第11章 对策论
微观经济学第11章博弈论1

4.3 博弈论的成长和发展
一、第一个研究高潮,本世纪40年代末和50年代初
1950年纳什提出“纳什均衡”(Nash equilibrium)概 念和证明纳什定理,发展非合作博弈的基础理论。 1950年Melvin Dresher和Merrill Flood在兰德公司(美国 空军)“囚徒的困境”(Prison’s dilemma)博弈实验, (Howard Raiffa)独立进行这个博弈实验; 1952-1953年期间(L. S. Shapley)和(D. B. Gillies)提 出“核”(Core)作为合作博弈的一般解概念 Shapley提出了合作博弈的“Shapley值”(Shapley value)概念等。 奥曼(R. J. Aumann)“40年代末50年代初是博弈论历 史上令人振奋的时期,原理已经破茧而出,正在试飞 它们的双翅,活跃着一批巨人。”
1
运输路线得益矩阵
单人博弈实质 个体最优化问题
-7000
-10000 -16000
运输路线扩展形
-10000
二、两人博弈
两人博弈即有两个博弈方的博弈 两人博弈最常见,研究最多,是最基本和有用 的博弈类型 囚徒困境、猜硬币、齐威王田忌赛马等都是两 人博弈 两人博弈有多种可能性,博弈方的利益方向可 能一致,也可以不一致
政府组织协调的 必要性和重要性
寡头1:低价(70) 寡头2:低价(70)
2.2 赌胜博弈
赌博、竞技等构成的博弈问题,在经济中 也有许多应用,赌胜博弈也是一类重要的 博弈问题,对经济竞争和合作也有很大启 示 赌胜博弈的特点是一方得等于另一方失, 不可能双赢,属于“零和博弈”
管理运筹学课件第13章-对策论

• 对策论基本概念 • 矩阵对策 • 连续对策 • 合作对策 • 非合作对策 • 对策论在实际问题中应用
01
对策论基本概念
对策论定义与特点
定义
对策论,又称博弈论,是研究决策过 程中理性决策者之间冲突与合作的数 学理论。
特点
对策论注重分析决策者之间的相互作 用和影响,以及决策结果的均衡性和 稳定性。
供应链管理
在供应链管理中,对策论可用于 协调供应商、制造商、销售商之 间的利益关系,优化供应链整体 效益。
金融市场投资决策
对策论可用于分析金融市场中的 投资决策问题,如股票交易、期 货交易等,帮助投资者制定最优 的投资策略。
军事领域应用案例
作战计划制定
01
对策论可用于分析敌我双方的作战能力和策略选择,帮助军事
指挥官制定最优的作战计划。
武器系统研发
02
在武器系统研发中,对策论可用于分析不同武器系统的性能优
劣和作战效能,为武器系统研发提供决策支持。
军事演习评估
03
对策论可用于评估军事演习的效果和参演部队的作战能力,为
军事训练提供改进建议。
社会领域应用案例
社会治安综合治理
对策论可用于分析社会治安问题中的各方利益关系和行为选择,提 出综合治理的策略和措施。
微分对策的求解方法
包括最大值原理、动态规划等方法。
连续对策求解方法
01
02
03
迭代法
通过不断迭代更新参与者 的策略,直到达到某个均 衡条件为止。
数值解法
利用数值计算的方法求解 连续对策的均衡解,如有 限差分法、有限元法等。
解析法
在某些特殊情况下,可以 通过解析的方法求解连续 对策的均衡解,如线性二 次型微分对策等。
对策论专题知识讲座

在甲方旳赢得矩阵中: A=[aij]m×n
i 行代表甲方策略 i=1, 2, …, m;j 列代表乙方策略 j=1, 2, …, n;aij 代表甲方取策略 i,乙方取策略 j,这一局势下 甲方旳益损值。此时乙方旳益损值为 -aij(零和性质)。
在考虑各方采用旳策略时,必须注意一种前提,就是 双方都是理智旳,即双方都是从各自可能出现旳最不利旳 情形选择一种最为有利旳情况作为决策旳根据。
10.4 矩阵对策旳矩阵降维
优超原则:
假设矩阵对策 G ={ S1, S2, A } 甲方赢得矩阵 A=[aij]mn 若存在两行(列),s 行(列)旳各元素均优于 t 行(列)旳元 素,即
asjatj j=1,2 … n ( ais ait i=1,2 … m )
称甲方策略s优超于t ( s优超于t)。
成立时,双方才有最优纯策略,并把(1,2)称为对策G在纯 策略下旳解,又称(1,2)为对策G旳鞍点。把其值V称之为对
策G={S1,S2,A}旳值。
10.3 矩阵对策旳混合策略
设矩阵对策 G = { S1, S2, A }。当
max i
min j
aij
min j
max i
aij
时,不存在最优纯策略。
人对策一样也是对策方在乎识到其他对策方旳存在,意识到其他 对策方对自己决策旳反应和反作用存在旳情况下谋求本身最大利 益旳决策活动。因而,它们旳基本性质和特征与两人对策是相同 旳,我们经常能够用研究两人对策一样旳思绪和措施来研究它们, 或将两人对策旳结论推广到多人对策。
但多人对策中出现了更多旳追求各自利益旳独立决策者,策 略旳相互依存关系也就更为复杂,对任一对策方旳决策引起旳反 应也就要比两人对策复杂得多。
应用经济学硕士研究生培养方案

应用经济学硕士研究生培养方案(学科代码:0202)一、培养目标本学科致力于培养具有严谨求实的学术作风,德、智、体全面发展,具有坚定正确的政治方向,具有扎实的经济学理论基础、合理的知识结构和宽广的知识面,具有独立从事经济研究的能力,能胜任经济类课程的教学,能胜任实际经济工作。
较为熟练地掌握一门外语并能阅读本学科的外文资料;毕业后可承担本学科的教学、科研工作和中高层次的经济管理工作;具有健康的心理和体魄。
二、学科专业1、区域经济学2、数量经济学3、财政学(含税收学)4、产业经济学5、统计学三、学习年限及应修学分全日制硕士研究生的学习年限一般为3年。
在完成培养要求的前提下,对少数学业优秀、科研成果突出的硕士生,可申请提前毕业,提前期一般不超过1年。
如确需延长学习年限的,延长期一般不超过1年。
至少须修满35学分,其中,课程学习32学分,实践环节3学分。
四、课程设置及考核方式(具体见课程设置与教学计划表)实践环节由科研实践和教学实践组成,科研实践必须参加校内外相关学科学术会议1次,撰写心得体会一份(计1学分);选听学科前沿系列讲座1次,至少6学时;撰写相关文献综述一份(计1学分)。
教学实践必须听课30学时,讲课30学时,提交教学大纲一份(计1学分)。
科研实践和教学实践均由导师负责考核。
五、培养方式研究生由导师及导师小组全面负责培养,以导师指导和本学科教师集体培养相结合为原则,建立和完善有利于学术群体作用的培养机制。
课程学习和研究并重;专业课的学习采取系统讲授、重点辅导、讨论讲座以及任课教师制定参考文献、书目,学习阅读后写综述和评论等多种形式。
加强研究生的自学能力、表达能力、写作能力、实际工作能力等的训练和培养。
六、学位(毕业)论文研究生在修完全部学位课程和修满所要求的总学分后,要在导师的指导下,进行学位(毕业)论文的研撰,由硕士研究生独立完成,论文写作时间不少于一年。
论文选题必须经过充分调查研究,查阅相关的文献,了解国内外本领域的研究历史和现状,选择本学科内有重要学术价值和实用价值、研究基础较为薄弱的问题,或能为解决当前、当地经济和社会发展的热点、难点问题以及为政府决策提供借鉴的问题作为论文选题;研究生确定了论文选题后,在论文写作之前,必须撰写开题报告,开题报告应包括论文选题的理由或意义、国内外有关该论题研究的现状及趋势、本人的详细研究计划、写作提纲、主要参考文献等内容。
《犯罪学》教学大纲(1)

天津广播电视大学开放教育法学专业《犯罪学》课程教学大纲第一部分大纲说明一、教学目的与要求通过犯罪学的学习,可以使学员掌握中国犯罪演变的历史,掌握我国各时期犯罪态势的变化和新型犯罪的发展变化,并且剖析其产生原因和治理对策,然后诉诸刑事政策与立法的修订。
尤其是在我国,治理犯罪的途径与手段,也决不仅止于刑罚,而是延伸到德法兼治的所有领域;可以说,整个社会都是运用犯罪学研究成果的舞台,对社会治安实行富于中国特色的综合治理也正基于此。
二、课内学时分配犯罪学课程3学分。
一个学期的课程。
课内学时54学时。
第二部分教学资源的配置和使用一、主要的教学资源(一)文字教材文字主教材为《犯罪学》,刘文成主编,群众出版社出版,它是教学与考试的主要依据。
同时还配置文字辅助教材。
(二)录音录象教材为适应远程开放教育的要求,满足自学需要,天津电大制作了《犯罪学》网络课程。
二、教学环节(一)自学自学是重要的学习方式,依据教学大纲的要求,保证足够的时间在听课基础上,全面系统认真阅读教材和指定参考书。
(二)面授辅导面授辅导是教学的重要方式,辅导教师要全面系统掌握教学大纲和教科书,通过讲解、辅导、答疑、组织讨论等方式帮助学生深入理解教材内容。
辅导课学习,以不少于课程内容时数的三分之一为宜。
(三)考试要求考核学生全面系统掌握教材内容的基础上,着重掌握重点、难点及运用所学基础理论分析我国各时期犯罪态势的变化和新型犯罪的发展变化,并且剖析其产生原因和治理对策,然后诉诸刑事政策与立法的修订。
题量适当并且难易搭配。
按照不同层次大致可分为:有一定难度的试题占总数的25%,中等难度的试题占总数的50%,比较容易的试题占总数的25%。
考试题型。
在一份试卷中,包括客观性试题,如填空、单项选择、多项选择;主观性试题,如名词解释、简答题、论述题,共六种题型。
根据本课程的特点,试题应引导学生掌握课程的基本内容,并重视提高理解与运用能力。
试题兼顾各种犯罪类型;兼顾主观性试题和客观性试题。
高级运筹学(博弈论书稿)-周晶

第章博弈论(对策论)第一节引言1.1博弈行为和博弈论在日常生活中,经常会看到一些相互之间具有斗争或竞争性质的行为。
譬如,两个人下棋,任何一个人在走某一步之前,都需要考虑对方是怎么走的,以及对方在他走了一步之后会怎么走,以至无穷。
高手与俗手的区别往往就在于高手能够考虑10步甚至20步以后的变化,最终的输赢不仅取决于你的决策,而且取决于你对手的决策,这就是博弈。
博弈与决策的根本区别在于是否考虑对方的行为,具有竞争或对抗性质的行为称为博弈行为。
在这类行为中,参加斗争或竞争的各方各自具有不同的目标和利益。
为了达到各自的目标和利益,各方必须考虑对手的各种可能的行动方案,并力图选取对自己最有利或最合理的方案。
比如战争活动中的双方,都力图选取对自己最有利的策略,千方百计去战胜对方;还比如在政治方面,国际间的谈判、各种政治力量间的较量、各国际集团之间的角逐等都无一不具有对抗性质;在经济活动中,各国之间、各公司企业之间的经济谈判,企业之间为争夺市场而进行的竞争等,举不胜举。
博弈论(game theory),就是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的理论与方法,即研究博弈行为中竞争各方是否存在着最合理行动方案,以及如何找到最合理行动方案的数学理论和方法。
也就是说,当一个主体,好比说一个人或一个企业的选择受到其他人、其他企业选择的影响,而且反过来影响到其他人、其他企业选择时的决策问题和均衡问题。
博弈论应是一种分析问题的方法,它被设计用来帮助我们理解所观察到的决策主体相互作用时的现象,其应用范围涉及经济学、政治学、犯罪学、军事、外交、国际关系、公共选择等各个领域。
博弈论思想的主要特征是各参与人所实施的行为方案(策略)相互依存,各方在冲突或合作后所实现的损益得失结果不仅取决于自己所采取的行为方案,同时也依赖于其他参与方所实施的行为方案,是各参与方行为方案组合的函数。
所以,博弈论在我国也被称为“对策论”。
第十一章博弈模型

• 用u1(a1,a2)表示对盟军产生的结果,即净胜场次, 称为盟军的效用函数.
盟军 德军 强化缺口 原地待命
向西进攻 盟军胜1场 盟军胜2场
向东撤退 无战斗 无战斗
1 0 M {mij}32 2 0
支付矩阵 2 1
东进 盟军败2场 盟军胜1场 (Payoff Matrix)
完全竞争: 零和博弈 (常数和博弈) u2(a1,a2)对应 –M
习题
• P411 ex1,ex3
11.5 效益的合理分配(合作对策)
例 甲乙丙三人合作经商,若甲乙合作获利7元, 甲丙合作获利5元,乙丙合作获利4元, 三人合作获利11元. 又知每人单干获利1元. 问三人合作时如何分配获利?
记甲乙丙三人分配为
x (x ,x ,x ) 123
x1 x2 x3 11
解不唯一
x1 x2 7 x1 x3 5
(5,3,3) (4,4,3)
x2 x3 4
(5,4,2)
x1, x2 , x3 1
……
怎样分配 更合理?
(1) Shapley合作对策
集合I {1,2, , n} 子集s I,实函数v(s)满足
v( ) 0 v(s1 s2 ) v(s1 ) v(s2 ), s1 s2
sSi (n s )!( s 1)!
1
w( s )
n!
nC|s|1
n1
s~子集 s中的元素数目, Si ~包含i的所有子集
[v(s) v(s \ i)] ~ i 对合作s 的“贡献” (i s)
w( s ) ~由s决定的“贡献”的权重
权重构成:|s|可能取值1~n, 先按此n等分;|s|=k的含有i的子
集个数有
C k 1 n 1
2019年中国科学技术大学863 管理科学综合(管理学、统计学与运筹学)考研初试大纲
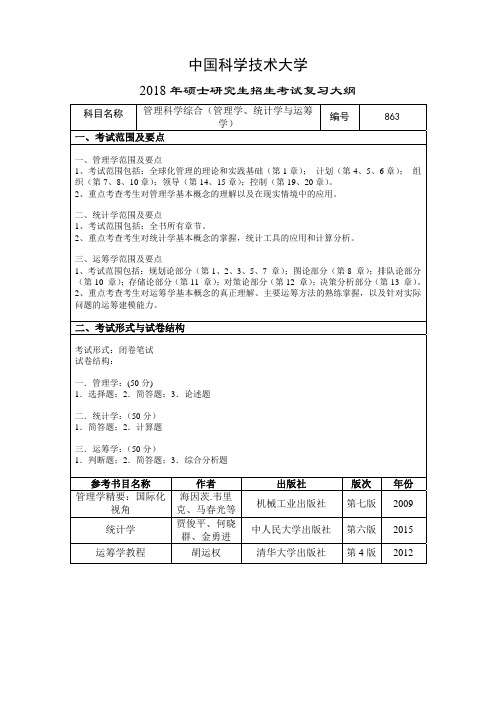
中国科学技术大学
2018年硕士研究生招生考试复习大纲
科目名称 管理科学综合(管理学、统计学与运筹
学)
编号 863 一、考试范围及要点
一、管理学范围及要点
1、考试范围包括:全球化管理的理论和实践基础(第1章);计划(第4、5、6章);组织(第7、8、10章);领导(第14、15章);控制(第19、20章)。
2、重点考查考生对管理学基本概念的理解以及在现实情境中的应用。
二、统计学范围及要点
1、考试范围包括:全书所有章节。
2、重点考查考生对统计学基本概念的掌握,统计工具的应用和计算分析。
三、运筹学范围及要点
1、考试范围包括:规划论部分(第1、
2、
3、5、7 章);图论部分(第8 章);排队论部分(第10 章);存储论部分(第11 章);对策论部分(第12 章);决策分析部分(第13 章)。
2、重点考查考生对运筹学基本概念的真正理解、主要运筹方法的熟练掌握,以及针对实际问题的运筹建模能力。
二、考试形式与试卷结构
考试形式:闭卷笔试
试卷结构:
一.管理学:(50分)
1.选择题;2.简答题;3.论述题
二.统计学:(50分)
1.简答题;2.计算题
三.运筹学:(50分)
1.判断题;2.简答题;3.综合分析题
参考书目名称作者出版社版次年份
管理学精要:国际化
视角
海因茨.韦里
克、马春光等
机械工业出版社第七版2009
统计学贾俊平、何晓
群、金勇进
中人民大学出版社第六版2015
运筹学教程胡运权清华大学出版社第4版2012。
Python最优化算法实战学习笔记

Python最优化算法实战第一章最优化算法概述1.1最优化算法简介最优化算法,即最优计算方法,也是运筹学。
涵盖线性规划、非线性规划、整数规划、组合规划、图论、网络流、决策分析、排队论、可靠性数学理论、仓储库存论、物流论、博弈论、搜索论和模拟等分支。
当前最优化算法的应用领域如下。
(1)市场销售:多应用在广告预算和媒体的选择、竞争性定价、新产品开发、销售计划的编制等方面。
如美国杜邦公司在20世纪50年代起就非常重视对广告、产品定价和新产品引入的算法研究。
(2)生产计划:从总体确定生产、储存和劳动力的配合等计划以适应变动的需求计划,主要采用线性规划和仿真方法等。
此外,还可用于日程表的编排,以及合理下料、配料、物料管理等方面。
(3)库存管理:存货模型将库存理论与物料管理信息系统相结合,主要应用于多种物料库存量的管理,确定某些设备的能力或容量,如工厂库存量、仓库容量,新增发电装机容量、计算机的主存储器容量、合理的水库容量等。
(4)运输问题:涉及空运、水运、陆路运输,以及铁路运输、管道运输和厂内运输等,包括班次调度计划及人员服务时间安排等问题。
(5)财政和会计:涉及预算、贷款、成本分析、定价、投资、证券管理、现金管理等,采用的方法包括统计分析、数学规划、决策分析,以及盈亏点分析和价值分析等。
(6)人事管理:主要涉及以下6个方面。
①人员的获得和需求估计。
②人才的开发,即进行教育和培训。
③人员的分配,主要是各种指派问题。
④各类人员的合理利用问题。
⑤人才的评价,主要是测定个人对组织及社会的贡献。
⑥人员的薪资和津贴的确定。
(7)设备维修、更新可靠度及项目选择和评价:如电力系统的可靠度分析、核能电厂的可靠度B风险评估等。
(8)工程的最佳化设计:在土木,水利、信息电子、电机、光学、机械、环境和化工等领域皆有作业研究的应用。
(9)计算机信息系统:可将作业研究的最优化算法应用于计算机的主存储器配置,如等候理论在不同排队规则下对磁盘、磁鼓和光盘工作性能的影响。
(NEW)运筹学教材编写组《运筹学》(第4版)笔记和课后习题(含考研真题)详解

线性规划问题的共同特征:
(1)每一个问题都用一组决策变量
表示某一方案,这组
决策变量的某一确定值就代表一个具体方案。一般这些变量的取值是非
负且连续的。
(2)存在有关的数据,如资源拥有量、消耗资源定额、创造新价值 量等,同决策变量构成互不矛盾的约束条件,这些约束条件可以用一组 线性等式或线性不等式来表示。
1.2 课后习题详解
本章无课后习题。
1.3 考研真题详解
本章只是对本课程的一个简单介绍,不是考试重点,所以基本上没 有学校的考研试题涉及到本章内容,因此,读者可以简单了解,不必作 为复习重点,本部分也就没有可选用的考研真题。Leabharlann 第2章 线性规划与目标规划
2.1 复习笔记
1.线性规划模型的概念及其一般形式
目 录
第1章 运筹学概论 1.1 复习笔记 1.2 课后习题详解 1.3 考研真题详解
第2章 线性规划与目标规划 2.1 复习笔记 2.2 课后习题详解 2.3 考研真题详解
第3章 对偶理论与灵敏度分析 3.1 复习笔记 3.2 课后习题详解 3.3 考研真题详解
第4章 运输问题 4.1 复习笔记 4.2 课后习题详解
2.线性规划问题的标准型及标准化 (1)线性规划的标准型
或
(2-4) (2-5) 线性规划的标准型要求:目标函数是Max型;约束条件是等式约 束;决策变量非负。 (2)线性规划的标准化方法
① 若要求目标函数实现最小化,即
,则只需将目标函数最
小化变换为求目标函数最大化,即令 ,于是得到
第13章 排队论
13.1 复习笔记 13.2 课后习题详解 13.3 考研真题详解 第14章 存储论 14.1 复习笔记 14.2 课后习题详解 14.3 考研真题详解 第15章 对策论基础 15.1 复习笔记 15.2 课后习题详解 15.3 考研真题详解 第16章 单目标决策 16.1 复习笔记 16.2 课后习题详解 16.3 考研真题详解 第17章 多目标决策 17.1 复习笔记
博弈论全套课件

三. 经典的博弈模型
1、“囚徒的困境”
关于博弈论,流传最广的是一个叫做“囚 徒 困 境 ” 的 故 事 。 这 个 博 弈 是 1950 年 图 克 (Tucker)提出的,这个博弈模型提出后曾引 发了大量的相关研究,也有许多关于“囚徒困 境”的版本。“囚徒困境”对博弈论的发展起 到了巨大的推动作用。可以说凡是讲博弈论, 都会说到这个经典的博弈模型。
在过去二三十年中,博弈论已成为社会科 学研究的一个重要方法。有人说,如果未来社 会科学还有纯理论的话,那就是博弈论。无论 是合作博弈还是非合作博弈都给我们提供了一 种系统的分析方法,使人们在其命运取决于他 人的行为时制定出相应的战略。特别是当许多 相互依赖的因素共存,没有任何决策能独立于 其它许多决策之外时,博弈论更是价值巨大。
最近十几年来,博弈论在经济学尤其是微 观经济学中得到了广泛的运用, 博弈论在许多 方面改写了微观经济学的基础,经济学家们已经 把研究策略相互作用的博弈论当作最合适的分 析工具来分析各类经济问题,诸如公共经济、 国际贸易、自然资源、企业管理等。在现代经 济学里,博弈论已经成为十分标准的分析工具。 除经济学以外, 博弈论目前在生物学、管理学 、国际关系、计算机科学、政治学、军事战略 和其他很多学科都有广泛的应用。现在已经有 愈来愈多的人开始关注、了解并学习博弈理论 。
博弈论(Game Theory)是一种关于游戏的 理论, 又叫做对策论, 是一门以数学为基础的、 研究对抗冲突中最优解问题的学科。事实上, 博弈论也正是衍生于古老的游戏,如象棋、围 棋、扑克等。
博弈论作为一门学科,是在20世纪50~60 年代发展起来的,当非零和博弈理论、特别是 不完全信息博弈理论获得充分发展时,才成为 现实。到20世纪70年代,博弈论正式成为主流 经济学研究的主要方法之一。1994年诺贝尔经 济学奖同时授予了纳什、泽尔腾、海萨尼三位 博弈论专家。2005年诺贝尔经济学奖又授予了 美国经济学家托马斯.谢林(Thomas Schelling)和以色列经济学家罗伯特.奥曼 (Robert Aumann),以表彰他们在合作博弈 方面的巨大贡献。
第10章对策论

i
( j = 1, 2," , m )
然后再找出各最大值中的最小值(最优支付)
min(max α ij ) = min α i* j = V2
j i j
这里 V2 = 2 我们把甲的最优赢得和乙的最优支付的这个公共值,称为矩阵对策的值,记作 VG , 即:
VG = max(min α ij ) = min(max α ij )
10.2 矩阵对策
矩阵对策就是有限零和二人对策,指的是参加对策的局中人只有两方(或二人) , 每一方局中人的可供选择策略数是有限多个,而且每一局对策结束时,一方的收入(或 赢得)等于另一方的支出(或称输出) ,换句话说,二方得失之和总是等于零。这类对 策比较简单,理论上也比较成熟,在实践中应用的也极为广泛。由于矩阵对策的理论奠 定了研究“对策现象”的基本思路,所以它是对策论中必须掌握的内容。 10.2.1 矩阵对策的数学模型 对于矩阵对策,我们用甲、乙表示两个局中人,假设甲有 m 个策略(又称纯策略) , 分别以 α1 , α 2 ," , α m 表示,乙有 n 个策略,分别以 β1 , β 2 ," , β n 表示。根据对策规定,若 (a , β ) 甲选用第 i 个策略,乙选用第 j 个策略,则称 i j 为一个纯局势,那么,甲的赢得可 以用 α ij 表示(若 α ij 是负数时,表示甲是支出而不是收入)。于是,甲的支付可以列成表
min α ij = α ij*
j
( i = 1, 2," , m )
然后在这些最小值中找到最大值(最优赢得) , 即:
max(min α ij ) = max α ij* = V1
i j i
在本对策 G 中, V1 = 2 局中人乙则和甲相反, 他的原则首先是在各纯策略 (列) 中找出最大值 (可靠支付) :
博弈论基础

博弈论博弈论(Game Theory),亦名“对策论”、“赛局理论”,属应用数学的一个分支,博弈论已经成为经济学的标准分析工具之一。
目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。
博弈论主要研究公式化了的激励结构间的相互作用。
是研究具有斗争或竞争性质现象的数学理论和方法。
也是运筹学的一个重要学科。
博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
生物学家使用博弈理论来理解和预测进化论的某些结果。
参见:行为生态学(behavioral ecology)。
约翰·冯·诺依曼博弈论是二人在平等的对局中各自利用对方的策略变换自己的对抗策略,达到取胜的目的。
博弈论思想古已有之,中国古代的《孙子兵法》就不仅是一部军事著作,而且算是最早的一部博弈论著作。
博弈论最初主要研究象棋、桥牌、赌博中的胜负问题,人们对博弈局势的把握只停留在经验上,没有向理论化发展。
博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
近代对于博弈论的研究,开始于策墨洛(Zermelo),波雷尔(Borel)及冯·诺伊曼(von Neumann)。
1928年,冯·诺依曼证明了博弈论的基本原理,从而宣告了博弈论的正式诞生。
1944年,冯·诺依曼和摩根斯坦共著的划时代巨著《博弈论与经济行为》将二人博弈推广到n人博弈结构并将博弈论系统的应用于经济领域,从而奠定了这一学科的基础和理论体系。
1950~1951年,约翰·福布斯·纳什(John Forbes Nash Jr)利用不动点定理证明了均衡点的存在,为博弈论的一般化奠定了坚实的策墨洛(Zermelo)基础。
纳什的开创性论文《n人博弈的均衡点》(1950),《非合作博弈》(1951)等等,给出了纳什均衡的概念和均衡存在定理。
此外,塞尔顿、哈桑尼的研究也对博弈论发展起到推动作用。
运筹学教程

1、填空题(6分,每空1分) 2、选择题(20分,每题2分) 3、名词解释(18分,每题6分) 4、简答题(36分,每题12分) 5、论述题(20分)
绪论
一、运筹学释义与发展简史
二、运筹学的基本信念 三、 运筹学主要分支简介 四、 运筹学解决问题的方法步骤 五、进度安排与学习建议
他估计到齐王由于上一次的大获全胜,这一次是不 会轻易更改这种对策的。
这使得孙膑在对局前便把握了主动权,有的放矢地 制定了“退一步,进两步”的策略。
孙膑决定用自己的下等马和国王的上等马比赛,而 用自己的上等马和国王的中等马比赛,中等马和国 王的下等马比赛。
比赛开始,第一场国王的马以极大的优势取得了胜 利,但在二、三场中田忌的马都取得了胜利。这次 国王不但没赢,反而输了一千金。
这类问题的解决方法是:先根据问题要达到的目标选 取适当的变量,问题的目标通过用变量的函数形式表示(称 为目标函数),对问题的限制条件用有关变量的等式或不等 式表达(称为约束条件)。当变量连续取值,且目标函数和 约束条件均为线性时,称这类模型为线性规划的模型 。
例 求解线性规划问题
max z 2x1 3x2 ,
定每方出上马、中马、下马各一匹各赛一局,每 局赌注是黄金一千两。 由于田忌的马比齐王同等级的马都要略逊一筹, 而在头一轮的比赛中,双方都是用同等级的马进 行对抗,所以齐王很快赢了全部三场,得到了三 千两黄金。
田忌的军师孙膑得知后,便 替田忌出了一个主意: 用自己的下等马和国王的上等马比赛,而用自己 的上等马和国王的中等马比赛,中等马和国王的 下等马比赛。
比赛开始,第一场国王的马以极 大的优势取得了 胜利。国王没有料到田忌的马竟然如此不堪一击, 为此俯仰大笑,得意不已。但美景不长,在二、 三场中田忌的马都取得了胜利。这一轮国王不但 没 赢,反而输了一千金。
运筹学(绪论)

五、运筹学在经济管理中应用的主要课题
• 6、人事管理:对人员的需求和使用的预测、 确定人员编制、人力资源开发、人员的合 理利用、人才评价体系、工资标准等。 • 7、设备维修与更新 • 8、可靠性分析 • 9、质量控制 • 10、项目选择、评估 • 11、城市公用事业和服务 • 12、工程优化设计与管理等
page27
四、运筹学在管理科学中的地位
• 管理科学的学科构架 • 2、技术方法部分: 决策方法、决策支持系统、计划与规划 技术、库存控制、技术经济、预测技术、 管理信息系统、管理系统工程、目标管 理、质量管理与保证、管理数学方法、 项目评估和可行性研究、价值工程、预 算与成本控制、时间-动作研究等。
page13
一、运筹学的发展及展望
• 2、运筹学的展望 • 1)运筹学发展过程中面临的一些问题: 抽象化风气日盛、大范围问题、高维问 题、体系厐杂等。 • 2)运筹学发展展望 • 运筹学应该在三个方面都应有所发展: 运筹学的学科体系、运筹学的应用及运 筹学的数学理论。
page14
二、运筹学的学科体系
page17
三、运筹学的定义与研究特点
• • 运筹学(Operational Research) 直译为 “运作研究”
运筹学是运用科学的方法(如分析、 试验、量化等)来决定如何最佳地运营和 设计各种系统的一门学科。运筹学对经济 管理系统中的人力、物力、财力等资源进 行统筹安排,为决策者提供有依据的最优 方案,以实现最有效的管理。 • 运筹学有广泛应用
page4
德州学院数学科学学院运筹学教案
情况介绍
• • 本课程设置的有关问题 教学要求
page5
目 录
第一章:绪论 第二章:线性规划 第三章:整数线性规划
第十章---博弈论初步精选全文完整版

甲 (式乙)
p.61
p.42
A B
混合策略组合及其支付也就有无限多的可能。
q.31 C 4,6 7,3
乙
.q72 D 9,1 2,8 9
不存在纯策略均衡时的混合策略均衡3
• 条件混合策略:参与人在假定其他参与人按某一概率选择某一策略
的条件下设计的对自己而言具有相对优势的(即期望支付最大的)混合 策略,称为“条件混合策略”。
• 对乙而言,如果假定甲合作,那么乙合作的支付为6,比不合作的支付 多1,因此合作是甲合作条件下乙的条件策略;假定甲不合作,那么乙的 条件策略是也不合作,乙若合作支付只有1,不合作则可得到3。
• 条件策略组合:参与人以其他参与人选择某一策略为条件的条件策略与
作为它的条件的对方策略之间的组合,称为“条件优势策略组合”或
• 假q2=定1-(q1p代1,入p甲2)与、乙(各q自1,的q2期)望的支取付值表从达0到式1有无,限经多整可理能可,得把:p2=1-p1和 E甲= p1(7-10q1)+5q1+2(式1); E乙= 5q1(2p1-1)-7p1+8(式2)
• 每个参与人需要确定,在另一参与人为其混合策略选择某个概率值时, 己方混合策略的概率向量应怎样取值,才能使自己的期望支付最大。
e点的坐标是p1=0.5,q1=0.7,则纳什均衡 时p2=0.5,q2=0.3 。
q1 1
本题中混合策略的纳什均衡还可表示为:
((p1 , p2),(q1 ,q2) )= ((0.5 , 0.5),(0.7 , 0.3) )。 0.7 本题中,只有唯一的这个纳什均衡点。
1
q1<0.7
p1= [0,1] q1 = 0.7
运筹学教材习题答案详解

显然用料最少的方案最优。
1.4A、B两种产品,都需要经过前后两道工序加工,每一个单位产品A需要前道工序1小时和后道工序2小时,每一个单位产品B需要前道工序2小时和后道工序3小时.可供利用的前道工序有11小时,后道工序有17小时.
3
B1:2.0
3
需要量(套)
200
150
问怎样下料使得(1)用料最少;(2)余料最少.
【解】第一步:求下料方案,见下表。
方案
一
二
三
四
五
六
七
八
九
十
十一
十二
十三
十四
需要量
B1:2.7m
2
1
1
1
0
0
0
0
0
0
0
0
0
0
300
B2:2m
0
1
0
0
3
2
2
1
1
1
0
0
0
0
450
A1:1.7m
0
0
1
0
0
1
0
2
1
0
3
2
1
0
《运筹学》
第1章线性规划
第2章线性规划的对偶理论
第3章整数规划
第4章目标规划
第5章运输与指派问题
第6章网络模型
第7章网络计划
第8章动态规划
第9章排队论
第10章存储论
第11章决策论
第12章对策论
习题一
1.1讨论下列问题:
进化稳定对策

第3章进化稳定对策张大勇最优化理论(optimization theory)和对策论(game theory,又称博弈论)是进化生物学中两个最常用的、非常相近的研究途径。
它们之间的主要区别体现在适用范围上:优化理论适用的情形是当一个个体的最优行为不依赖于其它个体的行为时,而对策论则适用于一个个体的最优行为依赖于其它个体如何行动的情形。
最优化理论的基本出发点是,自然选择总是倾向于使生物最有效地传递它们的基因,因而也将是最有效地从事各种活动,包括使它们在时间和能量分配方面达到最优状态。
第2章我们讨论生活史性状问题时采用的都是优化理论。
但是,最优化理论也遇到了一定困难,即在许多情况下普遍意义上的最佳策略往往并不存在。
一个个体采取某一对策是好还是坏不仅取决于这个对策本身,而且往往还取决于种群内其它个体所采取的对策是什么。
例如,一个雄性粪蝇在寻觅雌蝇时的最优占位往往取决于其它雄蝇停落在什么位置;在争夺配偶的战斗中,一个雄性动物的最佳对策经常取决于他的对手如何行动,有时退让是有利的,有时激烈争斗是更适合的。
在这些例子中,不存在一个任何情形下都一律适用的最佳对策。
这时我们观察到的自然界生物它们应该采取何种对策呢?为解决这一难题,Maynard Smith(1982;Maynard Smith & Price 1973)创造性地提出了一个全新概念––进化稳定对策,或称ESS(为英文全称evolutionarily stable strategy的简写)。
当种群内所有个体都采取了某个对策后,其它对策者都不能侵入该种群,那么这个对策就是进化上稳定的。
这个概念不强调绝对意义上的优化,而是从相对意义上寻求所谓的最佳:当种群完全是由ESS对策者组成的时候,ESS对策者的适合度将大于所有突变对策者的适合度。
因而,ESS 是一个弱化了的最优化概念(Ehrlich & Roughgarden 1987)。
本章的目的就是向读者介绍对策论在进化生物学中的应用,以及它的核心概念—进化稳定对策(关于ESS的综述包括有Maynard Smith 1982; Parker 1984; Hines 1987)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个自然的想法:对甲(乙)给出一个选取不同策略的概率分
布,以使甲(乙)在各种情况下的平均赢得(损失)最多(最 少)-----即混合策略。
求解混合策略的问题有图解法、迭代法、线性方程法和线性规
划法等,我们这里只介绍线性规划法,其他方法略。
例:设甲使用策略1的概率为x1′,使用策略2的概率为x2′ , 并设在最坏的情况下,甲赢得的平均值为V(未知)。
或将两人对策的结论推广到多人对策。
但多人对策中出现了更多的追求各自利益的独立决策者,策 略的相互依存关系也就更为复杂,对任一对策方的决策引起的反 应也就要比两人对策复杂得多。 与两人对策有本质区别的特点,即可能存在“破坏者”:其 策略选择对自身的得益没有任何影响,但却会影响其它对策方的 得益,有时这种影响甚至有决定性的作用。
6 0 3 得到 被第1行所优超
7 3
A3=
9
被第1列所优超
4 6 5.5
7 3
最终得到 A4= 4 6
对A4计算,用线性规划方法得到: (注意:余下的策略为3,4,1,2) 甲: X* = (0,0,1/15,2/15,0)T V=5 X*’= (0,0,1/3 ,2/3 ,0)T 乙: Y* = (1/10,1/10,0,0,0)T V=5 Y*’= (1/2 ,1/2 ,0,0,0)T 。
8y1+6y21 y1, y20
y1= 1/14
y2= 1/14 1/V= y1+y2=1/7 所以,V=7
返回原问题:
y1’= y1V = 1/2 y2’= y2V = 1/2
于是乙的最优混合策略为:
以 1/2 的概率选1;以 1/2 的概率选2 ,最优值 V=7。 当赢得矩阵中有非正元素时,V0 的条件不一定成立,可 以作下列变换: 选一正数 k,令矩阵中每一元素加上 k 得到 新的正矩阵A’,其对应的矩阵对策 G’= { S1, S2, A’} 与 G ={ S1, S2, A } 解相同,但VG = VG’ – k。
注:
– 利用优超原则化简赢得矩阵时,有可能将原对策问题 的解也划去一些(多解情况);
– 线性规划求解时有可能是多解问题。
10.3 矩阵对策的混合策略
设矩阵对策 G = { S1, S2, A }。当
max min aij min max aij
i j j i
时,不存在最优纯策略。
例:设一个赢得矩阵如下: min 5 9 5 A= 8 6 6 max 8 9 min 8
j
max 6
i
策略2
策略1
当甲取策略2 ,乙取策略1时,甲实际赢得8比预期的多2,
同样可求乙的最优混合策略:
设乙使用策略1的概率为 y1′ y1′+y2′=1 设乙使用策略2的概率为 y2′ y1′, y2′0 设在最坏的情况下,甲赢得的平均值为V。这也是乙损失的 平均值,越小越好。
作变换: y1= y1’/V , y2= y2’/V
建立线性模型: max y1+y2
s.t. 5y1+9y21
在甲方的赢得矩阵中:
A=[aij]m×n i 行代表甲方策略 i=1, 2, …, m;j 列代表乙方策略 j=1, 2, …, n;aij 代表甲方取策略 i,乙方取策略 j,这一局势下 甲方的益损值。此时乙方的益损值为 -aij(零和性质)。 在考虑各方采用的策略时,必须注意一个前提,就是 双方都是理智的,即双方都是从各自可能出现的最不利的
第11章 对策论
11.1 对策论基本概念 11.2 矩阵对策的最优纯策略 11.3 矩阵对策的混合策略 11.4 矩阵对策的矩阵降维
10.1 对策论基本概念
对策模型的三个基本要素: 1.局中人:参与对抗的各方;
2.策略集:局中人选择对付其它局中人的行动方案称为策略;
某局中人的所有可能策略全体称为策略集;
1和2分别称为局中人甲队、乙队的最优策略。由于双方必
然选择这一种策略,所以,这种策略又称为最优纯策略。
这种最优纯策略只有当赢得矩阵A=(aij)中等式
max min aij min max aij
i j j i
成立时,双方才有最优纯策略,并把(1,2)称为对策G在纯 策略下的解,又称(1,2)为对策G的鞍点。把其值V称之为对 策G={S1,S2,A}的值。
情形选择一种最为有利的情况作为决策的依据。
“齐王赛马”是一个矩阵策略。
“齐王赛马”齐王在各局势中的益损值表(单位:千金)
其中:齐王的策略集: S1={ 1, 2, 3, 4, 5, 6 },
田忌的策略集:S2={ 1, 2, 3, 4, 5, 6 }。
下面矩阵称齐王的赢得矩阵: 3 1 A= 1 -1 1 1 1 3 -1 1 1 1 1 1 3 1 1 -1 1 1 1 3 -1 1 -1 1 1 1 3 1 1 -1 1 1 1 3
3.一局势对策的益损值:局中人各自使用一个对策就形成了一
个局势,一个局势决定了各局中人的对策结果(量化)称为 该局势对策的益损值。
分类
(1)根据局中人的个数,分为二人对策和多人对策; (2)根据各局中人的赢得函数的代数和是否为零,可分为零和 对策和非零和对策; (3)根据局中人是否合作,又可分为合作对策和非合作对策; (4)根据局中人的策略集的个数,又分为有限对策和无限对策 (或连续对策); (5)也可根据局中人掌握信息的情况可分为完全信息对策、非 完全信息对策 (6)决策的行动顺序可分为静态对策、动态对策 (7)根据对策模型的数字特征又分为矩阵对策、连续对策、微 分对策、阵地对策、凸对策、随机对策。
10.4 矩阵对策的矩阵降维
优超原则: 假设矩阵对策 G ={ S1, S2, A } 甲方赢得矩阵 A=[aij]mn 若存在两行(列),s 行(列)的各元素均优于 t 行(列)的元 素,即 asjatj j=1,2 … n ( ais ait i=1,2 … m ) 称甲方策略s优超于t ( s优超于t)。 优超原则:当局中人甲方的策略t被其它策略所优超时,可 在其赢得矩阵A中划去第t行(同理,当局中人乙方的策略t被其 它策略所优超时,可在矩阵A中划去第t列)。 如此得到阶数较小的赢得矩阵A’,其对应的矩阵对策 G’= { S1, S2, A’} 与 G = { S1, S2, A } 等价,即解相同。
四、非零和对策 零和对策:一方的收益必定是另一方的损失。这种对策的 特点是不管各对策方如何决策,最后各对策方得益之和总是为 零。虽不等于0,但总是等于一个非零常数,称之为“常和对 策”。可以将零和对策本身看作是常和对策的特例。 “零和对策”和“常和对策”之外的所有对策都可被称为 “非零和对策”。非零和对策即意味着在不同策略组合(结果) 下各对策方的得益之和一般是不相同的。如前述囚徒困境就是 典型的非零和对策。 非零和对策是最一般的对策类型,而常和对策和零和对策 都是它的特例。在非零和对策中,存在着总得益较大的策略组 合和总得益较小的策略组合之间的区别,这也就意味着在对策 方之间存在着互相配合,争取较大的总得益和个人得益的可能 性。
三、多人非合作对策 有三个或三个以上对策方参加的对策就是“多人对策”。多
人对策同样也是对策方在意识到其他对策方的存在,意识到其他
对策方对自己决策的反应和反作用存在的情况下寻求自身最大利
益的决策活动。因而,它们的基本性质和特征与两人对策是相似 的,我们常常可以用研究两人对策同样的思路和方法来研究它们,
例:甲乙乒乓球队进行团体对抗赛,每队由三名球员组
成,双方都可排成三种不同的阵容,每一种阵容可以看作
一种策略,双方各选一种策略参赛。比赛共赛三局,规定 每局胜者得1分,输者得-1分,可知三赛三胜得3分,三赛二 胜得1分,三赛一胜得-1分,三赛三负得-3分。甲队的策略 集为S1={1,2,3},乙队的策略集为S2={1,2,3}。 根据以往比赛的资料,有甲队的赢得矩阵为A,如下所示,
10.2 矩阵对策的最优纯策略
二人有限零和对策(又称矩阵对策):
局中人为2;每个局中人的策略集的策略数目都是有限的; 每一局势的对策均有确定的损益值,并且对同一局势的两个局 中人的益损值之和为零。 通常将矩阵对策记为: G = {S1, S2, A}
S1:甲的策略集;
S2:乙的策略集;
A:甲的赢得矩阵。
A 1 2 3
1
1 1 3
2
请问这次比赛各队采用哪种阵容上场最为稳妥?
矩阵A中每行的最小元素分别为1,-3,-1。
在这些最少赢得中最好的结果是1,故甲队会采取策略1,无 论对手采取何策略,甲队至少得1分。对于乙队,{1,2,3} 可能带来的最少赢得,即A中每列的最大元素,分别为3,1,3。 乙队会采取2策略,确保甲队不会超过1分。
建立线性模型: min x1+x2 s.t. 5x1+8x21 9x1+6x21 x1, x20 x1= 1/21 x2= 2/21 1/V= x1+x2=1/7
所以,V=7
返回原问题: x1’= x1V= 1/3 x2’= x2V= 2/3 于是甲的最优混合策略为: 以1/3的概率选1, 以2/3的概率选2,最优值V=7。
一、完全信息静态对策 该对策是指掌握了参与人的特征、战略空间、支付函数 等知识和信息并且参与人同时选择行动方案或虽非同时但后 行动者并不知道前行动者采取了什么行动方案。 纳什均衡是一个重要概念。在一个战略组合中,给定其 他参与者战略的情况下,任何参与者都不愿意脱离这个组合, 或者说打破这个僵局,这种均衡就称为纳什均衡。 二、完全信息动态对策 在完全信息静态对策中,假设各方都同时选择行动。现 在情况稍复杂一些。如果各方行动存在先后顺序,后行的一 方会参考先行者的策略而采取行动,而先行者也会知道后行 者会根据他的行动采取何种行动,因此先行者会考虑自己行 动会对后行者的影响后选择行动。这类问题称为完全信息动 态对策问题。
