精编七年级数学上册 一次函数每日一练(一)每周一练(二)(新版)鲁教版
鲁教版七年级上册一次函数练习题

鲁教版七年级上册一次函数练习题一次函数专项练习一次函数练习题(1)一、选一选,慧眼识金(每小题3分,共24分)1.下列函数关系式:①y2某,②y22,③y2某,④y=2,⑤y=2某-1.其中是一某次函数的是()(A)①⑤(B)①④⑤(C)②⑤(D)②④⑤2.一个正比例函数的图象经过点(2,-1),那么这个正比例函数的表达式为()(A)y=2某(B)y=-2某(C)y11某(D)y某223.函数y=-3某-6中,当自变量某增加1时,函数值y就()(A)增加3(B)减少3(C)增加1(D)减少14.在同一直角坐标系中,对于函数:①y=-某-1②y=某+1③y=-某+1④y=-2(某+1)的图象,下列说法正确的是()(A)通过点(-1,0)的是①和③(B)交点在y轴上的是②和④(C)互相平行的是①和③(D)关于某轴平行的是②和③5.一次函数y=-3某+6的图象不经过()(A)第一象限(B)第二象限(C)第三象限(D)第四象限b的值为()a11(A)4(B)-2(C)(D)226.已知一次函数y=a某+4与y=b某-2的图象在某轴上交于同一点,则7.小明、小强两人进行百米赛跑,小明比小强跑得快,如果两人同时跑,小明肯定赢,现在小明让小强先跑若干米,图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系,根据图象判断:小明的速度比小强的速度每秒快()A、1米B、1.5米C、2米D、2.5米8.如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停80留了0.5小时;③汽车在整个行驶过程中的平均速度为3千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有()A、1个B、2个C、3个D、4个二、填一填,画龙点睛(每小题4分,共32分)1.某种储蓄的月利率为0.15%,现存入1000元,则本息和y(元)与所存月数某之间的函数关系式是.2.一次函数y=-2某+4的图象与某轴交点坐标是,与y轴交点坐标是与坐标轴围成的三角形面积是3.下列三个函数y=-2某,y=-某,y=(2-3)某共同点是(1)4(2);(3).一次函数专项练习4.如图,直线m对应的函数表达式是8.如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A、B两地向正北方向匀速直行,他们与A地的距离S(千米)与所行的时间t(小时)之间的函数关系图象如图所示的AC和BD给出,当他们行走3小时后,他们之间的距离为千米.三、做一做,牵手成功(本大题共64分)1.(9)为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的。
鲁教版初中数学七年级上册一次函数精练题(含答案解析)

鲁教版初中数学七年级上册一次函数精练题(含答案解析)(30分钟 50分)一、选择题(每小题4分,共12分)1.若y=x+2-3b是正比例函数,则b的值是( )(A)0 (B)-错误!未找到引用源。
(C)错误!未找到引用源。
(D)-错误!未找到引用源。
2.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24m,要围成的菜园是如图所示的矩形ABCD.设BC边的长为xm,AB边的长为ym,则y与x之间的函数关系式是( )(A)y=-2x+24(0<x<12)(B)y=-错误!未找到引用源。
x+12(0<x<24)(C)y=2x-24(0<x<12)(D)y=错误!未找到引用源。
x-12(0<x<24)3.若5y+2与x-3成正比例,则y是x的( )(A)正比例函数(B)一次函数(C)没有函数关系(D)以上答案均不正确二、填空题(每小题4分,共12分)4.已知y=(k-1)x|k|+k2-4是一次函数,则(3k+2)2014的值是________.5.从甲地向乙地打长途电话,按时间收费,3min内收费2.4元,超过3min的部分每1min收1元(不足1min按1min计),则时间t≥3(min)时,电话费y(元)与时间t(min)之间的函数关系式是________.6.已知|a+1|+(b-2)2=0,则函数y=(b+3)x-a+1-2b+b2的关系式是________,当x=-错误!未找到引用源。
时,y=________.三、解答题(共26分)7.(8分)已知:y与2x成正比例,且当x=3时,y=-12.求y与x的函数关系式.8.(8分)某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.方案一:每千克种子价格为4元,无论购买多少均不打折;方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次性购买超过3千克,则超过3千克的部分的种子价格打7折.(1)请分别求出方案一和方案二中购买的种子数量x(千克)和付款金额y(元)之间的函数关系式.(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.【拓展延伸】9.(10分)生态公园计划在园内的坡地上造一片有A,B两种树的混合林,需要购买这两种树苗共2000棵,种植A,B两种树苗的相关信息如表:项目品种单价(元/棵) 成活率劳务费(元/棵)A 15 95% 3B 20 99% 4设购买A种树苗x棵,造这片林的总费用为y元,解答下列问题:(1)写出y(元)与x(棵)之间的函数关系式;(2)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?答案解析1.【解析】选C.由正比例函数的定义可得:2-3b=0,解得b=错误!未找到引用源。
(新人教版)新版学年七年级数学上册 一次函数计算习题 (新版)鲁教版【提分必备】

⎩ ⎨一次函数计算(习题)例题示范例 1:如图,已知直线l 1 :y 2x ,直线l 2 与 x 轴交于点 A (1,0),与y 轴交于点 B (0,2),求直线l 1 与直线l 2 的交点 C 的坐标.解:设直线l 2 的解析式为 y kx b∵A (1,0),B (0,2) 把 A ,B 两点代入得,k b 00 b 2k 2解得 b 2 ∴ l 2 :y 2x 2∵直线l 1 与直线l 2 的交点为 C即C ( 1 ,1)2巩固练习1.如果点 A (-2,a )在一次函数y 1x 3的图象上,那么 a 的2值为( )A .-7B .3C .-1D .42.若正比例函数的图象经过点(2,6),则这个正比例函数的解析式为;3.若一次函数y=-x+a 的图象经过点A(1,-1),则a= ,它过点B(-2,);4.过点(-1 ,-3) 且与直线y=1-x 平行的直线的表达式是.5.一次函数y=-3x+9 的图象与x 轴的交点坐标是;与y 轴的交点坐标是;与坐标轴所围成的三角形的面积是.6.已知一次函数y=kx+b 的图象经过点(-3,2),且与直线y=-2x+4交于x 轴上的同一点,则该一次函数的表达式为.7.若一次函数y=ax+4 与y=bx-2 的图象在x 轴上相交于同一点,则b的值为.a8.(1)已知一次函数y=kx+b 的图象与y 轴交点的纵坐标为-2,且经过点(5,3),则该函数的表达式为;(2)若直线y=ax+5 经过一次函数y=4-3x 与y=2x-1 图象的交点,求a 的值为.9.已知y 是x 的一次函数,根据下表信息可知:a= ,b= ,c= .10.如图,直线l 的函数表达式为.⎨⎪⎨11. 一次函数 y k 1x b 1 的图象 l 1 与 y k 2 x b 2 的图象 l 2 相交于点P ,则方程组的解是 . y k x b5x 612.若关于 x ,y 的方程组 6 x 5 y 4m有无穷多组解,则关于 x ,的方程组4x 5 y710mx 7 y 11的解为 .13.已知某个一次函数的图象过点 A (-3,0),B (0,5),求这个函数的表达式.14. 如图,一次函数的图象经过点 A ,且与正比例函数 y =-x 的图象交于点B ,求该一次函数的表达式.思考小结1.函数图象经过一点(即点在直线上),坐标表达式;求交点坐标,两个函数的表达式,解方程组;已知两点坐标求一次函数表达式,利用.2.从数和形两方面说明y=x+1 和x+1=0 之间的联系:①从数的关系上看,函数y=x+1 的值等于 0,即方程x 1 0 ;②从图象上看,函数y=x+1 的图象与轴交点的就是方程x 1 0 的解.3.小明认为,一次函数y=kx+b 中,x 每增加 1,kx 增加了k,b 没有变,因此y 也增加了k.如图所示的一次函数图象中,x 从 1 变到2 时,函数值从3 变到 5,增加了 2,因此该一次函数中k 的值是 2.请你用待定系数法验证小明的说法.根据小明的思路,请你用两种方法求出下图中一次函数的表达式.。
鲁教版初中数学七年级上册《一次函数的图象》同步练习1

6.3 一次函数的图象一、填空题(1)一次函数的图象经过点(-1,2),且函数y的值随自变量x的增大而减小,请你写出一个符合上述条件的函数关系式________.(2)你能根据下列一次函数y=kx+b的草图,得到各图中k和b的符号吗?(3)若一次函数y=(2-m)x+m的图象经过第一、二、四象限时,m的取值范围是________,若它的图象不经过第二象限,m的取值范围是________.二、选择题(1)一水池蓄水20 m3,打开阀门后每小时流出5 m3,放水后池内剩下的水的立方数Q(m3)与放水时间t(时)的函数关系用图表示为()(2)两个受力面积分别为S A(米2)、S B(米2)(S A、S B为常数)的物体A、B,它们所受压强p(帕)与压力F(牛)的函数关系图象分别是射线l A、l B,则S A与S B的大小关系是()A.S A>S BB.S A<S BC.S A=S BD.不能确定(3)早晨,小强从家出发,以v1的速度前往学校,途中在一饮食店吃早点,之后以v2的速度向学校走去,且v1>v2,则表示小强从家到学校的时间t(分钟)与路程S(千米)之间的关系是()三、已知一次函数y=-2x-2(1)画出函数的图象.(2)求图象与x轴、y轴的交点A、B的坐标. (3)求A、B两点间的距离.(4)求△AOB的面积.(5)利用图象求当x为何值时,y≥0.参考答案一、(1)y=-x+1,y=-2x,y=-3x-1等,必须使k<0(2)①>>②><③<>④<<(3)m>2,m<0二、(1)D (2)B (3)A三、(1)如下图(2)A(-1,0)B(0,-2)(3)|AB|=5(4)S△AOB=1(5)x≤-1。
七年级数学上册一次函数 同步练习鲁教版

一次函数同步练习(一)填空1.直线y=-3x-6和两轴围成的三角形的周长为______;面积为______.2.直线y=x-1和直线y=x+1与y轴交点间的距离为______.3.直线y=kx+b过点P(3,2),且它交x轴,y轴的正半轴于A,B两点,若OA+OB=12,则此直线的解析式为______.4.已知y=y1+y2,y1=k1x,y2=k2x,当x=1时,y=3,且当x=1时,y1-y2=1,则函数y1,y2的解析式分别为______.(二)解下列各题5.已知一次函数y=mx-m+2,求(1)当m为何值时,它的图象过原点?(2)当m为何值时,它的图象过(0,5)?6.已知一次函数 y=mx-m+2,若它的图象过第一、第三、四象限,求m的取值X围.8.一次函数y=kx+b的图象过A(2,4),B(-1,5),求函数的解析式,并求出此函数图象与坐标轴围成的三角形的面积.9.已知函数y=kx+b,当x=8时,y=12;当x=2时,y=-3.求此函数的解析式.10.将下列二元一次方程变形成一次函数y=kx+b的形式,并求出每条直线与x轴、y轴的交点坐标,以及在x轴和y 轴上的截距.数是一次函数?并写出此函数.(1)试确定点 A(4,5),B(-2,3)是否在此函数的图象上?(2)求出在此图象上已知点关于原点的对称点的坐标.(1)当x=-2a时,对应的函数值;(1)当x=-9a2时,对应的函数值;(2)当y=4时,对应的x值.15.函数y=(a+1)xa2-a-1+2是一次函数时,求a的值.16.已知函数y=(2m-1)x+m+5,求m为何值时,(1)函数值随x的增大而增大;(2)函数值随x的增大而减小.17.已知函数y=(1-3k)x+2k+31,求当k是什么数时,(1)此函数值随x的增大而增大;(2)函数值随x的增大而减小.18.若一次函数图象过点A(2,-1)和B点,其中B是另一条直线19.若一次函数图象过点A(-1,2)和B点,其中B是另一条直线20.已知一次函数y=kx+b的图象过两点A(-3,2),B(5,0).(1)求k和b;(2)求此图象与坐标轴交点间的距离.21.已知一次函数y=kx+b的图象过两点A(2,-3),B(-4,-6).(1)求此函数的解析式;(2)求此图象与坐标轴两交点的坐标;(3)求(2)中两交点间的距离.22.一次函数y=kx+b的图象过两点A(1,5),B(-1,8),求:(1)此图象与坐标轴两交点的坐标;(2)此图象与坐标轴围成的三角形面积.23.已知一次函数y=kx+b的图象如图13-19所示,求k,b值及此函数的解析式.24.已知一次函数y=kx+b的图象如图13-20所示.(1)求k,b值及此函数解析式;(2)求A,B两点间的距离.25.已知一次函数y=kx+b的图象经过点(m,1)和点(-1,m),其中m>1,问k,b值的符号如何?26.若一次函数y=3x+b的图象与坐标轴所围成的三角形面积等于24,求b的值.27.已知一次函数y=kx+b的图象过两点A(-6,4),B(3,0),求此函数的解析式和其图象与坐标轴两交点的坐标.28.已知函数y=kx+1的图象上有一点A(1,a),A到原点的距离29.已知直线y=kx+2过点(-2,4).(1)求此直线的方程;(2)若此直线与x轴交于C点,且点A(5,-3)在直线上,且A点在x轴上的射影为B点,求△ABC的面积.30.设m是任意实数,证明一次函数y=mx-2m+1的图象必通过一个定点,并求出此点的坐标.31.某油箱存油60m3,每小时耗油8m3,写出油箱中剩余油量Q(m3)与用油时间t(小时)之间函数关系式,并作图.32.某工厂有一水池,容积1000升,池内原有水400升,今需将池注满.已知每分钟注入水20升,写出水池内水量Q与时间t(分)的函数解析式,并求出此函数的定义域.33.已知等腰三角形周长为10厘米,腰长为x,底边长为y,列出用x表示y的函数关系式,求出自变量取值X围并画出此函数的图象.34.某汽车油箱中存油20千克,油从管道中匀速流出,经210分钟流尽.(1)写出油箱中剩余油量y(千克)与流出时间x(分)之间的函数关系式;35.如图13-21所示,已知AA′,BB′是甲、乙两人在同一条路上步行的时间x与距离y之间函数关系的图象,求甲乙步行的时间x与距离y的关系式,并且求出他们的速度.36.在重为x、浓度为a%的食盐水中,加入重为y、浓度为b%的食盐水,使混合后的盐水浓度变成c%,求x与y的关系式,并作出此关系式的图象.37.汽车A在下午2时15分从甲地出发,开往乙地,途中发生故障停车6分钟,结果在当天下午3时57分到达乙地.汽车B在同一天下午2时28分从甲地出发,开往乙地,当天下午3时40分到达.若A,B行驶时保持固定的速度,求汽车B在A发生故障前追上A,追上的时刻是几时几分?38.根据记录,从地面向上,11千米以内,每升高1千米,气温降低6℃;又在11千米以上的高空,气温几乎不变.设在地面温度为20℃时,离地面距离x千米处的大气温度是y(℃),求x与y的关系式,并求出离地面4500米的高空,气温是多少?39.由记录知,从地面向上,11千米以内,每升高1千米,气温降低5℃;又在11千米以上的高空,气温几乎不变.设在地面温度为18℃时,离地面距离x千米处的大气温度是y(℃),求x,y的关系式,并求出离地面13000米的高空,气温是多少?40.从A地到B地的一条路,最初6千米是平地,接着3千米是上坡,最后4千米是下坡.一个人步行的速度,在平地上是每小时4千米,上坡每小时3千米,下坡每小时6千米.当他从A地出发,经过时间x(小时)后,到达距离为y(千米)的地方,求x与y的关系并作出其图象.41.从甲地到乙地的一条路,最初20千米是平地,接着6千米是上坡,最后10千米是下坡.一个人骑自行车的速度,在平地上是每小时10千米,上坡每小时6千米,下坡每小时12千米.当他从甲地出发经过时间x(小时)后,到达距离为y(千米)的地方,求x与y的关系.42.某油箱存油40升,每小时耗油10升,写出油箱中剩余油量Q(升)与用油时间t(小时)之间的函数关系式,并作图.43.如图13-22所示,有一块三角地ABC,底BC为60米,高AG为40米.现在要沿着BC建筑一座地基为矩形的大楼,若大楼的长为x,宽为y时,写出y与x的关系式(矩形的长在底BC上).44.在图13-23中,设两条直线l1和l2,分别是汽车在柏油路和公路上行驶时,所需牵引力F随载重量G而变化的图形.求l1,l2中F,G的关系式.45.某油箱存油80升,每小时耗油12升,写出油箱中剩余油量Q(升)与用油时间t(小时)之间的函数关系式和自变量t的取值X围,并作出此函数的图象草图.46.一根弹簧,挂5千克重物时,弹簧长为24厘米,以后每增加重量1千克,弹簧伸长1.5厘米,在弹性限度内,弹簧长l和悬挂重量w之间有何关系?并求出当w=10千克时,l等于多少?(三)作出下列函数的图象47.作出当a>0且b>0时,y=ax+b的图象(草图).48.作出当a>0且b<0时,y=ax+b的图象(草图).49.求作通过点(4,7),且与x轴成60°角的直线l.50.已知一次函数y=a2x-b,若其中a<0,b>0,画出它的图象(草图).51.作出当k2>0,k3<0,且满足k2>k3>k1时,函数y=kix+1(i=1,2,3)的图象(草图).52.作y=-2|x|+1的图象.53.作y=2|x|+1的图象.54.作函数y=-|x|-1的图象.55.作y=|x-2|+1的图象.(1)求作此函数的图象;(2)观察图象,问x取什么值时,y值大于1?(1)求作函数的图象;(2)x取何值时,y值小于2且大于-1?58.已知一次函数y=kx+3的图象与两坐标轴围成的三角形面积等于9,求k值,并画出这个函数图象.59.若一次函数的图象在x轴上的截距为-2,且过点(1,5).求这个函数的解析式并画出此函数的图象.关于y轴的对称图形.61.作出一次函数y=3x+1与y=3x-1的图象,并回答它们的位置关系.62.作y=4|x|-1的图象.值小于零.参考答案:(一)填空2.24.y1=2x,y2=x(二)解下列各题5.(1)2;(2)-3.6.m>2.提示:依题意要满足条件m>0且-m+2<0,所以m>2.7.A,D,E在;B,C不在..-4),在x轴上的截距为6,在y轴上的截距为-4;(2)y=2x-8,x轴交点(4,0),y轴交点(0,-8),x轴截距为4,y轴截距为-8.12.(1)点A在,点B不在;(2)(-4,-5).15.2.18.y=-2x+3.19.y=3x+5.25.k<0,b>0. 26.±12.+1的图象上.所以a=k+1,即k=a-1.因为A(1,a)到原点的距离30.(2,1).提示:由y=m(x-2)+1知当x=2时,恒有y=1而与m值无关,故一次函数y=mx-2m+1的图象必过定点(2,1).31.a=-8t+60(0≤t≤7.5).32.a=20t+400(0≤t≤30).33.y=-2x+10(2.5<x<5).35.甲:y=10x-5,10千米/小时;乙:y=4x+4,4千米/小时.为:y=10x-5.由B(-1,0)及B'(0,4)求出BB'的函数解析式为y=4x+4.所以甲的速度是每小时10千米,乙的速度是每小时4千米.37.下午3时7分.提示:设甲、乙两地的距离为1,A行驶在38.y=20-6x(0≤x≤11),-7℃.39.y=18-5x(0≤x≤11),-37℃.41.当0≤x≤2时,y=10x;当2<x≤3时,y=6x+8;当3<42.Q=-10t+40(0≤t≤4).44.l1为:G-10F=0,l2为:3G-20F=0.46.l=1.5w+16.5(w≥5),31.5厘米.提示:依题意得l=24+(w-5)×1.5=1.5w+16.5(w ≥5).(三)作出下列函数的图象47~63(略)。
七年级数学上册 一次函数计算习题 (新版)鲁教版

马明风整理⎩ ⎨一次函数计算(习题)例题示范例 1:如图,已知直线l 1 :y 2x ,直线l 2 与 x 轴交于点 A (1,0),与y 轴交于点 B (0,2),求直线l 1 与直线l 2 的交点 C 的坐标.解:设直线l 2 的解析式为 y kx b∵A (1,0),B (0,2) 把 A ,B 两点代入得,k b 00 b 2k 2解得 b 2 ∴ l 2 :y 2x 2∵直线l 1 与直线l 2 的交点为 C即C ( 1 ,1)2巩固练习1.如果点 A (-2,a )在一次函数y 1x 3的图象上,那么 a 的2值为( )A .-7B .3C .-1D .42.若正比例函数的图象经过点(2,6),则这个正比例函数的解析式为;3.若一次函数y=-x+a 的图象经过点A(1,-1),则a= ,它过点B(-2,);4.过点(-1 ,-3) 且与直线y=1-x 平行的直线的表达式是.5.一次函数y=-3x+9 的图象与x 轴的交点坐标是;与y 轴的交点坐标是;与坐标轴所围成的三角形的面积是.6.已知一次函数y=kx+b 的图象经过点(-3,2),且与直线y=-2x+4交于x 轴上的同一点,则该一次函数的表达式为.7.若一次函数y=ax+4 与y=bx-2 的图象在x 轴上相交于同一点,则b的值为.a8.(1)已知一次函数y=kx+b 的图象与y 轴交点的纵坐标为-2,且经过点(5,3),则该函数的表达式为;(2)若直线y=ax+5 经过一次函数y=4-3x 与y=2x-1 图象的交点,求a 的值为.9.已知y 是x 的一次函数,根据下表信息可知:a= ,b= ,c= .10.如图,直线l 的函数表达式为.马明风整理》》》》》》》》》积一时之跬步 臻千里之遥程《《《《《《《《《《《《马明风整理⎨⎪⎨11. 一次函数 y k 1x b 1 的图象 l 1 与 y k 2 x b 2 的图象 l 2 相交于点P ,则方程组的解是 . y k x b5x 612.若关于 x ,y 的方程组 6 x 5 y 4m 有无穷多组解,则关于x ,的方程组4x 5 y710mx 7 y 11的解为 .13.已知某个一次函数的图象过点 A (-3,0),B (0,5),求这个函数的表达式.14. 如图,一次函数的图象经过点 A ,且与正比例函数 y =-x 的图象交于点B ,求该一次函数的表达式.》》》》》》》》》积一时之跬步臻千里之遥程《《《《《《《《《《《《 思考小结1.函数图象经过一点(即点在直线上),坐标表达式;求交点坐标,两个函数的表达式,解方程组;已知两点坐标求一次函数表达式,利用.2.从数和形两方面说明y=x+1 和x+1=0 之间的联系:①从数的关系上看,函数y=x+1 的值等于 0,即方程x 1 0 ;②从图象上看,函数y=x+1 的图象与轴交点的就是方程x 1 0 的解.3.小明认为,一次函数y=kx+b 中,x 每增加 1,kx 增加了k,b 没有变,因此y 也增加了k.如图所示的一次函数图象中,x 从 1 变到2 时,函数值从3 变到 5,增加了 2,因此该一次函数中k 的值是 2.请你用待定系数法验证小明的说法.根据小明的思路,请你用两种方法求出下图中一次函数的表达式.马明风整理。
七年级数学上册 一次函数应用题习题 (新版)鲁教版

?? 一次函数应用题(习题)例题示范例 1:一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两.车.之.间.的.距.离.为y(km),图中的折线表示y 与x 之间的关系.根据图象解答下列问题:(1)求快车和慢车的速度;(2)求y 与x 之间的函数关系式,并写出自变量x 的取值范围.思路分析:A(0,900) 出发B(4,0) 两车相遇C( , ) 快车到站D(12,900) 慢车到站(1)由A,B 两点坐标可以得到:由D 点坐标可以得到:所以v快 150(km / h),v慢 75(km / h),所以C 点的横坐标为9006 .150(2)由分析可得:①AB 段是快车和慢车相向而行,根据k 的实际意义可得|k|=225,因为过第二、四象限,故k=-225,因为A(0,900),故b=900,所以AB 段表达式为y=-225x+900;②BC 段是快车和慢车背向而行,根据k 的实际意义可得|k|=225,因为过第一、三象限,故k=225,设y=225x+b,把B(4,0)代入,可得b=-900,所以BC段表达式为y=225x-900;③CD 段只有慢车在走,根据k 的实际意义可得|k|=75,因为过第一、三象限,故k=75,设y=75x+b,把D(12,900)代入,可得b=0,所以y=75x.225x 900 (0≤x ≤4)综上,y 225x 900 (4x ≤6)75x (6x ≤12)巩固练习1.在一条笔直的公路上有 A,B 两地,甲骑自行车从 A 地到 B 地;乙骑自行车从B 地到A 地,到达A 地后立即原路返回.如图是甲、乙两人离B 地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:(1)直接写出 A,B 两地之间的距离;(2)求出点M 的坐标,并解释该点坐标所表示的实际意义;(3)若两人之间的距离不超过 3km 时,能够用无线对讲机保持联系,求甲、乙两人能够用无线对讲机保持联系时x 的取值范围.O 1 2 x/h2.某地区一种商品的需求量y1(万件)、供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-36.当需求量为 0 时,即停止供应.当y1=y2 时,该商品的价格称为稳定价格,需求量称为稳定需求量.(1)求该商品的稳定价格与稳定需求量;(2)当价格在什么范围时,该商品的需求量低于供应量?(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4 万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?元/件)3.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y 与x 之间的函数关系.根据题中所给信息解答以下问题:(1)甲、乙两地之间的距离为k m;图中点C 表示的实际意义是;慢车的速度为,快车的速度为.(2)求线段BC 所表示的y 与x 之间的函数关系式,以及自变量x 的取值范围.(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.请直接写出第二列快车出发多长时间,与慢车相距 200km.【参考答案】巩固练习1. (1)A ,B 两地之间的距离是 30 km(2) M ( 2 ,20) ,该点坐标表示的实际意义是:两车出发3 2 h 时相遇,此时距离 B 地 20 km3(3) 3≤ x ≤11 9≤ x ≤25 15 5 2. (1)该商品的稳定价格是 32 元/件,稳定需求量是 28 万件(2)价格 x (元/件)满足32 < x <60 时,该商品的需求量低于供应量(3)6 元3. (1)960当两车行驶 6 h 时,快车到达乙地80 km/h ,160 km/h(2)y =240x -960(4≤x ≤6)(3)1.5 h。
鲁教版初中数学七年级上册《一次函数》同步练习1

6.2 一次函数一、填空题1.以下函数:①y =2x 2+x +1 ②y =2πr ③y =x 1 ④y =(2-1)x ⑤y =-(a +x )(a 是常数) ⑥s =2t 是一次函数的是________.2.当m =________时,y =(m -1)x 2m 是正比例函数.3.当k =________时,y =(k +1)x 2k +k 是一次函数.二、写出下列各题中x 与y 之间的关系式,并判断y 是否为x 的一次函数?是否为正比例函数?(1)小红去商店买笔记本,每个笔记本2.5元,小红所付买本款y (元)与买本的个数x (个)之间的关系.答:_______________________________________________________(2)等腰三角形的周长是18,若腰长为y ,底边长为x ,则y 与x 之间的关系.并求出x 的取值范围.答:_______________________________________________________(3)有一个长为120米,宽为110米的矩形场地准备扩建,使长增加x 米,宽增加y 米,且使矩形的周长为500米,则y 与x 的关系.答:_______________________________________________(4)据测试:拧不紧的水龙头每秒钟会滴下两滴水,每滴水约0.05毫升.小明同学在洗手时,没有把水龙头拧紧,当小明离开x 小时后水龙头滴了y 毫升水.y 与x 之间的关系.答:______________________________________________三、设某种储蓄的月利率为0.16%,现存入a (a >0)元本金.(1)写出本息和y (元)与所存月数x (月)之间的函数关系式.(2)当a =20000时,计算10个月后的本息和是多少元?四、容积为800公升的水池内已贮水200公升,若每分钟注入的水量是15公升,设池内的水量为Q(公升),注水时间为t(分).(1)请写出Q与t的函数关系式.(2)注水多长时间可以把水池注满?(3)当注水时间为0.2小时时,池中水量是多少?参考答案一、1.②④⑤⑥ 2.-1 3.1二、(1)y =2.5x 是一次函数,也是正比例函数(2)y =9-21x (0<x <9)是一次函数,不是正比例函数(3)y =20-x 是一次函数,不是正比例函数(4)y =360x 是一次函数,也是正比例函数三、(1)y =a (1+0.16%x )或写成y =a +0.16%ax(2)当a =20000,x =10时,y =20320四、(1)Q =200+15t(2)注水40分钟可以把水池注满(3)当注水0.2小时即12分钟时,池内有水380公升。
七年级数学上册 一次函数每日一练(一)每周一练(二)(新版)鲁教版

学 习 资 料 专 题一次函数每日一练(一)1.若一次函数 y =kx +b 的图象经过第一、三、四象限,则点 A (k,b )位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.若一次函数 y =(m -2)x -1 的图象经过第二、三、四象限,则 m 的取值范围是( ) A .m >0 B .m <0C .m >2D .m <23.若一次函数 y =kx +b 的图象不经过第三象限,也不经过原点, 则 k ,b 的取值范围是( ) A .k >0 且 b >0 B .k >0 且 b <0 C .k <0 且 b >0 D .k <0 且 b <04.已知直线 y =kx +b ,若 k +b =-5,kb =6,则该直线经过( )A .第二、四象限B .第一、二、三象限C .第一、三象限D .第二、三、四象限5.若 a 是非零实数,则直线 y =ax -a 一定经过( ) A .第一、二象限 B .第二、三象限 C .第三、四象限 D .第一、四象限6.已知一次函数 y =(m +2)x +1,若函数值 y 随 x 的增大而增大, 则 m 的取值范围是 .7.若一次函数 y =kx -1 中 y 随 x 的增大而减小,则这个一次函数的图象一定不经过第 象限.8.已知一次函数 y =kx +b ,若 y 随 x 的增大而减小,且 b >0,则它的图象大致是( )A .B .C .D .9.已知一次函数 y =kx +k ,若 y 随 x 的增大而增大,则它的图象大致是( )A .B .C .D .10. 已知一次函数 y =kx -2,若 y 随 x 的增大而减小,则它的图象大致是()A .B .C .D .11. 直线 y =2x -3 可以由直线 y =2x__单位而得到;直线 y =-3x +2 可以由直线 y =-3x单位而得到;直线 y =x +2 可以由直线 y =x -3单位而得到.1.8 1 2 每周一练(二)的运算结果应在( ) A .1 到 2 之间 B .2 到 3 之间C.3 到 4 之间 D .4 到 5 之间2.3.如图是国际数学家大会会标中的图案,其中四边形 ABCD 和四边形EFGH 都是正方形,若点 G 的坐标为(3,2),则点 D 的坐标为( )A .(5,3)B .(3,5)C .(5,5)D .(5,4)4.若等腰三角形的两边长 x ,y 满足方程组2x y 3 3x 2 y 8,则此等 腰三角形的周长为( ) A .3B .4C .4 或 5D .55.如图所示的计算程序中,y 与 x 之间的函数关系所对应的图象应为()A .B .C .D .35m6.如图,在 3×3 的正方形网格中有四个格点 A ,B ,C ,D ,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )A .A 点B .B 点C .C 点D .D 点7.定义运算“*”,规定 x *y =ax 2+by ,其中 a ,b 为常数,且 1*2=5,2*1=6,则 2*3= .8.5 的整数部分是_;若 m (4+m ) = .的小数部分是 m ,则9.若点 A (m +1,3m -5)到两坐标轴的距离相等,则 m 的值为.10. 点 A (-2,1)关于 y 轴对称的点的坐标是,关于原点对称的点的坐标是 .11. 已知线段 AB 与 x 轴交于点 C (2,0),若点 A ,点 B 的纵坐标分别为5 和-4,则△AOB 的面积为 .12. 直线 y mx n 的位置如图所示,化简:m n.13. 若函数 y (k 1)x k 2 1是正比例函数,则一次函数 y =kx -k不过第( )象限.A .一B .二C .三D .四7⎩ ⎩14.如图,在 Rt△ABC 中,∠ABC=90°,∠ACB=30°,将△ABC 绕点A按逆时针方向旋转15°后得到△AB1C1,B1C1 交AC 于点D.若AD= 2AB ,则△ABCC1第14 题图第15 题图15.如图,方格纸中的每个小方格都是边长为1 的正方形,A,B 两点在小方格的顶点上,在小方格的顶点上确定一点C,连接AB,AC,BC ,使△ABC 的面积为2,则满足条件的点C 的位置有个.16.解下列方程组2x 3y22(1)x 4 y113x 4 y 15 (2)4x 3y 10DB1 C2C17. 假如郑州市的出租车是这样收费的:起步价所包含的路程为0~1.5 千米,超过 1.5 千米的部分按每千米另收费.小刘说:“我乘出租车从市政府到郑州汽车站走了 4.5 千米,付车费 10.5 元.”小李说:“我乘出租车从省政府到郑州火车站走了 6.5 千米,付车费 14.5 元.” 问:(1)出租车的起步价是多少元?超过 1.5 千米后每千米收费多少元?(2)小张乘出租车从市政府到郑州东站(高铁站)走了 5.5 千米,应付车费多少元?18. 如图,在四边形 ABCD 中,AB =8,BC =1,∠DAB =30°,∠ABC =60°,四边形 ABCD 的面积为 5 ,求 AD 的长.DAB3【参考答案】1. D2. D3. C4. D5.D 6. m >-27. 一 8. A 9. C 10. D一次函数每日一练(一)11. 向下平移 3 个;向上平移 2 个;向上平移 5 个每周一练(二)1. C2. C3. A4. D5. D6.B7. 10 8. 2,3 9. 1 或 310. (2,1),(2,-1) 11. 912. n13. C 14. 6 215. 7 16.17. (1)出租车的起步价是 4.5 元,超过 1.5 千米后每千米收费 2元(2)小张应付车费 12.5 元 18. 233。
七年级上册数学鲁教版确定一次函数的表达式同步练习1

同步练习一、填空题(1)若一次函数y=kx-3k+6的图象过原点,则k=_______,一次函数的解析式为________.(2)若y-1与x成正比例,且当x=-2时,y=4,那么y与x之间的函数关系式为________.(3)随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势.年份(x)1999 2000 2001 2002 …入学儿童人数(y)2710 2520 2330 2140 …利用你所学的函数知识解决以下问题:①入学儿童人数y(人)与年份x(年)的函数关系是________.②预测该地区从________年起入学儿童人数不超过1000人.二、解答题1.汽车的油箱中的余油量Q(升)是它行驶的时间t(小时)的一次函数.某天该汽车外出时,油箱中余油量与行驶时间的变化关系如下图2:图2(1)根据图象,求油箱中的余油Q与行驶时间t的函数关系,并求出t的取值范围.(2)从开始算起,如果汽车每小时行驶40千米,当油箱中余油20升时,该汽车行驶了多少千米?2.小明买了一套现价为12万元的房子,购房时已付房款3万元,从第二年起,以后每年付房款5000元与上一年剩余欠款利息的和,已知剩余欠款的年利率为0.4%.(1)将第三年、第四年、第十年应付房款填入下列表格中:(2)若第x年(x≥2),小明家应交房款y元,请写出年付房款y与x的函数关系式.答_____________________________________________.3.我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.(1)若0<x≤6,请写出y与x的函数关系式.(2)若x>6,请写出y与x的函数关系式.(3)在同一坐标系下,画出以上两个函数的图象.(4)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?参考答案一、(1)2 2x (2)y =-23x +1(3)①y =2710-190(x -1999) ②2008 二、1.(1)Q =60-5t ,0≤t ≤12(2)当Q =20时,t =8,汽车行驶了320千米.2.(1)第三、四、十年分别应交房款5340元、5320元、5200元 (2)y =5000+[90000-5000(x -2)]×0.4%=5400-20x (x ≥2)3.(1)当0<x ≤6时,y =2x(2)当x >6时,y =12+3(x -6)即y =3x -6 (3)如上图: (4)该月用了11吨水.。
鲁教版七年级数学上册一次函数(二) 同步练习

一次函数(二) 同步练习一、选择题1.函数y=2x+3的图象一定通过点( )A.( 2,3 )B.(3,2)C.(1,5)D.(5,1)2.一次函数y=2x- 4的图象是由正比例函数y=2x 的图象( )A.向左平移4个单位长度得到B. 向右平移4个单位长度得到C.向上平移4个单位长度得到D.向下平移4个单位长度得到3. 一次函数y= -2x+6的图象与两坐标轴交于点A 、B,则△AOB 的面积等于( )A.12B.94.已知一次函数 y=2x-3, y= -3x+6, y=31-x+7, y=2)22(+-x 1=ax+b, y 2=bx+a 在同一坐标系中的图象可能是( )二、填空题6. 一次函数221-=x y 的图象与x 轴交于点 , 与y 轴交于点 . 时, 一次函数y= (m-2)x+6中, y 随x 的增大而增大.8.将正比例函数y= -2x 的图象向上平移3个单位后,得到的图象解析式是 .9. 将正比例函数y= 3x 的图象向右平移2个单位后,得到的图象解析式是 .10. 当m 满足时, 一次函数y= -2x+ m -6的图象与y 轴交于负半轴.三、简答题231+-=x y . (1)在直角坐标系中画出它的图象;(2)写出它与两坐标轴的交点坐标;(3)求出这条直线与坐标轴围成的三角形面积.ABC D12.动手做一做.向上平移4个单位长度13.已知一次函数y=(2m+2)x+(3-n),根据下列条件,请你求出m 、n 的取值X 围.(1) y 随x 的增大而增大;(2)直线与y 轴交点在x 轴下方;(3) 图象经过第二、三、四象限;14.根据下列条件,你能求出m 的取值X 围吗?试一试.(1) 一次函数y= (m-2)x+6+2m 的图象经过第一、二、三象限;(2)一次函数y= (m-2)x+6+2m 的图象经过第一、二、四象限;15.已知直线y=(2m+3)x+(4-n)和直线y=(n-2)x+4平行 ,且直线y=(2m+3)x+(4-n)和直线y=3x+(4+3 m)交于y 轴的同一点,试求m 与n 的值.16.对于一次函数y= (k-3)x+2k+6,陈成说它的图象不可能通过第一、三、四象限,你同意他的说法吗?为什么?1~5CDBCA6.(4,0)(0,-2). 7.m>2. 8. y= -2x+3. 9.y= 3x-6 10.m<6.11.(1) 图象略(2) (6,0),(0,2); (3)6. 12. y=4x+4, y=4x-4, y=4x-6.13.(1) m> -1; (2)n>3且m ≠ -1; (3) m<-1且n>3. 14.(1)⎩⎨⎧>+>-06202m m 得m>2; (2) 由⎩⎨⎧>+<-06202m m 得-3<m<2; 15. 解:由条件得:⎩⎨⎧-=+-=+n m n m 443232,得⎩⎨⎧=-=31n m . ⎩⎨⎧<+>-06203k k 得无解,所以他的说法正确.。
最新学年七年级数学上册 一次函数与几何综合(二)习题 (新版)鲁教版(考试必备)

一次函数与几何综合(二)(习题)1. 如图,一次函数 y =kx +b 的图象经过 A (-2,-1),B (1,3)两点, 并且与 x 轴交于点 C ,与 y 轴交于点 D ,则△AOB 的面积为 .第 1 题图 第 2 题图2. 如图,在平面直角坐标系中,点 A (-1,m )在直线 y =2x +3 上, 连结 OA ,将线段 OA 绕点 O 顺时针旋转 90°,点 A 的对应点B 恰好落在直线 y =-x +b 上,则 b 的值为 . 3. 如图,在平面直角坐标系 xOy 中,点 A 的坐标为(0,24),经过原点的直线 l 1 与经过点 A 的直线 l 2 相交于点 B (18,6).C 为线段 OB 上一动点(不与点 O ,B 重合),作 CD ∥y 轴交直线 l 2 于点 D ,过点 C ,D 分别向 y 轴作垂线,垂足分别为 F ,E ,若四边形 C DEF 是正方形,则点 C 的坐标为 . 第 3 题图 第 4 题图4. 如图,直线 AC 的表达式为 y 1 x 1,交 x 轴于点 C ,交 y2轴于点 D ,点 B 的坐标是(0,2),若 AB ⊥BC ,则△ABC 的面积为 .5. 如图,直线 y 1 x 1 与 x 轴、y 轴分别交于点 A ,B ,直线2 y x b 与 x 轴、y 轴分别交于点 C ,D ,两直线相交于点 P , 若 S △ ABD 4 ,则△APD 的面积为 .6. 如图,在平面直角坐标系 xOy 中,已知直线 l 1,l 2 相交于点A (2,1),点 B (8,4)在 l 1 上,l 2 的表达式为 y =3x -5.C 为 l 2 上的一个动点,且在点 A 右侧,若△ABC 的面积为 15,求点C 的坐标.l 2Cl 1Ax思考小结一次函数与几何综合解题思路坐标一次函数几何图形①要求坐标,;②要求函数表达式,;③要研究几何图形,., 【参考答案】巩固练习1. 522. 23. ( 72 24)7 7 4. 125. 206. C (4,7)思考小结1. ①利用函数表达式或线段长转坐标②待定系数法或 k ,b 的几何意义 ③坐标转线段长或 k ,b 的几何意义。
七年级数学上册 一次函数图象的应用习题 (新版)鲁教版

一次函数图象的应用(习题)例题示范例 1:已知一次函数 y =kx +b 与正比例函数 y =kbx ,它们在同一平面直角坐标系中的图象可能是( )A .B .C .D .思路分析:选项 A :假设一次函数 y =kx +b 图象正确,则 k <0,b>0,∴kb <0,由图象知,正比例函数可以与之共存,选项 A 正确; 选项 B :假设一次函数 y =kx +b 图象正确,则 k <0,b >0,∴kb <0,由图象知,正比例函数不能与之共存,选项 B 错误; 选项 C :假设一次函数 y =kx +b 图象正确,则 k >0,b <0,∴kb <0,由图象知,正比例函数不能与之共存,选项 C 错误; 选项 D :假设一次函数 y =kx +b 图象正确,则 k >0,b >0,∴kb >0,由图象知,正比例函数不能与之共存,选项 D 错误. 故选 A .例2:如图,若直线l1 : y1 k1x b1 与直线l2 : y2 k2 xb2 的交点坐标是(2,-1),则当y1 ≤y2 时,x 的取值范围是.思路分析:①找交点直线l1 : y1 k1x b1 与直线l2 : y2 k2 x b2 的交点坐标是(2,-1);②作直线过两直线交点作平行于y 轴的直线x=2;③定左右如图所示,在x=2 左侧,y1 y2 .综上,当y1 ≤y2 时,x 的取值范围是x≤2.巩固练习1.下列关于直线 y =-2x +1 的描述中,正确的是()A .图象必经过点(-2,1)B .图象经过第一、二、三象限C .当 x > 1时,y <02D .y 随 x 的增大而增大2. 若有意义,则函数 y =kx -1 的图象不经过第 象限.3. 如果直线 y =ax +b 经过第一、三、四象限,那么直线 y =bx +a 经过第象限,直线y bx 经过第a象限.4.正比例函数 y =2kx 的图象如图所示,则 y =(k -2)x +1-k 的图象可能是()A .B .C .D .5.一次函数 y =mx +2 与正比例函数 y =2mx (m 为常数,且 m ≠0) 在同一平面直角坐标系中的图象可能是( )A .B .C .D .6.两条直线y 1=ax +b 与y 2=bx +a 在同一平面直角坐标系中的图象可能是()A.B.C.D.7. 一次函数 y =kx +k 在平面直角坐标系中的图象可能是( )A .B .C .D .8.一次函数 y =mx -n 与正比例函数 y =mnx (m ,n 为常数,且mn ≠0)在同一平面直角坐标系中的图象中,一定不正确的是 ( )A .B .C .D .9.已知一次函数y 1x 1的图象如图所示,回答下列问题:2(1)当-1≤x <1 时,y 的取值范围是 ; (2)当 x >2 时,y 的取值范围是 ; (3)当 0<x ≤3 时,y 的取值范围是 ; (4)当 y ≥0 时,x 的取值范围是 .10. 已知一次函数 y 2x 2 的图象如图所示,回答下列问题:(1)当-1≤x <0 时,y 的取值范围是 ;(2)当 y >1 时,x 的取值范围是 ;(3)当-1≤y <2 时,x 的取值范围是.11.如图,直线 y 11x 与 y 2=-x +3 相交于点 A ,当 y 1<y 2 时, 2x 的取值范围是 .12. 如图,直线 y 1 x b 与 y 2=kx -1 相交于点 P ,点 P 的横坐标为-1,当 y 1>y 2 时,x 的取值范围是.13. 如图,直线 y1 x m 与直线 y 2=nx +4n (n ≠0)的交点的横坐标为-2,回答下列问题:(1)当 y 1>y 2 时,x 的取值范围是 ; (2)当 y 2>0 时,x 的取值范围是 .x+31思考小结1. 一次函数图象分析①只有一个一次函数图象时,根据函数的性质,判断k,b 的符号.②多个一次函数共存时,可以先假设其中一个正确,根据函数的性质,判断_的符号,然后用_的符号去验证.2. 如图,直线y kx b 经过A(-2,-1),B(-3,0)两点,则当1x kx b 0 时,x 的取值范围是.2思路分析:①观察图形,发现图中缺少y 1x 的图象,考虑作出函数2y1x 的图象,图象刚好过点2(填“A”或“B”);②通过找交点,,,求x 的取值范围.首先,三条直线的交点分别是,然后过交点作直线,分析得x 的取值范围是.【参考答案】巩固练习1. C2.二3.一、二、四,一、三4. B5.A6.A7.A8.A9. (1)1y≤3;(2)y<0;(3)1≤y 1 ;(4)x≤2 2 2 210. (1)0≤y2;(2)x1;(3)3≤x0 2 211. x 212. x 113. x 2 ;x 4思考小结1. ②k,b;k,b,另一个图象存在的合理性2. 3 x 2①划直线,定左右,x 3 ;②A③找交点,划直线,定左右,x 23 x 2。
七年级数学上册 一次函数与几何综合(二)习题 (新版)鲁教版
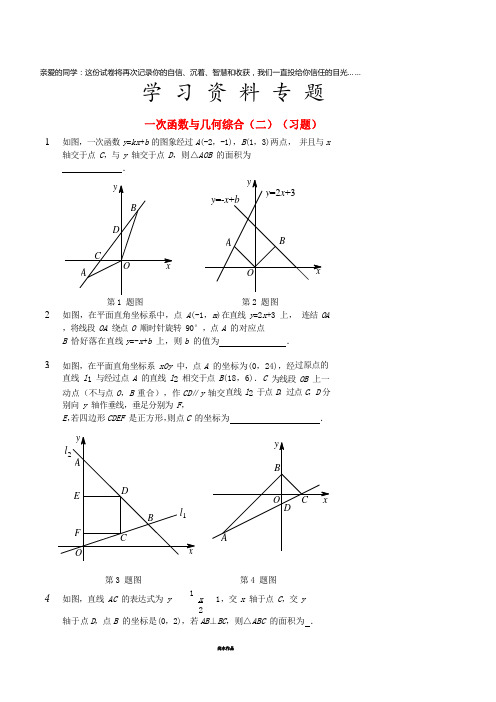
亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学 习 资 料 专 题一次函数与几何综合(二)(习题)1.如图,一次函数 y =kx +b 的图象经过 A (-2,-1),B (1,3)两点, 并且与 x轴交于点 C ,与 y 轴交于点 D ,则△AOB 的面积为 .第 1 题图第 2 题图2.如图,在平面直角坐标系中,点 A (-1,m )在直线 y =2x +3 上, 连结 OA ,将线段 OA 绕点 O 顺时针旋转 90°,点 A 的对应点 B 恰好落在直线 y =-x +b 上,则 b 的值为 .3.如图,在平面直角坐标系 xOy 中,点 A 的坐标为(0,24),经过原点的直线 l 1 与经过点 A 的直线 l 2 相交于点 B (18,6).C 为线段 OB 上一动点(不与点 O ,B 重合),作 CD ∥y 轴交直线 l 2 于点 D ,过点 C ,D 分别向 y 轴作垂线,垂足分别为 F , E ,若四边形 C DE F 是正方形,则点 C 的坐标为 .第 3 题图第 4 题图4. 如图,直线 AC 的表达式为 y 1x 1,交 x 轴于点 C ,交 y2 轴于点 D ,点 B 的坐标是(0,2),若 AB ⊥BC ,则△ABC 的面积为 .5. 如图,直线 y1x 1 与 x 轴、y 轴分别交于点 A ,B ,直线2y x b 与 x 轴、y 轴分别交于点 C ,D ,两直线相交于点 P , 若S △ ABD 4 ,则△APD 的面积为.6.如图,在平面直角坐标系 xOy 中,已知直线 l 1,l 2 相交于点A (2,1),点 B (8,4)在 l 1 上,l 2 的表达式为 y =3x -5.C 为 l 2 上的一个动点,且在点 A 右侧,若△ABC 的面积为 15,求点C 的坐标.l 2 Cl 1A x思考小结一次函数与几何综合解题思路坐标一次函数几何图形①要求坐标,;②要求函数表达式,;③要研究几何图形,., 【参考答案】 巩固练习 1.5 2 2. 2 3. ( 72 24)7 7 4. 12 5. 206. C (4,7)思考小结1. ①利用函数表达式或线段长转坐标②待定系数法或 k ,b 的几何意义 ③坐标转线段长或 k ,b 的几何意义。
最新学年七年级数学上册 一次函数图象的应用习题 (新版)鲁教版(考试必备)

一次函数图象的应用(习题)例题示范例 1:已知一次函数 y =kx +b 与正比例函数 y =kbx ,它们在同一平面直角坐标系中的图象可能是( )A .B .C .D .思路分析:选项 A :假设一次函数 y =kx +b 图象正确,则 k <0,b>0,∴kb <0,由图象知,正比例函数可以与之共存,选项 A 正确; 选项 B :假设一次函数 y =kx +b 图象正确,则 k <0,b >0,∴kb <0,由图象知,正比例函数不能与之共存,选项 B 错误; 选项 C :假设一次函数 y =kx +b 图象正确,则 k >0,b <0,∴kb <0,由图象知,正比例函数不能与之共存,选项 C 错误; 选项 D :假设一次函数 y =kx +b 图象正确,则 k >0,b >0,∴kb >0,由图象知,正比例函数不能与之共存,选项 D 错误. 故选 A .例2:如图,若直线l1 : y1 k1x b1 与直线l2 : y2 k2 xb2 的交点坐标是(2,-1),则当y1 ≤y2 时,x 的取值范围是.思路分析:①找交点直线l1 : y1 k1x b1 与直线l2 : y2 k2 x b2 的交点坐标是(2,-1);②作直线过两直线交点作平行于y 轴的直线x=2;③定左右如图所示,在x=2 左侧,y1 y2 .综上,当y1 ≤y2 时,x 的取值范围是x≤2.巩固练习1.下列关于直线 y =-2x +1 的描述中,正确的是()A .图象必经过点(-2,1)B .图象经过第一、二、三象限C .当 x > 1时,y <02D .y 随 x 的增大而增大2. 若有意义,则函数 y =kx -1 的图象不经过第 象限.3. 如果直线 y =ax +b 经过第一、三、四象限,那么直线 y =bx +a 经过第象限,直线y bx 经过第a象限.4.正比例函数 y =2kx 的图象如图所示,则 y =(k -2)x +1-k 的图象可能是()A .B .C .D .5.一次函数 y =mx +2 与正比例函数 y =2mx (m 为常数,且 m ≠0) 在同一平面直角坐标系中的图象可能是( )A .B .C .D .6.两条直线y 1=ax +b 与y 2=bx +a 在同一平面直角坐标系中的图象可能是()A.B.C.D.7. 一次函数 y =kx +k 在平面直角坐标系中的图象可能是( )A .B .C .D .8.一次函数 y =mx -n 与正比例函数 y =mnx (m ,n 为常数,且mn ≠0)在同一平面直角坐标系中的图象中,一定不正确的是 ( )A .B .C .D .9.已知一次函数y 1x 1的图象如图所示,回答下列问题:2(1)当-1≤x <1 时,y 的取值范围是 ; (2)当 x >2 时,y 的取值范围是 ; (3)当 0<x ≤3 时,y 的取值范围是 ; (4)当 y ≥0 时,x 的取值范围是 .10. 已知一次函数 y 2x 2 的图象如图所示,回答下列问题:(1)当-1≤x <0 时,y 的取值范围是 ;(2)当 y >1 时,x 的取值范围是 ;(3)当-1≤y <2 时,x 的取值范围是.11.如图,直线 y 11x 与 y 2=-x +3 相交于点 A ,当 y 1<y 2 时, 2x 的取值范围是 .12. 如图,直线 y 1 x b 与 y 2=kx -1 相交于点 P ,点 P 的横坐标为-1,当 y 1>y 2 时,x 的取值范围是.13. 如图,直线 y1 x m 与直线 y 2=nx +4n (n ≠0)的交点的横坐标为-2,回答下列问题:(1)当 y 1>y 2 时,x 的取值范围是 ; (2)当 y 2>0 时,x 的取值范围是 .x+31思考小结1. 一次函数图象分析①只有一个一次函数图象时,根据函数的性质,判断k,b 的符号.②多个一次函数共存时,可以先假设其中一个正确,根据函数的性质,判断_的符号,然后用_的符号去验证.2. 如图,直线y kx b 经过A(-2,-1),B(-3,0)两点,则当1x kx b 0 时,x 的取值范围是.2思路分析:①观察图形,发现图中缺少y 1x 的图象,考虑作出函数2y1x 的图象,图象刚好过点2(填“A”或“B”);②通过找交点,,,求x 的取值范围.首先,三条直线的交点分别是,然后过交点作直线,分析得x 的取值范围是.【参考答案】巩固练习1. C2.二3.一、二、四,一、三4. B5.A6.A7.A8.A9. (1)1y≤3;(2)y<0;(3)1≤y 1 ;(4)x≤2 2 2 210. (1)0≤y2;(2)x1;(3)3≤x0 2 211. x 212. x 113. x 2 ;x 4思考小结1. ②k,b;k,b,另一个图象存在的合理性2. 3 x 2①划直线,定左右,x 3 ;②A③找交点,划直线,定左右,x 23 x 2。
2019学年七年级数学上册 一次函数计算习题 (新版)鲁教版

⎩ ⎨一次函数计算(习题)例题示范例 1:如图,已知直线l 1 :y 2x ,直线l 2 与 x 轴交于点 A (1,0),与y 轴交于点 B (0,2),求直线l 1 与直线l 2 的交点 C 的坐标.解:设直线l 2 的解析式为 y kx b∵A (1,0),B (0,2) 把 A ,B 两点代入得,k b 00 b 2k 2解得 b 2 ∴ l 2 :y 2x 2∵直线l 1 与直线l 2 的交点为 C即C ( 1 ,1)2巩固练习1.如果点 A (-2,a )在一次函数y 1x 3的图象上,那么 a 的2值为( )A .-7B .3C .-1D .42.若正比例函数的图象经过点(2,6),则这个正比例函数的解析式为;3.若一次函数y=-x+a 的图象经过点A(1,-1),则a= ,它过点B(-2,);4.过点(-1 ,-3) 且与直线y=1-x 平行的直线的表达式是.5.一次函数y=-3x+9 的图象与x 轴的交点坐标是;与y 轴的交点坐标是;与坐标轴所围成的三角形的面积是.6.已知一次函数y=kx+b 的图象经过点(-3,2),且与直线y=-2x+4交于x 轴上的同一点,则该一次函数的表达式为.7.若一次函数y=ax+4 与y=bx-2 的图象在x 轴上相交于同一点,则b的值为.a8.(1)已知一次函数y=kx+b 的图象与y 轴交点的纵坐标为-2,且经过点(5,3),则该函数的表达式为;(2)若直线y=ax+5 经过一次函数y=4-3x 与y=2x-1 图象的交点,求a 的值为.9.已知y 是x 的一次函数,根据下表信息可知:a= ,b= ,c= .10.如图,直线l 的函数表达式为.2019年⎨⎪⎨11. 一次函数 y k 1x b 1 的图象 l 1 与 y k 2 x b 2 的图象 l 2 相交于点P ,则方程组的解是 . y k x b5x 612.若关于 x ,y 的方程组 6 x 5 y 4m 有无穷多组解,则关于x ,的方程组4x 5 y710mx 7 y 11的解为 .13.已知某个一次函数的图象过点 A (-3,0),B (0,5),求这个函数的表达式.14. 如图,一次函数的图象经过点 A ,且与正比例函数 y =-x 的图象交于点B ,求该一次函数的表达式.思考小结1.函数图象经过一点(即点在直线上),坐标表达式;求交点坐标,两个函数的表达式,解方程组;已知两点坐标求一次函数表达式,利用.2.从数和形两方面说明y=x+1 和x+1=0 之间的联系:①从数的关系上看,函数y=x+1 的值等于 0,即方程x 1 0 ;②从图象上看,函数y=x+1 的图象与轴交点的就是方程x 1 0 的解.3.小明认为,一次函数y=kx+b 中,x 每增加 1,kx 增加了k,b 没有变,因此y 也增加了k.如图所示的一次函数图象中,x 从 1 变到2 时,函数值从3 变到 5,增加了 2,因此该一次函数中k 的值是 2.请你用待定系数法验证小明的说法.根据小明的思路,请你用两种方法求出下图中一次函数的表达式.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数每日一练(一)
1.
若一次函数 y =kx +b 的图象经过第一、三、四象限,则点 A (k
,b )位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限
2.
若一次函数 y =(m -2)x -1 的图象经过第二、三、四象限,则 m 的取值范围是( ) A .m >0 B .m <0
C .m >2
D .m <2
3.
若一次函数 y =kx +b 的图象不经过第三象限,也不经过原点, 则 k ,b 的取值范围是( ) A .k >0 且 b >0 B .k >0 且 b <0 C .k <0 且 b >0 D .k <0 且 b <0
4.
已知直线 y =kx +b ,若 k +b =-5,kb =6,则该直线经过( )
A .第二、四象限
B .第一、二、三象限
C .第一、三象限
D .第二、三、四象限
5.
若 a 是非零实数,则直线 y =ax -a 一定经过( ) A .第一、二象限 B .第二、三象限 C .第三、四象限 D .第一、四象限
6.
已知一次函数 y =(m +2)x +1,若函数值 y 随 x 的增大而增大, 则 m 的取值范围是 .
7.
若一次函数 y =kx -1 中 y 随 x 的增大而减小,则这个一次函数的图象一定不经过第 象限.
8.
已知一次函数 y =kx +b ,若 y 随 x 的增大而减小,且 b >0,则它的图象大致是( )
A .
B .
C .
D .
9.
已知一次函数 y =kx +k ,若 y 随 x 的增大而增大,则它的图象大致是
( )
A .
B .
C .
D .
10. 已知一次函数 y =kx -2,若 y 随 x 的增大而减小,则它的图象大致是
(
)
A .
B .
C .
D .
11. 直线 y =2x -3 可以由直线 y =2x
__单位而得到;直
线 y =-3x +2 可以由直线 y =-3x
单位而得到;直线 y =x +2 可以由直线 y =x -3
单位而得到.
1.
8 1 2 每周一练(二)
的运算结果应在( ) A .1 到 2 之间 B .2 到 3 之间
C
.3 到 4 之间 D .4 到 5 之间
2.
3.
如图是国际数学家大会会标中的图案,其中四边形 ABCD 和四边形
EFGH 都是正方形,若点 G 的坐标为(3,2)
,则点 D 的坐标为( )
A .(5,3)
B .(3,5)
C .(5,5)
D .(5,4)
4.
若等腰三角形的两边长 x ,y 满足方程组2x y 3 3x 2 y 8
,则此等 腰三角形的周长为( ) A .3
B .4
C .4 或 5
D .5
5.
如图所示的计算程序中,y 与 x 之间的函数关系所对应的图象应为()
A .
B .
C .
D .
3
5
m
6.
如图,在 3×3 的正方形网格中有四个格点 A ,B ,C ,D ,以其中一
点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,
则原点是( )
A .A 点
B .B 点
C .C 点
D .D 点
7.
定义运算“*”,规定 x *y =ax 2+by ,其中 a ,b 为常数,且 1*2
=5,2*1=6,则 2*3= .
8.
5 的整数部分是
_;若 m (4+m ) = .
的小数部分是 m ,则
9.
若点 A (m +1,3m -5)到两坐标轴的距离相等,则 m 的值为
.
10. 点 A (-2,1)关于 y 轴对称的点的坐标是
,关于原
点对称的点的坐标是 .
11. 已知线段 AB 与 x 轴交于点 C (2,0),若点 A ,点 B 的纵坐标分别为
5 和-4,则△AOB 的面积为 .
12. 直线 y mx n 的位置如图所示,化简:m n
.
13. 若函数 y (k 1)x k 2 1是正比例函数,则一次函数 y =kx -k
不过第( )象限.
A .一
B .二
C .三
D .四
7
⎩ ⎩
14.如图,在 Rt△ABC 中,∠ABC=90°,∠ACB=30°,将△ABC 绕点A
按逆时针方向旋转15°后得到△AB1C1,B1C1 交AC 于
点D.若AD= 2
A
B ,则△ABC
C1
第14 题图第15 题图
15.如图,方格纸中的每个小方格都是边长为1 的正方形,A,B 两点在
小方格的顶点上,在小方格的顶点上确定一点C,连接AB,AC,BC ,使△ABC 的面积为2,则满足条件的点C 的位置有个.
16.解下列方程组
2x 3y
22
(1)
x 4 y
11
3x 4 y 15 (2)
4x 3y 10
D
B1 C
2
精品学习资料
C
17. 假如郑州市的出租车是这样收费的:起步价所包含的路程为
0~1.5 千米,超过 1.5 千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到郑州汽车站走了 4.5 千米,付车费 10.5 元.”
小李说:“我乘出租车从省政府到郑州火车站走了 6.5 千米,付车费 14.5 元.” 问:(1)出租车的起步价是多少元?超过 1.5 千米后每千米收费多少元?
(2)小张乘出租车从市政府到郑州东站(高铁站)走了 5.5 千米,应付车费多少元?
18. 如图,在四边形 ABCD 中,AB =8,BC =1,∠DAB =30°,
∠ABC =60°,四边形 ABCD 的面积为 5 ,求 AD 的长.
D
A
B
3
精品学习资料
【参考答案】
1. D
2. D
3. C
4. D
5.
D 6. m >-2
7. 一 8. A 9. C 10. D
一次函数每日一练(一)
11. 向下平移 3 个;向上平移 2 个;向上平移 5 个
每周一练(二)
1. C
2. C
3. A
4. D
5. D
6.
B
7. 10 8. 2,3 9. 1 或 3
10. (2,1),(2,-1) 11. 9
12. n
13. C 14. 6 2
15. 7 16.
17. (1)出租车的起步价是 4.5 元,超过 1.5 千米后每千米收费 2
元 (2)小张应付车费 12.5 元 18. 2
3
3
精品学习资料。
