2 《材料科学基础》第二章 晶体结构(下)PPT课件
合集下载
大学材料科学经典课件第二章材料的晶体结构

2) 方法同立方晶系, (hkil)为在四个 坐标轴的截距倒数的化简,自然可 保证关系式h+k+I=0。底面指数 为(0001),侧面的指数为(1010)。
晶系晶向与晶面指数
三、六方晶系晶面与晶向指数
2、晶向指数
标定方法:
1. 平移晶向(或坐标),让原 点为晶向上一点,取另一 点的坐标,有:
2. 并满足p+q+r=0 ;
1. 建立坐标系 结点为 原点,三棱为方向, 点阵常数为单位 (原 点在标定面以外,可 以采用平移法);
2. 晶面在三个坐标上的 截距a1 a2 a3 ;
3. 计算其倒数 b1 b2 b3 ;
4. 化成最小、整数比h: k:l ;
5. 放在圆方括号(hkl), 不加逗号,负号记在 上方 。
晶面指数特征:与原点位置无关;每一指数对应 一组平行的晶面。平行晶面的晶面指数相同,或
三、其他晶体学概念
5.两晶向之间的夹角: 在立方晶系中按矢量关系,晶向[u1v1w1]与[u2v2w2]
之间的夹角满足关系:
在立方晶系,晶面之间的夹角也就是为其法线的夹角, 用对应的晶向同样可以求出。
非立方晶系,晶面或晶向之间的夹角可以计算,但要 复杂许多。
第二节 纯金属常见的晶体结构
结构特点:以金属键结合,失去外层电子的金属离子与 自由电子的吸引力。无方向性,对称性较高的密堆 结构。
晶体结构则是晶体中实际 质点(原子、离子或分子) 的具体排列情况,它们能 组成各种类型的排列,因 此,实际存在的晶体结构 是无限的。
晶体结构和空间点阵的区别
晶体结和空间点阵的区别
三、晶面指数和晶相指数
.晶面(crystal face): 在晶格中由一系列原子所构成的平面
称为晶面。
晶系晶向与晶面指数
三、六方晶系晶面与晶向指数
2、晶向指数
标定方法:
1. 平移晶向(或坐标),让原 点为晶向上一点,取另一 点的坐标,有:
2. 并满足p+q+r=0 ;
1. 建立坐标系 结点为 原点,三棱为方向, 点阵常数为单位 (原 点在标定面以外,可 以采用平移法);
2. 晶面在三个坐标上的 截距a1 a2 a3 ;
3. 计算其倒数 b1 b2 b3 ;
4. 化成最小、整数比h: k:l ;
5. 放在圆方括号(hkl), 不加逗号,负号记在 上方 。
晶面指数特征:与原点位置无关;每一指数对应 一组平行的晶面。平行晶面的晶面指数相同,或
三、其他晶体学概念
5.两晶向之间的夹角: 在立方晶系中按矢量关系,晶向[u1v1w1]与[u2v2w2]
之间的夹角满足关系:
在立方晶系,晶面之间的夹角也就是为其法线的夹角, 用对应的晶向同样可以求出。
非立方晶系,晶面或晶向之间的夹角可以计算,但要 复杂许多。
第二节 纯金属常见的晶体结构
结构特点:以金属键结合,失去外层电子的金属离子与 自由电子的吸引力。无方向性,对称性较高的密堆 结构。
晶体结构则是晶体中实际 质点(原子、离子或分子) 的具体排列情况,它们能 组成各种类型的排列,因 此,实际存在的晶体结构 是无限的。
晶体结构和空间点阵的区别
晶体结和空间点阵的区别
三、晶面指数和晶相指数
.晶面(crystal face): 在晶格中由一系列原子所构成的平面
称为晶面。
材料科学基础第2章
化合物; C越小,越易形成固溶体
可编辑ppt
10
2.3.1 固溶体
固溶体(solid solution) :
合金组元通过溶解形成一种成分和性能均匀的、 且结构与组元之一相同的固相称为固溶体。
➢ 固溶体的最大特点是保持溶剂的晶体结构。
➢ 与固溶体晶格相同的组元为溶剂,一般在合金中 含量较多;另一组元为溶质,含量较少。
✓ 各向异性:由于在不同方向上的原子排列的紧密程 度不同使晶体在不同方向上的物理、化学和力学性 能不同。而一般整个晶体不显示各向异性,称为伪 等向性。
✓ 晶粒:组成晶体的结晶颗粒。 ✓ 多晶体:凡由两颗以上晶粒组成的晶体一般金属都
是多晶体。。
可编辑ppt
4
晶粒
可编辑ppt
5
Байду номын сангаас
多相合金
可编辑ppt
6
可编辑ppt
12
(3)按溶质原子在溶剂中的分布特点分类 无序固溶体:溶质原子在溶剂中任意分布, 无规律性。
有序固溶体:溶质原子按一定比例和有规 律分布在溶剂晶格的点阵或间隙里。
(4)按基体类型分类: 一次固溶体:以纯金属为基形成的固溶体。
二次固溶体:以化合物为基形成的固溶体。
可编辑ppt
13
固溶体的两种类型(置换和间隙)
中间相可以用分子式来大致表示其组成。
合金相的性质由以下三个因素控制: (1)电化学因素(电负性或化学亲和力因素)
电负性—化学亲和力越大越容易形成化合物,电负性 相近的元素容易形成固溶体。
(2)原子尺寸因素 △r=(rA-rB)/rA △r越大,越易形 成中间相。 △r越小,越易形成固溶体
(3)原子价因素(电子浓度因素): C电子=[A(100-x) +Bx]/100 C越大,越易形成
可编辑ppt
10
2.3.1 固溶体
固溶体(solid solution) :
合金组元通过溶解形成一种成分和性能均匀的、 且结构与组元之一相同的固相称为固溶体。
➢ 固溶体的最大特点是保持溶剂的晶体结构。
➢ 与固溶体晶格相同的组元为溶剂,一般在合金中 含量较多;另一组元为溶质,含量较少。
✓ 各向异性:由于在不同方向上的原子排列的紧密程 度不同使晶体在不同方向上的物理、化学和力学性 能不同。而一般整个晶体不显示各向异性,称为伪 等向性。
✓ 晶粒:组成晶体的结晶颗粒。 ✓ 多晶体:凡由两颗以上晶粒组成的晶体一般金属都
是多晶体。。
可编辑ppt
4
晶粒
可编辑ppt
5
Байду номын сангаас
多相合金
可编辑ppt
6
可编辑ppt
12
(3)按溶质原子在溶剂中的分布特点分类 无序固溶体:溶质原子在溶剂中任意分布, 无规律性。
有序固溶体:溶质原子按一定比例和有规 律分布在溶剂晶格的点阵或间隙里。
(4)按基体类型分类: 一次固溶体:以纯金属为基形成的固溶体。
二次固溶体:以化合物为基形成的固溶体。
可编辑ppt
13
固溶体的两种类型(置换和间隙)
中间相可以用分子式来大致表示其组成。
合金相的性质由以下三个因素控制: (1)电化学因素(电负性或化学亲和力因素)
电负性—化学亲和力越大越容易形成化合物,电负性 相近的元素容易形成固溶体。
(2)原子尺寸因素 △r=(rA-rB)/rA △r越大,越易形 成中间相。 △r越小,越易形成固溶体
(3)原子价因素(电子浓度因素): C电子=[A(100-x) +Bx]/100 C越大,越易形成
材料科学基础-§2-2 常见的晶体结构PPT课件

.
配位多面体是指物质结构中,与某个质点构成配位 关系而相邻结合的各个质点中心连线所构成的多面体。 该质点处于配位多面体的中心位置,而配位质点的中心 处于配位多面体的顶角上。
几种典型的配位形式及其相应的配位多面体
.
正、负离子半径比与阳离子配位数及配位多面体形状
实例
干冰 CO2
B2O3
SiO2 GeO2 闪锌矿
.
● 有效半径的确定 金属晶体 —— 两个相邻原子中心距的一半。 离子晶体 —— 一对相邻接触的阴、阳离子的中心距为离子 半径之和。 共价晶体—— 两个相邻键合离子的中心距为两离子的共价 半径之和。 原子或离子半径是晶体学中的重要参数
● 原子或离子半径大小对结构中质点排列方式影响很大。
● 原子或离子半径的概念并不十分严格,一种原子在不同
§2-2 常见的晶体结构
一. 晶体化学基本原理
1. 原子半径和离子半径 ● 原子半径或离子半径的概念
根据波动力学的观点,原子或离子围绕核运动的电子 在空间形成一个电磁场,其作用范围可视为球形。这个球 形的大小可视为原子或离子的体积,球的半径即为原子半 径或离子半径。 ● 原子或离子有效半径的概念
原子或离子在晶体结构中处于相接触时的半径。这种 状态下,离子或原子间的静电吸引和排斥作用达到平衡。
的晶体中,与不同的元素相结合,其半径可能发生变化。
● 离子晶体中存在极化,常是电子云向正离子方向移动,导
致正离子的作用范围变大,而负离子作用范围要变小。
● 共价键的增强和配位数的减少都可使原子或离子间距离缩
短,从而相应使半径减少。 .
2. 球体紧密堆积原理 球体最紧密堆积的基本类型 ① 单一质点的等大球体最紧密堆积,如纯金属晶体。 ② 几种质点的不等大球体的紧密堆积,如离子晶体。 等大球体的最密堆积 等大球体的最紧密排列平面有如 图的形式。在A球的周围有六个 球相邻接触,每三个球围成一个 空隙。其中一半是尖角向上的B 空隙,另一半是尖角向下的C空 隙,两种空隙相间分布。
配位多面体是指物质结构中,与某个质点构成配位 关系而相邻结合的各个质点中心连线所构成的多面体。 该质点处于配位多面体的中心位置,而配位质点的中心 处于配位多面体的顶角上。
几种典型的配位形式及其相应的配位多面体
.
正、负离子半径比与阳离子配位数及配位多面体形状
实例
干冰 CO2
B2O3
SiO2 GeO2 闪锌矿
.
● 有效半径的确定 金属晶体 —— 两个相邻原子中心距的一半。 离子晶体 —— 一对相邻接触的阴、阳离子的中心距为离子 半径之和。 共价晶体—— 两个相邻键合离子的中心距为两离子的共价 半径之和。 原子或离子半径是晶体学中的重要参数
● 原子或离子半径大小对结构中质点排列方式影响很大。
● 原子或离子半径的概念并不十分严格,一种原子在不同
§2-2 常见的晶体结构
一. 晶体化学基本原理
1. 原子半径和离子半径 ● 原子半径或离子半径的概念
根据波动力学的观点,原子或离子围绕核运动的电子 在空间形成一个电磁场,其作用范围可视为球形。这个球 形的大小可视为原子或离子的体积,球的半径即为原子半 径或离子半径。 ● 原子或离子有效半径的概念
原子或离子在晶体结构中处于相接触时的半径。这种 状态下,离子或原子间的静电吸引和排斥作用达到平衡。
的晶体中,与不同的元素相结合,其半径可能发生变化。
● 离子晶体中存在极化,常是电子云向正离子方向移动,导
致正离子的作用范围变大,而负离子作用范围要变小。
● 共价键的增强和配位数的减少都可使原子或离子间距离缩
短,从而相应使半径减少。 .
2. 球体紧密堆积原理 球体最紧密堆积的基本类型 ① 单一质点的等大球体最紧密堆积,如纯金属晶体。 ② 几种质点的不等大球体的紧密堆积,如离子晶体。 等大球体的最密堆积 等大球体的最紧密排列平面有如 图的形式。在A球的周围有六个 球相邻接触,每三个球围成一个 空隙。其中一半是尖角向上的B 空隙,另一半是尖角向下的C空 隙,两种空隙相间分布。
材料科学基础ppt

• 第六章 扩散与固态相变
– 第一节 扩散定律及其应用 – 第二节 扩散机制 – 第三节 影响扩散的因素与扩散驱动力 – 第四节 几个特殊的有关扩散的实际问题 – 第五节 固态相变中的形核 – 第六节 固态相变的晶体生长
• 第七章 陶瓷材料
导论
一·各种材料的概况
工程材料按属性可分为三类:金属材料、陶瓷材料和高分子材料。也可由此三个 相互组合而成的复合材料。按使用性能分类,则可分为主要利用其力学性能的结构材料和 主要利用其物理性能的功能材料。
• 第三章 晶体缺陷
– 第一节 点缺陷 – 第二节 位错的基本概念 – 第三节 晶体中的界面
• 第四章 材料的相结构及相图
– 第一节 材料的相结构 – 第二节 二元相图及其类型 – 第三节 复杂相图分析 – 第四节 相图的热力学基础
• 第五章 材料的凝固与气相沉积
– 第一节 材料凝固时晶核的形成 – 第二节 材料凝固时晶体的生长 – 第三节 固溶体合金的凝固 – 第四节 共晶合金的凝固 – 第五节 制造工艺与凝固组织 – 第六节 材料非晶态 – 第七节 材料的气—固转变
四. 晶面间距
1. 晶面间距:相邻两平行晶面间的距离。
2. 计算公式
对于各晶系的简单点阵,晶面间距与晶面指数 (hkl) 和点阵常数(a,b,c)之间有如下
关系:
立方晶系:
dhk la/h [2k2l2]1/2
四方晶系:
d h k1 l/h [2 (k 2 )/a 2 ( l/c )2 ] 1 /2
组织是指用金相观察方法观察材料内部时看到的涉及晶体或晶粒大小、方向、形状排 列状况等组成关系的组成物。不同的组织具有不同的力学性能和物理性能。
第一章 材料结构的基本知识
– 第一节 扩散定律及其应用 – 第二节 扩散机制 – 第三节 影响扩散的因素与扩散驱动力 – 第四节 几个特殊的有关扩散的实际问题 – 第五节 固态相变中的形核 – 第六节 固态相变的晶体生长
• 第七章 陶瓷材料
导论
一·各种材料的概况
工程材料按属性可分为三类:金属材料、陶瓷材料和高分子材料。也可由此三个 相互组合而成的复合材料。按使用性能分类,则可分为主要利用其力学性能的结构材料和 主要利用其物理性能的功能材料。
• 第三章 晶体缺陷
– 第一节 点缺陷 – 第二节 位错的基本概念 – 第三节 晶体中的界面
• 第四章 材料的相结构及相图
– 第一节 材料的相结构 – 第二节 二元相图及其类型 – 第三节 复杂相图分析 – 第四节 相图的热力学基础
• 第五章 材料的凝固与气相沉积
– 第一节 材料凝固时晶核的形成 – 第二节 材料凝固时晶体的生长 – 第三节 固溶体合金的凝固 – 第四节 共晶合金的凝固 – 第五节 制造工艺与凝固组织 – 第六节 材料非晶态 – 第七节 材料的气—固转变
四. 晶面间距
1. 晶面间距:相邻两平行晶面间的距离。
2. 计算公式
对于各晶系的简单点阵,晶面间距与晶面指数 (hkl) 和点阵常数(a,b,c)之间有如下
关系:
立方晶系:
dhk la/h [2k2l2]1/2
四方晶系:
d h k1 l/h [2 (k 2 )/a 2 ( l/c )2 ] 1 /2
组织是指用金相观察方法观察材料内部时看到的涉及晶体或晶粒大小、方向、形状排 列状况等组成关系的组成物。不同的组织具有不同的力学性能和物理性能。
第一章 材料结构的基本知识
材料科学基础第二章

y
[111]
x
[111]
例:画出晶向
[112 ]
2.立方晶系晶面指数
晶面指数的确定方法
(a)建立坐标系,结点为原点, 三棱为方向,点阵常数为单位 (原点在标定面以外,可以采 用平移法); (b)晶面在三个坐标上的截距a1 a2 a3 ; (c)计算其倒数 b1 b2 b3 ; (d)化成最小、整数比h:k:l ; 放在圆方括号(hkl),不加逗号, 负号记在上方 。
3.六方晶系晶面和晶向指数
三指数表示六方晶系晶面和晶向的缺点:晶体学上等价的 晶面和晶向不具有类似的指数。 例:
晶面指数
(11 0)
(100)
[010] [100]
从晶面指数上不能明确表示等同晶面,为了克服这一缺点, 采用a1、a2、a3及c四个晶轴, a1、a2、a3之间的夹角均 为120º ,晶面指数以(hkil)表示。 根据立体几何,在三维空间中独立的坐标轴不会超过三 个可证明 : i= - (h+k) 或 h+k+i=0
六方晶系
d hkl
h k l a b c
2 2 2
d hkl
a h2 k 2 l 2
1 l c
2
4 h 2 hk k 2 3 a2
注:以上公式是针对简单晶胞而言的,如为复杂晶胞, 例如体心、面心,在计算时应考虑晶面层数增加的影 响,如体心立方、面心立方、上下底(001)之间还有 一层同类型晶面,实际
[1 00 ]
[0 1 0]
[010]
[1 00]
y
[100]
x
[00 1]
大学材料科学基础第二章材料中的晶体结构

反过来: U = u - t; V = v - t; W = w
4.晶面间距(Interplanar crystal spacing)
两相邻近平行晶面间的垂直距离—晶面间 距,用dhkl表示,面间距计算公式见(1-6)。 通常,低指数的面间 距较大,而高指数的 晶面间距则较小 晶面间距愈大,该晶 面上的原子排列愈密 集;晶面间距愈小, 该晶面上的原子排列 愈稀疏。
晶体结构 = 空间点阵 + 结构单元
如:Cu, NaCl, CaF2有不同的晶体结构, 但都属于面心立方点阵。 思考题:空间点阵与布拉菲点阵。
三、 晶向指数与晶面指数
(Miller Indices of Crystallographic Directions and Planes) 在晶体中,由一系列原子所组成的平面称 为晶面,原子在空间排列的方向称为晶向。 晶体的许多性能都与晶体中的特定晶面和晶 向有密切关系。为区分不同的晶面和晶向, 采用晶面和晶向指数来标定。
5.晶带 (Crystal zone) 所有平行或相交于同一直线的晶面构 成一个晶带,此直线称为晶带轴。
晶带轴[u v w]与该晶带的晶面(h k l) 之间存在以下关系: hu + kv + lw = 0 凡满足此关系的晶面都属于以[u v w]为 晶带轴的晶带,律应用举例
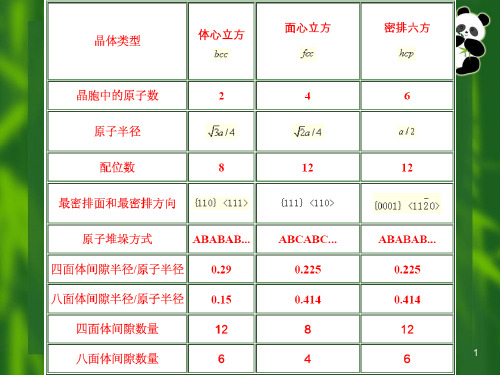
1 晶胞中原子数 (Number of Atoms in Unit Cell)
一个晶胞内所包含的原子数目。 体心立方晶胞:2个。 面心立方晶胞:4个。 密排六方晶胞:6个。
2 原子半径 r 与点阵常数 a 的关系
严格的说,原子半径并不是一个常数,它 随外界条件(温度)、原子结合键、配位数而 变,在理论上还不能精确地计算原子半径。 定义为晶胞中原子密排方向上相邻两原子 之间平衡距离的一半,用点阵常数表示。
4.晶面间距(Interplanar crystal spacing)
两相邻近平行晶面间的垂直距离—晶面间 距,用dhkl表示,面间距计算公式见(1-6)。 通常,低指数的面间 距较大,而高指数的 晶面间距则较小 晶面间距愈大,该晶 面上的原子排列愈密 集;晶面间距愈小, 该晶面上的原子排列 愈稀疏。
晶体结构 = 空间点阵 + 结构单元
如:Cu, NaCl, CaF2有不同的晶体结构, 但都属于面心立方点阵。 思考题:空间点阵与布拉菲点阵。
三、 晶向指数与晶面指数
(Miller Indices of Crystallographic Directions and Planes) 在晶体中,由一系列原子所组成的平面称 为晶面,原子在空间排列的方向称为晶向。 晶体的许多性能都与晶体中的特定晶面和晶 向有密切关系。为区分不同的晶面和晶向, 采用晶面和晶向指数来标定。
5.晶带 (Crystal zone) 所有平行或相交于同一直线的晶面构 成一个晶带,此直线称为晶带轴。
晶带轴[u v w]与该晶带的晶面(h k l) 之间存在以下关系: hu + kv + lw = 0 凡满足此关系的晶面都属于以[u v w]为 晶带轴的晶带,律应用举例
1 晶胞中原子数 (Number of Atoms in Unit Cell)
一个晶胞内所包含的原子数目。 体心立方晶胞:2个。 面心立方晶胞:4个。 密排六方晶胞:6个。
2 原子半径 r 与点阵常数 a 的关系
严格的说,原子半径并不是一个常数,它 随外界条件(温度)、原子结合键、配位数而 变,在理论上还不能精确地计算原子半径。 定义为晶胞中原子密排方向上相邻两原子 之间平衡距离的一半,用点阵常数表示。
无机材料科学基础第二章PPT课件

国际上通用的是密勒指数(Miller)
➢晶向指数:点阵中一维方向结点连线-行列:
行列平行方向-晶向(如:晶棱方向)
(1)建立坐标系,原点在待标晶向上
(2)选取该晶向上原点
以外的任一点P(xa,yb,zc)
zc
P
(3)将xa,yb,zc化简为互质
O
整数比u,v,w,且
yb
xa
u∶v∶w = xa∶yb∶zc
离子半径:离子中心到其作用力所及的有 效范围的距离。正、负离子都看成球体。离 子半径是衡量键性、键强、配位关系及极化 的重要数据。
2.6.2 球体紧密堆积原理
1、等大球体的最紧密堆积及其空隙:
【 紧密堆积结构】
Close-packed structures
ABABA.. packing
hcp & fcc
2、晶胞的分类
初级晶胞: 简单晶胞,只在平行六面体的八个角顶有阵点。
复合晶胞: 除角顶外,在其体心、面心或低心位置上也有 阵点。
3、描述晶胞的形状大小
晶胞的表示-晶胞参数
三条晶轴:a,b,c 轴间夹角:α,β,γ
4、晶系和布拉菲点阵
分类依据:棱长、夹角 七种类型:七大晶系 布拉菲点阵:14种
六方紧密堆积
hcp structure
(hexagonally-close packed)
ABCABC.. packing
立方紧密堆积
fcc structure
(face-centered cubic, 面心立方)
1、等大球体的最紧密堆积及其空隙:
(1)六方最紧密堆积:ABAB……紧密堆积 方式,密排面平行于(0001)。
• {100}=(100)+(010)+(001)
➢晶向指数:点阵中一维方向结点连线-行列:
行列平行方向-晶向(如:晶棱方向)
(1)建立坐标系,原点在待标晶向上
(2)选取该晶向上原点
以外的任一点P(xa,yb,zc)
zc
P
(3)将xa,yb,zc化简为互质
O
整数比u,v,w,且
yb
xa
u∶v∶w = xa∶yb∶zc
离子半径:离子中心到其作用力所及的有 效范围的距离。正、负离子都看成球体。离 子半径是衡量键性、键强、配位关系及极化 的重要数据。
2.6.2 球体紧密堆积原理
1、等大球体的最紧密堆积及其空隙:
【 紧密堆积结构】
Close-packed structures
ABABA.. packing
hcp & fcc
2、晶胞的分类
初级晶胞: 简单晶胞,只在平行六面体的八个角顶有阵点。
复合晶胞: 除角顶外,在其体心、面心或低心位置上也有 阵点。
3、描述晶胞的形状大小
晶胞的表示-晶胞参数
三条晶轴:a,b,c 轴间夹角:α,β,γ
4、晶系和布拉菲点阵
分类依据:棱长、夹角 七种类型:七大晶系 布拉菲点阵:14种
六方紧密堆积
hcp structure
(hexagonally-close packed)
ABCABC.. packing
立方紧密堆积
fcc structure
(face-centered cubic, 面心立方)
1、等大球体的最紧密堆积及其空隙:
(1)六方最紧密堆积:ABAB……紧密堆积 方式,密排面平行于(0001)。
• {100}=(100)+(010)+(001)
材料科学基础 ppt课件

当这对矛盾达到统一时,系统就达到平衡。 因为系统都具有最小自由能的倾向,由此确定的 点缺陷浓度即为该温度下的平衡浓度。
(5)结合键与性能
材料结合键的类型及键能大小对某些性能 有重要影响,主要表现在以下两个方面:
1.物理性能: (1)熔点的高低代表了材料稳定性的程度。物 质加热时,当热振动能足以破坏相邻原子间的稳 定结合时,便会发生熔化,所以熔点与键能值有 较好的对应关系:共价键、离子键化合物的熔点 较高,其中纯共价键金刚石具有最高熔点,金属 的熔点相对较低,但过渡族金属有较高的熔点, 特别是难熔金属W、Mo、Ta等熔点都很高。而具 有二次键结合的材料的熔点一般很低,如聚合物
2.根据排列次序建立了元素周期表,各个周 期中的元素的性质呈现相同的周期变化规 律,元素在周期表上的位置不仅决定了单 个原子的行为,也决定了材料中原子的结 合方式以及材料的化学性能和物理性能。
第二节 原子结合键
一.原子结合键 1.存在状态:凝聚态(液态和固态) 分类 2.一次键:结合力较强,包括离子键、共 价键和金属键。 3.二次键:结合力较弱,包括范德瓦耳斯 键和氢键。
二. 一次键
1.离子键
(1)通过电子转移形成稳定结构,存在于大 多数盐类、碱类和金属氧化物,如NaCI、MgO 、CuO、Mg2Si、CrO2。
(2) 基本特点是以离子为基本结合单位。
(3)一般离子晶体中正负离子静电引力较强 ,结合牢固。因此。其熔点和硬度均较高。 另外,在离子晶体中很难产生自由运动的电 子,因此,它们都是良好的电绝缘体。但当
电子云
原子核
电子云
原子核 a)理论电子云的分布
b)原子偶极矩的产生
4.氢键
氢键是一种特殊的分子间作用力,本质上与
范德瓦耳斯键一样,它是由氢原子同时与两个电
(5)结合键与性能
材料结合键的类型及键能大小对某些性能 有重要影响,主要表现在以下两个方面:
1.物理性能: (1)熔点的高低代表了材料稳定性的程度。物 质加热时,当热振动能足以破坏相邻原子间的稳 定结合时,便会发生熔化,所以熔点与键能值有 较好的对应关系:共价键、离子键化合物的熔点 较高,其中纯共价键金刚石具有最高熔点,金属 的熔点相对较低,但过渡族金属有较高的熔点, 特别是难熔金属W、Mo、Ta等熔点都很高。而具 有二次键结合的材料的熔点一般很低,如聚合物
2.根据排列次序建立了元素周期表,各个周 期中的元素的性质呈现相同的周期变化规 律,元素在周期表上的位置不仅决定了单 个原子的行为,也决定了材料中原子的结 合方式以及材料的化学性能和物理性能。
第二节 原子结合键
一.原子结合键 1.存在状态:凝聚态(液态和固态) 分类 2.一次键:结合力较强,包括离子键、共 价键和金属键。 3.二次键:结合力较弱,包括范德瓦耳斯 键和氢键。
二. 一次键
1.离子键
(1)通过电子转移形成稳定结构,存在于大 多数盐类、碱类和金属氧化物,如NaCI、MgO 、CuO、Mg2Si、CrO2。
(2) 基本特点是以离子为基本结合单位。
(3)一般离子晶体中正负离子静电引力较强 ,结合牢固。因此。其熔点和硬度均较高。 另外,在离子晶体中很难产生自由运动的电 子,因此,它们都是良好的电绝缘体。但当
电子云
原子核
电子云
原子核 a)理论电子云的分布
b)原子偶极矩的产生
4.氢键
氢键是一种特殊的分子间作用力,本质上与
范德瓦耳斯键一样,它是由氢原子同时与两个电
材料科学基础第2章

菱方 Rhombohedral a=b=c, α=β=γ≠90º
四方(正方)Tetragonal a=b≠c, α=β=γ=90º
立方 Cubic a=b=c, α=β=γ=90º
简单菱方
简单四方 体心四方
简单立方 体心立方 面心立方
简单三斜
简单单斜
底心单斜
简单正交
体心正交
底心正交
面心正交
简单六方
回转对称轴(n)1,2,3,4,6
宏观对称性 元素 对称面(m)
对称中心(i) 回转 — 反演轴 1,2,3,4,6
微观对称性
元素
滑动面 螺旋轴
a,b,c,n,d 21;31,32;41,43,42;61,65,62,64,63
点群(point group)—晶体中所有点对称元素的集合 根据晶体外形对称性,共有32种点群 空间群(space group)—晶体中原子组合所有可能方式 根据宏观、微观对称元素在三维空间的组合,可能存在 230种空间群(分属于32种点群)
原子半径(atomic radius) R
配位数(coordination number)
致密度(Efficiency of space filling)
N
K
nv
n 4 R3
3
VV
轴比(axial ratio) c/a
堆垛(Stacking) 密排结构(close-packed crystal structure) 最密排面(close-packed plane of atoms) fcc {1 1 1} ABCABCABC······ hcp{0 0 0 1} ABABABAB······
晶系
三斜Triclinic a≠b≠c ,α≠β≠γ
材料科学基础-第2章

a b c,
90o
13
14种Bravais点阵
3. 正交Orthorhombic: 简单正交 (4) 底心正交 (5) 体心正交 (6) 面心正交 (7)
a b c,
90
o
14
14种Bravais点阵
4. 六方Hexagonal:
简单六方(8)
a x
O
b
y
点阵矢量
ruvw ua vb wc
11
7种晶系,14种布拉菲Bravais点阵
晶系 Crystal systems 点阵参数 Lattice parameters 布拉维点阵类型 Types of Bravais lattice 简单三斜(1) 简单单斜(2) 底心单斜(3) 简单正交(4) 底心正交(5) 体心正交(6) 面心正交(7) 简单六方(8) 实例 Instances K2CrO7 -S CaSO4•H2O Fe3C Ga -S Mg, Zn Cd, Ni, As As, Sb, Bi -Sn, TiO2 Fe, Cr, Cu, Ag, Ni,V
abc
90
abc
90%以上 的金属具 有立方晶 系和六方 晶系
12
90
14种Bravais点阵
1. 三斜Triclinic :简单三斜(1)
a b c,
90
o
2. 单斜Monoclinic : 简单单斜(2) 底心单斜(3)
(321)取倒数为 0.333,0.5 ,1
Z
(321)
Y
X
(200)、(333)等是否存在? 具有公因子的晶面不存在
2 《材料科学基础》第二章 晶体结构(下)

思考题
Ca2+:000,½ ½ 0,½ 0 ½ ,0 ½ ½ F
-
:¼ ¼ ¼, ¾ ¾ ¼, ¾ ¼ ¾, ¼ ¾ ¾, ¾ ¾ ¾, ¼ ¼ ¾, ¼ ¾ ¼, ¾ ¼ ¼
思考题:
据晶体结构简要解释:
•为什么CaF2比NaCl容易形成弗仑克尔缺陷?
•为什么萤石结构中一般存在着负离子扩散机制?
了解
Al3+的分布原则符合鲍林规则:在同一层
和层与层之间, Al3+之间的距离应保持
最远。
空隙
α-Al2O3中的氧与铝的排列次序可写成: OAAlDOBAlEOAAlFOBAlDOAAlEOBAlFOAAlD……6层一个周期
Al3+的CN=6, Z=
O2-的CN= 4
2
属于刚玉型结构的晶体:
• 硅酸盐结构的特点:
2/3八面体间隙(A、B) 1/2八面体间隙(A) l/8四面体间隙(B) 全部立方体中心 1/2立方体中心
尖晶石
反尖晶石 纤锌矿 砷化镍 刚 玉 钛铁矿 橄榄石 氯化铯 萤 石 硅石型
二、硅酸盐晶体结构
1. 岛状结构
2. 组群状结构
3. 链状结构 4. 层状结构 5. 架状结构
•硅酸盐晶体的组成表征:
4:6:4AB2O4
4:6:4B(AB)O4 4:4MO 6:6MO 6:4M2O3 6:6:4ABO3 6:4:4A2BO4 8:8MO 8:4MO2 4:2MO2
1/8四面体间隙(A) 1/2八面体间隙(B) 1/8四面体间隙(B) 1/2八面体间隙(A、B) 1/2四面体间隙 全部八面体间隙 2/3八面体间隙
8
性质:硬度最高、极好的导热性、具半导体性能 与其结构相同的有硅、锗、灰锡、合成立方氮化硼等
材料科学基础-2

[111 ]
[ 1 11]
[1 1 1]
[1 1 1]
[11 1 ]
[1 1 1]
[1 1 1]
[1 1 1]
例:在一个面心立方晶胞中画出[012]、[123] 晶向。
晶面:通过空间点阵中任一组阵点的平面代表晶 体中的原子平面,称为晶面 晶面指数:表示晶体中点阵平面的指数,由晶面 与三个坐标轴的截距值所决定。 晶面指数的标定步骤: 建坐标:所定晶面不应通过原点; 求截距:求出待定晶面在三个坐标轴上的截距, 如果该晶面与某坐标轴平行,则其截距为∞; 取倒数:取三个截距值的倒数; 化整并加圆括号:将三个截距的倒数化为最小 整数h、k、l,并加圆括号,即(hkl),如果截距 为负值,则在负号标注在相应指数的上方。
正交
三、晶向指数与晶面指数(Miller指数)
晶向:空间点阵中各阵点列的方向代表晶体中原子排列的 方向,称为晶向,即空间点阵中任意两阵点的连接矢量。 晶向指数:表示晶体中点阵方向的指数。 晶向指数的确定步骤:
z
[ 1 11]
[112] • 建立坐标系; • 确定坐标值:在待定晶向上确定 [1 1 1] [1 1 0] 距原点最近的一个阵点的三个坐标值; • 化整并加方括号:将三个坐标值化为最小 [001] [111] 整数u、v、w,并加方括号。如有负值,在 [010] o 该数值上方标负号。 [100] [110]
• 在立方晶系中,具有相同指数的晶面和晶向 必定相互垂直。不适合其它晶系。 如: [121] (121) 即:晶向 [121] 为晶面 (121)的法向量。 ★ 因此,晶面指数可作为向量进行运算。
例:在一个面心立方晶胞中画出(102)、 (223) 晶面。
六方晶系的晶向指数和晶面指数
[ 1 11]
[1 1 1]
[1 1 1]
[11 1 ]
[1 1 1]
[1 1 1]
[1 1 1]
例:在一个面心立方晶胞中画出[012]、[123] 晶向。
晶面:通过空间点阵中任一组阵点的平面代表晶 体中的原子平面,称为晶面 晶面指数:表示晶体中点阵平面的指数,由晶面 与三个坐标轴的截距值所决定。 晶面指数的标定步骤: 建坐标:所定晶面不应通过原点; 求截距:求出待定晶面在三个坐标轴上的截距, 如果该晶面与某坐标轴平行,则其截距为∞; 取倒数:取三个截距值的倒数; 化整并加圆括号:将三个截距的倒数化为最小 整数h、k、l,并加圆括号,即(hkl),如果截距 为负值,则在负号标注在相应指数的上方。
正交
三、晶向指数与晶面指数(Miller指数)
晶向:空间点阵中各阵点列的方向代表晶体中原子排列的 方向,称为晶向,即空间点阵中任意两阵点的连接矢量。 晶向指数:表示晶体中点阵方向的指数。 晶向指数的确定步骤:
z
[ 1 11]
[112] • 建立坐标系; • 确定坐标值:在待定晶向上确定 [1 1 1] [1 1 0] 距原点最近的一个阵点的三个坐标值; • 化整并加方括号:将三个坐标值化为最小 [001] [111] 整数u、v、w,并加方括号。如有负值,在 [010] o 该数值上方标负号。 [100] [110]
• 在立方晶系中,具有相同指数的晶面和晶向 必定相互垂直。不适合其它晶系。 如: [121] (121) 即:晶向 [121] 为晶面 (121)的法向量。 ★ 因此,晶面指数可作为向量进行运算。
例:在一个面心立方晶胞中画出(102)、 (223) 晶面。
六方晶系的晶向指数和晶面指数
材料科学基础课件第二章--晶体结构

16
小结
1. 晶体结构是指晶体中原子或分子的排列情况,由空间点阵 与结构基元构成,晶体结构的形式是无限多的。
2. 空间点阵是把晶体结构中原子或分子等结构基元抽象为周
围环境相同的阵点之后,描述晶体结构的周期性和对称性的
图像。
17
2.1.2 晶向指数和晶面指数
(1) 晶向指数 晶向(crystal directions)—通 过晶体中任意两个原子中心连 成直线来表示晶体结构的空间 的各个方向。
些晶向可归为一个晶向族,用〈uvw〉表示。如
〈111〉 晶 向 族 包 括 [111] 、 [T11] 、 [1T1] 、 [11T] 、 [TT1]、[1TT]、[T1T]、[TTT];〈100〉晶向族包括 [100]、[010]、[001]、[T00]、[0T0]、[00T] 。
(4)同一晶向族中晶向上原子排列因对称关系而等同。
范德华键的特点及典型的分子晶体的性质:
范德华键(分子键)是通过“分子力”而产生的键合。分子力 包括三种力:葛生力(Keesen force)──极性分子中的固有 偶极矩产生的力,德拜力(Debye force)──感应偶极矩产生 的力,即极性分子和非极性分子之间的作用力,伦敦力 (London force)──非极性分子中的瞬时偶极矩产生的力。 当分子力不是唯一的作用力时,它们可以忽略不计。
2 晶体结构
晶体:物质是由原子、分子或离子按一定的空间 结构排列所组成的固体,其质点在空间的分布具 有周期性和对称性,因而晶体具有规则的外形。
1
晶体的宏观特征
石英
硫
2
钠长石 Na[AlSi3O8]
绿柱石 Be3Al2(SiO3)6
3
祖母绿Be3Al2[Si6O18]
小结
1. 晶体结构是指晶体中原子或分子的排列情况,由空间点阵 与结构基元构成,晶体结构的形式是无限多的。
2. 空间点阵是把晶体结构中原子或分子等结构基元抽象为周
围环境相同的阵点之后,描述晶体结构的周期性和对称性的
图像。
17
2.1.2 晶向指数和晶面指数
(1) 晶向指数 晶向(crystal directions)—通 过晶体中任意两个原子中心连 成直线来表示晶体结构的空间 的各个方向。
些晶向可归为一个晶向族,用〈uvw〉表示。如
〈111〉 晶 向 族 包 括 [111] 、 [T11] 、 [1T1] 、 [11T] 、 [TT1]、[1TT]、[T1T]、[TTT];〈100〉晶向族包括 [100]、[010]、[001]、[T00]、[0T0]、[00T] 。
(4)同一晶向族中晶向上原子排列因对称关系而等同。
范德华键的特点及典型的分子晶体的性质:
范德华键(分子键)是通过“分子力”而产生的键合。分子力 包括三种力:葛生力(Keesen force)──极性分子中的固有 偶极矩产生的力,德拜力(Debye force)──感应偶极矩产生 的力,即极性分子和非极性分子之间的作用力,伦敦力 (London force)──非极性分子中的瞬时偶极矩产生的力。 当分子力不是唯一的作用力时,它们可以忽略不计。
2 晶体结构
晶体:物质是由原子、分子或离子按一定的空间 结构排列所组成的固体,其质点在空间的分布具 有周期性和对称性,因而晶体具有规则的外形。
1
晶体的宏观特征
石英
硫
2
钠长石 Na[AlSi3O8]
绿柱石 Be3Al2(SiO3)6
3
祖母绿Be3Al2[Si6O18]
大学材料科学基础第2章 材料中的晶体结构PPT课件

30.10.2020
DALIAN JIAOTONG UNIVERSITY
21
2.点阵常数
晶胞棱边长度a、b、c与原子半径r之间 的关系:
体心立方结构(a=b=c) a = 4 (√3 /3) r
面心立方结构(a=b=c) a = 2 (√2 ) r 密排六方结构(a=b c) a = 2r
30.10.2020
阵点——构成空间点阵的每一个点
晶格——将阵点用一系列相互平行的直线连接 起来形成空间格架
晶胞——构成晶格的最基本单元
30.10.2020
DALIAN JIAOTONG UNIVERSITY
2
图2-1 晶体结构 a) 晶体 b) 晶格 c) 晶胞
30.10.2020
DALIAN JIAOTONG UNIVERSITY
式中, Ni 、 Nf 、 Nr分别表示位于晶胞内部、 面心和角顶上的原子数;m为晶胞类型参数, 立方晶系的m = 8,六方晶系的m =6。 体心立方 N = 1 + 81/8 = 2 面心立方 N = 6 1/2+ 81/8 = 4 密排六方 N = 3 + 2 1/2+ 121/6 = = 6
10
晶向指数间的关系
① 一个晶向指数代表着相互平行、方向一致的所有晶向; ② 若晶体中两晶向相互平行但方向相反,则晶向指数中的数
字相同,而符号相反。 ③晶向族——晶体中原子排列情况相同但空间位向不同的一
组晶向称为,用<UVW>表示。
立方晶系:<111> =
非立方晶系: <100> [100]、[010]、[001],因为在这三个 晶向上的原子间距分别为a、b、c,其上的原子排列情况 不同,性质亦不同,所以不能属于同一晶向族。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Na-Cl八面体共棱相连接而成。
•投影法
•布拉维格子 法
属于NaCl型结构的晶体很多,见下表。
4、CsCl型结构
化学式: CsCl
空间群:Pm3m 晶格参数:a0=0.411nm 结构:立方原始 格子
Cl-处于立方原始格子的八个角顶上,Cs+位于立方体中心, Cl-和 Cs+的CN均为8 。
Cl-做简单立堆方积, Cs+ 充填于 的全部 立中方,体阴空、隙阳离子配位数均
空间群: Fd3m; 晶格参数: a0=0.356nm
结构: 立方面心格子.
架状结构。碳原子位于立方面心的所有结点位置和交替分布在立 方体内四个1/8小立方体的中心;每个碳原子周围都有4个碳,碳 原子之间形成共价键。
晶胞中原子数Z= 8
性质:硬度最高、极好的导热性、具半导体性能 与其结构相同的有硅、锗、灰锡、合成立方氮化硼等
了解
8、金红石型结构
化学式:TiO2 空间群: P42/mnm 结构:四方原始格子
Ti4+位于四方原始格子结点位置,体中心Ti4+自成另一套四方原始格 子,O2-处于特定位置 O2-近似六方紧密堆积,Ti4+位于1/2的八面体空隙中,正负离子的 配位数分别是 6 和 3 。 Ti-O八面体以共棱方式排成链状,晶胞中心的链和四角的Ti-O八 面体链的排列方向相差90°,链与链之间是Ti-O八面体以共顶相连 Z=2 属于金红石型结构的晶体有:SnO2、PbO2、MnO2、MoO2、 WO2、MnF2、 MgF2、VO2
§2.3 无机非金属材料的晶体结构
一、典 型 结 构 类 型 二、硅酸盐晶体结构
12
整体概况
+ 概况1
您的内容打在这里,或者通过复制您的文本后。
概况2
+ 您的内容打在这里,或者通过复制您的文本后。
概况3
+ 您的内容打在这里,或者通过复制您的文本后。
一、典 型 结 构 类 型
1. 金刚石结构
7. 萤石型结构
S2-位于立方面心的结点位置,而Zn2+交错地分布于立方体内四个 1/8小立方体的中心。阴、阳离子的CN均4为 。
S2-做立方最紧堆密积,则Zn2+充填于 的1/2 空四隙面中体。阴、阳离子的 CN均为 。 4
Z=4
属于闪锌矿型结构的晶体:-SiC, GaAs, AlP, InSb等
其他方
S 2- :000, ½ ½ 0, ½ 0 ½, 0 ½ ½ Zn2+:¼ ¼ ¾ , ¼ ¾ ¼ , ¾ ¼ ¼ , ¾ ¾ ¾
为。
8
单位晶胞中的“分子”数Z=1
属于CsCl型结构的晶体:CsBr、CsI、NH4Cl
离子坐标:Cs+—½ ½ ½ ; Cl-—0 0 0
静电价规则
5、β-ZnS(闪锌矿)型结构 利用化学分子式 球数:四空:八空=1:2:1
化学式: ZnS
空间群: F44 3m
结构: 立方面格心子
静电平衡 Z- = Si = Z+/n
金刚石的各种晶体结构模型
摩氏硬度计
热导仪
2、石墨结构
化学式: C
空间群:P63/mmc, 晶格参数:a0=0.146nm,c0=0.670nm
结构:六方原始格子
层状结构。层内碳原子呈六方环状排列,每个碳原子与三个碳原 子以共价键相连;层间为分子键相连。
性质:碳原子有一个电子可以在层内移动,类似于金 属中的自由电子,平行层的方向具硬度低,有润滑感;良 好导电性; 石墨和金刚石是碳的两种同质多象变体。 人工合成的六方氮化硼与石墨结构相同。
举例说明结构对性能的影响。(C) 举例说明同质多晶现象。(C)
石墨烯- 2010年诺贝尔物理学奖
巴基球(C60)
巴基管(碳纳米管)
富勒烯家族-1996年诺贝尔化学奖
3、NaCl型结构
化学式: NaCl
空间群:Fm3m 晶格参数:a0=0.563nm
结构:立方面心 格子
Cl-做 立方最紧堆密积,Na+充填于
为。
6
的全部
八中面,体阴空、隙阳离子配位数均
单位晶胞中的“分子”数Z4=
空隙
其他方 法
描述晶体结构的方法:
坐标法 Cl-:000, ½ ½ 0, ½ 0 ½ , 0 ½ ½ Na+:00½,½00,0 ½ 0, ½ ½ ½ 球体密堆积法 Cl-按立方最紧密堆积方式堆积,Na+充填于 全部八面体空隙中,阴、阳离子配位数均为6 。 配位多面体连接法
结构:立方面心格子 Ca2+位于立方面心的结点上,F-位于立方体内八个1/8小立方体的中
心
立方紧密
全部 四面体
▪Ca2+做
8堆积 4,F-充填于 的 空隙。 正负离子的配位数分
别是 和简单。立方
1/2 立方体
▪ F-作
堆积,CCaa-2+F填立充方体共的棱相连空隙。
配4位多面体连接法: Z=
属于萤石型结构的晶体有: BaF2、PbF2、SnF2、CeO2、ThO2、UO2等 反萤石型结构:晶体结构与萤石完全相同,只是阴、阳离子位置完全互
坐标法
结构俯视图,数字为标高,0为 底面位置,25、50、75分别为
晶胞1/4、1/2、3/4的标高
投影法
Zn-S四面体以 共顶方式相连
配位多面体连接法 准 备
六方紧密堆积中空隙的位置和数量
6、α-ZnS(纤锌矿)型结构
化学式: ZnS
空间群: P63mc
结构:六方原格始子
S2-做六方最紧堆密积,Zn2+充填于 的1/2 空四隙面中体,阳离子和阴离子的
配位数都是 。
4
S2- :
Z= 2
4*1/6+4*1/12+1=2
属于纤锌矿型结构的晶体有:BeO、ZnO、A2lN*1等/3+Zn22*+1:/6+1=2
S2- :000, 2/3 1/3 1/2 Zn2+ :00u, 2/3 1/3 (u-1/2),其中u=0.875
书改错
7、萤石型结构
化学式: CaF2 空间群结构
8. 金红石型结构 Ax2型结构 9. 碘化镉型结构
4. CsCl型结构 AX型结构 10. 刚玉型结构 A2X3型结构
5. 闪锌矿型结构
11. 钙钛矿型结构 ABO3型结构
6. 纤锌矿型结构
12. 尖晶石型结构 AB2O4型结构
复习对称要
化学式: C
1、金刚石结构
换。如Li2O、Na2O、K2O等。
思考题
Ca2+:000,½ ½ 0,½ 0 ½ ,0 ½ ½ F - :¼ ¼ ¼, ¾ ¾ ¼, ¾ ¼ ¾, ¼ ¾ ¾, ¾ ¾ ¾, ¼ ¼ ¾, ¼ ¾ ¼, ¾ ¼ ¼
思考题:
据晶体结构简要解释: •为什么CaF2比NaCl容易形成弗仑克尔缺陷? •为什么萤石结构中一般存在着负离子扩散机制?
•投影法
•布拉维格子 法
属于NaCl型结构的晶体很多,见下表。
4、CsCl型结构
化学式: CsCl
空间群:Pm3m 晶格参数:a0=0.411nm 结构:立方原始 格子
Cl-处于立方原始格子的八个角顶上,Cs+位于立方体中心, Cl-和 Cs+的CN均为8 。
Cl-做简单立堆方积, Cs+ 充填于 的全部 立中方,体阴空、隙阳离子配位数均
空间群: Fd3m; 晶格参数: a0=0.356nm
结构: 立方面心格子.
架状结构。碳原子位于立方面心的所有结点位置和交替分布在立 方体内四个1/8小立方体的中心;每个碳原子周围都有4个碳,碳 原子之间形成共价键。
晶胞中原子数Z= 8
性质:硬度最高、极好的导热性、具半导体性能 与其结构相同的有硅、锗、灰锡、合成立方氮化硼等
了解
8、金红石型结构
化学式:TiO2 空间群: P42/mnm 结构:四方原始格子
Ti4+位于四方原始格子结点位置,体中心Ti4+自成另一套四方原始格 子,O2-处于特定位置 O2-近似六方紧密堆积,Ti4+位于1/2的八面体空隙中,正负离子的 配位数分别是 6 和 3 。 Ti-O八面体以共棱方式排成链状,晶胞中心的链和四角的Ti-O八 面体链的排列方向相差90°,链与链之间是Ti-O八面体以共顶相连 Z=2 属于金红石型结构的晶体有:SnO2、PbO2、MnO2、MoO2、 WO2、MnF2、 MgF2、VO2
§2.3 无机非金属材料的晶体结构
一、典 型 结 构 类 型 二、硅酸盐晶体结构
12
整体概况
+ 概况1
您的内容打在这里,或者通过复制您的文本后。
概况2
+ 您的内容打在这里,或者通过复制您的文本后。
概况3
+ 您的内容打在这里,或者通过复制您的文本后。
一、典 型 结 构 类 型
1. 金刚石结构
7. 萤石型结构
S2-位于立方面心的结点位置,而Zn2+交错地分布于立方体内四个 1/8小立方体的中心。阴、阳离子的CN均4为 。
S2-做立方最紧堆密积,则Zn2+充填于 的1/2 空四隙面中体。阴、阳离子的 CN均为 。 4
Z=4
属于闪锌矿型结构的晶体:-SiC, GaAs, AlP, InSb等
其他方
S 2- :000, ½ ½ 0, ½ 0 ½, 0 ½ ½ Zn2+:¼ ¼ ¾ , ¼ ¾ ¼ , ¾ ¼ ¼ , ¾ ¾ ¾
为。
8
单位晶胞中的“分子”数Z=1
属于CsCl型结构的晶体:CsBr、CsI、NH4Cl
离子坐标:Cs+—½ ½ ½ ; Cl-—0 0 0
静电价规则
5、β-ZnS(闪锌矿)型结构 利用化学分子式 球数:四空:八空=1:2:1
化学式: ZnS
空间群: F44 3m
结构: 立方面格心子
静电平衡 Z- = Si = Z+/n
金刚石的各种晶体结构模型
摩氏硬度计
热导仪
2、石墨结构
化学式: C
空间群:P63/mmc, 晶格参数:a0=0.146nm,c0=0.670nm
结构:六方原始格子
层状结构。层内碳原子呈六方环状排列,每个碳原子与三个碳原 子以共价键相连;层间为分子键相连。
性质:碳原子有一个电子可以在层内移动,类似于金 属中的自由电子,平行层的方向具硬度低,有润滑感;良 好导电性; 石墨和金刚石是碳的两种同质多象变体。 人工合成的六方氮化硼与石墨结构相同。
举例说明结构对性能的影响。(C) 举例说明同质多晶现象。(C)
石墨烯- 2010年诺贝尔物理学奖
巴基球(C60)
巴基管(碳纳米管)
富勒烯家族-1996年诺贝尔化学奖
3、NaCl型结构
化学式: NaCl
空间群:Fm3m 晶格参数:a0=0.563nm
结构:立方面心 格子
Cl-做 立方最紧堆密积,Na+充填于
为。
6
的全部
八中面,体阴空、隙阳离子配位数均
单位晶胞中的“分子”数Z4=
空隙
其他方 法
描述晶体结构的方法:
坐标法 Cl-:000, ½ ½ 0, ½ 0 ½ , 0 ½ ½ Na+:00½,½00,0 ½ 0, ½ ½ ½ 球体密堆积法 Cl-按立方最紧密堆积方式堆积,Na+充填于 全部八面体空隙中,阴、阳离子配位数均为6 。 配位多面体连接法
结构:立方面心格子 Ca2+位于立方面心的结点上,F-位于立方体内八个1/8小立方体的中
心
立方紧密
全部 四面体
▪Ca2+做
8堆积 4,F-充填于 的 空隙。 正负离子的配位数分
别是 和简单。立方
1/2 立方体
▪ F-作
堆积,CCaa-2+F填立充方体共的棱相连空隙。
配4位多面体连接法: Z=
属于萤石型结构的晶体有: BaF2、PbF2、SnF2、CeO2、ThO2、UO2等 反萤石型结构:晶体结构与萤石完全相同,只是阴、阳离子位置完全互
坐标法
结构俯视图,数字为标高,0为 底面位置,25、50、75分别为
晶胞1/4、1/2、3/4的标高
投影法
Zn-S四面体以 共顶方式相连
配位多面体连接法 准 备
六方紧密堆积中空隙的位置和数量
6、α-ZnS(纤锌矿)型结构
化学式: ZnS
空间群: P63mc
结构:六方原格始子
S2-做六方最紧堆密积,Zn2+充填于 的1/2 空四隙面中体,阳离子和阴离子的
配位数都是 。
4
S2- :
Z= 2
4*1/6+4*1/12+1=2
属于纤锌矿型结构的晶体有:BeO、ZnO、A2lN*1等/3+Zn22*+1:/6+1=2
S2- :000, 2/3 1/3 1/2 Zn2+ :00u, 2/3 1/3 (u-1/2),其中u=0.875
书改错
7、萤石型结构
化学式: CaF2 空间群结构
8. 金红石型结构 Ax2型结构 9. 碘化镉型结构
4. CsCl型结构 AX型结构 10. 刚玉型结构 A2X3型结构
5. 闪锌矿型结构
11. 钙钛矿型结构 ABO3型结构
6. 纤锌矿型结构
12. 尖晶石型结构 AB2O4型结构
复习对称要
化学式: C
1、金刚石结构
换。如Li2O、Na2O、K2O等。
思考题
Ca2+:000,½ ½ 0,½ 0 ½ ,0 ½ ½ F - :¼ ¼ ¼, ¾ ¾ ¼, ¾ ¼ ¾, ¼ ¾ ¾, ¾ ¾ ¾, ¼ ¼ ¾, ¼ ¾ ¼, ¾ ¼ ¼
思考题:
据晶体结构简要解释: •为什么CaF2比NaCl容易形成弗仑克尔缺陷? •为什么萤石结构中一般存在着负离子扩散机制?
