材料力学-拉、压杆件的变形分析
工程材料力学第四章轴向拉压杆的变形

拉(压)杆的纵向变形 (轴向变形) 基本情况下(等直杆,两端受轴向力):
纵向总变形Δl = l1-l (反映绝对变形量)
l 纵向线应变 (反映变形程度) l
1
fl
f ( x x)
x
f
l
x
x
沿杆长均匀分布 的荷载集度为 f 轴力图
fx
微段的分离体
y
pbd 2b 0
pd 2
13
所以
pd (2 10 Pa)(0.2m) -3 2 2(510 m)
6
4010 Pa 40 MPa
6
14
2.
如果在计算变形时忽略内压力的影响,则可认为
薄壁圆环沿圆环切向的线应变e(周向应变)与径向截面上
的正应力s 的关系符合单轴应力状态下的胡克定律,即
ν
亦即
- n
低碳钢(Q235):n = 0.24~0.28。
7
思考:等直杆受力如图,已知杆的横截面面积A和材料的 弹性模量E。
1.列出各段杆的纵向总变形ΔlAB,ΔlBC,ΔlCD以及整个 杆纵向变形的表达式。
2.横截面B, C及端面D的纵向位移与各段杆的纵向总变
形是什么关系?
uB L1
22
作业:4-7,4-91 Pa ~ 2.101011 Pa 200GPa ~ 210GPa
l 1 FN 胡克定律的另一表达形式: l E A
E
←单轴应力状态下的胡克定律
6
横向变形因数(泊松比)(Poisson’s ratio)
单轴应力状态下,当应力不超过材料的比例极限时,
杆件的四种基本变形

杆件的四种基本变形杆件变形的基本形式有四种,分别是拉伸或压缩、剪切、扭转、弯曲。
根据材料力学的内容,长度远大于截面尺寸的构件称为杆件,杆件的受力有各种情况,相应的变形就有各种形式。
1、拉伸或压缩这类变形就是由大小成正比方向恰好相反,力的促进作用线与杆件轴线重合的一对力引发的。
在变形上整体表现为杆件长度的弯曲或延长。
横截面上的内力称作轴力。
横截面上的形变原产为沿着轴线逆向的也已形变。
整个横截面形变对数成正比。
2、剪切这类变形就是由大小成正比、方向恰好相反、力的促进作用线相互平行的力引发的。
在变形上整体表现为受剪杆件的两部分沿外力作用方向出现相对错动。
横截面上的内力称作剪力。
横截面上的形变原产为沿着杆件横截面平面内的的乌形变。
整个横截面形变对数成正比。
3、扭转这类变形就是由大小成正比、方向恰好相反、促进作用面都旋转轴杆轴的两个力偶引发的。
整体表现为杆件上的任一两个横截面出现拖轴线的相对旋转。
横截面上的内力称作扭矩。
横截面上的形变原产为沿着杆件横截面平面内的的乌形变。
越紧邻横截面边缘,形变越大。
4、弯曲这类变形由旋转轴杆件轴线的纵向力,或由涵盖杆件轴线在内的横向平面内的一对大小成正比、方向恰好相反的力偶引发,整体表现为杆件轴线由直线变为曲线。
横截面上的内力称作弯矩和剪力。
在旋转轴轴线的横截面上,弯矩产生旋转轴横截面的也已形变,剪力产生平行于横截面的乌形变。
另外,受弯构件的内力有可能只有弯矩,没剪力,这时称作氢铵抠构件。
越紧邻构件横截面边缘,弯矩产生的也已形变越大。
理论力学中的杆件的变形分析

理论力学中的杆件的变形分析杆件在力学中扮演着重要的角色,广泛应用于各种工程领域。
在理论力学中,对于杆件的变形进行分析是十分重要的,它能帮助工程师和设计师预测和评估结构的性能和可靠性。
本文将介绍杆件的变形分析的基本原理和方法。
1. 弹性变形杆件受到外力作用时,会发生弹性变形。
在弹性变形情况下,杆件会迅速恢复到未受力状态,且不会发生永久形变。
弹性变形是基于胡克定律,即应力与应变成正比。
根据胡克定律,可以得到杆件的弹性形变的方程。
2. 杆件的拉伸和压缩当杆件受到拉伸或压缩作用时,会发生轴向变形。
在理论力学中,我们可以使用材料力学的知识来分析杆件的轴向变形。
拉伸和压缩是杆件最常见的变形形式,例如,建筑物的柱子或者桥梁的支撑杆件都会经历拉伸或压缩。
3. 杆件的弯曲当杆件受到弯曲力矩作用时,会发生弯曲变形。
弯曲是指杆件在垂直于其长度方向上发生形状改变。
在理论力学中,我们可以使用梁的理论来分析杆件的弯曲变形。
通过应力和应变的关系以及几何形状的考虑,可以计算出杆件在弯曲过程中的变形情况。
4. 杆件的扭转当杆件受到扭矩作用时,会发生扭转变形。
扭转是指杆件在一个固定的截面上,某一段杆件相对于其他段发生旋转。
通过扭转变形分析,我们可以计算出杆件在扭转过程中的变形情况。
杆件的变形分析对于在工程设计过程中非常重要。
通过对杆件的变形情况进行准确的分析,可以帮助工程师和设计师了解结构的性能和可靠性。
此外,在设计过程中,合理地选择材料和截面形状也是非常关键的,因为不同的材料和截面形状会直接影响杆件的变形情况。
总之,理论力学中的杆件的变形分析是一个复杂但重要的领域。
它涉及到弹性变形、拉伸和压缩、弯曲和扭转等不同类型的变形。
通过对杆件变形进行准确的分析,可以帮助工程师预测结构的行为,并确保结构的性能和安全性。
对于工程设计和结构优化来说,杆件的变形分析是一项必不可少的工作。
材料力学 杆件的变形计算
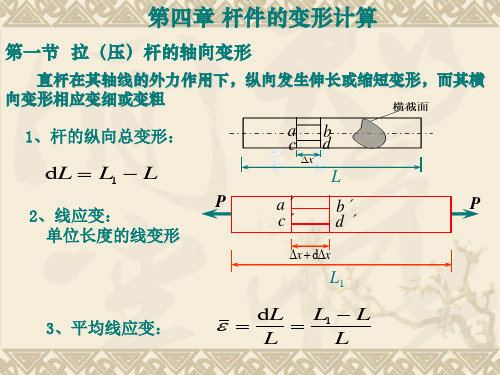
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
材料力学 第2章杆件的拉伸与压缩

第2章 杆件的拉伸与压缩提要:轴向拉压是构件的基本受力形式之一,要对其进行分析,首先需要计算内力,在本章介绍了计算内力的基本方法——截面法。
为了判断材料是否会发生破坏,还必须了解内力在截面上的分布状况,即应力。
由试验观察得到的现象做出平面假设,进而得出横截面上的正应力计算公式。
根据有些构件受轴力作用后破坏形式是沿斜截面断裂,进一步讨论斜截面上的应力计算公式。
为了保证构件的安全工作,需要满足强度条件,根据强度条件可以进行强度校核,也可以选择截面尺寸或者计算容许荷载。
本章还研究了轴向拉压杆的变形计算,一个目的是分析拉压杆的刚度问题,另一个目的就是为解决超静定问题做准备,因为超静定结构必须借助于结构的变形协调关系所建立的补充方程,才能求出全部未知力。
在超静定问题中还介绍了温度应力和装配应力的概念及计算。
不同的材料具有不同的力学性能,本章介绍了塑性材料和脆性材料的典型代表低碳钢和铸铁在拉伸和压缩时的力学性能。
2.1 轴向拉伸和压缩的概念在实际工程中,承受轴向拉伸或压缩的构件是相当多的,例如起吊重物的钢索、桁架第2章 杆件的拉伸与压缩 ·9··9·2.2 拉(压)杆的内力计算2.2.1 轴力的概念为了进行拉(压)杆的强度计算,必须首先研究杆件横截面上的内力,然后分析横截面上的应力。
下面讨论杆件横截面上内力的计算。
取一直杆,在它两端施加一对大小相等、方向相反、作用线与直杆轴线相重合的外力,使其产生轴向拉伸变形,如图2.2(a)所示。
为了显示拉杆横截面上的内力,取横截面把m m −拉杆分成两段。
杆件横截面上的内力是一个分布力系,其合力为N F ,如图2.2(b)和2.2(c)所示。
由于外力P 的作用线与杆轴线相重合,所以N F 的作用线也与杆轴线相重合,故称N F 为轴力(axial force)。
由左段的静力平衡条件0X =∑有:()0+−=N F P ,得=N F P 。
工程力学(材料力学)6拉压杆件的强度与变形问题

机械制造中的拉压杆件
机械制造中的拉压杆件主要用于 实现运动传递、力的传递和变形 等,如连杆、活塞杆、传动轴等。
这些杆件需要在高速、高温、重 载等极端条件下工作,因此需要 具备优异的力学性能和耐久性。
在机械制造中,拉压杆件的设计 和制造需要精确控制尺寸、形状 和材料,以确保其工作性能和可
靠பைடு நூலகம்。
其他工程领域中的拉压杆件
总结词
新型材料如碳纤维复合材料、钛合金等具有高强度、轻质等优点,在拉压杆件中得到广 泛应用。
详细描述
随着科技的不断发展,新型材料如碳纤维复合材料、钛合金等逐渐应用于拉压杆件的制 作。这些新型材料具有高强度、轻质、耐腐蚀等优点,能够提高杆件的力学性能和使用
寿命。
高性能的拉压杆件设计
总结词
通过优化设计,可以显著提高拉压杆件的性能。
刚度分析
对杆件的刚度进行分析, 可以确定其变形程度和承 载能力,为结构设计提供 依据。
拉压杆件的稳定性问题
稳定性定义
01
稳定性是指杆件在受到载荷作用时,保持其平衡状态的能力。
稳定性分析
02
通过稳定性分析,可以确定杆件在受到载荷作用时是否会发生
失稳现象,以及失稳的临界载荷。
稳定性要求
03
在工程应用中,杆件的稳定性需要满足一定的要求,以保证结
强度失效准则
当拉压杆件内部的应力达到或超过材料的屈服极限时,杆件会发生屈服失效, 丧失承载能力。
拉压杆件的强度计算
静力分析
根据外力的大小和方向,以及杆件的几何尺寸和材料属性,计算杆件内部的应力 分布。
动力分析
考虑动载荷的影响,分析杆件在振动、冲击等动态过程中的应力变化。
拉压杆件的强度校核
拉压杆应力、变形分析

通过这些数学模型,可以计算出在给定外力作用下物体的应 力和变形,从而对物体的力学性能进行评估。
应力与变形的实验验证
为了验证应力与变形的数学模型的正确性和可靠性,需要 进行实验验证。
实验中,可以通过测量物体的应力和变形数据,与数学模 型计算结果进行对比,以评估模型的准确性和适用范围。
05 拉压杆的优化设计
实验结果表明,拉压杆的应力分布不均匀,呈现 中间大、两端小的趋势。变形则表现为杆件中部 向下弯曲,两端向上翘起。
本研究采用有限元分析方法对拉压杆进行应力、 变形分析,得到了与实验结果较为一致的分析结 果,验证了有限元方法的可行性和有效性。
研究展望
虽然本研究取得了一定的成 果,但仍有许多问题需要进 一步探讨。例如,可以考虑 研究不同材料属性、不同截 面形状和不同边界条件等因 素对拉压杆应力、变形的影 响。
基于应力的优化设计
总结词
在基于应力的优化设计中,主要目标 是减小拉压杆的最大应力值,使其不 超过材料的许用应力。
详细描述
通过调整拉压杆的截面尺寸、长度、 材料等参数,可以改变其应力分布和 大小。常用的方法包括有限元分析和 数学优化算法。
基于变形的优化设计
总结词
基于变形的优化设计旨在减小拉压杆 的最大变形量,以确保其在工作过程 中具有良好的性能和精度。
根据应力的性质,可分为 拉应力和压应力;根据应 力的分布,可分为均匀应 力和非均匀应力。
应力状态
描述杆件内部各点的应力 状态,包括正应力和剪应 力。
拉压杆应力计算
轴向拉压杆
通过材料力学中的胡克定律计算拉压 杆的应力。
弯曲梁
扭转变形
利用扭矩和剪切模量计算扭转变形的 应力。
利用弯矩和剪力计算弯曲梁的应力。
材料力学之四大基本变形

WZ
IZ ymax
一、变形几何关系
( y)d d y
d
d
y
z
y
dx
y
CL8TU3-2
bh3
bh2
I Z 12 , WZ 6
d4
I Z 64
d3
, WZ 32
IZ
(D4 d 4)
64
D4
64
(1 4 )
WZ
D3
32
(1 4 )
(1)求支座反力
M A 0, M 0 RBl 0 M B 0, RAl M 0 0
(2)列剪力方程和弯矩方程
RB
M0 l
RA
M0 l
AC段 :
Q1
RA
M0 l
M1
RA x
M0 l
x
(0 x a)
CB段 :
Q2
返回
例3-1: 传动轴如图所示,转速 n = 500转/分钟,主动轮B输入功率NB= 10KW,A、 C为从动轮,输出功率分别为 NA= 4KW , NC= 6KW,试计算该轴的扭矩。
先计算外力偶矩
A
B
C x
mA
9550
NA n
9550 4 500
76.4Nm
mB
9550 NB n
9550 10 500
四大基本变形复习
1.轴向拉伸与压缩 2.剪切 3.扭转 4.弯曲
1.轴向拉压
受力特征:受一对等值、反向的纵向力,力的作用线与杆轴线 重合。 变形特征:沿轴线方向伸长或缩短,横截面沿轴线平行移动
材料力学第6章拉压杆件的应力变形分析与强度设计

解:首先分析钢杆和铝筒的受力:钢杆BC承受拉伸,铝筒承受 压缩。C点的位移等于钢杆的伸长量与铝筒的压缩量之和:
Rigid plate
F´P B
FP AsB Ea
Aa Es
Fixed rigid plate
A
FP
l l
C F´P
第2类习题 变形计算
长为1.2m、横截面面积为1.10×10-3m2的铝制筒放置在固定刚块上,直径 为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上,若二者轴线重合、载荷作 用线与轴线一致,且已知钢和铝的弹性模量分别为Es = 200GPa,Ea = 70GPa, FP = 60kN。试求钢杆上C处位移。
50mm。求铝板与钢板横截面上的最大正应力。
steel aluminum
Rigid plate
FNs
Es As Es As Ea Aa
FP
FNa
Ea Aa Es As Ea Aa
FP
TSINGHUA UNIVERSITY
1.复合材料柱横截面上正应力与FP、b0、b1、h和Ea、Es之间的关系式
图示由铝板和钢板组成的复合材料柱,纵向截荷FP通过刚性平板沿着柱的中心线施加 在其上。试:
1.导出复合材料柱横截面上正应力与FP、b0、b1、h和Ea、Es之间的关系式; 2.已知FP = 385kN;Ea = 70GPa,Es = 200GPa;b0 = 30mm,b1 = 20mm,h =
50mm。求铝板与钢板横截面上的最大正应力。
铝板
a
FNa EaFP
Aa
b0hsE2b1haE
钢板
s A F s N sE sb 0 h E sE F P a2 b 1 hb 0 hs E E sF 2 P b 1 haE
材料力学轴向拉伸和压缩第2节 杆的变形

一、纵向变形和线应变的概念
纵向变形
l l1l
纵向变形反映的是与杆件原长有关的绝对变形。
为了消除杆件原长度的影响,采用单位长度的变
形量来度量杆件的变形程度,称为纵向线应变,用
(3)计算各段杆的线应变
1
l1 l1
3.05 10 4
2
l2 l2
2.04 10 4
3
l3 l3
3.93 104
1
2
3
1
2
3
解(1)作轴力图
1
2
3
FN1 30kN
FN2 FN3 20kN
1
2
3
(2)计算纵向变形
l1
FN1l1 EA1
7.33105 m
l1 7.33 105 m l2
l3
FN3l3 EA3
1.18 104 m
FN 2l2 EA2
4.89 10 5 m
实验测定。
表2-1 几种常用材料的 E 和 的值
材料名称
铸铁 碳钢 合金钢 铝合金
铜
弹性模量 E(GPa)
80~160 196~216 206~216 70~72 100~120
泊松比
0.23~0.27 0.24~0.28 0.25~0.30 0.26~0.33 0.33~0.35
例2-3 钢制阶梯杆如图,已知轴向外力F1=50kN, F2 = 20kN,各段杆长为l1 = 150mm,l2 = l3 = 120mm, 截面直径为:d1 =d2 = 600mm,d3 = 300mm,钢的弹性 模量 E = 200GPa。求各段杆的纵向变形和线应变。
拉伸与压缩杆件的应力变形分析与强度计算 (2)

=l AD
l DE
l EB
l BC
= FNADlAD + FNDElDE + FNEBlEB + FNBClBC
Ec AAD
Ec ADE
Es AEB
Es ABC
=1.2106 m 0.6106 m 0.285106 m 0.857 106 m
=1.22810-6 m=1.22810-3 mm
在上述计算中,DE和EB段杆的横截面面积以及轴力虽然 都相同,但由于材料不同,所以需要分段计算变形量。
拉、压杆件的变形分析
a. 等直杆受图 示载荷作用,计算总变形。(各段 EA均相同)
l
n
Nili
i1 EA
1 EA
n
i 1
N
i
li
n
3
Δ l FNili
i EA i
Page 3
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉、压杆件的变形分析
x
Δ
l
l
需要指出的是,上述关于正应变的表达式只适用于杆
Page 10
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
第2章 拉伸与压缩杆件的应力变形分析与强度计算
轴力与轴力图 拉、压杆件横截面上的应力 拉、压杆件的强度设计 拉、压杆件的变形分析 拉伸与压缩时材料的力学性能 结论与讨论
Page 11
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
试求:直杆的总变形量。
Page 8
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
例题6
解:1. 作轴力图 由于直杆上作用有4个轴向 载荷,而且AB段与BC段杆横截 面面积不相等,为了确定直杆 横截面上的最大正应力和杆的 总变形量,必须首先确定各段 杆的横截面上的轴力。
材料力学-课件2-4拉杆的变形.胡克定律

EA L L
L
i
FNiLi
EAi
FN EA L E
A AL
在计算ΔL的L长度内,FN,E,A均 为常数。
在材料的线弹性范围内,正应力与线应变呈正比关系。
2、横向变形
△b=b1-b
b1 b
b
b
横向线应变
泊松比
例题 2.9
图示为一端固定的橡胶板条,若在加力前在 板表面划条斜直线AB,那么加轴向拉力后 AB线所在位置是?(其中ab∥AB∥ce)
α=300,杆长L=2m,杆的直径d=25mm,材
料的弹性模量E=2.1×105MPa,设在结点A处悬
挂一重物F=100kN,试求结点A的位移δA。
1
2
FNAB FNAC
X 0 C Y 0
F N F FN c N A AA C s C o C FiN F s n N AB F N c A 2cA s F B o oB isF n s 0 0
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等,所以上边纤维长,伸长量也大。
例题
2.10
例:图示直杆,其抗拉刚度为EA,试 求杆件的轴向变形△L,B点的位移 δB和C点的位移δC
A L
F
F
B
LAB
FL EA
B
C
L
C
B
FL EA
例题
2.11
图示结构,横梁AB是刚性杆,吊杆CD是等截面直杆,
B点受荷载P作用,试在下面两种情况下分别计算B点的位
拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
材料力学 杆件的变形计算
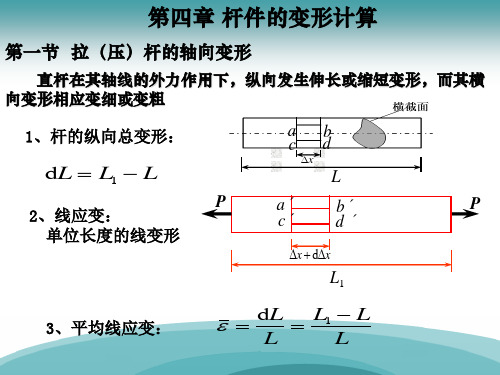
B
30oC2
C
C1
1.44mm
胡:请问,“ 弛其弦,以绳缓援之” 是什么意思 ?
郑:这是讲测量弓力时,先将弓的弦 松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说: 郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
400
400
FN KN 40
2)求伸长量
+
x l l AB lBC
-
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压,AC杆将伸长,而 F BC杆将缩短。
《材料力学》第三章 轴向拉压变形

第三章 轴向拉压变形
*四、温度应力、装配应力 一)温度应力:由温度引起杆变形而产生的应力(热应力) 。 温度引起的变形量—— L tL 1、静定问题无温度应力。 2、超静定问题存在温度应力。 二)装配应力——预应力、初应力:由于构件制造尺寸产生的制造误差,在装配时产生变形而引起的应 力。 1、静定问题无装配应力 2、超静定问题存在装配应力。 轴向拉压变形小结 一、拉压杆的变形(重点) 1、轴向变形:轴向尺寸的伸长或缩短。 2、横向变形:横向尺寸的缩小或扩大。 3、横向变形系数(泊松比) : 4、变形——构件在外力作用下或温度影响下所引起的形状尺寸的变化。 5、弹性变形——外力撤除后,能消失的变形。 6、塑性变形——外力撤除后,不能消失的变形。 3、横向变形系数 7、位移——构件内的点或截面,在变形前后位置的改变量。 8、正应变——微小线段单位长度的变形。
4、求变形: L
FN L EA
LAB
FNAB LAB 240 3.4 104 2.67(m m) EAAB 2.114.54
LCD 0.91mm LEF 1.74mm
5、求位移,变形图如图
LGH 1.63mm
D
LEF LGH DG LGH 1.70 mm EG
第三章 轴向拉压变形
第三章
一、概念 1、轴向变形:轴向尺寸的伸长或缩短。 2、横向变形:横向尺寸的缩小或扩大。 二、分析两种变形
轴向拉压变形
§3—1 轴向拉压杆的变形
b
L F F
b1
L1
1、轴向变形:Δ L=L1-L ,
L L F L (2) 、在弹性范围内: L N A
(1) 、轴向正应变线应变:
《材料力学》2-4拉(压)杆的变形.胡克定律

杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
1、纵向变形
LLL 绝对变形
线应变: 受力物体变形时,一点处沿 某一方向微小线段的相对变 形
当杆沿长度均匀变形时
L L
纵向线应变 (无量纲)
y
C
O
x
A
B
z △x
当杆沿长度非均匀变形时
αD
B1 BB2C1 C
FNCD
F
A
C
a
CC1
CL CCD ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LC FD LFN1 2CEL D A cLC o DsFCD
2Fa
EAcos2
B
4Fa
EAco3s
移δB。1、已经测出CD杆的轴向应变ε;2、已知CD杆 的抗拉刚度EA.
1. 已知ε
LCD
a
LCDa
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B2LCD 2a
2. 已知EA
LCD
FNCDa EA
mA 0
FNCD2F
B 2L 2 LC FN DCD 4EFFAaL0
例题
2.12
B
图示的杆系是由两根圆截面钢杆铰接而成。已知
L AB L AC F N EA L A C 2 EF c A o Ls
A
A AA
L AC
cos
FL
2EAcos2
材料力学中的拉伸与压缩性能分析

材料力学中的拉伸与压缩性能分析材料力学是研究物质在外力作用下的变形和破坏规律的学科,是现代工程学科的重要分支,具有广泛的应用前景。
在材料力学中,拉伸与压缩性能分析是研究材料强度和刚度的重要内容。
一、拉伸性能分析在材料力学中,桥梁、汽车、飞机等工程构件都要承受拉伸应力。
因此,对材料的拉伸强度进行分析是非常重要的。
拉伸性能分析的主要依据是拉伸试验,它是通过将试件铺在拉力试验机的压板上,载荷再逐渐增加,直到材料发生破坏。
在拉伸试验中,材料的应力为拉伸应力,而杆件的横截面积为受力面积。
因此,拉伸强度的计算公式为:σ = F/A其中,σ表示材料的拉伸应力,F表示施加于材料上的拉伸力,A表示杆件的横截面积。
由此可见,拉伸强度与杆件截面积成反比。
此外,还需要考虑拉伸应力引起的材料变形。
材料在受到拉伸载荷时,会发生形变,如图1所示。
当材料受到载荷时,会出现线性区、屈服点、硬化区等不同阶段的变形,这些阶段的变形特征对应不同的应力应变状态。
例如,屈服点就是达到应力最大值的点,之后材料发生残余形变。
因此,材料的拉伸强度应该包括塑性变形的影响。
图1 材料在拉伸过程中的应力应变曲线二、压缩性能分析与拉伸性能分析相似,压缩性能分析也是材料力学中的重要内容。
可以通过压缩试验来实现对材料压缩强度的分析。
压缩性能分析的公式为:σ = F/A其中,F表示受到的压力,A表示受力面积。
压缩强度与杆件横截面积成正比,直接影响杆件的承载能力。
压缩应力会引起材料的变形,抗压强度除了要考虑材料的承载能力,还必须考虑材料的稳定性。
许多材料在受到强压缩应力时容易发生失稳现象,这可能会导致杆件的严重变形,甚至破坏。
因此,在压缩信号中还必须考虑稳定性因素。
三、结论拉伸和压缩都是材料在外应力作用下的形变方式。
在材料力学中对材料的拉伸和压缩性能的准确分析具有重要意义。
拉伸和压缩试验可以通过一个标准进行,以便于比较不同材料之间的强度和刚度。
分析材料的拉伸和压缩性能可以为工程设计提供有效的参考,这也是材料力学研究的重要内容之一。
材料力学教案拉伸与压缩杆件的应力变形分析与强度计算

基础篇之二第2章拉伸与压缩杆件的应力变形分析与强度计算工程结构中的桅杆、旗杆、活塞杆,悬索桥、斜拉桥、网架式结构中的杆件或缆索,以及桥梁结构桁架中的杆件大都承受沿着杆件轴线方向载荷,这种载荷简称我轴向载荷。
承受轴向载荷的杆件将产生拉伸或压缩变形。
承受轴向载荷杆件的材料力学问题包括:杆件横截面上的内力、应力与变形分析与计算;材料的力学行为的实验结果;强度计算以及应变能计算。
这些问题虽然比较简单,但其中的基本概念与基本分析方法则具有普遍意义。
2-1 轴力与轴力图当所有外力均沿杆的轴线方向作用时,杆的横截面上只有轴力F N一种内力分量。
表示轴力沿杆轴线方向变化的图形,称为轴力图(diagram of normal forces)。
为了绘制轴力图,杆件上同一处两侧横截面上的轴力必须具有相同的正负号。
因此约定使杆件受拉的轴力为正;受压的轴力为负。
绘制轴力图的方法与步骤如下:首先,确定作用在杆件上的外载荷与约束力;其次,根据杆件上作用的载荷以及约束力,轴力图的分段点:在有集中力作用处即为轴力图的分段点;第三,应用截面法,用假想截面从控制面处将杆件截开,在截开的截面上,画出未知轴力,并假设为正方向;对截开的部分杆件建立平衡方程,确定轴力的大小与正负:产生拉伸变形的轴力为正,产生压缩变形的轴力为负;最后,建立F N-x坐标系,将所求得的轴力值标在坐标系中,画出轴力图。
【例题2-1】 已知:阶梯形直杆受力如图2-1所示。
试画出其轴力图。
图2-1 例题2-1解:因为在A、B、C、D四处都有集中力作用,所以AB、BC和CD三段杆的轴力各不相同。
应用截面法,在AB、BC和CD三段中容易截面处,分别将杆件截开,并且假设截开的横截面上的轴力均为正方向,即为拉力,如图2-2a所示。
然后分别对截开的三部分应用平衡方程0xF=∑即可确定AB 、BC 和CD 段杆横截面上的轴力,分别为:F N (CD )=200 kN ;F N (BC )=-(300-200)=100 kN ;F N (BC )=500+200-300=400 kN 。
拉压杆的变形

EA称为杆的拉压刚度,它是单位长度的杆产生单位长度的变形 所需的力。所以拉压刚度EA代表了杆件抵抗拉伸(压缩)变形 的能力。
因σ=FN/A、ε=Δl/l,故式(2-5)变为 σ=Eε (2-6
上式是胡克定律的另一表达式。它表明:在弹性限度内,正应力 与线应变成正比。
1.2横向变形
设图2-12所示拉、压杆在变形前、后的横向尺寸分别为d与d1, 则其横向变形Δd为
【例2-6】如图2-14(a)所示等截面直杆,已知 其原长l、横截 面积A、材料的容重γ、弹性模量E、受杆件自重和下端处集中力 F作用。求该杆下端面的位移ΔB。
【解】如图2-14(b)所示。距B端为x的横截面上的轴力为 FN(x)=F+γAx
微段dx如图2-14(c)所示。 略去两端内力的微小差值,则微段的变形为
=-0.975×10-3m=-0.975mm
各段柱的纵向线应变为
εBC=ΔlBC/lBC=-0.5mm/2000mm=2.5×10-4
εAB=ΔlAB/lAB=-0.975mm/1500mm=-6.5×10-4 全柱的总变形为两段柱的变形之和,即
Δl=ΔlBC+ΔlAB=-0.5mm-0.975mm=-1.475 mm
【解】由于上下两段柱的轴力不等,故两段柱 的变形要分别计算。各段柱的轴力为
FNBC=-100 kN 各段柱的纵向变形为
FNAB=-260 kN
ΔlBC=FNBC/EA = -100×103N×2m/10×109Pa× (0.2m)2 =-0.5×10-3m=-0.5mm
图2-13
ΔlAB=FNAB/EA= 260×103N×1.5m/10×109Pa×(0.2m)2
大量的实验表明,当杆的变形为弹性变形时,杆的纵向变形Δl与 外力F及杆的原长l成正比,而与杆的横截面面积A成反比,即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
何斌
Page 19
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉伸与压缩时材料的力学性能
应力-应变曲线 弹性力学性能 极限应力值——强度指标 韧性指标 单向压缩时材料的力学行为
何斌
Page 20
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
极限应力值——强度指标
屈服应力
在许多韧性材料的应力-应变曲线中,在弹性阶段之后,出现近
极限应力值——强度指标
颈缩与断裂
某些韧性材料(例如低碳 钢和铜),应力超过强度极限 以后,试样开始发生局部变 形,局部变形区域内横截面 尺寸急剧缩小,这种现象称 为颈缩(neck)。出现颈缩之后, 试样变形所需拉力相应减小, 应力-应变曲线出现下降阶段, 直至试样被拉断。
Page 24
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
elasticity or Young modulus),用E 表示。
对于应力-应变曲线初始阶段的非直线 段,工程上通常定义两种模量:
切线模量(tangent modulus),即曲线上 任一点处切线的斜率,用Et表示。
割线模量(secant modulus),即自原点 到曲线上的任一点的直线的斜率,用Es表示。
何斌
Page 26
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉伸与压缩时材料的力学性能
应力-应变曲线 弹性力学性能 极限应力值——强度指标 韧性指标 单向压缩时材料的力学行为
何斌
Page 27材料Fra bibliotek学第2章 拉伸与压缩杆件的应力变形·分析与强度计算
韧性指标
通过拉伸试验还可得到衡量材料韧性性能的指标—— 延伸率和截面收缩率:
Ec ADE
Es AEB
Es ABC
=1.2106 m 0.6106 m 0.285106 m 0.857 106 m
=1.22810-6 m=1.22810-3 mm
在上述计算中,DE和EB段杆的横截面面积以及轴力虽然 都相同,但由于材料不同,所以需要分段计算变形量。
何斌
Page 11
材料力学
AAB = 10×102 mm2 , BC 段 杆 的 横 截 面 面 积 ABC = 5×102 mm2;FP=60 kN;铜的弹性模量Ec=100 GPa,钢的弹性 模量Es=210 GPa;各段杆的长度如图中所示,单位为mm。
试求:直杆的总变形量。
何斌
Page 9
材料力学 何斌
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
何斌
Page 7
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
Negative Poisson's ratio
何斌
Page 8
材料力学
例题6
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉、压杆件的变形分析
变截面直杆,ADE段为铜制,EBC段为钢制;在A、D、 B、C等4处承受轴向载荷。已知:ADEB段杆的横截面面积
Page 13
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉伸与压缩时材料的力学性能
应力-应变曲线 弹性力学性能 极限应力值——强度指标 韧性指标 单向压缩时材料的力学行为
何斌
Page 14
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
应力-应变曲线
进行拉伸实验,首先需要将被试验的材料按国家标准制成标准 试样(standard specimen);然后将试样安装在试验机上,使试样承受 轴向拉伸载荷。通过缓慢的加载过程,试验机自动记录下试样所受 的载荷和变形,得到应力与应变的关系曲线,称为应力-应变曲线 (stress-strain curve)。
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
第2章 拉伸与压缩杆件的应力变形分析与强度计算
轴力与轴力图 拉、压杆件横截面上的应力 拉、压杆件的强度设计 拉、压杆件的变形分析 拉伸与压缩时材料的力学性能 结论与讨论
何斌
Page 12
材料力学 何斌
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉伸与压缩时材料的力学性能
GB/T6397-1986《金属拉伸试验试样》
标距 l
d
标距 l
l 10d 或 l 5d
l 11.3 A 或 l 5.65 A
d
何斌
Page 15
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
应力-应变曲线
脆性材料拉伸时的 应力-应变曲线
韧性金属材料拉伸 时的应力-应变曲线
工程塑料拉伸时的 应力-应变曲线
应变硬化
应力超过屈服应力或条 件屈服应力后,要使试样继 续变形,必须再继续增加载 荷。这一阶段称为强化 (strengthening)阶段。这一阶 段应力的最高限称为强度极
限 (strength limit), 用 σb表
示。
Page 23
材料力学 何斌
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
4~5倍。对于拉伸和压缩强
度极限不等的材料,拉伸强
拉、压杆件的变形分析
L
1、轴向变形: ΔL= L1 - L ,
(1)轴向线应变: L
L
L1
(2)虎克定律:
在弹性范围内, (当 p时)
b1 b
E
FN
A
L FN L
l
l
a1 a
(虎克定律的另一种表达方式)
EA
EA-抗拉(压)刚度
l-伸长为正,缩短为负
何斌
Page 3
材料力学
不再成正比关系。但是,如果在这一
阶段,卸去试样上的载荷,试样的变
形将随之消失。 这表明这一阶段内的变形都是弹性变形,因而包括线性弹性阶
段在内,统称为弹性阶段。弹性阶段的应力最高限称为弹性极限
(elastic limit),用σe表示。
大部分韧性材料比例极限与弹性极限极为接近,只有通过精密 测量才能加以区分。
何斌
Page 6
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉、压杆件的变形分析
Simon Denis Poisson Poisson’s ratio (1829)
Foam structures with a negative Poisson's ratio, Science, 235 1038-1040 (1987).
这两种模量统称为工程模量。
Page 18
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
弹性力学性能
比例极限 弹性极限
应力-应变曲线上,线性弹性区段 的应力最高限称为比例极限
(proportional limit),用σp表示。
线性弹性阶段之后,应力-应变
曲线上有一小段微弯的曲线,这表示
应力超过比例极限以后,应力与应变
拉、压杆件的变形分析
x
Δ l l
需要指出的是,上述关于正应变的表达式只适用于杆
件各处均匀变形的情形。
对于各处变形不均匀的情形,
必须考察杆件上沿轴向的微段
dx的变形,并以微段dx的相对变形
作为杆件局部的变形程度。 FPdx
x
Δdx = dx
EA x
dx
x
E
无论变形均匀与否,正应力与正应变的关系都是相同的。
似的水平段,这一阶段中应力几乎不变,而变形急剧增加,这种现 象称为屈服(yield) 。这一阶段曲线的最低点对应的应力值称为屈服
应力或屈服强度(yield stress),用σs表示。
何斌
Page 21
材料力学
0.2
何斌
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
极限应力值——强度指标
条件屈服应力
何斌
Page 5
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉、压杆件的变形分析
2、横向变形:
L
a a1 a, b b1 b
横向线应变: a b
a
b
在弹性范围内:
横向变形系数(泊松比)
L1
b1 b
a1 a
(Poisson ratio) 为材料的另一个弹性常数, 泊松比为无量纲量。
何斌
Page 16
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉伸与压缩时材料的力学性能
应力-应变曲线 弹性力学性能 极限应力值——强度指标 韧性指标 单向压缩时材料的力学行为
何斌
Page 17
材料力学
弹性模量
何斌
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
弹性力学性能
应力-应变曲线上的初始阶段通常都有一直 线段,称为线性弹性区,在这一区段内应力与应 变成正比关系,其比例常数,即直线的斜率称为 材 料 的 弹 性 模 量 ( 杨 氏 模 量 , modulus of
通过拉伸与压缩实验, 可以测得材料在轴向载荷作 用下,从开始受力到最后破 坏的全过程中应力和变形之 间的关系曲线,称为应力- 应变曲线。应力-应变曲线 全面描述了材料从开始受力 到最后破坏过程中的力学行 为。由此即可确定不同材料 发生强度失效时的应力值 (称为强度指标)和表征材 料塑性变形能力的韧性指标。
何斌
Page 28
材料力学
第2章 拉伸与压缩杆件的应力变形·分析与强度计算
拉伸与压缩时材料的力学性能
应力-应变曲线 弹性力学性能 极限应力值——强度指标 韧性指标 单向压缩时材料的力学行为
