第四章 杆件的变形计算
理论力学中的杆件的变形分析

理论力学中的杆件的变形分析杆件在力学中扮演着重要的角色,广泛应用于各种工程领域。
在理论力学中,对于杆件的变形进行分析是十分重要的,它能帮助工程师和设计师预测和评估结构的性能和可靠性。
本文将介绍杆件的变形分析的基本原理和方法。
1. 弹性变形杆件受到外力作用时,会发生弹性变形。
在弹性变形情况下,杆件会迅速恢复到未受力状态,且不会发生永久形变。
弹性变形是基于胡克定律,即应力与应变成正比。
根据胡克定律,可以得到杆件的弹性形变的方程。
2. 杆件的拉伸和压缩当杆件受到拉伸或压缩作用时,会发生轴向变形。
在理论力学中,我们可以使用材料力学的知识来分析杆件的轴向变形。
拉伸和压缩是杆件最常见的变形形式,例如,建筑物的柱子或者桥梁的支撑杆件都会经历拉伸或压缩。
3. 杆件的弯曲当杆件受到弯曲力矩作用时,会发生弯曲变形。
弯曲是指杆件在垂直于其长度方向上发生形状改变。
在理论力学中,我们可以使用梁的理论来分析杆件的弯曲变形。
通过应力和应变的关系以及几何形状的考虑,可以计算出杆件在弯曲过程中的变形情况。
4. 杆件的扭转当杆件受到扭矩作用时,会发生扭转变形。
扭转是指杆件在一个固定的截面上,某一段杆件相对于其他段发生旋转。
通过扭转变形分析,我们可以计算出杆件在扭转过程中的变形情况。
杆件的变形分析对于在工程设计过程中非常重要。
通过对杆件的变形情况进行准确的分析,可以帮助工程师和设计师了解结构的性能和可靠性。
此外,在设计过程中,合理地选择材料和截面形状也是非常关键的,因为不同的材料和截面形状会直接影响杆件的变形情况。
总之,理论力学中的杆件的变形分析是一个复杂但重要的领域。
它涉及到弹性变形、拉伸和压缩、弯曲和扭转等不同类型的变形。
通过对杆件变形进行准确的分析,可以帮助工程师预测结构的行为,并确保结构的性能和安全性。
对于工程设计和结构优化来说,杆件的变形分析是一项必不可少的工作。
材料力学 杆件的变形计算
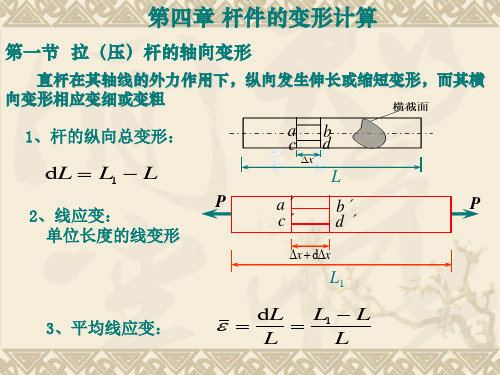
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
杆件的基本变形.

随外力产生或消失 随外力改变而改变 但有一定限度
截 面 法
根据空间任意力系的六个平衡方程
X 0 M
步骤: 1、切开 2、代替
x
Y 0
M
y
Z 0 M
z
0
0
0
求出内力分量
3、平衡
注意:
用截面法求内力和取分离体求约束反力的方法本质 相同。这里取出的研究对象不是一个物体系统或一个完 整的物体,而是物体的一部分。
拉 伸
压 缩
变形特点:杆轴沿外力方向伸长或缩短, 主要变形是长度的改变
屋 架 结 构 中 的 拉 压 杆
塔 式 结 构 中 的 拉 压 杆
桥 梁 结 构 中 的 拉 杆
剪 切 变形
受力特点:由垂直于杆轴方向的一对大小相等、 方向相反、作用线很近的横向外力引起的。
变形特点:二力之间的横截面产生相对错动变形 主要变形是横截面沿外力作用方向发生相对错动。
第四章 杆件的基本变形
杆件的外力与变形特点 内力及其截面杆件在外力作用下,形状和尺寸的变化。 二、杆件变形的形式 1、基本变形 轴向拉伸与压缩 剪切变形 扭转变形 弯曲变形 2、组合变形 同时发生两种或两种以上的变形形式
轴向拉伸或压缩变形
受力特点:作用线与杆轴重合的外力引起的。
螺 栓
连 接 键
销钉
螺 栓
扭 转 变 形
受力特点:由垂直于杆轴线平面内的力偶作用引起的
变形特点:相邻横截面绕杆轴产生相对旋转变形。
对称扳手拧紧镙帽
自 行 车 中 轴 受 扭
桥 体 发 生 扭 转 变 形
关于杆件变形能公式的推导

关于杆件变形能公式的推导杆件变形是指在受到外力作用下,杆件发生形变,这种形变可以用形变能来描述。
形变能是杆件弹性势能的一种表现形式,它是描述杆件形变程度的指标,与外力大小、杆件弹性系数、杆件长度和截面形状等相关。
要推导出杆件变形能公式,可以从杆件受力、应力、应变和势能等方面入手。
首先,杆件变形是由外力作用于杆件上引起的。
杆件在受力作用下会产生应力,应力是单位面积上的力。
杆件上的应变是指杆件在受力作用下,相应的长度变化。
根据胡克定律,应力与应变之间存在线性关系,可以表示为:σ=Eε其中,σ表示应力,E表示杨氏模量,ε表示应变。
接下来,考虑杆件的长度变化。
根据变形的几何关系,可知杆件长度的变化与应变之间存在关系。
设杆件在外力作用下发生的长度变化为ΔL,初始长度为L,变化后的长度为L',则有:ΔL=L'-L而杆件的应变ε可以表示为:ε=ΔL/L代入上述等式,可得:ΔL=εL将ε=σ/E代入,可以得到:PE=∫udV其中,V表示杆件的体积。
将杆件的应变ε替换进去,可以得到:PE=∫udV=∫σεdV=∫(σE)(ΔL/L)dV进一步展开,可以得到:PE = (∫ (σ E) ΔL dV) / L = (∫ (σ E) ΔL A dx) / L 其中,A表示杆件的截面积,x表示杆件的长度方向。
将ΔL=L'-L代入上式,可以得到:PE = (∫ (σ E) (L' - L) A dx) / L对式中的积分进行分解,可以得到:PE = ∫ (σ E A) (L' - L) dx / L再次代入ΔL=L'-L,可以得到:PE = ∫ (σ E A) ΔL dx / L由于σEA是常数,可以提到积分符号外,得到:PE = (σ E A) ∫ΔL dx / L杆件的长度与x成正比,对积分进行整理,可以得到:PE = (σ E A) ∫ L dx / L对上述积分进行求解,可以得到:因此,杆件的变形能可以表示为:PE=(σEA)L所以,杆件的变形能公式可以表达为:PE=Fδ其中,F表示外力,δ表示变形量。
第四章 杆件的变形计算

3)分别作AC1和BC2的垂线交于C0
A F B 30oC2 C
Cx CC2 0.277mm C y CC1 / sin30 CC 2 cot30
C1
1.44mm
C点总位移:
Cy
C C y C x 1.47mm
(此问题若用圆弧精确求解)
2
2
Cx
C0
T3 C
1)根据题意,首先画出扭矩图
T1 d1 A Mx N· m B T2 d2 C T3
2)AB 段单位长度扭转角:
1400
800
AB
M xAB GI pAB
+
x
1400 4 π 0.06 80 10 9 32 0.01375rad / m
3)BC 段单位长度扭转角: M xBC BC
M xi li j i 1 GI pi
n
请注意单位长度扭转角和相对扭转角的区别
例4-3 一受扭圆轴如图所示,已知:T1=1400N· m, T2=600N· m, T3=800N· m, d1=60mm,d2=40mm,剪切弹性模量G=80GPa,计 算最大单位长度扭转角。
T1 d1 A
T2 d2 B
第四章
• • • • •
杆件的变形计算
本部分主要内容:
拉压杆的轴向变形 圆轴的扭转变形与相对扭转角 梁的弯曲变形、挠曲线近似微分方程 用积分法求梁的弯曲变形 用叠加法求梁的弯曲变形
第一节 拉压杆的轴向变形
直杆在其轴线的外力作用下,纵向发生伸长或缩短变形, 而其横向变形相应变细或变粗 杆件在轴线方向的伸长
泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数, 可以通过实验测得。对于各向同性材料,可以证明三者之间存 在着下面的关系
第四章 杆件的变形 · 简单超静定问题

A1
、物理方程-变形与受力关系
FN 1 L1 FN 3 L3 cos E1 A1 E3 A3 补 充 方 程 (3)
F
FN1
A
FN3 FN2
、联立方程(1)、(2)、(3)可得:
x
FN1 FN 2 E3 A3 F E1 A1F cos2 ; FN 3 3 2E1 A1 cos E3 A3 2E1 A1 cos3 E3 A3
0.02 2 160 106
[ FN ] AD sin 50.24 1 0.75 / 0.752 1 [F ] 12.06 KN 2.5 AB
C 0.75m A 1m D D
(2)、B点位移
lCD
B lCD
[ FN ]lCD EA
D1 1.5m
l l
虎克定律 实验证明: 引入比例常数E,则
Fl l A FN l (虎克定律) Fl l EA EA
E——表示材料弹性性质的一个常数,称为拉压弹 性模量,亦称杨氏模量。单位:MPa、GPa. 例如一般钢材: E=200GPa。
EA——杆件的抗拉/压刚度
1)
O
1
B 4F
B
1
α α
2
FNAB FNAC
C
F F
X
0 0
FNAC sin FNAB sin 0
Y
A
LAB
FNAC cos FNAB cos F 0 F FNAC FNAB 2 cos F L FL LAC NAC EA 2 EA cos
轴向拉伸或压缩时的变形 刚度条件 超静定问题
轴向拉伸或压缩时的变形
第四章杆件的变形计算
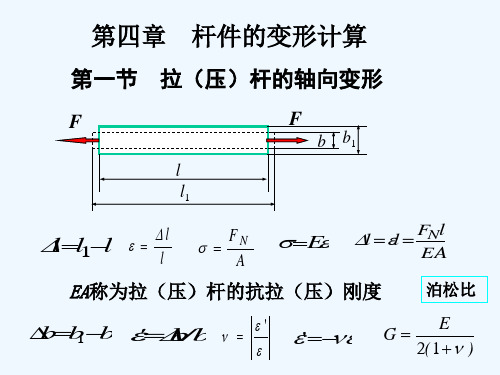
上式称为单位长度扭转角,用来表示扭转变形的大小, 其单位是rad/m。
当GIP越大,则θ越小,故称GIP为圆轴的抗扭刚度。 l Mx 两端相对扭转角 0 dx GI p
当Mx/GIP为常量时,上式为
M xl GI p
例4-3 某机器传动轴AC如图所示,已知轴材料的切变 模量G=80GPa ,轴直径d=45mm。求AB、BC及AC间 相对扭转角, 最大单位长度扭转角。 解 (1)内力分析
M l 80 0 . 4 4 x 2 BC rad 9.9412 10 rad BC GI 9 4 p 80 10 0 . 045 32
3 4 4 AC AB BC
( 1 . 12 10 9 . 94 10 ) rad 1.2 10 r
(5)列出转角方程和挠曲线方程
3 q q l (l x )3 6 E I 6 E I
3 4 2 q l q l q x 4q 2 2 w ( lx ) x ( x 64 l l x ) 2 4 E I 6 E I 2 4 E I 2 4 E I
(6) 求自由端挠度和转角
max 2
M xCA 6.68 10 3 GI p 200 10 9 0.06 4 / 32 0.0263rad/ m 1.5 /m
4 . 9 /m max
TB
A
TC
TA C
0.4m
B
0.4m
已知: n = 200r/min, PA = 60 kW, PB = 150kW, PC = 90kW, G=200GPa, dAB=0.06m, dBC= 0.04m。 试求: (1)轴两端截面相对转角 (2)最大单位长度扭转角
材料力学 杆件的变形计算

40kN A
60kN B
20kN C
400
400
9
40kN A
60kN B
20kN
C
1)求出轴力,并画出轴力图
400
400
FN KN 40
2)求伸长量
+
x l l AB lBC
-
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
ቤተ መጻሕፍቲ ባይዱ
FNBC l BC EABC
x0 x
5、杆的横向变形:
ac ac ac
6、x点处的横向线应变:
ac
ac
2
二、拉压杆的弹性定律
1、等内力拉压杆的弹性定律
P
P
2、变内力拉压杆的弹性定律
NN((xx))
x dx 内力在n段中分别为常量时
dL PL A
dL PL NL EA EA
※“EA”称为杆的抗拉压刚度。
(dx) N ( x)dx EA( x)
C
C2
C1
因此,C节点变形后将位于C3点
C3 C0
由于材料力学中的小变形假设,可
以近似用C1和C2处的圆弧的切线来代替 圆弧(以切代弧法),得到交点C0
14
[解]
1)分析节点C,求AC和BC的轴力(均预
A
先设为拉力)
F
B
30oC2
C
C1
y
FAC
F
30
FBC
C x
FAC sin 30 F 0 FAC 2F 80kN 拉 伸长
是刚刚走到这个知识领域的边缘,然而一旦对它有了充分的认 识,就将会在我们面 前展现出一个迄今为止只被人们神话般
第四章零件受力变形讲解

N
M 9550 D
D
n
637N m
-
作扭矩图 Tnmax=955N·m
圆轴扭转时横截面上的应力
1.圆轴扭转时的变形特征:
Me
Me
1)各圆周线的形状大小及圆周线之间的距离均无变 化;各圆周线绕轴线转动了不同的角度。 2)所有纵向线仍近似地为直线,只是同时倾斜了同
一角度 。
4.4.2 圆轴扭转时的应力
G
dj
dx
G Mn
GI p
Mn Ip
I p
2dA
A
IP是一个只决定于横截面的形状和大小的几何量,称 为横截面对形心的极惯性矩。
• 横截面上某点的切应力
T
的方向与扭矩方向相同,
并垂直于该点与圆心的
τ
连线
• 切应力的大小与其和圆
τ
心的距离成正比
注意:如果横截面是空心圆,空心部分没有应力 存在。
三.挤压的概念
构件发生剪切变形时,往往会受到挤压作用,这种 接触面之间相互压紧作用称为挤压。
构件受到挤压变形时,相互挤压的接触面称为挤压 面(A j y )。作用于挤压面上的力称为挤压力(F j y ),挤压 力与挤压面相互垂直。如果挤压力太大,就会使铆钉压 扁或使钢板的局部起皱 。
FFຫໍສະໝຸດ 四、挤压的实用计算单位是帕斯卡,简称帕,记作Pa,即l平方米 的面积上作用1牛顿的力为1帕,1N/m2=1Pa。
1MPa=106Pa
拉(压)杆的应力
假设轴力在横截面上的分布是均匀的,且方向
垂直于横截面。所以,横截面的正应力σ计算公式
为:
mn
F
F
σ= FN MPa A
6.5-杆件结构的变形计算

3
F2
B' F3
C
1
2
C'
Vε
1 2
Fδ
F--广义力(包括力和力偶) δ--广义位移 (包括线位移和角位移)
假设广义力按某一比例由零增致最后值对应的广义位移也由 零增致最后值.
对于线性结构,位移与荷载之间是线性关系,任一广
义位移,例如 2可表示为
δ2 C1F1 C2F2 C3F3
F2 (C1
2、变力功
当弹性杆件在力的作用下所产生的位移, 随力和变形的增加而增加时,力所作的 功为变力功。
W 1 Fl 2
6.5.2 杆件的弹性应变能
弹性体在外力的作用下将产生弹性变形,此时,外力 所作的功将转变为储存于弹性体内的能量。而当外力 逐渐减小时,弹性体的变形可逐渐恢复,储存在体内 的能量被释放而作功。
3、各类杆件结构在荷载作用下的位移公式 (1)梁和刚架
梁式杆的位移中弯矩的影响是主要的 ,位移计算 公式中取第一项便具有足够的工程精度
KP
M M P ds EI
(2)桁架
各杆为链杆,而且是同材料的等直杆。杆 内只有轴力,且处处相等。因而只取公式 中的第二项并简化为实用的形式
KP
A
a
(2) 若先在 C 截面加 F2, 然后在 B 截面加 F1.
B
F1
b
分别计算两种加力方法拉杆的应变能.
C
F2
(1)先在 B 截面加 F1,然后在 C 截面加 F2
(a)在 B 截面加 F1, B截面的位移为
B1
F1a EA
外力作功为
W1
1 2
F1δB1
F12a 2EA
(b)再在C上加 F2
材料力学课件 第四章扭转

直杆。
② 式中:T—横截面上的扭矩,由截面法通过外力偶矩求得。
—该点到圆心的距离。
Ip—截面极惯性矩,纯几何量,无物理意义。
17
Ip A 2dA 单位:mm4,m4。
③ 尽管由实心圆截面杆推出,但同样适用于空心圆截面杆,
只是Ip值不同。
一、传动轴的外力偶矩 传递轴的传递功率、转数与外力偶矩的关系:
m
9.55
P n
(kN
m)
其中:P — 功率,千瓦(kW) n — 转速,转/分(rpm)
m
7.024
P n
(kN
m)
其中:P — 功率,马力(PS) n — 转速,转/分(rpm)
m
7.121
P n
(kN
m)
其中:P — 功率,马力(HP) n — 转速,转/分(rpm)
22
[例2]有一阶梯形圆轴,如图(a)所示轴的直径分别d为1 50mm,d2 80mm 。扭转力偶矩分别为 Me1 0.8kN m ,Me2 1.2kN m ,M e3 2kN m。若 材料的许用切应力 [ ] 40MPa ,试校核该轴的强度。
解: 方法一(理论计算法) 用截面法求出圆轴各段的扭矩,如图(b)所示。 由扭矩图可见,CD段和DB段的直径相同,但DB段的扭矩大 于CD段,故这两段只要校核DB段的强度即可。AC段的扭矩 虽然也小于DB段,但其直径也比DB段小,故AC段的强度也 需要校核。
2GI p
W
U ;
64PR3n Gd 4
P K
;
K
Gd 4 64R3n
为弹簧常数。
36
[例3] 圆柱形密圈螺旋弹簧的平均直径为:D=125mm,簧丝直 径为:d =18mm,受拉力 P=500N 的作用,试求最大剪应力 的近似值和精确值;若 G =82GPa,欲使弹簧变形等于 6mm, 问:弹簧至少应有几圈?
杆件的变形及计算.

二、刚度设计
根据工程实际要求,对构件进行设计,以保证在确定的外载荷作用下,构件的弹性位移(最大位移 或指定位置处的位移)不超过规定的数值。于是: 1、对于拉压杆,刚度设计准则为
≤
ε为轴向线应变;[ε]为许用轴向线应变。 2、对于梁,刚度设计准则为
y ≤ y
≤
y和θ分别为梁的挠度和转角;[y]和[θ]分别为梁的许用挠度和许用转角。 3、对于受扭圆轴,刚度设计准则为
Q [ ] A
其中 Q 为剪切面上的剪力,由平衡条件求解;A 为剪切面面积;[τ]为材料的许用剪应力,单位 MPa。
二、挤压使用计算
在承载的情形下,连接件与其所连接的构件相互接触并产生挤压,因而在二者接触面的局部区域产生 较大的接触应力,称为挤压应力,用符号σjy表示,单位MPa。挤压应力是垂直与接触面的正应力。其可 导致接触的局部区域产生过量的塑性变形,而导致二者失效。 积压力为作用在接触面上的总的压力,用符号 Pjy 表示。 挤压面为接触面在挤压力作用线垂直平面上的投影,用符号 Ajy 表示。 其强度设计准则
≤
≤ l
φ和θ分别为圆轴指定两截面的相对扭转角和单位长度相对扭转角;[φ]和[φ/l]分别为相应的许 用值。
第二节 拉压杆强度设计与拉压杆伸缩量计算
一、拉压杆的强度设计
1、拉压杆横截面上的应力 内力系在横截面上均匀分布,横截面上正应力为:
N A
当杆件压缩时,上式同样适用。 σ的正负规定与轴力相同。拉应力为正,压应力为负。 2、拉压杆强度设计准则
Qmax Smax [ ] Ib
即
max [ ]
三、复杂受力时梁的强度计算
1、斜弯曲 可将梁在力P的作用下分解成在 Py、Pz 作用下的两个平 面弯曲的叠加。
材料力学 杆件的变形计算
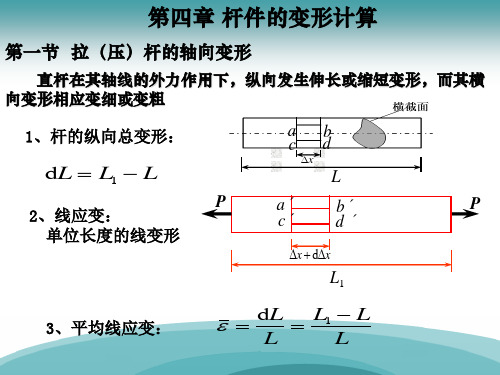
B
30oC2
C
C1
1.44mm
胡:请问,“ 弛其弦,以绳缓援之” 是什么意思 ?
郑:这是讲测量弓力时,先将弓的弦 松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说: 郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
400
400
FN KN 40
2)求伸长量
+
x l l AB lBC
-
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压,AC杆将伸长,而 F BC杆将缩短。
材料力学变形计算公式

材料力学变形计算公式材料力学这门学科啊,可真是充满了各种奇妙的知识和计算公式。
其中,变形计算公式那可是相当重要的一部分。
先来说说什么是变形。
想象一下,你用力拉一根橡皮筋,它是不是变长了?这就是变形。
而材料力学里研究的变形,可比拉橡皮筋复杂得多。
咱们就拿一根钢梁来举例吧。
假设这根钢梁要承受很大的重量,那它会发生什么样的变形呢?这时候变形计算公式就派上用场啦。
比如说,拉伸或压缩变形的计算公式是ΔL = FL / (EA) 。
这里的ΔL 表示变形量,F 是所受的力,L 是杆件的长度,E 是材料的弹性模量,A 是杆件的横截面面积。
我记得有一次在工地上,看到工程师们在计算一个大型起重机的起重臂的变形量。
他们拿着各种测量工具,神情专注,一边测量一边在本子上记录数据。
然后就开始运用这些变形计算公式来计算,看起重臂是否能够承受预期的重量,并且保证在工作过程中不会发生过度的变形。
再来说说扭转变形的计算公式。
扭转角φ = TL / (GIp) ,其中 T 是扭矩,L 是杆件的长度,G 是材料的剪切模量,Ip 是极惯性矩。
弯曲变形的计算公式就更复杂一些啦。
比如简支梁受集中力作用时,最大挠度的计算公式是 Ymax = Fl³ / (48EI) 。
这些变形计算公式在实际工程中可太重要了。
就像建造高楼大厦,如果不精确计算建筑材料的变形,那可就危险啦。
咱们在学习这些公式的时候,可不能死记硬背,得理解每个参数的含义和它们之间的关系。
比如说弹性模量 E ,它反映了材料抵抗变形的能力,不同的材料 E 值可不一样。
而且,在实际应用中,还得考虑很多因素的影响。
比如温度的变化、材料的缺陷等等。
总之啊,材料力学的变形计算公式虽然看起来有点复杂,但只要咱们用心去学,结合实际去理解,就能掌握好它们,为解决实际问题提供有力的工具。
所以,小伙伴们,别害怕这些公式,加油去探索材料力学的奇妙世界吧!。
杆线变形计算公式

杆线变形计算公式杆线变形是指在外力作用下,杆件产生的形变现象。
在工程中,对于杆线的变形计算是非常重要的,可以帮助工程师们设计出更加稳固和安全的结构。
杆线的变形计算可以利用公式来进行,下面我们就来介绍一下杆线变形计算的公式及其应用。
杆线的变形计算公式一般可以分为静力学方法和弹性力学方法两种。
静力学方法主要是根据杆线的受力分析,利用受力平衡方程来推导出变形的计算公式;而弹性力学方法则是根据杆线的弹性变形特性,利用弹性力学理论来推导出变形的计算公式。
下面我们将分别介绍这两种方法的计算公式及其应用。
静力学方法的计算公式一般可以通过受力平衡方程来推导得出。
对于简单的杆线结构,可以利用受力平衡方程来推导出杆线的变形计算公式,例如对于受均匀分布载荷作用的杆线,可以利用受力平衡方程推导出杆线的变形计算公式为:δ = PL / AE。
其中,δ为杆线的变形量,P为作用在杆线上的力,L为杆线的长度,A为杆线的截面积,E为杆线的弹性模量。
这个公式适用于受均匀分布载荷作用的简单杆线结构,可以方便地计算出杆线的变形量。
对于复杂的杆线结构,静力学方法的计算公式可能会比较复杂,需要进行更加详细的受力分析来推导出变形的计算公式。
在实际工程中,可以利用有限元分析等方法来进行复杂杆线结构的变形计算,得到更加精确的结果。
弹性力学方法的计算公式则是根据杆线的弹性变形特性来推导得出。
对于弹性杆线结构,可以利用弹性力学理论来推导出变形的计算公式,例如对于受集中力作用的弹性杆线,可以利用弹性力学理论推导出杆线的变形计算公式为:δ = F L / AE。
其中,δ为杆线的变形量,F为作用在杆线上的力,L为杆线的长度,A为杆线的截面积,E为杆线的弹性模量。
这个公式适用于受集中力作用的弹性杆线结构,可以方便地计算出杆线的变形量。
对于复杂的弹性杆线结构,弹性力学方法的计算公式同样可能会比较复杂,需要进行更加详细的弹性变形分析来推导出变形的计算公式。
在实际工程中,可以利用有限元分析等方法来进行复杂弹性杆线结构的变形计算,得到更加精确的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
首先要求出M 的数值
3M
jDB jDC jCB
+
x
180 π
M l xDC DC GI p
M l xCB CB GI p
180 3Ma 1 π GIp
M πGIp 540a
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
生命不止,奋斗不息
材料力学 Mechanics of Materials
g
在一段轴上,对单位长度扭转角公式进行积分,
就可得到两端相对扭转角j 。
dj
dx
dj M x
dx GI p 当 M x 为常数时:
GI p
j l M x dx
0 GI p
j M xl
GI p
同种材料阶梯轴扭转时:
j n M xili
A
F
B
30oC2
C
C1
y
FAC
F
30
FBC
C x
FAC sin 30 F 0 FAC 2F 80kN 拉 伸长
FBC FAC cos30 0 FBC 40 3kN 压 缩短
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
AMx N·m
+
T2
T3
d2
B
C
1400 800
x
1)根据题意,首先画出扭矩图
2)AB 段单位长度扭转角:
AB
M xAB GI pAB
80
1400 109 π
0.064
32
0.01375rad/ m
Hale Waihona Puke 3)BC段单位长度扭转角:
BC
M xBC GI pBC
80
800 109 π
0.044
32
0.03978rad/ m
求 : 1) 最大切应力; 2)j AC
M 2M
3M
D a C aB
2a A
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
M 2M
3M 1)画出扭矩图
D a C aB
Mx 2M M
2)求最大切应力
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
F
l
F
l FNl EA
l1
公式的适用条件:
1)线弹性范围以内,材料符合胡克定律
2)在计算杆件的伸长时,l 长度内其FN、A、l 均
应为常数,若为变截面杆或阶梯杆,则应进行分段 计算或积分计算。
x
B’
wB
w
B
某截面的法线方向与x轴 的夹角称为该截面的转角
x
挠度和转角的大小和截面所处的 x 方向的位
置有关,可以表示为关于 x 的函数。
挠度方程(挠曲线方程) 转角方程
w f1(x)
f2(x)
Cease to struggle and you cease to live.
生命不止,奋斗不息
生命不止,奋斗不息
材料力学 Mechanics of Materials
第三节 梁的弯曲变形,挠曲线近似微分方程
一、梁的变形
梁还必须有足够的刚度,即在受载后不至于发生过大的 弯曲变形,否则构件将无法正常工作。例如轧钢机的轧辊, 若弯曲变形过大,轧出的钢板将薄厚不均匀,产品不合格; 如果是机床的主轴,则将严重影响机床的加工精度。
+
x l l AB lBC
-
20
l AB
FNABl AB EA1
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBClBC EA2
20103 400 200103 240
0.167mm
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
Cease to struggle and you cease to live.
A
1m
F
B
30o
C
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压,AC杆将伸长,而 F BC杆将缩短。
C
C2
C1
因此,C节点变形后将位于C3点
生命不止,奋斗不息
材料力学 Mechanics of Materials
第一节 拉压杆的轴向变形
直杆在其轴线的外力作用下,纵向发生伸长或缩短变形,
而其横向变形相应变细或变粗
杆件在轴线方向的伸长
F l
l1
由胡克定律 Eε
得到轴向拉压变形公式
F l l1 l
纵向应变
FN
A
l
l
l FNl EA
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
F F1
A(x)
l x
F2
l1
l2
F
l FNdx l EA(x)
F3 l3
l n FNili
i1 EAi
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
b1 b
横向也会发生变形
F
F 横向应变
l l1
b b1 b
bb
通过试验发现,当材料在弹性范围内时,拉压杆的纵向应
变和横向应变存在如下的比例关系
泊松比
泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数,
T3=800N·m, d1=60mm,d2=40mm,剪切弹性模量G=80GPa,计 算最大单位长度扭转角。
T1 d1
A
T2
T3
d2
B
C
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
T1 d1
(此问题若用圆弧精确求解)
Cx 0.278mm
Cy 1.44mm
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
第二节 圆轴的扭转变形及相对扭转角
g dj
dx
在谈到圆轴扭转切应力公式的推导时,相距
i1 GI pi
相对扭转角的单位: rad
请注意单位长度扭转角和相对扭转角的区别
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
例4-3 一受扭圆轴如图所示,已知:T1=1400N·m, T2=600N·m,
为 dx 的两个相邻截面之间有相对转角dj
dj M x dx
GI p
取
dj M x
dx GI p
单位长度扭转角 用来表示扭转变形的大小
单位长度扭转角的单位: rad/m
GI p 抗扭刚度
GI p 越大,单位长度扭转角越小
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
3)分别作AC1和BC2的垂线交于C0
A
Cx CC2 0.277mm
F
C y CC1 / sin30 CC2cot30
B
30oC2
C
C1
1.44mm
C点总位移:
Cy
C C y 2 Cx 2 1.47mm
C0 Cx
材料力学 Mechanics of Materials
挠度和转角的正负号规定:
y
C’
A
C
x
B’
wB
w
B
x
在图示的坐标系中, 挠度 w 向上为正,向下为负。转 角规定截面法线与 x 轴夹角,逆时针为正,顺时针为负,
即在图示坐标系中挠曲线具有正斜率时转角 为正。
Cease to struggle and you cease to live.
C3 C0
由于材料力学中的小变形假设,可
以近似用C1和C2处的圆弧的切线来代替 圆弧(以切代弧法),得到交点C0
Cease to struggle and you cease to live.
生命不止,奋斗不息
材料力学 Mechanics of Materials
[解] 1)分析节点C,求AC和BC的轴力(均预先设为拉力)
生命不止,奋斗不息
材料力学 Mechanics of Materials
二、挠曲线近似微分方程
纯弯曲情况下 梁的中性层曲率与梁的弯矩之间的关系是:
横力弯曲情况下,若梁的跨度远大于梁的高度
时,剪力对梁的变形可以忽略不计。但此时弯 矩不再为常数。
