拉压杆的变形计算_图
合集下载
材料力学 杆件的变形计算
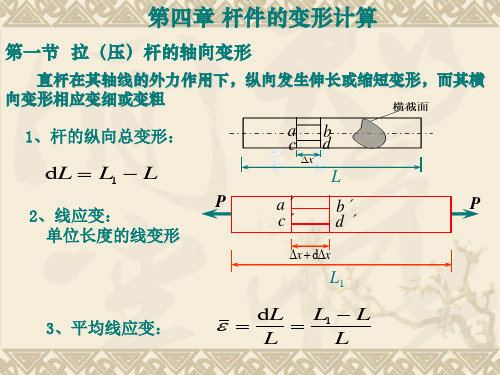
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa, ν = 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解:1) 求横截面正应力 :
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ,di = 15.3 mm, E=200 GPa, ν = 0.3, △l =0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N(x) N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移: 点总位移:
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段, 综合两段,最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆, 图示一等直圆杆,已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2)ϕ AC
材料力学-杆件的变形计算

EIz EIw M (x)dx C
再进行一次积分,可得到挠度方程
EIzw ( M (x)dx)dx Cx D
其中, C 和 D 是积分常数,需要经过边界条件或者连续条件来拟
定其大小。
❖ 边界条件:梁在其支承处旳挠度或转角是已知旳, 这么旳已知条件称为边界条件。
❖ 连续条件:梁旳挠曲线是一条连续、光滑、平坦旳 曲线。所以,在梁旳同一截面上不可能有两个不同 旳挠度值或转角值,这么旳已知条件称为连续条件。
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa,
= 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上旳正应力 σ (b) 螺栓旳横向变形△d
解:1) 求横截面正应力
l 0.04 7.4110-4
l 54 E 200 103 7.41104 148.2 MPa
M lBA BA GI p
180 7Ma π GI p
x
7 3
j
DB
2.33
第三节 梁旳变形
1、梁旳变形
梁必须有足够旳刚度,即在受载后不至于发生过大旳弯 曲变形,不然构件将无法正常工作。例如轧钢机旳轧辊,若 弯曲变形过大,轧出旳钢板将薄厚不均匀,产品不合格;假 如是机床旳主轴,则将严重影响机床旳加工精度。
dx
GI p
取
dj M x
dx GI p
单位长度扭转角 用来表达扭转变形旳大小
单位长度扭转角旳单位: rad/m
GI p 抗扭刚度
GI p 越大,单位长度扭转角越小
g
在一段轴上,对单位长度扭转角公式进行积分,
就可得到两端相对扭转角j 。
dj
dx
dj M x
再进行一次积分,可得到挠度方程
EIzw ( M (x)dx)dx Cx D
其中, C 和 D 是积分常数,需要经过边界条件或者连续条件来拟
定其大小。
❖ 边界条件:梁在其支承处旳挠度或转角是已知旳, 这么旳已知条件称为边界条件。
❖ 连续条件:梁旳挠曲线是一条连续、光滑、平坦旳 曲线。所以,在梁旳同一截面上不可能有两个不同 旳挠度值或转角值,这么旳已知条件称为连续条件。
例题4-2: 已知:l = 54 mm ,di = 15.3 mm,E=200 GPa,
= 0.3,拧紧后,△l =0.04 mm。 试求:(a) 螺栓横截面上旳正应力 σ (b) 螺栓旳横向变形△d
解:1) 求横截面正应力
l 0.04 7.4110-4
l 54 E 200 103 7.41104 148.2 MPa
M lBA BA GI p
180 7Ma π GI p
x
7 3
j
DB
2.33
第三节 梁旳变形
1、梁旳变形
梁必须有足够旳刚度,即在受载后不至于发生过大旳弯 曲变形,不然构件将无法正常工作。例如轧钢机旳轧辊,若 弯曲变形过大,轧出旳钢板将薄厚不均匀,产品不合格;假 如是机床旳主轴,则将严重影响机床旳加工精度。
dx
GI p
取
dj M x
dx GI p
单位长度扭转角 用来表达扭转变形旳大小
单位长度扭转角旳单位: rad/m
GI p 抗扭刚度
GI p 越大,单位长度扭转角越小
g
在一段轴上,对单位长度扭转角公式进行积分,
就可得到两端相对扭转角j 。
dj
dx
dj M x
工程力学第8章 变形及刚度计算

39
40
解 (1)静力方面 取结点 A为研究对象,分析其受 力如图 8.15(b)所示,列出平衡方程:
(2)几何方面
(3)物理方面 由胡克定律,有:
41
(4)补充方程 式(u)代入式(t),得:
再积分一次,得挠度方程
15
16
17
18
例8.5 图8.7所示等截面简支梁受集中力F作用,已 知梁的抗弯刚度为EI,试求C截面处的挠度yC和A截面 的转角θA。
19
解 取坐标系如图所示,设左、右两段任一横截面 形心的坐标、挠度和转角分别为x1,y1,θ1和x2,y2, θ2。梁的支反力为
20
2
3
8.1.2 横向变形及泊松比 定义
4
5
8.2 圆轴扭转时的变形和刚度计算
8.2.1 圆轴扭转时的变形 在7.6节中提到,圆轴扭转时的变形可用相对扭转角 φ来表示,而扭转变形程度可用单位长度扭转角θ来表示。 由7.6.2节中的式(d),即
6
8.2.2 刚度计算 有些轴,除了满足强度条件外,还需要对其变形加 以限制,如机械工程中受力较大的主轴。工程中常限制 单位长度扭转角θ不超过其许用值,刚度条件表述为
(3)物理方面 由胡克定律,可得:
37
(4)补充方程 将式(q)代入式(p),可得:
(5)求解 联立求解方程(o)和(r),可得:
38
由上例可以看出解超静定问题的一般步骤为: (1)选取基本体系,列静力平衡方程; (2)列出变形谐调条件; (3)物理方面,将杆件的变形用力表示; (4)将物理关系式代入变形谐调条件,得到补充 方程; (5)联立平衡方程和补充方程,求解未知量。
34
(1)静力方面 选取右端约束为多余约束,去掉该约束并代之以多 余支反力FB,如图8.14(b)所示,称为原超静定问题 的基本体系。所谓基本体系,是指去掉原超静定结构的 所有多余约束并代之以相应的多余支反力而得到的静定 结构。列出其平衡方程为:
《工程力学》第五章 杆件的变形与刚度计算

根据杆所受外力,作出其轴力图如 图 b所示。
(2)计算杆的轴向变形 因轴力FN和横截面面积A沿杆轴线变
化,杆的变形应分段计算,各段变形的 代数和即为杆的轴向变形。
l
FNili FN1l1 FN 2l2 FN 2l3
EAi
EA1
EA1
EA2
1 200 103
( 20 103 100 500
10 103 100 500
10 103 100 )mm 200
0.015mm
例5-2 钢制阶梯杆如图,已知
轴向外力F1=50kN,F2=20kN,
各段杆长为l1=150mm,
l2=l3=120mm,横截面面积为:
1
A1=A2=600mm2,A3=300mm2,
钢的弹性模量E=200GPa。求各
x
l 3
,ym
ax
9
Ml2 3E
I
xMl2 16EI
A
M 6EIl
(l 2
3b2 )
B
M 6EIl
(l 2
3a2 )
三、叠加法计算梁的变形
➢叠加法前提条件:弹性、小变形。 ➢叠加原理:梁在几个载荷共同作用下任一截面的挠度或转角, 等于各个载荷单独作用下该截面挠度或转角的代数和。
F1=2kN,齿轮传动力F2=1kN。主轴的许可变形为:卡盘 C处的挠度不超过两轴承间距的 1/104 ;轴承B处的转角
不超过 1/103 rad。试校核轴的刚度。
解(1)计算截面对中 性轴的惯性矩
Iz
D4
64
(1 4 )
804 (1 0.54 )mm4
64
188104 mm4
(2)计算梁的变形
拉压杆的变形

EA称为杆的拉压刚度,它是单位长度的杆产生单位长度的变形 所需的力。所以拉压刚度EA代表了杆件抵抗拉伸(压缩)变形 的能力。
因σ=FN/A、ε=Δl/l,故式(2-5)变为 σ=Eε (2-6
上式是胡克定律的另一表达式。它表明:在弹性限度内,正应力 与线应变成正比。
1.2横向变形
设图2-12所示拉、压杆在变形前、后的横向尺寸分别为d与d1, 则其横向变形Δd为
【例2-6】如图2-14(a)所示等截面直杆,已知 其原长l、横截 面积A、材料的容重γ、弹性模量E、受杆件自重和下端处集中力 F作用。求该杆下端面的位移ΔB。
【解】如图2-14(b)所示。距B端为x的横截面上的轴力为 FN(x)=F+γAx
微段dx如图2-14(c)所示。 略去两端内力的微小差值,则微段的变形为
=-0.975×10-3m=-0.975mm
各段柱的纵向线应变为
εBC=ΔlBC/lBC=-0.5mm/2000mm=2.5×10-4
εAB=ΔlAB/lAB=-0.975mm/1500mm=-6.5×10-4 全柱的总变形为两段柱的变形之和,即
Δl=ΔlBC+ΔlAB=-0.5mm-0.975mm=-1.475 mm
【解】由于上下两段柱的轴力不等,故两段柱 的变形要分别计算。各段柱的轴力为
FNBC=-100 kN 各段柱的纵向变形为
FNAB=-260 kN
ΔlBC=FNBC/EA = -100×103N×2m/10×109Pa× (0.2m)2 =-0.5×10-3m=-0.5mm
图2-13
ΔlAB=FNAB/EA= 260×103N×1.5m/10×109Pa×(0.2m)2
大量的实验表明,当杆的变形为弹性变形时,杆的纵向变形Δl与 外力F及杆的原长l成正比,而与杆的横截面面积A成反比,即
5-2拉压杆的变形计算汇总

F
a1
横向变形为 a = a 1- a
2.线应变——杆件单位长度内的变形量。
l l1 l 纵向线应变: l l a a1 a 横向线应变: a a
拉伸时, ﹥0, ' ﹤0;压缩时, ﹤0, ' ﹥0。 3.泊松比μ(横向变形系数) 实验结果表明:一定范围内,杆件的横向线应变 与纵向线应变的比值为一常数。即 ' =-
10kN
x
练习1.图示等截面直杆,其横截面面积A=4000cm2, 材料的弹性模量E=2×108Pa,试分别求上、下段的应力 和变形量。
300kN A B
3m
400kN
4m
C
小结: 1.应力与应变关系:
虎克定律:
Nl l EA
=E
2.拉压杆的变形计算
Nl l EA
应用时注意:N的正负要代入公式中计算。
A B C 30kN D
②分段计算变形量。 N ABl AB l AB EAAB
10kN
100
100
100
FN 20kN + 20103 100 0.02mm O 3 20010 500
-
△lBC = -0.01mm △lCD = -0.0167mm ③计算总变形量。 △l = △lAB + △lBC + △lCD = -0.0067mm
复习:
1.轴向拉压的受力特点和变形特点;
2.轴力的计算及轴力图的绘制
轴力的计算:N=∑F左或N=∑F右
轴力图作图规律:
左上右下,突变值等于外力的大小。
3.轴向拉(压)杆横截面上的正应力的计算。
杆件轴向拉伸与压缩_图文

极限应力(危险应力、失效应力):材料发生破坏或产生过大变形而 不能安全工作时的最小应力值,即材料丧失工作能力时的应力,以符号 σu表示,其值由实验确定。
许用应力:构件安全工作时的最大应力,即构件在工作时允许承受的
最大工作应力,以符号[σ]表示。计算公式为:
式中,n为安全系数,它是一个大于1的系数,一般来说,确定安全系数 时应考虑以下几个方面的因素。(1) 实际荷载与设计荷载的出入。(2) 材料 性质的不均匀性。(3) 计算结果的近似性。(4) 施工、制造和使用时的条件 影响。可见,确定安全系数的数值要涉及工程上的各个方面,不单纯是个 力学问题。通常,安全系数由国家制定的专门机构确定。
根据上述现象,对杆件内部的变形作如下假设:变形之前横截面为平 面,变形之后仍保持为平面,而且仍垂直于杆轴线,只是每个横截面沿 杆轴作相对平移。这就是平面假设。
ac
F
a' c'
F
b' d'
bd
11
建筑力学
推论:
1、等直拉(压)杆受力时没有发生剪切变形,因而横截 面上没有切应力。 2、拉(压)杆受力后任意两个横截面之间纵向线段的伸长 (缩短)变形是均匀的。亦即横截面上各点处的正应力 都相等。
p t
s M
10
建筑力学
拉(压)杆横截面上的正应力
推导思路:实验→变形规律→应力的分布规律→应力的计算公式
简单实验如下。用弹性材料做一截面杆(如下图),在受拉力前,在截 面的外表皮上画ab和cd两个截面,在外力F的作用下,两个截面ab和cd的 周线分别平行移动到a`b`和c`d`。根据观察,周线仍为平面周线,并且截 面仍与杆件轴线正交。
一般来说,在采用截面法之前不要使用力的可传性原理, 6
许用应力:构件安全工作时的最大应力,即构件在工作时允许承受的
最大工作应力,以符号[σ]表示。计算公式为:
式中,n为安全系数,它是一个大于1的系数,一般来说,确定安全系数 时应考虑以下几个方面的因素。(1) 实际荷载与设计荷载的出入。(2) 材料 性质的不均匀性。(3) 计算结果的近似性。(4) 施工、制造和使用时的条件 影响。可见,确定安全系数的数值要涉及工程上的各个方面,不单纯是个 力学问题。通常,安全系数由国家制定的专门机构确定。
根据上述现象,对杆件内部的变形作如下假设:变形之前横截面为平 面,变形之后仍保持为平面,而且仍垂直于杆轴线,只是每个横截面沿 杆轴作相对平移。这就是平面假设。
ac
F
a' c'
F
b' d'
bd
11
建筑力学
推论:
1、等直拉(压)杆受力时没有发生剪切变形,因而横截 面上没有切应力。 2、拉(压)杆受力后任意两个横截面之间纵向线段的伸长 (缩短)变形是均匀的。亦即横截面上各点处的正应力 都相等。
p t
s M
10
建筑力学
拉(压)杆横截面上的正应力
推导思路:实验→变形规律→应力的分布规律→应力的计算公式
简单实验如下。用弹性材料做一截面杆(如下图),在受拉力前,在截 面的外表皮上画ab和cd两个截面,在外力F的作用下,两个截面ab和cd的 周线分别平行移动到a`b`和c`d`。根据观察,周线仍为平面周线,并且截 面仍与杆件轴线正交。
一般来说,在采用截面法之前不要使用力的可传性原理, 6
胡克定律与拉压杆的变形

1.分段解法
FN1 = F2 − F1
FN2 = F2
(∆l )分段解法
=
FN1l1 EA
+
FN2l2 EA
=
(F2
− F1 )l1 EA
+
F2l2 EA
(∆l )分段解法
=
F2(l1 + EA
l2 )
−
F1l1 EA
2. 分解载荷法
(∆l
)分段解法
=
F2
( l1 + EA
l2
)
−
F1l1 EA
3. 比较
§9 连接部分的强度计算
连接实例 剪切与剪切强度条件 挤压与挤压强度条件 例题
单辉祖:工程力学(材料力学)
73
连接实例
单辉祖:工程力学(材料力学)
销钉
螺栓
耳片
74
单辉祖:工程力学(材料力学)
75
剪切与剪切强度条件
以耳片销钉为例介绍分析方法
单辉祖:工程力学(材料力学)
76
解:1. 破坏形式分析
单辉祖:工程力学(材料力学)
81
2. 许用载荷 [F]
n
τ
=
4F πd 2
≤ [τ
]
F ≤ πd 2[τ ] = 1.257 kN
4
o
σ bs
=
F
δd
≤ [σ bs ]
F ≤ δd[σ bs ] = 2.40 kN
p
σ max
=
F
(b − d )δ
≤ [σ ]
F ≤ (b − d )δ [σ ] = 3.52 kN
FN1 = FN1,F1 + FN1,F2 = −F1 + F2
第八章__变形及刚度计算

8×103 ×180 o = 0.40 / m < [θ ] 4 9 π × 0.110 80×10 × ×π 32
满足刚度条件
例:实心圆轴受扭,若将轴的直径减小一半 实心圆轴受扭, 时,横截面的最大切应力是原来的 8 倍? 圆轴的扭转角是原来的 16 倍?
τ max MT MT = = W p πd 3 16
又因为BD段内虽然轴力 又因为 段内虽然轴力 为常数, 为常数,但截面面积又分两 所以要分4段求变形 段求变形。 段,所以要分 段求变形。
∆L AE =
∑ ∆L
i
= ∆L AB + ∆L BC
FN图
+ ∆L CD + ∆L DE =
∑
FN l EA
§ 8-1 轴向拉压杆的变形
已知杆的长度、 受力如图。 例 已知杆的长度、截面面 积,受力如图。 材料的 弹性模量 E = 2.1 × 10 5 MPa。求杆的总变形 。
A1 = 250mm
50kN
2
A 2 = 200mm
30kN E
∆L AB
2
解:用直接法画轴力图 用直接法画轴力图
20kN
∆L AE =
∑ ∆L
i
= ∆L AB + ∆L BC
A B C D 1m 2m 1m 3m 10KN + – – 40KN 20KN
+ ∆L CD + ∆L DE =
∑
3
FN l EA
§8—2
圆杆扭转时的变形和刚度计算
一、扭转变形——扭转角 扭转变形 扭转角
MT 扭转角: 扭转角: ϕ = θdx = dx ∫ ∫0 GI p l
l
单位: 单位:rad
第四章 杆件的变形计算

3)分别作AC1和BC2的垂线交于C0
A F B 30oC2 C
Cx CC2 0.277mm C y CC1 / sin30 CC 2 cot30
C1
1.44mm
C点总位移:
Cy
C C y C x 1.47mm
(此问题若用圆弧精确求解)
2
2
Cx
C0
T3 C
1)根据题意,首先画出扭矩图
T1 d1 A Mx N· m B T2 d2 C T3
2)AB 段单位长度扭转角:
1400
800
AB
M xAB GI pAB
+
x
1400 4 π 0.06 80 10 9 32 0.01375rad / m
3)BC 段单位长度扭转角: M xBC BC
M xi li j i 1 GI pi
n
请注意单位长度扭转角和相对扭转角的区别
例4-3 一受扭圆轴如图所示,已知:T1=1400N· m, T2=600N· m, T3=800N· m, d1=60mm,d2=40mm,剪切弹性模量G=80GPa,计 算最大单位长度扭转角。
T1 d1 A
T2 d2 B
第四章
• • • • •
杆件的变形计算
本部分主要内容:
拉压杆的轴向变形 圆轴的扭转变形与相对扭转角 梁的弯曲变形、挠曲线近似微分方程 用积分法求梁的弯曲变形 用叠加法求梁的弯曲变形
第一节 拉压杆的轴向变形
直杆在其轴线的外力作用下,纵向发生伸长或缩短变形, 而其横向变形相应变细或变粗 杆件在轴线方向的伸长
泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数, 可以通过实验测得。对于各向同性材料,可以证明三者之间存 在着下面的关系
拉压杆的变形计算

FN1 =20kN (+) FN2 =-15kN ( - ) FN3 =- 50kN ( - ) max = 176.8MPa 发生在AB段.
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1
F1
A
(3) B截面的位移及AD杆的变形
Δl AB
ΔlCD
FN1l1 FN 2 l2 -4 2.53 10 m Δl BC 1.42 10-4 m EA1 EA2ⅢⅡⅠ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1 A
F1
FRD
FN3 FN2
F2
F1
FN 3 FRD 0 FN 3 50kN ( )
F1 F2 FN 2 0 FN 2 15kN ( )
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1
20
F1
称为泊松比 (Poisson’s ratio)
四、胡克定律 (Hooke’s law)
实验表明工程上大多数材料都有一个弹性阶段,在此 弹性范围内,正应力与线应变成正比. 由
E
FN A FN l Δl EA
Δl l
上式改写为
式中 E 称为弹性模量 (modulus of elasticity) ,EA称为抗拉
FN 3 l3 1.58 10-4 m EA3
uB ΔlCD Δl BC -0.3mm
Δl AD Δl AB Δl BC ΔlCD -0.47 10-4 mm
第7章 杆件的变形与刚度

32Tmax ⋅180 4 32 × 2000 ×180 d ≥4 = ×103 = 83.5mm G[θ ]⋅ π 2 80 ×109 × 0.3π 2
该圆轴直径应选择:d =83.5mm.
[例2]图示圆轴,已知mA =1.4kN.m, mB =0.6kN.m, mC =0.8kN.m;d1 =40mm,d2 =70mm; l1 =0.2m,l2 =0.4m; [τ]=60MPa,[θ]=1°/m,G=80GPa;试校核该轴的强度和刚 度,并计算两端面的相对扭转角。 mC
D
解:本题应分4段考虑。 π D4 I P1 = I P 2 = 32
d
A
a
1
2
B 3 b b
4
a
C
32 π D3 Wt1 = Wt 2 = 16 d4 π D3 (1 − 4 ) Wt 3 = Wt 4 = 16 D
I P3 = I P 4 =
π
(D4 − d 4 )
0.5kN.m 0.3kN.m 0.8kN.m 4 1 2 3
16mC
⊕
○ 1kN.m
π [τ ]
16 × 2000 3 = ×10 6 π 60 ×10
3
= 55.4mm
mA A
mB
mC
⑵按刚度条件
l1
B l C 2
2kN.m
⊕
○ 1kN.m
θ max = T ⋅ 180 ≤ [θ ] (°/m) GI p π π 4 Tmax 180 IP = d ≥ ⋅ 32 G[θ ] π
d2
mA
d1
mB
解: ⑴按强度校核
C
l2
A l1 B
0.6kN.m
T1 16mB τ1 = = Wt1 π d13 16 × 600 = = 47.7 MPa < [τ ] 3 π ×4
材料力学-课件2-4拉杆的变形.胡克定律

EA L L
L
i
FNiLi
EAi
FN EA L E
A AL
在计算ΔL的L长度内,FN,E,A均 为常数。
在材料的线弹性范围内,正应力与线应变呈正比关系。
2、横向变形
△b=b1-b
b1 b
b
b
横向线应变
泊松比
例题 2.9
图示为一端固定的橡胶板条,若在加力前在 板表面划条斜直线AB,那么加轴向拉力后 AB线所在位置是?(其中ab∥AB∥ce)
α=300,杆长L=2m,杆的直径d=25mm,材
料的弹性模量E=2.1×105MPa,设在结点A处悬
挂一重物F=100kN,试求结点A的位移δA。
1
2
FNAB FNAC
X 0 C Y 0
F N F FN c N A AA C s C o C FiN F s n N AB F N c A 2cA s F B o oB isF n s 0 0
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等,所以上边纤维长,伸长量也大。
例题
2.10
例:图示直杆,其抗拉刚度为EA,试 求杆件的轴向变形△L,B点的位移 δB和C点的位移δC
A L
F
F
B
LAB
FL EA
B
C
L
C
B
FL EA
例题
2.11
图示结构,横梁AB是刚性杆,吊杆CD是等截面直杆,
B点受荷载P作用,试在下面两种情况下分别计算B点的位
拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
材料力学 杆件的变形计算
必知弓力三石者,当弛其弦以绳缓擐之者,谓不张之,别以 一条 绳系两箭,乃加物一石张一尺、二石张二尺、三石张三 尺。其中 “两萧” 就是指弓的两端。 胡:郑老先生讲“每加物一石,则张一尺”。和我讲的完全是同一 个意思。您比我早1500 中就记录下这种正比关系,的确了不起, 真是令人佩服之至』我在1686 年《关于中国文字和语言的研究 和推测》一文中早就推崇过贵国的古代文化:“目前我们还只 是刚刚走到这个知识领域的边缘,然而一旦对它有了充分的认 识,就将会在我们面 前展现出一个迄今为止只被人们神话般
B
30oC2
C
C1
1.44mm
胡:请问,“ 弛其弦,以绳缓援之” 是什么意思 ?
郑:这是讲测量弓力时,先将弓的弦 松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说: 郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
400
400
FN KN 40
2)求伸长量
+
x l l AB lBC
-
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压,AC杆将伸长,而 F BC杆将缩短。
B
30oC2
C
C1
1.44mm
胡:请问,“ 弛其弦,以绳缓援之” 是什么意思 ?
郑:这是讲测量弓力时,先将弓的弦 松开,另外用绳子松松地套住弓 的两端,然后加重物,测量。
胡:我明白了。这样弓体就没有初始应力,处于自然状态。
郑:后来,到了唐代初期,贾公彦对我的注释又作了注疏,他说: 郑又云假令弓力胜三石,引之 中三尺者,此即三石力弓也。
400
400
FN KN 40
2)求伸长量
+
x l l AB lBC
-
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压,AC杆将伸长,而 F BC杆将缩短。
轴向拉压杆的变形

1.求出两杆的轴力
Fx 0 FN2 FN1 cos300 0 Fy 0 FN1 sin300 F 0
FN1 20kN(拉) FN 2 17.3kN(压)
A 1
F 2 30°
C
(a)
B
FN1
30
B
FN2
F
(b)
2.计算两杆的变形
l1
FN1l1 E1 A1
20 103 2 2 105 106 600 106
(60 103
1
20 103
2
30 103
1.5)
0.65 103 (m)
l 0.65 103 (m)
变形计算的应用:三角桁架节点位移的求法。
怎样画小变形放大图?
分析:
A
L1
图1
B L2
(1)、研究节点 C 的受力,确定各 杆的内力 FNi;
(2)、求各杆的变形量△Li ;
C
(3)、变形图严格画法,图中弧线;
60kN 80kN 50kN 30kN
解: 应用截面法求得各段横截 面上的轴力如下:
AB段 FN1 60kN BC段 FN2 60 80 20kN CD段 FN3 30kN
AB 1m 2m
(a) 60kN
CD 1.5m
30kN
20kN (b)
得各段横截面上的正应力为:
AB段 BC段 CD段
L FN L EA
----胡克定律
E——弹性模量与材料有关,单位——同应力。 EA——抗拉压刚度。
注意 ①当各段的轴力为常量时——
L L1 L2 L3
FNi Li EAi
②当轴力为x的函数时 N=N(x)——
L dL1 dL2 dL3
第7章 轴向拉压杆件的强度与变形计算

F NBC 56 . 6 kN (压力) F NBA 40 kN
(拉力)
(2)由强度条件确定各杆截面尺寸 对BA杆
A BA
d
4
2
F NBA
s
d
4 F NBA
s
17 . 8 mm
可取
d 18 mm
F NBC
对BC杆
A BC a
2
w
a
F NBC
【例】已知AB梁为刚体,CD为拉杆,拉杆直径
d=2cm,E=200GPa,FP=12kN, 求B点位移。
C 0.75m A D B
1m
1.5m
FP
解:(1)受力分析,求轴力
FN
F Ax
A
D
B
F Ay
1m
1.5m
FP
M
A
0
F P AB F N AD sin
FN
解:(1)受力分析, 求各杆轴力
F NBD
F x 0, Fy 0
2 F P 31 . 4 kN
(2)求各杆应力
BD
F NCD F P 22 . 2 kN
F NBD A BD F NCD A CD 22 . 2 kN 31 . 4 kN
CD
3
m
DD BB
AD AB
B B D D /(
AD AB
)
4 . 17 10
3
m
7.4 轴向拉压杆的强度计算
• 工作应力
FN A
• 失效:工作应力超过了杆件材料所能承受的极 限应力;
拉压杆的变形及刚度计算

胡克定律:
l FNl EA
上式只适用于在杆长为l长度内FN、E、A均为常
值的情况下,即在杆为l长度内变形是均匀的情况。
EA称为杆的拉压刚度
1.2 横向变形、泊松比 则横向正应变为:
a
a
当应力不超过一定限度时,横向应变
与轴向应变 之比的绝对值是一个常数。
横向变形因数或泊松比
法国科学家泊松(1781~1840) 于1829年从理论上推演得出的结果。 ,
FRA F2 F1 (10 30)
=-20kN (2)、计算各段杆件 横截面上的轴力
AB段: FNAB=FRA=-20kN
BD段: FNBD=F2=10kN
(3)、画出轴力图,如图(c)所示。
(4)、计算各段应力
AB段: BC段: CD段:
AB
FNAB AAC
20 103 500
40MPa
表4-1给出了常用材料的E、 值。
表8.1 常用材料的E、 值
材料名称 低碳钢 中碳钢
低合金钢 合金钢
灰口铸铁 球墨铸铁
铝合金 硬铝合金
混凝土 木材(顺纹) 木材(横纹)
牌号 Q235
45 16Mn 40CrNiMoA
LY12
E 200 ~ 210
205 200 210 60 ~ 162 150 ~ 180 71 380 15.2 ~ 36 9.8 ~ 11.8 0.49 ~ 0.98
例2 图示托架,已知 F 40 kN,圆截面钢杆
AB的直径 d 20 mm ,杆BC是工字钢,其
横截面面积为 1430mm,2 钢材的弹性模量
E 200GPa。求托架在F力作用下,
节点B的铅垂位移和水平位移? 解:(1)、取节点B为研究对象,求两杆轴力
