5-2拉压杆的变形计算汇总
合集下载
拉压杆的变形与变形能-5
§2-5拉伸或压缩时的变形1．沿杆件轴线的轴向变形如图2-23，设等直杆的原长为，横截面面积为。
在轴向力l A P 作用下，长度由l 变为。
杆件在轴线方向的伸长，即轴向变形为1ll l l −=Δ1 （1）由于杆内各点轴向应力σ与轴向应变ε为均匀分布，所以一点轴向线应变即为杆件的伸长除以原长l ：l Δl l Δ=ε （2） 由εσE =得ll E A N Δ= 所以EAPl EA Nl l ==Δ （2-6） 式（2-6）表示：当应力不超过比例极限时，杆件的伸长l Δ与拉力P 和杆件的原长度l 成正比，与横截面面积成反比。
这是胡克定律的另一种表达形式。
式中是材料弹性模量与拉压杆件横截面面积乘积，EA 越大，则变形越小，将EA 称为抗拉（压）刚度。
A EA 2．横向变形若在图2-23中，设变形前杆件的横向尺寸为，变形后相应尺寸变为，则横向变形为 b 1bb b b −=Δ1横向线应变可定义为bb Δ=′ε 由实验证明，在弹性范围内μεε=′ （2-7） μ为杆的横向线应变与轴向线应变代数值之比。
由于μ为反映材料横向变形能力的材料弹性常数，为正值，所以，一般冠以负号εεμ′−=，称为泊松比或横向变形系数。
ε′与ε的关系为μεε−=′ （2-8）3()()x Nx e σγ0 ()A dA A σσγ+=+在处0=x 0A A =即：按指数函数变化。
A 例2-6 图2-25所示为变截面杆，已知BD 段cm 21=A 2，DA 段42=A cm 2，kN ，kN 。
求AB 杆的变形5=AB l 1P 102=P Δ。
（材料的MPa ）310120×=E 解：首先分别求得BD 、DC 、CA 三段的轴力，N ，为1N 23N 51−=N kN ；52−=N kN ；53=N kN449311111005.1102101205.0105−−×−=×××××−==Δ=ΔEA l N l l BD （m ） 449322221052.0104101205.0105−−×−=×××××−==Δ=ΔEA l N l l DC （m ） 449333331052.0104101205.0105−−×=×××××==Δ=ΔEA l N l l CA（m ） 43211005.1−×−=Δ+Δ+Δ=Δl l l l AB （m ） AB l Δ的负号说明此杆缩短。
材料力学 杆件的变形计算
例题4-2: 已知：l = 54 mm ，di = 15.3 mm，E＝200 GPa， ν = 0.3，拧紧后，△l ＝0.04 mm。 试求：(a) 螺栓横截面上的正应力 σ (b) 螺栓的横向变形△d
解：1) 求横截面正应力 ：
ε=
∆l 0.04 = = 7.41×10-4 l 54
l = 54 mm ，di = 15.3 mm， E＝200 GPa， ν = 0.3， △l ＝0.04 mm
∆ac = a ′c′ − ac
∆ac ε′ = ac
二、拉压杆的弹性定律 1、等内力拉压杆的弹性定律 P P
PL NL dL = = EA EA
PL dL ∝ A
2、变内力拉压杆的弹性定律
N（x） N(x)
x dx dx 内力在n段中分别为常量时 内力在 段中分别为常量时
※“EA”称为杆的抗拉压刚度。 ※“ ”称为杆的抗拉压刚度。
C1
C点总位移： 点总位移：
∆C = ∆C y + ∆C x = 1.47mm
2 2
C0
Cx
(此问题若用圆弧精确求解) 此问题若用圆弧精确求解)
∆C x = 0.278mm ∆C y = 1.44mm
第二节 圆轴的扭转变形及相对扭转角
为 dx 的两个相邻截面之间有相对转角dϕ 的两个相邻截面之间有相对转角d
800 π × 0.04 4 80 ×109 32 = 0.03978rad / m
综合两段， 综合两段，最大单位扭转角应在BC 段 为 0.03978 rad/m
例4-5 图示一等直圆杆， 图示一等直圆杆，已知 d =40mm a =400mm G =80GPa, ϕ DB=1O , 求 : 1) 最大切应力 2）ϕ AC
拉压杆的变形计算
B 1 2
C
B
1 2
C
A
A
A'' （2）两杆的变形为
FN1l1 Fl Δl1 Δl2 （伸长） EA 2 EA cos
变形的几何条件相容是变形后，两杆仍应铰结在一起.
B 1 2
C
1
2
A
A''
l 1 A2
A A' A1
A
以两杆伸长后的长度BA1 和 CA2 为半径作圆弧相交于 A, 即为A点的新位置.AA 就是A点的位移. 因变形很小,故可过 A1，A2 分别做两杆的垂线，相交于 A 可认为
拉压杆的变形计算 (Calculation of axial deformation)
h1
F
h
b b1
F
l
l1
一、纵向变形 (Axial deformation)
1. 纵向变形 (Axial deformation)
2. 纵向应变 (Axial strain)
Δl l1 l Δl l
拉压杆的变形计算 (Calculation of axial deformation)
B 1 C
A
2
y B 1 2
C
FN1
1
FN2
2
A
x A
F 解：（1） 列平衡方程,求杆的轴力
Fx 0 Fy 0
FN1 FN 2
FN 2 sin FN1 sin 0 FN1 cos FN 2 cos F 0 F 2 cos
实验表明工程上大多数材料都有一个弹性阶段， 在此弹性范围内，正应力与线应变成正比.
《工程力学》第五章 杆件的变形与刚度计算
根据杆所受外力，作出其轴力图如 图 b所示。
（2）计算杆的轴向变形 因轴力FN和横截面面积A沿杆轴线变
化，杆的变形应分段计算，各段变形的 代数和即为杆的轴向变形。
l
FNili FN1l1 FN 2l2 FN 2l3
EAi
EA1
EA1
EA2
1 200 103
( 20 103 100 500
10 103 100 500
10 103 100 )mm 200
0.015mm
例5-2 钢制阶梯杆如图，已知
轴向外力F1=50kN，F2=20kN，
各段杆长为l1=150mm，
l2=l3=120mm，横截面面积为：
1
A1=A2=600mm2，A3=300mm2，
钢的弹性模量E=200GPa。求各
x
l 3
，ym
ax
9
Ml2 3E
I
xMl2 16EI
A
M 6EIl
(l 2
3b2 )
B
M 6EIl
(l 2
3a2 )
三、叠加法计算梁的变形
➢叠加法前提条件：弹性、小变形。 ➢叠加原理：梁在几个载荷共同作用下任一截面的挠度或转角， 等于各个载荷单独作用下该截面挠度或转角的代数和。
F1=2kN，齿轮传动力F2=1kN。主轴的许可变形为：卡盘 C处的挠度不超过两轴承间距的 1/104 ；轴承B处的转角
不超过 1/103 rad。试校核轴的刚度。
解（1）计算截面对中 性轴的惯性矩
Iz
D4
64
(1 4 )
804 (1 0.54 )mm4
64
188104 mm4
（2）计算梁的变形
杆件的变形计算
T1 d1
A
T2
T3
d2
B
C
Cease to struggle and you cease to live.
生命不止，奋斗不息
材料力学 Mechanics of Materials
T1 d1
AMx N·m
+
T2
T3
d2
B
C
1400 800
x
1）根据题意，首先画出扭矩图
2）AB 段单位长度扭转角：
AB
+
jAC1π80M G CB lpC IBM G BlA pB IA
180 7Ma π GI p
x 73jDB2.33
Cease to struggle and you cease to live.
生命不止，奋斗不息
材料力学 Mechanics of Materials
第三节 梁的弯曲变形，挠曲线近似微分方程
即在图示坐标系中挠曲线具有正斜率时转角 为正。
Cease to struggle and you cease to live.
生命不止，奋斗不息
材料力学 Mechanics of Materials
y
C’
A
C
x
挠度和转角的关系
B’
wB
w
B
x
w dy tan
dx
在小变形假设条件下
tan
wdytan
生命不止，奋斗不息
材料力学 Mechanics of Materials
M 2M
3M 1）画出扭矩图
D a C aB
Mx 2M M
2）求最大切应力
2a A
首先要求出M 的数值
第四章 杆件的变形计算
3）分别作AC1和BC2的垂线交于C0
A F B 30oC2 C
Cx CC2 0.277mm C y CC1 / sin30 CC 2 cot30
C1
1.44mm
C点总位移：
Cy
C C y C x 1.47mm
(此问题若用圆弧精确求解)
2
2
Cx
C0
T3 C
1）根据题意，首先画出扭矩图
T1 d1 A Mx N· m B T2 d2 C T3
2）AB 段单位长度扭转角：
1400
800
AB
M xAB GI pAB
+
x
1400 4 π 0.06 80 10 9 32 0.01375rad / m
3）BC 段单位长度扭转角： M xBC BC
M xi li j i 1 GI pi
n
请注意单位长度扭转角和相对扭转角的区别
例4-3 一受扭圆轴如图所示，已知：T1=1400N· m， T2=600N· m， T3=800N· m， d1=60mm，d2=40mm，剪切弹性模量G=80GPa，计 算最大单位长度扭转角。
T1 d1 A
T2 d2 B
第四章
• • • • •
杆件的变形计算
本部分主要内容:
拉压杆的轴向变形 圆轴的扭转变形与相对扭转角 梁的弯曲变形、挠曲线近似微分方程 用积分法求梁的弯曲变形 用叠加法求梁的弯曲变形
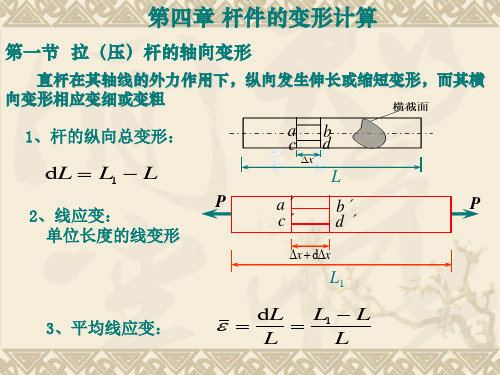
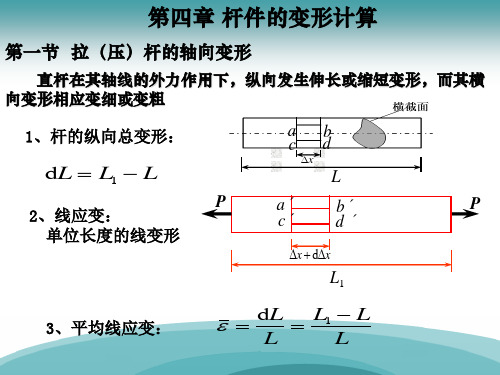
第一节 拉压杆的轴向变形
直杆在其轴线的外力作用下，纵向发生伸长或缩短变形， 而其横向变形相应变细或变粗 杆件在轴线方向的伸长
泊松比ν 、弹性模量 E 、切变模量G 都是材料的弹性常数， 可以通过实验测得。对于各向同性材料，可以证明三者之间存 在着下面的关系
《材料力学》2-4拉(压)杆的变形.胡克定律
拉（压）杆的变形.胡克定律`
杆件在轴向拉压时：
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
1、纵向变形
LLL 绝对变形
线应变: 受力物体变形时，一点处沿 某一方向微小线段的相对变 形
当杆沿长度均匀变形时
L L
纵向线应变 (无量纲)
y
C
O
x
A
B
z △x
当杆沿长度非均匀变形时
αD
B1 BB2C1 C
FNCD
F
A
C
a
CC1
CL CCD ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LC FD LFN1 2CEL D A cLC o DsFCD
2Fa
EAcos2
B
4Fa
EAco3s
移δB。1、已经测出CD杆的轴向应变ε；2、已知CD杆 的抗拉刚度EA.
1. 已知ε
LCD
a
LCDa
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B2LCD 2a
2. 已知EA
LCD
FNCDa EA
mA 0
FNCD2F
B 2L 2 LC FN DCD 4EFFAaL0
例题
2.12
B
图示的杆系是由两根圆截面钢杆铰接而成。已知
L AB L AC F N EA L A C 2 EF c A o Ls
A
A AA
L AC
cos
FL
2EAcos2
杆件在轴向拉压时：
沿轴线方向产生伸长或缩短——纵向变形 横向尺寸也相应地发生改变——横向变形
1、纵向变形
LLL 绝对变形
线应变: 受力物体变形时，一点处沿 某一方向微小线段的相对变 形
当杆沿长度均匀变形时
L L
纵向线应变 (无量纲)
y
C
O
x
A
B
z △x
当杆沿长度非均匀变形时
αD
B1 BB2C1 C
FNCD
F
A
C
a
CC1
CL CCD ccooss
C
C1
L/2
L/2
B
mA 0
FNCD
2F
cos
B1
LC FD LFN1 2CEL D A cLC o DsFCD
2Fa
EAcos2
B
4Fa
EAco3s
移δB。1、已经测出CD杆的轴向应变ε；2、已知CD杆 的抗拉刚度EA.
1. 已知ε
LCD
a
LCDa
D
FNCD
Fa
A
C 刚杆
B
L C1
L
2
2
B1
B2LCD 2a
2. 已知EA
LCD
FNCDa EA
mA 0
FNCD2F
B 2L 2 LC FN DCD 4EFFAaL0
例题
2.12
B
图示的杆系是由两根圆截面钢杆铰接而成。已知
L AB L AC F N EA L A C 2 EF c A o Ls
A
A AA
L AC
cos
FL
2EAcos2
轴向拉(压)杆的变形
（5-8） ε′没有量纲。
轴向拉（压）杆的变形
1.4 泊松比
实验表明，对于同一种材料，当应力不超过比例极
限时，横向线应变与纵向线应变之比的绝对值为常数。比
值ν称为泊松比，亦称横向变形系数。即
(5-9a)
由于这两个应变的符号恒相反，故有
ε'=-νε
(5-9b)
泊松比ν是材料的另一个弹性常数，由实验测得。工
程上常用材料的泊松比见表5-1。
轴向拉（压）杆的变形
工程力学
引入比例常数E，则上式可写为 （5-7）
上式称为胡克定律，这是胡克定律的另一形式。 由式（5-7）可看出，EA越大，杆件的变形Δl就越小，故称EA 为杆件抗拉（压）刚度。工程上常用材料的弹性模量见表5-1。
轴向拉（压）杆的变形
1.3 横向变形
在轴向力作用下，杆件沿轴向的方向伸长（缩 短）的同时，横向尺寸也将缩小（增大）。设横向 尺寸由b变为b1，如图5-8(b)所示，Δb= b1-b，则 横向线应变为
工程力学
轴向拉（压）杆的变形
轴向拉伸（或压缩）时，杆件的变 形主要表现为沿轴向的伸长（或缩短）， 即纵向变形。由实验可知，当杆沿轴向 伸长（或缩短）时，其横向尺寸也会相 应缩小（或增大），即产生垂直于轴线 方向的横向变形。
轴向拉（压）杆的变形
1.1 纵向变形
设一等截面直杆原长为l，横截面面积为A。在轴向拉力F 的作用下，长度由l变为l1，如图5-8（a）所示。杆件沿轴线方 向的伸长为Δl=l1－l，拉伸时Δl为正，压缩时Δl为负。
图5-8
轴向拉（压）杆的变形
杆件的伸长量与杆的原长有关，为了消除杆件长度 的影响，将Δl除以l，即以单位长度的伸长量来表征杆件 变形的程度，称为线应变或相对变形，用ε表形
轴向拉（压）杆的变形
1.4 泊松比
实验表明，对于同一种材料，当应力不超过比例极
限时，横向线应变与纵向线应变之比的绝对值为常数。比
值ν称为泊松比，亦称横向变形系数。即
(5-9a)
由于这两个应变的符号恒相反，故有
ε'=-νε
(5-9b)
泊松比ν是材料的另一个弹性常数，由实验测得。工
程上常用材料的泊松比见表5-1。
轴向拉（压）杆的变形
工程力学
引入比例常数E，则上式可写为 （5-7）
上式称为胡克定律，这是胡克定律的另一形式。 由式（5-7）可看出，EA越大，杆件的变形Δl就越小，故称EA 为杆件抗拉（压）刚度。工程上常用材料的弹性模量见表5-1。
轴向拉（压）杆的变形
1.3 横向变形
在轴向力作用下，杆件沿轴向的方向伸长（缩 短）的同时，横向尺寸也将缩小（增大）。设横向 尺寸由b变为b1，如图5-8(b)所示，Δb= b1-b，则 横向线应变为
工程力学
轴向拉（压）杆的变形
轴向拉伸（或压缩）时，杆件的变 形主要表现为沿轴向的伸长（或缩短）， 即纵向变形。由实验可知，当杆沿轴向 伸长（或缩短）时，其横向尺寸也会相 应缩小（或增大），即产生垂直于轴线 方向的横向变形。
轴向拉（压）杆的变形
1.1 纵向变形
设一等截面直杆原长为l，横截面面积为A。在轴向拉力F 的作用下，长度由l变为l1，如图5-8（a）所示。杆件沿轴线方 向的伸长为Δl=l1－l，拉伸时Δl为正，压缩时Δl为负。
图5-8
轴向拉（压）杆的变形
杆件的伸长量与杆的原长有关，为了消除杆件长度 的影响，将Δl除以l，即以单位长度的伸长量来表征杆件 变形的程度，称为线应变或相对变形，用ε表形
学习情境三 3.拉压杆的变形计算
580 600 200 702
(580 660) 700 2001202
l2
0.355 0.301 0.656(mm)
（2）上、下两部分的线应变之比
1
l1 l1
0.355 600
5.916 10 4
2
l2 l2
0.301 700
4.310 4
l 1 N l EA
＝E
虎克定律的另一种表达形式
上式表明： 在弹性范围内，应力与应变
成正比。
例 图 示 阶 梯 杆 ， 已 知 横 截 面 面 积 AAB=ABC=500mm2 ， ACD=300mm2，弹性模量E=200GPa。试求杆的总伸长。
解 ①作轴力图。
②分段计算变形量。
实验表明，在弹性范围内，杆件的纵向变形与
轴力N、杆长l 成正比，而与杆的横截面积A成反比。
即
l Nl
EA
上式称胡克定律。
E——称为弹性模量 E与材料性质有关，是衡量材料抵抗变形能力的
一个指标，大小由试验测定，单位为Pa。 EA——称为抗拉压刚度 它反映了杆件抵抗拉压变形的能力。
二、虎克定律
l Nl EA
l AB
N ABlAB EA AB
20 103 100 200 103 500 0.02mm
△lBC = -0.01mm △lCD = -0.0167mm
AB C 30kN
D 10kN
100 100 100
FN 20kN
+
O
－
x
10kN
③计算总变形量。
△l = △lAB + △lBC + △lCD = -0.0067mm
材料力学 杆件的变形计算
必知弓力三石者，当弛其弦以绳缓擐之者，谓不张之，别以 一条 绳系两箭，乃加物一石张一尺、二石张二尺、三石张三 尺。其中 “两萧” 就是指弓的两端。 胡：郑老先生讲“每加物一石，则张一尺”。和我讲的完全是同一 个意思。您比我早1500 中就记录下这种正比关系，的确了不起， 真是令人佩服之至』我在1686 年《关于中国文字和语言的研究 和推测》一文中早就推崇过贵国的古代文化：“目前我们还只 是刚刚走到这个知识领域的边缘，然而一旦对它有了充分的认 识，就将会在我们面 前展现出一个迄今为止只被人们神话般
B
30oC2
C
C1
1.44mm
胡：请问，“ 弛其弦，以绳缓援之” 是什么意思 ?
郑：这是讲测量弓力时，先将弓的弦 松开，另外用绳子松松地套住弓 的两端，然后加重物，测量。
胡：我明白了。这样弓体就没有初始应力，处于自然状态。
郑：后来，到了唐代初期，贾公彦对我的注释又作了注疏，他说： 郑又云假令弓力胜三石，引之 中三尺者，此即三石力弓也。
400
400
FN KN 40
2）求伸长量
+
x l l AB lBC
－
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压，AC杆将伸长，而 F BC杆将缩短。
B
30oC2
C
C1
1.44mm
胡：请问，“ 弛其弦，以绳缓援之” 是什么意思 ?
郑：这是讲测量弓力时，先将弓的弦 松开，另外用绳子松松地套住弓 的两端，然后加重物，测量。
胡：我明白了。这样弓体就没有初始应力，处于自然状态。
郑：后来，到了唐代初期，贾公彦对我的注释又作了注疏，他说： 郑又云假令弓力胜三石，引之 中三尺者，此即三石力弓也。
400
400
FN KN 40
2）求伸长量
+
x l l AB lBC
－
20
l AB
FNABl AB EAAB
40 10 3 400 200 10 3 800
0.1mm
伸长
lBC
FNBC l BC EABC
20103 400 0.167mm
200103 240
缩短
l lAB lBC 0.1 0.167 0.067mm 缩短
A
1m
F
B
30o
C
分析
A
B
通过节点C的受力分析可以判断AC 杆受拉而BC杆受压，AC杆将伸长，而 F BC杆将缩短。
杆的变形量计算公式
杆的变形量计算公式
杆件弯曲变形量可以通过杆件的杨氏模量、截面形状、杆件受力状态来计算。
下面是一般情况下杆的变形量计算公式：
1.直杆内力引起的弯曲变形量计算公式：
弯曲变形量(δ)=(M*L)/(E*I)
其中
δ为弯曲变形量
M为杆件的弯矩（Nm）
L为杆件的长度（m）
E为杆件的杨氏模量（Pa）
I为杆件的截面惯性矩（m^4）。
2.断面变形量引起的弯曲变形量计算公式：
弯曲变形量(δ)=(F*L)/(E*A)
其中
δ为弯曲变形量
F为杆件的力（N）
L为杆件的长度（m）
E为杆件的杨氏模量（Pa）
A为杆件的横截面积（m^2）。
这两个公式分别用于计算杆件在受到弯矩和受力作用下的弯曲变形量。
在实际应用中，根据杆件的不同形状和受力情况，可以选择相应的公式进
行计算。
此外，如果杆件的形状不规则，或杆件受力情况较为复杂，可以使用
数值方法来计算杆的变形量。
常用的数值方法包括有限元分析、杆件切割
法等。
综上所述，杆的变形量计算公式是根据杆件的弹性特性和几何形状推
导而来的。
通过这些公式，我们可以计算出杆件在受到弯矩和受力作用下
的弯曲变形量，为工程设计和结构分析提供了依据。
但在实际应用中，还
需要考虑一些特殊情况，并使用合适的数值方法进行计算。
轴向拉压杆的变形
1.求出两杆的轴力
Fx 0 FN2 FN1 cos300 0 Fy 0 FN1 sin300 F 0
FN1 20kN（拉） FN 2 17.3kN（压）
A 1
F 2 30°
C
(a)
B
FN1
30
B
FN2
F
(b)
2.计算两杆的变形
l1
FN1l1 E1 A1
20 103 2 2 105 106 600 106
(60 103
1
20 103
2
30 103
1.5)
0.65 103 (m)
l 0.65 103 (m)
变形计算的应用：三角桁架节点位移的求法。
怎样画小变形放大图？
分析：
A
L1
图1
B L2
（1）、研究节点 C 的受力，确定各 杆的内力 FNi；
（2）、求各杆的变形量△Li ；
C
（3）、变形图严格画法，图中弧线；
60kN 80kN 50kN 30kN
解： 应用截面法求得各段横截 面上的轴力如下：
AB段 FN1 60kN BC段 FN2 60 80 20kN CD段 FN3 30kN
AB 1m 2m
(a) 60kN
CD 1.5m
30kN
20kN (b)
得各段横截面上的正应力为：
AB段 BC段 CD段
L FN L EA
----胡克定律
E——弹性模量与材料有关，单位——同应力。 EA——抗拉压刚度。
注意 ①当各段的轴力为常量时——
L L1 L2 L3
FNi Li EAi
②当轴力为x的函数时 N=N(x)——
L dL1 dL2 dL3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F
a1
横向变形为 a = a 1- a
2.线应变——杆件单位长度内的变形量。
l l1 l 纵向线应变： l l a a1 a 横向线应变： a a
拉伸时， ﹥0， ' ﹤0；压缩时， ﹤0， ' ﹥0。 3.泊松比μ（横向变形系数） 实验结果表明：一定范围内，杆件的横向线应变 与纵向线应变的比值为一常数。即 ' =-
10kN
x
练习1．图示等截面直杆，其横截面面积A=4000cm2， 材料的弹性模量E=2×108Pa，试分别求上、下段的应力 和变形量。
300kN A B
3m
400kN
4m
C
小结： 1.应力与应变关系:
虎克定律:
Nl l EA
＝E
2.拉压杆的变形计算
Nl l EA
应用时注意：N的正负要代入公式中计算。
A B C 30kN D
②分段计算变形量。 N ABl AB l AB EAAB
10kN
100
100
100
FN 20kN + 20103 100 0.02mm O 3 20010 500
－
△lBC = -0.01mm △lCD = -0.0167mm ③计算总变形量。 △l = △lAB + △lBC + △lCD = -0.0067mm
复习：
1.轴向拉压的受力特点和变形特点；
2．轴力的计算及轴力图的绘制
轴力的计算：N=∑F左或N=∑F右
轴力图作图规律：
左上右下，突变值等于外力的大小。
3．轴向拉(压)杆横截面上的正应力的计算。
N A
第三节 拉压杆的变形及虎克定律
一、纵向变形和横向变形
l1
a1
F
l
F
a
F
l1
1. 纵向变形为 l=l1- l
作业：图示轴向受压柱的横截面面积为A＝0.8m2，承受 压力P=2000kN作用，已知柱长4m材料的弹性模量 E=2000MPa，试求该柱底截面所受应力及柱顶的位移。
P
二、虎克定律
Nl l EA
l 1 N l E A
＝E
虎克定律的另一种表达形式
上式表明： 在弹性范围内，应力与 应变 成正比。
例 图 示 阶 梯 杆 ， 已 知 横 截 面 面 积 AAB=ABC=500mm2 ， ACD=300mm2，弹性模量E=200GPa。试求杆的总伸长。 解 ①作轴力图。
二、虎克定律
实验表明，在弹性范围内，杆件的纵向变形与 轴力N、杆长l 成正比，而与杆的横截面积A成反比。 即
Nl l ቤተ መጻሕፍቲ ባይዱEA
上式称胡克定律。 E——称为弹性模量 E与材料性质有关，是衡量材料抵抗变形能力的 一个指标，大小由试验测定，单位为Pa。 EA——称为抗拉压刚度 它反映了杆件抵抗拉压变形的能力。