3.2 LU分解(录像用)
浅谈矩阵的LU分解和QR分解及其应用

浅谈矩阵的LU分解和QR分解及其应用基于理论研究和计算的需要,往往有必要把矩阵分解为具有某种特性的矩阵之积,这就是我们所说的矩阵分解.本文将介绍两种常用的矩阵分解方法,以及其在解线性方程组及求矩阵特征值中的应用.1.矩阵的LU 分解及其在解线性方程组中的应用1.1高斯消元法通过学习,我们了解到利用Gauss消去法及其一些变形是解决低阶稠密矩阵方程组的有效方法. 并且近些年来利用此类方法求具有较大型稀疏矩阵也取得了较大进展. 下面我们就通过介绍Gauss 消去法,从而引出矩阵的LU 分解及讨论其对解线性方程组的优越性.首先通过一个例子引入:(1.1)例1, 解方程组(1.2)(1.3)解. Step1 (1.1) ( 2) (1.3) 消去(1.3)中未知数, 得到4x2 x3 11 (1.4)Shep2 . (1.2) (1.4) 消去(1.4) 中的未知数x2x1 x2 x3 6 1有4x2x3 5 显然方程组的解为x* 2 上述过程相当于2x3 6 31 1 1 6 1 1 1 6 1 1 1 60 4 1 5 0 4 1 5 0 4 1 52 2 1 10 4 1 100 2 62)+ (r i 表示矩阵的i行)由此看出,消去法的基本思想是: 用逐次消去未知数的方法把原方程化为与 其等价的三角方程组 .下面介绍解一般 n 阶线性方程组的 Gauss 消去法 .a11a1nx 1b 1设AXb则n 阶线性方程组a n1annx nb nAX b (1.5) 并且 A 为非奇异矩阵 .通过归纳法可以将 AX b 化为与其等价的三角形方程,事实上: 及方程(1.5)为A 1 X b 1 ,其中A1Ab 1b(1) 设 a 1(11)0,首先对行计算乘数 mi1a i11m 111. 用 m i1乘 (1.5)的第一个方程加到第 i i 2,3, ,n 个方程上 .消去方程 (1.5)的第 2个方程直到第 n 个方程的未知数 x . a 111 得到与 (1.5) 等价的方程组A 2 b 2(1.6)其中 a ij 2a ij 1m i1a ij 1b i 2b i 1m i1b 11(2) 一般第 k 1 k n 1 次消去,设第 k 1步计算完成 . 即等价于A kX b k(1.7)a 111 a 112 a222且消去未知数 x 1,x 2, ,x k 1.其中 A kb 11简记作 b n 2由设 D i 0(i 1, ,k)及式 (1.8)有 a kk k设 a k (kk) 0 计 算 m ik a ik k/a k kk (ik= 1, n,ikn用 m ik aa ik k (i k 1, ,n) 消去 第k 1 个 方 程直 到第 n 个 方 程的 未知 数 x k . 得 到与 (1. 7等)价的 方 程组 A k 1X b k 1故由数学归纳法知,最后可以把原方程化成一个与原方程等价的三 角方程组 . 但是以上分析明显存在一个问题,即使 A 非奇异也无法保证 a ii i0, 需要把非奇异的条件加强 .D i 0. 即a11 D1 a11 0,Dkak1aikakk证明 利用数学归纳法证明引理的充分性 . 显然,当 k 1 时引理的充分性是成 立的,现在假设引理对 k 1是成立的,求证引理对 k 亦a ii i0 i 1,2 k 1 于是可用 Gauss 消去法将中,即a 111 a 121a 222A1 A ka kk a 11na 22nka knD 2a122 a 111 a 222a 222Dka n k ka n knnnD 3 a 111 a 222 a 333a2ka 111 a 222 a kk k(1.8)a k kka 222显然,由假设 a ii10 i 1,2 k ,利用(1.8) 亦可以推出D i 0(i 1, ,k) 从而由此前的分析易得;定理 1 如果n阶矩阵A的所有顺序主子式均不为零,则可通过Gauss消去法(不进行交换两行的初等变换) ,将方程组(1.5) 约化成上三角方程组,即a111a112a11n x1 b11a222 a22n x2 b22(1.9)a n n n x nb n n1.2矩阵LU 分解从而由以上讨论即能引出矩阵的LU 分解,通过高等代数我们得知对 A 施行行初等变换相当于用初等矩阵左乘A,即L1A1 A2 L1b 1 b2其中1m21 1L1m n1 0 1一般第k 步消元,,相当于L k A k A k 1 Lkb k b k 1重复这一过程,最后得到L n 1 L2L1A1A nn 1 2 11 n(1.10)L n 1 L2L1b 1 b n1m k 1,k 1m nk将上三角形矩阵A n记作U,由式(1.9)得到A=L11L21L n11U LU ,其中其中1m21 1m n1 m n2 1 由以上分析得;定理 2 (LU 分解) 设 A 为n阶矩阵,如果 A 的顺序主子式D i 0(i 1,2,, n 1). 则 A 可分解为一个单位下三角矩阵 L 和一个上三角矩阵 U的乘积,且这种分解是唯一的 .证明 由先前的分析得出存在性是显然的,即 A LU . 下证唯一性 ,设A LU CD 其中 L , C 为单位下三角矩阵, U , D 为上三角矩阵 . 由于D 1 L C UD 上式右端为上三角矩阵,左端为单位下三角矩阵,从而上式两端都 必须等于单位矩阵,故 U D , L C . 证毕.11 例 2 对于例子 1 系数矩阵矩阵 A 0 4 22 结合例 1,故1 0 0 1 1 1A LU0 1 0 0 4 121 10 2对于一般的非奇异矩阵, 我们可以利用初等排列矩阵 I ki (由交换单位矩阵 I的第 k 行与第 i k 行得到),即L 1I 1i 1A 1 A 2 ,L 1I 1i 1b 1 b21 1 (1.11) L k I ki kA k A k 1 ,L k I ki kb kbk 1(1.11)利用(1.11)得L n 1I n 1,i n 1 L 1I 1i 1A AU .简记做. 其中面就 n 情况来考察一下矩阵A AL4I 4i 4L 3I 3i 3L 2I 2i 2L 1I 1i 1A L 4 I 4i 4L 3I 4i 4 (I 4i 4I3i 3I 2i 2L 1I 4i 4I 3i 3I 2i 2) (I 4i 4 I 3i 3I 2i 2I 1i 1)A11 由 Gauss 消去法,得(I4i 4 I 3i 3L 2I 4i 4I 3i 3 )从而记从而容易的为单位下三角矩阵, 总结以上讨论可得如下定理.定理3 如果A非奇异矩阵,则存在排列矩阵P使PA LU 其中L为单位下三角矩阵,U 为上三角矩阵.1.3矩阵LU 分解的应用以上对非奇异矩阵 A 的LU 分解进行了全面的讨论,一下我们就简单介绍一下应用.对于矩阵A一旦实现了LU 分解,则解线性方程的问题,便可以等价于:(1) Ly b 求y (2) Ux=y , 求x (1.12)即,设 A 为非奇异矩阵,且有分解式 A LU ,其中三角矩阵。
LU分解法

(5)xn = yn ,对 i=n-1,…1
求 xi : xi =(yi -
Байду номын сангаас
n
(6)输出 xi (i=1,2,…n),结束 五、实验程序 (1)建立 LU_1.m 文件
(2)建立 backsub.m 文件
(3)建立 upsub.m 文件
(4)算法的实现: 输入 A=[-5 2 -1;1 0 3;3 1 6]得到 A;输入 B=[3 1 6;1 0 3;-5 2 -1] 得到 B; 在输入[L U]=LU_1(A),得到 L 和 U 的值。再输入[X]=backsub(A,B), 按回车得到 X 的值;载输入[Y]=upsub(A,B),按回车得到 Y 的值。
六、实验结果
七、实验结果分析:高斯消去法简单易行,计算量小且结果精确。可以算出多个 值。
实验总结:三角分法算出了 X 和 Y 值,高斯消去法算出了 RA,RB,n ,X 的值。 其中它们都可以解出 X 的值,且 X 的值完全相同。
实验报告一
一、实验名称:LU三角分法解线性方程组; 二、实验目的:熟练掌握LU三角分法的基本原理及其应用; 三、实验原理 设无行交换变换的高斯消去可求解一般线性方程组 AX=B, 则矩阵 A 可分解为 一个下三角形矩阵 L 和一个上三角形矩阵 U 的乘积:A=LU(L 的对角线元素 为 1,U 的对角线元素非零)。得到L和U后,可通过如下步骤得到X: (1) 利用前向替换法对方程组LY=B求解Y。(2)利用回代法对方程组UX =Y,求解X。 四、实验步骤 (1)输入 A,B; (2)对 j=1,2,…n 求 u1j : u1j = a1j ,对 i=1,2,…n 求 li1 : li1 = ai1 /u11; (3)对 r=1,2,…n 做如下步骤: ①urj = arj -
拟三对角矩阵的lu分解

拟三对角矩阵的lu分解
拟三对角矩阵的LU分解是指将一个矩阵分解成一个上三角矩阵和
一个下三角矩阵的乘积,即化为一串次三角形矩阵乘积之和;即将矩
阵A=LU,其中L是一个下三角矩阵,U是一个上三角矩阵。
如果矩阵
A是拟三角形矩阵,则LU分解的过程特别简单。
只需要计算出上三角形矩阵的主对角元素Uii,然后从上往下逐行计算出Uij(i为行号,j为列号)、Lij(i为行号,j为列号)即可。
另外,因为A是拟三角形矩阵,LU的过程中,只需要做单正(正则)
的三角形运算即可,不存在向量乘法等运算,所以,LU 分解是一种非
常高效的方法。
lu分解例题及解析

lu分解例题及解析Lu分解法是一种将矩阵分解为低秩矩阵的分解方法,主要应用于数据分析、图像处理等领域。
下面以一个例题来介绍Lu分解法的具体步骤及解析过程。
假设有如下矩阵A:$$\begin{bmatrix}2 & 1 & 4 \\8 & 7 & 2 \\6 & 3 & 5 \\\end{bmatrix}$$步骤1:选取矩阵A的第一行作为初始行,将其作为下三角矩阵L的第一行,确定上三角矩阵U的第一行,即:$$L=\begin{bmatrix}1 & 0 & 0 \\l_{21} & 1 & 0 \\l_{31} & 0 & 1 \\\end{bmatrix},U=\begin{bmatrix}u_{11} & u_{12} & u_{13} \\0 & u_{22} & u_{23} \\0 & u_{32} & u_{33} \\\end{bmatrix}$$那么,可以得到:$$\begin{bmatrix}2 & 1 & 4 \\8 & 7 & 2 \\6 & 3 & 5 \\\end{bmatrix}=\begin{bmatrix}1 & 0 & 0 \\& 1 & 0 \\& & 1 \\\end{bmatrix}\begin{bmatrix}& & \\& & \\& & \\\end{bmatrix}$$因此,需要确定L和U的未知量l21、l31、u11、u12、u13、u22、u23和u33。
步骤2:用第一行的元素对矩阵A进行初等变换,使得第一列的下两个元素都为0,即:$$\begin{bmatrix}2 & 1 & 4 \\8 & 7 & 2 \\6 & 3 & 5 \\\end{bmatrix}\xrightarrow{(R_2-4R_1)}\begin{bmatrix}2 & 1 & 4 \\0 & 3 & -14 \\6 & 3 & 5 \\\end{bmatrix}$$此时,可得到:$$\begin{bmatrix}2 & 1 & 4 \\8 & 7 & 2 \\6 & 3 & 5 \\\end{bmatrix}=\begin{bmatrix}1 & 0 & 0 \\& 1 & 0 \\& & 1 \\\end{bmatrix}\begin{bmatrix}u_{11} & u_{12} & u_{13} \\0 & ? & ? \\0 & ? & ? \\\end{bmatrix}$$可以看出,u11=2,u12=1,u13=4。
lu分解原理

LU分解是一种矩阵分解方法,可以将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积。
这种分解方法在数值计算中非常常用,可以用于求解线性方程组、求矩阵的行列式和逆矩阵等问题。
LU分解的原理比较简单,本文将对其进行详细介绍。
1. LU分解的定义LU分解是将一个矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积的过程,即A=LU。
其中,L是一个下三角矩阵,U是一个上三角矩阵。
下三角矩阵指除主对角线及其上方的元素外,其他元素均为0的矩阵;而上三角矩阵则是指除主对角线及其下方的元素外,其他元素均为0的矩阵。
2. LU分解的实现方法LU分解的实现方法有很多种,这里我们介绍其中的高斯消元法和克洛内克积分法。
(1)高斯消元法高斯消元法是一种经典的线性代数求解方法,它可以通过不断消元来把一个矩阵变成一个上三角矩阵。
具体来说,高斯消元法的过程如下:①首先将待分解的矩阵A赋值给一个新的矩阵U。
②初始化一个下三角矩阵L为单位矩阵。
③从第一行开始,对每一行做如下操作:a. 将该行的第一个非零元素除以该元素所在的系数,使其成为1。
b. 将该行的第一个元素下方的所有元素消为0,即对该行下面的所有行做如下操作:i. 将该行下面的行的第一个元素除以当前行第一个元素的值,使其变成0;ii. 将当前行乘以该行第一个元素的值,减去该行下面的行。
④最终得到的矩阵U就是原矩阵A的上三角矩阵,而L则是通过每一次操作中的系数变换所得到的下三角矩阵。
(2)克洛内克积分法克洛内克积分法是一种比较高效的LU分解方法,它采用矩阵的Kronecker积来进行分解。
具体来说,克洛内克积分法的过程如下:①首先将待分解的矩阵A赋值给一个新的矩阵U。
②将下三角矩阵L初始化为单位矩阵。
③对于每一列j,做如下操作:a. 将矩阵U的第j列中j行及其下方的元素除以U(j,j),使U(j,j)为1。
b. 将矩阵U的第j列下方的所有元素消为0,即对该列下面的所有列做如下操作:i. 将该列下面的列的第j行的元素除以当前列第j 行的元素值,使其变成0;ii. 将当前列乘以该列第j行的元素值,减去该列下面的列。
三阶矩阵的lu分解法试验总结

三阶矩阵的lu分解法试验总结LU分解是一种矩阵分解方法,将一个三阶矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积。
在试验中,我使用了LU分解法来分解三阶矩阵,并总结了一些关键的观察和结论。
首先,我使用了具有不同特性的几个三阶矩阵进行试验。
通过分解这些矩阵,我发现LU分解可以很好地解决线性方程组。
对于具有唯一解的矩阵,分解结果中的L矩阵是单位下三角矩阵,而U矩阵是上三角矩阵。
这两个矩阵的乘积即原始矩阵。
其次,我对矩阵的特殊性质进行了试验。
具体而言,我测试了非奇异矩阵、对角矩阵和可逆矩阵。
对于非奇异矩阵,LU分解仍然有效,并且分解结果中L和U的对角线上的元素均为非零值。
对于对角矩阵,分解结果中的L矩阵和U矩阵均为对角矩阵,并且相应对角线上的元素分别为原始矩阵对角线上的元素的累积乘积。
对于可逆矩阵,LU分解结果中的L和U矩阵仍然是可逆的,并且它们的乘积与原始矩阵相等。
在试验过程中,我还发现了一些有趣的现象。
特别是当原始矩阵具有一些特殊的性质时,LU分解具有一些特定的特征。
例如,如果原始矩阵的某个行或列是线性相关的,则分解过程中会出现零元素。
此外,如果原始矩阵是对称的,则分解结果中具有相同的性质。
此外,在试验过程中,我还探讨了LU分解的计算复杂度。
通过分析算法,我发现LU分解需要进行若干次基本操作,如乘法和加法。
由于分解结果中L矩阵的非零元素数量与原始矩阵的元素数量相等,而U 矩阵的非零元素数量小于原始矩阵的元素数量,所以LU分解的计算复杂度为O(n^3)。
这意味着在处理大规模矩阵时,LU分解可能会变得非常耗时。
最后,我还进行了一些数值试验,以验证LU分解的准确性。
我通过计算分解结果的乘积来验证它们是否与原始矩阵相等。
在我的试验中,分解结果与原始矩阵的乘积非常接近,差异可以归因于数值计算的舍入误差。
这进一步证明了LU分解的准确性和有效性。
综上所述,通过我的试验和总结,LU分解是一种有效的矩阵分解方法,特别适用于解决线性方程组。
矩阵a的lu分解

矩阵a的lu分解
通过矩阵a的LU分解,可以更快速地解决数学问题,这也是数值分析中常用
的方法之一。
矩阵是数学中一种重要的数据结构,它可以用来表示一组特定的值。
应用LU
分解的理论,可以将原有的矩阵a分解为一个下三角矩阵和一个上三角矩阵。
其中,下三角矩阵称为L(横向因子),上三角矩阵称为U(纵向因子)。
两个矩阵相乘,就可以得到比原来矩阵a更简单的矩阵,从而更容易计算。
LU分解是一种稳定的方法,可以有效地减少计算量,提高计算速度。
LU分解
本身很容易理解,但是要仔细分析它的特征。
LU分解以保持矩阵a的正定性为基础,可以避免矩阵的奇异性造成的计算错误。
另外,LU分解的计算可以在局部范
围内进行,这使其很容易用于分布式环境中的复杂计算。
事实上,LU分解的应用确实很广泛。
它不仅用于高精度的数据分析,而且在
非线性方程、积分处理和多元极值计算等领域都有应用。
此外,由于LU分解涉及
矩阵乘法,还有可能用于计算机图形学中的模糊图像建模和计算重建。
总之,矩阵a的LU分解是一种简单有效的数值分析方法,可以加快计算速度,提高计算精度,并具有多种应用前景。
未来,在不同的领域,我们仍会不断研究
LU分解的精妙之处,并以此改善计算的效率,开发出更多新的应用。
lu分解基本内容

lu分解基本内容一、什么是lu分解?LU分解(LU decomposition)是一种线性代数的分解方法,用于将矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
这种分解方法可以方便地解决线性方程组的求解、矩阵的求逆和矩阵的行列式计算等问题。
二、为什么需要lu分解?1. 线性方程组的求解:对于给定的线性方程组,可以通过LU分解将其转化为两个更简单的方程组进行求解,从而节省计算时间和资源。
2. 矩阵的求逆:通过LU分解可以得到矩阵的逆矩阵,从而可以方便地进行矩阵的运算和变换。
3. 矩阵的行列式计算:通过LU分解可以将矩阵的行列式转化为下三角矩阵和上三角矩阵的行列式的乘积,从而简化计算过程。
三、LU分解的步骤1. 将原始矩阵表示为一个下三角矩阵L和一个上三角矩阵U的乘积:A = LU。
2. 首先,通过高斯消元法将原始矩阵A转化为一个上三角矩阵U,同时记录每一步的消元操作。
3. 接下来,将记录的消元操作应用到一个单位下三角矩阵上,得到一个下三角矩阵L。
4. 最终得到的L和U就是原始矩阵A的LU分解结果。
四、如何应用LU分解?1. 求解线性方程组:将线性方程组的系数矩阵进行LU分解,然后利用分解结果求解方程组。
2. 求解矩阵的逆:将需要求逆的矩阵进行LU分解,然后利用分解结果求解矩阵的逆矩阵。
3. 计算矩阵的行列式:将矩阵进行LU分解,然后利用分解结果计算矩阵的行列式。
五、LU分解的优缺点1. 优点:- LU分解可以减少计算复杂度,提高求解速度。
- 通过LU分解可以方便地进行矩阵的运算和变换。
2. 缺点:- LU分解可能存在数值不稳定性的问题,导致分解结果的精度下降。
- LU分解可能需要较大的存储空间,对于大型矩阵计算可能会受到限制。
六、总结LU分解是一种常用的线性代数分解方法,可以将矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
它可以用于解决线性方程组的求解、矩阵的求逆和矩阵的行列式计算等问题。
通过LU分解可以方便地进行矩阵的运算和变换,提高计算效率。
数值实验三 LU分解法的优点

数值实验三LU分解法的优点一:实验目的给定矩阵A与向量b A=[nn−1⋮21n⋮32⋱……对称nn−1n]b=[1⋮0](1)求A的LU分解(2)利用A的LU分解解下列方程:①A*x=b ②A2∗x=b③A3∗x=b对第③题分析一下,如果先求M=A3,再解M*相比有何缺点?(3)利用A的LU分解法求A−1 ,其中n由自己选择,例如取n=5三:实验过程实验代码:Option Base 1Dim a() As Single, u() As Single, l() As SinglePrivate Sub Command1_Click()Dim m As Integer, p As Integer, n As Integer, k As Integer, i As Integer, j As Integer, s As Integer, t As Singlen = Val(Text1.Text)ReDim a(n, n), u(n, n), l(n, n)For i = 1 To nFor j = i To na(i, j) = n + i - ja(j, i) = n + i - jNextNextt = 0For k = 1 To nFor j = k To nt = 0For s = 1 To k - 1t = t + l(k, s) * u(s, j)Nextu(k, j) = a(k, j) - tNextIf k <> n ThenFor i = k + 1 To nt = 0For s = 1 To k - 1t = t + l(i, s) * u(s, k)Nextl(i, k) = (a(i, k) - t) / u(k, k)NextEnd IfNextFor m = 1 To nl(m, m) = 1NextFor i = 1 To nFor j = 1 To nText2.Text = Text2.Text & a(i, j) & vbCrLfNextNextFor i = 1 To nFor j = 1 To nText3.Text = Text3.Text & l(i, j) & vbCrLfNextNextFor i = 1 To nFor j = 1 To nText4.Text = Text4.Text & u(i, j) & vbCrLfNextNextEnd SubPrivate Sub Command2_Click()Dim y() As Single, x() As Single, b() As SingleDim n As Integer, k As Integer, i As Integer, j As Integer, s As Integer, t As Singlen = Val(Text1.Text)ReDim y(n), x(n), b(n)b(1) = 1For i = 2 To nb(i) = 0Next iFor k = 1 To nt = 0For s = 1 To k - 1t = t + l(k, s) * y(s)Nexty(k) = b(k) - tNextFor k = n To 1 Step -1t = 0For s = k + 1 To nt = t + u(k, s) * x(s)Nextx(k) = (y(k) - t) / u(k, k)NextFor i = 1 To nText5.Text = Text5.Text & x(i) & vbCrLfNextEnd SubPrivate Sub Command3_Click()Dim y() As Single, x() As Single, b() As SingleDim n As Integer, k As Integer, i As Integer, j As Integer, s As Integer, t As Single n = Val(Text1.Text)ReDim y(n), x(n), b(n)b(1) = 1For i = 2 To nb(i) = 0Next iFor i = 1 To 2For k = 1 To nt = 0For s = 1 To (k - 1)t = t + l(k, s) * y(s)Nexty(k) = b(k) - tNextFor k = n To 1 Step -1t = 0For s = k + 1 To nt = t + u(k, s) * x(s)Nextx(k) = (y(k) - t) / u(k, k)NextFor j = 1 To nb(j) = x(j)NextNextFor i = 1 To nText6.Text = Text6.Text & b(i) & vbCrLfNextEnd SubPrivate Sub Command4_Click()Dim y() As Single, x() As Single, b() As Single, v() As SingleDim n As Integer, k As Integer, i As Integer, j As Integer, s As Integer, t As Single n = Val(Text1.Text)ReDim y(n), x(n), b(n)b(1) = 1For i = 2 To nb(i) = 0Next iFor i = 1 To 3For k = 1 To nt = 0For s = 1 To (k - 1)t = t + l(k, s) * y(s)Nexty(k) = b(k) - tNextFor k = n To 1 Step -1t = 0For s = k + 1 To nt = t + u(k, s) * x(s)Nextx(k) = (y(k) - t) / u(k, k)NextFor j = 1 To nb(j) = x(j)NextNextFor i = 1 To nText7.Text = Text7.Text & b(i) & vbCrLfNextEnd SubPrivate Sub Command5_Click()EndEnd SubPrivate Sub Command6_Click()Dim y() As Single, x() As Single, b() As Single, v() As SingleDim n As Integer, k As Integer, i As Integer, j As Integer, s As Integer, t As Singlen = Val(Text1.Text)ReDim v(1 To n, 1 To n)ReDim y(1 To n)For i = 1 To nReDim b(1 To n)b(i) = 1For k = 1 To nt = 0For s = 1 To k - 1t = t + l(k, s) * y(s)Nexty(k) = b(k) - tNextFor k = n To 1 Step -1t = 0For s = k + 1 To nt = t + u(k, s) * v(s, i)Nextv(k, i) = (y(k) - t) / u(k, k)NextNextFor i = 1 To nFor j = 1 To nText8.Text = Text8.Text & v(i, j) & vbCrLfNextNextEnd Sub四:实验结果当n=10时A*x=b的解x1=【0 .5454544,-0.4999996,-3.971573E-07,2.5836E-07,-1.444715E-07,−18.344654E-08,-5.188799E-08,2.407111E-08,-3.632159E-08,4.545457E-02】A2∗x=b的解为x2=【0.5495862,-0.7727261,0.2499987,8.174827E-07,-4.631004E-07,−13.457071E-07,-2.65427E-07,9.026667E-08,-2.272733E-02,4.958682E-02】A3∗x=b的解为x3=【0.6883911,-1.172518,0.6363608,-0.1249981,-1.1815E-06−19.874508E-07,-7.902941E-07,1.136398E-02,-4.752079E-02,6.339223E-02】五:实验分析LU分解法比较简便迅速,当解多个系数矩阵为A的线性方程做时,LU分解法就显得特别优越,只要对系数矩阵做一次LU分解,以后只要解三角形方程即可。
lu分解的充要条件及证明

lu分解的充要条件及证明题目:LU分解的充要条件及证明引言:LU分解是线性代数中常用的一种矩阵分解方法,它将一个方阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积。
在实际问题的求解中,LU 分解有着广泛的应用,如线性方程组的求解、矩阵求逆等。
本文将从充要条件的角度出发,对LU分解进行详细的论述和证明。
一、LU分解的定义和基本概念LU分解是将一个n×n矩阵A分解为两个矩阵L和U相乘的形式,其中L 是一个下三角矩阵,U是一个上三角矩阵。
即,A=LU。
其中,下三角矩阵L的对角线元素均为1。
下面将给出LU分解的充要条件及证明。
二、充要条件的论述为了得到LU分解的充要条件,我们需要明确以下两个问题:1. 矩阵A是否存在LU分解?2. 如果存在LU分解,那么L和U的形式是否是唯一的?以下,我们将对上述两个问题进行逐步讨论。
2.1 矩阵A的非奇异性首先,我们需要确定矩阵A是否为非奇异矩阵。
如果A不是奇异矩阵,即A ≠0,则存在A的逆矩阵A^-1。
为了证明矩阵A的非奇异性是LU分解的充要条件,我们需要证明如果A是奇异矩阵,那么不存在LU分解。
证明思路:假设A是奇异矩阵,存在一个非零向量x使得Ax=0。
我们令L和U分别为A的LU分解矩阵,则有A=LU。
将其代入Ax=0可以得到LUx=0。
由于L和U都是三角矩阵,LUx=0意味着L(Ux)=0。
根据矩阵乘法的性质,我们可以推出Ux=0。
然而,对于非零向量x,如果Ux=0,则矩阵U的第一行必然存在一个为非零的元素,否则U为奇异矩阵,与U是上三角矩阵的定义相矛盾。
因此,我们可以得出结论:如果存在一个非零向量x使得Ax=0,那么矩阵U不能是上三角矩阵。
因此,如果A是奇异矩阵,则不存在LU分解。
综上所述,矩阵A的非奇异性是存在LU分解的充要条件。
2.2 L和U的唯一性接下来,我们研究如果A存在LU分解,L和U的形式是否是唯一的。
对于一个给定的矩阵A,其LU分解为A=LU。
matlab的lu分解 -回复

matlab的lu分解-回复Matlab的LU分解在数值线性代数中,LU分解是一种常用的矩阵分解方法,广泛应用于求解线性方程组、矩阵求逆和求解特征值等问题。
LU分解的基本思想是将一个矩阵分解为一个下三角矩阵L和一个上三角矩阵U的乘积,即A = LU。
在本文中,我们将深入探讨Matlab中的LU分解,介绍它的实现步骤以及一些应用案例。
首先,让我们来了解一下Matlab中LU分解的函数lufact。
该函数可用于计算矩阵A的LU分解,返回两个矩阵L和U以及一个置换向量P。
L 是一个单位下三角矩阵,U是一个上三角矩阵,P是一个置换向量,用于指示行交换的顺序。
在使用lufact函数之前,我们需要将问题转化为矩阵形式。
考虑一个线性方程组Ax = b,其中A是一个n×n的方阵,x是一个n维向量,b是一个n维向量。
我们可以将该方程组表示为矩阵形式Ax = b,其中A是一个n×n的矩阵,x和b是n维列向量。
现在我们将使用LU分解来解决这个线性方程组。
步骤1:导入数据和设置变量在开始之前,我们需要导入问题中的数据并设置相应的变量。
在Matlab 中,我们可以使用矩阵和向量来表示这些数据。
例如,我们可以使用矩阵A表示系数矩阵A,向量b表示常数向量b,向量x表示未知变量x。
matlabA = [1, 2, 3; 4, 5, 6; 7, 8, 10];b = [3; 6; 9];x = zeros(size(b));步骤2:进行LU分解接下来,我们可以使用lufact函数来计算矩阵A的LU分解。
matlab[L, U, P] = lufact(A);在这里,我们可以看到函数lufact将输入矩阵A分解为下三角矩阵L和上三角矩阵U,并返回一个置换向量P。
请注意,由于LU分解可能需要进行行交换,所以在求解线性方程组之前,我们需要根据置换向量P重新排列矩阵A和向量b。
步骤3:通过前/回代求解线性方程组现在,我们可以使用LU分解来求解线性方程组Ax = b。
三对角矩阵lu分解

三对角矩阵lu分解三对角矩阵,是一种特殊的矩阵,也称为三对角矩阵。
其特点是在主对角线的上下两条对角线上,每个非零元素仅在其对角线的相邻两条对角线上有一个元素。
因此,它的非零元素只有3个对角线上的元素。
在实际计算中,三对角矩阵常常是常见的。
为了方便的解决三对角矩阵的求解问题,可以使用LU分解方法。
LU 分解是一种数学问题处理技术,其旨在将矩阵分解成“下三角矩阵”和“上三角矩阵”的乘积形式,从而简化了复杂性。
下面将介绍三对角矩阵LU分解的具体过程。
1.确定矩阵形式:三对角矩阵中,对角线上的元素为主对角线元素,上下两条对角线上的元素为辅对角线元素。
为了利用LU分解方法,需要将三对角矩阵转化成下三角矩阵和上三角矩阵相乘的形式,因此需要确定要分解的三对角矩阵的形式。
2.分解下三角矩阵:首先,通过高斯消去法,将三对角矩阵转化为下三角矩阵的形式。
下三角矩阵是指在转换后,位于主对角线下方的所有元素都是零。
在这个过程中,需要逐列消去所有非零辅对角线元素。
此时,矩阵的主对角线上的所有元素将会被替换为与它处于同一列的辅对角线下方的元素之和。
这个过程需要重复执行,直到将矩阵转化成一个下三角矩阵。
3.分解上三角矩阵:接着,通过较简单的方法将下三角矩阵分解成上三角矩阵的形式。
上三角矩阵是指在转化后,位于主对角线上方的所有元素都是零。
在这个过程中,需要将矩阵的每一行上下翻转,然后再执行与第二步类似的高斯消去操作。
这个过程同样需要重复执行,直到将矩阵转化成一个上三角矩阵。
4.求解分解后的矩阵:在完成上述步骤之后,可以通过将分解后的下三角矩阵和上三角矩阵相乘,进而获得原始的三对角矩阵。
这个步骤只需要进行矩阵乘法运算即可。
通过上述步骤,可以利用LU分解方法求解三对角矩阵。
它比直接求逆矩阵的方法更加高效,也更适合在计算机上使用,因为它不需要进行倒置操作。
不过,在LU分解过程中,需要小心处理矩阵缩放问题和行转置等操作,以避免误差的出现。
python lu分解后回代法解三角方程ly=b及ux=y

python lu分解后回代法解三角方程
ly=b及ux=y
Python中,可以使用lu分解后回代法解三角方程ly=b及ux=y,其具体步骤如下:
1. 计算矩阵A的LU分解,使用`LU_decomposition`函数:
```python
L, U = LU_decomposition(A)
```
其中,`LU_decomposition`函数用于计算矩阵A的LU分解,返回L和U矩阵。
2. 使用L矩阵求解Ly=b:
```python
y = np.zeros_like(b)
n = A.shape(0)
# Solve Ly = b
for i in range(n):
y(i) = b(i)
for j in range(i):
y(i) -= L(i,j)*y(j)
y(i) /= L(i,i)
```
其中,`np.zeros_like(b)`用于创建与b具有相同形状的零矩阵,然后使用循环求解方程组。
3. 使用U矩阵求解Ux=y:
```python
x = np.zeros_like(b)
for i in range(n-1, -1, -1):
x(i) = y(i)
for j in range(i+1, n):
x(i) -= U(i,j)*x(j)
x(i) /= U(i,i)
```
其中,使用循环求解方程组,最终返回x向量作为方程组的解。
请注意,上述代码基于NumPy库实现,具体实现方式可能会因不同的库和版本而有所不同。
LU矩阵分解实例

例:给定一4阶矩阵42158721048366849A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,通过LU 分解求逆矩阵1A -。
解:算法过程为:1111()A L U U L u l----=⨯=⨯=⨯,第一步:求LU 矩阵设0000010203101111121320212222233031323333000000000000L U U U U LL U U U L U L L L U U L L L L U →⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⨯=↓⨯⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,通过(4)~(7)式可逐步进行矩阵L 和U 中元素的计算,如下所示:001122330000010102020303102030102030000000111110011212100213131003()1,(U )4,2,1,5,(L )8462,1, 1.5,444(U )7223,2210,10L L L L L U a U a U a U a a a a L L L U U U U a L U U a L U U a L U ======================-=-⨯==-=-⨯==-=计算的对角的第一行的第一列的第二行250,-⨯=2121200111313130011122222002211223232003211332323002311222(L )11()(812)23115()(8 1.52)33U 311202,615201,L 115()(4 1.5123L a L U U L a L U U U a L U L U U a L U L U L a L U L U U =-=⨯-⨯==-=⨯-⨯==--=-⨯-⨯==--=-⨯-⨯==--=⨯-⨯-的第二列(的第三行)(的第三列)33333003311332230) 1.25,U 59 1.550 1.2510.25;3U a L U L U L U ⨯==---=-⨯-⨯-⨯=(的第四行)经迭代计算,最后得到L 和U 矩阵为:第二步:求L 和U 矩阵的逆u ,l11,;u U l L --==(1)求U 矩阵的逆11000102030001020311121311121322232223333342150003000000002100000000.25U U U U u u u u U U U u u u u U U u u U u --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===↑⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦由式(9)可得矩阵U 的逆的各元素计算如下:000011010111110022122222110112022200332333332211(1),4111111(2)()(2),3436111(3)0.5()(00.5)0311()(2010.5)0.1254111(4)4()(14)22u U u u U u U U u U u U U U u U u U u U u U U =====-=-⨯=-===-=-⨯==-+=-⨯+⨯=-===-=-⨯=-12022313,,u u ,u u 12231333110113022303330011()(0(2)04)0311()(201(2)54) 4.54U u U u U U u U u U u U =-+=-⨯-+⨯==-++=-⨯+⨯-+⨯=-03u(2)求L 矩阵的逆1100001011101120212220212230313233303132330000001000000021*********.50.6667 1.251L l L L l l l L L L l l l L L L L l l l l --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===↓⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦由(8)式可得L 矩阵的逆的各元素计算如下001010002020002110303000311032201121113131113221223222(1)1,2,()3,5()(1.51(2)13) 1.9166673(2)2,()0.83333(3)() 1.251;l l L l l L l L l l L l L l L l l l L l l L l L l l l L l l ==-=-=-+==-++=-⨯+⨯-+⨯≈-=-=-=-+==-=-=213233=1,=1,(4)所以得到的逆矩阵为:(3)求A 的逆矩阵由式(10)可计算得到矩阵A 的逆,如下:10.250.1666670.125 4.5100000.33333002100000.5232100004 1.9166670.83333 1.2518.833334 3.66667 5.5 4.50.666670.33333005.333333 2.66667327.666667 3.3333354A u l-=⨯---⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⨯⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦--⎡⎤⎢-⎢=⎢--⎢--⎣⎦⎥⎥⎥⎥由程序计算出的结果如下:。
LU分解求逆
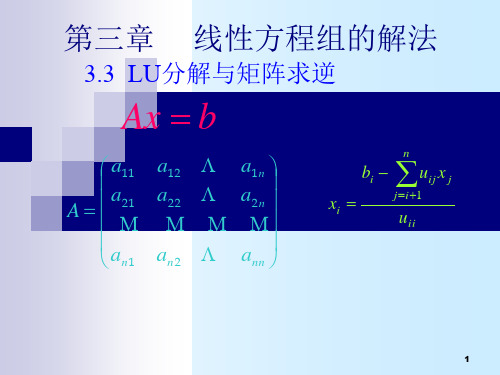
逐行算出U的元素 逐列算出L的元素
根据矩阵的乘法原理, A的第一行元素a1 j为
a1 j u1 j j 1,2 , , n
A的第r行元素主对角线 以右" 元素arj ( j r ,, n)为 "
导出U
arj lrk ukj
k 1
r
j r , , n
r 1,2,, n
9
同样,由
a11 a1r a a rr A r1 ar 1,r a anr n1
r
i r 1, , n
r 1,2,, n 1
U
arj lrk u kj 1 u rj
k 1
air lik u kr lir u rr
k 1
r 1
L
因此可以推导出
u 1 j a1 j ai 1 li 1 u11
j 1,2 ,, n
U
Ak Lk U k ,
(i ) det Ak det U k aii i 1
6
k
Gauss消去法 可以执行 定理3.1
( aiii ) 0 i 1, 2 , , n
det Ak 0 k 1, 2 , , n
若n阶方阵A的顺序主 子式D det A 0, k k
k阶顺序主子式
A
a1 k k akk ank
1 a1 n l 1 akn k 1 k ann l n1 l nk
L
( 1) ( ( a11 a11 ) a11 ) k n ( ( kakkk ) aknk ) (n ann) 1
matlablu分解函数

matlablu分解函数Matlab中的lu分解函数是一个十分常用的函数,它可以将矩阵分解成一个下三角矩阵和一个上三角矩阵的乘积,从而可以利用这个分解来求解线性方程组以及矩阵的逆。
1. lu分解函数的基本用法使用matlab中的lu函数可以很简单地进行矩阵的lu分解,lu 函数的语法为:[L, U] = lu(A)其中,A是要进行lu分解的矩阵,而lu函数将返回L和U两个矩阵,分别代表原矩阵分解后的下三角矩阵和上三角矩阵。
通过这两个矩阵,我们就可以很容易地求解线性方程组了。
2. 利用lu分解函数求解线性方程组对于一个线性方程组Ax=b,我们可以使用lu函数对系数矩阵A 进行lu分解,将其分解为L和U两个矩阵,进而可以将原方程组转化为Ly=b和Ux=y两个方程组,然后先利用Ly=b求解y,再利用Ux=y求解x。
若要使用matlab求解线性方程组,可以使用如下的语句:x = A\b;其中,A是系数矩阵,b是右侧矩阵,\操作符表示求解线性方程组。
3. 利用lu分解函数求解矩阵的逆如果要求解一个矩阵的逆,也可以使用lu分解函数来实现。
具体来说,如果我们要求解一个n阶矩阵A的逆矩阵,可以先对A进行lu分解,得到L和U两个矩阵,然后利用下面的公式来求解A的逆:A_inv = U \ (L \ eye(n));其中,eye(n)表示n阶单位矩阵。
这样,我们就可以利用matlab 中的lu函数来实现对矩阵的求逆操作。
4. lu分解函数的高级用法除了上面介绍的基本用法之外,matlab中的lu函数还有一些高级的用法。
比如,可以通过指定选项来控制lu函数的行为,比如选择部分主元(partial pivoting)或完全主元(complete pivoting),这可以提高矩阵分解的稳定性和精度。
具体来说,可以使用下面的语句来实现选项的设置:[L, U, P] = lu(A, 'vector');其中,'vector'表示使用部分主元选项,而'vectorized'表示使用完全主元选项。
matlablu分解函数

matlablu分解函数
Matlab中的LU分解函数是一种非常常用的线性代数函数,它可以将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
这个函数在数值计算和科学计算中非常有用,因为它可以帮助我们解决一些复杂的线性方程组问题。
LU分解函数的基本原理是将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积。
这个过程可以通过高斯消元法来实现。
在高斯消元法中,我们将矩阵转化为一个上三角矩阵,然后通过回代法来求解线性方程组。
但是,这种方法的计算量非常大,因为它需要进行大量的矩阵运算。
因此,我们可以使用LU分解函数来简化这个过程。
在Matlab中,我们可以使用lu函数来进行LU分解。
这个函数的基本语法是:
[L,U] = lu(A)
其中,A是要分解的矩阵,L是下三角矩阵,U是上三角矩阵。
这个函数返回的L和U矩阵可以用来解决线性方程组问题。
下面是一个简单的例子,演示了如何使用lu函数来解决线性方程组问题:
A = [1 2 3; 4 5 6; 7 8 9];
b = [1; 2; 3];
[L,U] = lu(A);
y = L\b;
x = U\y;
在这个例子中,我们首先定义了一个3x3的矩阵A和一个3x1的向量b。
然后,我们使用lu函数将A分解为L和U矩阵。
接下来,我们使用L和b来求解y向量,然后使用U和y来求解x向量。
最终,我们得到了线性方程组的解。
LU分解函数是Matlab中非常有用的一个函数,它可以帮助我们解决一些复杂的线性方程组问题。
如果你需要解决这样的问题,那么你应该学会如何使用这个函数。
python lu分解

python lu分解Python是一种功能强大的编程语言,它提供了许多用于数学计算和线性代数操作的库。
其中一个重要的库是NumPy,它提供了LU分解的函数。
LU分解是一种将一个矩阵分解成一个下三角矩阵和一个上三角矩阵的方法。
这种分解在解线性方程组和计算矩阵的逆时非常有用。
在NumPy中,我们可以使用`numpy.linalg.lu()`函数来执行LU分解。
以下是一个示例:```pythonimport numpy as np# 创建一个矩阵A = np.array([[4, 7, 3], [2, 5, 9], [8, 1, 6]])# 执行LU分解P, L, U = np.linalg.lu(A)# 打印结果print('P:', P)print('L:', L)print('U:', U)```在上面的示例中,我们首先创建了一个3x3的矩阵A。
然后,我们使用`numpy.linalg.lu()`函数对矩阵A进行LU分解,并将结果保存在P、L和U中。
最后,我们打印出这三个矩阵。
在LU分解中,P矩阵是一个置换矩阵,用于交换矩阵A的行。
L矩阵是一个下三角矩阵,它包含了A的行变换的信息。
U矩阵是一个上三角矩阵,它包含了A的列变换的信息。
通过LU分解,我们可以很容易地解线性方程组和计算矩阵的逆。
例如,如果我们有一个线性方程组Ax = b,其中A是一个已知的矩阵,x是未知向量,b是已知向量,我们可以使用LU分解来解这个方程组。
此外,LU分解还可以用来计算矩阵的行列式、秩和特征值等重要的线性代数运算。
它在数值计算和科学计算中被广泛应用。
总之,Python中的NumPy库提供了LU分解的函数,使我们能够方便地执行矩阵的LU分解,并利用这种分解来解线性方程组和进行其他重要的线性代数运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 矩阵的直接分解法
本节要点
掌握矩阵分解的概念
直接分解解方程组的步骤
直接分解的本质或理论来源 直接分解的递推计算公式 例子与算法
第3章 解线性方程组的直接方法
数理学院 陈文兵
m 1
k -1
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
由上可得Doolittle分解的递推公式 ukj akj lkm umj
m 1 k 1
j k, k 1, , n i k 1, ,n
a11 A1 [a11 ], A 2 a 21 a 11 a a 12 , , A k 21 a 22 a k1 a 12 a 22 a k2 a 1n a 2n a kk
都是非奇异,此处 k n.
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
3.2.4 矩阵直接分解的递推计算
假设 A LU
1 l 21 A (aij ) l31 l n1
(4)
先计算U的 第1行
Ax=b (1)
等价地写成
Ax=(LU)x=L(Ux ) = b (2)
令 Ux=y,则原线性方程组 Ax=b等价于下面两个方程组的求解:
Ly=b (3) 是否将求解问题复杂化? Ux=y (4) 于是可首先求解向量 y,使Ly=b; 然后求解 Ux=y,从而达到求解线性方程组 Ax=b的目的. 数理学院 陈文兵 第3章 解线性方程组的直接方法
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
3.2.1 矩阵分解的基本概念
定义1 给定n阶矩阵A,如果存在一个下三角形矩阵L与上三角 形U使得A=LU,就说A有三角分解。 这里,L和U的形式如下:
l11 l 21 l 22 L l31 l32 l n1 l n2 0 l nn u11 U u12 u 22 0 u13 u1n u 23 u 2n u 33 u 3n u nn
(2) a 3n -1
0
a1n (1) a 2n (2) a 3n a (n -1) nn
数理学院 陈文兵
第3章 解线性方程组的直接方法
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
分析第1次消元,目的要将第1列除第1行元素之外的所有元 素消去,其步骤是: 1、计算各行的消元因子:li1 a i1 / a11 , i 2,3,, n a ij a ij li1 * a1j , j 1,2,, n,i 2,3,, n 2、计算第i行:
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
由矩阵乘法运算可知:
a ij limu mj
m 1
n
i 1,2,, n; j 1,2,, n (1)
在进行第1次时,1)计算U的第1行.由(1)式,取i=1,则:
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY 3.2.3 直接分解的本质或理论来源
我们知道,对n阶线性方程组,高斯消元法消元要做n-1 次,观察下面的式子:
第1次 第2次 a12 a11 1 a (22) 0 0 0 0 0 第n 1次 a1n -1 a (1)-1 2n
l33 l n3
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
3.2.2 直接分解解方程组的步骤
假定我们能把矩阵A写成下列两个矩阵相乘的形式: A=LU ,其中L为下三角矩阵,U为上三角矩阵。这样我们可 以把线性方程组
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
这n-1次消元,实际上就是对系数矩阵A进行n-1次左乘运 算:
L n 1L n 2 L1A A ( n1) U 令L L n 1L n 2 L1 , 即有 LA U, 亦即: A L-1U LU, 这里令 L L-1
第3章 解线性方程组的直接方法
数理学TY OF INFORMATION SICENCE & TECHNOLOGY
另一种变化是减少前代过程,减少前代过程是基于考察高 斯消元法的结果。事实上,如果在对A做直接分解的同时,对 b向量也作相应的计算,于是得到Doolittle分解的一个改进递 推公式如下:
的系数矩阵作LU分解,并求方程组的解。
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
由于(3)、(4)是两个特殊的方程组,(3)是下三角方程组, (4)是上三角方程组,其算法非常简单,对(3)其递推计算 式为: 这是一
y1 b1 / l11 i -1 y (b lij yi ) / lii i i j1
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
定理:设A为n阶非奇异矩阵.则A有Doolittle分解的充分必要条件 是A的各阶顺序主子式 1 , 2 ,, n 均不为零.并且,当此条 件成立时,A的Doolittle分解是唯一的. 对上述定理也可表述为: 在Gauss消去法中,主元 a11 , a (1) ,, a (n -1) 全不为零的 22 nn 充分必要条件是矩阵A的顺序主子矩阵
个前代 过程,其 算法复 杂度为 n(n-1)/2 这是一 个回代 过程,其 算法复 杂度为 n(n+1)/2
i 2,3,, n
对(4)其递推计算式为:
x n y n / u nn n x ( y - u x ) / u i ij i ii i ji 1 i n - 1,,1
ukj akj lkm u mj
m 1 k 1
j k , k 1, , n i k 1 ,n , i k 1 ,n ,
lik ( aik lim u mk ) / u kk
m 1
k 1
b i b i b k lik k 1,2,, n
m 1 k -1 k
j k,, n
a kj l km u mj l kk u kj l km u mj u kj
m 1 m 1
k -1
故, u kj a kj l km u mj
m 1
k -1
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
a i1 lim u m1 (因为 u mj 0,当m j时 ) i 2,, n
m 1
1
a i1 li1u11 li1 a i1 / u11
在进行第k次时,1)计算U的第K行.由(1)式,取i=k,则:
a kj l km u mj (因为 lij 0,当 k时 ) m
lik (aik lim umk ) / ukk
m 1
k 1
k 1,2,, n
第3章 解线性方程组的直接方法
数理学院 陈文兵
NANJING UNIVERSITY OF INFORMATION SICENCE & TECHNOLOGY
矩阵分解的紧凑格式
在计算机程序中常常用这种方法解线性代数方程组。它 的优点是存储量很省。L和U中的三角零元素都不存储,就 是L的对角元素也因为都是1没有必要再记录在程序中,这样 只用一个n阶方阵就可以把L和U贮存起来。 即:下三角(包括对角元)存储L各元素,而上三角存储 U的元素。 再考察递推公式会发现A中任一元素aij只在计算lij (j<=i) 和uij(j>i)中用到一次以后就不再出现了,因而完全 可以利用原始数组A的单元,一个个逐次贮存L或U中的相应 元素.因此,紧凑格式只是在程序实现时在存储方式上的改 变,其算法本身未发生任何变化。
bi bi li1 * b1
从矩阵变换的角度来看,这次消元的实质是对矩阵A左 乘矩阵L1,即 L1A A1
a11 a12 1 0 a (1) l 1 22 21 (1) 其中,L1 l31 0 1 , A1 0 a 32 0 a (1) l n1 0 0 1 n2 a13 a (1) 23 (1) a 33 a (1) n3 a1n a (1) 2n (1) a 3n a (1) nn
