机械动力学第三章例3-3程序
机械系统动力学建模与分析(3)2012

(2)修改转动约束的运动函数。将Function (time)栏中的函
数表达式改写为“-15.0d * sin( 150 * time)”。
2. 创建碰撞力
本例中的碰撞力分两种情况,和小球相关的三对碰撞不考 虑摩擦力,球瓶和平台的碰撞考虑摩擦力,分别创建如下 。 (1)定义小球和滑块等物体的碰撞 将视图还原为前视图(Front<F>),点击创建碰撞力 (Contact)工具按钮,弹出创建碰撞力对话框,如图(a)所 示。在对话框“first solid”一栏中点击鼠标右键,点击浮动菜单 命令Contact_Solid—>Pick,然后在窗口中点取小球;在对话
spacing: 50mm
(4)显示Coordinate Windows
2. 建立球体
3. 建立地基
4. 设置初始条件
小球水平方向速度分量和垂直方向速度分量如下:
5. 建立测量
6. 进行仿真
7. 确定落地时的距离 (1)通过动画找到落地的时间
7. 确定落地时的距离 (2)利用测量曲线确定距离
3. 建立小球 (1)点击球体(Sphere)建摸工具按钮,然后在主窗 口栅格上的坐标(-70,30,0(mm))处按下鼠标 左键,拖动鼠标至坐标(-70,0,0(mm))处松开 左键,建立完成小球模型 。 (2)调整小球的质量 。将鼠标移至小球位置,点击 鼠标右键,在弹出的浮动菜单中选择菜单命令Part: PART_2—>Modify,于是弹出修改物体参数Modify Body对话框,在Define Mass By 栏中选择“User Input”选项,然后将Mass栏中的数字改为5.0,点击对 话框的OK按钮,完成对小球的质量修改。
机械动力学演示文稿(第三章)

r T r r
{ } {A( ) } [m]{A( ) }
r
T
r
r
r
T
r
r
T
r
2
r
nr
r
T
r
r
2 上式说明,第r阶固有频率平方ω nr 等于第r阶主刚度 K r 与第r阶主质量 M r (与单自由度公式类似)
的比值
{A( ) } [m]{A( ) } = M
s T r
{A } [m]{A( ) } = 0
模态刚度矩阵(主刚度矩阵)
[4-6]
可得
K1 0 [Φ ]T [k ][Φ ] = M 0
0 L K2 L M 0
例:前面求出
{A( ) }
1
1 = 2 ; 1
{A( ) }
2
1 =0 ; − 1
{A( ) }
3
1 = − 1 ; 1
[ ][ ]
“线性独立” 线性独立”
多自由度系统动能T,势能U表达式:
[4-4]
1 T & & {x} [m]{x} (10) 第r阶主振动动能 : Tr 2 1 T (11) 第r阶主振动势能 : U r U = {x} [k ]{x} 2 n 则: U = U 1 + U 2 + L + U n = ∑ U i (各阶主振动单独存在时 势能U i 之和) T=
模态矩阵
[Φ] = [{A(1) } {A(2 ) } {A(3) }]
1 1 1 = 2 0 − 1 1 − 1 1
[4-7]
1 2 1 m 0 0 1 1 1 T 求模态质量矩阵: M p = [Φ ] [m][Φ ] = 1 0 − 1 0 m 0 2 0 1 1 − 1 1 0 0 m 1 − 1 1 0 M 1 0 0 6 m 0 0 = 0 2m 0 = 0 M 2 0 0 3m 0 0 M3
机械系统动力学 第三章 机械系统运动微分方程的求解1

• 3-1机械系统运动方程求解方法-解析法 • 3-2机械系统的运动方程求解方法-数值法 • 3-3机械系统的运动方程求解方法-半解析数
值法
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
1.问题的提法 工程中大量的动力学问题都可以 归结于图3-1-1 单自由度振动系 统的力学模型,其动力学问题的数 学模型表示为常微分方程的初值 问题 控制方程:
n
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
在初始条件为 x(0) x0, x(0) x0 欠阻尼条件下,方程的定解
x(t)
ent ( x0
cos d t
x0
x0 d
sin dt)
[1
(
X st
)2 ]2 [2 (
)]2
sin(d t
)
n
n
上中的第一项为单自由度系统自由振动响应,当t
图3-1-1 单自由度振动系 统的力学模型
mx cx kx F(t)
满足初始条件:
x(0) x0, x(0) x0
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
2. 单自由度振动系统简谐激励作 用下的响应
运动微分方程:
mx cx kx F0 sin t
图3-1-1 单自由度振动系 统的力学模型
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动 2)特解
特解的求法很多,有比较系数法、旋转矢量法、拉 氏变换法等,较简单快捷的方法是旋转矢量法
设特解: x2(t) X sin(t )
代入方程 mx cx kx F0 sin t
机械设计第九版第三章3

断裂区
s-N疲劳曲线(应力比r恒定,不同的σmax对应的循环次数N)
多数零件在此阶段 破坏,即承受交变 应力1万次以上
静载 破坏
低周 疲劳
高周疲劳
无限寿命
任取一点, 横坐标为N,纵坐标为σrN
机械零件的疲劳大多发生在s-N曲线的CD段,可用 下式描述:
s N C ( NC N ND )
若应力每循环一次都对材料的破坏起相同的作用,则 应力 σ1 每循环一次对材料的损伤率即为1/N1,而循环了n1次 的σ1对材料的损伤率即为n1/N1。如此类推,循环了n2次的σ2 对材料的损伤率即为n2/N2,……。
当损伤率达到100%时,材料即发生疲劳破坏,故对应 于极限状况有:
n1 n2 n3 1 N 1 N 2 N3
为了度量含裂纹结构体的强度,在断裂力学中运用了 应力强度因子KI(或KⅡ、KⅢ)和断裂韧度KIC (或KⅡC、 KⅢC)这两个新的度量指标来判别结构安全性,即: KI<KIC时,裂纹不会失稳扩展。
KI≥KIC时,裂纹失稳扩展。 基于断裂力学的强度分析的步骤: (1)以无损探伤确定裂纹的形状、大小及分布(类似B超) (2)分析工作载荷,确定应力强度因子
设
σad=Kσσa+υσσm
安全系数计算公式改写为
s 1 Sca s ad
机械零件的疲劳强度计算3
三、单向不稳定变应力时的疲劳强度计算 不稳定变应力 非规律性 规律性 用统计方法进行疲劳强度计算 按损伤累积假说进行疲劳强度计算
规律性不稳定变应力示意图
s 4小于无限寿命时对应的应力s -1,可忽略
(2)在不可避免地要产生较大应力集中的结构处,可采 用减载槽来降低应力集中的作用。
西北工大版机械原理第3章平面机构的运动分析精品PPT课件

特点:
①该点涉及两个构件。
②绝对速度相同,相对速度为零。
③相对回转中心。 2)瞬心数目 若机构中有n个构件,则
P13
1 23
∵每两个构件就有一个瞬心
P12 P23
∴根据排列组合有
构件数 4 瞬心数 6
56
8
10 15 28
二、机构中瞬心的数目
若机构中有N个构件(包括机架),则
∵每两个构件就有一个瞬心
B A
E HE
1.位置分析 ①确定机构的位置(位形),绘制机构位置图。 ②确定构件的运动空间,判断是否发生干涉。
③确定构件(活塞)行程, 找出上下极限位置。 ④确定点的轨迹(连杆曲线),如鹤式吊。
2.速度分析 ①通过分析,了解从动件的速度变化规律是否满足 工作要求。如牛头刨 ②为加速度分析作准备。
∴根据排列组合有
K
C
2 N
N ( N 1) 2
三、机构中瞬心位置的确定
1. 通过运动副直接相联的两构件的瞬心位置确定
1)以转动副相联 的两构件的瞬心
2)以移动副相联的 两构件的瞬心
——转动副的中心。 P12
——移动副导路的 垂直方向上的
1
1
2
无穷远处。
P12 ∞ 2
3)以平面高副相联的两构件的瞬心
3.加速度分析的目的是为确定惯性力作准备。
方法: 图解法-简单、直观、精度低、求系列位置时繁琐。 解析法-正好与以上相反。
实验法-试凑法,配合连杆曲线图册,用于解决 实现预定轨迹问题。
3-2 用速度瞬心作平面机构的速度分析
一、速度瞬心(Instantaneous Center of Velocity——ICV) 速度瞬心(瞬心): 瞬时转动中心
机械设计第九版第三章3

表面处理之一喷丸
(4)适当提高零件的表面质量,特别是提高有应力集中 部位的表面加工质量,必要时表面作适当的防护处理。
(5)尽可能地减少或消除零件表面可能发生的初始裂纹 的尺寸,对于延长零件的疲劳寿命有着比提高材料性能更 为显著的作用。
3-3机械零件的抗断裂强度
机械零件的抗断裂强度
低应力脆断:在工程实际中,往往会发生工作应力小 于许用应力时所发生的突然断裂。 原因:结构内部裂纹和缺陷。 本质原因:对于高强度材料,抵抗裂纹扩展的能力随 着强度的增高而下降。用传统的强度理论计算高强度材料 结构的强度问题,就存在一定的危险性。 断裂力学:研究带有裂纹或带有尖缺口的结构或构件 的强度和变形规律的学科。
设
σad=Kσσa+υσσm
安全系数计算公式改写为
s 1 Sca s ad
机械零件的疲劳强度计算3
三、单向不稳定变应力时的疲劳强度计算 不稳定变应力 非规律性 规律性 用统计方法进行疲劳强度计算 按损伤累积假说进行疲劳强度计算
规律性不稳定变应力示意图
s 4小于无限寿命时对应的应力s -1,可忽略
给定任意两个参数, 其它三个可算出
r = -1 对称循环应力
r=0
脉动循环应力
r = 1 静应力
任意交变应力都可看作对称循环和静应力的叠加
任何交变应力的 研究可以转化为 对称循环和静应 力的研究
交变应力下,零件的主要损坏形式是疲劳断裂。 疲劳断裂过程: 1、零件表层产生微小裂纹 2、随着循环次数增加,微裂纹逐渐扩展 3、当剩余材料不足以承受载荷时,突然脆性断裂
纵坐标值=斜率×(横坐标值﹣直线与横坐标交点)
sm sS sa
3-2机械零件的疲劳强度
一、零件的极限应力线图
第03章 机器人的运动学和动力学

教案首页课程名称农业机器人任课教师李玉柱第3章机器人运动学和动力学计划学时 3教学目的和要求:1.概述,齐次坐标与动系位姿矩阵,了解平移和旋转的齐次变换;2.机器人的运动学方程的建立与求解*;3.机器人的动力学*重点:1.机器人操作机运动学方程的建立及求解;2.工业机器人运动学方程3.机器人动力学难点:1. 机器人动力学方程及雅可比矩阵基本原理思考题:1.简述齐次坐标与动系位姿矩阵基本原理。
2.连杆参数及连杆坐标系如何建立?3.机器人动力学方程及雅可比矩阵基本原理是什么?第3章机器人运动学和动力学教学主要内容:3.2 齐次坐标与动系位姿矩阵3.3 齐次变换3.4 机器操作机运动学方程的建立与求解3.5 机器人运动学方程3.6 机器人动力学本章将主要讨论机器人运动学和动力学基本问题。
先后引入了齐次坐标与动系位姿矩阵、齐次变换,通过对机器人的位姿分析,介绍了机器人运动学方程;在此基础上有对机器人运动学方程进行了较为深入的探讨。
3.1 概述机器人,尤其是关节型机器人最有代表性。
关节型机器人实质上是由一系列关节连接而成的空间连杆开式链机构,要研究关节型机器人,必须对运动学和动力学知识有一个基本的了解。
分析机器人连杆的位置和姿态与关节角之间的关系,理论称为运动学,而研究机器人运动和受力之间的关系的理论则是动力学。
3.2 齐次坐标与动系位姿矩阵3.2.1 点的位置描述在关节型机器人的位姿控制中,首先要精确描述各连杆的位置。
为此,先定义一个固定的坐标系,其原点为机器人处于初始状态的正下方地面上的那个点,如图3-1(a)所示。
记该坐标系为世界坐标系。
在选定的直角坐标系{A}中,空间任一点P的位置可以用3×1的位置向量A P表示,其左上标表示选定的坐标系{A},此时有A P=XYZ P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦式中:P X、P Y、P Z—点P在坐标系{A}中的三个位置坐标分量,如图3-1(b)。
3.2.2 齐次坐标将一个n维空间的点用n+1维坐标表示,则该n+1维坐标即为n维坐标的齐次坐标....。
自由度机械系统动力学

1. 解析法
d
t t0 Je 0 Me()
(3.4.6)
若
Me()ab
则
再求出其 反函数
t
t0
Je b
ln ab ab0
f (t)
(3.4.7)
若
d
tt0Je 0abc2
演讲完毕,感谢观 看
(3.4.8)
一、等效力和等效力矩 二、等效质量和等效转动惯量
等效力学模型
等效原则: 等效构件具有的动能=各构件动能之和
M e
n j 1
m
j
vSj v
2
J
j
j
v
2
J e
n j 1
m
j
vSj
2
J
j
j
2
(3.3.3)
等效质量和等效转动惯量与传动比有关, 而与机械驱动构件的真实速度无关
2W()
Je()
(3.4.3)
若
是以表达式
给出,且为可积函数时,
(3.4.3)可得到解析解。
但是
常常是以线
图或表格形式给出,则只
能用数值积分法来求解。
常用的数值积分法有梯形
法和辛普生法。
运动方程式的求解方法
一、等效力矩是位置的函数时运动方程的求解
二、等效转动惯量是常数、等效力矩是角速度的函数时运动方程
单自由度机械系统可以采用等效力学模型来进行研究,即系统的动力学问题转化为一个等效构件的动力学问题来研究,可以 使问题得到简化。
当取作定轴转动的构件作为等效构件时,作用于系统上 的全部外力折算到该构件上得到等效力矩,系统的全部 质量和转动惯量折算到该构件上得到等效转动惯量。
当取作直线运动的构件作为等效构件时,作用于系统上 的全部外力折算到该构件上得到等效力,系统的全部质 量和转动惯量折算到该构件上得到等效质量。
E420-理论力学-动力学第三章部分习题解答

动力学第三章部分习题解答3-3 取套筒B 为动点,OA 杆为动系 根据点的复合运动速度合成定理r e a v v v +=可得:l v v ω==e 0a 30cos ,l v v v BC B ω332a === 研究AD 杆,应用速度投影定理有:030cos D A v v =,l v D ω334=再取套筒D 为动点,BC 杆为动系,根据点的复合运动速度合成定理r D BC D v v v +=将上式在x 轴上投影有:r D BC D v v v +-=-,l v v v BC D D ω332r =+-=3-4 AB 构件(灰色物体)作平面运动, 已知A 点的速度s A O v A /0cm 4510==ωAB 的速度瞬心位于C ,应用速度瞬心法有:rad/s 23==AC v A AB ω BC v AB B ω=,设OB 杆的角速度为ω,则有rad/s 415==OB v B ω 设P 点是AB 构件上与齿轮I 的接触点, 该点的速度:CP v AB P ω=齿轮I 的角速度为:rad/s 61==r v PI ω a v e vr vA vDv rD v A vB P v CAB ωI ω3-6 AB 杆作平面运动,取A 为基点 根据基点法公式有:BA A B v v v +=将上式在AB 连线上投影,可得0,01==B O B v ω因此,041ωω==AB v A AB因为B 点作圆周运动,此时速度为零,因此只有切向加速度(方向如图)。
根据加速度基点法公式n t BA BAA B aaa a ++=将上式在AB 连线上投影,可得n060cos BA A B a a a +=-,r a B 205.2ω-=201231ωα-==B O a B B O (瞬时针)3-7 齿轮II 作平面运动,取A 为基点有nt BA BA A B a a a a ++= n t 1BA BA a a a a ++=将上式在x 投影有:n 1cos BA a a a -=-β由此求得:212n 2cos 2r a a r a BAII βω+==再将基点法公式在y 轴上投影有:2t2sin r a a II BA αβ==,由此求得22sin r a II βα=再研究齿轮II 上的圆心,取A 为基点n t n t2222A O AO A O O aaa aa++=+将上式在y 轴上投影有2sin 2t t 22βαa r a a II AO O ===, B vBAv A vAa Ba t BA an BA atBA anBA axyt2A Oa n 2AO a xyn 2O a t 2Oa由此解得:)(2sin 2121t 221r r a r r a OO O +=+=βα再将基点法公式在x 轴上投影有:n1n22A O O a a a -=- 由此解得:2cos 1n2a a a O -=β,又因为221n 212)(O O O r r a ω+= 由此可得:)(2cos 21121r r a a O O +-±=βω3-9 卷筒作平面运动,C 为速度瞬心, 其上D 点的速度为v ,卷筒的角速度为r R vDC v -==ω 角加速度为rR ar R v -=-== ωα 卷筒O 点的速度为:rR vRR v O -==ω O 点作直线运动,其加速度为 rR aRr R R v va O O -=-==研究卷筒,取O 为基点,求B 点的加速度。
机械动力学第三章作业(答案)

3-1 某弹簧质量系统1k ,m ,具有自然频率1f ,第2个弹簧2k 串联于第一个弹簧,其自然频率降至1/21f ,求以1k 表示的2k 。
解:1112k f m π= (1)121212111k k k kk k k ==++1221121122()k k f f m k k π==+ (2)122(1)2(2)k k k +== ,则 123k k =3-2 如图所示,杆a 与弹簧1k 和2k 相连,弹簧3k 置于杆a 的中央,杆b 与弹簧 3k 和 4k 相连,质量m 置于杆b 的中央。
设杆a 和杆b 为质量和转动惯矩可忽略的刚性杆,并能在图示平面内自由移动和转动。
求质量m 上、下振动的固有频率。
解:1114x k =2214x k = 1233122x x x k +=+ 4412x k = 12341111161644e x k k k k ∴=+++ 1234111111161644e ek x k k k k ==+++所以n 1234114111122()44e k f m m k k k k ππ==+++ (2)n f ωπ=3-3求图中系统的固有频率,悬臂梁端点的刚度分别是1k 及3k ,悬臂梁的质量忽略不计。
解: 1k 和2k 为串联,等效刚度为:212112k k k k k +=。
(因为总变形为求和)12k 和3k 为并联(因为12k 的变形等于3k 的变形),则:2132312132121312123k k k k k k k k k k k k k k k k +++=++=+=123k 和4k 为串联(因为总变形为求和),故:424132312143243142141234123k k k k k k k k k k k k k k k k k k k k k k k k e ++++++=+=故:m k en =ω3-4求图所示系统的固有频率,刚性杆的质量忽略不计。
机械原理第3版课件第三章

v
生无限值惯性力,并由此对凸轮产
生冲击
a
+∞
—— 刚性冲击
-∞
s = c0 c1 v = ds dt = c1 回程运动方程: a = dv dt = 0
边界条件
运动始点:=0, s=h 运动终点: = ,s=0
s = h (1 ) h v = ω a = 0 Nhomakorabeaf
从动件在运动起始、中点 和终止点存在柔性冲击 适用于中速轻载场合
f
O
f/2
4h2/f2
c)五次多项式运动规律 表达式为
v = ds / dt = C1 2C2 3C3 2 4C4 3 5C5 4 a = dv / dt = 2C2 2 6C3 2 12C4 2 2 20C5 2 3 s = C0 C1 C2 2 C3 3 C4 4 C5 5
推程边界条件
在始点处:=0, s1=0, v1=0, a1=0; 在终点处: = Φ s2=h, v2=0, a2=0; 解得待定系数为
C0=0,C1=0,C2=0,C3=10h/Φ 3,C4=-15/ Φ4,C5=6h/ Φ5
位移方程式为
S=10hφ 3/ Φ3-15hφ4/Φ4+6hφ5/Φ5
第二节
凸轮机构基本运动参数设计
一、凸轮工作转角的确定
二、从动件运动规律设计
一、凸轮工作转角的确定
s
*从动件在远停处对应 的转角s——远停角。
h
0
0
120º
s
180º
300º
360º
120º
西北工业大学机械原理课后答案第3章

O OO OP 2P 3F 23(P 24Pl 3(P 34)(a)(b)Pl 3Pl 6A 1题3-6在图a 所示的四杆机构中,第三章平面机构的运动分析题3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P j 直接标注在图上)解:题3-4在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3的传动比w1/w3.C 2P 12P 23St -解:1)计算此机构所有瞬心的数目K N (N1)2152) 为求传动比 < 3需求出如下三个瞬心 R 6、P 36、P 13如图3-2所示。
; 1 巳6只33) 传动比 仁3计算公式为: —3P 16P 13I AB =60mm , l cD =90mm , l AD =|Bc =120mm , w 2=10rad/s ,试用瞬心P134 C 4L CP 12AM B3P iP 34CBMF 24F 34P ?4(d)Pl 4法求:V B3I AB2IAB lBPI32.56rad sV ClCR 3 3 0.4m s量得 1 26.42 226.6P 3434B P 233 22A ,D- i Pl4P 12 1(a)P 131) 当0 =165。
时,点C 的速度Vc ;2) 当$ =165。
时,构件3的BC 线上速度最小的一点 E 的位置及速度的大小; 3) 当Vc=O 时,0角之值(有两个解)解:1)以选定比例尺,绘制机构运动简图。
(图3-3 )2)求V c ,定出瞬心P 13的位置。
如图 3-3 (a )3)定出构件3的BC 线上速度最小的点 E 的位置。
因为BC 线上速度最小的点必与 P 13点的距离最近,所以过 P 13点引BC 线延长线的垂线交于 E 点。
如图3-3 (a )v E1ER 3 3 0.375ms4)当V C 0时,P 13与C 点重合,即AB 与BC 共线有两个位置。
作出 V C 0的两个位置。
题3-12在图示的各机构中,设已知各构件的尺寸、原动件 1以等角速度3 1顺时针方向转动。
机械动力学第三章课件

变换后积分
d t0 dt 0 ( )
t
t t0
d 0 ( )
= (t)
2. 等效构件的角加速度
d d d d dt d dt d
二、等效转动惯量是常数,等效力矩是速度的函数时
以电动机驱动的鼓风机、搅拌机、离心泵以及车床等之类机械属于这种情况。这些 机器的驱动力是速度的函数,而生产阻力是常数或者是速度的函数,机器的速比是常 数。因此,其等效力矩仅仅是速度的函数,而等效转动惯量是常数,此时,用力矩形 式的运动方程式求解比较方便。 d 2 dJe Je Me dt 2 d 分离变量
图a
图b
机械的运动方程式
一、机械运动方程的一般表达式
机械系统的运动方程式为:dE=dW
对于如图之曲柄滑块机构:
2 2 2 dE d ( J 1 12 / 2 m 2v S / 2 J / 2 m 3 v / 2) 2 S2 2 3
dW ( M 1 1 F 3v 3)dt Ndt
说明:
对一个单自由度的机械系统的运动研究可简化为对该 系统的一个具有等效转动惯量Je(),在其上作用有等
效力矩Me( , ,t)的假想构件的运动的研究。 等效构件
具有等效转动惯量,其上作 用有等效力矩的等效构件
原机械系统等效 动力学模型
二、机械系统的等效动力学模型(续)
2. 等效质量和等效力 选滑块为曲柄滑块机构的等效构件
2. 驱动力 驱动力是指驱使原动机运动的力,其变化规律取决于 原动机的机械特性。 原动机的机械特性:指原动机发出的驱动力与运动参 数之间的关系。
额定转矩:特性曲线上N点所
对应的转矩。
西北工业大学机械原理课后答案第3章1
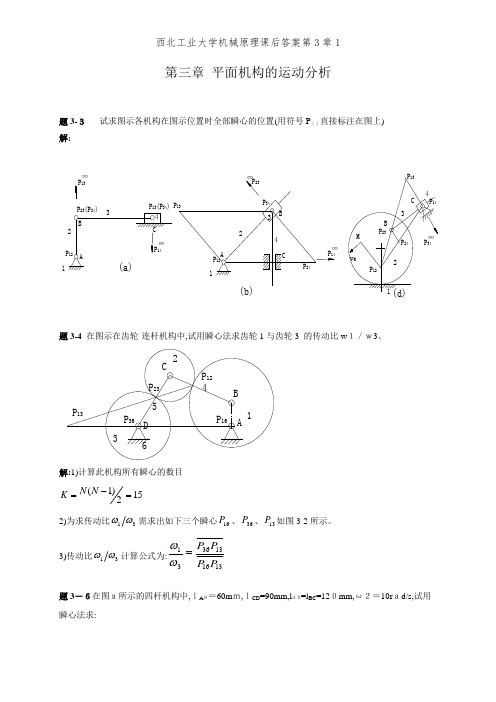
第三章 平面机构的运动分析题3-3 试求图示各机构在图示位置时全部瞬心的位置(用符号P ij直接标注在图上) 解:1P 13(P 34)13∞题3-4 在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3 的传动比w 1/w3、P 13P 23P 363D 652C 4B P 16A 1P 12解:1)计算此机构所有瞬心的数目152)1(=-=N N K2)为求传动比31ωω需求出如下三个瞬心16P 、36P 、13P 如图3-2所示。
3)传动比31ωω计算公式为:1316133631P P P P =ωω题3-6在图a所示的四杆机构中,lA B=60m m,lCD =90mm,l AD=l BC =120mm,ω2=10r ad/s,试用瞬心法求:231) 当φ=165°时,点C 的速度Vc;2) 当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小; 3) 当Vc=0时,φ角之值(有两个解)解:1) 以选定比例尺,绘制机构运动简图。
(图3-3 ) 2)求V C ,定出瞬心P13的位置。
如图3-3(a)s rad BP ll v l AB AB B 56.21323===μωω s m CP v l C 4.0313==ωμ 3)定出构件3的BC 线上速度最小的点E 的位置。
因为BC 线上速度最小的点必与P 13点的距离最近,所以过P 13点引BC 线延长线的垂线交于E 点。
如图3-3(a)s m EP v l E 375.0313==ωμ4)当0=C v 时,P 13与C点重合,即AB 与BC 共线有两个位置。
作出0=C v 的两个位置。
量得 ︒=4.261φ ︒=6.2262φ题3-12 在图示的各机构中,设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度。
解:a)速度方程:32233C C C B C B C v v v v v +=+=加速度方程:r C C k C C C t B C n B C B t C nC a a a a a a a a 232323333++=++=+b) 速度方程:2323B B B B v v v +=加速度方程:r B B K B B B t B nB a a a a a 2323233++=+c) 速度方程:2323B B B B v v v +=加速度方程:r B B K B B B t B nB a a a a a 2323233++=+题3-14 在图示的摇块机构中,已知l AB =30mm,l AC=100mm,lBD =50mm,lDE =40mm 。
3-3动力学分析

{ f } = [ N ]{δ }e
{σ } = [ D ][ B ]{δ } = [ S ]{δ }
e
{ε } = [ B ]{δ }
e
e
位移,应变和应力都是随时间t变化的函数 变化的函数. 位移,应变和应力都是随时间 变化的函数.
§3-3 动力学分析
根据达朗贝尔原理, 根据达朗贝尔原理,引入惯性力和阻尼力之后结构仍 处于平衡状态. 处于平衡状态. 动态分析中仍采用虚位移原理建立单元特性方程, 动态分析中仍采用虚位移原理建立单元特性方程,根 据整体平衡条件和与静力分析相同的集成方式, 据整体平衡条件和与静力分析相同的集成方式,得到结 构的平衡方程. 构的平衡方程.
§3-3 动力学分析
4.固有特性分析 . 结构固有特性由结构本身决定,与外部载荷无关, 结构固有特性由结构本身决定,与外部载荷无关,由 模态参数定量描述. 模态参数定量描述. 模态参数包括固有频率,模态振型,模态质量, 模态参数包括固有频率,模态振型,模态质量,模态 刚度和模态阻尼比等,最重要的参数是固有频率, 刚度和模态阻尼比等,最重要的参数是固有频率,模态振 型和模态阻尼比. 型和模态阻尼比. 固有特性分析就是对模态参数进行计算,目的: 固有特性分析就是对模态参数进行计算,目的: 避免结构出现共振和有害的振型; 避免结构出现共振和有害的振型;为响应分析提供必 要依据. 要依据.
等参数单元概念
解决办法——坐标变换 坐标变换 解决办法
斜四边形单元,作连接对边中点的直线, 斜四边形单元,作连接对边中点的直线,作为ξ轴和η 取其交点为原点, 值分别为± , 轴,取其交点为原点,令四边上的ξ值, η值分别为± 1, 使整体坐标(x, 下的斜四边形 变换为局部坐标( 下的斜四边形, 使整体坐标 ,y)下的斜四边形,变换为局部坐标 ξ ,η) 下的矩形. 下的矩形.
机械动力学第3章

(3.1-8)
x(0) x0 , x(0) x0
我们关心的是,系统在受到初始扰动的作用后, 是否和单自由度系统一样发生自由振动? • • 两个坐标是否有相同的随时间变化规律? 如果有,那么这一随时间变化的规律是什么, 是否是简谐函数?
8
3.1无阻尼自由振动
21 22
描述了系统发生固有频率为 n 2 的自由振动时 x1 (t ) x2 (t ) 的大小。
u u
16
它们分别反应了系统以某个固有频率作自由振动时 的形状或振型 ,表示为
f.特征向量
u u
u 11 1 u 11 1 r 1 u 21 u 12 1 u 12 2 r 2 u 22
确定u 1 和 u 2
u 21 r1
2 n1 m1 k 11
比较r1和r2的大小??
u
11
k
12
k k
22
k
12 2 n1
m
2
u 22 r2
2 n 2 m1 k 11
(3.1-21)
u
12
k
12
22
k
12 2 n2
m
2
u u
11
12
描述了系统发生固有频率为 n1 的自由振动时 x1 (t ) x2 (t ) 的大小;
22ຫໍສະໝຸດ (3.1-20)
13
3.1无阻尼自由振动
3.1.1 固有模态振动
从而得到 n1
n 2 ,且
n1
n2
理论力学-c3-3

2
3
➢ 若正方体绕对角线运动, =
Ԧ =
2
6 3
Ԧ + Ԧ + ,
3
Ԧ + Ԧ + ,则
1
2 2
= ⋅ Ԧ =
2
12
12
平行轴定理
转轴, 平行,距离为。刚体绕穿过质心的轴转动惯量为 ,则
绕轴的转动惯量为
= + 2
(1)啤酒瓶(2)你和镜中人(3)四门塔
22
小结
定点运动,刚体角动量和动能
Ԧ = መ ⋅ ,
1
= ⋅ መ ⋅
2
若取惯量主轴为坐标轴,则
1
መ = 0
0
Ԧ = 1 Ԧ + 2 Ԧ + 3 ,
0
2
0
0
0
3
1
= 1 2 + 2 2 + 3 2
1
2 ,
6
= = 0
2 Τ6
0
0
2
መ =
=
0
2 Τ6
0
6
2
0
0
Τ6
9
2
መ =
6
上式中为单位矩阵,满足
⋅ =
角动量为
2
Ԧ = መ ⋅ =
6
动能为
1
2 2
= ⋅ Ԧ =
2
12
正方体绕质心的角动量与角速度同方向,动能正比于角速度大小
′
−
−
−
′
−
′
机械原理A-3-3

内,这时1 构件与2构件仅有一面受力。 R21如图1 所示。 当外力P 的作用线位于接触表面ab之 外,这时1 构件除了移动之外,还要发 生倾转。R21如图2 所示。 当外力P 的作用线平行移动轴线并距 移动轴线h 远时,1构件除了移动之外,
还要发生倾转。R21如图3 所示。
1)、移动副中摩擦力的确定 Q----载荷和自重 P-----驱动力 N21---法向反力 F21---摩擦力
F21
方向:F21总是与V21方向相反
大小:当摩擦系数f一定时, F21与N21成反比。
F21=fN21
对于不同的接触面(即运动副元素的几何形 状),N21在Q为定值时,N21的表达式形式是不同 的。如下所示:
Q 3 构件: R23 R43 0
21 1 构件: R23 R41 0 43 M 1 R21 h 3 23
w14
R41
M1
R23 1 h 2 R21
4
3
R12 3 2
v23 w34
R12 R21 R32
选
N
R21 M 1 h Q Q 图长
N21 Q F21 f N21 f Q
N21 sin Q 2
2
N21 sin
Q
F21 f N21 f sin fVQ
sin 2)、移动副中总反力的确定:
fV
f
---称为当量摩擦系数。
N21与F21 同是2 构件作用于1 构件 的力,故将它们合成一总反力R21.
平衡条件为:
Y
0
Mo 0
Md M r
Q R21
机械原理程序

机械原理程序
机械原理程序如下:
1. 引力计算程序:
输入物体的质量和重力加速度,计算并输出物体所受到的引力。
公式为:F = m * g,其中F为引力,m为物体质量,g为重力
加速度。
2. 简单机械计算程序:
输入施加在物体上的力和物体的移动距离,计算并输出所做的功。
公式为:W = F * d,其中W为做功,F为力,d为移动距离。
3. 杆的弯曲应变计算程序:
输入杆的长度、杨氏模量和施加在杆上的力,计算并输出杆的弯曲应变。
公式为:ε = F * L / (E * A),其中ε为弯曲应变,F
为力,L为长度,E为杨氏模量,A为横截面积。
4. 滑动轴承润滑油计算程序:
输入滑动轴承的载荷和运转速度,计算并输出所需的润滑油体积。
根据轴承的类型和工作条件选择适当的润滑油,并根据经验公式计算润滑油体积。
5. 传动比计算程序:
输入两个齿轮的齿数,计算并输出传动比。
公式为:传动比 = 齿轮2的齿数 / 齿轮1的齿数。
6. 弹簧刚度计算程序:
输入弹簧的压缩或拉伸长度和施加的力,计算并输出弹簧的刚度。
公式为:刚度 = 施加的力 / 压缩或拉伸长度。
以上是一些常见的机械原理程序,用于计算和解决与机械原理相关的问题。
根据输入的参数和公式,程序能够准确地计算出所需的结果,方便工程师和技术人员在实际工作中的应用。
