第一部分 专题七 选考内容
高职院校单独招生考试英语复习指导通用版第一部分基础知识梳理专题七形容词和副词

gh, enough等。例如:
Someone thinks it is hard to learn English. 有人认为学英语很难。
You should work hard. 你应该努力工作。
典例剖析
1. What a
cough! You seem C ill.
A. terribly; terribly B. terrible; terrible C. terrible; terribly
形容词和副词
复习指南
命题探究
考题中对形容词、副词的考查,其考点主要分为以下三类: (1)形容词、副词在具体语境中的正确使用。 (2)形容词、副词比较级、最高级的变化规则、用法及固定搭配。 (3)同义词、近义词和易混词的词义辨析。
考点一 形容词的基本用法
1.形容词的句法功能
(1)作定语:说明名词的性质和特征,通常置于名词之前。但是当形容词修饰不定代词 (如something, anything等)作定语时,要后置。例如:
考点三 易混形容词和副词辨析
2.易混副词辨析 (11)also,too,as well和either。
考点三 易混形容词和副词辨析
2.易混副词辨析 (12)how long,how soon,how often和how far。
考点三 易混形容词和副词辨析
2.易混副词辨析 (13)too...to和...enough to。
busy—busily; happy—happily; heavy—heavily
③ 以e
ly。特殊情况要去掉e
ly y。例如:
wide—widely; brave—bravely; true—truly; terrible—terribly
贵阳专版2019届中考语文总复习第1部分积累与运用专题7名著阅读习题1(有答案)

专题七名著阅读(一)(时间:45分钟)1.名著阅读。
不必说碧绿的菜畦,光滑的石井栏,高大的皂荚树,紫红的桑椹;也不必说鸣蝉在树叶里长吟,肥胖的黄蜂伏在菜花上,轻捷的叫天子(云雀)忽然从草间直窜向云霄里去了。
单是周围的短短的泥墙根一带,就有无限趣味。
油蛉在这里低唱,蟋蟀们在这里弹琴。
翻开断砖来,有时会遇见蜈蚣;还有斑蝥,倘若用手指按住它的脊梁,便会拍的一声,从后窍喷出一阵烟雾。
何首乌藤和木莲藤缠络着,木莲有莲房一般的果实,何首乌有拥肿的根……这段文字出自__鲁迅__(作者)写的散文《__从百草园到三味书屋__》,它是散文集《__朝花夕拾__》中的一篇,这是作者“从记忆中抄出来”的一部回忆性散文集。
2.名著阅读。
回得五庄观,那大仙又让道童抬一大锅油出来,架起干柴,发起烈火。
顷刻间,那油锅热腾腾。
大圣见那台下西边有一个石狮子,便咬破舌尖,把石狮子喷了一口,叫声“变”,变作他本身模样。
油锅滚透后,大仙说:“把孙行者抬下去!”二十个小仙扛将起来,往锅里一掼,“砰”的一声响,溅起些滚油点子,把那小道士们脸上烫了几个燎浆大泡!只听得烧火的小童喊道:“锅漏了!”原来是一个石狮子在锅里。
以上文字出自《西游记》,这位大仙是__镇元大仙__(名字),他惩治唐僧师徒四人是因为__孙悟空推倒(毁掉)了人参果树__。
3.名著阅读。
“先生!”祥子低着头,声音很低,可是很有力:“先生另找人吧!这个月的工钱,你留着收拾车吧:车把断了,左边的灯碎了块玻璃;别处倒都好好的呢。
”选文中的“先生”是指__曹先生__,祥子叫先生“另找人”的原因是__祥子拉车摔伤了曹先生__(事件)。
4.名著阅读。
“我是被压迫的,瞧,那就是压迫者!由于他,所有一切我热爱过的,尊敬过的,祖国、父母、爱人、子女他们全死亡了!所有我仇恨的一切,就在那里!”船长不愿这艘战舰的残骸骨跟“复仇号”的光荣残骸相混,他把战舰引向东方。
第二天,可怕的打击开始了!此语段出自《__海底两万里__》,文段中的船长是__尼摩__(人物)。
高考物理二轮总复习精品课件 第一编 核心专题突破 专题7 热学(选考) 专题七 热学(选考)

(2)若气体质量一定,p、V、T均发生变化,则选用理想气体状态方程列式求
解。
命题角度2关联气体问题
与活塞、液柱相联系的“两团气”问题,要注意寻找“两团气”之间的压强、
体积或位移关系,列出辅助方程,最后联立求解。
命题角度3气体状态变化的图像问题
命题角度4与热力学第一定律综合问题
温馨提示气体等压膨胀(压缩)时,气体对外界(外界对气体)做功W=pΔV。
0
可知当体积
增大时,单位体积内分子个数变少,分子的密集程度变小,A错误;气体压强
产生的原因是大量气体分子对容器壁的持续的、无规则撞击,压强增大并
不是因为分子间斥力增大,B错误;普通气体在温度不太低、压强不太大的
情况下才能看作理想气体,C错误;温度是气体分子平均动能的标志,大量气
体分子的速率呈现“中间多、两边少”的规律,温度变化时,大量分子的平均
板和冷热两端管等构成。高压氮气由喷嘴切向流入涡流室中,然后以螺旋
方式在环形管中向右旋转前进,分子热运动速率较小的气体分子将聚集到
环形管中心部位,而分子热运动速率较大的气体分子将聚集到环形管边缘
部位。气流到达分离挡板处时,中心部位气流与分离挡板碰撞后反向,从A
端流出,边缘部位气流从B端流出。下列说法正确的是(
内外气体对活塞的压力差大于重力沿汽缸壁的分力,故汽缸内气体缓慢地
将活塞往外推,最后汽缸水平,缸内气压等于大气压。汽缸、活塞都是绝热
的,故缸内气体与外界没有发生热传递,汽缸内气体压强作用将活塞往外推,
气体对外做功,根据热力学第一定律ΔU=Q+W得:气体内能减小,故缸内理
想气体的温度降低,分子热运动的平均速率减小,并不是所有分子热运动的
数学二轮专题7选考部分第1讲坐标系与参数方程

高考二轮专题复习
返回目录
命题角 度
素养清单
真题示例
2019·全国卷
极坐 标、极
Ⅱ,22 2019·全国卷
坐标方 逻辑推理 Ⅲ,22 程的求 数学运算 2018·全国卷
解及其 应用
Ⅰ,22 2017·全国卷
Ⅱ,22
典例回顾
(1)求C2的直角坐标 方程; (2)若C1与C2有且仅 有三个公共点,求C1 的方程.
所以θ的取值范围是π4,π2. 所以P点轨迹的极坐标方程为ρ=4cos θ,θ∈π4,π2.
高考二轮专题复习
返回目录
2.(2017·全国卷Ⅱ)在直角坐标系xOy中,以坐标原
点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1
的极坐标方程为ρcos θ=4.
(1)M为曲线C1上的动点,点P在线段OM上,且满足
为xy= =a1+ -4t t, (t为参数). (1)若a=-1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为 17,求a.
高考二轮专题复习
返回目录
解析 (1)曲线C的普通方程为x92+y2=1.
当a=-1时,直线l的普通方程为x+4y-3=0.
x+4y-3=0, 由x92+y2=1,
高考二轮专题复习
返回目录
在Rt△OPQ中,ρcosθ-π3=|OP|=2, 经检验,点P2,π3在曲线ρcosθ-π3=2上, 所以l的极坐标方程为ρcosθ-π3=2.
高考二轮专题复习
返回目录
(2)设P(ρ,θ),在Rt△OAP中,|OP|=|OA|cos θ= 4cos θ,即 ρ=4cos θ.因为P在线段OM上,且AP⊥OM,
高考二轮专题复习
返回目录
专题七 第1讲 分子动理论、气体及热力学定律

真题再做
解析:(1)过程①中,气体由a到b,体积V
不变、T升高,则压强增大,A错; 过程②中,气体由b到c,体积V变大,对外 界做功,B对; 过程④中,气体由d到e,温度T降低,内能ΔU减小,体积V不变,
气体不做功,根据热力学第一定律 ΔU=Q+W得Q<0,即气体
温度均为T0.现用电热丝缓慢加热汽缸中的气体,直至活塞刚
好到达b处.求此时汽缸内气体的温度以及在此过程中气体 对外所做的功.重力加速度大小为g.
做真题•明考向 建体系•记要点 研考向•提能力 限训练•通高考 首页 上页 下页 尾页
真题再做
解析:(1)气体的内能不考虑气体自身重力的影响,故气体的 内能不包括气体分子的重力势能,A错;实际气体的内能包 括气体的分子动能和分子势能两部分,B、E对;气体整体源自B.过程②中气体对外界做正功
C.过程④中气体从外界吸收了热量 D.状态c、d的内能相等 E.状态d的压强比状态b的压强小
做真题•明考向
建体系•记要点
研考向•提能力
限训练•通高考
首页
上页 下页
尾页
真题再做
(2)如图, 容积为 V 的汽缸由导热材料制成, 面积为 S 的活塞将汽缸分成容积相等的上下两部分,汽缸 上部通过细管与装有某种液体的容器相连,细管上 有一阀门 K.开始时, K 关闭, 汽缸内上下两部分气 体的压强均为 p0.现将 K 打开,容器内的液体缓慢 V 地流入汽缸,当流入的液体体积为 时,将 K 关闭,活塞平衡时 8 V 其下方气体的体积减小了 .不计活塞的质量和体积,外界温度保 6 持不变,重力加速度大小为 g.求流入汽缸内液体的质量.
7专题七:金属及其化合物 之 铁及其化合物 以及无机推断
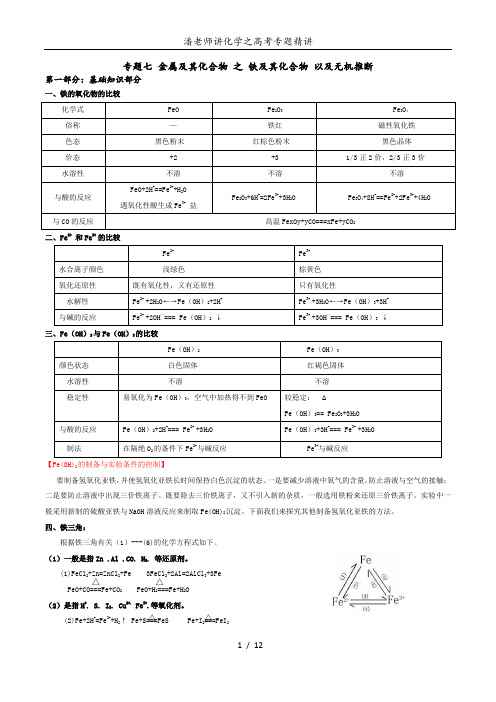
专题七 金属及其化合物 之 铁及其化合物 以及无机推断第一部分:基础知识部分一、铁的氧化物的比较二、Fe 2+和Fe 3+的比较三、Fe (OH )2与Fe (OH )3的比较【Fe(OH)2的制备与实验条件的控制】要制备氢氧化亚铁,并使氢氧化亚铁长时间保持白色沉淀的状态。
一是要减少溶液中氧气的含量,防止溶液与空气的接触;二是要防止溶液中出现三价铁离子。
既要除去三价铁离子,又不引入新的杂质,一般选用铁粉来还原三价铁离子。
实验中一般采用新制的硫酸亚铁与NaOH 溶液反应来制取Fe(OH)2沉淀。
下面我们来探究其他制备氢氧化亚铁的方法。
四、铁三角:根据铁三角有关(1)---(6)的化学方程式如下。
(1)一般是指Zn .Al .CO. H 2. 等还原剂。
(1)FeCl 2+Zn=ZnCl 2+Fe 3FeCl 2+2Al=2AlCl 3+3Fe FeO+CO===Fe+CO 2 FeO+H 2===Fe+H 2O (2)是指H +. S. I 2. Cu 2+.Fe 3+.等氧化剂。
(2)Fe+2H +=Fe 2++H 2↑ Fe+S===FeS Fe+I 2===FeI 2△ △△ △Fe+Cu 2+=Fe 2++Cu Fe+2Fe 3+=3Fe 2+(3)(5)是指Cl 2. Br 2. O 2. HNO 3. KMnO 4等氧化剂。
(3)2Fe 2++Cl 2=2Fe 3++2Cl-2Fe 2++Br 2=2Fe 3++2Br -4Fe(OH)2+O 2+2H 2O=4Fe(OH)3 3Fe 2++4H ++NO 3-=3Fe 3++NO↑+2H 2O5Fe 2++MnO 4-+8H +=Mn 2++5Fe 3++4H 2O(4)一般是指Fe. Cu. HI. H 2S.等还原剂. (4) 2Fe 3++Cu=Cu 2++2Fe 2+Fe 3++Fe=3Fe 2+2Fe 3++2I -=2Fe 2++I 2↓ 2Fe 3++H 2S=2Fe 2++S↓+2H +(5)是指Cl 2. Br 24等氧化剂。
数学讲义:第一部分 专题七 数 列
专题七 ⎪⎪⎪数 列[题组全练]1.(2017·全国卷Ⅰ)记S n 为等差数列{a n }的前n 项和.若a 4+a 5=24,S 6=48,则{a n }的公差为( )A .1B .2C .4D .8解析:选C 设等差数列{a n }的公差为d ,则由⎩⎪⎨⎪⎧a 4+a 5=24,S 6=48,得⎩⎪⎨⎪⎧a 1+3d +a 1+4d =24,6a 1+6×52d =48,即⎩⎪⎨⎪⎧2a 1+7d =24,2a 1+5d =16,解得d =4. 2.已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7=( ) A .21 B .42 C .63D .84解析:选B 设{a n }的公比为q ,由a 1=3,a 1+a 3+a 5=21,得1+q 2+q 4=7,解得q 2=2(负值舍去).∴a 3+a 5+a 7=a 1q 2+a 3q 2+a 5q 2=(a 1+a 3+a 5)q 2=21×2=42.3.(2017·全国卷Ⅲ)等差数列{a n }的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{a n }前6项的和为( )A .-24B .-3C .3D .8解析:选A 设等差数列{a n }的公差为d , 因为a 2,a 3,a 6成等比数列,所以a 2a 6=a 23, 即(a 1+d )(a 1+5d )=(a 1+2d )2. 又a 1=1,所以d 2+2d =0. 又d ≠0,则d =-2,所以{a n }前6项的和S 6=6×1+6×52×(-2)=-24.4.若{a n }是等差数列,首项a 1>0,a 2 017+a 2 018>0,a 2 017·a 2 018<0,则使前n 项和S n>0成立的最大正整数n 是( )A .2 017B .2 018C .4 034D .4 035解析:选C 因为a 1>0,a 2 017+a 2 018>0,a 2 017·a 2 018<0,所以d <0,a 2 017>0,a 2 018<0,所以S 4 034=4 034(a 1+a 4 034)2=4 034(a 2 017+a 2 018)2>0,S 4 035=4 035(a 1+a 4 035)2=4 035a 2 018<0,所以使前n 项和S n >0成立的最大正整数n 是4 034. 5.(2018·全国卷Ⅲ)等比数列{a n }中,a 1=1,a 5=4a 3. (1)求{a n }的通项公式;(2)记S n 为{a n }的前n 项和.若S m =63,求m . 解:(1)设{a n }的公比为q ,由题设得a n =q n -1.由已知得q 4=4q 2,解得q =0(舍去)或q =-2或q =2. 故a n =(-2)n-1或a n =2n -1.(2)若a n =(-2)n -1,则S n =1-(-2)n3.由S m =63,得(-2)m =-188,此方程没有正整数解. 若a n =2n -1,则S n =1-2n 1-2=2n-1.由S m =63,得2m =64,解得m =6. 综上,m =6.[系统方法]1.等差(比)数列基本运算的解题思路 (1)设基本量a 1和公差d (公比q ).(2)列、解方程(组):把条件转化为关于a 1和d (q )的方程(组),求出a 1和d (q )后代入相应的公式计算.2.等差、等比数列性质问题的求解策略(1)抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.(2)数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题.(3)利用数列性质进行运算时,要注意整体思想的应用(如第2题),可以减少计算量,此方法还适用于求函数值、求函数的解析式等问题.[题组全练]1.《张丘建算经》卷上第22题为:“今有女善织,日益功疾.初日织五尺,今一月日织九匹三丈.”其意思为今有一女子擅长织布,且从第2天起,每天比前一天多织相同量的布,若第一天织5尺布,现在一个月(按30天计)共织390尺布.则该女子最后一天织布的尺数为( )A .18B .20C .21D .25解析:选C 依题意得,织女每天所织的布的尺数依次排列形成一个等差数列,设为{a n },其中a 1=5,前30项和为390,于是有30(5+a 30)2=390,解得a 30=21,即该织女最后一天织21尺布.2.(2017·全国卷Ⅱ)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )A .1盏B .3盏C .5盏D .9盏解析:选B 每层塔所挂的灯数从上到下构成等比数列,记为{a n },则前7项的和S 7=381,公比q =2,依题意,得S 7=a 1(1-27)1-2=381,解得a 1=3.3.我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:第一步:构造数列1,12,13,14,…,1n .第二步:将数列的各项乘以n ,得数列(记为)a 1,a 2,a 3,…,a n . 则a 1a 2+a 2a 3+…+a n -1a n 等于( ) A .n 2 B .(n -1)2 C .n (n -1)D .n (n +1)解析:选C a 1a 2+a 2a 3+…+a n -1a n=n 1·n 2+n 2·n 3+…+n n -1·n n =n 2⎣⎡⎦⎤11×2+12×3+…+1(n -1)n=n 2⎝⎛⎭⎫1-12+12-13+…+1n -1-1n=n 2·n -1n=n (n -1).[系统方法]解决数列与数学文化问题的3步骤[由题知法][典例] (2017·全国卷Ⅰ)记S n 为等比数列{a n }的前n 项和.已知S 2=2,S 3=-6. (1)求{a n }的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列. [解] (1)设{a n }的公比为q .由题设可得⎩⎪⎨⎪⎧a 1(1+q )=2,a 1(1+q +q 2)=-6. 解得⎩⎪⎨⎪⎧a 1=-2,q =-2.故{a n }的通项公式为a n =(-2)n . (2)由(1)可得S n =(-2)×[1-(-2)n ]1-(-2)=-23+(-1)n 2n +13. 由于S n +2+S n +1=-43+(-1)n2n +3-2n +23=2⎣⎡⎦⎤-23+(-1)n 2n +13=2S n ,故S n +1,S n ,S n +2成等差数列.[类题通法] 证明{a n }是等差或等比数列的基本方法[应用通关](2018·全国卷Ⅰ)已知数列{a n }满足a 1=1,na n +1=2(n +1)a n .设b n =a nn .(1)求b 1,b 2,b 3;(2)判断数列{b n }是否为等比数列,并说明理由; (3)求{a n }的通项公式. 解:(1)由条件可得a n +1=2(n +1)na n . 将n =1代入得,a 2=4a 1,而a 1=1,所以a 2=4. 将n =2代入得,a 3=3a 2,所以a 3=12. 从而b 1=1,b 2=2,b 3=4.(2)数列{b n }是首项为1,公比为2的等比数列. 由条件可得a n +1n +1=2a nn ,即b n +1=2b n ,又b 1=1,所以数列{b n }是首项为1,公比为2的等比数列. (3)由(2)可得a n n=2n -1,所以a n =n ·2n -1.角度一 公式法求和[例1] (2018·厦门质检)已知数列{a n }满足a 1=1,a n +1=3a n2a n +3,n ∈N *.(1)求证:数列⎩⎨⎧⎭⎬⎫1a n 为等差数列;(2)设T 2n =1a 1a 2-1a 2a 3+1a 3a 4-1a 4a 5+…+1a 2n -1a 2n -1a 2n a 2n +1,求T 2n . [解] (1)证明:由a n +1=3a n2a n +3, 得1a n +1=2a n +33a n =1a n +23,所以1a n +1-1a n =23.又a 1=1,则1a 1=1,所以数列⎩⎨⎧⎭⎬⎫1a n 是首项为1,公差为23的等差数列.(2)设b n =1a 2n -1a 2n-1a 2n a 2n +1=⎝⎛⎭⎫1a 2n -1-1a 2n +11a 2n,由(1)得,数列⎩⎨⎧⎭⎬⎫1a n 是公差为23的等差数列,所以1a 2n -1-1a 2n +1=-43,即b n =⎝⎛⎭⎫1a2n -1-1a 2n +11a 2n =-43×1a 2n, 所以b n +1-b n =-43⎝⎛⎭⎫1a2n +2-1a 2n =-43×43=-169. 又b 1=-43×1a 2=-43×⎝⎛⎭⎫1a 1+23=-209, 所以数列{b n }是首项为-209,公差为-169的等差数列,所以T 2n =b 1+b 2+…+b n =-209n +n (n -1)2×⎝⎛⎭⎫-169=-49(2n 2+3n ).[类题通法] 公式法求数列和问题需过“三关”角度二 分组求和法求和[例2] (2018·珠海模拟)已知等差数列{a n }的首项为a ,公差为d ,n ∈N *,且不等式ax 2-3x +2<0的解集为(1,d ).(1)求数列{a n }的通项公式a n ;(2)若b n =3a n +a n -1,n ∈N *,求数列{b n }的前n 项和T n .[解](1)易知a ≠0,由题设可知⎩⎨⎧1+d =3a ,1·d =2a ,解得⎩⎪⎨⎪⎧a =1,d =2.故数列{a n }的通项公式为a n =1+(n -1)·2=2n -1.(2)由(1)知b n =32n -1+2n -1-1,则T n =(3+1)+(33+3)+…+(32n -1+2n -1)-n=(31+33+…+32n -1)+(1+3+…+2n -1)-n=31(1-9n )1-9+(1+2n -1)n 2-n=38(9n -1)+n 2-n . [类题通法] 分组求和法求数列和的关键点角度三 用裂项相消法求和[例3] (2017·全国卷Ⅲ)设数列{a n }满足a 1+3a 2+…+(2n -1)a n =2n . (1)求{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n +1的前n 项和.[解] (1)因为a 1+3a 2+…+(2n -1)a n =2n , 故当n ≥2时,a 1+3a 2+…+(2n -3)a n -1=2(n -1). 两式相减得(2n -1)a n =2,所以a n =22n -1(n ≥2). 又由题设可得a 1=2,满足上式, 从而{a n }的通项公式为a n =22n -1. (2)记⎩⎨⎧⎭⎬⎫a n 2n +1的前n 项和为S n .由(1)知a n 2n +1=2(2n +1)(2n -1)=12n -1-12n +1. 则S n =1-13+13-15+…+12n -1-12n +1=1-12n +1=2n 2n +1.[类题通法] 裂项相消法求数列和问题的步骤角度四 用错位相减法求和[例4] (2017·天津高考)已知{a n }为等差数列,前n 项和为S n (n ∈N *),{b n }是首项为2的等比数列,且公比大于0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4.(1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b 2n -1}的前n 项和(n ∈N *).[解] (1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q (q >0). 由已知b 2+b 3=12,得b 1(q +q 2)=12, 而b 1=2,所以q 2+q -6=0. 又因为q >0,解得q =2.所以b n =2n . 由b 3=a 4-2a 1,可得3d -a 1=8.① 由S 11=11b 4,可得a 1+5d =16.②由①②,解得a 1=1,d =3,由此可得a n =3n -2.所以数列{a n }的通项公式为a n =3n -2,数列{b n }的通项公式为b n =2n . (2)设数列{a 2n b 2n -1}的前n 项和为T n , 由a 2n =6n -2,b 2n -1=2×4n -1,得a 2n b 2n -1=(3n -1)×4n ,故T n =2×4+5×42+8×43+…+(3n -1)×4n ,③4T n =2×42+5×43+8×44+…+(3n -4)×4n +(3n -1)×4n +1,④③-④,得-3T n =2×4+3×42+3×43+…+3×4n -(3n -1)×4n +1=12×(1-4n )1-4-4-(3n -1)×4n +1=-(3n -2)×4n +1-8.故T n =3n -23×4n +1+83.所以数列{a 2n b 2n -1}的前n 项和为3n -23×4n +1+83. [类题通法] 错位相减法求数列和问题的步骤[考法全析]一、曾经这样考1.[利用a n 与S n 的关系求S n ](2015·全国卷Ⅱ)设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n =________.解析:由已知得a n +1=S n +1-S n =S n +1S n , 两边同时除以S n +1S n ,得1S n +1-1S n=-1,故数列⎩⎨⎧⎭⎬⎫1S n 是以-1为首项,-1为公差的等差数列,则1S n =-1+(n -1)×(-1)=-n ,所以S n =-1n . 答案:-1n[启思维] 本题通过等式a n +1=S n S n +1考查了a n 与S n 关系的转化及应用,通过构造新数列来求解.一般地,对于既有a n ,又有S n 的数列题,应充分利用公式a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2,有时将a n 转化为S n ,有时将S n 转化为a n ,要根据题中所给条件灵活变动.应注意对n =1的检验.二、还可能这样考2.[累加法或累乘法求数列的通项]已知数列{a n }满足a 1=2,a n -a n -1=n (n ≥2,n ∈N *),则a n =__________.解析:由题意可知,a 2-a 1=2,a 3-a 2=3,…,a n -a n -1=n (n ≥2), 以上式子累加得,a n -a 1=2+3+…+n . 因为a 1=2,所以a n =2+(2+3+…+n )=2+(n -1)(2+n )2=n 2+n +22(n ≥2).因为a 1=2满足上式,所以a n =n 2+n +22.答案:n 2+n +22[启思维] (1)本题数列的递推公式可转化为a n +1=a n +f (n ),通常采用等差数列通项公式的求解方法——累加法(逐差相加法)求解.即先将递推公式化成a n +1-a n =f (n ),然后分别把n =1,2,3,…,n -1代入上式,便会得到(n -1)个等式,最后添加关于a 1的等式,把n 个等式相加之后,就会直接得到该数列的通项公式.(2)对于递推公式可转化为a n +1a n=f (n )的数列,因为其类似于等比数列,故通常采用等比数列通项公式的求解方法——累乘法(逐商相乘法)求解.即分别将n =1,2,3,…,n -1代入上式,便会得到(n -1)个等式,最后添加关于a 1的等式,这n 个等式相乘之后,就会直接得到该数列的通项公式.如[增分集训]第2题.3.[构造法求数列的通项]已知数列{a n }满足a 1=2,a n +1=2a n2+a n(n ∈N *),则a n =________. 解析:因为a n +1=2a n 2+a n ,所以1a n +1-1a n =12. 因为a 1=2,即1a 1=12,所以数列⎩⎨⎧⎭⎬⎫1a n 是首项为12,公差为12的等差数列,所以1a n =12+(n -1)×12=n 2,故a n =2n .答案:2n[启思维] (1)本题递推公式是形如a n +1=sa nta n +s的递推关系,可采用取倒数的方法,将递推式变形为1a n +1-1a n =t s,从而可构造出数列⎩⎨⎧⎭⎬⎫1a n ,其首项为1a 1,公差为t s .(2)对于递推式a n +1=pa n +q (p ,q 为常数),①当p =1时,{a n }为等差数列;②当p ≠0,q =0时,{a n }为等比数列;③当p ≠0,q ≠0时,可利用待定系数法,将递推式转化为a n +1+q p -1=p ⎝⎛⎭⎫a n +q p -1,从而可构造出数列⎩⎨⎧⎭⎬⎫a n +q p -1,其首项为a 1+qp -1(不等于0),公比为p .如[增分集训]第3题.[增分集训]1.(2018·全国卷Ⅰ)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6=________.解析:∵S n =2a n +1,∴当n ≥2时,S n -1=2a n -1+1, ∴a n =S n -S n -1=2a n -2a n -1, 即a n =2a n -1.当n =1时,a 1=S 1=2a 1+1,得a 1=-1.∴数列{a n }是首项a 1为-1,公比q 为2的等比数列, ∴S n =a 1(1-q n )1-q =-1(1-2n )1-2=1-2n ,∴S 6=1-26=-63. 答案:-632.已知在数列{a n }中,a n +1=nn +2a n (n ∈N *),且a 1=4,则数列{a n }的通项公式a n =__________.解析:由a n +1=n n +2a n ,得a n +1a n =nn +2,故a 2a 1=13,a 3a 2=24,a 4a 3=35,…,a n a n -1=n -1n +1(n ≥2), 以上式子累乘得,a n a 1=13·24·35·…·n -2n ·n -1n +1=2n (n +1).因为a 1=4,所以a n =8n (n +1)(n ≥2).因为a 1=4满足上式,所以a n =8n (n +1).答案:8n (n +1)3.(2019届高三·陕西实验中学模拟)已知数列{a n }中,a 1=3,且点P n (a n ,a n +1)(n ∈N *)在直线4x -y +1=0上,则数列{a n }的通项公式a n =__________.解析:因为点P n (a n ,a n +1)在直线4x -y +1=0上, 所以4a n -a n +1+1=0. 所以a n +1+13=4⎝⎛⎭⎫a n +13. 因为a 1=3,所以a 1+13=103.故数列⎩⎨⎧⎭⎬⎫a n +13是首项为103,公比为4的等比数列.所以a n +13=103×4n -1,故数列{a n }的通项公式为a n =103×4n -1-13.答案:103×4n -1-13[典例细解][例1] (2017·全国卷Ⅰ)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N :N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A .440B .330C .220D .110[解析] 设第一项为第1组,接下来的两项为第2组,再接下来的三项为第3组,依此类推,则第n 组的项数为n ,前n 组的项数和为n (n +1)2.由题意可知,N >100,令n (n +1)2>100, 得n ≥14,n ∈N *,即N 出现在第13组之后.易得第n 组的所有项的和为1-2n 1-2=2n -1,前n 组的所有项的和为2(1-2n )1-2-n =2n +1-n -2.设满足条件的N 在第k +1(k ∈N *,k ≥13)组,且第N 项为第k +1组的第t (t ∈N *)个数, 若要使前N 项和为2的整数幂,则第k +1组的前t 项的和2t -1应与-2-k 互为相反数,即2t -1=k +2,∴2t =k +3,∴t =log 2(k +3), ∴当t =4,k =13时,N =13×(13+1)2+4=95<100,不满足题意; 当t =5,k =29时,N =29×(29+1)2+5=440;当t >5时,N >440. 故所求N 的最小值为440. [答案] A[启思维] 本题在创新情境中考查了等差数列与等比数列的求和公式,是具有综合拓展性的客观题的压轴题.数列试题的创新多是材料背景创新,通常融入“和”与“通项”的关系,与生产生活、社会热点相结合,考查考生的阅读能力的同时,也考查数学素养中的逻辑推理、计算能力,培养了考生的创新意识.另外,创新迁移类型试题还有以下特点:(1)新知识“开幕”,别开生面,新的知识主要是新的符号、定义、法则、图表等,或介绍新的思维方法,着眼于应用;(2)类比、推广;(3)以高中数学内容为材料,“偷梁换柱”“移花接木”,创设新情境,演化新问题.[例2] (2013·全国卷Ⅰ)设△A n B n C n 的三边长分别为a n ,b n ,c n ,△A n B n C n 的面积为S n ,n =1,2,3,….若b 1>c 1,b 1+c 1=2a 1,a n +1=a n ,b n +1=c n +a n 2,c n +1=b n +a n2,则( ) A .{S n }为递减数列 B .{S n }为递增数列C .{S 2n -1}为递增数列,{S 2n }为递减数列D .{S 2n -1}为递减数列,{S 2n }为递增数列 [解析] 由b n +1=a n +c n 2,c n +1=b n +a n2, 得b n +1+c n +1=a n +12(b n +c n ),(*)b n +1-c n +1=-12(b n -c n ),由a n +1=a n 得a n =a 1,代入(*)得b n +1+c n +1=a 1+12(b n +c n ),∴b n +1+c n +1-2a 1=12(b n +c n -2a 1),∵b 1+c 1-2a 1=2a 1-2a 1=0, ∴b n +c n =2a 1>|B n C n |=a 1,所以点A n 在以B n ,C n 为焦点且长轴长为2a 1的椭圆上(如图).由b 1>c 1得b 1-c 1>0,所以|b n +1-c n +1|=12(b n -c n ),即|b n -c n |=(b 1-c 1)·⎝⎛⎭⎫12n -1,所以当n 增大时|b n -c n |变小,即点A n 向点A 处移动,即边B n C n 上的高增大,又|B n C n |=a n =a 1不变,所以{S n }为递增数列.[答案] B[启思维] 交汇问题是将各主干知识“联姻”“牵手”、交叉渗透等综合考查主干知识的常见问题,覆盖面广.本题将数列与几何交汇,增大了试题难度,较好地考查了考生的数形结合思想、逻辑思维能力,其实质是考查数列的递推关系式、椭圆的定义及性质,此题对考生的数学抽象、逻辑推理、直观想象要求较高.[知能升级]1.数列与其他知识的交汇问题主要体现在以下两点:(1)以数列知识为纽带,在数列与函数、方程、不等式、解析几何的交汇处命题,主要考查利用函数观点、不等式的方法解决数列问题,往往涉及与数列相关的不等式证明、参数的范围等.(2)以数列知识为背景的新概念、创新型问题,除了需要用到数列知识外,还要运用函数、不等式等相关知识和方法,特别是题目条件中的“新知识”是解题的钥匙,此类问题往往思维难度较大,通常作为压轴题出现.2.解决此类问题的关键是理解题意,将核心问题提炼出来,运用数列、函数、解析几何的相关知识求解,主要考查了转化与化归思想的应用.[增分集训]1.斐波那契数列{a n }满足:a 1=1,a 2=1,a n =a n -1+a n -2(n ≥3,n ∈N *).若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前n 项所占的格子的面积之和为S n ,每段螺旋线与其所在的正方形所围成的扇形面积为c n ,则下列结论错误的是( )A .S n +1=a 2n +1+a n +1a nB .a 1+a 2+a 3+…+a n =a n +2-1C .a 1+a 3+a 5+…+a 2n -1=a 2n -1D .4(c n -c n -1)=πa n -2a n +1解析:选C 对于选项A ,由题图可知,S 2=a 2a 3,S 3=a 3a 4,S 4=a 4a 5,…,则S n +1=a n +1a n +2=a n +1(a n +1+a n )=a 2n +1+a n +1a n ,故A 项正确;对于选项B ,a 1+a 2+a 3+…+a n =a n +2-1=a n +1+a n -1⇔a 1+a 2+a 3+…+a n -1=a n +1-1⇔a 1+a 2+a 3+…+a n -2=a n -1⇔a 1+a 2+a 3+…+a n -3=a n -1-1⇔…⇔a 1=a 3-1⇔1=2-1,故B 项正确;对于选项C ,当n =1时,a 1≠a 2-1,故C 项错误;对于选项D,4(c n -c n -1)=4⎝⎛⎭⎫πa 2n 4-πa 2n -14=π(a n +a n -1)(a n-a n -1)=πa n -2a n +1,故D 项正确.2.已知函数f (x )在R 上的图象是连续不断的一条曲线,当x >0时,f (x )<2,对任意的x ,y ∈R ,f (x )+f (y )=f (x +y )+2成立,若数列{a n }满足a 1=f (0),且f (a n +1)=f ⎝⎛⎭⎫a na n +3,n ∈N *,则a 2 018的值为( )A .2 B.62×32 017-1 C.22×32 017-1D.22×32 016-1解析:选C 令x =y =0得f (0)=2,所以a 1=2. 设x 1,x 2是R 上的任意两个数,且x 1<x 2, 则x 2-x 1>0,因为当x >0时,f (x )<2,所以f (x 2-x 1)<2,即f (x 2)=f (x 2-x 1+x 1)=f (x 2-x 1)+f (x 1)-2<2+f (x 1)-2=f (x 1), 所以f (x )在R 上是减函数. 因为f (a n +1)=f ⎝⎛⎭⎫a na n +3,所以a n +1=a n a n +3,即1a n +1=3a n +1,所以1a n +1+12=3⎝⎛⎭⎫1a n +12,因为1a 1+12=1, 所以⎩⎨⎧⎭⎬⎫1a n+12是以1为首项,3为公比的等比数列,所以1a n +12=3n -1,即a n =22×3n -1-1. 所以a 2 018=22×32 017-1. 3.数列{a n }中,a 1=12,a n +1=na n (n +1)(na n +1)(n ∈N *),若不等式3n 2+1n +ta n ≥0恒成立,则实数t 的取值范围是____________.解析:由a n +1=na n(n +1)(na n +1),得1(n +1)a n +1-1na n=1,又1a 1=2,所以数列⎩⎨⎧⎭⎬⎫1na n 是首项为2,公差为1的等差数列,则1na n =n +1,即a n =1n (n +1), 从而不等式3n 2+1n +ta n ≥0恒成立等价于-t ≤3n +n +4恒成立,易知当n =2时,3n +n +4取得最小值152,所以-t ≤152,即t ≥-152. 所以实数t 的取值范围是⎣⎡⎭⎫-152,+∞.答案:⎣⎡⎭⎫-152,+∞ [高考大题通法点拨]数列问题重在“归”——化归[思维流程][策略指导]利用化归思想可探索一些一般数列的简单性质.等差数列与等比数列是数列中的两个特殊的基本数列,高考中通常考查的是非等差、等比数列问题,应对的策略就是通过化归思想,将其转化为这两种数列.[典例] 已知数列{a n }的前n 项和S n =3n 2+8n ,{b n }是等差数列,且a n =b n +b n +1. (1)求数列{b n }的通项公式;(2)令c n =(a n +1)n +1(b n +2)n,求数列{c n }的前n 项和T n .[破题思路] 第(1)问[规范解答](1)由题意知当n ≥2时,a n =S n -S n -1=6n +5. 当n =1时,a 1=S 1=11, 符合上式. 所以a n =6n +5. 设数列{b n }的公差为d.由⎩⎪⎨⎪⎧ a 1=b 1+b 2,a 2=b 2+b 3,即⎩⎪⎨⎪⎧ 11=2b 1+d ,17=2b 1+3d ,解得⎩⎪⎨⎪⎧b 1=4,d =3. 所以b n =3n +1.(2)由(1)知c n =(6n +6)n +1(3n +3)n =3(n +1)·2n +1. 由T n =c 1+c 2+…+c n ,得T n =3×[2×22+3×23+…+(n +1)×2n +1],2T n =3×[2×23+3×24+…+(n +1)×2n +2],两式作差,得-T n =3×[2×22+23+…+2n +1-(n +1)×2n +2]=3×⎣⎢⎡⎦⎥⎤4+4(1-2n )1-2-(n +1)×2n +2 =-3n ·2n +2,所以T n =3n ·2n +2.[关键点拨] 等差、等比数列基本量的计算模型 [对点训练](2018·福州模拟)已知数列{a n }中,a 1=1,a 2=2,a n +1=3a n -2a n -1(n ≥2,n ∈N *).设b n =a n +1-a n .(1)证明:数列{b n }是等比数列;(2)设c n =b n(4n 2-1)2n,求数列{c n }的前n 项的和S n .解:(1)证明:因为a n +1=3a n -2a n -1(n ≥2,n ∈N *),b n =a n +1-a n , 所以b n +1b n =a n +2-a n +1a n +1-a n =(3a n +1-2a n )-a n +1a n +1-a n =2(a n +1-a n )a n +1-a n =2,又b 1=a 2-a 1=2-1=1,所以数列{b n }是以1为首项,以2为公比的等比数列. (2)由(1)知b n =1×2n -1=2n -1,因为c n =b n(4n 2-1)2n,所以c n =12(2n +1)(2n -1)=14⎝⎛⎭⎫12n -1-12n +1,所以S n =c 1+c 2+…+c n=14⎝⎛⎭⎫1-13+13-15+…+12n -1-12n +1 =14⎝⎛⎭⎫1-12n +1=n 4n +2. [总结升华]对于数列的备考:一是准确掌握数列中a n 与S n 之间的关系,这是解决数列问题的基础;二是重视等差与等比数列的复习,熟悉其基本概念、公式和性质,这是解决数列问题的根本;三是注意数列与函数、不等式等的综合问题,掌握解决此类问题的通法;四是在知识的复习和解题过程中体会其中所蕴含的数学思想方法,如分类讨论、数形结合、等价转化、函数与方程思想等.[专题跟踪检测](对应配套卷P180) 一、全练保分考法——保大分1.已知等差数列的前3项依次为a ,a +2,3a ,前n 项和为S n ,且S k =110,则k 的值为( )A .9B .11C .10D .12解析:选C 由a ,a +2,3a 成等差数列,得公差为2,且2(a +2)=a +3a ,解得a =2,所以S k =2k +k (k -1)2×2=k 2+k =110,解得k =10或k =-11(舍去). 2.(2018·云南模拟)已知数列{a n }是等差数列,若a 1-1,a 3-3,a 5-5依次构成公比为q 的等比数列,则q =( )A .-2B .-1C .1D .2解析:选C 依题意,注意到2a 3=a 1+a 5,2a 3-6=a 1+a 5-6,即有2(a 3-3)=(a 1-1)+(a 5-5),即a 1-1,a 3-3,a 5-5成等差数列;又a 1-1,a 3-3,a 5-5依次构成公比为q 的等比数列,因此有a 1-1=a 3-3=a 5-5(若一个数列既是等差数列又是等比数列,则该数列是一个非零的常数列),q =a 3-3a 1-1=1. 3.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难.次日脚痛减一半,六朝方得至其关.要见次日行里数,请公仔细算相还.”其意思是“有一个人走378里,第一天健步行走,从第二天起脚痛,每天走的路程是前一天的一半,走了6天后到达目的地.”则第三天走了( )A .60里B .48里C .36里D .24里解析:选B 由题意得每天走的路程构成等比数列{a n },其中q =12,S 6=378,则S 6=a 1⎝⎛⎭⎫1-1261-12=378,解得a 1=192,所以a 3=192×14=48.4.已知递减的等差数列{a n }中,a 3=-1,a 1,a 4,-a 6成等比数列.若S n 为数列{a n }的前n 项和,则S 7的值为( )A .-14B .-9C .-5D .-1解析:选A 设数列{a n }的公差为d ,由题可知d <0,因为a 1,a 4,-a 6成等比数列,所以a 24=a 1×(-a 6),即(a 1+3d )2=a 1×(-a 1-5d ).又a 3=a 1+2d =-1,联立可解得d =-1或d =25(舍去).因为d =-1,所以a 1=1,所以S 7=-14.5.若数列{a n }是正项数列,且a 1+a 2+…+a n =n 2+n ,则a 1+a 22+…+a nn 等于( )A .2n 2+2nB .n 2+2nC .2n 2+nD .2(n 2+2n )解析:选A ∵a 1+a 2+…+a n =n 2+n ,① ∴当n =1时,a 1=2,解得a 1=4. 当n ≥2时,a 1+a 2+…+a n -1=(n -1)2+n -1.② ①-②,得a n =2n ,∴a n =4n 2.当n=1时上式也成立.∴a nn=4n,则a1+a22+…+a nn=4(1+2+…+n)=4×n(1+n)2=2n2+2n.6.已知正项等比数列{a n}的前n项和为S n,且S8-2S4=5,则a9+a10+a11+a12的最小值为()A.10 B.15C.20 D.25解析:选C由题意可得a9+a10+a11+a12=S12-S8,由S8-2S4=5可得S8-S4=S4+5,由等比数列的性质可得S4,S8-S4,S12-S8成等比数列,则S4(S12-S8)=(S8-S4)2,综上可得a9+a10+a11+a12=S12-S8=(S4+5)2S4=S4+25S4+10≥2S4·25S4+10=20,当且仅当S4=5时等号成立,综上可得a9+a10+a11+a12的最小值为20.7.设{a n}是由正数组成的等比数列,S n为其前n项和.已知a2a4=1,S3=7,则其公比q等于________.解析:∵{a n}是由正数组成的等比数列,∴数列{a n}的公比q>0.由a2a4=1,得a23=1,∴a3=1.∵S3=7,∴a1+a2+a3=1q2+1q+1=7,即6q2-q-1=0,解得q=12或q=-13(舍去).故q=1 2.答案:1 28.在各项均为正数的等比数列{a n}中,a m-1a m+1=2a m(m≥2),数列{a n}的前n项积为T n.若T2m-1=512,则m的值为________.解析:由等比数列的性质,得a m+1a m-1=a2m=2a m.又数列{a n}的各项均为正数,所以a m =2.又T2m-1=(a m)2m-1=22m-1=512,所以2m-1=9,所以m=5.答案:59.设数列{a n}的前n项和为S n,且a1=1,a n+a n+1=12n(n∈N*),则S2n-1=________.解析:因为a1=1,a n+a n+1=12n(n∈N*),所以S2n-1=a1+(a2+a3)+…+(a2n-2+a2n-1)=1+122+124+…+122n-2=1-⎝⎛⎭⎫14n1-14=43⎣⎡⎦⎤1-⎝⎛⎭⎫14n.答案:43⎣⎡⎦⎤1-⎝⎛⎭⎫14n10.(2018·成都模拟)已知等差数列{a n}的前n项和为S n,a2=3,S4=16,n∈N*.(1)求数列{a n}的通项公式;(2)设b n =1a n a n +1,求数列{b n }的前n 项和T n . 解:(1)设数列{a n }的公差为d , ∵a 2=3,S 4=16, ∴a 1+d =3,4a 1+6d =16, 解得a 1=1,d =2. ∴a n =2n -1. (2)由题意,b n =1(2n -1)(2n +1)=12⎝⎛⎭⎫12n -1-12n +1,∴T n =b 1+b 2+…+b n=12⎣⎡⎦⎤⎝⎛⎭⎫1-13+⎝⎛⎭⎫13-15+…+⎝⎛⎭⎫12n -1-12n +1 =12⎝⎛⎭⎫1-12n +1 =n2n +1. 11.(2019届高三·南宁二中、柳州高中联考)已知a 1=2,a 2=4,数列{b n }满足:b n +1=2b n +2且a n +1-a n =b n .(1)求证:数列{b n +2}是等比数列; (2)求数列{a n }的通项公式.解:(1)证明:由题知,b n +1+2b n +2=2b n +2+2b n +2=2,∵b 1=a 2-a 1=4-2=2,∴b 1+2=4,∴数列{b n +2}是以4为首项,2为公比的等比数列. (2)由(1)可得,b n +2=4·2n -1,故b n =2n +1-2.∵a n +1-a n =b n , ∴a 2-a 1=b 1, a 3-a 2=b 2, a 4-a 3=b 3, …a n -a n -1=b n -1.累加得,a n -a 1=b 1+b 2+b 3+…+b n -1(n ≥2), a n =2+(22-2)+(23-2)+(24-2)+…+(2n -2) =2(1-2n )1-2-2(n -1)=2n +1-2n ,故a n =2n +1-2n (n ≥2).∵a 1=2符合上式,∴数列{a n }的通项公式为a n =2n +1-2n (n ∈N *).12.已知数列{a n }是等差数列,a 2=6,前n 项和为S n ,{b n }是等比数列,b 2=2,a 1b 3=12,S 3+b 1=19.(1)求{a n },{b n }的通项公式; (2)求数列{b n cos(a n π)}的前n 项和T n . 解:(1)∵数列{a n }是等差数列,a 2=6, ∴S 3+b 1=3a 2+b 1=18+b 1=19,∴b 1=1, ∵b 2=2,数列{b n }是等比数列,∴b n =2n -1.∴b 3=4,∵a 1b 3=12,∴a 1=3, ∵a 2=6,数列{a n }是等差数列, ∴a n =3n .(2)由(1)得,令C n =b n cos(a n π)=(-1)n 2n -1,∴C n +1=(-1)n +12n ,∴C n +1C n=-2,又C 1=-1, ∴数列{b n cos(a n π)}是以-1为首项,-2为公比的等比数列, ∴T n =-1×[1-(-2)n ]1+2=-13[1-(-2)n ].二、强化压轴考法——拉开分1.已知数列{a n }的前n 项和为S n ,且a 1=2,S n +1=4a n +2,则a 12=( ) A .20 480 B .49 152 C .60 152D .89 150解析:选B 由S 2=4a 1+2,得a 1+a 2=4a 1+2,联立a 1=2,解得a 2=8.又a n +2=S n +2-S n +1=4a n +1-4a n ,∴a n +2-2a n +1=2(a n +1-2a n ),∴数列{a n +1-2a n }是以a 2-2a 1=4为首项,以2为公比的等比数列,∴a n +1-2a n =4×2n -1=2n +1,∴a n +1-2a n 2n +1=1,∴a n +12n +1-a n2n =1,∴数列⎩⎨⎧⎭⎬⎫a n 2n 是以a 12=1为首项,以1为公差的等差数列,∴a n2n =1+(n -1)=n ,∴a n =n ·2n ,∴a 12=12×212=49 152.2.已知a 1=1,a n =n (a n +1-a n )(n ∈N *),则数列{a n }的通项公式是( ) A .2n -1 B.⎝⎛⎭⎫n +1n n -1C .n 2D .n解析:选D 因为a n =n (a n +1-a n )=na n +1-na n ,所以na n +1=(n +1)a n ,所以a n +1a n =n +1n ,所以a n =a n a n -1·a n -1a n -2·…·a 2a 1·a 1=n n -1·n -1n -2 (2)1·1=n .3.(2018·郑州模拟)已知数列{a n }满足a 1=1,|a n +1-a n |=1n (n +2).若a 2n +1>a 2n -1,a 2n +2<a 2n (n ∈N*),则数列{(-1)n a n }的前40项的和为( )A.1920B.325462C.4184D.2041解析:选D 由题意可得a 2n +1-a 2n -1>0,a 2n +2-a 2n <0,则a 2n +1-a 2n -1>a 2n +2-a 2n , 所以a 2n +1-a 2n +2>a 2n -1-a 2n .① 而|a 2n +1-a 2n +2|=1(2n +1)(2n +3),|a 2n -1-a 2n |=1(2n -1)(2n +1),即|a 2n +1-a 2n +2|<|a 2n -1-a 2n |.② 综合①②,得a 2n -1-a 2n <0, 即a 2n -1-a 2n =-1(2n -1)(2n +1).裂项,得a 2n -a 2n -1=12×⎝⎛⎭⎫12n -1-12n +1.综上可得,数列{(-1)n a n }的前40项的和为(a 2-a 1)+(a 4-a 3)+…+(a 40-a 39)=12×⎣⎡⎦⎤⎝⎛⎭⎫1-13+⎝⎛⎭⎫13-15+…+⎝⎛⎭⎫139-141=2041. 4.(2019届高三·河北“五个一名校联盟”联考)在正整数数列中,由1开始依次按如下规则,将某些数染成红色.先染1;再染两个偶数2,4;再染4后面最邻近的3个连续奇数5,7,9;再染9后面的最邻近的4个连续偶数10,12,14,16;再染此后最邻近的5个连续奇数17,19,21,23,25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,…,则在这个红色子数列中,由1开始的第2 018个数是( )A .3 971B .3 972C .3 973D .3 974解析:选B 由题意可知,第1组有1个数,第2组有2个数,…,根据等差数列的前n 项和公式,可知前n 组共有n (n +1)2个数.由于2 016=63×(63+1)2<2 018<64×(64+1)2=2 080,因此,第2 018个数是第64组的第2个数.由于第1组最后一个数是1,第2组最后一个数是4,第3组最后一个数是9,…,第n 组最后一个数是n 2,因此,第63组最后一个数为632,632=3 969,第64组为偶数组,其第1个数为3 970,第2个数为3 972,故选B.5.(2019届高三·南昌调研)设数列{a n }的前n 项和为S n ,若a 1=3且当n ≥2时,2a n =S n ·S n -1(n ∈N *),则数列{a n }的通项公式a n =________.解析:当n ≥2时,由2a n =S n ·S n -1可得2(S n -S n -1)=S n ·S n -1,∴1S n -1-1S n =12,即1S n -1S n -1=-12,∴数列⎩⎨⎧⎭⎬⎫1S n 是首项为13,公差为-12的等差数列,∴1S n =13+⎝⎛⎭⎫-12·(n -1)=5-3n 6,∴S n =65-3n.当n ≥2时,a n =12S n S n -1=12×65-3n ×65-3(n -1)=18(5-3n )(8-3n ),又a 1=3,∴a n =⎩⎪⎨⎪⎧3,n =1,18(5-3n )(8-3n ),n ≥2. 答案:⎩⎪⎨⎪⎧3,n =1,18(5-3n )(8-3n ),n ≥2 6.(2018·开封模拟)已知数列{a n }满足[2-(-1)n ]a n +[2+(-1)n ]a n +1=1+(-1)n ×3n (n ∈N *),则a 25-a 1=________.解析:∵[2-(-1)n ]a n +[2+(-1)n ]a n +1=1+(-1)n ×3n ,∴当n =2k (k ∈N *)时,a 2k +3a 2k +1=1+6k ,当n =2k -1(k ∈N *)时,3a 2k -1+a 2k =1-6k +3,∴a 2k +1-a 2k -1=4k -1,∴a 25=(a 25-a 23)+(a 23-a 21)+…+(a 3-a 1)+a 1=(4×12-1)+(4×11-1)+…+(4×1-1)+a 1=4×12×(12+1)2-12+a 1=300+a 1,∴a 25-a 1=300.答案:300三、加练大题考法——少失分1.已知等差数列{a n }的前n 项和为S n ,S 7=0,a 3-2a 2=12(n ∈N *). (1)求数列{a n }的通项公式a n ;(2)求数列⎩⎨⎧⎭⎬⎫a n +162n +2的前n 项和S n .解:(1)设等差数列{a n }的公差为d ,由已知得⎩⎪⎨⎪⎧7a 1+7×62d =0,a 1+2d -2(a 1+d )=12,解得⎩⎪⎨⎪⎧a 1=-12,d =4,所以a n =4n -16.(2)由(1)知a n =4n -16,所以a n +162n +2=4n -16+162n +2=n2n , 所以S n =12+222+323+…+n 2n ,两边同乘以12,得12S n =122+223+324+…+n -12n +n 2n +1, 两式相减,得12S n =12+122+123+124+…+12n -n 2n +1=12⎝⎛⎭⎫1-12n 1-12-n2n +1=1-n +22n +1,所以S n =2-n +22n . 2.设数列{a n }的前n 项和为T n =2n -14(n ∈N *).(1)求{a n }的通项公式;(2)若数列{b n }满足b n =log 2a n ,数列{b n }的前n 项和为S n ,定义[x ]为不小于x 的最小整数,求数列⎩⎨⎧⎭⎬⎫⎣⎡⎦⎤S n n 2的前n 项和R n .解:(1)因为数列{a n }的前n 项和为T n =2n -14,所以a 1=T 1=21-14=14.当n ≥2时,a n =T n -T n -1=2n -14-2n -1-14=2n -3,当n =1时,a 1=14符合上式.故a n =2n -3.(2)由(1)可知,b n =log 2a n =n -3,则数列{b n }是首项为-2,公差为1的等差数列,其前n 项和S n =n 22-52n ,则S n n 2=12-52n .因为当n ≥1时,S n n 2=12-52n 单调递增,所以S 112=-2,当2≤n ≤5时,-34≤S nn 2≤0,当n ≥6时,112≤S n n 2<12,所以R 1=-2,当2≤n ≤5时,R n =-2+0+0+…+0=-2, 当n ≥6时,R n =-2+(n -5)·1=n -7,所以R n =⎩⎪⎨⎪⎧-2,1≤n ≤5,n -7,n ≥6.3.已知等差数列{a n }的前n 项和为S n (n ∈N *),且a 2=3,S 5=25. (1)求数列{a n }的通项公式; (2)若数列{b n }满足b n =1S n ·S n +1,记数列{b n }的前n 项和为T n ,证明:T n <1.解:(1)设等差数列{a n }的公差为d.因为a 2=3,S 5=25,所以⎩⎪⎨⎪⎧a 1+d =3,5(2a 1+4d )2=25,解得⎩⎪⎨⎪⎧a 1=1,d =2,所以a n =2n -1.(2)证明:由(1)知,a n =2n -1, 所以S n =n (1+2n -1)2=n 2. 所以b n =1n 2·(n +1)2=1n (n +1)=1n -1n +1.所以T n =b 1+b 2+b 3+…+b n =⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1n -1n +1=1-1n +1<1.4.(2017·山东高考)已知{x n }是各项均为正数的等比数列,且x 1+x 2=3,x 3-x 2=2. (1)求数列{x n }的通项公式;(2)如图,在平面直角坐标系xOy 中,依次连接点P1(x 1,1),P 2(x 2,2),…,P n +1(x n +1,n +1)得到折线P 1P 2…P n +1,求由该折线与直线y =0,x =x 1,x =x n +1所围成的区域的面积T n .解:(1)设数列{x n }的公比为q ,由已知得q >0.由题意得⎩⎪⎨⎪⎧x 1+x 1q =3,x 1q 2-x 1q =2.所以3q 2-5q -2=0.因为q >0,所以q =2,x 1=1, 因此数列{x n }的通项公式为x n =2n -1.(2)过P 1,P 2,…,P n +1向x 轴作垂线,垂足分别为Q 1,Q 2,…,Q n +1. 由(1)得x n +1-x n =2n -2n -1=2n -1,记梯形P n P n +1Q n +1Q n 的面积为b n ,由题意得b n=(n+n+1)2×2n-1=(2n+1)×2n-2,所以T n=b1+b2+…+b n=3×2-1+5×20+7×21+…+(2n-1)×2n-3+(2n+1)×2n-2.①又2T n=3×20+5×21+7×22+…+(2n-1)×2n-2+(2n+1)×2n-1.②①-②得-T n=3×2-1+(2+22+…+2n-1)-(2n+1)×2n-1=32+2(1-2n-1)1-2-(2n+1)×2n-1.所以T n=(2n-1)×2n+12.。
(新高考适用)2023版高考历史二轮总复习 第1部分 专题7 求生——近代化道路探索与社会转型课件

【解析】 由1912—1918年中国机器需用器具净进口值统计表可 知,中国机器生产需要的器具进口值总趋势是有较快增长,说明辛亥革 命后和一战期间我国民族工业得到较快发展,故选D项;1912—1918年 我国社会思潮主要是实业救国和民主共和,而不仅是实业救国,且材料 并未体现社会思潮,排除A项;题干仅提到机器需用器具的进口值,并 没有与其他产业进行比较,所以没法得出近代产业结构变化的结论,排 除B项;题干中并没有提到进口的机器需用器具是国家投入,所以不能 得出国家对工业建设投入加大的结论,排除C项。
话题二 冲击转型——探索近代化的曲折道路
“近代”是相对于“传统”而言的,传统社会和现代社会是两种不 同性质的社会,由传统社会向现代社会变迁的过程就是近代化的过程。 中国近代化也叫现代化,以经济领域工业化、市场化,政治领域的民主 化、法制化和思想领域的人性化、科学化为主要标志。这是整个世界近 代化最为主要的发展线索,中国近代历史也不例外。
第一部分
两大板块 纵横贯通 优势互补 珠联璧合
第二编 中国近现代史
板块二 专题纵向贯通——让理解更深刻 专题七 求生——近代化道路探索与社会转型
话题一 近代中国经济的调适与转型
通过中国近现代社会经济的变动,充分认识整体的世界经济对中国 经济的影响,认识一个国家经济发展要顺应世界发展潮流的重要性及社 会转型的相关策略。
A.使清政府开始早期近代化尝试 B.刺激列强掀起瓜分中国的狂潮 C.导致外国侵略势力发展到北京 D.加强了中国与西方世界的联系
【解析】 据材料“中国与西洋的关系更加密切”并结合所学知识 可知,第二次鸦片战争以后,面对内忧外患,洋务派(在中央以恭亲王奕
、文祥为代表;在地方以曾国藩、李鸿章、左宗棠、张之洞为代表)掀 起了洋务运动,向西方学习技术,开启了中国近代化的历程,故选A 项;19世纪末,《马关条约》的签订刺激列强掀起瓜分中国的狂潮,排 除B项;条约签订前,外国侵略势力已发展到北京,排除C项;鸦片战争 后,中国已被迫卷入资本主义世界市场,排除D项。
物理二轮 第一部分 专题七 学案 直流电路和交流电路
本 学 案 栏 目 开 关
答案
AC
巧学妙解王荣誉出品
易混辨析
专题七 学案13
1.正弦式交变电流的变化规律(线圈在中性面位置开始计时) 表达式
本 学 案 栏 目 开 关
图象
磁通量 电动势
Φ = Φmcos ωt= BScos ωt e = Emsin ωt = NBSωsin ωt u = Umsin ωt = REm sin ωt R+ r i = Imsin ωt = Em sin ωt R+ r
由于矩形闭合导线框 ABCD 的电阻不可忽略, 则其电阻会发热,
本 学 案 栏 目 开 关
故闭合导线框的功率应大于 12 W,D 错误.
答案 C
巧学妙解王荣誉出品
考题 3 例3 对变压器和远距离输电的考查
巧学妙解王荣誉出品
专题七 学案13
(3)可直接应用“部分电路中 R、I、U 的关系”中的两个结论: ①任一电阻 R 阻值增大,必引起通过该电阻的电流 I 的减小和 I↓ 该电阻两端电压 U 的增大,即 R↑→ U↑ ②任一电阻 R 阻值增大,必将引起与之并联的支路中电流 I 的增大和与之串联的各电阻两端电压 U 串的减小.即 I并↑ R↑→ U串↓
效 值
平 均 值
计算通过电路横截面的 电荷量
巧学妙解王荣誉出品
专题七 学案13
突破练习 3. (2013· 海南· 3)通过一阻值 R=100 Ω 的电阻
本 学 案 栏 目 开 关
的交变电流如图 5 所示, 其周期为 1 s. 电 阻两端电压的有效值为 A.12 V B.4 10 V C.15 V D.8 5 V ( B )
图5
巧学妙解王荣誉出品
第一阶段 专题七 化学与技术——应用化

高考对化学与技术的考查是以Ⅱ卷大题或选做大题的 形式出现,试题的综合性较强,常常选取某一化工生产作为 核心来考查反应原理、设备结构、绿色工艺等问题,不仅检 测了学生对核心知识的掌握程度,而且检查了化学知识的深、 广度。主要的考查内容有: (1)水处理技术:硬水的软化、海水的淡化、污水的处 理等; (2)自然资源的开发利用:依托海水元素的提取、氯碱工 业、合成氨工业、硫酸工业、纯碱工业等综合考查化学反应 原理、新技术、新设备的应用等; (3)化学材料的制造与应用。 返回
返回
(4)常见的工业生产流程的主线和核心:
规律:主线主产品、分支副产品、回头为循环。 核心考点:物质的分离操作、除杂试剂的选择、生产条 件的控制、三废处理及能量的综合利用等。 返回
1.无机非金属材料的生产
类型 举例 主要成分或生产原理 陶瓷 将黏土与水的混合物通过高温煅烧制成 普通玻璃的主要成分为 Na2SiO3、CaSiO3 和 SiO2, 传 生产原理为 统 高温 硅 玻璃 Na2CO3+SiO2=====Na2SiO3+CO2↑ 酸 高温 CaCO3+SiO2=====CaSiO3+CO2↑ 盐 材 主 要 成 分 是 硅 酸 三 钙 (3CaO· 2) 、 硅 酸 二 钙 SiO 料 水泥 (2CaO· 2)、铝酸三钙(3CaO· 2O3)、铁铝酸钙 SiO Al (4CaO· 2O3· 2O3)等 Al Fe
备考策略指导
考什么
高考前沿快讯
怎么考 知识点一 知识点二 知识点三
第 一 阶 段
专 题 七
知识升级
考点锁定 难点速通
课堂——强化落实
课时检测
课下——达标检测
返回
返回
在新课标高考中,本部分为选考模块,主要是大题,以 简答题为主,有时也综合化学计算的内容。本部分在新课标高 考中体现的思想:关注化学在社会发展和科技进步中的作用, 引导考生认识化学与生产、生活的密切联系,应用化学知识开 发新材料、新能源,解决有关环境问题等。考查的主要题型包
2019学年高中语文选修唐诗宋词选读:专题七第一板块菩萨蛮(小山重叠金明灭)含答案

词是唐五代时兴起的一种配合音乐歌唱的新体诗。
它在隋唐之际已经产生,中唐以后逐渐有较多文人从事创作,晚唐五代趋于繁荣,而极盛于宋代。
唐五代时,词的表现内容逐步开拓,词的情感和意境进一步深化;诗歌中新的审美追求对词的内在特质的形成产生了重要的影响。
词人的出现及其性格特征的趋同性、词集的出现与词之主体风格的形成,则意味着词作为一种独立文体已经确立。
而且唐五代词的美学理想、艺术精神和表现特征,直接启迪了北宋词,唐五代时期成为词萌芽、成熟和发展的重要阶段。
唐五代词主要有花间词和南唐词两大词派。
(一)花间词花间词派是以晚唐词人温庭筠、五代前蜀词人韦庄为代表,以写男女相思离别为主要特征的词派,亦称作“西蜀词派”。
温词秾艳华美,韦词疏淡明丽,代表该派的两种风格,其他人的词作多蹈袭温韦余风。
(二)南唐词南唐词以宫廷为中心,以君臣为主体,以“二主一相”(中主李璟、后主李煜父子和中主朝宰相冯延巳)为代表,他们凭借共同的高雅而全面的文化修养和艺术情趣,以及独特的个性禀赋和情感体验,赋予南唐词独特的感伤情调和开阔的词境,确立了他们结束“花间”开启北宋的承上启下的词史地位。
1.掌握词的相关文学常识,能够区别诗与词的不同点。
2.能够通过对温庭筠、韦庄词的鉴赏,初步了解花间词的艺术风格。
3.能通过对冯延巳、李璟、李煜词的鉴赏,初步了解南唐词的艺术特色。
4.通过体会鉴赏唐五代词的语言风格和表达技巧,掌握鉴赏词作的规律和技巧。
1.《菩萨蛮》(小山重叠金明灭)这首词是体现温庭筠词作浓艳华美风格的代表作。
历来对这首词的评赏与接受,见仁见智,颇为纷纭。
因此,学习时可对文本进行细读和多元解读,把鉴赏的重心放在表达技巧的分析与鉴赏上,如刻画描写人物的方法等。
2.《菩萨蛮》(人人尽说江南好)韦词如清新明丽之芙蓉。
学习时可在通读词意的基础上,赏析词中直抒胸臆的词句,领会韦庄词“显而疏”的艺术特色;赏析词中“江南”、“老”和“还乡”等词语反复出现的表达效果;赏析词的上下片中“情”与“景”交替变化的结构安排的艺术效果。
贵阳专版2019届中考语文总复习第1部分积累与运用专题7名著阅读习题1 含答案

专题七名著阅读(一)(时间:45分钟)1.名著阅读。
不必说碧绿的菜畦,光滑的石井栏,高大的皂荚树,紫红的桑椹;也不必说鸣蝉在树叶里长吟,肥胖的黄蜂伏在菜花上,轻捷的叫天子(云雀)忽然从草间直窜向云霄里去了。
单是周围的短短的泥墙根一带,就有无限趣味。
油蛉在这里低唱,蟋蟀们在这里弹琴。
翻开断砖来,有时会遇见蜈蚣;还有斑蝥,倘若用手指按住它的脊梁,便会拍的一声,从后窍喷出一阵烟雾。
何首乌藤和木莲藤缠络着,木莲有莲房一般的果实,何首乌有拥肿的根……这段文字出自__鲁迅__(作者)写的散文《__从百草园到三味书屋__》,它是散文集《__朝花夕拾__》中的一篇,这是作者“从记忆中抄出来”的一部回忆性散文集。
2.名著阅读。
回得五庄观,那大仙又让道童抬一大锅油出来,架起干柴,发起烈火。
顷刻间,那油锅热腾腾。
大圣见那台下西边有一个石狮子,便咬破舌尖,把石狮子喷了一口,叫声“变”,变作他本身模样。
油锅滚透后,大仙说:“把孙行者抬下去!”二十个小仙扛将起来,往锅里一掼,“砰”的一声响,溅起些滚油点子,把那小道士们脸上烫了几个燎浆大泡!只听得烧火的小童喊道:“锅漏了!”原来是一个石狮子在锅里。
以上文字出自《西游记》,这位大仙是__镇元大仙__(名字),他惩治唐僧师徒四人是因为__孙悟空推倒(毁掉)了人参果树__。
3.名著阅读。
“先生!”祥子低着头,声音很低,可是很有力:“先生另找人吧!这个月的工钱,你留着收拾车吧:车把断了,左边的灯碎了块玻璃;别处倒都好好的呢。
”选文中的“先生”是指__曹先生__,祥子叫先生“另找人”的原因是__祥子拉车摔伤了曹先生__(事件)。
4.名著阅读。
“我是被压迫的,瞧,那就是压迫者!由于他,所有一切我热爱过的,尊敬过的,祖国、父母、爱人、子女他们全死亡了!所有我仇恨的一切,就在那里!”船长不愿这艘战舰的残骸骨跟“复仇号”的光荣残骸相混,他把战舰引向东方。
第二天,可怕的打击开始了!此语段出自《__海底两万里__》,文段中的船长是__尼摩__(人物)。
2022年人教版中考化学复习第一部分基础考点过关 专题七 常见的酸和碱

专题七常见的酸和碱命题点1溶液的酸碱性与pH1. (2019北京)一些食物的pH范围如下,其中呈碱性的是()A. 柠檬汁(2.0~3.0)B. 番茄汁(4.0~4.4)C. 牛奶(6.3~6.6)D. 鸡蛋清(7.6~8.0)2. (2019宜昌)下列人体内的一些液体和排泄物的正常pH范围中,酸性最强的是()A. 血浆(7.35~7.45)B. 胃液(0.9~1.5)C. 唾液(6.6~7.1)D. 胆汁(7.1~7.3)3. (2019重庆B)头发油腻是因为油脂的分泌,清洗时碱性溶液效果更好。
从pH角度考虑效果最好的洗发水的pH为()A. 8B. 7C. 6D. 44. (2019天津)一些物质的近似pH如图,下列有关说法正确的是()第4题图A. 苹果汁的酸性比纯鲜牛奶的酸性弱B. 肥皂水的碱性比炉具清洁剂的碱性强C. 厕所清洁剂与炉具清洁剂能混用D. 人被某些蚊虫叮咬后可涂抹肥皂水以减轻痛痒5. (2019铁岭)下列常见的三种溶液:①澄清石灰水①食盐水①食醋,pH大小关系是()A. ①>①>①B. ①>①>①C. ①>①>①D. ①>①>①6. (2019本溪)下列有关溶液酸碱性的说法错误的是()A. pH=7的溶液呈中性B. pH>7的溶液一定呈碱性C. pH<7的雨水一定是酸雨D. 酸溶液的pH越小酸性越强7. (2019滨州)下列有关测定氢氧化钠溶液pH的实验操作或描述,你认为正确的是()A. 用镊子夹取pH试纸直接伸入氢氧化钠溶液中测量B. 先用蒸馏水将pH试纸润湿,再用滴管吸取氢氧化钠溶液滴到pH试纸上测量C. 用洁净干燥的玻璃棒蘸取氢氧化钠溶液滴到pH试纸上,再与标准比色卡对照D. 用pH试纸测得该氢氧化钠溶液的pH=12.68. (2017北京)如图所示,在白色点滴板1~6的孔穴中,分别滴加2滴紫色石蕊溶液。
第8题图(1)孔穴6中溶液变为蓝色,说明碳酸钾溶液显____________(填“酸性”或“碱性”)。
专题七振动与波动光分析

专题七 选考模块
简谐运动和受迫振动
本考点是高考的重点,考向主要有:(1)简谐运 动的特征;(2)共振的条件及特点;(3)单摆运动的规 律.
栏目 导引
专题七 选考模块
[知识提炼] 1.简谐运动的五个特征 (1)动力学特征:F=-kx. (2)运动学特征:简谐运动为变加速运动,远离平衡位置时, x、F、a、Ep 均增大,v、Ek 均减小,靠近平衡位置时则相反. (3)运动的周期性特征:相隔 T 或 nT(n 为正整数)的两个时刻 振子处于同一位置且振动状态相同.
栏目 导引
专题七 选考模块
[典题例析] (2016·重庆巴蜀中学模拟)一列沿着 x 轴正方向传播的 横波,在 t=0 时刻的波形如图甲所示,图甲中某质点的振动 图象如图乙所示.下列说法正确的是( ABD )
栏目 导引
专题七 选考模块
A.图乙表示质点 L 的振动图象 B.该波的波速为 0.5 m/s C.t=8 s 时质点 M 的位移为零 D.在 4 s 内 K 质点所经过的路程为 3.2 m E.质点 L 经过 1 s 沿 x 轴正方向移动 0.5 m
栏目 导引
专题七 选考模块
描述简谐运动的物理量变化的判断 (1)分析简谐运动中各物理量的变化情况时,一定要以位移为 桥梁,位移增大时,振动质点的回复力、加速度、势能均增 大,速度、动能均减小;反之,则产生相反的变化. (2)质点的振动方向可以通过下一时刻质点位移的变化来判 定,下一时刻位移如果增加,振动质点就远离平衡位置,下 一时刻位移如果减小,振动质点就靠近平衡位置.
栏目 导引
专题七 选考模块
[典题例析] (2016·辽宁朝阳联考)一质点做简谐运动的图象如图所 示,下列说法正确的是( ABE )
(宁夏)职教高考考点解析与高分突破:语文 第一部分专题七

③ 但不甚浓厚
⑤句有“虽”,③句有“但”,两句构成转折关系,
④ 所以引以为快
衔接紧密,排除A项;
⑤ 中国人“自然”的观念中虽偶杂有道家的神秘主义
A.②③④⑤①
B.②①⑤③④
C.⑤③②④①
D.⑤③②①④
②①④三句关系紧密,①句解说②句(①句的“彼 此”照应②句的“自然”和“中国人”),②①两 句是④句的原因,再结合句意,当知⑤③句在前,
Hale Waihona Puke 知识精讲 一、语言表达连贯 (二)保持结构、句式的一致性
结构、句式的一致性表现在:
第一,语言中常有些排比句、对偶句,这就要求结构上保持统一,破坏了这种统一,也 就破坏了连贯性;
第二,用陈述句还是疑问句,用主动句还是被动句,合说还是分说,不同的句式或不同 的表达方式也会涉及连贯问题;
第三,复句中的分句与分句间有并列、转折、递进、选择、因果、假设、条件等关系, 如果注意不到这一点,可能会破坏分句间的逻辑联系,从而影响句意的连贯。
小贴士 此例题是句序排列题。 句序排列题:是指将次序混乱的句子重新调整, 使之排列有序,语意贯通。
知识精讲 一、语言表达连贯 (三)保持顺序的合理性
连贯的句子之间具有不可随意更改的逻辑性,它遵循一定的规律: 或以空间为序,从上到下、从左到右、从外到内等; 或以时间为序,从早到晚、从过去到现在等; 或以事物发展前后为序; 或以人们的认识规律为序,由易到难、由浅入深、由表及里、由感性认识 到理性认识等; 或以主次、轻重为序等。
深圳中考专题7 文学常识

C.庄周是战国时期的哲学家,道家代表人物。《庄子》是庄周及其后学的著作集, 为道家经典之一。道家提倡“道法自然,无为而治”的观点。
D.《三国演义》是我国第一部章回体长篇历史演义小说,作者是元末明初的罗贯中。
D.《木兰诗》中“对镜帖花黄”,“花黄”是古代妇女的一种面部装饰物,一般是未出阁女 子的装饰,所以后来就有了“黄花闺女”之说。
返回目录
第一部分
基础知识
14. 下列表述正确的一项是( B )
A.杜甫,字子美,自号“少陵野老”,唐代伟大的浪漫主义诗人,他被后人称为“诗史”,他的诗 被称为“诗圣”。《茅屋为秋风所破歌》展现了一个生活贫困,却舍己为人、关心天下“寒士”、忧国忧 民的诗人形象。
D.《雁门太守行》中的“行”和《茅屋为秋风所破歌》中的“歌”都是古代 诗歌的一种体裁。
返回目录
第一部分
基础知识
7. 下列有关文学文化常识的表述,不正确的一项是( A )
A.《庄子》现存 33 篇,《北冥有鱼》选自内篇《秋水》,《庄子与惠子游于濠
梁之上》选自外篇《逍遥游》。
B.《核舟记》是明代著名的江南才子、文学家魏学洢所写的说明性文章,出
A.《陋室铭》的“铭”和《爱莲说》的“说”都是古代的一种文体。 B.敬称表示尊敬客气的态度,也叫“尊称”,如卿、大兄、愚、鄙人 等。 C.《阿长与〈山海经〉》和《藤野先生》选自鲁迅的散文集《朝花夕拾》。 D.《出师表》选自晋陈寿的《三国志》。出师表是军队出征前统帅向君 王所上的奏疏。
返回目录
第一部分
D.《皇帝的新装》是波兰儿童文学家安徒生的代表作之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲 选修4-4 坐标系与参数方程考点一 极坐标方程及其应用[典例感悟][典例1] (2017·全国卷Ⅱ)在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 1的极坐标方程为ρcos θ=4.(1)M 为曲线C 1上的动点,点P 在线段OM 上,且满足|OM |·|OP |=16,求点P 的轨迹C 2的直角坐标方程;(2)设点A 的极坐标为⎝⎛⎭⎫2,π3,点B 在曲线C 2上,求△OAB 面积的最大值. [解] (1)设P 的极坐标为(ρ,θ)(ρ>0),M 的极坐标为(ρ1,θ)(ρ1>0). 由题设知|OP |=ρ,|OM |=ρ1=4cos θ. 由|OM |·|OP |=16,得C 2的极坐标方程ρ=4cos θ(ρ>0). 因此C 2的直角坐标方程为(x -2)2+y 2=4(x ≠0). (2)设点B 的极坐标为(ρB ,α)(ρB >0),由题设知|OA |=2,ρB =4cos α,于是△OAB 的面积S =12|OA |·ρB ·sin ∠AOB =4cos α·⎪⎪⎪⎪sin ⎝⎛⎭⎫α-π3=2sin ⎝⎛⎭⎫2α-π3-32≤2+ 3. 当α=-π12时,S 取得最大值2+ 3.所以△OAB 面积的最大值为2+ 3.[方法技巧]1.求曲线的极坐标方程的一般思路曲线的极坐标方程问题通常可利用互换公式转化为直角坐标系中的问题求解,然后再次利用互换公式即可转化为极坐标方程.熟练掌握互换公式是解决问题的关键.2.解决极坐标交点问题的一般思路一是将极坐标方程化为直角坐标方程,求出交点的直角坐标,再将其转化为极坐标;二是将曲线的极坐标方程联立,根据限制条件求出交点的极坐标.[演练冲关]1.(2016·全国卷Ⅰ)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =a cos t ,y =1+a sin t ,(t 为参数,a >0).在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2:ρ=4cos θ.(1)说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程;(2)直线C 3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C 1与C 2的公共点都在C 3上,求a .解:(1)消去参数t 得到C 1的普通方程为x 2+(y -1)2=a 2,则C 1是以(0,1)为圆心,a 为半径的圆.将x =ρcos θ,y =ρsin θ代入C 1的普通方程中,得到C 1的极坐标方程为ρ2-2ρsin θ+1-a 2=0.(2)曲线C 1,C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2-2ρsin θ+1-a 2=0,ρ=4cos θ.若ρ≠0,由方程组得16cos 2θ-8sin θcos θ+1-a 2=0, 由已知tan θ=2, 即sin θ=2cos θ,可得16cos 2θ-8sin θcos θ=0,从而1-a 2=0,解得a =-1(舍去)或a =1.当a =1时,极点也为C 1,C 2的公共点,且在C 3上. 所以a =1.考点二 参数方程及其应用[典例感悟][典例2] (2017·全国卷Ⅰ)在直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =3cos θ,y =sin θ(θ为参数),直线l 的参数方程为⎩⎪⎨⎪⎧x =a +4t ,y =1-t(t 为参数).(1)若a =-1,求C 与l 的交点坐标; (2)若C 上的点到l 距离的最大值为17,求a . [解] (1)曲线C 的普通方程为x 29+y 2=1.当a =-1时,直线l 的普通方程为x +4y -3=0,由⎩⎪⎨⎪⎧x +4y -3=0,x 29+y 2=1解得⎩⎪⎨⎪⎧x =3,y =0或⎩⎨⎧x =-2125,y =2425.从而C 与l 的交点坐标为(3,0),-2125,2425.(2)直线l 的普通方程为x +4y -a -4=0, 故C 上的点(3cos θ,sin θ)到l 的距离为 d =|3cos θ+4sin θ-a -4|17=|5sin (θ+φ)-a -4|17⎝⎛⎭⎫0<φ<π2,tan φ=34.当a ≥-4时,d 的最大值为a +917 ,由题设得a +917=17,解得a =8;当a <-4时,d 的最大值为-a +117, 由题设得-a +117=17,解得a =-16.综上,a =8或a =-16.[方法技巧]参数方程化为普通方程的方法及参数方程的应用(1)将参数方程化为普通方程的过程就是消去参数的过程,常用的消参方法有代入消参、加减消参、三角恒等式消参等,往往需要对参数方程进行变形,为消去参数创造条件.(2)在与直线、圆、椭圆有关的题目中,参数方程的使用会使问题的解决事半功倍,尤其是求取值范围和最值问题,可将参数方程代入相关曲线的普通方程中,根据参数的取值条件求解.[演练冲关]2.已知曲线C :x 24+y 29=1,直线l :⎩⎪⎨⎪⎧x =2+t ,y =2-2t(t 为参数).(1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|PA |的最大值与最小值.解:(1)曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos θ,y =3sin θ(θ为参数).直线l 的普通方程为2x +y -6=0.(2)曲线C 上任意一点P (2cos θ,3sin θ)到l 的距离为d =55|4cos θ+3sin θ-6|. 则|PA |=d sin 30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43. 当sin(θ+α)=-1时,|PA |取得最大值,最大值为2255.当sin(θ+α)=1时,|PA |取得最小值,最小值为255.考点三 极坐标方程与参数方程的综合应用[典例感悟][典例3] (2017·全国卷Ⅲ)在直角坐标系xOy 中,直线l 1的参数方程为⎩⎪⎨⎪⎧x =2+t ,y =kt (t为参数),直线l 2的参数方程为⎩⎪⎨⎪⎧x =-2+m ,y =m k (m 为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)-2=0,M 为l 3与C 的交点,求M 的极径.[解] (1)消去参数t 得l 1的普通方程l 1:y =k (x -2); 消去参数m 得l 2的普通方程l 2:y =1k (x +2).设P (x ,y ),由题设得⎩⎪⎨⎪⎧y =k (x -2),y =1k (x +2).消去k 得x 2-y 2=4(y ≠0).所以C 的普通方程为x 2-y 2=4(y ≠0).(2)C 的极坐标方程为ρ2(cos 2θ-sin 2θ)=4(0<θ<2π,θ≠π).联立⎩⎪⎨⎪⎧ρ2(cos 2θ-sin 2θ)=4,ρ(cos θ+sin θ)-2=0 得cos θ-sin θ=2(cos θ+sin θ).故tan θ=-13,从而cos 2θ=910,sin 2θ=110.代入ρ2(cos 2θ-sin 2θ)=4得ρ2=5,所以交点M 的极径为 5.[方法技巧]解决极坐标方程与参数方程综合问题的方法(1)在参数方程或极坐标方程应用不够熟练的情况下,我们可以先将其化成直角坐标的普通方程,这样思路可能更加清晰.(2)对于一些运算比较复杂的问题,用参数方程计算会比较简捷. (3)利用极坐标方程解决问题时,要注意题目所给的限制条件及隐含条件.[演练冲关]3.(2017·成都模拟)在直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cos α,y =2+2sin α(α为参数),直线l 的参数方程为⎩⎨⎧x =3-32t ,y =3+12t (t 为参数).在以坐标原点O 为极点,x 轴的正半轴为极轴的极坐标系中,过极点O 的射线与曲线C 相交于不同于极点的点A ,且点A 的极坐标为(23,θ),其中θ∈⎝⎛⎭⎫π2,π. (1)求θ的值;(2)若射线OA 与直线l 相交于点B ,求|AB |的值. 解:(1)由题意知,曲线C 的普通方程为x 2+(y -2)2=4, ∵x =ρcos θ,y =ρsin θ, ∴曲线C 的极坐标方程为(ρcos θ)2+(ρsin θ-2)2=4,即ρ=4sin θ. 由ρ=23,得sin θ=32, ∵θ∈⎝⎛⎭⎫π2,π, ∴θ=2π3.(2)由题,易知直线l 的普通方程为x +3y -43=0, ∴直线l 的极坐标方程为ρcos θ+3ρsin θ-43=0. 又射线OA 的极坐标方程为θ=2π3(ρ≥0),联立,得⎩⎪⎨⎪⎧θ=2π3(ρ≥0),ρcos θ+3ρsin θ-43=0,解得ρ=4 3.∴点B 的极坐标为⎝⎛⎭⎫43,2π3, ∴|AB |=|ρB -ρA |=43-23=2 3.[课时跟踪检测]1.(2017·石家庄质检)在平面直角坐标系xOy 中,直线l 的参数方程是⎩⎪⎨⎪⎧x =2+t cos α,y =t sin α(t 为参数),以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为ρ2cos 2θ+2ρ2sin 2θ=12,且直线l 与曲线C 交于P ,Q 两点.(1)求曲线C 的直角坐标方程及直线l 恒过的定点A 的坐标; (2)在(1)的条件下,若|AP |·|AQ |=6,求直线l 的普通方程. 解:(1)∵x =ρcos θ,y =ρsin θ,∴C 的直角坐标方程为x 2+2y 2=12. 直线l 恒过的定点为A (2,0).(2)把直线l 的方程代入曲线C 的直角坐标方程中得,(sin 2α+1)t 2+4(cos α)t -8=0. 由t 的几何意义知|AP |=|t 1|,|AQ |=|t 2|. ∵点A 在椭圆内,这个方程必有两个实根, ∴t 1t 2=-8sin 2α+1,∵|AP |·|AQ |=|t 1t 2|=6, ∴81+sin 2α=6,即sin 2α=13,∵α∈(0,π), ∴sin α=33,cos α=±63, ∴直线l 的斜率k =±22,因此,直线l 的方程为 y =22(x -2)或y =-22(x -2). 2.(2017·郑州质检)在平面直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =2cos φ,y =sin φ(φ为参数),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线C 2是圆心为⎝⎛⎭⎫3,π2,半径为1的圆.(1)求曲线C 1的普通方程,C 2的直角坐标方程;(2)设M 为曲线C 1上的点,N 为曲线C 2上的点,求|MN |的取值范围. 解:(1)消去参数φ可得C 1的普通方程为x 24+y 2=1.由题可知,曲线C 2的圆心的直角坐标为(0,3), ∴C 2的直角坐标方程为x 2+(y -3)2=1. (2)设M (2cos φ,sin φ),曲线C 2的圆心为C 2, 则|MC 2|=(2cos φ)2+(sin φ-3)2=4cos 2φ+sin 2φ-6sin φ+9=-3sin 2φ-6sin φ+13=-3(sin φ+1)2+16.∵-1≤sin φ≤1,∴|MC 2|min =2,|MC 2|max =4. 根据题意可得|MN |min =2-1=1,|MN |max =4+1=5, 即|MN |的取值范围是[1,5].3.(2017·合肥模拟)在平面直角坐标系xOy 中,圆C 的参数方程为⎩⎨⎧x =-5+2cos t ,y =3+2sin t(t 为参数),在以原点O 为极点,x 轴的非负半轴为极轴建立的极坐标系中,直线l 的极坐标方程为ρcos ⎝⎛⎭⎫θ+π4=- 2. (1)求圆C 的普通方程和直线l 的直角坐标方程;(2)设直线l 与x 轴,y 轴分别交于A ,B 两点,点P 是圆C 上任意一点,求A ,B 两点的极坐标和△PAB 面积的最小值.解:(1)由⎩⎪⎨⎪⎧x =-5+2cos t ,y =3+2sin t ,消去参数t ,得圆C 的普通方程为(x +5)2+(y -3)2=2. 由ρcos ⎝⎛⎭⎫θ+π4=-2,得ρcos θ-ρsin θ=-2, 所以直线l 的直角坐标方程为x -y +2=0.(2)直线l 与x 轴,y 轴的交点分别为A (-2,0),B (0,2),化为极坐标为A (2,π),B ⎝⎛⎭⎫2,π2. 设点P 的坐标为(-5+2cos t,3+2sin t ),则点P 到直线l 的距离为d =|-5+2cos t -3-2sin t +2|2=⎪⎪⎪⎪-6+2cos ⎝⎛⎭⎫t +π42,所以d min =42=2 2.又|AB |=22, 所以△PAB 面积的最小值是S min =12×22×22=4.4.(2018届高三·西安八校联考)在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=2sin θ,θ∈[)0,2π.(1)求曲线C 的直角坐标方程;(2)在曲线C 上求一点D ,使它到直线l :⎩⎨⎧x =3t +3,y =-3t +2(t 为参数)的距离最短,并求出点D 的直角坐标. 解:(1)由ρ=2sin θ,θ∈[0,2π),可得ρ2=2ρsin θ. 因为ρ2=x 2+y 2,ρsin θ=y ,所以曲线C 的直角坐标方程为x 2+(y -1)2=1.(2)由直线l 的参数方程⎩⎪⎨⎪⎧x =3t +3,y =-3t +2(t 为参数),消去t 得直线l 的普通方程为y =-3x +5.因为曲线C :x 2+(y -1)2=1是以G (0,1)为圆心、1为半径的圆,(易知C ,l 相离) 设点D (x 0,y 0),且点D 到直线l :y =-3x +5的距离最短, 所以曲线C 在点D 处的切线与直线l :y =-3x +5平行. 即直线GD 与l 的斜率的乘积等于-1,即y 0-1x 0×(-3)=-1,又x 20+(y 0-1)2=1,可得x 0=-32(舍去)或x 0=32,所以y 0=32, 即点D 的直角坐标为⎝⎛⎭⎫32,32.5.(2018届高三·广东五校联考)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎨⎧x =2cos α,y =sin α(α为参数),以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,曲线C 2的极坐标方程为ρsin ⎝⎛⎫θ+π4=4 2. (1)求曲线C 1的普通方程与曲线C 2的直角坐标方程;(2)设P 为曲线C 1上的动点,求点P 到曲线C 2上点的距离的最小值.解:(1)由曲线C 1:⎩⎪⎨⎪⎧x =2cos α,y =sin α得曲线C 1的普通方程为x 22+y 2=1.由曲线C 2:ρsin ⎝⎛⎭⎫θ+π4=42得,22ρ(sin θ+cos θ)=42, 即曲线C 2的直角坐标方程为x +y -8=0. (2)易知椭圆C 1与直线C 2无公共点,椭圆上的点P (2cos α,sin α)到直线x +y -8=0的距离为d =|2cos α+sin α-8|2=|3sin (α+φ)-8|2,其中φ是锐角且tan φ= 2.所以当sin(α+φ)=1时,d 取得最小值82-62.6.(2017·成都模拟)在平面直角坐标系xOy 中,倾斜角为α⎝⎛⎭⎫α≠π2的直线l 的参数方程为⎩⎪⎨⎪⎧x =1+t cos α,y =t sin α(t 为参数).以坐标原点为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程是ρcos 2θ-4sin θ=0.(1)写出直线l 的普通方程和曲线C 的直角坐标方程;(2)已知点P (1,0).若点M 的极坐标为⎝⎛⎭⎫1,π2,直线l 经过点M 且与曲线C 相交于A ,B 两点,设线段AB 的中点为Q ,求|PQ |的值.解:(1)∵直线l 的参数方程为⎩⎪⎨⎪⎧x =1+t cos α,y =t sin α(t 为参数),∴直线l 的普通方程为y =tan α·(x -1).由ρcos 2 θ-4sin θ=0得ρ2cos 2 θ-4ρsin θ=0,即x 2-4y =0. ∴曲线C 的直角坐标方程为x 2=4y .(2)∵点M 的极坐标为⎝⎛⎭⎫1,π2,∴点M 的直角坐标为(0,1). 又直线l 经过点M ,∴1=tan α·(0-1), ∴tan α=-1,即直线l 的倾斜角α=3π4.∴直线l 的参数方程为⎩⎨⎧x =1-22t ,y =22t(t 为参数).代入x 2=4y ,得t 2-62t +2=0.设A ,B 两点对应的参数分别为t 1,t 2. ∵Q 为线段AB 的中点,∴点Q 对应的参数值为t 1+t 22=622=3 2.又点P (1,0)是直线l 上对应t =0的点,则|PQ |=⎪⎪⎪⎪⎪⎪t 1+t 22=3 2.7.(2017·南昌模拟)在平面直角坐标系xOy 中,曲线C 1过点P (a,1),其参数方程为⎩⎨⎧x =a +2t ,y =1+2t(t 为参数,a ∈R).以O 为极点,x 轴非负半轴为极轴,建立极坐标系,曲线C 2的极坐标方程为ρcos 2θ+4cos θ-ρ=0.(1)求曲线C 1的普通方程和曲线C 2的直角坐标方程;(2)已知曲线C 1与曲线C 2交于A ,B 两点,且|PA |=2|PB |,求实数a 的值.解:(1)∵曲线C 1的参数方程为⎩⎪⎨⎪⎧x =a +2t ,y =1+2t ,∴其普通方程为x -y -a +1=0.∵曲线C 2的极坐标方程为ρcos 2θ+4cos θ-ρ=0, ∴ρ2cos 2θ+4ρcos θ-ρ2=0,∴x 2+4x -x 2-y 2=0,即曲线C 2的直角坐标方程为y 2=4x .(2)设A ,B 两点所对应的参数分别为t 1,t 2,由⎩⎪⎨⎪⎧y 2=4x ,x =a +2t ,y =1+2t ,得2t 2-22t +1-4a=0.Δ=(22)2-4×2(1-4a )>0,即a >0,由根与系数的关系得⎩⎨⎧t 1+t 2=2,t 1·t 2=1-4a2,根据参数方程的几何意义可知|PA |=2|t 1|,|PB |=2|t 2|, 又|PA |=2|PB |,∴2|t 1|=2×2|t 2|,即t 1=2t 2或t 1=-2t 2.当t 1=2t 2时,有⎩⎨⎧t 1+t 2=3t 2=2,t 1·t 2=2t 22=1-4a2,解得a =136>0,符合题意.当t 1=-2t 2时,有⎩⎨⎧t 1+t 2=-t 2=2,t 1·t 2=-2t 22=1-4a2,解得a =94>0,符合题意.综上所述,实数a 的值为136或94.8.(2017·贵阳检测)在直角坐标系xOy 中,曲线C 1的参数方程为⎩⎪⎨⎪⎧x =4+3cos t ,y =5+3sin t (其中t 为参数),以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ.(1)求曲线C 1的普通方程和C 2的直角坐标方程;(2)若A ,B 分别为曲线C 1,C 2上的动点,求当AB 取最小值时△AOB 的面积.解:(1)由⎩⎪⎨⎪⎧x =4+3cos t ,y =5+3sin t得C 1的普通方程为(x -4)2+(y -5)2=9.由ρ=2sin θ得ρ2=2ρsin θ,将x 2+y 2=ρ2,y =ρsin θ代入上式,得C 2的直角坐标方程为x 2+(y -1)2=1. (2)如图,当A ,B ,C 1,C 2四点共线,且A ,B 在线段C 1C 2上时,|AB |取得最小值,由(1)得C 1(4,5),C 2(0,1),∴kC 1C 2=5-14-0=1,则直线C 1C 2的方程为x -y +1=0,∴点O 到直线C 1C 2的距离d =12=22,又|AB |=|C 1C 2|-1-3=(4-0)2+(5-1)2-4=42-4,∴S △AOB =12d |AB |=12×22×(42-4)=2- 2.第二讲 选修4-5 不等式选讲考点一 绝对值不等式的解法[典例感悟][典例1] (2017·全国卷Ⅰ)已知函数f (x )=-x 2+ax +4,g (x )=|x +1|+|x -1|. (1)当a =1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[-1,1],求a 的取值范围. [解] (1)当a =1时,不等式f (x )≥g (x )等价于 x 2-x +|x +1|+|x -1|-4≤0.①当x <-1时,①式化为x 2-3x -4≤0,无解;当-1≤x ≤1时,①式化为x 2-x -2≤0,解得-1≤x ≤1; 当x >1时,①式化为x 2+x -4≤0, 解得1<x ≤-1+172.所以f (x )≥g (x )的解集为x -1≤x ≤-1+172.(2)当x ∈[-1,1]时,g (x )=2.所以f (x )≥g (x )的解集包含[-1,1],等价于当x ∈[-1,1]时,f (x )≥2.又f (x )在[-1,1]的最小值必为f (-1)与f (1)之一,所以f (-1)≥2且f (1)≥2,得-1≤a ≤1. 所以a 的取值范围为[-1,1].[方法技巧]绝对值不等式的常用解法(1)基本性质法:对a ∈R +,|x |<a ⇔-a <x <a ,|x |>a ⇔x <-a 或x >a . (2)平方法:两边平方去掉绝对值符号.(3)零点分区间法:含有两个或两个以上绝对值符号的不等式,可用零点分区间法脱去绝对值符号,将其转化为与之等价的不含绝对值符号的不等式(组)求解.(4)几何法:利用绝对值的几何意义,画出数轴,将绝对值转化为数轴上两点的距离求解.(5)数形结合法:在直角坐标系中作出不等式两边所对应的两个函数的图象,利用函数图象求解.[演练冲关]1.(2017·全国卷Ⅲ)已知函数f (x )=|x +1|-|x -2|. (1)求不等式f (x )≥1的解集;(2)若不等式f (x )≥x 2-x +m 的解集非空,求m 的取值范围. 解:(1)f (x )=⎩⎪⎨⎪⎧-3,x <-1,2x -1,-1≤x ≤2,3,x >2.当x <-1时,f (x )≥1无解;当-1≤x ≤2时,由f (x )≥1,得2x -1≥1,解得1≤x ≤2; 当x >2时,由f (x )≥1,解得x >2. 所以f (x )≥1的解集为{x |x ≥1}.(2)由f (x )≥x 2-x +m ,得m ≤|x +1|-|x -2|-x 2+x .而|x +1|-|x -2|-x 2+x ≤|x |+1+|x |-2-x 2+|x |=-⎝⎛⎭⎫|x |-322+54≤54, 且当x =32时,|x +1|-|x -2|-x 2+x =54.故m 的取值范围为⎝⎛⎦⎤-∞,54. 考点二 不等式的证明[典例感悟][典例2] (2016·全国卷Ⅱ)已知函数f (x )=⎪⎪⎪⎪x -12+⎪⎪⎪⎪x +12,M 为不等式f (x )<2的解集.(1)求M ;(2)证明:当a ,b ∈M 时,|a +b |<|1+ab |. [解](1)f (x )=⎩⎪⎨⎪⎧-2x ,x ≤-12,1,-12<x <12,2x ,x ≥12.当x ≤-12时,由f (x )<2得-2x <2,解得x >-1;当-12<x <12时,f (x )<2恒成立;当x ≥12时,由f (x )<2得2x <2,解得x <1.所以f (x )<2的解集M ={x |-1<x <1}.(2)证明:由(1)知,当a ,b ∈M 时,-1<a <1,-1<b <1, 从而(a +b )2-(1+ab )2=a 2+b 2-a 2b 2-1=(a 2- 1)·(1-b 2)<0.因此|a +b |<|1+ab |.[方法技巧] 证明不等式的常用方法不等式证明的常用方法有比较法、分析法、综合法、反证法等. (1)如果已知条件与待证结论直接联系不明显,则考虑用分析法.(2)如果待证的是否定性命题、唯一性命题或以“至少”“至多”等方式给出的问题,则考虑用反证法.(3)如果待证不等式与自然数有关,则考虑用数学归纳法.在必要的情况下,可能还需要使用换元法、构造法等技巧简化对问题的表述和证明.[演练冲关]2.(2017·全国卷Ⅱ)已知a >0,b >0,a 3+b 3=2.证明: (1)(a +b )(a 5+b 5)≥4; (2)a +b ≤2.证明:(1)(a +b )(a 5+b 5)=a 6+ab 5+a 5b +b 6 =(a 3+b 3)2-2a 3b 3+ab (a 4+b 4) =4+ab (a 2-b 2)2≥4.(2)因为(a +b )3=a 3+3a 2b +3ab 2+b 3 =2+3ab (a +b )≤2+3(a +b )24(a +b )=2+3(a +b )34,所以(a +b )3≤8,因此a +b ≤2.考点三 含绝对值不等式的恒成立问题[典例感悟][典例3] (2017·合肥质检)已知函数f (x )=|x -m |-|x +3m |(m >0). (1)当m =1时,求不等式f (x )≥1的解集;(2)对于任意实数x ,t ,不等式f (x )<|2+t |+|t -1|恒成立,求m 的取值范围. [解] (1)当m =1时,f (x )=⎩⎪⎨⎪⎧-4,x ≥1,-2x -2,-3<x <1,4,x ≤-3.由f (x )≥1,得⎩⎪⎨⎪⎧-2x -2≥1,-3<x <1或x ≤-3,解得x ≤-32,∴不等式f (x )≥1的解集为⎩⎨⎧⎭⎬⎫xx ≤-32.(2)不等式f (x )<|2+t |+|t -1|对任意的实数x ,t 恒成立,等价于对任意的实数x ,f (x )<(|2+t |+|t -1|)min 恒成立,即[f (x )]max <(|2+t |+|t -1|)min ,∵f (x )=|x -m |-|x +3m |≤|(x -m )-(x +3m )|=4m ,|2+t |+|t -1|≥|(2+t )-(t -1)|=3, ∴4m <3,又m >0,∴0<m <34.即m 的取值范围为⎝⎛⎭⎫0,34. [方法技巧]已知不等式恒成立求参数范围问题的解法[演练冲关]3.(2017·洛阳统考)已知f (x )=|2x -1|-|x +1|.(1)将f (x )的解析式写成分段函数的形式,并作出其图象;(2)若a +b =1,对∀a ,b ∈(0,+∞),1a +4b ≥3f (x )恒成立,求x 的取值范围.解:(1)由已知,得f (x )=⎩⎨⎧-x +2,x <-1,-3x ,-1≤x ≤12,x -2,x >12,函数f (x )的图象如图所示.(2)∵a ,b ∈(0,+∞),且a +b =1, ∴1a +4b =⎝⎛⎭⎫1a +4b (a +b ) =5+⎝⎛⎭⎫b a +4a b ≥5+2b a ·4ab =9,当且仅当b a =4a b,即a =13,b =23时等号成立.∵1a +4b ≥3(|2x -1|-|x +1|)恒成立, ∴|2x -1|-|x +1|≤3, 结合图象知-1≤x ≤5, ∴x 的取值范围是[-1,5].[课时跟踪检测]1.(2017·云南调研)已知函数f (x )=|x +1|+|m -x |(其中m ∈R). (1)当m =2时,求不等式f (x )≥6的解集;(2)若不等式f (x )≥6对任意实数x 恒成立,求m 的取值范围. 解:(1)当m =2时,f (x )=|x +1|+|2-x |,①当x <-1时,f (x )≥6可化为-x -1+2-x ≥6,解得x ≤-52;②当-1≤x ≤2时,f (x )≥6可化为x +1+2-x ≥6,无实数解; ③当x >2时,f (x )≥6可化为x +1+x -2≥6,解得x ≥72.综上,不等式f (x )≥6的解集为xx ≤-52或x ≥72.(2)法一:因为|x +1|+|m -x |≥|x +1+m -x |=|m +1|,由题意得|m +1|≥6,即m +1≥6或m +1≤-6,解得m ≥5或m ≤-7,即m 的取值范围是(-∞,-7]∪[5,+∞).法二:①当m <-1时,f (x )=⎩⎪⎨⎪⎧-2x +m -1,x <m ,-m -1,m ≤x ≤-1,2x +1-m ,x >-1,此时,f (x )min =-m -1,由题意知,-m -1≥6, 解得m ≤-7,所以m 的取值范围是m ≤-7. ②当m =-1时,f (x )=|x +1|+|-1-x |=2|x +1|, 此时f (x )min =0,不满足题意.③当m >-1时,f (x )=⎩⎪⎨⎪⎧-2x +m -1,x <-1,m +1,-1≤x ≤m ,2x +1-m ,x >m ,此时,f (x )min =m +1,由题意知,m +1≥6,解得m ≥5, 所以m 的取值范围是m ≥5.综上所述,m 的取值范围是(-∞,-7]∪[5,+∞).2.(2017·郑州模拟)已知a >0,b >0,函数f (x )=|x +a |+|x -b |的最小值为4. (1)求a +b 的值; (2)求14a 2+19b 2的最小值.解:(1)因为|x +a |+|x -b |≥|a +b |,所以f (x )≥|a +b |,当且仅当(x +a )(x -b )<0时,等号成立,又a >0,b >0,所以|a +b |=a +b ,所以f (x )的最小值为a +b ,所以a +b =4.(2)由(1)知a +b =4,b =4-a ,14a 2+19b 2=14a 2+19(4-a )2=1336a 2-89a +169=1336⎝⎛⎭⎫a -16132+1613,故当且仅当a =1613,b =3613时,14a 2+19b 2取最小值为1613. 3.(2018届高三·湖南五市十校联考)设函数f (x )=|x -1|-2|x +a |. (1)当a =1时,求不等式f (x )>1的解集;(2)若不等式f (x )>0在x ∈[2,3]上恒成立,求a 的取值范围.解:(1)a =1,f (x )>1⇔|x -1|-2|x +1|>1⇔⎩⎪⎨⎪⎧x ≤-1,-x +1+2(x +1)>1或⎩⎪⎨⎪⎧ -1<x ≤1,-x +1-2(x +1)>1或⎩⎪⎨⎪⎧x >1,x -1-2(x +1)>1⇔-2<x ≤-1或-1<x <-23或x ∈∅⇔-2<x <-23,故不等式f (x )>1的解集为⎝⎛⎭⎫-2,-23. (2)f (x )>0在x ∈[2,3]上恒成立⇔|x -1|-2|x +a |>0在x ∈[2,3]上恒成立⇔|2x +2a |<x -1⇔1-x <2x +2a <x -1⇔1-3x <2a <-x -1在x ∈[2,3]上恒成立⇔(1-3x )max <2a <(-x -1)min ⇔-5<2a <-4⇔-52<a <-2.故a 的取值范围为⎝⎛⎭⎫-52,-2. 4.(2017·宝鸡质检)已知函数f (x )=|2x -a |+|2x +3|,g (x )=|x -1|+2. (1)解不等式|g (x )|<5;(2)若对任意x 1∈R ,都存在x 2∈R ,使得f (x 1)=g (x 2)成立,求实数a 的取值范围. 解:(1)由||x -1|+2|<5得-5<|x -1|+2<5,所以-7<|x -1|<3,解得-2<x <4,则不等式|g (x )|<5的解集为{x |-2<x <4}.(2)因为对任意x 1∈R ,都存在x 2∈R ,使得f (x 1)=g (x 2)成立,所以{y |y =f (x )}⊆{y |y =g (x )},又f (x )=|2x -a |+|2x +3|≥|(2x -a )-(2x +3)|=|a +3|,g (x )=|x -1|+2≥2,所以|a +3|≥2,解得a ≥-1或a ≤-5, 所以实数a 的取值范围为{a |a ≥-1或a ≤-5}.5.(2018届高三·湘中名校联考)已知函数f (x )=|x -2|+|2x +a |,a ∈R. (1)当a =1时,解不等式f (x )≥5;(2)若存在x 0满足f (x 0)+|x 0-2|<3,求实数a 的取值范围. 解:(1)当a =1时,f (x )=|x -2|+|2x +1|. 由f (x )≥5得|x -2|+|2x +1|≥5.当x ≥2时,不等式等价于x -2+2x +1≥5,解得x ≥2,所以x ≥2;当-12<x <2时,不等式等价于2-x +2x +1≥5,即x ≥2,所以解集为空集;当x ≤-12时,不等式等价于2-x -2x -1≥5,解得x ≤-43,所以x ≤-43.故原不等式的解集为⎩⎨⎧⎭⎬⎫xx ≤-43或x ≥2.(2)f (x )+|x -2|=2|x -2|+|2x +a |=|2x -4|+|2x +a |≥|2x +a -(2x -4)|=|a +4|,∵原命题等价于(f (x )+|x -2|)min <3,即|a +4|<3,∴-7<a <-1.即实数a 的取值范围为(-7,-1).6.已知函数f (x )=|2x -1|+|2x +a |,g (x )=x +3. (1)当a =-2时,求不等式f (x )<g (x )的解集;(2)设a >-1,且当x ∈⎣⎡⎭⎫-a 2,12时,f (x )≤g (x ),求a 的取值范围. 解:(1)当a =-2时,不等式f (x )<g (x )化为|2x -1|+|2x -2|-x -3<0.设函数y =|2x -1|+|2x -2|-x -3,则y =⎩⎨⎧-5x ,x <12,-x -2,12≤x ≤1,3x -6,x >1.其图象如图所示.从图象可知,当且仅当x ∈(0,2)时,y <0.所以原不等式的解集是{x |0<x <2}.(2)当x ∈⎣⎡⎫-a 2,12时,f (x )=1+a .不等式f (x )≤g (x )化为1+a ≤x +3.所以x ≥a -2对x ∈⎣⎡⎭⎫-a 2,12都成立.故-a 2≥a -2,即a ≤43.从而a 的取值范围是⎝⎛⎦⎤-1,43. 7.(2017·贵阳检测)已知|x +2|+|6-x |≥k 恒成立. (1)求实数k 的最大值;(2)若实数k 的最大值为n ,正数a ,b 满足85a +b +22a +3b=n .求7a +4b 的最小值. 解:(1)因为|x +2|+|6-x |≥k 恒成立, 设g (x )=|x +2|+|6-x |,则g (x )min ≥k .又|x +2|+|6-x |≥|(x +2)+(6-x )|=8,当且仅当-2≤x ≤6时,g (x )min =8, 所以k ≤8,即实数k 的最大值为8.第 21 页 共 21 页(2)由(1)知,n =8,所以85a +b +22a +3b=8, 即45a +b +12a +3b =4,又a ,b 均为正数, 所以7a +4b =14(7a +4b )⎝ ⎛⎭⎪⎫45a +b +12a +3b =14[](5a +b )+(2a +3b )⎝ ⎛⎭⎪⎫45a +b +12a +3b =14⎣⎢⎡⎦⎥⎤4+1+4(2a +3b )5a +b +5a +b 2a +3b ≥14×(5+4)=94, 当且仅当4(2a +3b )5a +b =5a +b 2a +3b,即a =5b =1552时,等号成立,所以7a +4b 的最小值是94. 8.设a ,b ,c ∈R +,且a +b +c =1.求证:(1)2ab +bc +ca +c 22≤12; (2)a 2+c 2b +b 2+a 2c +c 2+b 2a ≥2.证明:(1)因为1=(a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ca ≥4ab +2bc +2ca +c 2,当且仅当a =b 时等号成立.所以2ab +bc +ca +c 22=12(4ab +2bc +2ca +c 2)≤12. (2)因为a 2+c 2b ≥2ac b ,b 2+a 2c ≥2ab c ,c 2+b 2a ≥2bc a, 所以a 2+c 2b +b 2+a 2c +c 2+b 2a≥⎝⎛⎭⎫ac b +ab c +⎝⎛⎭⎫ab c +bc a +⎝⎛⎭⎫ac b +bc a=a ⎝⎛⎭⎫c b +b c +b ⎝⎛⎭⎫a c +c a +c ⎝⎛⎭⎫a b +b a ≥2a +2b +2c =2,当且仅当a =b =c =13时等号成立.。
