2008年普通高等学校招生全国统一考试数学卷(福建.文)含详解
2008年高考数学试卷(福建.文)含详解

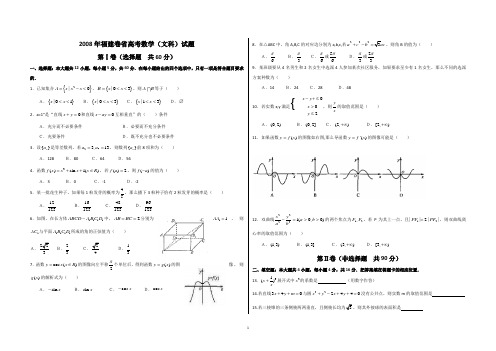
数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.¢ (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件 (3)设|a n |是等左数列,若a 2=3,a 1=13,则数列{a n }前8项的和为 A.128 B.80 C.64 D.56 (4)函数f (x )=x 3+sin x +1(x ∈R),若f (a )=2,则f (-a )的值为 A.3 B.0 C.-1 D.-2 (5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是A.12125 B.16125 C.48125 D.96125(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.223 B.23 C.24 D.13(7)函数y =cos x (x ∈R)的图象向左平移2个单位后,得到函数y=g(x )的图象,则g(x )的解析式为A.-sin xB.sin xC.-cos xD.cos x(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若a 2+c 2-b 3,则角B 的值为A.6πB.3πC.6π或56πD.3π或23π(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48(10)若实数x、y满足10,0,2,x yxx-+≤⎧⎪⎨⎪≤⎩则yx的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) (11)如果函数y=f(x)的图象如右图,那么导函数y=f(x)的图象可能是(12)双曲线22221x ya b-=(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PE2|,则双曲线离心率的取值范围为A.(1,3)B.(1,3)C.(3,+∞)D. [3,+∞]第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置.(13)(x+1x)9展开式中x2的系数是.(用数字作答)(14)若直线3x+4y+m=0与圆x2+y2-2x+4y+4=0没有公共点,则实数m的取值范围是 . (153,则其外接球的表面积是.(16)设P是一个数集,且至少含有两个数,若对任意a、b∈P,都有a+b、a-b、ab、ab∈P(除数b≠0)则称P是一个数域,例如有理数集Q是数域,有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数集Q ⊆M ,则数集M 必为数域;④数域必为无限集.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分) 已知向量(sin ,cos ),(1,2)m A A n ==-,且0.m n = (Ⅰ)求tan A 的值;(Ⅱ)求函数()cos 2tan sin (f x x A x x =+∈R )的值域. (18)(本小题满分12分)三人独立破译同一份密码.已知三人各自破译出密码的概率分别为111,,,543且他们是否破译出密码互不影响.(Ⅰ)求恰有二人破译出密码的概率;(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由. (19)(本小题满分12分)如图,在四棱锥P —ABCD 中,侧面P AD ⊥底面ABCD ,侧棱P A =PD 2,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC=2,O 为AD 中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PB 与CD 所成角的余弦值; (Ⅲ)求点A 到平面PCD 的距离. (20)(本小题满分12分)已知{a n }是正数组成的数列,a 1=11,n n a a +)(n ∈N *)在函数y =x 2+1的图象上. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)若列数{b n }满足b 1=1,b n +1=b n +2n a,求证:b n ·b n +2<b 2n +1. (21)(本小题满分12分)已知函数32()2f x x mx nx =++-的图象过点(-1,-6),且函数()()6g x f x x '=+的图象关于y 轴对称.(Ⅰ)求m 、n 的值及函数y =f (x )的单调区间;(Ⅱ)若a >0,求函数y =f (x )在区间(a -1,a +1)内的极值. (22)(本小题满分14分)如图,椭圆2222:1x y C a b+=(a >b >0)的一个焦点为F (1,0),且过点(2,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)若AB 为垂直于x 轴的动弦,直线l :x =4与x 轴交于点N , 直线AF 与BN 交于点M . (ⅰ)求证:点M 恒在椭圆C 上; (ⅱ)求△AMN 面积的最大值.2008年普通高等学校招生全国统一考试(福建卷)数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.∅ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解:若00x y x ay +=-=与互相垂直,则0x ay -=的斜率必定为1,1a =,反之显然 (3):设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 A.128 B.80 C.64 D.56 解:因为{}n a 是等差数列,278313886422a a ++=⨯=⨯=∴S(4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为 A.3 B.0 C.-1 D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125 B.16125 C.48125 D.96125解:独立重复实验服从二项分布4(3,)5B ,21234148(2)55125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭(6)如图,在长方体ABCD -A 1B 1C 1D 1中, AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为B.23D.13解:连11A C ,则11AC A ∠为AC 1与平面A 1B 1C 1D 1所成角.112AB BC AC AC ==⇒==11AA = 1111113sin 3AA AC AC A AC =⇒∠==∴ (7)函数cos ()y x x R =∈的图象向左平移2π个单位后,得到函数()y g x =的图象,则()g x 的解析式为A.sin x -B. sin xC.cos x -D.cos x 解:()cos()sin 2y g x x x π==+=-(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c,若222a cb +-=,则角B 的值为 A.6π B.3π C.6π或56π D.3π或23π解:由222a +c -b得222(a +c -b )2ac即cos =2B ,6B π⇒=(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种(10)若实数x 、y 满足10,0,2,x y x y -+≤⎧⎪>⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞)AA解:由题设1y x ≥+,所以11y x x ≥+,又01211x y <≤-≤-=,因此2y x≥ 又yx可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
2008年普通高等学校招生全国统一考试理科数学(福建卷)

A.
B.
的图象,则m的值可以为() C.-
D.-
10. 在△ABC中,角A、B、C的对边分别为a、b、c,若a2+c2-b2= ac,则角B的值为
A.
B.
C. 或
D. 或
11. 双曲线 A.(1,3)
(a>0,b>0)的两个焦点为F1、F2,若P为其上一点,且|PF1|=2|PF2|,则双曲线离心率的取值范围为()
,求a的取值范围.
22. (本小题满分14分)
已知函数f(x)=ln(1+x)-x1
(Ⅰ)求f(x)的单调区间;
(Ⅱ)记f(x)在区间
(n∈N*)上的最小值为bx令an=ln(1+n)-bx。
(ⅰ)如果对一切n,不等式
恒成立,求实数c的取值范围;
(ⅱ)求证:
。
B.
C.(3,+ )
D.
12. 如图所示为函数y=f(x),y=g(x)的导函数的图象,那么y=f(x),y=g(x)的图象可能是( )
A.
B.
C.
D.
二、填空题
13. 若(x-2)5=a5x5+a4x4+a3x3+a2x2+a1x+a0,则a1+a2+a3+a4+a5=__________。(用数字作答)
成绩合格与否均互不影响。 (Ⅰ)求他不需要补考就可获得证书的概率; (Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求 的数学期望E 。
21. 已知椭圆
的一个焦点是F(1,0),O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程; (Ⅱ)设过点F的直线l交椭圆于A、B两点,若直线l绕点F任意转动,总有
高考试卷 全国普通高校招生统一考试数学(福建卷 文科)(附答案 全字版)

高考试卷全国普通高校招生统一考试数学(福建卷文科)(附答案全字版)自己整理的高考试卷全国普通高校招生统一考试数学(福建卷文科)(附答案全字版)相关文档,希望能对大家有所帮助,谢谢阅读!2008年全国普通高校招生统一考试(文史)(福建卷)卷一(选择题60分)1.选择题:共12个分题,每个分题5分,共60分。
在每个子问题中给出的四个选项中,只有一个符合主题的要求。
(1)如果设置a={x | x2-xB.(0,2)C.(2,)d[2,) (11)如果函数y=f(x)的像如右图所示,那么导函数y=f(x)的像可能是(12)双曲线(a > 0,b > 0)的两个焦点是F1和F2,如果p是它的上点,并且B.(1,3)C.(3, )D.[3,]卷二(非选择题90分)二、填空:这个大题有4个小题,每题4分,共16分,填在答题卡的相应位置。
(13)(x)9展开式中x2的系数为。
(用数字回答)(14)如果直线3x 4y m=0与圆x2 y2-2x 4y 4=0之间没有公共点,则实数m的取值范围为。
(15)如果三棱锥的三个侧边相互垂直,并且侧边的长度都相同,则外切球面的表面积为。
(16)设p为一个数字集,至少包含两个数字。
如果有的话,(1)数字字段必须包含两个数字,0和1;整数集是一个数域;如果有理数集QM,那么数集M一定是数域;(4)数域必须是无限集合。
正确命题的序号是。
(填写你认为正确的命题序号)三、答题:这个大题有6个小题,共74分。
答案应写书面说明,证明过程或计算步骤。
(17)(这个小问题满分12分)向量已知,且(I)求tanA的值;()求函数r)的值域。
(18)(本项满分12分)三个人独立破译同一个密码。
已知三个人破译密码的概率分别为,是否破译密码互不影响。
()找到恰好两个人破译密码的概率;(二)“密码破解”和“密码未破解”的概率是多少?说明理由。
(19)(这个小问题满分12分)如图所示,在金字塔P-ABCD中,侧边PAD是底部ABCD,侧边PA=PD=,底部ABCD是直角梯形,其中BCAD,AB ADAMN面积最大值。
2008高考福建数学理科试卷含详细解答(全word版)080629

2008年普通高等学校招生全国统一考试(福建卷)数 学(理工类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为A.1B.2C.1或2D.-1解:由2320a a -+=得12a =或,且101a a -≠≠得2a ∴=(纯虚数一定要使虚部不为0) (2)设集合{|0}1xA x x =<-,{|03}B x x =<<,那么“m ∈A ”是“m ∈B ”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件解:由01xx <-得01x <<,可知“m A ∈”是“m B ∈”的充分而不必要条件 (3)设{a n }是公比为正数的等比数列,若151,16a a ==,则数列{}n a 前7项的和为A.63B.64C.127D.128解:由151,16a a ==及{a n }是公比为正数得公比2q =,所以771212712S -==- (4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为A.3B.0C.-1D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是 A.16625B.96625C. 192625D. 256625解:独立重复实验4(4,)5B ,22244196(2)55625P k C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭A(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为B.C.D.解:连11A C 与11B D 交与O 点,再连BO,则1OBC ∠为BC 1与平面BB 1D 1D所成角.111OC COS OBC BC ∠=,1OC =,1BC =15C O S O B C∴∠= (7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种 (8)若实数x 、y 满足100x y x -+≤⎧⎨>⎩ 则yx 的取值范围是A.(0,1)B.(]0,1C.(1,+∞)D.[)1,+∞解:由已知1y x ≥+,111y x x x x +==+,又0x >,故yx的取值范围是(1,)+∞(9)函数()cos ()f x x x R =∈的图象按向量(,0)m 平移后,得到函数'()y f x =-的图象, 则m 的值可以为A.2πB.πC.-πD.-2π 解:()sin y f x x '=-=,而()cos ()f x x x R =∈的图象按向量(,0)m 平移后得到cos()y x m =-,所以cos()sin x m x -=,故m可以为2π. (10)在△ABC 中,角ABC 的对边分别为a 、b 、c ,若222(a +c -b ,则角B 的值为A.6π B.3π C.6π或56πD.3π或23π解: 由222(a +c -b 得222(a +c -b )2ac cos Bsin B ∴,又在△中所以B 为3π或23π(11)双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞解:如图,设2PF m =,12(0)F PF θθπ∠=<≤,当P 在右顶点处θπ=,22ce a ===∵1cos 1θ-<≤,∴(]1,3e ∈另外也可用三角形的两边和大于第三边,及两边差小于第三边,但要注意前者可以取到等号成立,因为可以三点一线. 也可用焦半径公式确定a 与c 的关系。
【历年高考经典】2008年文科数学试题及答案-福建卷

2008年普通高等学校招生全国统一考试(福建卷)文科数学第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2|0A x x x =-<,{}|03B x x =<<,则AB 等于( )A.{}|01x x << B.{}|03x x << C.{}|13x x <<D.∅2.a=1”是“直线0x y +=和直线0x ay -=互相垂直”的( )条件A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 3.设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项和为( )A.128B.80C.64D.564.函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为( )A.3B.0 C.-1D.-25.某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是( )A.12125B.16125 C.48125 D.961256.如图,在长方体1111ABCD A BC D -中,2AB BC ==分别为11AA =,则1AC 与平面1111A B C D 所成的角的正弦值为( )A.3B.23C.4D.137.函数cos ()y x x R =∈的图像向左平移2π个单位后,得到函数()y g x =的图像,则()g x 的解析式为( )A.sin x - B.sin xC.cos x -D.cos x8.在△ABC 中,角A,B,C 的对应边分别为a,b,c,若222a cb +-=,则角B 的值为( )A.6πB.3π C.6π或56πD.3π或23π9.某班级要从4名男生和2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )A.14 B.24 C.28 D.4810.若实数x,y 满足{02x y x y -+≤>≤,则yx的取值范围是( ) A.(0,2)B.(0,2] C.(2,)+∞D.[2,)+∞11.如果函数()y f x =的图像如右图,那么导函数'()y f x =的图像可能是( )12.双曲线22221(0,0)x y a b a b-=>>的两个焦点为12,F F ,若P 为其上一点,且12||2||PF PF =,则双曲线离心率的取值范围为( )A.(1,3)B.(1,3]C.(3,)+∞D.[3,)+∞第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.13. 91()x x+展开式中3x 的系数是 (用数字作答)14.若直线340x y m ++=与圆222440x y x y +-++=没有公共点,则实数m 的取值范围是15.,则其外接球的表面积是 16.设P 是一个数集,且至少含有两个数,若对任意,a b P ∈,都有,,,aa b a b ab P b+-∈(除数0b ≠),则称P 是一个数域。
2008高考福建数学文科试卷含详细解答

2008年普通高等学校招生全国统一考试(福建卷)数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.∅ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解:若00x y x ay +=-=与互相垂直,则0x ay -=的斜率必定为1,1a =,反之显然 (3):设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 A.128 B.80 C.64 D.56 解:因为{}n a 是等差数列,278313886422a a ++=⨯=⨯=∴S(4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为 A.3 B.0 C.-1 D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125 B.16125 C.48125 D.96125解:独立重复实验服从二项分布4(3,)5B ,21234148(2)55125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭(6)如图,在长方体ABCD -A 1B 1C 1D 1中, AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.3B.23C.4D.13AB解:连11A C ,则11AC A ∠为AC 1与平面A 1B 1C 1D 1所成角.11222AB BC AC AC ==⇒==,又11AA = 1111113sin 3AA AC AC A AC =⇒∠==∴ (7)函数cos ()y x x R =∈的图象向左平移2π个单位后,得到函数()y g x =的图象,则()g x 的解析式为A.sin x -B. sin xC.cos x -D.cos x 解:()cos()sin 2y g x x x π==+=-(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若2223a c b ac +-=,则角B 的值为 A.6π B.3π C.6π或56π D.3π或23π解:由222a +c -b 3ac 得222(a +c -b )32ac 即3cos B ,6B π⇒=(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种(10)若实数x 、y 满足10,0,2,x y x y -+≤⎧⎪>⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) 解:由题设1y x ≥+,所以11y x x≥+,又01211x y <≤-≤-=,因此2y x ≥又yx可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
2008年普通高等学校招生全国统一考试数学卷(福建.文)含详解

2008年普通高等学校招生全国统一考试数学卷(福建.文)含详解数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.¢ (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件 (3)设|a n |是等左数列,若a 2=3,a 1=13,则数列{a n }前8项的和为 A.128 B.80 C.64 D.56 (4)函数f (x )=x 3+sin x +1(x ∈R),若f (a )=2,则f (-a )的值为 A.3 B.0 C.-1 D.-2 (5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125 B.16125 C.48125 D.96125(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.3 B.23 C.4 D.13(7)函数y =cos x (x ∈R)的图象向左平移2π个单位后,得到函数y=g(x )的图象,则g(x )的解析式为 A.-sin x B.sin x C.-cos x D.cos x(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若a 2+c 2-b ac ,则角B 的值为 A.6π B.3π C.6π或56π D.3π或23π(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48(10)若实数x 、y 满足10,0,2,x y x x -+≤⎧⎪⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) (11)如果函数y=f (x )的图象如右图,那么 导函数y=f (x )的图象可能是(12)双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PE 2|,则双曲线离心率的取值范围为A.(1,3)B.(1,3)C.(3,+∞)D. [3,+∞]第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. (13)(x +1x)9展开式中x 2的系数是 .(用数字作答) (14)若直线3x+4y +m =0与圆x 2+y 2-2x +4y +4=0没有公共点,则实数m 的取值范围是 . (15,则其外接球的表面积是 . (16)设P 是一个数集,且至少含有两个数,若对任意a 、b ∈P ,都有a+b 、a-b 、ab 、ab∈P (除数b ≠0)则称P 是一个数域,例如有理数集Q 是数域,有下列命题: ①数域必含有0,1两个数; ②整数集是数域;③若有理数集Q ⊆M ,则数集M 必为数域;④数域必为无限集.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分) 已知向量(sin ,cos ),(1,2)m A A n ==-,且0.m n =(Ⅰ)求tan A 的值;(Ⅱ)求函数()cos 2tan sin (f x x A x x =+∈R )的值域. (18)(本小题满分12分)三人独立破译同一份密码.已知三人各自破译出密码的概率分别为111,,,543且他们是否破译出密码互不影响. (Ⅰ)求恰有二人破译出密码的概率;(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由. (19)(本小题满分12分)如图,在四棱锥P —ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA =PD ,底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC=2,O 为AD 中点. (Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PB 与CD 所成角的余弦值; (Ⅲ)求点A 到平面PCD 的距离. (20)(本小题满分12分)已知{a n }是正数组成的数列,a 1=11n a +)(n ∈N *)在函数y =x 2+1的图象上. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)若列数{b n }满足b 1=1,b n +1=b n +2n a,求证:b n ·b n +2<b 2n +1. (21)(本小题满分12分)已知函数32()2f x x mx nx =++-的图象过点(-1,-6),且函数()()6g x f x x '=+的图象关于y 轴对称. (Ⅰ)求m 、n 的值及函数y =f (x )的单调区间;(Ⅱ)若a >0,求函数y =f (x )在区间(a -1,a +1)内的极值. (22)(本小题满分14分)如图,椭圆2222:1x y C a b+=(a >b >0)的一个焦点为F (1,0),且过点(2,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)若AB 为垂直于x 轴的动弦,直线l :x =4与x 轴交于点N ,直线AF 与BN 交于点M . (ⅰ)求证:点M 恒在椭圆C 上; (ⅱ)求△AMN 面积的最大值.2008年普通高等学校招生全国统一考试(福建卷)数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.∅ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解:若00x y x ay +=-=与互相垂直,则0x ay -=的斜率必定为1,1a =,反之显然 (3):设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 A.128 B.80 C.64 D.56 解:因为{}n a 是等差数列,278313886422a a ++=⨯=⨯=∴S(4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为 A.3 B.0 C.-1 D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125B.16125 C.48125 D.96125解:独立重复实验服从二项分布4(3,)5B ,21234148(2)55125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭(6)如图,在长方体ABCD -A 1B 1C 1D 1中, AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.3B.23C.4D.13解:连11A C ,则11AC A ∠为AC 1与平面A 1B 1C 1D 1所成角.112AB BC AC AC ==⇒==,又11AA =A1111113sin 3AA AC AC A AC =⇒∠==∴ (7)函数cos ()y x x R =∈的图象向左平移2π个单位后,得到函数()y g x =的图象,则()g x 的解析式为 A.sin x - B. sin x C.cos x - D.cos x解:()cos()sin 2y g x x x π==+=-(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若222a c b +-=,则角B 的值为 A.6π B.3πC.6π或56πD.3π或23π解:由222a +c -b得222(a +c -b )= 2ac即cos B 6B π⇒=(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48 解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种(10)若实数x 、y 满足10,0,2,x y x y -+≤⎧⎪>⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) 解:由题设1y x ≥+,所以11y x x ≥+,又01211x y <≤-≤-=,因此2y x≥ 又yx可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
2008高考福建数学文科试卷含详细解答(全word版)080626

2008年普通高等学校招生全国统一考试(福建卷)数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.∅ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解:若00x y x ay +=-=与互相垂直,则0x ay -=的斜率必定为1,1a =,反之显然 (3):设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 A.128 B.80 C.64 D.56 解:因为{}n a 是等差数列,278313886422a a ++=⨯=⨯=∴S(4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为 A.3 B.0 C.-1 D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125 B.16125 C.48125 D.96125解:独立重复实验服从二项分布4(3,)5B ,21234148(2)55125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭(6)如图,在长方体ABCD -A 1B 1C 1D 1中, AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.3B.23C.4D.13A解:连11A C ,则11AC A ∠为AC 1与平面A 1B 1C 1D 1所成角.11222AB BC AC AC ==⇒==11AA = 1111113sin 3AA AC AC A AC =⇒∠==∴ (7)函数cos ()y x x R =∈的图象向左平移2π个单位后,得到函数()y g x =的图象,则()g x 的解析式为A.sin x -B. sin xC.cos x -D.cos x 解:()cos()sin 2y g x x x π==+=-(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若2223a c b ac +-=,则角B 的值为 A.6π B.3π C.6π或56π D.3π或23π解:由222a +c -b 3ac 得222(a +c -b )32ac 即3cos B ,6B π⇒=(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种(10)若实数x 、y 满足10,0,2,x y x y -+≤⎧⎪>⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) 解:由题设1y x ≥+,所以11y x x ≥+,又01211x y <≤-≤-=,因此2y x≥ 又yx可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
2008年普通高等学校招生全国统一考试数学(福建卷·理科)(附答案,完全word版)

2008年普通高等学校招生全国统一考试(福建卷)数学(理工农医类)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为( ) A .1B .2C .1或2D .1-2.设集合01x A xx ⎧⎫=<⎨⎬-⎩⎭,{}03B x x =<<,那么“m ∈A ”是“m ∈B ”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件3.设{a n }是公比为正数的等比数列,若11a =,516a =,则数列{a n }前7项的和为( ) A .63B .64C .127D .1284.函数3()sin 1()f x x x x =++∈R ,若f (a )=2,则()f a -的值为( ) A .3B .0C .1-D .2-5.某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是( ) A .16625B .96625C . 192625D . 2566256.如图,在长方体1111ABCD A BC D -中,AB =BC =2,AA 1=1,则BC 1与 平面BB 1D 1D 所成角的正弦值为( ) A.3B .5C .5D .57.某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( ) A .14 B .24 C .28 D .48 8.若实数x 、y 满足100x y x -+⎧⎨>⎩≤,,则yx 的取值范围是( ) A .(0,1)B .(]01,C .(1,+∞)D .[)1+∞,9.函数()cos ()f x x x =∈R 的图象按向量(m ,0) 平移后,得到函数()y f x '=-的图象,则m 的值可以为( )ABC DA 1D 1C 1B 1A .2π B .πC .-πD .2π-10.在△ABC 中,角A B C ,,的对边分别为a b c ,,,若222()tan a c b B +-=,则角B 的值为( ) A .6π B .3π C .6π或56πD .3π或23π11.双曲线22221x y a b-=(00)a b >>,的两个焦点为F 1,F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为( ) A .(1,3)B .(]13,C .(3,+∞)D .[)3+∞,12.已知函数y =f (x ),y =g (x )的导函数的图象如图,那么y =f (x ),y =g (x )的图象可能是( )第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. 13.若55432543210(2)x a x a x a x a x a x a -=+++++,则a 1+a 2+a 3+a 4+a 5=__________.(用数字作答)14.若直线340x y m ++=与圆1cos 2sin x y θθ=+⎧⎨=-+⎩(θ为参数)没有公共点,则实数m 的取值范围是 .15,则其外接球的表面积是 . 16.设P 是一个数集,且至少含有两个数,若对任意a b P ∈,,都有a b +,a b -,ab ,a b∈P (除数0b ≠),则称P 是一个数域.例如有理数集Q是数域;数集{}F a b =+∈Q ,也是数域.有下列命题:①整数集是数域;②若有理数集M ⊆Q ,则数集M 必为数域;③数域必为无限集;④存在无穷多个数域.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上))xA .B .C .D .三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知向量(sin cos )A A =,m,1)=-n ,1=m n ,且A 为锐角.(Ⅰ)求角A 的大小;(Ⅱ)求函数()cos 24cos sin ()f x x A x x =+∈R 的值域.18.(本小题满分12分)如图,在四棱锥P-ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA =PDABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点. (Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PB 与CD 所成角的大小;(Ⅲ)线段AD 上是否存在点Q ,使得它到平面PCD若存在,求出AQQD的值;若不存在,请说明理由.19.(本小题满分12分) 已知函数321()23f x x x =+-. (Ⅰ)设{}n a 是正数组成的数列,前n 项和为n S ,其中13a =.若点211(2)n n n a a a ++-,(n ∈*N )在函数()y f x '=的图象上,求证:点()n n S ,也在()y f x '=的图象上;(Ⅱ)求函数f (x )在区间(1)a a -,内的极值.20.(本小题满分12分) 某项考试按科目A 、科目B 依次进行,只有当科目A 成绩合格时,才可继续参加科目B 的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A 每次考试成绩合格的概率均为23,科目B 每次考试成绩合格的概率均为12.假设各次考试成绩合格与否均互不影响.(Ⅰ)求他不需要补考就可获得证书的概率;(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求ξ的数学期望E ξ.A BCO DP21.(本小题满分12分)如图,椭圆22221(0)x y a b a b+=>>的一个焦点是F (1,0),O 为坐标原点.(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形,求椭圆的方程;(Ⅱ)设过点F 的直线l 交椭圆于A ,B 两点.若直线l 绕点F 任意转动,恒有222OA OB AB +<,求a 的取值范围.22.(本小题满分14分) 已知函数()ln(1)f x x x =+-. (Ⅰ)求f (x )的单调区间;(Ⅱ)记f (x )在区间[]0π,(n ∈*N )上的最小值为n b ,令ln(1)n n a n b =+-.(Ⅲ)如果对一切nc 的取值范围; (Ⅳ)求证:13132112242421n na a a a a a a a a a a a -+++<……….2008年普通高等学校招生全国统一考试(福建卷)数学(理工农医类)参考答案一、选择题:本大题考查基本概念和基本运算.每小题5分,满分60分. 1.B 2.A 3.C 4.B 5.B 6.D 7.A 8.C 9.A 10.D 11.B 12.D二、填空题:本大题考查基础知识和基本运算.每小题4分,满分16分. 13.3114.(0)(10)-+∞,,∞ 15.9π16.③④三、本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.17.本小题主要考查平面向量的数量积计算、三角函数的基本公式、三角恒等变换、一元二次函数的最值等基本知识,考查运算能力.满分12分. 解:(Ⅰ)由题意得3sin cos 1m n A A =-=,12sin 1sin 662A A ππ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭,.由A 为锐角得66A ππ-=,3A π=. (Ⅱ)由(Ⅰ)知1cos 2A =,所以2213()cos22sin 12sin 2sin 2sin 22f x x x x x x ⎛⎫=+=-+=--+ ⎪⎝⎭因为x ∈R ,所以[]sin 11x ∈-,,因此,当1sin 2x =时,f (x )有最大值32. 当sin 1x =-时,()f x 有最小值3-,所以所求函数f (x )的值域是332⎡⎤-⎢⎥⎣⎦,.18.本小题主要考查直线与平面的位置关系、异面直线所成角、点到平面的距离等基本知识,考查空间想象能力、逻辑思维能力和运算能力.满分12分. 解法一:(Ⅰ)证明:在△PAD 中PA =PD ,O 为AD 中点,所以PO ⊥AD ,又侧面PAD ⊥底面ABCD ,平面PAD 平面ABCD =AD ,PO ⊂平面PAD , 所以PO ⊥平面ABCD .(Ⅱ)连结BO ,在直角梯形ABCD 中,BC ∥AD ,AD =2AB =2BC ,有OD ∥BC 且OD =BC ,所以四边形OBCD 是平行四边形, 所以OB ∥DC .由(Ⅰ)知,PO ⊥OB ,∠PBO 为锐角, 所以∠PBO 是异面直线PB 与CD 所成的角. 因为AD =2AB =2BC =2,在Rt △AOB 中,AB =1,AO =1, 所以OBA B CODPQ在Rt △POA 中,因为APAO =1,所以OP =1,在Rt △PBO 中,tan ∠PBO=PG PBO BO ==∠=. 所以异面直线PB 与CD所成的角是arctan2. (Ⅲ)假设存在点Q ,使得它到平面PCD的距离为2. 设QD =x ,则12DQC S x =△,由(Ⅱ)得CD =OB在Rt △POC 中,PC = 所以PC =CD =DP ,2(2)42PCD S ==△, 由P DQC Q PCD VV --=,得111132322x ⨯⨯=⨯,解得322x =<, 所以存在点Q 满足题意,此时13AQ QD =. 解法二:(Ⅰ)同解法一.(Ⅱ)以O 为坐标原点,OC OD OP ,,的方向分别为x 轴、y 轴、z 轴的正方向,建立空间直角坐标系O xyz -,依题意,易得(010)A -,,,(110)B -,,,(100)C ,,,(010)D ,,,(001)P ,,, 所以(110)(111)CD PB =-=--,,,,,.cos 32PB CD PB CD PB CD<>===,, 所以异面直线PB 与CD 所成的角是arccos3(Ⅲ)假设存在点Q ,使得它到平面PCD 的距离为2, 由(Ⅱ)知(101)(110)CP CD =-=-,,,,,.设平面PCD 的法向量为n =(x 0,y 0,z 0).则00n CP n CD ⎧=⎪⎨=⎪⎩,,所以000000x z x y -+=⎧⎨-+=⎩,,即000x y z ==, 取x 0=1,得平面PCD 的一个法向量为n =(1,1,1). 设(00)(11)(10)Q y yCQ y -=-,, ≤≤,,, ,由32CQ n n=,得2=, 解得12y =-或y =52(舍去), 此时1322AQ QD ==,,所以存在点Q 满足题意,此时13AQ QD =. 19.本小题主要考查函数极值、等差数列等基本知识,考查分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.满分12分. (Ⅰ)证明:因为321()23f x x x =+-,所以2()2f x x x '=+, 由点211(2)()n n n a a a n ++-∈*N ,在函数()y f x '=的图象上, 得221122n n n n a a a a ++-=+,即11()(2)0n n n n a a a a +++--=,又*0()n a n >∈N ,所以12n n a a +-=,又因为13a =, 所以数列{}n a 是以3为首项,公差为2的等差数列. 所以2(1)32=22n n n S n n n -=+⨯+,又因为2()2f n n n '=+,所以()n S f n '=, 故点()n n S ,也在函数()y f x '=的图象上.(Ⅱ)解:2()2(2)f x x x x x '=+=+,由()0f x '=,得02x x ==-或.当x 变化时,()f x ',()f x 的变化情况如下表:注意到(1)12a a --=<,从而①当12a a -<-<,即21a -<<-时,()f x 的极大值为2(2)3f -=-,此时()f x 无极小值; ②当10a a -<<,即01a <<时,()f x 的极小值为(0)2f =-,此时()f x 无极大值; ③当2a -≤或10a -≤≤或1a ≥时,()f x 既无极大值又无极小值.20.本小题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题,解决问题的能力.满分12分.解:设“科目A 第一次考试合格”为事件1A ,“科目A 补考合格”为事件A 2;“科目B 第一次考试合格”为事件1B ,“科目B 补考合格”为事件2B .(Ⅰ)不需要补考就获得证书的事件为A 1·B 1,注意到A 1与B 1相互独立, 则1111211()()()323P A B P A P B =⨯=⨯=. 答:该考生不需要补考就获得证书的概率为13. (Ⅱ)由已知得,ξ=2,3,4,注意到各事件之间的独立性与互斥性,可得1112(2)()()P P A B P A A ξ==+2111114.3233399=⨯+⨯=+= 112112122(3)()()()P P A B B P A B B P A A B ξ==++21121112111143223223326699=⨯⨯+⨯⨯+⨯⨯=++=, 12221212(4)()()P P A A B B P A A B B ξ==+121112111113322332218189=⨯⨯⨯+⨯⨯⨯=+=, 故44182349993E ξ=⨯+⨯+⨯=.答:该考生参加考试次数的数学期望为83.21.本小题主要考查直线与椭圆的位置关系、不等式的解法等基本知识,考查分类与整合思想,考查运算能力和综合解题能力.满分12分.解法一:(Ⅰ)设M ,N 为短轴的两个三等分点, 因为△MNF 为正三角形,所以OF =,即1=223b,解得b 2214a b =+=,因此,椭圆方程为22143x y +=. (Ⅱ)设1122()()A x y B x y ,,,. (ⅰ)当直线 AB 与x 轴重合时,22222224(1)OA OB a AB a a +==>,,因此,恒有222OA OB AB +<. (ⅱ)当直线AB 不与x 轴重合时,设直线AB 的方程为:1x my =+,代入22221x y a b+=,整理得22222222()20a b m y b my b a b +++-=,所以222212122222222b m b a b y y y y a b m a b m-+=-=++,. 因为恒有222OA OB AB +<,所以∠AOB 恒为钝角. 即11221212()()0OA OB x y x y x x y y ==+<,,恒成立.2121212121212(1)(1)(1)()1x x y y my my y y m y y m y y +=+++=++++222222222222(1)()21m b a b b m a b m a b m +-=-+++22222222220m a b b a b a a b m -+-+=<+.又a 2+b 2m 2>0,所以22222220m a b b a b a -+-+<对m ∈R 恒成立, 即2222222a b m a a b b >-+对m ∈R 恒成立.当m ∈R 时,222a b m 最小值为0,所以22220a a b b -+<.2222a a b b <-,2224(1)a a b b <-=,因为a >0,b >0,所以a <b 2,即210a a -->,解得a >a <(舍去),即a >,综合(i )(ii ),a 的取值范围为⎫+⎪⎪⎝⎭∞.解法二:(Ⅰ)同解法一,(Ⅱ)解:(i )当直线l 垂直于x 轴时,x =1代入22222221(1)1A y b a y a b a-+==,. 因为恒有|OA |2+|OB |2<|AB |2,222(1)4A A y y+<,21Ay >,即21a a->1,解得a >a < (舍去),即a > (ii )当直线l 不垂直于x 轴时,设11()A x y ,,22()B x y ,.设直线AB 的方程为y =k (x -1)代入22221x y a b+=,得(b 2+a 2k 2)x 2-2a 2k 2x + a 2 k 2-a 2 b 2=0,故22222212122222222a k a k a b x x x x b a k b a k -+==++,因为恒有|OA |2+|OB |2<|AB |2,所以x 21+y 21+ x 22+ y 22<( x 2-x 1)2+(y 2-y 1)2, 得x 1x 2+ y 1y 2<0恒成立.x 1x 2+ y 1y 2= x 1x 2+k 2(x 1-1) (x 2-1)=(1+k 2) x 1x 2-k 2(x 1+x 2)+ k 222222222222222222222222222()(1)a k a b a k a a b b k a b k k k b a k b a k b a k --+-=+-+=+++.由题意得(a 2-a 2 b 2+b 2)k 2-a 2 b 2<0对k ∈R 恒成立.①当a 2-a 2 b 2+b 2>0时,不合题意;②当a 2-a 2 b 2+b 2=0时,a ③当a 2-a 2 b 2+b 2<0时,a 2-a 2(a 2-1)+ (a 2-1)<0,a 4-3a 2 +1>0,解得a 2>a 2>a >a .综合(i )(ii ),a 的取值范围为⎫+⎪⎪⎝⎭∞.22.本小题主要考查函数的单调性、最值、不等式、数列等基本知识,考查运用导数研究函数性质的方法,考查分析问题和解决问题的能力,满分14分. 解法一:(Ⅰ)因为()ln(1)f x x x =+-,所以函数定义域为(1-,+∞),且1()111x f x x x-'=-=++. 由()0f x '>得10x -<<,()f x 的单调递增区间为(1-,0); 由()0f x '<得x >0,()f x 的单调递增区间为(0,+∞).(Ⅱ)因为()f x 在[0,n ]上是减函数,所以()ln(1)n b f n n n ==+-, 则ln(1)ln(1)ln(1)n n a n b n n n n =+-=+-++=.(ⅰ)2n ==++1>=,又lim lim 1x x→==,因此c <1,即实数c 的取值范围是(-∞,1). < 因为2135(21)246(2)n n ⎡⎤-⎢⎥⎣⎦……3222133557(21)(21)11246(2)2121n n n n n -+=<++…,所以135(21)246(2)n n -<……)n ∈*N ,则113135(21)224246(2)n n -+++………1<….13132112242421()n na a a a a a n a a a a a a -+++<∈*N ……….解法二:(Ⅰ)同解法一.(Ⅱ)因为f (x )在[]0n ,上是减函数,所以()ln(1)n b f n n n ==+-, 则ln(1)ln(1)ln(1)n n a n b n n n n =+-=+-++=.(ⅰ)因为<n ∈*N<对n ∈*N 恒成立.则2c n <+n ∈*N 恒成立.设()2g n n =+,n ∈*N ,则c <g (n )对n ∈*N 恒成立.考虑[)()21g x x x =+∈+∞,.因为12211()1(2)(22)11021x g x x x x x -+=-++=<-=+′,所以()g x 在[)1+∞,内是减函数;则当n ∈*N 时,g (n )随n 的增大而减小,又因为42lim ()lim(2x x x x g n n →∞→∞+=+===1.所以对一切()1n g n ∈>*N ,.因此1c ≤,即实数c 的取值范围是(]1-∞,.<下面用数学归纳法证明不等式135(21))246(2)n n n -<∈*N …….①当n =1时,左边=12<右边.不等式成立. ②假设当n=k时,不等式成立.即135(21)246(2)k k -<……当n=k +1时,13521(21)212462(22)222222k k k k k k k k ∙∙∙∙∙++<=++++=…(-)…()=<=,即1n k =+时,不等式成立综合①,②得,不等式135(21))246(2)n n n ∙∙∙∙∙∙∙∙-<∈*N ……成立.所以135(21)246(2)n n ∙∙∙∙∙∙∙∙-<……113135(21)224246(2)n n ∙∙∙∙∙∙∙∙∙∙-+++………1<…相信能就一定能即13132112242421()n na a a a a a n a a a a a a -+++<∈*N ……….8、这个世界并不是掌握在那些嘲笑者的手中,而恰恰掌握在能够经受得住嘲笑与批忍不断往前走的人手中。
2008年福建高考理科数学试卷与答案解析(文字版)

2021年**高考理科数学试卷及答案解析(文字版 )第一卷〔选择题共60 分〕一、选择题:本大题共 12 小题,每题 5 分,共 60 分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
(1)假设复数 (a 2-3a+2)+(a-1)i 是纯虚数,那么实数a 的值为A.1B.2C.1或 2D.-1(2)设集合 A={ x|x < 0 },B={ x|0<x <3}, 那么“ m A 〞是“ m B 〞的 x 1A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件n }是公比为正数的等比数列,假设a 1 5那么数列{ n }前7项的 (3)设{ a =7,a =16, a和为A.63B.64C.127D.128(4)函数 f(x)= x 3 +sinx+1(x R ),假设f(a)=2,那么f(-a)的值为A.3B.0C.-1D.-2(5)某一批花生种子,如果每1 粒发芽的概率为4,那么播下 4 粒种子恰有 25粒发芽的概率是A.16B. 96C. 192D. 256625 625625625(6)如图,在长方体1 1 11 中,AB=BC=2, AA 1=1,那么BC 1 与平面ABCD-A B C DBB 1D 1D 所成角的正弦值为A.6 B.2 5C.15 D.103555(7)某班级要从 4 名男生、 2 名女生中选派 4 人参加某次社区效劳,如果要求至少有 1 名女生,那么不同的选派方案种数为A.14B.24C.28D.48(8)假设实数 x、y 满足x-y+1 ≤0,那么y的取值X围是xx>0A. (0,1)B. (0,1)C. (1,+∞ )D. [1, +∞](9)函数 f(x)=cosx(x)(x R)的图象按向量(m,0)平移后,得到函数y= -f ′ (x)的图象,那么m 的值可以为A. B. C.- D. -2 2(10)在△ ABC 中,角A 、、、、 2 223ac ,那么角BB C 的对边分别为 a b c,假设 (a +c -b )tanB=的值为A. B. C.或5D.或2636633(11)双曲线x2y 21〔a>0,b>0〕的两个焦点为F 1、F2 ,假设 P 为其上一点,且|PF 1|=2|PF2|,a 2b2那么双曲线离心率的取值X围为A.(1,3)B. 1,3C.(3,+ )D. 3,(12) 函数y=f(x), y=g(x)的导函数的图象如以下列图,那么y=f(x),y=g(x)的图象可能是第二卷〔非选择题共90 分〕二、填空题:本大题共4 小题,每题 4 分,共 16 分,把答案填在答题卡的相应位置.(13〕假设 (x-2)5=a5x5+a4x4+a3x3+a2x2 +a1x+a0,那么 a1+a2+a3+a4+a5=__________.( 用数字作答 ) x=1+cos(14)假设直线 3x+4y+m=0 与圆y=-2+sin〔为参数〕没有公共点,那么实数m 的取值X围是.〔15〕假设三棱锥的三个侧面两两垂直,且侧棱长均为3 ,那么其外接球的外表积是.〔16〕设 P 是一个数集,且至少含有两个数,假设对任意a、 b∈ P,都有 a+b、a-b, ab、ab ∈ P 〔除数 b ≠ 0 〕,那么称P是一个数域.例如有理数集Q是数域;数集F a b 2 a,b Q 也是数域.有以下命题:①整数集是数域;②假设有理数集Q M ,那么数集M必为数域;③数域必为无限集;④存在无穷多个数域.其中正确的命题的序号是.〔把你认为正确的命题的序号都填上〕三、解答题:本大题共6 小题,共74 分 .解容许写出文字说明,证明过程或演算步骤.〔17〕〔本小题总分值12 分〕向量m=(sin A,cosA),n= (3, 1) ,m·n=1,且A为锐角.〔Ⅰ〕求角 A 的大小;〔Ⅱ〕求函数f ( x) cos2 x 4cos Asin x(x R) 的值域.〔18〕〔本小题总分值12 分〕如图,在四棱锥P-ABCD 中,那么面 PAD ⊥底面 ABCD ,侧棱 PA=PD=2 ,底面ABCD为直角梯形,其中BC∥ AD, AB⊥ AD , AD=2AB =2BC=2, O 为 AD 中点 .〔Ⅰ〕求证:PO⊥平面 ABCD ;〔Ⅱ〕求异面直线PB 与 CD 所成角的大小;〔Ⅲ〕线段 AD 上是否存在点Q,使得它到平面PCD 的距离为3AQ ?假设存在,求出2QD的值;假设不存在,请说明理由.〔19〕〔本小题总分值12 分〕函数 f ( x)1 x 3 x2 2 .3〔Ⅰ〕设 { a n } 是正数组成的数列,前n 项和为 S n ,其中 a 1=3. 假设点(a ,a22a ) (n ∈nn 1n 1N*) 在函数 y=f ′ (x)的图象上,求证:点〔n, S n 〕也在 y=f ′ ( x)的图象上;〔Ⅱ〕求函数 f(x)在区间〔 a-1, a 〕内的极值 .〔20〕〔本小题总分值 12 分〕某项考试按科目 A 、科目 B 依次进展,只有当科目A 成绩合格时,才可继续参加科目B 的考试。
2008高考福建数学理科试卷含详细解答(全word版)080629

2008年普通高等学校招生全国统一考试(福建卷)数 学(理工类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)若复数2(32)(1)a a a i -++-是纯虚数,则实数a 的值为A.1B.2C.1或2D.-1解:由2320a a -+=得12a =或,且101a a -≠≠得2a ∴=(纯虚数一定要使虚部不为0) (2)设集合{|0}1xA x x =<-,{|03}B x x =<<,那么“m ∈A ”是“m ∈B ”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件解:由01xx <-得01x <<,可知“m A ∈”是“m B ∈”的充分而不必要条件 (3)设{a n }是公比为正数的等比数列,若151,16a a ==,则数列{}n a 前7项的和为A.63B.64C.127D.128解:由151,16a a ==及{a n }是公比为正数得公比2q =,所以771212712S -==- (4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为A.3B.0C.-1D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是 A.16625B.96625C. 192625D. 256625解:独立重复实验4(4,)5B ,22244196(2)55625P k C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭A(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为B.C.D.解:连11A C 与11B D 交与O 点,再连BO,则1OBC ∠为BC 1与平面BB 1D 1D 所成角.111OC COS OBC BC ∠=,1OC =,1BC=1COS OBC ∴∠== (7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种 (8)若实数x 、y 满足100x y x -+≤⎧⎨>⎩ 则yx 的取值范围是A.(0,1)B.(]0,1C.(1,+∞)D.[)1,+∞解:由已知1y x ≥+,111y x x x x +==+,又0x >,故yx的取值范围是(1,)+∞(9)函数()cos ()f x x x R =∈的图象按向量(,0)m 平移后,得到函数'()y f x =-的图象, 则m 的值可以为A.2πB.πC.-πD.- 2π解:()sin y f x x '=-=,而()cos ()f x x x R =∈的图象按向量(,0)m 平移后得到cos()y x m =-,所以cos()sin x m x -=,故m可以为2π. (10)在△ABC 中,角ABC 的对边分别为a 、b 、c ,若222(a +c -b ,则角B 的值为A.6π B.3π C.6π或56πD.3π或23π解: 由222(a +c -b 3ac 得222(a +c -b )3cos = 22sin B ac B 即3cos cos = 2sin BB B3sin B ∴,又在△中所以B 为3π或23π(11)双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞解:如图,设2PF m =,12(0)F PF θθπ∠=<≤,当P 在右顶点处θπ=,222(2)4cos 254cos 2m m m ce a θθ+-===-∵1cos 1θ-<≤,∴(]1,3e ∈另外也可用三角形的两边和大于第三边,及两边差小于第三边,但要注意前者可以取到等号成立,因为可以三点一线. 也可用焦半径公式确定a 与c 的关系。
2008年普通高等学校招生全国统一考试数学卷(全国Ⅱ.文)含详解

2008年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至10页. 考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.不能答在试题卷上.3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式:如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ,那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(012)k k n kk n P k C p p k n -=-=,,,,一、选择题1.若sin 0α<且tan 0α>是,则α是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( )A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,3.原点到直线052=-+y x 的距离为( ) A .1B .3C .2D .54.函数1()f x x x=-的图像关于( )A .y 轴对称B . 直线x y -=对称C . 坐标原点对称D . 直线x y =对称5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <cB .c <a <bC . b <a <cD . b <c <a6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8-7.设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( ) A .1 B .12C .12-D .1-8.正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( ) A .3B .6C .9D .189.44)1()1(x x +-的展开式中x 的系数是( )A .4-B .3-C .3D .410.函数x x x f cos sin )(-=的最大值为( ) A .1B .2 C .3D .211.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 的双曲线的离心率为( ) A .221+ B .231+ C . 21+ D .31+12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( ) A .1 B .2C .3D .22008年普通高等学校招生全国统一考试文科数学(必修+选修I)第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答)15.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(22)M ,,则ABF △的面积等于 .16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) 在ABC △中,5cos 13A =-,3cos 5B =. (Ⅰ)求sinC 的值;(Ⅱ)设5BC =,求ABC △的面积. 18.(本小题满分12分)等差数列{}n a 中,410a =且3610a a a ,,成等比数列,求数列{}n a 前20项的和20S .19.(本小题满分12分)甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹.根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2.设甲、乙的射击相互独立.(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率. 20.(本小题满分12分)如图,正四棱柱1111ABCD A BC D -中,124AA AB ==,点E 在1CC 上且EC E C 31=. (Ⅰ)证明:1AC ⊥平面BED ; (Ⅱ)求二面角1A DE B --的大小. 21.(本小题满分12分)设a ∈R ,函数233)(x ax x f -=.(Ⅰ)若2=x 是函数)(x f y =的极值点,求a 的值;(Ⅱ)若函数()()()[02]g x f x f x x '=+∈,,,在0=x 处取得最大值,求a 的取值范围. 22.(本小题满分12分)设椭圆中心在坐标原点,(20)(01)A B ,,,是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点. (Ⅰ)若6ED DF =,求k 的值; (Ⅱ)求四边形AEBF 面积的最大值.AB CD EA 1B 1C 1D 12008年普通高等学校招生全国统一考试 文科数学试题(必修+选修Ⅰ)参考答案和评分参考评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要 考查内容比照评分参考制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和 难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数.选择题不给中间分.一、选择题1.C 2.B 3.D 4.C 5.C 6.D 7.A 8.B 9.A 10.B 11.B 12.C 二、填空题13.2 14.420 15.216.两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.1.若sin 0α<且tan 0α>是,则α是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角 【答案】C【解析】sin 0α<,α在三、四象限;tan 0α>,α在一、三象限,∴选C 2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( )A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,【答案】B【解析】{}1,0,1,2--=M ,{}3,2,1,0,1-=N ,∴{}1,0,1-=N M 【高考考点】集合的运算,整数集的符号识别 3.原点到直线052=-+y x 的距离为( ) A .1B .3C .2D .5【答案】D【解析】52152=+-=d【高考考点】点到直线的距离公式4.函数1()f x x x=-的图像关于( ) A .y 轴对称 B . 直线x y -=对称 C . 坐标原点对称 D . 直线x y =对称【答案】C 【解析】1()f x x x=-是奇函数,所以图象关于原点对称 【高考考点】函数奇偶性的性质5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <cB .c <a <bC . b <a <cD . b <c <a【答案】C 【解析】由0ln 111<<-⇒<<-x x e,令x t ln =且取21-=t 知b <a <c6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8-【答案】D【解析】如图作出可行域,知可行域的顶点是A (-2,2)、B(32,32)及C(-2,-2) 于是8)(min -=A z7.设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( )A .1B .12C .12-D .1-【答案】A【解析】ax y 2'=,于是切线的斜率a y k x 2'1===,∴有122=⇒=a a8.正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( ) A .3 B .6C .9D .18【答案】B【解析】高360sin 32=︒=h ,又因底面正方形的对角线等于32,∴底面积为 6332212=⨯⨯⨯=S ,∴体积63631=⨯⨯=V【备考提示】在底面积的计算时,要注意多思则少算 9.44)1()1(x x +-的展开式中x 的系数是( )A .4-B .3-C .3D .4【答案】A【解析】41666141404242404-=-+=-+C C C C C C 【易错提醒】容易漏掉1414C C 项或该项的负号10.函数x x x f cos sin )(-=的最大值为( ) A .1 B .2 C .3D .2【答案】B【解析】)4sin(2cos sin )(π-=-=x x x x f ,所以最大值是2【高考考点】三角函数中化为一个角的三角函数问题【备考提示】三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题 11.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 的双曲线的离心率为( ) A .221+ B .231+ C . 21+ D .31+【答案】B【解析】由题意BC c =2,所以c c AC 3260sin 220=⨯⨯=,由双曲线的定义,有c a c c BC AC a )13(2322-=⇒-=-=,∴231131+=-==a c e 【高考考点】双曲线的有关性质,双曲线第一定义的应用12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( ) A .1 B .2C .3D .2【答案】C【解析】设两圆的圆心分别为1O 、2O ,球心为O ,公共弦为AB ,其中点为E ,则21EO OO 为矩形,于是对角线OE O O =21,而3122222=-=-=AE OA OE ,∴321=O O 【高考考点】球的有关概念,两平面垂直的性质13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 【答案】 2【解析】λ+a b =)32,2(++λλ则向量λ+a b 与向量(47)=--,c 共线274322=⇒--=++⇔λλλ14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答) 【答案】 420【解析】4202701501621026110=+=+C C C C15.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(22)M ,,则ABF △的面积等于 .【答案】 2 【解析】设过M的直线方程为)2(2-=-x k y ,由0)1(444)2(22222=-+-⇒⎩⎨⎧=-=-k kx x k xy x k y ∴k x x 421=+,2221)1(4kk x x -=,由题意144=⇒=k k ,于是直线方程为x y = 421=+x x ,021=x x ,∴24=AB ,焦点F (1,0)到直线x y =的距离21=d∴ABF △的面积是216.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)【答案】两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.三、解答题17.解:(Ⅰ)由5cos 13A =-,得12sin 13A =, 由3cos 5B =,得4sin 5B =. ··········································································· 2分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=. ····································· 5分(Ⅱ)由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===. ··········································· 8分 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=. ····················· 10分18.解:设数列{}n a 的公差为d ,则3410a a d d =-=-, 642102a a d d =+=+,1046106a a d d =+=+. ················································································ 3分 由3610a a a ,,成等比数列得23106a a a =,即2(10)(106)(102)d d d -+=+, 整理得210100d d -=,解得0d =或1d =.······················································································· 7分 当0d =时,20420200S a ==. ······································································ 9分 当1d =时,14310317a a d =-=-⨯=, 于是2012019202S a d ⨯=+207190330=⨯+=. ············································· 12分 19.解:记12A A ,分别表示甲击中9环,10环,12B B ,分别表示乙击中8环,9环,A 表示在一轮比赛中甲击中的环数多于乙击中的环数,B 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数,12C C ,分别表示三轮中恰有两轮,三轮甲击中环数多于乙击中的环数.(Ⅰ)112122A A B A B A B =++,··································································· 2分 112122()()P A P A B A B A B =++ 112122()()()P A B P A B P A B =++112122()()()()()()P A P B P A P B P A P B =++0.30.40.10.40.10.40.2=⨯+⨯+⨯=. ····························································· 6分(Ⅱ)12B C C =+, ······················································································ 8分22213()[()][1()]30.2(10.2)0.096P C C P A P A =-=⨯⨯-=,332()[()]0.20.008P C P A ===,1212()()()()0.0960.0080.104P B P C C P C P C =+=+=+=. ··························· 12分 20.解法一:依题设,2AB =,1CE =.(Ⅰ)连结AC 交BD 于点F ,则BD AC ⊥.由三垂线定理知,1BD AC ⊥. ········································································· 3分 在平面1ACA 内,连结EF 交1AC 于点G ,由于1AA ACFC CE== 故1Rt Rt A AC FCE △∽△,1AAC CFE ∠=∠, CFE ∠与1FCA ∠互余.于是1AC EF ⊥. 1AC 与平面BED 内两条相交直线BD EF ,都垂直, 所以1AC ⊥平面BED . ·················································································· 6分 (Ⅱ)作GH DE ⊥,垂足为H ,连结1A H .由三垂线定理知1A H DE ⊥,故1A HG ∠是二面角1A DE B --的平面角.························································ 8分EF =CE CF CG EF ⨯==EG ==. AB CDEA 1B 1C 1D 1 FH G13EG EF =,13EF FD GH DE ⨯=⨯=又1AC ==113AG AC CG =-=.11tan A GA HG HG∠== 所以二面角1A DE B --的大小为 ················································· 12分 解法二:以D 为坐标原点,射线DA 为x 轴的正半轴, 建立如图所示直角坐标系D xyz -.依题设,1(220)(020)(021)(204)B C E A ,,,,,,,,,,,.(021)(220)DE DB ==,,,,,,11(224)(204)AC DA =--=,,,,,. ······························ 3分 (Ⅰ)因为10AC DB =,10AC DE =, 故1AC BD ⊥,1AC DE ⊥. 又DBDE D =,所以1AC ⊥平面DBE . ·················································································· 6分 (Ⅱ)设向量()x y z =,,n 是平面1DA E 的法向量,则DE ⊥n ,1DA ⊥n .故20y z +=,240x z +=.令1y =,则2z =-,4x =,(412)=-,,n . ····················································· 9分1AC <>,n 等于二面角1A DE B --的平面角, 11114cos 42AC AC AC <>==,n n n 所以二面角1A DE B --的大小为arccos42. ················································· 12分21.解:(Ⅰ)2()363(2)f x ax x x ax '=-=-.因为2x =是函数()y f x =的极值点,所以(2)0f '=,即6(22)0a -=,因此1a =. 经验证,当1a =时,2x =是函数()y f x =的极值点. ········································· 4分 (Ⅱ)由题设,3222()336(3)3(2)g x ax x ax x ax x x x =-+-=+-+. 当()g x 在区间[02],上的最大值为(0)g 时,(0)(2)g g ≥,即02024a -≥.故得65a ≤. ································································································ 9分 反之,当65a ≤时,对任意[02]x ∈,, 26()(3)3(2)5g x x x x x +-+≤23(210)5xx x =+- 3(25)(2)5xx x =+- 0≤,而(0)0g =,故()g x 在区间[02],上的最大值为(0)g . 综上,a 的取值范围为65⎛⎤-∞ ⎥⎝⎦,. ··································································· 12分22.(Ⅰ)解:依题设得椭圆的方程为2214x y +=, 直线AB EF ,的方程分别为22x y +=,(0)y kx k =>. ····································· 2分 如图,设001122()()()D x kx E x kx F x kx ,,,,,,其中12x x <,且12x x ,满足方程22(14)4k x +=, 故21x x =-=.①由6ED DF =知01206()x x x x -=-,得021215(6)77x x x x =+==; 由D 在AB 上知0022x kx +=,得0212x k=+.所以212k =+, 化简得2242560k k -+=,解得23k =或38k =. ······················································································ 6分 (Ⅱ)解法一:根据点到直线的距离公式和①式知,点E F ,到AB的距离分别为1h ==2h ==······················································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 1525(14k =+==≤当21k =,即当12k =时,上式取等号.所以S 的最大值为 ························ 12分 解法二:由题设,1BO =,2AO =.设11y kx =,22y kx =,由①得20x >,210y y =->, 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ···································································································· 9分===当222x y =时,上式取等号.所以S 的最大值为 ······································· 12分。
2008年福建省数学(文科)高考试卷及答案

第6课 黄河颂 新诗
一、重点字词
1.给下列加点字注音。
巅diān 澎湃péng pài 狂澜lán 屏píng障 哺bǔ育
2.用恰当词语填空。
(1)惊涛澎湃,/掀起万丈狂澜;/浊流宛转,/结成九曲连环。
◇词语解释:P37 注释1、3、4、6、7、9、10、11;P38 注释 2、3、5、6、7、9、10、11、14、15、16、17、18、19
◇通假字:“扳”通“攀”,牵,引
◇文言归纳:《三点一测》P37-38 六至八
1.仲永变化的三个阶段(根本原因:不使学)
(1)五岁:指物作诗立就,文理皆有可观者(2)十二三岁:不能称前时之闻(3)又七年:泯然众人矣
二、重点句子背记知识清单
将下列句子翻译成现代汉语
l.即书诗四句,并自为其名。他当即写了四句诗,并且自己题写了名字。
点拨:重点理解“书”“为”等词。
2.自是指物作诗立就,其文理皆有可观者。
从此,指着东西让他作诗,他立刻就能完成,其中文采和道理都有值得看的地方。
点拨:重点理解“自是”“就”“之”“理”等词。
☆第2课 《爸爸的花儿落了》 小说
P.43注释 ① 选自《城南旧事》,林海音,台湾作家
1.线索 ——(1)“花”:以花喻人(共出现4次)(2)毕业典礼(时间顺序)
2.题目:一语双关(花的凋谢象征爸爸的去世)
3.伏笔:爸爸病情的恶化(第11、32、54、55段)
4.插叙(现实与回忆交替出现):第13-31段、
第3课 丑小鸭 童话
一、重点字词
1.给下列加点字注音。讪shàn笑 吐绶shòu鸡 沼zhǎo泽 木屐jī
2008年福建省数学(文科)高考试卷及答案

线性代数复习题一、填空题1. 11111111---x 是关于x 的一次多项式,该式中一次项的系数是________。
2. 已知四阶行列式D 中第三列元素依次为1-,2,0,1,它们的余子式依次分别为5,3,7-,4,则D =_______。
3. 已知333222111=D ,则=+-131211A A A _______________。
4. 已知矩阵n s ij c C B A ⨯=)(,,满足CB AC =,则A 与B 分别是___________阶矩阵。
5. 已知⎪⎪⎪⎭⎫ ⎝⎛=40060852b A 是奇异阵,则=b _________。
6. 设方阵A 满足0322=--E A A ,则=-1A ___________。
7. 设⎪⎪⎪⎪⎪⎭⎫⎝⎛-=1100210000120025A ,则=-1A ________________。
8. ⎪⎪⎭⎫ ⎝⎛-=1011A ,k 为自然数,则=k A _______________。
9. 若A 为n 阶方阵,且E AA T =,则=A 或 。
10.若n 阶方阵A 的秩小于n ,则A 的行列式等于_______ ____。
11.设A 为3阶方阵,且3=A ,则*1A A -+=_____________。
12.已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200020002A ,满足B A AB +=,则=B _____________。
13.设A 为n 阶方阵,且2=A ,则=A 2 ,=*A 。
14.若A 为n 阶方阵,且E AA T =,1-=A 则=+E A 。
15.设A 为5阶方阵,且21=A ,试求=--1*)3(A ________。
16.已知矩阵⎪⎪⎪⎭⎫ ⎝⎛=054032100A ,则=)(A R _____________.17.设向量组T )1,2,1,1(1=α,T )2,0,0,1(2=α,T k ),8,4,1(3---=α线性相关,则参数k =_____ 。
(精编精校)2008年普通高等学校招生全国统一考试(福建卷)文科数学 解析版
2008年福建卷省高考数学(文科)试题第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2|0A x x x =-<,{}|03B x x =<<,则AB 等于( )A.{}|01x x <<B.{}|03x x <<C.{}|13x x <<D.∅2.a=1”是“直线0x y +=和直线0x ay -=互相垂直”的( )条件A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 3.设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项和为( )A.128B.80 C.64 D.564.函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为( )A.3B.0 C.-1D.-25.某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是( ) A.12125B.16125 C.48125 D.961256.如图,在长方体1111ABCD A B C D -中,2AB BC ==分别为11AA =,则1AC 与平面1111A B C D 所成的角的正弦值为( )A.223B.23C.24D.137.函数cos ()y x x R =∈的图像向左平移2π个单位后,得到函数()y g x =的图像,则()g x 的解析式为( )A.sin x - B.sin xC.cos x -D.cos x8.在△ABC 中,角A,B,C 的对应边分别为a,b,c,若2223a c b ac +-=,则角B 的值为( )A.6π B.3π C.6π或56πD.3π或23π9.某班级要从4名男生和2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )A.14 B.24 C.28 D.4810.若实数x,y 满足{002x y x y -+≤>≤,则yx的取值范围是( ) A.(0,2)B.(0,2] C.(2,)+∞D.[2,)+∞11.如果函数()y f x =的图像如右图,那么导函数'()y f x =的图像可能是( )12.双曲线22221(0,0)x y a b a b-=>>的两个焦点为12,F F ,若P 为其上一点,且12||2||PF PF =,则双曲线离心率的取值范围为( )A.(1,3)B.(1,3]C.(3,)+∞D.[3,)+∞第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置. 13. 91()x x+展开式中3x 的系数是 (用数字作答)14.若直线340x y m ++=与圆222440x y x y +-++=没有公共点,则实数m 的取值范围是 15.若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是16.设P 是一个数集,且至少含有两个数,若对任意,a b P ∈,都有,,,aa b a b ab P b+-∈(除数0b ≠),则称P 是一个数域。
2008年普通高等学校招生全国统一考试(福建卷)

2008年普通高等学校招生全国统一考试(福建卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第2至第4页。
全卷满分150分,考试时间120分钟。
参考公式:如果事件A 、B 互斥,那么 球的表面积公式P (A +B )=P (A )+P (B ) 24R S π=如果事件A 、B 相互独立,那么 其中R 表示球的半径 P(A·B)=P(A)+P(B)第一卷(选择题60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
⑴若复数i a a a )1()23(2-++-是纯虚数,则实数a 的值为( ) A )1 B )2 C )1或2 D )-1 ⑵设集合}01|{<-=x xx A ,}30|{<<=x x B ,那么“A m ∈”是“B m ∈”的( ) A )充分而不必要条件 B )必要而不充分条件C )充要条件D )既不充分也不必要条件⑶设}{n a 是公比为正数的等比数列,若16,151==a a ,则数列}{n a 的前7项的和为( ) A )63 B )64 C )127 D )128⑷函数)(1sin )(3R x x x x f ∈++=,若2)(=a f ,则)(a f -的值为( ) A )3 B )0 C )-1 D )-2 ⑸某一批花生种子,如果每1粒发芽的概率为54,那么播下4粒种子恰有2粒发芽的概率是( ) A )62516 B )62596 C )625192 D )625256⑹如图,在长方体1111D C B A ABCD -中,1,21===AA BC AB , 则1BC 与平面D D BB 11所成角的正弦值为( )A )36 B )552 C )515 A )510⑺某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )A )14B )24C )28D )48⑻若实数⎩⎨⎧>≤+-001x y x ,则x y的取值范围是( )A ))1,0(B )]1,0(C )),1(+∞D )),1[+∞D 1C 1ABB 1CDA 1⑼函数)(cos )(R x x x f ∈=的图象按向量)0,(m 平移后,得到函数)(x f y '-=的图象,则m 的值可以为( )A )2π B )π C )π- D )2π- ⑽在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,若ac B b c a 3tan )(222=-+,则角B 的值为( )A )6π B )3π C )6π或65π D )3π或32π ⑾双曲线)0,0(12222>>=-b a by a x 的两个焦点为1F 、2F ,若P 为其上一点,且||2||21PF PF =,则双曲线离心率的取值范围是( )A ))3,1(B )]3,1(C )),3(+∞D )),3[+∞ ⑿已知函数)(),(x g y x f y ==的导函数的图象如右图, 那么)(),(x g y x f y ==的图象可能是( )第二卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分。
2008年福建高考数学试卷

2008年普通高等学校招生全国统一考试(福建理科)数 学(理工农医类)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)若复数(a 2-3a +2)+(a-1)i 是纯虚数,则实数a 的值为 A.1B.2C.1或2D.-1(2)设集合A={x |1x x -<0},B={x |0<x <3},那么“m ∈A ”是“m ∈B ”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件(3)设{a n }是公比为正数的等比数列,若a 1=7,a 5=16,则数列{a n }前7项的和为A.63B.64C.127D.128(4)函数f (x )=x 3+sin x +1(x ∈R ),若f (a )=2,则f (-a )的值为 A.3B.0C.-1D.-2(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下4粒种子恰有2粒发芽的概率是A.16625B.96625C.192625D.256625(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2, AA 1=1, 则BC 1与平面BB 1D 1D 所成角的正弦值为A.3B.552 C.5D.5(7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48(8)若实数x 、y 满足 x-y+1≤0,则y x的取值范围是x>0A. (0,1)B. (0,1)C. (1,+∞)D. [1, +∞](9)函数f (x )=cos x (x )(x ∈R )的图象按向量(m,0) 平移后,得到函数y = -f ′(x )的图象,则m 的值可以为A.2πB.πC.-πD.-2π(10)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c , 若(a 2+c 2-b 2)tan B ,则角B的值为A. 6πB.3πC.6π或56π D.3π或23π(11)双曲线12222=-by ax (a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞(12)已知函数y =f (x ), y =g (x )的导函数的图象如下图,那么y =f (x ),y =g (x )的图象可能是第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. (13)若(x -2)5=a 5x 5+a 4x 4+a 3x 3+a 2x 2+a 1x +a 0,则a 1+a 2+a 3+a 4+a 5=__________.(用数字作答) x =1+cos θ(14)若直线3x+4y+m=0与圆 y =-2+sin θ (θ为参数)没有公共点,则实数m 的取值范围是 .(15)若三棱锥的三个侧面两两垂直,,则其外接球的表面积是 . (16)设P 是一个数集,且至少含有两个数,若对任意a 、b ∈P ,都有a +b 、a -b , ab 、a b∈P (除数b ≠0),则称P 是一个数域.例如有理数集Q 是数域;数集{}=+∈也是数域.有下列命题:F a b Q,①整数集是数域;②若有理数集Q M⊆,则数集M必为数域;③数域必为无限集;④存在无穷多个数域.其中正确的命题的序号是.(把你认为正确的命题的序号都填上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)已知向量m=(sin A,cos A),n=1)-,m·n=1,且A为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数()cos24cos sin()=+∈的值域.f x x A x x R如图,在四棱锥P-ABCD 中,则面PAD ⊥底面ABCD ,侧棱PA =PD ,底面ABCD为直角梯形,其中BC ∥AD , AB ⊥AD , AD =2AB =2BC =2, O 为AD 中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PB 与CD 所成角的大小;(Ⅲ)线段AD 上是否存在点Q ,使得它到平面PCD 2?若存在,求出AQ QD的值;若不存在,请说明理由.(19)(本小题满分12分) 已知函数321()23f x x x =+-.(Ⅰ)设{a n }是正数组成的数列,前n 项和为S n ,其中a 1=3.若点211(,2)n n n a a a ++-(n ∈N*)在函数y =f ′(x )的图象上,求证:点(n , S n )也在y =f ′(x )的图象上;(Ⅱ)求函数f (x )在区间(a -1, a )内的极值.某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试。
2008年普通高等学校招生全国统一考试数学(福建卷·理科)(附答案,完全word版)

2008年普通高等学校招生全国统一考试数 学(理工农医类)(福建卷)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)若复数(a 2-3a +2)+(a-1)i 是纯虚数,则实数a 的值为 A.1B.2C.1或2D.-1(2)设集合A={x |1xx -<0},B={x |0<x <3},那么“m ∈A ”是“m ∈B ”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件(3)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n }前7项的和为 A.63B.64C.127D.128(4)函数f (x )=x 3+sin x +1(x ∈R ),若f (a )=2,则f (-a )的值为 A.3B.0C.-1D.-2(5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是 A.16625B.96625C. 192625D. 256625(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为A.3B.5C.5D.(7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为 A.14B.24C.28D.48(8)若实数x 、y 满足100x y x -+≤⎧⎨>⎩,则y x 的取值范围是A.(0,1)B.(]0,1C.(1,+∞)D.[)1,+∞(9)函数f (x )=cos x (x )(x ∈R )的图象按向量(m,0) 平移后,得到函数y =-f ′(x )的图象,则m 的值可以为 A.2πB.πC.-πD.-2π(10)在△ABC 中,角ABC 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B ,则角B 的值为 A.6π B.3π C.6π或56πD.3π或23π(11)又曲线22221x y a b==(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PF 2|,则双曲线离心率的取值范围为 A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞(12)已知函数y =f (x ),y =g (x )的导函数的图象如下图,那么y =f (x ),y =g (x )的图象可能是第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. (13)若(x -2)5=a 3x 5+a 5x 4+a 3x 3+a 2x 2+a 1x +a 0,则a 1+a 2+a 3+a 4+a 5=__________.(用数字作答) x =1+cos θ(14)若直线3x+4y+m=0与圆 y =-2+sin θ(θ为参数)没有公共点,则实数m 的取值范围是 .(15,则其外接球的表面积是 . (16)设P 是一个数集,且至少含有两个数,若对任意a 、b ∈R ,都有a +b 、a -b , ab 、ab∈P(除数b ≠0),则称P 是一个数域.例如有理数集Q 是数域;数集{},F a b Q =+∈也是数域。
高考福建数学文科试卷含详细解答(全word版)080626

2008年普通高等学校招生全国统一考试(福建卷)数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.∅ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解:若00x y x ay +=-=与互相垂直,则0x ay -=的斜率必定为1,1a =,反之显然 (3):设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 A.128 B.80 C.64 D.56 解:因为{}n a 是等差数列,278313886422a a ++=⨯=⨯=∴S(4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为 A.3 B.0 C.-1 D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125 B.16125 C.48125 D.96125解:独立重复实验服从二项分布4(3,)5B ,21234148(2)55125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ (6)如图,在长方体ABCD -A 1B 1C 1D 1中, AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.3B.23C.4D.13A解:连11A C ,则11AC A ∠为AC 1与平面A 1B 1C 1D 1所成角.112AB BC AC AC ==⇒==11AA = 1111113sin 3AA AC AC A AC =⇒∠==∴ (7)函数cos ()y x x R =∈的图象向左平移2π个单位后,得到函数()y g x =的图象,则()g x 的解析式为A.sin x -B. sin xC.cos x -D.cos x 解:()cos()sin 2y g x x x π==+=-(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c,若222a cb +-=,则角B 的值为 A.6π B.3π C.6π或56π D.3π或23π解:由222a +c -b得222(a +c -b )= 22ac即cos =2B ,6B π⇒=(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种(10)若实数x 、y 满足10,0,2,x y x y -+≤⎧⎪>⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) 解:由题设1y x ≥+,所以11y x x ≥+,又01211x y <≤-≤-=,因此2y x≥ 又yx可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.¢ (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件 (3)设|a n |是等左数列,若a 2=3,a 1=13,则数列{a n }前8项的和为 A.128 B.80 C.64 D.56 (4)函数f (x )=x 3+sin x +1(x ∈R),若f (a )=2,则f (-a )的值为 A.3 B.0 C.-1 D.-2 (5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是A.12125 B.16125 C.48125 D.96125(6)如图,在长方体ABCD -A 1B 1C 1D 1中,AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为A.3 B.23 C.4D.13(7)函数y =cos x (x ∈R)的图象向左平移2个单位后,得到函数y=g(x )的图象,则g(x )的解析式为A.-sin xB.sin xC.-cos xD.cos x(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若a 2+c 2-b ,则角B 的值为A.6π B.3π C.6π或56π D.3π或23π(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48(10)若实数x 、y 满足10,0,2,x y x x -+≤⎧⎪⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞) (11)如果函数y=f (x )的图象如右图,那么 导函数y=f (x )的图象可能是(12)双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PE 2|,则双曲线离心率的取值范围为A.(1,3)B.(1,3)C.(3,+∞)D. [3,+∞]第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. (13)(x +1x)9展开式中x 2的系数是 .(用数字作答) (14)若直线3x+4y +m =0与圆x 2+y 2-2x +4y +4=0没有公共点,则实数m 的取值范围是 . (15,则其外接球的表面积是 . (16)设P 是一个数集,且至少含有两个数,若对任意a 、b ∈P ,都有a+b 、a-b 、ab 、a b∈P (除数b ≠0)则称P 是一个数域,例如有理数集Q 是数域,有下列命题: ①数域必含有0,1两个数;②整数集是数域;③若有理数集Q ⊆M ,则数集M 必为数域;④数域必为无限集.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分) 已知向量(sin ,cos ),(1,2)m A A n ==-,且0.m n = (Ⅰ)求tan A 的值;(Ⅱ)求函数()cos 2tan sin (f x x A x x =+∈R )的值域. (18)(本小题满分12分)三人独立破译同一份密码.已知三人各自破译出密码的概率分别为111,,,543且他们是否破译出密码互不影响.(Ⅰ)求恰有二人破译出密码的概率;(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大?说明理由. (19)(本小题满分12分)如图,在四棱锥P —ABCD 中,侧面P AD ⊥底面ABCD ,侧棱P A =PD 底面ABCD 为直角梯形,其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC=2,O 为AD 中点.(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PB 与CD 所成角的余弦值; (Ⅲ)求点A 到平面PCD 的距离. (20)(本小题满分12分)已知{a n }是正数组成的数列,a 1=11n a +)(n ∈N *)在函数y =x 2+1的图象上. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)若列数{b n }满足b 1=1,b n +1=b n +2n a,求证:b n ·b n +2<b 2n +1. (21)(本小题满分12分)已知函数32()2f x x mx nx =++-的图象过点(-1,-6),且函数()()6g x f x x '=+的图象关于y 轴对称.(Ⅰ)求m 、n 的值及函数y =f (x )的单调区间;(Ⅱ)若a >0,求函数y =f (x )在区间(a -1,a +1)内的极值. (22)(本小题满分14分)如图,椭圆2222:1x y C a b+=(a >b >0)的一个焦点为F (1,0),且过点(2,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)若AB 为垂直于x 轴的动弦,直线l :x =4与x 轴交于点N , 直线AF 与BN 交于点M . (ⅰ)求证:点M 恒在椭圆C 上; (ⅱ)求△AMN 面积的最大值.2008年普通高等学校招生全国统一考试(福建卷)数 学(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于 A.{x |0<x <1} B.{x |0<x <3} C.{x |1<x <3} D.∅ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} (2)“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件解:若00x y x ay +=-=与互相垂直,则0x ay -=的斜率必定为1,1a =,反之显然 (3):设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项的和为 A.128 B.80 C.64 D.56 解:因为{}n a 是等差数列,278313886422a a ++=⨯=⨯=∴S(4)函数3()sin 1()f x x x x R =++∈,若()2f a =,则()f a -的值为A.3B.0C.-1D.-2解:3()1sin f x x x -=+为奇函数,又()2f a =∴()11f a -=故()11f a --=-即()0f a -=.(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 A.12125 B.16125 C.48125 D.96125解:独立重复实验服从二项分布4(3,)5B ,21234148(2)55125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭(6)如图,在长方体ABCD -A 1B 1C 1D 1中, AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为B.23D.13解:连11AC ,则11AC A ∠为AC 1与平面A 1B 1C 1D 1所成角.112AB BC AC AC ==⇒==,又11AA= 1111113sin 3AA AC AC A AC =⇒∠==∴ (7)函数cos ()y x x R =∈的图象向左平移2π个单位后,得到函数()y g x =的图象,则()g x 的解析式为A.sin x -B. sin xC.cos x -D.cos x 解:()cos()sin 2y g x x x π==+=-(8)在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c,若222a cb +-=,则角B 的值为 A.6π B.3π C.6π或56π D.3π或23π解:由222a +c -b得222(a +c -b )=22ac即cos = 2B ,6B π⇒=(9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A.14B.24C.28D.48解:6人中选4人的方案4615C =种,没有女生的方案只有一种,所以满足要求的方案总数有14种(10)若实数x 、y 满足10,0,2,x y x y -+≤⎧⎪>⎨⎪≤⎩则y x 的取值范围是A.(0,2)B.(0,2)C.(2,+∞)D.[2,+∞)AA解:由题设1y x ≥+,所以11y x x ≥+,又01211x y <≤-≤-=,因此2y x≥ 又yx可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
(11)如果函数y=f (x )的图象如右图,那么导函数y=f (x )的图象可能是解:由原函数的单调性可以得到导函数的正负情况依次是正→负→正→负,只有答案A 满足.(12)双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,若P 为其上一点,且|PF 1|=2|PE 2|,则双曲线离心率的取值范围为 A.(1,3)B.(]1,3C.(3,+∞)D.[)3,+∞解:如图,设2PF m =,12(0)F PF θθπ∠=<≤,当P 在右顶点处θπ=,22c e a ===∵1cos 1θ-<≤,∴(]1,3e ∈另外也可用三角形的两边和大于第三边,及两边差小于第三边,但要注意前者可以取到等号成立,因为可以三点一线. 也可用焦半径公式确定a 与c 的关系。
第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. (13)(x +1x)9展开式中x 2的系数是 .(用数字作答) 解:992991rr r r r C x C x x --⎛⎫= ⎪⎝⎭,令9233r r -==得,3984C ∴= (14)若直线340x y m ++==0与圆222440x y x y +-++=没有公共点,则实数m 的取值范围是 .解:圆心为(1,2)-,要没有公共点,根据圆心到直线的距离大于半径可得1d r =>=,即55m ->,m ∈∞∞ (-,0)(10,+) (15,则其外接球的表面积是 . 解:依题可以构造一个正方体,其体对角线就是外接球的直径.23r = ,249S r ππ==(16)设P 是一个数集,且至少含有两个数,若对任意a 、b ∈P ,都有a+b 、a-b 、ab 、a b∈P (除数b ≠0)则称P 是一个数域,例如有理数集Q 是数域,有下列命题:①数域必含有0,1两个数; ②整数集是数域;③若有理数集Q ⊆M ,则M 必为数域;④数域必为无限集.其中正确的命题的序号是 .(把你认为正确的命题的序号都填上) 解:①数集P 有两个元素,a b , ,则一定有0,1aa a a-==(设0a ≠),正确; ②整数集不是数域,11,2,2Z Z Z ∈∈∉但是;③令数集M Q =,则1M④数域有1,一定有1+1=2,1+2=3,推下去必然包含整数集,因而为无限集。
