偏导数的物理几何意义
《偏导数的概念》课件

偏导数的几何意义
偏导数在几何上表示函数曲面在某一 点处的切线斜率。
对于二元函数z=f(x,y),其在点(x0,y0) 处的偏导数即为该点处曲面切线的斜 率。
偏导数的计算方法
通过求导法则进行计算:链式法则、乘积法则、商的法则、复合函数求导 法则等。
对于多元函数的偏导数,需要分别对各个自变量求导,然后根据具体问题 选择合适的方向进行计算。
商的乘积。
乘积法则
对于两个函数的乘积,其偏导数为各 自函数的偏导数的乘积加上各自函数 对另一变量的导数的乘积。
反函数法则
对于反函数的偏导数,等于原函数在 该点的导数的倒数。
03
CATALOGUE
偏导数在几何中的应用
曲线的切线
总结词
偏导数可以用来求曲线的切线。
详细描述
在几何学中,曲线的切线是曲线在某一点的邻近线段的行为。通过偏导数,我 们可以找到曲线在某一点的切线斜率,从而确定切线的方向和位置。
描述热量在物体中的传递和扩散过程。
电场与磁场
总结词
偏导数在电场和磁场的研究中也有着重要的应用,它可 以帮助我们理解和描述电场和磁场的变化规律。
详细描述
电场和磁场是物理学中两个重要的物理量,它们描述了 电荷和电流产生的场。在研究电场和磁场时,我们常常 需要用到偏导数来描述它们的变化规律。通过偏导数, 我们可以计算出电场和磁场在不同位置的值,从而更好 地理解和描述电场和磁场的变化规律。
THANKS
感谢观看
边际分析
边际分析
偏导数提供了对经济变量边际变化的度量,即当其他条件保持不变时,某一变量变化一 个单位所引起的另一变量的变化量。
边际成本和边际收益
在决策分析中,偏导数用于计算边际成本和边际收益,帮助企业了解产品定价、产量决 策的合理性。
第二节 偏导数

V k , T V, T P P k
从而
P V
V T
T P
kT V2
k P
V k
kT PV
1
.
2019年12月24日星期二
徐州工程学院数理学院
上页 下页 返回 结束
警告各位!
偏导数 z 是一个整体记号, 不能拆分. x
不能像一元函数那样将 z , z 看成是
2019年12月24日星期二
徐州工程学院数理学院
上页 下页 返回 结束
1997年研究生考题, 选择, 3分
f
(
x,
y)
x2
xy
y2
( x, y) (0,0)在点(0,0)处( C
).
0 ( x, y) (0,0)
A. 连续,偏导数存在;
B. 连续,偏导数不存在; C. 不连续,偏导数存在; D. 不连续,偏导数不存在.
x y
z 与 x , y 的商.
2019年12月24日星期二
徐州工程学院数理学院
上页 下页 返回 结束
例7 求 u e x xy2z3 的偏导数 .
解:
u e xxy2z3 (1 y2 ) ;
x
u e xxy2z3 2x y ; y
u e xxy2z3 (3z2 ) . z
函数有相应的增量 (称为关于x的偏增量), 即
x z f ( x0 x, y0 ) f ( x0 , y0 )
如果极限
lim x z lim f ( x0 x, y0 ) f ( x0 , y0 )
x0 x x0
偏导数的几何意义

偏导数的几何意义实验目的:通过实验加深学生对偏导数定义的理解掌握偏导数的几何意义并从直观上理解二阶混合偏导数相等的条件背景知识:一偏导数的定义在研究一元函数时.我们从研究函数的变化率引入了导数概念.对于多元函数同样需要讨论它的变化率.但多元函数的变化量不只一个,因变量与自变量的关系要比一元函数复杂的多.所以我们首先考虑多元函数关于其中一个自变量的变化率,以二元函数= 为例,如果只有自变量变化,而自变量y固定(即看作常量),这时它就是的一元函数,这函数对x的导数,就称为二元函数z对于的偏导数,即有如下定义定义设函数z= 在点的某一邻域内有定义,当y固定在,而在处有增量时,相应的函数有增量- ,如果(1)存在,则称此极限为函数= 在点处对的偏导数,记做, , ,或例如,极限(1)可以表为=类似的,函数z= 在点处对的偏导数定义为记做, , 或如果函数= 在区域D内每一点( )处对的偏导数都存在,那么这个偏导数就是的函数,它就称为函数= 对自变量的偏导函数,记做, , ,或类似的,可以定义函数= 对自变量的偏导函数,记做, , ,或由偏导数的概念可知, 在点处对的偏导数显然就是偏导函数在点处的函数值,就像一元函数的导函数一样,以后在不至于混淆的地方也把偏导函数简称为偏导数.至于求= 的偏导数,并不需要用新的方法,因为这里只有一个自变量在变动,另外一个自变量看作是固定的,所以仍旧是一元函数的微分法问题,求时,只要把暂时看作常量而对求导;求时,则只要把暂时看作是常量,而对求导数.偏导数的概念还可以推广导二元以上的函数,例如三元函数在点( )处对的偏导数定义为=其中( )是函数的定义域的内点,它们的求法也仍旧是一元函数的微分法问题例求的偏导数解= ,=二偏导数的几何意义二元函数= 在点的偏导数的几何意义设为曲面= 上的一点,过点作平面,截此曲面得一曲线,此曲线在平面上的方程为= ,则导数,即偏导数,就是这曲线在点处的切线对轴的斜率.同样,偏导数的几何意义是曲面被平面所截得的曲线在点处的切线对的斜率三偏导数的几何意义我们知道,如果一元函数在某点具有导数,则它在该点必定连续,但对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续.这是因为各偏导数存在只能保证点P沿着平行于坐标轴的方向趋于P 时,函数值趋于,但不能保证点P按任何方式趋于 P 时,函数值都趋于.例如,函数= ={在点(0,0)对的偏导数为同样有但是我们在前面的学习中知道这函数在点(0,0)并不连续四二阶混合偏导数设函数= 在区域D内具有偏导数= , =那么在D内, 都是的函数.如果这里两个函数的偏导数也存在,则它们是函数= 的二阶偏导数,按照对变量求导次序的不同有下列四个二阶偏导数:,,其中第二 ,第三个偏导数称为混合偏导数例2 设,求, , ,,从例子中,我们看到两个二阶混合偏导数相等,即, =我们再看用maple作求的图形第一个图形为第二个图形为从图中我们看到两个连续的偏导函数,它们是相等的这不是偶然的,事实上我们有下述定理定理如果函数= 的两个二阶混合偏导数及在区域D里连续,那么在该区域内这两个二阶混合偏导数必定相等换句话说,二阶混合偏导数在连续的条件下与求导的次序无关。
偏导数知识点公式总结

偏导数知识点公式总结一、偏导数的概念1.1 偏导数的定义偏导数是多元函数对其中一个自变量的导数。
对于一个函数 $f(x_1, x_2, ..., x_n)$,它的偏导数 $\frac{\partial f}{\partial x_i}$ 表示在$x_i$方向上的变化率。
偏导数的定义可以表示为:$$\frac{\partial f}{\partial x_i} = \lim_{\Delta x_i \to 0} \frac{f(x_1, x_2, ..., x_i + \Delta x_i, ..., x_n) - f(x_1, x_2, ..., x_i, ..., x_n)}{\Delta x_i}$$1.2 偏导数的图示解释偏导数可以通过函数曲面的切线来解释。
对于函数 $z = f(x, y)$,在点$(x_0, y_0, z_0)$处的偏导数 $\frac{\partial f}{\partial x}$可以理解为曲面在$x$方向的斜率,即曲面在$x$方向上的变化率。
同样地,$\frac{\partial f}{\partial y}$表示曲面在$y$方向上的变化率。
这样的解释有助于我们更直观地理解偏导数的含义。
二、偏导数的性质2.1 对称性对于二元函数 $f(x, y)$,它的偏导数满足对称性,即$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$。
这一性质表明,在计算混合偏导数时,可以不必考虑自变量的顺序。
2.2 连续性在函数的定义域内,若偏导数存在且连续,则函数规定可微。
这一性质是偏导数与函数连续性的关系,对于函数的导数性质有着重要的影响。
2.3 性质总结:和与积对于函数 $u = u(x, y)$ 和 $v = v(x, y)$,它们的偏导数具有和与积的运算法则。
偏导数的物理几何意义

偏导数的物理几何意义一偏导数的定义在研究一元函数时.我们从研究函数的变化率引入了导数概念.对于多元函数同样需要讨论它的变化率.但多元函数的变化量不只一个,因变量与自变量的关系要比一元函数复杂的多.所以我们首先考虑多元函数关于其中一个自变量的变化率,以二元函数=为例,如果只有自变量变化,而自变量y固定(即看作常量),这时它就是的一元函数,这函数对x的导数,就称为二元函数z对于的偏导数,即有如下定义定义设函数z= 在点的某一邻域内有定义,当y固定在,而在处有增量时,相应的函数有增量- ,如果(1)存在,则称此极限为函数= 在点处对的偏导数,记做, , ,或例如,极限(1)可以表为=类似的,函数z= 在点处对的偏导数定义为记做, , 或如果函数= 在区域D内每一点( )处对的偏导数都存在,那么这个偏导数就是的函数,它就称为函数= 对自变量的偏导函数,记做, , ,或类似的,可以定义函数= 对自变量的偏导函数,记做, , ,或由偏导数的概念可知, 在点处对的偏导数显然就是偏导函数在点处的函数值,就像一元函数的导函数一样,以后在不至于混淆的地方也把偏导函数简称为偏导数.至于求= 的偏导数,并不需要用新的方法,因为这里只有一个自变量在变动,另外一个自变量看作是固定的,所以仍旧是一元函数的微分法问题,求时,只要把暂时看作常量而对求导;求时,则只要把暂时看作是常量,而对求导数.偏导数的概念还可以推广导二元以上的函数,例如三元函数在点( )处对的偏导数定义为=其中( )是函数的定义域的内点,它们的求法也仍旧是一元函数的微分法问题例求的偏导数解= ,=二偏导数的几何意义二元函数= 在点的偏导数的几何意义设为曲面= 上的一点,过点作平面,截此曲面得一曲线,此曲线在平面上的方程为= ,则导数,即偏导数,就是这曲线在点处的切线对轴的斜率.同样,偏导数的几何意义是曲面被平面所截得的曲线在点处的切线对的斜率三偏导数的几何意义我们知道,如果一元函数在某点具有导数,则它在该点必定连续,但对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续.这是因为各偏导数存在只能保证点P沿着平行于坐标轴的方向趋于P 时,函数值趋于,但不能保证点P按任何方式趋于P 时,函数值都趋于.例如,函数= ={在点(0,0)对的偏导数为同样有但是我们在前面的学习中知道这函数在点(0,0)并不连续四二阶混合偏导数设函数= 在区域D内具有偏导数= , =那么在D内, 都是的函数.如果这里两个函数的偏导数也存在,则它们是函数= 的二阶偏导数,按照对变量求导次序的不同有下列四个二阶偏导数:,,其中第二,第三个偏导数称为混合偏导数例2 设,求, , ,,从例子中,我们看到两个二阶混合偏导数相等,即, =我们再看用maple作求的图形第一个图形为第二个图形为从图中我们看到两个连续的偏导函数,它们是相等的这不是偶然的,事实上我们有下述定理定理如果函数= 的两个二阶混合偏导数及在区域D里连续,那么在该区域内这两个二阶混合偏导数必定相等换句话说,二阶混合偏导数在连续的条件下与求导的次序无关。
偏导数的几何意义

偏导数得几何意义ﻫ实验目得:通过实验加深学生对偏导数定义得理解掌握偏导数得几何意义并从直观上理解二阶混合偏导数相等得条件ﻫ背景知识:一偏导数得定义在研究一元函数时、我们从研究函数得变化率引入了导数概念、对于多元函数同样需要讨论它得变化率、但多元函数得变化量不只一个,因变量与自变量得关系要比一元函数复杂得多、所以我们首先考虑多元函数关于其中一个自变量得变化率,以二元函数= 为例,如果只有自变量变化,而自变量y固定(即瞧作常量),这时它就就是得一元函数,这函数对x 得导数,就称为二元函数z对于得偏导数,即有如下定义定义设函数z= 在点得某一邻域内有定义,当y固定在,而在处有增量时,相应得函数有增量- ,如果(1)存在,则称此极限为函数=在点处对得偏导数,记做, ,,或例如,极限(1)可以表为=类似得,函数z=在点处对得偏导数定义为记做,,或如果函数= 在区域D内每一点( )处对得偏导数都存在,那么这个偏导数就就是得函数,它就称为函数= 对自变量得偏导函数,记做, ,,或类似得,可以定义函数= 对自变量得偏导函数,记做,,,或由偏导数得概念可知,在点处对得偏导数显然就就是偏导函数在点处得函数值,就像一元函数得导函数一样,以后在不至于混淆得地方也把偏导函数简称为偏导数、至于求=得偏导数,并不需要用新得方法,因为这里只有一个自变量在变动,另外一个自变量瞧作就是固定得,所以仍旧就是一元函数得微分法问题,求时,只要把暂时瞧作常量而对求导;求时,则只要把暂时瞧作就是常量,而对求导数、偏导数得概念还可以推广导二元以上得函数,例如三元函数在点()处对得偏导数定义为=其中()就是函数得定义域得内点,它们得求法也仍旧就是一元函数得微分法问题例求得偏导数解= ,=二偏导数得几何意义二元函数= 在点得偏导数得几何意义设为曲面= 上得一点,过点作平面,截此曲面得一曲线,此曲线在平面上得方程为= ,则导数,即偏导数,就就是这曲线在点处得切线对轴得斜率、同样,偏导数得几何意义就是曲面被平面所截得得曲线在点处得切线对得斜率三偏导数得几何意义我们知道,如果一元函数在某点具有导数,则它在该点必定连续,但对于多元函数来说,即使各偏导数在某点都存在,也不能保证函数在该点连续、这就是因为各偏导数存在只能保证点P沿着平行于坐标轴得方向趋于P 时,函数值趋于,但不能保证点P按任何方式趋于P 时,函数值都趋于、例如,函数= ={在点(0,0)对得偏导数为同样有但就是我们在前面得学习中知道这函数在点(0,0)并不连续四二阶混合偏导数设函数= 在区域D内具有偏导数=, =那么在D内,都就是得函数、如果这里两个函数得偏导数也存在,则它们就是函数= 得二阶偏导数,按照对变量求导次序得不同有下列四个二阶偏导数:,,其中第二,第三个偏导数称为混合偏导数例2 设,求, ,,,从例子中,我们瞧到两个二阶混合偏导数相等,即,=我们再瞧用maple作求得图形第一个图形为第二个图形为从图中我们瞧到两个连续得偏导函数,它们就是相等得这不就是偶然得,事实上我们有下述定理定理如果函数=得两个二阶混合偏导数及在区域D里连续,那么在该区域内这两个二阶混合偏导数必定相等换句话说,二阶混合偏导数在连续得条件下与求导得次序无关。
3.1-2 偏导数与高阶偏导

f yx ( x 2x, y 1y) f xy ( x 3x, y 4y)
由 于f xy , f yx连 续, 令x 0, y 0得 : f xy ( x , y ) f yx ( x , y )
( x0 , y0 ) 处的函数值。偏导函数简称偏导数。
偏导数的概念还可以推广到二元以上的多元函数。例如三元
函数 u f ( x, y, z ) 在点 ( x, y, z ) 处对 x 的偏导数定义为
函数 u f ( x, y, z ) 在点 ( x , y, z ) 处对 x 的偏导数定义为 f ( x x , y , z) f( x , y , z) f x ( x , y , z ) lim 。 x 0 x 5
第三节
偏导数与全微分
第五章
多元函数微分学及其应用
3.1 偏导数概念与几何意义
1.函数 z f ( x , y ) 在点 M 0 ( x0 , y0 ) 处的偏导数的定义
定义 3.1 设 z f ( x, y) 在点 M0 ( x0 , y0 ) 的某一邻域 N ( M0 )
上有定义,当 y 固定在 y0 而 x 在 x0 处有增量 x 时 ,相应地 函数有增量 f ( x0 x, y0 ) f ( x0 , y0 ) ,
f xy (0,0) f yx (0,0)
例1 中 2 y 2 y 2 y 2 y , 而例 2 中 , xy yx xy yx
问:混合偏导数相等需要什么条件?
18
第五章
多元函数微分学及其应用
定理 3.1:如果 f xy ( x, y) , f yx ( x, y) 在点 ( x, y) 的某邻域 内连续,则有 f xy ( x, y) f yx ( x, y) 。
偏导数的几何意义.doc

Ax偏导数的儿何意义实验目的:通过实验加深学生对偏导数定义的理解掌握偏导数的几何意义并从直观上理解二 阶混合偏导数相等的条件背景知识:一偏导数的定义在研究一无函数吐我们从研究函数的变化率引入了导数概念.对于多元函数同样需要讨论 它的变化率.但多元函数的变化量不只一个,因变量与自变最的关系要比一元函数复杂的多. 所以我们首先考虑多元函数关于其中一-个自变量的变化率,以二元函数z= /(了疗)为例, 如果只有自变量工变化,而自变量y 固定(即看作常量),这时它就是X 的一元函数,这函数 对X 的导数,就称为二元函数Z 对于才的偏导数,即有如下定义定义设函数z= *')在点的某一•邻域内有定义,当y 固定在V 。
,而工在工。
处有增量• A*时,相应的函数有增量/(x 0 4-Ax,^) _ /(x 0,^0)f(x 0 +Ax,y 0)-f(x 0,y 0) lim ---------------------------------如果 Ax (1)存在,则称此极限为函数z=在点”°疗°)处对汗的偏导数,记做例如,极限(1)可以表为 f(x 0 +Ax,y 0)-f(x 0,y 0) hgy°)蚣。
类似的,函数z= ,(兀、)在点(冲疗°)处对歹的偏导数定义为尚 栈尚九(%必)dzlim 敏T O Rxo,Vo +Ay)・地,dz记做分5 X■命如果函数2= 了3疗)在区域D内每一点(&')处对工的偏导数都存在,那么这个偏导数就是工溜的函数,它就称为函数Z = /(工1)对自变量式的偏导函数,记做 & 堂凯瓦,气或九(")类似的,可以定义函数z= /(兀力对自变量W的偏导函数,记做dz山偏导数的概念可知,/3'力在点(如儿)处对工的偏导数九成。
/)显然就是偏导函数九3',)在点成°疗°)处的函数值,就像-•元函数的导函数-•样,以后在不至于混淆的地方也把偏导函数简称为偏导数.至于求z=的偏导数,并不需要用新的方法,因为这里只有一个自变量在变动,另外dz一个自变量看作是固定的,所以仍旧是一元函数的微分法问题,求欲时,只要把*暂时看作常最而对工求导;求莎时,则只要把式智时看作是常量,而对V求导数.偏导数的概念还可以推广导二元以上的函数,例如三元函数〃 = /(兀MZ)在点(、,yz)处对式的偏导数定义为岫Rx +Ax, y ,z)・Rx ,y ,z)九(X'V’z) = A XT O A X其中(X'W'Z)是函数〃 = /3,V,z)的定义域的内点,它们的求法也仍旧是一元函数的微分法问题例求z = / sin 2y的偏导数dz解瓦=2xsin 2〉,dzdy _ 2/COS2〉二偏导数的几何意义二元函数z= '3,)在点3o,Wo)的偏导数的几何意义疗° J3o,〉o)) u o77*(工疗)[心r、』y-y^\耳口设为曲面z = J、…上的一点,过°点作平面/ 气截此曲面得•曲线,此曲线在平面^=^0上的方程为Z = /(X,%),则导数小/3'")"・命即偏导数兀(%必),就是这曲线在"。
8.2-2偏导数的几何意义及偏导数存在与连续的关系

偏 导数存在与连续的
关系
第八章多元函数微分学 第2节偏导数及其在经济分析中的应用
主讲 韩华
1 -几何意义
经济数学
微积分
偏导数人(X。成0) 就 是曲面被平面 y = yQ 所 截 得 的 曲 线在点处的切线 对x轴的斜率.
O
1 -几何意义
经济数学--微积分
偏导数人(乂0 9 No ) 就 是 曲 面 被 平 面 X = x0 所 截 得 的曲线在点 M。处 的切线对 p轴的斜 率.
点处并不连续.偏导数存在宀连续.
微积分
谢谢
T导数存在与连续的关系
一元函数中在某点可导—►连续, 多元
函数中在某点偏导数存在斗连续,
= i 例如,函数 f (x,y)
2 x2y, x 2 + y 2 丰 0
+ , X2
y2
2
,
、0,
x2+ y2= 0
依定义知在(0,0)处,fx (0,0) = fy (0,0) = 0. 但函数在该
偏导数几何意义

偏导数几何意义偏导数是多元函数微积分中的一个重要概念,它用来描述函数在某个方向上的变化率。
偏导数的几何意义主要包括以下几个方面:1. 偏导数的定义偏导数是指在多元函数中,固定其他变量不变,仅对某个变量进行微小的变化时,函数的变化率。
如果函数$f(x_1,x_2,...,x_n)$在$x_i$处的偏导数存在,那么它的偏导数可以表示为$f_{x_i}(x_1,x_2,...,x_n)$。
对于二元函数$f(x,y)$,$f_x$表示函数在$x$轴方向上的变化率,$f_y$表示函数在$y$轴方向上的变化率。
2. 偏导数与方向导数偏导数描述了函数在某个方向上的变化率,因此它与方向导数密切相关。
方向导数是指函数在某个方向上的变化率,可以表示为$\frac{\partial f}{\partial\boldsymbol{u}}$,其中$\boldsymbol{u}$是方向向量。
在某个点上,如果函数在所有方向上的变化率都存在,那么这些变化率就构成了一个向量,称之为梯度向量。
3. 偏导数与曲面偏导数可以用来描述曲面的性质。
对于任意的曲面,如果它在某个点处的偏导数存在,那么这个曲面在这个点处有一个唯一的切平面。
这个切平面与$x_i$轴的夹角就是$f_{x_i}$的值,它描述了曲面在这个方向上的变化率。
使用偏导数可以求解曲面的最大值和最小值。
对于一个具有偏导数的函数$f(x_1,x_2,...,x_n)$,可以使用偏导数方法求得$f$的最值点,即令所有$n$个偏导数都等于零,然后求解方程组。
最大值和最小值点就是$f$的极值点。
偏导数还可以用来描述曲线的性质。
考虑一个函数$f(x,y)$和一条曲线$C$,如果曲线$C$落在$f=0$的等高线上,那么曲线$C$在这个点处的斜率等于$f$在这个点处的梯度向量在曲线$C$方向的投影,即$\nabla f(x,y)\cdot\frac{d\boldsymbol{x}}{dt}$。
偏导数在几何上的应用

感谢您的观看
THANKS
详细描述
梯度是一个向量,其大小等于函数在该点的方向导数的最大值,其方向则是该方向导数最大的方向。梯度的计算 涉及到偏导数的计算,可以通过对偏导数进行向量运算得到。
偏导数与高斯公式和格林公式
总结词
高斯公式和格林公式是微积分中的重要公式,它们涉及到偏导数的概念,可以用来解决某些几何问题 。
详细描述
高斯公式和格林公式分别描述了三维空间和二维平面中体积分和曲线积分与偏导数的关系。它们在计 算几何形状的体积、表面积、曲线长度等几何量时非常有用。通过这些公式,我们可以将复杂的几何 问题转化为相对简单的积分问题,从而方便地求解。
偏导数与函数图像的凹凸性
总结词
偏导数可以用来判断函数图像的 凹凸性。
详细描述
如果一个函数在某一点的偏导数 大于零,则该点附近的函数图像 是凹的;如果偏导数小于零,则 该点附近的函数图像是凸的。
偏导数与函数图像的单调性
总结词
偏导数可以用来判断函数图像的单调性。
详细描述
如果一个函数在某一点的偏导数大于零,则该点附近函数值是递增的;如果偏 导数小于零,则该点附近函数值是递减的。这为研究函数的单调性提供了重要 的几何解释。
偏导数在几何上的应用
目录 CONTENT
• 偏导数的几何意义 • 偏导数在几何优化问题中的应用 • 偏导数在解决几何问题中的具体
应用 • 偏导数在几何中的其他应用
01
偏导数的几何意义
偏导数与切线斜率
总结词
偏导数可以用来描述函数图像上某一 点的切线斜率。
详细描述
在几何上,偏导数表示函数在某一点 处沿某一方向的变化率,即切线的斜 率。对于二元函数,偏导数可以表示 空间曲面在某一点的切平面。
偏导数概念及其计算

计算多元函数的偏导数
计算多元函数$f(x, y, z)$在点$(a, b, c)$处的 偏导数,即求$frac{partial f}{partial x}(a, b, c)$、$frac{partial f}{partial y}(a, b, c)$和 $frac{partial f}{partial z}(a, b, c)$,可以通 过求导法则和链式法则进行计算。
曲面的法线向量
法线向量是垂直于曲 面切平面的向量。
法线向量在几何上表 示曲面在该点的切线 方向。
通过偏导数计算切平 面,进而得到法线向 量。
05
偏导数的计算Байду номын сангаас例
计算一元函数的偏导数
计算一元函数$f(x)$在$x=a$处的偏 导数,即求$f'(a)$,可以通过求导法 则和链式法则进行计算。
例如,对于函数$f(x) = x^3 + 2x^2 + x$,在$x=1$处的偏导数为$f'(1) = 3 times 1^2 + 2 times 1 + 1 = 6$。
Hessian矩阵是对称矩阵,其行列式值表示函数在某一点的 凹凸性。
要点二
详细描述
Hessian矩阵是一个对称矩阵,即其转置矩阵与原矩阵相 等。Hessian矩阵的行列式值可以用来判断函数在某一点 的凹凸性,如果行列式值为正,则函数在这一点处为凸函 数;如果行列式值为负,则函数在这一点处为凹函数。此 外,Hessian矩阵还可以用来计算函数的极值点和鞍点。
详细描述
对于指数函数f(x, y) = e^(x*y),其偏导数可以通过链式法则和指数法则进行计算。具 体地,f'_x = e^(x*y) * y,f'_y = e^(x*y) * x。
偏导数的几何意义
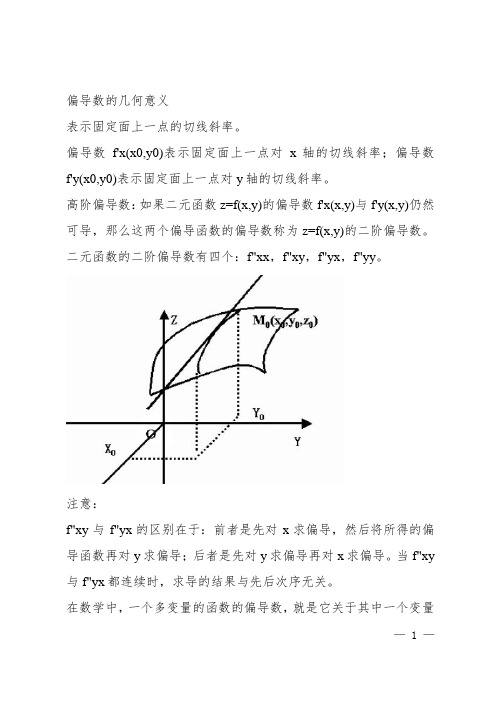
— 1 —
偏导数的几何意义
表示固定面上一点的切线斜率。
偏导数f'x(x0,y0)表示固定面上一点对x 轴的切线斜率;偏导数f'y(x0,y0)表示固定面上一点对y 轴的切线斜率。
高阶偏导数:如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。
二元函数的二阶偏导数有四个:f"xx ,f"xy ,f"yx ,f"yy 。
注意:
f"xy 与f"yx 的区别在于:前者是先对x 求偏导,然后将所得的偏导函数再对y 求偏导;后者是先对y 求偏导再对x 求偏导。
当f"xy 与f"yx 都连续时,求导的结果与先后次序无关。
在数学中,一个多变量的函数的偏导数,
就是它关于其中一个变量
的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
偏导数在向量分析和微分几何中是很有用的。
二元函数偏导数的几何意义

二元函数偏导数的几何意义
对于二元函数偏导数的几何意义,可以概括为某一点上的切线斜率,也就是有两个自变量的函数y关于某一自变量x的偏导数表示这个切
线斜率。
在这种情况下,该函数在某一点(x,y)开始沿着该切线的
方向走,斜率值表示该方向的变化程度,也就是说,该函数随着一个
自变量的变化应该沿着切线的变化而变化。
比如对于一个常见的函数,例如y=2x+3,在(3,9)点处求偏导数,
首先根据定义先求到偏导数,即dy/dx=2,这说明斜率的值是2。
这就很
有趣的表明函数在着个点以切线方向增加2倍的变化量。
比如,假如
函数有一个1%的变化,那么切线也有2%的变化,y值也会改变2%。
另外,当偏导数为负时,函数也就沿着负的斜率变化而变化,于是该
函数的变化也会变小,又或者也可以理解为函数的斜率在减小。
总的来说,二元函数的偏导数能够准确地描述某一点上切线的斜率,
也就是说该函数随着其中一个自变量的变化,另一自变量也有一定的
变化幅度。
同时,偏导数也可以用来进行函数处处可导性的判断,如
果偏导数不为0,那么该函数就是处处可导的。
偏导数的几何意义_概述说明以及解释

偏导数的几何意义概述说明以及解释1. 引言1.1 概述在数学分析和微积分中,偏导数是一个重要的概念。
它们被广泛应用于各个领域,如优化问题、几何体参数化与曲线拟合以及物理学中的场和流动问题等。
偏导数的几何意义不仅能帮助我们理解函数在给定点处的变化率,还能揭示函数曲面切平面方向和法线方向上的斜率。
1.2 文章结构本文将首先介绍偏导数的定义,然后深入探讨偏导数在几何上的含义。
接着,我们将讨论偏导数在实际问题中的应用场景,并对其进行详细说明。
最后,我们将解释常见的偏导数计算方法并推导其中涉及到的公式。
1.3 目的本文旨在帮助读者全面理解偏导数在几何上的意义,并能够应用于实际问题中。
通过阐述偏导数计算方法和公式推导过程,读者将获得更深入和全面的知识。
此外,本文还将总结关键观点并提出未来可能研究方向,为读者进一步探索奠定基础。
以上就是本文“1. 引言”部分的详细内容。
2. 偏导数的几何意义:2.1 偏导数的定义:在多元函数中,偏导数是指对于一个变量求导时,其他变量保持不变。
对于一个函数$f(x_1, x_2,...,x_n)$,它关于第$i$个自变量$x_i$的偏导数表示为$\frac{\partial f}{\partial x_i}$。
2.2 几何意义一: 曲面切平面方向的斜率:偏导数的一种几何意义是描述曲面在某一点处切平面的斜率。
具体来说,考虑一个二元函数$f(x,y)$,我们可以将其看作是一个曲面。
在这个曲面上取一点$(x_0,y_0,f(x_0,y_0))$,此时$x$轴和$y$轴为该点的坐标轴,而斜率为偏导数$\frac{\partial f}{\partial x}(x_0,y_0)$和$\frac{\partial f}{\partial y}(x_0,y_0)$所组成的向量就是切平面在该点上的法向量。
2.3 几何意义二: 曲面上某点法线方向的斜率:另一种几何意义是描述曲面上任意一点处法线方向(垂直于曲面)的斜率。
偏导数

偏 导 数
一、偏导数
二、偏导数几何意义
及与连续的关系 三、高阶偏导数 四、小结、思考题
一、偏导数的定义及其计算法
定义 设函数 z f ( x , y ) 在点 ( x0 , y0 ) 的某一邻 域内有定义,当 y 固定在 y0 而 x 在 x0 处有增量 x 时,相应地函数有增量 f ( x0 x, y0 ) f ( x0 , y0 ),
_______;
2.
z xy z e ( x y ), 则 x
z y
________.
2 2x csc , y y
2x 2x 2 csc y y
e xy ( xy x 2 1)
e ( xy y 1)
xy 2
f ( x0 x , y0 ) f ( x0 , y0 ) 如果 lim 存在,则称 x 0 x 此极限为函数 z f ( x , y )在点( x0 , y0 )处对 x
的偏导数,记为
zx z f , , x0 x x0 x x x y y y y
0 0
2 3
f x 0,1 , f x 1, 0 , f y 0, 2 , f y 2, 0 .
解: f
x y 2 x, f x 0,1 1, f x 1, 0 2;
f x 3 y2 , y
f y 0, 2 12,
f y 2, 0 2
三、高阶偏导数
设 z = f (x , y)在域 D 内存在连续的偏导数
z f x ( x, y ) , x
z f y ( x, y ) y
则称它们是z = f ( x , y ) 若这两个偏导数仍存在偏导数, 的二阶偏导数 . 按求导顺序不同, 有下列四个二阶偏导 数: 2 2 z z z z f x y ( x, y ) ( ) ( ) 2 f x x ( x, y ); y x x y x x x
偏导数的概念

1 t
x2 e 4t
2
2 5 x t 2
4
2 x e 4 t .
u 1 x t
x2 e 4t
x 2 2t
x2 3 1 2 4t t xe .
2u x
类似地,可定义函数z=f(x,y)在点(x0,y0)处对y的偏导数
为
z f ( x0 , y0 y ) f ( x0 , y0 ) lim . y ( x0 , y0 ) y0 y
又可记为
f , f y ( x0 , y0 )或z y ( x0 , y0 ). y ( x0 , y0 )
z=f(x,y)中,得z=f(x,y0),然后对x求导数fx(x,y0),再以
x=x0代入.两种做法是一致的.因为在这个过程中,y为
常数y0.
例1 求函数 f ( x, y ) x 2 2 xy y 2 在点(1,3)处对x和y的 偏导数.
解
f x ( x, y ) 2 x 2 y
z z 3 2 2 2 3 解 x 9 x y , 3x y 6 xy , y x
2 z 2z 2 2 3 3 x 18 xy , 6 xy 6 y , 2 xy x
2z 2 18 x y, 2 y
2z 3x 2 18 xy 2 . yx
V R , T P T V . P R
P V T RT R V RT 2 1. V T P VP V P R
偏导数的记号是个整体记号,不能看作分子与分
母之商,否则这三个偏导数的积将是1.这一点与一元 dy 函数导数记号 是不同的,dy 可看成函数的微分dy dx dx 与自变量微分dx之商.
偏导数几何意义(课资参考)

.
❖偏导数的符号
❖偏导函数
z x
x x0 y y0
,
f x
x x0 y y0
,
zx xx0 ,
y y0
fx(x0, y0) .
如果函数zf(x, y)在区域D内每一点(x, y)处对x的偏导数 都存在, 那么f(x, y)对x的偏导数是x、y的函数, 这个函数称为 函数zf(x, y)对x的偏导函数(简称偏导数), 记作
§8.2 偏 导 数
一、偏导数的定义及其计算法 二、高阶偏导数
一、偏导数的定义及其计算法
❖偏导数的定义
设函数zf(x, y)在点(x0, y0)的某一邻域内有定义, 若极限
lim f (x0 x, y0) f (x0, y0)
x0
x
存在, 则称此极限为函数zf(x, y)在点(x0, y0)处对x的偏导数, 记作
z , x
f , x
zx , 或 fx(x, y) .
一、偏导数的定义及其计算法
❖偏导数的定义
f x (x0,
y0)
lim
x0
f
(x0
x,
y0) x
f
(x0,
y0)
.
❖偏导数的符号
❖偏导函数
z x
x x0 y y0
,
f x
x x0 y y0
,
zx xx0 ,
y y0
fx(x0, y0) .
解 r
x
x r
y
y.
x x2 y2 z2 r y x2 y2 z2 r
❖偏导数的几何意义 fx(x0, y0)[ f(x, y0)]x是截线zf(x, y0)在点(x0, y0)处的切线Tx
偏导数几何意义

通过偏导数可以判断多元函数在某个区域内的单调性和极值情况。在隐函数中,偏导数可以帮助我们判断函数在某个 特定区域内的性质。
解决实际问题
偏导数在实际问题中有着广泛的应用,如经济学中的边际分析、物理学中的场论等。在隐函数中,偏导 数可以帮助我们解决一些实际问题,如求解曲线的切线方程、法线方程等。
THANKS
感谢观看
06
总结与展望
本次课程总结回顾
01
偏导数定义及计算
02
偏导数的几何意义
偏导数是一元函数导数的推广,反映 的是多元函数在某一点沿某一坐标轴 方向的变化率。通过本次课程,我们 深入理解了偏导数的定义,并掌握了 其计算方法。
偏导数在几何上表示空间曲面在某一 点处沿某一坐标轴方向的切线斜率。 这一几何意义为我们提供了直观理解 多元函数局部性质的工具。
性质。例如,在曲面上,切平面和法线可以用于定义曲面的定向、曲率
以及曲面上的测地线等概念。
03
偏导数与方向导数关系
方向导数定义及性质
方向导数定义
方向导数是函数在某一点沿某一方向的 变化率。对于二元函数$z = f(x, y)$,在 点$P(x_0, y_0)$处沿方向$l$(与$x$轴 正向夹角为$alpha$)的方向导数定义为 $lim_{rho to 0} frac{f(x_0 + Delta x, y_0 + Delta y) - f(x_0, y_0)}{rho}$,其 中$rho = sqrt{(Delta x)^2 + (Delta y)^2}$,$Delta x = rho cos alpha$, $Delta y = rho sin alpha$。
判断非极值点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏导数的物理几何意义
偏导数是多元函数微分学中的重要概念,它描述了函数在其中一点沿
着一些坐标轴的变化率。
在物理学中,偏导数有着重要的几何和物理意义。
以下是偏导数的物理几何意义的详细解释:
1.变化率:函数的一阶偏导数描述了函数在其中一点的变化率。
在物
理学中,这可以理解为物理量在该点的变化率。
例如,在空间中考虑一个
以时间t为参数的三维位置矢量函数r(t)=(x(t),y(t),z(t)),其中x、y
和z分别是位置矢量在x、y和z轴的分量。
三个分量的一阶偏导数分别
是x的速度、y的速度和z的速度,它们描述了位置矢量在每个轴上的变
化率。
2.切线和切平面:二元函数的两个偏导数代表了函数图像上的切线和
切平面。
在物理学中,这对于描述曲线和曲面的切线和切平面是非常重要的。
例如,在二维平面上考虑一个函数z=f(x,y),其中x和y是平面上
的坐标变量。
函数的偏导数∂z/∂x和∂z/∂y分别表示函数图像上的沿着x轴
和y轴方向的切线斜率。
这意味着我们可以借助偏导数来找到函数图像上
的切线和切平面,从而描述函数在其中一点的局部行为。
3. 法向量:在多元函数的高阶偏导数中,Hessian矩阵的特征向量
对应的特征值具有重要的物理和几何意义。
特别地,Hessian矩阵是一个
对称矩阵,它描述了函数图像局部的二次曲率信息。
Hessian矩阵的特征
向量对应的特征值是曲面在该点法向量的方向和曲率。
例如,在二维平面
上考虑一个函数z = f(x, y),其中x和y是平面上的坐标变量。
Hessian矩阵的特征向量对应的特征值描述了曲面在该点的法向量方向和
曲率大小,这对于描述曲面的形态和弯曲性质具有重要作用。
4.极值点:在多元函数中,偏导数可以帮助我们找到函数的极值点。
在物理学中,这对于优化和最优化问题的求解是非常重要的。
例如,考虑一个具有多个变量的能量函数E(x,y,z),其中x、y和z是能量函数的自变量。
函数的偏导数∂E/∂x,∂E/∂y和∂E/∂z可以帮助我们找到能量函数的极小值点,这在工程和科学应用中广泛用于优化问题和最优化算法。
综上所述,偏导数在物理学中有着重要的几何和物理意义。
它们描述了函数的变化率、切线和切平面、法向量、以及极值点等信息,对于描述物理过程、解决优化问题和研究几何性质等方面起着重要的作用。
