2011届山东省济宁市高三第一次模拟考试理科数学试题
2011年高考理科数学试题及详细答案(山东卷)

考点:指数函数的图像与性质。 专题:计算题。 分析:先将点代入到解析式中,解出a的值,再根据特殊三角函数值进 行解答. 解答:解:将(a,9)代入到y=3x中,得3a=9, 解得a=2. ∴ = .
故选D. 点评:对于基本初等函数的考查,历年来多数以选择填空的形式出现. 在解答这些知识点时,多数要结合着图象,利用数形结合的方式研究, 一般的问题往往都可以迎刃而解. 4.(2011•山东)不等式|x﹣5|+|x+3|≥10的解集是( ) A.[﹣5,7] B.[﹣4,6] C.(﹣∞,﹣ 5]∪[7,+∞) D.(﹣∞,﹣4]∪[6,+∞) 考点:绝对值不等式的解法。 专题:计算题。 分析:解法一:利用特值法我们可以用排除法解答本题,分别取x=0, x=﹣4根据满足条件的答案可能正确,不满足条件的答案一定错误,易 得到答案. 解法二:我们利用零点分段法,我们分类讨论三种情况下不等式的解, 最后将三种情况下x的取值范围并起来,即可得到答案. 解答:解:法一:当x=0时,|x﹣5|+|x+3|=8≥10不成立 可排除A,B 当x=﹣4时,|x﹣5|+|x+3|=12≥12成立 可排除C 故选D 法二:当x<﹣3时 不等式|x﹣5|+|x+3|≥10可化为:﹣(x﹣5)﹣(x+3)≥10 解得:x≤﹣4 当﹣3≤x≤5时 不等式|x﹣5|+|x+3|≥10可化为:﹣(x﹣5)+(x+3)=8≥10恒不成立 当x>5时 不等式|x﹣5|+|x+3|≥10可化为:(x﹣5)+(x+3)≥10 解得:x≥6 故不等式|x﹣5|+|x+3|≥10解集为:(﹣∞,﹣4]∪[6,+∞) 故选D 点评:本题考查的知识点是绝对值不等式的解法,其中利用零点分段法 进行分类讨论,将绝对值不等式转化为整式不等式是解答本题的关键. 5.(2011•山东)对于函数y=f(x),x∈R,“y=|f(x)|的图象关于y轴 对称”是“y=f(x)是奇函数”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条 件 D.既不充分也不必要条件
山东省济宁一中2011届高三第一次质量检测(数学理)

济宁市第一中学2011届高三教学质量第一次检测数学(理科)试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知函数()21f x x x =+-,集合(){}|M x x f x ==,(){}|N y y f x ==,则( )A .M N =B .M N ÝC .MN =∅D .M N Þ 2.命题2:,560p x R x x ∃∈-+<,则( )A .2:,560p x R x x ⌝∃∈-+≥ B .2:,560p x R x x ⌝∀∈-+<C .2:,560p x R x x ⌝∀∈-+>D .2:,560p x R x x ⌝∀∈-+≥3.已知函数()()32212f x ax a x =+-+,若1x =-是()y f x =的一个极值点,则a 的值为( )A .2-B .2C .27D .4 4.命题“若,p q ⌝则”是真命题,则下列命题一定是真命题的是( )A .若,p q 则B .若,p q ⌝则C .若,q p ⌝则D .若,q p ⌝⌝则5.将函数()lg 1y x =-的图像进行变换,使所得函数的图像与函数lg y x =的图像关于y 轴对称,这种变换是 ( )A .向左平移1个单位B . 向右平移1个单位C .向上平移1个单位D . 向下平移1个单位 6.若1122a a -<,则a 的取值范围是( )A .1a ≥B .0a >C .01a <<D .01a ≤≤7.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,那么函数解析式为2y x =,值域为{}1,4的“同族函数”共有( ) A . 7个 B . 8个C . 9个D . 10个8.设()f x 是定义在R 上以6为周期的函数,函数()f x 在()0,3上单调递减,且()y f x =的图像关于直线3x =对称,则下面结论中正确的是( )A . ()()()1.5 3.5 6.5f f f <<B . ()()()3.5 1.5 6.5f f f <<C . ()()()6.5 3.5 1.5f f f <<D . ()()()1.5 6.5 3.5f f f << 9.()203sin x x dx π+⎰是( )A .2318π+ B .2314π+ C . 2314π- D .2318π- 10.曲线313y x x =+在点41,3⎛⎫⎪⎝⎭处的切线与坐标轴围成的三角形的面积为( )A .19B .29C .13D .2311.给出下列四个命题,其中为真命题的为( )①“,x R ∃∈使得213x x +>”的否定是“,x R ∀∈都有213x x +≤”;②“2m =-”是“直线()210m x my +++=与直线()()2230m x m y -++-=相互垂直” 的必要不充分条件;③设圆()2222040x y Dx Ey F D E F ++++=+->与坐标轴有四个交点,分别为()()()()1212,0,,0,0,,0,A x B x C y D y ,则12120x x y y -=;④函数()sin f x x x =-的零点个数有3个. A .①④B .②④C . ①③D .②③12.设定义域为R 的函数()lg 1,10, 1x x f x x ⎧-≠⎪=⎨=⎪⎩,则关于x 的方程()()20f x bf x c ++=有7个不同实数解的充要条件 ( )A . 00b c <>且B .00b c ><且C .00b c <=且D .00b c ≥=且二、填空题:本大题共4小题,每小题4分,共16分.13.已知命题p :231x ->,命题q :()212log 50x x +-<,则p q ⌝⌝是的 _条件(填充分不必要条件、必要不充分条件、充要条件). 14.若对于任意[]1,1a ∈-,函数()()2442f x x a x a =+-+-的值恒大于零,则x 的取值范围是________. 15.已知命题:,p x R ∃∈使tan 1x =,命题2:320q x x -+<的解集是{}|12x x <<,下列结论:①命题“p q ∧”是真命题;②命题“p q ∧⌝”是假命题;③命题“p q ⌝∨”是真命题;④命题“p q ⌝∨⌝”是假命题;其中正确的为______.(只填序号即可)16. 已知函数()x f 的导函数为()x f ',且满足()()2'232xf x x f +=,则()=5'f .三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤17.(满分12分)已知函数()32log f x x =+,[]1,9x ∈,若函数()()()22g x f x f x =+⎡⎤⎣⎦(I )求函数()g x 的定义域; (Ⅱ)求函数()g x 的值域.18.(满分12分)已知a 是实数,函数2()()f x x x a =-.(Ⅰ)若(1)3f '=,求a 的值及曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)求()f x 在区间[]2,0上的最大值.19.(满分12分)设命题()2:431p x -≤;命题()()2:2110q x a x a a -+++≤,若⌝p是⌝q 的必要不充分条件,求实数a 的取值范围. 20.(满分12分)设某物体一天中的温度T 是时间t 的函数,已知32()(0)T t at bt ct d a =+++≠,其中温度的单位是℃,时间的单位是小时.中午12:00相应的0t =,中午12:00以后相应的t 取正数,中午12:00以前相应的t 取负数(如早上8:00相应的t =-4,下午16:00相应的t =4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.(I )求该物体的温度T 关于时间t 的函数关系式;(II )该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?21.(满分12分)对于函数()f x ,若()f x x =,则称x 为()f x 的“不动点”;若()f f x x=⎡⎤⎣⎦则称x 为()f x 的“稳定点”函数()f x 的“不动点”和“稳定点”的集合分别记为A 和B ,即(){}|A x f x x ==,(){}|B x f f x x ==⎡⎤⎣⎦. (Ⅰ) 求证:A B ⊆;(Ⅱ)若()()21,f x ax a x R =-∈,且A B =≠∅,求实数a 的取值范围.22.(满分14分)已知函数()b f x ax c x=++(),,a b c 是常数是奇函数且满足()512f =,()1724f =. (Ⅰ)求a 、b 、c 的值;(Ⅱ)是判断函数()f x 在10,2⎛⎫⎪⎝⎭上的单调性并说明理由;(Ⅲ)试求函数()f x 在()0,+∞上的最小值.参考答案一、选择题 DDBCA,CCBAA,CC二、填空题 13.充分不必要;14.3x >或1x <;15.①②③④;16.6 三、解答题17.解:(1)函数()()()22g x f x f x=+⎡⎤⎣⎦满足21919x x ≤≤⎧⎨≤≤⎩,…………………………2分 解得13x ≤≤,即函数()()()22g x f x f x =+⎡⎤⎣⎦的定义域为[]1,3………………4分(2)[]1,3x ∈,[]3log 0,1x ∴∈………………………………………………………5分()()()22g x f x f x =+⎡⎤⎣⎦()22332log 2log x x =+++ 233log 6log 6x x =++()23log 33x =+-…………………………………………9分当3log 0x =时, ()min 6g x =,当3log 1x =时, ()max 13g x =,………………11分 即函数()g x 的值域为[]6,13.………………………………………………………12分18.(Ⅰ)()232f x x ax '=-,由'(1)3f =易得a =0,从而可得曲线()y f x =在(1,(1))f 处的切线方程为320.x y --= …………………………………………………………4分(Ⅱ)先求出可能的极值点x 1=0,x 2=23a ,再讨论极值点与区间[0,2]端点的位置关系.令'()0f x =,得1220,3ax x ==. 当20,3a≤即0a ≤时,()f x 在[0,2]上单调递增, max ()(2)84f x f a ==-;…6分 当22,3a≥即3a ≥时,()f x 在[0,2]上单调递减, max ()(0)0f x f ==;……8分 当202,3a <<即03a <<时,()f x 在2[0,]3a 上单调递减,在2[,2]3a上单调递增,函数f (x )(0≤ x ≤2)的最大值只可能在x =0或x =2处取到,因为f (0)=0,f (2)=8-4a ,令f (2) ≥ f (0),得a ≤ 2,所以max 84,02;()0,2 3.a a f x a -<≤⎧=⎨<<⎩…………11分 综上,max84,2;()0, 2.a a f x a -≤⎧=⎨>⎩……………………………………………………12分 19. 解:由p 得1431x -≤-≤,所以112x ≤≤,...............................3分 由q 得1a x a ≤≤+,......................................................6分 又因p ⌝是q ⌝的必要非充分条件,所以p 是q 的充分非必要条件,..............8分所以1211a a ⎧≤⎪⎨⎪+>⎩或1211a a ⎧<⎪⎨⎪+≥⎩,解得102a ≤≤.................................12分 20.(满分12分)解:(1) 因为232T at bt c '=++,而()()44T T ''-=, 故488488a b c a b c ++=-+,∴ ()()()106004641648315860488488a T d b T a b c d c T a b c d d a b c a b c=⎧==⎧⎪⎪=-=-+-+=⎪⎪⇒⎨⎨=-=+++=⎪⎪⎪⎪=++=-+⎩⎩ . ∴()3360(1212)T t t t t =-+-≤≤.……………………………………………6分(2) 233T t '=-, 由 ()011T t t t '==-=得或 当t 在]2,2[-上变化时,()()T t T t '与的变化情况如下表:由上表知当62)(21取到最大值时或t T t t =-=,答:在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.............12分 21. (1)证明:当A φ=显然成立,当A φ≠时,对0x A ∀∈,有()00f x x =成立,所以()()000f f x f x x ==⎡⎤⎣⎦,即0x B ∈,所以A B ⊆..........................4分 (2)由()f f x x =⎡⎤⎣⎦得()221a ax x -=,即3422210a x a x a x -+--=又因A=B ,所以342221a x a x a x -+--可分解为()()22211ax x a x ax a --+-+并且方程2210a x ax a +-+=与210ax x --=有相同的根或无实根............8分 当0a =时,{}1A B ==-,显然成立,当0a ≠时, 由2210a x ax a +-+=得2110ax x a++-=,显然不可能与方程210ax x --=有相同的根,所以11410a a ⎛⎫--<⎪⎝⎭,解得34a <又方程210ax x --=有实根,所以140a +≥,解得14a ≥- 所以1344a -≤<且0a ≠ 综上所述, 1344a -≤<.................................................12分.22.解:(1)函数()f x 是奇函数,∴()()0f x f x -+=,即 0bb axc ax c x x--++++=,0c ∴=.由()512f =,()1724f =,得52a b +=,17224b a +=,解得12,2a b ==. ∴12,,02a b c ===..................................................4分 (2)由(1)得,()122f x x x =+, ()'2122f x x =-,当10,2x ⎛⎫∈ ⎪⎝⎭时,21022x <<,则2122x >.∴()'0f x <,函数()f x 在10,2⎛⎫⎪⎝⎭上为减函数.............................8分(3)由()'21202f x x =-=,0x >,得12x =.当12x >时,2122x <,∴()'0f x >,即函数()f x 在1,2⎛⎫+∞ ⎪⎝⎭上为增函数.又由(2)知12x =处是函数的最小值点, 即函数()f x 在()0,+∞上的最小值为122f ⎛⎫= ⎪⎝⎭...................14分。
济宁市2011年高中阶段学校招生考试数学试题及答案(word版)

☆绝密级 试卷类型A济宁市二○一一年高中阶段学校招生考试数 学 试 题注意事项:1.本试题分第Ⅰ卷和第Ⅱ卷两部分,共10页.第Ⅰ卷2页为选择题,30分;第Ⅱ卷8页为非选择题,70分;共100分.考试时间为120分钟.2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上. 每题选出答案后,都必须用2B 铅笔把答题卡上对应题目的答案标号(ABCD)涂黑,如需改动,必须先用橡皮擦干净,再改涂其他答案.3.答第Ⅱ卷时,将密封线内的项目填写清楚,并将座号填写在第8页右侧,用钢笔或圆珠笔直接答在试卷上.考试结束,试题和答题卡一并收回.第I卷(选择题 共30分)一、选择题(下列各题的四个选项中,只有一顶符合题意,每小题3分,共30分) 1. 计算-1-2的结果是A. -1B.1C.-3D.3 2. 下列等式成立的是A.532a a a =+ B.a a a =-23C .632a a a =∙ D.632)(a a = 3. 如果一个等腰三角形的两边长分别是5 cm ,6 cm ,那么此三角形的周长是A. 15 cmB. 16 cmC. 17 cmD. 16 cm 或17 cm 4. 下列计算正确的是A 5=B .2=C.= D .2= 5. 已知关于x 方程02=++a bx x 有一个根是)0(≠-a a ,则a-b 的值为A .-1B .0C .1D .2 6.已知//AE BD ,∠1=120o,∠2=40o,则∠C 的度数是A.10 ºB.20 ºC.30 ºD.40 º7.在2x □2xy □2y 的空格□中,分别填上“+”或“﹣”,在所得的代数式中,能构成完全平方式的概率是A. 1B.34 C. 12 D. 148..已知二次函数2y ax bx c =++中,其函数y 与自变量x 之间的部分对应值如下表所示:x… 0 1 2 3 4 … y…4114…点A (1x ,1y )、B (2x ,2y )在函数的图象上,则当112x <<,234x <<时,1y 与2y 的大小关系正确的是A .12y y >B .12y y < C. 1y ≥2yD .1y ≤2y9. 如图,△ABC 的周长为30cm ,把△ABC 的边AC 对折,使顶点A 和C 重合,折痕交BC 边于点D ,交AC 边于点E ,AE =4 cm ,连接AD ,则△ABD 的周长是 A .22cm B. 20cm C. 18cm D. 15cm 10. 如图,是某几何体的三视图及相关数据,则下面判断正确是 A. a >c B. b >c C. a 2+4b 2=c 2D. a 2+b 2=c 2第9☆绝密级试卷类型A济宁市二○一一年高中阶段学校招生考试数学试题第Ⅱ卷(非选择题共70分)二、填空题(每小题3分,共15分;只要求填写最后结果)11. 反比例函数xmy1-=的图象在第一、三象限,则m的取值范围是 .12. 将二次函数245y x x=-+化为2()y x h k=-+的形式,则y= .13. 如图,在Rt△ABC中,∠C=90º,∠A=60º,BC=4 cm,以点C为圆心,以3 cm的长为半径作圆,则⊙C与AB的位置关系是.14. 如图,观察每一个图中黑色正六边形的排列规律,则第10个图中黑色正六边形有个.15. 如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD BE=,AE与CD交于点F,AG CD⊥于点G,则=AFFG.第1个图第2个图第3个图…DCAFBEG三、解答题(共55分,解答应写出文字说明、证明过程或推演步骤) 16.(5分)计算:22()a b ab b a a a--÷- 17.(5分)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作直线EF ⊥BD ,分别交AD 、BC 于点E 和F. 求证:四边形BEDF 是菱形.18.(6分)日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估.如图,上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°方向,海检船以21海里/时的速度向正北方向行驶,下午2时海检船到达B 处,这时观测到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P 的距离?(参考数据:331212 sin36.9,tan36.9,sin67.5,tan67.554135≈≈≈≈)19.(6分)某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的出甲、乙、丙三人.投票结果统计如图一:其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:图二是某同学根据上表绘制的一个不完整的条形图。
高考理科数学试题及详细答案山东卷

2011 年一般高等学校招生全国一致考试 ( 山东卷 )理科数学第 I 卷(共 60 分)一 . 选择题:本大题共 12 小题,每题5 分,共 60 分。
在每题给出的四个选项中,只有一项为哪一项切合题目要求的。
1.( 2011?山东)设会合 2)M={x|x +x ﹣ 6< 0} , N={x|1 ≤x ≤3} ,则 M ∩N=(A .[1, 2)B .[1, 2]C .( 2, 3]D .[2, 3]2.( 2011?山东)复数 z=( i 是虚数单位)在复平面内对应的点位于象限为()A .第一象限B .第二象限C .第三象限D .第四象限3.( 2011?山东)若点( a , 9)在函数y=3x的图象上,则 tan 的值为()A .0B .C . 1D .4.( 2011?山东)不等式 |x ﹣ 5|+|x+3| ≥10 的解集是()A .[﹣ 5, 7]B .[ ﹣4, 6]C .(﹣ ∞,﹣ 5]∪ [7, +∞)D .(﹣ ∞,﹣ 4]∪ [6, +∞)5.( 2011?山东)对于函数y=f ( x ),x ∈ R , “y=|f ( x ) |的图象对于 y 轴对称 ”是 “y=f ( x )是奇函数 ”的()A .充足而不用要条件B .必需而不充足条件C .充要条件D .既不充足也不用要条件6.( 2011?山东) 若函数 f ( x )=sin ωx ( ω> 0)在区间 上单一递加, 在区间上单一递减, 则 ω=()A .8B . 2C .D .7.( 2011?山东)某产品的广告花费x 与销售额 y 的统计数据以下表 广告花费 x (万元) 4 2 3 5 销售额 y (万元) 49263954依据上表可得回归方程中的 为,据此模型预告广告花费为6 万元时销售额为()A .63.6 万元B .65.5 万元C . 67.7 万元D .72.0 万元8.( 2011?山东)已知双曲线=1( a > 0,b > 0)的两条渐近线均和圆C : x 2+y 2﹣ 6x+5=0 相切,且双曲线的 右焦点为圆 C 的圆心,则该双曲线的方程为()A .B .=1C .=1 D . =19.( 2011?山东)函数 的图象大概是( )1A .B.C.D .10.( 2011?山东)已知 f( x)是 R 上最小正周期为 2 的周期函数,且当0≤x< 2 时, f ( x)=x 3﹣x,则函数y=f (x)的图象在区间 [0, 6]上与 x 轴的交点的个数为()A .6B. 7C. 8D. 911.(2011?山东)如图是长和宽分别相等的两个矩形.给定以下三个命题:① 存在三棱柱,其正(主)视图、俯视图以以下图;② 存在四棱柱,其正(主)视图、俯视图以以下图;③ 存在圆柱,其正(主)视图、俯视图以以下图.此中真命题的个数是()A .3B. 2C. 1D. 012.(2011?山东)设 A ,A ,A,A4是平面直角坐标系中两两不一样的四点,若(λ∈ R),123(μ∈ R),且,则称 A 3, A 4调解切割 A 1,A 2,已知点 C( c, 0),D ( d, O)( c, d∈R)调解切割点 A ( 0, 0), B( 1,0),则下边说法正确的选项是()A .C 可能是线段 AB 的中点 B .D 可能是线段 AB 的中点C.C, D 可能同时在线段AB 上D .C, D 不行能同时在线段AB 的延伸线上第 II卷(共90分)2二、填空题:本大题共 4 小题,每题 4 分,共 16 分.13.( 2011?山)行如所示的程序框,入l=2 , m=3, n=5 ,出的y 的是_________.14.( 2011?山)若( x)6式的常数60,常数 a 的_________.15.( 2011?山)函数 f ( x) =(x>0),察:1,f (x) =f ( x)=f 2(x) =f ( f1( x))=,f 3(x) =f ( f2( x))=,f 4(x) =f ( f3( x))=,⋯依据以上事,由推理可得:当 n∈ N* 且 n≥2 , f n( x) =f ( f n﹣1( x)) = _________.16.( 2011?山)已知函数f( x)=log a x+x b( a>0,且 a≠1).当 2< a< 3< b< 4 ,函数 f( x)的零点 x0∈( n,*三、解答(共 6 小,分74 分)17.( 2011?山)在ABC 中,内角 A , B ,C 的分a, b, c,已知(Ⅰ )求的;(Ⅱ)若,b=2,求△ ABC的面S.318.( 2011?山东)红队队员甲、乙、丙与蓝队队员 A 、B 、 C 进行围棋竞赛,甲对 A ,乙对 B,丙对 C 各一盘,已知甲胜 A ,乙胜 B,丙胜 C 的概率分别为,,,假定各盘竞赛结果互相独立.(Ⅰ )求红队起码两名队员获胜的概率;(Ⅱ)用ξ表示红队队员获胜的总盘数,求ξ的散布列和数学希望Eξ.19.( 2011?山东)在以下图的几何体中,四边形 ABCD 为平行四边形,∠ ACB=90 °,EA ⊥平面 ABCD ,EF∥ AB ,FG∥ BC ,EG∥ AC . AB=2EF .(Ⅰ)若 M 是线段 AD 的中点,求证:GM ∥平面 ABFE ;(Ⅱ)若 AC=BC=2AE ,求平面角 A ﹣ BF﹣ C 的大小.20.( 2011?山东)等比数列 {a n} 中. a1,a2,a3分别是下表第一、二、三行中的某一个数.且a1?a2?a3中的任何两个数不在下表的同一列.第一列第二列第三列第一行3210第二行6414第三行9818(Ⅰ)求数列 {a n} 的通项公式;(Ⅱ)如数列 {b n} 知足 b n=a n+(﹣ 1)lna n,求数列b n的前 n 项和 s n.21.( 2011?山东)某公司拟建筑以下图的容器(不计厚度,长度单位:米),此中容器的中间为圆柱形,左右两端均为半球形,依据设计要求容器的体积为立方米,且l≥2r.假定该容器的建筑花费仅与其表面积相关.已知圆柱形部分每平方米建筑花费为 3 千元,半球形部分每平方米建筑花费为c(c> 3)千元.设该容器的建筑花费为y 千元.(Ⅰ)写出 y 对于 r 的函数表达式,并求该函数的定义域;(Ⅱ)求该容器的建筑花费最小时的r.22.( 2011?山东)已知直线 l 与椭圆 C:交于 P( x1,y1),Q( x2,y2)两不一样点,且△ OPQ 的面积 S△OPQ=,此中 O 为坐标原点.(Ⅰ)证明 x12+x 22和 y12+y 22均为定值;(Ⅱ)设线段 PQ 的中点为 M ,求 |OM|?|PQ|的最大值;(Ⅲ)椭圆 C 上能否存在点 D,E,G,使得 S△ODE=S△ODG=S△OEG=?若存在,判断△ DEG 的形状;若不存在,请说明原因.42011 年一般高等学校招生全国一致考试( 山东卷 )理科数学参照答案与试题分析一 . 选择题:本大题共12 小题,每题5 分,共 60 分。
高三数学第一次模拟考试理济宁市一模,含解析新人教A版

济宁市高三模拟考试数学(理工类)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部份,满分l50分,考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回.注意事项:1.答第I 卷前,考生务必将自己的姓名,考号填写在答题卡上2.选择题答案利用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号,非选择题答案利用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚.参考公式:若是事件A 、B 互斥,那么P(A+B)=P(A)+P(B). 若是事件A 、B 独立,那么P(A·B)=P(A)·P(B). 第I 卷(选择题共60分)一、选择题:本大题共l2小题.每小题5分。
共60分.在每小题给出的四个选项中。
只有一项是符合题目要求的. 1.复数2=()1ii z -,则复数1z +在复平面上对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限 【答案】D【解析】221z=()122i i i ii==---,所以1112z i +=-,对应点位1(1,)2-,选D.2.已知全集U=R ,集合A={2(+1)y |y ln x ,x R =∈},集合B={21x ||x |-≤},则如图所示的阴影部份表示的集合是A .{01>3x |x x ≤<或}B .{|0<1x x ≤}C .{|>3x x }D .{|13x x ≤≤} 【答案】A【解析】2A={(+1)}0y|y ln x ,x R {y y }=∈=≥,{13}B x x =≤≤,图中阴影部份为集合()U AB ,所以{1>3}UB x x x =<或,所以(){01>3}U A B x x x =≤<或,选A.3.下列命题中正确的有①设有一个回归方程y =2—3x ,变量x 增加一个单位时,y 平均增加3个单位;②命题P :“2000,--1>0x R x x ∃∈”的否定⌝P :“,102x R x -x-∀∈≤”;③设随机变量X 服从正态散布N(0,1),若P(X>1)=p ,则P(-1<X<0)=12-p ; ④在一个2×2列联表中,由计算得k 2=6.679,则有99%的把握确认这两个变量间有关系. A .1个 B .2个 C .3个 D .4个 本题可以参考独立性查验临界值表【答案】C【解析】①变量x 增加一个单位时,y 平均减少3个单位,所以错误。
济宁一中届模拟检测一理科数学试题目

济宁一中届模拟检测一理科数学试题目济宁一中2011届第一次模拟测试 数学(理)试题 2011.3一、选择题(本题共12小题,每题5分,共60分) 1.计算:=--+ii i 21)1)(2(2(A )2 (B )2- (C )2i(D )2i -2.已知a 、b 为直线,α、β为平面.在下列四个命题中, ① 若a ⊥α,b ⊥α,则a ∥b ; ② 若 a ∥α,b ∥α,则a ∥b ;③ 若a ⊥α,a ⊥β,则α∥β; ④ 若α∥b ,β∥b ,则α∥β.正确命题的个数是 (A) 1 (B) 3(C) 2 (D) 0 3.已知函数()()01f x x ≤≤的图象的一段圆弧(如图所示)1201x x<<<则(A )1212()()f x f x x x < (B )1212()()f x f x x x =(C )1212()()f x f x x x > (D )前三个判断都不正确4.将4名司机和8名售票员分配到四辆公共汽车上,每辆车上分别有1名司机和2名售票员,则可能的分配方案种数是 (A)4444242628A A CC C (B)44242628A A A A(C)44242628A CC C(D)242628C C C5.有下列四个命题:1p :若0a b ⋅=,则一定有a b ⊥; 2p : ∃x 、y ∈R, sin(x-y)=sinx-siny; 3p : (0,1)(1,)a ∀∈+∞,函数12()1xf x a-=+都恒过定点⎪⎭⎫⎝⎛2,21; 4p :方程220xy Dx Ey F ++++=表示圆的充要条件是2240D E F +-≥.其中假命题的是(A)1p ,4p (B)2p ,4p (C )1p ,3p(D) 2p ,4p6.定义在R 上的偶函数f (x )在[)∞+,0上递增,0)31(=f ,则满足)(log 81x f >0的x 的取值范围是(A)()∞+,0 (B)()∞+⎪⎭⎫ ⎝⎛,221,0 (C)⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛2,2181,0 (D) ⎪⎭⎫ ⎝⎛21,07.右图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积约(A)523 (B)521(C )519 (D)5168.将一张坐标纸折叠一次,使点(10,0)与(-6,8)重合,则与点(-4,2)重合的点是(A ) (4,-2) (B ) (4,-3) (C ) (3, 23) (D ) (3,-1) 9.平面上有四个互异的点A 、B 、C 、D ,满足(AB-BC )·(AD -CD )=0,则三角形ABC 是(A )直角三角形 (B ) 等腰三角形(C ) 等腰直角三角形(D ) 等边三角形10.已知函数f (x )的图象过点(0,-5),它的导数'()f x =4x 3-4x ,则当f (x )取得最大值-5时,x 的值应为(A) -1 (B) 0 (C) 1 (D) ±111.要测量底部不能到达的电视塔AB 的高度,在CA点测得塔顶A 的仰角是45°,在D 点测得塔顶A 的仰角是30°,并测得水平面上的∠BCD =120°,CD =40m,则电视塔的高度为(A)102m (B)20m (C )203m (D)40m12.已知函数f(x)=x9x3m ⋅-+m+1对x ∈(0,∞+)的图象恒在x 轴上方,则m 的取值范围是 (A ) 2-22<m <2+22 (B ) m <2 (C)m<2+22(D ) m ≥2+22二、填空题(本题共4小题,每题4分,共16分)13.观察下列各式9-1=8,16-4=12,25-9=16,36-16=20…,这些等式反映了自然数间 的某种规律,设n 表示自然数,用关于n 的等式表示为 .14. 如图,正六边形ABCDEF 的两个顶点A 、D 为椭圆的两个焦点,其余4个顶点在椭圆上,则该椭圆的离心率为____________________.ADFECB15.一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,测的刹车后t 秒内列车前进的距离为2270.45S t t =-米,则列车刹车后 秒车停下来,期间列车前进了 米.16.执行右边的程序框图,输出的T 为( )三、解答题(本题共6小题,共74分) 17. ( 本题满分12分 ) 已知函数否 是 ?f x x x x x()cos sin cos sin =--442(1)求f x ()的最小正周期;(2)若x ∈⎡⎣⎢⎤⎦⎥02,π,求f x ()的最大值,最小值.18. ( 本题满分12分 )某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,遇到红灯时停留的时间都是2min. (1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;(2)求这名学生在上学路上因遇到红灯停留的总时间ξ的分布列及期望.19.( 本题满分12分 )已知)0(3,2)(,≥x x f x 成等差数列.又数列,3,)0}({1=>a a a n n 中此数列的前n 项的和S n (+∈N n )对所有大于1的正整数n 都有)(1-=n nS f S . (1)求数列}{na 的第n+1项;(2)若nn n a a b 1,11+是的等比中项,且T n 为{b n }的前n 项和,求T n.20. ( 本题满分12分 )如图,已知直角梯形ABCD 的上底2BC =,1//,2BC AD BC AD =,CD AD ⊥,平面PDC ⊥平面ABCD ,PCD∆是边长为2的等边三角形。
数学_2011年山东省某校高考数学一模试卷(理科)_(含答案)

2011年山东省某校高考数学一模试卷(理科)一、选择题(共12小题,每小题5分,满分60分) 1. 设全集为R ,集合A ={x|1x ≤1},则∁R A =( )A {x|0≤x <1}B {x|0<x ≤1}C {x|0<x <1}D {x|x ≥1或x <0} 2. (1+2i2−i )2011=( )A 1B −1C iD −i3. 某程序框图如图所示,该程序运行后输出的k 的值是( )A 4B 5C 6D 74. 已知sinθ=45,sinθ−cosθ>1,则sin2θ=( ) A −2425 B −1225 C −45 D 24255. 定义在R 上的偶函数f(x)在[0, +∞)上递增,f(13)=0,则满足f(log 18x)>0x 的取值范围是( )A (0,12)∪(2,+∞) B (0, +∞) C (0,18)∪(12,2) D (0,12)6. 公差不为零的等差数列{a n }中,a 2,a 3,a 6成等比数列,则其公比q 为( ) A 1 B 2 C 3 D 47. 某教师一天上3个班级的课,每班开1节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5节和第6节不算连上),那么这位教师一天的课表的所有排法有( )A 474种B 77种C 462种D 79种8. 已知向量a →=(x −1,2),b →=(4,y),若a →⊥b →,则9x +3y 的最小值为( ) A 2√3 B 6 C 12 D 3√29. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积是( ) A 12π B 4√3π C 3π D 12√3π 10. 已知双曲线x 2−y 22=1的焦点为F 1、F 2,点M 在双曲线上且MF 1→⋅MF 2→=0,则点M 到x轴的距离为( ) A 43B 53C2√33D √311. 点P 是曲线x 2−y −2ln √x =0上任意一点,则点P 到直线4x +4y +1=0的最小距离是( )A √22(1−ln2) B √22(1+ln2) C √22(12+ln2) D 12(1+ln2)12. 设实数x ,y 满足约束条件{x −y −2≤0x +2y −5≥0y ≤2,则u =2xyx 2+y 2的取值范围是( )A [310,1) B [12,1] C [310,12] D [35,1]二、填空题(共4小题,每小题4分,满分16分)13. 已知(ax −√x)9的展开式中x 3的系数为9,则常数a 的值为________.14. 已知数列{a n }满足a 1=23,且对任意的正整数m ,n 都有a m+n =a m ⋅a n ,若数列{a n }的前n 项和为S n ,则S n =________.15. 不等式|x −1|<1表示的平面区域落在抛物线y 2=4x 内的图形的面积是________. 16. 下列命题中:(1)α=2kπ+π3(k ∈Z)是tanα=√3的充分不必要条件; (2)函数f(x)=|2cosx −1|的最小正周期是π;(3)△ABC 中,若cosAcosB >sinAsinB ,则△ABC 为钝角三角形;(4)若a +b =0,则函数y =asinx −bcosx 的图象的一条对称轴方程为x =π4; 其中是真命题的为________.三、解答题(共6小题,满分74分)17. 已知函数f(x)=sin2x +acos 2x (a ∈R ,a 为常数),且π4是函数y =f(x)的零点.(1)求a 的值,并求函数f(x)的最小正周期;(2)若x ∈[0, π2],求函数f(x)的值域,并写出f(x)取得最大值时x 的值.18. 某考生参加2011年大学自主招生考试,面试时从两道数学题,一道物理题,一道化学题中任选两道回答,该考生答对每一道数学题、物理题、化学题的概率依次为0.9,0.8,0.7,(1)求该考生恰好抽到两道数学题并都答对的概率;(2)求该考生在这次面试中答对试题个数X 的分布列和数学期望.19. 如图,四棱锥P −ABCD 中,AB ⊥AD ,CD ⊥AD ,PA ⊥底面ABCD ,PA =AD =CD =2AB =2,M 为PC 的中点. (1)求证:BM // 平面PAD ;(2)在平面PAD 内找一点N ,使MN ⊥平面PBD ,并求直线PC 与平面PBD 所成角的 正弦值.20. 已知抛物线方程C:y 2=2px(p >0),点F 为其焦点,点N(3, 1)在抛物线C 的内部,设点M 是抛物线C 上的任意一点,|MF →|+|MN →|的最小值为4. (1)求抛物线C 的方程;(2)过点F 作直线l 与抛物线C 交于不同两点A 、B ,与y 轴交于点P ,且PF →=λ1FA →=λ2FB →,试判断λ1+λ2是否为定值?若是定值,求出该定值并证明;若不是定值,请说明理由. 21. 已知数列{a n }中,a 1=2,a n −a n−1−2n =0(n ≥2, n ∈N). (1)写出a 2、a 3的值(只写结果)并求出数列{a n }的通项公式; (2)设b n =1a n+1+1a n+2+1a n+3+⋯+1a 2n,若对任意的正整数n ,当m ∈[−1, 1]时,不等式t 2−2mt +16>b n 恒成立,求实数t 的取值范围.22. 已知向量p →=(a −3,x),q →=(x +a,x),f(x)=p →⋅q →,且m ,n 是方程f(x)=0的两个实根,(1)设g(a)=m 3+n 3+a 3,求g(a)的最小值;(2)若不等式lnx −bx <x 2在x ∈[1, +∞)上恒成立,求实数b 的取值范围;(3)对于(1)中的函数y =g(a),给定函数ℎ(x)=c(xlnx −x 3),(c <0),若对任意的x 0∈[2, 3],总存在x 1∈[1, 2],使得g(x 0)=ℎ(x 1),求实数c 的取值范围.2011年山东省某校高考数学一模试卷(理科)答案1. A2. D3. A4. A5. A6. C7. A8. B9. C10. C11. B12. D13. 114. 2−2n+13n15. 16√2316. (1)(3)(4)17. 解:(1)由于π4是函数y=f(x)的零点,即x=π4是方程f(x)=0的解,从而f(π4)=sinπ2+acos2π4=0,则1+12a=0,解得a=−2.所以f(x)=sin2x−2cos2x=sin2x−cos2x−1,则f(x)=√2sin(2x−π4)−1,所以函数f(x)的最小正周期为π.(2)由x∈[0, π2],得2x−π4∈[−π4, 3π4],则sin(2x−π4)∈[−√22, 1],则−1≤√2sin(2x−π4)≤√2,−2≤√2sin(2x−π4)−1≤√2−1,∴ 值域为[−2, √2−1].当2x−π4=2kπ+π2(k∈Z),即x=kπ+38π时,f(x)有最大值,又x∈[0, π2],故k =0时,x =38π,f(x)有最大值√2−1.18. 解:(1)该考生恰好抽到两道数学题并都答对的概率P =C 22C 42×0.9×0.9=0.135(2)X 的可能取值为0,1,2P(x =0)=0.1×0.1+0.2×0.3+2(0.1×0.3+0.1×0.2)C 42=17600P(x =2)=0.9×0.9+0.8×0.7+2(0.9×0.7+0.9×0.8)C 42=407600 P(x =1)=1−17600−407600=176600E(X)=20=1.65 19. 证明:(1)取PD 的中点E ,连接EM ,EA ,则EM // AB ,且EM =AB 所以四边形ABME 为平行四边形,所以BM // AE又AE ⊂平面PAD ,BM 不在平面PAD 内,∴ BM // 平面PAD ; 解:(2)以A 为原点,AB ,AD ,AP 分别为x ,y ,z 轴,建立空间直角坐标系 则B(1, 0, 0),C(2, 2, 0),D(0, 2, 0),P(0, 0, 2),M(1, 1, 1),E(0, 1, 1)假设存在满足题意的点,则在平面PAD 内,设N(0, y, z)MN →=(−1,Y −1,Z −1),PB →=(1,0,−2),DB →=(1,−2,0){MN →⋅DB →=0˙,得y =12,z =12,所以N =(0,12,12),即N 是AE 的中点,此时MN ⊥平面PBD , 设直线PC 与平面PBD 所成的角为θ, 易得PC →=(2,2,−2),MN →=(−1,−12,−12) 设PC →与MN →的夹角为α,则cosα=|PC →||MN →|˙=−√23,sinθ=−cosα=√23故直线PC 与平面PBD 所成角的正弦值为√2320. 解:(1)准线方程为l :x =−p2,点M 到l 的距离设为d ,由抛物线定义,|MF →|+|MN →|=d +|MN →|≥3+p2=4,p =2,所以y 2=4x . (2)设A(x 1, y 1),B(x 2, y 2),F(1, 0)由题意知直线l 的斜率k 存在且不等于0, 设l:y =k(x −1),则P(0, −k),由PF →=λ1FA →=λ2FB →知(1, k)=λ1(x 1−1, y 1)=λ2(x 2−1, y 2)∴ k =λ1y 1=λ2y 2∵ k ≠0,∴ λ1=k y 1,λ2=ky 2,λ1+λ2=k ×y 1+y 2y 1y 2,将y =k(x −1)代入y 2=4x 得y 2−4k y −4=0,y 1+y 2=4k,y 1⋅y 2=−4∴y 1+y 2y 1y 2=−4k×14=−1k,∴ λ1+λ2=k ×(−1k)=−1为定值.21. 解:(1)∵ a 1=2,a n −a n−1−2n =0(n ≥2, n ∈N)∴ a 2=6,a 3=12当n ≥2时,a n −a n−1=2n ,a n−1−a n−2=2(n −1),…,a 3−a 2=2×3,a 2−a 1=2×2,∴ a n −a 1=2[n +(n −1)+...+3+2], ∴ a n =2[n +(n −1)+⋯+3+2+1]=2n(n+1)2=n(n +1)当n =1时,a 1=1×(1+1)=2也满足上式, ∴ 数列{a n }的通项公式为a n =n(n +1) (2)b n =1a n+1+1a n+2++1a 2n=1(n+1)(n+2)+1(n+2)(n+3)++12n(2n+1)=1(n+1)−1(n+2)+1(n+2)−1(n+3)++12n −1(2n+1)=1(n+1)−1(2n+1)=n2n 2+3n+1=1(2n+1n)+3令f(x)=2x +1x (x ≥1),则f′(x)=2−1x 2,当x ≥1时,f ′(x)>0恒成立 ∴ f(x)在x ∈[1, +∞)上是增函数,故当x =1时,f(x)min =f(1)=3 即当n =1时,(b n )max =16要使对任意的正整数n ,当m ∈[−1, 1]时,不等式t 2−2mt +16>b n 恒成立,则须使t 2−2mt +16>(b n )max =16,即t 2−2mt >0,对∀m ∈[−1, 1]恒成立,∴ {t 2−2t >0t 2+2t >0,解得,t >2或t <−2,∴ 实数t 的取值范围为(−∞, −2)∪(2, +∞) 22. 解:(1)f(x)=x 2+(a −3)x +a 2−3a 有两个实根, 所以△≥0,解得a ∈[−1, 3] 由题意{m +n =3−amn =a 2−3ag(a)=m 3+n 3+a 3=(m +n)[(m +n)2−3mn]+a 3=3a 3−9a 2+27,a ∈[−1, 3] g′(a)=9a(a −2)=0,解得a =0或2 g(0)=g(3)=27,g(−1)=g(2)=15 所以最小值为15.(2)若不等式lnx −bx <x 2在x ∈[1,+√∞)上恒成立,即x 2−lnx +bx >0恒成立,解得b>x(lnx−x2)令ℎ(x)=x(lnx−x2),x∈[1, +∞)则ℎ′(x)=1+lnx−3x2,x∈[1, +∞)−6x,x∈[1, +∞)则ℎ′′(x)=1x∵ ℎ′′(x)=1−6x<0在[1, +∞)恒成立x∴ ℎ′(x)=1+lnx−3x2,在区间[1, +∞)为减函数则ℎ′(x)≤ℎ′(1)=−2<0恒成立∴ ℎ(x)=x(lnx−x2)在区间[1, +∞)递减则ℎ(x)≤ℎ(1)=−1故b>−1(3)由(1)得对任意的x0∈[2, 3],g(x0)∈[15, 27]由(2)得函数ℎ(x)=c(xlnx−x3),(c<0),在区间[1, 2]单调递增则ℎ(1)=−c≤ℎ(x)≤ℎ(2)=c(2ln2−8)若对任意的x0∈[2, 3],总存在x1∈[1, 2],使得g(x0)=ℎ(x1),则−c≤15且c(2ln2−8)≥27解得:−15≤c≤272ln2−8。
山东省济宁一中2011届高三下学期4月模拟测试(数学)

济宁一中2011届高三年级模拟考试数 学 试 题2011.4第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设A 、B 是两个非空集合,定义运算A ×B ={x |x ∈A ∪B ,且x ∉A ∩B },已知A ={x |y =2x -x 2},B ={y |y =2x,x >0},则A ×B =( )A .∪(2,+∞) B. D .2. 命题“对任意的x ∈R,x 3-x 2+1≤0”的否定是( )A .不存在x ∈R,x 3-x 2+1≤0B .存在x ∈R,x 3-x 2+1≤0C .存在x ∈R,x 3-x 2+1>0D .对任意的x ∈R,x 3-x 2+1>03. 已知函数f (x )=⎩⎪⎨⎪⎧(3a -2)x +6a -1(x <1),a x(x ≥1),在(-∞,+∞)上单调递减,那么实数a的取值范围是( )A .(0,1)B .(0,23)C .[38,23)D .[38,1)4.若复数2(R,12a ia i i -∈+为虚数单位)是纯虚数,则实数a 的值为A.4B. 4-C.1D. 1-5.已知在等比数列{}n a 中,1346510,4a a a a +=+=,则等比数列{}n a 的公比q 的值为A.14B.12C.2D. 86.若函数)(log )(b x x f a +=的大致图象如右图,其中b a ,(0a >且1a ≠)为常数,则函数b a x g x+=)(的大致图象是A B C D7.某计算机程序每运行一次都随机出现一个五位的二进制数A =A 的各位数中,)5,4,3,2(,11==k a a k出现0的概率为31,出现1的概率为32.记54321a a aaa ++++=ξ,当程序运行一次时,ξ的数学期望E ξ= A .827 B .1681 C .113 D .65818.已知圆C:()()()22240x a y a -+-=>及直线:30l x y -+=,当直线l C 被截得弦长为a 等于 AB .2-C 1D 19.双曲线221mx y +=的虚轴长是实轴长的2倍,则m 等于 A .14-B .4-C . 4D .1410.设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥≥-≤--,0,0,0,023y x y x y x 若目标函数)0,0(>>+=b a by ax z 的最大值1,则b a 11+的最小值为 ( )A .625B .38C .311D .411.已知函数1|)(|,]1,0[,44)(2>∈-=x f x x ax x x f 的不等式关于时的解集为空集,则满足条件的实数a 的取值范围是( )A .⎥⎦⎤ ⎝⎛∞-43,B .),43(+∞C .}43{D .[)+∞,112.(理)从6名学生中选4人分别从事A 、B 、C 、D 四项不同的工作,若甲、乙两人不能从事A 工作,则不同的选派方案共有( )A .280B .240C .180D .96(文).若函数f (x )=x 3-3x +a 有3个不同的零点,则实数a 的取值范围是( ) A .B .(-2,2)C .(-∞,-1)D .(1,+∞)二、填空题:本大题共4小题,每小题4分,共16分。
(2011济宁一模)山东省济宁市2011届高三第一次模拟考试word试题部分(数学理)
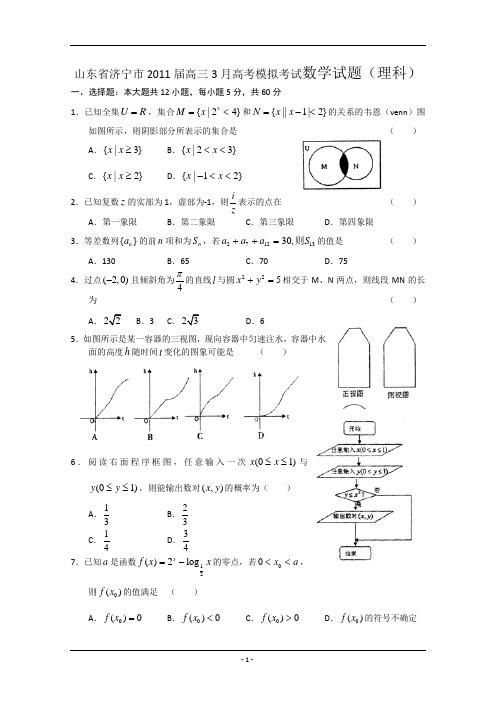
山东省济宁市2011届高三3月高考模拟考试数学试题(理科)一、选择题:本大题共12小题,每小题5分,共60分1.已知全集U R =,集合{|24}x M x =<和{||1|2}N x x =-<的关系的韦恩(venn )图如图所示,则阴影部分所表示的集合是( )A .{|3}x x ≥B .{|23}x x <<C .{|2}x x ≥D .{|12}x x -<<2.已知复数z 的实部为1,虚部为-1,则iz表示的点在( )A .第一象限B .第二象限C .第三象限D .第四象限3.等差数列{}n a 的前n 项和为n S ,若27121330,a a a S ++=则的值是 ( )A .130B .65C .70D .754.过点(2,0)-且倾斜角为4π的直线l 与圆225x y +=相交于M 、N 两点,则线段MN 的长为( )A .22B .3C .23D .65.如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的图象可能是 ( )6.阅读右面程序框图,任意输入一次(01)x x ≤≤与(01)y y ≤≤,则能输出数对(,)x y 的概率为( )A .13 B .23 C .14 D .347.已知a 是函数12()2log xf x x =-的零点,若00x a <<,则0()f x 的值满足 ( )A .0()0f x =B .0()0f x <C .0()0f x >D .0()f x 的符号不确定8.已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=+>><<为奇函数,该函数的部分图象如图所示,EFG ∆是边长为2的等边三角形,则(1)f 的值为( )A .32-B .62-C .3D .3-9已知函数2010()sin x f x x e x =++,令1213()(),()(),(n n f x f x f x f x f x f x f x f x +''''==== ,则2011()f x =( )A .sin xx e +B .cos xx e +C .sin xx e -+D .cos xx e -+10.已知1:0,:420x x x p q m x-≤+-≤,若p q 是的充分条件,则实数m 取值范围是( )A .22m >+B .22m ≤+C .2m ≥D .6m ≥11.已知抛物线22(0)y px p =>上一点(1,)(0)M m m >到其焦点的距离为5,双曲线221x y a-=的左顶点为A ,若双曲线的一条渐近线与直线AM 平行,则实数a 的值是( )A .125B .19C .15D .1312.给定两个长度为1的平面向量OA OB和,它们的夹角为90︒,如图所示,点C 在以O 为圆心的圆弧AB 上运动,若CO xOA yOB =+,其中,x y R ∈,则x y +的最大值是( )A .1B .2C .3D .2二、填空题:本大题共4小题,每小题4分,共16分。
2011届山东省济宁一中高三模拟测试(基本能力)

济宁一中2011届高三年级模拟考试基本能力试题2011.04本试卷分第I卷和第II卷两部分,共12页,满分100分。
考试用时100分钟。
请将1-70题选择题答案填涂在答题卡上,填空及71-74题答案写在答题纸上,答在试卷上的题目无效。
第Ⅰ卷(共30分)一、一个民族想要站在科学的最高峰,就一刻也不能没有理论思维。
1.毛泽东在《七律·人民解放军占领南京》一诗中写道:“宜将剩勇追穷寇,不可沽名学霸王”。
这句诗借用西楚霸王(项羽)本可以凭优势兵力消灭刘邦,却怕落下“不义”之名而丧失机会的典故,告诫人们“宜将剩勇追穷寇”的道理。
这一典故给我们的哲学启示是A.世界上一切事物都是变化发展的B.主观和客观是具体的历史的统一C.当量的积累达到一定程度时,就应不失时机促成事物的飞跃与发展D.发挥主观能动性必须以尊重客观规律为基础2.用网络搜索引擎查询“遗传与变异”的定义,下列查询结果中最为可靠的应该是①在“百度百科”中找到的②在“百度文库”中找到的③在“人民教育出版社”网站中找到的④在“中国国家数字图书馆”中找到的A.①②B.①③C.③④D.②④3.子路问君子,子曰:“修己以敬。
”曰:“如斯而己乎?”曰:“修己以安人。
”曰:“如斯而己乎?”曰:“修己以安百姓……”子路与孔子的对话揭示了君子的三重境界:修养自己严肃认真做事;修养自己使别人安乐;修养自己使百姓安乐。
现代国家公务员同样需要“修己”,若以孔子“修已”思想衡量,应该①守责而不失范②为民而不为己③尚公而不趋利④让权而不谋权A.①②③B.②③④C.①②④D.①③④4.人造金属电池可提供相当于常规电池10倍的电力,不需要维修,充电次数可达1000次以上,使用寿命比铅蓄电池长4~5倍,而且不会污染环境。
它给我们的哲学启示是A.人的意识具有能动作用,可以改变规律B.人具有主观能动性,可以随意创造新的事物C.人们可以根据客观条件,创造出自然界原本没有的事物D.人可以改变自然界的客观性,从而创造新的事物5.意境不是意和境的简单相加,而是意和境和谐,并在此基础上生出“景外之意”、“象外之象”、“韵外之致”。
山东省济宁市高三数学第一次模拟考试试题理

2018—2019学年度济宁市高考模拟考试数学(理工类)试题2019.3本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.考试结束后,将本试卷和答题卡一并收回.注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上.第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}(){}2230,ln 1,A x x x B x y x A B =--≤==-⋂=则A ,[1,3]B .(1,3] c .[2,3] D .[-l ,+∞) 2.若复数21z i=+,其中i 为虚数单位,则下列结论正确的是 A .z 的虚部为1-B .2z =C .2z 为纯虚数D .z 的共轭复数为1i -- 3.执行如图所示的程序框图,若输入a 的值为1-,则输出的S 的值是A .12-B .12 C .74 D .6320 4.若变量,x y 满足221020x y x z x y y ⎧+≤⎪≥=+⎨⎪≥⎩,则的最大值是A .5-B .1C .2D .55.函数()f x 是定义在R 上的奇函数,且()()()()11,19,2019f x f x f f +=-==若则A .9-B .9C .3-D .06.已知平面α,直线,m n ,满足n α⊂,则“//m n ”是“//m α”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件7.若sin 3sin cos cos 22x x x x ππ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭,则 A .310 B .310- c .34 D .34- 8.下图为某市国庆节7天假期的楼房认购量与成交量的折线图,小明同学根据折线图对这7天的认购量(单位:套)与成交量(单位:套)作出如下判断:①日成交量的中位数是16;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月7日认购量的增幅大于10月7日成交量的增幅.则上述判断正确的个数为A .0B .1C .2D .39.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的体积为A .823π B .6πC .6πD .8π10.已知函数()()sin 3cos 0f x x x ωωω=+>的零点构成一个公差为2π的等差数列,把函数()f x 的图象沿x 轴向右平移6π个单位,得到函数()g x 的图象.关于函数()g x ,下列说法正确的是A .在,42ππ⎡⎤⎢⎥⎣⎦上是增函数 B .其图象关于直线2x π=对称 C .函数()g x 是偶函数 D .在区间2,63ππ⎡⎤⎢⎥⎣⎦上的值域为3,2⎡⎤-⎣⎦ 11.已知双曲线()2222:10x y C a b a b-=>0,>的左、右焦点分别为12F F 、,实轴长为4,渐近线方程为121,42y x MF MF =±-=,点N 在圆2240x y y +-=上,则1MN MF +的最小值为A .27+B .5C .6D .712.已知当()1,x ∈+∞时,关于x 的方程()ln 30x x a x a +-+=有唯一实数解,则a 所在的区间是A .(3,4)B .(4,5)C .(5,6)D .(6.7)第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.某学校从编号依次为01,02,…,90的90个学生中用系统抽样(等间距抽样)的方法抽取一个样本,已知样本中相邻的两个组的编号分别为14,23,则该样本中来自第四组的学生的编号为 ▲ .14.()()522x y x y +-的展开式中,24x y 的系数为 ▲ .(用数字作答).15.如图所示,在正方形OABC 内随机取一点,则此点取自黑色部分的概率为 ▲ .16.在△ABC 中,记3,.m CB AC n CB m n =-=⊥若.则sinA 的最大值为 ▲ .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(本小题满分12分)等差数列{}n a 的公差为正数,11a =,其前n 项和为n S ;数列{}n b 为等比数列,12b =, 且222312,10b S b S =+=.(I)求数列{}{}n n a b 与的通项公式;(Ⅱ)设1n n nc b S =+,求数列{}n c 的前n 项和n T .18.(本小题满分12分)如图,在四棱锥P —ABCD 中,底面ABCD 为平行四边形,PA ⊥底面ABCD ,60,3,23,3ABC AB AD AP ∠====.(I)求证:平面PCA ⊥平面PCD ;(Ⅱ)设E 为侧棱PC 上的一点,若直线BE 与底面ABCD 所成的角为45°,求二面角E AB D --的余弦值.19.(本小题满分12分)某学校为了了解全校学生的体重情况,从全校学生中随机抽取了100人的体重数据,结果这100人的体重全部介于45公斤到75公斤之间,现将结果按如下方式分为6组:第一组[45,50),第二组[50,55),…,第六组[70,75),得到如下图(1)所示的频率分布直方图,并发现这100人中,其体重低于55公斤的有15人,这15人体重数据的茎叶图如图(2)所示,以样本的频率作为总体的概率.(I)求频率分布直方图中,,a b c 的值;(Ⅱ)从全校学生中随机抽取3名学生,记X 为体重在[55,65)的人数,求X 的概率分布列和数学期望;(III)由频率分布直方图可以认为,该校学生的体重ξ近似服从正态分布()2,N μσ,其中()260,25.220.9545P μσμσξμσ==-≤<+>若,则认为该校学生的体重是正常的.试判断该校学生的体重是否正常?并说明理由.20.(本小题满分12分) 已知椭圆()222210x y C a b a b +=>>:的离心率为33,且椭圆C 过点231,3P ⎛⎫ ⎪ ⎪⎝⎭. (I)求椭圆C 的方程;(Ⅱ)设椭圆C 的右焦点为F ,直线l 与椭圆C 相切于点A ,与直线3x =相交于点B ,求证:AFB ∠的大小为定值.21.(本小题满分12分)已知函数()()ln 1f x x a x a a R =-+-∈.(I)讨论()f x 的单调性;(Ⅱ)若)(),0a x e f x ⎡∈+∞≥⎣时,恒成立,求实数a 的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知点M 的直角坐标为(1,0),直线l 的参数方程为21222x t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数);以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为2sin 2cos p θθ=.(I)求直线l 的普通方程和曲线C 的直角坐标方程;(Ⅱ)直线l 和曲线C 交于A ,B 两点,求2211MA MB +的值.23.(本小题满分10分)选修4—5:不等式选讲 已知函数()()0,0f x x a x b a b =-++>>. (I)当1a b ==时,解不等式()2f x x >+; (Ⅱ)若()f x 的值域为[2,+∞),求证:11111a b +≥++.。
山东省济宁市高三数学第一次模拟考试 理(济宁市一模,含解析)新人教A版

2013年济宁市高三模拟考试数学(理工类)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分l50分,考试时间120分钟。
考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答第I 卷前,考生务必将自己的姓名,考号填写在答题卡上2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号,非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚. 参考公式:如果事件A 、B 互斥,那么P(A+B)=P(A)+P(B). 如果事件A 、B 独立,那么P(A·B)=P(A)·P(B). 第I 卷(选择题共60分)一、选择题:本大题共l2小题.每小题5分。
共60分.在每小题给出的四个选项中。
只有一项是符合题目要求的. 1.复数2=()1ii z -,则复数1z +在复平面上对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限 【答案】D【解析】221z=()122i i i ii==---,所以1112z i +=-,对应点位1(1,)2-,选D.2.已知全集U=R ,集合A={2(+1)y |y ln x ,x R =∈},集合B={21x ||x |-≤},则如图所示的阴影部分表示的集合是A .{01>3x |x x ≤<或}B .{|0<1x x ≤}C .{|>3x x }D .{|13x x ≤≤} 【答案】A【解析】2A={(+1)}0y|y ln x ,x R {y y }=∈=≥,{13}B x x =≤≤,图中阴影部分为集合()U A B I ð,所以{1>3}U B x x x =<或ð,所以(){01>3}U A B x x x =≤<I 或ð,选A. 3.下列命题中正确的有①设有一个回归方程$y =2—3x ,变量x 增加一个单位时,y 平均增加3个单位;②命题P :“2000,--1>0x R x x ∃∈”的否定⌝P :“,102x R x -x-∀∈≤”;③设随机变量X 服从正态分布N(0,1),若P(X>1)=p ,则P(-1<X<0)=12-p ; ④在一个2×2列联表中,由计算得k 2=6.679,则有99%的把握确认这两个变量间有关系. A .1个 B .2个 C .3个 D .4个 本题可以参考独立性检验临界值表 P(K 2≥k) 0.50.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.535 7.879 10.828【答案】C【解析】①变量x 增加一个单位时,y 平均减少3个单位,所以错误。
开始模拟1

高三模拟考试一数学试题(理科) 2011.2本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
考试时间120分钟,满分150分.第Ⅰ卷(选择题共60分)一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}A x x x =<->1或1,2{log 0}B x x =>,则A B =A. {}|x x >1 B.{}|x x >0 C.{}|x x <-1D.{}|x x x <->1或12.记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( ) A.1440种B.720种 C.960种 D.480种3.设1z i =-(i 是虚数单位),则22z z+= A. 1i -- B.1i -+C. 1i -D.1i +4.在△ABC 中,已知向量AB AC 与满足,()0||||AB AC BC AB AC +⋅=,且12||||AB AC AB AC ⋅=,则△ABC 为A.三边均不相等的三角形 B.直角三角形 C.等腰非等边三角形 D.等边三角形5.某校数学教研组为了解学生学习数学的情况,采用分层抽样的方法从高一600人、高二680人、高三720人中,抽取50人进行问卷调查,则高一、高二、高三抽取的人数分别是A.15,16,19 B.15,17,18 C.14,17,19 D.14,16,206.曲线313y x x =+在点4(,)31处的切线与坐标轴围成的三角形面积为 A.1 B.19 C.13 D.237.设⎪⎩⎪⎨⎧<+≥=4)1(4)21()(x x f x x f x,,,则)3(log 2f 等于 A.823- B.111 C.191D.2418.如图为一个几何体的三视图,左视图和主视图均为矩形, 俯视图为正三角形,尺寸如图,则该几何体的全面积为2732B.123 C.24 D.2423+9.等差数列{}n a 的前项和为n S ,若37108a a a +-=,1144a a -=,则13S 等于 A.152B.154 C.156D.15810.已知函数()2sin(2)f x x ϕ=+,若()2f α=,则()12f πα+的值为A.3 B.3± C.1 D.与ϕ和α有关11. 若点P 为共焦点的椭圆1C 和双曲线2C 的一个交点,12F F 、分别是它们的左右焦点,设椭圆离心率为1e ,双曲线离心率为2e ,若120PF PF ⋅=,则221211e e += A.1 B.2 C.3 D.412.定义在R 上的函数()f x 满足()()f x f x -=,(1)(1)f x f x +=-,且当[0,2]x ∈时,2()log (31)f x x =+,则(2010)(2011)f f +-的值为3A.1 B.2 C.3 D.4第Ⅱ卷(非选择题 共90分)二、 填空题:本大题共4小题,每小题4分,共16分.13.抛物线24y x =上的一点M 到焦点的距离为1,则点M 的纵坐标是 .14.不等式212<-+x x 的解集是 . 15.在如图所示的算法流程图中,输出S 的值为 . 16. 已知函数()f x 满足1(1)()f x f x +=,且()f x 是偶函数, 当[0,1]x ∈时,()f x x =,若在区间[1,3]-内,函数()()g x f x kx k=--有4个零点,则实数k 的取值范围是 .三. 解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知数列{}n a 是首项为1,公比为(0)q q >的等比数列,并且13212,,2a a a 成等差数列. (Ⅰ)求q 的值;(Ⅱ)若数列{}n b 满足n n b a n =+,求数列{}n b 的前n 项和n T .18.(本小题满分12分)已知向量(cos sin ,3cos ),(cos sin ,2sin )m x x x n x x x =+=-,若函数()f x m n =⋅, (Ⅰ)求函数()f x 的单调递增区间;(Ⅱ)在ABC ∆中,,,a b c 分别是角,,A B C 的对边,且1,2a b c =+=,()1f A =,求ABC ∆的面积.19. (本小题满分12分)四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,底面ABCD 是边长为2的正方形,又PA PD =,60APD ∠=︒,E 、G 分别是BC 、PE 的中点。
山东省济宁市数学高三上学期理数第一次模拟考试试卷

山东省济宁市数学高三上学期理数第一次模拟考试试卷姓名:________ 班级:________ 成绩:________一、选择题. (共12题;共24分)1. (2分)(2020·陕西模拟) 已知集合,,则()A .B .C .D .2. (2分)(2018·吕梁模拟) 已知复数,则()A .B .C .D . 53. (2分) (2016高一上·历城期中) 已知函数f(x)与g(x)的图象在R上不间断,由表知函数y=f(x)﹣g(x)在下列区间内一定有零点的是()x﹣10123f(x)﹣0.677 3.011 5.432 5.9807.651g(x)﹣0.530 3.451 4.890 5.241 6.892A . (﹣1,0)B . (0,1)C . (1,2)D . (2,3)4. (2分)已知服从正态分布N(μ,σ2)的随机变量,在区间(μ﹣σ,μ+σ),(μ﹣2σ,μ+2σ)和(μ﹣3σ,μ+3σ)内取值的概率分别为68.3%,95.4%和99.7%.某大型国有企业为10000名员工定制工作服,设员工的身高(单位:cm)服从正态分布N(173,52),则适合身高在163~178cm范围内员工穿的服装大约要定制()A . 6830套B . 9540套C . 8185套D . 9755套5. (2分)小孟进了一批水果.如果他以每斤一块二的价格出售,那他就会赔4元;如果他以每斤一块五的价格出售,一共可以赚8元.现在小孟想将这批水果尽快出手,以不赔不赚的价格卖出,那么每千克水果应定价为()元.A . 2.6B . 2.2C . 2.8D . 1.36. (2分)(2017·锦州模拟) 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形,俯视图是圆心角为的扇形,则该几何体的侧面积为()A . 2B . 4+πC . 4+ πD . 4+π+ π7. (2分)执行如图所示的程序框图,若输入的n的值是100,则输出的变量S和T的值依次是()A . 2 500,2 500B . 2 550,2 550C . 2 500,2 550D . 2 550,2 5008. (2分) (2017高二上·廊坊期末) 方程x2+2x+n2=0(n∈[﹣1,2])有实根的概率为()A .B .C .D .9. (2分)用数学归纳法证明不等式(n≥2,n∈N+)时,第一步应验证不等式()A .B .C .D .10. (2分) (2017高三上·嘉兴期中) 为了得到函数的图象,可以将函数的图象()A . 向右平移个单位B . 向右平移个单位C . 向左平移个单位D . 向左平移个单位11. (2分)已知,,则是的()A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件12. (2分) (2020高二上·榆树期末) 若抛物线的焦点坐标为,则()A . 12B . 6C . 3D .二、填空题. (共4题;共4分)13. (1分)已知| |=8,| |=15,| + |=17,则与的夹角θ为________.14. (1分)(2017·南开模拟) (x﹣)n的展开式中只有第5项的二项式系数最大,则它的展开式中常数项是________.15. (1分)已知f(x)=x2 , g(x)=()x﹣m,若对任意x1∈[﹣1,3],总存x2∈[0,2],在使得f(x1)≥g(x2)成立,则实数m的取值范围是________.16. (1分)(2019·哈尔滨模拟) 关于函数 ,下列说法正确的是________(填上所有正确命题序号).(1)是的极大值点;(2)函数有且只有1个零点;(3)存在正实数,使得恒成立;(4)对任意两个正实数,且,若,则 .三、解答题. (共7题;共70分)17. (15分)(2016高二下·临泉开学考) 设数列{an}的前n项和为Sn ,已知a1=1,,n∈N* .(1)求a2的值;(2)求数列{an}的通项公式;(3)证明:对一切正整数n,有.18. (10分)(2018·全国Ⅱ卷文) 如图,在三角锥中, , ,为的中点.(1)证明:平面 ;(2)若点在棱上,且MC=2MB,求点C到平面POM的距离.19. (10分) (2015高二下·仙游期中) 袋中装着标有数字1、2、3、4、5的小球各2个,从袋中任取3个小球,每个小球被取出的可能性都相等,用ξ表示取出的3个小球上的最大数字,求:(1)取出的3个小球上的数字互不相同的概率;(2)随机变量ξ的概率分布列和数学期望.20. (10分)(2017·南通模拟) 已知椭圆C:mx2+3my2=1(m>0)的长轴长为,O为坐标原点.(1)求椭圆C的方程和离心率.(2)设点A(3,0),动点B在y轴上,动点P在椭圆C上,且点P在y轴的右侧.若BA=BP,求四边形OPAB面积的最小值.21. (5分) (2018高三上·福建期中) 函数 .(I)求的单调区间;(II)若,求证: .22. (10分) (2019高二下·吉林月考) 己知圆的参数方程为,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为.(1)将圆的参数方程化为普通方程,将圆的极坐标方程化为直角坐标方程;(2)圆,是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.23. (10分) (2016高一上·嘉兴期中) 已知函数f(x)=x2﹣ax﹣2a2(x∈R).(1)关于x的不等式f(x)<0的解集为A,且A⊇[﹣1,2],求a的取值范围;(2)是否存在实数a,使得当x∈R时,成立.若存在给出证明,若不存在说明理由.参考答案一、选择题. (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题. (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题. (共7题;共70分) 17-1、17-2、17-3、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、23-1、23-2、。
