等体积1
7.3 等体....过程

M CV PdV CV VdP RCV dT RPdV CP PdV CV PdV 又: R = CP - CV
PdV VdP
M
RdT
CP = CV
CVVdP CP PdV
CV PdV CV VdP
M
RCV dT
RPdV
CP PdV CV PdV
QV CV
M
(T2 T1 )
定体摩尔热容CV,可以由理论计算得出, 也可以由实验测出。下页表中给出几 种气体的CV,的实验值。
表 几种气体摩尔热容的实验值(在1.013X105Pa、25oC时)
气体
单原子气体 氦(He) 氖(Ne) 氩(Ar) 双原子分子 氢(H2) 氮(N2) 氧(O2) 一氧化碳(CO)
CV (T2 T1 )
5、比热容(比热)
前面给出的摩尔热容是针对理想气体而言的,对于液体、固 体等构成的系统,当在某一微小过程中吸热dQ,温度升高dT, 则定义: dQ C 为系统在该过程中的热容, C=
dT
单位J· K-1。
由于系统的热容 C 与系统的质量有关,故把单位质量的热 容称为比热容(简称比热)c,其单位为J· -1 · -1。 K kg 热容C 与比热容(简称比热)c 的关系为:
pdV
V1
绝热膨胀过程中,系统对外作的功,是靠内能减少实现的, 故温度降低;绝热压缩过程中,外界对气体作功全用于增加气 体内能,故温度上升。
dV
V2
V
下面我们来推导绝热方程: M dE CV dT 0 dE dWa
dWa PdV M 0= CV dT PdV
PV M RT
小学1-5年级数学公式及概念大全
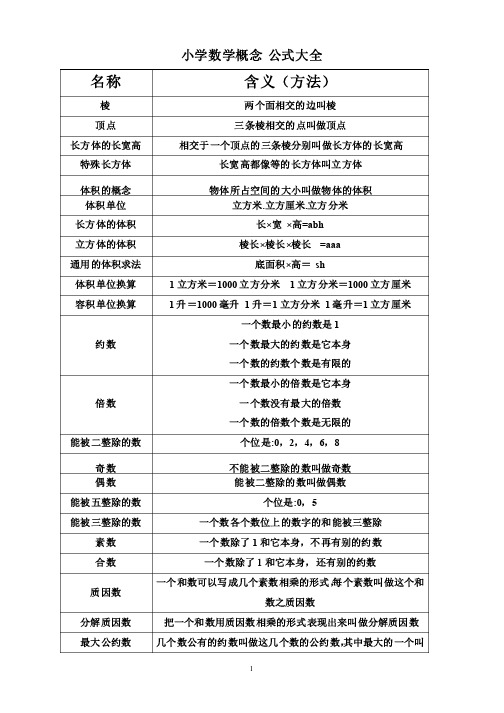
小学数学概念公式大全名称含义(方法)棱两个面相交的边叫棱顶点三条棱相交的点叫做顶点长方体的长宽高相交于一个顶点的三条棱分别叫做长方体的长宽高特殊长方体长宽高都像等的长方体叫立方体体积的概念物体所占空间的大小叫做物体的体积体积单位立方米.立方厘米.立方分米长方体的体积长×宽×高=abh立方体的体积棱长×棱长×棱长=aaa通用的体积求法底面积×高=sh体积单位换算1立方米=1000立方分米1立方分米=1000立方厘米容积单位换算1升=1000毫升1升=1立方分米1毫升=1立方厘米约数一个数最小的约数是1 一个数最大的约数是它本身一个数的约数个数是有限的倍数一个数最小的倍数是它本身一个数没有最大的倍数一个数的倍数个数是无限的能被二整除的数个位是:0,2,4,6,8奇数不能被二整除的数叫做奇数偶数能被二整除的数叫做偶数能被五整除的数个位是:0,5能被三整除的数一个数各个数位上的数字的和能被三整除素数一个数除了1和它本身,不再有别的约数合数一个数除了1和它本身,还有别的约数质因数一个和数可以写成几个素数相乘的形式,每个素数叫做这个和数之质因数分解质因数把一个和数用质因数相乘的形式表现出来叫做分解质因数最大公约数几个数公有的约数叫做这几个数的公约数,其中最大的一个叫做这几个数的最大公约数互质数公约数只有1的两个数叫互质数约数时的最大公约数小数是大数的约数,小数就是这两个数的最大公约数互质数最大公约数两个数是互质数,它们最大公约数是1最小公倍数几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做最小公倍数分数大小的比较分子相同的两个数分母小的那个数比较大,分母相同的两个数分子大的那个数比较大假分数分子比分母大或分子和分母相等的分数叫做假分数,假分数大于或等于1带分数一个整数和一个真分数合成的数叫带分数分数的基本性质分母或分子同时扩大或缩小相同的倍数分数的大小不变约分把一个分数的分子和分母同时除以它们的公约数(1除外)化成和原来分数相等的分数通分把异分母分数分别化成和原来分数相等的同分母分数同分母加减法只把分子相加减分母不变异分母加减法先通分然后按照同分母加减法进行计算带分数加减法整数部分和分数部分分别相加减再把所得数合并起来计算顺序在一个算式里只有加减法或只有乘除法从左往右依次计算在一个算式里有加减法又有乘除法先算乘除法再算加减法有括号的先算括号里的有括号的算式有括号的算式要先算小括号里的运算再算中括号里的什么加加法把两个数合并成一个数的运算叫加法什么叫减法已知两个加数的和与其中的一个加数,求另一个加数的运算方法关系式单价×数量=总价速度×时间=路程工作效率×工作时间=工作总量本金×利率×时间=利息保险金额×保险费率×保险时间=保险费应纳税收入×税率=应缴税款商不变的性质被除数和除数同时扩大或缩小相同的倍数商不变什么叫乘法求几个相同加数的简便运算叫乘法什么叫除法已知两个因数的积与其中一个因数求另一因数的运算叫除法面积单位平方米,平方厘米,平方分米长方形面积长×宽=ab正方形面积边长×边长=aa面积单位换算1平方分米=100平方厘米1平方米=100平方分米长方形长方形的对边相等,四个角都是直角正方形正方形的四条边都相等,四个角都是直角长方形周长(长+宽)×2=(a+b)×a+b)×22正方形周长边长×4=a×a×44长度单位换算1千米=1000米1分米=10厘米1米=10分米=100厘米1厘米=10毫米重量单位换算1吨=1000千克1千克=1000克小数的四则混合运算小数的四则混合运算的运算顺序和整数四则混合运算的运算顺序相同土地面积单位换算平方千米100公顷1000平方米100平方分米100平方厘米平行四边形面积底×高=ab三角形面积底×高÷2=ab÷ab÷22梯形面积(上底+下底)×高÷2=(a+b)×(a+b)×h÷h÷h÷22什么叫方程含有未知数的等式什么叫方程的解使方程左右两边相等的未知数的值什么叫解方程求方程的解的过程叫解方程什么叫百分比表示一个数的百分之几的数叫做百分数百分数的写法用带有百分号“%”的数来表示小数化百分数只要把小数点向右移动两位,在最后添上百分号就行了百分数化小数只要把百分号去掉小数点向左移动两位百分数化分数把百分数改写成分母是100的分数,再把能约分的约成最简分数分数乘整数用分数的分子和整数相乘的积做分子,分母不变分数乘分数用分子相乘的积做分子,分母相乘的积做分母分数乘带分数先把带分数化成假分数,然后按照分数乘法的法则进行计算分数乘小数先把小数化成分数后再计算分数除法已知两个因数的积与其中一个因数,求另一因数的运算整数除分数的方法整数乘这个分数的倒数分数除以带分数先把带分数化成假分数然后计算小数除以分数一般把小数化成分数再计算小数分数四则混合运算顺序与整数四则混合运算顺序相同什么叫圆心圆的最中心一点叫圆心什么叫半径圆心到圆上任意一点的线段叫做半径用字母R表示什么叫直径通过圆心并且两端都在圆心上的线段叫做直径用字母D表示直径与半径的关系d=2r r=d/2π圆的周长是直径的三倍多一点这是一个固定的数,叫π=3.14 圆周长直径×π圆面积π×半径×半径如何区分闰年公历年份是四的倍数的都是闰年,公历年份是整百数时必须是四百的倍数才是闰年直线直线可以无限延长线段线段是直线上两点间的一段射线一端可以无限延长并且只有一个端点什么叫锐角小于90度的角叫锐角什么叫钝角大于90度而小于180度的角叫钝角什么叫平角当角的两边方向相反成一条直线时这样的角叫做平角平角=180度什么叫周角角的一边绕它的顶点旋转一周所成的角叫做周角周角=360度什么叫四边形四条线段围成的图形叫四边形什么叫平行四边形两组对边分别平行的四边形叫做平行四边形平行四边形的底和高每组对边之间的距离叫做平行四边形的高,和高垂直的对边叫做平行四边形的底特殊的平行四边形长方形和正方形的两组对边也分别平行,它们是特殊的平行四边形什么叫三角形三条线段围成图形叫三角形围成三角形的每条线段叫三角形的边每两条线段的交点叫三角形的顶点三角形的特性三角形的特性是稳定性锐角三角形三个角都是锐角的三角形钝角三角形有一个角是钝角的三角形直角三角形有一个角是直角的三角形等腰三角形两条边相等的三角形等边三角形三条边相等的三角形叫等边三角形又叫正三角形三角形的高和底从三角形的一个角的顶点向它的对边画一条垂线,顶点到垂足间的线段叫三角形的高,这个角的对边叫三角形的底什么叫梯形只有一组对边平行的四边形叫梯形什么叫等腰梯形两腰相等的梯形叫等腰梯形什么叫分数把物体平均分成几分取其中的1份或几分叫分数小数的基本性质小数的末尾添上0或者去掉0小数的大小不变小数点位置的移动引起小数大小的变化(扩大)小数点向右移动一位,原来的数扩大10倍,小数点向右移动二位,原来的数扩大100倍,小数点向右移动三位,原来的数扩大1000倍小数点位置的移动引起小数大小的变化(缩小)小数点向左移动一位,原来的数缩小10倍,小数点向左移动二位,原来的数缩小100倍,小数点向左移动三位,原来的数缩小1000倍有余数的除法计算有余数的除法余数一定要比除数小圆柱体体积底面积×高=SH圆锥体体积1/3×等底等高的圆柱体体积=1/3SH条形统计图条形统计图可以容易看出各种数量的多少折线统计图不但容易看出各种数量的多少还可以清楚的表示出数量的增减变化情况比比的前项相当于被除数、相当于分子;比的后项相当于除数、相当于分母,比值相当于商、相当于分数值比的基本性质比的前项和后项同时扩大或缩小相同的倍数比值不变比例尺图上距离÷实际距离=比例尺图上距离/比例尺=实际距离图上距离=实际距离÷比例尺什么叫比例式表示两个比相等的式子叫比例式,组成比例的四个数叫做比例的项,两端的两个项叫做外项,中间的两项叫做内项比例的基本性质两个内项积等于两个外项积什么叫解比例求比例中的未知项叫解比例正比例路程/时间=速度(一定)总价/数量=单价(一定)生产的数量/生产的时间=生产效率反比例X×X×Y=KY=K(一定)等体积等高圆锥的底面积是圆柱的三倍圆柱的底面积是圆锥的1/3等体积等面积圆锥的高是圆柱的的三倍圆柱的高是圆锥的1/3等高的圆锥和圆柱圆柱的体积等于圆锥的三倍圆柱的体积比圆锥的体积大2倍圆锥体积等于圆柱体积的1/3圆锥体积比圆柱体积少2/3圆柱体侧面积S侧=CHC=π×直径=2×π×R 圆柱体表面积S表=S侧+2S底圆柱体底面积S底=π×R×R×R R圆柱体半径(r)R=D/2R=C/2×π圆柱体体积V=SH圆环S圆环=π×(R×r)R×R R-r×r×r)ππ=圆周率立方体表面积棱长×棱长×6=a×a×66a×a×a×长方体地表面积(长×宽+长×高+宽×高)×2=(A×H)×H)×22H+B×H)×B+A×H+B×A×B+A×B+A×H+B×加法交换律a+b=b+a加法结合律(a+b)-c=a-(b+c)减法的性质a-b-c=a-(b+c)乘法交换率a×a×b b =b×a乘法结合律(a×(b×a)(b×a)c=a×(b×(a×b)×b)×b)×c=a×c=a×乘法分配律(a+b)×c+b×c cc+b×c=a×c+b×c=a×a+b)×c=a×。
体积长度重量等换算与面积计算公式

体积长度重量等换算与面积计算公式一、体积的换算公式:体积常用的单位有立方米(m³),立方厘米(cm³),立方毫米(mm³),升(L),立方英尺(ft³),立方英寸(in³)等。
下面是一些常用的体积换算公式:1.1 立方米(m³)转立方厘米(cm³):1 m³ = 1,000,000 cm³;1.2 立方米(m³)转立方毫米(mm³):1 m³ = 1,000,000,000 mm³;1.3立方米(m³)转升(L):1m³=1000L;1.5 立方英尺(ft³)转立方英寸(in³):1 ft³ ≈ 1728 in³;1.6 立方英寸(in³)转立方厘米(cm³):1 in³ ≈ 16.3871 cm³。
二、长度的换算公式:长度的常用单位有米(m)、厘米(cm)、毫米(mm)、千米(km)、英尺(ft)、英寸(in)、码(yd)等。
下面是一些常用的长度换算公式:2.1 米(m)转厘米(cm):1 m = 100 cm;2.2 米(m)转毫米(mm):1 m = 1000 mm;2.3 米(m)转千米(km):1 m = 0.001 km;2.4 英尺(ft)转米(m):1 ft ≈ 0.3048 m;2.5 英寸(in)转厘米(cm):1 in ≈ 2.54 cm;2.6 码(yd)转米(m):1 yd ≈ 0.9144 m。
三、重量的换算公式:重量常用的单位有千克(kg)、克(g)、毫克(mg)、吨(t)、磅(lb)等。
下面是一些常用的重量换算公式:3.1 千克(kg)转克(g):1 kg = 1000 g;3.2 千克(kg)转毫克(mg):1 kg = 1,000,000 mg;3.3 千克(kg)转吨(t):1 kg = 0.001 t;3.4 磅(lb)转千克(kg):1 lb ≈ 0.4536 kg;3.5 磅(lb)转克(g):1 lb ≈ 453.5924 g;四、面积的计算公式:面积常用的单位有平方米(m²),平方厘米(cm²),平方毫米(mm²),公顷(ha),英亩(acre)等。
小学1-6年级数学几何问题知识总结

小学数学几何问题一图形的认识、测量量的计量一、长度单位是用来测量物体的长度的。
常用的长度单位有:千米、米、分米、厘米、毫米。
二、长度单位:三、面积单位是用来测量物体的表面或平面图形的大小的。
常用面积单位:平方千米、公顷、平方米、平方分米、平方厘米。
四、测量和计算土地面积,通常用公顷作单位。
边长100米的正方形土地,面积是1公顷。
五、测量和计算大面积的土地,通常用平方千米作单位。
边长1000米的正方形土地,面积是1平方千米。
六、面积单位:(100)七、体积单位是用来测量物体所占空间的大小的。
常用的体积单位有:立方米、立方分米(升)、立方厘米(毫升)。
八、体积单位:(1000)九、常用的质量单位有:吨、千克、克。
十、质量单位:十一、常用的时间单位有:世纪、年、季度、月、旬、日、时、分、秒。
十二、时间单位:(60)十三、高级单位的名数改写成低级单位的名数应该乘以进率;低级单位的名数改写成高级单位的名数应该除以进率。
十四、常用计量单位用字母表示:二平面图形【认识、周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长短无关。
角的大小的计量单位是(°)。
三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角是钝角;等于180度的角是平角;等于360度的角是周角。
四、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
五、三角形是由三条线段围成的图形。
围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
六、三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。
按边分,可以分为等边三角形、等腰三角形和任意三角形。
体积公式单位

体积公式单位体积公式是用于计算三维空间中物体所占空间大小的数学表达式。
不同的物体形状有不同的体积公式。
以下是一些常见形状的体积公式及其单位:+1.立方体:体积= 边长^3。
单位通常是立方米(m^3)、立方厘米(cm^3)或立方毫米(mm^3)等。
例如,一个边长为2米的立方体的体积是2^3 = 8立方米。
2.球体:体积= (4/3) × π × 半径^3。
单位与立方体相同,可以是立方米、立方厘米等。
例如,一个半径为1米的球体的体积大约是4.19立方米(取π为3.14)。
3.圆柱体:体积= π × 半径^2 × 高。
单位同样可以是立方米、立方厘米等。
例如,一个半径为1米、高为2米的圆柱体的体积是大约6.28立方米。
4.圆锥体:体积= (1/3) × π × 半径^2 × 高。
单位与其他形状相同。
例如,一个底面半径为1米、高为3米的圆锥体的体积是大约3.14立方米。
5.长方体(或矩形体):体积= 长× 宽× 高。
单位与其他形状相同,如立方米、立方厘米等。
例如,一个长为2米、宽为1米、高为3米的长方体的体积是6立方米。
这些公式中的π(Pi)是一个数学常数,近似值为3.14159。
在实际应用中,可能需要根据具体情况选择合适的单位。
在科学和工程领域,通常使用国际单位制(SI)中的单位,如立方米(m^3)或立方厘米(cm^3)。
在其他领域,如日常生活或某些特定行业,可能会使用其他单位,如立方英寸(in^3)或立方英尺(ft^3)等。
等体积法

又在直角三角形 PCB 中,由 PB=10,BC=4,可得 PC= 2 21
于是 SBCD
1 2
SBCP
=2
21 ,
VDBCM
=VM DBC
1 Sh 3
10
7
A
C B
题型一:换底面求体积
典例1:如图,在边长为2的正方体AC1中,BC1交B1C于点O.
1求证:BC1 面B1CD. 2 求四面体B1 BC1D的体积.
题型二:点到面的距离
(1)直接法:由定义作出垂线段并计算,用线面和面面垂直的判定及性质来作;
(2)转移法:若直线 AB / / 平面,则直线 AB 上任意一点到平面的距离相等;
等体积法求三棱锥体积和高
等体积法
由于三棱锥是由4个三角形围成的四面体,任何一个三角形都可以 看成其底面。在求体积时灵活变换底面,但是三棱锥的体积保持不变, 这种方法我们称为“等体积法”,它是三棱锥求体积的巧妙方法。
例:如图,在三棱锥中,PA,AB,AC两两垂直,
P
求三棱锥C-PAB的体积
V VC PAB VP ABC APBC VBPAC
A
O
C
BM
练习 3:如图,已知三棱锥 A —BPC 中,AP⊥PC, AC⊥BC,M 为 AB 中点, D 为 PB 中点,且△PMB 为正三角形。 (Ⅰ)求证:平面 ABC⊥平面 APC; (Ⅱ)若 BC=4,AB =20,求三棱锥 D—BCM 的体积.
证明:(Ⅰ) PMB为正三角形,D Fra bibliotek PB 的中点,
6 3
D
F
C
A
B
练 习 2 :( 2018 全 国 卷 Ⅱ) 如 图 , 在 三 棱 锥 P A B C中 , AB BC 2 2 , PA PB PC AC 4, O 为 AC 的中点. P
固体物理答案 第1章

固体物理习题.1 如果将等体积球分别排列成下列结构,设x表示刚球所占体积与总体积之比,证明:结构 简单立方 体心立方 面心立方 六角密排 金刚石 证明: (1)简单立方:设晶格常数为,球半径为,则,如右图所示,晶胞内包含一个原子,(2)体心立方:在简单立方的体心增加一球,则立方单元内包含二个原子,(3)面心立方:在简单立方的六个面心上分别增加一个球,则立方单元内包含4个原子,(4)六角密排:如左图所示晶胞内包含6个原子,,晶胞的高用表示,则晶胞的体积=(5)金刚石:在面心立方结构的四条互不相邻的体对角线中心分别加一原子,则原胞内包含8个原子,且1.2试证六方密排堆积中证: 由上题可知 ,则1.3证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证明:根据题根据,则计算可得倒格子基矢(需有运算过程):与体心立方基矢相比这正好是以为晶格常数的体心立方格子的基矢。
同理可证体心立方晶格的倒格子是晶格常数为的面心立方格子。
1.4证明:倒格子原胞体积为,其中为正格子原胞体积。
证:有正格子基矢与倒格子基矢之间的关系:则倒格子体积。
1.5证明倒格子矢量垂直于密勒指数为的晶面系。
证:根据密勒指数的定义,晶面在基矢上的截距分别为,作矢量显然这三个矢量互不平行,均落在晶面上,且有同理,故倒格矢垂直于的晶面系。
1.6对于简单立方晶格,证明密勒指数为的晶面系,面间距满足,其中为立方边长。
证:由上题可知,倒格矢垂直于密勒指数为的晶面系,对于简单立方,两两垂直,则面间距而,所以。
1.7写出体心立方和面心立方晶格结构的金属中,最近邻和次近邻的原子数。
若立方边长为,写出最近邻和次近邻的原子间距。
解:最近邻次近邻原子数原子间距原子数原子间距体心立方 8 6面心立方 12 61.8画出体心立方和面心立方晶格结构的金属在(100),(110),(111)面上的原子排列。
答:略1.9指出立方晶格(111)面和(100)面,(111)面和(110)面的交线的晶向。
高考数学立体几何专题:等体积法(一)

第一个问题:如下图所示:计算:上顶点P 到底面ABC 的距离P h 。
第一种情况:底面ABC 的垂线过上顶点P 。
例题一:已知:在三棱锥ABC P -中:直线⊥PA 底面ABC 。
计算:点P 到底面ABC 的距离P h 。
解答:直线⊥PA 底面ABC ,直线PA 上点P 是上顶点,直线PA 上点A 是底面ABC 上一点PA ⇒是点P 到底面ABC 的距离,PA h P =。
例题二:已知:如下图所示,直线⊥PQ 平面ABC 。
计算:点P 到底面ABC 的距离P h 。
解答:直线⊥PQ 平面ABC ,直线PQ 上点P 是上顶点,直线PQ 上点D 是平面ABC 上一点PD ⇒是点P 到平面ABC 的距离,PD h P =。
第二种情况:底面ABC 的垂线不过上顶点P 。
例题一:已知:在三棱锥ABC P -中:点D 和点E 分别为AB 和PA 的中点,⊥DE 平面ABC 。
计算:点P 到底面ABC 的距离。
解答:点D 和点E 分别为AB 和PA 的中点DE ⇒是PAB ∆的中位线PB DE //⇒,⊥DE 底面ABC⊥⇒PB 底面ABC ,直线PB 上的点P 是上顶点,直线PB 上的点B 在底面ABC 上⇒点P 到底面ABC 的距离为PB 。
例题二:已知:在三棱柱111C B A ABC -中,点P 是棱1BB 的中点,⊥1AB 底面ABC 。
计算:点P 到底面ABC 的距离。
解答:过点P 作1AB 的平行线交AB 于点Q 。
如下图所示:⊥1AB 底面ABC ,⊥⇒PQ AB PQ 1//平面ABC ,直线PQ 上的点P 是上顶点,直线PQ 上的点Q 在底面ABC 上⇒点P 到底面ABC 的距离为PQ 。
第二个问题:如下图所示:计算:三棱锥ABC P -的体积。
P ABC ABC P h S V ⨯⨯=∆-31,其中P h 是上顶点P 到底面ABC 的距离。
问题:第一个问题中解决的上顶点P 到底面ABC 的距离,都会有一个共同特点,底面ABC 有一条垂线。
梁、板、柱等体积常用计算公式

常用计算公式(一)基础1.带形基础(1)外墙基础体积=外墙基础中心线长度×基础断面面积(2)内墙基础体积=内墙基础底净长度×基础断面面积+T形接头搭接体积其中T形接头搭接部分如图示。
V=V1+V2=(L搭×b×H)+ L搭〔bh1/2+2(B-b/2×h1/2×1/3)〕=L搭〔b×H+h1(2b+B/6)〕式中:V——内外墙T形接头搭接部分的体积;V1——长方形体积,如T形接头搭接示意图上部所示,无梁式时V1=0;V2——由两个三棱锥加半个长方形体积,如T形接头搭接示意图下部所示,无梁式时V= V2 ;H——长方体厚度,无梁式时H=0;2.独立基础(砼独立基础与柱在基础上表面分界)(1)矩形基础:V=长×宽×高(2)阶梯形基础:V=∑各阶(长×宽×高)(3)截头方锥形基础:V=V1+V2=H1/6×[A×B+(A+a)(B+b)+a×b]+A×B×h2截头方锥形基础图示式中:V1——基础上部棱台部分的体积(m3 )V2——基础下部矩形部分的体积(m3 )A,B——棱台下底两边或V2矩形部分的两边边长(m)a,b——棱台上底两边边长(m)h1——棱台部分的高(m)h2——基座底部矩形部分的高(m)(4)杯形基础基础杯颈部分体积(m3 )V3=abh3式中:h3——杯颈高度V3_——杯口槽体积(m3 )V4= h4/6+[A×B+(A+a)(B+b)+a×b]式中:h4—杯口槽深度(m)。
杯形基础体积如图7—6所示:V=V1+V2+V3-V4式中:V1,V2,V3,V4为以上计算公式所得。
3. 满堂基础(筏形基础)有梁式满堂基础体积=(基础板面积×板厚)+(梁截面面积×梁长)无梁式满堂基础体积=底板长×底板宽×板厚4. 箱形基础箱形基础体积=顶板体积+底板体积+墙体体积5.砼基础垫层基础垫层工程量=垫层长度×垫层宽度×垫层厚度(二)柱1.一般柱计算公式:V=HF式中:V——柱体积;H——柱高(m)F——柱截面积2.带牛腿柱如图所示V=(H × F)+牛腿体积×n=(h × F)+[(a ×b ×h1)+a × b V2 h2/2]n =h ×F+a ×b ×(h1+h2/2)n式中:h——柱高(m);F——柱截面积a.b——棱台上底两边边长;h1——棱台部分的高(m)h2——基座底部矩形部分的高(m);n——牛腿个数3.构造柱:V=H ×(A×B+0.03×b×n)式中:H—构造柱高(m); A.B—构造柱截面的长和宽b—构造柱与砖墙咬槎1/2宽度;n—马牙槎边数(三)梁1.一般梁的计算公式(梁头有现浇梁垫者,其体积并入梁内计算)V=Lhb式中:h—梁高(m);b—梁宽;L—梁长2.异形梁(L、T、十字型等梁)V=LF式中:L—梁长;F—异型梁截面积3.圈梁圈梁体积V=圈梁长×圈梁高×圈梁宽4.基础梁V=L×基础梁断面积式中:V—基础梁体积(m3);L—基础梁长度(m)。
中考物理专题突破6 质量和密度综合计算题

专题突破04 质量和密度综合计算题题型一 等质量、等体积、等密度问题在计算中常隐含三个条件:质量不变,如水结成冰;体积不变,如瓶子装水、装其他液体问题,溢水法问题;密度不变,如样品问题。
1.等质量问题(冰熔化为水)(1)冰、水相互转化,质量将保持不变,10:9:=冰水V V 。
(2)冰、水相互转化,总体积变化了V ,则发生物态变化的冰体积为10V ,发生物态变化的水体积为9V 。
2.等体积问题(1)溢水法测体积,通过测量溢出水的质量,计算出水的体积,从而获得物体的体积。
(2)换液法测体积,通过装满的液体(密度已知)之间的质量差,求出容器的容积。
3.等密度问题样品密度和整个物体的密度相等。
【例1】医院里有一只氧气瓶,它的容积为10dm 3,里面装有密度为2.5kg/m 3的氧气,氧气的质量是 g ;某次抢救病人用去了10g 氧气,则瓶内剩余氧气的密度为 。
【例2】如图所示,乌鸦为了喝到瓶中的水,每次将一个质量为0.01kg 的小石头投入容积为3×10﹣4m 3盛有0.2kg 的水的瓶中,当投入25个相同的小石头后,水面恰好升到瓶口,已知水的密度ρ水=1.0×103kg/m 3,求:(1)瓶内小石头的总体积;(2)小石头的密度。
题型二 空心问题方法:通过比较实心体积与总体积的大小关系,进行相应的判断和计算。
即:算出被测物体的体积。
已知条件测ρm =V ,若已知测V V =,则为实心,否则为空心;【例3】a、b是两个由同种材料制成的金属球,它们的质量分别为256g、120g,体积分别为32cm3、24cm3.在这两个金属球中,如果有一个是实心的,那么()A.这个实心球是a,金属的密度是8g/cm3B.这个实心球是a,金属的密度是5g/cm3C.这个实心球是b,金属的密度是8g/cm3D.这个实心球是b,金属的密度是5g/cm3【例4】有A、B、C三个由同种材料制成的金属球,它们的质量分别为128g、400g、60g,体积分别为16cm3、50cm3、12cm3.则金属球A的密度为g/cm3.在A、B、C三个金属球中,若只有一个是空心的,那么这个空心球的空心体积为cm3,若把空心球的空心部分灌满水,则这个球的平均密度为g/cm3.(小数点后保留1位)题型三图像问题【考点解释】m-ρ图像ρ-v图像①注意横、纵坐标分别代表的参数;若纵坐标为质量m,横坐标为体积v。
等体积法
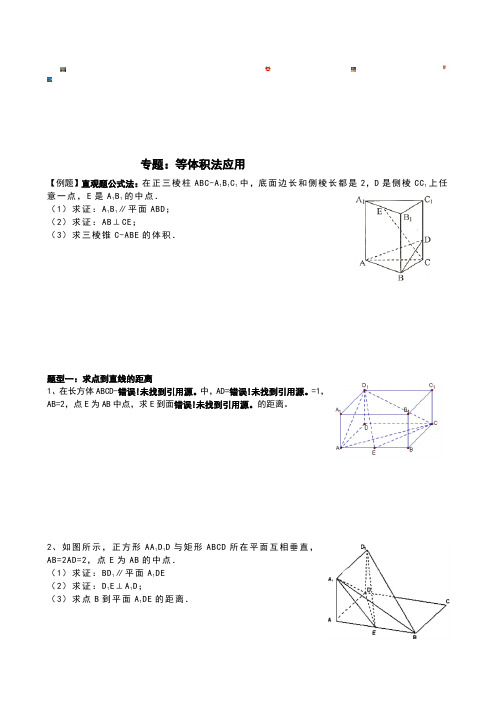
专题:等体积法应用
【例题】直观题公式法:在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A
1B1的中点.
(1)求证:A1B1∥平面ABD;
(2)求证:AB⊥CE;
(3)求三棱锥C-ABE的体积.
题型一:求点到直线的距离
1、在长方体ABCD-错误!未找到引用源。
中,AD=错误!未找到引用源。
=1,AB=2,点E为AB中点,求E到面错误!未找到引用源。
的距离。
2、如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,
AB=2AD=2,点E为AB的中点.
(1)求证:BD1∥平面A1DE
(2)求证:D1E⊥A1D;
(3)求点B到平面A1DE的距离.
3、如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.(1)求证:AB1⊥面A1BD;
(2)求点C到平面A1BD的距离.
题型二:求椎体体积
1、如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
(1)求证:DE∥面PBC;
(2)求证:AB⊥PE;
(3)求三棱锥B-PEC的体积.
2、三棱锥P-ABC中,PA=PB=PC,∠ACB=90°,AC=CB=2.
(1)求证:平面PAB⊥平面ABC;
(2)当∠PCB=60°时,求三棱锥A-PCB的体积.。
1m3等于多少nm3

1m3等于多少nm31m3等于1000nm3当我们谈论物理量时,它的单位是非常重要的。
从天文学、物理学、化学和生物学等多种领域,到家居科技和日常生活,单位换算是不可缺少的一环。
由于单位的重要性,它必须有一个准确的衡量方式来使其大家都能接受,并遵守相同的标准。
因此,给出一个可接受的单位换算系统,这两个量之间可以进行换算,这也有助于大家理解更多有关它们的知识。
以1m3等于1000nm3为例:1m3体积指1米立方,它表示单位面积为1平方米内垂直向上方向延伸1米时所得到的空间体积。
另外,1000nm3意味着体积为1立方微米。
1立方微米的体积等于1平方微米的面积的体积沿垂直方向延伸1微米时所得到的空间体积。
准确地说,在较大单位到较小单位之间的换算公式是:1m3 = 1000nm3(1m3 = 1000x10-9 m3)。
除了在家庭日常用品和新闻等之外,1m3等于1000nm3的概念在天文学领域同样重要。
在天文学中,物体之间的距离大多以光秒表示,然而它的测量规范尺度从数量级到惊人的光年时。
所以,在表达物体之间的距离时,需要对单位的大小进行换算,从而更准确地表示它们的实际距离。
此外,1m3等于1000nm3的概念还可以在医学或生物学方面使用。
在医学计量学中,医生非常有必要知道一物体的体积大小,以便更精确地测量药物的含量。
因此,正确的单位换算往往被不同领域的专家应用,以便更准确地测量药物的体积,而这种概念也会帮助他们更准确地计量其方程式中所使用的药物。
总而言之,1m3等于1000nm3是一种单位换算,用于从大到小改变实物的大小。
这种概念不仅用于工程计算场景,也可以用于家庭用品,也可以用于天文学和医学等其他领域。
这是一种有效的单位换算,有助于准确判断实物的大小。
三大守恒课件高二上学期化学人教版选择性必修1

离子种类: Na+、H+、CO32- 、HCO3- 、OH-: n(Na+)×1、n(H+)×1、n(CO32-)×2、n(HCO3-)×1、n(OH-)×1
电荷守恒: n(Na+)+n(H+)=2n(CO32- )+n(HCO3- )+n(OH-)
同除体积V: c(Na+)+c(H+)=2c(CO32- )+c(HCO3- )+c(OH-)
(2)CH3COONa溶液: c( Na+ ) + c ( H+ ) = c ( CH3COO– ) + c ( OH– )
(3)CH3COOH与CH3COONa等浓度等体积混合溶液:
c( Na+ ) + c ( H+ ) = c ( CH3COO– ) + c ( OH– )
小结
书写电荷守恒式必须注意: ①准确判断并找全溶液中阴、阳离子的种类; ②弄清离子浓度和电荷浓度的关系:系数看价态。
同除体积V: c(Na+)+c(H+)=2c(CO32- )+c(HCO3- )+c(OH-)
(1) Na2S 溶液 阳离子种类: Na+ 、H+ 阴离子种类: OH– 、 S2– 、 HS–
c (Na+ ) + c ( H+ ) = c ( OH– ) + 2c ( S2–) + c ( HS– )
(3)Na2SO3
c(Na+)=2[c( HSO3-) + c( SO32- )+ c(H2SO3 )]
小结
书写元素质量守恒式必须注意: ①通过溶质的化学式(混合溶液须考虑各溶质的含量)列出特定元素 的原子(或原子团)间的定量关系(特定元素一般为非H非O元素)。 ②找出特征元素在水溶液中的所有存在形式。
一炭单位的名词解释

一炭单位的名词解释炭是一种具有高热值和低灰分的燃料,广泛应用于能源、冶金和化工等行业。
在煤炭和石油资源日益匮乏的今天,对炭及其相关单位的研究和了解变得尤为重要。
本文将解释一炭单位,让我们更好地理解和应用于炭领域。
一炭单位是炭的体积密度单位,用于描述炭在一定条件下的密实程度。
一炭单位的定义是:1炭单位等于1立方米体积的炭质材料所具有的质量。
也就是说,当炭的体积为1立方米时,其质量就是一炭单位。
为什么需要引入一炭单位?这是因为炭的用途广泛,与其他能源相比,它有较高的热值和较低的灰分含量,因此被广泛应用于工业生产和民用需求。
而炭的体积密度对于储运以及计量等环节都非常重要。
不同类型的炭在炭单位上有所差异,例如木炭、煤炭、活性炭等,它们的体积和质量之间的关系不同,因此一炭单位的引入可以有效标准化炭的计量和管理。
一炭单位的计算方法有多种,根据所使用的炭的类型和特性不同,计算方法也会有所差异。
例如,对于木炭来说,可以根据木材的密度和含水率来计算出一炭单位的质量。
而对于煤炭来说,不同种类的煤炭有不同的密度和烟煤率,因此计算一炭单位的方法也不尽相同。
在能源和冶金等相关领域,一炭单位常被用来作为炭质材料的定量指标,用以评估和比较不同类型炭的性能。
考虑到不同炭质材料的特性和用途,一炭单位可以帮助我们了解炭的密实程度和热值等相关指标,从而为炭的选择和应用提供参考。
除了一炭单位之外,还有其他与炭密度相关的单位和指标,如堆密度和相对密度等。
堆密度是指炭在自重状态下堆积所占据的表观体积密度,它可以通过将炭装填到容器中并进行振实后得出。
而相对密度是指炭质材料的质量与相等体积水的质量之比,在炭领域中也有一定的应用。
总结起来,一炭单位是用于描述炭质材料体积密度的单位之一,作为炭的计量和性能评估指标具有重要意义。
通过对一炭单位的解释,我们可以更好地理解和应用于炭领域,并为相关行业的发展和创新提供支持。
虽然一炭单位本身只是一个技术术语,但它背后蕴含的深度和应用意义却值得我们深入探索。
有关等质量和等体积混合后溶液浓度的计算[1]
![有关等质量和等体积混合后溶液浓度的计算[1]](https://img.taocdn.com/s3/m/ac9e200876c66137ee061971.png)
有关等质量和等体积混合后溶液浓度的计算例题解析]:例题:已知25%氨水的密度0.91g/cm3,5%氨水的密度为0.98g/cm3,若将上述两溶液等体积混合,所得氨水溶液的质量分数()A.等于15%B.大于15%C.小于15%D.无法确定解法一:设所取溶液的体积为VmL,则混合后溶液的质量分数为[25%×V/0.91+5%×V/0.98]/(V×0.91+V×0.98)=15.37%>15%。
解法二:由氨水的浓度与密度的关系可知氨水的浓度越大,密度越小。
当将上述两种溶液等质量混合时,溶液的质量分数为15%。
当将两种溶液等体积混合时,25%氨水的质量小于5%氨水的质量。
即等同于在等质量混合的基础上又增加了5%氨水的质量,故混合液的质量分数小于15%。
[解题反思]:所谓反思,就是从一个新的角度,多层次、多角度地对问题及解决问题的思维过程进行全面的考察、分析和思考,从而深化对问题的理解,优化思维过程,提示问题本质,探索一般规律,沟通知识间的相互联系,促进知识的同化和迁移,并进而产生新的发现。
做到不仅要一题一得,更要一题多得,既能使知识得到不断的弥补、完善,又能举一反三。
通过对该题的分析可知,不仅可以利用计算手段判断混合后溶液质量分数的大小,也可以通过以等质量混合为参照进行判断的方法解题。
当采用对比方法解题时,应立足于溶液的密度与溶液浓度之间的变化关系:①以氨水、乙醇等溶液为代表:该类溶液的密度比水的密度小[d(aq)<d水],且溶液的浓度越大,溶液的密度越小。
将不同浓度的同种溶液混合时,等质量混合后溶液的质量分数大于等体积混合后溶液的质量分数。
②以硫酸溶液为代表:此类溶液的密度比水的密度大[d(aq)>d水],且溶液的浓度越大,溶液的密度越大。
将不同浓度的同种溶液混合时,等质量混合后溶液的质量分数小于等体积混合后溶液的质量分数。
因此,通过对解题方法的反思,实现一题多解,总结解题规律,做到举一反三。
内切球的等体积法公式(一)

内切球的等体积法公式(一)
内切球的等体积法公式
1. 问题描述
内切球是指一个球与由三个平面围成的三角形的每个平面都相切。
内切球的等体积法公式用于计算内切球的半径。
2. 公式推导
步骤1:计算三角形的面积
三角形的面积可以通过海伦公式计算,即:[S = ]
其中,(a)、(b)、(c) 分别为三角形的三边长,(p) 表示半周长:[p = (a + b + c)]
步骤2:计算内切球的半径
内切球的半径可以通过等体积法计算,即:[r = ]
其中,(V) 表示三角形的体积。
3. 解释说明
以一个具体的三角形为例,计算该三角形的内切球半径。
假设三角形的三边长分别为(a = 5)、(b = 6)、(c = 7),根据步骤1计算面积:
[p = (5 + 6 + 7) = 9]
[S = = 9]
假设三角形的体积为(V = 10),根据步骤2计算内切球半径:
[r = = = ]
所以,该三角形的内切球半径为()。
总结
通过内切球的等体积法公式,我们可以方便地计算一个三角形的内切球半径。
这个公式在实际应用中具有很大的实用价值,尤其在几何学和计算机图形学领域。
等体积法的原理及应用

等体积法的原理及应用1. 等体积法简介等体积法是一种物理实验方法,通过测量物质在不同条件下等体积时的性质变化,从而得到物质的相关参数或性质的定量信息。
等体积法主要用于固体和液体的实验研究,特别是在材料科学、地球化学、环境科学等领域得到广泛应用。
2. 等体积法的原理等体积法的原理基于以下基本假设:1.物质的体积在不同条件下基本保持不变;2.物质在等体积状态下的性质变化与所施加的条件具有相关性。
根据以上原理,我们可以通过保持测试物质的体积恒定,并测量物质在不同条件下的性质变化,进而推导出物质的相关参数。
3. 等体积法的应用案例3.1 固体材料的应用等体积法在固体材料研究中有广泛的应用,以下列举几个具体的案例:•材料的热膨胀系数测量:通过测量材料在不同温度下的线膨胀系数,可以进一步推导出热膨胀系数的相关参数,用于工程设计和材料选择等方面。
•材料的磁性测量:通过在不同磁场下测量材料的磁性变化,可以研究材料的磁性特性,例如磁化率和磁导率等。
•材料的力学性能分析:通过测量材料在不同应力下的体积变化,可以得到材料的弹性模量、屈服强度等重要参数,用于材料的强度和韧性评估。
3.2 液体的应用等体积法在液体研究中也有广泛的应用,以下列举几个具体的案例:•液体的密度测量:通过保持液体的体积不变,并测量其质量,可以计算出液体的密度,用于确定物质的纯度和浓度。
•溶液的浓度测定:通过测量溶液在不同浓度下的体积变化,可以推导出溶液的浓度,并进行溶液稀释等操作。
•液体的表面张力测量:通过测量液体在不同表面积下的液滴形态变化,可以计算出液体的表面张力,用于研究液体的表面性质和界面现象。
4. 结论等体积法是一种常用的物质性质研究方法,通过测量物质在等体积条件下的性质变化,可以获得物质的相关参数,具有重要的科学研究和工程应用价值。
在固体材料和液体领域,等体积法都有广泛的应用,可以用于研究材料的热性能、磁性能、力学性能等,以及液体的密度、溶液浓度、表面性质等。
物理等体积问题

物理等体积问题通常涉及到体积不变的物体或系统,需要我们运用相关的物理知识和公式来解答。
以下是一些常见的物理等体积问题:
气体等体积变化问题:这类问题通常涉及到气体在等体积变化过程中的状态变化,需要运用理想气体状态方程(PV=nRT)来解答。
其中,P表示压强,V表示体积,n表示摩尔数,R表示气体常数,T表示温度。
液体等体积问题:这类问题通常涉及到液体在等体积容器中的高度变化,需要运用液体压强公式(p=ρgh)来解答。
其中,ρ表示液体的密度,g表示重力加速度,h表示高度。
固体等体积问题:这类问题通常涉及到固体在等体积容器中的形状变化,需要运用固体压强公式(p=F/S)来解答。
其中,F表示作用在固体上的压力,S表示受力面积。
需要注意的是,在解决物理等体积问题时,要明确问题的条件和要求,选择合适的物理公式和模型进行分析和计算。
同时,要注意单位的统一和换算,确保计算结果的准确性和可靠性。
当量直径1

当量直径
因为实际颗粒的形状都是不规则 如何用一个尺寸描述其大小呢? 把颗粒看成一个相当的球, 该球体的直径作为颗粒的粒径. 由于相当的物理量不同, 就有不同的粒径.一般可分为: 1 等体积球当量径 dv 2 等表面积球当量径 ds
3 等比表面积球当量径 dsv 4 等沉降速度球当量径 又称为斯托克斯径 dst 5 等投影面积球当量径 da 6 等投影周长圆当量径 dL
1等体积球当量径dv2等表面积球当量径ds?3等比表面积球当量径dsv?4等沉降速度球当量径?又称为斯托克斯径dst?5等投影面积球当量径da6等投影周长圆当量径d?6等投影周长圆当量径dlv实际颗粒的体积36?vdv?12s实际颗粒的表面积?sds?2s3v2s3v666svddddsvd???????3?4斯托克斯stokes径是指与颗粒具有相同密度且在相同的沉降介质中具有相同沉降速度的颗粒直径
1 2
dv
3
6V
s
v ---实际颗粒的体积
S---实际颗粒的表面积
ds
3
6v d sv s
6
6 2 d sv 2 s
4 斯托克斯(stokes)径是指与颗粒具有相同 密度且在相同的沉降介质中具有相同沉降 速度的颗粒直径.具体计算方法在后面介绍. 5 da=(4A/π)1/2 A ---实际颗粒的投影面积 6 dL=L/π L ---实际颗粒投影的周长
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等积变形问题:
常用等量关系为:①形状面积变了,周长没变;
②容器形状改变,但容积没变
③原料体积=成品体积
1.用直径为90mm的圆柱形玻璃杯(已装满水)向一个由底面积为1251252
mm内高为81mm的长方体铁盒倒水时,玻璃杯中的水的高度下降多少mm?(结果保留)
2、现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?
3.一个长方形的周长长为26cm,这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,求长方形的长
4.将一个底面直径30厘米,高8厘米的圆锥形容器中倒满水,再将水倒入一只底面直径10厘米的圆柱形空容器里,圆柱形容器中的水面有多高?
5.将棱长为20cm的正方体铁块锻造成一个长为100cm,宽为5cm的长方体铁块,求长方体铁块的高度。
6.将棱长为20cm的正方体铁块没入盛水量筒中,已知量筒底面积为12cm2,问量筒中水面升高了多少cm?
配套问题:
1.有28名工人生产螺栓和螺母,每人每小时平均生产螺栓12个或螺母18个,应如何分配生
120个劳力修建水库,平均每天每个劳力能挖土5 m3或运土3m3,为
?
25人组织的小分队参加防汛抗洪斗争,若每人每小时可装泥土18袋或每2人每小时可抬泥土14袋,如何安排好人力,才能使装泥和抬泥密切配合,而正好清
15个机轴或10个轴承。
一根机轴和两个轴
2米布可以裁上衣3件,或裁裤子4条,现有花呢240米,为了使
6、机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工。
