2011届中考数学第一轮专题复习课件9
合集下载
中考数学专题复习课件 --- 第九讲不等式与不等式组
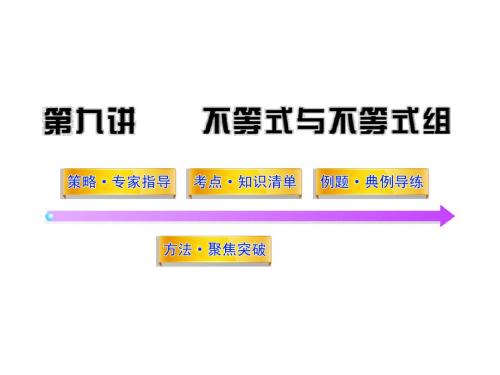
7.(2010·湘潭中考)解不等式2(x-1)＜x+1，并求它的非负整 数解. 【解析】原不等式可化为2x-x＜1+2，∴x＜3，
∴它的非负整数解为0，1，2.
5 2x 3 8.(2011·南京中考)解不等式组 x 1 x ,并写出不等式组 3 2
的整数解.
5 2x 3 ① , 【解析】 x 1 x 3 2 ②
政府补贴.农民田大伯到该商城购买了冰箱、彩电各一台，可
以享受多少元的补贴?
(2)为满足农民需求，商场决定用不超过85 000元采购冰箱、 彩电共40台，且冰箱的数量不少于彩电数量的 5 . 若使商场获
6
利最大,请你帮助商场计算应该购进冰箱、彩电各多少台？最 大获利是多少?
【解析】(1)(2 420+1 980)×13%=572(元). (2)设冰箱采购x台，则彩电采购(40-x)台，根据题意得
甲： 7 当 时，租车费用为7×2 000+3×1 800=19 400(元)； 甲： 4 所以，当 时，租车费用最便宜，费用为18 800元. 6 乙：
1.(2010·温州中考)某班级从文化用品市场购买了签字笔和 圆珠笔共15支，所付金额大于26元，但小于27元.已知签字笔 每支2元，圆珠笔每支1.5元，则其中签字笔购买了_____支. 【解析】设签字笔购买了x支，则购买圆珠笔(15-x)支，由题
3
表示出来.
【解析】去分母，得3(x-1)≤1+x,
去括号，得3x-3≤1+x,
移项，合并同类项，得2x≤4,
系数化为1，得x≤2.
把解集在数轴上表示出来如图所示：
1 2 x 1 5 ① 4.(2010 ·毕节中考)解不等式组 3x 2 , 并把解 1 ＜x ② 2 2 集在数轴上表示出来.
2011中考数学全套复习课件(共52)专题8
根类型之二 图形规律型 据一组相关图案的变化规律， 据一组相关图案的变化规律，从中总结图形的变化 所反映的规律， 所反映的规律，其中以图形为载体的变化规律最 常见，猜想这种规律时， 常见，猜想这种规律时，需要把图形的变化规律 仔细观察，对图形进行对照，最终得到结论. 仔细观察，对图形进行对照，最终得到结论
专题训练(八 归纳、 专题训练 八) 归纳、猜想与说理判断
所谓归纳、 所谓归纳、猜想问题指的是给出一组具有某种特定 关系的数，式，图形，或是给出与图形有关的操 关系的数， 图形， 变化过程，要求通过观察，分析，推理， 作，变化过程，要求通过观察，分析，推理，探 求其中所蕴含的规律， 求其中所蕴含的规律，进而归纳或猜想出一般性 的结论．常见类型： 数字猜想型 数字猜想型； 数式规律 的结论．常见类型：(1)数字猜想型；(2)数式规律 图象变化猜想型； 数形结合猜想型 数形结合猜想型； 型；(3)图象变化猜想型；(4)数形结合猜想型；(5) 图象变化猜想型 坐标变化型．热点知识：数与式的运算，因式分 坐标变化型．热点知识：数与式的运算， 平面直角坐标系，三角形，特殊四边形， 解，平面直角坐标系，三角形，特殊四边形，几 何变换，图形的组合等知识． 何变换，图形的组合等知识．
专题训练(八 归纳、 专题训练 八) 归纳、猜想与说理判断
深圳] 例1 [2010深圳 观察下列算式，用你所发现的规 深圳 观察下列算式， 律得出22010的末位数字是 的末位数字是( ) 律得出 的末位数字是 21＝2, 22＝4, 23＝8, 24＝16, 25＝32, 26＝64, 27＝128, 28＝256，… ， A.2 B．4 C．6 D．8 ． ． ．
专题训练(八 归纳、 专题训练 八) 归纳、猜想与说理判断
2011中考数学全套复习课件(共52)第1课时
第1课时
实数的有关概念
类型之一 实数的概念及分类 命题角度： 命题角度： 1．有理数与无理数的概念 ． 2．实数的分类 ． 巴中] 例1 [2010巴中 下列各数： ，0， ， 巴中 下列各数： ， ， cos60°， ，0.303003 … (两个“3”之间依次多 两个“ 之间依次多 ° 两个 一个“ ， － 无理数个数为( ) 一个“0”)，1－ 中，无理数个数为 A．2个 B．3个 C．4个 D．5个 ． 个 ． 个 ． 个 ． 个
第1课时
考点一 实数的概念及分类 1．按定义分类 ．
实数的有关概念
实数
第1课时
考点一 实数的概念及分类 1．按正负分类 ．
实数的有关概念
实数
[注意 注意] 注意 (1)任何分数都是有 任何分数都是有 理数， 理数， (2)0既不是正数， 既不是正数， 既不是正数 也不是负数， 也不是负数，但0是 是 自然数． 自然数． (3)常见的几种无理 常见的几种无理 根号型： 数：①根号型：② 三角函数型; 三角函数型 ③构 造型； 有关的. 造型；④与π有关的 有关的
第1课时
实数的有关概念
类型之四 创新应用题 命题角度： 命题角度： 1．探究数字规律 ． 2．探究图形与数字的变化关系 ． 南宁] 例4,[2010南宁 古希腊数学家把数 南宁 古希腊数学家把数1,3,6,10,15,21，… ， 叫做三角形数， 它有一定的规律性， 叫做三角形数 ， 它有一定的规律性 ， 若把第一个三 角形数记为a 第二个三角形数记为a 角形数记为 1， 第二个三角形数记为 2， …，第 n个 ， 个 三角形数记为a 计算a 三角形数记为 n， 计算 2－ a1，a3－ a2，a4－ a3，…， ， 由此推算a 由此推算 100－a99＝________，a100＝________. ，
2011届中考数学备考复习课件：2.3《一元一次不等式(组)及其解法》
第13课时 一元一次不 课时 等式（ 等式（组）及其解法
1．用不等号连接而成的式子叫不等式；只含有一 ．用不等号连接而成的式子叫不等式； 个未知数，并且未知数的次数是1， 个未知数，并且未知数的次数是 ，并且两边都是 整式的不等式，叫做一元一次不等式． 整式的不等式，叫做一元一次不等式． 2．不等式的性质： ．不等式的性质： （1）不等式的两边都加上（或减去）同一个整式， ）不等式的两边都加上（或减去）同一个整式， 不等号方向不变。 不等号方向不变。 2）不等式的两边都乘以（或除以）同一个正数， （2）不等式的两边都乘以（或除以）同一个正数， 不等号方向不变。 不等号方向不变。 （3）不等式的两边都乘以（或除以）同一个负数， ）不等式的两边都乘以（或除以）同一个负数， 不等号方向改变。 不等号方向改变。
6．一元一次不等式与一次函数的联系： ．一元一次不等式与一次函数的联系： 解一元一次不等式ax + b < 0 或 ax + b > 0 可以看着是求一次函数 y = ax + b 的 图象在x轴上方或下方方自变量 轴上方或下方方自变量x的取值范 图象在 轴上方或下方方自变量 的取值范 围。
【例1】（2010年毕节）解不等式 】 组
1 − 2( x − 1) ≤ 5 3x − 2 1 2 < x+ 2
，
并把解集在数轴上表示出来．
．（09深圳 例2．（ 深圳）先阅读理解下面的例题，再按要 ．（ 深圳）先阅读理解下面的例题， 求解答： 求解答： 2 例题：解一元二次不等式. 例题：解一元二次不等式 x − 9 > 0 x 2 − 9 = ( x + 3)( x − 3) 解：∵ ∴ ( x + 3)( x − 3) > 0 由有理数的乘法法则“两数相乘，同号得正” 由有理数的乘法法则“两数相乘，同号得正”，有 1） 2） （1） x + 3 > 0 （2） x + 3 < 0 解不等式组（ ）， ），得 解不等式组（1），得， x > 3 解不等式组（ ）， ），得 解不等式组（2），得， x < −3 x>3 故 ( x + 3)( x − 3) > 0 的解集为 x < −3 2 x > 3 x < −3 x −9 > 0 或， 5x + 1 即一元二次不等式 的解集为 <0 2x − 3 或. 问题： 的解集. 问题：求分式不等式 的解集
1．用不等号连接而成的式子叫不等式；只含有一 ．用不等号连接而成的式子叫不等式； 个未知数，并且未知数的次数是1， 个未知数，并且未知数的次数是 ，并且两边都是 整式的不等式，叫做一元一次不等式． 整式的不等式，叫做一元一次不等式． 2．不等式的性质： ．不等式的性质： （1）不等式的两边都加上（或减去）同一个整式， ）不等式的两边都加上（或减去）同一个整式， 不等号方向不变。 不等号方向不变。 2）不等式的两边都乘以（或除以）同一个正数， （2）不等式的两边都乘以（或除以）同一个正数， 不等号方向不变。 不等号方向不变。 （3）不等式的两边都乘以（或除以）同一个负数， ）不等式的两边都乘以（或除以）同一个负数， 不等号方向改变。 不等号方向改变。
6．一元一次不等式与一次函数的联系： ．一元一次不等式与一次函数的联系： 解一元一次不等式ax + b < 0 或 ax + b > 0 可以看着是求一次函数 y = ax + b 的 图象在x轴上方或下方方自变量 轴上方或下方方自变量x的取值范 图象在 轴上方或下方方自变量 的取值范 围。
【例1】（2010年毕节）解不等式 】 组
1 − 2( x − 1) ≤ 5 3x − 2 1 2 < x+ 2
，
并把解集在数轴上表示出来．
．（09深圳 例2．（ 深圳）先阅读理解下面的例题，再按要 ．（ 深圳）先阅读理解下面的例题， 求解答： 求解答： 2 例题：解一元二次不等式. 例题：解一元二次不等式 x − 9 > 0 x 2 − 9 = ( x + 3)( x − 3) 解：∵ ∴ ( x + 3)( x − 3) > 0 由有理数的乘法法则“两数相乘，同号得正” 由有理数的乘法法则“两数相乘，同号得正”，有 1） 2） （1） x + 3 > 0 （2） x + 3 < 0 解不等式组（ ）， ），得 解不等式组（1），得， x > 3 解不等式组（ ）， ），得 解不等式组（2），得， x < −3 x>3 故 ( x + 3)( x − 3) > 0 的解集为 x < −3 2 x > 3 x < −3 x −9 > 0 或， 5x + 1 即一元二次不等式 的解集为 <0 2x − 3 或. 问题： 的解集. 问题：求分式不等式 的解集
2011中考数学全套复习课件(共52)专题9
专题训练(九 专题训练 九) 动态型问题
针对训练2.[2010厦门 如图矩形 厦门] 如图矩形ABCD的边 、AB 的边AD、 针对训练 厦门 的边 分别与⊙ 相切于点 相切于点E、 ， ＝ 求的长； 分别与⊙O相切于点 、F，AE＝ .(1)求的长；(2) 求的长 分别交射线DA、 于点 若AD＝ ＋5，直线 ＝ ，直线MN分别交射线 、DC于点 分别交射线 M、 N， ∠ DMN＝60° ， 将直线 沿射线DA方 、 ， ＝ ° 将直线MN沿射线 方 沿射线 向平移， 设点D到直线的距离为 到直线的距离为d， 向平移 ， 设点 到直线的距离为 ， 当 1≤d≤4时 ， 时 请判断直线MN与⊙O的位置关系，并说明理由． 的位置关系， 请判断直线 与 的位置关系 并说明理由．
专题训练(九 专题训练 九) 动态型问题
针 对 训 练 1.[2009 包 头 ] 如 图 在 △ABC 中 ， AB=AC=10cm,BC＝8cm,点D为AB的中点 的中点.(1)若点 ＝ 点 为 的中点 若点 P在线段 上以 厘米 秒的速度由 点向 点运动 ， 在线段BC上以 厘米/秒的速度由 点向C点运动 在线段 上以3厘米 秒的速度由B点向 点运动， 同时点Q在线段 上由C点向 点运动． 若点Q 在线段CA上由 点向A点运动 同时点 在线段 上由 点向 点运动 ． ① 若点 的运动速度与点P的运动速度相等 经过1秒后 的运动速度相等， 秒后， 的运动速度与点 的运动速度相等 ， 经过 秒后 ， 是否全等； 若点Q的运动速度与 △BPD与△CQP是否全等；②若点 的运动速度与 与 是否全等 的运动速度不相等， 点 P的运动速度不相等， 当点 的运动速度为多少 的运动速度不相等 当点Q的运动速度为多少 能够使△ 时，能够使△BPD与△CQP 与 全等？ 若点 若点Q以 全等？(2)若点 以②中的运动速度 从点C出发 出发， 从点 出发，点P以原来的运 动速度 以原来的运 从点B同时出发 都逆时针沿△ 同时出发， 从点 同时出发，都逆时针沿△ABC 三边运动，求经过多长时间点P与点 三边运动，求经过多长时间点 与点 Q第一次在△ABC的哪条边上相遇？ 第一次在△ 的哪条边上相遇？ 第一次在 的哪条边上相遇
2011届中考数学备考复习课件：3.7《多边形、四边形与平行四边形》
5．平行四边形的判定: ．平行四边形的判定 (1)两组对边分别平行的四边形是平行四边形 两组对边分别平行的四边形是平行四边形. 两组对边分别平行的四边形是平行四边形 (2)一组对边平行且相等的四边形是平行四边形 一组对边平行且相等的四边形是平行四边形. 一组对边平行且相等的四边形是平行四边形 (3) 两组对边分别相等的四边形是平行四边形 两组对边分别相等的四边形是平行四边形. (4) 两组对角相等的四边形是平行四边形 两组对角相等的四边形是平行四边形. (5)对角线互相平分的四边形是平行四边形 对角线互相平分的四边形是平行四边形. 对角线互相平分的四边形是平行四边形
4．平行四边形的性质： ．平行四边形的性质： （1）边的关系：两组对边分别平行且相等。 ）边的关系：两组对边分别平行且相等。 （2）角的关系：两组对角分别相等；邻角 ）角的关系：两组对角分别相等； 互补。 互补。 （3）对角线的关系：对角线互相平分。 ）对角线的关系：对角线互相平分。 （4）对称性：平行四边形是中心对称图形， ）对称性：平行四边形是中心对称图形， 对角线的交点是对称中心。 对角线的交点是对称中心。
第27课时 多边形、四边形 课时 多边形、 与平行四边形
180 0 (n − 2) 1.多边边形的内角和公式为
为大于2的整数）；多边形的外角和为 （n为大于 的整数）；多边形的外角和为 为大于 的整数）； 3600。 2．正多边形的概念：各条边都相等、各 ．正多边形的概念：各条边都相等、 内角都都相等的多边形是正多边形。 内角都都相等的多边形是正多边形。 3．平行四边形定义：两组对边分别平行 ．平行四边形定义： 的四边形叫做平行四边形。 的四边形叫做平行四边形。
四川资阳)如图 例1.( 09四川资阳 如图，已知□ABCD的对 四川资阳 如图， 角线AC、BD相交于点O，AC =12，BD=18， ， ， 的长． ， 且△AOB的周长l=23，求AB的长．
2011届中考数学备考复习课件：1.9《一元二次方程根的判别式及根与系数的关系》
x1 x2 p
x1 x2 q
例1．(广州)已知：关于 1 0
的两个实数根的倒数和为3，求m的值．
例2．（中山）已知关于x的方程.
x (m 2) x 2m 1 0
2
（1）求证:方程有两个不相等的实数根. （2）当m为何值时，方程的两根互为相 反数？并求出此时方程的解.
第9课时 一元二次方程根的 判别式及根与系数的关系
1．一元二次方程 ax bx c 0(a 0) b 2 4ac 的根的判别式△＝ 当△＞0时，方程有两个不相等的实数根； 当△＝0时，方程有两个相等的实数根， 当△＜0时，方程没有实数根．
2
2.一元二次方程的根与系数的关系 ax 2 bx c 0(a 0) (1)如果一元二次方程 的两个根是x1 , x 2 ,那么， c b x1 x 2 x1 x2 a a x 2 px q 0 (2)如果方程 的 x1 , x 2 两个根是 ，那么，
x x 例3．（河南）已知， 1 , 2 2 是关于x的一元二次方程 x 6 x k 0 2 2 的两个实数根，且 x1 x2 x1 x2 115 2 2 (1)求k的值；（2）求 x1 x2 8 的值.
2011届中考数学备考复习课件：2.7《反比例函数》
y 3 A（角坐标系xOy中，一次 ．（07汕头 如图， ．（ 汕头） k2 函数y＝k1x＋b的图象与反比例函数 y = x 两点。 的图象交于A(1，4)、B(3，m)两点。 (1)求一次函数的解析式； 求一次函数的解析式； 求一次函数的解析式 的面积。 (2)求△AOB的面积。 求
1.（09肇庆）如图 1，已知一次函数 （ 肇庆 肇庆） ， y1 = x + m 为常数） （m为常数）的图象与反比例 k 函 y2 = x 为常数） 数 （k为常数）的图象相交于点A （1，3）． ， ）． （1）求这两个函数的解析式及其图象的另一交 ） 的坐标； 点B的坐标； 的坐标 y1 ≥ y2 （2）观察图象，写出使函数值 ）观察图象， 的自变 的取值范围． 量X的取值范围． 的取值范围
第17课时 课时
反比例函数
1． 反比例函数及其图象 ． 那么， 那么，y 的反比例函数。 是x的反比例函数。 的反比例函数 反比例函数的图象是双曲线， 反比例函数的图象是双曲线，它有两 个分支， 个分支，可用描点法画出反比例函数 的图象
k 如果 y = x ( k 是常数 , k ≠ 0 )
,
2．反比例函数的性质 ． 当K>0时，图象的两个分支分别在一、三象 时 图象的两个分支分别在一、 限内，在每个象限内， 随 的增大而减小 的增大而减小； 限内，在每个象限内， y随x的增大而减小； 当K<0时，图象的两个分支分别在二、四象 时 图象的两个分支分别在二、 限内，在每个象限内， 随 的增大而增大 的增大而增大。 限内，在每个象限内，y随x的增大而增大。 3．待定系数法 ． 先设出式子中的未知数， 先设出式子中的未知数，再根据条件求出未 知系数， 知系数，从而写出这个式子的方法叫做待定 系数法可用待定系数法求一次函数、 系数法可用待定系数法求一次函数、二次函 数和反比例函数的解析式。 数和反比例函数的解析式。
1.（09肇庆）如图 1，已知一次函数 （ 肇庆 肇庆） ， y1 = x + m 为常数） （m为常数）的图象与反比例 k 函 y2 = x 为常数） 数 （k为常数）的图象相交于点A （1，3）． ， ）． （1）求这两个函数的解析式及其图象的另一交 ） 的坐标； 点B的坐标； 的坐标 y1 ≥ y2 （2）观察图象，写出使函数值 ）观察图象， 的自变 的取值范围． 量X的取值范围． 的取值范围
第17课时 课时
反比例函数
1． 反比例函数及其图象 ． 那么， 那么，y 的反比例函数。 是x的反比例函数。 的反比例函数 反比例函数的图象是双曲线， 反比例函数的图象是双曲线，它有两 个分支， 个分支，可用描点法画出反比例函数 的图象
k 如果 y = x ( k 是常数 , k ≠ 0 )
,
2．反比例函数的性质 ． 当K>0时，图象的两个分支分别在一、三象 时 图象的两个分支分别在一、 限内，在每个象限内， 随 的增大而减小 的增大而减小； 限内，在每个象限内， y随x的增大而减小； 当K<0时，图象的两个分支分别在二、四象 时 图象的两个分支分别在二、 限内，在每个象限内， 随 的增大而增大 的增大而增大。 限内，在每个象限内，y随x的增大而增大。 3．待定系数法 ． 先设出式子中的未知数， 先设出式子中的未知数，再根据条件求出未 知系数， 知系数，从而写出这个式子的方法叫做待定 系数法可用待定系数法求一次函数、 系数法可用待定系数法求一次函数、二次函 数和反比例函数的解析式。 数和反比例函数的解析式。
2011届中考数学备考复习课件：4.2《与圆有关的计算》
第32课时 与圆有关的计算 课时
1．弧长公式：在半径为的圆中，如果圆心 ．弧长公式：在半径为的圆中， 角为， 角为，则它所对的弧长为 l = nπR 。
180
2．扇形的面积和周长：如果扇形的半径为 ．扇形的面积和周长： nπR 0，扇形的周长等 + 2R R，圆心角为 ，圆心角为n 180 2 nπR lR 于 ；扇形的面积为 或 S= 360 2 中为弧长）。 （其L中为弧长）。 中为弧长
D A O B
别是 ．将两边长分别是4cm和6cm的矩形 和 的矩形 以其一边所在的直线为轴旋转一周， 以其一边所在的直线为轴旋转一周，所 ． 得圆柱体表面积为
例3．（贵州）如图，已知AB是⊙O的 ．（贵州）如图，已知 是 的 ．（贵州 直径， 直径，点C在⊙O上，且AB=13， 在 上 ， BC=5 ． 的值． （1）求 sin ∠BAC ） 的值． （2）如果 ）如果OD⊥AC，垂足为 ，求AD ⊥ ，垂足为D， 的长． 的长． （3）求图中阴影部分的面积（精确到 ）求图中阴影部分的面积（ 0.1）． ）． C
例1．（株洲）如下图中每个阴影部分是 ．（株洲） ．（株洲 以多边形各顶点为圆心， 为半径的扇形 为半径的扇形， 以多边形各顶点为圆心，1为半径的扇形， 并且所有多边形的每条边长都大于2， 并且所有多边形的每条边长都大于 ，则 个多边形中， 第n个多边形中，所有扇形面积之和是 个多边形中 （结果保留π）.
3．圆锥的侧面展开图是扇形，这个扇 ．圆锥的侧面展开图是扇形， 形的弧长等于圆锥的底面周长即 2∏R 其中R为底面圆的半径 为底面圆的半径）； （其中 为底面圆的半径）； 扇形半径等于圆锥的母线长l。 扇形半径等于圆锥的母线长 。圆锥的侧 S侧 rl；圆锥的全面 面积公式为 = π ； 积等于侧面积与底面积的和。 积等于侧面积与底面积的和。
1．弧长公式：在半径为的圆中，如果圆心 ．弧长公式：在半径为的圆中， 角为， 角为，则它所对的弧长为 l = nπR 。
180
2．扇形的面积和周长：如果扇形的半径为 ．扇形的面积和周长： nπR 0，扇形的周长等 + 2R R，圆心角为 ，圆心角为n 180 2 nπR lR 于 ；扇形的面积为 或 S= 360 2 中为弧长）。 （其L中为弧长）。 中为弧长
D A O B
别是 ．将两边长分别是4cm和6cm的矩形 和 的矩形 以其一边所在的直线为轴旋转一周， 以其一边所在的直线为轴旋转一周，所 ． 得圆柱体表面积为
例3．（贵州）如图，已知AB是⊙O的 ．（贵州）如图，已知 是 的 ．（贵州 直径， 直径，点C在⊙O上，且AB=13， 在 上 ， BC=5 ． 的值． （1）求 sin ∠BAC ） 的值． （2）如果 ）如果OD⊥AC，垂足为 ，求AD ⊥ ，垂足为D， 的长． 的长． （3）求图中阴影部分的面积（精确到 ）求图中阴影部分的面积（ 0.1）． ）． C
例1．（株洲）如下图中每个阴影部分是 ．（株洲） ．（株洲 以多边形各顶点为圆心， 为半径的扇形 为半径的扇形， 以多边形各顶点为圆心，1为半径的扇形， 并且所有多边形的每条边长都大于2， 并且所有多边形的每条边长都大于 ，则 个多边形中， 第n个多边形中，所有扇形面积之和是 个多边形中 （结果保留π）.
3．圆锥的侧面展开图是扇形，这个扇 ．圆锥的侧面展开图是扇形， 形的弧长等于圆锥的底面周长即 2∏R 其中R为底面圆的半径 为底面圆的半径）； （其中 为底面圆的半径）； 扇形半径等于圆锥的母线长l。 扇形半径等于圆锥的母线长 。圆锥的侧 S侧 rl；圆锥的全面 面积公式为 = π ； 积等于侧面积与底面积的和。 积等于侧面积与底面积的和。
2011届中考数学备考复习课件：4.10《概率计算》
P 实验的总次数
通常有两种方法来求：一是列表法；二 是树状图法。
例1．（09肇庆）掷一个骰子，观察向上 一面的点数，求下列事件的概率： （1）点数为偶数； （2）点数大于 2 且小于5
例2．（广东）甲、乙、丙三名学生各自随机选 择到A、B两个书店购书． （1）求甲、乙两名学生在不同书店购书的概率； （2）求甲、乙、丙三名学生在同一书店购书的 概率．
例3．（江苏连云港）九年级1班将竞选 出正、副班长各1名，现有甲、乙两位男 生和丙、丁两位女生参加竞选． （1）男生当选班长的概率是 ； （2）请用列表或画树状图的方法求出两 位女生同时当选正、副班长的概率．
第40课 概率计算
1 必然事件： 发生的概率为 1.事件：确定事件 不可能事件： 发生的概率为0
不确定事件：发生的概率大于0小于1。
2.概率：表示一件事发生的可能性的大小； 3.机会：不确定事件经过多次试验使之趋于稳定 状态时，这个事件的成功率，我们把这种成功 率表示一件事件发生的可能性，即机会。 4.随机事件的概率通常用机会来表示。某事件发 生的概率为多少，也就是说这件事发生的机会 是多少。
通常有两种方法来求：一是列表法；二 是树状图法。
例1．（09肇庆）掷一个骰子，观察向上 一面的点数，求下列事件的概率： （1）点数为偶数； （2）点数大于 2 且小于5
例2．（广东）甲、乙、丙三名学生各自随机选 择到A、B两个书店购书． （1）求甲、乙两名学生在不同书店购书的概率； （2）求甲、乙、丙三名学生在同一书店购书的 概率．
例3．（江苏连云港）九年级1班将竞选 出正、副班长各1名，现有甲、乙两位男 生和丙、丁两位女生参加竞选． （1）男生当选班长的概率是 ； （2）请用列表或画树状图的方法求出两 位女生同时当选正、副班长的概率．
第40课 概率计算
1 必然事件： 发生的概率为 1.事件：确定事件 不可能事件： 发生的概率为0
不确定事件：发生的概率大于0小于1。
2.概率：表示一件事发生的可能性的大小； 3.机会：不确定事件经过多次试验使之趋于稳定 状态时，这个事件的成功率，我们把这种成功 率表示一件事件发生的可能性，即机会。 4.随机事件的概率通常用机会来表示。某事件发 生的概率为多少，也就是说这件事发生的机会 是多少。
2011届中考数学备考复习课件：2.2《方程(组)的应用(二)》
例4.（广东）将一条长为 （广东）将一条长为20cm的铁丝剪 的铁丝剪 成两段， 成两段，并以每一段铁丝的长度为周长做 成一个正方形． 成一个正方形． (1)要使这两个正方形的面积之和等于 要使这两个正方形的面积之和等于 17cm2，那么这段铁丝剪成两段后的长度 分别是多少? 分别是多少? (2)两个正方形的面积之和可能等于 两个正方形的面积之和可能等于 12cm2吗? 若能，求出两段铁丝的长度； 若能，求出两段铁丝的长度； 若不能，请说明理由． 若不能，请说明理由．
．（贵阳 例1．（贵阳）汽车产业的发展，有效促 ．（贵阳）汽车产业的发展， 进我国现代化建设． 进我国现代化建设．某汽车销售公司 2005年盈利 年盈利1500万元，到2007年盈利 万元， 年盈利 万元 年盈利 2160万元，且从 万元， 年到2007年，每 万元 且从2005年到 年到 年 年盈利的年增长率相同． 年盈利的年增长率相同． 年盈利多少万元？ （1）该公司 ）该公司2006年盈利多少万元？ 年盈利多少万元 （2）若该公司盈利的年增长率继续保持 ） 不变，预计2008年盈利多少万元？ 年盈利多少万元？ 不变，预计 年盈利多少万元
第12课时 方程（组） 课时 方程（ 的应用（ 的应用（二）
1．增长率问题：原产量为a，平均年增长率为 ．增长率问题： a(1 x，则一年后产量a(1 + x) ，二年后产量为 + x) 2 …… n年后量为 (1 + x) n 年后量为 。 a 利润 2．利润问题：利润 售价 进价，利润率 进价 售价—进价 ．利润问题：利润=售价 进价，利润率= 3．本息和 本金 利息．利息 本金× 利率 期 本金+利息 ．本息和=本金 利息．利息=本金 × 数 4．数字问题：一个三位数百位数字为 ，十 ．数字问题：一个三位数百位数字为a， 位数字为b，百位数字为c， 位数字为 ，百位数字为 ，则这个三位数可表 示为100a+10b+c． 示为 ． 5.面积与周长等与几何方面有关的问题． 面积与周长等与几何方面有关的问题． 面积与周长等与几何方面有关的问题
2011届中考数学备考复习课件：2.8《二次函数的图象与性质》
2
（1）求二次函数的表达式，并在右图中 ）求二次函数的表达式， 画出它的图象； 画出它的图象； 2 − （2）求证：对任意实数 ，点 M ( m， m ) ）求证：对任意实数m， 都不在这个二次函数的图象上． 都不在这个二次函数的图象上．
y = ax 2 + bx + c 例3．二次函数 ．
第18课时 课时
二次函数的图象与性质
二次函数及其图象 1.如果 如果y=ax2+bx+c(a,b,c是常数， 是常数， 如果 是常数 a≠0),那么，y叫做 的二次函数。 那么， 叫做 的二次函数。 叫做x的二次函数 那么 2.二次函数的图象是抛物线，可用描点 二次函数的图象是抛物线， 二次函数的图象是抛物线 法画出二次函数的图象。 法画出二次函数的图象。 3.抛物线的顶点、对称轴和开口方向 抛物线的顶点、 抛物线的顶点 b 4ac − b 2 抛物线y=ax2+bx+c(a≠0)的顶点是 (− 2a , 4a ) 抛物线 的顶点是 b 对称轴是 x = − ，当a>0时，抛物线开 时 2a 口向上， 口向上，当a<0时，抛物线开口向下。 时 抛物线开口向下。 4.抛物线 抛物线y=a(x+h)2+k(a≠0)的顶点是 抛物线 的顶点是 ），对称轴是 （-h，k），对称轴是 ， ），对称轴是x=-h.
．（常州 例1．（常州）二次函数 ．（常州） 的部分对应值如下表： 的部分对应值如下表：
y = ax + bx + c
2
x
y
轴为 = x 值 y=
…
−3
−2
0
1
3
−5
5 7
…
…
7
0
（1）求二次函数的表达式，并在右图中 ）求二次函数的表达式， 画出它的图象； 画出它的图象； 2 − （2）求证：对任意实数 ，点 M ( m， m ) ）求证：对任意实数m， 都不在这个二次函数的图象上． 都不在这个二次函数的图象上．
y = ax 2 + bx + c 例3．二次函数 ．
第18课时 课时
二次函数的图象与性质
二次函数及其图象 1.如果 如果y=ax2+bx+c(a,b,c是常数， 是常数， 如果 是常数 a≠0),那么，y叫做 的二次函数。 那么， 叫做 的二次函数。 叫做x的二次函数 那么 2.二次函数的图象是抛物线，可用描点 二次函数的图象是抛物线， 二次函数的图象是抛物线 法画出二次函数的图象。 法画出二次函数的图象。 3.抛物线的顶点、对称轴和开口方向 抛物线的顶点、 抛物线的顶点 b 4ac − b 2 抛物线y=ax2+bx+c(a≠0)的顶点是 (− 2a , 4a ) 抛物线 的顶点是 b 对称轴是 x = − ，当a>0时，抛物线开 时 2a 口向上， 口向上，当a<0时，抛物线开口向下。 时 抛物线开口向下。 4.抛物线 抛物线y=a(x+h)2+k(a≠0)的顶点是 抛物线 的顶点是 ），对称轴是 （-h，k），对称轴是 ， ），对称轴是x=-h.
．（常州 例1．（常州）二次函数 ．（常州） 的部分对应值如下表： 的部分对应值如下表：
y = ax + bx + c
2
x
y
轴为 = x 值 y=
…
−3
−2
0
1
3
−5
5 7
…
…
7
0
2011届中考数学备考复习课件：1.1《实数的概念》
．（09湛江 例1．（ 湛江）如图，一只蚂蚁从 点沿数 ．（ 湛江）如图，一只蚂蚁从A点沿数 轴向右直爬2个单位到达点 个单位到达点B， 轴向右直爬 个单位到达点 ，A 点表示 − 2， 点所表示的数为m 设B点所表示的数为 点所表示的数为 的值； （1）求m 的值； ） m − 1 + (m + 6)0 的值。 的值。 （2）求 ）
实数的运算： 8．实数的运算：先乘除后加减有括号先算括号 里面的；同一级运算按照从左至右的顺序进行。 里面的；同一级运算按照从左至右的顺序进行。 9．近似数、有效数字与科学计数法： 近似数、有效数字与科学计数法： a × 10 n 的形式（ （1）把一个数写成 的形式（其中 1 ≤ a < 10 n是整数），这种记数法叫科学计数法。 是整数），这种记数法叫科学计数法。 ），这种记数法叫科学计数法 近似数： （2）近似数：一般地一个近似数四舍五入到哪一 就说这个近似数精确到哪一位。 位，就说这个近似数精确到哪一位。 （3）有效数字：一个近似数，从左边第一个不是 有效数字：一个近似数， 的数字起到精确到的数位止， 0的数字起到精确到的数位止，所有的数字都叫做 这个数的有效数字。 这个数的有效数字。
从一做起 做到第一
第一章第1课时
实数的概念
要点、 要点、考点聚焦 基础训练 典型例题解析
1、实数的分类 、
整数 有理 数 实数 无理 数 分数 负整数 正分数 负分数 有限小数或循环小数
正无理数 负无理数
无限不循环小数
2.数轴：规定了原点、 2.数轴：规定了原点、正方向和单位长度的直线 数轴 叫做数轴(画数轴时， 叫做数轴(画数轴时，要注意上述规定的三要素缺 一个不可) 实数与数轴上的点是一一对应的。 一个不可)，实数与数轴上的点是一一对应的。数 轴上的点所表示的数，从左到右逐渐增大。 轴上的点所表示的数，从左到右逐渐增大。 只有符号不同的两个数，称为互为相反数， 3．只有符号不同的两个数，称为互为相反数， 零的相反数是零，从数轴上看， 零的相反数是零，从数轴上看，互为相反数的 两个数所对应的点关于原点对称． 两个数所对应的点关于原点对称．互为相反数 的两个数和为0 的两个数和为0。 绝对值：从数轴上看， 4．绝对值：从数轴上看，一个数的绝对值就是 表示这个数的点与原点的距离. 表示这个数的点与原点的距离.
2011届中考数学考点专题复习14
应用题1．（2009南宁）南宁市狮山公园计划在健身区铺设广场砖．现有甲、乙两个工程队参加竞标，甲工程队铺设广场砖的造价y 甲（元）与铺设面积()2m x 的函数关系如图12所示；乙工程队铺设广场砖的造价y乙（元）与铺设面积()2mx 满足函数关系式：y kx =乙．（1）根据图12写出甲工程队铺设广场砖的造价y 甲（元）与铺设面积()2mx 的函数关系式；（2）如果狮山公园铺设广场砖的面积为21600m ，那么公园应选择哪个工程队施工更合算？解：（1）当0500x ≤≤时，设1y k x =甲，把()50028000，代入上式得： 11280002800050056500k k =∴==，56y x ∴=甲 ···························································································································· 2分 当500x ≥时，设2y k x b =+甲，把()50028000，、()100048000，代入上式得： 2250028000100048000k b k b +=⎧⎨+=⎩ ··········································································································· 3分 解得：2408000k b =⎧⎨=⎩·················································································································· 4分408000y x ∴=+甲()()560500408000500x x y x x <⎧⎪∴=⎨+⎪⎩甲≤≥ ··························································································· 5分 （2）当1600x =时，401600800072000y =⨯+=甲 ····················································· 6分1600y k =乙 ····················································································· 7分①当y y <乙甲时，即：720001600k <得：45k > ···························································································································· 8分②当y y >乙甲时，即：720001600k >得：045k << ······················································································································ 9分③当y y =乙甲时，即720001600k =，45k ∴=答：当45k >时，选择甲工程队更合算，当045k <<时，选择乙工程队更合算，当45k =时，选择两个工程队的花费一样． ········································································· 10分2（09钦州）小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示．根据图中的数据（单位：m ），解答下列问题：（1）写出用含x 、y 的代数式表示的地面总面积；63y22x客厅卧室厨房卫生间（2）已知客厅面积比卫生间面积多21m 2，且地面总面积是卫生间面积的15倍，铺1m 2地砖的平均费用为80元，求铺地砖的总费用为多少元？解：（1）地面总面积为：（6x ＋2y ＋18）m 2； ································································· 4分（2）由题意，得6221,6218152.x y x y y -=⎧⎨++=⨯⎩ ···························································· 6分解之，得4,3.2x y =⎧⎪⎨=⎪⎩ ···························································································· 8分 ∴地面总面积为：6x ＋2y ＋18＝6×4＋2×32＋18＝45（m 2）． ················ 9分∵铺1m 2地砖的平均费用为80元，∴铺地砖的总费用为：45×80＝3600（元）． ·············································· 10分3（09湖南）为迎接“建国60周年”国庆，我市准备用灯饰美化红旗路，需采用A 、B 两种不同类型的灯笼200个，且B 灯笼的个数是A 灯笼的32。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二、“三角形和等腰三角形”给你留下多少？ 尝试填写下列知识点（并在脑海中构建知识体系）
1、_______________________叫三角形。 按边可分为 ， 按角可分为__________________． 2、＿＿＿＿＿＿＿＿＿＿＿＿＿＿叫等边三角形， __________ 叫等腰三角形， ＿＿＿＿＿＿＿＿＿＿＿＿＿＿叫不等边三角形. 三角形的性质是________________________.
三、下列例题请先做做，看自己有无“漏洞”如果有 请偿试写出“病因”． 例1（1）若等腰三角形的底边长为10cm， 则腰长x的取值范围是＿＿＿＿＿＿＿＿． （2）若等腰三角形的腰长为10cm， 则底边长x的取值范围是＿＿＿＿＿＿＿＿． （3）若等腰三角形的周长是6， 则底边长x的取值范围是＿＿＿＿＿＿＿＿．
初中数学复习
第15课时 三角形和等腰三角形
一、下列各题已有解答的有“病”吗？如果有“病”， 请写出“病因”。没有解答的，你认为易让别人犯错 的“陷阱”在哪儿？ 1．等腰三角形两边长分别是4和9，则周长是（ C ） A．17 B．22 C．17或22 D．19.5 ▲错因分析或陷阱是 ____________________________________ ▲正确解答是 ____________________________________
4．（2008恩施自治州）为了让州城居民有更多休闲 和娱乐的地方，政府又新建了几处广场，工人师傅在 铺设地面时，准备选用同一种正多边形地砖.现有下面 几种形状的正多边形地砖，其中不能进行平面镶嵌的 是（D） A．正三角形 B．正方形 C．正五边形 D．正六边形 ▲错因分析或陷阱是 _____________________________________ ▲正确解答是 _____________________________________
3、 锐角三角形的三条高交于三角形的 直角三角形的三条高交于三角形的 钝角三角形的三条高交于三角形的
叫三角形的高， ， ， 。 叫三角形的中线，
三角形的中线交于三角形的内部； 叫三角形的角平分线， 三角形的角平分线交于三角形的内部； 三角形的高线、中线和角平分线都是线段。
4、三角形具有 ，三角形的内角和等于＿＿＿＿＿． 5、 叫做三角形的外角， 三角形的外角和等于 ＿＿，三角形外角的性质是＿＿＿＿＿ 6、等腰三角形的性质1 ＿＿＿＿＿＿＿， 等腰三角形的性质2 ； 等腰三角形的判定定理 ； 等边三角形的判定定理1 ， 判定定理2 ， 判定定理3＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿．
2．如图，AD是△ABC的高，则以AD为高的 三角形 共有（ A ）个 A．2 B．3 C．4 D．6 ▲错因分析或陷阱 ______________________________ ▲正确解答是 _______________________________
A
B
C E D
Hale Waihona Puke 3．已知等腰三角形一腰上的中线将三角形的 周长分成9cm和15cm两部分，则这个三角形 的腰长和底边长是6cm和12cm或10cm和 4cm ▲错因分析或陷阱是 ____________________________________ ______________________ ▲正确解答是 ____________________________________ _________________________
例8．(2008年西宁市) 如图2，将一副三角板折叠放在一起， 使直角的顶点重合于点，则 例9．（2008年南京市）若等腰三角形的一个外角为70°， 则它的底角为
例10．（2008乌鲁木齐）在一次数学课上， 王老师在黑板上画出图6，并写下了四个等式：① AB DC ， ② BE CE ， ③ B C ，④ BAE CDE 要求同学从这四个等式中选出两个作为条件， 推出是等腰三角形．请你试着完成王老师提出的要求， 并说明理由．（写出一种即可） 已知： 求证：是等腰三角形． A D 证明：
E
B 图6
C
四、你能以知识点或题型给上面例题分类？ 你认为这些题目的典型性怎么样？ 你有没有发现解题规律或数学思想方法？ 有什么补充？请先写下来，以便交流。
例2.若三角形的三边长分别为 5、2x-1和8，则x的取值范围是 ______． 例3．已知等腰三角形的两边之比是 3：4 ，其周长为110cm ， 求三边长＿＿＿＿＿＿＿＿．
例4（1）若三角形三个外角之比是2：3：4， 则三个内角之比是 （2）若三角形三个内角之比是2：3：4， 则三个外角之比是 例5．在△ABC中，OB平分∠ABC，OC平分∠ACB （1）若∠ABC=60°，∠ACB=40°，则∠BOC=＿ ＿＿ （2）若∠A=80°，则∠BOC=＿＿＿＿ （3）若∠A=100°，则∠BOC=＿＿＿＿ （4）若∠A=m°，则∠BOC=＿＿＿＿ （5）∠BOC和∠A之间的关系是＿＿＿＿＿