5.3.1+平行线的性质
第五章相交线与平行线5.3.1平行线的性质

40
题目已知:AB∥CD
找出的截线只能是CF,由图可知:
∠ C和 ∠ 1
构成同位角。
∠C和∠AEC构成内错角。
∠C和∠BEC 构成同旁内角。
利用平行线的 性质,以上三种类 型的角,存在着什 么样的数量关系?
已知:如图所示,AG//CF,AB//CD, ∠A=40
复习回顾 平行线的判定方法:
1、同位角相等 2、内错角相等 3、同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、 内错角、同旁内角各有什么关系呢?
交流合作,探索发现 猜一猜∠1和∠2相等吗?
a
b
2 1
c
心动
不如行动
合作交流一
65°
c
1 2 65°
a
b
是不是任意一条直线去
截平行线a、b,所得的同位 角都相等呢?
水平镜面后被发射,此时∠1=∠2 , ∠3=∠4 。
(2 )发射光线BC与EF也平行吗?
已知:如图所示, ∠ADE=60 °, ∠B=60 °, ∠AED=40 ° (1)求证:DE∥BC;
(2)求∠C的度数。
已知:如图所示,直线a、b被 c、d 所截,且c⊥a,c⊥b. 求证:∠1=∠2.
已知:如图所示,∠1=∠2,CE∥BF 求证: AB∥CD. ∵ CE∥BF E ∴∠1=∠B A 1 ∵∠1=∠2 ∴∠2=∠B C ∴ AB∥CD
110
°
已知: AB∥CD ,∠1=110 ° 求:∠2,∠3, ∠4的度数
110 °
已知:如图所示,AG//CF,AB//CD, ∠A=40
求:∠C的度数。
平行线的性质(分层作业)【解析版】

5.3.1平行线的性质分层作业基础训练1.如图,直线a b ∥,直线l 与a ,b 分别交于点A ,B ,过点A 作AC b 于点C ,若160 ,则2 的度数为()A .120°B .60°C .45°D .30°【答案】D 【分析】根据垂直的定义可得90ACB ,再根据平行线的性质可得160ABC ,最后根据角的和差即可解答.【详解】解:∵AC b 于点C ,∴90ACB ,∵a b ∥,∴160ABC ,∴2906030 .故选:D .【点睛】本题主要考查了平行线的性质、垂直的定义等知识点,掌握两直线平行、同位角相等是解答本题的关键.2.如图,直尺一边BC 与量角器的零刻度线AD 平行,已知EOD 的读数为65 ,设OE 与BC 交于点F ,则BFE 的度数等于()A .135B .115C .105D .100【答案】B 【分析】本题考查平行线性质和邻补角定义,根据平行线性质结合EOD ,推出BFO ,再结合邻补角即可解题.【详解】解:如图,BC AD ∵ ,65BFO EOD ,180115BFE BFO .故选:B .3.如图,将木条,a b 与c 钉在一起,且木条a 与木条c 交于点,180,260O .要使木条a 与b 平行,则木条a 绕点O 顺时针旋转的度数至少为()A .10B .20C .30D .50【答案】B【详解】如图.因为当260AOC 时,OA b ∥,所以要使木条a 与b 平行,木条a 绕点O 顺时针旋转的度数至少为806020 .4.如图,下列推理及括号中所注明的推理依据错误的是()A .∵AD BC ∥,180BAD D (两直线平行,同旁内角互补)B .∥∵AB CD ,180BCD ABC (两直线平行,同旁内角互补)C .13 ∵,AB CD ∥(内错角相等,两直线平行)D .DAM CBM ∵,AD BC ∥(同位角相等,两直线平行)【答案】A【分析】本题考查的是平行线的判定与性质,利用平行线的判定方法与性质逐一分析即可得到答案,熟记平行线的判定方法与平行线的性质是解本题的关键.【详解】解:∵AD BC ∥,180BAD ABC (两直线平行,同旁内角互补),故A 符合题意;∥∵AB CD ,180BCD ABC (两直线平行,同旁内角互补),故B 不符合题意;13 ∵,AB CD ∥(内错角相等,两直线平行),故C 不符合题意;DAM CBM ∵,AD BC ∥(同位角相等,两直线平行),故D 不符合题意;故选A5.如图,小颖绘制一个潜望镜原理示意图,两个平面镜的镜面AB 与CD 平行,入射光线a 与出射光线b 平行.若入射光线a 与镜面AB 的夹角145 ,则4 的度数为()A .30B .45C .60D .90【答案】B 【分析】本题考查了平行性的性质.熟练掌握平行线的性质定理是解题的关键.由题意知,21 ,3=4 ,由AB CD ,可得32 ,进而可求4 .【详解】解:由题意知,入射光线与镜面的夹角等于反射光线与镜面的夹角,即21 ,3=4 ,∵AB CD ,∴3245 ,∴445 ,故选:B .6.如图,直线a b ,直线l 与直线a 相交于点P ,与直线b 相交于点Q ,PM l 于点P ,若155 ,则2 的度数为()A .35B .55C .125D .145【答案】A【分析】本题考查了平行线性质,根据两直线平行,同位角相等,平角的定义计算即可.【详解】如图,∵a b ,155 ,∴3155 ,∵34180,4920 ,∴18035243 ,故选A .7.如图,,,ABF BFE E F 为直线CD 上两点,且BF 平分ABE .若1108 ,则2 的度数为()A .36B .54C .72D .80【答案】A【解析】略8.一块直角三角板和直尺按如图所示的方式放置.若155 ,则2 的度数是.【答案】35°【解析】略9.如图,一艘船在海面上航行,到达B 处时,看到灯塔A 在它的北偏东45 方向,达到C 处时,看到灯塔A 在它的北偏西30 方向.则BAC .【答案】75 /75度【分析】本题考查方向角,关键是掌握方向角的定义.过A 作AD BE ,则AD CF ∥,由方向角的定义得到4530ABE ACF ,,然后由平行线的性质可得答案.【详解】解:过A 作AD BE ,则AD CF ∥,由题意得:4530ABE ACF ,,∵AD BE ,AD CF ∥,∴4530BAD ABE CAD ACF ,,∴75BAC BAD CAD ,故答案为:75 .10.如图,一把长方形直尺沿直线断开并错位摆放,点E 、D 、B 、F 在同一条直线上,若131ADE ,则DBC 的度数为.【答案】49 /49度【分析】本题主要考查了平行线的性质,邻补角的定义.先根据邻补角的性质求得ADF 的度数,再根据平行线的性质求解即可.【详解】解:∵131ADE ,∴49ADF ,∵AD BC ∥,∴49DBC ADF .故答案为:49 .11.生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA 垂直于地面AE 于A ,CD 平行于地面AE ,则ABC BCD °.【答案】270【分析】过点B 作BF AE ,如图,由于CD AE ∥,则BF CD ∥,根据两直线平行,同旁内角互补得180BCD CBF ,由AB AE 得AB BF ,即90ABF ,于是得到结论.本题主要考查了平行线的性质,正确作出辅助线,并熟记两直线平行,同旁内角互补是解决问题的关键.【详解】解:过点B 作BF AE ,如图,∵CD AE ∥,∴BF CD ∥,∴180BCD CBF ,∵AB AE ,∴AB BF ,∴90ABF ,90180270ABC BCD ABF CBF BCD .故答案为:270.12.如图,直线12l l ∥,AB 交1l 于点D ,BC 交2l 于点E ,若132 ,2120 ,则3 度.【答案】92【分析】本题考查了平行线的性质,过点B 作1BF l ∥,得出22188DBF FBE ,进而318092DBF 根据即可求解.【详解】解:如图所示,过点B 作1BF l ∥,则3180DBF ,∵12l l ∥,∴2BF l ∥,∴1FBE ,∴22188DBF FBE ,∴318092DBF ,故答案为:92.13.如图,已知AB CD ∥,100ABE ,40BEC ,则ECD 的度数为.【答案】120 /120度【分析】此题考查了平行线的判定和性质.过E 作EF AB ∥,根据平行线的性质及角的和差求解即可.【详解】解:过E 作EF AB ∥,∵AB CD ∥,∴AB CD EF ∥∥,B BEF ,180C CEF ,100ABE ∵,100BEF ,40BEC ∵,1004060CEF BEF BEC ,180120C CEF ,故答案为:120 .14.一副三角板按如图所示方式叠放,两三角板的斜边互相平行,则∠ 等于.【答案】105 /105度【分析】本题考查三角板中角度的计算,掌握两直线平行,内错角相等是解题的关键.【详解】过点E 作EF AD ,如图,由题可知45A ,60C ,又∵两三角板的斜边互相平行,BC AD∴EF AD BC ,∴45AEF A ,45CEF C∴6045105AEF CEF C A ,度答案为:105 .15.如图,点F 在AC 上,FG AB 于点G ,FB 与CD 相交于点H ,且180BHC GFB .(1)求证:CD AB .在下列解答中,填空:证明:∵180BHC GFB (已知)___①___(对顶角相等)∴___②___180GFB (等量代换)∴CD FG ∥(③)∴AGF ___④___(两直线平行,同位角相等)又∵FG AB (已知)∴90AGF (垂直的定义.)∴ADC ___⑤___(等量代换)∴CD AB (垂直的定义)(2)若CD 平分ACB ,且40ACB ,求AFG 的度数.【答案】(1)BHC DHF ;DHF ;同旁内角互补,两直线平行;ADC ;90(2)20【分析】(1)证明180DHF GFB 得CD FG ∥,从而AGF ADC ,然后再证明90ADC 即可;(2)由角平分线的定义得20ACD ,然后利用平行线的性质可求出AFG 的度数.【详解】(1)证明:∵180BHC GFB (已知)BHC DHF (对顶角相等)∴180DHF GFB (等量代换)∴CD FG ∥(同旁内角互补,两直线平行)∴AGF ADC (两直线平行,同位角相等)又∵FG AB (已知)∴90AGF (垂直的定义.)∴90ADC (等量代换)∴CD AB (垂直的定义)故答案为:BHC DHF ;DHF ;同旁内角互补,两直线平行;ADC ;90 ;(2)∵CD 平分ACB ,且40ACB ,∴1202ACD ACB .∵CD FG ∥,∴20AFG ACD【点睛】本题考查了平行线的判定与性质,对顶角相等,垂直的定义,角平分线的定义,熟练掌握平行线的判定与性质是解答本题的关键.16.如图所示,有两艘油轮在海面上,油轮N 在油轮M 的正东方向,并且在M 、N 两处分别测得小岛P 在北偏东65 和北偏西45 的方向,那么在P 处测得M 、N 的张角MPN 的度数为多少?【答案】110【分析】本题考查了方位角的计算,平行线的性质与判定;过点P 作PC AM ∥于点C ,根据平行线的性质即可求解.【详解】解:如图,过点P 作PC AM ∥于点C ,∵AM BN ∥,PC BN ∥,AMP MPC ,BNP NPC ,65AMP ∵,45BNP ,65MPC AMP ,45NPC BNP ,110MPN MPC NPC .17.如图,CD AB 于D ,点F 是BC 上任意一点,FE AB 于E ,且12 ,=60B .试求ADG 的度数.【答案】60【分析】本题考查了平行线的判定和性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.由,CD AB FE AB ,则CD EF ∥,则2BCD ,从而证得BC DG ,即可得到B ADG .【详解】解:CD AB FE AB ∵,,,CD EF ∥24,又12,∵14,,BC DG ∥60.ADG B 能力提升18.如图,123l l l ∥∥,则下列各式中,正确的是()A.312B .23190C .123180D .231180【答案】C【解析】略19.如图所示,,CD AB OE ∥平分,60AOD D ,80EOF ,则BOF 为()A .35B .40C .25D .20【答案】B 【分析】本题考查了平行线的性质,角平分线的定义,以及角的和差关系.由平行线的性质和角平分线的定义求得120,60AOD AOE ,即可求出BOF 的度数.【详解】解:∵CD AB ∥,∴180AOD D ,∵60D ,∴180********AOD D ,∵OE 平分AOD ,∴60AOE AOD ,∵80EOF ,∴180180608040BOF AOE EOF .故选:B .20.如图,AB ∥CD ,F 为AB 上一点,FD ∥EH ,且FE 平分AFG ,过点F 作FG EH 于点G ,且2AFG D ,则下列结论:①40D ;②290D EHC ;③FD 平分HFB ;④FH 平分GFD .其中正确结论的个数是()A .1个B .2个C .3个D .4个【答案】A 【分析】根据角平分线的性质和平行线的性质解答.延长FG ,交CH 于I ,构造出直角三角形,利用直角三角形两锐角互余解答.【详解】解:延长FG ,交CH 于I .∥∵AB CD ,BFD D ,AFI FIH ,FD EH ∵∥,EHC D ,FE ∵平分AFG ,22FIH AFE EHC ,390EHC ,30EHC ,30D ,22303090D EHC ,40D ①错误;290D EHC ②正确,FE ∵平分AFG ,30260AFI ,30BFD ∵,90GFD ,90GFH HFD ,可见,HFD 的值未必为30 ,GFH 未必为45 ,只要和为90 即可,FD ③平分HFB ,FH ④平分GFD 不一定正确.故选:A .【点睛】本题考查了角平分线的性质和平行线的性质,二者有机结合,难度较大,需要作出辅助线,对能力要求较高.21.已知直线m n ∥,将一块含30 角的直角三角板ABC 按如图所示的方式放置,使A ,B 两点分别落在直线m ,n 上.若165 ,则2 的度数是.【答案】35 /35度【分析】本题考查了平行线的性质,三角板的属性,根据题意,得到123 ,代入计算即可.【详解】如图,∵m n ∥,∴123 ,∵165 ,330 ,∴21335 ,故答案为:35 .22.如图,ABCD 为一长条形纸带,AD CB ∥,将ABCD 沿EF 折叠,C 、D 两点分别与C D 、对应,若122 ,则AEF 的度数为.【答案】108 /108度【分析】本题考查平行线的性质,翻折变换,由题意122 ,设2x ,则12DEF FED x ¢Ð=Ð=Ð=,构建方程即可解决问题.【详解】解:由翻折的性质可知:DEF FED ,∵AD CB ∥,1DEF ,∵122 ,∴设2x ,则12DEF FED x ¢Ð=Ð=Ð=,2180DEF D EF ∵,5180x ,36x ,223108AEF D EF x x x ¢\Ð=Ð+Ð=+==°,故答案为:108 .23.已知直线MN PQ ∥,现将一副直角三角板作如图摆放,且60,45CAB DEF .下列结论:①AB DF ∥;②150ACE ;③65MAC ;④NAB DFE ,其中正确结论的序号为.【答案】①②④【分析】本题考查平行线的判断和性质,三角板中角度的计算.内错角相等,两直线平行,判断①,邻补角求出ACE 的度数,判断②,过点B 作BG MN ∥,利用平行线的判定和性质,判断③和④.掌握平行线的判定方法和性质,是解题的关键.【详解】解:由题意,得:90,90ABC EDF ,∴90FDB ABC ,∴AB DF ∥,故①正确;∵60,45CAB DEF ,∴30ACB ,45DFE ,∴180150ACE ACB ;故②正确;过点B 作BG MN ∥,∵MN PQ ∥,∴BG MN PQ ∥∥,∴45GBE DEF ,∴45NAB ABG ABC GBE ,∴45NAB DFE ,180135MAB ABG ,∴13575MAC BAC ;故③错误,④正确;故答案为:①②④.24.如图,已知点E 、F 在直线AB 上,点N 在线段CD 上,ED 与FN 交于点M ,C 1 ,23 ,(1)求证:AB CD ;(2)若40D ,80EMF ,求AEP 的度数.【答案】(1)见解析(2)120【分析】本题主要查了平行线的判定和性质:(1)根据23 ,可得CP FN ∥,从而得到C FND ,继而得到1FND ,即可求证;(2)根据CP FN ∥,可得280EMF ,再由AB CD ,可得40FED D ,即可求解.【详解】(1)证明:∵23 ,∴CP FN ∥,∴C FND ,又∵C 1 ,∴1FND ,∴AB CD ;(2)解:∵CP FN ∥,∴280EMF ,又∵AB CD ,∴40FED D ,∴28040120AEP FED .拔高拓展25.在综合与实践课上,老师以“两条平行线AB ,CD 和一块含60 角的直角三角尺EFG (90EFG ,60EGF )”为主题开展数学活动.(1)如图①,若直角三角尺的60 角的顶点G 放在CD 上,21 ,求1 的度数;(2)如图②,小颖把直角三角尺的两个锐角的顶点E ,G 分别放在AB 和CD 上,请你探索并说明AEF 与FGC 之间的数量关系;(3)如图③,小亮把直角三角尺的直角顶点F 放在CD 上,30 角的顶点E 放在AB 上.若AEG ,CFG ,则AEG 与CFG 的数量关系是什么(用含 , 的式子表示)?请说明理由.【答案】(1)160(2)90AEF FGC ,理由见解析(3)300 .理由见解析【详解】解:(1)因为AB CD ∥,所以1EGD .因为2180EGF EGD ,21 ,所以1601180 ,解得160 .(2)如图,过点F 作∥FP AB .因为CD AB ∥,所以FP AB CD ∥∥,所以AEF EFP ,FGC GFP ,所以AEF FGC EFP GFP EFG .因为90EFG ,所以90AEF FGC .(3)300 .理由如下:因为AB CD ∥,所以180AEF CFE ,即30930900180AEG CFG ,整理可得180120300 .。
5.3.1《 平行线的性质》教材解读-人教版数学七年级下册

5.3.1《平行线的性质》教材解读一、课标内容《课程标准》相关内容:1.在探索直线平行的性质的过程中,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
2.进一步发展空间观念,体会通过合情推理探索数学结论,运用演绎推理加以证明的过程,在多种形式下的数学活动中,发展合情推理和演绎推理的能力。
3.经历观察、操作、想象、推理、交流等活动,培养学生参与活动和交流合作的意识。
4.敢于发表自己的想法,勇于质疑、敢于创新,养成认真勤奋、独立思考、合作交流等学习习惯,形成严谨求实的科学态度。
二、教材分析(一)教材的地位作用《平行线的性质》是新人教版七年级数学下册第五章第三小节的内容,本节课是在学生已经学习了同位角、内错角、同旁内角和平行线的判定的基础上进行教学的。
这节课是空间与图形领域的基础知识,在以后的学习中经常要用到。
它为今后三角形内角和、三角形全等、三角形相似等知识的学习奠定了理论基础。
(二)知识要点及重难点平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补。
重点:探究平行线的性质。
难点:明确平行线的性质和判定的区别。
三、教材编写特点教材由平行线的判定引入对平行线性质的研究,既渗透了图形的判定和性质之间的互逆关系,又体现了知识的连贯性,平行线的三条性质都是需要证明的,但是为了与学生思维发展水平相适应,性质1是通过操作确认的方式得出的,在性质1的基础上经过进一步推理,得到性质2和性质3,这一过程体现了由实验几何到论证几何的过渡,渗透了简单推理,体现了数学在培养良好思维品质方面的价值。
四、教学建议教材所选的例题及课后练习题1,都是平行线性质的直接运用,较为简单。
练习题2是平行线判定和性质的综合运用,是为了让学生区分判定和性质,推理也比较简单。
考虑到学生还处于几何初步阶段,进度不可过快,教师可以设计一些有两步推理的证明题,让学生填充理由。
在应用知识的过程中,组织学生进行讨论,结合题目的已知条件和结论,让学生自己总结出判定和性质的区别,只有自己构造起的知识,才能真正被灵活应用。
(新人教版)数学七年级下册:5.3.1《平行线的性质(第2课时)》教学设计(两套)

5.3.2平行线的性质(第2课时)平行线的性质(二)教学目标1.经历观察、操作、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力.2.理解两条平行线的距离的含义,了解命题的含义,会区分命题的题设和结论.3.能够综合运用平行线性质和判定解题. 重点、难点重点:平行线性质和判定综合应用,两条平行的距离,命题等概念. 难点:平行线性质和判定灵活运用. 教学过程 一、复习引入1.平行线的判定方法有哪些?(注意:平行线的判定方法三种,另外还有平行公理的推论)2.平行线的性质有哪些.3.完成下面填空.已知:如图,BE 是AB 的延长线,AD ∥BC,AB ∥CD,若∠D=100°,则∠C=_____, ∠A=______,∠CBE=________.4.a ⊥b,c ⊥b,那么a 与c 的位置关系如何?为什么?cb二、进行新课1.例1 已知:如上图,a ∥c,a ⊥b,直线b 与c 垂直吗?为什么?学生容易判断出直线b 与c 垂直.鉴于这一点,教师应引导学生思考:(1)要说明b ⊥c,根据两条直线互相垂直的意义, 需要从它们所成的角中说明某个角是90°,是哪一个角?通过什么途径得来?(2)已知a ⊥b,这个“形”通过哪个“数”来说理,即哪个角是90°.(3)上述两角应该有某种直接关系,如同位角关系、内错角关系、同旁内角关系,你能确定它们吗?让学生写出说理过程,师生共同评价三种不同的说理. 2.实践与探究(1)下列各图中,已知AB ∥EF,点C 任意选取(在AB 、EF 之间,又在BF 的左侧).请测量各图中∠B 、∠C 、∠F通过上述实践,试猜想∠B 、∠F 、∠C 之间的关系,写出这种关系,试加以说明.E D C B AFECBAFECBA(1) (2) 教师投影题目:学生依据题意,画出类似图(1)、图(2)的图形,测量并填表,并猜想:∠B+∠F=∠C.在进行说理前,教师让学生思考:平行线的性质对解题有什么帮助? 教师视学生情况进一步引导:①虽然AB ∥EF,但是∠B 与∠F 不是同位角,也不是内错角或同旁内角. 不能确定它们之间关系.②∠B 与∠C 是直线AB 、CF 被直线BC 所截而成的内错角,但是AB 与CF 不平行.能不能创造条件,应用平行线性质,学生自然想到过点C 作CD ∥AB,这样就能用上平行线的性质,得到∠B=∠BCD.③如果要说明∠F=∠FCD,只要说明CD 与EF 平行,你能做到这一点吗?以上分析后,学生先推理说明, 师生交流,教师给出说理过程.FEDCB A作CD ∥AB,因为AB ∥EF,CD ∥AB,所以CD ∥EF(两条直线都与第三条直线平行, 这两条直线也互相平行).所以∠F=∠FCD(两直线平行,内错角相等).因为CD ∥AB.所以∠B=∠BCD(两直线平行,内错角相等).所以∠B+∠F=∠BCF. (2)教师投影课本P23探究的图(图5.3-4)及文字.①学生读题思考:线段B 1C 1,B 2C 2……B 5C 5都与两条平行线的横线A 1B 5和A 2C 5垂直吗?它们的长度相等吗?②学生实践操作,得出结论:线段B 1C 1,B 2C 2……,B 5C 5同时垂直于两条平行直线A1B5和A 2C 5,并且它们的长度相等.③师生给两条平行线的距离下定义.学生分清线段B 1C 1的特征:第一点线段B 1C 1两端点分别在两条平行线上,即它是夹在这两条平行线间的线段,第二点线段B 1C 1同时垂直这两条平行线. 教师板书定义:(像线段B 1C 1)同时垂直于两条平行线, 并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离.④利用点到直线的距离来定义两条平行线的距离.F EDCBA教师画AB ∥CD,在CD 上任取一点E,作EF ⊥AB,垂足为F.学生思考:EF 是否垂直直线CD?垂线段EF 的长度d 是平行线AB 、CD 的距离吗? 这两个问题学生不难回答,教师归纳:两条平行线间的距离可以理解为:两条平行线中,一条直线上任意一点到另一条直线的距离.教师强调:两条平行线的距离处处相等,而不随垂线段的位置改变而改变. 3.了解命题和它的构成.(1)教师给出下列语句,学生分析语句的特点.①如果两条直线都与第三条直线平行,那么这条直线也互相平行; ②等式两边都加同一个数,结果仍是等式; ③对顶角相等;④如果两条直线不平行,那么同位角不相等.这些语句都是对某一件事情作出“是”或“不是”的判断. (2)给出命题的定义.判断一件事情的语句,叫做命题.教师指出上述四个语句都是命题,而语句“画AB ∥CD”没有判断成分,不是命题.教师让学生举例说明是命题和不是命题的语句. (3)命题的组成.①命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项. ②命题的形成.命题通常写成“如果……,那么……”的形式,“如果”后接的部分是题设,“那么”后接的部分是结论.有的命题没有写成“如果……,那么……”的形式,题设与结论不明显,这时要分清命题判断了什么事情,有什么已知事项,再改写成“如果……,那么……”形式. 师生共同分析上述四个命题的题设和结论,重点分析第②、③语句. 第②命题中,“存在一个等式”而且“这等式两边加同一个数”是题设, “结果仍是等式”是结论。
5.3.1平行线的性质

b
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126° 即 ∠2=54° ,∠3=126°, ∠4=54°。
小结与回顾:
(1)请你谈谈本节课的收获和感受。 (2)说说平行线的“判定”与“性质”有什么不同?
已知
同位角相等 内错角相等 同旁内角互补
o o ∠ 2=110 ∠ 3=110 o
B
D
达标测试 2、如图,一条公路两次拐弯前后两条路 互相平行。第一次拐的角∠B是142゜,
第二次 拐的角∠C是多少度?为什么?
C B
∠C=142
o
∵两直线平行,内错角相等
达标测试
3、如图直线 a ∥ b,直线b垂直于直 线c,则直线a垂直于直线c吗? a⊥b ?
已知角之间的关系(相等或互补),得到两直线平行 的结论是平行线的判定。 已知两直线平行,得到角之间的关系(相等或互补) 的结论是平行线的性质。
范例
例2、如图, AB∥DC ,GM、HN分别是
∠ BGH 、∠DHF的平分线,GM、HN有 E 什么关系?为什么? G A B
H C F N M
D
练习
2、如图, AB∥DC ,GM、HN分别是
∠AGH 、∠ GHD的平分线,GM、HN有 E 什么关系?为什么? G A B
M H C F N
D
3、如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度? a 解: 1
∵ ∠2=∠1 (对顶角相等) ∴ ∠2=∠1 =54° ∵ a∥b(已知) ∴ ∠4=∠1=54°(两直线平行,同位角相等)
c a b
根据右图,填空: E ①如果∠1=∠C, 4 1 A B 同位角相等,两直线平行 ) 3 2 那么__∥__( AB CD ② 如果∠1=∠B 那么__ EC ∥__ BD ( 内错角相等,两直线平行 ) D C ③ 如果∠2+∠B=180°, EC ∥__ 那么__ ) BD ( 同旁内角互补,两直线平行
5.3 平行线的性质

5.3.1平行线的性质(一)学习目标1.使学生理解平行线的性质和判定的区别.2.使学生掌握平行线的三个性质,并能运用它们作简单的推理.学习过程一、复习:如图,填空⑴∵∠1=∠5(已知),∴∥( ,两直线平行).⑵∵∠3=∠5(已知),∴∥( ,两直线平行).⑶∵∠3+∠6=180°(已知),∴∥( ,两直线平行).二、新知探究1.实验观察,发现平行线第一个性质请学生画出下图进行实验观察.设l1∥l2,l3与它们相交,请度量∠1和∠2的大小,你能发现什么关系?请同学们再作出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?平行线性质1:两直线平行,同位角相等.2.演绎推理,发现平行线的其它性质(1)已知:如图,直线AB,CD被直线EF所截,AB∥CD.求证:∠1= ∠2.由此可得:平行线性质2:两直线平行,角相等.(2)已知:如图2-64,直线AB,CD被直线EF所截,AB∥CD.求证:∠1+∠2=180°.由此可得:平行线性质3:两直线平行,.3.平行线判定与性质的区别与联系区别:(1)性质:,.(2)判定:,.联系:它们的条件和结论是互逆的,性质与判定要证明的问题是不同的.练习1.填空(括号内填根据)①∵∠1=∠3(已知),∴∥()②∵a∥b(已知),∴∠1+∠2=180°()③如图: ∵AB ∥CD (已知)∴∠1= ∠3 ()又∠3= ∠2 ()∴∠1= ∠2又∵∠4+ ∠2 =180 ゜()∴∠1+ ∠4 =180 ゜例1.如图,已知∠1=∠2,∠3=110°,求∠4的度数?练习2.如图所示,已知∠B=60°,∠BDE=120°,问∠C与∠AED相等吗?为什么?3.如图,AB∥CD,AD∥BC,求证:∠A=∠CCA BC D12345FE678ab123cD5.3.1 平行线的性质(二)学习目标1.进一步巩固平行线性质和判定,培养推理能力和有条件表达能力;2.能够综合运用平行线性质和判定解题.学习过程一.复习1.平行线的判定方法有哪些?平行线的性质有哪些?2.如图1,已知直线a、b被直线c所截,在括号内为下面各小题的推理填上适当的根据: (1) ∵a∥b (已知),∴∠1=∠3 ( );(2) ∵∠1=∠3 (已知),∴a∥b( );(3) ∵a∥b (已知),∴∠1+∠4=180º ( );(4)∵∠1+∠4=180º (已知),∴a∥b( );二、例题巩固例1一块梯形铁片的残余部分如图,量得∠A=75º,∠B=72º,梯形的另外两个角分别是多少度? 练习1.如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.例2 如图所示.已知:AD∥BC,∠AEF=∠B,求证:AD∥EF.练习2.⑴回答:如图①∠3=∠B,则∥,依据是②∠2+∠A=180°, 则∥,依据是;③∠1=∠4,则∥,依据是④GC ∥EF,AB ∥EF, 则∥,依据是;⑵如图所示,已知:∠1=∠2,求证:∠3+∠4=180°.⑶如图所示,已知,∠1=∠2,∠A=∠D.求证:AB∥CDFEDCBAab123c4图1FEDCBA21EDBA EDCBA FECBA5.3.1 平行线的性质与判定学习目标2. 进一步巩固平行线性质和判定,培养推理能力和有条件表达能力; 2.能够综合运用平行线性质和判定解题. 学习过程1.复习⑴ 如图1,点E 在CD 上,点F 在AB 上,G 是AD 延长线上一点。
5.3.1平行线的性质

练习
1.如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少 度?
解:
a
∵ ∠1= 54°(已知)
1 2 4
对顶角相等) ∴ ∠2=∠1 =54°(________
b
∵ a∥b(已知)
∴ ∠2+∠3=180° _________________ (两直线平行 ,同旁内角互补)3
∴ ∠3= 180°- ∠2= 180° -54°=126°
E C
(已知)
(同位角相等,两直线平行)
D
B
(2)∵ DE∥BC (已证明) 又∵∠AED=40° (已知) ∴∠C= ∠ AED=40 ° (两直线平行,同位角相等)
4.如图,已知AG//CF,AB//CD,∠A=40,求 ∠C的度数。 G
解:如图 ∵ AG//CF(已知)
∴ ∠A=∠1
F
A
1
∴ ∠4=∠1=54° ________________ (两直线平行 ,同位角相等)
2.如图,D是AB上一点,E是AC上一点,∠ADE=60 °, ∠B=
60 °,∠AED=40° (1)DE和BC平行吗?为什么?
(2) ∠C是多少度,为什么?
A
解:(1)∵∠ADE=60 ° ∠B=60 ° ∴∠ADE=∠B (等量代换) ∴DE∥BC
c
a
2 3 1
b
平行线的性质3 两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
平行线的性质3 两条平行线被第三条直线所截,同旁内角互补。 简单说成:两直线平行,同旁内角互补。
c
a
2 3 1
【应用格式】
b
∵ a∥b (已知) ∴ ∠3+∠2=1800 (两直线平行,同旁内角互补)
平行线的性质

5.3.1 平行线的性质【学习目标】1使学生掌握平行线的三个性质,并能应用它们进行简单的推理论证;2使学生经过对比后,理解平行线的性质和判定的区别和联系.【学习重点】平行线的三个性质及其应用.【学习难点】正确理解性质与判定的区别和联系,并正确运用它们去推理证明.【学习过程】一、学前准备:1、已知直线AB 及其外一点P,画出过点P的AB 的平行线。
2、回答:如图(1)∠3=∠B,则EF∥AB,依据是____________________________(2)∠2+∠A=180°,则DC∥AB,依据是___________________________________(3)∠1=∠4,则GC∥EF,依据是_________________________________________(4) GC ∥EF,AB ∥EF,则GC∥AB,依据是_______________________________思考:平行线的判定方法有哪三种?它们是先知道什么……、后知道什么?二、实践探究:1、问题:根据同位角相等,内错角相等,同旁内角互补可以判定两直线平行,反过来如果两直线平行,同位角,内错角、同旁内角之间有什么关系呢?猜一猜:如果a//b,∠1和∠2相等吗?结论:平行线的性质1两条平行线被第三条直线所截,___________.简写为:两直线平行,___________符号语言: ∵a∥b( )∴∠___=∠_____( ).如图:已知a//b,那么∠2与∠3相等吗?为什么?结论:平行线的性质2两条平行线被第三条直线所截,_____________简写为:两直线平行,________________符号语言:∵a∥b( )∴∠___=∠_____( ).如图,已知a//b,那么∠2与∠4有什么关系呢?为什么?结论:平行线的性质3两条平行线被第三条直线所截,________________.简写为:两直线平行,____________符号语言: ∵a∥b( )∴∠___=∠_____( ).思考:平行线的性质有哪三种?它们是先知道什么……、后知道什么?和判定有什么不同?已知角之间的关系(相等或互补),得到两直线平行的结论,是平行线的_____。
5.3.1《平行线的性质》重难点专项练习【六大题型】(解析版)

5.3.1《平行线的性质》重难点题型专项练习考查题型一 两直线平行同位角相等的应用典例1.(2022秋·重庆铜梁·七年级校考阶段练习)如图,直线a ,b 被直线c 所截,若a b ∥,2110Ð=°,则1Ð的度数为( )A .70°B .75°C .80°D .85°【答案】A【分析】由a b ∥,根据两直线平行,同位角相等,即可求得3Ð的度数,又由邻补角的定义即可求得1Ð的度数.【详解】解:如图:∵a b ∥,2110Ð=°,∴32110Ð=Ð=°,∵13180Ð+Ð=°,∴170=°∠.故选:A .【点睛】此题考查了平行线的性质与邻补角的定义.解题的关键是熟练掌握平行线的性质,正确运用数形结合思想.变式1-1.(2022·四川德阳·模拟预测)如图,直线//a b ,将三角尺的直角顶点放在直线b 上,如果260Ð=°,那么1Ð的度数为( )A .30°B .40°C .50°D .60°【答案】A【分析】根据平行线的性质求出3Ð,由平角性质可知1180390ÐÐ=°--°即可得出结论.【详解】如图://a b Q ,2360\Ð=Ð=°,1180903180906030\Ð=°-°-Ð=°-°-°=°,故选:A .【点睛】本题考查了平行线的性质,熟练运用平行线的性质推理是解题的关键.变式1-2.(2022·宁夏固原·校考模拟预测)如图,把一个三角尺的直角顶点放在直尺的一边上,如果123Ð=°,那么2Ð的大小为( )A .23°B .46°C .57°D .67°【答案】D【分析】根据余角的定义求出3Ð,再根据两直线平行,同位角相等可得23ÐÐ=.【详解】解:∵123Ð=°,∴3902367°°Ð=-=°,∵直尺的两边互相平行,∴2367Ð=Ð=°.故选:D .【点睛】本题考查了平行线的性质,熟记性质并准确识图是解题的关键.变式1-3.(2022秋·陕西西安·七年级校考期中)如图,将直尺与30°角的三角尺叠放在一起,若165Ð=°,则2Ð的大小是( )A .45°B .55°C .65°D .75°【答案】B【分析】由30°三角尺可知360Ð=°,由平角可求4Ð,再根据平行线的性质可知24ÐÐ=.【详解】解:如图:由30°三角尺可知360Ð=°,∵1+3+4180ÐÐÐ=°,∴418013180656055Ð=°-Ð-Ð=°-°-°=°,由平行线的性质可知2455Ð=Ð=°.故选:B .【点睛】本题考查了平行线的性质及直角三角形的性质,充分运用三角板和直尺的几何特征是解题的关键.考查题型二 两直线平行内错角相等的应用典例2.(2021·新疆乌鲁木齐·校考一模)如图,直线12l l ∥,直角三角板的直角顶点C 在直线1l 上,一锐角顶点B 在直线2l 上,若135Ð=°,则2Ð的度数是( )A .65°B .55°C .45°D .35°【答案】B【分析】先根据角的和差求出3Ð的度数,然后根据平行线的性质求解即可.【详解】解:如图,135Ð=°Q ,90ACB Ð=°,390155\Ð=°-Ð=°,又12l l ∥,2355\Ð=Ð=°.故选:B .【点睛】本题考查了平行线的性质,掌握两直线平行,内错角相等是解题的关键.变式2-1.如图,AB CD P ,40B Ð=°,则ECD Ð的度数为( )A .160°B .140°C .50°D .40°【答案】B【分析】利用平行线的性质先求解DCB Ð,再利用邻补角的性质求解ECD Ð即可.【详解】解:∵AB CD P ,40B Ð=°,∴40DCB B Ð=Ð=°,∴180140ECD DCB Ð=°-Ð=°,故选B .【点睛】本题考查的是平行线的性质,邻补角的性质,熟知两直线平行,内错角相等是解题的关键.变式2-2.(2022·河南洛阳·统考一模)如图,ACD Ð是ABC V 的外角,AB CE ∥,80BAC Ð=°,35DCE Ð=°,则ACB Ð的度数为( )A .55°B .65°C .75°D .85°【答案】B【分析】由80AB CE BAC Ð=°,∥可得80ACE Ð=°,进而即可求ACB Ð;【详解】∵80AB CE BAC Ð=°,∥,∴80BAC ACE Ð=Ð=°,∵35DCE Ð=°,∴()18065ACB ACE DCE Ð=°-Ð+Ð=°.故选:B.【点睛】本题主要考查平行线的性质,掌握“两直线平行,内错角相等”定理是解题的关键.变式2-3.如图,直线AB ,CD 被直线DE 所截,AB CD ∥,140Ð=°,则D Ð的度数为( )A .20°B .40°C .50°D .140°【答案】B【分析】根据两直线平行内错角相等可得出答案.【详解】解:∵AB CD ∥,140Ð=°,∴140D Ð=Ð=°,故选:B .【点睛】本题考查了平行线的性质,熟知两直线平行,内错角相等是解本题的关键.考查题型三 两直线平行同旁内角互补的应用典例3.(2022春·黑龙江哈尔滨·七年级校考阶段练习)如图,已知直线AB CD ∥,130GEF Ð=°,135EFH Ð=°,则12Ð+Ð的度数为( )A .35°B .45°C .65°D .85°【答案】D【分析】由130GEF Ð=°,135EFH Ð=°可得1324265°Ð+Ð+Ð+Ð=,由AB CD P 得34180Ð+Ð=°,进而可求出12Ð+Ð的度数.【详解】解:如下图所示,∵130GEF Ð=°,∴13130°Ð+Ð=,∵135EFH Ð=°,∴24135°Ð+Ð=,∴1324265°Ð+Ð+Ð+Ð=∵AB CD P ,∴34180Ð+Ð=°,∴121324(34)26518085°Ðа+Ð=Ð+Ð+Ð+Ð-+Ð=°=-,故选:D .【点睛】本题考查了平行线的性质,解题的关键是根据平行线的性质找出图中角度之间的关系.变式3-1.如图,已知直线a b ∥,把三角板的直角顶点放在直线b 上.若140Ð=°,则2Ð的度数为( )A .140°B .130°C .120°D .110°【答案】B【分析】根据互余计算出3904050Ð=°-°=°,再根据平行线的性质由a b ∥得到21803130Ð=°-Ð=°.【详解】解:∵1+3=90Ðа,∴3904050Ð=°-°=°,∵a b ∥,∴23180Ð+Ð=°.∴218050130°°=Ð=-°.故选:B .【点睛】本题考查了平行线的性质,熟记性质并准确识图是解题的关键.变式3-2.(2022秋·福建福州·七年级校考期中)如图,AB CD P ,170=°∠,则2Ð=( )A .70°B .80°C .110°D .120°【答案】C【分析】先利用对顶角相等,再利用两直线平行,同旁内角互补得出答案.【详解】解:170Ð=°Q ,3170\Ð=Ð=°,//AB CD Q ,2180318070110\Ð=°-Ð=°-°=°.故选:C .【点睛】此题主要考查了平行线的性质,对顶角相等,熟练掌握性质是解答题的关键.变式3-3.如图,AC BD ∥,AE 平分BAC Ð交BD 于点E ,若166а=,则2Ð= ( )A .123°B .128°C .132°D .142°【答案】A【分析】如图:根据平角的定义及角平分线的性质求得3Ð的度数,再根据平行线的性质求解即可.【详解】解:如图:∵166Ð=°,∴180118066114BAC Ð=°-Ð=°-°=°,∵AE 平分BACÐ∴1131145722BAC °°Ð=Ð=´=,∵AC BD ∥,∴23180Ð+Ð=°,∴2180318057123Ð=°-Ð=°-°=°.故选:A .【点睛】本题主要考查了平行线的性质、角平分线的定义等知识点,灵活运用平行线的性质是解答本题的关键.考查题型四 根据平行线的性质探究角的关系典例4.(2022秋·重庆铜梁·七年级校考期中)如图,已知AB DE ∥,且∠C=110°,则∠1与∠2的数量关系为__________________ .【答案】2170Ð=Ð+°【分析】过点C 作CF AB ∥,则CF AB DE ∥∥,根据平行线的性质可得角之间的关系,从而∠1与∠2的数量关系即可求解.【详解】解:过点C 作CF AB ∥,如图:则CF AB DE ∥∥,∴1BCF Ð=Ð,2180DCF Ð+Ð=°,∵110BCD Ð=°,∴1101101DCF BCF Ð=°-Ð=°-Ð,∴11012180°-Ð+Ð=°,∴2170Ð=Ð+°.故答案为:2170Ð=Ð+°.【点睛】本题考查了平行线的性质,解题的关键是作出平行线,利用平行线的性质得出角之间的关系.变式4-1.(2022·浙江杭州·杭州绿城育华学校校考模拟预测)如图,已知AB CD ∥,CE BF ∥,则B C Ð+Ð= ______ .【答案】180°##180度【分析】根据两直线平行,同位角相等与两直线平行,同旁内角互补,得到EHB C Ð=Ð,180EHB B Ð+Ð=°,等量代换即可求得B C Ð+Ð的值.【详解】解:如图,设AB 与CE 交于点H ,∵AB CD ∥,CE BF ∥,∴EHB C Ð=Ð,180EHB B Ð+Ð=°,∴180B C Ð+Ð=°.故答案为:180°.【点睛】此题考查了平行线的性质.解题的关键是注意两直线平行,同位角相等与两直线平行,同旁内角互补定理的应用,注意数形结合思想的应用.变式4-2.(2022秋·内蒙古乌海·七年级校考期中)如图,AB ∥EF ,则∠A ,∠C ,∠E 满足的数量关系是______.【答案】360A C E Ð+Ð+Ð=°【分析】根据两直线平行,同旁内角互补可直接得到答案.【详解】如下图所示,过点C 作//CD AB ,∵//CD AB ,∴180A ACD Ð+Ð=°(两直线平行,同旁内角互补),∵//AB EF ,//CD AB ,∴//CD EF ,∴180E DCE Ð+Ð=°(两直线平行,同旁内角互补),∴360A ACD E DCE Ð+Ð+Ð+Ð=°,∴360A ACE E Ð+Ð+Ð=°,∴在原图中360A C E Ð+Ð+Ð=°,故答案为:360A C E Ð+Ð+Ð=°.【点睛】本题考查平行直线的性质,解题的关键是熟练掌握两直线平行,同旁内角互补.变式4-3.(2022秋·山东青岛·七年级统考期末)如图,直线AB//CD ,∠AEM =2∠MEN ,∠CFM =2∠MFN ,则∠M 和∠N 的数量关系是________.【答案】∠EMF=23∠ENF【分析】利用平行线的性质以及已知条件解决问题即可.【详解】解:过点M 作MJ ∥AB ,过点N 作NK ∥AB .∵AB ∥CD ,∴MJ ∥AB ∥CD ,NK ∥AB ∥CD ,∴∠EMJ=∠AEM ,∠FMJ=∠CFM ,∠ENK=∠AEN ,∠FNK=∠CFN ,∴∠EMF=∠AEM+∠CFM ,∠ENF=∠AEN+∠CFN ,∵∠AEM=2∠MEN ,∠CFM=2∠MFN ,∴∠AEM+∠CFM=23(∠AEN+∠CFN ),即∠EMF=23∠ENF .故答案为:∠EMF=23∠ENF .【点睛】本题考查平行线的性质,解题的关键是学会探究规律的方法,属于中考常考题型.考查题型五 利用平行线的性质求角的度数典例5.(2022秋·北京西城·七年级期中)如图,若AB CD ∥,EF 与AB ,CD 分别相交于点E ,F ,EP EF ^,EFD Ð平分线与EP 相交于点P ,20BEP Ð=°,则PFD Ð=__________°.【答案】35°【分析】由题可求出BEF Ð,然后根据两直线平行,同旁内角互补可知DFE Ð,根据角平分线的定义可得到结果.【详解】∵EP EF ^,∴90PEF Ð=°,∵20BEP Ð=°,∴110BEF PEF BEP Ð=Ð+Ð=°,∵AB CD P ,∴18070EFD BEF Ð=°-Ð=°,∵FP 平分EFD Ð,∴1352PFD EFD Ð=Ð=°.【点睛】本题考查了平行线的性质与角平分线的定义,以及三角形的内角和定理,注意数形结合思想是解题关键.变式5-1.(2022春·黑龙江哈尔滨·七年级哈尔滨市第四十九中学校校考阶段练习)如图,已知AB EF ∥,BC DE ∥,若70B Ð=°,则E Ð=________°.【答案】110【分析】先根据“两直线平行,内错角相等”得出BGE Ð,再根据“两直线平行,同旁内角互补”得出答案.【详解】如图所示.∵AB EF ∥,∴70B B G E Ð=Ð=°.∵BC DF ∥,∴180BGE E Ð+Ð=°,∴180110E B G E Ð=°-Ð=°.故答案为:110.【点睛】本题主要考查了平行线的性质,灵活选择平行线的性质是解题的关键.变式5-2.如图,AB CD ∥,若40A Ð=°,26C Ð=°,则∠E=______.【答案】66°##66度【分析】如图所示,过点E 作EF AB ∥,则AB CD EF ∥∥,根据两直线平行内错角相等分别求出4026AEF CEF =°=°∠,∠,则66AEC AEF CEF =+=°∠∠∠.【详解】解:如图所示,过点E 作EF AB ∥,∵EF AB AB CD ∥,∥,∴AB CD EF ∥∥,∴4026AEF A CEF C ==°==°∠∠,∠∠,∴66AEC AEF CEF =+=°∠∠∠,故答案为:66°.【点睛】本题主要考查了平行线的性质,正确作出辅助线求出4026AEF CEF =°=°∠,∠是解题的关键.变式5-3.将一块长方形纸折成如图的形状,若已知1=110а,则2Ð=____°.【答案】55【分析】根据平行线的性质以及折叠的性质,即可得到2Ð的度数.【详解】解:如图所示:∵AB CD P ,∴1==110ACD Ðа,∵由折叠可知122ECD ACD Ð=Ð=Ð,∴2=55а,故答案为:55.【点睛】本题主要考查了平行线的性质和折叠的性质,根据题意正确作出辅助线是解答本题的关键.考查题型六 平行线的判定与性质的综合应用典例6.(2022秋·陕西渭南·七年级统考期中)如图,已知点B 、C 在线段AD 的异侧,连接、AB CD ,点E 、F 分别是线段、AB CD 上的点,连接CE BF 、,分别与AD 交于点G ,H ,且AEG AGE Ð=Ð,C DGC Ð=Ð.(1)求证:AB CD ∥;(2)若180AGE AHF °Ð+Ð=,求证:B C Ð=Ð;(3)在(2)的条件下,若117BFC C Ð=Ð,求AHB Ð的度数.【答案】(1)证明见解析(2)证明见解析(3)70°【分析】(1)只需要证明AEG C Ð=Ð即可证明AB CD ∥;(2)先证明HGE AHF =∠∠得到BF CE P 则B AEG =∠∠,再由AEG C Ð=Ð即可证明B C Ð=Ð;(3)根据平行线的性质得到180BFC C Ð+Ð=°,AHB DGC Ð=Ð,再结合已知条件求出C Ð的度数即可得到答案.【详解】(1)证明:∵AEG AGE Ð=Ð,C DGC Ð=Ð,AGE DGC Ð=Ð,∴AEG C Ð=Ð,∴AB CD ∥;(2)证明:∵180180AGE HGE AGE AHF +=°+=°∠∠,∠∠,∴HGE AHF =∠∠,∴BF CE P ,∴B AEG =∠∠,又∵AEG C Ð=Ð,∴B C Ð=Ð;(3)解:由(2)得BF CE P ,∴180BFC C Ð+Ð=°,AHB DGC Ð=Ð,又∵117BFC C Ð=Ð,∴111807C C +=°∠∠,∴70C Ð=°,∴70AHB DGC C ===°∠∠∠.【点睛】本题主要考查了平行线的性质与判定,对顶角相等,熟知平行线的性质与判定条件是解题的关键.变式6-1.(2022秋·广东东莞·七年级统考期中)如图,点B ,C 在线段AD 的异侧,点E ,F 分别是线段AB ,CD 上的点,已知12Ð=Ð,3C Ð=Ð.(1)求证:AB CD ∥;(2)若24180Ð+Ð=°,求证:180BFC C Ð+Ð=°;(3)在(2)的条件下,若3021BFC Ð-°=Ð,求B Ð的度数.【答案】(1)见解析(2)见解析(3)50B Ð=°【分析】(1)已知12Ð=Ð,所以32Ð=Ð,又因为3C Ð=Ð,可以得出1CÐ=Ð即可判定AB CD ∥;(2)已知23ÐÐ=,24180Ð+Ð=°,可以得出//BF EC ,即可得出180BFC C Ð+Ð=°;(3)由(1)(2)可知AB CD ∥,//BF EC ,可以得出1C Ð=Ð,180BFC C Ð+Ð=°;可以得出30212BFC C Ð-°=Ð=Ð,可以得出C Ð,又因为1C B Ð=Ð=Ð,即可求出B Ð的度数.【详解】(1)证明:12Ð=ÐQ ,3C Ð=Ð,23ÐÐ=,1C \Ð=Ð,//AB CD \;(2)证明:24180Ð+Ð=°Q ,23ÐÐ=,34180\Ð+Ð=°,//BF EC \,180BFC C \Ð+Ð=°;(3)180BFC C Ð+Ð=°Q ,30212BFC C Ð-°=Ð=ÐQ ,230BFC C \Ð=Ð+°,230180C C \Ð+°+Ð=°,50C \Ð=°,130BFC \Ð=°,//AB CD Q ,180B BFC \Ð+Ð=°,50B \Ð=°.【点睛】本题考查了对顶角相等,平行线的性质与判定,掌握平行线的性质与判定是解题的关键.变式6-2.如图,已知12AB CD Ð=Ð∥,.(1)求证:EF NP ∥;(2)若FH 平分EFG Ð,交CD 于点H ,交NP 于点O ,且14010FHG Ð=°Ð=°,,求FGD Ð的度数.【答案】(1)见解析(2)60°【分析】(1)根据平行线的性质及等量代换得出1BNP Ð=Ð,即可判定EF NP ∥;(2)过点F 作FM AB ∥,根据平行公理得出AB FM CD ∥∥,根据平行线的性质及角平分线定义得到50GFH EFH Ð=Ð=°,根据三角形外角性质求解即可.【详解】(1)证明:∵AB CD ∥,50GFH EFH Ð=Ð=°∴2BNP Ð=Ð,∵12Ð=Ð,∴1BNP Ð=Ð,∴EF NP ∥;(2)解:如图,过点F 作FM AB ∥,∵AB CD ∥,∴AB FM CD ∥∥,∴14010EFM HFM FHG Ð=Ð=°Ð=Ð=°,,∴50EFH EFM HFM Ð=Ð+Ð=°,∵FH 平分EFG Ð,∴50GFH EFH Ð=Ð=°,∴60FGD GHF HFG Ð=Ð+Ð=°.【点睛】此题考查了平行线的判定与性质,角平分线的定义,熟记平行线的判定与性质是解题的关键.变式6-3.(2022秋·福建福州·七年级校考期中)如图,在ABC V 中,AGF ABC ÐÐ=,12180Ð+Ð=°.(1)求证:DE BF ∥;(2)若DE AC ^,2140Ð=°,求AFG Ð的度数.【答案】(1)见解析(2)50°【分析】(1)由于AGF ABC ÐÐ=,可判断GF BC ∥,则1CBF ÐÐ=,由12180Ð+Ð=°得出2180CBF ÐÐ+=°判断出BF DE ∥;(2)由BF DE ∥,BF AC ^得到DE AC ^,由2140Ð=°得出140Ð=°,得出AFG Ð的度数.【详解】(1)解:BF DE ∥,理由如下:AGF ABC ÐÐ=Q ,GF \BC ∥,1CBF ÐÐ\=,12180Ð+Ð=°Q ,2180CBF ÐÐ\+=°,BF \DE ∥;(2)解:BF Q DE ∥,BF AC ^,DE AC \^,12180Ð+Ð=°Q ,2140Ð=°,140Ð\=°,904050AFG Ð\=°-°=°.【点睛】本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等,同旁内角互补.。
《5.3.1 平行线的性质》教案、导学案、同步练习

《5.3.1 平行线的性质》教案第1课时平行线的性质【教学目标】1.理解平行线的性质;(重点)2.能运用平行线的性质进行推理证明.(重点、难点)【教学过程】一、情境导入窗户内窗的两条竖直的边是平行的,在推动过程中,两条竖直的边与窗户外框形成的两个角∠1、∠2有什么数量关系?二、合作探究探究点一:平行线的性质如图,AB∥CD,BE∥DF,∠B=65°,求∠D的度数.解析:利用“两直线平行,内错角相等,同旁内角互补”的性质可求出结论.解:∵AB∥CD,∴∠BED=∠B=65°.∵BE∥FD,∴∠BED+∠D=180°,∴∠D=180°-∠BED=180°-65°=115°.方法总结:已知平行线求角度,应根据平行线的性质得出同位角相等,内错角相等,同旁内角互补.再结合已知条件进行转化.探究点二:平行线与角平分线的综合运用如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD 的度数.解析:先利用GF ∥CE ,易求∠CAG ,而∠PAG =12°,可求得∠PAC =48°.由AP 是∠BAC 的角平分线,可求得∠BAP =48°,从而可求得∠BAG =∠BAP +∠PAG =48°+12°=60°,即可求得∠ABD 的度数.解:∵FG ∥EC ,∴∠CAG =∠ACE =36°.∴∠PAC =∠CAG +∠PAG =36°+12°=48°.∵AP 平分∠BAC ,∴∠BAP =∠PAC =48°.∵DB ∥FG ,∴∠ABD =∠BAG =∠BAP +∠PAG =48°+12°=60°.方法总结:(1)利用平行线的性质可以得出角之间的相等或互补关系,利用角平分线的定义,可以得出角之间的倍分关系;(2)求角的度数,可把一个角转化为一个与它相等的角或转化为已知角的和差.探究点三:平行线性质的探究应用如图,已知∠ABC .请你再画一个∠DEF ,使DE ∥AB ,EF ∥BC ,且DE 交BC 边与点P .探究:∠ABC 与∠DEF 有怎样的数量关系?并说明理由.解析:先根据题意画出图形,再根据平行线的性质进行解答即可.解:∠ABC 与∠DEF 的数量关系是相等或互补.理由如下:如图①,因为DE ∥AB ,所以∠ABC =∠DPC .又因为EF ∥BC ,所以∠DEF =∠DPC ,所以∠ABC =∠DEF .如图②,因为DE ∥AB ,所以∠ABC +∠DPB =180°.又因为EF ∥BC ,所以∠DEF =∠DPB ,所以∠ABC +∠DEF =180°.故∠ABC 与∠DEF 的数量关系是相等或互补.方法总结:画出满足条件的图形时,必须注意分情况讨论,即把所有满足条件的图形都要作出来.三、板书设计平行线的性质⎩⎨⎧⎭⎬⎫两直线平行,同位角相等两直线平行,内错角相等两直线平行,同旁内角互补求角的大小或说明角之间的数量关系【教学反思】平行线的性质是几何证明的基础,教学中注意基本的推理格式的书写,培养学生的逻辑思维能力,鼓励学生勇于尝试.在课堂上,力求体现学生的主体地位,把课堂交给学生,让学生在动口、动手、动脑中学数学第2课时平行线的性质和判定及其综合运用【教学目标】1.掌握平行线的性质与判定的综合运用;(重点、难点)2.体会平行线的性质与判定的区别与联系.【教学过程】一、复习引入问题:平行线的判定与平行线的性质的区别是什么?判定是已知角的关系得平行关系,性质是已知平行关系得角的关系.两者的条件和结论刚好相反,也就是说平行线的判定与性质是互逆的.二、合作探究探究点一:先用判定再用性质如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF ∥AB.(1)CE与DF平行吗?为什么?(2)若∠DCE=130°,求∠DEF的度数.解析:(1)由∠1+∠DCE=180°,∠1+∠2=180°,可得∠2=∠DCE,即可证明CE∥DF;(2)由平行线的性质,可得∠CDF=50°.由DE平分∠CDF,可得∠CDE=1 2∠CDF=25°.最后根据“两直线平行,内错角相等”,可得到∠DEF的度数.解:(1)CE∥DF.理由如下:∵∠1+∠2=180°,∠1+∠DCE=180°,∴∠2=∠DCE,∴CE∥DF;(2)∵CE∥DF,∠DCE=130°,∴∠CDF=180°-∠DCE=180°-130°=50°.∵DE平分∠CDF,∴∠CDE=12∠CDF=25°.∵EF∥AB,∴∠DEF=∠CDE=25°.方法总结:根据题目中的数量找出各量之间的关系是解这类问题的关键.从角的关系得到直线平行用平行线的判定,从平行线得到角相等或互补的关系用平行线的性质,二者不要混淆.探究点二:先用性质再用判定如图,已知DF∥AC,∠C=∠D,CE与BD有怎样的位置关系?说明理由.解析:由图可知∠ABD和∠ACE是同位角,只要证得同位角相等,则CE∥BD.由平行线的性质结合已知条件,稍作转化即可得到∠ABD=∠C.解:CE∥BD.理由如下:∵DF∥AC,∴∠D=∠ABD.∵∠C=∠D,∴∠ABD=∠C,∴CE∥BD.方法总结:解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.探究点三:平行线性质与判定中的探究型问题如图,AB∥CD,E,F分别是AB,CD之间的两点,且∠BAF=2∠EAF,∠CDF=2∠EDF.(1)判定∠BAE,∠CDE与∠AED之间的数量关系,并说明理由;(2)∠AFD与∠AED之间有怎样的数量关系?解析:平行线中的拐点问题,通常需过拐点作平行线.解:(1)∠AED=∠BAE+∠CDE.理由如下:如图,过点E作EG∥AB.∵AB∥CD,∴AB∥EG∥CD,∴∠AEG=∠BAE,∠DEG=∠CDE.∵∠AED=∠AEG+∠DEG,∴∠AED=∠BAE+∠CDE;(2)同(1)可得∠AFD =∠BAF +∠CDF .∵∠BAF =2∠EAF ,∠CDF =2∠EDF ,∴∠BAE +∠CDE =32∠BAF +32∠CDF =32(∠BAF +∠CDF )=32∠AFD ,∴∠AED =32∠AFD .方法总结:无论平行线中的何种问题,都可转化到基本模型中去解决,把复杂的问题分解到简单模型中,问题便迎刃而解.三、板书设计⎭⎬⎫同位角相等内错角相等同旁内角互补判定性质两直线平行【教学反思】本节内容的重点是平行线的性质及判定的综合,直接运用了“∵”“∴”的推理形式,为学生创设了一个学习推理的环境,逐步培养学生的逻辑推理能力.因此,这一节课有着承上启下的作用,比较重要.本节内容的难点是理解平行线的性质和判定的区别,并在推理中正确地应用.由于学生还没有学习命题的概念和命题的组成,不知道判定和性质的本质区别和联系是什么,所以在教学中,应让学生通过应用和讨论,体会到如果已知角的关系,推出两直线平行,就是平行线的判定;反之,如果两直线平行,得出角的关系,就是平行线的性质《5.3.1 平行线的性质》导学案第1课时 平行线的性质【学习目标】:1.掌握两直线平行,同位角、内错角相等,同旁内角互补,并能熟练运用.2.通过独立思考,小组合作,运用猜想、推理的方法,提升自己利用图形分析问题的能力.3.激情投入,全力以赴,培养严谨细致的学习习惯.【重点】:平行线的性质.【难点】:根据平行线的性质进行推理.【自主学习】一、知识链接平行线的判定方法有哪几种?二、新知预习如图,直线a与直线b平行,直线c与它们相交.(1)量一量:用量角器量图中8个角的度数.(2)说一说:由测量的结果,你发现∠1与∠5、∠2与∠6、∠3与∠7、∠4与∠8、∠3与∠6、∠4与∠5、∠3与∠5、∠4与∠6的大小有什么关系?(3)想一想:(2)中的各对角分别是什么角?(4)议一议:两条平行直线被第三条直线所截,所得的同位角、内错角、同旁内角有什么关系?三、自学自测1.如图,直线a∥b,∠1=70°,那么∠2的度数是()A.50°B.60°C.70°D.80°2.下列说法中,(1)同位角相等,两直线平行;(2)两直线平行,同旁内角互补;(3)内错角相等,两直线平行;(4)同一平面内,垂直于同一直线的两条直线平行.其中是平行线的性质的是()A.(1)和(3)B.(2)C.(4)D.(2)和(4)【课堂探究】要点探究探究点:平行线的性质问题1:画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:角∠1 ∠2 ∠3 ∠4度数角∠5 ∠6 ∠7 ∠8度数观察:∠1~ ∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想.猜想:两条平行线被第三条直线所截,同位角 .思考:再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?问题2:如图,已知a//b,那么∠2与∠3相等吗?为什么?问题3:如图,已知a//b,那么∠2与∠4有什么关系呢?为什么?例1.如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?例2:小明在纸上画了一个∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他设计出多少种方法测出∠A的度数?【当堂检测】1.如图,已知平行线AB、CD被直线AE所截(1)从∠1=110°可以知道∠2 是多少度吗,为什么?(2)从∠1=110°可以知道∠3是多少度吗,为什么?(3)从∠1=110°可以知道∠4 是多少度吗,为什么?2.如图,一条公路两次拐弯的前后两条路互相平行.第一次拐弯时∠B是142°,第二次拐弯时∠C是多少度?为什么?3.如图,直线 a ∥ b,直线b垂直于直线c,那么直线a垂直于直线c吗?4.如果有两条直线被第三条直线所截,那么必定有()A.内错角相等B.同位角相等C.同旁内角互补D.以上都不对5.(1)如图1,若AB∥DE , AC∥DF,试说明∠A=∠D.请补全下面的解答过程,括号内填写依据.解: ∵ AB∥DE( )∴∠A=_______ ( )∵AC∥DF( )∴∠D=______ ( )∴∠A=∠D ( )(2)如图2,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.解: ∵ AB∥DE( )∴∠A= ______ ( )∵AC∥DF( )∴∠D+ _______=180° ( )∴∠A+∠D=180°()6.【拓展题】如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?5.3.1 平行线的性质第2课时平行线的性质和判定及其综合运用【学习目标】:1.进一步熟悉平行线的判定方法和性质.2.运用平行线的性质和判定进行简单的推理和计算.【重点】:平行线的判定方法和性质.【难点】:平行线的性质和判定的综合运用.【自主学习】一、知识链接1.平行线的判定方法有哪些?2.平行线的性质有哪些?二、新知预习1.两条直线被第三条直线所截,同位角、内错角相等,或者说同旁内角互补,这句话对吗?2.自主归纳:(1)两直线平行,同位角,内错角,同旁内角 .(2)不难发现,平行线的判定,反过来就是,注意它们之间的联系和区别.(3)运用平行线的性质时,不要忽略前提条件“”,不要一提同位角或内错角,就认为是相等的.【课堂探究】一、要点探究探究点:平行线的性质和判定及其综合应用例1.如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B = 60°,∠AED=40°.(1)DE和BC平行吗?为什么?(2)∠C是多少度?为什么?做一做:已知AB∥CD,∠1 = ∠2.试说明:BE∥CF.例2.如图,AB∥CD,猜想∠A、∠P 、∠PCD的数量关系,并说明理由.例3.如图,若AB//CD ,你能确定∠B 、∠D 与∠BED 的大小关系吗?说说你的看法.【变式题1】如图,AB//CD ,探索∠B 、∠D 与∠DEB 的大小关系 .【变式题2】如图,AB ∥CD,则∠A ,∠C 与∠E 1,∠E 2,…,∠E n 有什么关系?【变式题3】如图,若AB ∥CD, 则∠A ,∠C 与各拐角之间有什么关系?EDC BA【当堂检测】1.填空:如图,(1)∠1= 时,AB∥CD.(2)∠3= 时,AD∥BC.2.直线a,b与直线c相交,给出下列条件:①∠1= ∠2;②∠3= ∠6;③∠4+∠7=180°;④∠3+ ∠5=180°,其中能判断a//b的是( )A. ①②③④ B .①③④ C. ①③ D. ④3. 有这样一道题:如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数. 请补全下列解答过程.解:过点E作EF//AB.∵AB//CD(已知),∴ // (平行于同一直线的两直线平行).∴∠A+∠ =180°,∠C+∠ =180°(两直线平行,同旁内角互补).又∵∠A=100°,∠C=110°(已知),∴∠ = °, ∠ = °.∴∠AEC=∠1+∠2= °+ ° = °.4.已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.5.如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.第五章相交线与平行线5.3.1《平行线的性质》同步练习一、单选题(共15题;共30分)1、如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20o,那么∠2的度数是( )A、30°B、25°C、20°D、15°2、如图所示BC//DE,∠1=108°,∠AED=75°,则∠A的大小是()A、60°B、33°C、30°D、23°3、两条平行直线被第三条直线所截,下列命题中正确的是()A、同位角相等,但内错角不相等B、同位角不相等,但同旁内角互补C、内错角相等,且同旁内角不互补D、同位角相等,且同旁内角互补4、一架飞机向北飞行,两次改变方向后,前进的方向与原来的航行方向平行,已知第一次向左拐50°,那么第二次向右拐()A、40°B、50°C、130°D、150°5、如图,下列说法正确的是()A、若AB//CD,则∠1=∠2B、若AD//BC,则∠B+∠BCD=180ºC、若∠1=∠2,则AD//BCD、若∠3=∠4,则AD//BC6、下列图形中,由AB//CD能得到∠1=∠2的是()A、 B、C、 D、7、下列语句:①两条不相交的直线叫做平行线;②过直线外一点有且只有一条直线与已知直线垂直;③若AB=BC,则点B是AC的中点;④若两角的两边互相平行,则这两个角一定相等;其中说法正确的个数是()A、1B、2C、3D、48、同一平面内,两条不重合的直线的位置关系是()A、平行或垂直B、平行或相交C、平行、相交或垂直D、相交9、下列生活实例中;①交通道口的斑马线;②天上的彩虹;③体操的纵队;④百米跑道线;⑤火车的平直铁轨线.其中属于平行线的有()A、1个B、2个C、3个D、4个10、如图,AB∥CD,∠A=46°,∠C=27°,则∠AEC的大小应为()A、19°B、29°C、63°D、73°11、如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,∠2的度数为()A、95°B、65°C、85°D、35°12、如图,已知:AB∥CD,CE分别交AB、CD于点F、C,若∠E=20°,∠C=45°,则∠A的度数为()A、5°B、15°C、25°D、35°13、如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=()A、20°B、25°C、30°D、35°14、如图,若a∥b,则下列选项中,能直接利用“两直线平行,内错角相等”判定∠1=∠2的是()A、 B、C、 D、15、如图,如果AB∥CD,那么图中相等的内错角是()A、∠1与∠5,∠2与∠6B、∠3与∠7,∠4与∠8C、∠5与∠1,∠4与∠8D、∠2与∠6,∠7与∠3二、填空题(共5题;共10分)16、如图,已知:∠A=∠F,∠C=∠D,求证:BD∥EC,下面是不完整的说明过程,请将过程及其依据补充完整.证明:∵∠A=∠F(已知)∴AC∥________,________∴∠D=∠1________又∵∠C=∠D(已知)∴∠1=________________∴BD∥CE ________17、如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为________ 度(用关于α的代数式表示).18、如图所示,一条公路两次拐弯后和原来的方向相同,即拐弯前、•后的两条路平行,若第一次拐角是150°,则第二次拐角为________ .19、如图,把含有60 º角的三角尺ABC的直角顶点C放在直线DE上,当AB∥DE。
5.3.1 平行线的性质(2)

5.布置作业
教科书 习题5.3 第7、8、14题, 复习题5 第6题
从来没有人读书,只有人在书中读自己, 发现自己或检查自己.
——罗曼·罗兰
答:CD∥EF.
A
G1D E
C
2 F
B
2.综合运用,巩固提高
理由如下: ∵ ∠AGD =∠ACB ,
A G1D
∴ GD∥BC.
E
∵∠1和∠3是内错角,
C3 2
F
B
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠2=∠3.
∵∠2和∠3是同位角,
∴ CD∥EF(同位角相等,两直线平行).
3.应用迁移,拓展升华
∴∠E=∠__2_( 两直线平行,内错角相等 )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
辅助线:为帮助解题而添加的线 辅助线一般画成虚线
1,过转折点作平行线 2,利用平行线相关性质
4.归纳小结
(1)平行线的性质与判定的区别是什么? (2)在解决具体问题过程中,你能区别 什么时候需要使用平行线的性质,什么时 候需要使用平行线的判定吗?
答: BE∥CF.
A
B
E F
C
D
2.综合运用,巩固提高
理由如下:
∵ BE平分∠ABC,
∴
1
1 2
ABC.
同理 2 1 BCD.
2
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
A
1
E
2
C
B F D
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行).
2.综合运用,ACB, ∠1=∠2,CD与EF平行吗?为什么?
5.3.1平行线的性质

回答:如图
(1)∠3=∠B,则EF∥AB,依据是
同位角相等,两直线平行
(2)∠2+∠A=180°,则DC∥AB, 依据是 同旁内角互补,两直线平行 (3)∠1=∠4,则GC∥EF,依据是
内错角相等,两直线平行
(4) GC∥EF,AB∥EF,则GC∥AB, 依据是 平行于同一直线的两直线平行. (5)EF⊥BC,AB⊥BC,则EF∥AB, 依据是 平面内,垂直于同一直线的两直线平行.
比一比
平行线的“判定”与“性质”有什么不
判定:已知角的关系得平行的关系. 推平行,用判定. 性质:已知平行的关系得角的关系. 知平行,用性质.
已知 判定
同位角相等 内错角相等 同旁内角互补
得到
两直线平行
性质 已知
得到
4.如图,已知AB、CD、EF互相平行,且 ∠ABE =70°,∠ECD = 150°,则 ∠BEC =________.
整理归纳: 平行线的性质 性质1:两直线平行,同位角相等. ∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等) 性质2:两直线平行,内错角相等. ∵a∥b( 已知 ) ∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补. ∵a∥b( 已知 ) ∴ ∠1+∠4=180° (两直线 平行,同旁内角互 补)
1.已知:如图,a// b ,那么3与2有什么关系? 解: ∠ 2 = ∠3,理由如下: ∵ a∥b ∴∠1= ∠2( 两直线平行,同位角相等 ) ∠1 又∵∠3 = ___(对顶角相等), ∴∠ 2 = ∠3.
平行线的性质2 两条平行线被第三条直线所截,内错角相等 简单说成:两直线平行,内错角相等。
2014年春人教版义务教育教科书数学7年级下册5.3.1平行线的性质

5.3.1平行线的性质学习范围:课本19页——21页练习学习目标:1、了解平行线的性质2、能够进行推理说明平行线的性质。
学习重、难点:重点:探索并掌握平行线的性质,能用平行线性质进行简单的推理和计算.难点:能区分平行线的性质和判定学习过程:1、平行线的判定定理1中“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”。
其中同位角是条件,两条直线平行是结论,那么把这个结论反过来成立吗?即:“如果两条平行线被第三条直线所截,那么同位角相等。
”成立吗?2、带着上面的问题认真学习课本19页,并完成课本上的填空。
3、性质1:两条 被第三条直线所截,同位角 。
可以简单的说:性质2:性质3:4、学习20页思考,并完成课本上的填空。
左图中:a ∥b,说明2∠+3∠=1800(提示:应该性质1) a bc 3215、自主学习20页例题学效测试:6、判断题(1)两条直线被第三条直线所截,则同旁内角互补.( )(2)两条直线被第三条直线所截,如果同旁内角互补,那么同位角相等.( )7、如图:直线a ∥b,1∠=540,那么2∠,3∠,4∠各是多少度?8、如图(3),AB ∥EF,∠ECD=∠E,则CD ∥AB.说理如下:因为∠ECD=∠E,所以CD ∥EF( )又AB ∥EF,所以CD ∥AB( ).a bc 4321FE D C B A同步训练:判断题.1.两条直线被第三条直线所截,则同旁内角互补.( )2.两条直线被第三条直线所截,如果同旁内角互补,那么同位角相等.( )3.两条平行线被第三条直线所截,则一对同旁内角的平分线互相平行.( )选择题1.∠1和∠2是直线AB 、CD 被直线EF 所截而成的内错角,那么∠1和∠2 的大小关系是( )A.∠1=∠2B.∠1>∠2;C.∠1<∠2D.无法确定2.一个人驱车前进时,两次拐弯后,按原来的相反方向前进, 这两次拐弯的角度是( )A.向右拐85°,再向右拐95°;B.向右拐85°,再向左拐85°C.向右拐85°,再向右拐85°;D.向右拐85°,再向左拐95° 填空1. 如图(1),若AD ∥BC,则______=_______,∠_______=∠_______,∠ABC+_______=180°;若DC ∥AB,则∠______=∠_______,∠________= ∠__________,∠ABC+∠_________=180°.2.如图(3),AB ∥EF,∠ECD=∠E,则CD ∥AB.说理如下:因为∠ECD=∠E,所以CD ∥EF( )又AB ∥EF, 所以CD ∥AB( ).解答(选做题)如图,已知:DE ∥CB,∠1=∠2,求证:CD 平分∠ECB.87654321D CB A F E D CB A E 21D CB。
人教版初一数学 5.3.1 平行线的性质PPT课件

探究新知 两直线平行,内错角相等吗?
探究新知
已知:如图,直线l1//l2,∠1和∠2是直线l1,l2被 直线l3 截出的内错角.
求证:∠1=∠2. 证明:∵l1//l2(已知), ∴∠1=∠3(两直线平行,同位角相等). 又∵∠2=∠3(对顶角相等), ∴∠1=∠2(等量代换).
探究新知 两直线平行,同旁内角有什么关系?
课后作业
1.教材第20页 练习第1,2题,第22, 23页习题5.3第2,4,5题. 2.七彩作业.
探究新知
学生活动三【典例精讲】 例 如图,已知平行线AB,CD 被直线AE 所截. (1)从∠1=110°可以知道∠2是多少度吗?为什么? 解:∠2=110°. 理由:两直线平行,内错角相等.
探究新知
例 如图,已知平行线AB,CD 被直线AE 所截. (2)从∠1=110°可以知道∠3是多少度吗?为什么? 解:∠3=110°. 理由:两直线平行,同位角相等.
回顾复习
通过上题可知平行线的判定方法有什么? 1.同位角相等,两直线平行. 2.内错角相等,两直线平行. 3.同旁内角互补,两直线平行.
反过来,如果两条直线平行,那么同位角、内错 角、同旁内角各有什么关系呢?
探究新知
学生活动一【一起探究】 我们知道,同位角相等,两直线平行;反过来,
若两直线平行,同位角会有什么关系?
探究新知
例 如图,已知平行线AB,CD 被直线AE 所截. (3)从∠1=110°可以知道∠4是多少度吗?为什么? 解:∠4=70°. 理由:两直线平行,同旁内角互补.
拓展应用
如图,将一个三角尺的直角顶点放在直尺的一
边上,当∠1=35°时,∠2的度数为( C )
A.35°
B.45°
平行线的性质(1)-

北
北
•B
41°
A•
如图,F在直线DF上,B在直线AC上, 若∠ AGB= ∠ EHF, ∠ C= ∠ D 则∠ A= ∠ F,为什么?
D
E
F
H
G
A
BC
本节小 结
同位角相等 内错角相等 同旁内角互补
判定 性质
两直线平 行
再见
即:两直线平行,同位角相等
性质2 两条平行线被第三条直线所截,内错角相等
即:两直线平行,内错角相等
性质3 两条平行线被第三条直线所截,同旁内角互补
即:两直线平行,同旁内角互补
; 宠物DR 宠物DR ;
过程给了它缤纷;生命本没有芳香,过程给了它花香;生命本是一朵白色的纸花,过程给了它活力。法布尔的《昆虫记》告诉我们:生命的意义在于去发现、去挖掘、去体现。生命是美丽的,生命的美丽,永远是展现在她的进取之中,就像大树的美丽,是展现在它负势向上高耸入云的蓬 勃生机中;像雄鹰的美丽,是展现在它搏风击雨如苍天之魂的翱翔中;像江河的美丽,是展现在它波涛汹涌一泻千里的奔流中……法布尔的《昆虫记》也告诉我们我们的生命不是天地间的过客,也不是时光的影子,我们的生命是自然的花朵,是岁月的果实,我们是宇宙间充满激情、梦想、力 量和智慧的创造者,我们正以自己的奋斗展现着人类生命的美丽。法布尔的《昆虫记》还告诉我们生命是伟大的,生命给予我们一切,生命让世界变得更美丽。有了生命才有了生活,有了生活才有了生命,生命让生活充满活力,我们要珍惜生命、赞叹生命、感谢生命。 纵观历史,我们可 以发现,历史上那些伟人、那些为人们所怀念和称颂的人、那些被认为实现了生命意义的人,都是对社会发展做出了极大贡献的人;而历史上那些坏人之所以是坏人,就是因为他们被认为是对社会发展起到破坏作用的人。揭开中国历史的篇章,有多少人的生命
5.3.1平移

课题:5.3.1平行线的性质重点难点:知识点一:平行线的性质性质1:两直线平行,同位角相等m//n ∴∠1=∠3性质2:两直线平行,内错角相等m//n ∴∠3=∠2性质3:两直线平行,同旁内角互补m//n ∴∠2+∠4=180º知识点二:平行线的性质与判定的联系与区别区别:性质由形到数,用于推导角的关系并计算判定由数到形,用于判定两直线平行联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关典型例题分析:题型一:平行线性质的基本应用例1:已知:AB//CD,直线EF分别交AB,CD于E,EG平分∠BEF,∠1=40º求:∠2的度数题型二:平行线性质的灵活应用——一题多解例2:如图,AB//CD,EPF为折线,试探究∠P与∠AEP与∠PFC的关系,并给出证明。
题型三:平行线性质与判定的综合运用例3:已知:∠AED=70º,∠ACB=70º,CD平分∠ACB.求:∠EDC的度数例4:已知:AD//BC,∠A=∠C.求证:AB//CD同步练习:1.已知:如图,∠1=∠2,∠C=∠D,试说明∠A=∠F.2.如下图,AM//CN(1)求∠MAB+∠ABC+∠BCN的度数(2)求∠MAE+∠AEF+∠EFC+∠FCN的度数(3)根据(1)(2)题,你能探究出一个结论吗?你能直接写出这一结论3.如图,已知DE//BC,∠D:∠DBC=2:1,∠1=∠2,求∠DEB 的度数.4.已知:如图,AB//CD,被直线EF 所截交AB,CD 于M,N,MP 平分∠EMB,NQ 平分∠MND,那么MP//NQ,为什么?5.如图所示,已知:AE 平分∠BAC ,CE 平分∠ACD ,且AB ∥CD .求证:∠1+∠2=90°6.如图所示,已知:∠1=∠2,求证:∠3+∠4=180°7.已知:如图,AB//CD,分别探究下图中∠APC 与∠PAB 、∠PCD 的关系.达标检测:一、选择题:1、如图5,∠1和∠2互补,那么图中平行的直线有()A、ba// B、dc// C、ed// D、ec//图5 图62、下列条件中,能得到互相垂直的是()A、对顶角的平分线B、平行线的同位角的平分线C、平行线的内错角的平分线D、邻补角的平分线3、如图6,nm//,那么∠1、∠2、∠3的关系是()A、∠1+∠2+∠3=360° B、∠1+∠2-∠3=180°C、∠1-∠2+∠3=180°D、∠1+∠2+∠3=180°二、解答题:1、如图7,点A在直线MN上,且MN//BC,求证∠BAC+∠B+∠C=180º2、如图,M、N、T在同一直线上,且∠1=∠3,∠P=∠T,求证:∠M=∠R。
5、3、1平行线的性质
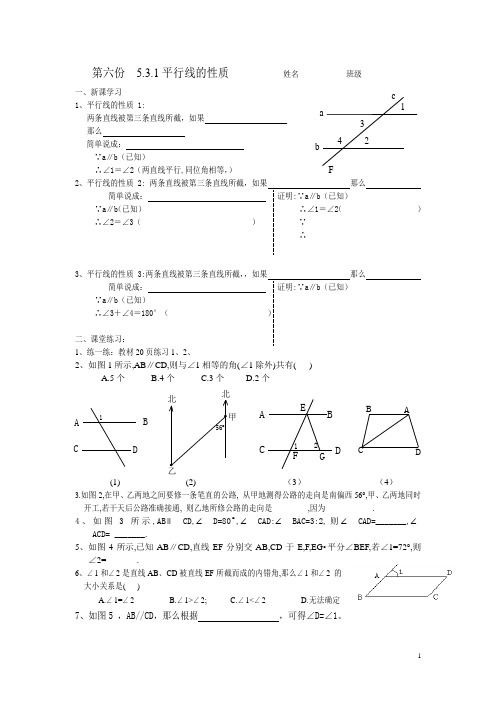
D C B AD C B A 1G FE D C B A 12第六份 5.3.1平行线的性质 姓名____________班级______________一、新课学习 1、平行线的性质 1: 两条直线被第三条直线所截,如果那么简单说成: ∵a ∥b (已知)∴∠1=∠2(两直线平行,同位角相等,)2、平行线的性质那么∵a ∥b ()∴∠2=∠3(3、平行线的性质 那么∵a ∥b ∴∠3二、课堂练习:1、练一练:教材20页练习1、2、2、如图1所示,AB ∥CD,则与∠1相等的角(∠1除外)共有( )A.5个B.4个C.3个D.2个(1) (2) (3) (4)3.如图2,在甲、乙两地之间要修一条笔直的公路, 从甲地测得公路的走向是南偏西56°,甲、乙两地同时开工,若干天后公路准确接通, 则乙地所修公路的走向是_________,因为____________. 4、如图3所示,AB ∥ CD,∠ D=80°,∠ CAD:∠ BAC=3:2,则∠ CAD=_______,∠ ACD=•_______. 5、如图4所示,已知AB ∥CD,直线EF 分别交AB,CD 于E,F,EG •平分∠BEF,若∠1=72°,则∠2=_______.6、∠1和∠2是直线AB 、CD 被直线EF 所截而成的内错角,那么∠1和∠2 的大小关系是( ) A.∠1=∠2 B.∠1>∠2; C.∠1<∠2 D.无法确定7、如图5 ,AB//CD ,那么根据 ,可得∠D=∠1。
如果AD//BC ,根据 可得∠B=∠1 图(5)8、AB ∥CD ,∠1=100°,求∠2、∠3、∠4、∠5的度数,并说明根据?9、EF 过△ABC 的一个顶点A ,且EF ∥BC ,如果∠B =40°,∠2=75°,那么∠1、∠3、∠C 、∠BAC +∠B +∠C 各是多少度,并说明依据?10、如图,BCD 是一条直线,∠A=75°,∠1=53°,∠2=75°,求∠B 的度数.E21DCBA11、如图,已知∠1=110°,∠2=110°,∠3=70°,求∠4的度数.4321DCBA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精练目标:巩固新知
精练方式:讲练结合
精练内容:
(1)如图2—69已知:AB∥CD,MG平分∠AMN,NH平分∠DNM,说明:MG∥NH
(2)如图2—70已知:AB∥CD,∠A=∠C,说明:AD∥BC
(3)如图2—71,EG⊥AB,CD⊥AB,说明:EG∥CD
M
有效小结与作业设计
小结:平行线的性质是怎样的?几何语言怎样描述?平行线的性质和判定的区别和联系是什么?
如果我们把上面的三条判定方法,从反而思考和研究,即把条件和结论交换一下,便得到以下三条平行线的性质(板书) (1)两条直线平行,同位角相等(2)两条直线平行,内错角相等(3)两条直线平行,同旁内角互补。这节课我们就是要研究它们是否成立(板书课题)
由于每个问题的条件和结论交换所得到的新的问题不一定正确,如:“对顶角相等”是成立的,但它的反面问题“相等的角是对顶角”就不成立,又如:“两直线相交成直角,这两条直线互相垂直”,它的反面问题是“两条直线互相垂直,这两条直线相交所成的角是直角”,它们同时成立所以上面三条性质还不能说是正确的,因此只能说是猜想,即:猜想(1):两直线平行,同位角相等;猜想(2):两直线平行,内错角相等;猜想(3):两直线平行,同旁内角互补(在教学过程中,把上面三条性质前面加上“猜想”两字就行精讲目标:演绎推理,发现平行线的性质
精讲方式:探究式精讲
精讲内容:
1实验观察,发现平行线第一个性质(方法)
下面先对第一个猜想进行实验观察请学生画出图2—63(1)
设a∥b,c与它们相交,请度量∠1和∠2的大小,你能发现什么
关系?(∠1=∠2)这是偶然的吗?请同学们在用图2—63(1),再作
出直线l4,再度量一下∠3和∠4的大小,你还能发现它们有什么关系?(∠3=∠4)由这两次实验活动,你能发现什么规律?(说明猜想1是成立的)由于猜想1是由实践活动证实成立的因此,我们把它当方法(板书:把上述猜想改为平行线性质1,并在后面加上“方法”两字)平行线性质1(方法):两直线平行,同位角相等
凤台四中专业性有效教学设计方案
年级学科
课题
5.3.1平行线的性质
时间
主讲教师
教学课时
1课时
课型
新授课
教学目标
目标:使学生掌握平行线的三个性质,并能应用它们进行简单的推理论证;使学生经过对比后,理解平行线的性质和判定的区别和联系;通过推理论证教学,培养学生的分析问题和解决问题的能力;培养学生从特殊到一般发现问题的能力;培养学生逆向思维的能力
重点:平行线的三个性质及其应用
难点:正确理解性质和判定的区别和联系以及运用它们去推理证明
有效导入
导入目标:激发学生探索的兴趣
导入方式:问题导入
导入内容:
我们学了哪些判定平行的方法?在学生回答的基础上,教师用投影的形式打出其中三条(1)同位角相等,两直线平行(方法) (2)内错角相等,两直线平行(方法) (3)同旁内角互补,两直线平行(方法)
