上海交大附中2010-2011学年度第一学期_高三数学第一次月考试卷[1].doc
交大附中浦东实验高中2011届第一学期第一次月考高三数学试卷

上海交大附中浦东实验高中2021届第一学期第一次月考高三数学试卷 〔总分值150分,考试时间120分钟〕 (2021-9) 一、填空题〔10*4分=40分〕 1、由数字1,2,3,4,5可以组成无重复数字的 个三位偶数。
2、假设61⎪⎭⎫ ⎝⎛-x x 展开式中常数项等于 3、假设4名男生,4名女生排成一排,女生不排两端,那么有_________种不同排法。
4、(2–x )7=a 0+a 1x+a 2x 2+……+a 7x 7,那么a 1+a 2+……+a 7= 。
5、从1,2,3,4,5五个数字中,任意有放回地连续抽取三个数字,那么三个数字完全不...同.的 概率是_________. 6、假设()441043x a x a a x +⋅⋅⋅++=+,那么()()2312420a a a a a +-++的值为_______ 7、将5本不同的书全发给4名同学,每名同学至少有一本书的不同的分法是__________. 8、设m 、n 是异面直线,m 、k 也是异面直线,那么n 、k 的位置关系是__ __ . 9、学校A 有学生200人,学校B 有学生300人,学校C 有学生500人,从这三所学校的学 生中用分层抽样的方法共得到20人当代表,那么学校A 、B 、C 依次抽得的人数是___ __ 10、求值:0123456789999999999922222C C C C C C C C C C -+-+-+-+-= . 二、选择题:〔9*4分=36分〕 11、用1,2,3,4四个数字可以组成数字不重复的自然数的个数 〔 〕 A 、64 B 、60 C 、24 D 、256 12、3张不同的电影票全局部给10个人,每人至多一张,那么有不同分法的种数是 〔 〕 A 、2160 B 、120 C 、240 D 、720 13、要排一张有5个独唱和3个合唱的节目表,如果合唱节目不能排在第一个,并且合唱节目不能相邻,那么不同排法的种数是〔 〕 A 、 B 、 C 、 D 、 14、5个人排成一排,其中甲、乙两人至少有一人在两端的排法种数有 〔 〕 A 、6 B 、24 C 、84 D 、48 15、空间四个点,那么“这四个点中有三点在同一直线上〞是“这四个点在同一平面上〞的〔 〕A 、充分非必要条件;B 、必要非充分条件;C 、充要条件;D 、非充分非必要条件.16、甲、乙两学生在一学期里屡次检测中,其数学成绩的平均分相等,•但他们成绩的方差 学校_________________班级____________姓名_______________学号___________ ………………………...………………………装…………………………订…………………………..线……………….…………………………… ______________学生答题不准超过此线不 等,那么正确评价他们的数学学习情况的是 〔 〕A .学习水平一样B .成绩虽然一样,但方差大的学生学习潜力大C .虽然平均成绩一样,但方差小的学习成绩稳定D .方差较小的学习成绩不稳定,忽高忽低17、假设样本1,2,3,x 的平均数为5,又样本1,2,3,x ,y 的平均数为6,那么样本..1,2,3,x ,y 的方差是〔 〕A 、26.0B 、32.5C 、41.5D 、5.718、用数字1,2,3,4,5组成没有重复数字的五位数,其中小于50000的偶数有 〔 〕A 、24B 、36C 、46D 、6019、某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下 方式分成六组:每一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15 秒……第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班人数的百分比为x ,成绩大于等于15秒且小于17秒的学生人数 为y ,那么从频率分布直方图中可以分析出x 和y 分别为 〔 〕A .0.9,35B . 0.9,45C .0.1,35D .0.1,45 三、解答题 20、〔14分〕解方程:112312-=+x x x P P P21、〔14分〕证明题:如图:两直线a 、b 平行,直线c 与a 、b 相交,那么:直线a 、b 、c 三线共面〔要求写出、求证、证明〕。
2010年上海交通大学附属中学高一数学上

数学试卷(满分100分,90分钟完成,允许使用计算器,答案一律写在答题纸上)命题:段长荣 审核:杨逸峰 校对:纪爱萍一.填空题:(共12小题,每小题3分)1. A={1},B={x|x ⊆A},用列举法表示集合B 的结果为_________。
2. 已知集合A={(x,y)|y=x+3},B={(x,y)|y=3x-1},则A ∩B=________。
3. 写出x>1的一个必要非充分条件__________。
4. 不等式11x≤的解集为_____________。
(用区间表示) 5. 命题“已知x 、y ∈R ,如果x+y ≠2,那么x ≠0或y ≠2.”是_____命题。
(填“真”或“假”)6. 集合A={x|(a-1)x 2+3x-2=0}有且仅有两个子集,则a=_________。
7. 若不等式|ax+2|<6的解集为(-1,2),则实数a 等于_________。
8. 不等式24x x ->x 的解集是____________。
9. 已知a 2+b 2=1,则___________。
10. Δ和 各代表一个自然数,且满足1∆+9=1,则当这两个自然数的和取最小 值时,Δ=_______, =_______.11. 已知集合A={-1,2},B={x|mx+1>0},若A ∪B=B ,则实数m 的取值范围是_________。
12. 如果关于x 的三个方程x 2+4ax-4a+3=0,x 2+(a-1)x+a 2=0,x 2+2ax-2a=0中,有且只有一个方程有实数解,则实数a 的取值范围是_______________。
二.选择题:(共4小题,每题3分)13. 设命题甲为“0<x<5”,命题乙为“|x-2|<3”,那么甲是乙的: ( )(A )充分非必要条件;(B )必要非充分条件; (C )充要条件; (D )既非充分又非必要条件14. 下列命题中正确的是:( )(A )若ac>bc ,则a>b(B) 若a 2>b 2,则a>b(C )若ba 11>,则a<b (D) 若b a <,则a<b15. 设x>y>0,则下列各式中正确的是:( )(A )x>2x y +>(B )>2x y+>y(C )x>2x y +> y > (D )> y >2x y+16. 下列每组中两个函数是同一函数的组数共有:( )(1)f(x)=x 2+1和f(v)=v 2+1(2)y =y =(3)y=2x ,x ∈{0,1}和y=215166x x ++,x ∈{0,1} (4)y=1和y=x 0(5)和y(6)y=x 和y (A )1组 (B )3组(C )2组(D )4组三.解答题:(共5小题,本大题要有必要的过程)17. (本题8分)已知集合{}1A x x a =-≤,{}2540B x x x =-+>,且A B φ= ,求实数a 的取值范围。
2017-2018学年上海市交通大学附属中学高一数学上第一次月考试题(含答案)

上海交通大学附属中学2017-2018学年度第一学期高一数学月考一 试卷一、填空题(1-6题每题4分,7-12题每题5分)1.用列举法表示方程22320,x x x R --=∈的解集是____________.2.已知集合2{1,},{1,}A m B m =-=,且A B =,则m 的值为____________.3.设集合{1,2,6},{2,4},{|15,}A B C x x x R ===-≤≤∈,则()A B C =____________.4.已知关于x 的一元二次不等式20ax x b ++>的解集为(,2)(1,)-∞-+∞,则a b -=____________.5.设集合{}3(,)|1,(,)12y U x y y x A x y x ⎧-⎫==+==⎨⎬-⎩⎭,则U A =ð____________.6.不等式21x+≥+____________. 7.已知x R ∈,命题“若25x <<,则27100x x -+<”的否命题是____________.8.设[]:13,:1,25x x m m αβ-≤≤∈-+,α是β的充分条件,则m ∈____________.9.若对任意x R ∈,不等式22(1)(1)10a x a x ----<恒成立,则实数a 值范围是____________.10.向50名学生调查对A 、B 两事件的态度,有如下结果:赞成A 的人数是全体的五分之三,其余的不赞成,赞成B 的比赞成A 的多3人,其余的不赞成;另外,对A 、B 都不赞成的学生数比对A 、B 都赞成的学生数的三分之一多1人. 问对A 、B 都赞成的学生有____________人11.设[]x 表示不超过x 的最大整数(例如:[5.5]5,[ 5.5]6=-=-),则2[]5[]60x x -+≤的解集为____________.12.已知有限集123{,,,,}(2)n A a a a a n =≥. 如果A 中元素(1,2,3,,)i a i n =满足1212n n a a a a a a =+++,就称A 为“复活集”,给出下列结论:①集合⎪⎪⎩⎭是“复活集”; ②若12,a a R ∈,且12{,}a a 是“复活集”,则124a a >;③若*12,a a N ∈,则12{,}a a 不可能是“复活集”;④若*i a N ∈,则“复活集”A 有且只有一个,且3n =.其中正确的结论是____________.(填上你认为所有正确的结论序号)二、选择题(每题5分)13.若集合P 不是集合Q 的子集,则下列结论中正确的是( )A. Q P ⊆B. P Q =∅C. P Q ≠∅D. P Q P ≠14.集合{}*|4|21|A x x N =--∈,则A 的非空真子集的个数是( ) A. 62 B. 126 C. 254 D. 51015.已知,,a b c R ∈,则下列三个命题正确的个数是( )①若22ac bc >,则a b >; ②若|2||2|a b ->-,则22(2)(2)a b ->- ③若0a b c >>>,则a a c b b c+>+; ④若0,0,4,4a b a b ab >>+>>,则2,2a b >>A. 1B. 2C. 3D. 416.若实数,a b 满足0,0a b ≥≥且0ab =,则称a 与b 互补,记(,)a b a b ϕ=-,那么(,)0a b ϕ=是a 与b 互补的( )A. 必要而不充分的条件B. 充分而不必要的条件C. 充要条件D. 既不充分也不必要条件 三、解答题17. (本题满分14分)已知关于x 的不等式250ax x a-<-的解集为M (1)4a =时,求集合M ;(2)若3M ∈且5M ∉,求实数a 的取值范围18.(本题满分14分)解关于x 的不等式2(2)(21)60a x a x -+-+>19.(本题满分16分)已知函数()|1||2|f x x x =+--(1)求不等式()1f x ≥的解集;(2)若不等式2()f x x x m ≥-+的解集非空,求m 的取值范围20.(本题满分14分)某商场在促销期间规定:商场内所有商品标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:4000.230110⨯+=(元),设购买商品得到的优惠率=购买商品获得的优惠额商品的标价。
上海交大附中2011届高三上学期第一次月考(数学)

上海交大附中2011届高三上学期第一次月考(数学)一、填空题:本大题共14小题,每小题4分,共56分。
1.集合2{|1,}M y y x x R ==-+∈,2{|lg(4)}N x y x ==-,则M N ⋂=(2,1]-。
解:(,1]M =-∞,(2,2)N =-。
2.设{|110,}A x x x N =≤≤∈,2{|280,}B x x x x R =+-=∈, 全集U R =,则右图中阴影表示的集合中的元素为4-。
解:{2,4}B =-,4A -∉。
3. 有4个命题:①很多男生爱踢足球;②所有男生都不爱踢足球;③至少有一个男生不爱踢足球;④所有女生都爱踢足球。
其中是命题“所有男生都爱踢足球”的否定命题的是 ③ 。
4. 函数22()1x f x x =+,则111()()()(1)(2)(3)(4)432f f f f f f f ++++++=72。
解:1(1)2f =,2222222111()()111111x x x f x f x x x x x+=+=+=++++。
∴11117()()()(1)(2)(3)(4)343222f f f f f f f ++++++=+=。
5.不等式(0x +的解集为(,3]{3}-∞-⋃。
解:22090x x +≤⎧⎨-≥⎩或290x -=⇒233x x x ≤-⎧⎨≤-≥⎩或或3x =±。
6.若点(2,4)既在函数2ax by +=的图象上,又在它的反函数的图象上,则函数的解析式是322xy -+=。
解:244222a ba b++⎧=⎪⎨=⎪⎩⇒2241a b a b +=⎧⎨+=⎩⇒123a b ⎧=-⎪⎨⎪=⎩。
7.设函数1()2ax f x x a+=+在区间(2,)-+∞上是增函数,那么a 的取值范围是[1,)+∞。
解:22222121()22ax a a a f x a x a x a+-+-==-++,对称中心为(2,)a a -。
上海交通大学附属中学10-11学年度高二上学期期末试卷(数学)
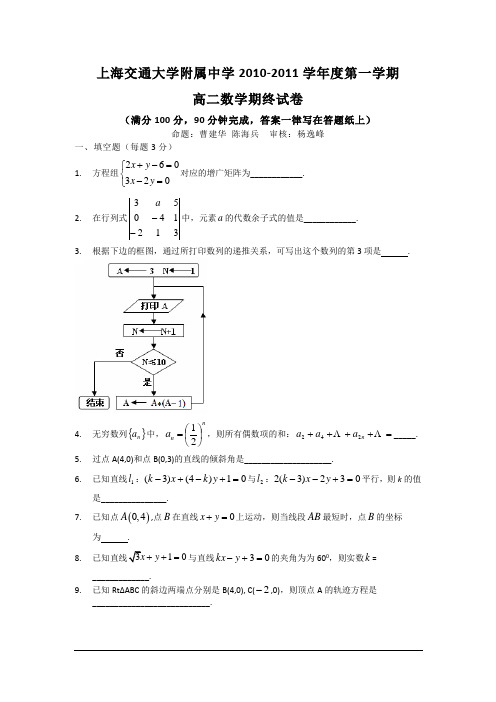
上海交通大学附属中学2010-2011学年度第一学期高二数学期终试卷(满分100分,90分钟完成,答案一律写在答题纸上)命题:曹建华 陈海兵 审核:杨逸峰一、填空题(每题3分)1. 方程组260320x y x y +-=⎧⎨-=⎩对应的增广矩阵为____________. 2. 在行列式31214053--a 中,元素a 的代数余子式的值是____________.3. 根据下边的框图,通过所打印数列的递推关系,可写出这个数列的第3项是 .4. 无穷数列{}n a 中,nn a ⎪⎭⎫ ⎝⎛=21,则所有偶数项的和:=++++ΛΛn a a a 242_____. 5. 过点A(4,0)和点B(0,3)的直线的倾斜角是____________________.6. 已知直线1l :01)4()3(=+-+-y k x k 与2l :032)3(2=+--y x k 平行,则k 的值是_______________.7. 已知点()0,4A ,点B 在直线0x y +=上运动,则当线段AB 最短时,点B 的坐标为 .8. 310x y ++=与直线03=+-y kx 的夹角为为600,则实数k = _____________.9. 已知RtΔABC 的斜边两端点分别是B(4,0), C(2-,0),则顶点A 的轨迹方程是___________________________.10. 已知椭圆221102x y m m +=--,长轴在y 轴上. 若焦距为4,则m = . 11. 与圆22(2)1x y +-=相切,且在两坐标轴上截距相等的直线共有________条.12. 若关于x 的方程212+=-kx x 恰有两个实根,则k 的取值范围是_________________.13. 在等差数列{a n }中,1a 为首项,n S 是其前n 项的和,将2)(1n a a S n n +=整理为12121a a n S n n +=后可知:点ΛΛ),,(,),2,(),1,(222111nS a P S a P S a P n n n (n 为正整数)都在直线12121a x y +=上,类似地,若{n b }是首项为1b ,公比为)1(≠q q 的等比数列,n T 是其前n 项的和,则点ΛΛ),,(,),,(),,(222111n n n T b P T b P T b P (n 为正整数)在直线__________________________________上.14. 在ABC ∆中,设a 、b 、c 分别是A ∠、B ∠、C ∠所对的边长,且满足条件a b c 2,2==,则ABC ∆面积的最大值为________________.二、选择题(每题3分)15. 设{(,)|(2)()0}A x y x y x y =+--=,2{(,)|}0x y B x y x y +=⎧=⎨-=⎩则“x A ∈”是“x B ∈”的( )A 、充分不必要条B 、必要不充分条件C 、充要条件D 、既不是充分条件,也不是必要条件16. 点()M x y 00,是圆()0222>=+a a y x 内不为圆心的一点,则直线200a y y x x =+与该圆的位置关系是 ( )A 、相切B 、相交C 、相离D 、相切或相交17. 已知直线2x =及4x =与函数2log y x =图像的交点分别为,A B ,与函数lg y x =图像的交点分别为,C D ,则直线AB 与CD ( )A 、相交,且交点在第I 象限B 、相交,且交点在第II 象限C 、相交,且交点在第IV 象限D 、相交,且交点在坐标原点18. 在ABC ∆中,O 是平面ABC 上的一点,点P 满足()++=λ,),0(+∞∈λ,则直线AP 过ABC ∆的( )A 、垂心B 、重心C 、内心D 、外心三、解答题(10分+12分+12分+12分)19. 求圆心在直线0=+y x 上,且过圆02410222=-+-+y x y x 与圆082222=-+++y x y x 的交点的圆的方程。
交大附中第一学期第一次月考

交大附中高一第一次月考数学试题一、选择题(本大题共 10 小题,每小题 4 分,共 40 分,)1、已知全集 = {0,1,2,3,4},集合 = {1,2,3},集合 = {0,2,4},则集合( ) ∩ =A.{0,4}B.{2,3,4}C.{0,2,4}D. {0,2,3,4}2、下面关于集合的表述正确的个数是( )①{2,3} ≠ {3,2};②{( , )| + = 1} = { | + = 1};③{ | > 1} = { | > 1}A.个 B .个 C .个 D .个3、已知点( , )在映射的作用下的象是( + , 2 − ),则在映射的作用下,点(5,1)的原象是( )A.(2,1)B.(2,3)C.(3,4)D.(6,9)4、已知函数A. B. C. D.5、已知函数 = ( )是定义在上的奇函数,当 ≥ 0时, ( ) = 2 2 − ,则(−1) = ( )A.−3B.−1C.D.6、函数的定义域为( )A.(−∞, −1] ∪ [1, +∞) B .[−1,1]C.[−1,0) ∪ (0,1]D.7、若函数 ( ) = 2 − 2( − 1) + 2在区间(−∞, 5)上递减,则实数的取值范围A. > 6B. ≥ 6C. < 6D. ≤ 68、函数 ( ) = √ 2 − 2 − 3的单调递增区间是( )A.(−∞, −1]B.(−∞, 1]C.[1, +∞)D.[3, +∞)9、已知函数的定义域为,则实数的取值范围是( )A.(0,1)B.[0,1)C.(0,1]D.[0,1]10、已知函数 ( ) = 2 − 2 在定义域[−1, ]上的值域是[−1,3],则实数的取值范围是( )A.[1,3]B.[−1,1]C.[−1,3]D.[0,3]( ) = √ 1− 22 − 1二.填空题(本大题共 4 小题,每小题 5 分,共 20 分)11、已知0 < < 2,则函数 = (8 − 3)上的最大值是__________.三.解答题(本大题共 4 小题,每小题 10 分,共 40 分)15、(本题 10 分)已知集合 = {| 2 − 3≤ 10}, = {|+ 1 ≤ ≤ 2 + 1}.(1)若 = 3,求⋂(∁);(2)若⋃ = ,求实数的取值范围.16、(本题 10 分)已知函数() = { 2 − 1, −1 < < 2.9 − 3, ≥ 2的值;(2)画出 = ()的图象,并指出单调增区间.17、(本题 10 分)已知()是二次函数,且满足(0) = (5) = 0,(1) = −8.(1)求()的解析式;(2)设函数()在∈ [, + 1]上的最小值为(),求()的表达式.18、(本题 10 分)已知函数()是定义在上的减函数,且满足:(1) = −2,对任意, ∈ 都有( + ) = () + (). (1)求(0),(2)的值;(2)判断()的奇偶性,并证明;(3)当 > 0时,解关于的不等式:(2) − 2() < () + 4.。
上海交大附中2010届高三数学上学期期中考试沪教版 新课标

上海交通大学附属中学2010届高三上学期高三数学期中试卷(满分150分, 考试时间120分钟,答案请写在答题纸上)一.填空题 (本大题满分56分)本大题有14题,考生应在答题纸相应编号的空格内直接写结果,每个空格填对得4分,否则一律得零分.1.设A 、B 是非空数集,定义:{|,}A B a b a A b B ⊕=+∈∈,若{1,2}A =,{3,4,5}B =,则B A ⊕的子集个数为;2.若函数()f x ax b =+(0)a ≠有一个零点是1,则2()g x bx ax =-的零点是 ;3.已知tan 2α=,则2211sin cos 23αα+= ;4.若等差数列{}n a 的前5项和5S =25,且7a =13,则1a =_____;5.已知数列{}n a 满足=n a 4(1,2,3,4)( 5 ,)n n n a n n N -=⎧⎨-≥∈⎩ ,则2009a =___________;6.在等比数列{a n }中,首项a 1<0,则{a n }是递增数列的充要条件是公比q 满足_______; 7.设函数)52sin(2)(ππ+=x x f ,若对任意x R ∈,都有)()()(21x f x f x f ≤≤成立,则21x x -的最小值为 ;8.将函数tan(3)4y x π=-的图像上的各点经过怎样的平移_________________,可以得到函数tan3y x =-的图像?9.已知函数)sin(ϕω+=x y (0)ω>与直线21=y 的交点中,距离最近的两点间距离为3π,那么ω=________;10.数列}{n a 满足122,1a a ==,并且nn n n n n n n a a a a a a a a ⋅-=⋅-++--1111(2≥n ),则数列的第100项为 ______;11.1n →∞=,则实数a 的值为 ___________;12.已知函数()f x 在定义域R 上为增函数,且()0f x <,则()()2g x x f x =在(, 0-∞)的单调性为_________________;13.设非常值函数()f x 是R 上的偶函数,对任意的x R ∈都有(6)()(3)f x f x f +=+,试写出同时满足上述两个条件的一个函数解析式___________;14.用n 个不同的实数a 1,a 2,…,a n 可得n !个不同的排列,每个排列为一行1 2 31 32 2 13 2 3 1 3 1 2 3 2 1写成一个n !行的数阵.对第i 行a i 1,a i 2,┄,a in ,记b i = -a i 1+2a i 2-3 a i 3+…+(-1)n na in , i =1,2,3,…,n ! .例如,用1,2,3可得数阵如右,由于此数阵中每一列各数之和都是12,所以,b 1+b 2+…+b 6=-12+2⨯12-3⨯12=-24.那么,在用1,2,3,4,5形成的数阵中, b 1+b 2+…+b 120= .二.选择题(本大题满分16分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号的空格内直接写结果,选对得4分,否则一律得零分。
高三第一次月考数学试卷

高三第一次月考数学试卷一、选择题(每题5分,共60分)1.已知集合A={x∣x2−3x−4≤0},则A的解集为:A. (−1,4]B. [−1,4]C. (−∞,−1]∪[4,+∞)D. [−4,3]2.复数z=1+i2i的共轭复数为:A. 1−iB. 1+iC. −1+iD. −1−i3.函数f(x)=log2(x2−2x−3)的定义域为:A. (−∞,−1)∪(3,+∞)B. (−1,3)C. [−1,3]D. (−∞,−1]∪[3,+∞)4.已知向量a=(1,2),b=(3,−1),则a⋅b=:A. 1B. -1C. 5D. -55.下列函数中,在区间(0,+∞)上单调递增的是:A. y=x1B. y=x2−2xC. y=log21xD. y=2x6.已知等差数列{an}的前n项和为Sn,若a1=1,S3=−3,则a2+a4=:A. -4B. -2C. 0D. 27.下列命题中,正确的是:A. 若a>b,则ac2>bc2B. 若a>b,c>d,则a−d>b−cC. 若a>b,c>d,则ac>bdD. 若a>b,则a1<b18.已知函数f(x)=sin(2x+6π),则f(6π)的值为:A. 21B. −21C. 23D. −239.已知抛物线y2=2px(p>0)的焦点为F,准线为l,过F的直线与抛物线交于A,B两点,交准线l于D,若BF=3FA,则∣AB∣∣DF∣=:A. 21B. 31C. 32D. 4310.已知函数f(x)=ln(x+1)−x+1ax在其定义域内单调递增,则实数a的取值范围是:A. (−∞,1]B. [−1,+∞)C. (−∞,−1]D. [1,+∞)11.已知椭圆C:a2x2+b2y2=1(a>b>0)的左、右焦点分别为F1,F2,过F1的直线与椭圆C交于A,B两点,若∣BF2∣=2∣AF2∣,4cos∠AF1F2=10,则C的离心率为:A. 22B. 23C. 35D. 3612.已知函数f(x)={(3a−1)x+4a,log ax,x<1x≥1是(−∞,+∞)上的减函数,则实数a的取值范围是:A. (0,71]B. [71,31)C. (0,31]D. [31,1)二、填空题(每题5分,共20分)1.若x,y∈R,且xy=2,则x2+y2的最小值为 _______。
上海交通大学附属中学2010―2011学年度第一学期高三相关历史月考

上海交通大学附属中学2010―2011学年度第一学期高三相关历史月考上海交通大学附属中学2010―2011学年度第一学期高三相关历史月考(满分150分,120分钟完成。
答案一律写在答题纸上)一、选择题(共60分,每题2分,每题只有一个正确答案。
) 1.动荡不安的伊拉克是当今世界关注的焦点,伊拉克所在的两河流域是世界闻名的发祥地之一,下列哪一文明成果出自该地区 A.金字塔 B.佛教C.《汉谟拉比法典》D.种姓制度 2.古埃及象形文字的书写材料其中最为普遍的材料是 A.石质材料 B.陶片 C.木料 D.纸草 3.人们常说四大文明古国,即古埃及、巴比伦、印度、中国,但近几十年来,国际学术界倾向于更具概括力的“四大文明区”的说法,即东地中海文明区、南亚次大陆文明区、东亚文明区、中南美印第安文明区。
那么下列不属于中南美印第安文明区的文明是 A.玛雅文明 B.阿兹特克文明 C.印加文明 C.亚述文明 4.被称为“古典时代”的希腊,政治民主、经济发展、文化繁荣,它是古代希腊城邦制度的全盛时期,尤其以雅典为典范。
期间涌现了不少英雄般的人物,下列不属于这一时期的杰出人物是 A.亚里士多德 B.伯利克里 C.希罗多德D.盲人诗人荷马 5.西罗马帝国灭亡以后,东罗马帝国在历史上又延续了大约 A.500多年B.800多年C.1000多年D.1200多年 6.“法律条文没有作出规定的,法官就不能受理。
譬如有公民的奴隶被人拐走或偷跑掉,此公民要求法律受理就要找法官,向他申明:根据某某法律,我认为此奴隶应归我所有。
法官确认后才能受理。
”这一描述主要说明罗马法 A.重视法律程序 B.保留习惯旧俗 C.强调法官至上 D.体现人人平等 7.人们在一座古老建筑的墙上发现了一幅画(右图)它反映了西欧中世纪某个阶段的政教关系。
其特征是 A.教皇拥有至高无上的权威 B.教皇成了君主的人质 C.教皇和君主各执权柄、互不干涉 D.教皇和君主相互依存、相互利用8.一位哲人说过:“这(文艺复兴)是一次人类从来没有经历过的最伟大的、进步的变革,是一个需要巨人并产生了巨人的时代”。
上海交通大学附属中学高三数学月考试卷

上海交通大学附属中学高三数学月考试卷(理)(说明:本试卷满分150分,考试时间120分钟。
本套试卷另附答题纸,每道题的解答必须写在答题纸的相应位置,本卷上任何解答都不作评分依据...........................。
) 一、填空题(本大题满分56分,每题4分,填错或不填在正确的位置一律得零分) 1.已知复数z 满足i z i =-)1(,则z = 2.已知集合{}{}lg(1),213S x y x T x x ==-=-≤,则ST =_________.3.在等差数列{}n a 中,已知137=a ,2915=a ,则通项公式n a =_____________.4.若P 是圆012422=++-+y x y x 上的动点,则P 到直线02434=+-y x 的最小距离是_____________.5.某区有200名学生参加数学竞赛,随机抽取10名学生成绩如下:则总体标准差的点估计值是 .(精确到0.01) 6.函数3sin sin()y x x π=+的最大值是______________.7.二项式9)1(xx -展开式中的常数项为 .8.已知曲线12C C ,的极坐标方程分别为π4cos 002ρθρθ⎛⎫=< ⎪⎝⎭,≥≤,cos 3ρθ=,则曲线1C 与2C 交点的一个极坐标为 .9.若12332lim 21112=⋅+⋅-++-∞→n n n n n a a ,则=a 。
10.已知)(x f 是最小正周期为2的函数,当(1,1]x ∈-时,()f x =若在区间(3,5]上ax x f =)(有两个不相等的实数根,则实数a 的取值范围是___________11.某校学生在上学路上要经过2个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是13,遇到红灯时停留的时间都是2分钟.则该校某个学生在上学路上因遇到红灯停留的总时间ξ的均值等于 分钟.12.设直线m 与平面α相交但不.垂直,则下列所有正确的命题序号是 . ①在平面α内有且只有一条直线与直线m 垂直; ②过直线m 有且只有一个平面与平面α垂直;成 绩 人 数40 1150 60 221370 80 90③与直线m 平行的直线不.可能与平面α垂直; ④与直线m 垂直的直线不.可能与平面α平行; ⑤与直线m 平行的平面不.可能与平面α垂直. 13.已知定义域为R 的偶函数)(x f ,对于任意R x ∈,满足)2()2(x f x f -=+。
[高一数学]2010-2011学年度北方交大附中高一第一学期月考练习2010108
![[高一数学]2010-2011学年度北方交大附中高一第一学期月考练习2010108](https://img.taocdn.com/s3/m/c995f754cf84b9d528ea7aa9.png)
2010-2011学年度北方交大附中高一第一学期月考练习 2010.10.8班级__________ 姓名__________ 成绩____________一、选择题(每小题3分,共30分)1. 设全集{}21012U =--,,,,,{}210A =--,,,{}012B =,,,则()U A B = ð( )A .{}0B .{}21--,C .{}12,D .{}012,,2. 下列函数中,在区间(0)+∞,上是增函数的是( )A .32y x =-B .1y x=C .2y x =-D .22y x =-3.函数y =) A .32⎡⎫+∞⎪⎢⎣⎭,B .32(2)2⎡⎫+∞⎪⎢⎣⎭ ,,C .32(2)2⎛⎫+∞ ⎪⎝⎭,,D .(2)(2)-∞+∞ ,, 4. 下列函数是奇函数的是( )A .21y x =-B .||1y x =+C .1y x x=+D .2y x x =+5. 函数()||xf x x =的图象是( )DC BA6. 如果二次函数21y ax bx =++的图象的对称轴是1x =,并且通过点(17)A -,,则a ,b 的值分别是( ) A .2,4B .2,4-C .2-,4D .2-,4-7. 定义在R 上的偶函数,且()f x 在[)0+∞,上为增函数,则(2)f -,(π)f -,(3)f 的大小顺序是( )A .(π)(2)(3)f f f -<-<B .(π)(2)(3)f f f ->->C .(π)(3)(2)f f f -<<-D .(π)(3)(2)f f f ->>-8. 已知函数2()1f x ax ax =++,若对于任意实数x ,都有()0f x >成立,则实数a 的取值范围是( )A .(04),B .[)04,C .(]04,D .[04],9. 定义在R 上的函数()f x 满足()()()f x y f x f y +=+(x 、y ∈R ),当0x <时()0f x >,则函数()f x 在[]a b ,上( ) A .有最小值()f aB .有最大值()f bC .有最小值()f bD .有最大值2a b f +⎛⎫⎪⎝⎭10.设集合{}01234S A A A A A =,,,,,在S 上定义运算 为:i j k A A A = ,其中||k i j =-,i ,0j =,1,2,3,4.那么满足条件21()i j A A A A = ()i j A A S ∈,的有序数对()i j ,共有( ) A .12个 B .8个C .6个D .4个二、填空题(每小题4分,共32分)11.设:f A B →,其中{}()|A B x y x y ==∈R ,,,:()()f x y x y x y →+-,,,那么A 中元素(13),的象为_____________.B 中元素(13),的原象为____________.12.若函数()23f x x =-的值域为[18]-,,则其定义域为_____________,定义在R 上的函数(|1|)y f x =-的增区间为______________. 13.若2()23f x x x =-+,则(2)f x -=___________,(38)f -_____(39)f (填“>”或“<”)14.设2|1|2||1()1||11x x f x x x --⎧⎪=⎨>⎪+⎩,≤,,,则12f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦_________,若()1f a =-,则a =________. 15.函数223(50)y x x x =--+-≤≤的值域为__________.16.若函数2()2(1)2f x x a x =+-+在(]4-∞,上是减函数,则实数a 的取值范围是___________. 17.函数()(||1)f x x x =-的减区间为_____________.18.已知定义在R 上的奇函数()f x 是增函数,则下列说法正确的是_________.⑴(0)0f =;⑵()y f x =-是减函数;⑶1()y f x =是减函数⑷()()y f x f x =⋅是增函数;⑸(1)1y f x =-+的图象关于(11),对称. 三、解答题(共38分)19.已知集合{}|121P x a x a =++≤≤,{}2|310Q x x x =-≤.⑴ 若3a =,求()R P Q ð⑵ 若P Q ⊆,求实数a 的图象过点(15),.20.已知函数()f x 的解析式;⑴ 求函数()f x 的解析式; ⑵ 求函数()f x 定义域;⑶ 证明:函数()f x 在12⎛⎫+∞ ⎪⎝⎭,上是减函数.21.已知函数()f x 是定义在R 上的函数,当0x >时,()5f x =⑴ 求函数()f x 在R 上的解析式;⑵ 说明函数()f x 在R 上的单调性;(说清理由,不必证明) ⑶ 或a 满足2(34)(1)f a a f a -+>+,求a 的取值范围.22.已知函数2()1f x ax bx =++,(a ,b 为实数),x ∈R ,()(0)()()(0)f x x F x f x x >⎧=⎨-<⎩⑴ 若(1)0f -=且函数()f x 的值域为[)0+∞,,求()F x 的表达式;⑵ 在⑴的条件下,当[22]x ∈-,时,()()g x f x kx =-是单调函数,求实数k 的取值范围;⑶ 设0m n ⋅<,0m n +>,0a >且()f x 为偶函数,判断()()F m F n +能否大于零?。
【数学】上海市交通大学附属中学2010-2011学年高二上学期期末考试(新疆班)

上海交通大学附属中学2010-2011学年度第一学期内高二数学期末试卷(2011年1月12日)命题:宋向平 审核:杨逸峰一. 填空题(本大题满分36分)本大题共有12题,只要求在答题纸相应题序的空格内直接填写结果,每个空格填对得3分,否则一律得零分.1. 的共轭复数是是虚数单位)(2i i -_____ 2--i ___________ .2. 已知复数z 满足1(z i iz i +=-是虚数单位),则z =_____________.i -3. 已知z 是纯虚数,iz -+12是实数,则=z i 2- 4. 已知423)1()43()3(i i i z +++-=,求z = 505. 5的值是 .-16 6. 若关于x 的一实系数元二次方程20x px q ++=有一个根为1i +,则p q +=________07. 设复数1z i =+,则20122012⎛⎫+=_____________.28. 若C z ∈且|22|,1|22|i z i z --=-+则的最小值是_____________.39. 在复平面上,已知直线l 上的点所对应的复数z 满足3z i z i +=--,则直线l 的倾斜角为 3arctan 2π-(结果用反三角函数值表示) 10. z z C z z z z z 1212122222402,,,∈-+==||,那么以|z 1|为直径的圆的面积为______.4π11. 用一个平面去截正方体。
其截面是一个多边形,则这个多边形的边数最多是 6条12. 已知空间四边形ABCD ,E 、F 分别是BC 、AD 中点,5EF =,8AB =,6CD =,则AB 与CD 所成的角的大小为_________90二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A 、B 、C 、D 的A 1四个结论,其中有且只有一个结论是正确的.13. 若复数z=a+bi(a 、b ∈R),则下列正确的是 (B )(A ) 2z >2z (B ) 2z =2z (C ) 2z <2z (D ) 2z =z 2 14.在复平面内,若复数12ω=-对应的向量为OA ,复数2ω对应的向量为OB ,则向量AB 对应的复数是( D )(A )1 (B )1- (C(D)15. 如图,正方体1111A B C D A B C D -中,若E F G 、、分别为棱BC 、1C C 、11B C 的中点,1O 、2O 分别为四边形11ADD A 、1111A B C D 的中心,则下列各组中的四个点不在..同一个平面上的是( B ) (A )11A C O D 、、、 (B )D E G F 、、、(C )1A E F D 、、、 (D )12G E O O 、、、16. 若a b 、为异面直线,直线c ∥a ,则c 与b 的位置关系是( ) (A )相交 (B )异面 (C )平行 (D ) 异面或相交三.解答题(本大题满分48分)本大题共有4题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.17. (本小题满分10分)已知复数z 1满足(1+i )z 1=-1+5i , z 2=a -2-i , 其中i 为虚数单位,a ∈R, 若21z z -<|z 1|,求a 的取值范围.解:由题意得 z 1=ii ++-151=2+3i , 于是21z z -=i a 24+-=4)4(2+-a ,1z =13.4)4(2+-a <13,得a 2-8a +7<0,1<a <7.18. (本小题满分12分)如图,长方体1111D C B A ABCD -中, AD=2,AB=AD=4,62AA 1=,点E 是AB 的中点,点F 是1AA 的中点。
上海交通大学附属中学度高一数学上学期期末试卷

上海交通大学附属中学2010-2011学年度第一学期高一数学期终考试卷本试卷共有22道试题,满分100分,考试时间90分钟。
请考生用钢笔或圆珠笔将答案写在答题卷上(本试卷允许使用计算器,凡属用计算器所得之值,如无特别说明,请精确到小数点后3位)一、填空题(本大题满分42分)本大题共有14题,只要求直接填写结果,每个空格填对得3分,否则一律得零分。
1、 已知集合A ={x ∣|x -1|>1},则A =R ð____________。
2、 不等式lg(1)1x -<的解集是_________。
(用区间表示)3、 过点P (4,2)的幂函数是________函数。
(填“奇函数”、“偶函数”、“非奇非偶函数”、“既奇又偶函数”)4、 若函数y A ,值域为B ,则A ∩B =____________。
5、 已知函数3()2x f x +=,1()f x -是()f x 的反函数,若16mn =(m ,n ∈R +),则11()()f m f n --+的值为______________。
6、 函数2lg(82)y x x =+-的单调递增区间是__________。
7、 给出函数1()x x f x e e -=+,若0()()f x f x ≥对一切x ∈R 成立,则0x =________。
8、 设2()lg2x f x x +=-,则2()()2x f f x+的定义域为_________。
9、 若函数()f x (x ∈R )的图像关于点M (1,2)中心对称,且()f x 存在反函数1()f x -,若(4)0f =,则1(4)f -=___________。
10、用二分法求得函数f (x )=x 3+2x 2+3x +4在(-2,-1)内的零点是_______。
(精确到0.1)11、已知函数223y x x =-+在区间[0,m ]上的最大值为3,最小值为2,则实数m 的取值范围是______________。
上海交大附中2011届高三摸底考试(数学)

上海交通大学附属中学2010-2011学年度第一学期高三数学摸底试卷(满分150分,120分钟完成,答案一律写在答题纸上)命题:宋向平 审核:杨逸峰一、填空题:本大题共14小题,每小题4分,共56分。
1. 不等式的解集为________________________2. 函数是 (填奇偶性)3. 行列式的值是4. 已知复数则=-z z 2____________ 5.的展开式中,的系数等于 6.双曲线方程为,则它的焦点坐标为____________ 7.若,则_________。
8. 在△ABC 中,若b =1,c =,,则a = 。
9. 已知向量,b 满足,,与b 的夹角为60°,则10. 执行右图所示的程序框图,若输入,则输出的值为 。
11. 如图,二面角的大小是60°,线段.,与l 所成的角为30°.则与平面所成的角的正弦值是_________.12. 将6位志愿者分成4组,其中两个各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有 种(用数字作答)。
13. 已知函数满足:,则__________.14. 若数列满足:对任意的,只有有限个正整数使得成立,记这样的的个数为,则得到一个新数列.例如,若数列是,则数列是.已知对任意的,,则 , .二、选择题:本大题共4小题,每小题5分,共20分。
15. 已知,则的最小值是( )(A )3 (B )4 (C ) (D )211 16. 已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是( )(A )2 (B ) (C ) (D )17. 样本中共有五个个体,其值分别为,若该样本的平均值为1,则样本方差为(A ) (B ) (C ) (D )218. 若直线y=x+b 与曲线有公共点,则b 的取值范围是(A ) (B )(C ) (D )三、解答题:本大题共5题,74分。
19. (本小题满分12分)已知函数,其图象过点).21,6(π (1)求ϕ的值;(2)将函数的图象上各点的横坐标缩短到原来的,纵坐标不变,得到函数的图象,求函数在上的最大值和最小值。
上海交通大学附属中学2010

上海交通大学附属中学2010-2011学年度第一学期高一数学期终考试卷本试卷共有22道试题,满分100分,考试时间90分钟。
请考生用钢笔或圆珠笔将答案写在答题卷上命题:杨逸峰 审核:杨逸峰(本试卷允许使用计算器,凡属用计算器所得之值,如无特别说明,请精确到小数点后3位)一、填空题(本大题满分42分)本大题共有14题,只要求直接填写结果,每个空格填对得3分,否则一律得零分。
1、 已知集合A ={x ∣|x -1|>1},则A =R ð____________。
2、 不等式lg(1)1x -<的解集是_________。
(用区间表示)3、 过点P (4,2)的幂函数是________函数。
(填“奇函数”、“偶函数”、“非奇非偶函数”、“既奇又偶函数”)4、 若函数y A ,值域为B ,则A ∩B =____________。
5、 已知函数3()2x f x +=,1()f x -是()f x 的反函数,若16mn =(m ,n ∈R +),则11()()f m f n --+的值为______________。
6、 函数2lg(82)y x x =+-的单调递增区间是__________。
7、 给出函数1()x x f x e e -=+,若0()()f x f x ≥对一切x ∈R 成立,则0x =________。
8、 设2()lg2x f x x +=-,则2()()2x f f x+的定义域为_________。
9、 若函数()f x (x ∈R )的图像关于点M (1,2)中心对称,且()f x 存在反函数1()f x -,若(4)0f =,则1(4)f -=___________。
10、用二分法求得函数f (x )=x 3+2x 2+3x +4在(-2,-1)内的零点是_______。
(精确到0.1)11、 已知函数223y x x =-+在区间[0,m ]上的最大值为3,最小值为2,则实数m 的取值范围是______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海交大附中2010-2011学年度第一学期
高三数学第一次月考试卷
一、填空题:本大题共14小题,每小题4分,共56分。
1.集合2{|1,}M y y x x R ==-+∈,2{|lg(4)}N x y x ==-,则
M N ⋂=——————。
2.设{|110,}A x x x N =≤≤∈,2{|280,}B x x x x R =+-=∈,
全集U R =,则右图中阴影表示的集合中的元素为________
3. 有4个命题:①很多男生爱踢足球;②所有男生都不爱踢足
球;③至少有一个男生不爱踢足球;④所有女生都爱踢足球。
其中是命题“所有男生都爱踢足球”的否定命题的是 __________。
4. 函数22()1x f x x =+,则111()()()(1)(2)(3)(4)432
f f f f f f f ++++++=______。
5.
不等式(0x +的解集为___________________。
6.若点(2,4)既在函数2ax b y +=的图象上,又在它的反函数的图象上,则函数的解析式是__________。
7.设函数1()2ax f x x a
+=+在区间(2,)-+∞上是增函数,那么a 的取值范围是___________。
8. 若221 1()log 1 1
x x f x x x ⎧-≤=⎨+>⎩ ,1()f x -是()f x 的反函数,则_______________。
9.若1x >-,(5)(2)()1
x x f x x ++=+的最小值是________。
10. 已知偶函数()f x 在区间[0,)+∞单调增加,则满足1
(21)()3f x f -<的x 取值范围是____________。
11.函数()lg(6),()a f x x a R x
=+-∈的值域为R ,则实数a 的取值范围是__________。
12. 建造一个容积为318m , 深为2m 的长方形无盖水池,如果池底和池壁每2m 的造价分别为200元和150元,那么水池的最低造价为_____________元。
13.已知函数()||,()f x x x px q x R =++∈,给出下列四个命题:①
()f x 为奇函数的充要条件是0q =;②)(x f 的图象关于点
(0,)q 对称;③当0p =时,方程()0f x =的解集一定非空;④
方程()0f x =的解的个数一定不超过两个。
其中所有正确命题的序号是 。
14.请把下列命题补充完整,并使之成为真命题:
若函数3()2x f x +=的图像与函数)(x g 的图像关于直线________对称,则函数
)(x g =______ (填上你认为可以成为真命题的一种情况即可,两个空位都填对,方能得分)。
二、选择题:本大题共4小题,每小题5分,共20分。
15. 命题“对任意的x R ∈,都有3210x x -+≤”的否定是 ( C )
()A 不存在x R ∈,使得3210x x -+≤ ()B 存在x R ∈,使得3210x x -+≤
()C 存在x R ∈,使得3210x x -+> ()D 对任意的x R ∈,都有3210x x -+>
16. 已知函数2()() 1 (0)f x ax b c x a =+++≠是偶函数,其定义域为[,]a c b -,则点(,)a b 的
轨迹是 ( ) ()A 线段 ()B 直线的一部分 ()C 点 ()D 圆锥曲线
17. 若不等式12x x a ++->在R 上恒成立,则a 的取值范围 ( )
()A 一切实数 ()B (3,3]-
()C (,3)-∞- ()D (,3)-∞ 18. 对于函数131()(2)2
x x f x x =-⋅和实数m 、n ,下列结论中正确的是 ( ) ()A 若n m <,则f m f n ()()< ()B 若f m f n ()()<,则22m n <;
()C 若f m f n ()()<,则33m n <; ()D 上述命题都不正确。
三、解答题:本大题共5题,74分。
19.(本小题满分12分)
命题P :“函数()22
x x a f x =+在区间[4,)+∞上递增”;命题Q :“ 22()log log a g x x x =- 在区间[4,)+∞上递增”。
若命题P 与命题Q 有且仅有一个真,求实数a 的集合。
20.(本小题满分12分,第1小题7分,第2小题5分)
甲、乙两商场同时促销原售价为2000元的某种型号的彩电,甲商场一律按销售价的8折促销,即按原价的80%销售;乙商场按如下方式促销,买一台优惠2.5%,买两台优惠5%,买三台优惠7.5%,以此类推,即每多买一台,每台再优惠2.5个百分点,但每台最低价不能低于1500元,某公司需购买这种型号的彩电x 台(*x N ∈),若到甲商场购买的费用为()f x 元,到乙商场购买的费用为()g x 元。
(1) 分别求出函数()f x 、()g x 的关系式;
(2) 问去哪家商场购买花费较少?并说明理由。
21.(本小题满分14分,第1小题6分,第2小题8分)
已知正数a 、b 、c 满足1=++c b a ,
(1) 192
; (2) 求113113113+++++c b a 的最大值。
22.(本小题满分18分,第1小题4分,第2小题8分,第3小题6分)
已知函数()f x ax ,其中0a >。
(1) 若2(1)(1)f f =-,求a 的值;
(2) 证明:当1a ≥时,函数()f x 在区间[0,)+∞上为单调函数,并指出是增还是减;
(3) 若函数()f x 在区间[1,)+∞上是增函数,求a 的取值范围。
23.(本小题满分18分,第1小题6分,第2小题6分,第3小题6分)
已知函数()f x 是定义在[2,2]-上的奇函数,当[2,0)x ∈-时,31()2f x tx x =-
(t 为常数)。
(1) 求函数()f x 的解析式;
(2) 当[2,6]t ∈时,求()f x 在[]2,0-上的最小值,及取得最小值时的x ,并猜想()f x 在[0,2]上的单调递增区间(不必证明);
(3) 当9t ≥时,证明:函数()y f x =的图象上至少有一个点落在直线14y =上。
