第三章练习题及参考解答
第三章控制对象的动态特性习题与参考解答

第三章控制对象的动态特性习题与参考解答3-1 什么是自衡特性?具有自衡特性被控过程的系统框图有什么特点?1)在扰动作用破坏其平衡工况后,被控过程在没有外部干预的情况下自动恢复平衡的特性,称为自衡特性。
2)被控过程输出对扰动存在负反馈。
3-2 什么是单容过程和多容过程?1)单容:只有一个储蓄容量。
2)多容:有一个以上储蓄容量。
3-3 什么是控制通道和扰动通道(干扰通道)?对于不同的通道,对象的特性参数(K、T、τ)对控制有什么不同的影响?对于一个被控对象来说,输入量是扰动量和操纵变量,而输出是被控变量。
由对象的输入变量至输出变量的信号联系称为通道。
操纵变量至被控变量的信号联系称为控制通道;扰动量至被控变量的信号联系称为扰动通道。
一般来说,对于不同的通道,对象的特性参数(K、T、τ)对控制作用的影响是不同的。
对于控制通道:放大系数K大,操纵变量的变化对被控变量的影响就大,即控制作用对扰动的补偿能力强,余差也小;放大系数K小,控制作用的影响不显著,被控变量的变化缓慢。
但K太大,会使控制作用对被控变量的影响过强,使系统的稳定性下降。
在相同的控制作用下,时间常数T大,则被控变量的变化比较缓慢,此时对象比较平稳,容易进行控制,但过渡过程时间较长;若时间常数T小,则被控变量变化速度快,不易控制。
时间常数太大或太小,在控制上都将存在一定困难,因此,需根据实际情况适中考虑。
滞后时间τ的存在,使得控制作用总是落后于被控变量的变化,造成被控变量的最大偏差增大,控制质量下降。
因此,应尽量减小滞后时间τ。
对于扰动通道:放大系数K大对控制不利,因为,当扰动频繁出现且幅度较大时,被控变量的波动就会很大,使得最大偏差增大;而放大系数K小,既使扰动较大,对被控变量仍然不会产生多大影响。
时间常数T大,扰动作用比较平缓,被控变量变化较平稳,对象较易控制。
纯滞后的存在,相当于将扰动推迟τ0时间才进入系统,并不影响控制系统的品质;而容量滞后的存在,则将使阶跃扰动的影响趋于缓和,被控变量的变化相应也缓和些,因此,对系统是有利的。
人工智能教程习题及答案第3章习题参考解答

第三章确定性推理方法习题参考解答3.1 练习题3.1 什么是命题?请写出3个真值为T 及真值为F 的命题。
3.2 什么是谓词?什么是谓词个体及个体域?函数与谓词的区别是什么?3.3 谓词逻辑和命题逻辑的关系如何?有何异同?3.4 什么是谓词的项?什么是谓词的阶?请写出谓词的一般形式。
3.5 什么是谓词公式?什么是谓词公式的解释?设D= {1,2} ,试给出谓词公式( x)( y)(P(x,y) Q(x,y))的所有解释,并且对每一种解释指出该谓词公式的真值。
3.6对下列谓词公式分别指出哪些是约束变元?哪些是自由变元?并指出各量词的辖域。
(1)( x)(P(x, y) ( y)(Q(x, y) R(x, y)))(2)( z)( y)(P(z, y) Q(z, x)) R(u, v)(3)( x)(~ P( x, f (x )) ( z)(Q(x,z) ~ R(x,z)))(4)( z)(( y)(( t)(P(z, t) Q(y, t)) R(z, y))(5)( z)( y)(P(z, y) ( z)(( y)(P(z, y) Q(z, y) ( z)Q(z, y))))什么是谓词公式的永真性、永假性、可满足性、等价性及永真蕴含?3.7什么是置换?什么是合一?什么是最一般的合一?3.8判断以下公式对是否可合一;若可合一,则求出最一般的合一:3.9(1)P(a,b) ,P(x, y)(2)P(f(z),b) ,P(y, x)(3)P(f(x), y) ,P(y, f(a))(4)P(f(y), y,x) ,P(x, f(a), f(b))(5)P(x, y) ,P(y, x)什么是范式?请写出前束型范式与SKOLEM 范式的形式。
3.10什么是子句?什么是子句集?请写出求谓词公式子句集的步骤。
3.113.12谓词公式与它的子句集等值吗?在什么情况下它们才会等价?3.13 把下列谓词公式分别化为相应的子句集:(1)( z)( y)(P(z, y) Q(z, y))(2)( x)( y)(P(x, y) Q(x, y))(3)( x)( y)(P(x, y) (Q(x, y) R(x, y)))(4)( x)( y)( z)(P(x, y) Q(x, y) R(x, z))(5)( x)( y)( z)( u)( v)( w)(P(x, y,z,u,v,w) (Q(x, y, z,u, v, w) ~R(x, z, w)))3.14 判断下列子句集中哪些是不可满足的:(1)S {~ P Q,~ Q,P,~ P}(2)S {P Q,~ P Q,P ~ Q,~ P ~ Q}(3)S {P(y) Q(y), ~ P(f(x)) R(a)}(4)S {~ P(x) Q(x), ~ P(y) R(y), P(a),S(a),~ S(z) ~ R(z)}(5)S {~ P(x) ~ Q(y) ~ L(x, y), P(a), ~ R(z) L(a, z), R(b), Q(b)}(6)S {~ P(x) Q(f(x), a), ~ P(h(y)) Q(f(h(y)), a) ~ P(z)}(7)S {P(x) Q(x) R(x),~ P(y) R(y),~Q(a),~ R(b)}(8)S {P(x) Q(x),~ Q(y) R(y), ~ P(z) Q(z),~ R(u)}3.15 为什么要引入Herbrand 理论?什么是H 域?如何求子句集的H 域?3.16 什么是原子集?如何求子句集的原子集?3.17 什么是H 域解释?如何用域D 上的一个解释I 构造H 域上的解释I *呢?3.18 假设子句集S={P(z) ∨Q(z),R(f(t))} ,S 中不出现个体常量符号。
教科版小学科学四年级下册第三章岩石与土壤练习题(附答案) (3)

教科版小学科学四年级下册第三章岩石与土壤练习题(附答案)一、教科版四年级下册科学第三章岩石与土壤选择题1.石英、长石、云母三种矿物中最硬的是( )。
A. 长石B. 石英C. 云母【答案】 B【解析】【解答】在三种矿物中,硬度由大到小依次是:石英、长石和云母。
B选项符合题意。
故答案为:B。
【分析】本题考查的是矿物硬度的比较。
2.形状六面体,每个面都是菱形的矿物是( )。
A. 石英B. 方解石C. 方铅矿D. 石盐【答案】 B【解析】【解答】方解石是一种碳酸钙矿物,天然碳酸钙中最常见的就是它。
因此,方解石是一种分布很广的矿物。
方解石的晶体形状多种多样,它们的集合体可以是一簇簇的晶体,形状为六面体,每个面都是菱形。
B选项符合题意。
故答案为:B。
【分析】本题考查的是方解石的特点。
3.下列岩石中容易分离成层的是( )。
A. 花岗岩B. 石灰岩C. 板岩【答案】 C【解析】【解答】板岩的特点是容易分离成层。
C选项符合题意。
故答案为:C。
【分析】板岩种浅变质岩,由粘土质、粉砂质沉积岩或中酸性凝灰质岩石、沉凝灰岩经轻微变质作用形成。
其岩性致密,具板状构造,有明显的板状劈理。
板岩颗粒结构紧密,透水性差,硬度高,耐磨度好,是墙地饰材的理想产品。
4.小伟检查一种矿物的硬度时,发现这种矿物用铜钥匙刻划不出痕迹,但能用小刀划出痕迹,这种矿物的硬度是( )。
A. 软B. 较软C. 较硬D. 硬【答案】 C【解析】【解答】可以用小刀画出痕迹,但是铜钥匙划不出痕迹的矿物其硬度是较硬。
C 选项符合题意。
故答案为:C。
【分析】在对矿物的硬度进行划分等级时,我们可以借助指甲、铜钥匙和小刀。
指甲可以划出痕迹的是软,指甲划不出但铜钥匙可以划出痕迹的是较软,铜钥匙划不出但是小刀可以划出的是较硬,而小刀也划不出痕迹的是硬。
5.用稀盐酸滴在下列矿物中能冒气泡的是()。
A. 石灰岩B. 石英C. 方铅矿D. 赤铁矿【答案】 A【解析】【解答】用稀盐酸滴在下列矿物中能冒气泡的是石灰岩,A选项符合题意,故答案为:A。
第3章CPU构成习题参考解答

6.按照图 3.3 所示的双总线数据通路,写出 SUB R2,R3 指令取指阶段和执行阶段的 微操作序列。 答:SUB R2,R3。这是一条减法指令,属于寄存器寻址方式,操作数和结果都存在寄 存器中。其功能是用寄存器 R2 的内容减去 R3 的内容,结果存入寄存器 R2 中。其指令流程 如表 3.26: 表 3.26 SUB R2,R3 指令双总线流程分析表 步骤 ( 1) ( 2) ( 3) ( 4) ( 5) 微 操 作 (PC)→MAR; (PC)+1→C (C ) →PC; M[MAR] →MDR (MDR)→IR (R2)-(R3)→C (C)→R2 控 制 信 号 解 释 PCOUT1、 CPMAR、 EMAR、 指令地址送到 MAR , PC RD、+1、CPC 内容和 1 相加后送 C。 COUT、CP2PC、SMDR MDROUT1、CP1IR 完成 PC 的修改, 将读出的 指令送 MDR。 将读出的指令送 IR,取指 阶段完成。
表 3.27 SUB R2,R3 指令三总线流程分析表 步骤 ( 1) ( 2) ( 3) ( 4) 微 操 作 (PC)→MAR; (PC)+1→PC M[MAR] →MDR (MDR)→IR (R2)-(R3)→R2 控 制 信 号 解 释 PCOUT3、 CPMAR、 EMAR、 指令地址送到 MAR , PC RD、+1、CP1PC 内容和 1 相加后送 PC。 SMDR MDROUT3、CP1IR R2OUT2 、 R3OUT3 、 ADD、PC1R1 将读出的指令送 MDR。 将读出的指令送 IR,取指 阶段完成。 R2 减去 R3 的内容后送 R2。
8.根据表 3.7 分析,参考表 3.8,说明此模型机有几种指令格式。 答:模型机有如下 9 种指令格式: ⑴ 31 27 26 22 21 17 16 0 OP ra rb C2 指令:LOAD、STORE、LOADA、ADDI、ANDI 和 ORI 使用此格式。 ⑵ 31 27 26 22 21 0 OP ra C1 指令:LOADR、STORER 和 LOADR 使用此格式。 ⑶ 31 27 26 22 21 17 16 12 11 0 OP ra rc 未用 指令:NEG、NOT 使用此格式。 ⑷ 31 27 26 22 21 17 16 12 11 OP 未用 rb rc 未用 指令:BRxx 使用此格式。 ⑸ 31 27 26 22 21 17 16 12 11 OP ra rb rc 未用 指令:BRLxx 使用此格式。 ⑹ 31 27 26 22 21 17 16 12 11 OP ra rb rc 未用 0 指令:ADD、SUB、AND 和 OR 使用此格式。 ⑺ 31 27 26 22 21 17 16 5 4 未用 3 2 C4 3 2 C4 0 0 0
第三章 整式及其加减专题练习及答案 解析版

第三章 整式及其加减专题练习学校:___________姓名:___________班级:___________学号:___________一、单选题(每小题3分,共30分)1.下列计算正确的是( )A .527x y xy +=B .321x x −=C .22234x y yx x y −=−D .338x x x += 2.已知423x y −与2n x y 是同类项,则n 的值为( )A .1B .2C .3D .43.下列说法中正确的是( )A .单项式2πx 的次数和系数都是2B .单项式2m n 和2n m 是同类项C .多项式2234x y xy +−是三次三项式D .多项式221x x −+−的项是2x ,2x 和1 4.定义一种新运算:2a b a b ⊗=−.例如232231⊗=⨯−=,则()()2x y x y +⊗−化简后的结果是( )A .33x y −+B .yC .3x y −−D .3y 5.如图是一个正方体的平面展开图,若原正方体中相对面上的两个数字之和均为5,则x y z ++的值为( )A .4B .5C .6D .7 6.如果2312M x x =++,235N x x =−+−,则M 与N 的大小关系是( ) A .M N >B .M N <C .M N =D .与x 的大小有关 7.在式子2532x x −,22x y π,1x y +,25y −中,多项式的个数是( ) A .1 B .2 C .3 D .4 8.若221m m +=-,则2324m m −−=( )A .1−B .1C .5−D .59.已知5x y −=,3a b +=−,则()()y b x a −−+的值为( )A .8B .8−C .2D .2−10.正方形ABCD 在数轴上的位置如图所示,点A 、B 对应的数分别为2−和1−,若正方形ABCD 绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点C 所对应的数为0;则翻转2022次后,点C 所对应的数是( )A .2020B .2021C .2022D .2023二、填空题(每小题3分,共15分)11.k =______时()2232353x k xy xy y −−++−中不含xy 项 12.已知a ,b 互为相反数,m ,n 互为倒数,p 是最小的正整数,则102()||2020a b mn p ++−=__________.13.当2022x =时,代数式35ax bx ++的值为1,则当2022x =−时,35ax bx ++的值为__________.14.如图是一个“数值转换机”,若输入的数 1.5x =−,则输出的结果为____.15.如图,是由一些点组成的图形,按此规律,当20n =时图形中点的个数为 __.三、解答题(16题8分,17题6分,18题6分,19题7分,20题10分,21题9分,22题9分,共55分)16.化简:(1)()()2235x x x −+−−+(2)()()2222312x x x x x −+−−−+17.先化简,再求值:()()2222352mn m m mn m mn ⎡⎤−−+−−+⎣⎦, 其中m ,n 满足()2120m n −++=.18.某同学做一道数学题:已知两个多项式A 、B ,计算2A B +,他误将“2A B +”看成“2A B +”,求得的结果是2927x x −+,已知232B x x =+−,求2A B +的正确答案.19.如图,已知长方形的宽为a ,两个空白处分别是半径为a ,b 的四分之一圆.(1)用含a 、b 的式子表示阴影部分的面积;(结果保留π)(2)当6a =,2b =时,求出阴影部分的面积.20.已知:22321A a ab a =+−−,21B a ab =−+−(1)求()432A A B −−的值;(2)若2A B +的值与a 的取值无关,求b 的值.21.仔细观察下列等式:第一个:225183−=⨯第二个:229587−=⨯第三个:22139811−=⨯第四个:221713815−=⨯……(1)请你写出第六个等式:___________;(2)请写出第n 个等式:___________;(用含字母n 的等式表示);(3)运用上述规律,计算:811813897899⨯+⨯++⨯+⨯.22.在数轴上点A 表示数a ,点B 表示数b ,点 C 表示数c ,a 是多项式2241x x −−+的二次项系数,b 是最大的负整数,单项式2412x y −的次数为c .(1)a =_________,b =_________,c =__________(2)若将数轴在点B 处折叠,则点A 与点C __________重合。
复式记账法练习题及参考答案

第三章复式记账同步强化练习题一、单项选择题1、复式记账法对每项经济业务都以相等的金额()中进行登记。
A、一个账户B、两个账户C、全部账户D、两个或两个以上的账户2、预付供应单位材料货款,负债及所有者权益类账户的期末余额一般在()。
A、借方B、借方和贷方C、贷方D、借方或贷方3、所有者权益类账户的期末余额根据()计算。
A、借方期末余额=借方期初余额+借方本期发生额—贷方本期发生额B、借方期末余额=借方期初余额+贷方本期发生额—借方本期发生额C、贷方期末余额=贷方期初余额+贷方本期发生额—借方本期发生额D、贷方期末余额=贷方期初余额+借方本期发生额—贷方本期发生额4、借贷记账法下的“借”表示{ }A、费用增加B、负债增加C、所有者权益增加D、收入增加5、应收账款账户的期初余额为借方2000元,本期借方发生额8000元,本期贷方发生额6000元,该账户的期末余额为()。
A、借方4000元B、贷方8000元C、负5000元D、贷方5000元6、办公室用转账支票购办公用品,其会计分录为()。
A、借:管理费用B、借:库存商品C、借:管理费用D、借:银行存款贷:现金贷:银行存款贷:银行存款贷:管理费用7、下列错误中,能够通过试算平衡查找的有()。
A、重记经济业务B、漏记经济业务C、借贷方向相反D、借贷金额不等8、采用托收承付结算方式,办理托收手续后,应作的会计分录为()。
A、借:银行存款贷:主营业务收入应交税金—应交增值税(销项税额)B、借:其他货币资金—在途资金贷:主营业务收入应交税金—应交增值税(销项税额)C、借:应收账款贷:主营业务收入应交税金—应交增值税(销项税额)D、借:应收票据贷:主营业务收入二、多项选择题1、复式记账法的优点包括()。
A、进行试算平衡B、了解经济业务的来龙去脉C、简化账簿登记工作D、检查账户记录的正确性2、复式记账法是指对发生的每一笔经济业务都要()进行登记的一种记账方法。
A、在同一会计期间内B、以相等的金额C、在相互联系的两个或两个以上的账户中D、同时3、试算平衡表中,试算平衡的公式有()。
【精选】光纤通信课后习题解答第3章习题参考答案

第三章 光纤的传输特性1.简述石英系光纤损耗产生的原因,光纤损耗的理论极限值是由什么决定的?答:(1)(2)光纤损耗的理论极限值是由紫外吸收损耗、红外吸收损耗和瑞利散射决定的。
2.当光在一段长为10km 光纤中传输时,输出端的光功率减小至输入端光功率的一半。
求:光纤的损耗系数α。
解:设输入端光功率为P 1,输出端的光功率为P 2。
则P 1=2P 2光纤的损耗系数()km dB P P km P P L /3.02lg 1010lg 102221===α 3.光纤色散产生的原因有哪些?对数字光纤通信系统有何危害?答:(1)按照色散产生的原因,光纤的色散主要分为:模式(模间)色散、材料色散、波导色散和极化色散。
(2)在数字光纤通信系统中,色散会引起光脉冲展宽,严重时前后脉冲将相互重叠,形成码间干扰,增加误码率,影响了光纤的传输带宽。
因此,色散会限制光纤通信系统的传输容量和中继距离。
4.为什么单模光纤的带宽比多模光纤的带宽大得多?答:光纤的带宽特性是在频域中的表现形式,而色散特性是在时域中的表现形式,即色散越大,带宽越窄。
由于光纤中存在着模式色散、材料色散、波导色散和极化色散四种,并且模式色散>>材料色散>波导色散>极化色散。
由于极化色散很小,一般忽略不计。
在多模光纤中,主要存在模式色散、材料色散和波导色散;单模光纤中不存在模式色散,而只存在材料色散和波导色散。
因此,多模光纤的色散比单模光纤的色散大得多,也就是单模光纤的带宽比多模光纤宽得多。
光纤损耗吸收损耗本征吸收杂质吸收原子缺陷吸收紫外吸收 红外吸收氢氧根(OH -)吸收 过渡金属离子吸收散射损耗弯曲损耗5.均匀光纤纤芯和包层的折射率分别为n 1=1.50,n 2=1.45,光纤的长度L=10km 。
试求:(1)子午光线的最大时延差;(2)若将光纤的包层和涂敷层去掉,求子午光线的最大时延差。
解:(1) 1sin 21111⎪⎪⎭⎫ ⎝⎛-=-=n n C Ln n C L n CL c M θτ () s 1.72145.150.110350.1105μ=⎪⎭⎫⎝⎛-⨯⨯=km km (2)若将光纤的包层和涂敷层去掉,则n 2=1.01sin 21111⎪⎪⎭⎫ ⎝⎛-=-=n n C Ln n C L n CL c M θτ () s 5210.150.110350.1105μ=⎪⎭⎫⎝⎛-⨯⨯=km km 6.一制造长度为2km 的阶跃型多模光纤,纤芯和包层的折射率分别为n 1=1.47,n 2=1.45,使用工作波长为1.31μm ,光源的谱线宽度Δλ=3nm ,材料色散系数D m =6ps/nm·km ,波导色散τw =0,光纤的带宽距离指数γ=0.8。
电磁场与电磁波(第4版)第3章部分习题参考解答
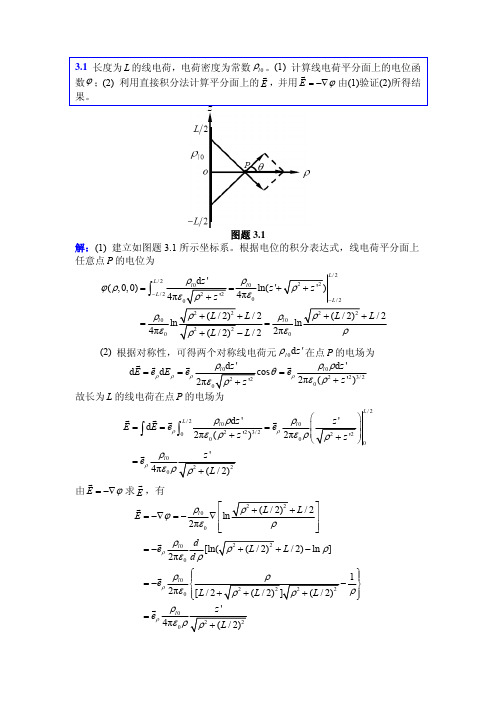
ρ ≥ a 时, E = −∇ϕ = −eρ
G
G ∂ ∂ρ
3.4 已知 y > 0 的空间中没有电荷,试判断下列函数中哪些是可能的电位解? (1) e− y cosh x ;(2) e− y cos x ;(3) e− 2 sin x cos x ;(4) sin x sin y sin z 。 解:在电荷体密度 ρ = 0 的空间,电位函数应满足拉普拉斯方程 ∇ 2ϕ = 0 。
∂2 − y ∂2 − y ∂2 − y (e cosh x) + 2 (e cosh x) + 2 (e cosh x) = 2e− y cosh x ≠ 0 (1) ∂x 2 ∂y ∂z −y 所以函数 e cosh x 不是 y > 0 空间中的电位解; ∂2 − y ∂2 − y ∂2 − y (e cos x) + 2 (e cos x) + 2 (e cos x) = −e− y cos x + e− y cos x = 0 (2) ∂x 2 ∂y ∂z −y 所以函数 e cos x 是 y > 0 空间中可能的电位解; ∂ − 2 ∂ ∂ (e sin x cos x) + 2 (e− 2 sin x cos x) + 2 (e − 2 sin x cos x) (3) 2 ∂x ∂y ∂z
G ρ = −eρ l 0 2πε 0 G = eρ
ρl 0 4πε 0 ρ
⎧ ρ 1⎫ ⎪ ⎪ − ⎬ ⎨ 2 2 2 2 ρ⎪ ⎪[ L / 2 + ρ + ( L / 2) ] ρ + ( L / 2) ⎩ ⎭ z'
ρ 2 + ( L / 2) 2
3.2 点电荷 q1 = q 位于 P 1 ( − a, 0, 0) ,另一点电荷 q2 = −2q 位于 P 2 ( a, 0, 0) ,求空间的 零电位面。 解:两个点电荷 + q 和 −2q 在空间产生的电位 ⎤ q 1 ⎡ 2q ϕ ( x, y , z ) = − ⎢ ⎥ 2 2 2 2 2 2 4 πε 0 ⎢ ( ) ( ) ⎥ x a y z x a y z + + + − + + ⎣ ⎦ 1 2 − =0 令 ϕ ( x, y, z ) = 0 ,则有 2 2 2 2 ( x + a) + y + z ( x − a) + y 2 + z 2
第三章 习题解答-2.0
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔; (2)(S)-2-溴-丁烷; (3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷; (7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(J. Org. Chem. 2013, 78, 6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
《化工热力学章节习题及解答》第三章 例题

另外,还需要理想气体等压热容的数据,查附录A-4得到,得到异丁烷的理想气体等压热容是
(J mol-1K-1)
初态是T0=300K,P0=0.1MPa的理想气体;终态是T=360K的饱和蒸汽,饱和蒸汽压可以从Antoine方程计算,查附录A-2,得
性质
沸点或蒸汽压
U/Jg-1
H/Jg-1
S/Jg-1K-1
饱和蒸汽
340℃或14.59MPa
2464.5
2622.0
5.3359
总性质
2464500(J)
2622000(J)
5335.9(JK-1)
所以, J; J; JK-1。
又因为,是一个等容过程,故需要吸收的热为 J
7. 压力是3MPa的饱和蒸汽置于1000cm3的容器中,需要导出多少热量方可使一半的蒸汽冷凝?(可忽视液体水的体积)
解:以1g为基准来计算。
(1)对于绝热可逆膨胀,Q=0,W=-1000ΔU,S2=S1,
从 Pa,查附录C-1,得到 , 940.87Jg-1, ,
则 和
由于可确定膨胀后仍处于汽液两相区内,终态压力就是饱和蒸汽压,从 Pa查 , ; ,
从
则W=-1000(U2-U1)=278.45(kJ)
(2)再恒容加热成饱和蒸汽,W=0,
解:由Maxwell关系式
左边= ;
又因为 ,右边= ,由此可以得到
(这种体积关系一般能成立,故方程有一定的可靠性)。
5.试证明 ,并说明 。
解:由定义 ;
右边= =左边。
代入理想气体状态方程, 可以得到
6.证明(a)在汽液两相区的湿蒸汽有 。(b)在临界点有 。
高中数学(必修一)第三章 函数的概念与性质幂函数 练习题

高中数学(必修一)第三章 函数的概念与性质幂函数 练习题(含答案解析)学校:___________姓名:___________班级:_____________一、单选题1.下列幂函数中,定义域为R 的是( ) A .1y x -= B .12y x -=C .13y x =D .12y x = 2.已知幂函数n y x =在第一象限内的图像如图所示,若112,2,,22n ⎧⎫∈--⎨⎬⎩⎭则与曲线1C 、2C 、3C、4C 对应的n 的值依次为( )A .12-、2-、2、12B .2、12、2-、12-C .2、12、12-、2-D .12-、2-、12、23.四个幂函数在同一平面直角坐标系中第一象限内的图象如图所示,则幂函数12y x =的图象是( )A .①B .①C .①D .①4.下列函数中,既是偶函数,又满足值域为R 的是( ) A .y =x 2B .1||||y x x =+C .y =tan|x |D .y =|sin x |5.如下图所示曲线是幂函数y =xα在第一象限内的图象,已知α取±2,±12四个值,则对应于曲线C 1,C 2,C 3,C 4的指数α依次为( )A .-2,-12,12,2B .2,12,-12,-2C .-12,-2,2,12 D ..2,12,-2,-126.若幂函数()f x 经过点,且()8f a =,则=a ( )A .2B .3C .128D .5127.函数()0a y x x =≥和函数()0xy a x =≥在同一坐标系下的图像可能是( )A .B .C .D .8.式子)A .1633- B .1633--C .1633+D .1633-+9.对,a b ∈R ,记{},max ,,a a ba b b a b ≥⎧=⎨<⎩,函数()}2maxf x x -=的图象可能是( )A .B .C .D .二、解答题10.设函数()222f x x x =-+,[],1,x t t t R ∈+∈(1)求实数t 的取值范围,使()y f x =在区间[],1t t +上是单调函数; (2)求函数()f x 的最小值. 11.已知幂函数()223m m y x m --=∈Z 的图像与x 、y 轴都无交点,且关于y 轴对称,求m 的值,并画出它的草图.12.已知幂函数()()25mf x m m x =+-在()0,∞+上单调递增.(1)求()f x 的解析式;(2)若()31f x x k >+-在[1,1]-上恒成立,求实数k 的取值范围. 13.设函数()f x 是定义在R 上的奇函数,且()21x ax b f x x +=++.(1)求实数a ,b 的值;(2)当x ∈⎤⎦,不等式()()22f x mx x ≥-有解,求实数m 的取值范围.三、填空题14.若点(2,4)P ,0(3,)Q y 均在幂函数()y f x =的图象上,则实数0y =_____.15.已知实数a ,b 满足等式a 12=b 13,下列五个关系式:①0<b<a<1;①-1<a<b<0;①1<a<b ;①-1<b<a<0;①a =b.其中可能成立的式子有________.(填上所有可能成立式子的序号) 16.函数3223125y x x x =--+在[0,3]上的最大值等于__________.17.定义{}()max ,()a ab a b b a b ≥⎧=⎨<⎩,则{}2max 1,2x x x +--的最小值为_________.参考答案:1.C【分析】直接根据幂函数的定义域可直接判断,偶次根式被开方式必须大于等于0才有意义,分式则必须分母不为0【详解】对选项A,则有:0x≠对选项B,则有:0x>对选项C,定义域为:R对选项D,则有:0x≥故答案选:C2.C【解析】本题可根据幂函数的图像与性质并结合题目中的图像即可得出结果.【详解】由幂函数的图像与性质可知:在第一象限内,在1x=的右侧部分的图像,图像由下至上,幂的指数依次增大,故曲线1C、2C、3C、4C对应的n的值依次为:2、12、12-、2-,故选:C.【点睛】本题考查幂函数的图像与性质,在第一象限内,幂函数在1x=的右侧部分的图像,图像由下至上,幂的指数依次增大,考查数形结合思想,是简单题.3.D【解析】由幂函数12y x=为增函数,且增加的速度比较缓慢作答.【详解】幂函数12y x=为增函数,且增加的速度比较缓慢,只有①符合.故选:D.【点睛】本题考查幂函数的图象与性质,属于基础题.4.C【分析】由函数的值域首先排除ABD,对C进行检验可得.【详解】选项A,B中函数值不能为负,值域不能R,故AB错误,选项D值域为[]0,1,故D也错误,那么选项C为偶函数,当3(,)22xππ∈时,tan tany x x==,值域是R,因此在定义域内函数值域为R,故选:C5.B【分析】在图象中,作出直线1x m =>,根据直线x m =和曲线交点的纵坐标的大小,可得曲线1C ,2C ,3C ,4C 相应的α应是从大到小排列.【详解】在图象中,作出直线1x m =>,直线x m =和曲线的交点依次为,,,A B C D , 所以A B C D y y y y >>>,所以C A B D m m m m αααα>>>, 所以A B C D αααα>>>,所以可得曲线1C ,2C ,3C ,4C 相应的α依次为 2,12,-12,-2 故选:B【点睛】本题主要考查幂函数的图象和性质,意在考查学生对这些知识的理解掌握水平. 6.A【解析】设幂函数()f x x α=,代入点求出3α=,即可求解.【详解】设()f x x α=,因为幂函数()f x 经过点,所以f α==, 解得3α=,所以()38f a a ==,解得2a =, 故选:A 7.C【分析】按照x y a =和a y x =的图像特征依次判断4个选项即可.【详解】()0a y x x =≥必过(0,0),()0xy a x =≥必过(0,1),D 错误;A 选项:由x y a =图像知1a >,由a y x =图像可知01a <<,A 错误;B 选项:由x y a =图像知01a <<,由a y x =图像可知1a >,B 错误;C 选项:由x y a =图像知01a <<,由a y x =图像可知01a <<,C 正确. 故选:C. 8.A【分析】利用根式与分数指数幂互化和指数幂运算求解.【详解】231322333⎛⎫=-÷ ⎪⎝⎭, 21131326223333--=-=-,故选:A 9.A【分析】由()}2maxf x x -=2x -的较大者,在同一平面直角坐标系中作出两个函数的图象,取图象较高者即可得()f x 的图象.【详解】y =2y x 都是偶函数,当0x >时,12y x =在()0,∞+上单调递增,2yx 在()0,∞+上单调递减,当1x =2x -=在同一平面直角坐标系中作出y =和2yx 的图象,如图:()}2maxf x x -=2x -的较大者,所以()f x 图象是两个图象较高的,故选:A.10.(1)(][),01,-∞⋃+∞;(2)()2min21,01,0122,1t t f x t t t t ⎧+≤⎪=<<⎨⎪-+≥⎩【解析】(1)由题可得11t +≤或1t ≥,解出即可;(2)讨论对称轴在区间[],1t t +的位置,根据单调性即可求出. 【详解】(1)()f x 的对称轴为1x =,要使()y f x =在区间[],1t t +上是单调函数, 则11t +≤或1t ≥,解得0t ≤或1t ≥, 即t 的取值范围为(][),01,-∞⋃+∞;(2)()f x 的对称轴为1x =,开口向上,则当1t ≥时,()f x 在[],1t t +单调递增,()()2min 22f x f t t t ∴==-+,当11t t <<+,即01t <<时,()()min 11f x f ==,当11t +≤,即0t ≤时,()f x 在[],1t t +单调递减,()()2min 11f x f t t ∴=+=+,综上,()2min21,01,0122,1t t f x t t t t ⎧+≤⎪=<<⎨⎪-+≥⎩. 11.1m = ;草图见祥解【分析】根据幂函数的性质,可得到2230m m --<,再有图像关于y 对称,即可求得m 的值. 【详解】因为幂函数223()m m y x m Z --=∈的图像与坐标轴无交点,所以2230m m --<,解得13m -<<,又因为m Z ∈,所以0,1,2m =,因为图像关于y 对称,所以幂函数为偶函数, 当0m =时,则3y x -=为奇函数,不满足题意; 当1m =时,则4y x -= 为偶函数,满足题意; 当2m =时,则3y x -=为奇函数,不满足题意; 综上所述:1m = 草图(如下)【点睛】本题考查幂函数的性质和图像,需熟练掌握幂函数的性质和图像. 12.(1)2()f x x = (2)(),1-∞-【分析】(1)根据幂函数的定义和()f x 的单调性,求出m 得值; (2)结合第一问求出的2()f x x =,利用函数的单调性,解决恒成立问题. (1)()f x 是幂函数,则251m m +-=,2m ∴=或-3,()f x 在(0,)+∞上单调递增,则2m =所以2()f x x =; (2)()31f x x k >+-即2310x x k -+->,要使此不等式在[1,1]-上恒成立,只需使函数()231g x x x k =-+-在[1,1]-上的最小值大于0即可.①()231g x x x k =-+-在[1,1]-上单调递减,①()()11min g x g k ==--, 由10k -->,得1k <-.因此满足条件的实数k 的取值范围是(),1-∞-. 13.(1)0a =,0b = (2)1,4⎛⎤-∞ ⎥⎝⎦【分析】(1)根据定义在R 上的奇函数的性质以及定义即可解出;(2)由(1)可知,()21x f x x =+,根据分离参数法可得()()22112m x x ≤+-,再求出()()22112x x +-的最大值,即得解. (1)因为函数()f x 是定义在R 上的奇函数,所以()00f a ==,()()1111022f f b b-+-=+=+-,解得0b =,检验可知函数()21xf x x =+为奇函数,故0a =,0b =. (2)由(1)可知,()21x f x x =+,而x ∈⎤⎦,所以 ()()22f x mx x ≥-可化为()()22112m x x ≤+-,设[]23,4t x =∈,则()()()()[]222219121224,1024x x t t t t t ⎛⎫+-=+-=--=--∈ ⎪⎝⎭,而不等式()()22f x mx x ≥-有解等价于()()22max11412m x x ⎡⎤⎢⎥≤=+-⎢⎥⎣⎦,故实数m 的取值范围为1,4⎛⎤-∞ ⎥⎝⎦.14.9【分析】设出幂函数的解析式,代入P 点坐标求得这个解析式,然后令3x =求得0y 的值.【详解】设幂函数为()f x x α=,将()2,4P 代入得24,2αα==,所以()2f x x =,令3x =,求得2039y ==.【点睛】本小题主要考查幂函数解析式的求法,考查幂函数上点的坐标,属于基础题. 15.①①①【分析】在同一坐标系中画出函数121y x =,132y x =的图象,结合函数图象,进行动态分析可得,当01b a <<<时,当1a b <<时,当1a b ==时,1132a b =可能成立,10b a -<<<、10a b -<<<时,12a 没意义,进而即可得到结论【详解】10b a -<<<、10a b -<<<时,12a 没意义,①①不可能成立;’画出121y x =与132y x =的图象(如图), 已知1132x x m ==,作直线y m =, 若0m =或1,则a b =,①能成立; 若01m <<,则01b a <<<,①能成立;若1m ,则1a b <<,①能成立,所以可能成立的式子有①①①,故答案为①①①.【点睛】本题主要考查幂函数的图象与性质,意在考查灵活应用所学知识解答问题的能力,以及数形结合思想的应用,属于中档题. 数形结合是根据数量与图形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法,.函数图象是函数的一种表达形式,它形象地揭示了函数的性质,为研究函数的数量关系提供了“形”的直观性.归纳起来,图象的应用常见的命题探究角度有:1、确定方程根的个数;2、求参数的取值范围;3、求不等式的解集;4、研究函数性质.16.5【分析】对3223125y x x x =--+求导,根据单调性求最大值.【详解】3223125y x x x =--+,则266126(2)(1)y x x x x '=--=-+当2x >时,0y '>,此时函数3223125y x x x =--+单调递增;当12x -<<时,0y '<,此时函数3223125y x x x =--+单调递减;当1x <-时,0y '>,此时函数3223125y x x x =--+单调递增.则函数3223125y x x x =--+在区间[0,2]内单调递减,在区间[2,3]内单调递增当0x =时,5y =,当3x =时,4y =-所以函数3223125y x x x =--+在0x =处取到最大值5所以函数3223125y x x x =--+在区间[0,3]上的最大值是5.故答案为:5.17.1【分析】根据题干中max 函数的定义,可以得到所求函数为分段函数,求出每一段的最小值,取其中的最小值即可 【详解】令212x x x +-=-得:3x =-或1x =,由题意可得:{}2221,3max 1,22,311,1x x x x x x x x x x x ⎧+-≤-⎪+--=--<<⎨⎪+-≥⎩,画出函数对应的图像如下:由图可得:当1x =时,{}2max 1,2x x x +--最小,代入解析式可得:最小值为1故答案为:1。
计量经济学(第四版)第三章练习题及答案
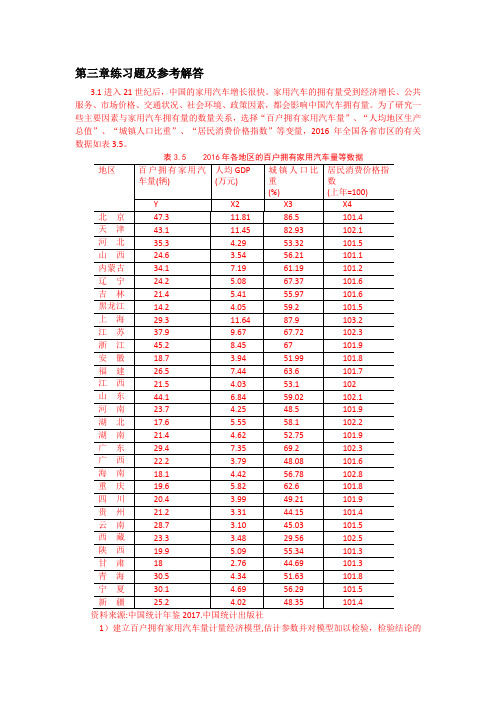
第三章练习题及参考解答3.1进入21世纪后,中国的家用汽车增长很快。
家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量,2016年全国各省市区的有关数据如表3.5。
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。
第三章习题解答及参考答案

(
)
①
2 式中 m 为整数。令 u = αr ,显然上式是 u 的周期函数,周期为 2π ,故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数:
其中,
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有:
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ;两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明,要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少? 解:取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的 空间频率成分不受到有限孔径的渐晕效应的影响,故透镜的口径 D 应满足条件:
第3章 习题及参考解答

第3章习题及参考解答1.指出下列各指令中源操作数和目的操作数的寻址方式。
(1)MOV DI,100(2)MOV CX.100[SI](3)MOV [SI],AX(4)ADD AX,[BX+DI](5)AND AX,BX(6)MOV DX,[1000](7)MOV BX,[BP+DI+100](8)PUSHF(9)SUB [1050],CX(10)AND DH,[BP+4]解源操作数目的操作数(1)立即寻址寄存器寻址(2)变址寻址寄存器寻址(3)寄存器寻址寄存器间接寻址(4)基址加变址寻址寄存器寻址(5)寄存器寻址寄存器寻址(6)直接寻址寄存器寻址(7)基址加变址寻址寄存器寻址(8)寄存器寻址寄存器间接寻址(9)寄存器寻址直接寻址(10)变址寻址寄存器寻址2.试述指令MOV AX,2000H和MOV AX,DS:[2000H]的区别?解区别有三条:(1)MOV AX,2000H对源操作数是立即寻址,而MOV AX.[2000H]对源操作数是直接寻址;(2)前者功能是把立即数2000H送入AX中,而后者是把内存2000H单元与2001H单元的内容取出送入AX 中;(3)两者的机器代码不同,执行速度也不同,前者执行时间快,后者执行时间慢。
4.若DS=4000H,BX=0800H,[40800H]=05AOH,[40802H]=2000H,求执行指令LDS SI,[BX]后,DS与SI中的内容。
若上题中的DS换成ES,其他条件不变,求执行指令LES DI,[BX]后,ES与DI 中的内容。
解SI=05AOH,DS=2000HDI=05AOH,ES=2000H5.若AX=98ABH,BX=A8BCH。
求执行指令ADD AX,BX后,AX与BX中的内容,并指出SF,ZF,AF,PF,CF和OF的状态。
解AX=4167H,BX=A8BCH,SFZFAFPFCFOF=001011B。
6.若CX=6700H,DX=78FFH,CF=1。
固态电子论_第三章习题参考解答

第7题
以硅半导体中掺金为例说明如下:
金原子具有1个价电子。
如果金(Au)原子将价电子电离出去,则在硅半导体中产生一个深施主能级 EtD ,
l
l
令 l' l 1,得到,
k (x a) f (x l'a) f (x l'a) k (x)
l '
l '
eika 1,ka 2n,k 2n
a
在第一布里渊区,
k
a
, a
(n 0,1,2,......)
如下图所示:
Ec
Au Au
Ei
0.35eV
EtD
E
如果金(Au)原子获得一个外来电子,则在硅半导体中产生一个深受主能级 EtA ,
如下图所示:
Au Au
Ec
0.54eV
Ei
EtA
E
第8题(参考第1章倒格子、第2章能带表示的课件)
(1) 图3-41是能带图的简约布里渊区表示法。
第Ⅱ能带原本在第二布里渊区,通过移动1个倒格矢 Gh后落入第一布里渊区的。第Ⅲ能带
在第一布里渊区内,k
1 2a
,
1 2a
,得到,
k 0,k 1 2a
当 k 0 , 电子能量,
Emin Ek 0 0
当 k 1 , 电子能量, 2a
第三章图形的平移与旋转练习题及答案全套一

情景再现:你对以上图片熟悉吗?请你回答以下几个问题: (1)汽车中的乘客在乘车过程中,身高、体重改变了吗?乘客所处的地理位置改变了吗?(2)传送带上的物品,比如带有图标的长方体纸箱,向前移动了20米,它上面的图标移动了多少米?(3)以上都是我们常见的平移问题,认真想一想,你还能举一些平移的例子吗?1.如图1,面积为5平方厘米的梯形A ′B ′C ′D ′是梯形ABCD 经过平移得到的且∠ABC =90°.那么梯形ABCD 的面积为________,∠A ′B ′C =________. 图1 2.在下面的六幅图中,(2)(3)(4)(5)(6)中的图案_________可以通过平移图案(1)得到的.图23.请将图3中的“小鱼”向左平移5格.图34.请欣赏下面的图形4,它是由若干个体积相等的正方体拼成的.你能用平移分析这个图形是如何形成的吗?一、填空:1、如下左图,△ABC 经过平移到△A ′B ′C ′的位置,则平移的方向是______,平移的距离是______,约厘米______.2、如下中图,线段AB 是线段CD 经过平移得到的,则线段AC 与BC 的关系为( )A.相交B.平行C.相等D.平行且相等3、如下右图,△ABC 经过平移得到△DEF ,请写出图中相等的线段______,互相平行的线段______,相等的角______.(在两个三角形的内角中找) 4、如下左图,四边形ABCD 平移后得到四边形EFGH ,则:①画出平移方向,平移距离是_______;(精确到0.1cm )②HE=_________,∠A=_______,∠A=_______. ③DH=_________=_______A=_______. 5、如下右图,△ABC 平移后得到了△DEF ,(1)若∠A=28º,∠E=72º,BC=2,则∠1=____º,∠F=____º,EF=____º;(2)在图中A 、B 、C 、D 、E 、F 六点中,选取点_______和点_______,使连结两点的线段与AE 平行. 6、如图,请画出△ABC 向左平移4格后的△A 1B 1C 1,然后再画出△A 1B 1C 1向上平移3格后的△A 2B 2C 2,若把△A 2B 2C 2看成是△ABC 经过一次平移而得到的,那么平移的方向是______,距离是____的长度. 二、选择题:7、如下左图,△ABC 经过平移到△DEF 的位置,则下列说法:①AB ∥DE ,AD=CF=BE ; ②∠ACB=∠DEF ; ③平移的方向是点C 到点E 的方向; ④平移距离为线段BE 的长. 其中说法正确的有( ) A.个 B.2个 C.3个 D.4个8、如下右图,在等边△ABC 中,D 、E 、F 分别是边BC 、AC 、AB 的中点,则△AFE 经过平移可以得到( ) A.△DEF B.△FBD C.△EDC D.△FBD 和△EDC三、探究升级:1、如图,△ABC 上的点A 平移到点A 1,请画出平移后的图形△A 1B 1C 1.3、 △ABC 经过平移后得到△DEF ,这时,我们可以说△ABC 与△DEF 是两个全等三角形,请你说出全等三角形的一些特征,并与同伴交流.4、如下图中,有一块长32米,宽24米的草坪,其中有两条宽2米的直道把草坪分为四块,则草坪的面积是______.5、利用如图的图形,通过平移设计图案,并用一句诙谐、幽默的词语概括你所画的图形.一、填空、选择题:1、图形的旋转是由____和____决定的,在旋转过程中位置保持不动的点叫做____,任意一对对应点与旋转中心连线所成的角叫做_____.2、如下图,如果线段MO 绕点O 旋转90°得到线段NO ,在这个旋转过程中,旋转中心是_______,旋转角是_______,它时______°.§3.3图形的平移与旋转§3.2图形的平移与旋转§3.1图形的平移与旋转3、如图,在下列四张图中不能看成由一个平面图形旋转而产生的是( )4、请你先观察图,然后确定第四张图为( ) 4、 如下左图,△ABC 绕着点O 旋转后得到△DEF ,那么点A 的对应点是_______,线段AB 的对应线段是_____,_____的对应角是∠F.6、如下中图,△ABC 与△BDE 都是等腰三角形,若△ABC 经旋转后能与△BDE 重合,则旋转中心是________,旋转了______°.7、如下右图,C 是AB 上一点,△ACD 和△BCE 都是等边三角形,如果△ACE 经过旋转后能与△DCB 重合,那么旋转中心是_______,旋转了______°,点A 的对应点是_______. 二、解答题:8、如图11.4.7,△ABC 绕顶点C 旋转某一个角度后得到△A ′B ′C ,问:(1)旋转中心是哪一点? (2)旋转角是什么? (3)如果点M 是BC 的中点,那么经过上述旋转后,点M 转到了什么位置?9、观察下列图形,它可以看作是什么“基本图形”通过怎样的旋转而得到的? 三、探究升级10、如图,△ACE 、△ABF 都是等腰三角形,∠BAF=∠CAE=90°,那么△AFC 是哪一点为旋转中心,旋转多少度之后能与另一个三角形重合?点F 的对应点是什么?一、选择题1.平面图形的旋转一般情况下改变图形的( )A.位置B.大小C.形状D.性质2.9点钟时,钟表的时针和分针之间的夹角是( )A.30° B.45° C.60° D.90°3.将平行四边形ABCD 旋转到平行四边形A ′B ′C ′D ′的位置,下列结论错误的是( )A.AB =A ′B ′B.AB ∥A ′B ′C.∠A =∠A ′D.△ABC ≌△A ′B ′C ′ 二、填空题4.钟表上的指针随时间的变化而移动,这可以看作是数学上的_______.5.菱形ABCD 绕点O 沿逆时针方向旋转到四边形D C B A '''',则四边形D C B A ''''是________.6.△ABC 绕一点旋转到△A ′B ′C ′,则△ABC 和△A ′B ′C ′的关系是_______.7.钟表的时针经过20分钟,旋转了_______度.8.图形的旋转只改变图形的_______,而不改变图形的_______. 三、解答题9.下图中的两个正方形的边长相等,请你指出可以通过绕点O 旋转而相互得到的图形并说明旋转的角度. 10.在图中,将大写字母H 绕它右上侧的顶点按逆时针方向旋转90°,请作出旋转后的图案.11.如图,菱形A ′B ′C ′D ′是菱形ABCD 绕点O 顺时针旋转90°后得到的,你能作出旋转前的图形吗? 12.Rt △ABC ,绕它的锐角顶点A 分别逆时针旋转90°、180°和顺时针旋转90°,(1)试作出Rt △ABC 旋转后的三角形;(2)将所得的所有三角形看成一个图形,你将得到怎样的图形?13.如图,将右面的扇形绕点O 按顺时针方向旋转,分别作出旋转下列角度后的图形: (1)90°;(2)180°;(3)270°.你能发现将扇形旋转多少度后能与原图形重合吗?14.如图,分析图中的旋转现象,并仿照此图案设计一个图案.看一看:下列三幅图案分别是由什么“基本图形”经过平移或旋转而得到的?1.2.3.试一试:怎样将下图中的甲图变成乙图? 做一做:1、如图①,在正方形ABCD 中,E 是AD 的中点,F 是BA 延长线上的一点,AF =21AB , (1)△ABE ≌△ADF .吗?说明理由。
《高等代数1》复习练习题(三)——第三章 线性方程组(参考解答)

《高等代数1》复习练习题(三)——第三章线性方程组(解答)(供2017级数学与应用数学专业使用)一、填空题1、设23(,2,1),(2,3,0),(1,1,1)T T T k ααα1==-=-,则当1k =-时,向量组321,,ααα线性相关. 2、设矩阵⎪⎪⎪⎭⎫⎝⎛-=403212221A ,向量(,1,1)Ta α=,已知向量组,A αα线性相关,则1a =-.3、设向量组123(,0,),(,,0),(0,,)T T T a c b c a b ααα===线性相关,则,,a b c 必满足关系式 abc=0 .4、线性方程组121232343414,,,x x a x x a x x a x x a -=-=-=-=有解的充分必要条件是_____________.5、设33⨯矩阵A 的秩()1r A =,23(1,1,2),(2,0,1),(1,2,3)T T T ααα1===是线性方程组AX β=的三个特解,则对应导出组0AX =的基础解系是121323,αααααα---中任意两个向量.6、设33⨯矩阵A 的秩()2r A =,A 的各行元素之和均为零,则齐次线性方程组0AX =的通解是(1,1,1)T k .7、若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ有非零解,则=λ1.8、设齐次线性方程组12312312300x x x x kx x kx x x ++=⎧⎪++=⎨⎪++=⎩只有零解,则k 应满足的条件是1k ≠.9、.齐次线性方程组1231231232302340x x x x ax bx x x x ++=⎧⎪++=⎨⎪++=⎩有非零解,当且仅当,a b 满足关系式1(1)2a b =+.10、若线性方程组b AX =有解,且秩()A r =,则秩()A =r .二、选择题 1、设12,,,s ααα均为n 维向量,下列结论不正确的是 ( B ).(A)若对任意一组不全为零的数12,,,s k k k ,都有1122+++≠s s k k k ααα0,则12,,,s ααα线性无关.(B)若12,,,s ααα线性相关,则对任意一组不全为零的数12,,,s k k k ,都有1122+++=s s k k k ααα0.(C)向量组12,,,s ααα线性无关的充分必要条件是此向量组的秩为s . (D)向量组12,,,s ααα线性无关的必要条件是其中任意两个向量线性无关.2、设向量组123(,2,1),(2,,0),(1,1,1)TTTt t ααα===-线性无关,则( D ).(A )3t ≠-且2t ≠. (B )3t =或2t =-. (C )3t =-或2t =. (D )3t ≠且2t ≠-.3、设向量T T T T )4,0,1,1(,)1,3,0,2(,)5,1,2,0(,)2,2,1,1(4321=-===αααα,则向量组4321,,,αααα的秩等于( C ).(A)1. (B) 2. (C)3. (D)4. 4、设12,,,m ααα是一n 维向量组,它的秩12(,,,)=<m r r m ααα,则下面说法不正确的是( A ).(A)向量组12,,,m ααα中任意一个向量都能由其余向量线性表出.(B)向量组12,,,m ααα线性相关.(C)向量组12,,,m ααα与其任一极大无关组等价.(D)向量组12,,,m ααα中任意r 个线性无关的向量都构成其极大无关组.5、设0=AX 是非齐次方程组AX β=所对应的导出组,则下列结论正确的是 ( D ).(A)若0=AX 仅有零解,则AX β=有唯一解.(B)若0=AX 有非零解,则AX β=有无穷多解. (C)若AX β=有无穷多解,则0=AX 仅有零解. (D)若AX β=有无穷多解,则0=AX 有非零解.6、若A 是n 阶方阵,β是n 维非零向量,且齐次线性方程组0=AX 有非零解,则下列结论中不会发生的是( B ).(A)AX β=无解. (B)AX β=有唯一解. (C)AX β=有无穷多解. (D)()r A n <.7、非齐次线性方程组AX β=中未知量个数为n ,方程个数为m ,()r A r =,则 ( A )(A)r m =时,AX β=有解. (B)r n =时,AX β=有唯一解. (C)m n =时,AX β=有唯一解. (D)r n <时,AX β=有无穷多解. 8、设A 为m n ⨯矩阵,且()1r A n =-,12,αα是非齐次线性方程组AX β=的两个不同的解向量,k 为任意常数,则0AX =的通解为( A ).(A )12()k αα-; (B )12()k αα+; (C )1k α; (D )2k α. 9、设12,,,s ααα均为n 维向量,下列结论正确的是( B ) .(A) 若1122s s k k k ααα+++=0,则12,,,s ααα线性相关.(B) 若对任意一组不全为零的数12,,,s k k k ,都有1122s s k k k ααα+++≠0,则12,,,s ααα线性无关.(C) 若12,,,s ααα线性相关,则对任意一组不全为零的数12,,,s k k k ,都有1122s s k k k ααα+++=0.(D) 若12000s ααα+++=0,则12,,,s ααα线性无关.三、判断题 1、如果当120n k k k ===≠时,11220n n k k k ααα+++=,则向量组12,,,nααα线性相关. ( √ )2、如果12(,,,),1,2,,i i i in a a a i s α==线性相关,则向量组1212(,,,,,,,),1,2,,i i i in i i im a a a b b b i s β==也线性相关.( X )3、若123,,,αααβ线性相关,则β可由向量组123,,ααα线性表出.( X )4、若β不能由向量组123,,ααα线性表出,则123,,,αααβ线性无关.( X )5、若向量12,,,s ααα线性相关,则其中每一个向量皆可由其余向量线性.( X )6、非齐次线性方程组的两个解的和不再是它的解. ( √ )7、方程个数小于未知量个数的线性方程组必有无穷多个解. ( X )8、设12,αα线性相关,12,ββ也线性相关,则1122,αβαβ++线性相关. ( X )9、若线性方程组AX β=有无穷多个解,则0AX =一定有非零解. ( √ ) 10、若线性方程组0AX =有非零解,则AX β=一定有无穷多解.( X ) 四、计算题1、求向量组1234(1,1,2,4),(0,3,1,2),(3,0,7,14),(1,1,2,0),T T T T αααα=-===-5(2,1,5,6)T α=的秩及一个极大线性无关组,并用极大线性无关组线性表示其余向量.解:对以12345,,,,ααααα为列的矩阵作行初等变换化为阶梯形矩阵.1234510312103121301103303(,,,,)21725011014214060224210312131203303011010000000011000440000010301011010001100000ααααα⎛⎫⎛⎫ ⎪ ⎪--⎪ ⎪=→⎪ ⎪⎪⎪--⎝⎭⎝⎭⎛⎫⎛⎫⎪⎪ ⎪ ⎪→→ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎛⎫⎪⎪→ ⎪⎪⎝⎭所以,向量组12345,,,,ααααα的秩是3,124,,ααα是其一个极大线性无关组,且31251243,ααααααα=+=++.2、已知向量组123(0,1,1),(,3,1),(,1,0)T TT a b βββ=-==与向量组123(1,2,3),(2,1,1),(3,0,1)T TT ααα=-=-=具有相同的秩,且3β可由123,,ααα线性表出,求,a b .解:令1231231233(,,),(,,),(,,,)A B A αααβββαααβ===则由条件可知,A 与B ,A 与A 由相同的秩.因为1233123123(,,,)2101036123110051031231231000105103510510300015b b A b b b b b b b b αααβ⎛⎫⎛⎫⎪ ⎪==→--- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎛⎫⎛⎫⎪ ⎪ ⎪⎪→-→ ⎪⎪⎪⎪- ⎪⎝⎭⎝⎭12300004(,,)131041041110110110110041004a b a b a b B a b βββ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪==→→ ⎪⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭ ⎪⎝⎭⎛⎫⎪- ⎪→ ⎪ ⎪- ⎪⎝⎭所以,2=秩A =秩B =秩A ,于是10,1045a b b -=-=,故20,5a b ==. 3、设四元非齐次线性方程组=AX β的系数矩阵A 的秩为2,已知它的三个解向量为123,,ηηη,其中123(4,3,2,1),(1,3,5,1),(2,6,3,2)===-T T T ηηη,求该方程组的通解.解:因为123,,ηηη是=AX β的解,所以12(3,0,3,0)T ηη-=-,13(6,3,1,1)T ηη-=---是0AX =的解,且1213,ηηηη--线性无关.又因为()2r A =,所以0AX =的基础解系含有两个解向量,于是1213,ηηηη--是0AX =的一个基础解系.故=AX β的通解是1112213()()c c ηηηηη+-+-(12,c c F ∈)4、设向量1234,,,αααα是齐次线性方程组0AX =的一个基础解系,若112223334441,,,t t t t βααβααβααβαα=+=+=+=+,试问:当实数t 满足什么关系时,1234,,,ββββ也是0AX =的一个基础解系?解:因为1234,,,αααα是0AX =的基础解系,所以1234,,,αααα的线性组合1234,,,ββββ也是0AX =的解. 因此,当1234,,,ββββ线性无关时,1234,,,ββββ也是0AX =的一个基础解系.因为12341234100100(,,,)(,,,)010001t t t t ββββαααα⎛⎫⎪⎪= ⎪⎪⎝⎭所以,1234,,,ββββ线性无关⇔1234||0ββββ≠⇔410010010010001ttt tt=-≠⇔1t ≠±.故当1t ≠±时,1234,,,ββββ也是0AX =的一个基础解系.5、设3阶非零矩阵A 的每一个列向量都是方程组1231231232020330x x x x x ax x x x +-=⎧⎪-+=⎨⎪+ -=⎩的解,求常数a 和行列式A .解:设123(,,)A βββ=,其中123,,βββ是A 的列向量,则123,,βββ不全为零,且是已知方程组的解,于是已知方程组由非零解,从而其系数矩阵行列式为零,即11211221034120313023a a a ---=-+=-+=--所以12a =. 设已知方程组的系数矩阵为B ,则B O ≠,且123123(,,)(,,)(0,0,0)BA B B B B O ββββββ====若||0A ≠,则A 可逆,从而111()()B BE B AA BA A OA O ---=====,矛盾,所以||0A =.6、讨论常数a 为何值时,线性方程组123123123112ax x x x ax x x x ax ++=⎧⎪++=⎨⎪+ +=-⎩无解、有唯一解、有无穷多解?在有无穷多解的情况下,求出其全部解.解:对线性方程组的增广矩阵作行初等变换得22111011120024211101130113112112112112011300(2)(1)2(2)a a a a a a a A a a a a aa a a a a a a a a ⎛⎫⎛⎫--+--+⎛⎫⎪ ⎪ ⎪=→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪→-- ⎪ ⎪+-+⎝⎭1)当1a =时,秩1A =≠秩2A =,方程组无解. 2)当1,2a ≠-时,秩3A ==秩A ,方程组有唯一解. 3)当2a =-时,秩2A ==秩3A <,方程组有无穷多解:13231,1x x x x =+=+(3x 是自由未知量)7、已知方程组⎪⎩⎪⎨⎧=-=+++=+--330)1(31432321321x ax x a x x x x x ,问a 为何值时,此方程组:(1)有唯一解;(2)无解;(3)有无穷多解?在有无穷多解的情况下,试用其导出组的基础解系表出全部解.解:对线性方程组的增广矩阵作行初等变换得21411141114111310012101210330330233112012100(3)(1)3A a a a a a a a a a a a a a ------⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=+→-+→-+ ⎪ ⎪ ⎪⎪ ⎪ ⎪--+-+⎝⎭⎝⎭⎝⎭-⎛⎫⎪→-+ ⎪ ⎪+-+⎝⎭1)当1,3a ≠-时,秩3A ==秩A ,方程组有唯一解.2)当1a =时,秩2A =≠秩3A =,方程组无解.3)当3a =-时,秩2A ==秩3A <,方程组有无穷多解:132314,1x x x x =-+=--(3x 是自由未知量)8、讨论常数,a b 为何值时,线性方程组1231231234324ax x x x bx x x bx x ++=⎧⎪++=⎨⎪+ +=⎩无解、有唯一解、有无穷多解?在有无穷多解的情况下,求出其全部解.解:对线性方程组的增广矩阵作行初等变换得1140114301142113113101212140010010114210121012011420014200(1)142a ab a a a a A bb b b b a a a a ab b b ab b a b ab -----⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=→→ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭--⎛⎫⎛⎫⎪ ⎪→→-- ⎪ ⎪⎪ ⎪--+--+⎝⎭⎝⎭1)当11,2a b =≠或0b =时,秩2A =≠秩3A =,方程组无解.2)当1,0a b ≠≠时,秩3A ==秩A ,方程组有唯一解. 3)当11,2a b ==时,秩2A ==秩3A <,方程组有无穷多解: 1322,2x x x =-=(3x 是自由未知量)9、对于线性方程组123123123322x x x x x x x x x λλλλ++=-⎧⎪++=-⎨⎪++=-⎩(1)λ取何值时,方程组无解、有唯一解、有无穷多解;(2)在方程组有无穷多解时,试用其对应齐次线性方程组的基础解系表示方程组通解.解:对线性方程组的增广矩阵作行初等变换得2211301133112011011211200233112011001101120(2)(1)3(1)A λλλλλλλλλλλλλλλλλλλλλλ⎛⎫----⎛⎫⎪ ⎪=-→-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎛⎫----⎛⎫ ⎪ ⎪→--→-- ⎪ ⎪ ⎪ ⎪--+--⎝⎭⎝⎭(1)1)当2λ=-时,秩2A =≠秩3A =,方程组无解. 2)当1,2λ≠-时,秩3A ==秩A ,方程组有唯一解. 3)当1λ=时,秩1A ==秩3A <,方程组有无穷多解.(2)在方程组有无穷多解时,与原方程组同解方程组为1232x x x ++=-,令230x x ==,得特解0(2,0,0)γ=-.与原方程组同解方程组对应的齐次线性方程组同解方程组为1230x x x ++=,所以对应的齐次线性方程组的基础解系为12(1,1,0),(1,0,1)ηη=-=-.所以原方程组的通解为:01122k k γγηη=++(12,k k 是任意数). 五、证明题1、设向量组123,,ααα线性无关,证明向量组12αα+,23αα+,31αα+也线性无关.证明:设112223331()()()0k k k αααααα+++++=则131122233()()()0k k k k k k ααα+++++=因为123,,ααα线性无关,所以131223000k k k k k k +=⎧⎪+=⎨⎪+=⎩解得1230k k k ===,故122331,,αααααα+++线性无关.2、证明向量组12233441,,,αααααααα++++线性相关. 证明:设112223334441()()()()0k k k k αααααααα+++++++=则141122233344()()()()0k k k k k k k k αααα+++++++=考虑齐次线性方程组141223340000k k k k k k k k +=⎧⎪+=⎪⎨+=⎪⎪+=⎩其系数行列式1001100110110011001111001100110010011=-=-=所以齐次线性方程组有非零解. 于是存在不全为零的数1234,,,k k k k ,使得112223334441()()()()0k k k k αααααααα+++++++=成立,故12233441,,,αααααααα++++线性相关.3、设向量组123,,ααα线性无关,证明向量组1223312,2,32αααααα---也线性无关.证明:设112223331(2)(2)(32)0k k k αααααα-+-+-=则131122233(22)()(23)0k k k k k k ααα-+-++-+=因为123,,ααα线性无关,所以1312232200230k k k k k k -=⎧⎪-+=⎨⎪-+=⎩解得1230k k k ===,故1223312,2,32αααααα---线性无关.4、设向量组123,,ααα线性无关,证明向量组123123,2322,αααααα++-+123355ααα+-线性相关.证明:设112321233123()(2322)(355)0k k k ααααααααα+++-+++-=则123112321233(23)(35)(225)0k k k k k k k k k ααα+++-+++-=因为123,,ααα线性无关,所以1231231232303502250k k k k k k k k k ++=⎧⎪-+=⎨⎪+-=⎩ 解得1323192,95k k k k =-=,取35k =,得1219,2k k =-=使得 112321233123()(2322)(355)0k k k ααααααααα+++-+++-=故123123123,2322,355ααααααααα++-++-线性相关.5、已知向量组1234,,,αααα线性无关,证明向量组12233441,,,αααααααα+++-也线性无关.证明:设112223334441()()()()0k k k k αααααααα++++++-=则141122233344()()()()0k k k k k k k k αααα-++++++=因为1234,,,αααα线性无关,所以141223340000k k k k k k k k -=⎧⎪+=⎪⎨+=⎪⎪+=⎩解得12340k k k k ====,故12233441,,,αααααααα+++-线性无关.6、设12,,,s ααα均为n 维列向量,A 是n n ⨯矩阵,试证明: (1)若12,,,s ααα线性相关,则12,,,s A A A ααα也线性相关;(2)若A 可逆,且12,,,s A A A ααα线性相关,则12,,,s ααα也线性相关.证明:(1)因为12,,,s ααα线性相关,所以存在不全为零的数12,,,s k k k ,使得1122440k k k ααα+++=从而有11221122()00s s s s k A k A k A A k k k A αααααα+++=+++==故12,,,s A A A ααα线性相关.(2)因为12,,,s A A A ααα线性相关,所以存在不全为零的数12,,,s k k k ,使得1122440k A k A k A ααα+++=从而有11221122()0s s s s A k k k k A k A k A αααααα+++=+++=由A 可逆,得1122440k k k ααα+++=.故12,,,s ααα线性相关.7、已知向量组123,,ααα与122331,,αααααα+++ (1)证明123,,ααα与122331,,αααααα+++等价;(2)证明123,,ααα线性相关的充分必要条件是122331,,αααααα+++线性相关.证明:(1)首先,122331,,αααααα+++显然可由123,,ααα线性表示. 其次,由1122331212233131223311[()()()]21[()()()]21[()()()]2ααααααααααααααααααααα⎧=+-+++⎪⎪⎪=+++-+⎨⎪⎪=-+++++⎪⎩可知,123,,ααα可由122331,,αααααα+++线性表示. 故123,,ααα与122331,,αααααα+++等价.8、已知非齐次线性方程组123423423412340221(3)21321x x x x x x x x a x x x x x bx + + +=⎧⎪ ++=⎪⎨ - +--=-⎪⎪+ ++=-⎩ 有3个线性无关的解,证明:系数矩阵A 的秩等于2,并求,a b 的值及方程组的通解.证明:设123ξξξ,,是方程组的3个线性无关解,则1213ξξξξ--,是导出组0AX =的两个解.若1213()()0k l ξξξξ-+-=,则有123()0k l k l ξξξ+--=,于是由123ξξξ,,线性无关可得0k l ==,所以1213ξξξξ--,是导出组0AX =的两个线性无关解,因此,0AX =的基础解系所含向量个数不少于2,即有4()2A -≥秩. 所以有()2A ≤秩.因为系数矩阵111101220132321A a b ⎛⎫ ⎪⎪= ⎪--- ⎪⎝⎭,有一个2阶子式111001=≠,所以有()A ≤2秩,故()=2A 秩.对增广矩阵A 做行初等变换,有313242311110111100122101221=013210132132110123111110012210010000010r r r r r r A a a b b a b -++⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪−−−→ ⎪ ⎪-------- ⎪ ⎪-----⎝⎭⎝⎭⎛⎫⎪⎪−−−→ ⎪- ⎪-⎝⎭于是由()=2A 秩,有1010a b -=⎧⎨-=⎩,即11a b =⎧⎨=⎩.因此有31324212311110111100122101221=012210122132111012211111010111012210122100000000000000000000r r r r r r r r A -++-⎛⎫⎛⎫⎪ ⎪⎪ ⎪−−−→⎪⎪--------⎪ ⎪-----⎝⎭⎝⎭---⎛⎫⎛⎫⎪⎪⎪ ⎪−−−→−−−→ ⎪ ⎪⎪⎪⎝⎭⎝⎭故方程组的通解为1342341122x x x x x x =-++⎧⎨=--⎩.9、设12,,,n ααα均为n 维线性无关列向量,A 是n n ⨯矩阵,试证明:12,,,n A A A ααα线性无关⇔A 可逆.证明:(⇒)因为12n ααα,,,线性无关,所以以12n ααα,,,为列的n n ⨯矩阵12()n B ααα=可逆.因为12,,,n A A A ααα线性无关,所以矩阵1212()()n n C A A A A AB αααααα===可逆,从而1A CB -=可逆.(⇐)若有数12n k k k ,,,,使得11220s n k A k A k A ααα+++=则有1122()0n n A k k k ααα+++=由A 可逆可得11220s n k k k ααα+++=因为12,,,n ααα线性无关.所以120n k k k ====,故12,,,nA A A ααα线性无关.。
第三章作业参考答案

第三章本-量-利分析一、单项选择题1.不是本量利关系基本公式的是( A )。
A.利润=单位贡献毛益×销售量-变动成本B.利润=单价×销售量-(销售量×单位变动成本+固定成本)C.利润=销售收入×贡献毛益率-固定成本D.利润=销售收入-固定成本-变动成本2.下列等式不成立的是( B )。
A.安全边际率+盈亏临界点作业率=lB.安全边际率+贡献毛益率=1C.变动成本率+贡献毛益率=lD.贡献毛益率×安全边际率=销售利润率3.某企业生产产品A,单位变动成本10元,年产销量均为5 000件,年固定成本10 000元,单位售价15元,则总的贡献毛益为( C )。
A.5 000 B.15 000 C.25 000 D.115 000 4.某企业只生产销售一种产品,该产品单位售价8元,单位变动成本5元,年固定成本为30 000元,则该产品的盈亏临界点销售额为( D )元。
注意:销售额与销售量的区别A.10 000 B.30 000 C.50 000 D.80 0005.其他条件不变,单价提高,则盈亏临界点( C )。
A.提高 B.不变 C.下降 D.A、B、C都有可能6. 在各种盈亏临界图中,( B )更符合变动成本法的思路。
A. 传统式B. 贡献毛益式C. 利量式D.单位式7.某产品的单价为10元,单位变动成本为5元,固定成本为20 000元,目标净利润为13 400元,所得税率为33%,则实现目标净利润的销售量为( A )。
【13400/(1-33%)+20000】/5A.8 000件 B.6 680件 C.8 0000件 D.66 800件8.正常盈利情况下,对利润最敏感的因素是( C )。
A.单位变动成本 B.固定成本 C.单价 D.销售量二、多项选择题1.其他因素不变时,会引起企业利润上升的有( ABCD )。
A.单价上升 B.销量增加C.单位变动成本下降 D.固定成本下降2.下列因素上升时,会导致盈亏临界点上升的因素为( BC )。
计量经济学第三章练习题及参考全数解答

第三章练习题及参考解答为研究中国各地域入境旅行状况,成立了各省市旅行外汇收入(Y ,百万美元)、旅行社职工人数(X1,人)、国际旅行人数(X2,万人次)的模型,用某年31个省市的截面数据估量结果如下:ii i X X Y 215452.11179.00263.151ˆ++-= t= R 2= 92964.02=RF= n=311)从经济意义上考察估量模型的合理性。
2)在5%显著性水平上,别离查验参数21,ββ的显著性。
3)在5%显著性水平上,查验模型的整体显著性。
练习题参考解答:(1)由模型估量结果可看出:从经济意义上说明,旅行社职工人数和国际旅行人数均与旅行外汇收入正相关。
平均说来,旅行社职工人数增加1人,旅行外汇收入将增加百万美元;国际旅行人数增加1万人次,旅行外汇收入增加百万美元。
这与经济理论及体会符合,是合理的。
(2)取05.0=α,查表得048.2)331(025.0=-t因为3个参数t 统计量的绝对值均大于048.2)331(025.0=-t ,说明经t 查验3个参数均显著不为0,即旅行社职工人数和国际旅行人数别离对旅行外汇收入都有显著阻碍。
(3)取05.0=α,查表得34.3)28,2(05.0=F ,由于34.3)28,2(1894.19905.0=>=F F ,说明旅行社职工人数和国际旅行人数联合起来对旅行外汇收入有显著阻碍,线性回归方程显著成立。
表给出了有两个说明变量2X 和.3X 的回归模型方差分析的部份结果:表 方差分析表1)回归模型估量结果的样本容量n 、残差平方和RSS 、回归平方和ESS 与残差平方和RSS 的自由度各为多少?2)此模型的可决系数和调整的可决系数为多少? 3)利用此结果能对模型的查验得出什么结论?可否确信两个说明变量2X 和.3X 各自对Y 都有显著阻碍?练习题参考解答:(1) 因为总变差的自由度为14=n-1,因此样本容量:n=14+1=15因为 TSS=RSS+ESS 残差平方和RSS=TSS-ESS=66042-65965=77 回归平方和的自由度为:k-1=3-1=2 残差平方和RSS 的自由度为:n-k=15-3=12(2)可决系数为:2659650.99883466042ES RTSS S === 修正的可决系数:222115177110.998615366042i i e n R n k y --=-=-⨯=--∑∑ (3)这说明两个说明变量2X 和.3X 联合起来对被说明变量有很显著的阻碍,可是还不能确信两个说明变量2X 和.3X 各自对Y 都有显著阻碍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章练习题及参考解答3.1 第三章的“引子”中分析了,经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”等变量,2011年全国各省市区的有关数据如下:表3.6 2011年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2012.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果?3) 你认为模型还可以如何改进?【练习题3.1参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++回归结果如下:由F 统计量为17.87881, P 值为0.000001,可判断模型整体上显着, “人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”等变量联合起来对百户拥有家用汽车量有显着影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“交通工具消费价格指数”分别对百户拥有家用汽车量都有显着影响。
2)X2的参数估计值为5.9911,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近6辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.5231,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.5231辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-2.2677,表明随着家用汽车使用成本的提高, “交通工具消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少2.2677辆。
3)模型的可决系数为0.6652,说明模型中解释变量变解释了百户拥有家用汽车量变动的66.52%,还有33.48%未被解释。
影响百户拥有家用汽车量的因素可能还有交通状况、社会环境、政策因素等,还可以考虑纳入一些解释变量。
但是使用更多解释变量或许会面临某些基本假定的违反,需要采取一些其他措施。
3.2 表3.7是1994年-2011年中国的出口货物总额(Y)、工业增加值(X2)、人民币汇率(X3)的数据:表3.7 出口货物总额、工业增加值、人民币汇率数据资料来源: 中国统计年鉴2012.中国统计出版社.1)建立出口货物总额计量经济模型: 12233t t t t Y X X u βββ=+++,估计参数并对模型加以检验。
2)如果再建立如下货物总额计量经济模型: 12233ln ln t t t t Y X X u ααα=+++,估计参数并对模型加以检验。
3)分析比较两个模型参数估计结果的经济意义有什么不同。
【练习题3.2参考解答】建议学生独立完成3.3 经研究发现,家庭书刊消费受家庭收入及户主受教育年数的影响,表中为对某地区部分家庭抽样调查得到样本数据:表3.8 家庭书刊消费、家庭收入及户主受教育年数数据1) 作家庭书刊消费(Y )对家庭月平均收入(X )和户主受教育年数(T )的多元线性回归:123i i i i Y X T u βββ=+++利用样本数据估计模型的参数,对模型加以检验,分析所估计模型的经济意义和作用。
2)作家庭书刊消费(Y )对户主受教育年数(T )的一元回归,获得残差E1;再作家庭月平均收入(X )对户主受教育年数(T )的一元回归,并获得残差E2。
3)作残差E1对残差E2的无截距项的回归:212i E E v α=+,估计其参数。
4)对比所估计的2ˆβ和2ˆα后,你对家庭书刊消费(Y )对家庭月平均收入(X )和户主受教育年数(T )的多元线性回归的参数的性质有什么认识?【练习题3.3 参考解答】:1)作回归 123i i i i Y X T u βββ=+++ ,结果为:检验:模型f 统计量显着、各解释变量参数的t 检验都显着.估计结果表明家庭月平均收入(X )每增加1元,家庭书刊消费(Y )平均将增加0.08645元。
户主受教育年数(T )每增加1年,家庭书刊消费(Y )平均将增加52.37031元。
2)作家庭书刊消费(Y )对户主受教育年数(T )的一元回归,获得残差E1生成E1=RESID作家庭月平均收入(X )对户主受教育年数(T )的一元回归,并获得残差E2:生成E2=RESID3)作残差E1对残差E2的无截距项的回归:212i E E v α=+,估计其参数4)对比:所估计的2ˆ0.08645β=和2ˆ0.08645α=,这正说明了多元回归中的2ˆβ是剔除户主受教育年数(T )的影响或者说保持户主受教育年数(T )不变的情况下,家庭月平均收入(X )对家庭书刊消费(Y )的影响,也就是偏回归系数。
3.4为了分析中国税收收入(Y )与国内生产总值(X2)、财政支出(X3)、商品零售价格指数(X4)的关系,利用1978-2007年的数据,用EViews 作回归,部分结果如下:表3.9 回归结果Dependent Variable: LNY Method: Least SquaresDate: 06/30/13 Time: 19:39 Sample: 1978 2007Included observations: 30VariableCoeffic ientStd. Error t-StatisticProb.C-2.75530.6400.000267080LNX20.4512343.1748310.0038LNX30.6271330.1615660.0006X40.0056451.7955670.0842R-squared0.987591 Mean dependent var8.341376Adjusted R-squared S.D. dependent var 1.357225S.E. of regression Akaike info criterion-0.707778Sum squared resid 0.662904Schwarz criterion-0.520952Log likelihood14.61668F-statisticDurbin-Watson stat 0.616136Prob(F-statistic)0.00000填补表中空缺的数据,并分析回归的结果,并评价所估计参数的经济意义。
【练习题3.4参考解答】建议学生独立完成3.5 已知某商品的需求量(Y)、价格(X 2)和消费者收入(X 3),下表给出了解释变量2X 和.3X 对Y 线性回归方差分析的部分结果:表3.10 方差分析表1)回归模型估计结果的样本容量n 、来自回归的平方和(ESS)、回归平方和ESS 与残差平方和RSS 的自由度各为多少?2)此模型的可决系数和修正的可决系数为多少?3)利用此结果能对模型的检验得出什么结论?能否认为模型中的解释变量2X 和3X 联合起来对某商品的需求量Y 的影响是否显着?本例中能否判断两个解释变量2X 和3X 各自对某商品的需求量Y 也都有显着影响?【练习题3.5参考解答】:1) n=19+1=20来自回归的平方和(ESS)的自由度为k-1=3-1=2残差平方和RSS 的自由度为 n-k=20-3=172) 可决系数∑∑--=-=-=222)(11Y Y e TSS RSS TSS RSS TSS R ii=377067.19+70895.00=447962.192R =212011(1)1(10.8417)0.8231203n R n k ----=--=-- 3) F=188533.60/4170.2941=45.2087或者 F =222030.841745.1955113110.8417n k R k R --⋅=⨯=---- 所以可以认为模型中的解释变量2X 和3X 联合起来对某商品的需求量(Y)的影响显着但是,判断判断两个解释变量2X 和.3X 各自对某商品的需求量Y 也都有显着影响需要t 统计量,而本例中缺t 统计量,还不能作出判断。
3.6为了分析居民银行存款变动的趋势,由《中国统计年鉴》取得1994年-2011年居民年底存款余额、城镇居民家庭人均可支配收入、农村居民家庭人均纯收入、国民总收入、人均GDP 、居民消费价格总指数等数据:表3.11 居民年底存款余额等数据资料来源: 中国统计年鉴2011.中国统计出版社.1)如果设定线性回归模型:12233445566t t Y X X X X X u ββββββ=++++++,你预期所估计的各个参数的符号应该是什么?2)用OLS 法估计参数,模型参数估计的结果与你的预期是否相符合?对这个计量模型的估计结果你如何评价?3) 如果另外建立线性回归模型:15566t t Y X X u βββ=+++,用OLS 法估计其参数,你对该模型有什么评价?【练习题3.6参考解答】建议学生独立完成3.7在第二章练习题2.7的基础上,联系自己所学的专业将模型改造成多元线性回归模型,并自己去收集样本数据,用本章的方法估计和检验这个多元线性回归模型,你如何评价自己所做的这项研究?【练习题3.7参考解答】本题无参考解答。
