用对偶单纯形法求解线性规划问题
管理运筹学多选 简答

管理运筹学多选 简答多选:3.对取值无约束的变量x j 通常令x j =x j ′- x j 〞,其中x j ′≥0,x j 〞≥0,在用单纯形法求得的最优解中,不可能出现的是最后的情形。
4.线性规划问题maxZ=X 1+CX 2其中4≤c≤6,一1≤a≤3,10≤b≤12,则当c=6 a=-1 b=10和c=4 a=3 b=12时,该问题的最优目标函数值分别达到上界或下界。
9.下列数学模型,只有B 为非线性规划模型(模型中a .b .c 为常数;θ为可取某一常数值的参变量,x ,Y 为变量),因为它所表达的列变量是不够的。
10.下列模型中,不属于线性规划问题的标准形式的是前三个模型,只有最后一个才是标准的。
4.在下图中,根据(a ) 生成的支撑树有三个b 、c 、d ,如下:7.在下图各边中,平行边有e 1 、 e 2、 e 5 、 e 6, e 1等边则是非平行边。
下列知识点可出简答题1. 简答:运筹学的数学模型有哪些优点?答:(1)通过模型可以为所要考虑的问题提供一个参考轮廓,指出不能直接看出的结果。
(2)节省时间和费用。
(3)模型使人们可以根据过去和现在的信息进行预测,可用于教育训练,训练人们看到他们决策的结果,而不必作出实际的决策。
( 4)数学模型有能力揭示一个问题的抽象概念,从而能更简明地揭示出问题的本质。
(5)数学模型便于利用计算机处理一个模型的主要变量和因素,并易于了解一个变量对其他变量的影响。
这些都是使得运筹学能够快速发展的有利条件。
2. 简答:运筹学的系统特征是什么?答:运筹学的系统特征可以概括为以下四点:(1)用系统的观点研究功能关系(2)应用各学科交叉的方法(3)采用计划方法(4)为进一步研究揭露新问题。
新发现的问题,可能要求用修正过去的模型、输入新的数据以及调整以前类似项目的解,获得解决。
6.简答:根据已知条件建立线性规划数学模型某工厂生产A 、B 、C 三种产品,每种产品的原材料消耗量、机械台时消耗量以及这些资源的限量,单位产品的利润如下表所示:根据客户订货,三种产品的最低月需要量分别为200,250和100件,最大月销售量分别为250,280和120件。
河北1233工程大学运筹学试题及答案

河北工程大学~学年第学期期末考试试卷题号一二三四五六七八九十总分评分评卷教师一、写出下列线性规划问题的对偶问题:(8 分)MIN Z5X1 6 X 27 X 3X15X 23X315约束条件5X1 6X2 10X3 20X1X 2X35X10, X20, X 3不受限制二、用图解法求解下列线性规划问题:(10 分)MAX Z10X15X 23X14X 29约束条件 5 X12X 28X1, X20三、用沃戈法求下列运输问题的初始基本可行解(12 分)销地甲乙丙丁产量产地1412411162210391038511622销量814121448四、用对偶单纯形法求解线性规划问题:(12 分)MIN Z 4X112X218X3X13X33约束条件2X2 2X35X130五、某公司安排五名工作人员到五个不同岗位上工作。
但必须对上岗人员进行培训。
由于五名工作人员的经历不同,文化水平也有差异,故所需培训时间也不相同。
如下表所示培工训B1B2B3B4B5时作人间员A7598111A29127119A854693A736964A5467511问如何分配这五名人员的工作,使总的培训时间最短(12 分)六、若某产品中有一外购件,年需求量为10000件,单价为100 元。
由于该件可在市场采购,故定货提前期为零,并设不允许缺货。
已知每组织一次采购需2000 元,每年每件的存贮费为该件单价的10%,试求经济定货批量及每年的最小存贮加上采购的总费用。
(10 分)七、、某工程项目各项活动的逻辑关系如表所示,试绘制网络图,并确定关键路线。
(12 分)工序名称紧前工序花费时间(天)A—3B—2C—2D—2E B2F C2G F、 D3H A、E、G4八、已知线性规划问题:( 12 分)MAX Z 2X1X2X3X1X2X36约束条件X12X24X1,X2,X30用单纯形法求解得最终单纯形表如下表所示:X1X X X X 2345X61111O1X51003111 C-Z-3-1-2j j试说明分别发生下列变化时,新的最优解是什么( 1)目标函数变为 MAX Z= 2X123+3X +X6 3(2)约束条件右项由变为44九、已知赢得矩阵为1 7 13A0 29 试用图解法求解此对策。
(完整版)对偶单纯形法详解

一、什么是对偶单纯形法?
对偶单纯形法是应用对偶原理求解原始 线性规划的一种方法——在原始问题的单 纯形表格上进行对偶处理。
注意:不是解对偶问题的单纯形法!
二、对偶单纯形法的基本思想 1、对“单纯形法”求解过程认识的提升— —
从更高的层次理解单纯形法 初始可行基(对应一个初始基本可行解)
3 4
x1, x2 , x3, x4, x5 0
以此形式进行列表求解,满足对偶单纯形 法的基本条件,具体如下:
CB
XB
0
x4
0
x5
cj -2 -3 -4 0 0
xj b
x1 x2 x3 x4 x5
-3
-1 -2 -1 1 0
-4
-2 1 -3 0 1
-Z
0
-2 -3 -4 0 0
比
值 -2/-2 --- -4/-3 --- ---
2/5
11/5
-2 -3 -4 0 0 x1 x2 x3 x4 x5
0 1 -1/5 -2/5 1/5 1 0 7/5 -1/5 -2/5
cj-zj
0
0 0 -3/5 -8/5 -1/5
最优解: X*=(11/5,2/5, 0, 0, 0)T,
最优值: minW= -maxZ* = -[11/5×(-2)+2/5×(-3)]= 28/5
将三个等式约束两边分别乘以-1,然后
列表求解如下:
CB
XB
0
y3
0
y4
0
y5
-Z
比
cj yj b
-3 -9 0 y1 y2 y3
00 y4 y5
-2
-1 -1 1 0 0
运筹学作业2(清华版第二章部分习题)答案

运筹学作业2(第二章部分习题)答案2.1 题 (P . 77) 写出下列线性规划问题的对偶问题:(1)123123123123123m ax 224..34223343500,z x x x s t x x x x x x x x x x x x =++⎧⎪++≥⎪⎪++≤⎨⎪++≤⎪≥≥⎪⎩无约束,;解:根据原—对偶关系表,可得原问题的对偶规划问题为:123123123123123m ax 235..223424334,0,0w y y y s t y y y y y y y y y y y y =++⎧⎪++≤⎪⎪++≤⎨⎪++=⎪≥≤≤⎪⎩(2)1111m in ,1,,,1,,0,1,,;1,,m n ij ij i j n ij ij i j nij ij j j ij z c x c x a i m c x b j nx i m j n====⎧=⎪⎪⎪==⎪⎨⎪⎪==⎪⎪≥==⎪⎩∑∑∑∑ 解:根据原—对偶关系表,可得原问题的对偶规划问题为:11m ax 1,,;1,,m n i i j ji j i j ij i w a u b v u v c i m j n u ==⎧=+⎪⎪⎪+≤⎨⎪==⎪⎪⎩∑∑ j 无约束,v 无约束2.2判断下列说法是否正确,为什么?(1) 如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解; 答:错。
因为:若线性规划的原问题存在可行解,且其对偶问题有可行解,则原问题和可行问题都将有最优解。
但,现实中肯定有一些问题是无最优解的,故本题说法不对。
例如原问题1212212m ax 31..30,0z x x x x s t x x x =++≥⎧⎪≤⎨⎪≥≥⎩有可行解,但其对偶问题1211212m in 33..10,0w y y y s t y y y y =+≥⎧⎪+≥⎨⎪≤≥⎩无可行解。
(2) 如果线性规划的对偶问题无可行解,则原问题也一定无可行解;答:错,如(1)中的例子。
《运筹学》试题及答案(六)

《运筹学》试题及答案(六)《运筹学》试题及答案第⼆章线性规划的基本概念⼀、填空题1.线性规划问题是求⼀个线性⽬标函数_在⼀组线性约束条件下的极值问题。
2.图解法适⽤于含有两个变量的线性规划问题。
3.线性规划问题的可⾏解是指满⾜所有约束条件的解。
4.在线性规划问题的基本解中,所有的⾮基变量等于零。
5.在线性规划问题中,基可⾏解的⾮零分量所对应的列向量线性⽆关6.若线性规划问题有最优解,则最优解⼀定可以在可⾏域的顶点(极点)达到。
7.线性规划问题有可⾏解,则必有基可⾏解。
8.如果线性规划问题存在⽬标函数为有限值的最优解,求解时只需在其基可⾏解_的集合中进⾏搜索即可得到最优解。
9.满⾜⾮负条件的基本解称为基本可⾏解。
10.在将线性规划问题的⼀般形式转化为标准形式时,引⼊的松驰数量在⽬标函数中的系数为零。
11.将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左_端加⼊松弛变量。
12.线性规划模型包括决策(可控)变量,约束条件,⽬标函数三个要素。
13.线性规划问题可分为⽬标函数求极⼤值和极⼩_值两类。
14.线性规划问题的标准形式中,约束条件取等式,⽬标函数求极⼤值,⽽所有变量必须⾮负。
15.线性规划问题的基可⾏解与可⾏域顶点的关系是顶点多于基可⾏解16.在⽤图解法求解线性规划问题时,如果取得极值的等值线与可⾏域的⼀段边界重合,则这段边界上的⼀切点都是最优解。
17.求解线性规划问题可能的结果有⽆解,有唯⼀最优解,有⽆穷多个最优解。
18.如果某个约束条件是“≤”情形,若化为标准形式,需要引⼊⼀松弛变量。
19.如果某个变量X j为⾃由变量,则应引进两个⾮负变量X j′,X j〞,同时令X j=Xj ′-Xj。
20.表达线性规划的简式中⽬标函数为max(min)Z=∑c ij x ij。
21..(2.1 P5))线性规划⼀般表达式中,a ij表⽰该元素位置在i⾏j列。
⼆、单选题1.如果⼀个线性规划问题有n个变量,m个约束⽅程(mA.m个 B.n个 C.Cn m D.Cmn个2.下列图形中阴影部分构成的集合是凸集的是 A3.线性规划模型不包括下列_ D要素。
线性规划课后题答案(张干宗)
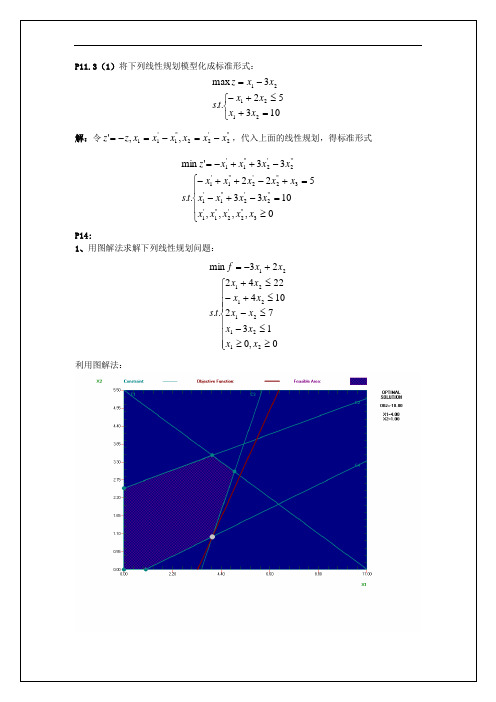
P11.3(1)将下列线性规划模型化成标准形式:⎩⎨⎧=+≤+--=10352..3max 212121x x x x t s x x z 解:令"2'22"1'11,,'x x x x x x z z -=-=-=,代入上面的线性规划,得标准形式⎪⎩⎪⎨⎧≥=-+-=+-++--++-=0,,,,1033522..33'min 3"2'2"1'1"2'2"1'13"2'2"1'1"2'2"1'1x x x x x x x x x x x x x x t s x x x x z P14:1、用图解法求解下列线性规划问题:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤-≤-≤+-≤++-=0,013721042242..23min 212121212121x x x x x x x x x x t s x x f 利用图解法:于是得最优解为(4,1),最优值为-10。
P15:2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥-≥+-=06063222..26max 21212121x x x x x x t s x x z 解:利用图解法于是最优解为(6,0),最优值为36。
P15.3⎪⎪⎩⎪⎪⎨⎧≥≥≥+≤+≤+--=0,0121272172..27min 21212121210x x x x x x x x t s x x x 解:利用图解法求得有无穷多最优解,都落在一个线段上,该线段的两个端点是:)3/7,3/7(),0,3()2()1(==x x于是全部的最优解可以表示成)1(x与)2(x的凸组合,即.10,)1()2()1(*≤≤-+=αααx x x最优值都是-21。
P16:1、 解:设ij x 表示第i 台机床加工第j 类产品的产量,于是可得数学模型⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤+≤+≤+≤++++++++++++++++=.6,5,4,3,2,1,0900600700850..)(80)(64)(72)(32)(28)(40max 464335322421161514131211461635152414431332122111j x x x x x x x x x x x x x t s x x x x x x x x x x x x f j P16:2、 解:设j x 表示第j 食品的采购量,于是可得数学模型13、某养鸡场有一万只鸡,用动物饲料和谷物饲料混合喂养,每天每只鸡平均吃混合饲料0.5公斤,其中动物饲料占的比例不得少于1/5。
《卫生管理运筹学》习题集

《卫生管理运筹学》习题集一、线性规划1.某医学院动物房饲养某种动物供教学与科研使用,设每头该种动物每天至少需700g蛋白质、30g矿物质、100mg维生素.现有5种饲料可供选用,各种饲料每千克营养成分含量及单价如表2-27所示:表2-27 各种饲料的营养素含量及价格饲料蛋白质(g)矿物质(g)维生素(mg) 价格(元/千克)1 3 1.0 0.5 0.22 2 0.5 1.0 0.73 1 0.2 0.2 0.44 6 2.0 2.0 0.35 18 0.5 0.8 0.8要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案(建立问题的线性规划模型,不求解).2.某食品厂用原料A、B、C加工成3种不同类型的食品甲、乙、丙.已知各种类型食品中A、B、C的含量,原料成本,各种原料每月的限制用量,3种食品的单位加工费及售价如表2-28所示:表2-28 3种原料与食品的相关数据食品原料成本每月限制用量原料甲乙丙(元/千克)(kg)A≥60%≥15% 2.00 2000B 1.50 2500C≤20%≤60%≤50% 1.00 1200加工费(元/千克)0.50 0.40 0.30售价(元/千克) 3.40 2.85 2.25问该厂每月生产这3种类型食品各多少千克,使得到的利润为最大?试建立这个问题的线性规划数学模型.3.用图解法求解下列线性规划问题,并指出各问题是具有唯一最优解、多重最优解、无界解或无可行解.(1)2146Min x x Z += 1 221≥+x x..t s 5.14321≥+x x 0,21≥x x (2)2184Max x x Z += 1022 21≤+x x..t s 8 21≥+-x x 0,21≥x x(3)21Max x x Z += 246821≥+x x12 6421-≥+x x4 2 2≥x0,21≥x x(4)2123Max x x Z -=1 21≤+x x..t s 42221≥+x x 0,21≥x x (5)2193Max x x Z += 223 21≤+x x 4 21≤+-x x..t s 6 2≤x 052 21≤-x x.t .s0,21≥x x(6)2143Max x x Z +=82 21≤+-x x12 2 21≤+x x12 2 21≤+x x0,21≥x x4.用单纯形法解线性规划问题 (1)2153Max x x Z +=4 1≤x12 2 2≤x 182321≤+x x0,21≥x x(2)322Min x x Z +-=2 2 321=+-x x x13 32≤-x x 2 32≤-x x0,,321≥x x x5. 表2-29中给出某线性规划问题计算过程中的一个单纯形表,目标函数为321228Max Z x x x ++=,约束条件为≤,表中4x 、5x 、6x 为松弛变量,表中解的目标函数值Z =14.表2-29 单纯形表.t .s.t .s.t .s(1)g a ~的值;(2)表中给出的解是否为最优解.6.用大M 法求解下列线性规划问题,并指出问题的解属于哪一类: (1)32154Max x x x Z ++=1823321≥++x x x4 2 21≤+x x5 321=-+x x x 0,,321≥x x x(2)3212Max x x x Z ++= 4224321≥++x x x 20 42 21≤+x x 16284 321≤++x x x 0,,321≥x x x (3)21Max x x Z +=.t .s.t .s246821≥+x x 1264 21-≥+x x 42 2≥x 0,21≥x x(4)432132Max x x x x Z -++= 15 32 321=++x x x 20 5 2 321=++x x x 10 2 4321=+++x x x x 0,,,4321≥x x x x (5)321436Min x x x Z ++= 30 1≥x 50 2≤x..t s 203≥x 120 321=++x x x0,,321≥x x x7.写出下列线性规划问题的对偶问题 (1)321210Max x x x Z ++=102 321≤++x x x..t s 20 4 321≤++x x x 0,,321≥x x x(2)43214323Min x x x x Z +-+=3432 4321≤++-x x x x.t .s.t .s543 432-≥++x x x 24732 4321=---x x x x01≥x ,04≤x ,2x 、3x 无约束 (3)321765Min x x x Z ---=153 5 321≥-+-x x x201065 321≤+--x x x5 321-=--x x x 01≤x ,02≥x ,3x 无约束 8.用对偶单纯形法求解下列线性规划问题: (1)321432Min x x x Z ++= 3 2 321≥++x x x..t s 43 2 321≥+-x x x 0,,321≥x x x (2)32123Min x x x Z ++=6 321≤++x x x4 31≥-x x 3 32≥-x x 0,,321≥x x x9.已知线性规划问题用单纯形法计算时得到的初始单纯形表及最终单纯形表如表2-30所示,请将表中空白处数字填上.表2-30 初始与最终单纯形表.t .s.t .s.t .s… … …10.某出版单位有4500个空闲的印刷工时和4000个空闲的装订工时,拟用于下列4种图书的印刷和装订.已知各种书每册所需的印刷和装订工时如表2-31所示:表2-31 4种图书的印刷与装订所需资源及利润设j x 为第j 种书的出版数(单位:千册),据此建立如下线性规划模型:432134Max x x x x Z +++=45483 4321≤+++x x x x..t s 403 2 4321≤+++x x x x 0,,,4321≥x x x x用单纯形法求解得最终单纯形表如表2-32所示,试回答下列问题(各问题条件互相独立):表2-32 最终单纯形表(1)据市场调查第4种书最多只能销5000册,当销量多于5000时,超量部分每册降价2元,据此找出新的最优解;(2)经理对不出版第2种书提出意见,要求该种书必须出2000册,求此条件下最优解;(3)作为替代方案,第2种书仍须出2000册,印刷由该厂承担,装订工序交别的厂承担,但装订每册的成本比该厂高0.5元,求新的最优解;(4)出版第2种书的另一方案是提高售价,若第2种书的印刷加装订成本合计每册6元,则该书售价应为多高时,出版该书才有利?二、特殊的线性规划1. 试述运输问题数学模型的特征,为什么模型的(nm+)个约束中最多只有(1-+nm)个是独立的?2. 如何把一个产销不平衡的运输问题(含产大于销和销大于产)转化为产销平衡的运输问题.3. 某药厂有三个生产基地A1、A2、A3,分别向四个地区医药公司B1、B2、B3、、B4供货,每个基地的产量和各公司的需要量(单位:吨)以及单位运费(百元)见表3-17.(1) 分别用西北角法和最小元素法求初始调动方案,并比较其费用;(2) 如何安排调运方案,使总费用最少?表3-17 药厂基地至医药公司的单位运费表B1 B2 B3 B4基地的产量(t)单位运费(单位:百元)A1A2A3医药公司的需要量(t)10 6 20 11 15 12 7 9 20 25 6 14 16 18 5 5 15 15 104. 已知某运输问题的产销平衡表,单位运价表及给出的一个调运方案分别见表3-18和表3-19.试判断所给出的调运方案是否最优?如果是最优,说明理由.如果不是最优,请给出最优调运方案.表3-18 单位运价表表3-19 产销平衡表及某一调运方案5. 已知某运输问题的产销平衡表,最优调运方案及单位运价表分别如表3-20和表3-21所示.由于从产地2至销地B 的道路因故暂时封闭,故需对表3-20的调运方案进行修正.试用尽可能方便的方法重新找出最优调运方案.表3-20 产销平衡表及某一调运方案表3-21 单位运价表6. 利用隐枚举法求解下面规划问题:12312312313123Max 4322534(1)433(2)s.t.1(3),,01Y x x x x x x x x x x x x x x =++-+≤⎧⎪++≥⎪⎨+≥⎪⎪=⎩或 7. 某医药公司拟在某省城东、西两个区设立门市部,共有5个位置A 1、A 2、A 3、A 4、A 5可供选用.不同位置所需的投资额及预期利润如表3-22所示.规定在东区A 1、A 2、A 3中至多选两点;在西区A 4、A 5中至少选一点,问如何选址可使预期总利润最大?表3-22 不同位置的投资、利润表门 市 部 A 1 A 2 A 3 A 4 A 5 总投资额(万元)投资额(万元)20 30 25 40 45 100年利润(万元)10252025308. 某校篮球队拟从编号为1,2,3, 4, 5, 6的六名预备队员中,选拔三名正式队员,要求他们的平均身高尽可能高.此外,入选队员尚须符合下列条件:① 至少有一名后卫;② 2号和5号只能入选一名;③ 最多入选一名中锋;④ 2号或4号入选,6号就不得入选.这些预备队员的有关情况见表3-23.试问:哪三名预备队员应当入选?只需建立数学模型.9. 指派问题的实质是什么?简述求解指派问题的匈牙利法基本原理. 10. 利用匈牙利法求解下列指派问题:4411(1).Min ij ij i j Y b x ===∑∑()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎩⎪⎪⎪⎨⎧====∑∑==161512111514161517161213121097:)4,3,2,1,(1,011s.t.4141ij ij j ij i ij b j i x x x 效率矩阵为4411(2).Max ij iji j Y a x ===∑∑()⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎩⎪⎪⎪⎨⎧====∑∑==1379111114134128711691715:)4,3,2,1,(1,011.s.t 4141ij ij j ij i ij a j i x x x 效率矩阵为11. 某医院的五位大夫A 1、A 2、A 3、A 4和A 5从家中直接出诊,各去五个家庭病床B 1、B 2、B 3、B 4 和B 5中的一个.从每位大夫的家到每个家庭临床的路程见表3-24.怎样安排他们的出诊任务,方能使其总路程最短?表3—24 路程表 表3—25 工作效率表表3-23 队员条件预备队员编号位置 身高(m ) 1 中锋 1.93 2 中锋 1.91 3 前锋 1.87 4 前锋 1.86 5 后卫 1.80 6后卫1.8512. 某中医院准备指派赵、钱、孙、李充当老中医大夫周、吴 、郑 、王的助手.根据过去的经验,他们在一起工作的效率如表3—25所示.如何搭配可使他们的总工作效率最高?13. 某医学院为了活跃学术气氛,决定下周举办能源、交通、材料和生物工程四个专题讲座.每个讲座在下周下午各举办一次,每个下午不许多于一个讲座.根据详细的调查资料,估计每天下午不能出席的学生人数如表3—26所示.试从缺席的学生人数最少着想,设计一个讲座日程表.14. 某医疗器械厂拟派四名推销员甲、乙、丙、丁各去四座城市A 、B 、C 、D 推销产品.由于这些推销员的能力和经验各不相同,他们去各地推销而使该厂获取的利润预计如表3—27所示.试制定可获最大利润的指派方案.表3—26 缺席人数表表3—27 利润表AB C D 利润(万元)甲 37 27 28 35 乙 40 34 29 28 丙 33 24 32 35 丁28 322524(刘国旗)三、目标规划1.试述目标规划的数学模型与一般线性规划数学模型的相同和不同之处. 2.为什么求解目标规划时要提出满意解的概念,它同最优解有什么区别? 3.某医用器械厂生产甲、乙两种仪器,甲仪器每件可获利600元,乙每件可获利400元.生产过程中每件甲、乙所需台时数分别为2和3个单位,需劳动工时数分别为4和2个单位.设厂方在计划期内可提供机器台时数100个单位,B 1 B 2 B 3 B 4 B 5 路 程(km )A 1 11 14 24 21 21 A 2 14 19 15 29 25 A 3 20 17 7 28 11 A 4 10 18 16 15 19 A 51912192817周 吴 郑 王工作效率赵 11 9 10 1 钱 1 9 3 13 孙 5 8 5 12 李811011能源 交通 材料生物工程 缺 席 人 数星期一40 60 20 50 星期二 30 40 30 40 星期三 20 30 20 60 星期四 30 20 30 30 星期五20103010劳动工时数120个单位,如果劳动力不足尚可组织工人加班,厂领导制定了下列目标:(1) 计划期内利润达18 000元; (2) 机器台时数充分利用; (3) 尽量减少加班的工时数;(4) 甲产品产量达22件,乙产品产量达18件. 试给出该多目标问题的数学模型.4.地市级电视台考虑怎么安排娱乐、新闻和商业节目的播出时间,以获得最好效益.依据法律,该台每天允许广播12小时,其中商业节目用以赢利,每分钟可收入250美元,新闻节目每分钟需支出40美元,娱乐节目每播送一分钟消耗17.5美元.按法律规定,正常情况下商业节目只能占广播时间的20%,每小时至少安排5分钟新闻节目.问每天的广播节目该如何安排?优先级如下:P 1: 满足法律要求;P 2: 每天的纯收入最大.试建立该问题的目标规划模型.5. 用图解法找出下列目标规划问题的满意解:11233212111222123312(1)Min 2424s.t.28,0;,0(1,2,3)i i Z p d p d p d x x d d x x d d x x d d x x d d i +++-+-+-++-=++⎧-++-=⎪-+-=⎪⎨++-=⎪⎪≥≥=⎩ 13223111211122223312(2)Min ()62245s.t.515,0;,0(1,2,3)i i Z p d p d p d d x x d d x x d d x d d x x d d i +-+--+-+-++-=+++⎧++-=⎪++-=⎪⎨+-=⎪⎪≥≥=⎩ 112233412111222133124412(3)Min ()4002500s.t.3000.40.3240,0;,0(1,2,3,4)i i Z P d d P d P d x x d d x x d d x d d x x d d x x d d i ++---+-+-+-++-=+++⎧++-=⎪++-=⎪⎪+-=⎨⎪++-=⎪⎪≥≥=⎩ 6. 用单纯形法求解本章习题中第3题的解.7. 试用单纯形法求解下列目标规划:1122233123121112221233(1)Min ()211s.t.210810560;,0(1,2,3)ii i Z Pd P d d P d x x x x x d d x x d d x x d d x d d i +-+--+-+-++-=+++⎧++=⎪-+-=⎪⎪++-=⎨⎪++-=⎪⎪≥≥=⎩ 1122333123111232212333(2)Min ()360210s.t.200;,0(1,2,3)ii i Z p d p d p d d x x x d d x x x d d x x x d d x d d i -+-+-+-+-++-=+++⎧+++-=⎪-++-=⎪⎨+-+-=⎪⎪≥≥=⎩ 112233412111222123314412(3)Min ()244312s.t.82,0;,0(1,2,3,4)i i Z p d d p d p d x x d d x x d d x x d d x d d x x d d i ++-+-+-+-+-++-=+++⎧++-=⎪++-=⎪⎪++-=⎨⎪+-=⎪⎪≥≥=⎩ 8. 某企业生产两种产品A 、B ,产品A 售出后每件可获利10元,产品B 信出后每件可获利8元.生产每件产品A 需3小时的装配时间,每件产品B 需2小时的装配时间.可用的装配时间共计为每周120小时,但允许加班.在加班时间内生产的产品每件的获利分别降低1 元.加班时间限定每周不超过40小时,企业希望总获利最大.试凭自己经验确定优先级别,并建立该问题的目标规划模型.(刘国旗)四、动态规划1.如图5-3所示,求从始点A到终点E的最短路线及其长度.图5-3 A到E的线路图2.某药厂有五套新设备,拟分配给所属的三个车间.各车间将不同套数的设备投入生产后,每年创造的产值(单位:万元)如表5-44所示.表5-44 不同设备的产值表问应怎样分配这五套新设备,才能使整个药厂所获得的总产值最大,并求最大总产值.3.有一部货车给某医药公司4个零售点共卸下6箱药物,各零售点出售该药物所得的利润如表5-45所示.求在各零售点各卸下几箱药物,才能使所获得的总利润最大?并求最大总利润.表5-45 不同零售点的利润表4.某药厂根据市场的要求,明年头6个月的交货任务如表5-46所示.表中数字为月底的交货量.该厂的生产能力为每月400件,该厂仓库的存储能力为300件,已知每百件货物的生产费用为10000元,在进行生产的月份工厂要支出管理费4000元,仓库保管费为每百件货物每月1000元,假定开始时及6月底交货后无存货,问每月各应生产多少件产品,才能既满足交货任务又能使总费用最少?表5-46 需求量表5.某药厂生产一种药品,该产品在来年前四个月的估计销售量如表5-47所示.该项药品的生产准备费为每批500元,每件的生产费为1元,每件的存储费为每月1元.假定1月初的存货为100件,5月初的存货为0件,求该厂在这四个月内的最优生产计划.表5-47 销售量表6.某医药公司考虑为某种新产品定价,该产品的单价拟从每件5元、6元、7元、8元这四个价格中选其中一个,每年年初允许价格变动,但变动幅度不能超过1元.该公司预计该产品畅销只有五年,五年后将被淘汰,根据销售情况的预测,在价格不同的情况下各年的预计利润值如表5-48所示.请制定一条最优定价策略,使五年内所获利润总值最大.表5-48 预计利润值表(单位:万元)7.某药厂生产三种药品,各种药品的重量与利润如表5-49所示.现将这三种药品运往市场出售,运输能力总重量不超过6吨,问应如何安排,才能使总利润最大?表5-49 重量与利润值表8.某旅行者外出旅行,需将5件物品装入包中,包裹总重量不超过13千克.物品的单件重量及效用价值如表5-50所示.问如何装这些物品,才能使总价值最大?表5-50 重量与价值表9.如果要考虑某种医疗设备在今后4年内的更新问题,并且新的设备成本是6.7万元,使用t 年后的残值在t ≤ 4时,s (t )= 4- t ;t > 4时,s (t )=0;使用t 年后每年所创造的利润在t ≤ 4时,tt p +=14)(.开始时设备已使用了两年,其余数据不变,问每年年初应如何作出决策,才能使四年内所获得的总利润最大.五、网络分析与网络计划1.已知无向图1G ={1V ,1E }、2G ={2V ,2E }、3G ={3V ,3E }、4G ={4V ,4E },其中:1V ={1v ,2v ,3v ,4v ,5v },1E ={(1v ,2v ),(1v ,3v ),(1v ,4v ),(2v ,3v ),(2v ,4v ),(3v ,4v ),(3v ,5v ),(4v ,5v )}; 2V ={1v ,2v ,3v ,4v ,5v },2E ={(1v ,2v ),(2v ,3v ),(2v ,3v ),(3v ,4v ),(3v ,5v ),(4v ,5v )}; 3V ={1v ,2v ,3v ,4v },3E ={(1v ,2v ),(2v ,3v ),(2v ,3v ),(3v ,4v )}; 4V ={1v ,2v ,3v ,4v ,5v },4E ={(1v ,2v ),(2v ,3v ),(2v ,4v ),(3v ,5v ),(4v ,5v )}. (1)试求这四个图的图解,并判断是否连通图. (2)试问2G ,3G ,4G 是否1G 真子图和生成子图.(3)试判断1G 中1μ={1v ,2v ,3v ,4v ,5v }、2μ={1v ,2v ,3v ,4v ,5v ,3v ,1v }、3μ={1v ,2v ,3v ,5v ,4v ,1v }、4μ={1v ,3v ,2v ,4v ,3v ,5v }是否为开链、闭链、初等链、圈.2.有向图D =(V ,A ),其中:V ={1v ,2v ,3v ,4v ,5v },A ={(1v ,2v ),(1v ,3v ),(2v ,4v ),(2v ,5v ),(3v ,2v ),(4v ,3v ),(4v ,5v )}. (1)试求D 及其基础图的图解.(2)试判断1μ={1v ,2v ,3v ,4v ,5v }、2μ={2v ,5v ,4v ,3v ,2v }、3μ={1v ,3v ,4v ,5v ,2v ,1v }4μ={1v ,3v ,2v ,4v ,3v ,2v ,5v }、5μ={2v ,4v ,3v ,2v ,}是否为开链、闭链、初等链、路、回路.3.分别用避圈法和破圈法求下列网络的的最小树: (1)(2)(3)4.在六个居民小区中建立一个有线电视网,假设各小区有线网建设费用仅与架线距离有关,六个小区相互间的距离(单位百米)见表6-12.试选择架线方案使有线电视网的建设费用最低.表6-12 六个小区相互间的距离(单位百米)5.在下列网络中:(1)用Dijkstra标号法求从S点到T点的最短距离以及最短路;(2)用逐次逼近法求S点到各点的最短距离以及最短路.图习题6-56.在下列网络中试求v1到各点的最短距离.7.某零件生产经毛胚、机加工、热处理和检验四道工序,在满足同样的技术要求前提下,各道工序有不同的实施方案,其费用(元)如表6-13,试确定一个生产费用最低的加工方案.表6-13 各道工序不同的实施方案及其费用8.在下面网络中,弧旁的括号标注了弧的容量和流量.试求(1)所有的截集及截量;(2)最大流;(3)最小截集.9.试求下面网络中v (f )=4的最小费用流,图中弧旁数字为(ij b ,ij r ).10.试求下面网络的最小费用最大流,图中弧旁数字为(ij b ,ij r ).图习题6-1011.表6-14给出某运输问题的产销平衡表与单位运价表,将此问题转化为最小费用最大流问题.画出网络图并进行求解.表6-14 某运输问题的产销平衡表与单位运价表12.指出下列统筹图的错误,若有可能进行更正.图习题6-12(a)(b)(c)(d)13.根据作业明细表绘制网络图:(1)工序明细表见表6-15:表6-15 工序明细表(2)工序明细表见表6-16:表6-16 工序明细表14.已知网络图,计算(1)各结点的最早时间和最迟时间;(2)各工序的最早开工、最早完工、最迟开工和最迟完工时间.图习题6-14-1图习题6-14-215.已知表6-17所列资料,要求:(1)绘制网络图;(2)计算各工序的最早开工、最早完工、最迟开工、最迟完工时间和总时差;(3)确定关键路线.表6-17 各工序的逻辑关系及时间16.已知一个车库基建工程的作业明细表如表6-18所示,要求:(1)工程从开始施工到全部结束的最短周期;(2)如果工序l拖10天,对整个工程有何影响;(3)如果工序j的工序时间由12天缩短到8天,对整个工程进度有何影响;(4)为保证整个工程进度在最短周期内完成,工序I最迟在哪天开工;(5)如果要求工程在75天完工,要不要采取措施?应从哪些方面采取措施?表6-18 车库基建工程的作业明细表17.在第16题中,试确定70天内完工,又使工程费用最低的施工方案.各工序的正常进度和赶工进度的工序时间及费用情况如表6-19.表6-19 各工序的正常进度和赶工进度的时间及费用18.某工程各工序的工序时间及需要人数如表6-20.现有人数10人,试确定工程完工时间最短的工程进度计划.表6-20 各工序的工序时间及需要人数19.某计划项目的资料如表6-21,要求:(1)绘制网络图并计算每个工序的期望时间和方差以及总工期的期望和方差;(2)分别判断总工期提前3天完成以及延迟不超过5天完成的可能性大小.表6-21 项目的有关资料六、存贮1.为什么要进行存贮管理?2.存贮管理中两个主要的决策变量是什么?3.说明存贮管理中各种费用的含义.4.简要说明解决存储问题的5个步骤.5.基本经济订货模型的适用条件是什么?6.利用计算机模拟解决存贮问题的优点和缺点是什么?7.某医院需要某种人工心脏瓣膜每月20只左右,每只年保存费用10元,订货后可立即到货,每次订货费75元.问每次最优订货量是多少?多长时间订货一次?年最小总存贮费用是多少?8.某防疫站每月需要某杀毒剂100千克,因为预防疾病的需要不允许缺货.供应科每天可以配制此杀毒剂20千克,每次启动配制费用为800元,每千克杀毒剂每天存贮费用为0.1元.问每次启动配制多少使存贮总费用最小?多少天启动配制一次?9.某医院需要某种人工关节每月50个,订货后很快就到货,使用每个人工关节获利50元,保存每个人工关节每年75元,但缺货造成收入损失较大,估计为每个每年720元.问每月最优订货量是多少?每年最低总存贮费用是多少?10.一个医院每月需要心脏起博器10个,医院进价是1000元/个,每次订货费用是50元,存贮费用是货价的12%.问你还需要什么信息来计算最优订货量?假如符合基本EOQ模型,最低总存贮费用和最优订货量各是多少?假如订货—到货间隔变成7天,存货为多少时就应该订货?11.医药商店每月售出200台理疗机,生产厂家每月可生产1000台,每台价格1000元.每年存贮费用是平均存货价值的10%,每次订货费用500元,每年365天营业.为了不使顾客失望,在缺货时从临近同类医药商店以每台1060元的价格购进卖给顾客,问最优订货量是多少?最小总存贮费用是多少?12.SARS流行期间,某市防疫站对从疫区归来人员进行监测,被监测人员自愿购买能提高免疫能力的中药煎剂预防SARS.每份煎剂成本10元,售出18元,但如防疫站订购过量,剩余的煎剂第二天作废.疫区归来人员中自愿购买煎剂的人数服从正态分布,平均数500人,标准差100人.问市防疫站订购多少份中药煎剂使经济损失为最小?七、排队1.某诊所只有一名医生,来就诊的患者人数服从泊松分布,平均每小时4人;医生诊断时间服从负指数分布,平均每人需12分钟,求:(1)诊所的各项工作指标;(2)患者不必等待的概率.2.某医院门诊部只有一名医生,病人平均20分钟到达一个,医生对每个病人的诊治时间平均为15分钟,上述两种时间均为负指数分布.若该门诊希望到达的病人90%以上能有座位,则该医院至少应设置多少个座位?3.某牙科诊所只有一位大夫和一个电动连体式牙科综合治疗仪,另备3个供患者排队等待的椅子.若一旦椅子坐满患者,后到的患者立即离开.患者按泊松流每小时到达1人,大夫为每位患者的诊疗时间服从负指数分布,平均为1.25小时.求:(1)患者到达便可看病的概率;(2)诊所里有1位或2位病人的概率;(3)系统其它运行指标.4.设某医院内科危重病房1位护士负责5个床位,病床经常住满.每个病人的需求服从泊松分布,平均每2小时1次,病人每次的护理时间服从负指数分布,平均为20分钟.试求:(1)没有病人需要护理的概率;(2)等待护理的病人平均数;(3)若该护士负责6个病人的护理,其它各项条件不变,则上述(1)(2)的结果又如何?(4)若希望至少45%时间内所有病人都不需要护理,求该护士最多负责护理的病人数.5.某医院机关文书室有3名打字员,每名打字员每小时能打6份文件.若该室平均每小时收到15份要打的文件.假设该室为M/M/C/∞/∞系统.(1)求3名打字员忙于打字的概率;(2)该室主要运行指标;(3)若打字员分工包打不同科室的文件,每名打字员都平均每小时接到5份文件,试计算此情况下该室的各项工作指标,并与(2)比较.6.某电话交换台的呼叫强度服从平均每分钟4次的泊松分布,最多有6条线同时通话,每次通话时间服从平均0.5分钟的负指数分布.呼叫不通时,呼叫自动消失.试求:(1)系统空闲的概率;(2)呼叫不通的概率;(3)平均通话线路数.7.某院一台血液分析仪每份血样检测时间为3分钟,血样按泊松分布平均每小时到达18份.试求主要工作指标和仪器空闲概率.8.某医院有一个取药窗口,患者按泊松分布平均每小时到达10人.药剂员发药时间(小时))~2t.试求该药房空闲的概率和其它运行指标.N(1.0,05.09.到达只有一名医生诊所的病人有两类:急诊病人和普通病人.当急诊病人到达时,医生将暂停正在治疗的普通病人而为其服务.同类型病人按FCFS服务规则进行.已知两类病人到达均服从泊松分布,急诊病人平均每天2人,普通病人每天6人;医生为两类病人治疗时间相同且服从负指数分布,平均每小时2人,若一天按8小时工作时间计算,试求:(1)两类病人分别在系统内的平均等待时间;(2)两类病人分别在系统内的平均队长.10.某工厂设备维修部要求维修的设备按泊松分布到达,平均每天17.5台.维修部工人每人每天平均维修10台,服从负指数分布.已知每名工人工资每天60元,因设备维修而造成的停产损失为每台每天300元.试确定该维修部的最佳工人数(停产损失费和工资支付费总和最小).八、决策分析1.某药厂要确定下一计划期内某药品的生产批量,根据经验并通过市场调查,已知药品销路好、一般和较差的概率分别为0.3、0.5和0.2,采用大批量生产可能获得的利润分别为20万元、12万元和8万元,中批量生产可能获得的利润分别为16万元、16万元和10万元,小批量生产可能获得的利润分别为12万元、12万元和12万元.试用最大可能准则和期望值准则进行决策.2.某农场种植了价值10000元的中药材,但目前因害虫的侵袭而受到严重的威胁,场长必须决定是否喷洒农药.喷洒农药将耗费1000元.如果他决定喷洒农药,只要一周内不下雨,就可以挽救全部药材;而如果一周内有雨,就只能挽救50%的药材.反之,如果他决定不喷洒农药,只要一周内不下雨,就将损失全部药材;若一周内有雨,就能自动救活60%的药材.试用最大可能准则和期望值准则进行决策.假设场部气象站估计一周内下雨的概率为0.7.3.某药厂决定某药品的生产批量时,调查了这一药品的销路好、销路差两种自然状态发生的概率,和大、中、小三种批量生产方案的投资金额,以及它们在不同销路状态下的效益值,如表9-8所示.试用决策树法进行决策.表9-8 不同方案在不同状态下的益损值(万元)方案投资金额药品销路2s (销路好) 7.0)(2=s P 3s (销路差) 3.0)(3=s P1a (大批量生产) 10 20 -15 2a (中批量生产) 8 18 -103a (小批量生产) 5 16 -84.某厂在产品开发中经过调查研究,取得如下有关资料:一开始就有引进新产品和不引进新产品两种方案.在决定引进新产品时,估计需投入科研试制费7万元,估计其它企业以相同产品投入市场参与竞争的概率为0.6,无竞争的概率为0.4.在无竞争的情况下,该厂有大规模生产、一般规模生产和小规模生产三种方案,其收益分别为20万元、16万元和12万元.在有竞争的情况下,该厂和竞争企业都有上述三种规模的生产方案,有关数据如表9-9所示.试用决策树法进行决策.表9-9 不同方案在不同状态下的益损值(万元)竞争企业生产规模 大 一般 小5.某地有10万人口,当地卫生机构拟对人群的某种疾病作一次检查.现在,需要就采用哪种检查方式的问题作出决策.有三种方式可供选择:第一,全体人口普查;第二,只检查高危人群;第三,所有的人都不检查.假设人群的疾病分布状况和预期的检查结果以及检查治疗费用的有关资料如表9-10、9-11所示.为了使总费用最少,应选择哪种方案?试用决策树来分析.表9-10 不同人群的检查结果实 际 情 况检查 高 危 险 组 低 危 险 组 结果 阳性 阴性 合计 阳性 阴性 合计阳性 1900 3600 5500 3040 15360 18400 阴性 100 14400 14500 160 61440 61660 合计 2000 18000 20000 3200 76800 80000表9-11 检查和治疗费用(元/人)项目 费用 全人口普查 3 重点检查 4 真阳性病人早期治疗 10 假阳性病人早期治疗 5 晚期治疗 1006.某医院制剂室生产某种药品有三种方案,大批量生产、中批量生产、小批量生产;该药品治疗的疾病情况也有三种:大流行、局部流行、不流行.出现哪种概率全然不知,获利情况如表9-12所示.试用乐观准则、悲观准则、折衷准则(7.0=λ)、后悔值准则进行决策.表9-12 不同方案在不同状态下的益损值(元)方 案自 然 状 态1s (疾病大流行) 2s (局部流行) 3s (不流行)1a (大批量生产) 600 400 -200 2a (中批量生产) 400 250 -1003a (小批量生产) 100 150 507.实施某一卫生服务计划,有4个可供选择的方案1a ,2a ,3a ,4a ,每个方案都面临三种可能的自然状态321,,s s s ,各相应的益损值如表9-13所示,假定不知道各自然状态发生的概率.试用各种准则进行决策.(折衷系数6.0=λ)表9-13 不同方案在不同状态下的益损值(万元)方 案自 然 状 态1s 2s 3s。
运筹学习题答案(第二章)

page 5 4/15/2021
School of Management
运筹学教程
第二章习题解答
minW b1y1 b2y2 bmym
m
aijyi
cj
( j 1,2,,n1)
对偶问题: stim1 aijyi cj
( j n1 1,n1 2,,n)
i1 yi 0
(i 1,,m1)
yi无约束( j m1 1,,m)
School of Management
运筹学教程
第二章习题解答
page 25 4/15/2021
max W 2 y 1 4 y 2 3 y 3
(1) 对偶问题:
3 y1 4 y 2 2 y 3 60
st
2 y1 y1 3
y2 y2
2 2
y3 y3
40 80
y 1 , y 2 , y 3 0
max Z x1 2 x2 x3
x1 x2 x3 2
st
x1 2 x1
x
2
x
2
x
3
x
1 3
2
.
x1 0, x2 0, x3无约束
(1)写出其对偶问题;(2)利用对偶问题性质证明 原问题目标函数值z≤1。
page 13 4/15/2021
School of Management
Cj-Zj
32 2 0 0 0
┆ ┆ ┆ ┆┆ ┆ ┆ ┆ ┆
0 X4 5/4 0 0 (d) (l) -1/4 -1/4
3 X1 25/4 1 0 (e) 0 3/4 (i)
2 X2 5/2 0 1 (f) 0 (h) 1/2
Cj-Zj
0 (k) (g) 0 -5/4 (j)
对偶单纯形法(经典运筹学)

解:问题化为标准型 max Z 2 x1 x 2 5 x1 x 2 x3 2 x 2 x3 x 4 5 s.t 6x xx 9 xx 2 2 6 x3 3 5 5 9 44 x1 , x 2 , x3,x 4,x5 0
X1 X2 X3 X4 X 5
2 检 0 1 -1 1 2 -4 0 -2 1 1 -6 0 0 1 0 0 0 0 1
Z Z-10
X1 1 X4 0
5 5 -9
X5 0
4
14 13 X1 X 2 X 3
检
X1 X4
0 1 0 0 0 0 0 1
X4
X5
-1/4 Z-31/4 1/4 1/2 11/4 1/2
所在行的基变量出基 则取br
4、以ari0 为主元素进行换基迭代 ,得一新的单纯形表, 转2
例:用对偶单纯形法 求解下列问题 max Z 2 x1 x 2 x1 x 2 x3 5 2x x 5 11 9 2 3 最优解 X ( ,) s.t 4 4 4 x 6 x 9 2 3 31 x1 , x 2 ,Z x3 0 最优值
-1/2 0 -1/2 0 -2 3/2 1 0
X2
-1/4 9/4
11 9 1 最优解 X ( ,, 0, , 0 ) 4 4 2 初始基 B (P ) 1,P 4,P 5 31 最优值 Z 不是典则形式 4
注意:对偶单纯形法仅限于初始基B对应 可用对偶单 的典则形式中目标函数的系数(检 纯形法 验数)均≤0的情形。 B的典则形式
对偶单纯形法是求解对偶规划的一种方法 × 对偶单纯形法:利用对偶理论得到的一个 求解线性规划问题的方法
单纯形法(原始单纯形法)的两个条件:
用对偶单纯形法求解线性规划问题

例4-7 用对偶单纯形法求解线性规划问题Min z =5x 1+3x 2X 1 - 6 x 2 A 4在表4-17中,b=-16<0,而yA 0,故该问题无可行解. 注意:对偶单纯形法仍是求解原问题 ,它是适用于当原问题无可行基 ,且所有检验数均为负的情况.若原问题既无可行基,而检验数中又有小于0的情况.只能用人工变量法求解.在计算机求解时,只有人工变量法,没有对偶单纯形法.3.对偶问题的最优解由对偶理论可知,在原问题和对偶问题的最优解之间存在着密切的关系 从求解原问题的最优单纯形表中,得到对偶问题的最优解.(1)设原问题(P)为Min z= exs.t.-2 X i + 3x 2 A 6A 0 (j=1,2 )解:将问题转化为 XjMax z = -5X 1 -3 x 2 s.t. 2x i - 3xX 3 = -6-3 x i + 6 X2+ x 4A -4Xj其中,X 3 , X 4 ,3,4 )A 0 (j=1,2 为松弛变量,可以作为初始基变量,单纯形表见表4-17.,可以根据这些关系,Xj > 0 (j=1,2 , 3,4 )则标准型 (LP) 为AX b s.t.X0Max z=CXAX b s.t.X0其对偶线性规划(D )为Max z=b T Y AX b s.t.X0用对偶单纯形法求解 时,有 Pj=-e i , c j =0 (LP ),得最优基B 和最优单纯形表 T ( B )。
对于(LP )来说,当j=n+iT (B )中,对于检验数,有(b n+1,b n+2・・・b n+m) = (C n+i , c n+2…,c n+m ) -C B B -1(Pn +1,Pn+2 …,Pn+m ) =- C B B -1(-I)于是,Y*= (b n+1,b n+2…b n+m T 。
可见,在(LP )的最优单纯形表中,剩余变 量对应的检验数就是对偶问题的最优解。
同时,在最优单纯形表 T ( B )中,由于剩余变量对应的系数 所以从而,在最优单纯形表b n +2 …bB 1 = ( -y n+1 , -y n+2 …-y n+m )例 4-8 求下列线性规划问题的对偶问题的最优解。
对偶单纯形法的条件

对偶单纯形法的条件对偶单纯形法是线性规划中一种重要的求解方法,主要用于解决线性规划问题的对偶问题。
它通过对原问题进行转化和运算,求解出对偶问题的最优解,从而得到原问题的最优解。
对偶单纯形法是基于单纯形法的扩展,具有更广泛的适用性和更高效的求解效果。
对于使用对偶单纯形法求解线性规划问题,需要满足以下条件:1. 原问题必须是标准形式的线性规划问题:目标函数为最小化形式,约束条件为等式形式,并且所有变量的取值范围为非负数。
2. 原问题必须存在可行基本解:可行基本解是指满足所有约束条件的解,可以通过单纯形法或其他方法求得。
3. 原问题的最优解必须有限:即原问题存在最优解,不是无界的。
在满足以上条件的基础上,使用对偶单纯形法求解线性规划问题的步骤如下:步骤一:建立对偶问题根据原问题的约束条件和目标函数,建立对偶问题的目标函数和约束条件。
对偶问题的目标函数为原问题的约束条件的系数构成的向量与对偶变量的乘积之和,约束条件为原问题的目标函数的系数构成的向量与对偶变量之和等于对偶约束条件的系数构成的向量。
步骤二:初始化给定初始对偶变量的取值,通常取为0,然后计算初始对偶解。
步骤三:判断最优性根据当前对偶解,判断原问题的最优性。
如果原问题的最优性条件满足,则停止计算,得到最优解;否则,进行下一步。
步骤四:选择换入变量根据当前对偶解,选择换入变量。
具体方法是在对偶约束条件中,选择不满足约束条件且对偶变量目标函数系数最小的变量作为换入变量。
步骤五:选择换出变量根据换入变量,选择换出变量。
具体方法是在换入变量所对应的约束条件中,选择满足约束条件且使对偶解最小的变量作为换出变量。
步骤六:更新对偶解根据换入、换出变量,更新对偶解。
具体方法是用换入变量替换对应的换出变量,计算新的对偶解。
重复步骤三到六,直到原问题的最优性条件满足为止。
最终得到原问题的最优解和对偶问题的最优解。
对偶单纯形法的优点在于它能够通过解决对偶问题来求解原问题,从而减少了计算量,提高了求解效率。
对偶单纯形法无界解的判断标准

对偶单纯形法无界解的判断标准在线性规划领域,对偶单纯形法是一种常用的方法,用于求解线性规划问题。
在实际应用中,我们经常会遇到线性规划问题的无界解情况,对偶单纯形法的无界解判断标准成为了至关重要的问题。
本文将从深度和广度的角度对对偶单纯形法无界解的判断标准进行全面评估和探讨,以便读者能够更全面、深刻地理解这一概念。
让我们对对偶单纯形法做一个简要的概述。
对偶单纯形法是一种基于单纯形法的线性规划算法,通过不断迭代求解对偶问题的最优解来间接地求解原始问题的最优解。
对于一个线性规划问题,若原始问题存在最优解,则其对偶问题也存在最优解,且二者的最优值相等。
对偶单纯形法在实际应用中具有重要的价值。
接下来,让我们探讨对偶单纯形法无界解的判断标准。
对于一个线性规划问题,首先需要构建对偶问题并利用对偶单纯形法求解最优解。
当对偶问题的最优解存在且对应的原始问题的解为无界时,我们称其为原问题存在无界解。
对偶单纯形法无界解的判断标准主要包括以下几点:1. 主对偶定理:根据主对偶定理,如果原始问题存在最优解,则对偶问题也存在最优解,且二者的最优值相等。
若对偶问题存在无界解,则原始问题解为无界。
2. 对偶单纯形表的检验数:在对偶单纯形法的迭代过程中,我们需要对对偶单纯形表的检验数进行检查。
若检验数中存在正值,则说明对偶问题的解并非最优解,同时也可以说明原问题的解为无界。
3. 对偶问题的最优解判断:在对偶单纯形法的迭代过程中,需要判断对偶问题是否存在最优解。
若对偶问题不存在最优解,则原问题的解必为无界。
4. 原始问题的去线性化:通过对原始问题进行去线性化处理,得到一个辅助问题。
若辅助问题的解为有界,则原问题的解也必为有界;若辅助问题的解为无界,则原问题的解为无界。
以上是对偶单纯形法无界解的判断标准的几个关键点,通过这些判断标准,我们能够更清晰地判断原始问题的解是否存在无界。
在个人观点方面,我认为对偶单纯形法无界解的判断标准是线性规划领域中的重要问题之一。
运筹学习题答案注释(第2章)

运筹学习题答案及注释2.3 已知某求极大化线性规划问题用单纯形法求解时的初始单纯形表及最终单纯形表如表2-32所示,求表中各括弧内未知数的值。
注释:由题中初始单纯形表及、最终单纯形表,我们可以看出:在初始单纯形表中,先选x 1进基,选x 5出基,做变换;然后再选x 2进基,选x 6出基,做变换,则得到最终单纯形表。
2.7 给出线性规划问题。
max 432142x x x x z +++=st. ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤++≤++≤+≤++0,,,966283432132143221421x x x x x x x x x x x x x x x要求:(1)写出其对偶问题;(2)已知原问题最优解为X*=(2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
解:(1)其对偶问题为: min 43219668y y y y w +++=st. ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+≥++≥+++≥++0,,,9143224321314324321421y y y y y y y y y y y y y y y y(2)用单纯形法解原问题,将原问题化成标准形式如下:max 87654321000042x x x x x x x x z +++++++=st. ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥=+++=+++=++=+++0,,,,,,,96628387654321832174326215421x x x x x x x x x x x x x x x x x x x x x x x因此,可得如下单纯形表:因1≥0,所以选x 进基,因(10/3)/(5/3)≤3/1≤(8/3)/(1/3),故选x 出基,则得所以,最优解为:X*=(2,2,4,0,0,0,0,1),代入目标函数得z =16。
其对偶问题得最优解为:X*=(4/5,3/5,1,0,0,0,0,4/5),代入目标函数得w =16。
2.9 用对偶单纯形法求解下列线性规划问题。
对偶单纯形法(经典运筹学)

X1 X2 X3 X4 X5 检 X3 -2 -1 0 -3 -1 1 0 0 0 0 Z -3
X4
X5
-4 -3 0
1 2 0
1
0
0
1
-6
3
不 可 行
即max Z 2 x1 x2
3 3x1 x 2 x3 4 x 3x x4 6 1 2 s.t x5 3 x1 2 x 2 x1 , x 2 , x3 , x 4 , x5 0
-1/3 0 -1/3 0 2/3 1
X 3 X4 X5 0 -3/5 -2/5 Z+12/5 1 -1 -1 0
X2 0 X1 1
1 0
0 0
1/5 4/5 6/5 -2/5 -3/5 3/5
3 6 最优解X ( ,, 0, 0, 0 ) 5 5 最优值Z 12 5
则取xi0 为入基变量
1
1
令X N 0 得X B B b 0 得基本可行解 X 1 B b,0
1
1
1 、若所有的检验数 CN B 1 N 0 , 则X 1为最优解
2、检验数 C N C B B 1 N中存在一个分量 0, 且该分量对应的列 向量中所有的分量 0, 则目标函数值在可行解 域内无上界
1、确定出基变量: 设br =min{bi | bi <0} 则取br所在行的基变量 为出基变量 即取X4为出基变量 2、确定入基变量: 原则: 保持检验行系数≤0
i i0 设 min | a ri 0 a ri a ri 0
1 21 3
X1 检 -2/3 X3 -5/3 X2 4/3 X5 -5/3 X1 检 0 X3 0 X3 X4 0 -1/3 1 0 0
2、线性规划问题的对偶问题

3 y1 + y2 30
y 1, y 2 0
得到另外一个数学模型:
min s = 120 y1 + 50 y2
s.t. 4 y1 + 2y2 50 3 y1+ y2 30 (2.2)
y 1, y 2 0
模型(2.1)和模型(2.2) 既有区别又有 联系。联系在于它们都是关于家具 厂的模型并且使用相同的数据,区 别在于模型反映的实质内容是不同 的。模型(2.1)是站在家具厂经营者 立场追求销售收入最大,模型(2.2) 是则站在家具厂对手的立场追求所 付的租金最少。
max Z=2x1+3x2 s.t. 2x1+2x2 12 4x1 16 5x2 15 x1,x2 0
6 5 4 3 2 1 1 2 3 4 5 6 ① 2X+2y<=12 X=3 X=4
点(3,3)是最优解, z*=15 当A的资源变为13小 时,z*=16,说明A的边 际价格是1,即影子 价格是1。
约束条件右端项 目标函数变量的系数
目标函数变量的系数 约束条件右端项
• 例2-7:写出下列线性规划的对偶问题
min z=7x1+4x2-3x3 s.t. -4x1+2x2-6x3≤24 -3x1-6x2-4x3≥15 5x2+3x3=30 x1≤0,x2取值无约束,x3≥0
Max w=24y1+15y2+30y3
引入变量 y1 , y2’,y2” 写出对偶问题
max g = 5 y1+ 4y2’- 4y2” s.t. y1 +2y2’- 2y2” 2 y1 3 -y1 + y2’- y2” -5 y1, y2’,y2” 0
线性规划习题答案

习题一P .361. 一个毛纺厂用羊毛和兔毛生产A,B,C 三种混纺毛料,生产1单位产品需要的原料如下表所示.三种产品的单位利润分别是4,1,5.每月可购进的原料限额为羊毛8000单位,兔毛3000单位,问此毛纺厂应如何安排生产能获得最大利润?解:设生产A,B,C 三种产品的量分别是123,,x x x ,则模型为123123123123max 4538000..243000,,0z x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩2. 某饲料厂生产的一种饲料由6种配料混合配成.每种配料中所含营养成分A,B 以及单位配料购入价由下表所示.每单位饲料中至少含9单位的A,19单位的B.问饲料厂如何配方,使得饲料成本最低且满足要求?解:设每单位饲料中每种配料所需的量为()1,2,3,4,5,6i x i =,则有1234561345623456123456min 3530605027122229..33219,,,,,0z x x x x x x x x x x x s t x x x x x x x x x x x =+++++++++≥⎧⎪++++≥⎨⎪≥⎩4. 某产品的一个完整单位包括四个A 零件和三个B 零件.这两种零件(A 和B)由两种不同的原料制成,而这两种原料可利用的数量分别是100单位和200单位.三个车间进行生产,而每个车间制造零件的方法各不相同.下表中给出每个生产班组的原料耗用量和每一种零件的产量.目标是要确定每一个车间的生产班组数使得产品的配套数达到最大.解:设每个车间的生产组数分别为123,,x x x ,则可生产()()123123768594min ,43x x x x x x y ++++⎧⎫=⎨⎬⎩⎭个单位产品,则线性规划如下:123123123123123max 853*********..76845943,,0yx x x x x x s t x x x y x x x yx x x ++≤⎧⎪++≤⎪⎪++≥⎨⎪++≥⎪⎪≥⎩6. 设123,,,A A A 三地各有某种纺织原料90,30,70吨,需要调运给12345,,,,B B B B B 五地,后者各需要80,10,30,50,20吨.从()1,2,3i A i =到(1,2,3,4,5)j B j =的路程(千米)如下表所示.现要求设计一个调拨方案,使得总运输吨公里数最少.解: 设从()1,2,3i A i =运往()1,2,3,4,5j B j =的运量为ij x ,则线性规划模型为如下形式,其中ij c 表示从i A 到j B 的运价。
用对偶单纯形法求解线性规划问题

用对偶单纯形法求解线性规划问题对偶单纯形法是一种常用于求解线性规划问题的方法。
它通过对原始线性规划问题进行对偶化,将原问题转化为对偶问题,并通过迭代的方式逐步优化,最终得到最优解。
本文将详细介绍对偶单纯形法的基本原理和步骤,并通过一个实例来演示其具体应用。
对偶单纯形法的基本原理是基于线性规划的对偶性理论。
根据对偶性理论,对于原始线性规划问题的最优解,一定存在一个对偶问题,其最优解与原问题的最优解相等。
因此,我们可以通过求解对偶问题来得到原问题的最优解。
对偶问题的形式如下:最大化 W = b'y约束条件为:A'y ≤ c其中,A是原始线性规划问题的约束矩阵,b是原始问题的目标函数系数矩阵,c是原始问题的约束条件矩阵,y是对偶问题的变量向量。
对偶单纯形法的步骤如下:步骤1: 初始化将原始线性规划问题转化为标准型,并初始化基变量和非基变量的初始解。
步骤2: 计算对偶变量值根据对偶问题的约束条件,计算对偶变量的初始值。
步骤3: 计算对偶目标函数值根据对偶问题的目标函数,计算初始的对偶目标函数值。
步骤4: 检验最优性判断当前解是否为最优解。
如果是,则终止算法;否则,进入下一步。
步骤5: 选择入基变量和出基变量根据当前解,选择一个入基变量和一个出基变量。
步骤6: 更新解通过列生成法或其他方法,更新当前解。
步骤7: 更新对偶变量和对偶目标函数值根据更新后的解,更新对偶变量和对偶目标函数值。
步骤8: 转至Step 4重复步骤4至步骤7,直到找到最优解。
下面以一个具体的线性规划问题为例来演示对偶单纯形法的应用。
假设有以下线性规划问题:最大化 Z = 3x1 + 5x2约束条件为:2x1 + x2 ≤ 10x1 + 3x2 ≤ 15x1, x2 ≥ 0首先,将原始问题转化为标准型:最大化 Z = 3x1 + 5x2约束条件为:2x1 + x2 + s1 = 10x1 + 3x2 + s2 = 15x1, x2, s1, s2 ≥ 0初始化基变量和非基变量的初始解为:x1 = 0, x2 = 0, s1 = 10, s2 = 15根据对偶问题的约束条件,计算对偶变量的初始值:y1 = 0, y2 = 0根据对偶问题的目标函数,计算初始的对偶目标函数值:W = 0检验最优性,发现当前解不是最优解,需要进入下一步。
线性规划的对偶与对偶单纯形法

x1 x 2 x3 3 s.t . x1 4 x 2 7 x3 9 x 0, x 0, x 0 2 3 1
min Z c1 x1 c2 x2 cn xn
对 偶 问 题 的 定 义
a11 a12 a21 a22 s.t . a m1 a m 2 x1 , x2 , , xn
将最优解 y1 , y 2的值代入约束条件,得第3个约束为严格 不等式,由互补松弛性得 x3 0, 又由于 y1 , y 2的值均大于 零,因此原问题的两个约束条件应取等式,故有
3 x1 x2 x3 1 x1 2 x2 3 x3 2
求解后得到 x1 4/7, x2 5 / 7, 故原问题的最优解为 x ( x1 , x2 , x3 )T (4 / 7, 5 / 7, 0) T f min 23 / 7
max z b1 y1 b2 y2 bm y m
a11 y1 a21 y 2 am1 y m ( , )c1 a12 y1 a22 y 2 am 2 y m ( , )c2 a y a y a y (, )c 2n 2 mn m n 1n 1 y j 0(符号不限 , 或 0)i 1 ~ m
1616231381514141521232172152723215245211524min682680038100016100106000min682680038100016100106000261383161610031800012000380001500x2060160000523000051000021000005600x2013540至此右端项的所有分量都已非负当前的迭代点已是一个对偶可行的饿基本可行解因而也是最优解即最优解为相应的目标函数值为100540单纯形法是在基本可行解中寻找满足最优性条件简约价值系数非负的最优解对偶单纯形法则是在所有满足最优性条件简约价值系数非负的最优解中寻找满足可行的最优解单纯形法与对偶单纯形法对偶的经济解释1原始问题是利润最大化的生产计划问题称为m种资源的影子价格shadowprice原始和对偶问题都取得最优解时最大利润maxzmin3资源影子价格的性质影子价格越大说明这种资源越是相对紧缺影子价格越小说明这种资源相对不紧缺如果最优生产计划下某种资源有剩余这种资源的影子价格一定等于0种资源的边际利润4产品的机会成本机会成本表示减少一件产品所节省的资源可以增加的利润增加单位资源可以增加的利润减少一件产品可以节省的资源在利润最大化的生产计划中1边际利润大于0的资源没有剩余2有剩余的资源边际利润等于03安排生产的产品机会成本等于利润4机会成本大于利润的产品不安排生产
民航运筹学_中国民用航空飞行学院中国大学mooc课后章节答案期末考试题库2023年

民航运筹学_中国民用航空飞行学院中国大学mooc课后章节答案期末考试题库2023年1.同一目标约束的一对偏差变量,至少有一个取值为0。
参考答案:正确2.目标规划问题一定存在最优解参考答案:错误3.在目标规划求解中,若高级别目标不能满足时,其后的低级别目标也一定不能满足。
参考答案:错误4.对于只有两个决策变量的目标规划问题,可用图解法求解。
参考答案:正确5.在用单纯形法求解目标规划时,利用最小比值法确定换出变量。
参考答案:正确6.目标规划的满意解不可能出现()参考答案:di+>0,di- >07.用图解法求解目标规划问题,满意解在图中可能是()参考答案:(A)(B)(C)之一8.以下叙述不正确的是()参考答案:目标规划模型用单纯形法求解时,某些情况也需增加人工变量9.以下叙述正确的是()参考答案:目标规划模型的约束中含绝对约束和目标约束10.产地个数为m销地个数为n的平衡运输问题的系数矩阵为A,则有r(A)≤m+n-1。
参考答案:错误11.表示作业法实质上是求解运输问题的单纯形法。
参考答案:正确12.按最小元素法(或Vogel法)给出的初始基可行解,从每一个空格出发可以找到唯一的闭回路。
参考答案:正确13.下列结论正确的有( )参考答案:表上作业法使用的条件是产量等于销量的平衡问题_用位势法判断一个解是否最优时,得出的位势值存在且唯一_任何运输问题都存在可行解14.有m个产地n个销地的平衡运输问题模型具有特征有( )参考答案:有mn个变量,m+n个约束_系数矩阵的秩等于m+n-1_有m+n-1个基变量,mn-m-n+1个非基变量15.当迭代到运输问题最优解时,如果有某非基变量的检验数等于0,则说明该运输问题有()参考答案:多重最优解16.在求解运输问题的表上作业法中,空格的检验数值应等于()参考答案:(闭回路上奇数次顶点运价之和)-(闭回路上偶数次顶点运价之和)17.关于产销不平衡的运输问题,下列叙述正确的是()参考答案:当产大于销时,只在运价表右端增加一列Bn+1,运价为零,销量为bn+1即可18.产销平衡的运输问题的数学模型系数矩阵的Pij中只有两个元素取1,其余为0,这两个1的元素位于()参考答案:第i行和第m+j行19.运输问题是一类特殊的线性规划问题,因而求解的结果为()参考答案:可能出现唯一最优解或多重最优解20.对偶单纯形法适用于下列线性规划:在求目标函数最大值时,所有非基变量的检验数都小于等于0,但存在某些基变量的值为负数参考答案:正确21.在对偶单纯形法中,因为总存在<0的bi,选取数值最小的作为第r行,令br=min{bi},其对应变量xr为换出基的变量。
管理运筹学多选 简答

管理运筹学多选 简答多选:3.对取值无约束的变量x j 通常令x j =x j ′- x j 〞,其中x j ′≥0,x j 〞≥0,在用单纯形法求得的最优解中,不可能出现的是最后的情形。
4.线性规划问题maxZ=X 1+CX 2其中4≤c≤6,一1≤a≤3,10≤b≤12,则当c=6 a=-1 b=10和c=4 a=3 b=12时,该问题的最优目标函数值分别达到上界或下界。
9.下列数学模型,只有B 为非线性规划模型(模型中a .b .c 为常数;θ为可取某一常数值的参变量,x ,Y 为变量),因为它所表达的列变量是不够的。
10.下列模型中,不属于线性规划问题的标准形式的是前三个模型,只有最后一个才是标准的。
4.在下图中,根据(a ) 生成的支撑树有三个b 、c 、d ,如下:7.在下图各边中,平行边有e 1 、 e 2、 e 5 、 e 6, e 1等边则是非平行边。
下列知识点可出简答题1. 简答:运筹学的数学模型有哪些优点?答:(1)通过模型可以为所要考虑的问题提供一个参考轮廓,指出不能直接看出的结果。
(2)节省时间和费用。
(3)模型使人们可以根据过去和现在的信息进行预测,可用于教育训练,训练人们看到他们决策的结果,而不必作出实际的决策。
( 4)数学模型有能力揭示一个问题的抽象概念,从而能更简明地揭示出问题的本质。
(5)数学模型便于利用计算机处理一个模型的主要变量和因素,并易于了解一个变量对其他变量的影响。
这些都是使得运筹学能够快速发展的有利条件。
2. 简答:运筹学的系统特征是什么?答:运筹学的系统特征可以概括为以下四点:(1)用系统的观点研究功能关系(2)应用各学科交叉的方法(3)采用计划方法(4)为进一步研究揭露新问题。
新发现的问题,可能要求用修正过去的模型、输入新的数据以及调整以前类似项目的解,获得解决。
6.简答:根据已知条件建立线性规划数学模型某工厂生产A 、B 、C 三种产品,每种产品的原材料消耗量、机械台时消耗量以及这些资源的限量,单位产品的利润如下表所示:根据客户订货,三种产品的最低月需要量分别为200,250和100件,最大月销售量分别为250,280和120件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4-7用对偶单纯形法求解线性规划问题.
Min z =5x1+3x
2
≥6
s.t.-2 x1 + 3x
2
≥4
3 x1 - 6 x
2
Xj≥0(j=1,2)
解:将问题转化为
Max z = -5 x1 - 3 x
2
+ x3 = -6
s.t. 2 x1 - 3x
2
-3 x1 + 6 x
+ x4≥-4
2
Xj≥0(j=1,2,3,4)
其中,x3 ,x4为松弛变量,可以作为初始基变量,单纯形表见表4-17.
在表4-17中,b=-16<0,而y≥0,故该问题无可行解.
注意: 对偶单纯形法仍是求解原问题,它是适用于当原问题无可行基,且所有检验数均为负的情况.
若原问题既无可行基,而检验数中又有小于0的情况.只能用人工变量法求解.
在计算机求解时,只有人工变量法,没有对偶单纯形法.
3.对偶问题的最优解
由对偶理论可知,在原问题和对偶问题的最优解之间存在着密切的关系,可以根据这些关系,从求解原问题的最优单纯形表中,得到对偶问题的最优解.
(1)设原问题(p)为
Min z=CX
s.t. ⎩⎨
⎧≥=0
X b
AX
则标准型(LP)为
Max z=CX
s.t. ⎩
⎨⎧≥=0X b
AX
其对偶线性规划(D )为
Max z=b T Y s.t. ⎩
⎨
⎧≥=0X b
AX
用对偶单纯形法求解(LP ),得最优基B 和最优单纯形表T (B )。
对于(LP )来说,当j=n+i 时,有Pj=-e i ,c j =0
从而,在最优单纯形表T (B )中,对于检验数,有
(σn+1,σn+2…σn+m )=(c n+1,c n+2…,c n+m )-C B B -1(Pn +1,Pn+2…,Pn+m )=- C B B -1 (-I)
于是,Y*=(σn+1,σn+2…σn+m )T 。
可见,在(LP )的最优单纯形表中,剩余变量对应的检验数就是对偶问题的最优解。
同时,在最优单纯形表T (B )中,由于剩余变量对应的系数 所以
B -1 =(-y n+1,-y n+2…-y n+m )
例4-8 求下列线性规划问题的对偶问题的最优解。
Min z =6x 1+8x 2 s.t. x 1 + 2x 2≥20
3 x 1 + 2x 2≥50
Xj ≥0(j=1,2)
解: 将问题转化为
Max z =-6x 1-8x 2
s.t. -x 1 — 2x 2 + x 3=20
-3 x 1 - 2x 2+ x 4 =50
Xj ≥0(j=1,2,3,4)
用对偶单纯形法求解如表
表4-18 例4-8单纯形表
在引入松弛变量化为标准型之后,约束等式两侧同乘-1,能够立即得到检验数全部非正的原规划基本解,可以直接建立初始对偶单纯形表进行求解,非常方便。
对于有些线性规划模型,如果在开始求解时不能很快使所有检验数非正,最好还是采用单纯形法求解。
因为,这样可以免去为使检验数全部非正而作的许多工作。
从这个意义上看,可以说,对偶单纯形法是单纯形法的一个补充。
除此之外,在对线性规划进行灵敏度分析中有时也要用到对偶单纯形方法,可以简化计算。
例4-9:求解线性规划问题:
Min f = 2x1 + 3x2 + 4x3
S.t. x1 + 2x2 + x3 ≥3
2x1 - x2 + x3 ≥4
x1 , x2 , x3 ≥0
标准化:Max z = - 2x1 - 3x2 - 4x3
s.t. -x1-2x2-x3+x4= -3
-2x1+x2-3x3+x5= -4
x1,x2,x3,x4,x5 ≥0。
