线性规划单纯形法(例题)
求单纯形表中的未知数例题

求单纯形表中的未知数例题以下是一个求解线性规划问题的例题,涉及到单纯形法。
假设有如下线性规划问题:
最大化: 4x + 6y
约束条件:
x + 2y <= 12
x + y <= 8
x, y >= 0
目标函数系数:4 和6。
约束条件的系数分别是:1、2、1 和1。
首先,我们需要构建一个初始单纯形表。
在这个表中,我们有两个基变量和两个非基变量。
基变量的系数是约束条件的系数,而非基变量的系数是目标函数的系数。
初始单纯形表如下:
在这个表中:
B列是基变量的检验数,表示的是当前解是否可行或最优。
非基变量的检验数表示的是当非基变量进入基变量时,目标函数的增加值。
我们将其设置为负无穷,表示这是一个入基变量,其增加量可以被任意大。
最后一行的两个问号表示的是非基变量的值,我们将其设置为待求解的值。
然后,我们开始迭代。
在每一次迭代中,我们都会找到一个入基变量和出基变量,然后更新单纯形表。
这个过程会一直持续到所有的检验数都满足最优性条件(即所有的B列的值都大于等于0)。
运筹学单纯形法的例题

可行域在x1+3x2=7与4x1+2x2=9之下__
3
.
05.07.2020
练习㈠用图解法
5
4 4x1+x2=9
3
2
1 (2.25,0)
0
1
2
3
4
5
6
7
4
.
05.07.2020
练习㈠. 单纯形表
1 31 0 7 4 20 1 9
填入第一个约束的数据.
填入第二个约束的数据.
5
.
05.07.2020
❖至少有一个非基变量的检验数为正,但它的系 数全为非正,则无有限最优解;
❖所有非基变量的检验数全为非正,已有最优解, 但若其中至少有一个的检验数为0,且它的系 数中有2正4 的,则可能有. 无穷多个最优0解5.07.。2020
基变量列中_x_5_换为_x_1_,
改CB列,_-_M__换为_4__.
Excel
17
.
05.07.2020
练习㈢用图解法和单纯形法求 如下线性规划问题的最优解:
Max z =4 x1 + x2 x1 + 3x2 ≥ 7
s.t. 4x1 + 2x2 ≥ 9 x1 , x2 ≥ 0
可行域在直线 x1+3x2=7之上__
s.t. 4x1 + 2x2 -x4+x6=9
基引是进谁两?个这 理x“1里?,x人“2 ,工x-”3 如变,x4何量,x5处”,x6≥0
x5 ,x620
.
05.07.2020
练习㈢.用单纯形法
Max z=4x1+x2+0x3+0x4 -Mx5 –Mx6
线性规划单纯形法(清华2)

增加单位产品甲(x1)比乙对目标函数 的贡献大(检验数最大),把非基变量 x1换成基变量,称x1为进基变量,而把 基变量x4换成非基变量,称x4为出基变 量。 (在选择出基变量时,一定保证消去系 统为正消去系统)(最小比值原则)
增加单位产品甲(x1)比乙对目标函数 的贡献大(检验数最大),把非基变量 x1换成基变量,称x1为进基变量,而把 基变量x4换成非基变量,称x4为出基变 量。 (在选择出基变量时,一定保证消去系 统为正消去系统)(最小比值原则)
因为B为一个基, det(B)<>0
有 XB = B-1b- B-1N XN
S = CB B-1b + (CN- CB B-1N ) XN
令非基变量XN = 0 则
Xt = (XB , XN) =( B-1b , 0)为基础解, 其目标函数值为 S = CB B-1b 只要XB = B-1b 0, Xt =( B-1b , 0) 0
X为基础可行解, B就是可行基。
另外,若满足 CN- CB B-1N 0 则对任意的 x 0 有 S = CX CB B-1b
即对应可行基B的可行解x为最优解。
定理1-5(最优解判别准则)
对于可行基B ,若
C - CB B-1A 0
则对应于基B的基础可行解x就是基础最 优解,此时的可行基就是最优基。 C - CB B-1A为检验数。 由于基变量的检验数:CB - CB B-1B = 0
c2
Ct= …… cn X=
x2
0= …… xn
0
….. 0
并且
r(A)=m<n.
1.最优解判别定理:
不妨假设 A=(B , N)(B为一个基)
相应地有 Xt= (XB , XN)
第2章线性规划建模及其单纯形法

2x1+x2≤40 3x2≤75 x1 ,x2 ≥ 0
7
这是一个典型的利润最大化的生产计划问题。 其中,“Max”是英文单词“Maximize”的缩写,含 义为“最大化”; “s.t.”是“subject to”的缩写,表示“满足于…”。 因此,上述模型的含义是:在给定条件限制下,求 使目标函数z达到最大的x1 ,x2的取值
a21x1 + a22x...2 + … + a2nxn≤ b2 am1x1 + am2x2 + … + amnxn≤ bm
x1 , x2 , … , xn≥0
20
•标准形式 •目标函数: Max z=c1x1 + c2x2 + … + cnxn
•约束条件: a11x1 + a12x2 + … + a1nxn=b1 a21x1 + a22x...2 + … + a2nxn=b2 am1x1 + am2x2 + … + amnxn=bm x1 , x2 , … , xn≥0
4 x1 + 2 x2 + 3 x3 - 9 x4≥ 39 6 x2 + 2 x3 + 3 x4≤-58 x1 , x3 , x4 ≥0
31
解8x3:+7首x4先;,将目标函数转换成极大化:令z=-f=3x1–5x2– 其次考虑约束,有3个不等式约束,引进松弛变量 x5 ,x6 ,x7 ≥0 ; 由于x2无非负限制,可令x2=x2’-x2”,其中x2’≥0 x2”≥0 由于第3个约束右端项系数为-58,于是把该式两端乘 以-1。 于是,我们可以得到以下标准形式的线性规划问题:
单纯形法求解线性规划问题例题

单纯形法求解线性规划问题例题线性规划问题(LinearProgrammingProblem,LPP)是指由一系列约束条件和优化目标函数组成的数学最优化模型,它可以用于解决各种单位时间内最高效率的分配问题。
在求解LPP的过程中,单纯形法(Simplex Method)是最主要的优化算法之一。
单纯形法的原理是采用一组基本变量的拿破仑表示法,一步步构造出线性规划问题的最优解。
下面我们来看一个例子:有公司向农户出售两种农药,甲和乙,每瓶甲农药售价3元,每瓶乙农药售价2元,公司每天有200瓶甲农药和150瓶乙农药,问该公司售出多少瓶甲农药和乙农药,能每天获得最大收益?该问题可表示为下述线性规划模型:最大化 $3x_1+2x_2$约束条件:$x_1+x_2le 200$$2x_1+x_2le 150$$x_1,x_2ge 0$由上述模型可知,有两个未知量$x_1$和$x_2$,它们分别代表出售的甲农药和乙农药的瓶数。
单纯形法的基本思想是采用一组基本变量表示未知量,将未知量$x_1$和$x_2$表示为由两个基本变量$y_1$和$y_2$组成的拉格朗日变换系数矩阵形式,即:$x_1+x_2=y_1+y_2$$2x_1+x_2=m(y_1+y_2)$其中,m是一个系数,根据上面的约束条件,m取200/150=4/3,则:$x_1=y_1+frac{1}{3}y_2$$x_2=y_2-frac{1}{3}y_2$由此可以得到该问题的新的线性规划模型:最大化 $3y_1+2(frac{4}{3})y_2$约束条件:$y_1+y_2le 200$$y_2le 150$$y_1,y_2ge 0$可以看出,该问题所构建出来的新的线性规划模型比原来的模型更加容易求解。
我们将建立单纯形表,以便求出最优解。
首先列出单纯形表:$begin{array}{|c|c|c|c|c|c|c|}hline& y_1 & y_2 & S_1 & S_2 & f & b hline1 & 1 & 1 & 1 & 0 & 3 & 200 hline2 & 0 & 1 & 0 & 1 & 4/3 & 150 hlineend{array}$其中,$y_1$和$y_2$是基本变量,$S_1$和$S_2$是可行解系数,$f$是目标函数系数,$b$是右端项。
补全单纯形表例题

补全单纯形表例题
单纯形法是线性规划问题的一种求解方法。
在给定的线性规划问题中,我们首先找到一个初始解,然后通过迭代的方式找到最优解。
以下是一个简单的线性规划问题的单纯形法求解过程:
例题:
目标函数:最大化 z = 3x + 4y
约束条件:
1. x + 2y <= 12
2. 2x + y <= 10
3. x, y >= 0
初始单纯形表:
x y z c b
1 0 -
2 -1 30 + 40 4 0
2 0 -1 2 30 + 40
3 0
3 1 0 0 0 0 12
4 2 0 0 0 0 10
迭代步骤:
1. 从最后一行开始,检查是否满足所有约束条件。
发现第3个约束条件不满足,即x+2y>12,说明我们可以增加y的取值以减小x的取值。
2. 将第4列中的y增加1,得到新的单纯形表:
x y z c b
1 0 -
2 -1 30 + 40 4 -4
2 0 -1 2 30 + 40
3 -2
3 1 0 1 0 -2 6
4 2 0 1 0 -1 5
3. 检查新的单纯形表,所有约束条件都满足。
现在我们有了初始解,x=0, y=1。
将这个解代入目标函数得到z=30+41=4。
因此,初始最优解是(x=0, y=1, z=4)。
两阶段单纯形法例题详解

两阶段单纯形法引言在线性规划中,两阶段单纯形法是一种常用的求解方法。
它通过两个阶段的迭代,逐步优化目标函数值,从而找到最优解。
本文将详细介绍两阶段单纯形法的步骤和原理。
步骤两阶段单纯形法主要分为两个阶段:人工变量法和单纯形法。
人工变量法•将目标函数按照线性规划的标准形式化简。
•引入人工变量(artificial variables)来转换非标准化的约束条件为等式形式。
•新增的人工变量构成的目标函数为目标是最小化的。
•利用单纯形法求解这个新增的最小化目标函数,得到一个初始可行解。
•如果初始可行解的目标函数值为0,说明原问题有解;如果目标函数值不为0,则原问题无解。
单纯形法•判断初始基本可行解是否是最优解,如果不是,则进行下面的优化步骤。
•选择一个入基变量(entering variable),即将要进入基本解的变量。
•选择一个出基变量(leaving variable),即将要离开基本解的变量。
•使用基本变量和非基本变量之间的约束方程来计算新的基本解。
•迭代以上步骤,直到找到满足优化条件的最优解。
示例假设有一个线性规划问题如下:max Z = 5x1 + 3x2subject tox1 + 2x2 <= 62x1 + x2 >= 4x1, x2 >= 0首先,将目标函数和约束条件标准化,得到以下形式:max Z = 5x1 + 3x2subject to-x1 - 2x2 <= -62x1 + x2 >= 4x1, x2 >= 0然后,采用人工变量法引入人工变量(s1和s2),得到以下形式:max Z = 5x1 + 3x2subject to-x1 - 2x2 + s1 = -62x1 + x2 - s2 = 4x1, x2, s1, s2 >= 0接下来,我们利用单纯形法求解最小化目标函数s1 + s2的初始可行解。
根据单纯形表格的形式,我们可以得到初始表格如下:Cj | -1 | -1 | 0 | 0 |------- |----|----|----|----|Cb | 0 | 0 | 1 | 1 |------- |----|----|----|----|Var. |x1 |x2 |s1 |s2 |------- |----|----|----|----|-1 | -1 | -2 | 1 | 0 |------- |----|----|----|----|0 | 2 | 1 | 0 | -1 |按照单纯形法的步骤,我们选取入基变量s1和出基变量x2,进行迭代计算,得到新的表格:Cj | -1 | -4 | 1 | -3 |------- |----|----|----|----|Cb | 0 | 2 | -1 | 2 |------- |----|----|----|----|Var. |x1 |s2 |s1 |x2 |------- |----|----|----|----|-1 | -1 | 0 | 1 | 2 |------- |----|----|----|----|2 | 2 | 0 | 0 | -1 |继续迭代,直到得到满足优化条件的最优解。
用对偶单纯形法求解线性规划问题

例4-7用对偶单纯形法求解线性规划问题.Min z =5x1+3x2≥6s.t.-2 x1 + 3x2≥43 x1 - 6 x2Xj≥0(j=1,2)解:将问题转化为Max z = -5 x1 - 3 x2+ x3 = -6s.t. 2 x1 - 3x2-3 x1 + 6 x+ x4≥-42Xj≥0(j=1,2,3,4)其中,x3 ,x4为松弛变量,可以作为初始基变量,单纯形表见表4-17.在表4-17中,b=-16<0,而y≥0,故该问题无可行解.注意: 对偶单纯形法仍是求解原问题,它是适用于当原问题无可行基,且所有检验数均为负的情况.若原问题既无可行基,而检验数中又有小于0的情况.只能用人工变量法求解.在计算机求解时,只有人工变量法,没有对偶单纯形法.3.对偶问题的最优解由对偶理论可知,在原问题和对偶问题的最优解之间存在着密切的关系,可以根据这些关系,从求解原问题的最优单纯形表中,得到对偶问题的最优解.(1)设原问题(p)为Min z=CXs.t. ⎩⎨⎧≥=0X bAX则标准型(LP)为Max z=CXs.t. ⎩⎨⎧≥=0X bAX其对偶线性规划(D )为Max z=b T Y s.t. ⎩⎨⎧≥=0X bAX用对偶单纯形法求解(LP ),得最优基B 和最优单纯形表T (B )。
对于(LP )来说,当j=n+i 时,有Pj=-e i ,c j =0从而,在最优单纯形表T (B )中,对于检验数,有(σn+1,σn+2…σn+m )=(c n+1,c n+2…,c n+m )-C B B -1(Pn +1,Pn+2…,Pn+m )=- C B B -1 (-I)于是,Y*=(σn+1,σn+2…σn+m )T 。
可见,在(LP )的最优单纯形表中,剩余变量对应的检验数就是对偶问题的最优解。
同时,在最优单纯形表T (B )中,由于剩余变量对应的系数 所以B -1 =(-y n+1,-y n+2…-y n+m )例4-8 求下列线性规划问题的对偶问题的最优解。
线性规划单纯形法(例题)资料

线性规划单纯形法(例题)《吉林建筑工程学院城建学院人文素质课线性规划单纯形法例题》⎪⎩⎪⎨⎧≥=++=+++++=⎪⎩⎪⎨⎧≥≤+≤++=0,,,24261553).(002max ,,0,24261553).(2max 14.18432142132143214321212121x x x x x x x x x x t s x x x x z x x x x x x x x t s x x z 标准型得到该线性规划问题的,分别加入松驰变量在上述线性规划问题中法求解线性规划问题。
分别用图解法和单纯形)】(页【为初始基变量,选择43,x x)1000(00)0010(01)2050(12)6030(24321=⨯+⨯-==⨯+⨯-==⨯+⨯-==⨯+⨯-=σσσσ为出基变量。
为进基变量,所以选择41x x3/1)6/122/10(00)0210(03/1)3/1240(10)1200(24321-=⨯+-⨯-==⨯+⨯-==⨯+⨯-==⨯+⨯-=σσσσ为出基变量。
为进基变量,所以选择32x x24/724/528/11012/112/124/1100021110120124321-=⨯+-⨯-=-=-⨯+⨯-==⨯+⨯-==⨯+⨯-=)()()()(σσσσ4334341522max ,)43,415(),(2112=+⨯=+===x x z x x X TT 故有:所以,最优解为⎪⎪⎩⎪⎪⎨⎧≥=++=+=+++++=⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤+=0,,,,18232424).(0002max ,,,0,182312212).(52max 24.185432152142315432154321212121x x x x x x x x x x x x t s x x x x x z x x x x x x x x x t s x x z 标准型得到该线性规划问题的,分别加入松驰变量在上述线性规划问题中法求解线性规划问题。
线性规划单纯形法(例题)

《吉林建筑工程学院城建学院人文素质课线性规划单纯形法例题》⎪⎩⎪⎨⎧≥=++=+++++=⎪⎩⎪⎨⎧≥≤+≤++=0,,,24261553).(002max ,,0,24261553).(2max 14.18432142132143214321212121x x x x x x x x x x t s x x x x z x x x x x x x x t s x x z 标准型得到该线性规划问题的,分别加入松驰变量在上述线性规划问题中法求解线性规划问题。
分别用图解法和单纯形)】(页【为初始基变量,选择43,x x)1000(00)0010(01)2050(12)6030(24321=⨯+⨯-==⨯+⨯-==⨯+⨯-==⨯+⨯-=σσσσ为出基变量。
为进基变量,所以选择41x x3/1)6/122/10(00)0210(03/1)3/1240(10)1200(24321-=⨯+-⨯-==⨯+⨯-==⨯+⨯-==⨯+⨯-=σσσσ为出基变量。
为进基变量,所以选择32x x24/724/528/11012/112/124/1100021110120124321-=⨯+-⨯-=-=-⨯+⨯-==⨯+⨯-==⨯+⨯-=)()()()(σσσσ4334341522max ,)43,415(),(2112=+⨯=+===x x z x x X TT 故有:所以,最优解为⎪⎪⎩⎪⎪⎨⎧≥=++=+=+++++=⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤+=0,,,,18232424).(0002max ,,,0,182312212).(52max 24.185432152142315432154321212121x x x x x x x x x x x x t s x x x x x z x x x x x x x x x t s x x z 标准型得到该线性规划问题的,分别加入松驰变量在上述线性规划问题中法求解线性规划问题。
线性规划经典例题

线性规划经典例题一、问题描述某工厂生产两种产品A和B,每天可用的原料有限,而每种产品的制造需要不同数量的原料。
产品A每单位利润为10元,产品B每单位利润为8元。
产品A每天的制造时间为6小时,产品B每天的制造时间为4小时。
已知制造一个单位的产品A需要2小时,而制造一个单位的产品B需要1小时。
工厂的目标是最大化每天的利润。
二、数学建模1. 定义变量:- x1: 每天制造的产品A的单位数量- x2: 每天制造的产品B的单位数量2. 建立目标函数:目标函数为最大化每天的利润,即:Maximize Z = 10x1 + 8x23. 建立约束条件:- 原料的限制:每天可用的原料有限,产品A每单位需要2单位原料,产品B每单位需要3单位原料。
因此,原料的约束条件为:2x1 + 3x2 ≤ 原料数量- 时间的限制:每天的制造时间有限,产品A每单位需要2小时制造,产品B每单位需要1小时制造。
因此,时间的约束条件为:2x1 + x2 ≤ 制造时间- 非负约束:每天制造的产品数量不能为负数,因此,非负约束条件为:x1 ≥ 0x2 ≥ 0三、求解线性规划问题利用线性规划的求解方法,可以求解出最优解。
1. 图形法:通过绘制约束条件的直线或曲线,找到目标函数的最大值所在的区域。
2. 单纯形法:单纯形法是一种常用的求解线性规划问题的方法。
通过迭代计算,找到目标函数的最大值所在的点。
四、数值计算为了方便计算,我们假设原料数量为20单位,制造时间为10小时。
1. 图形法:绘制约束条件的直线或曲线,找到目标函数的最大值所在的区域。
在本例中,约束条件的直线为:2x1 + 3x2 ≤ 202x1 + x2 ≤ 10绘制直线后,找到目标函数的最大值所在的区域。
2. 单纯形法:利用单纯形法,可以求解出最优解。
根据约束条件和目标函数,可以构建如下的单纯形表格:| 基变量 | x1 | x2 | 原料数量 | 制造时间 | 目标函数 ||--------|----|----|----------|----------|---------|| x3 | 0 | 0 | 20 | 10 | 0 || x1 | 1 | 0 | 2 | 2 | 10 || x2 | 0 | 1 | 3 | 1 | 8 |通过迭代计算,可以得到最优解为:x1 = 5x2 = 0最大利润为:50元五、结果分析根据数值计算的结果,最优解为每天制造5个单位的产品A,不制造产品B,可以获得最大利润为50元。
单纯形法及例题解析

= a11a22-a12a21
三阶行列式
a11 a12 a13 a21 a22 a23 a31 a32 a33
= a11a22a33+a12a23a31+a13a21a32-
a13a22a31-a11a23a32-a12a21a33
练习
14 3 -5 2 1 36 1
10 0 -5 2 3 33 5
x4
x5
0
x3
2
[1]
0
1
0
-1/2
1
0
x4
16
4
0
0
1
0
4
3
x2
3
0
1
0
0
1/4
-
Cj-Zj
2
0
0
0
-3/4
Cj
CB
XB
b
2
x1
2
0
x4
8
3
x2
3
Cj-Zj
单纯形表
2
3
0
x1
x2
x3
1
0
1
0
0
-4
0
1
0
0
0
-2
0
0
θ
x4
x5
0
-1/2
-
1
[2]
4
0
1/4
12
0
1/4
单纯形表
Cj
2
3
0
0
0
θ
CB
矩阵的乘法
A =(aij)m s B =(bij)s n C =AB =(cij)m n
cij = ai1b1j+ai2b2j+ … +aisbsj
线性规划和其单纯形法习题

优解变为 X
求证: (C C)( X X 0 ) 0
0
2
5
6
2
F
0
4
5
2
0
5 已知某线性规划问题旳约束条件为
2x1 x2 x3
25
st. 4xx11
3x2 7 x2
x3
x4 2x4
x5
30 85
x1 x2 x3 x4 x5 0
判断下列各点是否为该线性规划问题可行域上旳顶点:
X (5,15, 0, 20, 0)
X (9, 7, 0, 0,8) X (15, 5,10, 0, 0)
项目 X1 X2 X3 X4
X5
X4 6 (b) (c) (d) 1 0
X5 1 -1
3 (e) 0 1
Cj-ZJ
(a) -1 2
00
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj-ZJ
0
-7 (j) (k) (l)
6、设 X 0 是线性规划问题 max z CX , AX b, X 0
x1 0, x2 0, x3无约束
3 对下述线性规划问题找出全部基解,指出那些是基可行 解,并拟定最优值。
min
Z
5x1
2x 2
3x 3
2x 4
x 2x 3x 4x 7
s.t. 21x1
2
2x 2
3
x 3
4
2x 4
3
x 0( j 1,...., 4) j
4、已知线性规划问题 :
性规划旳目旳函数为 max Z 5x1 3x2约束形式为
线性规划与单纯形法

第1章 线性规划与单纯形法1、用图解法求解下列线性规划问题,并指出问题具有唯一最优解、无穷最优解、无界解还是无可行解。
⎪⎩⎪⎨⎧≥≥+≥++=0x x 42x 4x 66x 4x 3x 2x minz )a (21212121, ⎪⎩⎪⎨⎧≥≥+≤++=0x ,x 124x 3x 2x 2x 2x 3x maxz )b (21212121⎪⎩⎪⎨⎧≤≤≤≤≤++=8x 310x 512010x 6x x x maxz )c (212121⎪⎩⎪⎨⎧≥≤+-≥-+=0x ,x 23x 2x 2x 2x 6x 5x maxz )d (21212121 2、用单纯形法求解下列线性规划问题。
⎪⎩⎪⎨⎧≥≤+≤++=0x ,x 82x 5x 94x 3x 5x 10x maxz )a (21212121⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+=0x ,x 5x x 242x 6x 155x x 2x maxz )b (2121212213、用大M 法和两阶段法求解下列线性规划问题,并指出属于哪一类解。
⎪⎪⎩⎪⎪⎨⎧≥≥-≥+-≥+++-=0x x x 0x 2x 2x 2x 6x x x 2x x 2x maxz )a (3,2,132******** ⎪⎩⎪⎨⎧≥≥+≥++++=0x ,x ,x 62x 3x 82x 4x x x 3x 2x minz )b (321213213214、已知线性规划问题的初始单纯形表(如表1所示)和用单纯形法迭代后得到的表(如表2所示)如下,试求括弧中未知数a ~l 的值。
表25、某厂生产Ⅰ、Ⅱ、Ⅲ三种产品,都分别经A 、B 两道工序加工。
设A 工序可分别在设备A 1或A 2上完成,有B 1、B 2、B 3三种设备可用于完成B 工序。
已知产品Ⅰ可在A 、B 任何一种设备上加工;产品Ⅱ可在任何规格的A 设备上加工,但完成B 工序时,只能在B 1设备上加工;产品Ⅲ只能在A 2与B 2设备上加工。
线性规划经典例题

线性规划经典例题线性规划是一种数学优化方法,用于解决线性约束条件下的最优化问题。
在实际应用中,线性规划经常被用于资源分配、生产计划、运输问题等方面。
下面将介绍一个经典的线性规划例题,并详细解答。
例题描述:某公司生产两种产品A和B,每个产品的生产需要消耗不同的资源。
已知每天可用的资源有:材料1,材料2和工时。
产品A每个单位需要消耗2单位的材料1,3单位的材料2和1单位的工时;产品B每个单位需要消耗4单位的材料1,1单位的材料2和3单位的工时。
公司每天可用的材料1、材料2和工时分别为30单位、20单位和15单位。
产品A的利润为5单位,产品B的利润为4单位。
公司希望在满足资源约束条件的前提下,最大化利润。
解答步骤:步骤1:确定决策变量首先,我们需要确定决策变量,也就是我们要求解的问题的变量。
在这个例题中,我们需要确定两个决策变量:x表示生产的产品A的数量,y表示生产的产品B的数量。
步骤2:建立目标函数目标函数是我们要优化的目标,即最大化利润。
根据题目中给出的信息,我们可以得到目标函数:Maximize Z = 5x + 4y步骤3:建立约束条件约束条件是我们在问题中需要满足的限制条件。
根据题目中给出的信息,我们可以得到以下约束条件:2x + 4y ≤ 30 (材料1的约束条件)3x + y ≤ 20 (材料2的约束条件)x + 3y ≤ 15 (工时的约束条件)x, y ≥ 0 (非负约束条件)步骤4:求解最优解将目标函数和约束条件带入线性规划模型中,我们可以使用各种求解方法来求解最优解。
这里我们使用单纯形法求解。
首先,将约束条件转化为等式形式,得到标准型的线性规划问题:2x + 4y + s1 = 303x + y + s2 = 20x + 3y + s3 = 15其中,s1、s2、s3是松弛变量。
接下来,构建初始单纯形表格:| x | y | s1 | s2 | s3 | RHS |-------------------------------------------s1 | 2 | 4 | 1 | 0 | 0 | 30 |s2 | 3 | 1 | 0 | 1 | 0 | 20 |s3 | 1 | 3 | 0 | 0 | 1 | 15 |-------------------------------------------Z | -5 | -4 | 0 | 0 | 0 | 0 |进行单纯形法迭代计算,得到最优解:| x | y | s1 | s2 | s3 | RHS |-------------------------------------------s1 | 0 | 2 | 1 | -2 | 0 | 10 |s2 | 0 | -2 | -3 | 7 | 0 | -10 |x | 1 | 0 | -2 | 3 | 0 | 5 |-------------------------------------------Z | 0 | 0 | 5 | -4 | 0 | 25 |根据单纯形法的计算结果,最优解为x=5,y=0,利润最大值为25。
运筹学第四版第二章线性规划及单纯形法

方案的制定受到那些现实条件制约:
确定约束条件
人力资源(劳动力)的限制: 9x1 4x2 360
设备工时的限制:
4x1 5x2 200
原材料资源的限制:
3x1 10x2 300
此外,决策变量的取值不应为负值即 x1 0, x2 0
6
综上所述,我们得到了这个问题的数学模型
目标函数 约束条件
大?
项目
Ⅰ
设备A (h)
0
设备B (h)
6
调试工序(h) 1
利润(元) 2
Ⅱ 每天可用能力
5
15
2
24
表1-2
1
5
1
12
其数学模型为:
max Z 2x1 x2
5x2 15
6xx11
2x2 x2
24 5
x1, x2 0
13
例3:捷运公司在下一年度的1~4月份的4个月内拟租用仓库
堆放物资。已知各月份所需仓库面积列于下表1-3。仓库租
借费用随合同期而定,期限越长,折扣越大,具体数字见表
1-4。租借仓库的合同每月初都可办理,每份合同具体规定
租用面积和期限。因此该厂可根据需要,在任何一个月初办
理租借合同。每次办理时可签一份合同,也可签若干份租用
面积和租用期限不同的合同。试确定该公司签订租借合同的
最优决策,目的是使所租借费用最少。
14
max Z 70 x1 120 x2
9x1 s.t. 43xx11
x1,
4x2 5x2 10x2 x2 0
360 200 300
资源约束
非负约束
其中 约束条件可记 s.t (subject to), 意思为“以… 为条件“、”假定“、”满足“之意。
线性规划(单纯形法)
不难看出x 可作为初始基变量,列单纯形表计算。 不难看出 4、x5可作为初始基变量,列单纯形表计算。
单纯形法的进一步讨论- 单纯形法的进一步讨论-人工变量法
Page 17
故人为添加两个单位向量,得到人工变量单纯形法数学模型: 故人为添加两个单位向量,得到人工变量单纯形法数学模型: max Z = 3x1 − x2 − x3 + 0x4 + 0x5-Mx6 − Mx7
x1 − 2x2 + x3 + x4 = 11 − 4x + x + 2x − x + x = 10 1 2 3 5 6 − 2x1 + x3 + x7 = 1 x j ≥ 0, j = 1,2,L,7
确定换出变量。根据下式计算并选择θ 选最小的θ对应基 ② 确定换出变量。根据下式计算并选择 ,选最小的 对应基
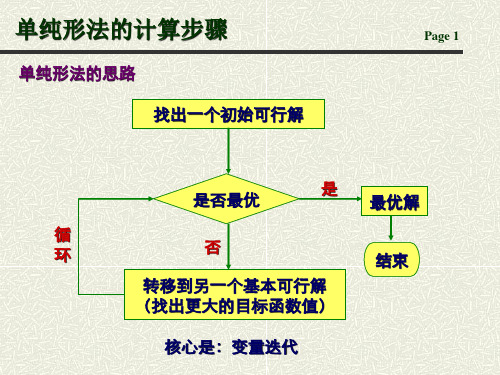
单纯形法的计算步骤
③
Page 6
用换入变量xk替换基变量中的换出变量,得到一个新的基。 用换入变量 替换基变量中的换出变量,得到一个新的基。 替换基变量中的换出变量 对应新的基可以找出一个新的基可行解, 对应新的基可以找出一个新的基可行解,并相应地可以画出 一个新的单纯形表。 一个新的单纯形表。
4 4 2
1 0 0 0
0 0 1 0
0 -2 1/2 -3/2
1/4 1/2 -1/8 -1/8
0 1 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《吉林建筑工程学院城建学院人文素质课线性规划单纯形法例题》
⎪⎩⎪
⎨⎧≥=++=+++++=⎪⎩
⎪
⎨⎧≥≤+≤++=0,,,24
261553).(002max ,,0,24
261553).(2max 14.1843214213
214
321432121212
1x x x x x x x x x x t s x x x x z x x x x x x x x t s x x z 标准型得到该线性规划问题的,分别加入松驰变量在上述线性规划问题中法求解线性规划问题。
分别用图解法和单纯形)】
(页【为初始基变量,选择43,x x
)1000(00)0010(01
)2050(12)6030(24321=⨯+⨯-==⨯+⨯-==⨯+⨯-==⨯+⨯-=σσσσ
为出基变量。
为进基变量,所以选择41x x
3
/1)6/122/10(00
)0210(03
/1)3/1240(10)1200(24321-=⨯+-⨯-==
⨯+⨯-==⨯+⨯-==⨯+⨯-=σσσσ
为出基变量。
为进基变量,所以选择32x x
24
/724/528/11012/112/124/1100
021110120124321-=⨯+-⨯-=-=-⨯+⨯-==⨯+⨯-==⨯+⨯-=)()()()(σσσσ
433
4341522max ,)4
3,415(
),(2112=
+⨯=+===x x z x x X T
T 故有:所以,最优解为
⎪⎪⎩
⎪⎪⎨
⎧≥=+
+=+=+
++++=⎪⎪⎩⎪⎪⎨
⎧≥≤+≤≤+=0,,,,18232424).(0002max ,,,0
,182312212
).(52max 24.185432152142315
43215432121212
1x x x x x x x x x x x x t s x x x x x z x x x x x x x x x t s x x z 标准型得到该线性规划问题的,分别加入松驰变量在上述线性规划问题中法求解线性规划问题。
分别用图解法和单纯形)】
(页【
)000010(00001000000000100520200052300010254321=⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-=σσσσσ)()()()( 为出基变量。
为进基变量,所以选择42x x
10051002/5102/150000
00051000
00150052
300510254321=⨯+⨯+⨯-=-=-⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-=)()()()()(σσσσσ 为出基变量为进基变量,所以51x x
3
/23/12053/1006/113/122/153/1000
02051000
02150050120500254321-=⨯+⨯+-⨯-=-=-⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-==⨯+⨯+⨯-=)()()()()(σσσσσ 34
6522max ,6,2,0,02X *
T *=⨯+⨯==z
为最优解。
)(明:单纯形表得计算结果表。
