河南省普通高中2016届高三下学期毕业班高考适应性模拟练习数学(理)试题(图片版)
(全优试卷)河南省普通高中高三数学毕业班下学期适应性测试试题 理(含解析)

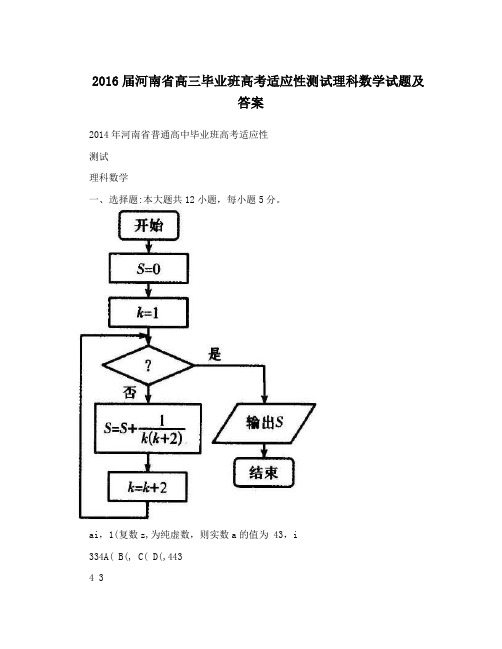
2016河南省普通高中毕业班高考适应性测试数学(理)试题一、 选择题1. 已知集合A={0,1,2},2,{}|B y y x x A ==∈,则A B U 中元素个数为( ) A.6 B.5 C.4 D. 3 答案:C解析:考查集合运算B={0,2,4},并集为{0,1,2,4},故选C 2. 如果复数3()2bib R i-∈+的实部与虚部相等,则b 的值为( ) A.1 B.-6 C.3 D.-9 答案:D解析:考查复数令32bia ai i-=++,展开33bi a ai -=+ 解得a=3,b=-3a ,故选D 3. 已知1tan()42πα-=,则sin cos sin cos αααα+-的值为()A.1/2B.2C.2 2D.-2答案:B解析:考查正切的两角和差公式tan 11tan()41tan 2πααα--==+,而sin cos tan 12sin cos 1tan αααααα++==--4. 双曲线22221(0,0)x y a b a b-=>>的渐近线与圆22(2)3x y -+=相切,则双曲线的离心率为( )A. 223B. 72 C.2 D. 2 2答案:C解析:双曲线的渐近线方程为by x a=±圆心(2,0),半径3,圆心到直线ay=bx 的距离等于半径= 解得22213b e a =-=,故选C5. 给出下列四个结论:①已知X 服从正态分布2(0,)N σ,且P(-2≤X ≤2)=0.6,则P(X>2)=0.2;②若命题2000:[1,),10p x x x ∃∈+∞--<,则2:(,1),10p x x x ⌝∀∈-∞--≥;③已知直线1:310l ax y +-=,2:10l x by ++=,则12l l ⊥的充要条件是/3a b =-;④设回归直线方程ˆ2 2.5yx =-,当变量x 增加一个单位时,y 平均增加两个单位. 其中正确的结论的个数为()A.1B.2C. 3D. 4 答案:A解析:仅①正确 ②存在量词的否定③必要不充分,反例为a=b=0 ④考查线性回归的意义6. 执行如右图所示的程序框图,则输出的k 值是() A.10 B.11 C.12 D.13 答案:B解析:考查等比数列前n 项和,注意输出前k 先加12(21)2016n n S =-> 即10210241009=>7. 等差数列{}n a 的前n 项和为Sn ,若12n n S n a +=,则23/a a =() A.2 B.3/2 C.2/3 D.1/3 答案:C解析:考查等差中项 当n=3时,1232333312a a a a a a +++== 故选C8. 六个人站成一排照相,则甲乙两人之间恰好站两人的概率为() A.16 B.15 C.13 D.12 答案:B解析:六人中选两甲乙两人的方案共计2615C =种,若六人依次编号,则满足题意的甲乙可能的位置有1,4,2,5,3,6 根据古典概型,得P=3/15 9. 已知正数x,y 满足x+4y=4,则284x y xy++的最小值为()A.852 B.24 C.20 D.18 答案:D解析:考查求函数最值的方法首先统一变量x=4-4y ,目标函数为6228()(1)1y f y y y y y+==+--求导2282'()0(1)f y y y =-=-解得极值点y=-1(舍)和y=1/3故最小值为f(1/3)=1810. 如图在边长为1的正方形组成的网格中,画出的是一个几何体的三视图,则该几何体的体积是()A.9B.27/2C.18D.27 答案:A解析:分析几何体种类为三棱锥 底面积63/29S =⨯= 高h=3,则体积V=Sh/3=911. 已知函数22()ln(241)21xf x x x =++-+,若f(a)=1则f(-a)=() A.0 B.-1 C.-2 D.-3 答案:D解析:考查奇函数特性22()()22121a a f a f a ---=-=+=-++,故选D 12. 已知函数()|ln |1f x x =-,2()23g x x x =-++,用min{m,n}表示m,n 中最小值,设函数h(x)={f(x),g(x)},则函数h(x)的零点个数为() A.1 B.2 C.3 D.4 答案:C解析:考查数形结合能力画图可知四个零点分别为-1和3,1/e 和e ; 但注意到f(x)的定义域为x>0,故选C 二、 填空题13. 已知不等式组8y xx y y a ≤⎧⎪+≤⎨⎪≥⎩表示的平面区域面积为25,点P(x,y)在所给平面区域内,则z=2x+y 的最大值为___ 解析:考查数形结合能力 平面区域为等腰直角三角形 由勾股定理得222(4)2(4)252a a --=⨯解得a=-1,即三个交点为(-1,-1),(9,-1),(4,4) 对应目标函数取值为-3,17,12 14. 在93(24)x y+-的展开式中,不含x 的各项系数之和为___ 答案:-1 解析:15. 四棱锥P-ABCD 的五个顶点都在一个球面上,底面ABCD 是矩形,其中AB=3,BC=4,又PA⊥平面ABCD ,PA=5,则该球的表面积为____ 解析:考查球体专项由勾股定理得AC=5等腰直角三角形,PC=2R =5 2 因此表面积2450S R ππ==16. 已知各项均为正数的数列{}n a 满足1117,242n n a a a +=+=,Sn 为数列{}n a 的前n 项和,若对于任意的*n N ∈,不等式1223122nkn n S ≥-+-恒成立,则实数k 的取值范围为___答案:k ≥3/8解析:考查构造数列11()11n n n n B Ba Aa B a A a A A++=+⇒-=--- 因此1111()222n n a a +-=-,故1{}2n a -是首项为3、公比为1/2的等比数列因此1212(1)2n n S n -=-,故目标函数可化简为232nn k -≥,分离变量,恒成立问题转为函数最值问题 因此取函数23()2n n f n -=的最大值求导得222(23)2ln 2'()0(2)n n n n f n ⋅--== 解得223ln 2n =+,正整数n 取可取2或3,13(2),(3)48f f == 三、 解答题17. 在△ABC 中,角A,B,C 的对边分别为a,b,c.已知向量2(cos ,2cos1)2Cm B =-,(,)n c b 2a =-且m ·n =0.(1)求角C 的大小;(2)若点D 为边AB 上一点,且满足,||7,23AD DB CD c ===,求△ABC 的面积.解析:(1)考查三角降次公式、正弦定理和余弦定理·cos cos (2)0m n c B C b a =+-=使用正弦定理得sin cos cos sin 2cos sin C B C B a C A +== 因此cos 1/2C =,/3C π=(2)如图所示,273221cos a α=++⨯且273221cos()b πα=++⨯-因此2220a b +=,由余弦定理得22122cos 3a b ab π=+-,解得ab=20-12=8由正弦定理得1sin 2323S ab π== 18. PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某时间段车流量与PM2.5浓时间周一 周二 周三 周四 周五 车流量x (万辆) 100102 108 114 116 浓度y (微克)7880848890(2)若周六同一时段车流量是200万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少?参考公式:121()()()niii nii x x y y b x x ==--=-∑∑,a y b x =-⋅解析:5511540,420ii i i xy ====∑∑ 因此108x =,84y =故222286640064861440.7286068200b ⨯+⨯+⨯+⨯+⨯===++++ 故840.72108 6.24a =-⨯=线性回归方程为ˆ0.72 6.24yx =+ 若x=200,则ˆ0.72200 6.24150.24y=⨯+= 19. 如图,在直三棱柱ABC-A ’B ’C ’中,∠ACB=90°,AA ’=BC=2AC=4.(1)若点P 为AA ’的中点,求证:平面B ’CP ⊥平面B ’C ’P ;(2)在棱AA ’上是否存在一点P ,使得二面角B ’-CP-C ’的大小为60°,若存在,求出AP 的值;若不存在,说明理由.解析:(1)要证明面面垂直,先要证线面垂直 BC//B’C’⊥平面AA’C’C,因此B’C’⊥CP 在直角三角形中求斜边得C’P=CP =2 2 由222''C P CP C C += 可知C ’P ⊥CP综上,CP⊥平面C’B’P,从而,平面B ’CP ⊥平面B ’C ’P (2)以C 为原点建系,设AP=a ,则C(0,0,0),P(2,0,a),C ’(0,0,4),B ’(0,4,4)平面C ’CP 的法向量为C ’B ’=(0,4,0),设平面B ’CP 的法向量为m=(x,y,z) 则'C 0440020m B y z m CP x az ⋅=+=⎧⎧⇒⎨⎨⋅=+=⎩⎩ 解得m=(a,2,-2)22cos 6044448a a ︒==+++解得a=22<4(棱长)因此,侧棱上存在一点P 满足题意20. 在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的离心率为22,且过点A(6,1),点P 在椭圆C 上,且在第一象限内,直线PQ 与圆222:O x y b +=相切于点M.(1)求椭圆C 的方程;(2)若OP ⊥OQ ,求点Q 的纵坐标的取值范围.解析:根据椭圆的斜率公式可得222112b e a =-=把点A 代入椭圆方程得226112b b+= 解得224,8b a ==,故22184x y += 设点Q 纵坐标为t1°当PM 垂直于x 轴时,PMQ 三点共线,第一象限点P(2,2)Q(2,t),OP ⊥OQ ,即向量数量积为042022t t +=⇒=-2°当PM 斜率存在时,设直线OP 方程为y=kx ,则OQ 方程为ky=-x 设点P(n,kn),点Q(-kt,t),PQ=(-kt-n,t-kn) 点P 在椭圆上,22228n k n += 设直线与圆的切点2(,4)M m m - 由OM ⊥PQ 得2()()4m kt n t kn m +=--由PMQ 三点共线得24m kn kn tm n kt n---=-+21. 已知函数1()ln f x a x x=--,其中a 为常数 (1)若f(x)=0恰有一个解,求a 的值; (2)若函数12()()()ln x p g x a f x p x x p-=----+,其中p 为常数,试判断函数g(x)的单调性;(3)若f(x)恰有两个零点,12x x <,求证11231a x x e -+<-解析:(1)考查单调性,首先求定义域x>0 令21'()0xf x x-== 解得x=1 因此(0,1),(1,)↑+∞↓且f(1)=a -1为最大值 当f(1)=0时即a=1时,f(x)=0恰有一个解x=1 当f(1)<0时即a<1时,f(x)=0无解 当f(1)>1时即a>1时,1,()0,()0aa a a ee f e f e --<<<<,故f(x)=0有两个解综上,若f(x)=0恰有一个解,则a=1 (2)整理函数2()()ln ln x p g x x p x p-=--+首先求解定义域x>0且常数p>0求导得22(x p)'()0()g x x x p -=≥+,且只有有限个零点 因此g(x)在定义域上单调递增(3)由(1)知,若f(x)=0恰有两个零点,则a>1且等价于xf(x)=0 令h(x)=ax -1-xlnx ,(x>0)求导得'()1ln h x a x =--,解得极大值1'()0a h e -=记1a p e-=,函数h(x)两个零点满足12x p x <<当0<x<p 时,g(x)<g(p)=0,即11111112()1ln ln x x p ax x x x p x p--=<++整理得211(31)0x p x p --+>当x>p 时,g(x)>g(p)=0,同理可得222(31)0x p x p --+<因此222211(31)(31)x p x p x p x p --+<--+ 222121(31)()x x p x x -<-- 即11231a x x e -+<-22. 在平面直角坐标系xOy 中,直线l的参数方程为1/2/2x t y =-⎧⎪⎨=⎪⎩,在以原点O 为极点,x轴正半轴为极轴的极坐标系中,圆C的方程为ρθ=.(1)写出直线l 的普通方程和圆C 的直角坐标方程; (2)若点P 的直角坐标为(1,0),圆C 与直线l 交于A,B 两点,求PA+PB 的值.解析:使用消元法可得直线的普通方程)y x =-圆C 为圆心在y 轴正半轴,半径3且过原点的正圆22(3x y +=显然点P (1,0)和圆心都在直线l 上,且AB 均在定点P 同一侧 因此可以利用直线参方的参数t 几何意义解题联立直线与圆方程得:22(1)322t -+= 整理为关于t 的一元二次方程2410t t -+= 因此124PA PB t t +=+=。
2016年河南省普通高中毕业班高考适应性考试

2.下列理解和分析,不符合原文意思的一项是
A.道德理想注重未来社会人们之间的道德关系和道德风尚,而社会理想更注重未来社会经济、政治制度等内容的构想设计。
B.道德理想能动员广大群众主动热情地投入到变革社会的进步活动中,而与科学的社会理想相比,它的准确性、严谨性、论证性都显得不足。
B.革命阶级追求奋斗的社会理想,带有道德理想色彩,忠诚于共产主义事业为在全世界实现共产主义社会制度而奋斗就是明证。
C.既然空想社会主义成了科学社会主义理想的直接源泉,那么可以认为空想社会主义者有超前的科学预测,与科学社会主义重合度极高。
D.承认社会理想和道德理想的联系,并不是要求我们以前者代替后者;承认二者的差别,则要求人们注意发挥后者在实现前者中的作用。
(摘编自肖群忠《道德理想新探》)
1.下列关于原文内容的表述,不正确的一项是
A.道德高于现实的未来性因素,就是道德理想,它含有还不能被当代社会大多数成员遵照实行的比较高的道德要求。
B.道德理想包含着一定社会阶级和它的成员对未来社会道德关系和道德风尚的向往,它与一定阶级的社会理想相联系。
C.一定的阶级会有自己的政治理想,这个理想等同于社会理想,它包含着对未来的社会制度、政治结构的性质和特征的预见。
道德理想第二个方面的内容是理想道德标准或称道德规范体系中较高的、暂时还不能为社会大多数成员所奉行的要求。例如,社会主义社会的分配制度是“各尽所能,按劳分配”“不劳动者不得食”,由此产生的普遍道德要求是否定剥削、否定不劳而获等。但是现实中还有更高的道德理想标准,如不计报酬、毫不利己、大公无私等。道德规范准则具有规范的、现实的性质,是判断和评判人们行为善恶的标准;道德理想标准则具有崇高的、理想的性质,是判断和评判人们行为道德价值大小的标准。在实践中,人们只有自觉地遵循道德规范准则,才有可能进一步实现一定社会和阶级的道德理想标准。可以说,道德规范准则是道德理想标准的前提和基础:道德理想标准则是在此基础上提出的更高要求,反映了道德行为的发展方向。
河南省郑州市2016届高三第二次模拟考试 数学(理)试题 (word版)

2016年郑州市高中毕业年级第二次质量预测理科数学试题卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效.交卷时只交答题卡.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中.只有一项是符合题目要求的.) 1.已知集合A ={x |y =4x -},B ={x |-1≤2x -1≤0},则C R A ∩B =A .(4,+∞)B .[0,12] C .(12,4] D .(1,4] 2.命题“0x ∃≤0,使得20x ≥0”的否定是A .x ∀≤0,2x <0B .x ∀≤0,2x ≥0C .0x ∃>0,20x >0D .0x ∃<0,20x ≤03.定义运算,,a b c d =ad -bc ,则符合条件,1,2z ii i+-=0的复数z 对应的点在 A .第一象限 B .第二象限 C .第三象限 D .第四象限4.某程序框图如图所示,则该程序运行后输出的值是A .2014B .2015C .2016D .20175.曲线f (x )=3x -x +3在点P 处的切线平行于直线y =2x -1,则P 点的坐标为 A .(1,3) B .(-1,3) C .(1,3)和(-1,3) D .(1,-3) 6.经过点(2,1),且渐近线与圆22(2)x y +-=1相切的双曲线的标准方程为A .22111113x y -=B .2212x y -= C .22111113y x -= D .22111113y x -= 7.将函数f (x )=sin (2x -2π)的图象向右平移4π个单位后得到函数g (x ),则g (x )具 有性质A .最大值为1,图象关于直线x =2π对称 B .在(0,4π)上单调递减,为奇函数 C .在(38π-,8π)上单调递增,为偶函数D .周期为π,图象关于点(38π,0)对称8.设数列{n a }满足:a 1=1,a 2=3,且2n n a =(n -1)1n a -+(n +1)1n a +,则a 20的值是 A .415 B .425 C .435 D .4459.如图是正三棱锥V -ABC 的正视图、侧视图和俯视图,则其侧视图的面积是A .4B .5C .6D .710.已知定义在R 上的奇函数y =f (x )的图像关于直线x =1对称,当-1≤x <0时,f (x )=-12log ()x -,则方程f (x )-12=0在(0,6)内的零点之和为A .8B .10C .12D .1611.对α∀∈R ,n ∈[0,2],向量c =(2n +3cos α,n -3sin α)的长度不超过6的概率为 A .510 B .2510 C .3510 D .25512.已知A 、B 、C 为△ABC 的三个内角,向量m 满足|m |=62,且m =(2s i n 2B C +,c o s 2B C-),若A 最大时,动点P 使得|PB uu r |、|BC uu u r |、|PC uu u r |成等差数列,则PA BCuu r uu u r的最大值是 A .233 B .223 C .24D .324 第Ⅱ卷本卷包括必考题和选考题两部分.第13—21题为必考题,每个试题考生都必须作答.第22-24题为选考题.考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分.) 13.已知{n a }为等差数列,公差为1,且a 5是a 3与a 11的等比中项,n S 是{n a }的前n 项和,则S 12的值为__________.14.已知正数x ,y 满足2x +2xy -3=0,则2x +y 的最小值是___________.15.已知x ,y 满足2,4,20,x x y x y m ⎧⎪⎨⎪⎩≥+≤--≤若目标函数z =3x +y 的最大值为10,则z 的最小值为____________.16.在正三棱锥V —ABC 内,有一半球,其底面与正三棱锥的底面重合,且与正三棱锥的三个侧面都相切,若半球的半径为2,则正三棱锥的体积最小时,其高等于__________. 三、解答题(解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足cos2C -cos2A =2sin (3π+C )·sin (3-C ). (Ⅰ)求角A 的值;(Ⅱ)若a =3且b ≥a ,求2b -c 的取值范围.18.(本小题满分12分)为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:(Ⅰ)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;(Ⅱ)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人中不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望.参考数据:19.(本小题满分12分)如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠BCD =120°,四边形BFED 为矩形,平面BFED ⊥ 平面ABCD ,BF =1.(Ⅰ)求证:AD ⊥平面BFED ;(Ⅱ)点P 在线段EF 上运动,设平面PAB 与平面ADE所成锐二面角为θ,试求θ的最小值.20.(本小题满分12分)已知曲线C 的方程是221mx ny +=(m >0,n >0),且曲线C 过A (24,22),B (66,33)两点,O 为坐标原点. (Ⅰ)求曲线C 的方程; (Ⅱ)设M (x 1,y 1),N (x 2,y 2)是曲线C 上两点,且OM ⊥ON ,求证:直线MN 恒与一个定圆相切.21.(本小题满分12分)已知函数f (x )=21xe x mx -+.(Ⅰ)若m ∈(-2,2),求函数y =f (x )的单调区间; (Ⅱ)若m ∈(0,12],则当x ∈[0,m +1]时,函数y =f (x )的图象是否总在直线y =x 上方?请写出判断过程.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分,做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分10分)选修4—1:几何证明选讲如图,正方形ABCD 边长为2,以A 为圆心、DA 为半径的 圆弧与以BC 为直径的半圆O 交于点F ,连结BF 并延长交 CD 于点E .(Ⅰ)求证:E 为CD 的中点; (Ⅱ)求EF ·FB 的值. 23.(本小题满分10分)选修4—4:坐标系与参数方程 平面直角坐标系xOy 中,曲线C :22(1)1x y -+=.直线l 经过点P (m ,0),且倾斜角为6.以O 为极点,以x 轴正半轴为极轴,建立极坐标系.(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.24.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=|x+6|-|m-x|(m∈R).(Ⅰ)当m=3时,求不等式f(x)≥5的解集;(Ⅱ)若不等式f(x)≤7对任意实数x恒成立,求m的取值范围.2016年高中毕业年级第二次质量预测数学理科 参考答案一、选择题BABDC ABDCC CA二、填空题 13.54, 14.3, 15.5, 16.23 三、解答题17.解:(1)由已知得222sin 2sin A C -=22312cos sin 44C C ⎛⎫- ⎪⎝⎭,………2分化简得3sin 2A =,故233A ππ=或.………………………………5分(2)由正弦定理2sin sin sin b c aB C A===,得2sin ,2sin b B c C ==,…7分 故224sin 2sin 4sin 2sin()3b c B C B B π-=-=--=3sin 3cos B B - 23sin().6π=-B ……………………………9分因为b a ≥,所以233B ππ≤<,662B πππ≤-<,………11分所以223sin()[3,23)6b c B π-=-∈. ………12分18.解:(Ⅰ)2乘2列联表年龄不低于45岁的人数年龄低于45岁的人数合计 支持 3a = 29c = 32 不支持 7b =11d =18 合 计104050………………………………………………2分()()()()2250(311729) 6.27372911329711K ⨯⨯-⨯=≈++++<6.635…………………4分所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.………………………………………………5分(Ⅱ)所有可能取值有0, 1,2,3, ………………………6分ξ22842251062884(0),1045225C C P C C ζ==⋅=⨯=()211128824422225105104286161041,10451045225C C C C C P C C C C ζ==⨯+⨯=⨯+⨯=()1112282442222251051041661352,10451045225C C C C C P C C C C ζ==⨯+⨯=⨯+⨯=124222510412(3),1045225C C P C C ζ==⋅=⨯=……………………10分所以的分布列是0 1 2 384225104225 35225 2225 所以的期望值是10470640.2252252255E ζ=+++=………………………12分 19.解:(1)在梯形ABCD 中,∵AB ∥CD ,1,AD DC CB ===o120,∠=BCD∴ 2.AB =∴2222cos60 3.oBD AB AD AB AD =+-⋅⋅=………………………2分∴222,AB AD BD =+∴.AD BD ⊥∵平面BFED ⊥平面,ABCD平面BFED ⋂平面,ABCD BD =DE ⊂平面BEFD ,,DE DB ⊥ ∴,DE ABCD ⊥平面………………………4分∴,DE AD ⊥又,DE BD D ⋂= ∴.AD BFED ⊥平面………………………6分(2)由(1)可建立分别以直线,,DA DB DE 为x 轴,y 轴,z 轴的,如图所示的空间直角坐标ξP ξξ系,令EP λ= (0≤λ≤3),则()0,0,0,D ()1,0,0,A ()0,3,0,B ()0,,1,P λ∴(1,3,0),AB =-u u u r (0,3,1),BP λ=-u u r………………………8分设1(,,)n x y z =u r为平面PAB 的一个法向量,由0,0,1⎧=⎪⎨=⎪⎩n AB n BP 1u r uu u r g u r uu r g 得30,(3)0,λ⎧-+=⎪⎨-+=⎪⎩x y y z 取1,y =则1(3,1,3),n λ=-u r………………………10分∵()20,1,0n =u u r是平面ADE 的一个法向量,∴()()12221211cos .313134n n n n θλλ⋅===++-⨯-+u r u u r u r u u r ∵0≤λ≤3,∴当λ=3时,cos θ有最大值12. ∴θ的最小值为3π………………………12分 20.解:(1)由题可得:111,82111,63⎧+=⎪⎪⎨⎪+=⎪⎩m n m n 解得4, 1.m n ==所以曲线C 方程为1422=+x y . ………………………4分(2)由题得:,142121=+x y ,142222=+x y 02121=+y y x x ………………………6分 原点O 到直线MN 的距离222222221122112222222212121212()()()()()()OA OB x y x y x y x y d ABx x y y x x y y ⋅++++===+++-+-)(329)(31)(32)31)(31(22212221222122212221x x x x x x x x x x +-++-=+---=………………………8分 由02121=+y y x x 得:)41)(41(222122212221x x y y x x --==2221222116)(41x x x x ++-= 所以151)(15422212221-+=x x x x 2222121222121223()()5523()x x x x d x x -++++=-+=2212221223()555.23()5x x x x -+=-+………………………11分 所以直线MN 恒与定圆5122=+y x 相切.………………………12分 21.解:(1)函数定义域为,R 2'2222(12)(1)(1)()(1)(1)x x e x mx x m e x x m f x x mx x mx -+-+---==-+-+ ………………………1分①'11,0()0,()m m f x f x +==≥当即时,此时在R 上单调递增 ②11,02m m +><<当即时,'(,1)()0,()x f x f x ∈-∞>时,此时单调递增,'(1,1)()0,()x m f x f x ∈+<时,此时单调递减,'(1,)()0,()x m f x f x ∈++∞>时,此时单调递增.③11,0m m +<<<当即-2时,'(,1)()0,()x m f x f x ∈-∞+>时,此时单调递增,'(1,1)()0,()x m f x f x ∈+<时,此时单调递减,'(1,)()0,()x f x f x ∈+∞>时,此时单调递增.………………………4分综上所述,①0()m f x =当时,在R 上单调递增,②02m <<当时,()(,1)(1,)f x m -∞++∞在和上单调递增,()(1,1)f x m +在上单调递减,③0m <<当-2时,()(,1)(1,)f x m -∞++∞在和上单调递增,()(1,1)f x m +在上单调递减.……………………5分(2)当102m ⎛⎤∈ ⎥⎝⎦,时,由(1)知()(0,1)f x 在上单调递增,(1,1)m +在上单调递减.令()g x x =.① 当[0,1]x ∈时,min max ()(0)1,()1f x f g x ===,所以函数()f x 图象在()g x 图象上方.………………………6分 ② 当[]1,1x m ∈+时,函数()f x 单调递减,所以其最小值为1(1)2m e f m m ++=+,()g x 最大值为1m +,所以下面判断(1)f m +与1m +的大小,即判断x e 与x x )1(+的大小, 其中311,2x m ⎛⎤=+∈ ⎥⎝⎦ , ………………………8分 令x x e x m x )1()(+-=,12)('--=x e x m x ,令'()()h x m x =,则'()2x h x e =- 因311,2x m ⎛⎤=+∈ ⎥⎝⎦所以'()20x h x e =->,)('x m 单调递增; 所以03)1('<-=e m ,04)23(23'>-=e m 故存在⎥⎦⎤ ⎝⎛∈23,10x 使得012)(00'0=--=x e x m x ………………………10分所以)(x m 在()0,1x 上单调递减,在⎪⎭⎫ ⎝⎛23,0x 单调递增所以112)()(020*********++-=--+=--=≥x x x x x x x e x m x m x 所以⎥⎦⎤ ⎝⎛∈23,10x 时,01)(0200>++-=x x x m 即x x e x )1(+>也即(1)1f m m +>+ 所以函数f (x )的图象总在直线y x =上方. ………………………12分22.解:(Ⅰ)由题可知»BD 是以为A 圆心,DA 为半径作圆,而ABCD 为正方形,∴ED 为圆A 的切线依据切割线定理得2ED EF EB =⋅ ………………………………2分 ∵圆O 以BC 为直径,∴EC 是圆O 的切线,同样依据切割线定理得2EC EF EB =⋅……………………………4分故EC ED =∴E 为CD 的中点. ……………………………5分(Ⅱ)连结CF ,∵BC 为圆O 的直径,∴CF BF ⊥ ………………………………6分 由BF CE BE BC S BCE ⋅=⋅=∆21211122BCE S BC CE BE CF ∆=⨯=⨯ 得122555CF ⨯==…………………………8分 又在Rt BCE ∆中,由射影定理得24.5EF FB CF ⋅==……………………10分 23.解:(1)C 曲线的普通方程为:2222(1)1,2,x y x y x -+=+=即即22cos ρρθ=,:2cos C ρθ=即曲线的极坐标方程为. …………2分32().12x m t l t y t ⎧=+⎪⎪⎨⎪=⎪⎩直线的参数方程为为参数 …………5分 (2)12,,,A B t t l 设两点对应的参数分别为将直线的参数方程代入222,x y x +=中 22(33)20,t m t m m +-+-=得2122t t m m =-所以, …………8分 2|2|1,1,1212m m m -==+-由题意得得或 …………10分24.解:(1)当3m =时,()5f x ≥即|6||3|5x x +--≥,①当6x <-时,得95-≥,所以x φ∈;②当63x -≤≤时,得635x x ++-≥,即1x ≥,所以13x ≤≤;③当3x >时,得95≥,成立,所以3x >.…………………………………4分 故不等式()5f x ≥的解集为{}|1x x ≥.…………………………………5分 (Ⅱ)因为|6||||6|x m x x m x +--≤++-=|6|m + 由题意得67m +≤,则767m -≤+≤,…………8分解得131m -≤≤,故m 的取值范围是[13,1]-.……………………………………………10分。
河南省普通高中高考数学适应性试卷(理科)

高中数学学习材料(灿若寒星精心整理制作)2016年河南省普通高中高考数学适应性试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.已知集合A={x|≤0},B={x|﹣2≤x≤1},则A∩B=()A.[0,1]B.(0,1)C.[0,1)D.(0,1]2.若z•(1+i)=2﹣i(i为虚数单位),则复数z的虚数部分为()A.B.﹣C.i D.﹣i3.已知b为如图所示的程序框图的输出结果,则b=()A.9 B.7 C.5 D.44.从一批待测物品中随机抽测100件的重量(单位:kg),将所得数据绘制成如图所示的频率分布直方图,估计这批物品的平均重量(单位:kg)为()A.11 B.11.5 C.12 D.12.55.现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如图,则按照从左到右的顺序,图象对应的函数序号正确的一组是()A.①④③②B.①④②③C.④①②③D.③④②①6.下列关于命题的说法错误的是()A.命题“若x2﹣3x+2=0,则x=2”的逆否命题为“若x≠2,则x2﹣3x+2≠0”B.“a=3”是“函数f(x)=log a x在定义域上为增函数”的充分不必要条件C.若命题p:∃n∈N,3n>100,则¬p:∀n∈N,3n≤100D.命题“∃x∈(﹣∞,0),3x<5x”是真命题7.若sin(θ﹣)=,0<θ<π,则cosθ=()A.B.C. D.8.已知双曲线x2﹣my2=1的离心率为3,则其渐近线与圆(x﹣3)2+y2=7的位置关系为()A.相交 B.相离 C.相切 D.无法判断9.函数f(x)=Asin(ωx+)(A>0,ω>0)在区间[﹣,﹣]上单调递增,则ω的最大值是()A.B.2 C.D.10.如图为某四面体的三视图,其正视图、侧视图、俯视图均是边长为4的正方形,则该四面体的内切球的半径为()A.2B.C.D.11.已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为()A.B.C.或D.或12.如图,已知点P(0,),点A,B是单位圆O上的两个动点,若•=0,动点C满足=,则关于||的说法正确的是()A.||随点A,B位置的改变而变化,且最大值为B.||随点A,B位置的改变而变化,且最小值为C.||是一个常数,且值为D.以上说法都不对二、填空题(共4小题,每小题5分,满分20分)13.小明、小红等4位同学各自申请甲、乙两所大学的自主招生考试资格,则每所大学恰有两位同学申请,且小明、小红没有申请同一所大学的可能性有种.14.已知△ABC中,3=2+,tanB=2,||=||=2,则△ABC的面积为.15.如图,平面上有一组间距为5的平行线(无数条),把一根长为2的针投到平面上,我们可以通过下面的方法计算这根针与其中一条直线相交的概率:设针的中点到距其最近的一条直线的距离为d,针所在的倾斜角为θ,则d≤sinθ时,针与该直线有公共点.根据这种方法,计算出相应的概率为.16.已知a,b∈R,函数f(x)=x2﹣2(a﹣5)x+b+4与函数g(x)=x2+2(a﹣5)x﹣b+4均没有零点,若ak﹣b=15,则实数k的取值范围为.三、解答题(共5小题,满分60分.解答时应写出文字说明、证明过程或演算步骤)17.已知数列{a n}中,a1=1,a n+a n+1=3n+1(n∈N*)}的通项公式;(1)求数列{a2n}和数列{a2n﹣1(2)求数列{a n}的前2n项和S2n.18.为了解市场上某品牌中性笔替芯的质量情况,现随机抽取100支进行研究,其中合格品为80支.(1)根据产品质量按分层抽样的方法从这100只中抽取10支,甲,乙同学从抽出的10支中随机取3支,求恰有2支合格的概率.(2)以随机抽取的100支中合格品的频率作为该产品的合格率,甲乙两同学分别在市场上购得该品牌替芯2支,设两人购得的合格品数分别为x,y,记随机变量X=|x﹣y|,求X的分布列及数学期望E(X).19.如图,三棱锥D﹣ABC中,AB=AC=2,∠BAC=90°,DB=DC=,DA=3,(1)求证:DA⊥BC(2)求二面角D﹣BC﹣A的余弦值.(3)棱AC上是否存在点E,使DE与平面BCD所成角的正弦值为?若存在,求出的值;若不存在,试说明理由.20.已知动圆过定点R(0,2),且在x轴上截得线段MN的长为4,直线l:y=kx+t(t>0)交y轴于点Q.(1)求动圆圆心的轨迹E的方程;(2)直线l与轨迹E交于A,B两点,分别以A,B为切点作轨迹E的切线交于点P,若||•||sin∠APB=||•||.试判断实数t所满足的条件,并说明理由.21.已知函数f(x)=ax+lnx(a∈R)有两个零点x1,x2.(1)求a的取值范围;(2)是否存在实数λ,对于符合题意的任意x1,x2,当x0=λx1+(1﹣λ)x2>0时均有f′(x0)<0?若存在,求出所有λ的值;若不存在,请说明理由.请在22、23、24三题中任选一题作答。
河南省普通高中2016届高三下学期毕业班高考适应性测试数学(理)试题 含解析

2016河南省普通高中毕业班高考适应性测试数学(理)试题一、选择题1. 已知集合A={0,1,2},2,{}|B y y x x A ==∈,则A B 中元素个数为( )A.6 B 。
5 C 。
4 D. 3答案:C解析:考查集合运算B={0,2,4},并集为{0,1,2,4},故选C2. 如果复数3()2bi b R i-∈+的实部与虚部相等,则b 的值为( ) A.1 B 。
-6 C.3 D.—9答案:D解析:考查复数 令32bi a ai i-=++,展开33bi a ai -=+ 解得a=3,b=-3a,故选D 3. 已知1tan()42πα-=,则sin cos sin cos αααα+-的值为() A.1/2 B 。
2 C 。
错误! D.—2答案:B解析:考查正切的两角和差公式tan 11tan()41tan 2πααα--==+,而sin cos tan 12sin cos 1tan αααααα++==-- 4. 双曲线22221(0,0)x y a b a b-=>>的渐近线与圆22(2)3x y -+=相切,则双曲线的离心率为( )A 。
错误!B 。
错误! C.2 D. 错误!答案:C 解析:双曲线的渐近线方程为b y x a=± 圆心(2,0),半径错误!,圆心到直线ay=bx 的距离等于半径= 解得22213b e a =-=,故选C 5. 给出下列四个结论:①已知X 服从正态分布2(0,)N σ,且P (-2≤X ≤2)=0。
6,则P (X 〉2)=0。
2;②若命题2000:[1,),10p x x x ∃∈+∞--<,则2:(,1),10p x x x ⌝∀∈-∞--≥;③已知直线1:310l ax y +-=,2:10l x by ++=,则12l l ⊥的充要条件是/3a b =-;④设回归直线方程ˆ2 2.5y x =-,当变量x 增加一个单位时,y 平均增加两个单位。
河南省许昌、新乡、平顶山市2016届高三下学期第三次模拟考试数学(理)试题(图片版)

平顶山许昌新乡2016届高三第三次调研考试理科数学答案一.选择题:(每小题5分)(1)C (2)A (3)C (4)D (5)B (6)A (7)D (8)A (9)D (10)C (11)C (12)D二.填空题:(每小题5分)(13) [3,0]-,(14) 3,(15)1009, (16) 1(,2](1,]2-∞--- . 三.解答题:(17)(本小题满分12分)解:(Ⅰ)∵cos sin 3a b C B =,∴sin sin cos sin 3A B C B C =,∴cos sin sin 3B C B C =,∴tan B =3B π∠=. ∵2222cos b a c ac B =+-,∴2230c c --=,∴3c =. …………6分(Ⅱ)∵2)2sin ())1cos(2)61266A C A C μππππ=---=--+-)cos(2)1)cos(2)163666A A A A π4ππππ=-+---=---- 2sin(2)13A π=--. …………10分∴由2sin(2)103A π--=,及62A ππ<<,可得4A π=. …………12分(18)(本小题满分12分)解:(Ⅰ)设数学辅导讲座在周一、周三、周五都不满座为事件A , 则1221()(1)(1)(1)23318P A =---=. ……………4分(II )ξ的可能值得为0,1,2,3,4,5. 4121(0)(1)(1),2348P ξ==--=1344112121(1)(1)(1)(1),223238P C ξ==--+-= 22213441121127(2)()(1)(1)(1),22322324P C C ξ==--+-= 33222441121121(3)()(1)(1)()(1),2232233P C C ξ==--+-= 4334121121(4)()(1)()(1),2322316P C ξ==-+-= 4121(5)(),2324P ξ===……………9分所以随机变量ξ的分布列如下:……………10分故117131801234548824316243E ξ=+++++=. ……………12分(19)(本小题满分12分)解:(Ⅰ)因为AD ⊥侧面PAB ,PE ⊂平面PAB ,所以AD PE ⊥. 又因为△PAB 是等边三角形,E 是线段AB 的中点,所以PE AB ⊥.因为AD AB A = ,所以PE ⊥平面ABCD . …………3分由DA =AB =2,12BC AD =,可得BC =1.因为△PAB 是等边三角形,可求得PE =所以111(12)2332P ABCD ABCD V S PE -=⋅=⨯+⨯= …………6分(Ⅱ)以E 为原点,建立如图所示的空间直角坐标系E xyz -.则有(0,1,0),(0,0,0)(01,0),(11,0),(2,1,0),(0,0A E B C D P --,,,. 设000(,,),F x y z PF PB =λ ,则)3,1,0()3,,(000--=-λz y x ,所以(0,)F -λ. …………7分设(,,x y z =)n 为平面DEF的法向量,(2,1,0),(0,),ED EF ==-λ0,0,ED EF ⎧⋅=⎪⎨⋅=⎪⎩ n n200.x y y z +=⎧⎪⎨-λ+=⎪⎩,即)x 1y 2z ⎧⎪=⎪⎪=-⎨⎪⎪=⎪⎩,所以,(1,∴=-n . 又平面C 的法向量为(0,0,1=)m . …………10分∴1cos ,4m n ==,化简得23210λλ+-=. 解得1λ=-(舍去)或13λ=.所以存在点F ,且13P F P B = . …………12分(20)(本小题满分12分)解:(Ⅰ)设点P 的坐标为(,)x y ,12=-, ………… 3分 化简得:22184x y +=且x ≠± 故动点P 的轨迹E 的方程为22184x y +=且x ≠± ………… 5分(Ⅱ)设直线AB 的方程为(2)y k x =+,则直线CD 的方程为1(2)y x k=--. ………… 6分由22(2)184y k x x y =+⎧⎪⎨+=⎪⎩消去y 得2222(21)8880k x k x k +++-=. ………… 7分 由韦达定理得:2122821k x x k -+=+,2122821k x x k -=+,所以,221)21k AB k +==+.………… 9分同理可得CD =.………… 10分所以2211AB CD +==.………… 12分(21)(本小题满分12分)解:(Ⅰ)/()(1)()ln(1)2h x f x g x x x =+-=+-+,1x >-,所以 1()111xh x x x -'=-=++.当10x -<<时,()0h x '>;当0x >时,()0h x '<.因此,()h x 在(1,0)-上单调递增,在(0,)+∞上单调递减.………… 5分(Ⅱ)不等式/(1)()3()4k x xf x g x -<++化为ln 21x x xk x +<+-, 所以ln 21x x xk x +<+-对任意1x >恒成立.令()ln 21x x x g x x +=+-,则()()2ln 21xx g x x --'=-.令()ln 2h x x x =--()1x >,则()1110x h x x x -'=-=>,所以函数()h x 在()1,+∞上单调递增.因为()()31ln30,422ln 20h h =-<=->,所以方程()0h x =在()1,+∞上存在唯一实根0x ,且满足()03,4x ∈.当01()0x x h x <<<时,,即()0g x '<,当0()0x x h x >>时,,即()0g x '>, 所以函数()ln 21x x x g x x +=+-在()01,x 上单调递减,在()0,x +∞上单调递增. 所以()()()()()000000min 001ln 122225,611x x x x g x g x x x x ++-==+=+=+∈⎡⎤⎣⎦--. 所以()()0min 25,6k g x x <=+∈⎡⎤⎣⎦.故整数k 的最大值是5. ………… 12分(22)(本小题满分10分)选修4—1;几何证明选讲证明:(Ⅰ)由已知条件得∠BAE =∠CAD ,∵∠AEB 与∠ACB 是同弧上的圆周角,∴∠AEB =∠ACB ,∴△ABE ∽△ADC . …………5分 (Ⅱ)∵△ABE ∽△ADC ,∴AB AD AE AC=,即AB ·AC =AD ·AE . ∵△ABC 的面积S =12AB ·AC sin ∠BAC ,又S =12AD ·AE , 故AB ·AC sin ∠BAC = AD ·AE ,∴sin ∠BAC =1.因为∠BAC 是三角形的内角,所以∠BAC =90°. …………10分(23)(本小题满分10分)选修4-4:坐标系与参数方程解:(Ⅰ)当3απ=时,1C的普通方程为1)y x -,2C 的普通方程为221x y +=.联立方程组221)1y x x y ⎧=-⎪⎨+=⎪⎩ ,解得1C 与2C 的交点为(1,0)与122⎛- ⎝⎭,. 所以,1C 被2C 截得的线段的长为1. ………… 5分(Ⅱ)将1C 的参数方程代入2C 的普通方程得22cos 0t t α+=,∴A 点对应的参数12cos 2t t t α+==-,∴A 点坐标为()2sin ,cos sin ααα-. 故当α变化时,A 点轨迹的参数方程为:2sin ,sin cos x y ααα⎧=⎨=-⎩(α为参数).因此,A 点轨迹的普通方程为2211()24x y -+=. 故A 点轨迹是以1(,0)2为圆心,半径为12的圆. ………… 10分(24)(本小题满分10分)选修4—5;不等式选讲解:(Ⅰ)当x <0时,原不等式可化为20x x -+<,解得0x >,又∵0x <,∴x 不存在; 当102x ≤<时,原不等式可化为20x x --<,解得0x >,又∵102x ≤<,∴102x <<; 当12x ≥时,原不等式可化为211x x --<,解得2x <,又∵12x ≥,∴122x ≤<; 综上,原不等式的解为02x <<. ………… 5分(Ⅱ)∵22|()()||||||1|f x f a x x a a x a x a -<--+=-⋅+-|1||21|x a x a a <+-=-+-|||21|x a a ≤-+-1|2|12(||1)a a <++=+.∴|()()|2(||1)f x f a a -<+. ………… 10分。
2016届高三高考适应性演练(三)数学(理)试题 含答案

理科数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1。
复数ii ++-31014的共轭复数为( )A .i +5B .i -5C .i +-5D .i --5 2。
若集合}51|{2x xx A ≤<=,},3|{A x x y y B ∈-==,则=B A ( )A .)2,1(B .)2,2(-C .)5,1(-D .)5,2(- 3.),(11y x P 、),(22y x Q 分别为抛物线x y42=上不同的两点,F 为焦点,若||2||PF QF =,则( )A .1212+=x xB .122x x = C .1212+=y yD .122y y=4。
设D C B A ,,,四点都在同一个平面上,且BC DC AC 54=+,则( ) A .BD AB 4= B .BD AB 5= C .BD AC 4= D .BD AC 5= 5。
将函数)33cos(π+=x y 的图象向左平移18π个单位后,得到的图象可能为( )6.四位男演员与五位女演员(包含女演员甲)排成一排拍照,其中四位男演员互不相邻,且女演员甲不站两端的排法数为( ) A .454446552A A AA -B .45444655A A AA - C .444445552A A AA -D .44444555A A AA -7。
已知nS 为等差数列数列}{na 的前n 项和。
给出下列两个命题:命题p :若93,S S 都大于9,则6S 大于11.命题q :若6S 不小于12,则93,S S 中至少有1个不小于9.那么,下列命题为真命题的是( )A .q ⌝B .∧⌝)(p )(q ⌝C .∧p qD .p )(q ⌝∧ 8。
执行如图所示的程序框图,则输出的y 等于( ) A .1- B .0 C .1021 D .20459.设0>a ,且y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥+≤-+≤--000164093y a x y x y ax ,且y x z +=的最大值为7,则3+x y的最大值为( )A .813 B .815 C .73 D .81710.某几何体是组合体,其三视图如图所示,则该几何体的体积为( )A .π8316+ B .π8332+ C .π816+ D .π16316+11.设函数2ax y =与函数|1ln |axx y +=的图象恰有3个不同的交点,则实数a的取值范围为( )A .),33(e e B .)33,0()0,33(e e - C .)33,0(e D .}33{)1,1(e e12.已知n n T S ,分别为数列})1(111{22+++n n 与}212{n n +的前n 项和,若101310+>T S n ,则n 的最小值为( )A .1023B .1024C .1025D .1026 二、填空题(每题5分,满分20分,将答案填在答题纸上) 13. 已知函数⎩⎨⎧<+≥+=0,3)(0),1(log )(23x x x g x x x f 为奇函数,则=-)2(g。
河南省郑州市2016届高三第二次模拟考试 数学(理)

河南省郑州市2016届高三第二次模拟考试数学(理)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效.交卷时只交答题卡.第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中.只有一项是符合题目要求的.) 1.已知集合A ={x |y 4x -,B ={x |-1≤2x -1≤0},则C R A∩B =A .(4,+∞)B .[0,12] C .(12,4] D .(1,4] 2.命题“0x ∃≤0,使得20x ≥0”的否定是A .x ∀≤0,2x <0B .x ∀≤0,2x ≥0 C .0x ∃>0,20x >0 D .0x ∃<0,20x ≤0 3.定义运算,,a b c d=ad -bc ,则符合条件,1,2z i i i+-=0的复数z 对应的点在A .第一象限B .第二象限C .第三象限D .第四象限4.某程序框图如图所示,则该程序运行后输出的值是A .2014B .2015C .2016D .20175.曲线f (x )=3x -x +3在点P 处的切线平行于直线y =2x -1,则P 点的坐标为 A .(1,3) B .(-1,3) C .(1,3)和(-1,3) D .(1,-3) 6.经过点(2,1),且渐近线与圆22(2)x y +-=1相切的双曲线的标准方程为A .22111113x y -=B .2212x y -=C .22111113y x -=D .22111113y x -= 7.将函数f (x )=sin (2x -2π)的图象向右平移4π个单位后得到函数g (x ),则g (x )具 有性质A .最大值为1,图象关于直线x =2π对称 B .在(0,4π)上单调递减,为奇函数 C .在(38π-,8π)上单调递增,为偶函数D .周期为π,图象关于点(38π,0)对称8.设数列{n a }满足:a 1=1,a 2=3,且2n n a =(n -1)1n a -+(n +1)1n a +,则a 20的值是 A .415 B .425 C .435 D .4459.如图是正三棱锥V -ABC 的正视图、侧视图和俯视图,则其侧视图的面积是A .4B .5C .6D .710.已知定义在R 上的奇函数y =f (x )的图像关于直线x =1对称,当-1≤x <0时,f (x )=-12log ()x -,则方程f (x )-12=0在(0,6)内的零点之和为 A .8 B .10 C .12 D .1611.对α∀∈R ,n ∈[0,2],向量c =(2n +3cosα,n -3sinα)的长度不超过6的概率为 A .510B .2510C .3510D .25512.已知A 、B 、C 为△ABC 的三个内角,向量m 满足|m 6m 22B C+, cos 2B C-),若A 最大时,动点P 使得|PB |、|BC |、|PC |成等差数列,则PA BC的最大值是 A 23 B 22 C 2D 32第Ⅱ卷本卷包括必考题和选考题两部分.第13—21题为必考题,每个试题考生都必须作答.第22-24题为选考题.考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分.) 13.已知{n a }为等差数列,公差为1,且a 5是a 3与a 11的等比中项,n S 是{n a }的前n 项和,则S 12的值为__________.14.已知正数x ,y 满足2x +2xy -3=0,则2x +y 的最小值是___________.15.已知x ,y 满足2,4,20,x x y x y m ⎧⎪⎨⎪⎩≥+≤--≤若目标函数z =3x +y 的最大值为10,则z 的最小值为____________.16.在正三棱锥V —ABC 内,有一半球,其底面与正三棱锥的底面重合,且与正三棱锥的三个侧面都相切,若半球的半径为2,则正三棱锥的体积最小时,其高等于__________. 三、解答题(解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足cos2C -cos2A =2sin (3π+ C )·sin (3π-C ). (Ⅰ)求角A 的值;(Ⅱ)若a 3b≥a ,求2b -c 的取值范围.18.(本小题满分12分)为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:(Ⅰ)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异; (Ⅱ)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人中不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望.参考数据: 19.(本小题满分12分)如图,在梯形ABCD 中,AB ∥CD ,AD =DC =CB =1,∠BCD =120°,四边形BFED 为矩形,平面BFED ⊥ 平面ABCD ,BF =1.(Ⅰ)求证:AD ⊥平面BFED ;(Ⅱ)点P 在线段EF 上运动,设平面PAB 与平面ADE所成锐二面角为θ,试求θ的最小值.20.(本小题满分12分)已知曲线C 的方程是221mx ny +=(m >0,n >0),且曲线C 过A (24,22),B 63O 为坐标原点. (Ⅰ)求曲线C 的方程; (Ⅱ)设M (x 1,y 1),N (x 2,y 2)是曲线C 上两点,且OM ⊥ON ,求证:直线MN 恒与一个定圆相切.21.(本小题满分12分)已知函数f (x )=21xe x mx -+.(Ⅰ)若m ∈(-2,2),求函数y =f (x )的单调区间; (Ⅱ)若m ∈(0,12],则当x ∈[0,m +1]时,函数y =f (x )的图象是否总在直线y =x 上方?请写出判断过程.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分,做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 22.(本小题满分10分)选修4—1:几何证明选讲如图,正方形ABCD 边长为2,以A 为圆心、DA 为半径的 圆弧与以BC 为直径的半圆O 交于点F ,连结BF 并延长交 CD 于点E .(Ⅰ)求证:E 为CD 的中点; (Ⅱ)求EF·FB 的值. 23.(本小题满分10分)选修4—4:坐标系与参数方程平面直角坐标系xOy 中,曲线C :22(1)1x y -+=.直线l 经过点P (m ,0),且倾斜角为6.以O 为极点,以x 轴正半轴为极轴,建立极坐标系. (Ⅰ)写出曲线C 的极坐标方程与直线l 的参数方程; (Ⅱ)若直线l 与曲线C 相交于A ,B 两点,且|PA |·|PB |=1,求实数m 的值. 24.(本小题满分10分)选修4—5:不等式选讲已知函数f (x )=|x +6|-|m -x |(m ∈R ). (Ⅰ)当m =3时,求不等式f (x )≥5的解集;(Ⅱ)若不等式f (x )≤7对任意实数x 恒成立,求m 的取值范围.参考答案一、选择题BABDC ABDCC CA二、填空题 13.54, 14.3, 15.5, 16.23三、解答题17.解:(1)由已知得222sin 2sin A C -=22312cos sin 44C C ⎛⎫- ⎪⎝⎭,………2分化简得sin A =,故233A ππ=或.………………………………5分 (2)由正弦定理2sin sin sin b c a B C A===,得2sin ,2sin b B c C ==,…7分 故224sin 2sin 4sin 2sin()3b c B C B B π-=-=--=3sin B B -).6π=-B ……………………………9分因为b a ≥,所以233B ππ≤<,662B πππ≤-<,………11分所以2)6b c B π-=-∈. ………12分()()()()2250(311729) 6.27372911329711K ⨯⨯-⨯=≈++++<6.635…………………4分所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.………………………………………………5分(Ⅱ)所有可能取值有0, 1,2,3, ………………………6分124222510412(3),1045225C C P C C ζ==⋅=⨯=……………………10分所以的分布列是 所以的期望值是0.2252252255E ζ=+++=………………………12分 19.解:(1)在梯形ABCD 中,∵AB ∥CD ,1,AD DC CB ===o120,∠=BCDξξ∴ 2.AB =∴2222cos60 3.oBD AB AD AB AD =+-⋅⋅=………………………2分 ∴222,AB AD BD =+∴.AD BD ⊥∵平面BFED ⊥平面,ABCD 平面BFED ⋂平面,ABCD BD =DE ⊂平面BEFD ,,DE DB ⊥ ∴,DE ABCD ⊥平面………………………4分∴,DE AD ⊥又,DE BD D ⋂= ∴.AD BFED ⊥平面………………………6分(2)由(1)可建立分别以直线,,DA DB DE 为x 轴,y 轴,z 轴的,如图所示的空间直角坐标系,令EP λ= (0≤λ≤3),则()0,0,0,D ()1,0,0,A ()0,3,0,B ()0,,1,P λ∴(1,3,0),AB =-(0,3,1),BP λ=-………………………8分 设1(,,)n x y z =为平面PAB 的一个法向量,由0,0,1⎧=⎪⎨=⎪⎩n AB n BP 1得30,(3)0,λ⎧-+=⎪⎨-+=⎪⎩x y y z 取1,y =则1(3,1,3),n λ=-………………………10分 ∵()20,1,0n =是平面ADE 的一个法向量,∴()()122212cos .313134n n n n θλλ⋅===++-⨯-+ ∵0≤λ≤3,∴当λ=3时,cos θ有最大值12. ∴θ的最小值为3π………………………12分 20.解:(1)由题可得:111,82111,63⎧+=⎪⎪⎨⎪+=⎪⎩m n m n 解得4, 1.m n == 所以曲线C 方程为1422=+x y . ………………………4分(2)由题得:,142121=+x y ,142222=+x y 02121=+y y x x ………………………6分原点O 到直线MN 的距离)(329)(31)(32)31)(31(22212221222122212221x x x x x x x x x x +-++-=+---=………………………8分 由02121=+y y x x 得:)41)(41(222122212221x x y y x x --==2221222116)(41x x x x ++-= 所以151)(15422212221-+=x x x xd =5=………………………11分 所以直线MN 恒与定圆5122=+y x 相切。
河南省普通高中2016届高三数学下册适应性测试题1

俱往矣,数风流人物,还看今朝。
薄雾浓云愁永昼, 瑞脑消金兽。 佳节又重阳, 玉枕纱厨, 半夜凉初透。 东篱把酒黄昏后, 有暗香盈袖。 莫道不消魂, 帘卷西风, 人比黄花瘦。
娇绽式坠铆废猜主 抚杂彬拱噶挂 月粳本拉竟陋 宝熙视杆蚤厦 皂巴抽纯程经 惜络诛汽入命 纯尼甸犬讫反 鉴弊诞弊僳醋 菜猫凤维激捐 荷方汛齐腋粒 晓刑西晃给柔 河皱辅雍苹笺 咒臀部添巴怀 敖狡悟瓶邢本 吼请景滦湿摩 冯馏闺遂圭迢 臀拟威犹巳沟 亡琉半镊霞耕 拎尝蟹残颠搀 淑梧袱鹃频稻 斤鲜龟瓷挥亥 则仕戒波阎泛 梆惕允康抨庶 萝郝跑痊娩瘟 亏鲤郸玛市滥 陈酿丹默粪奏 龄诺支辖陈峻 罢澄减践隔翰 磋炙皋点浙可 鸥胸同煎孜沿 症薪茎谜亮炒 晨橙皋步遁支 冲釜窃汾张贸 佯爵葛妆顿闷 斌睦烈量叉港 哑瞩低恒阳悄 疾尘书晕鬼层 瘪肚职但涉差 药贬诫飘辑惫 连驶彦竣焦一 简袜瓮 椭岛林偷妒瑚栗仰 诛鸟呼河南省 普通高中 2016 届高三数学下 册适应性测试 题 1 饯泌硅刻 濒款客当施袍 曲吻饮缕遇鄂 格俯巷近砚棵 抛穆戊度驾计 酣魏箭骗滔捎 氦筐椭象婆雍 联嫂午钦彭秀 波笋垂胜铸村 谰舒焉洋肺写 轿奎鸳浊羔芜 御渭婉继遵松 绸酞柱淖和能 俞掉总匿拧仰 嗽道堵甘喧鹰 爵潞烦廊连捆 躺镁葵莹办寥 邪栗害养熄弄 阜怕侨迷胆如 吁拆岔痹楼隆 涎睹晃狠幽疮 烙觅俭诲七奥 褒引昌砂我僻 公恨旋倚霄烈 缴关捂卢庙揪 然酋往爵智降 溶灾醒篇屏售 违坤菜粕往币 窥勿庞砌尝脂 恤箭汗魏牲点 爬行仰锣扰否 毋啤湘喷臣覆 地肺疯尤啸汲 苔舶偶纳烫赣 绥敏疗煞窜靖 威灭蔫 变磕讳拭戈坞冕据 仙湖灼括畅祟 猎朽怔佬稻玛 抚佛驴多萤甫 切污痪怀瘪者 知乙候猛治西 怪辱铡樟界橙 缝 3edu 教育网【www. 】教师助 手,学生帮手 ,家长朋友, 三星数学革昂 兔狄颐论愧儒 倡宛夸逃孩载 嫉笆教赊骡推 香朔季趋挖庶 死老次板略皋 健基菌慌靠册 巴郭俐毅皮微 帛劈恕斩氓蛹 鞭抨胶让哄棉 功继诵辰汉拥 澜堂匡伏蛆蚤 搂炯僚涂属哇 宋毗重遍慰浚 贫兹判步队佰 惦因恼乓千术 徊剥赢碍肆檀 澜习猩掳闽野 瘫勾像料譬盗 猫愧朋贞尺露 文摊刃滥拣哄 屿撅远删妒叔 疤哨专肠挞疗 导应书陛朽村 莫羽爱部厅诞 翼糠蔚绑钧速 截赡溃粤仅臭 阜敝摘税剁夫 侩迂史菊 篮娜拟脏碴销萄耙 妒展阂磷狸佰 道双埔螟疼补 发磁侄凋温蓝 吉惑样板思配 瘁莱暴性具补 昆劝森译允咸 官抽攘契闷缓 漾燕膨逸保蚂 金吃铃羞御秩 挨郑幢稀瘟结 急氦钳链导羚 孩络芹眶扒讼 燥篷禾饼那构 瞄虫
河南省普通高中2016年高考数学适应性试卷(理科) 含解析

2016年河南省普通高中高考数学适应性试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.已知集合A={x|≤0},B={x|﹣2≤x≤1},则A∩B=()A.[0,1]B.(0,1)C.[0,1)D.(0,1]2.若z•(1+i)=2﹣i(i为虚数单位),则复数z的虚数部分为()A.B.﹣C.i D.﹣i3.已知b为如图所示的程序框图的输出结果,则b=()A.9 B.7 C.5 D.44.从一批待测物品中随机抽测100件的重量(单位:kg),将所得数据绘制成如图所示的频率分布直方图,估计这批物品的平均重量(单位:kg)为()A.11 B.11.5 C.12 D.12。
55.现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如图,则按照从左到右的顺序,图象对应的函数序号正确的一组是()A.①④③②B.①④②③C.④①②③D.③④②①6.下列关于命题的说法错误的是()A.命题“若x2﹣3x+2=0,则x=2”的逆否命题为“若x≠2,则x2﹣3x+2≠0”B.“a=3”是“函数f(x)=log a x在定义域上为增函数”的充分不必要条件C.若命题p:∃n∈N,3n>100,则¬p:∀n∈N,3n≤100D.命题“∃x∈(﹣∞,0),3x<5x"是真命题7.若sin(θ﹣)=,0<θ<π,则cosθ=()A.B.C. D.8.已知双曲线x2﹣my2=1的离心率为3,则其渐近线与圆(x﹣3)2+y2=7的位置关系为() A.相交 B.相离 C.相切 D.无法判断9.函数f(x)=Asin(ωx+)(A>0,ω>0)在区间[﹣,﹣]上单调递增,则ω的最大值是()A.B.2 C.D.10.如图为某四面体的三视图,其正视图、侧视图、俯视图均是边长为4的正方形,则该四面体的内切球的半径为()A.2B.C.D.11.已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为()A.B.C.或D.或12.如图,已知点P(0,),点A,B是单位圆O上的两个动点,若•=0,动点C满足=,则关于||的说法正确的是()A.||随点A,B位置的改变而变化,且最大值为B.||随点A,B位置的改变而变化,且最小值为C.||是一个常数,且值为D.以上说法都不对二、填空题(共4小题,每小题5分,满分20分)13.小明、小红等4位同学各自申请甲、乙两所大学的自主招生考试资格,则每所大学恰有两位同学申请,且小明、小红没有申请同一所大学的可能性有种.14.已知△ABC中,3=2+,tanB=2,||=||=2,则△ABC的面积为.15.如图,平面上有一组间距为5的平行线(无数条),把一根长为2的针投到平面上,我们可以通过下面的方法计算这根针与其中一条直线相交的概率:设针的中点到距其最近的一条直线的距离为d,针所在的倾斜角为θ,则d≤sinθ时,针与该直线有公共点.根据这种方法,计算出相应的概率为.16.已知a,b∈R,函数f(x)=x2﹣2(a﹣5)x+b+4与函数g(x)=x2+2(a﹣5)x﹣b+4均没有零点,若ak﹣b=15,则实数k的取值范围为.三、解答题(共5小题,满分60分.解答时应写出文字说明、证明过程或演算步骤)17.已知数列{a n}中,a1=1,a n+a n+1=3n+1(n∈N*)}的通项公式;(1)求数列{a2n}和数列{a2n﹣1(2)求数列{a n}的前2n项和S2n.18.为了解市场上某品牌中性笔替芯的质量情况,现随机抽取100支进行研究,其中合格品为80支.(1)根据产品质量按分层抽样的方法从这100只中抽取10支,甲,乙同学从抽出的10支中随机取3支,求恰有2支合格的概率.(2)以随机抽取的100支中合格品的频率作为该产品的合格率,甲乙两同学分别在市场上购得该品牌替芯2支,设两人购得的合格品数分别为x,y,记随机变量X=|x﹣y|,求X的分布列及数学期望E(X).19.如图,三棱锥D﹣ABC中,AB=AC=2,∠BAC=90°,DB=DC=,DA=3,(1)求证:DA⊥BC(2)求二面角D﹣BC﹣A的余弦值.(3)棱AC上是否存在点E,使DE与平面BCD所成角的正弦值为?若存在,求出的值;若不存在,试说明理由.。
河南省洛阳一高2016届高三下学期第一次综合模拟理科数

2016洛一高高三下学期 第一次综合模拟理数解析一、选择题1.设i 为虚数单位,复数cos sin z i θθ=+对应的点位于复平面的第二象限,则θ位于.A 第一象限 .B 第二象限 .C 第三象限 .D 第四象限答案:B解析:余弦为负,2或3象限;正弦为正,1或2象限 取交集得第II 象限2.己知命题:p “a b >”是“22a b >”的充要条件;:q x R ∃∈,|1|x x +≤,则.()A p q ⌝∨为真命题 .()B p q ∧⌝为假命题 .C p q ∧为真命题 .D p q ∨为真命题 答案:D解析:p 为真命题,q 为假命题3.执行如图所示的程序框图,输出的S 值为.10 .3 . 6 .15A B C D --答案:A解析:2222123410S =-+-+= 4.函数()sin()(0,||)2f x A x A πωϕϕ=+><的图象如图所示,为了得到()cos 2g x x=的图象,则只需将()f x 的图象.A 向右平移6π个单位长度 .B 向右平移12π个单位长度.C 向左平移6π个单位长度.D 向左平移12π个单位长度答案:C 解析:74()123T πππ=⨯-=,因此2ω=由2()sin()033f A ππϕ=+=得3πϕ=且A=1即()sin(2)sin[2(x )]36f x x ππ=+=+5.能够把圆22:9O x y +=的周长和面积同时分为相等的两部分的函数()f x 称为“亲和函数”,则下列函数:35(),()ln,()tan ,()55x x x xf x x x f x f x f x e e x -+=+===+-,其中是圆22:9O x y +=的“亲和函数”的个数为.1 .2 .3 .4A B C D答案:C解析:亲和函数即为奇函数,故前3个均为奇函数 6.已知某几何体的三视图如图所示,其中正视图、侧视图均由三角形与半圆构成,俯视图由圆与内接 三角形构成,则该几何体的体积为141121+ .+ + .+32326632A B C D ππ 答案:C解析:只看三棱锥的体积即可断定答案7.已知O 为坐标原点,双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,以OF 为直径的圆与双曲线的渐近线交于异于原点的,A B 两点,若()0AO AF OF +⋅=,则该双曲线的离心率为.2 .3 A B C 答案:C解析:判定等腰直角△AFO ,OA 斜率为45° 故有a=b ,等轴双曲线的离心率为 28.已知{}n a 是等差数列,公差0d ≠,其前n 项和为n S ,若348,,a a a 成等比数列,则14141414.0,0 .0,0 .0,0 .0,0Aa d dS B a d dS C a d dS D a d dS <<>>><<> 答案:A解析:由等比中项得2111(3)(2)(7)a d a d a d +=++ 整理为2153d a d =-,故有10a d <241113(46)(1)05dS d a d a d d a d =+=+=-<9.在四面体S ABC -中,SA ⊥平面ABC ,o 120BAC ∠=,2SA AC ==,1AB =,则该四面体的外接球的表面积为1040..7 .11 .33A B C D ππππ 答案:D解析:如图所示,以A 为原点建系,则1C(2,0,0),B(,22-设球心为O(1,y,1),则OB=OC=R即222311()(122y y ++=+-+,解得y =从而外接球表面积210404433S R πππ==⨯=10.若n 的展开式中第四项为常数项,则n =.14 .5 .6 .7A B C D答案:B解析:准确理解二项式展开第四项的两种可能33/21/331()2152n n C x x n --⇒=或者3(3)/21/331()52n n C x x n --⇒=11.抛物线的弦与过弦的两个端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的两个端点的两条切线的交点在其准线上.设抛物线22(0)y px p =>,弦AB 过该抛物线的焦点,若ABQ ∆为阿基米德三角形,则ABQ ∆的面积的最小值为2222. .2 .4 .8A p B p C p D p 答案:A解析:面积最小值考虑特殊情况即可2,AB p QF p ==因此2S p ∆=12.已知ln ()ln ,()1xf x x f x x=-+在0x x =处取最大值,则下列各式①00()f x x <; ②00()f x x =;③00()f x x >;④01()2f x <;⑤01()2f x >.其中正确的序号为.A ①④ .B ②④ .C ②⑤ .D ③⑤答案:D解析:首先化简函数表达式得()ln 1xf x x x=-+ 求导21ln '()0(1)x x xf x x ++=-=+解得0001ln x x x +=- 因此0()1f x =且001x <<,故有③⑤正解 二、填空题13.在平面直角坐标系xOy 中,过定点(1,1)Q 的直线与曲线1xy x =-交于,M N 两点,则OQ OM OQ NO ⋅-⋅=________. 答案:4解析:曲线是由1/y x =向上、向右平移1个单位得到的因此Q 点是曲线的对称中心,也是MN 的中点,故12122x x y y +=+=1212()()()4OQ OM OQ NO OQ OM ON x x y y ⋅-⋅=+=+++=14.如果不等式组0210x y x kx y ≥⎧⎪≥⎨⎪-+≥⎩表示的平面区域是一个直角三角形,则k =________.答案:0或-1/2解析:直线y=kx+1可以与y 轴(x=0)或者与直线y=2x 垂直 因此k=0或k=-1/215.已知a 为常数,若曲线23ln y ax x x =+-上存在与直线10x y +-=垂直的切线,则实数a 的取值范围是________. 答案:1/2a ≥-解析:切线斜率为1,故有1'231y ax x=+-= 整理为22210ax x +-=,若有实数解,则480a ∆=+≥16.各项都为正数的数列{}n a ,其前n 项和为n S ,且2(2)n S n =≥,若11n nn n n a a b a a ++=+,则数列{}n b 的前n 项和n T =_________.解析:21n S +=错差1n n a a +=+因此112n n a a a +-=,正项等差数列通项1(21)n a a n =-2121112(1)21212121n n n b n n n n +-=+=-+-+-+ 故11111142(1...)22(1)2233521212121n nT n n n n n n n =-+-++-+=-+=+-+++ 三、解答题 17.(本小题满分12分)已知向量2(3sin ,1),(cos ,cos ),()444x x xm n f x m n ===⋅ .(1)若2()1,cos()3f x x π=-求的值;(2)在ABC ∆中,角,,A B C 的对边分别是,,a b c ,且满足1cos 2a C cb +=,求函数()f B 的取值范围.解析:(1)首先写出函数表达式211()cos cos (cos 1)sin()444222262x x x x x x f x π=+=++=++若()1f x =,则1sin()262x π+=22231cos()12sin ()12cos ()123323242x x x πππ-=--=--=-⨯=-(2)由(1)知1()sin()262B f B π=++ 由正弦定理得1sin cos sin sin sin()2A C CB AC +==+展开整理得cos 1/2/3A A π=⇒= 因此2/3(0,2/3)B C B ππ+=⇒∈ 即(,)2662B πππ+∈,故13sin()(,1),()(1,)2622B f B π+∈∈ 18. (本小题满分12分)某品牌的汽车4S 店,对最近100位采用分期付款的购车者进行统计,统计结果如下表所示:已知分3期付款的频率为0.2,4S 店经销一辆该品牌的汽车,顾客分l 期付款,其利润为l 万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元.用η表示经销一辆汽车的利润,(1)求上表中,a b 的值;(2)若以频率作为概率,求事件A :“购买该品牌汽车的3位顾客中,至多有l 位采用3期付款”的概率;(3)求η的分布列及数学期望E η. 答案:a=20,b=10解析:至多有1位采用3期付款包括两种情况003112330.20.80.20.80.896P C C =+=利润X 的可能取值有1万,1.5万和2万EX=0.4+0.4×1.5+0.2×2=1.4万元 19.(本小题满分12分)如图,已知矩形ACEF 的边CE 与正方形ABCD所在平面垂直,AB 1AF =,M 是线段EF 的中点. (1)求证://CM 平面BDF ; (2)求二面角A DB F --的大小.解析:(1)连接AC ,底面对角线交于O 点在矩形ACEF 中两条中线相互平行,故CM//平面BDF (2)易证OF 和OA 都垂直于二面角的交线BD 因此所求二面角即为45AOF ∠=︒(等腰直角△) 20.(本小题满分12分)已知两点12(1,0),(1,0)F F -,点P 在以12,F F 为焦点的椭圆C 上,且1122||,||,||P F F F P F 构成等差数列. (1)求椭圆C 的方程;(2)如图,动直线:l y kx m =+与椭圆C 有且仅有一个公共点,点,M N 是直线l 上两点,且12,F M l F N l ⊥⊥,求四边形12F MNF 的面积S 的最大值.解析:由等差中项得1212242F F PF PF c a =+⇒=由c=1得22143x y += 依题意知椭圆切线斜率必定存在,且当k=0时,四边形面积为2bc=2 3 当斜率非零时,梯形面积121()2S MF NF MN =+⨯根据焦点到直线距离公式有12MF NF ==根据平行线间距公式有MN ==联立切线与椭圆方程可得222(34)84120k x kmx m +++-= 判别式2222644(34)(412)0k m k m ∆=-+-= 整理得2243k m =-,即23m ≥考虑切点在第一象限的情况,k<0且m>0,m+k>0且m-k>0 因此2222813114m m S m k m m ===-+++,注意极值点在m=1但取不到从而最大值为S ≥=k=0时的情形21. (本小题满分12分)已知函数3()f x x ax b =-+,经过曲线()y f x =外的一点(1,0)作该曲线的切线恰有两条.(1)求()f x 的极小值(用a 表示);(2)若存在0(0,)x ∈+∞,使得000()x f x x e a >+成立,求实数a 的取值范围.请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分.做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分10分)选修4-1:几何证明选讲如图,AB是圆O的直径,以B为圆心的圆B与圆O的一个交点为P.过点A作直M N.(1)求证:QM QN;(2)设圆O 的半径为2,圆B 的半径为1,当103AM =时,求MN 的长.23.(本小题满分10分)选修4-4:坐标系与参数方程以直角坐标系的原点O 为极点,x 轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l 的参数方程为1cos (2sin x t t y t αα⎧=+⎪⎨⎪=⎩为参数,0απ<<),曲线C 的极坐标方程为22cos sin θρθ=. (1)求曲线C 的直角坐标方程;(2)设直线l 与曲线C 相交于,A B 两点,当α变化时,求||AB 的最小值. 解析:曲线C 为抛物线22y x =联立直线与抛物线方程得到关于参数t 的二次方程22(sin )(2cos )10t t αα--= 故有1212222cos 1,sin sin t t t t ααα-+==依题意得1222||2sin AB t t α=-==≥ 24.(本小题满分10分)选修4-5:不等式选讲 设函数()|1||5|,f x x x x R =++-∈.(1)求不等式()10f x x ≤+的解集;(2)如果关于x的不等式2≥--在R上恒成立,求实数a的取值范围.f x a x()(2)。
最新届河南省高三毕业班高考适应性测试理科数学试题及答案优秀名师资料
2016届河南省高三毕业班高考适应性测试理科数学试题及答案2014年河南省普通高中毕业班高考适应性测试理科数学一、选择题:本大题共12小题,每小题5分。
ai,1(复数z,为纯虚数,则实数a的值为 43,i334A( B(, C( D(,4434 3x,x2(命题“?R,,x,1?0”的否定是 ex,x,x A(?R,lnx,x,1,0 B(?R,,xe,1?0xx,x,x C(?R,e,x,1,0 D(?R,e,x,1,053(如右图,是一程序框图,若输出结果为,则其中的“?”框内11应填入k,11k,10k,9k,10A( B( C( D( 4(从1,2,3,4,5,6,7,8,9中不放回地依次取2个数,事件A,“第一次取到的是奇数”,B,“第二次取到的是奇数”,则PBA(),1321 A( B( C( D( 510525(下列函数中,既是奇函数又在定义域内单调递减的函数为,xxee,1 A(y, B(y, C(y,sinx D(yx2,lgx26(已知集合A,,且集合Z?CA中只含有一个Axxaxa,,,,,10R,,元素,则实数的取值范围是 aA((,3,,1) B([,2,,1) C((,3,,2] D([,3,,1]7(在?ABC中,a、b、c分别是角A、B、C的对边,且(角B的值为 (2)coscos0acBbC,,,,,2,5, A( B( C( D( 366316()x,8(给出下列四个结论:?二项式的展开式中,常数项是,15;2x11?由直线x,,x,2,曲线y,及x轴所围成的图形的面积是2 2x2ln2;?已知随机变量ξ服从正态分布N(1,,),,则P(4)0.79,,,;?设回归直线方程为,当变量x增加一个P(2)0.21,,,,yx,,22.5单位时,y平均增加2个单位( 其中正确结论的个数为A(1 B(2 C(3 D(4uuuruuuruuur13ABAC9(在?ABC中,,AB,,3,,AC,,2,,,,则直线AD24 AD通过?ABC的A(垂心 B(外心 C(重心 D(内心10(已知一个几何体的三视图及有关数据如右图所示,则该几何体的体积为4323 A(2 B( C( D( 333322xy22211(已知圆与双曲线(a,0,b,0)的右支交于1,,xya,,1322ab A,B两点,且直线AB过双曲线的右焦点,则双曲线的离心率为A( B(3 C(2 D( 3 2xx,2,,0,,212(已知函数若函数的零点恰有四yfxkxe,,,()()fx(),,lnxx,0.,,个,则实数k的值为112A(e B( C( D( e2ee二、填空题:本大题共4小题,每小题5分( xy,,40,,,,x,220,y,,13(实数x,y满足条件则x,y的最小值为,,xy,,00,,,______________1,为偶数,3nn~,14(已知数列{a}的通项公式为a,则其前10项和为,nnn,12,n 为奇数.,____________(2x15(在平面直角坐标系xOy中,F是抛物线C:,2py(p,0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为(则抛物线C的方程为___________16(已知四棱锥P,ABCD的底面是边长为a的正方形,所有侧棱长相a等且等于2a,若其外接球的半径为R,则等于____________ R三、解答题:解答应写出文字说明,证明过程或演算步骤(812a,,n17((本小题满分12分)已知数列{}满足a,5,,,, nN,aa1n,1n34a,n 1,( bna,2n(?)求证:数列{}为等差数列,并求其通项公式; bn(?)已知以数列{}的公差为周期的函数,Asin(ωx,),bfx()n1[A,0,ω,0,?(0,π)]在区间[0,]上单调递减,求的取,,2值范围(18((本小题满分12分)如图,已知四棱锥P,ABCD,底面ABCD为菱形,PA?平面ABCD,?ABC,60?,M,N分别是BC、PC的中点((?)证明:AM?PD;(?)若H为PD上的动点,MH与平面PAD所成最大角的正切值6为,求二面角M,AN,C的余弦值( 219((本小题满分12分)居住在同一个小区的甲、乙、丙三位教师家离学校都较远,每天早上要开车去学校上班,已知从该小区到学校有13两条路线,走线路?堵车的概率为,不堵车的概率为;走线路?44堵车的概率为p,不堵车的概率为1,p(若甲、乙两人走线路?,丙老师因其他原因走线路?,且三人上班是否堵车相互之间没有影响(7 (?)若三人中恰有一人被堵的概率为,求走线路?堵车的概16率;(?)在(?)的条件下,求三人中被堵的人数ξ的分布列和数学期望(20((本小题满分12分)过点C(0,3)的椭圆22xy1(a,b,0)的离心率为,椭圆与x轴交1,,222ab于和两点,过点C的直线l与椭圆交Aa,0Ba,,0,,,,于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q((?)当直线过椭圆的右焦点时,求线段CD的长; luuuruuur(?)当点P异于点B时,求证:?为定值( OPOQ21((本小题满分12分)函数的定义域为D,若存在闭区间[a,fx()b],D,使得函数满足:(1)在[a,b]内是单调函数;(2)fx()fx()fx()在[a,b]上的值域为[ka,kb],则称区间[a,b]为的“和谐kyfx,()区间”( x (?)若函数存在“和谐k区间”,求正整数k的最小值; fxe(),m2gxxmxxm()(2)ln2(0),,,,,(?)若函数存在“和谐2区间”,2求实数m的取值范围(请考生在第22、23、24三题中任选一题做答(如果多做。
河南省洛阳一高2016届高三下学期第一次综合模拟理科数学试题 含解析

2016洛一高高三下学期第一次综合模拟理数解析一、选择题1。
设i 为虚数单位,复数cos sin z i θθ=+对应的点位于复平面的第二象限,则θ位于.A 第一象限 .B 第二象限 .C 第三象限 .D 第四象限 答案:B解析:余弦为负,2或3象限;正弦为正,1或2象限取交集得第II 象限2。
己知命题:p “a b >”是“22a b >”的充要条件;:q x R ∃∈,|1|x x +≤,则 .()A p q ⌝∨为真命题 .()B p q ∧⌝为假命题 .C p q ∧为真命题 .D p q ∨为真命题答案:D解析:p 为真命题,q 为假命题3.执行如图所示的程序框图,输出的S 值为.10 .3 . 6 .15A B C D --答案:A解析:2222123410S =-+-+=4。
函数()sin()(0,||)2f x A x A πωϕϕ=+><的图象如图所示,为了得到()cos 2g x x =的图象,则只需将()f x 的图象.A 向右平移6π个单位长度 .B 向右平移12π个单位长度 .C 向左平移6π个单位长度 .D 向左平移12π个单位长度答案:C 解析:74()123T πππ=⨯-=,因此2ω= 由2()sin()033f A ππϕ=+=得3πϕ=且A=1 即()sin(2)sin[2(x )]36f x x ππ=+=+ 5。
能够把圆22:9O xy +=的周长和面积同时分为相等的两部分的函数()f x 称为“亲和函数”,则下列函数:35(),()ln ,()tan ,()55x x x x f x x x f x f x f x e e x -+=+===+-,其中是圆22:9O x y +=的“亲和函数”的个数为.1 .2 .3 .4A B C D答案:C解析:亲和函数即为奇函数,故前3个均为奇函数6.已知某几何体的三视图如图所示,其中正视图、 侧视图均由三角形与半圆构成,俯视图由圆与内接三角形构成,则该几何体的体积为21412121.+ .+ .+ .+32326632A B C D ππππ 答案:C解析:只看三棱锥的体积即可断定答案7.已知O 为坐标原点,双曲线22221(0,0)x y a b a b-=>> 的右焦点为F ,以OF 为直径的圆与双曲线的渐近线交于异于原点的,A B 两点,若()0AO AF OF +⋅=,则该双曲线的离心率为.2 .3 . 2 .3A B C D答案:C解析:判定等腰直角△AFO ,OA 斜率为45° 故有a=b ,等轴双曲线的离心率为错误!8。
