2017年秋季新版沪科版八年级数学上学期14.2、三角形全等的判定同步练习6
沪科版数学八年级上册(基础练习)14.2《三角形全等的判定》

14.2《三角形全等的判定》基础练习
第1课时《SAS》
一、选择题
1.如图,AC、BD相交于点O,∠1=∠2,若用“SAS”说明△ACB≌△BDA,则还需要加上条件()
A.AD=BC B.BD=AC C.∠D=∠C D.OA=AB
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠DEF,补充下哪一条件后,能应用“SAS”判定△ABC≌△DEF()
A.AC=DF B.BE=CF C.∠A=∠D D.∠ACB=∠DFE
3.如图,AC与BD相交于点P,AP=DP,则需要“SAS”证明△APB≌△DPC,还需添加的条件是()
A.BA=CD B.PB=PC C.∠A=∠D D.∠APB=∠DPC
4.下列两个三角形全等的是()
A.①②B.②③C.③④D.①④
5.如图是将长方形纸片沿对角线折叠得到的,图中(包括实线、虚线在内)共有全等三角形()对.
A.2 B.3 C.4 D.5
6.如图,如果AD∥BC,AD=BC,AC与BD相交于O点,则图中的全等三角形一共有()
A.3对B.4对C.5对D.6对
7.如图,任意画一个△ABC(AC≠BC),在△ABC所在平面内确定一个点D,使得△ABD与△ABC全等,则符合条件的点D有()
A.1个B.2个C.3个D.4个
二、填空题
8.如图,在△ABC和△A′B′C′中,AB=A′B′,BC=B′C′,∠B=∠B′,则△ABC和△A′B′C′.
9.要使两个三角形全等,至少需个对应元素相等,其中至少有一组对应相。
沪科版八年级上册《全等三角形》同步练习(含详细答案)
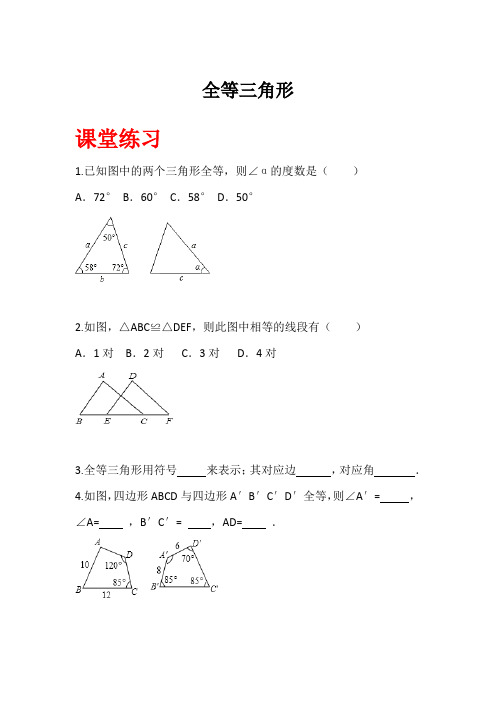
全等三角形
课堂练习
1.已知图中的两个三角形全等,则∠α的度数是()
A.72°B.60°C.58°D.50°
2.如图,△ABC≌△DEF,则此图中相等的线段有()
A.1对B.2对C.3对D.4对
3.全等三角形用符号来表示;其对应边,对应角.
4.如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′= ,∠A= ,B′C′= ,AD= .
5.如图所示是一个等边三角形,按下列要求分割图形
(1)用1条线段把图①分割成2个全等三角形图形(2)用3条线段把图②分割成3个全等三角形图形(3)用3条线段把图③分割成4个全等三角形图形
答案解析
1.D精讲精析:∵图中的两个三角形全等.a与a,c与c分别是对应边,那么它们的夹角就是对应角,
∴∠α=50°.
2.D精讲精析:∵△ABC≌△DEF∴AB=DE,AC=DF,BC=EF,∵BC=EF,即BE+EC=CF+EC,∴BE=CF.即有4对相等的线段.
3. ≌;相等;相等精讲精析:全等三角形用符号≌来表示;其对应边:相等,对应角:相等.
4.120°;70°;12;6精讲精析:由题意得:∠A′=∠120°,∠A=∠D=70°,B′C′=BC=12,AD=A′D′=6.
5.精讲精析:解:如图:①作高;
②作角平分线;
③连接各中点.。
沪科版八年级数学上第14章全等三角形检测题(含答案)

沪科版八年级数学上第14章全等三角形检测题(含答案)经过翻转、平移后,能够完全重合的两个三角形叫做全等三角形。
接下来我们一起来练习沪科版八年级数学上第14章全等三角形检测题。
沪科版八年级数学上第14章全等三角形检测题(含答案)一、选择题(每小题3分,共30分)1. 下列说法正确的是( )A.形状相同的两个三角形全等B.面积相等的两个三角形全等C.完全重合的两个三角形全等D.所有的等边三角形全等2. 如图所示,分别表示△ABC的三边长,则下面与△一定全等的三角形是()C D3. 在△中,∠∠,若与△全等的一个三角形中有一个角为95°,那么95°的角在△中的对应角是( )A.∠B.∠C.∠DD.∠∠4. 在△ABC和△中,AB= ,∠B=∠ ,补充条件后仍不一定能保证△ABC≌△ ,则补充的这个条件是( )A.BC=B.∠A=∠C.AC=D.∠C=∠5. 如图所示,点B、C、E在同一条直线上,△ABC与△CDE 都是等边三角形,则下列结论不一定成立的是()A.△ACE≌△BCDB.△BGC≌△AFCC.△DCG≌△ECFD.△ADB≌△CEA6. 要测量河两岸相对的两点的距离,先在的垂线上取两点,使,再作出的垂线,使在一条直线上(如图所示),可以说明△≌△,得,因此测得的长就是的长,判定△≌△最恰当的理由是()A.边角边B.角边角C.边边边D.边边角7. 已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是()A.∠A与∠D互为余角B.∠A=∠2C.△ABC≌△CEDD.∠1=∠28. 在△和△FED 中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件( )A.AB=EDB.AB=FDC.AC=FDD.∠A=∠F9. 如图所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE,其中一定正确的是()A.①②③B.②③④C.①③⑤D.①③④10. 如图所示,在△中,>,∥ =,点在边上,连接,则添加下列哪一个条件后,仍无法判定△与△全等()A. ∥B.C.∠ =∠D.∠ =∠二、填空题(每小题3分,共24分)11.(2019?黑龙江齐齐哈尔中考)如图,点B,A,D,E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是.(只填一个即可)12. 如图,在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是.13.6个边长相等的正方形的组合图形如图所示,则∠1+∠2+∠3= .14.如图所示,已知在等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE= 度.15.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .16.如图所示,在△ABC中,∠C=90°,AD平分∠CAB,BC=8 cm,BD=5 cm,那么点D到直线AB的距离是cm.17.如图所示,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的面积是.18.如图所示,已知在△ABC中,∠A=90°,AB=AC,CD平分∠ACB,DE⊥BC于E,若BC=15 cm,则△DEB的周长为cm.三、解答题(共46分)19.(6分)(2019?重庆中考)如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.20.(8分)如图所示,△ABC≌△ADE,且∠CAD=10°∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB 的度数.21.(6分)如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC. 求证:(1)EC=BF;(2)EC⊥BF.22.(8分) 如图所示,在△ABC中,∠C=90°,AD是∠BAC 的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.证明:(1)CF=EB;(2)AB=AF+2EB.23.(9分)如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC. 24.(9分)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)过点B作BF⊥CE于点F,交CD于点G(如图①),求证:AE=CG;(2)过点A作AH⊥CE,交CE的延长线于点H,并交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明. 第14章全等三角形检测题参考答案1. C 解析:能够完全重合的两个三角形全等,故C正确;全等三角形大小相等且形状相同,形状相同的两个三角形相似,但不一定全等,故A错;面积相等的两个三角形形状和大小都不一定相同,故B错; 所有的等边三角形不全等,故D错.2. B 解析:A.与三角形有两边相等,但夹角不一定相等,二者不一定全等;B.与三角形有两边及其夹角相等,二者全等;C.与三角形有两边相等,但夹角不相等,二者不全等;D.与三角形有两角相等,但夹边不相等,二者不全等.故选B.3. A 解析:一个三角形中最多有一个钝角,因为∠∠,所以∠B和∠只能是锐角,而∠是钝角,所以∠ =95°.4. C 解析:选项A满足三角形全等判定条件中的边角边,选项B满足三角形全等判定条件中的角边角,选项D满足三角形全等判定条件中的角角边,只有选项C 不满足三角形全等的条件.5. D 解析:∵△ABC和△CDE都是等边三角形,∴ BC=AC,CE=CD,∠BCA=∠ECD=60°,∴∠BCA+∠ACD=∠ECD+∠ACD,即∠BCD=∠ACE.在△BCD和△ACE中,∴△BCD≌△ACE(SAS),故A成立.∵△BCD≌△ACE,∴∠DBC=∠CAE.∵∠BCA=∠ECD=60°,∴∠ACD=60°.在△BGC和△AFC中,∴△BGC≌△AFC,故B成立.∵△BCD≌△ACE,∴∠CDB=∠CEA,在△DCG和△ECF中,∴△DCG≌△ECF,故C成立.6. B 解析:∵ BC⊥AB,DE⊥BD,∴∠ABC=∠BDE.又∵ CD=BC,∠ACB=∠DCE,∴△EDC≌△ABC(ASA). 故选B.7. D 解析:∵ AC⊥CD,∴∠1+∠2=90°.∵∠B=90°,∴∠1+∠A=90°,∴∠A=∠2.在△ABC和△CED中,∴△ABC≌△CED,故B、C选项正确,选项D错误.∵∠2+∠D=90°,∴∠A+∠D=90°,故A选项正确.8. C 解析:因为∠C=∠D,∠B=∠E,所以点C与点D,点B与点E,点A与点F是对应顶点,AB的对应边应是FE,AC的对应边应是FD,根据AAS,当AC=FD时,有△ABC≌△FED.9. D 解析:∵ AB=AC,∴∠ABC=∠ACB.∵ BD平分∠ABC,CE平分∠ACB,∴∠ABD=∠CBD=∠ACE=∠BCE.∴①△BCD≌△CBE(ASA).由①可得CE=BD, BE=CD,∴ AB-BE=AC-DC,即AE=AD. 又∠A=∠A,∴③△BDA≌△CEA (SAS).又∠EOB=∠DOC,所以④△BOE≌△COD(AAS).故选D.10. C 解析:A.∵∥,∴∠ =∠ .∵,∴△≌△,故本选项可以证出全等.B.∵ =,∠ =∠,∴△≌△,故本选项可以证出全等.C.由∠ =∠证不出△≌△,故本选项不可以证出全等.D.∵∠ =∠,∠ =∠,,∴△≌△,故本选项可以证出全等.故选C.11. BC=EF或∠BAC=∠EDF或∠C=∠F或AC∥DF等解析:由BD=AE,可得AB=DE.由BC∥EF,可得∠B=∠E.要使△ABC≌△DEF,需添加的一个条件是BC=EF或∠BAC=∠EDF或∠C=∠F或AC∥DF等.12.13. 135°解析:观察图形可知:△ABC≌△BDE,∴∠1=∠DBE.又∵∠DBE+∠3=90°,∴∠1+∠3=90°.∵∠2=45°,∴∠1+∠2+∠3=∠1+∠3+∠2=90°+45°=135°.14. 60 解析:∵△ABC是等边三角形,∴∠ABD=∠C,AB=BC.∵ BD=CE,∴△ABD≌△BCE,∴∠BAD=∠CBE.∵∠ABE+∠EBC=60°,∴∠ABE+∠BAD=60°,∴∠APE=∠ABE+∠BAD=60°.15. 55°解析:在△ABD与△ACE中,∵∠1+∠CAD=∠CAE +∠CAD,∴∠1=∠CAE.又∵ AB=AC,AD=AE,∴△ABD ≌△ACE(SAS).∴∠2=∠ABD.∵∠3=∠1+∠ABD=∠1+∠2,∠1=25°,∠2=30°,∴∠3=55°.16. 3 解析:由∠C=90°,AD平分∠CAB,作DE⊥AB于E,所以D点到直线AB的距离是DE的长.由角平分线的性质可知DE=DC.又BC=8 cm,BD=5 cm,所以DE=DC=3 cm.所以点D到直线AB的距离是3 cm.17. 31.5 解析:作OE⊥AC,OF⊥AB,垂足分别为E、F,连接OA.∵ OB,OC分别平分∠ABC和∠ACB,OD⊥BC,∴ OD=OE=OF.=×OD×BC+×OE×AC+×OF×AB=×OD×(BC+AC+AB)=×3×21=31.5.18. 15 解析:因为CD平分∠ACB,∠A=90°,DE⊥BC,所以∠ACD=∠ECD,CD=CD,∠DAC=∠DEC,所以△ADC≌△EDC,所以AD=DE,AC=EC,所以△DEB的周长=BD+DE+BE=BD+AD+BE.又因为AB=AC,所以△DEB的周长=AB+BE=AC+BE=EC+BE=BC=15 cm.19. 分析:∠ADB与∠FCE分别是△ADB与△FCE的两个内角,若能证明这两个三角形全等,则可证明∠ADB=∠FCE.这两个三角形中已具备一边(AB=FE)和一角(∠B=∠E)的条件,若能证明BD=EC,利用“SAS”即可证明这两个三角形全等,所需条件根据线段的和差关系容易得出.证明:∵ BC=DE,∴ BC+CD=DE+CD,即BD=CE.在△ABD与△FEC中,∴△ABD≌△FEC(SAS).20. 分析:由△ABC≌△ADE,可得∠DAE=∠BAC=(∠EAB-∠CAD),根据三角形外角的性质可得∠DFB=∠FAB+∠B.因为∠FAB=∠FAC+∠CAB,即可求得∠DFB的度数;根据三角形外角的性质可得∠DGB=∠DFB -∠D,即可得∠DGB的度数.解:∵△ABC≌△ADE,∴∠DAE=∠BAC=(∠EAB-∠CAD)=.∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°,∠DGB=∠DFB-∠D=90°-25°=65°.21. 分析:首先根据角之间的关系推出再根据边角边定理,证明△≌△,最后根据全等三角形的性质定理,得知.根据角的转换可求出.证明:(1)因为,所以.又因为在△与△中,所以△≌△ . 所以.(2)因为所以即22. 分析:(1)根据角平分线的性质“角平分线上的点到角两边的距离相等”可得点D到AB的距离=点D到AC的距离,即CD=DE.再根据Rt△CDF≌Rt△EDB,得CF=EB.(2)利用角平分线的性质证明△ADC≌△ADE,∴ AC=AE,再将线段AB进行转化.证明:(1)∵ AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴ DE=DC.又∵ BD=DF,∴ Rt△CDF≌Rt△EDB(HL),∴ CF=EB.(2)∵ AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴△ADC≌△ADE,∴ AC=AE,∴ AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.23. 证明:∵ DB⊥AC ,CE⊥AB,∴∠AEC=∠ADB=90°. 在△ACE与△ABD中,∴△ACE≌△ABD (AAS),∴ AD=AE.在Rt△AEF与Rt△ADF中,∴ Rt△AEF≌Rt△ADF(HL),∴∠EAF=∠DAF,∴ AF平分∠BAC.24.⑴证明:因为BF⊥CE于点F,所以∠CFB=90°,所以∠ECB+∠CBF=90°.又因为∠ACE +∠ECB=90°,所以∠ACE =∠CBF .因为AC=BC, ∠ACB=90°,所以∠A=∠CBA=45°.又因为点D是AB的中点,所以∠DCB=45°.因为∠ACE =∠CBF,∠DCB=∠A,AC=BC,所以△CAE≌△BCG,所以AE=CG.(2)解:BE=CM.证明:∵∠ACB=90°,∴∠ACH +∠BCF=90°.∵ CH⊥AM,即∠CHA=90°,∴∠ACH +∠CAH=90°,∴∠BCF=∠CAH.∵ CD为等腰直角三角形斜边上的中线,∴ CD=AD.∴∠ACD=45°.在△CAM与△BCE中,BC=CA ,∠BCF=∠CAH,∠CBE=∠ACM,我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。
沪科新版八年级(上) 中考题同步试卷:14.2 三角形全等的判定(03)

沪科新版八年级(上)中考题同步试卷:14.2 三角形全等的判定(03)一、选择题(共2小题)1.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,其中正确的结论有()A.0个B.1个C.2个D.3个2.如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若CE=3,且∠ECF =45°,则CF的长为()A.2B.3C.D.二、填空题(共3小题)3.如图,AC是矩形ABCD的对角线,AB=2,BC=2,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=.4.如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是.5.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE,BE,则∠AEB的度数为.三、解答题(共25小题)6.如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连接BD,与AC交于点E,连接AD,CD.(1)求证:△ABC≌△ADC;(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.7.如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC 中点,BD平分∠ABC,点F在AB上,且BF=BC.求证:(1)DF=AE;(2)DF⊥AC.8.已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE;(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.9.如图,△ABC和△EFD分别在线段AE的两侧,点C,D在线段AE上,AC=DE,AB ∥EF,AB=EF.求证:BC=FD.10.如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE 交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.11.已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:(1)△CDE≌△DBF;(2)OA=OD.12.如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.13.如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.14.如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.15.在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.16.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.17.如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.18.已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.(1)如图1,连接BD,AF,则BD AF(填“>”、“<”或“=”);(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.19.如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.20.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB =CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.21.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB;(2)AF=2CD.22.如图,在△ABC中,AB=AC,分别以B、C为圆心,BC长为半径在BC下方画弧.设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD(1)求证:AD平分∠BAC;(2)若BC=6,∠BAC=50°,求弧DE、弧DF的长度之和(结果保留π).23.如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.求证:(1)△EAB≌△EDC;(2)∠EFG=∠EGF.24.如图,四边形ABCD是正方形,点E在直线BC上,连接AE.将△ABE沿AE所在直线折叠,点B的对应点是点B′,连接AB′并延长交直线DC于点F.(1)当点F与点C重合时如图(1),易证:DF+BE=AF(不需证明);(2)当点F在DC的延长线上时如图(2),当点F在CD的延长线上时如图(3),线段DF、BE、AF有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.25.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.求证:AC=DF.26.如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.(1)求证:DE=AB.(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求的长.27.如图,∠1=∠2,∠3=∠4,求证:AC=AD.28.如图,AC=DC,BC=EC,∠ACD=∠BCE.求证:∠A=∠D.29.如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.(1)求证:CF=AD;(2)若∠ACB=90°,试判断四边形BFCD的形状,并说明理由.30.如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD.沪科新版八年级(上)中考题同步试卷:14.2 三角形全等的判定(03)参考答案一、选择题(共2小题)1.D;2.A;二、填空题(共3小题)3.;4.90°;5.30°;三、解答题(共25小题)6.;7.;8.;9.;10.;11.;12.;13.;14.;15.;16.;17.;18.=;19.;20.;21.;22.;23.;24.;25.;26.;27.;28.;29.;30.;。
沪科版八年级上册数学第14章 全等三角形含答案(模拟题)

沪科版八年级上册数学第14章全等三角形含答案一、单选题(共15题,共计45分)1、如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图所示),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是()A.边角边B.角边角C.边边边D.边边角2、如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需()A.AB=DCB.OB=OCC.∠C=∠DD.∠AOB=∠DOC3、某同学把一块三角形的玻璃打碎成三块(如图所示),在要到玻璃店去配一块完全一样的玻璃,应带第()块去配.A.①B.②C.③D.①②③都不可以4、如图:AB=AD,AE平分∠BAD,则图中有()对全等三角形。
A.2B.3C.4D.55、两个直角三角形中,如果有一条直角边对应相等.则:①若斜边上的高对应相等.那么这两个直角三角形全等;②若直角的平分线相等,那么这两个直角三角形全等;③若斜边上的中线对应相等,那么这两个直角三角形全等;④两个直角三角形都有一个锐角是30°,那么这两个直角三角形全等.其中正确命题的个数有()A.1个B.2个C.3个D.4个6、如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形()A.1对B.2对C.4对D.8对7、下列结论是正确的是()A.全等三角形的对应角相等B.对应角相等的两个三角形全等C.有两条边和一角对应相等的两个三角形全等D.相等的两个角是对顶角8、下列说法正确的是()A.顺次连接任意一个四边形四边的中点,所得到的四边形一定是平行四边形 B.平行四边形既是中心对称图形,又是轴对称图形 C.对角线相等的四边形是矩形 D.只要是证明两个直角三角形全等,都可以用“HL”定理9、如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么∠ABC的大小是( )A.40°B.45°C.50°D.60°10、如图,在Rt△ABC中,AC=BC=2,将△ABC绕点A逆时针旋转60°,连接BD,则图中阴影部分的面积是()A.2 ﹣2B.2C. ﹣1D.411、如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有( )对.A.2B.3C.4D.512、如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD 的中点,则AE的长为()A.6B.C.5D.13、如图,在△ABC和△DEF中,满足AB=DE,∠B=∠E,如果要判定这两个三角形全等,添加的条件错误的是()A. BC=EFB. AC=DFC.∠ A=∠ DD.∠ C=∠ F14、如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是()A.AASB.SASC.ASAD.SSS15、如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,有如下五个结论:①AO⊥ BC;②OD=OE;③△OEF是等边三角形;④△OEF≌△CEF;⑤∠OEF=54°则上列说法中正确的个数是()A. 2B. 3C. 4D. 5二、填空题(共10题,共计30分)16、阅读后填空:已知:如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OA=OD.分析:要证OA=OD,可证ABO≌ DCO;要证ABO≌ DCO,可先证ABC≌ DCB得出AB=DC这个结论;而用________可证ABC≌ DCB(填SAS或AAS或HL).17、如图,在Rt△ABC中,∠ACB = 90°,,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =________.18、如图,△ABC的顶点分别为A(0,3),B(﹣4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是________.19、如图,A,D,F,B在同一直线上,AE=BC,且AE∥BC.添加一个条件________ ,使△AEF≌△BCD.20、如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E,某同学分析图形后得出以下结论,上述结论一定正确的是________(填代号).①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△B CE.21、如图的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD.则△AED的周长为________cm.22、如图,,,.点,为线段上两点.现存在以下条件:① ;② ;③;④ .请在以上条件中选择一个条件,使得一定和全等,则这个条件可以为________.(请写出所有正确的答案)23、如图,已知∠ACB=∠DBC,请增加一个条件,使△ABC≌△DCB,你添加的条件为________.24、如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:⑴∠AFC=∠AFE⑵BF=DE⑶∠BFE=∠BAE⑷∠BFD=∠CAF.其中正确的结论是________(填写所正确结论的序号),25、如图,AC,BD相交于点O,AC=BD,AB=CD,写出图中两对相等的角________.三、解答题(共5题,共计25分)26、如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,AB=6,FC=4,求线段DB的长.27、如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30º,EF⊥AB,垂足为F,连结DF.(1)求证:AC=EF;(2)求证:四边形ADFE是平行四边形.28、如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,连接NC、BE交于点P.探究:试判断BE和CN的位置关系和数量关系,并说明理由.应用:Q是线段BC的中点,若BC=6,求PQ29、已知:在矩形中,是对角线,于点,于点.求证:30、已知:AD是△ABC中BC边上的中线,延长AD至E,使DE=AD,连接BE,求证:△ACD≌△EBD.参考答案一、单选题(共15题,共计45分)1、B2、B3、C4、B5、D6、C7、A8、A9、B10、C11、B12、B13、B14、B15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、30、。
沪科版八年级数学上册第14章-全等三角形知识例题讲解与练习

第14章 全等三角形【知识剖析】一、全等形:能够完全重合的两个图形,叫做全等形. 二、全等三角形的有关概念1、全等三角形的定义:能够完全重合的两个三角形,叫做全等三角形.2、全等三角形的对应元素:全等三角形中,互相重合的边叫做对应边;互相重合的角叫做对应角;互相重合的顶点叫做对应顶点.3、全等三角形的性质:全等三角形的对应边相等,对应角相等.注:用全等符号“≌”表示两个全等三角形时,通常把表示对应顶点的字母写在对应位置上.[例1] 如图,将△ABC 绕其顶点B 顺时针旋转一定角度后得到△DBE ,请说出图中两个全等三角形的对应边和对应角.[例2] (1)如图,△ABE 与△CED 是全等三角形,可表示为△ABE ≌_______,其中∠A=30°,∠B=70°,AB=3cm ,则∠D=_____,∠DEC =_____,CD=_____.(2)如图,△ABC ≌△DCB ,若CD=4cm ,∠A=28°,∠DBC=35°,则AB=_____,∠D=_____,∠ABC=_______.(3)如图,△AOB ≌△COD ,若CD=2cm ,∠B=45°,则AB=_____,∠D=______.[例3] 如图,△ACB ≌△A /CB /,∠A /CB=30°,∠ACB/=110°,则∠ACA/=______.[例4] 如图,在Rt △ABC 中,∠ACB=90°,且AC=BC=4cm ,已知△BCD ≌△ACE ,则四边形AECD 的面积是_________.[例5] 如图,将△ABC 沿直线DE 折叠后,使得点B 与点A 重合,已知AC=5cm ,△ADC 的周长为17cm ,则BC 的长为_______.[例6] 如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C /处,折痕为EF ,若∠EFC /=125°,那么∠ABE 的度数为________.三、全等三角形的判定 1、“边角边”定理:两边和它们的夹角对应相等的两个三角形全等.(SAS )ABC 和△DEF 中,AB DEB E BC EF =⎧⎪∠=∠⎨⎪=⎩ABC ≌△DEF 2、.(ASA ) 在△ABC 和△DEF 中,∵ B EBC EF C F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF 3、“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等.(AAS ) 在△ABC 和△DEF 中,∵B EC F AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF4、“边边边”定理:三边对应相等的两个三角形全等.(SSS)在△ABC和△DEF中,∵AB DE BC EF AC DF=⎧⎪=⎨⎪=⎩∴△ABC≌△DEF另外,判定两个直角三角形全等还有另一种方法.:斜边和一条直角边对应相等的两个直角三角形全等.(HL)在Rt△ABC和Rt△DEF中,∵AB DEAC DF=⎧⎨=⎩∴ Rt△ABC≌Rt△DEF四、全等三角形的证明思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AASASAASAAASSASAASSSSHLSAS[例7]如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.[例8]如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.求证:∠ACE=∠DBF.[例9]如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.[例10] 如图,AC=DF,AD=BE,BC=EF.求证:AC∥DF.[例11]如图,AD是△ABC中BC边上的中线,求证:1()2AD AB AC<+[例12]如图,AB∥CD,EC、EB分别平分∠BCD和∠CBA,点E在AD上,求证:BC=AB+CD.[例13]如图,已知△ABC中,AC=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF 的直角顶点D放在AC的中点上(直角三角形的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.(1)在图(1)中,DE交AB于M,DF交BC于N.①证明DM=DN;②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的.若不发生变化,求出其面积. (2)继续旋转至图(2)的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)继续旋转至图(3)的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明.【综合练习】一、选择题1、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A、3个B、2个C、1个D、0个2、下列说法正确的是()A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等3、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是()A. 相等B. 不相等C. 互余或相等D. 互补或相等4、已知△ABC≌△DEF,若∠A=50°,∠C=30°,则∠E等于()A. 30°B. 50°C.60°D.100°5、已知△ABC和△DEF中,∠B=∠E,∠C=∠F,若要△ABC≌△DEF,只要满足下列条件中的()A. AB=DFB.BC=DFC. AC=DED.BC=EF6、如图,AB=AC,EB=EC,那么图中的全等三角形共有()A. 1对B. 2对C.3对D.4对7、某同学不小心把一块三角形玻璃打碎,变成了如图所示的三块,现在要到玻璃店去配一块完全一样的玻璃,那么应带()去,才能配好.A. ①B.②C.③D.任意一块8、已知:的三边分别为,的三边分别为,且有,则与().A.一定全等 B.不一定全等 C.一定不全等 D.无法确定9、如图,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有( )A、△ABD≌△AFDB、△AFE≌△ADCC、△AEF≌△DFCD、△ABC≌△ADE(第9题)(第10题)(第11题)10、如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有()A.1个 B.2个C.3个D.4个11、如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为( )A、18B、32C、28D、2412、如果D是△ABC中BC边上一点,并且△ADB≌△ADC,则△ABC是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形二、填空题13、已知:△ABC ≌△A ′B ′C ′,∠A=∠A ′,∠B=∠B ′,∠C=70°,AB=15cm ,则∠C ′=_________,A ′B ′=__________.14、如图,在△ABC 和△FED ,AD=FC ,AB=FE ,当添加条件__________时,就可得到△ABC ≌△FED.(只需填写一个你认为正确的条件)(第14题) (第15题) (第16题)15、如图,BE ,CD 是△ABC 的高,且BD =EC ,判定△BCD ≌△CBE 的依据是 . 16、如图,在△ABC 中,AD=DE ,AB=BE ,∠A=80°,则∠CED=_____.17、如图,△ABC ≌△ADE ,BC 的延长线交DA 于点F ,交DE 于点G ,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB=_________.18、如图是重叠的两个直角三角形,将其中一个直角三角形沿BC 方向平移得到△DEF.如果AB=8cm ,BE=4cm ,DH=3cm ,那么图中阴影部分面积为_______cm 2. 三、解答题19、如图,在△ABC 中,F 为AC 的中点,E 为AB 上一点,D 为EF 延长线上一点,∠A=∠ACD.求证://CD AE .20、如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,已知EH=EB=3,AE=4,求CH 的长.21、如图,已知AD为△ABC的中线,试比较AB+AC与2AD的大小.22、如图,∠ABC=90°,AB=AC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E、F.求证:EF=CF-AE.23、(1)如图(1),A、E、F、C在同一条直线上,AE=CF,DE⊥AC,BF⊥AC,若AB=CD. 求证:BD平分EF;(2)若将图形变为图(2),其余条件不变,上述结论是否成立?请说明理由.24、如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B、C 在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:BD=DE+CE;(2)若直线AE绕点A旋转到图(2)的位置(BD<CE)时,其余条件不变,问BD与DE、CE 的关系如何?请给予证明;(3)若直线AE绕点A旋转到图(3)的位置(BD>CE)时,其余条件不变,问BD与DE、CE 的关系如何?请直接写出结果,不需证明.。
沪科版八年级数学全等三角形判定(6)(含答案)

沪科版八年级数学全等三角形判定(6)(含答案)课堂练习1.如图,△ADC≌△EDC≌△EDB,则∠B的度数为( )A.20°B.30°C.40°D.45°2.如图,在四边形ACBO中,AC=BC,∠A=∠B=90°,∠1=35°,则∠BCA的度数为( )A.145°B.130°C.110°D.70°3.如图,∠E=∠F=90°,∠B=∠C,AE=AF,有下列结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( )A.1个B.2个C.3个D.4个4.如图,AD=AB,∠C=∠E,∠CDE=55°,则∠ABE=___________.5.如图,在四边形ABCD中,AB=CD,AD=BC,∠A=100°,,则∠C=________.6.如图,在△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE.求证:△ABD≌△AEC.7.工人师傅常用角尺平分一个任意角做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合.过角尺顶点C作射线OC由做法得△MC≌△NOC的依据是( )A.AASB.SASC.ASAD.SSS8.如图,AD是△ABC中BC边上的高,下列能使△ABD≌△ACD的条件是A.AB=ACB.∠BAC=90°C.BD=ACD.∠B=45°9.如图,在△ABC中,AB>AC,D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF.则下列条件中,添加后仍无法判定△BFD与△EDF全等的是()A.EF∥ABB.BF=CFC.∠A=∠DFED.∠B=∠DEF10.如图,AC=DC,BC=EC,请你添加一个适当的条件:_______使得△ABC≌△DEC.11.如图,用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A1O1B1=∠AOB的依据是_________.12.如图,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.求证:BO=DO.13.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,求CH的长.14.如图,一张长方形纸片沿对角线剪开(如图①),得到两张三角形纸片(如图②),再将这两张三角形纸片摆成如图③形式,使点B、F、C、D在同一条直线上.(1)求证:AB⊥ED;(2)若PB=BC,请找出图中与此条件有关的对全等三角形,并给予证明.1.B2.C3.C4.125°5.100°6.∵∠BAC=∠DAE,∴∠BAC-∠BAE=∠DAE-∠BAE,即∠CAE=∠DAB.又AB=AE,AD=AC,∴△ABD≌△AEC7.D 8.A 9.C10.DE=AB11.SSS12.∵∠1=∠2,AC=AC,∠3=∠4,∴△ABC≌△ADC(ASA).∴AB=AD.∴△AOB≌△AOD(SAS).∴BO=DO13.在△ABC中,AD⊥BCCE⊥AB,∴∠AEH=∠ADB=90°∵∠EAH+∠AHE=90°,∠DHC+∠BCH=90°,∠EHA=∠DHC,∴∠EAH=∠BCH.∵∠AEH =∠BEC=90°,EH=EB,∴△AEH≌△CEB.∴AE=CE.∵EH=EB=3,AE=4,∴CH=114.(1)由于△ABC与△DEF是一张长方形纸片沿对角线剪开而得到的两张三角形纸片…∠ACB=90°,△ABC≌△DEF.∴∠A∠D.在△ANP和△DNC中,∠ANP=∠DNC,∴,∠APN=∠DCN∵∠ACB=90°∴∠DCN=90°.∴∠APN=90°,∴AB⊥ED(2)答案不唯一,如△ABC≌△DBP证明如下:在△ABC和△DBP 中,∠A=∠D,∠B=∠B,PB=BC,∴△ABC≌△DBP。
沪科版数学八年级上册(培优练习)14.2《三角形全等的判定》

14.2.1《三角形全等的判定》培优练习第1课时《SAS》一、选择题1.下列条件中,满足△ABC≌△A'B'C'的是()A.AB=A'B',AC=A'C',∠B=∠B' B.AB=A'B',BC=B'C',∠A=∠A'C.AC=A'C',BC=B'C',∠C=∠C' D.AC=A'C',BC=B'C',∠B=∠B'2.如图,AB=12m,CA⊥AB于A,DB上AB于B,且AC=4m.点P从点B向点A运动,每分走1m;点Q从点B向点D运动,每分走2m.P,Q两点同时出发,运动()min后,△CAP≌△PBQ.A.2 B.3 C.4 D.5二、填空题3.如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从点B以1m/min的速度向点A运动;点Q从点B以2m/min的速度向点D运动,P,Q两点同时出发,运动min后,△CAP≌△PBQ.4.如图,AB与CD相交于点E,AE=CE,如果根据“SAS”可以判定△ADE≌△CBE,那么只需要补充一个条件.三、解答题5.如图,AB=DB,BC=BE,∠1=∠2,试说明△ABE≌△DBC.第2课时《ASA》培优练习一、选择题1.如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是()A.∠B=∠C B.∠D=∠E C.∠BAC=∠EAD D.∠B=∠E2.如图所示,已知AB∥CD,AD∥BC,那么图中共有全等三角形()A.8对B.4对C.2对D.1对二、填空题3.如图,∠1=∠2,∠3=∠4,则图中全等三角形有对.4.△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“ASA”判定,还需要加条件;若加条件AB=AC,则可用判定.三、解答题5.如图B、C、E三点在同一直线上,AC∥DE,AC=CE,∠ACD=∠B,求证:△ABC≌△CDE.第3课时《SSS》培优练习一、选择题1.若干个正六边形拼成的图形中,下列三角形与△ACD全等的有()A.△BCE B.△ADF C.△ADE D.△CDE2.在四边形ABCD和四边形A'B'C'D'中,已知AB=A'B',BC=B'C',CD=C'D',∠A=∠A'.要使四边形ABCD≌四边形A'B'C'D',可以增加的条件是()A.∠B=∠B' B.∠C=∠C' C.∠D=∠D' D.DA=D'A'二、填空题3.如图所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明≌或≌.4.在平面直角坐标系中,点A(1,2),B(6,5),C(5,2),存在点E,使△AEC和△ABC 全等,写出所有满足条件的E点的坐标.三、解答题5.如图,AB=AE,AC=AD,BD=CE,△ABC≌△AED吗?试说明.第4课时《其他判定两个三角形全等的条件》培优练习一、选择题1.如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有()A.4 组B.3 组C.2 组D.1 组2.如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是()A.相等B.不相等C.互余或相等D.互补或相等二、填空题3.如图,AB∥CD,AD∥BC,图中全等三角形共有对.4.如图,AB=AC,若利用“ASA”来说明△ABE≌△ACD,则还需补充的条件是;若利用“AAS”来说明△ABE≌△ACD,则还需补充的条件是.三、解答题5.如图,已知AD∥CE,∠1=∠2.(1)试说明AB∥CD;(2)若点D为线段BE中点,试说明△ABD≌△CDE.第5课时《两个直角三角形全等的判定》培优练习一、选择题1.在平面直角坐标系内,点O为坐标原点,A(﹣4,0),B(0,3).若在该坐标平面内有以点P(不与点A、B、O重合)为一个顶点的直角三角形与Rt△ABO全等,且这个以点P 为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的三角形个数为()A.9 B.7 C.5 D.32.如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的直角三角形有()A.3对B.4对C.5对D.6对二、填空题3.如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A 点出发以2/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动秒时,△DEB与△BCA全等.4.已知Rt△ABC的两直角边不相等,如果要画一个三角形与Rt△ABC全等,且使所画三角形两条直角边与Rt△ABC的两条直角边分别在同一条直线上(Rt△ABC本身不算),那么满足上述条件的三角形最多能画出个.三、解答题5.(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE 的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE 的关系如何?请予以证明.第6课时《全等三角形的判定方法的综合》培优练习一、选择题1.小明用五根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是()A.∠A=∠C B.∠ABC=∠CDA C.∠ABD=∠CDB D.∠ABD=∠C2.如图,在△ABC中,AB=AC,点D是△ABC外一点,连接AD、BD、CD,且BD交AC于点O,在BD上取一点E,使得AE=AD,∠EAD=∠BAC.若∠ACB=70°,则∠BDC的度数为()A.30°B.40°C.50°D.60°二、填空题3.如图,把△ABC的中线CD延长到E,使DE=CD,连接AE,若AC=4且△BCD的周长比△ACD的周长大1,则AE=.4.如图,在平面直角坐标系中,已知点A(0,3),点B(9,0),且∠ACB=90°,CA=CB,则点C的坐标为.三、解答题5.如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.(1)判断BF与AC的数量关系并说明理由;(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.参考答案第1课时1.解:AB=A'B',AC=A'C',∠B=∠B',不符合SAS,选项A不满足△ABC≌△A'B'C';AB=A'B',BC=B'C',∠A=∠A',不符合SAS,选项B不满足△ABC≌△A'B'C';AC=A'C',BC=B'C',∠C=∠C',符合SAS,选项C满足△ABC≌△A'B'C';AC=A'C',BC=B'C',∠B=∠B',不符合SAS,选项D不满足△ABC≌△A'B'C'.故选:C.2.解:设t min后△CAP≌△PBQ,由题意的,AP=AB﹣BP=12﹣t,BQ=2t,当△CAP≌△PBQ时,AP=BQ,即12﹣t=2t,解得:t=4,即4 min后△CAP≌△PBQ.故选:C.3.解:设t min后△CAP≌△PBQ,由题意的,AP=AB﹣BP=12﹣t,BQ=2t,当△CAP≌△PBQ时,AP=BQ,即12﹣t=2t,解得:t=4,即4 min后△CAP≌△PBQ.故答案为:4.4.解:需要补充条件DE=BE,∵在△DAE和△BCE中,∴△ADE≌△CBE(SAS),故答案为:DE=BE.5.证明:∵∠1=∠2,∴∠ABE=∠DBC,在△ABE和△DBC中,,∴△ABE≌△DBC(SAS).第2课时1.解:∠BAC=∠EAD,理由是:∵∠BAC=∠EAD,∴∠BAC+∠CAE=∠EAD+∠CAE,∴∠BAE=∠CAD,在△ACD和△ABE中,,∴△ACD≌△ABE(SAS),选项A、选项B,选项D的条件都不能推出△ACD≌△ABE,只有选项C的条件能推出△ACD ≌△ABE,故选:C.2.解:∵AB∥CD,AD∥BC,∴∠CAD=∠ACB,∠BDA=∠DBC,∠BAC=∠DCA,∠ABD=∠CDB,又∵AC、BD为公共边,∴△ACD≌△CAB、△BAD≌△DCB(ASA);∴AD=BC,AB=CD,∴△AOD≌△COB、△AOB≌△COD(ASA).所以全等三角形有:△AOD≌△COB、△AOB≌△COD、△ACD≌△CAB、△BAD≌△DCB,共4对;故选B.3.解:连接AC,∵∠1=∠2,BD=BD,∠3=∠4,∴△ABD≌△CBD(ASA),∴AB=BC,∵∠1=∠2,BE=BE,∴△ABE≌△CBE,(SAS),∵∠3=∠4,∴△ADF≌△CDF,同理,△AED≌△CED,△ABF≌△CBF,△ABD≌△CBD.△AEF≌△CEF 所以共有6对故答案为:6.4.解:△ABC中,AD⊥BC于D,要使△ABD≌△ACD,若根据“ASA”判定,还需要加条件∠DAB=∠DAC.理由:∵∠BAD=∠CAD,AD=AD,∠ADB=∠ADC,∴△ABD≌△ACD(ASA).若添加AB=AC,则全等的理由是HL,故答案为∠BAD=∠CAD,HL.5.证明:∵AC∥DE,∴∠ACB=∠E,∠ACD=∠D,∵∠ACD=∠B,∴∠D=∠B,在△ABC和△EDC中,∴△ABC≌△CDE(AAS).第3课时1.解:根据图象可知△ACD和△ADE全等,理由是:∵根据图形可知AD=AD,AE=AC,DE=DC,在△ACD和△AED中,,∴△ACD≌△AED(SSS),故选:C.2.解:添加的条件是DA=D′A′.连接BD,B′D′,∵在△ABD和△A′B′D′中,∴△ABC≌△A′B′C′(SAS),∴∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,BD=B′D′,在△BCD和△B′C′D′,∴△ACD≌△A′C′D′(SSS),∴∠DBC=∠D′B′C′,∠C=∠C′,∠BDC=∠B′D′C′∴∠ABC=∠A′B′C′,∠ADC=∠A′D′C′,∴四边形ABCD≌四边形A′B′C′D′,故选:D.3.解:在△ACD和△BDC中,,∴△ACD≌△BDC(SSS);在△ABD和△BAC中,,∴△ABD≌△BAC(SSS).故答案为:△ACD;△BDC;△ABD;△BAC.4.解:如图所示:有3个点,△ACE和△ACB全等,点E的坐标是:(0,5),(0,﹣1),(6,﹣1),故答案为:(0,5)或(0,﹣1)或(6,﹣1).5.△ABC≌△AED,证明:∵BD=CE,∴BC=ED,在△ABC和△AED中,,∴△ABC≌△AED.第4课时1.解:第①组AB=DE,∠B=∠E,∠C=∠F,满足AAS,能证明△ABC≌△DEF.第②组AB=DE,∠B=∠E,BC=EF满足SAS,能证明△ABC≌△DEF.第③组∠B=∠E,BC=EF,∠C=∠F满足ASA,能证明△ABC≌△DEF.所以有3组能证明△ABC≌△DEF.故选:B.2.解:第一种情况,当两个三角形全等时,是相等关系,第二种情况,如图,AC=AC′,高CD=C′D′,∴∠ADC=∠AD′C′,在Rt△ACD和Rt△AC′D′中,,Rt△ACD≌Rt△AC′D′(HL),∴∠CAD=∠C′AD′,此时,∠CAB+∠C′AB=180°,是互补关系,综上所述,这两个三角形的第三条边所对的角的关系是“相等或互补”.故选:D.3.解:∵AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).故图中的全等三角形共有4对.故答案为4.4.解:∵∠A=∠A,AB=AC,∴只需补充∠B=∠C,即可利用“ASA”来说明△ABE≌△ACD.∵∠A=∠A,AB=AC,∴只需补充∠AEB=∠ADC,即可利用“AAS”来说明△ABE≌△ACD.故答案为:∠B=∠C;∠AEB=∠ADC.5.解:(1)∵AD∥CE,∵∠1=∠2,∴∠ADC=∠1,∴AB∥CD;(2)∵AD∥CE,∴∠ADB=∠CED,∵D 是BE中点,∴BD=DE,在△ABD和△CDE中,∴△ABD≌△CDE(AAS).第5课时1.解:如图:分别以OA、OB、AB为边作与Rt△ABO全等的三角形各有3个,则所有符合条件的三角形个数为9.故选:A.2.解:∵BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°,∵AC=AB,∵∠CAE=∠BAD,∴△AEC≌△ADB;∴CE=BD,∵AC=AB,∵∠BEC=∠CDB=90°,∴△BCE≌△CBD;∴BE=CD,∴AD=AE,∵AO=AO,∴△AOD≌△AOE;∵∠DOC=∠EOB,∴△COD≌△BOE;∴OB=OC,∵AB=AC,∴CF=BF,AF⊥BC,∴△ACF≌△ABF,△COF≌△BOF.∵∠ABO=∠ACO共6对,故选D.3.解:①当E在线段AB上,AC=BE时,△ACB≌△BED,∵AC=4,∴BE=4,∴AE=8﹣4=4,∴点E的运动时间为4÷2=2(秒);②当E在BN上,AC=BE时,∵AC=4,∴BE=4,∴AE=8+4=12,∴点E的运动时间为12÷2=6(秒);③当E在线段AB上,AB=EB时,△ACB≌△BDE,这时E在A点未动,因此时间为0秒;④当E在BN上,AB=EB时,△ACB≌△BDE,AE=8+8=16,点E的运动时间为16÷2=8(秒),故答案为:0,2,6,8.4.解:如图所示:△AMC,△EFC,△EGC,△HGC,△HFC,△BCN,△MNC共7个,故答案为:7.5.解:(1)∵∠BAC=90°,BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°,∵∠ABD+∠BAE=90°,∠CAE+∠BAE=90°∴∠ABD=∠CAE,∵AB=AC,在△ABD和△CAE中,∵,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∵AE=AD+DE,∴BD=DE+CE;(2)BD=DE﹣CE;∵∠BAC=90°,BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°,∴∠ABD+∠DAB=∠DAB+∠CAE,∴∠ABD=∠CAE,∵AB=AC,在△ABD和△CAE中,∵,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∴AD+AE=BD+CE,∵DE=BD+CE,∴BD=DE﹣CE.第6课时1.解:∵AB=CD,AD=CB又BD=DB∴△ABD≌△CDB∴∠A=∠C,∠ABD=∠CDB;又∠ABD=∠CDB,∠CBD=∠ADB∴∠ABC=∠CDA,∠ABD与∠C不是对应角不相等.故选:D.2.解:∵∠BAC=∠EAD∴∠BAC﹣∠EAC=∠EAD﹣∠EAC即:∠BAE=∠CAD在△ABE和△ACD中∴△ABE≌△ACD (SAS)∴∠ABD=∠ACD.∵∠BOC是△ABO和△DCO的外角∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC∴∠ABD+∠BAC=∠ACD+∠BDC∴∠BAC=∠BDC∵∠ACB=65°,AB=AC∴∠ABC=∠ACB=70°∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°∴∠BDC=∠BAC=40°.故选:B.3.解:∵CD为△ABC的中线,∴AD=BD,在△ADE和△BDE中,∴△ADE≌△BDE,∴AE=BC,∵△BCD的周长比△ACD的周长大1,∴CD+BD+BC=AC+AD+CD+1,∴BC=AC+1=4+1=5,∴AE=5.故答案为5.4.解:如图,过点C作CE⊥OA,CF⊥OB,∵∠AOB=90°,∴四边形OECF是矩形,∴∠ECF=90°,∵∠ACB=90°,∴∠ACE=∠BCE在△ACE和△BCF中,,∴△ACE≌△BCF,∴CE=CF,∵四边形OECF是矩形,∴矩形OECF是正方形,∴OE=OF,∵AE=OE﹣OA=OE﹣3,BF=OB﹣OF=9﹣OF,∴OE=OF=6,∴C(6,6),故答案为:(6,6);5.解:(1)BF=AC,理由是:如图1,∵AD⊥BC,BE⊥AC,∴∠ADB=∠AEF=90°,∵∠ABC=45°,∴△ABD是等腰直角三角形,∴AD=BD,∵∠AFE=∠BFD,∴∠DAC=∠EBC,在△ADC和△BDF中,∵,∴△ADC≌△BDF(AAS),∴BF=AC;(2)NE=AC,理由是:如图2,由折叠得:MD=DC,∵DE∥AM,∴AE=EC,∵BE⊥AC,∴AB=BC,∴∠ABE=∠CBE,由(1)得:△ADC≌△BDF,∵△ADC≌△ADM,∴△BDF≌△ADM,∴∠DBF=∠MAD,∵∠DBA=∠BAD=45°,∴∠DBA﹣∠DBF=∠BAD﹣∠MAD,即∠ABE=∠BAN,∵∠ANE=∠ABE+∠BAN=2∠ABE,∠NAE=2∠NAD=2∠CBE,∴∠ANE=∠NAE=45°,∴AE=EN,∴EN=AC.。
沪科版数学八年级上册14.2三角形全等的判定专题训练及答案

14.2 三角形全等的判定专题一 利用全等进展测量1. 1805年,法国拿破仑率军与德军在莱茵河激战,德军在河北岸Q处,如图,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸O处调整好自己的帽子,使视线恰好擦过帽舌边沿看到敌军兵营Q处,然后后退到B 点,这时他的视点恰好能落在O 处,于是他命令部下测量他脚站的B 处与O 点之间的距离,并下令按这个距离炮轰敌兵营,法军能命中吗?说明理由.2.某同学根据数学知识原理制作了如下图的一个测量工具----拐尺,其中O 为AB 的中点,CA ⊥AB ,BD ⊥AB ,CA =BD ,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.专题二 全等三角形中的探究题3.如下图,在△ABC 中, ∠C =90,AC =10㎝,BC =5㎝,一条线段PQ =AB ,P ,Q 两点分别在AC 和过A 点且垂直于ACP 点运动到AC 上什么位置时, △ABC 才能和△APQ 全等?4.如图(1),AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE .〔1〕试判断AC 与CE 的位置关系,并说明理由.〔2〕假设将CD 沿CB 方向平移得到图(2)(3)(4)(5)的情形,其余条件不变,此时第〔1〕问中AC 与CE 的位置关系还成立吗?结论还成立吗?请说明理由.5.能够互相重合的多边形叫做全等形,即如果两个多边形对应角相等,对应边相等,那B A O PQ CAB D O x 隔离房么两个多边形一定全等。
但判定两个三角形全等只需三组对应量相等即可,如SAS ,SSS 等,但如果要判定两个四边形全等仅有四组量对应相等是不够的,必须具备至少五组量对应相等.〔1〕请写出两个四边形全等的一种判定方法〔五组量对应相等〕;〔2〕如图,简要说明你的判定方法是正确的;〔3〕举例说明仅有四边对应相等的两个四边形不一定全等〔画出图形并简要说明理由〕.【知识要点】1.判断两个三角形全等的方法有:SAS,ASA,AAS,SSS,直角三角形除了上述判断方法外,还可以利用“HL 〞判断.2.在三边或两边及其夹角或两角及其夹边的情况下,可以利用尺轨作图作出符合条件的三角形.3.三角形具有稳定性,即三角形三边确定的情况下,其形状和大小就固定了.【温馨提示】1.在书写两个三角形全等时,对应的顶点要写在对应的位置上.2.判断两个直角三角形全等共有五种判定方法,除“HL 〞外,还可以利用一般三角形全等的方法进展判断.3.注意全等三角形性质和判定的综合运用.【方法技巧】1.证明三角形全等的一般思路是:(1)如果有两条对应边相等,还应寻找它们的夹角或第三边对应相等;(2)如果有一个角和一条边对应相等,还应寻找另一个角相等;(3)如果有两个角对应相等,还应寻找一条边对应相等.2.证明线段或角相等时,常常先证明线段或角所在的三角形全等.当图形中找不到这些线段或角所在的全等三角形时,应考虑添加适当的辅助线.参考答案AO ∥PQ ,所以∠AOB =∠Q .因为AB =OP ,∠ABO =∠POQ ,所以△ABO≌△POQ ,所以BO = OQ ,即距离敌营距离等于BO ,所以法军能命中.2.解:如图,使AC 与房间内壁在一条直线上,且C 与一端点接触,然后人在BD 的延长线上移动至F ,使F 、O 、E 三点正好在一条直线上,记下F 点,这时量出DF 长,即为房间深度CE .理由如下:由∠A =∠B =90°,OA =OB ,∠EOA =∠FOB ,所以△EAO ≌△FBO ,得BF =AE ,那么BF -BD =AE -AC ,即DF =CE . 3.解:要使△ABC 和△APQ 全等,由于∠P AQ =∠C =90,PQ =AB ,那么只需AP =BC 或AP =AC ,由HL 即知它们全等,从而得P 点在A 点或AC 的中点处时△APQ 和△ABC 全等.:〔1〕AC ⊥CE ,可确定△ABC ≌△CDE ,得∠ACB =∠E ,因为∠ACB +∠ECD =∠E +∠ECD =90°,所以∠ACE =180°-90°=90°,所以AC ⊥CE .图(2)(3)(4)(5)四种情况,结论仍然成立,理由同上.E C A O B D F5.解:〔1〕∠D=∠D′,AD=A′D′,DC=D′C′,BC=B′C′,AB=A′B′,〔2〕连接AC, 在△ADC 和△A′D′C′中,因为AD=A′D′,∠D=∠D′,DC=D′C′,所以△ADC≌△A′D′C′,那么AC=A′C′,从而得△ACB≌△A′C′B′,从而得到四边形ABCD和四边形A′B′C′D′的对应角,对应边均相等,即有四边形ABCD≌四边形A′B′C′D′;〔3〕举一个凸四边形和凹四边形.。
秋八年级数学上册 14.2 三角形全等的判定(1)练习题(无答案)沪科版(2021年整理)

2017年秋八年级数学上册14.2 三角形全等的判定(1)练习题(无答案)(新版)沪科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年秋八年级数学上册14.2 三角形全等的判定(1)练习题(无答案)(新版)沪科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年秋八年级数学上册14.2 三角形全等的判定(1)练习题(无答案)(新版)沪科版的全部内容。
D C B A14.2 三角形全等的判定(1)1、如图1,AB ∥CD,AB=CD ,BE=DF ,则图中有多少对全等三角形( )A.3B.4 C 。
5 D.62、如图2,AB=AC ,AD=AE ,欲证△ABD ≌△ACE,可补充条件( )A.∠1=∠2 B 。
∠B=∠C C 。
∠D=∠E D 。
∠BAE=∠CAD3、如图3,AD=BC,要得到△ABD 和△CDB 全等,可以添加的条件是( )A 。
AB ∥CD B.AD ∥BC C.∠A=∠CD 。
∠ABC=∠CDA4、如图4,AB 与CD 交于点O ,OA=OC ,OD=OB ,∠AOD=________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC,AD 平分∠BAC,请补充完整过程说明△ABD ≌△ACD 的理由. ∵AD 平分∠BAC , ∴∠________=∠________(角平分线的定义)。
在△ABD 和△ACD 中,∵___________________, ∴△ABD ≌△ACD ( )6、如图6,已知AB=AD ,AC=AE ,∠1=∠2,求证∠ADE=∠B 。
沪科版八年级数学上册14.2.2 用角边角判定三角形全等 (习题课件)【新版】

【思路点拨】 要紧扣旋转只改变图形位置,而不改变图形的大小这 一特征分析.
返回
第十四章 全等三角形
第2节 三角形全等的判定 第2课时 用角边角判定三角形全等
1
2
3
4
5
6
7
8
9
10
11
12
两角和它们的___夹__边___分别相等的两个三角形全等.
其书写模式为:在△ABC和△A′B′C′中,
A ∠__A__′,
_A_B__
A'
B',
B _∠__B_′_,
证明:∵AD为△ABC的中线,∴BD=CD,
∵CF⊥AD,BE⊥AD,∴∠CFD=∠BED=90°.
∵∠CDF =∠BDE,∴∠DCF=∠DBE.
在△BED和△CFD中,∵∠BED =∠CFD,
∠DBE =∠DCF,BD=CD
∴△BED≌△CFD(ASA).
返回
5.如图,已知点E在△ABC的外部,点D在BC边上, DE交AC于F,若∠1=∠2=∠3,AC=AE, 求证:△ABC≌△ADE.
EF.∵AB∥DE,∴∠B=∠E.∵AC∥DF,∴∠ACB
B E ,
=∠DFE.在△ABC和△DEF中,BC EF ,
ACB DFE ,
∴△ABC≌△DEF.
∴AC=DF.
返回
8.让我们一起动手来做一个折纸游戏吧!如图所示,取一 张长方形的纸ABCD,将其折叠,使D点与B点重合, EF为折痕,观察图形,图中有全等的三角形吗?如果 有,请给出理由;如果没有,请说明原因.
返回
9.(阜阳期末)如图, BD⊥AC于点D, CE⊥AB于点E, AD =AE. 求证:BE=CD.
沪科版八年级数学上册课时作业 14.2.3 三边分别相等的两个三角形全等(SSS)

沪科版数学八年级上册课时作业第14章全等三角形14.2三角形全等的判定第3课时三边分别相等的两个三角形全等(SSS)基础达标1. 如图所示,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )A. 三角形的稳定性B. 两点之间线段最短C. 两点确定一条直线D. 垂线段最短2. 如图,在△ABC中,AB=AC,EB=EC,则可以直接用“SSS”判定( )A. △ABD△△ACDB. △ABE△△ACEC. △BDE△△CDED. 以上答案都不对3. 如图所示,△ABC是不等边三角形,DE=BC,分别以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )A. 8个B. 6个C. 4个D. 2个4. 如图,已知AB=DF,AC=DE,如果用“SSS”证明△ABC△△DFE,还需添加条件.(填写一个你认为正确的答案即可)5. 如图,在△ABD与△ACE中,已知AB=AC,BD=CE,AD=AE,△1=20°,则△2=.6. 用直尺和圆规作一个角等于已知角,如图,能得出△A′O′B′=△AOB的依据是.7. 如图,已知AD=BC,AE=FC,DF=BE,求证:△B=△D.巩固提升8. 如图所示,已知AB=CD,AD=CB,则下列结论中不一定正确的是( )A. AB△DCB. △B=△DC. △A=△CD. AB=BC9. 已知下列条件,能画出唯一△ABC的是( )A. AB=4,BC=5,△BAC=50°B. AB=4,BC=3,AC=5C. △A=60°,△B=45°,△C=75°D. △C=90°,AB=610. 如图,在△ABC中,AB=AC,D,E两点在BC上,且AD=AE,BD=CE.若△BAD=30°,△DAE=50°,则△BAC的度数为.11. 在如图所示的6×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边BC且全等的所有格点三角形的个数是个.12. 一个平分角的仪器如图所示,其中AB=AD,BC=DC,求证:△BAC=△DAC.13. 如图,已知AB=AC,点D在BE上,且AD=AE,BD=CE.求证:△3=△1+△2.14. 如图,已知AB=DC,DB=AC.(1)求证:△ABD=△DCA.(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?15. 如图所示,AD=CB,E,F是AC上两动点,且有DE=BF.(1)若E,F运动至如图①的位置,且AF=CE,求证:△ADE△△CBF.(2)若E,F运动至如图②的位置,且AF=CE,那么上述结论△ADE△△CBF还成立吗?为什么?(3)AD和CB平行吗?请你任选其中一图加以说明.图①图②参考答案1. A2. B3. C4. BE=CF(或BC=EF)5. 20°6. SSS7. 证明:△AE=FC,△AE-EF=FC-EF,即AF=CE.在△ADF与△CBE中,AD BCAF CEDF BE⎧⎪⎨⎪⎩=,=,=,△△ADF△△CBE.(SSS)△△B=△D.(全等三角形的对应角相等) 8. D 9. B10. 110°11. 312. 证明:在△ABC与△ADC中,AB ADBC DCAC AC⎧⎪⎨⎪⎩=,=,=,△△ABC△△ADC(SSS),△△BAC=△DAC.13. 证明:在△ABD和△ACE中,△AB=AC,AD=AE,BD=CE,△△ABD△△ACE(SSS),△△BAD=△1,△ABD=△2,△△3=△BAD +△ABD , △△3=△1+△2.14. (1)证明:连接AD .在△ABD △△DCA 中,()AB DC AD DA DB AC ⎧⎪⎨⎪⎩=,=,公共边=, △△ABD △△DCA (SSS ).△△ABD =△DCA .(全等三角形的对应角相等) (2)解:作辅助线的意图是构造全等三角形.15. (1)证明:△AF =CE ,△AF +EF =CE +EF ,即AE =CF .在△ADE 和△CBF 中,AD CB DE BF AE CF ⎧⎪⎨⎪⎩=,=,=, △△ADE △△CBF .(SSS )(2)解:成立.△AF =CE ,△AF -EF =CE -EF ,即AE =CF . 同(1)证得△ADE △△CBF .(3)解:AD △CB .△△ADE △△CBF ,(已证) △△A =△C .△AD △BC .。
沪科版八年级数学上册课时作业 14.2.3 三边分别相等的两个三角形全等(SSS)

沪科版数学八年级上册课时作业第14章全等三角形14.2三角形全等的判定第3课时三边分别相等的两个三角形全等(SSS)基础达标1. 如图所示,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )A. 三角形的稳定性B. 两点之间线段最短C. 两点确定一条直线D. 垂线段最短2. 如图,在△ABC中,AB=AC,EB=EC,则可以直接用“SSS”判定( )A. △ABD△△ACDB. △ABE△△ACEC. △BDE△△CDED. 以上答案都不对3. 如图所示,△ABC是不等边三角形,DE=BC,分别以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )A. 8个B. 6个C. 4个D. 2个4. 如图,已知AB=DF,AC=DE,如果用“SSS”证明△ABC△△DFE,还需添加条件.(填写一个你认为正确的答案即可)5. 如图,在△ABD与△ACE中,已知AB=AC,BD=CE,AD=AE,△1=20°,则△2=.6. 用直尺和圆规作一个角等于已知角,如图,能得出△A′O′B′=△AOB的依据是.7. 如图,已知AD=BC,AE=FC,DF=BE,求证:△B=△D.巩固提升8. 如图所示,已知AB=CD,AD=CB,则下列结论中不一定正确的是( )A. AB△DCB. △B=△DC. △A=△CD. AB=BC9. 已知下列条件,能画出唯一△ABC的是( )A. AB=4,BC=5,△BAC=50°B. AB=4,BC=3,AC=5C. △A=60°,△B=45°,△C=75°D. △C=90°,AB=610. 如图,在△ABC中,AB=AC,D,E两点在BC上,且AD=AE,BD=CE.若△BAD=30°,△DAE=50°,则△BAC的度数为.11. 在如图所示的6×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边BC且全等的所有格点三角形的个数是个.12. 一个平分角的仪器如图所示,其中AB=AD,BC=DC,求证:△BAC=△DAC.13. 如图,已知AB=AC,点D在BE上,且AD=AE,BD=CE.求证:△3=△1+△2.14. 如图,已知AB=DC,DB=AC.(1)求证:△ABD=△DCA.(2)在(1)的证明过程中,需要作辅助线,它的意图是什么?15. 如图所示,AD=CB,E,F是AC上两动点,且有DE=BF.(1)若E,F运动至如图①的位置,且AF=CE,求证:△ADE△△CBF.(2)若E,F运动至如图②的位置,且AF=CE,那么上述结论△ADE△△CBF还成立吗?为什么?(3)AD和CB平行吗?请你任选其中一图加以说明.图①图②参考答案1. A2. B3. C4. BE=CF(或BC=EF)5. 20°6. SSS7. 证明:△AE=FC,△AE-EF=FC-EF,即AF=CE.在△ADF与△CBE中,AD BCAF CEDF BE⎧⎪⎨⎪⎩=,=,=,△△ADF△△CBE.(SSS)△△B=△D.(全等三角形的对应角相等) 8. D 9. B10. 110°11. 312. 证明:在△ABC与△ADC中,AB ADBC DCAC AC⎧⎪⎨⎪⎩=,=,=,△△ABC△△ADC(SSS),△△BAC=△DAC.13. 证明:在△ABD和△ACE中,△AB=AC,AD=AE,BD=CE,△△ABD△△ACE(SSS),△△BAD=△1,△ABD=△2,△△3=△BAD +△ABD , △△3=△1+△2.14. (1)证明:连接AD .在△ABD △△DCA 中,()AB DC AD DA DB AC ⎧⎪⎨⎪⎩=,=,公共边=, △△ABD △△DCA (SSS ).△△ABD =△DCA .(全等三角形的对应角相等) (2)解:作辅助线的意图是构造全等三角形.15. (1)证明:△AF =CE ,△AF +EF =CE +EF ,即AE =CF .在△ADE 和△CBF 中,AD CB DE BF AE CF ⎧⎪⎨⎪⎩=,=,=, △△ADE △△CBF .(SSS )(2)解:成立.△AF =CE ,△AF -EF =CE -EF ,即AE =CF . 同(1)证得△ADE △△CBF .(3)解:AD △CB .△△ADE △△CBF ,(已证) △△A =△C .△AD △BC .。
八年级数学上册14.2三角形全等的判定(1)练习题(无答案)沪科版

D C B A14.2 三角形全等的判定(1)1、如图1,AB ∥CD,AB=CD ,BE=DF ,则图中有多少对全等三角形( )A.3B.4 C 。
5 D.62、如图2,AB=AC ,AD=AE ,欲证△ABD ≌△ACE,可补充条件( )A.∠1=∠2 B 。
∠B=∠C C 。
∠D=∠E D 。
∠BAE=∠CAD3、如图3,AD=BC,要得到△ABD 和△CDB 全等,可以添加的条件是( )A 。
AB ∥CD B.AD ∥BC C.∠A=∠CD 。
∠ABC=∠CDA4、如图4,AB 与CD 交于点O ,OA=OC ,OD=OB ,∠AOD=________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC,AD 平分∠BAC,请补充完整过程说明△ABD ≌△ACD 的理由. ∵AD 平分∠BAC , ∴∠________=∠________(角平分线的定义)。
在△ABD 和△ACD 中,∵___________________, ∴△ABD ≌△ACD ( )6、如图6,已知AB=AD ,AC=AE ,∠1=∠2,求证∠ADE=∠B 。
7、如图,已知AB=AD ,若AC 平分∠B AD,问AC 是否平分∠BCD ?为什么?8、如图,在△ABC和△DEF中,B、E、F、C,在同一直线上,下面有4个条件,请你在其中选3个作为题设,余下的一个作为结论,写一个真命题,并加以证明。
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.9、如图⑴,AB⊥BD,DE⊥BD,点C是BD上一点,且BC=DE,CD=AB.⑴试判断AC与CE的位置关系,并说明理由.⑵如图⑵,若把△CDE沿直线BD向左平移,使△CDE的顶点C与B重合,此时第⑴问中AC与BE的位置关系还成立吗?(注意字母的变化)尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
