北京2010年中考各区一模数学试题分类(四边形)

合集下载

2010年北京市大兴区初三数学一模试题及答案

A DCB（图1）大兴区2010年中考一模试题第I 卷（选择题，共32分）一、选择题（本题共32分，每小题4分）在下列各题的四个备选答案中，只有一个是正确的，请将正确答案前的字母填涂在答题卡上． 1．15-的相反数是（）A ．5-B ．5C ． 15-D ．152．2008年末某市常住人口约为人，将用科学记数法表示为（）A ．426310⨯ B ．42.6310⨯ C ．62.6310⨯ D ．70.26310⨯ 3．如图1，AD BC ∥，BD 平分ABC ∠，且110A ∠=︒，则D ∠的度数为（）A ．70︒B ．35︒C ．55︒D ．110︒ 4. 妈妈在菜市场买了五种水果，质量分别为（单位：千克）：0.5，1，1.5，1，1，则这组数据的平均数和中位数分别为（）A ．1，1.5B ．2.5，1C ．1.5，1D ．1，15．若两圆的半径分别为5和7，圆心距为2，则这两圆的位置关系是（）A ．内含B ．内切C ．相交D ．外切6．一个布袋中有4个除颜色外其余都相同的小球，其中3个白球，1个红球．从袋中任意摸出1个球是白球的概率是（） A ．43 B ．41 C ．32 D ．31 7．把代数式322a a a -+分解因式，下列结果中正确的是（） A ．2(1)a a - B ．2(1)a a - C ．2(1)a a + D ．(1)(1)a a a +-8. 如图2，点A 、B 、C 、D 为圆O 的四等分点，动点P 从圆心O 出发，沿O C D O ---的路线作匀速运动．设运动时间为t 秒,APB ∠的度数为y 度，则下列图象中表示y 与t 之间函数关系最恰当的是（）（图2 ）2第II 卷（共88分）二、填空题（本题共16分, 每小题4分）9．若实数,a b 2(1)0b -=，则代数式2ab a -的值为 . 10．已知反比例函数ky x=的图象经过点()1,4, 则k = .11.如图3，ABC △的三个顶点A 、B 、C的坐标分别为()3,3、()6,4、()4,6，则BC 边上的高为．(图3)12.如图4所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n 个图形需要黑色棋子的个数是．三、解答题（本题共30分, 每小题5分）13．计算：101(2sin60(π-1)4-︒+.14．解不等式组：4(3),1 1.6x x x ->⎧⎪⎨<⎪⎩第1个图形第2个图形第3个图形第4个图形(图4)初三模考试题精心整理汇编京睿试题库 :..第 3 页共 15 页..: 为了孩子的将来保驾护航EBCA FDBCAD E15. 已知：如图5，点A 、E 、F 、C 在同一条直线上，AD BC =，AE CF =，A C ∠=∠．求证：DF BE =．图516.计算22111a a a ---17．已知直线l 与直线2y x =平行，且与直线y x m =-+交于点()2,0, 求m 的值及直线l 的解析式.18．如图6，在梯形ABCD 中，AD BC ∥，90A ∠=︒，45C ∠=︒，DE EC =，4AB =2AD =，求BE 的长．（图6）4B（图7）四、解答题（本题共20分, 第19题5分，第20题6分，第21题5分，第22题4分） 19．如图7，已知AB 是O ⊙的直径，O ⊙过BC 的中点D ，且90DEC ∠=︒．（1）求证：DE 是O ⊙的切线；（2）若30C ∠=°，CE =O ⊙的半径．20．某区政府为进一步改善人民居住环境，准备在街道两边种植梧桐、柳树、小叶榕、香樟、杨树，种植哪种树取决于居民的喜爱情况．为此，政府派出社会调查小组在本区内随机调查了部分居民，并将结果绘制成如下扇形统计图和条形统计图．请根据统计图，完成下列问题：（1）本次调查了多少名居民？其中喜爱柳树的居民有多少人？（2）请补全条形统计图；（3）请根据此项调查，对该区在街道两边种植哪种树提出一条合理化建议．初三模考试题精心整理汇编京睿试题库 :..第 5 页共 15 页..: 为了孩子的将来保驾护航21．列方程或方程组解应用题某中学拟组织九年级师生外出．下面是年级组长李老师和小芳同学有关租车问题的对话：李老师：“客运公司有60座和45座两种型号的客车可供租用，60座客车每辆每天的租金比45座客车每辆每天的租金多200元．”小芳：“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车外出参观，一天的租金共计5000元．”根据以上对话，求客运公司60座和45座的客车每辆每天的租金分别是多少元？22. 如图8-1、9-1，现将二张形状、大小完全相同的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合．分别在图8-1、图9-1中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，按所采裁图形的实际大小，在图8-2中拼成正方形，在图9-2中拼成一个角是135 的三角形．要求：（1）裁成的两部分在拼成几何图形时要互不重叠且不留空隙；（2）所拼出的几何图形的各顶点必须与小正方形的顶点重合.6五、解答题（本题共22分, 第23题7分，第24题7分，第25题8分）23. 如图10-1，四边形ABCD 是正方形，G 是CD 边上的一个动点(点G 与C 、D 不重合)，以CG 为一边在正方形ABCD 外作正方形CEFG ，连结BG ，DE ．我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系：（1）①请直接写出图10-1中线段BG 、线段DE 的数量关系及所在直线的位置关系；②将图10-1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α，得到如图10-2、如图10-3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图10-2证明你的判断．（2）将原题中正方形改为矩形（如图10-4～10-6），且,,,AB a BC b CE ka CG kb ==== (,0)a b k ≠ ，试判断（1）①中得到的结论哪个成立，哪个不成立？并写出你的判断，不必证明.（3）在图10-5中，连结DG 、BE ，且14,2,2a b k ===，则22BE DG += ．初三模考试题精心整理汇编京睿试题库 :..第 7 页共 15 页..: 为了孩子的将来保驾护航24. 若12,x x 是关于x 的一元二次方程20(0)ax bx c a ++=≠的两个根，则方程的两个根12,x x 和系数,,a b c 有如下关系：1212,bcx x x x aa+=-⋅=. 我们把它们称为根与系数关系定理. 如果设二次函数2(0)y ax bx c a =++≠的图象与x 轴的两个交点为12(,0),(,0)A x B x .利用根与系数关系定理我们又可以得到A 、B 两个交点间的距离为：12AB x x =-= 请你参考以上定理和结论，解答下列问题:设二次函数2(0)y ax bx c a =++>的图象与x 轴的两个交点为12(,0),(,0)A x B x ，抛物线的顶点为C ，显然ABC ∆为等腰三角形.（1）当ABC ∆为等腰直角三角形时，求24;b ac -的值（2）当ABC ∆为等边三角形时，24b ac -= .（3）设抛物线21y x kx =++与x 轴的两个交点为A 、B ，顶点为C ，且90ACB ∠=︒,试问如何平移此抛物线，才能使60ACB ∠=︒？25．已知抛物线22y x x a=-+（0a<）与y轴相交于点A，顶点为M.直线12y x a=-分别与x轴，y轴相交于B C，两点，并且与直线AM相交于点N.(1)填空：试用含a的代数式分别表示点M与N的坐标，则()()M N，，，；(2)如图11，将NAC△沿y轴翻折，若点N的对应点N′恰好落在抛物线上，AN'与x轴交于点D，连结CD，求a的值和四边形ADCN的面积；(3)在抛物线22y x x a=-+（0a<）上是否存在一点P，使得以P A C N，，，为顶点的四边形是平行四边形？若存在，求出P点的坐标；若不存在，试说明理由.（图11）8初三模考试题精心整理汇编京睿试题库 :..第 9 页共 15 页..: 为了孩子的将来保驾护航大兴区2010年中考一模试题初三数学参考答案及评分标准一、选择题（本题共32分，每小题4分） 1．D15-的相反数是512． C用科学记数法表示为62.6310⨯ 3． B由已知得70ABC ∠=︒，35ABD ∠=︒，所有35ADB ∠=︒． 4. D这组数据的平均数为1，中位数分别为1 5．B由已知，两圆的半径差与圆心距相等，这两圆位置关系为内切． 6．A从袋中任意摸出1个球是白球的概率34P =． 7． A3222(1)a a a a a -+=- 8． C动点P 从O C -过程中，APB ∠从90︒到45︒，动点P 从C D -过程中，APB ∠保持45︒不变，动点P 从D O - 过程中，APB ∠从45︒到90︒，故选Ｃ二、填空题（本题共16分, 每小题4分） 9． 6-30a -=，3a =，10b -=，1b =，26ab a -=-． 10．4144k =⨯=． 11．由已知坐标的AC AB ==BC =，BC边上的高为 12．(2)n n +或22n n +或2(1)1n +-由已知观察图形，可得到规律为(2)n n +或22n n +或2(1)1n +- 三、解答题（本题共30分, 每小题5分）13．解：()1012sin 60π14-⎛⎫+︒+- ⎪⎝⎭431=-+………………………………………………………… 4分10A BCDEH F53=+……………………………………………………………5分14．解：解不等式①，得 4x >；…………………………………………………………2分解不等式②，得6x <． …………………………………………………………4分所以原不等式组的解集为46x <<． ……………………………………………………5分15．证明：∵AE CF =，∴AE EF CF EF +=+∴AF EC =………………………………………………………… 1分在ADF △和CBE △中，AD CB A C AF CE =⎧⎪∠=∠⎨⎪=⎩…………………………………………………………3分∴ADF CBE △≌△．……………………………………………4分 ∴DF BE =．……………………………………………5分16．解：2212111(1)(1)1a a a a a a a -=---+--……………………………………… 1分21(1)(1)(1)(1)a a a a a a +=-+-+- ……………………………………… 2分2(1)(1)(1)a a a a -+=+- ……………………………………… 3分1(1)(1)a a a -=+- ……………………………………… 4分11a =+ ……………………………………… 5分17．解：依题意，点()2,0在直线y x m =-+上，∴012m =-⨯+． ……………………………………… 1分 ∴ 2m =． ……………………………………… 2分由直线l 与直线2y x =平行，可设直线l 的解析式为2y x b =+．……3分 ∵点()2,0在直线l 上,∴022b =⨯+．∴4b =-． ……………………………………… 4分故直线l 的解析式为24y x =-．……………………………………… 5分 18．解：如图，分别过点D 、E 作DF BC ⊥于点F ，EH BC ⊥于点H ．∴EH D F ∥，90DFB DFC EHB EHC ∠=∠=∠=∠=︒．（第18题图）初三模考试题精心整理汇编B第19题图又90A ∠=︒，AD BC ∥， ∴90ABC ∠=︒．∴四边形ABFD 是矩形． ∵4AB =，2AD =，∴2BF AD ==，4DF AB ==．………………………………… 1分在Rt DFC △，45C ∠=︒，∴45FDC ∠=︒，∴FDC C ∠=∠．∴4FC DF ==． …………………………………2分又∵DE EC =，EH D F ∥，∴122EH DF ==． …………………………………3分∴2HC EH ==． ∴2FH =．∴4BH =． …………………………………4分在Rt EBH △中，∴BE 分说明：本题答案不唯一，其他解法，只要正确，请参照本评分标准给分．四、解答题（本题共20分, 第19题5分，第20题6分，第21题5分，第22题4分） 19．（1）证明：连接OD ． ······· 1分点D 为BC 的中点，点O 为AB 的中点． ∴OD 为ABC △的中位线，∴OD AC ∥ ··························· 2分 ∵90DEC ∠=︒， ∴90DEC ODE ∠=∠=︒ ∴DE OD ⊥，∴DE 是O ⊙的切线 ······················· 3分（2）解：连接AD ， ∵AB 为直径， ∴90BDA ∠=︒． ∵90DEC ∠=︒在Rt CED △中，cos CEC CD ∠=cos30︒=4CD = 4分∵点D 为BC 的中点，∴4BD CD==，∴AC AB=，∴30B C∠=∠=︒．在Rt ABD△中，cosDBBAB∠=，4cos30AB︒=，AB∴O⊙························ 5分说明：本题答案不唯一，其他解法，只要正确，请参照本评分标准给分．20．解：（1）8010800÷=%，800320280808040----=，即本次调查了800名居民，其中喜爱柳树的居民有40人．….2分（2）如图．……………………………………………………………………….4分（3）建议多种植香樟树．（注：答案不惟一）……………………………………6分21．解：设客运公司60座和45座客车每天每辆的租金分别为x元和y元．···· 1分由题意，列方程组200425000x yx y-=⎧⎨+=⎩，．····················· 3分解之得900700.xy=⎧⎨=⎩，······························ 4分答：客运公司60座和45座的客车每辆每天的租金分别是900元和700元…………….5分说明：本题答案不唯一，其他解法，只要正确，请参照本评分标准给分．22.初三模考试题精心整理汇编五、解答题（本题共22分, 第23题7分，第24题7分，第25题8分）23．⑴①BG DE=；BG DE⊥； (1)②①中得到的结论仍然成立…………………………………………………2分证明：∵四边形ABCD和四边形EFGC分别是正方形，∴CG CE=．BC CD=，90ECG BCD∠=∠=︒．∴ECG DCG BCD DCG∠+∠=∠+∠，即DCE BCG∠=∠．∴BCG DCE△≌△，∴DE BG=，∴CED BGC∠=∠，∵CQE DQG∠=∠90CQE BGC∠+∠=︒，∴90GOE∠=︒，∴DE BG⊥……………………………………4分⑵BG DE⊥成立；……………………………………5分BG DE=不成立…………………………………….6分⑶2225BE DG+=……………………………………7分24 ．⑴ 解：当ABC△为等腰直角三角形时，过C作CD AB⊥，垂足为D，则2AB CD=………………………………………………1分∵抛物线与x轴有两个交点，∴0>△，∴2244b ac b ac-=-∵AB又∵244b ac CDa-=，∵0a≠，242b ac-………………………………2分∴()222444b acb ac--=∵240b ac-≠．∴244b ac -=…………………………………………3分 ⑵当ABC △为等边三角形时，24b ac -12=………………4分⑶∵90ACB ∠=︒， ∴24b ac -4=．即244k -=，∴k =±分因为向左或向右平移时，ACB ∠的度数不变，所有只需要将抛物线21y x =±+向上或向下平移使60ACB ∠=︒，然后向左或向右平移任意个单位即可．设向上或向下平移后的抛物线解析式为：21y x m =±++， ∵平移后60ACB ∠=︒，∴2412b ac -=， ∴2m =-．∴抛物线21y x kx =++向下平移2个单位后，向左或向右平移任意个单位都能使ACB ∠的度数由90︒变为60︒.…………………………………………………………7分25.（1）()411133M a N a a ⎛⎫-- ⎪⎝⎭，，，.……………1分（2）由题意得点N 与点N '关于y 轴对称，∴N '4133a a ⎛⎫-- ⎪⎝⎭，， ∵N '在22y x x a =-+上初三模考试题精心整理汇编∴21168393a a a a -=++，∴10a =（不合题意，舍去），294a =-.……………2分∴343N ⎛⎫ ⎪⎝⎭-，，∴点N 到y 轴的距离为3. ∵940A ⎛⎫- ⎪⎝⎭，，N ' 334⎛⎫ ⎪⎝⎭，， ∴直线AN '的解析式为94y x =-，……………………3分它与x 轴的交点为9(,0)4D点D 到y 轴的距离为94． ∴1919918932222416ADCN ACN ACD S S S =+=⨯⨯+⨯⨯=△△.……………4分（3）在抛物线上存在点P ，使得以P 、A 、C 、N 为顶点的四边形是平行四边形，当点1P在y 轴的左侧时，若1ACP N 是平行四边形，则1P N 平行且等于AC ，∴把N 向上平移2a -个单位得到1P ，坐标为4733a a ⎛⎫- ⎪⎝⎭，，………………………5分 27168393a a a a -=-+ ∴30a =（不舍题意，舍去），438a =-，∴117(,)28P -…………………………………………………………………6分当点2P 在y 轴的右侧时，若2AP CN 是平行四边形，则AC 与2P N 互相平分， ∴2,OA OC OP ON ==． ∴2P 与N 关于原点对称，241(,)33P a a -，………………………………………………7分∴21168393a a a a =++， ∴50a =（不合题意，舍去），6158a =-， ∴25528P ⎛⎫- ⎪⎝⎭，． ∴存在这样的点11728P ⎛⎫- ⎪⎝⎭，或25528P ⎛⎫- ⎪⎝⎭，，能使得以P A C N ，，，为顶点的四边形是平行四边形．…………………………………………………………………8分。

2010年北京石景山区一模数学试题及答案

第Ⅰ卷（共 32 分）
一、选择题（本题共 32 分，每小题 4 分）在每个小题给出的四个备选答案中，只有一个是正确的，请将所选答案前的字母按规定要求填涂在答题纸第 1-8 题的相应位置上． 1． 3 的倒数是 A．
1 3
B．
1 3
C． 3
D． 3
2．据中新社报道：2010 年我国粮食产量将达到 540 000 000 吨，用科学记数法表示这个数字为 A． 0.5410

图1
图2
石景山区 2010 年初三第一次统一练习暨毕业考试试卷
本资料由教育城编辑整理 QQ: 471701103 更多资料：/SearchDatum.aspx
教育城：
初三数学参考答案
阅卷须知：为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可．若考生的解法与本解法不同，正确者可参照评分参考给分，解答右端所注分数，表示考生正确做到这一步应得的累加分数．一、选择题（本题共 32 分，每小题 4 分）题号答案 1 A 2 C 3 D 4 B 5 C 6 B 7 B 8 A
教育城：
石景山区 2010 年初三第一次统一练习暨毕业考试
数学试卷
考生须知题号分数 1．本试卷共 8 页．全卷共七道大题，25 道小题． 2．本试卷满分 120 分，考试时间 120 分钟． 3．在试卷密封线内准确填写区（县）名称、毕业学校、姓名和准考证号． 4．考试结束后，将试卷和答题纸一并交回．一二三四五六七总分
第 8 题图
A
B
C
D
第Ⅱ卷（共 88 分）
二、填空题（本题共 16 分，每小题 4 分） 9．在函数 y

北京2010年中考各区一模数学试题分类(切线的证明与圆中的计算).doc

21.已知：如图，⊙O 是ABC ∆的外接圆，AB 为⊙O 直径，且AB PA ⊥于点A ，AC PO ⊥于点M （1）求证：PC 是⊙O 的切线；（2）当2=OM ，42cos =B 时，求PC 的长。

［崇文一模］ 20.如图，AB 是半圆⊙O 的直径，过点O 作弦AD 的垂线交半圆⊙O 于点E ，交AC 于点C ，使BED C ∠=∠ （1）判断直线AC 与圆O 的位置关系，并证明你的结论。

（2）若8=AC ，54cos =∠BED ，求AD 的长。

［延庆一模］20．如图，AB 为⊙O 的直径，AD 平分BAC ∠交⊙O 于点D ，AC 交AC DE ⊥的延长线于点E ，B BF A ⊥交AD 的延长线于点F ，（1）求证：DE 是⊙O 的切线；（2）若,3=DE ⊙O 的半径为5，求BF 的长．［西城一模］21．如图，ABC △内接于O ，AB AC =．点D 在O 上，AD AB ⊥于点A ，AD 与BC 交于点E ，点F 在DA 的延长线上，AF AE =．（1）求证：BF 是O 的切线；（2）若4AD =，4cos 5ABF ∠=，求BC 的长．O FEDCBAM B PO AC F E DCBAODCBAO21．如图，⊙O 的直径AB=4，C 、D 为圆周上两点，且四边形OBCD 是菱形，过点D 的直线EF ∥AC ，交BA 、BC 的延长线于点E 、F ．（1）求证：EF 是⊙O 的切线；（2）求DE 的长．［门头沟一模］20. 已知：如图，BE 是⊙O 的直径，CB 与⊙O 相切于点B ，OC ∥DE 交⊙O 于点D ，CD 的延长线与BE 的延长线交于A 点.（1）求证：AC 是⊙O 的切线；（2）若AD ＝4，CD ＝6，求tan ∠ADE 的值.［丰台一模］20．已知：如图，AB 为⊙O 的直径，⊙O 过AC 的中点D ，DE ⊥BC 于点E ．（1）求证：DE 为⊙O 的切线；（2）若DE =2，tan C =21，求⊙O 的直径．［石景山一模］20．已知：如图，AB 为⊙O 的直径，弦OD AC //,BD 切⊙O 于B ,联结CD ．（1）判断CD 是否为⊙O 的切线，若是请证明；若不是请说明理由．（2）若2=AC ,6=OD ,求⊙O 的半径． OF E DCBAOE D C B A20．已知：如图，在△ABC 中，AB=BC ，D 是AC 中点，BE 平分∠ABD 交AC 于点E ，点O 是AB 上一点，⊙O 过B 、E 两点, 交BD 于点G ，交AB 于点F ．（1）求证：AC 与⊙O 相切；（2）当BD=2，sinC=12时，求⊙O 的半径．［平谷一模］19. 已知，如图，直线MN 交⊙O 于A,B 两点，AC 是直径，AD 平分∠CAM 交⊙O 于D ，过D 作DE ⊥MN 于E ．（1）求证：DE 是⊙O 的切线；（2）若6DE =cm ，3AE =cm ，求⊙O 的半径.［大兴一模］19．如图7，已知AB 是⊙O 的直径，⊙O 过BC 的中点D ，且︒=∠90DEC ．（1）求证：DE 是⊙O 的切线；（2）若30C ∠=°，32=CE ，求⊙O 的半径．［密云一模］19．如图，等腰三角形ABC 中，AC ＝BC ＝6，AB ＝8．以BC 为直径作⊙O 交AB 于点D ，交AC 于点G ，DF ⊥AC ，垂足为F ，交CB 的延长线于点E ．（1）求证：直线EF 是⊙O 的切线；（2）求sin ∠E 的值． AF DO E B G C AE DOBC（图7）23．如图，平行四边形ABCD 中，以A 为圆心，AB 为半径的圆交AD 于F ，交BC 于G ，延长BA 交圆于E.（1）若ED 与⊙A 相切，试判断GD 与 ⊙A 的位置关系，并证明你的结论；（2）在（1）的条件不变的情况下，若 GC ＝CD ＝5，求AD 的长.［海淀一模］20. 已知：如图，⊙O 为ABC ∆的外接圆，BC 为⊙O 的直径，作射线BF ，使得BA 平分CBF ∠，过点A 作AD BF ⊥于点D .(1)求证：DA 为⊙O 的切线； (2)若1BD =，1tan 2BAD ∠=，求⊙O 的半径.［昌平一模］20．已知：如图，点D 是⊙O 的直径CA 延长线上一点，点B 在⊙O 上，且.OA AB AD == （1）求证：BD 是⊙O 的切线；（2）若点E 是劣弧BC 上一点，AE 与BC 相交于点F ，且8BE =，5tan 2BFA ∠=，求⊙O 的半径长.（第23题图） F OD CBAFE DCBAO［朝阳一模］ 21．（本小题满分5分）如图，点B 、C 、D 都在⊙O 上，过点C 作AC ∥BD 交OB 延长线于点A ，连接CD ，且∠CDB=∠OBD=30°，DB=63cm ．（1）求证：AC 是⊙O 的切线；（2）求⊙O 的半径长；（3）求由弦CD 、BD 与弧BC 所围成的阴影部分的面积（结果保留π）．［东城一模］20．如图，在⊙O 中，AB 是直径，AD 是弦，∠ADE = 60°，∠C = 30°．（1）判断直线CD 是否为⊙O 的切线，并说明理由；（2）若CD = 33 ，求BC 的长．OBCDEA。

2010北京一模数学试题汇编--复数、算法、集合、简易逻辑、推理与证明、平面几何、坐标系与参数方程

平面几何1. （崇文·理·题3）已知PA 是O 的切线，切点为A ，2PA =，AC 是O 的直径，PC 交O 于点B ，30PAB ∠=，则O 的半径为（）PAA ．1B ．2CD ．【解析】 C ；30,2tan30PAPCA PABCA ∠=∠===2. （东城·理·题3）如图，已知AB 是⊙O 的一条弦，点P 为AB 上一点，PC OP ⊥，PC 交⊙O 于C ，若4AP =，2PB =，则PC 的长是（）A ．3B ．C ．2 DOPCB A【解析】 B ；延长CP 交于圆上一点，得到一条圆的弦，易知P 点为该弦的中点，有28PC PA PB =⋅=．3. （丰台·理·题9）在平行四边形ABCD 中，点E 是边AB 的中点，DE 与AC 交于点F ，若AEF ∆的面积是12cm ，则CDF ∆的面积是 2cm ．【解析】 4；EB取CD 的中点G ，连结BG 交AC 于H ，则∵BE DG ∥且1122BE AB CD DG ===，∴四边形BEDG 为平行四边形 ∴AF FH HC == ∴44DFC AEF S S ==△△4. （海淀·理·题10）如图，AB 为O 的直径，且8AB =，P 为OA 的中点，过P 作O 的弦CD ，且:3:4C PP D =，则弦CD 的长度为．【解析】 7；由8AB =得2,6AP PB ==．由已知和相交弦定理得 :3:4CP PD AP PB CP PD ⋅=⋅⎧⎨=⎩，解得34CP PD =⎧⎨=⎩．于是347CD CP PD =+=+=．5. （石景山·理·题10）已知曲线C 的参数方程为cos ,2sin ,x y θθ=⎧⎨=-+⎩()θ为参数，则曲线C 的普通方程是；点A 在曲线C 上，点(,)M x y 在平面区域22020210x y x y y -+⎧⎪+-⎨⎪-⎩≥≤≥上，则AM 的最小值是．【解析】22(2)1x y ++=，32； C 是圆22(2)1x y ++=；不等式组的可行域如图阴影所示，A 点为(0,1)-、M 为10,2⎛⎫⎪⎝⎭时，||AM 最短，长度是32．6. （西城·理·题12）如图，PC 切O 于点C ，割线PAB 经过圆心O ，弦C D A B ⊥于点E ．已知O 的半径为3，2PA =，则PC = ．OE = ．B【解析】 94,5； 22(26)164PC PA PB PC =⋅=⨯+=⇒=；连结OC ，知OC PC ⊥，于是5PO =，2239235CO OE OP PE =⋅⇒==+．BCOE PDA7. （宣武·理·题11）若,,A B C 是O ⊙上三点，PC 切O ⊙于点C ，110,40ABC BCP ∠=︒∠=︒，则AOB ∠的大小为．【解析】 60︒；如图，弦切角40PCB CAB ∠=∠=︒，于是18030ACB CAB ABC ∠=︒-∠-∠=︒，从而260AOB ACB ∠=∠=︒．POCBA8. （朝阳·理·题12）如图，圆O 是ABC ∆的外接圆，过点C 的切线交AB 的延长线于点D ，3CD AB BC ===，则BD 的长为；AC 的长为．【解析】 4,()24CD DB DA DB AB BD BD =⋅=⋅+⇒=．又由DCB CAB∠=∠知BCD ACD∆≅∆．于是BC BD CDAC CD AD==．即3BD ACAC CD===9.（西城·理·题12）如图，PC切O于点C，割线PAB经过圆心O，弦C D A B⊥于点E．已知O的半径为3，2PA=，则PC=．OE=．B【解析】94,5；22(26)164PC PA PB PC=⋅=⨯+=⇒=；连结OC，知OC PC⊥，于是5PO=，2239235CO OE OP PE=⋅⇒==+．BCO EPDA坐标系与参数方程1.（海淀·理·题4）在平面直角坐标系xOy中，点P的直角坐标为(1,．若以原点O为极点，x轴正半轴为极轴建立极坐标系，则点P的极坐标可以是（）A．π1,3⎛⎫-⎪⎝⎭B．4π2,3⎛⎫⎪⎝⎭C．π2,3⎛⎫-⎪⎝⎭D．4π2,3⎛⎫-⎪⎝⎭【解析】C；易知2ρ==，()π2π3k k θ=-∈Z ．2. （朝阳·理·题9）已知圆的极坐标方程为2cos ρθ=，则圆心的直角坐标是；半径长为．【解析】 ()1,0,1；由22cos ρρθ=，有222x y x +=，即圆的直角坐标方程为()2211x y -+=．于是圆心坐标为()1,0，半径为1．3. （崇文·理·题11）将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩（θ为参数）化成普通方程为．【解析】 ()2214x y -+=；由12cos ,2sin x y θθ-==知()2214x y -+=．4. （石景山·理·题11）如图，已知PE 是圆O 的切线．直线PB 交圆O 于A 、B 两点，4PA =，12AB =，AE =．则PE 的长为_____，ABE ∠的大小为________．POEBA【解析】 8，30︒；24(412)64PE PA PB =⋅=⨯+=，则8PE =；由222P EP A A E =+，可知90PAE ∠=︒，即90BAE ∠=︒，由tan AE ABE AB ∠=，得30ABE ∠=︒．5. （西城·理·题11）将极坐标方程2cos ρθ=化成直角坐标方程为．【解析】2220x y x +-=； 2222cos 2x y x ρρθ=⇒+=．6. （东城·理·题12）圆的极坐标方程为sin 2cos ρθθ=+，将其化成直角坐标方程为，圆心的直角坐标为．【解析】 2215(1)()24x y -+-=，11,2⎛⎫⎪⎝⎭；222sin 2cos 2x y y x ρρθρθ=+⇒+=+．7. （东城·理·题12）圆的极坐标方程为sin 2cos ρθθ=+，将其化成直角坐标方程为，圆心的直角坐标为．【解析】 2215(1)()24x y -+-=，11,2⎛⎫⎪⎝⎭；222sin 2cos 2x y y x ρρθρθ=+⇒+=+．8. （宣武·理·题12）若直线:0l x =与曲线:x a C y φφ⎧=⎪⎨=⎪⎩（φ为参数，0a >）有两个公共点,A B ，且||2AB =，则实数a 的值为；在此条件下，以直角坐标系的原点为极点，x 轴正方向为极轴建立坐标系，则曲线C 的极坐标方程为．【解析】22,4cos 20ρρθ-+=；曲线C ：22()2x a y -+=，点C 到l 的距离为2a=，因此||22A B a ==⇒=；222(2cos )(2sin )ρθθ-+=，即24cos 20ρρθ-+=．9. （丰台·理·题12）在平面直角坐标系xOy 中，直线l 的参数方程为11x y t =⎧⎨=+⎩（参数t ∈R ），圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩（参数[)0,2πθ∈），则圆心到直线l 的距离是．直线方程为1y x =+，圆的方程为()2211x y -+=．于是圆心()1,0到直线10x y -+=．复数1. （海淀·理·题1）在复平面内，复数1iiz =-（i 是虚数单位）对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解析】 C ；()()1i 1i i 1i iz -==--=--，该复数对应的点位于第三象限．2. （丰台·理·题1）如果1i1ia z a -=+为纯虚数，则实数a 等于（）A ．0B ．1-C ．1D ．1-或1 【解析】 D ；设i z x =，0x ≠则1ii 1i a x a -=+()1i 0ax a x ⇔+-+=100ax a x +=⎧⇔⎨+=⎩11a x =⎧⇔⎨=-⎩或11a x =-⎧⎨=⎩．3. （石景山·理·题1）复数21i+等于（）A ．2i -B ．2iC ．1i -D ．1i + 【解析】 C ；22(1i)2(1i)1i 1i (1i)(1i)2--===-++-．4. （东城·理·题1）i 是虚数单位，若12ii(,)1ia b a b +=+∈+R ，则a b +的值是（） A ．12- B ．2- C ．2 D ．12【解析】 C ；12i (12i)(1i)3i 1i (1i)(1i)2++-+==++-，于是31222a b +=+=． 5. （朝阳·理·题1）复数112i i ++等于（）A ．12i +B ．12i -C ．12-D ．12【解析】 D ；计算容易有1i 11i 22+=+．6. （海淀·文·题1）在复平面内，复数()i 1i -（i 是虚数单位）对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解析】 A ；()i 1i 1i -=+，对应的点为()1,1位于第一象限．7. （丰台·文·题1）复数1i1iz -=+化简的结果等于（）A ．i -B ．iC ．2i -D ．2i 【解析】 A ；1i1i z -=+()()()21i 2i i 1i 1i 2--===-+-．8. （石景山·文·题1）复数21i+等于（）A ．2i -B ．2iC ．1i -D ．1i + 【解析】 C ；22(1i)2(1i)1i 1i (1i)(1i)2--===-++-．9. （东城·文·题1）计算复数1i1i-+的结果为（）A ．i -B ．iC ．1-D ．1 【解析】 A ；21i (1i)i 1i 2--==-+．10. （朝阳·文·题1）复数22(1)i i+等于（） A ．2 B ．-2 C ．2i - D ．2i 【解析】 C ；()221221i ii i +==--．11. （宣武·理·题3）若复数z 满足2i 1iz=+，则z 对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解析】 B ；2i(1i)22i z =+=-+．12. （宣武·文·题4）设i 是虚数单位，则复数(1i)2i z =+⋅所对应的点落在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【解析】 B ；22i z =-+．13. （西城·文·题9）i 是虚数单位，1i 1i +=+ ．【解析】 11i 22+；11i 1ii i 1i 22-++=+=+．14. （西城·理·题9）若(2i)i i a b -=+，其中,a b ∈R ，i 为虚数单位，则a b += ．【解析】 3；2i i a b +=+1,2a b ⇒==．15. （崇文·理·题9）如果复数()()2i 1i m m ++（其中i 是虚数单位）是实数，则实数m =___________．【解析】 1-；()()()()223i 1i 1mm m m i m ++=-++．于是有3101m m +=⇒=-．16. （崇文·文·题10）如果复数()()2i 1i m m ++（其中i 是虚数单位）是实数，则实数m =___________．【解析】 -1；()()()()223i 1i 1m m m m m i ++=-++．于是有3101m m +=⇒=-．算法1. （丰台·文·题3）在右面的程序框图中，若5x =，则输出i 的值是（）A ．2B ．3C ．4D ．5 【解析】 C ；51337109325→→→→，对应的4i =．2. （石景山·理·题4）一个几何体的三视图如图所示，那么此几何体的侧面积（单位：2cm ）为（） A ．80 B ．60 C ．40 D ．20【解析】 A ；几何体如图，是正四棱锥，底边长8，侧面底边上的高为5，因此侧面积为1854802⨯⨯⨯=．3. （西城·理·题5）阅读右面的程序框图，运行相应的程序，输出的结果为（）A ．1321B ．2113C ．813D ．138【解析】 D ；1,1,220x y z ===<；1,2,320x y z ===<；，8,13,2120x y z ===>，故输出138．4. （东城·理·题5）如图是一个算法的程序框图，若该程序输出的结果为45，则判断框中应填入的条件是（）A ．4?T >B ．4?T <C ．3?T >D ．3?T <【解析】 B ；循环一次得：12,1,2i T S ===；两次得：1123,2,263i T S ===+=；三次得：2134,3,3124i T S ===+=；四次得：3145,4,4205i T S ===+=，此时需要跳出循环，故填4?T <．5. （东城·文·题5）按如图所示的程序框图运算，若输入6x =，则输出k 的值是（） A ．3 B ．4 C ．5 D ．6【解析】 B ；6x =，0k =，13x =，1k =，27x =，2k =，55x =，3k =，111x =，4k =，111100x =>，跳出循环，输出4k =．6. （石景山·文·题6）已知程序框图如图所示，则该程序框图的功能是（）A ．求数列1n ⎧⎫⎨⎬⎩⎭的前10项和()n *∈NB ．求数列12n ⎧⎫⎨⎬⎩⎭的前10项和()n *∈NC ．求数列1n ⎧⎫⎨⎬⎩⎭的前11项和()n *∈ND ．求数列12n ⎧⎫⎨⎬⎩⎭的前11项和()n *∈N注意n 和k 的步长分别是2和1．7. （西城·文·题6）阅读右面的程序框图，运行相应的程序，输出的结果为（）A ．1321B ．2113C ．813D ．138【解析】 D ；1,1,220x y z ===<；1,2,320x y z ===<；，8,13,2120x y z ===>，故输出138．8. （海淀·理科·题7）已知某程序框图如图所示，则执行该程序后输出的结果是（）第 7 题A ．1-B ．1C ．2D ．12【解析】 A ；∵()20100mod 3i ==，∴对应的1a =-．9. （朝阳·文·题11）如图，下程序框图的程序执行后输出的结果是．【解析】 55；10.（宣武·文·题12）执行如图程序框图，输出S的值等于．12题图【解析】20；运算顺序如下===→===→===→===>，1,1,23,4,36,10,410,20,54A S i A S i A S i A S i输出S，故20S=．11.（崇文·理·题12）（崇文·文·题12）某程序框图如图所示，该程序运行后输出,M N的值分别为．【解析】 13，21；n 4次运行后43i =>，于是有13,21M N ==．12. （丰台·理·题13）在右边的程序框图中，若输出i 的值是4，则输入x 的取值范围是．【解析】 (]2,4；∵328228x x ->⇔>，322810x x ->⇔>，32104x x ->⇔>，3242x x ->⇔>∴要使得刚好进行4次运算后输出的82x>，则有24x<≤．13.（朝阳·理·题13）右边程序框图的程序执行后输出的结果是．【解析】625；将经过i次运行后的,n S值列表如下．i 1 2 3 4 5 ．．．m．．．25n 3 5 7 9 11 21m+51 S 1 4 9 16 25 2m625 于是625S=．14.（海淀·文·题13）已知程序框图如图所示，则执行该程序后输出的结果是_______________．【解析】12；∵()202mod 3i ==，∴对应的12a =．集合简易逻辑推理与证明1. （崇文·文·题1）已知全集U =R ，集合{}|12A x x =->，{}2|680B x x x =-+<，则集合()U A B =ð （）A ．{}|14x x -≤≤B ．{}|23x x <≤C ． {}|23x x <≤D ．{}|14x x -<< 【解析】 D ；容易解得{3A x x x =>或者}0x <，{}26B x x =<<．于是()U A B =ð{}23x x <≤．2. （西城·理·题1）设集合{|1}P x x =>，2{|0}Q x x x =->，则下列结论正确的是（） A ．P Q = B ．P Q R = C ．P Q Ü D ．Q P Ü【解析】 C ；(1,)P =+∞，(,0)(1,)Q =-∞+∞．3. （宣武·理·题1）设集合20.3{|0},2P x x m =-=≤，则下列关系中正确的是（） A ．m P ⊂ B ．m P ∉ C ．{}m P ∈ D ．{}m PÞ 【解析】 D ；{|0P x x =≤≤，0.3022m <=<<，故m P ∈，因此{}m P Þ4. （崇文·理·题1）已知全集U =R ，集合{}|12A x x =->，{}2|680B x x x =-+<，则集合()U A B =ð（）A ．{}|14x x -≤≤B ．{}|14x x -<<C ．{}|23x x <≤D ． {}|23x x <≤ 【解析】 D ；容易解得{3A x x x =>或者}0x <，{}26B x x =<<．于是()U A B =ð{}23x x <≤．5. （西城·文·题1）设集合{|1}P x x =>，{|(1)0}Q x x x =->，下列结论正确的是（） A ．P Q = B ．P Q R = C ．P Q Ü D ．Q P Ü 【解析】 C ；(1,)P =+∞，(,0)(1,)Q =-∞+∞．6. （宣武·文·题1）设集合{|4},sin 40A x x m ==︒≤，则下列关系中正确的是（） A ．m A ⊂ B ．m A ⊄ C ．{}m A ∈ D ．{}m A ∉ 【解析】 D ；正确的表示法，m A ∈，{}m A Þ，{}m A ∉．7. （东城·理·题2）设全集{33,}I x x x =-<<∈Z ，{1,2}A =，{2,1,2}B =--，则()I A B ð等于（） A ．{1} B ．{1,2} C ．{2} D ．{0,1,2} 【解析】 D ；{2,1,0,1,2}I =--，{0,1}I B =ð，故(){0,1,2}I A B =ð．8. （石景山·文·题2）已知命题 :p x ∀∈R ，2x ≥，那么命题p ⌝为（） A ．,2x x ∀∈R ≤ B ．,2x x ∃∈<R C ．,2x x ∀∈-R ≤ D ．,2x x ∃∈<-R 【解析】 B ；全称命题的否定是存在性命题，将∀改为∃，然后否定结论．9. （东城·文·题2）设集合{1,2,4,6}A =，{2,3,5}B =，则韦恩图中阴影部分表示的集合（） A ．{2} B ．{3,5} C ．{1,4,6} D ．{3,5,7,8}【解析】 B ；阴影部分表示{3,5}U AB =ð．10. （丰台·理·题2）设集合[)1{|(),0,}2x M y y x ==∈+∞，(]2{|log ,0,1}N y y x x ==∈，则集合M N 是（）A ．[)(,0)1,-∞+∞B ．[)0,+∞C ．(],1-∞D ．(,0)(0,1)-∞ 【解析】 C ；(]0,1M =，(],0N =-∞，因此(],1MN =-∞．11. （石景山·理·题2）已知命题 :p x ∀∈R ，2x ≥，那么命题p ⌝为（） A ．,2x x ∀∈R ≤ B ．,2x x ∃∈<RC ．,2x x ∀∈-R ≤D ．,2x x ∃∈<-R 【解析】 B ；全称命题的否定是存在性命题，将∀改为∃，然后否定结论．12. （朝阳·文·题2）命题:0p x ∀>，都有sin 1x -≥，则（） A ．:0p x ⌝∃>，使得sin 1x <- B ．:0p x ⌝∀> ，使得sin 1x <- C ．:0p x ⌝∃>，使得sin 1x >- D ．:0p x ⌝∀>，使得sin 1x -≥ 【解析】 A ；由命题的否定容易做出判断．13. （海淀·文·题7）给出下列四个命题：①若集合A 、B 满足A B A =，则A B ⊆；②给定命题,p q ，若“p q ∨”为真，则“p q ∧”为真； ③设,,a b m ∈R ，若a b <，则22am bm <；④若直线1:10l ax y ++=与直线2:10l x y -+=垂直，则1a =．其中正确命题的个数是（）A ．1B ．2C ．3D ．4 【解析】 B ；命题①和④正确．14. （丰台·文·题7）若集合{}0,1,2P =，10(,),,20x y Q x y x y P x y ⎧⎫-+>⎧⎪⎪=∈⎨⎨⎬--<⎩⎪⎪⎩⎭，则Q 中元素的个数是（）A ．3B ．5C ．7D ．9 【解析】 B ；(){},|12,,Q x y x y x y P =-<-<∈，由{}0,1,2P =得x y -的取值只可能是0和1．∴()()()()(){}0,0,1,1,2,2,1,0,2,1Q =，含有5个元素．15. （崇文·文·题8）如果对于任意实数x ，[]x 表示不超过x 的最大整数．例如[]3.273=，[]0.60=．那么“[][]x y =”是“1x y -<”的 ( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【解析】 A ；由[][][][]1,1x x x y y y <+<+≤≤．于是有[][]()[][]1111x y x y x y -=+<-<+-=-则1x y -<．不妨设33,24x y ==，于是3331424x y -=-=<．但是[][]1,0.x y ==16. （东城·文·题9）已知命题3:(1,),log 0p x x ∀∈+∞>，则p †为．【解析】 030(1,),log 0x x ∃∈+∞≤；全称命题的否定为存在命题．17. （宣武·文·题10）命题“任意常数列都是等比数列”的否定形式是．【解析】存在一个常数列不是等比数列；全称命题的否定是存在性命题． 18. （海淀·理·题11）给定下列四个命题：① “π6x =”是“1sin 2x =”的充分不必要条件；② 若“p q ∨”为真，则“p q ∧”为真；③ 若a b <，则22am bm <；④ 若集合A B A =，则A B ⊆．其中为真命题的是（填上所有正确命题的序号）．【解析】 ①，④；19. （海淀·理·题14）在平面直角坐标系中，点集(){}22,|1A x y xy =+≤，{(,)|4,0,340}B x y x y x y =-≤≥≥，则⑴点集(){}1111(,)3,1,,P x y x x y y x y A ==+=+∈所表示的区域的面积为_____； ⑵点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为．【解析】 π；18π+．；⑴如左图所示，点集P 是以()3,1为圆心1为半径的圆，其表示区域的面积为π； ⑵如右图所示，点集Q 是由三段圆弧以及连结它们的三条切线段围成的区域，其面积为()1π433451π18π2OPQ OABP PCDQ OFEQ S S S S ++++=⨯⨯+++⨯+=+△．20. （海淀·文·题14）在平面直角坐标系中，点集(){}22,|1A x y xy =+≤，(){},|11,11B x y x y =--≤≤≤≤，则⑴点集(){}1111(,)3,1,,P x y x x y y x y A ==+=+∈所表示的区域的面积为_____； ⑵点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为．【解析】π，12π+；⑴如左图所示，点集P 是以()3,1为圆心1为半径的圆，其表示区域的面积为π；⑵ 如右图所示，点集Q 是由四段圆弧以及连结它们的四条切线段围成的区域，其面积为12π+．。

2010北京各区县一模综合题试题分类汇编

各区县一模综合题试题分类汇编例1：（顺义）8在正方形ABCD 中，点E 为BC 边的中点，点F 在对角线AC 上，连接FB 、FE 。

当点F 在AC 上运动时，设AF=x ，△BEF 的周长为y ，下列图象中，能表示y 与x 的函数关系的图象大致是（）例2：（1）（海淀）8．如图，点E 、F 是以线段BC 为公共弦的两条圆弧的中点，6BC =，点A 、D 分别为线段EF 、BC 上的动点。

连接AB 、AD ，设BD x =，22AB AD y -=，下列图象中，能表示y 与x 的函数关系的图象是（）（2）（昌平）8．如图，在半径为1的⊙O 中，直径AB 把⊙O 分成上、下两个半圆，点C 是上半圆上一个动点（C 与点A 、B 不重合），过点C 作弦CD AB ⊥，垂足为E ，OCD ∠的平分线交⊙O 于点P ，设,CE x AP y ==，下列图象中，最能刻画y 与x 的函数关系的图象是（）例3：（东城）8．方程2310x x +-=的根可视为函数3y x =+的图象与函数1y x=的图象交点的横坐标，那么用此方法可推断出方程3210x x +-=的实根0x 所在的范围（） A ．010x -<< B ．001x << C ．012x << D ．023x <<例4：（1）（平谷）8．如图，已知⊙O 是以数轴的原点O 为圆心，半径为1的圆，45AOB ∠=︒,点P 在数轴上运动，若过点P 且与OA 平行的直线与⊙O 有公共点，设x OP =，则x 的取值范围是（）A ．B ．C ．D ．海淀第8题图yO x x OO昌平第8题图E PO CBDA ．－1≤x ≤1 B．≤x ≤2 C ．0≤x ≤2 D ．x ＞2（2）（宣武）8．如图，正方形ABCD 的边长为2，将长为2的线段QF 的两端放在正方形相邻的两边上同时滑动。

如果点Q 从点A 出发，沿图中所示方向按A D CB A →→→→滑动到点A 为止，同时点F 从点B 出发，沿图中所示方向按B A DC B →→→→滑动到B 点为止，那么在这个过程中，线段QF 的中点M 所经过的路线围成的图形面积为（） A ．2 B ．π-4 C ．πD ．1-π二、1、例1：（朝阳）12．如图，△ABC 中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边做垂线，画出一个新的等腰直角三角形，如此继续下去，直到所画直角三角形的斜边与△ABC 的BC 边重叠为止，此时这个三角形的斜边长为_____．例2：（海淀）12．如图，n +1个边长为2的等边三角形有一条边在同一直线上，设△211B D C 的面积为1S ，△322B D C 的面积为2S ，…，△1n n n B D C +的面积为n S ，则2S = ；n S =____ （用含n 的式子表示）2．代数找规律例1：（房山）12．一组按规律排列的式子：2581114916,,,,...(0)a a a a a --≠，其中第8个式子是，第n 个式子是（n 为正整数）．3．几何计算例1：（1）（东城）12．如图，P 为边长为2的正三角形中任意一点，连接PA 、PB 、P C ，过P 点分别做三边的垂线，垂足分别为D 、E 、F ，则PD+PE+PF= ；阴影部分的面积为_________．（2）（石景山）12．已知：如图，直角△ABC 中，︒=∠90ACB ，1==BC AC ，的圆心为A ，如果图中两个阴影部分的面积相等，那么AD 的长是．朝阳第12题图海淀第12题图平谷第8题图宣武第8题图4．分类讨论例1：（宣武）12．如图，在第一象限内作与x 轴的夹角为︒30的射线OC ，在射线OC 上取一点A ，过点A 作x AH ⊥轴于点H 。

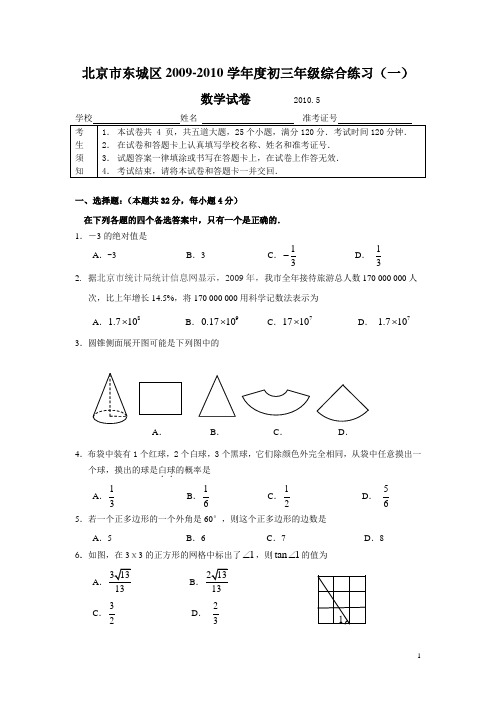
2010年北京市东城区中考一模数学试卷(word版含评分标准)

1北京市东城区2009-2010学年度初三年级综合练习（一）数学试卷 2010.5一、选择题：（本题共32分，每小题4分）在下列各题的四个备选答案中，只有一个是正确的．1．－3的绝对值是A ．-3B ．3C ．13-D ． 132. 据北京市统计局统计信息网显示，2009年，我市全年接待旅游总人数170 000 000人次，比上年增长14.5%，将170 000 000用科学记数法表示为 A ．81.710⨯ B ．90.1710⨯ C ．71710⨯ D ． 71.710⨯ 3．圆锥侧面展开图可能是下列图中的4．布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球．．的概率是 A ．13 B ．16 C ．12 D ． 565．若一个正多边形的一个外角是60°，则这个正多边形的边数是A ．5B ．6C ．7D ．8 6．如图，在3ⅹ3的正方形的网格中标出了1∠，则tan1∠的值为A B C ．32 D ． 23A ．B ．C ．D ．ACDE 7．某人要去夏威夷旅游，统计了该城市一周中午的温度（华氏温度标准）如图所示，如果用m 代表这组数据的中位数，f 代表众数，a 代表平均数，则 A. f a m << B. m f a << C. a f m << D. f m a << 8．方程2310x x +-=的根可视为函数3yx =+的图象与函数1y x=的图象交点的横坐标，那么用此方法可推断出方程3210x x +-=的实根0x 所在的范围是 A ．010x -<< B ．001x << C ．012x <<D ．023x <<二、填空题：（本题共16分，每小题4分）9x 的取值范围是．10．若⊙O 的半径为5厘米，圆心O 到弦AB 的距离为3厘米，则弦长AB 为厘米． 11.在实数范围内分解因式：32a ab -= ． 12.如图，P 为边长为2的正三角形中任意一点，连接PA 、PB 、P C ，过P 点分别做三边的垂线，垂足分别为D 、E 、F ，则 PD+PE+PF= ；阴影部分的面积为__________.三、解答题：（本题共30分，每小题5分） 13. 计算：201()(1)2sin 602π-++-︒+14. 解不等式组31422x x x ->-⎧⎨<+⎩，并把它的解集表示在数轴上．15.如图，ABC ∆与ADE ∆均为等腰直角三角形，90BAC EAD ∠=∠=︒，求证：BAE CAD ∆≅∆.B C16．已知2(1)()3x x x y ---=-，求222x y xy +-的值．17．列方程或方程组解应用题：.A 、B 两种机器人都被用来搬运化工原料，A 型机器人比B 型机器人每小时多搬运30kg ，A 型机器人搬运900kg 与B 型机器人搬运600kg 所用时间相等，两种机器人每小时分别搬运多少化工原料？18．已知：二次函数2y ax bx c =++(0)a ≠中的x y ，满足下表：（1）m 的值为；（2）若1()A p y ，，2(1)B p y+，两点都在该函数的图象上，且0p <，试比较1y 与2y 的大小.四、解答题：（本题共20分，每小题5分）19．如图，在梯形ABCD 中，AD ∥BC ，∠B=90°，AD=2，BC=5，E 为DC 中点，tanC=34．求AE 的长度．20．如图，在⊙O 中，AB 是直径，AD 是弦，∠ADE = 60°，∠C = 30°．（1）判断直线CD 是否为⊙O 的切线，并说明理由；（2）若CD = 33 ，求BC 的长．1521．某中学体育俱乐部的老师对学生的体能进行摸底测试，考试项目有跳绳、仰卧起坐等，体育老师随机从全校3600名学生中抽取统计了100名学生60秒跳绳的成绩，列出的频数分布直方图如下（每个分组包括左端点，不包括右端点）：（1）求60秒跳绳的成绩在140—160次的人数；（2）若将此直方图转化为扇形统计图，求（1）中人数所在扇形统计图中圆心角的度数；（3）请你估计一下全校大概有多少名学生60秒跳绳的次数在100次以上？22．人们经常利用图形的规律来计算一些数的和. 如在边长为1的网格图1中，从左下角开始，相邻的黑折线围成的面积分别是1，3，5，7，9，11，13，15，17 ，它们有下面的规律： 1+3=22 ； 1+3+5=32 ； 1+3+5+7=42 ； 1+3+5+7+9=52 ；……（1）请你按照上述规律，计算1+3+5+7+9+11+13的值，并在图1中画出能表示该算式的图形；（2）请你按照上述规律，计算第n 条黑折线与第1n -条黑折线所围成的图形面积；（3）请你在边长为1的网格图2中画出下列算式所表示的图形. 1+8=32 ； 1+8+16=52 ； 1+8+16+24=72 ；1+8+16+24+32=92 .五、解答题：（本题共22分，第23、24题每题7分，第25题8分）23. 已知抛物线C 1：22y x x =-的图象如图所示，把C 1的图象沿y 轴翻折，得到抛物线C 2的图象，抛物线C 1与抛物线C 2的图象合称图象C 3．（1）求抛物线C 1的顶点A 坐标，并画出抛物线C 2（2）若直线y kx b =+与抛物线2(0)y ax bx c a =++≠且只有一个交点时,称直线与抛物线相切. 若直线y x b =+与抛物线C 1相切，求b 的值；（3）结合图象回答，当直线y x b =+与图象C 3 点时，b 的取值范围．FE QP NMD C BAAB CDM24．如图，在平面直角坐标系中，A（0），B（2）.把矩形OABC 逆时针旋转30︒得到矩形111OA B C .（1）求1B 点的坐标；（2）求过点（2，0）且平分矩形111OA B C 面积的直线l 方程；（3）设（2）中直线l 交y 轴于点P ，直接写出1PC O ∆与11PB A ∆的面积和的值及1POA∆与11PBC ∆的面积差的值.25．如图，正方形ABCD 的对角线AC 与BD 相交于点M ，正方形MNPQ 与正方形ABCD全等，射线MN 与MQ 不过A 、B 、C 、D 四点且分别交ABCD 的边于E 、F 两点. （1）求证：ME=MF ；（2）若将原题中的正方形改为矩形，且24BC AB ==，其他条件不变，探索线段ME 与线段MF 的数量关系.北京市东城区2009-2010学年度初三年级综合练习（一）数学参考答案 2010.5一、选择题：（本题共32分，每小题4分）二、填空题：（本题共16分，每小题4分）9. 3x ≥-， 10. 8， 11. ()()a a b a b-+，12..2. 三、解答题：（本题共30分，每小题5分） 201()(1)2sin 602π-++-︒13.解:原式＝412=+- …………………………………………4分 5=5= ………………………………………………………………5分14.解：31422x x x ->-⎧⎨<+⎩12x x >-⎧⇒⎨<⎩12x ⇒-<<. ∴原不等式组的解集是12x -<<. ……………………………3分在数轴上表示为：……………………………………5分15.证明：ABC △与AED △均为等腰直角三角形，AB AC ∴=，AE AD =，90BAC EAD ∠=∠= . ··························································· 3分BAC CAE EAD CAE ∴∠+∠=∠+∠.即BAE CAD ∠=∠. ············································································································· 4分在BAE △与CAD △中，ABCDE MFEDCBA,,.AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩BAE CAD ∴△≌△. ……………5分16．解：2(1)()3x x x y ---=- ，223x x x y ∴--+=-．………………………2分3x y ∴-=. ……………………………………3分22222()39x y xy x y ∴+-=-==． ……………………………………5分17．解：设B 型机器人每小时搬运x kg 化工原料，则A 型机器人每小时搬运(30)x +kg 化工原料.A 型机器人搬运900kg 与B 型机器人搬运600kg 所用时间相等，∴90060030x x=+. …………………2分解此分式方程得：60x =.检验：当60x =时，(30)0x x +≠，所以60x =是分式方程的解. …………………4分当60x =时，3090x +=.答：A 型机器人每小时搬运90kg 化工原料，B 型机器人每小时搬运60kg 化工原料. ………………………………………………………………………………………………5分 18．解：（1）m = 0 . ………2分（2）0p < ，11p p ∴<+<，又因为抛物开口向上，对称轴为1x =， ∴12y y >. …………5分四、解答题：（本题共20分，每小题5分）19．解：过点E 作BC 的垂线交BC 于点F ，交AD 的延长线于点M . ………1分在梯形ABCD 中，AD ∥BC ，E 是DC 的中点， ∴∠M=∠MFC ，DE=CE .在△MDE 和△FCE 中，∠M=∠MFC ， ∠DEM=∠CEF ，DE=CE .∴△MDE ≌△FCE .∴EF = ME ，DM=CF . ………………3分∵AD=2，BC=5，∴DM=CF=23. 在Rt △FCE 中，tanC=34=CFEF，∴EF = ME =2. ………4分在Rt △AME 中，AE =265)232(222=++. …5分 20. 解：（1）CD 是⊙O 的切线．……………………1分证明：连接OD ．∵∠ADE =60°，∠C =30°，∴∠A =30°． ∵OA=OD ，∴∠ODA=∠A =30°．∴∠ODE=∠ODA+∠ADE =30°+60°=90°． ∴OD ⊥CD ． ∴CD 是⊙O 的切线．……………………………3分（2）在Rt △ODC 中，∠ODC =90°， ∠C =30°， CD =33． ∵tan C =CDOD， ∴OD=CD ·tan C =33×33=3．∴OC=2OD =6．∵OB=OD =3，∴BC=OC -OB =6-3=3．…………………………………………5分 21. 解：（1）60秒跳绳的成绩在140—160次的人数为：1003826148410-----=（人）．…………………1分（2）（1）中人数所在扇形统计图中圆心角的度数为：1036036100⨯︒=︒．…………………4分（3）估计全校60秒跳绳的次数在100次以上的学生人数为：381410436002376100+++⨯=（名）． ………………5分22．（1）1+3+5+7+9+11+13=72． …………………1分算式表示的意义如图（1）．…………………2分（2）第n 条黑折线与第1n -条黑折线所围成的图形面积为21n -. …………………3分（3）算式表示的意义如图（2）、（3）等. …………………5分（1）（2）（3）五、解答题：（本题共22分，第23、24题每题7分，第25题8分）23．解：（1）顶点坐标A（1，-1）. …………………1分……………………………………………………………………………………2分（2）2(1)2(2)y x by x x=+⎧⎨=-⎩把（1）式代入（2）整理得：230x x b--=.940b∆=+=，94b=-. …………………4分（3）2(1)2(2)y x by x x=+⎧⎨=+⎩把（1）式代入（2）整理得：20x x b+-=.140b∆=+=，14b=-. …………………6分∴当直线y x b=+与图象C3有两个交点时，b的取值范围为：9144b-<<-. …………………7分24. 解：（1）由已知可得：2,90OA AB A ==∠=︒，11130,4BOA BOA OB OB ∴∠=∠=︒==.又1AOA ∠ 为旋转角，130AOA ∴∠=︒.160B OA ∴∠=︒. …………………1分过点1B 作1B E OA ⊥于点E ，在1Rt B OE ∆中，1160,4B OE OB ∠=︒=，12,OE B E ∴==1(2,B ∴. …………………2分（2）设F 为11AC 与1OB 的交点，可求得(1F . …………………4分设直线l 的方程为y kx b =+，把点（2，0）、（102,k b k b=+⎧⎪=+解得：k b ⎧=⎪⎨=⎪⎩∴直线l 的方程为y =+. …………………5分（3）…………………7分25．（1）证明：过点M 作MG ⊥BC 于点G ，MH ⊥CD 于点H . ∴∠MGE=∠MHF=090.∵M 为正方形对角线AC 、BD 的交点，∴MG=MH .又∵∠1+∠GMQ=∠2+∠GMQ=090， ∴∠1=∠2.在△MGE 和△MHF 中∠1=∠2， MG=MH ， ∠MGE=∠MHF .F 21HGE QPNBDMCA∴ME=MF . ………………3分（2）解：①当MN 交BC 于点E ，MQ 交CD 于点F 时.过点M 作MG ⊥BC 于点G ，MH ⊥CD 于点H .∴∠MGE=∠MHF=090.∵M 为矩形对角线AC 、BD 的交点， ∴∠1+∠GMQ=∠2+∠GMQ=090. ∴∠1=∠2.在△MGE 和△MHF 中，∠1=∠2∠MGE=∠MHF ∴△MGE ∽△MHF . ∴MHMGMF ME =. ∵M 为矩形对角线AB 、AC 的交点，∴MB=MD=MC又∵MG ⊥BC ，MH ⊥CD ，∴点G 、H 分别是BC 、DC 的中点. ∵24BC AB ==， ∴BC MH AB MG 21,21==. ∴21=MF ME . ………………4分 ②当MN 的延长线交AB 于点E ，MQ 交BC 于点F 时. 过点M 作MG ⊥AB 于点G ，MH ⊥BC 于点H .∴∠MGE=∠MHF=090.∵M 为矩形对角线AC 、BD 的交点， ∴∠1+∠GMQ=∠2+∠GMQ=090. .∴∠1=∠2.在△MGE 和△MHF 中，∠1=∠2， ∠MGE=∠MHF .NP∴MHMGMF ME =. ∵M 为矩形对角线AC 、BD 的交点，∴MB=MA=MC .又∵MG ⊥AB ，MH ⊥BC ，∴点G 、H 分别是AB 、BC 的中点. ∵24BC AB ==，∴AB MH BC MG 21,21==. ∴2=MFME. ………………5分 ③当MN 、MQ 两边都交边BC 于E 、F 时.过点M 作MH ⊥BC 于点H .∴∠MHE=∠MHF =∠NMQ=090. ∴∠1=∠3，∠2=∠4.∴△MEH ∽△FEM ，FMH ∽△FEM .∴ME MH FE FM =，FM MHFE EM=. ∵M 为正方形对角线AC 、BD 的交点， ∴点M 为AC 的中点.又∵MH ⊥BC ，∴点M 、H 分别是AC 、BC 的中点. ∵24BC AB ==，∴AB=2. ∴MH=1. ∴1FM FM ME MH EF EF ==⋅， 1EM EMMF MH EF EF==⋅. ∴11122222=+=+EF EM FM MF ME . ………………6分 ④当MN 交BC 边于E 点，MQ 交AD 于点F 时. 延长FM 交BC 于点G .易证△MFD ≌△MGB . ∴MF=MG .同理由③得22111MG ME +=. ∴22111ME MF +=. ………………7分综上所述：ME 与MF 的数量关系是21=MF ME 或2=MFME 或11122=+MF ME . …8分。

北京市各区县2010年以来一模二模中的四边形综合题

四边形综合题（2010昌平一模）1．(1)已知：如图1，△ABC 中，分别以AB 、AC 为一边向△ABC 外作正方形ABGE 和ACHF ，直线AN ⊥BC 于N ，若EP AN ⊥于P ，FQ AN ⊥于Q . 判断线段EP FQ 、的数量关系，并证明； (2)如图2，梯形ABCD 中，AD ∥BC , 分别以两腰AB 、CD 为一边向梯形ABCD 外作正方形ABGE 和DCHF ，线段AD 的垂直平分线交线段AD 于点M ，交BC 于点N ，若EP M N ⊥于P ，FQ MN ⊥于Q ．(1)中结论还成立吗？请说明理由.图2FF图1HN Q GHMPEP QGEDCBAN CBA（2010延庆一模）2. 在图25-1至图25-3中，点B 是线段AC 的中点，点D 是线段CE 的中点．四边形BCGF 和CDHN 都是正方形．AE 的中点是M ．（1）如图25-1，点E 在AC 的延长线上，点N 与点G 重合时，点M 与点C 重合，求证：FM = MH ，FM⊥MH ；（2）将图25-1中的CE 绕点C 顺时针旋转一个锐角，得到图25-2，求证：△FMH 是等腰直角三角形；（3）将图25-2中的CE 缩短到图25-3的情况，△FMH 还是等腰直角三角形吗？（不必说明理由）（相似形）图25-1AHC (M )DEBFG (N )G图25-2AHCDEBFNM AH CDE图25-3BFG MN（2010昌平二模）3．如图1，在菱形ABCD 中，点E F 、分别为边AD CD 、上的动点（都与菱形的顶点不重合），连接EF 、BE 、BF .（1）若60A ∠=，且AE CF AB +=，判断BEF ∆的形状，并说明理由；（2）在（1）的条件下，设菱形的边长为a ，求BEF ∆面积的最小值.CDAB 图2（备用）AB CE DF图1（2010崇文一模）4. 在ABC ∆中，︒=∠45ACB ，点D （与点B 、C 不重合）为射线BC 上一动点，连接AD ，以AD 为一边且在AD 右侧作正方形ADEF 。

2010年北京怀柔数学一模试题及答案

NM DC BA怀柔区2010年初三一模数学试卷下面各题均有四个选项，其中只有一个．．是符合题意的． 1．21-的倒数为( ) A. 2 B. 2- C.21D. 21- 2．二次根式2-x 有意义，则x 的取值范围是( )A. 2≥xB. 2≤xC. 2>xD. 2<x 3．已知如图，AB ∥CD,CN 交AB 于点M,若∠C=38，则∠AMN=( ) A. 38 B. 132C. 142D. 1524．下列图形中，既是轴对称图形，又是中心对称图形的是( )5．布袋中装有2个红球，3个白球，4个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球．．的概率是( ) A.92 B. 31 C. 94D. 1 6．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数均是9.2环，方差分别为：58.02=甲S ，52.02=乙S ，56.02=丙S ，48.02=丁S ，则成绩最稳定的是（）A ．甲B ．乙C ．丙D ．丁7．一元二次方程041)1(2=+--m mx x m 有实数根，则m 的取值范围是（） A. 0>m B. 1m 0≠≥且m C. 1≠m D. 1m 0≠>且m8．在直角梯形ABCD 中，AB ∥CD ,BC ⊥DC 于点C, AB=2,CD=3,∠D=45,动点P 从D 点出发，沿DC以每秒1个单位长度的速度移动,到C 点停止．过P 点作PQ 垂直于直．线．AD ，垂足为Q ．设P 点移动的时间为t 秒，△DPQ 与直角梯形ABCD 重叠部分的面积为S, 下列图象中，能表示S 与t 的函数关系的图象大致是( )A B C D二、填空题（本题共16分，每小题4分） 9．已知042=-++y x ，则x+y= .10．已知如图，正方形ABCD 是⊙O 的内接四边形，E 是⌒BC 上一点，则∠AED= °.11．圆心在x 轴上的两圆相交于A 、B 两点,已知A 点坐标为(-3,2)，则B 点坐标是． 12．已知如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD=2，BC=DC=5，点P 在BC 上移动，则当PA+PD 取最小值时，△APD 中边AP 上的高为 .三、解答题（本题共30分，每小题5分）13．计算：)3(60tan )21(813--+--- . 14．分解因式：y x xy 34-.15．解不等式组：3(2)8,1.23x x x x ++⎧⎪-⎨⎪⎩＜≤.16．已知如图，∠1＝∠2，∠C ＝∠D ．求证：AC ＝BD ．17．王大伯承包了25亩土地，今年春季改种茄子和西红柿两种大棚蔬菜，总支出44000元。

北京市丰台区2010年一模初三数学试卷(含答桉)

欢迎访问h t t p ://b l o g .s i n a.c o m .c n /b e i j i n g s t ud y丰台区2010年初三毕业及统一练习数学试卷一、选择题（共8小题，每小题4分，满分32分）下列各题均有四个选项，其中只有一个..是符合题意的．1．3的倒数是A ．3B ．3−C ．13D ．13−2．今年初，惊闻海地发生地震，中国政府和人民在第一时间作出支援海地的决定：1月13日，中国红十字会向海地先期捐款1000000美元，将1000000用科学记数法表示为A ．51010×B ．6101×C ．7101.0×D ．5101×3．下列图形中，不是三棱柱的表面展开图的是A ．B ．C ．D ．4．如果半径分别为2cm 和3cm 的两圆外切，那么这两个圆的圆心距是A ．1cmB ．5cmC ．1cm 或5cmD ．小于1cm 或大于5cm 5．某小组7名同学积极参加支援“希望工程”的捐书活动，他们捐书的册数分别是（单位：本）：10，12，10，13，10，15，17，这组数据的众数和中位数分别是A ．10，12B ．10，13C ．10，10D ．17，106．在1，2，3三个数中任取两个，组成一个两位数，则组成的两位数是偶数的概率为A ．13B ．12C ．14D ．167．不等式组⎨⎧−≥−,12x 的解集在数轴上表示正确的是AB ．CD．8．如图所示是张老师晚上出门散步时离家的距离y与时间x 之间的函数关系的图象，若用黑点表示张老师家的位置，则张老师散步行走的路线可能是A ．B ．C ．D ．欢迎访问h t t p ://bl o g.s i na .c om .c n /b ei j i ng st u d y二、填空题（共4小题，每小题4分，满分16分）9．在函数y中，自变量x 的取值范围是___________．10．分解因式：324b b a −=．11．若一个正n 边形的一个内角为144°，则n 等于．12．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你观察图中正方形A 1B 1C 1D 1，A 2B 2C 2D 2，A 3B 3C 3D 3……每个正方形四条边上的整点的个数．按此规律推算出正方形A 10B 10C 10D 10四条边上的整点共有个．三、解答题（共6小题，每小题5分，满分30分）13．计算：21|22sin 602010−+−°+−（π）．．解方程：0222=−−x x ．15．已知：如图，□ABCD 中，点E 是AD 的中点，延长CE 交BA 的延长线于点F ．求证：AB=AF ．16．已知：x 022=−,求代数式11)1(222++−−x xx x 的值．17．如图，一次函数b kx y +=1的图象与反比例函数xmy =2的图象相交于A 、B 两点．（1）求出这两个函数的解析式；（2）结合函数的图象回答：当自变量x 的取值范围满足什么条件时，21y y <？EBCDAF欢迎访问h t t p ://b l o g.s i n a .c om .c n /b ei j i ng s t u d y 18．列方程或方程组解应用题：中国2010年上海世博会第三期预售平日门票分为普通票和优惠票，其中普通票每张150元人民币，优惠票每张90元人民币．某日一售票点共售出1000张门票，总收入12.6万元人民币．那么，这一售票点当天售出的普通票和优惠票各多少张？注：优惠票的适用对象包括残疾人士、老年人（1950年12月31日前出生的）、学生、身高超过1.20米的儿童、现役军人．四、解答题（共4小题，每小题5分，满分20分)19．已知：如图，梯形ABCD 中，DC ∥AB ，AD =BC ，对角线AC 、BD 交于点O ，∠COD =60°，若CD =3，AB =8，求梯形ABCD 的高．20．已知：如图，AB 为⊙O 的直径，⊙O 过AC 的中点D ，DE ⊥BC 于点E ．（1）求证：DE 为⊙O 的切线；（2）若DE =2，tan C =21，求⊙O 的直径．21．国家教育部规定“中小学生每天在校体育活动时间不低于1小时”．某中学为了了解学生体育活动情况，随机抽查了520名毕业班学生，调查内容是：“每天锻炼是否超过1小时及未超过1小时的原因”．以下是根据所得的数据制成的统计图的一部分．根据以上信息，解答下列问题：（1）每天在校锻炼时间超过1小时的人数是；（2）请将图2补充完整；（3）2010年我市初中毕业生约为9.6万人，请你估计今年全市初中毕业生中每天锻炼时间超过1小时的学生约有多少万人？BCDOA图1图2欢迎访问h t t p :://b l o g.s i n a .c o m.c n /b e i j i n gs t u d y22．在图1中，正方形ABCD 的边长为a ，等腰直角三角形FAE 的斜边AE ＝2b ，且边AD 和AE 在同一直线上．操作示例当2b ＜a 时，如图1，在BA 上选取点G ，使BG ＝b ，连结FG 和CG ，裁掉△FAG 和△CGB 并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH ．思考发现小明在操作后发现：该剪拼方法就是先将△FAG 绕点F 逆时针旋转90°到△FEH 的位置，易知EH 与AD 在同一直线上．连结CH ，由剪拼方法可得DH =BG ，故△CHD ≌△CGB ，从而又可将△CGB 绕点C 顺时针旋转90°到△CHD 的位置．这样，对于剪拼得到的四边形FGCH （如图1），过点F 作FM ⊥AE 于点M （图略），利用SAS 公理可判断△HFM ≌△CHD ，易得FH =HC =GC =FG ，∠FHC =90°．进而根据正方形的判定方法，可以判断出四边形FGCH 是正方形．实践探究（1）正方形FGCH 的面积是；（用含a ，b 的式子表示）（2）类比图1的剪拼方法，请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展小明通过探究后发现：当b ≤a 时，此类图形都能剪拼成正方形，且所选取的点G 的位置在BA 方向上随着b 的增大不断上移．当b ＞a 时（如图5），能否剪拼成一个正方形？若能，请你在图5中画出剪拼成的正方形的示意图；若不能，简要说明理由．五、解答题（共3小题，共22分)23．（本小题满分7分）已知二次函数22−+−=m mx x y ．（1）求证：无论m 为任何实数，该二次函数的图象与x 轴都有两个交点；（2）当该二次函数的图象经过点（3，6）时，求二次函数的解析式；（3）将直线y =x 向下平移2个单位长度后与（2）中的抛物线交于A 、B 两点（点A 在点B 的左边），一个动点P 自A 点出发，先到达抛物线的对称轴上的某点E ，再到达x 轴上的某点F ，最后运动到点B ．求使点P 运动的总路径最短的点E 、点F 的坐标，并求出这个最短总路径的长．图3AE图4图22b＝a a ＜2b ＜2ab ＝aF 图12b ＜a图5Ab ＞a欢迎访问h t t p ://b l og .s i n a .c om .c n /b e i j i ng s t u d y24．（本小题满分7分）直线CD 经过BCA ∠的顶点C ，CA=CB ．E 、F 分别是直线CD 上两点，且BEC CFA α∠=∠=∠．（1）若直线CD 经过BCA ∠的内部，且E 、F 在射线CD 上，请解决下面两个问题：①如图1，若90,90BCA α∠=∠=��，则EFBE AF −（填“>”，“<”或“=”号）；②如图2，若0180BCA <∠<��，若使①中的结论仍然成立，则α∠与BCA ∠应满足的关系是；（2）如图3，若直线CD 经过BCA ∠的外部，BCA α∠=∠，请探究EF 、与BE 、AF 三条线段的数量关系，并给予证明．25．（本小题满分8分）已知抛物线22−−=x x y ．（1）求抛物线顶点M 的坐标；（2）若抛物线与x 轴的交点分别为点A 、B （点A 在点B 的左边），与y 轴交于点C ，点N 为线段BM 上的一点，过点N 作x 轴的垂线，垂足为点Q ．当点N 在线段BM 上运动时（点N 不与点B ，点M 重合），设NQ 的长为t ，四边形NQAC 的面积为S ，求S 与t 之间的函数关系式及自变量t 的取值范围；（3）在对称轴右侧的抛物线上是否存在点P ，使△PAC 为直角三角形?若存在，求出所有符合条件的点P 的坐标；若不存在，请说明理由．ABCE FDD ABCE FADFC EB图1图2图3欢迎访问h t t p://b l og .s in a .c om .c n/b e i j i n g s t u d y丰台区2010年初三毕业及统一练习数学参考答案及评分标准一、选择题（共8小题，每小题4分，满分32分）题号12345678答案CBDBAACD二、填空题（共4小题，每小题4分，满分16分）9．3≥x 10．)2)(2(b a b a b −+11．1012．80三、解答题（共6小题，每小题5分，满分30分）13．解：原式=12324113+×−+−--------4分=41．--------------5分14．解法一：12122=−+−x x ，--------------1分3)1(2=−x ，--------------2分31±=−x ，--------------3分31±=x ．-------------4分∴原方程的解为311+=x ，312−=x ．---5分解法二：a =1，b =−2，c =−2，△=0128442>=+=−ac b ,------2分∴312322242±=±=−±−=a ac b b x ．------4分∴原方程的解为311+=x ，12−=x ．--5分15．证明：∵四边形ABCD 是平行四边形，∴AB ∥CD 且AB=CD ．∴∠F =∠2,∠1=∠D ．---------------1分∵E 为AD 中点，∴AE =ED .---------------2分在△AEF 和△DEC 中21F D AE ED ∠=∠⎧⎪∠=∠⎨⎪=⎩，，，∴△AEF ≌△DEC ．--------------3分∴AF =CD .---------------4分∴AB =AF .--------------5分16．解：原式=22(1)1)(1)1x x x x x −++−+（------------1分=2111x x x x −+++------------2分=112+−+x x x ．-------------3分∵022=−x ，∴22=x ．∴原式=111112=++=+−+x x x x ．-------------5分17．解：（1）由图象知反比例函数xmy =2的图象经过点B (4，3)，∴43m =．∴m =12．----------1分∴反比例函数解析式为212y x=．----------2分由图象知一次函数b kx y +=1的图象经过点A (－6，－2)，B (4，3),∴⎩⎨⎧=+−=+−.3426　，b k b k 解得⎪⎩⎪⎨⎧==．121b k ---------3分∴一次函数解析式为1112y x =+．--------4分（2）当0<x <4或x <－6时，21y y <．------5分18．解：设当日售出普通票x 张，则售出优惠票（1000-x ）张，------1分根据题意,得:150x +90（1000-x ）=126000，------3分解方程得x =600．------4分∴1000-600=400．答：当日这一售票点售出普通票600张，优惠票400张．-------5分欢迎访问h t t p ://b l og .si n a .co m n /b e i j四、解答题（共4小题，每小题5分，满分20分）19.解：过点C 作CE ∥DB ，交AB 的延长线于点E ．∴∠ACE =∠COD =60°．-----------------1分又∵DC ∥AB ，∴四边形DCEB 为平行四边形．----------------2分∴BD =CE ，BE =DC =3，AE =AB +BE =8+3=11．----------------3分又∵DC ∥AB ，AD =BC ，∴DB =AC =CE ．∴△ACE 为等边三角形．∴AC =AE =11，∠CAB =60°．--------------------------------------------------4分过点C 作CH ⊥AE 于点H ．在Rt △ACH 中，CH =AC ·sin ∠CAB =11×2．∴梯形ABCD --------------------------------------------------5分20.（1）证明：联结OD ．∵D 为AC 中点,O 为AB 中点,∴OD 为△ABC 的中位线．∴OD ∥BC ．-----------1分∵DE ⊥BC ，∴∠DEC =90°.∴∠ODE =∠DEC =90°.∴OD ⊥DE 于点D .∴DE 为⊙O 的切线．------------2分（2）解：联结DB ．∵AB 为⊙O 的直径,∴∠ADB =90°．∴DB ⊥AC ．∴∠CDB =90°.∵D 为AC 中点,∴AB=AC ．在Rt △DEC 中，∵DE =2,tan C =21,∴EC =4tan =CDE .-------------------------3分由勾股定理得：DC =2.在Rt △DCB 中，BD=tan =⋅C DC ．由勾股定理得：BC =5.∴AB=BC =5.---------------------------4分∴⊙O 的直径为5.---------------------------5分21.解：(1)每天在校锻炼时间超过1小时的人数是人；-----------------1分(2)填图正确；-----------------3分(3)每天在校锻炼时间超过1小时的学生约为7．2万人.-----------5分22．解：（1）a 2+b 2；------------------1分（2）剪拼成的新正方形示意图如图2—图4中的正方形FGCH ．联想拓展：能剪拼成正方形.示意图如图5．正确画出一个图形给1分.图2B图3图5图4(G )欢迎访问h t t p ://bl o g .s in a .c o m .c n /b ei j i ng st ud y五、解答题（共3小题，满分22分）23．（1）证明：令y =0,则022=−+−m mx x ．∵△)2(4)(2−−−=m m 842+−=m m =4)2(2+−m ,---------------------------1分又∵0)2(2≥−m ，∴04)2(2>+−m ．即△>0．∴无论m 为任何实数，一元二次方程022=−+−m mx x 总有两不等实根．∴该二次函数图象与x 轴都有两个交点．-----------------------------2分（2）解：∵二次函数22−+−=m mx x y 的图象经过点（3，6）,∴62332=−+−m m .解得21=m .∴二次函数的解析式为23212−−=x x y .----------------------------3分（3）解：将x y =向下平移2个单位长度后得到解析式为：2−=x y .----------------------------4分解方程组⎪⎩⎪⎨⎧−−=−=．，232122x x y x y 得⎪⎪⎩⎪⎪⎨⎧−==．，232111y x ⎩⎨⎧−==．，1122y x ∴直线2−=x y 与抛物线23212−−=x x y 的交点为．，)1,1()23,21(−−B A ∴点A 关于对称轴41=x 的对称点是)23,0('−A ,点B 关于x 轴的对称点是)1,1('B .设过点'A 、'B 的直线解析式为b kx y +=．∴⎪⎩⎪⎨⎧=+−=．，123b k b 解得∴直线''B A 的解析式为2325−=x y .∴直线''B A 与x 轴的交点为)0,53(F .-----------------------------------------------5分与直线41=x 的交点为)87,41(−E .-----------------------------------------------6分则点)87,41(−E 、)0,53(F 为所求．过点'B 做''''H AA H B 的延长线于点⊥，∴25'=H B ，1'=HA .在Rt △H B A ''中，229''''22=+=H A H B B A .∴所求最短总路径的长为''B A FB EF AE =++292=-----------------------------------------------7分O5232k b ⎧=⎪⎪⎨⎪=−⎪⎩，欢迎访问h t t p :://b l og .s i n a .c om .c n /b e i j i n g s t u d y 24．解：（1）EF =AF BE −；-----------------------------------------------1分(2)∠α+∠BCA =180°；-----------------------------------------------3分(3)探究结论：EF=BE+AF .-----------------------------------------------4分证明：∵∠1+∠2+∠BCA =180°,∠2+∠3+∠CFA =180°.又∵∠BCA =∠α=∠CFA ，∴∠1=∠3.------------------5分∵∠BEC =∠CFA =∠α,CB =CA ,∴△BEC ≌△CFA .-----------------6分∴BE=CF ,EC=AF .∴EF=EC+CF=BE+AF .-------------------7分25．解：（1）∵抛物线219()24y x =−−∴顶点M 的坐标为⎟⎠⎞⎜⎝⎛−49,21．--------1分（2）抛物线与22y x x=−−与x 轴的两交点为A (-1,0)，B （2，0）．设线段BM 所在直线的解析式为b kx y +=．∴⎪⎩⎪⎨⎧−=+=+.4921,02b k b k 解得3,23.k b ⎧=⎪⎨⎪=−⎩∴线段BM 所在直线的解析式为323−=x y ．---------2分设点N 的坐标为),(t x −．∵点N 在线段BM 上，∴323−=−x t .∴223x t =−+．∴S 四边形NQAC ＝S △AOC ＋S 梯形OQNC 21121112(2)(2)322333t t t t =××++−+=−++．-----------3分∴S 与t 之间的函数关系式为331312++−=t t S ，自变量t 的取值范围为490<<t ．------4分（3）假设存在符合条件的点P ，设点P 的坐标为P （m ，n ），则21>m 且22−−=m m n ．222(1)PA m n =++，222)2(++=n m PC，52=AC ．分以下几种情况讨论：①若∠PAC ＝90°，则222AC PA PC +=．∴⎪⎩⎪⎨⎧+++=++−−=.5)1()2(,222222n m n m m m n 解得251=m ，12−=m ．∵21>m ．∴25=m ．∴⎟⎠⎞⎜⎝⎛47,251P ．-----------6分②若∠PCA ＝90°，则222AC PC PA +=．∴⎪⎩⎪⎨⎧+++=++−−=.5)2()1(,222222n m n m m m n 解得233=m ，04=m ．∵21>m ，∴23=m ．∴⎟⎠⎞⎜⎝⎛−45,232P ．当点P 在对称轴右侧时，PA ＞AC ，所以边AC 的对角∠APC 不可能是直角．∴存在符合条件的点P ，且坐标为⎟⎠⎞⎜⎝⎛47,251P ，⎟⎠⎞⎜⎝⎛−45,232P ．----------------8分123。

2010年北京市中考数学试卷-含答案详解

北京市2010年高级中等学校招生考试一、选择题（本大题共8小题，共32.0分。

在每小题列出的选项中，选出符合题目的一项）1.−2的倒数是( )A. −B.C. −2D. 22.2010年6月3日，人类首次模拟火星载人航天飞行试验“火星—500”正式启动，包括中国志愿者王跃在内的6名志愿者踏上了为期12480小时的“火星之旅”.将12480用科学记数法表示应为( )A. 12.48×103B. 0.1248×105C. 1.248×104D. 1.248×1033.如图，在△ABC中，点D，E分别在AB，AC边上，DE//BC，若AD∶AB=3∶4，AE=6，则AC等于( )A. 3B. 4C. 6D. 84.若菱形两条对角线的长分别为6和8，则这个菱形的周长为( )A. 20B. 16C. 12D. 105.从1，2，3，4，5，6，7，8，9，10这十个数中随机取出一个数，取出的数是3的倍数的概率是( )A. B. C. D.6.将二次函数y=x 2−2x+3化为y=(x−ℎ)2+k的形式，结果为( )A. y=(x+1)2+4B. y=(x−1)2+4C. y=(x+1)2+2D. y=(x−1)2+27.10名同学分成甲、乙两队进行篮球比赛，他们的身高(单位：cm)如下表所示：队员1队员2队员3队员4队员5甲队177176175172175乙队170175173174183设两队队员身高的平均数依次为甲，乙，身高的方差依次为，，则下列关系中完全正确的是( )A. 甲= 乙，>B. 甲= 乙，<C. 甲> 乙，>D. 甲< 乙，<8.美术课上，老师要求同学们将下图所示的白纸只沿虚线裁开，用裁开的纸片和白纸上的阴影部分围成一个立体模型，然后放在桌面上，下面四个示意图中，只有一个符合上述要求，那么这个示意图是( )A. B.C. D.二、填空题（本大题共5小题，共21.0分）9.若二次根式有意义，则x的取值范围是________．10.分解因式：m 3−4m=________．11.如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，连接OC，若OC=5，CD=8，则AE= ________．12.下图为手的示意图，在各个手指间标记字母A，B，C，D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→⋯的方式)从A开始数连续的正整数1，2，3，4，…，当数到12时，对应的字母是________；当字母C第201次出现时，恰好数到的数是________；当字母C第2n+1次出现时(n为正整数)，恰好数到的数是_________(用含n的代数式表示)．13.阅读下列材料：小贝遇到一个有趣的问题：在矩形ABCD中，AD=8cm，AB=6cm.现有一动点P按下列方式在矩形内运动：它从A点出发，沿着与AB边夹角为45°的方向作直线运动，每次碰到矩形的一边，就会改变运动方向，沿着与这条边夹角为45°的方向作直线运动，并且它一直按照这种方式不停地运动，即当P点碰到BC边，沿着与BC边夹角为45°的方向作直线运动，当P点碰到CD边，再沿着与CD边夹角为45°的方向作直线运动……如图1所示．问P点第一次与D点重合前与边相碰几次，P点第一次与D点重合时所经过的路径的总长是多少．小贝的思考是这样开始的：如图2，将矩形ABCD沿直线CD折叠，得到矩形A 1B 1CD.由轴对称的知识，发现P 2P 3=P 2E，P 1A=P 1E．请你参考小贝的思路解决下列问题：(1)P点第一次与D点重合前与边相碰________次；P点从A点出发到第一次与D点重合时所经过的路径的总长是________cm；(2)进一步探究：改变矩形ABCD中AD，AB的长，且满足AD>AB.动点P从A点出发，按照阅读材料中动点的运动方式，并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上．若P点第一次与B点重合前与边相碰7次，则AB∶AD的值为________．三、计算题（本大题共2小题，共10.0分）14.计算：．15.解分式方程四、解答题（本大题共10小题，共57.0分。

2010年北京市中考数学试卷(含答案)

2010年北京市高级中等学校招生考试数学试卷学校姓名准考证号考生须知 1．本试卷共6页，共五道大题，25道小题，满分120分。

考试时间120分钟。

2．在试卷和答题卡上准确填写学校名称、姓名和准考证号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题、作图题用2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5．考试结束，将本试卷、答题卡和草稿纸一并交回。

一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个‧‧是符合题意的．1．2-的倒数是 A ．12- B ．12C ．2-D ．22．2010年6月3日，人类首次模拟火星载人航天飞行试验“火星 — 500”正式启动，包括中国志愿者王跃在内的6名志愿者踏上了为期12 480小时的“火星之旅”. 将12 480用科学记数法表示应为 A ．312.4810⨯ B ．50.124810⨯ C ．41.24810⨯ D ．31.24810⨯ 3．如图，在△ABC 中，点D E 、分别在边上，DE ∥BC ，若:3:4AD AB =，6AE =，则AC 等于AB AC 、A. 3B. 4C. 6D. 8 4．若菱形两条对角线的长分别为6和8，则这个菱形的周长为A ．20B ．16C ．12D ．105．从 1，2，3，4，5，6，7，8，9，10这十个数中随机取出一个数，取出的数是3的倍数的概率是A ．15B ．310C ．13 D ．126．将二次函数223y x x =-+化为2()y x h k =-+的形式，结果为A ．2(1)4y x =++B ．2(1)4y x =-+C ．2(1)2y x =++D ．2(1)2y x =-+ 7．10名同学分成甲、乙两队进行篮球比赛，他们的身高（单位：cm ）如下表所示：队员1 队员2 队员3 队员4 队员5 甲队 177 176 175 172 175 乙队170175173174183设两队队员身高的平均数依次为x 甲，x乙，身高的方差依次为2S 甲，2S 乙，则下列关系中完全正确的是 A ．x x =甲乙，22S S>乙甲B ．x x =甲乙，22S S<乙甲 C．x x >甲乙，22S S >乙甲D ．x x <甲乙，22S S<乙甲8．美术课上，老师要求同学们将右图所示的白纸只沿虚线裁开，用裁开的纸片和白纸上的阴影部分围成一个立体模型，然后放在桌面上，下面四个示意图中，只有一个‧‧‧‧符合上述要求，那么这个示意图是A BC D 二、填空题（本题共16分，每小题4分）9．若二次根式21x -有意义，则x 的取值范围是． 10．分解因式：34m m -= .11．如图，AB 为⊙O 的直径，弦CD AB ⊥，垂足为点E ，连结OC ，若5OC =，8CD =，则AE = ．12．右图为手的示意图，在各个手指间标记字母 A ，B ，C ，D.请你按图中箭头所指方向（即 A →B →C →D →C→B →A →B →C → … 的方式）从 A 开始数连续的正整数 1，2，3，4，…，当数到 12 时，对应的字母是；当字母C 第201次出现时，恰好数到的数是；当字母C 第21n +次出现时（n 为正整数），恰好数到的数是（用含n 的代数式表示）.三、解答题（本题共30分，每小题5分） 13．计算：101201043tan 603-⎛⎫-+--︒ ⎪⎝⎭.14．解分式方程 312422x x x -=--．15．已知：如图，点A B C D 、、、在同一条直线上，EA AD ⊥，FD AD ⊥，AE DF =，AB DC =．求证：ACE DBF ∠=∠．16．已知关于 x 的一元二次方程 2410x x m -+-= 有两个相等的实数根，求m 的值及方程的根．17．列方程或方程组解应用题：2009年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米，其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米，问生产运营用水和居民家庭用水各多少亿立方米．18．如图，直线23y x =+与x 轴交于点A ，与y 轴交于点B ．（1）求A ，B 两点的坐标；（2）过B 点作直线BP 与x 轴交于点P ，且使2OP OA =，求△ABP 的面积．四、解答题（本题共20分，每小题5分）19．已知：如图，在梯形ABCD 中，AD ∥BC ，2AB DC AD ===，4BC =．求B ∠的度数及AC 的长．20．已知：如图，在△ABC 中，D 是AB 边上一点，⊙O 过D B C 、、三点，290DOC ACD ∠=∠=︒．（1）求证：直线AC 是⊙O 的切线；（2）如果75ACB ∠=︒，⊙O 的半径为2，求BD 的长．21．根据北京市统计局公布的2006—2009年空气质量的相关数据，绘制统计图如下： 2006—2009年北京全年市区空气质量达到二级和好于二级的天数统计图由统计图中的信息可知，北京全年市区空气质量达到二级和好于二级的天数与上一年相比，增加最多的是年，增加了天；（2）表1是根据《中国环境发展报告（2010）》公布的数据绘制的2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比的统计表，请将表1中的空缺部分补充完整（精确到1%）；表1 2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比统计表城市北京上海天津昆明杭州广州南京成都沈阳西宁百分比91% 84% 100% 89% 95% 86% 86% 90% 77%（3）根据表1中的数据将十个城市划分为三个组，百分比不低于95%的为A 组，不低于85%且低于95%的为B 组，低于85%的为C 组．按此标准，C 组城市数量在这十个城市中所占的百分比为 %；请你补全右边的扇形统计图．22．阅读下列材料：小贝遇到一个有趣的问题：在矩形ABCD 中，8AD =cm ，6AB =cm ．现有一动点P 按下列方式在矩形内运动：它从A 点出发，沿着与AB 边夹角为45︒的方向作直线运动，每次碰到矩形的一边，就会改变运动方向，沿着与这条边夹角为45︒的方向作直线运动，并且它一直按照这种方式不停地运动，即当P 点碰到BC 边，沿与BC 边夹角为45︒的方向作直线运动，当P 点碰到CD 边，再沿着与CD 边夹角为45︒的方向作直线运动，…，如图1所示．问P 点第一次与D 点重合前‧‧‧与边相碰几次，P 点第一次与D 点重‧合时‧‧所经过的路径的总长是多少．小贝的思考是这样开始的 : 如图2，将矩形ABCD 沿直线CD 折叠，得到矩形11A B CD ．由轴对称的知识，发现232P P P E =，11P A PE =. 请你参考小贝的思路解决下列问题：（1）P 点第一次与D 点重合前‧‧‧与边相碰次；P 点从A 点出发到第一次与D 点重合时‧‧‧所经过的路径的总长是 cm ；（2）进一步探究：改变矩形ABCD 中AD 、AB 的长，且满足AD AB >．动点P 从A 点出发，按照阅读材料中动点的运动方式，并满足前后连续两次与边相碰的位置在矩形ABCD 相邻的两边上. 若P 点第一次与B 点重合前‧‧‧与边相碰7次，则:A B A D 的值为 .2009年十个城市空气质量达到二级和好于二级的天数占全年天数百分比分组统计图图1图2五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．已知反比例函数ky x=的图象经过点(31)A -，．（1）试确定此反比例函数的解析式；（2）点O 是坐标原点，将线段OA 绕O 点顺时针旋转30°得到线段OB ，判断点B 是否在此反比例函数的图象上，并说明理由；（3）已知点(36)P m m +，也在此反比例函数的图象上（其中 0m <），过P 点作x 轴的垂线，交x 轴于点M ．若线段PM 上存在一点Q ，使得△OQM 的面积是12，设Q 点的纵坐标为n ，求2239n n -+的值．24．在平面直角坐标系xOy 中，抛物线22153244m my x x m m -=-++-+与x 轴的交点分别为原点O 和点A ，点(2,)B n 在这条抛物线上．（1）求B 点的坐标；（2）点P 在线段 OA 上，从O 点出发向A 点运动，过P 点作x 轴的垂线，与直线 OB 交于点E ，延长PE 到点D ，使得ED PE =，以PD 为斜边，在PD 右侧作等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）．① 当等腰直角三角形 PCD 的顶点 C 落在此抛物线上时，求OP 的长；② 若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位（当Q 点到达O 点时停止运动，P 点也同时停止运动）．过Q 点作x 轴的垂线，与直线AB 交于点F ，延长QF 到点M ，使得FM QF =，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN （当Q 点运动时，M 点、N 点也随之运动）．若P 点运动到 t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻t 的值．25．问题：已知△ABC 中，2B A C A C B ∠=∠，点D 是△ABC 内的一点，且AD CD =，BD BA =．探究DBC∠与ABC ∠度数的比值．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明.（1）当90BAC ∠=︒时，依问题中的条件补全右图．观察图形，AB 与AC 的数量关系为；当推出15DAC ∠=︒时，可进一步可推出DBC ∠的度数为；可得到DBC ∠与ABC ∠度数的比值为．（2）当90BAC ∠≠︒时，请你画出图形，研究DBC ∠与ABC ∠度数的比值是否与（1）中的结论相同，写出你的猜想并加以证明．2010年北京市高级中等学校招生考试数学试卷答案一、选择题 1.A ， 2.C ， 3.D ， 4.A ， 5.B ， 6.D ， 7.B ， 8.B ，二、填空题 9. x ≥21， 10. m (m +2)(m -2)， 11. 2， 12. B 、603、6n +3；三、解答题13. 解：原式=3-1+43-3=2+33。

2010年西城区一模数学试卷及答案

北京市西城区2010年抽样测试初三数学试卷 2010.5一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一．个．是符合题意的 1．4-的绝对值等于A ．4B ．14 C ．14- D ．4- 2．据统计，今年春节期间，北京市居民在京旅游人数约为2410000人次，同比增长17.6%．将2410000用科学记数法表示应为A ．70.24110⨯B ．62.4110⨯C ．524.110⨯D ．424110⨯ 3．如图，AB 是O 直径，弦CD AB ⊥于点E ．若8CD =，3OE =，则O 的直径为A ．5B ．6C ．8D ．104．若一个正多边形的一个内角是144°，则这个多边形的边数为A ．12B ．11C ．10D ．9 5|3|0y +=，则()2xy -的值为A ．6-B ．9C ．6D ．9- 6．对于一组数据：85，83，85，81，86．下列说法中正确的是 A ．这组数据的平均数是85 B ．这组数据的方差是3.2 C ．这组数据的中位数是84 D ．这组数据的众数是867．在平面直角坐标系中，对于平面内任一点()P a b ，若规定以下两种变换： ①()()f a b a b =--，，，如()()1212f =--，，． ②()()g a b b a =，，．如()()1331g =，，．按照以上变换，那么()()f g a b ，等于 A ．()b a --，B ．()a b ，C ．()b a ，D．()a b --，8．小明将一张正方形包装纸，剪成图1所示形状，用它包在一个棱长为10的正方体的表面（不考虑接缝），如图2所示．小明所用正方形包装纸的边长至少为A ．40B ．30+C ．D ．10+图2图1二、填空题（本题共16分，每小题4分）9．若分式241x x ++的值为零，则x 的值为．10．分解因式：2816ax ax a -+= ．11．如图，在ABC △中，D 、E 分别为AB 、AC 边上的点，DE BC ∥．若3AD =，5DB =， 1.2DE =，则BC = ． 12．在平面直角坐标系中，我们称边长为1且顶点的横纵坐标均为整数的正方形为单位格点正方形．如图，菱形ABCD 的四个顶点坐标分别是()80-，，()04，，()80，，()04-，，则菱形ABCD 能覆盖的单位格点正方形的个数是个；若菱形n n n n A B C D 的四个顶点坐标分别为()20n -，，()0n ，，()20n ，，()0n -，（n 为正整数），则菱形n n n n A B C D 能覆盖的单位格点正方形的个数为（用含有n 的式子表示）．三、解答题（本题共30分，每小题5分）13()101|199920103-⎛⎫--+- ⎪⎝⎭．14．解不等式组()245221.3x x x x ⎧++⎪⎨-<⎪⎩≤，把它的解集在数轴上表示出来，并求它的整数解． 32E D CB A15．已知：如图，A 、B 、C 、D 四点在一条直线上，且AB DC =，ECD FBA ∠=∠，A D ∠=∠．求证：AE DF =．GFEDCBA16．已知12x y =，求2222x x xy y ⋅-+222x y yx yx y -++-的值．17．列方程或方程组解应用题“家电下乡”农民得实惠，根据“家电下乡”的有关政策：农户每购买一件家电，国家将按每件家电售价的13%补贴给农户．小明的爷爷2009年5月份购买了一台彩电和一台洗衣机，他从乡政府领到了390元补贴款．若彩电的售价比洗衣机的售价高1000元，问一台彩电和一台洗衣机的售价各是多少元？18．已知：如图，在梯形ABCD 中，AD BC ∥，45B ∠=°，105BAC ∠=°，4AD CD ==．求BC 的长．DCB A四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）19．某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑．某校要从甲、乙两种品牌电脑中各选购一种型号的电脑．（1）写出所有可能的选购方案（利用树状图或列表法表示）；（2）如果（1）中各种选购方案被选中的可能性相同，那么B型号电脑被选中的概率是多少？20．如图，将直线4y x=沿y轴向下平移后，得到的直线与x轴交于点94A⎛⎫⎪⎝⎭，，与双曲线()0ky xx=>交于点B．（1）求直线AB的解析式；（2）若点B的纵坐标为m，求k的值（用含有m的式子表示）．21．如图，ABC△内接于O，AB AC=．点D在O上，AD AB⊥于点A，AD与BC 交于点E，点F在DA的延长线上，AF AE=．（1）求证：BF是O的切线；（2）若4AD=，4cos5ABF∠=，求BC的长．22．在ABC △中，BC a =，BC 边上的高2h a =，沿图中线段DE 、CF 将ABC △剪开，分成的三块图形恰能拼成正方形CFHG ，如图1所示．图1HG请你解决如下问题：在A B C '''△中，B C a ''=，B C ''边上的高12h a =．请你设计两种不同的分割方法，将A B C '''△沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图2、图3中，画出分割线及拼接后的图形．图2C′B′A′图2C′B′A′五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．已知：关于x 的方程()231230mx m x m --+-=．（1）求证：m 取任何实数量，方程总有实数根；（2）若二次函数()213123y mx m x m =--+-的图象关于y 轴对称． ① 求二次函数1y 的解析式；② 已知一次函数222y x =-，证明：在实数范围内，对于x 的同一个值，这两个函数所对应的函数值12y y ≥均成立；（3）在（2）条件下，若二次函数23y ax bx c =++的图角经过点()50-，，且在实数范围内，对于x 的同一个值，这三个函数所对应的函数值132y y y ≥≥均成立，求二次函数23y ax bx c =++的解析式．24．如图1，在ABCD 中，AE BC ⊥于点E ，E 恰为BC 的中点，tan 2B =．（1）求证：AD AE =；（2）如图2，点P 在线段BE 上，作EF DP ⊥于点F ，连结AF ．求证：DF EF -；（3）请你在图3中画图探究：当P 为线段EC 上任意一点（P 不与点E 重合）时，作EF 垂直直线DP ，垂足为点F ，连结AF ．线段DF 、EF 与AF 之间有怎样的数量关系？直接写出你的结论．图1EDCBA图2PF ABCDE图3ABCDE25．如图，在平面直角坐标系xOy中，一次函数y =+的图象与x 轴交于点A ，与y 轴交于点B ，点C 的坐标为()30，，连结BC ．（1）求证：ABC △是等边三角形；（2）点P 在线段BC 的延长线上，连结AP ，作AP 的垂直平分线，垂足为点D ，并与y 轴交于点E ，分别连结EA 、EC 、EP ．① 若6CP =，直接写出AEP ∠的度数；来源：港中数学网 ② 若点P 在线段BC 的延长线上运动（P 不与点C 重合），AEP ∠的度数是否变化？若变化，请说明理由；若不变，求出AEP ∠的度数；（3）在（2）的条件下，若P 从C 点出发在BC 的延长线上匀速运动，速度为每秒1个单位长度．EC 与AP 交于点F ，设AEF △的面积为1S ，CFP △的面积为2S ，12y S S =-，运动时间为()0t t >秒时，求y 关于t 的函数关系式．初三数学试卷答案及评分参考 2010.5阅卷须知：1.解答右端所注分数，表示考生正确做到这一步应得的累加分数。

北京2010西城区一模数学试卷及答案

北京市西城区2010年抽样测试一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1. -4的绝对值等于A . 4B . 41C . -41 D . -4 2. 据统计，今年春节期间，北京本市居民在京旅游人数为2 410 000人次，同比增长17.6%.将2 410 000用科学记数法表示应为. 710241.0⨯ B . 61041.2⨯ C . 5101.24⨯ D . 410241⨯3．如图，AB 是⊙O 直径，弦CD ⊥AB 于点E .若CD ＝8，OE =3，则⊙O 的直径为A . 5B . 6C .8D . 10 4．若一个正多边形的一个内角是144°，则这个多边形的边数为 A . 12 B . 11 C .10 D . 9 5．0312=++-y x ，则2()xy -的值为A .－6B . 9C .6D . －96．对于数据：85，83，85，81，86．下列说法中正确的是（）A ．这组数据的中位数是84B ．这组数据的方差是3.2C ．这组数据的平均数是85D ．这组数据的众数是867．在平面直角坐标系中，对于平面内任一点P ()b a ,若规定以下两种变换：①),(),(b a b a f --=．如)2,1()2,1(--=f②),(),(a b b a g =．如)1,3()3,1(=g按照以上变换，那么()),(b a g f 等于A ．()a b --,B ．()b a ,C ．()a b ,D ． ()b a --,8．小明将一张正方形包装纸，剪成图1所示形状，用它包在一个棱长为10的正方体的表面（不考虑接缝），如图2所示．小明所用正方形包装纸的边长至少为A . 40 B.2230+ C . 220 D . 21010+二、填空题（本题共16分，每小题4分）9．若分式142++x x 的值为零，则x 的值为． 10．分解因式：=+-a ax ax 1682 ．11．如图，在△ABC 中，D 、E 分别AB 、AC 边上的点，DE ∥BC ．若AD ＝3，DB ＝5，DE ＝1.2，则BC ＝．12．在平面直角坐标系中，我们称边长为1、且顶点的横、纵坐标均为整数的正方形为单位格点正方形．如图，在菱形ABCD中，四个顶点坐标分别是（－8,0），（0,4），（8,0），（0，－4），则菱形ABCD 能覆盖的单位格点正方形的个数是个；若菱形A n B n C n D n 的四个顶点坐标分别为（－2n ,0），（0,n ），（2n ，0），（0，－n ）（n 为正整数），则菱形A n B n C n D n能覆盖的单位格点正方形的个数为（用含有n 的式子表示）.三、解答题（本题共30分，每小题5分）13．计算：01)20101999()31(2318-+----.14．解不等式组⎪⎩⎪⎨⎧<-+≤+.321),2(542x x x x 把它的解集在数轴上表示出来，并求它的整数解.15．已知：如图，A 、B 、C 、D 四点在一条直线上，且AB =CD ，∠A=∠D ，∠ECD=∠FBA .求证： AE =DF .16．已知21=y x ，求y x y y x y x y xy x x -++-⋅+-2222222的值.CAE D B C BE AF DG17．列方程或方程组解应用题：“家电下乡”农民得实惠，根据“家电下乡”的有关政策：农户每购买一件家电，国家将按每件家电售价的13%补贴给农户．小明的爷爷2009年5月份购买了一台彩电和一台洗衣机，他从乡政府领到了390元补贴款．若彩电的售价比洗衣机的售价高1000元，问一台彩电和一台洗衣机的售价各是多少元？18．已知：如图，在梯形ABCD 中，AD ∥BC ，∠B=45°，∠BAC=105°，AD =CD =4．求BC 的长．四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）19．某电脑公司现有A ，B ，C 三种型号的电脑和D ，E 两种型号的打印机．某校要从其中选购一台电脑和一台打印机送给山区小学．(1) 写出所有选购方案(利用树状图或列表方法表示）；(2) 已知A 、D 是甲厂生产的产品，B 、C 、E 是乙厂生产的产品．如果（1）中各种选购方案被选中的可能性相同，那么甲厂生产的产品被选中的概率是多少？20．如图，将直线x y 4=沿y 轴向下平移后，得到的直线与x 轴交于点A （0,49），与双曲线k y x =（0x >）交于点B ．（1）求直线AB 的解析式；（2）若点B 的纵坐标为m ，求k 的值（用含m 的代数式表示）．D A B C21．如图，△ABC 内接于⊙O ，且AB ＝AC ，点D 在⊙O 上，AD ⊥AB 于点A ，AD 与BC 交于点E ，F 在DA 的延长线上，且AF ＝AE ．（1）求证：BF 是⊙O 的切线；(2）若AD ＝4，54cos =∠ABF ，求BC 的长．22．在△ABC 中， BC ＝a ，BC 边上的高h ＝a 2，沿图中线段DE 、CF 将△ABC 剪开，分成的三块图形恰能拼成正方形CFHG ，如图1所示．请你解决如下问题：已知：如图2，在△A ′B ′C ′中， B ′C ′＝a ，B ′C ′边上的高h ＝a 21．请你设计两种不同的分割方法，将△A ′B ′C ′沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图2、图3中，画出分割线及拼接后的图形．五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．已知关于x 的方程032)1(32=-+--m x m mx ．（1）求证：无论m 取任何实数时，方程总有实数根；（2）若关于x 的二次函数32)1(321-+--=m x m mx y 的图象关于y 轴对称．①求这个二次函数的解析式；②已知一次函数222-=x y ，证明：在实数范围内，对于x 的同一个值，这两个函数所对应的函数值y 1≥y 2均成立；（3）在（2）的条件下，若二次函数y 3＝ax 2＋bx ＋c 的图象经过点（－5，0），且在实数范围内，对于x 的同一个值，这三个函数所对应的函数值y 1≥y 3≥y 2均成立．求二次函数y 3＝ax 2＋bx ＋c 的解析式.A ′B ′C ′ 图3 A ′B′ C ′ 图424．如图1，在□ABCD 中，AE ⊥BC 于E ，E 恰为BC 的中点，2tan =B .（1）求证：AD =AE ；（2）如图2，点P 在BE 上，作EF ⊥DP 于点F ，连结AF . 求证：AF EF DF 2=-；（3）请你在图3中画图探究：当P 为射线E C 上任意一点（P 不与点E 重合）时，作EF ⊥DP 于点F ，连结AF ，线段DF 、EF 与AF 之间有怎样的数量关系？直接写出你的结论.25．如图，在平面直角坐标系xOy 中，一次函数333+=x y 的图象与x 轴交于点A ，与y 轴交于点B ，点C 的坐标为（3,0），连结BC ．（1）求证：△ABC 是等边三角形；（2）点P 在线段BC 的延长线上，连结AP ，作AP 的垂直平分线，垂足为点D ，并与y 轴交于点E ，分别连结EA 、EP ．①若CP ＝6，直接写出∠AEP 的度数；②若点P 在线段BC 的延长线上运动（P 不与点C 重合），∠AEP 的度数是否变化？若变化，请说明理由；若不变，求出∠ADP 的度数；（3）在（2）的条件下，若点P 从C 点出发在BC 的延长线上匀速运动，速度为每秒1个单位长度． EC 与AP 于点F ，设△AEF 的面积为S 1，△CFP 的面积为S 2，y ＝S 1－S 2，运动时间为t （t >0）秒时，求y 关于t 的函数关系式．图1 E B C A D 图3 E B CA D 图2 E CB A D F P初三数学试卷答案及评分参考 2010.5阅卷须知：1.解答右端所注分数，表示考生正确做到这一步应得的累加分数。

2010年中考数学试题分类(精选版)：多边形与平行四边形

2010年中考数学试题分类汇编多边形与平行四边形一、选择题1. (2010年四川眉山市)．如图，每个小正方形的边长为1，A 、B 、C 是小正方形的顶点，则∠ABC 的度数为（）A ．90°B ．60°C ．45°D ．30°【答案】C2.（2010福建龙岩）下列图形中，单独选用一种图形不能进行平面镶嵌的图形是（）A. 正三角形B. 正方形C. 正五边形D. 正六边形【答案】C3．（2010年北京顺义）若一个正多边形的一个内角是120°，则这个正多边形的边数是A ．9B ．8C ．6D ．4 【答案】C4. （2010年台湾省）图(十)为一个平行四边形ABCD ，其中H 、G 两点分别在BC 、 CD 上，AH ⊥BC ，AG ⊥CD ，且AH 、AC 、AG 将∠BAD 分成 ∠1、∠2、∠3、∠4四个角。

若AH =5，AG =6，则下列关系何者正确？ (A) ∠1=∠2 (B) ∠3=∠4 (C) BH =GD (D) HC =CG 【关键词】平行四边形【答案】A二、填空题1.（2010年福建福州）14.如图，在□ABCD 中，对角线AC 、BD 相交于点O ，若AC=14，BD=8，AB=10，则△OAB 的周长为 . 【答案】212.（2010年福建宁德）如图，在□ABCD 中，AE ＝EB ，AF ＝2，则FC 等于_____．【答案43.(2010年山东滨州)如图,平行四边形ABCD 中, ∠ABC=60°,E 、F 分别在CD、BC 的延长线上,AE ∥BD,EF ⊥BC,DF=2,则EF 的长为ABC EFAB CD G H 12 3 4 图(十)FEDC BA【答案】4.（2010年福建宁德）如图，在△ABC 中，点E 、F 分别为AB 、AC 的中点．若EF 的长为2，则BC 的长为___________. 【答案】4三、解答题1. (2010年福建晋江)如图，请在下列四个关系中，选出两个恰．．．当．的关系作为条件，推出四边形ABCD 是平行四边形，并予以证明．（写出一种即可）关系：①AD ∥BC ，②CD AB =，③C A ∠=∠，④︒=∠+∠180C B ．已知：在四边形ABCD 中，，；求证：四边形ABCD 是平行四边形．解：已知：①③，①④，②④，③④均可,其余均不可以. （解法一）已知：在四边形ABCD 中，①AD ∥BC ，③C A ∠=∠.……………………（2分）求证：四边形ABCD 是平行四边形．证明：∵ AD ∥BC∴︒=∠+∠180B A ，︒=∠+∠180D C ………………………………………（5分） ∵C A ∠=∠，∴D B ∠=∠∴四边形ABCD 是平行四边形…………………………………………………（8分）（解法二）已知：在四边形ABCD 中，①AD ∥BC ，④︒=∠+∠180C B .………………（2分）AB CD第4题图 F A E BC D求证：四边形ABCD 是平行四边形．证明：∵︒=∠+∠180C B ，∴AB ∥CD ……………………………………………………………………（5分）又∵AD ∥BC∴四边形ABCD 是平行四边形．…………………………………………………（8分）（解法三）已知：在四边形ABCD 中，②CD AB =，④︒=∠+∠180C B .………………（2分）求证：四边形ABCD 是平行四边形．证明：∵︒=∠+∠180C B ，∴AB ∥CD ……………………………………………………………………（5分）又∵CD AB =∴四边形ABCD 是平行四边形．…………………………………………………（8分）（解法四）已知：在四边形ABCD 中，③C A ∠=∠，④︒=∠+∠180C B .………………（2分）求证：四边形ABCD 是平行四边形．证明：∵︒=∠+∠180C B ，∴AB ∥CD ……………………………………………………………………（4分） ∴︒=∠+∠180D A ………………………………………………………………（6分）又∵C A ∠=∠ ∴D B ∠=∠∴四边形ABCD 是平行四边形．…………………………………………………（8分）2. (2010年浙江衢州)已知：如图，E ，F 分别是ABCD 的边AD ，BC 的中点．求证：AF =CE ．证明：方法1：∵ 四边形ABCD 是平行四边形，且E ，F 分别是AD ，BC 的中点，∴ AE = CF ． ……2分又 ∵ 四边形ABCD 是平行四边形，∴ AD ∥BC ，即AE ∥CF ．∴ 四边形AFCE 是平行四边形． ……3分 ∴ AF =CE ．……1分方法2：∵ 四边形ABCD 是平行四边形，且E ，F 分别是AD ，BC 的中点， ∴ BF =DE ． ……2分又 ∵ 四边形ABCD 是平行四边形， ∴ ∠B =∠D ，AB =CD ．A D E FB C ADEFBC(第19题)∴ △ABF ≌△CDE ．……3分 ∴ AF =CE ． ……1分3．（2010浙江省嘉兴）如图，在□ABCD 中，已知点E 在AB 上，点F 在CD 上且AE ＝CF ．（1）求证：DE ＝BF ；（2）连结BD ，并写出图中所有的全等三角形．（不要求证明）【关键词】平行四边形的判定与性质、全等三角形【答案】（1）在□ABCD 中，AB //CD ，AB =CD ．∵AE =CF ，∴BE =DF ，且BE //DF ． ∴四边形BFDE 是平行四边形． ∴BF DE ． …5分（2）连结BD ，如图，图中有三对全等三角形： △ADE ≌△CBF ， △BDE ≌△DBF ，△ABD ≌△CDB ． …3分4. (2010年山东滨州)如图，四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点.(1)请判断四边形EFGH 的形状？并说明为什么.(2)若使四边形EFGH 为正方形，那么四边形ABCD 的对角线应具有怎样的性质？解：(1) 四边形EFGH 为平行四边形，连接AC ∵E 、F 分别是AB 、BC 的中点，EF ∥AC ，EF=21AC. 同理HG ∥AC ，HG=21AC. ∴EF ∥HG, EF=HG.∴四边形EFGH 是平行四边形(2) 四边形ABCD 的对角线垂直且相等.5.（2010年江苏泰州）如图，四边形ABCD 是矩形，∠EDC =∠CAB ，∠DEC =90°．(1)求证：AC ∥DE ；(2)过点B 作BF ⊥AC 于点F ，连结EF ，试判断四边形BCEF 的形状，并说明理由．BE（第3题）AB CD【答案】⑴在矩形ABCD 中，AC ∥DE ，∴∠DCA =∠CAB ，∵∠EDC =∠CAB ， ∴∠DCA =∠EDC ，∴AC ∥DE ； ⑵四边形BCEF 是平行四边形．理由：由∠DEC =90°，BF ⊥AC ，可得∠AFB =∠DEC =90°，又∠EDC =∠CAB ，AB=CD ，∴△DEC ≌△AFB ，∴DE =AF ，由⑴得AC ∥DE ， ∴四边形AFED 是平行四边形，∴AD ∥EF 且AD =EF ， ∵在矩形ABCD 中，AD ∥BC 且AD =BC ， ∴EF ∥BC 且EF =BC ，∴四边形BCEF 是平行四边形．【关键词】矩形的性质平行四边形的判定全等三角形的判定6.（2010年福建晋江）如图，请在下列四个关系中，选出两个恰当．．．．的关系作为条件，推出四边形ABCD 是平行四边形，并予以证明．（写出一种即可）关系：①AD ∥BC ，②CD AB =，③C A ∠=∠，④︒=∠+∠180C B ．已知：在四边形ABCD 中，，；求证：四边形ABCD 是．【关键词】平行四边形的判定【答案】已知：①③，①④，②④，③④均可,其余均不可以. （解法一）已知：在四边形ABCD 中，①AD ∥BC ，③C A ∠=∠.……………………（2分）求证：四边形ABCD 是平行四边形．证明：∵ AD ∥BC∴︒=∠+∠180B A ，︒=∠+∠180D C ∵C A ∠=∠，∴D B ∠=∠ ∴四边形ABCD 是平行四边形（解法二）已知：在四边形ABCD 中，①AD ∥BC ，④︒=∠+∠180C B . 求证：四边形ABCD 是平行四边形．证明：∵︒=∠+∠180C B ， ∴AB ∥CD 又∵AD ∥BC∴四边形ABCD 是平行四边形．（解法三）已知：在四边形ABCD 中，②CD AB =，④︒=∠+∠180C B . 求证：四边形ABCD 是平行四边形．证明：∵︒=∠+∠180C B ， ∴AB ∥CD 又 ∵CD AB =∴四边形ABCD 是平行四边形．（解法四）已知：在四边形ABCD 中，③C A ∠=∠，④︒=∠+∠180C B . 求证：四边形ABCD 是平行四边形．证明：∵︒=∠+∠180C B ， ∴AB ∥CD∴︒=∠+∠180D A 又∵C A ∠=∠ ∴D B ∠=∠∴四边形ABCD 是平行四边形． 7.（2010年贵州毕节地区）如图，已知： ABCD 中，BCD ∠的平分线CE 交边AD 于E ，ABC ∠的平分线BG 交CE 于F ，交AD 于G ．求证：AE DG =．【关键词】平行四边形、角平分线【答案】证明：∵ 四边形ABCD 是平行四边形（已知），AD BC ∴∥，AB CD =（平行四边形的对边平行，对边相等）GBC BGA ∴∠=∠，BCE CED ∠=∠（两直线平行，内错角相等）又∵ BG 平分ABC ∠，CE 平分BCD ∠（已知）ABG GBC ∴∠=∠，BCE ECD ∠=∠（角平分线定义） ABG GBA ∴∠=∠，ECD CED ∠=∠．AB AG ∴=，CE DE =（在同一个三角形中，等角对等边） AG DE ∴=AG EG DE EG ∴-=-，即AE DG =．分7.（2010年重庆市潼南县）如图,四边形ABCD 是边长为2的正方形，点G 是BC 延长线上一点，连结AG ，点E 、F 分别在AG 上，连接BE 、DF ，∠1=∠2 ， ∠3=∠4. ABC E FG【关键词】全等三角形【答案】解：（1）∵四边形ABCD 是正方形∴AB=AD在△ABE 和△DAF 中⎪⎩⎪⎨⎧∠=∠=∠=∠3412DA AB∴△ABE ≌△DAF -----------------------4分（2）∵四边形ABCD 是正方形∴∠1+∠4=900∵∠3=∠4∴∠1+∠3=900∴∠AFD=900----------------------------6分在正方形ABCD 中， AD ∥BC∴∠1=∠AGB=300在Rt △ADF 中，∠AFD=900AD=2∴AF=3 DF =1----------------------------------------8分由(1)得△ABE ≌△ADF ∴AE=DF=1∴EF=AF-AE=13- -----------------------------------------10分8.（2010年江苏宿迁）如图，在□ABCD 中，点E 、F 是对角线AC 上两点，且AE =CF ．求证：∠EBF =∠FDE ．【关键词】平行四边形【答案】证明：连接BD 交AC 于O 点 …… 1分∵四边形ABCD 是平行四边形∴OA=OC ，OB=OD ………………3分又∵AE=CF ∴OE=OF∴四边形BEDF 是平行四边形 …… 6分 ∴∠EBF=∠EDF …………… 8分9.（2010年浙江宁波）如图1，有一张菱形纸片ABCD ，8=AC ，6=BD .（1）请沿着AC 剪一刀，把它分成两部分，把剪开的两部分拼成一个平行四边形，在图2中用实数画出你所拼成的平行四边形;若沿着BD 剪开，请在图3中用实线画出拼成的平行四边形;并直接写出这两个平行四边形的周长。

(10)2018-2020年北京中考数学复习各地区模拟试题分类(10)——四边形参考答案

∵四边形 ABCD 是平行四边形，
∴AB∥CD，AD＝BC＝10，
∴∠BAF＝∠DFA，
∵DC＝16，
∴DF＝DC﹣CF＝16﹣6＝10，
∴AD＝DF，
∴∠DAF＝∠DFA，
∴∠BAF＝∠DAF，
∴AF 平分∠DAB．
13．【解答】（1）证明：∵四边形 ABCD 是平行四边形，
∴AD＝BC，AD∥BC，
∴MA＝ME＜BM， ∴点 M 不在 AB 的垂直平分线上， ∴点 M 不在∠AOB 的角平分线上，故②错误， ③如图 3 中，作 PM∥OA 交 AB 于 M．
∵PM∥OA， ∴∠BMP＝∠BAO＝60°，∠BPM＝∠AOB＝60°， ∴△PMB 是等边三角形， ∴PB＝PM＝AQ， ∵PE⊥BM， ∴EM＝BM， ∵∠AQD＝∠MPD，∠ADQ＝∠MQP，AQ＝PM， ∴△ADQ≌△MDP（AAS）， ∴AD＝DM， ∴DE＝DM+ME= 12AM+ 12BM= 12（AM+BM）= 12AB，故③正确，故答案为①③． 6．【解答】解：①如图 1，
故存在两个中点四边形 MNPQ 是正方形．故答案为：①②③④．
8．【解答】解：①如图，连接 AC，BD 交于 O， ∵四边形 ABCD 是菱形，连接 AC，BD 交于 O，过点 O 直线 MP 和 QN，分别交 AB，BC，CD，AD 于 M，N，P，Q，则四边形 MNPQ 是平行四边形，故存在无数个四边形 MNPQ 是平行四边形；故正确； ②如图，当 PM＝QN 时，四边形 MNPQ 是矩形，故存在无数个四边形 MNPQ 是矩形；故正确； ③如图，当 PM⊥QN 时，存在无数个四边形 MNPQ 是菱形；故正确； ④当四边形 MNPQ 是正方形时，MQ＝PQ，则△AMQ≌△DQP（AAS）， ∴AM＝QD，AQ＝PD， ∵PD＝BM， ∴AB＝AD， ∴四边形 ABCD 是正方形，当四边形 ABCD 为正方形时，四边形 MNPQ 是正方形，故存在无数个四边形 MNPQ 是正方形；故④错误；故答案为①②③．

2010年北京各区一模数学试题复数、算法、集合、简易逻辑、推理与证明、平面几何

2010年北京各区一模数学试题复数、算法、集合、简易逻辑、推理与证明、平面几何D1.2. （丰台·理·题9）在平行四边形ABCD 中，点E 是边AB 的中点，DE 与AC交于点F ，若AEF ∆的面积是12cm ，则CDF ∆的面积是 2cm ．【解析】 4；HG FED CBA取CD 的中点G ，连结BG 交AC 于H ，则∵BE DG ∥且1122BE AB CD DG ===， ∴四边形BEDG 为平行四边形 ∴AF FH HC == ∴44DFCAEFS S ==△△3. （海淀·理·题10）如图，AB 为O 的直径，且8AB =，P 为OA 的中点，过P 作O 的弦CD ，且:3:4CP PD =，则弦CD 的长度为．【解析】7；由8AB =得2,6AP PB ==．由已知和相交弦定理得 :3:4CP PD AP PB CP PD ⋅=⋅⎧⎨=⎩，解得34CP PD =⎧⎨=⎩．于是347CD CP PD =+=+=．4. （石景山·理·题10）已知曲线C 的参数方程为cos ,2sin ,x y θθ=⎧⎨=-+⎩()θ为参数，则曲线C 的普通方程是；点A 在曲线C 上，点(,)M x y 在平面区域22020210x y x y y -+⎧⎪+-⎨⎪-⎩≥≤≥上，则AM 的最小值是．【解析】22(2)1x y ++=，32； C是圆22(2)1x y ++=；不等式组的可行域如图阴影所示，A 点为(0,1)-、M 为10,2⎛⎫ ⎪⎝⎭时，||AM 最短，长度是32． C A 2-2y xO5. （西城·理·题12）如图，PC 切O 于点C ，割线PAB 经过圆心O ，弦CD AB ⊥于点E ．已知O 的半径为3，2PA =，则PC = ．OE = ．AD E OCB【解析】94,5；22(26)164PC PA PB PC=⋅=⨯+=⇒=；连结OC，知OC PC⊥，于是5PO=，2239235CO OE OP PE=⋅⇒==+．BCO EPDA6.（宣武·理·题11）若,,A B C是O⊙上三点，PC切O⊙于点C，110,40ABC BCP∠=︒∠=︒，则AOB∠的大小为．【解析】60︒；如图，弦切角40PCB CAB∠=∠=︒，于是18030ACB CAB ABC∠=︒-∠-∠=︒，从而260AOB ACB∠=∠=︒．PO CBA7.（朝阳·理·题12）如图，圆O是ABC∆的外接圆，过点C的切线交AB的延长线于点D，3CD AB BC===，则BD的长为；AC的长为．ODCB【解析】 374,．()24CD DB DA DB AB BD BD =⋅=⋅+⇒=．又由DCB CAB ∠=∠知BCD ACD ∆≅∆．于是BC BD CDAC CD AD==．即33727BD AC AC CD ==⇒=．8. （西城·理·题12）如图，PC 切O 于点C ，割线PAB 经过圆心O ，弦CD AB ⊥于点E ．已知O 的半径为3，2PA =，则PC = ．OE = ．AD E OCB【解析】 94,5；22(26)164PC PA PB PC =⋅=⨯+=⇒=；连结OC ，知OC PC ⊥，于是5PO =，2239235COOE OP PE =⋅⇒==+． BCOE PDA坐标系与参数方程1. （海淀·理·题4）在平面直角坐标系xOy 中，点P的直角坐标为(1,．若以原点O 为极点，x 轴正半轴为极轴建立极坐标系，则点P 的极坐标可以是（）A ．π1,3⎛⎫- ⎪⎝⎭B ．4π2,3⎛⎫ ⎪⎝⎭C ．π2,3⎛⎫- ⎪⎝⎭ D ．4π2,3⎛⎫- ⎪⎝⎭ 【解析】C ；易知2ρ=，()π2π3k k θ=-∈Z ．2. （朝阳·理·题9）已知圆的极坐标方程为2cos ρθ=，则圆心的直角坐标是；半径长为．【解析】 ()1,0,1；由22cos ρρθ=，有222x y x +=，即圆的直角坐标方程为()2211x y -+=．于是圆心坐标为()1,0，半径为1．3. （崇文·理·题11）将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩（θ为参数）化成普通方程为．【解析】 ()2214x y -+=；由12cos ,2sin x y θθ-==知()2214x y -+=．4. （石景山·理·题11）如图，已知PE 是圆O 的切线．直线PB 交圆O 于A 、B 两点，4PA =，12AB =，43AE =．则PE 的长为_____，ABE ∠的大小为________．POEBA【解析】 8，30︒；24(412)64PE PA PB =⋅=⨯+=，则8PE =；由222PE PA AE =+，可知90PAE ∠=︒，即90BAE ∠=︒，由3tan AE ABE AB ∠==，得30ABE ∠=︒．5. （西城·理·题11）将极坐标方程2cos ρθ=化成直角坐标方程为．【解析】2220x y x +-=； 2222cos 2x y x ρρθ=⇒+=．6. （东城·理·题12）圆的极坐标方程为sin 2cos ρθθ=+，将其化成直角坐标方程为，圆心的直角坐标为．【解析】 2215(1)()24x y -+-=，11,2⎛⎫⎪⎝⎭； 222sin 2cos 2x y y xρρθρθ=+⇒+=+．7. （东城·理·题12）圆的极坐标方程为sin 2cos ρθθ=+，将其化成直角坐标方程为，圆心的直角坐标为．【解析】 2215(1)()24x y -+-=，11,2⎛⎫⎪⎝⎭； 222sin 2cos 2x y y xρρθρθ=+⇒+=+．8. （宣武·理·题12）若直线:0l x =与曲线:x a C y φφ⎧=⎪⎨=⎪⎩（φ为参数，0a >）有两个公共点,A B ，且||2AB =，则实数a 的值为；在此条件下，以直角坐标系的原点为极点，x 轴正方向为极轴建立坐标系，则曲线C 的极坐标方程为．【解析】22,4cos 20ρρθ-+=；曲线C ：22()2x a y -+=，点C 到l2a =，因此||22AB a==⇒=；222(2cos )(2sin )ρθθ-+=，即24cos 20ρρθ-+=．9. （丰台·理·题12）在平面直角坐标系xOy 中，直线l 的参数方程为11x y t =⎧⎨=+⎩（参数t ∈R ），圆C 的参数方程为cos 1sin x y θθ=+⎧⎨=⎩（参数[)0,2πθ∈），则圆心到直线l 的距离是．直线方程为1y x =+，圆的方程为()2211x y -+=．于是圆心()1,0到直线10x y -+=复数1. （海淀·理·题1）在复平面内，复数1ii z =-（i 是虚数单位）对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解析】 C ；()()1i 1i i 1i iz -==--=--，该复数对应的点位于第三象限．2. （丰台·理·题1）如果1i1i a z a -=+为纯虚数，则实数a 等于（） A ．0 B ．1- C ．1 D ．1-或1 【解析】 D ；设i z x =，0x ≠则1ii 1i a x a -=+()1i 0ax a x ⇔+-+=100ax a x +=⎧⇔⎨+=⎩11a x =⎧⇔⎨=-⎩或11a x =-⎧⎨=⎩．3. （石景山·理·题1）复数21i+等于（） A ．2i - B ．2i C ．1i -D ．1i + 【解析】 C ；22(1i)2(1i)1i 1i (1i)(1i)2--===-++-．4. （东城·理·题1）i 是虚数单位，若12ii(,)1i a b a b +=+∈+R ，则a b +的值是（）A ．12-B ．2- C ．2D ．12【解析】C ；12i (12i)(1i)3i1i (1i)(1i)2++-+==++-，于是31222a b +=+=． 5. （朝阳·理·题1）复数112ii ++等于（） A ．12i + B ．12i - C ．12- D ．12 【解析】D ；计算容易有1i 11i 22+=+．6. （海淀·文·题1）在复平面内，复数()i 1i -（i 是虚数单位）对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解析】 A ；()i 1i 1i -=+，对应的点为()1,1位于第一象限．7. （丰台·文·题1）复数1i1i z -=+化简的结果等于（） A ．i - B ．i C ．2i - D ．2i 【解析】 A ；1i1i z -=+()()()21i 2i i 1i 1i 2--===-+-．8. （石景山·文·题1）复数21i+等于（） A ．2i - B ．2i C ．1i -D ．1i + 【解析】 C ；22(1i)2(1i)1i 1i (1i)(1i)2--===-++-．9. （东城·文·题1）计算复数1i1i-+的结果为（） A ．i - B ．i C ．1- D ．1 【解析】 A ；21i (1i)i 1i 2--==-+．10. （朝阳·文·题1）复数22(1)i i+等于（） A ．2 B ．-2 C ．2i - D ．2i 【解析】 C ；()221221i ii i +==--． 11. （宣武·理·题3）若复数z 满足2i 1iz=+，则z 对应的点位于（） A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限【解析】 B ；2i(1i)22i z =+=-+． 12. （宣武·文·题4）设i 是虚数单位，则复数(1i)2i z =+⋅所对应的点落在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解析】 B ；22i z =-+． 13. （西城·文·题9）i 是虚数单位，1i 1i +=+ ．【解析】 11i22+；11i 1i i i 1i 22-++=+=+．14. （西城·理·题9）若(2i)i i a b -=+，其中,a b ∈R ，i 为虚数单位，则a b += ．【解析】 3；2i i a b +=+1,2a b ⇒==． 15. （崇文·理·题9）如果复数()()2i 1i m m ++（其中i 是虚数单位）是实数，则实数m =___________．【解析】 1-；()()()()223i 1i 1m m m m i m ++=-++．于是有3101m m +=⇒=-． 16. （崇文·文·题10）如果复数()()2i 1i m m ++（其中i 是虚数单位）是实数，则实数m =___________．【解析】 -1；()()()()223i 1i 1m m m m m i ++=-++．于是有3101m m +=⇒=-．算法1. （丰台·文·题3）在右面的程序框图中，若5x =，则输出i 的值是（）x> 109i = i + 1NY 输出i结束x = 3x -2i = 0输入x开始A ．2B ．3C ．4D ．5 【解析】 C ；51337109325→→→→，对应的4i =．2. （石景山·理·题4）一个几何体的三视图如图所示，那么此几何体的侧面积（单位：2cm ）为（）A ．80B ．60C ．40D ．20【解析】A ；几何体如图，是正四棱锥，底边长8，侧面底边上的高为5，因此侧面积为1854802⨯⨯⨯=．3.（西城·理·题5）阅读右面的程序框图，运行相应的程序，输出的结果为（）A．1321B．2113C．813D．138【解析】D；1,1,220x y z===<；1,2,320x y z===<；，8,13,2120x y z===>，故输出138．4.（东城·理·题5）如图是一个算法的程序框图，若该程序输出的结果为45，则判断框中应填入的条件是（）A．4?T>B．4?T<C．3?T>D．3?T<【解析】B ；循环一次得：12,1,2i T S ===；两次得：1123,2,263i T S ===+=；三次得：2134,3,3124i T S ===+=；四次得：3145,4,4205i T S ===+=，此时需要跳出循环，故填4?T <．5. （东城·文·题5）按如图所示的程序框图运算，若输入6x =，则输出k 的值是（）A ．3B ．4C ．5D ．6【解析】B ； 6x =，0k =，13x =，1k =，27x =，2k =，55x =，3k =，111x =，4k =，111100x =>，跳出循环，输出4k =．6. （石景山·文·题6）已知程序框图如图所示，则该程序框图的功能是（）A ．求数列1n ⎧⎫⎨⎬⎩⎭的前10项和()n *∈N B ．求数列12n ⎧⎫⎨⎬⎩⎭的前10项和()n *∈N C ．求数列1n ⎧⎫⎨⎬⎩⎭的前11项和()n *∈N D ．求数列12n ⎧⎫⎨⎬⎩⎭的前11项和()n *∈N【解析】注意n和k的步长分别是2和1．7.（西城·文·题6）阅读右面的程序框图，运行相应的程序，输出的结果为（）A．1321B．2113C．813D．138【解析】D；1,1,220x y z===<；1,2,320x y z===<；，8,13,2120x y z ===>，故输出138．8. （海淀·理科·题7）已知某程序框图如图所示，则执行该程序后输出的结果是（）第 7 题A ．1-B ．1C ．2D ．12【解析】A ；∵()20100mod 3i ==，∴对应的1a =-．9. （朝阳·文·题11）如图，下程序框图的程序执行后输出的结果是．【解析】55；将经过i次运行后的,n S值列表如下．于是S=5510.（宣武·文·题12）执行如图程序框图，输出S的值等于．12题图【解析】20；运算顺序如下===→===→===→===>1,1,23,4,36,10,410,20,54A S i A S i A S i A S i，输出S，故20S=．11.（崇文·理·题12）（崇文·文·题12）某程序框图如图所示，该程序运行后输出,M N的值分别为．【解析】13，21；依据程序框图画出运行n 次后,,M N i 的值．n1 2 3 i2 3 4 M2 5 13 N3 8 21 4次运行后43i =>，于是有13,21M N ==．12. （丰台·理·题13）在右边的程序框图中，若输出i 的值是4，则输入x 的取值范围是．【解析】(]2,4；∵328228->⇔>，x xx x->⇔>，322810x x->⇔>->⇔>，3242x x32104∴要使得刚好进行4次运算后输出的82x>，则有24<≤．x13.（朝阳·理·题13）右边程序框图的程序执行后输出的结果是．【解析】625；将经过i 次运行后的,n S 值列表如下．i1 2 3 4 5 ．．． m ．．．25 n3 5 7 9 11 21m + 51 S 14 9 16 25 2m 625 于是625S =．14. （海淀·文·题13）已知程序框图如图所示，则执行该程序后输出的结果是_______________．结束输出 a i = i +1否是a = 1-1ai ≥ 20a = 2 , j = 1开始【解析】12；a = -1 , j = 3a = 12, j = 2a = 2 , j = 1∵()202mod 3i ==，∴对应的12a =．集合简易逻辑推理与证明1. （崇文·文·题1）已知全集U =R ，集合{}|12A x x =->，{}2|680B x x x =-+<，则集合()UA B = （）A ．{}|14x x -≤≤B ．{}|23x x <≤C ． {}|23x x <≤D ．{}|14x x -<< 【解析】 D ；容易解得{3A x x x =>或者}0x <，{}26B x x =<<．于是()UA B ={}23x x <≤．2. （西城·理·题1）设集合{|1}P x x =>，2{|0}Q x x x =->，则下列结论正确的是（）A ．P Q =B ．P Q R =C ．P Q D ．Q P 【解析】 C ；(1,)P =+∞，(,0)(1,)Q =-∞+∞．3. （宣武·理·题1）设集合20.3{|0},2P x x m =-=≤，则下列关系中正确的是（） A ．m P ⊂ B ．m P ∉ C ．{}m P ∈ D ．{}m P 【解析】 D ；{|0P x x =≤≤，0.3022m <=<<，故m P ∈，因此{}m P4. （崇文·理·题1）已知全集U =R ，集合{}|12A x x =->，{}2|680B x x x =-+<，则集合()UA B =（）A ．{}|14x x -≤≤B ．{}|14x x -<<C ．{}|23x x <≤D ． {}|23x x <≤ 【解析】 D ；容易解得{3A x x x =>或者}0x <，{}26B x x =<<．于是()UA B ={}23x x <≤． 5. （西城·文·题1）设集合{|1}P x x =>，{|(1)0}Q x x x =->，下列结论正确的是（）A ．P Q =B ．P Q R =C ．P QD ．Q P 【解析】 C ；(1,)P =+∞，(,0)(1,)Q =-∞+∞．6. （宣武·文·题1）设集合{|4},sin 40A x x m ==︒≤，则下列关系中正确的是（） A ．m A ⊂ B ．m A ⊄ C ．{}m A ∈ D ．{}m A ∉ 【解析】 D ；正确的表示法，m A ∈，{}m A ，{}m A ∉．7. （东城·理·题2）设全集{33,}I x x x =-<<∈Z ，{1,2}A =，{2,1,2}B =--，则()IA B 等于（）A ．{1}B ．{1,2}C ．{2}D ．{0,1,2} 【解析】 D ；{2,1,0,1,2}I =--，{0,1}IB =，故(){0,1,2}IA B =．8. （石景山·文·题2）已知命题 :p x ∀∈R ，2x ≥，那么命题p ⌝为（） A ．,2x x ∀∈R ≤ B ．,2x x ∃∈<R C ．,2x x ∀∈-R ≤ D ．,2x x ∃∈<-R 【解析】 B ；全称命题的否定是存在性命题，将∀改为∃，然后否定结论．9. （东城·文·题2）设集合{1,2,4,6}A =，{2,3,5}B =，则韦恩图中阴影部分表示的集合（）A ．{2}B ．{3,5}C ．{1,4,6}D ．{3,5,7,8}【解析】B ；阴影部分表示{3,5}UA B =．10. （丰台·理·题2）设集合[)1{|(),0,}2xM y y x ==∈+∞，(]2{|log ,0,1}N y y x x ==∈，则集合M N 是（）A ．[)(,0)1,-∞+∞B ．[)0,+∞C ．(],1-∞D ．(,0)(0,1)-∞ 【解析】 C ；(]0,1M =，(],0N =-∞，因此(],1M N =-∞． 11. （石景山·理·题2）已知命题 :p x ∀∈R ，2x ≥，那么命题p ⌝为（） A ．,2x x ∀∈R ≤ B ．,2x x ∃∈<R C ．,2x x ∀∈-R ≤ D ．,2x x ∃∈<-R 【解析】 B ；全称命题的否定是存在性命题，将∀改为∃，然后否定结论．12. （朝阳·文·题2）命题:0p x ∀>，都有sin 1x -≥，则（）A ．:0p x ⌝∃>，使得sin 1x <-B ．:0p x ⌝∀> ，使得sin 1x <-C ．:0p x ⌝∃>，使得sin 1x >-D ．:0p x ⌝∀>，使得sin 1x -≥【解析】 A ；由命题的否定容易做出判断．13. （海淀·文·题7）给出下列四个命题：①若集合A 、B 满足A B A =，则A B ⊆；②给定命题,p q ，若“p q ∨”为真，则“p q ∧”为真； ③设,,a b m ∈R ，若a b <，则22am bm <；④若直线1:10l ax y ++=与直线2:10l x y -+=垂直，则1a =．其中正确命题的个数是（）A ．1B ．2C ．3D ．4【解析】 B ；命题①和④正确．14. （丰台·文·题7）若集合{}0,1,2P =，10(,),,20x y Q x y x y P x y ⎧⎫-+>⎧⎪⎪=∈⎨⎨⎬--<⎩⎪⎪⎩⎭，则Q 中元素的个数是（）A ．3B ．5C ．7D ．9【解析】 B ；(){},|12,,Q x y x y x y P =-<-<∈，由{}0,1,2P =得x y -的取值只可能是0和1． ∴()()()()(){}0,0,1,1,2,2,1,0,2,1Q =，含有5个元素．15. （崇文·文·题8）如果对于任意实数x ，[]x 表示不超过x 的最大整数．例如[]3.273=，[]0.60=．那么“[][]x y =”是“1x y -<”的 ( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【解析】 A ；由[][][][]1,1x x x y y y <+<+≤≤．于是有[][]()[][]1111x y x y x y -=+<-<+-=-则1x y -<．不妨设33,24x y ==，于是3331424x y -=-=<．但是[][]1,0.x y ==16. （东城·文·题9）已知命题3:(1,),log 0p x x ∀∈+∞>，则p 为．【解析】030(1,),log 0x x ∃∈+∞≤；全称命题的否定为存在命题．17. （宣武·文·题10）命题“任意常数列都是等比数列”的否定形式是．【解析】存在一个常数列不是等比数列；全称命题的否定是存在性命题．18. （海淀·理·题11）给定下列四个命题：① “π6x =”是“1sin 2x =”的充分不必要条件； ② 若“p q ∨”为真，则“p q ∧”为真；③ 若a b <，则22am bm <；④ 若集合A B A =，则A B ⊆．其中为真命题的是（填上所有正确命题的序号）．【解析】 ①，④；19. （海淀·理·题14）在平面直角坐标系中，点集(){}22,|1A x y x y =+≤， {(,)|4,0,340}B x y x y x y =-≤≥≥，则⑴点集(){}1111(,)3,1,,P x y x x y y x y A ==+=+∈所表示的区域的面积为_____；⑵点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为．【解析】 π；18π+．；⑴如左图所示，点集P 是以()3,1为圆心1为半径的圆，其表示区域的面积为π； ⑵如右图所示，点集Q 是由三段圆弧以及连结它们的三条切线段围成的区域，其面积为()1π433451π18π2OPQ OABP PCDQ OFEQS S S S ++++=⨯⨯+++⨯+=+△．20. （海淀·文·题14）在平面直角坐标系中，点集(){}22,|1A x y x y =+≤， (){},|11,11B x y x y =--≤≤≤≤，则 ⑴点集(){}1111(,)3,1,,P x y x x y y x y A ==+=+∈所表示的区域的面积为_____；⑵点集{}12121122(,),,(,),(,)Q x y x x x y y y x y A x y B ==+=+∈∈所表示的区域的面积为．【解析】 π，12π+；⑴如左图所示，点集P 是以()3,1为圆心1为半径的圆，其表示区域的面积为π；⑵如右图所示，点集Q是由四段圆弧以及连结它们的四条切线段围成的区域，其面积为．12π。

2010年北京石景山数学一模答案

GFEDCB A 石景山区2010年初三第一次统一练习暨毕业考试试卷初三数学参考答案阅卷须知：为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可．若考生的解法与本解法不同，正确者可参照评分参考给分，解答右端所注分数，表示考生正确做到这一步应得的累加分数．一、选择题（本题共32分，每小题4分）二、填空题（本题共16分，每小题4分）9．3->x ；10．))((2b a b a a -+； 11．109； 12．ππ2．三、解答题（本题共30分，每小题5分）13．解：原式133325-+--=……………………………………4分36+-= ………………………………………………5分14．解：解不等式①， 3-<x …………………………………………2分4分5分15．条件： ② ③ ④ ，结论： ① ……………… 1分证明： ∵ CD AB =∴ BD AC = ……………………………………………… 2分 ∵ FBG EAG ∠=∠∴ FBD EAD ∠=∠……………………… ………… 3分在△ACE 和△BDF 中⎪⎩⎪⎨⎧=∠=∠=BD AC FBD EAD BF AE ∴ △ACE ≌△BDF （SAS ） ………………………………… 4分∴ D ACE ∠=∠ ……………………………………………… 5分条件： ① ③ ④ ，结论： ② 证明：∵ FBG EAG ∠=∠ ∴ FBD EAD ∠=∠∵ AE BF =，ACE D ∠=∠ ∴ △ACE ≌△BDF （AAS ） ∴ BD AC = ∴ CD AB =条件： ① ② ④ ，结论： ③ 证明：∵ CD AB = ∴ BD AC =∵ FBG EAG ∠=∠ ∴ FBD EAD ∠=∠ ∵ ACE D ∠=∠∴ △ACE ≌△BDF （ASA ） ∴ AE BF =16．解：原式211)2(212+--+-⋅-=x x x x x 2112+--+-=x x x x ……………………………………………1分 2332++-=x x …………………………………………3分当0832=-+x x 时，832=+x x …………………………………4分原式283+-=103-= ………………………………………5分 17．解：根据题意，得：)0,2(A ，)32,0(B …………………1分在Rt △AOB 中，4)32(222=+=AB ，︒=∠30DBA ，…2分∴︒=∠30DCA ，6=+=AB OA OCRt △DOC 中，32tan =∠=DCO OC OD∴)0,6(C ，)32,0(-D …………………………………………3分设直线CD 的解析式为：32-=kx y∴ 3260-=k ，解得33=k ………………………………5分所以直线CD 的解析式为3233-=x y18．解：设该农场种植A 种草莓x 亩，B 种草莓)6(x -亩 ………1分依题意，得：460000)6(200040120060=-⨯+⨯x x …………2分解得：5.2=x , 5.36=-x ……………………………………3分 (2)由)6(21x x -≥，解得2≥x 设农场每年草莓全部被采摘的收入为y 元，则：4800008000)6(200040120060+-=-⨯+⨯=x x x y ……4分 ∴当2=x 时，y 有最大值为464000………………………………5分答：(l)A 种草莓种植2.5亩, B 种草莓种植3.5亩．(2) 若种植A 种草莓的亩数不少于种植B 种草莓的一半，那么种植A 种草莓2亩时，可使农场每年草莓全部被采摘的总收入最多.四、解答题（本题共20分，每小题5分）19．解：如图，过A 、D 作AE ⊥BC 于E 、DF ⊥BC 于F …………1分设 x AB AD 2==Rt △ABE 中，︒=︒-︒=∠3090120BAE20．解：（1）判断：CD 是⊙O 的切线证明：联结OC ………………………………1分∵ OD AC //∴∠A =∠BOD ,∠ACO =∠COD ∵ OC OA =∴∠A =∠ACO∴∠BOD =∠COD ∵ OC OB =, OD 为公共边 ∴△BOD ≌△COD ∴∠B =∠OCD∵ BD 是⊙O 的切线，AB 为直径 ∴ ∠︒=90ABD∴ ∠︒=90OCD …………………………………………2分 ∴ CD 是⊙O 的切线（2) 联结BC 交OD 于E∵ CD 和BD 都是⊙O 的切线 ∴CD =BD ，∠CDO =∠BDO ∴ BC ⊥OD ,CE BE =，︒=∠90OBD ∴△OBE ∽△ODB∴ OBOE ODOB = …………………………………………3分由CE BE =,OB OA = 得OE 为△ABC 的中位线即121==AC OE∴ OBOB 16= 得6±=OB (舍负) ………………………………5分∴ ⊙O 的半径为6．注：还可以证明△ABC ∽△ODB21. 解：（1）20，0.04 ，50; 图略 …………………………………3分（2）第二小组：105≤<a ……………………………………………4分（3）(0.16＋0.40)×1000=560. …………………………………………5分22．（1）16 …………………………………………1分（2）各2分五、解答题（本题满分7分）23．解：（1）△=(2k-7)2-4k （k+3）>0 k <4049……………………………………………………2分 ∵k 为非负整数，∴k=0，1∵()03722=++-+k x k kx 为一元二次方程∴k=1 ………………………………………………………………3分 (2)把k=1代入方程得x 2-5x+4=0, 解得x 1=1, x 2=4 ∵m<n∴m=1，n=4 …………………………………………………………… 4分把m=1，n=4代入ax y =与xb y 3+=可得a =4，b=1 …………………………………………………………5分 (3)把y=c 代入x y 4=与xy 4= 可得A(4c ，c) B(c 4,c)，由AB=23，可得c 4－4c =23 解得c 1=2, c 2=－8，经检验c 1=2, c 2=－8为方程的根。