2018年江苏省高考数学模拟试卷(9)(含详细答案)
2018届江苏高考数学模拟试卷(1)(含答案)

2018届江苏高考数学模拟试卷(1)数学I一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上......... 1.已知集合{02},{11}A x x B x x =<<=-<<,则A B U = ▲ .2. 设复数1a +=-i z i(i 是虚数单位,a ∈R ).若z 的虚部为3,则a 的值为 ▲ .3.一组数据5,4,6,5,3,7的方差等于 ▲ .4.右图是一个算法的伪代码,输出结果是 ▲ .5.某校有B A ,两个学生食堂,若甲、乙、丙三名学生各自随机选择其中的一个食堂用餐,则此三人不在同一食堂用餐的概率为 ▲ .6. 长方体1111ABCD A B C D -中,111,2,3AB AA AC ===,则它的体积等于 ▲ .7.若双曲线2213x y a -=的焦距等于4,则它的两准线之间的距离等于 ▲ .8. 若函数()22xx af x =+是偶函数,则实数a 等于 ▲ .9. 已知函数f (x )=2sin(ωx +φ)(ω>0).若f (π3)=0,f (π2)=2,则实数ω的最小值为 ▲ .S ←0 a ←1 For I From 1 to 3a ←2×a S ←S +a End For Print S (第4题)10. 如图,在梯形ABCD 中,,2,234,//CD AD AB CD AB ====,,如果 ⋅-=⋅则,3= ▲ .11.椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,若椭圆上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则椭圆C 的离心率的取值范围是 ▲ .12.若数列12{}(21)(21)n n n +--的前k 项的和不小于20172018,则k 的最小值为 ▲ .13. 已知24παπ<<,24πβπ<<,且22sin sin sin()cos cos αβαβαβ=+,则tan()αβ+的最大值为▲ .14. 设,0a b >,关于x 的不等式3232x xx xa N Mb ⋅-<<⋅+在区间(0,1)上恒成立,其中M , N 是与x 无关的实数,且M N >,M N -的最小值为1. 则ab的最小值为___▲___.二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证 明过程或演算步骤.15.如图,在ABC ∆中,已知7,45AC B =∠=o,D 是边AB 上的一点,3,120AD ADC =∠=o . 求:(1)CD 的长; (2)ABC ∆的面积.16.如图,在四棱锥S-ABCD 中,底面ABCD 是平行四边形,E ,F 分别是AB ,SC 的中点. (1)求证:EF ∥平面SAD ; A D CB(2)若SA=AD ,平面SAD ⊥平面SCD ,求证:EF ⊥AB .17.如图,有一椭圆形花坛,O 是其中心,AB 是椭圆的长轴,C 是短轴的一个端点. 现欲铺设灌溉管道,拟在AB 上选两点E ,F ,使OE =OF ,沿CE 、CF 、F A 铺设管道,设θ=∠CFO ,若OA =20m ,OC =10m , (1)求管道长度u 关于角θ的函数;(2)求管道长度u 的最大值.18.在平面直角坐标系xOy 中,已知圆222:C x y r +=和直线:l x a =(其中r 和a 均为常数,且0r a <<),M 为l 上一动点,1A ,2A 为圆C 与x 轴的两个交点,直线1MA ,2MA 与圆C 的另一个交点分别为,P Q .(1)若2r =,M 点的坐标为(4,2),求直线PQ 方程; (2)求证:直线PQ 过定点,并求定点的坐标.19.设R k ∈,函数2()ln 1f x x x kx =+--,求: (1)1=k 时,不等式()1f x >-的解集; (2)函数()x f 的单调递增区间;(3)函数()x f 在定义域内的零点个数.20.设数列{}n a ,{}n b 分别是各项为实数的无穷等差数列和无穷等比数列. (1)已知06,12321=+-=b b b b ,求数列{}n b 的前n 项的和n S ;(2)已知数列{}n a 的公差为d (0)d ≠,且11122(1)22n n n a b a b a b n +++⋅⋅⋅+=-+,求数列{}n a ,{}n b 的通项公式(用含n ,d 的式子表达); (3)求所有满足:11n n n na b b a ++=+对一切的*N n ∈成立的数列{}n a ,{}n b .数学Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两题,并在相应的答题区域内作答.................... 若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. A .选修4—1:几何证明选讲(本小题满分10分) 如图,在△ABC 中,90BAC ∠=,延长BA 到D ,使得AD =12AB ,E ,F 分别为BC ,AC 的中点,求证:DF =BE .B .选修4—2:矩阵与变换 (本小题满分10分)已知曲线1C :221x y +=,对它先作矩阵1002A ⎡⎤=⎢⎥⎣⎦对应的变换,再作矩阵010m B ⎡⎤=⎢⎥⎣⎦对应的变换(其中0≠m ),得到曲线2C :2214x y +=,求实数m 的值.C .选修4—4:坐标系与参数方程 (本小题满分10分)已知圆C的参数方程为12cos 2sin x y θθ=+⎧⎪⎨=⎪⎩, , (θ为参数),直线l 的参数方程为1cos sin x t y t αα=+⎧⎨=⎩, , (t 为参数,0 ααπ<<π≠2,且),若圆C 被直线lα的值.D .选修4—5:不等式选讲 (本小题满分10分)对任给的实数a 0a ≠()和b ,不等式()12a b a b a x x ++-⋅-+-≥恒成立,求实数x 的取值范围.【必做题】第22、23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文 字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,在直三棱柱ABC -A 1B 1C 1中,A A 1=AB =AC =1,AB ⊥AC ,M ,N 分别是棱CC 1,BC 的 中点,点P 在直线A 1B 1上.(1)求直线PN 与平面ABC 所成的角最大时,线段1A P 的长度;(2)是否存在这样的点P ,使平面PMN 与平面ABC 所成的二面角为6π. 如果存在,试确定点P 的位置;如果不存在,请说明理由.(第21—A 题)BECFDA123.(本小题满分10分)设函数()sin cos n n f θθθ=+,其中n 为常数,n ∈*N , (1)当(0,)2πθ∈时, ()f θ是否存在极值?如果存在,是极大值还是极小值?(2)若sin cos a θθ+=,其中常数a 为区间[内的有理数. 求证:对任意的正整数n ,()f θ为有理数.2018高考数学模拟试卷(1)数学Ⅰ答案一、填空题答案:1. {12}x x -<<2. 5 3.53 4. 14 5. 43 6.4 7. 1 8. 1 9. 3 10.2311. 111(,)(,1)322⋃.解:422111232c a c e e c a>-⎧⇒<<≠⎨≠⎩且,故离心率范围为111(,)(,1)322⋃.12. 10解:因为对任意的正整数n ,都有1212)12)(12(211--=--++n n n n n 1-1, 所以⎭⎬⎫⎩⎨⎧--+)12)(12(21n n n的前k 项和为 1)1)(2(221)1)(2(221)1)(2(221322211--++--+--+k kk12112112112112112113221---++---+---=+k k 12111--=+k 使2018201712111≥--+k ,即2018121≥-+k ,解得10≥k ,因此k 的最小值为10.13. -4解:因为24ππ<<βα,,所以βαβαsin sin cos cos ,,,均不为0.由βαβαβαcos cos )sin(sin sin 22+=,得βαβαβαβαsin cos cos sin tan tan sin sin +=,于是αββαtan 1tan 1tan tan +=,即βαβαβαtan tan tan tan tan tan +=, 也就是βαβα22tan tan tan tan =+,其中βαtan tan ,均大于1. 由βαβαβαtan tan 2tan tan tan tan22⋅≥+=⋅,所以34tan tan ≥βα.令()341tan tan 1-,--∞∈=βαt , βαβαβαβαβαtan tan 1tan tan tan tan 1tan tan )tan(22-=-+=+21-+=tt 4-≤,当且仅当1-=t 时取等号.14.4+解:32()32xxx x a f x b ⋅-=⋅+,则23()6l n2()0(32)xx x a b f x b +'=>⋅+恒成立,所以()f x 在(0,1)上单调递增, 132(0),(1)132a a f f b b --==++,∴()f x 在(0, 1)上的值域为132(,)132a ab b --++,M x f N <<)( 在(0,1)上恒成立,故mi n 321()1321(32)(1)a a ab M N b b b b --+-=-==++++,所以2342a b b =++,所以2344a b b b=++≥.所以min ()4ab=+.二、解答题答案15.解:(1)在ACD ∆中,由余弦定理得2222cos AC AD CD AD CD ADC =+-⋅∠,2227323cos120CD CD =+-⨯⋅o ,解得5CD =.(2)在BCD ∆中,由正弦定理得sin sin BD CD BCD B =∠,5sin 75sin 45BD =o o,解得BD = 所以BDC BD CD ADC CD AD S S S BCD ACD ABC ∠⋅+∠⋅=+=∆∆∆sin 21sin 2111535sin120560222+=⨯⨯+⨯⨯oo 758+=.16. 解(1)取SD 的中点G ,连AG ,FG .在SCD ∆中,因为F ,G 分别是SC ,SD 的中点, 所以FG ∥CD ,12FG CD =. 因为四边形ABCD 是平行四边形,E 是AB 的中点, 所以1122AE AB CD ==,AE ∥CD . 所以FG ∥AE ,FG=AE ,所以四边形AEFG 是平行四边形,所以EF ∥AG .因为AG ⊂平面SAD ,EF ⊄平面SAD ,所以EF ∥平面SAD . (2)由(1)及SA=AD 得,AG SD ⊥.因为平面SAD ⊥平面SCD ,平面SAD ⋂平面SCD =SD ,AG ⊂平面SAD , 所以AG ⊥平面SCD ,又因为SCD CD 面⊂,所以AG ⊥CD . 因为EF ∥AG ,所以EF ⊥CD , 又因为CD AB //,所以EF ⊥AB .17. 解:(1)因为θsin 01=CF ,θtan 10=OF ,θtan 10-20=AF , 所以θθθθsin cos 102020tan 1002sin 02-+=-+=++=AF CF CE u , AE DCS FG其中,552cos 0<<θ. (2)由 θθsin cos 102020-+=u ,得θθ2'sin cos 0201-=u ,令21cos 0'==θ,u , 当 21cos 0<<θ时,0'>u ,函数)(θu 为增函数;当552c o s 21<<θ时,0'<u ,函数)(θu 为减函数. 所以,当21cos =θ,即3πθ=时,310203sin21102020max +=⨯-+=πu (m )所以,管道长度u 的最大值为)(31020+m.18. 解:(1)当2r =,(4,2)M 时,则1(2,0)A -,2(2,0)A ,直线1MA 的方程:320x y -+=,解224320x y x y ⎧+=⎨-+=⎩得86(,)55P .直线2MA 的方程:20x y --=,解22420x y x y ⎧+=⎨--=⎩得(0,2)Q -.所以PQ 方程为220x y --=.(2)由题设得1(,0)A r -,2(,0)A r ,设(,)M a t ,直线1MA 的方程是()ty x r a r =++,与圆C 的交点11(,)P x y , 直线2MA 的方程是()ty x r a r=--,与圆C 的交点22(,)Q x y ,则点11(,)P x y ,22(,)Q x y 在曲线[()()][()()]0a r y t x r a r y t x r +-+---=上, 化简得2222222()2()()0a r y ty ax r t x r ---+-=, ①又11(,)P x y ,22(,)Q x y 在圆C 上,圆C :2220x y r +-=, ②①-2t ×②得22222222222()2()()()0a r y ty ax r t x r t x y r ---+--+-=,化简得2222()2()0a r y t ax r t y ----=.所以直线PQ 方程为2222()2()0a r y t ax r t y ----=.令0y =得2r x a =,所以直线PQ 过定点2(,0)r a.19.解(1)k =1时,不等式()1f x >-即2ln 0x x x +->,设2()l n g x x x x =+-,因为2121()210x x g x x x x-+'=+-=>在定义域(0,)+∞上恒成立,所以g (x )在(0,)+∞上单调递增,又(1)0g =,所以()1f x >-的解集为(1,)+∞.(2)2121()2(0)x kx f x x k x x x-+'=+-=>,由()0f x '≥得2210x kx -+≥……(*). (ⅰ)当280k ∆=-≤,即k -≤≤(*)在R 上恒成立,所以()f x 的单调递增区间为(0,)+∞. (ⅱ)当k >时,280k ∆=->,此时方程2210x kx -+=的相异实根分别为12x x ==,因为12120,2102k x x x x ⎧+=>⎪⎪⎨⎪=>⎪⎩,所以120x x <<,所以()0f x '≥的解集为(0,[)44k k -+∞U , 故函数f (x )的单调递增区间为)+∞和.(ⅲ)当k <-时,同理可得:,0,21,020212121<<∴⎩⎨⎧<=+>=x x kx x x x ()f x 的单调递增区间为(0,)+∞.综上所述,当k >()f x的单调递增区间为)+∞和;当k ≤()f x 的单调递增区间为(0,)+∞. (3)据(2)知①当k ≤时,函数()f x 在定义域(0,)+∞上单调递增,令210,0x kx x ⎧-->⎨>⎩得2k x +>,取}m =,则当x >m 时,2()10f x x kx >-->.设01x <<,21max{1,}x kx k λ--<--=,所以()l n f x x λ<+,当0x e λ-<<时,()0f x <,取m i n {1,}n e λ-=,则当(0,)x n ∈时,()0f x <,又函数()f x 在定义域(0,)+∞上连续不间断,所以函数()f x 在定义域内有且仅有一个零点.②当22>k 时,()f x 在12(0,)(,)x x +∞和上递增,在12(,)x x 上递减, 其中012,0122211=+-=+-kx x kx x则2221111111()ln 1ln (21)1f x x x kx x x x =+--=+-+-211ln 2x x =--.下面先证明ln (0)x x x <>:设x x x h -=ln )(),由1()xh x x-'=>0得01x <<,所以h (x )在(0,1)上递增,在(1,)+∞上递减,01)1()(m a x <-==h x h ,所以()0h x <)0(>x ,即 ln (0)x x x <>.因此,047)21(2)(212111<---=--<x x x x f ,又因为)(x f 在12(,)x x 上递减,所以21()()0f x f x <<,所以()f x 在区间2(0,)x 不存在零点.由①知,当x m >时,()0f x >,()f x 的图象连续不间断,所以()f x 在区间2(,)x +∞上有且仅有一个零点. 综上所述,函数()f x 在定义域内有且仅有一个零点.20.解(1)设{}n b 的公比为q ,则有063=+-q q ,即2(2)(23)0q q q +-+=,所以2q =-,从而1(2)3nn S --=.(2)由11122(1)22n n n a b a b a b n +++⋅⋅⋅+=-+得112211(2)22nn n a b a b a b n --++⋅⋅⋅+=-+,两式两边分别相减得2(2)nn n a b n n =⋅≥.由条件112a b =,所以*2(N )n n n a b n n =⋅∈,因此111(1)2(2)n n n a b n n ---=-⋅≥,两式两边分别相除得12(2)1n n a n q n a n -⋅=≥-,其中q 是数列{}n b 的公比.所以122(1)(3)2n n a n q n a n ---⋅=≥-,上面两式两边分别相除得2221(2)(3)(1)n n n a a n n n a n ---=≥-.所以312234a a a =,即1121(2)3()4a d a a d +=+,解得113a d a d ==-或,若d a 31-=,则04=a ,有024444==⋅b a 矛盾,所以1a d =满足条件,所以2,nn n a dn b d==.(3)设数列{}n a 的公差为d ,{}n b 的公比为q , 当q =1时,112n n b b b ++=,所以112n na b a +=,所以数列{}n a 是等比数列,又数列{}n a 是等差数列,从而数列{}n a 是各项不为0的常数列,因此112b =,经验证,110,2n n a a b =≠=满足条件.当1q ≠时,由11n n n n a b b a ++=+得1111(1)n dn a b q q dn a d-+=++-……(*) ①当d>0时,则1d a n d ->时,10n n a a +>>,所以111dn a dn a d +>+-此时令112dn a dn a d +<+-得12d a n d->,因为112d a d a d d -->所以,当12d a n d ->时,1112dn a dn a d +<<+-. 由(*)知,10,0b q >>. (ⅰ)当q >1时,令11(1)2n b q q-+>得121log (1)qn b q >++,取11122max{,1log }(1)q d a M d b q -=++,则当1n M >时,(*)不成立. (ⅱ)当0<q <1时,令11(1)1n b q q -+<得111log (1)qn b q >++,取12121max{,1log }(1)q d a M d b q -=++,则当2n M >时,(*)不成立. 因此,没有满足条件的数列{}n a ,{}n b .②同理可证:当d <0时,也没有满足条件的数列{}n a ,{}n b .综上所述,所有满足条件的数列{}n a ,{}n b 的通项公式为110,2n n a a b =≠=(*N n ∈).数学Ⅱ(附加题)答案21.【选做题】答案A .选修4—1:几何证明选讲 解:取AB 中点G ,连结GF ,12AD AB =,AD AG ∴=,又90BAC ∠=, 即AC 为DG 的垂直平分线, ∴ DF = FG ………………① ,又E 、F 分别为BC 、AC 中点, 1//2EF AB BG EF BG ==∴ 四边形BEFG 为平行四边形, ∴ FG = BE …………② 由①②得BE =DF .B .选修4—2:矩阵与变换 解:010********m m BA ⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,设P ()00,x y 是曲线1C 上的任一点,它在矩阵BA 变换作用下变成点(),P x y ''',则000020210x my x m y x y '⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦⎣⎦,则002x my y x '=⎧⎨'=⎩,即0012x y y x m'=⎧⎪⎨'=⎪⎩, 又点P 在曲线1C 上,则22214x y m''+=,'p 在曲线2C 上,则14''22=+x y , 故21m =,所以,1m =±.C .选修4—4:坐标系与参数方程 解:圆的直角坐标方程为()(2214x y -+-=,直线的直角坐标方程为()1y k x =-()tan k α=,因为圆C 被直线l,∴=k =,即tan α=, 又0πα≤<,∴α=π3或2π3.D .选修4—5:不等式选讲 解:由题知,aba b a x x ++-≤-+-21恒成立,故|1||2|x x -+-不大于aba b a ++-的最小值 ,∵||||2|||≥|a b a b a b a b a -++++-=,当且仅当()()0≥a b a b +-时取等号, ∴aba b a ++-的最小值等于2.∴x 的范围即为不等式|x -1|+|x -2|≤2的解,解不等式得1522≤≤x .【必做题】答案22. 解:如图,以A 为原点建立空间直角坐标系,则A 1(0,0,1),B 1(1,0,1), M (0,1,12),N (12,12,0)设10),1,0,(<<=λλp .则)0,0,(1λ=A ,)1,0,(11λ=+=A ;)1,21,21(--=λ, (1)∵()0,0,1=m 是平面ABC 的一个法向量.=><=∴|,cos |sin m θ45)21(1141)21(|100|22+-=++--+λλ∴当12λ=时,θ取得最大值,此时sin θ=,tan 2θ=即:当12λ=时, θ取得最大值,此时tan 2θ=. 故P A 1的长度为21.(2)=)21,21,21(-,由(1))1,21,21(--=λ,设(),,x y z =n 是平面PMN 的一个法向量.则111022211()022x y z x y z λ⎧-++=⎪⎨⎪-+-=⎩得123223y x z x λλ+⎧=⎪⎨-⎪=⎩令x =3,得y =1+2λ,z=2-2λ, ∴()3,12,22λλ=+-n , ∴|cos ,|<>=m n 4210130λλ++=(*)∵△=100-4⨯4⨯13=-108<0,∴方程(*)无解∴不存在点P 使得平面PMN 与平面ABC 所成的二面角为30º. 23. 解:(1)当(0,)2πθ∈时,设22()sin cos (sin cos )0n n f n θθθθθ--'=->,等价于0cos sin 22>---θθn n .(ⅰ)n =1时,令,>0)('f θ得110sin cos θθ->,解得04πθ<<,所以()f θ在(0,)4π上单调递增,在(,)42ππ上单调递减,所以()f θ存在极大值,无极小值.(ⅱ)n =2时,()f θ=1,()f θ既无极大值,也无极小值. (ⅲ)3n ≥时,令,>0)('f θ得sin cos θθ>,所以42ππθ<<,所以()f θ在(0,)4π上单调递减,在(,)42ππ上单调递增,所以()f θ存在极小值,无极大值.(3)由22sin cos sin cos 1a θθθθ+=⎧⎪⎨+=⎪⎩得:21sin cos 2a θθ-= , 所以sin θ,cos θ是方程22102a x ax --+=的两根, x =,∴()((2nnnnna a f θ+=+=⎝⎭⎝⎭,当k n 2=为偶数时,()()()()()()()()]222222[(2]222222[(2222222244222224244222222kn n n n n kn nn nnnna a C a C a a C a C a a-++-+-+=-++-+-+=--+-+----当12+=k n 为奇数时,()()()()()()()()]2222222[(22222222(222222122442222214244222222kn n n n n n n knn nn nn n nnna C a C a C a C a C a C a a -++-+-+=-++-+-+=--+-+------∵a为[内的有理数,m n C,2n为正整数,∴()fθ为有理数.。
2018年高考数学江苏卷及答案解析

数学试卷 第1页(共24页) 数学试卷 第2页(共24页)绝密★启用前江苏省2018年普通高等学校招生全国统一考试数 学本试卷共160分.考试时长120分钟.参考公式:锥形的体积公式13V Sh =,其中S 是椎体的底面积,h 是椎体的高。
一、填空题:本大题共14小题,每小题5分,共计70分. 1.已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么AB = .2.若复数z 满足i 12i z =+,其中i 是虚数单位,则z 的实部为 .3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 .4.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 .5.函数()f x =的定义域为 .6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 .7.已知函数ππsin(2)()22y x ϕϕ=+-<<的图象关于直线π3x =对称,则ϕ的值是 .8.在平面直角坐标系xOy 中,若双曲线22221(0)x y a b a b-=>>0,的右焦点(,0)F c 到一条渐近线的距离为2,则其离心率的值是 . 9.函数()f x 满足(4)()()f x f x x +=∈R ,且在区间(2,2]-上,()cos (2)2102x x f x x x π⎧⎪⎪=⎨⎪+⎪⎩0<≤,(-2<≤),,则((15))f f 的值为 . 10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .11.若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点,则()f x 在[1,1]-上的最大值与最小值的和为 .12.在平面直角坐标系xOy 中,A 为直线:2l y x =上在第一象限内的点,点(5,0)B ,以AB 为直径的圆C 与直线l 交于另一点D .若0AB CD =,则点A 的横坐标为 .13.在ABC △中,角A ,B ,C 所对应的边分别为a ,b ,c ,120ABC ∠=,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为 .14.已知集合{21,}A x x n n ==-∈*N ,{2,}n B x x n ==∈*N .将AB 的所有元素从小到大依次排列构成一个数列{}n a ,记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为 .毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共24页) 数学试卷 第4页(共24页)二、解答题:本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥. 求证:(Ⅰ)AB ∥平面11A B C ; (Ⅱ)平面11ABB A ⊥平面1A BC .16.(本小题满分14分)已知α,β为锐角,4tan 3α=,cos()αβ+=.(Ⅰ)求cos2α的值; (Ⅱ)求tan()αβ-的值.数学试卷 第5页(共24页) 数学试卷 第6页(共24页)17.(本小题满分14分)某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧MPN (P 为此圆弧的中点)和线段MN 构成,已知圆O 的半径为40米,点P 到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD ,大棚Ⅱ内的地块形状为CDP △,要求点A ,B 均在线段MN 上,C ,D 均在圆弧上.设OC 与MN 所成的角为θ.(Ⅰ)用θ分别表示矩形ABCD 和CDP △的面积,并确定sin θ的取值范围; (Ⅱ)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C过点1)2,焦点1(F,2F ,圆O 的直径为12F F .(Ⅰ)求椭圆C 及圆O 的方程;(Ⅱ)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; ②直线l 与椭圆C 交于A ,B 两点.若OAB △,求直线l 的方程.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共24页) 数学试卷 第8页(共24页)19.(本小题满分16分)记()f x ',()g x '分别为函数()f x ,()g x 的导函数.若存在0x ∈R ,满足00()()f x g x =且00()()f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.(Ⅰ)证明:函数()f x x =与2()22g x x x =+-不存在“S 点”; (Ⅱ)若函数2()1f x ax =-与()ln g x x =存在“S 点”,求实数a 的值;(Ⅲ)已知函数2()f x x a =-+,e ()xb g x x=.对任意0a >,判断是否存在0b >,使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”,并说明理由.20.(本小题满分16分)设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项1b ,公比为q 的等比数列. (Ⅰ)设10a =,11b =,2q =若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围; (Ⅱ)若110a b =>,m ∈*N,q ∈,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,1n m =+…,均成立,并求d 的取值范围(用1b ,m ,q 表示).数学试卷 第9页(共24页) 数学试卷 第10页(共24页)数学Ⅱ(附加题)本试卷均为非选择题(第21题~第23题). 本卷满分40分,考试时间为30分钟.21.【选做题】本题包括A ,B ,C ,D 四小题,请选定其中两小题并作答...........,若多做,则按作答的前两小题评分、解答时应写出文字说明、证明过程或演算步骤。
2018年江苏省高考数学试卷及解析

2018年江苏省高考数学试卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5.00分)已知集合A={0,1,2,8},B={﹣1,1,6,8},那么A∩B=.2.(5.00分)若复数z满足i•z=1+2i,其中i是虚数单位,则z的实部为.3.(5.00分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为.4.(5.00分)一个算法的伪代码如图所示,执行此算法,最后输出的S的值为.5.(5.00分)函数f(x)=的定义域为.6.(5.00分)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为.17.(5.00分)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.8.(5.00分)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为.9.(5.00分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x)=,则f(f(15))的值为.10.(5.00分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.11.(5.00分)若函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[﹣1,1]上的最大值与最小值的和为.12.(5.00分)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为.13.(5.00分)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.214.(5.00分)已知集合A={x|x=2n﹣1,n∈N*},B={x|x=2n,n∈N*}.将A∪B 的所有元素从小到大依次排列构成一个数列{a n},记S n为数列{a n}的前n项和,则使得S n>12a n+1成立的n的最小值为.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14.00分)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.16.(14.00分)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.17.(14.00分)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D 均在圆弧上.设OC与MN所成的角为θ.3(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(16.00分)如图,在平面直角坐标系xOy中,椭圆C 过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB 的面积为,求直线l的方程.19.(16.00分)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在4x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x﹣2不存在“S点”;(2)若函数f(x)=ax2﹣1与g(x)=lnx存在“S点”,求实数a的值;(3)已知函数f(x)=﹣x2+a,g(x)=.对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.20.(16.00分)设{a n}是首项为a1,公差为d的等差数列,{b n}是首项为b1,公比为q的等比数列.(1)设a1=0,b1=1,q=2,若|a n﹣b n|≤b1对n=1,2,3,4均成立,求d的取值范围;(2)若a1=b1>0,m∈N*,q∈(1,],证明:存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,并求d的取值范围(用b1,m,q表示).数学Ⅱ(附加题)【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.(10.00分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若PC=2,求BC的长.5B.[选修4-2:矩阵与变换](本小题满分10分)22.(10.00分)已知矩阵A=.(1)求A的逆矩阵A﹣1;(2)若点P在矩阵A对应的变换作用下得到点P′(3,1),求点P的坐标.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的方程为ρsin (﹣θ)=2,曲线C的方程为ρ=4cosθ,求直线l被曲线C截得的弦长.D.[选修4-5:不等式选讲](本小题满分0分)24.若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内6作答,解答时应写出文字说明、证明过程或演算步骤.25.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.26.设n∈N*,对1,2,……,n的一个排列i1i2……i n,如果当s<t时,有i s>i t,则称(i s,i t)是排列i1i2……i n的一个逆序,排列i1i2……i n的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n(k)为1,2,…,n的所有排列中逆序数为k的全部排列的个数.(1)求f3(2),f4(2)的值;(2)求f n(2)(n≥5)的表达式(用n表示).72018年江苏省高考数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5.00分)已知集合A={0,1,2,8},B={﹣1,1,6,8},那么A∩B={1,8} .【分析】直接利用交集运算得答案.【解答】解:∵A={0,1,2,8},B={﹣1,1,6,8},∴A∩B={0,1,2,8}∩{﹣1,1,6,8}={1,8},故答案为:{1,8}.【点评】本题考查交集及其运算,是基础的计算题.2.(5.00分)若复数z满足i•z=1+2i,其中i是虚数单位,则z的实部为2.【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案.【解答】解:由i•z=1+2i,得z=,8∴z的实部为2.故答案为:2.【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.(5.00分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为90.【分析】根据茎叶图中的数据计算它们的平均数即可.【解答】解:根据茎叶图中的数据知,这5位裁判打出的分数为89、89、90、91、91,它们的平均数为×(89+89+90+91+91)=90.故答案为:90.【点评】本题考查了利用茎叶图计算平均数的问题,是基础题.4.(5.00分)一个算法的伪代码如图所示,执行此算法,最后输出的S的值为8.9【分析】模拟程序的运行过程,即可得出程序运行后输出的S值.【解答】解:模拟程序的运行过程如下;I=1,S=1,I=3,S=2,I=5,S=4,I=7,S=8,此时不满足循环条件,则输出S=8.故答案为:8.【点评】本题考查了程序语言的应用问题,模拟程序的运行过程是解题的常用方法.5.(5.00分)函数f(x)=的定义域为[2,+∞).【分析】解关于对数函数的不等式,求出x的范围即可.【解答】解:由题意得:≥1,10解得:x≥2,∴函数f(x)的定义域是[2,+∞).故答案为:[2,+∞).【点评】本题考查了对数函数的性质,考查求函数的定义域问题,是一道基础题.6.(5.00分)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为0.3.【分析】(适合理科生)从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,根据概率公式计算即可,(适合文科生),设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,根据概率公式计算即可【解答】解:(适合理科生)从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,故选中的2人都是女同学的概率P==0.3,(适合文科生),设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,11故选中的2人都是女同学的概率P==0.3,故答案为:0.3【点评】本题考查了古典概率的问题,采用排列组合或一一列举法,属于基础题.7.(5.00分)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.【分析】根据正弦函数的对称性建立方程关系进行求解即可.【解答】解:∵y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,∴2×+φ=kπ+,k ∈Z,即φ=kπ﹣,∵﹣φ<,∴当k=0时,φ=﹣,故答案为:﹣.【点评】本题主要考查三角函数的图象和性质,利用正弦函数的对称性建立方程关系是解决本题的关键.128.(5.00分)在平面直角坐标系xOy 中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为2.【分析】利用双曲线的简单性质,以及点到直线的距离列出方程,转化求解即可.【解答】解:双曲线=1(a>0,b>0)的右焦点F (c,0)到一条渐近线y=x的距离为c,可得:=b=,可得,即c=2a,所以双曲线的离心率为:e=.故答案为:2.【点评】本题考查双曲线的简单性质的应用,考查转化思想以及计算能力.9.(5.00分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f (x)=,则f(f(15))的值为.【分析】根据函数的周期性,进行转化求解即可.13【解答】解:由f(x+4)=f(x)得函数是周期为4的周期函数,则f(15)=f(16﹣1)=f(﹣1)=|﹣1+|=,f ()=cos ()=cos =,即f(f(15))=,故答案为:【点评】本题主要考查函数值的计算,根据函数的周期性结合分段函数的表达式利用转化法是解决本题的关键.10.(5.00分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,14多面体的中心为顶点的多面体的体积为:2×=.故答案为:.【点评】本题考查几何体的体积的求法,考查空间想象能力以及计算能力.11.(5.00分)若函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[﹣1,1]上的最大值与最小值的和为﹣3.【分析】推导出f′(x)=2x(3x﹣a),x∈(0,+∞),当a≤0时,f′(x)=2x(3x ﹣a)>0,f(0)=1,f(x)在(0,+∞)上没有零点;当a>0时,f′(x)=2x (3x﹣a)>0的解为x>,f(x)在(0,)上递减,在(,+∞)递增,由f(x)只有一个零点,解得a=3,从而f(x)=2x3﹣3x2+1,f′(x)=6x(x﹣1),x ∈[﹣1,1],利用导数性质能求出f(x)在[﹣1,1]上的最大值与最小值的和.【解答】解:∵函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,∴f′(x)=2x(3x﹣a),x∈(0,+∞),①当a≤0时,f′(x)=2x(3x﹣a)>0,函数f(x)在(0,+∞)上单调递增,f(0)=1,f(x)在(0,+∞)上没有零15点,舍去;②当a>0时,f′(x)=2x(3x﹣a)>0的解为x >,∴f(x)在(0,)上递减,在(,+∞)递增,又f(x)只有一个零点,∴f ()=﹣+1=0,解得a=3,f(x)=2x3﹣3x2+1,f′(x)=6x(x﹣1),x∈[﹣1,1],f′(x)>0的解集为(﹣1,0),f(x)在(﹣1,0)上递增,在(0,1)上递减,f(﹣1)=﹣4,f(0)=1,f(1)=0,∴f(x)min=f(﹣1)=﹣4,f(x)max=f(0)=1,∴f(x)在[﹣1,1]上的最大值与最小值的和为:f(x)max+f(x)min=﹣4+1=﹣3.【点评】本题考查函数的单调性、最值,导数的运算及其应用,同时考查逻辑思维能力和综合应用能力,是中档题.12.(5.00分)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D .若=0,则点A的横坐标为3.16【分析】设A(a,2a),a>0,求出C的坐标,得到圆C的方程,联立直线方程与圆的方程,求得D 的坐标,结合=0求得a值得答案.【解答】解:设A(a,2a),a>0,∵B(5,0),∴C (,a),则圆C的方程为(x﹣5)(x﹣a)+y(y﹣2a)=0.联立,解得D(1,2).∴=.解得:a=3或a=﹣1.又a>0,∴a=3.即A的横坐标为3.故答案为:3.【点评】本题考查平面向量的数量积运算,考查圆的方程的求法,是中档题.13.(5.00分)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c 的最小值为9.【分析】根据面积关系建立方程关系,结合基本不等式1的代换进行求解即可.【解答】解:由题意得acsin120°=asin60°+csin60°,17即ac=a+c,得+=1,得4a+c=(4a+c)(+)=++5≥2+5=4+5=9,当且仅当=,即c=2a时,取等号,故答案为:9.【点评】本题主要考查基本不等式的应用,利用1的代换结合基本不等式是解决本题的关键.14.(5.00分)已知集合A={x|x=2n﹣1,n∈N*},B={x|x=2n,n∈N*}.将A∪B 的所有元素从小到大依次排列构成一个数列{a n},记S n为数列{a n}的前n项和,则使得S n>12a n+1成立的n的最小值为27.【分析】采用列举法,验证n=26,n=27即可.【解答】解:利用列举法可得:当n=26时,A∪B中的所有元素从小到大依次排列,构成一个数列{a n},所以数列{a n}的前26项分别1,3,5,7,9,11,13,15,17,19,21,23.25,…41,2,4,8,16,32.S26=,a27=43,⇒12a27=516,不符合题意.当n=27时,A∪B中的所有元素从小到大依次排列,构成一个数列{a n},18所以数列{a n}的前26项分别1,3,5,7,9,11,13,15,17,19,21,23.25,…41,43,2,4,8,16,32.S27==546,a28=45⇒12a28=540,符合题意,故答案为:27.【点评】本题考查了集合、数列的求和,属于中档题.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14.00分)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.【分析】(1)由⇒AB∥平面A1B1C;(2)可得四边形ABB1A1是菱形,AB1⊥A1B,19由AB1⊥B1C1⇒AB1⊥BC⇒AB1⊥面A1BC,⇒平面ABB1A1⊥平面A1BC.【解答】证明:(1)平行六面体ABCD﹣A1B1C1D1中,AB∥A1B1,AB∥A1B1,AB⊄平面A1B1C,A1B1⊂∥平面A1B1C⇒AB∥平面A1B1C;(2)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,⇒四边形ABB1A1是菱形,⊥AB1⊥A1B.在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1⇒AB1⊥BC.∴⇒AB1⊥面A1BC,且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC.【点评】本题考查了平行六面体的性质,及空间线面平行、面面垂直的判定,属于中档题.16.(14.00分)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.【分析】(1)由已知结合平方关系求得sinα,cosα的值,再由倍角公式得cos2α的值;(2)由(1)求得tan2α,再由cos(α+β)=﹣求得tan(α+β),利用tan(α20﹣β)=tan[2α﹣(α+β)],展开两角差的正切求解.【解答】解:(1)由,解得,∴cos2α=;(2)由(1)得,sin2,则tan2α=.∵α,β∈(0,),∴α+β∈(0,π),∴sin(α+β)==.则tan(α+β)=.∴tan(α﹣β)=tan[2α﹣(α+β)]==.【点评】本题考查三角函数的恒等变换及化简求值,考查同角三角函数基本关系式的应用,是中档题.17.(14.00分)某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D 均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;21(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.【分析】(1)根据图形计算矩形ABCD和△CDP的面积,求出sinθ的取值范围;(2)根据题意求出年总产值y的解析式,构造函数f(θ),利用导数求f(θ)的最大值,即可得出θ为何值时年总产值最大.=(40sinθ+10)•80cosθ【解答】解:(1)S矩形ABCD=800(4sinθcosθ+cosθ),S△CDP =•80cosθ(40﹣40sinθ)=1600(cosθ﹣cosθsinθ),当B、N重合时,θ最小,此时sinθ=;当C、P重合时,θ最大,此时sinθ=1,∴sinθ的取值范围是[,1);(2)设年总产值为y,甲种蔬菜单位面积年产值为4t,乙种蔬菜单位面积年产值为3t,22则y=3200t(4sinθcosθ+cosθ)+4800t(cosθ﹣cosθsinθ)=8000t(sinθcosθ+cosθ),其中sinθ∈[,1);设f(θ)=sinθcosθ+cosθ,则f′(θ)=cos2θ﹣sin2θ﹣sinθ=﹣2sin2θ﹣sinθ+1;令f′(θ)=0,解得sinθ=,此时θ=,cosθ=;当sinθ∈[,)时,f′(θ)>0,f(θ)单调递增;当sinθ∈[,1)时,f′(θ)<0,f(θ)单调递减;∴θ=时,f(θ)取得最大值,即总产值y最大.答:(1)S=800(4sinθcosθ+cosθ),矩形ABCDS△CDP=1600(cosθ﹣cosθsinθ),sinθ∈[,1);θ=时总产值y最大.【点评】本题考查了解三角形的应用问题,也考查了构造函数以及利用导数求函数的最值问题,是中档题.2318.(16.00分)如图,在平面直角坐标系xOy中,椭圆C 过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB 的面积为,求直线l的方程.【分析】(1)由题意可得.,又a2﹣b2=c2=3,解得a=2,b=1即可.(2)①可设直线l的方程为y=kx+m,(k<0,m>0).可得.由,可得(4k2+1)x2+8kmx+4m2﹣4=0,△=(8km)2﹣4(4k2+1)(4m2﹣4)=0,解得k=﹣,m=3.即可②设A(x1,y1),B(x2,y2),联立直线与椭圆方程得(4k2+1)x2+8kmx+4m2﹣4=0,24O到直线l的距离d=,|AB|=|x2﹣x1|=,△OAB的面积为S===,解得k=﹣,(正值舍去),m=3.即可【解答】解:(1)由题意可设椭圆方程为,∵焦点F1(﹣,0),F2(,0),∴.∵∴,又a2﹣b2=c2=3,解得a=2,b=1.∴椭圆C 的方程为:,圆O的方程为:x2+y2=3.(2)①可知直线l与圆O相切,也与椭圆C,且切点在第一象限,∴可设直线l的方程为y=kx+m,(k<0,m>0).由圆心(0,0)到直线l 的距离等于圆半径,可得.由,可得(4k2+1)x2+8kmx+4m2﹣4=0,△=(8km)2﹣4(4k2+1)(4m2﹣4)=0,25可得m2=4k2+1,∴3k2+3=4k2+1,结合k<0,m>0,解得k=﹣,m=3.将k=﹣,m=3代入可得,解得x=,y=1,故点P 的坐标为(.②设A(x1,y1),B(x2,y2),由⇒k <﹣.联立直线与椭圆方程得(4k2+1)x2+8kmx+4m2﹣4=0,|x2﹣x1|==,O到直线l的距离d=,|AB|=|x2﹣x1|=,△OAB的面积为S===,解得k=﹣,(正值舍去),m=3.∴y=﹣为所求.【点评】本题考查了椭圆的方程,直线与圆、椭圆的位置关系,属于中档题.2619.(16.00分)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x﹣2不存在“S点”;(2)若函数f(x)=ax2﹣1与g(x)=lnx存在“S点”,求实数a的值;(3)已知函数f(x)=﹣x2+a,g(x)=.对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.【分析】(1)根据“S点”的定义解两个方程,判断方程是否有解即可;(2)根据“S点”的定义解两个方程即可;(3)分别求出两个函数的导数,结合两个方程之间的关系进行求解判断即可.【解答】解:(1)证明:f′(x)=1,g′(x)=2x+2,则由定义得,得方程无解,则f(x)=x与g(x)=x2+2x﹣2不存在“S 点”;(2)f′(x)=2ax,g′(x)=,x>0,由f′(x)=g′(x )得=2ax,得x=,f ()=﹣=g ()=﹣lna2,得a=;27(3)f′(x)=﹣2x,g′(x)=,(x≠0),由f′(x0)=g′(x0),假设b>0,得b=﹣>0,得0<x0<1,由f(x0)=g(x0),得﹣x02+a==﹣,得a=x02﹣,令h(x)=x2﹣﹣a=,(a>0,0<x<1),设m(x)=﹣x3+3x2+ax﹣a,(a>0,0<x<1),则m(0)=﹣a<0,m(1)=2>0,得m(0)m(1)<0,又m(x)的图象在(0,1)上连续不断,则m(x)在(0,1)上有零点,则h(x)在(0,1)上有零点,则存在b>0,使f(x)与g(x)在区间(0,+∞)内存在“S”点.【点评】本题主要考查导数的应用,根据条件建立两个方程组,判断方程组是否有解是解决本题的关键.20.(16.00分)设{a n}是首项为a1,公差为d的等差数列,{b n}是首项为b1,公比为q的等比数列.(1)设a1=0,b1=1,q=2,若|a n﹣b n|≤b1对n=1,2,3,4均成立,求d的取值范围;28(2)若a1=b1>0,m∈N*,q∈(1,],证明:存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,并求d的取值范围(用b1,m,q表示).【分析】(1)根据等比数列和等差数列的通项公式,解不等式组即可;(2)根据数列和不等式的关系,利用不等式的关系构造新数列和函数,判断数列和函数的单调性和性质进行求解即可.【解答】解:(1)由题意可知|a n﹣b n|≤1对任意n=1,2,3,4均成立,∵a1=0,q=2,∴,解得.即≤d ≤.证明:(2)∵a n=a1+(n﹣1)d,b n=b1•q n﹣1,若存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,则|b1+(n﹣1)d﹣b1•q n﹣1|≤b1,(n=2,3,…,m+1),即b1≤d ≤,(n=2,3,…,m+1),∵q∈(1,],∴则1<q n﹣1≤q m≤2,(n=2,3,…,m+1),∴b1≤0,>0,因此取d=0时,|a n﹣b n|≤b1对n=2,3,…,m+1均成立,29下面讨论数列{}的最大值和数列{}的最小值,①当2≤n≤m 时,﹣==,当1<q ≤时,有q n≤q m≤2,从而n(q n﹣q n﹣1)﹣q n+2>0,因此当2≤n≤m+1时,数列{}单调递增,故数列{}的最大值为.②设f(x)=2x(1﹣x),当x>0时,f′(x)=(ln2﹣1﹣xln2)2x<0,∴f(x)单调递减,从而f(x)<f(0)=1,当2≤n≤m 时,=≤(1﹣)=f ()<1,因此当2≤n≤m+1时,数列{}单调递递减,故数列{}的最小值为,∴d的取值范围是d∈[,].【点评】本题主要考查等比数列和等差数列以及不等式的综合应用,考查学生的30运算能力,综合性较强,难度较大.数学Ⅱ(附加题)【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.(10.00分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若PC=2,求BC的长.【分析】连接OC,由题意,CP为圆O的切线,得到垂直关系,由线段长度及勾股定理,可以得到PO的长,即可判断△COB是等边三角形,BC的长.【解答】解:连接OC,因为PC为切线且切点为C,所以OC⊥CP.因为圆O的半径为2,,所以BO=OC=2,,所以,31所以∠COP=60°,所以△COB为等边三角形,所以BC=BO=2.【点评】本题主要考查圆与直线的位置关系,切线的应用,考查发现问题解决问题的能力.B.[选修4-2:矩阵与变换](本小题满分10分)22.(10.00分)已知矩阵A=.(1)求A的逆矩阵A﹣1;(2)若点P在矩阵A对应的变换作用下得到点P′(3,1),求点P的坐标.【分析】(1)矩阵A=,求出det(A)=1≠0,A可逆,然后求解A的逆矩阵A﹣1.(2)设P(x,y),通过•=,求出=,即可得到点P的坐标.【解答】解:(1)矩阵A=,det(A)=2×2﹣1×3=1≠0,所以A可逆,从而:A的逆矩阵A﹣1=.(2)设P(x,y),则•=,所以=A﹣1=,32因此点P的坐标为(3,﹣1).【点评】本题矩阵与逆矩阵的关系,逆矩阵的求法,考查转化思想的应用,是基本知识的考查.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的方程为ρsin (﹣θ)=2,曲线C的方程为ρ=4cosθ,求直线l被曲线C截得的弦长.【分析】将直线l、曲线C的极坐标方程利用互化公式可得直角坐标方程,利用直线与圆的相交弦长公式即可求解.【解答】解:∵曲线C的方程为ρ=4cosθ,∴ρ2=4ρcosθ,⇒x2+y2=4x,∴曲线C是圆心为C(2,0),半径为r=2得圆.∵直线l的方程为ρsin (﹣θ)=2,∴﹣=2,∴直线l的普通方程为:x ﹣y=4.圆心C到直线l的距离为d=,∴直线l被曲线C截得的弦长为2.【点评】本题考查了极坐标方程化为直角坐标方程、直线与圆的相交弦长关系、点到直线的距离公式,属于中档题.33D.[选修4-5:不等式选讲](本小题满分0分)24.若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.【分析】根据柯西不等式进行证明即可.【解答】解:由柯西不等式得(x2+y2+z2)(12+22+22)≥(x+2y+2z)2,∵x+2y+2z=6,∴x2+y2+z2≥4是当且仅当时,不等式取等号,此时x=,y=,z=,∴x2+y2+z2的最小值为4【点评】本题主要考查不等式的证明,利用柯西不等式是解决本题的关键.,【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.25.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.34【分析】设AC,A1C1的中点分别为O,O1,以{}为基底,建立空间直角坐标系O﹣xyz,(1)由|cos|=可得异面直线BP与AC1所成角的余弦值;(2)求得平面AQC1的一个法向量为,设直线CC1与平面AQC1所成角的正弦值为θ,可得sinθ=|cos|=,即可得直线CC1与平面AQC1所成角的正弦值.【解答】解:如图,在正三棱柱ABC﹣A1B1C1中,设AC,A1C1的中点分别为O,O1,则,OB⊥OC,OO1⊥OC,OO1⊥OB,故以{}为基底,建立空间直角坐标系O﹣xyz,35∵AB=AA1=2,A(0,﹣1,0),B (,0,0),C(0,1,0),A1(0,﹣1,2),B1(,0,2),C1(0,1,2).(1)点P为A1B1的中点.∴,∴,.|cos|===.∴异面直线BP与AC1所成角的余弦值为:;(2)∵Q为BC的中点.∴Q ()∴,,设平面AQC1的一个法向量为=(x,y,z),由,可取=(,﹣1,1),设直线CC1与平面AQC1所成角的正弦值为θ,sinθ=|cos|==,36∴直线CC1与平面AQC1所成角的正弦值为.【点评】本题考查了向量法求空间角,属于中档题.26.设n∈N*,对1,2,……,n的一个排列i1i2……i n,如果当s<t时,有i s>i t,则称(i s,i t)是排列i1i2……i n的一个逆序,排列i1i2……i n的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n(k)为1,2,…,n的所有排列中逆序数为k的全部排列的个数.(1)求f3(2),f4(2)的值;(2)求f n(2)(n≥5)的表达式(用n表示).【分析】(1)由题意直接求得f3(2)的值,对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置,由此可得f4(2)的值;(2)对一般的n(n≥4)的情形,可知逆序数为0的排列只有一个,逆序数为137的排列只能是将排列12…n中的任意相邻两个数字调换位置得到的排列,f n(1)=n﹣1.(2),当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排为计算f n+1(2)=f n(2)+f n(1)列,n+1在新排列中的位置只能是最后三个位置,可得f n+1+f n(0)=f n(2)+n,则当n≥5时,f n(2)=[f n(2)﹣f n﹣1(2)]+[f n﹣1(2)﹣f n﹣2(2)]+…+[f5(2)﹣f4(2)]+f4(2),则f n(2)(n≥5)的表达式可求.【解答】解:(1)记μ(abc)为排列abc得逆序数,对1,2,3的所有排列,有μ(123)=0,μ(132)=1,μ(231)=2,μ(321)=3,∴f3(0)=1,f3(1)=f3(2)=2,对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置.因此,f4(2)=f3(2)+f3(1)+f3(0)=5;(2)对一般的n(n≥4)的情形,逆序数为0的排列只有一个:12…n,∴f n(0)=1.逆序数为1的排列只能是将排列12…n中的任意相邻两个数字调换位置得到的排列,f n(1)=n﹣1.(2),当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排为计算f n+1列,n+1在新排列中的位置只能是最后三个位置.因此,f n(2)=f n(2)+f n(1)+f n(0)=f n(2)+n.+1当n≥5时,f n(2)=[f n(2)﹣f n﹣1(2)]+[f n﹣1(2)﹣f n﹣2(2)]+…+[f5(2)38﹣f4(2)]+f4(2)=(n﹣1)+(n﹣2)+…+4+f4(2)=.因此,当n≥5时,f n(2)=.【点评】本题主要考查计数原理、排列等基础知识,考查运算求解能力和推理论证能力,是中档题.39。
2018年江苏省高考数学一模试卷(解析卷)
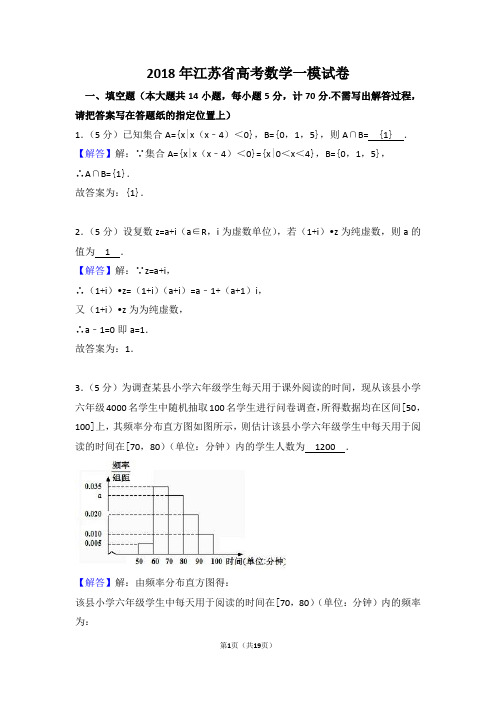
2018年江苏省高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B={1} .【解答】解:∵集合A={x|x(x﹣4)<0}={x|0<x<4},B={0,1,5},∴A∩B={1}.故答案为:{1}.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为1.【解答】解:∵z=a+i,∴(1+i)•z=(1+i)(a+i)=a﹣1+(a+1)i,又(1+i)•z为为纯虚数,∴a﹣1=0即a=1.故答案为:1.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为1200.【解答】解:由频率分布直方图得:该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的频率为:1﹣(0.005+0.035+0.020+0.010)×10=0.3,∴估计该县小学六年级4000名学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为:4000×0.3=1200.故答案为:1200.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为1.【解答】解:根据题意知,执行程序后,输出函数y=,当x=0时,y=e0=1.故答案为:1.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.【解答】解:口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,从袋中一次随机摸出2个球,基本事件总数n==6,摸出的2个球的编号之和大于4包含的基本事件有:(1,4),(2,3),(2,4),(3,4),共4个,∴摸出的2个球的编号之和大于4的概率为p=.故答案为:.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p 的值为6.【解答】解:∵双曲线的方程,∴a2=4,b2=5,可得c==3,因此双曲线的右焦点为F(3,0),∵抛物线y2=2px(p>0)的焦点与双曲线的右焦点重合,∴=3,解之得p=6.故答案为:6.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是(﹣∞,2] .【解答】解:函数y=e x﹣a的值域为A∵e x=2,∴值域为A=[2﹣a,+∞).又∵A⊆[0,+∞),∴2﹣a≥0,即a≤2.故答案为:(﹣∞,2].8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.【解答】解:∵(tanα﹣1)(tanβ﹣1)=2,可得:tanα+tanβ+1=tanαtanβ,∴tan(α+β)=═﹣1,∵锐角α,β,可得:α+β∈(0,π),∴α+β=.故答案为:.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是(0,] .【解答】解:由函数y=sinωx,图象过原点,若ω<0,图象在x轴下方单调递减,∴ω>0,因为y=Sinωx在[0,2π]单调递增,说明其至少在[0,2π]单调递增,则其周期至少8π,∴,即.故答案为:(0,]10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为4034.【解答】解:因为S n为等差数列{a n}的前n项和,且{a n}的前2017项中的奇数项和为2018,=a1+a3+a5+…+a2017=1009×(a1+a2017)×=2018,得a1+a2017═4.所以S奇则S2017=(a1+a2017)=2017×2=4034故答案为:4034.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是[1,).【解答】解:由0≤x≤3可得f(x)∈[0,],x>3时,f(x)∈(0,1).画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)﹣m有四个不同的零点,∴函数y=f(x)与y=m的图象有4个交点,由图象可得m的取值范围为[1,),故答案为:[1,).12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为﹣.【解答】解:【解法一】设P(x1,y1),Q(x2,y2);则y1=k(x1﹣3)①,+(y2﹣1)2=1②;由=3,得,即,代入②得+=9;此方程表示的圆心(0,3)到直线kx﹣y﹣3k=0的距离为d≤r;即≤3,解得﹣≤k≤0.∴实数k的最小值为﹣.【解法二】设P(x,y),Q(x0,y0);则+(y0﹣1)2=1①;由=3,得,即,代入①化简得x2+(y﹣3)2=9;∴点P的轨迹是圆心为(0,3),半径为3的圆的方程,又点P在直线kx﹣y﹣3k=0上,如图所示;则直线与该圆有公共点,即圆心到直线的距离为d≤r;∴≤3,解得﹣≤k≤0;∴实数k的最小值为﹣.故答案为:﹣.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为24.【解答】解:建立如图的直角坐标系,则A(,),B(0,0),那么容易得到C(0,5)时,D的位置可以有三个位置,其中D1(﹣,),D2(﹣,0),D3(﹣,),此时=(﹣,﹣),=(﹣,﹣),=(﹣,﹣5),=(﹣,﹣),则•=21,•=24,•=22.5,则的最大值为24,故答案为:24.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为100.【解答】解:∵ksin2B+sinAsinC>19sinBsinC,由正弦定理可得:kb2+ac>19bc,∴k>,又∵c﹣b<a<b+c,∴﹣b﹣c<﹣a<b﹣c,∴<19+()=20﹣()2=100﹣(﹣10)2,当=10时,20﹣()2取得最大值20×10﹣102=100.∴k≥100,即实数k的最小值为100.故答案为:100二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.【解答】证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.又AB1⊂侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C⊂平面A1MC,所以AB⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.【解答】解:(1)因为c=,则由正弦定理,得sinC=sinB.…(2分)又C=2B,所以sin2B=sinB,即2sinBcosB=sinB.…(4分)又B是△ABC的内角,所以sinB>0,故cosB=.…(6分)(2)因为=,所以cbcosA=bacosC,则由余弦定理,得b2+c2﹣a2=b2+a2﹣c2,得a=c.…(10分)从而cosB==,…(12分)又0<B<π,所以sinB==.从而cos(B+)=cosBcos﹣sinBsin=.…(14分)17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?【解答】解:(1)在图甲中,连接MO交EF于点T.设OE=OF=OM=R,在Rt△OET中,因为∠EOT=∠EOF=60°,所以OT=,则MT=0M﹣OT=.从而BE=MT=,即R=2BE=2.故所得柱体的底面积S=S扇形OEF ﹣S△OEF=πR2﹣R2sin120°=﹣,又所得柱体的高EG=4,所以V=S×EG=﹣4.答:当BE长为1(分米)时,折卷成的包装盒的容积为﹣4立方分米.(2)设BE=x,则R=2x,所以所得柱体的底面积S=S扇形OEF﹣S△OEF=πR2﹣R2sin120°=(﹣)x2,又所得柱体的高EG=6﹣2x,所以V=S×EG=(﹣2)(﹣x3+3x2),其中0<x<3.令f(x)=﹣x3+3x2,0<x<3,则由f′(x)=﹣3x2+6x=﹣3x(x﹣2)=0,解得x=2.列表如下:所以当x=2时,f(x)取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q 的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;=a n对任意(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.【解答】解:(1)由题意,可得a=(a n+d)(a n﹣d)+λd2,化简得(λ﹣1)d2=0,又d≠0,所以λ=1.(2)将a1=1,a2=2,a3=4,代入条件,可得4=1×4+λ,解得λ=0,所以a=a na n﹣1,所以数列{a n}是首项为1,公比q=2的等比数列,+1所以a n=2n﹣1.欲存在r∈[3,7],使得m•2n﹣1≥n﹣r,即r≥n﹣m•2n﹣1对任意n∈N*都成立,则7≥n﹣m•2n﹣1,所以m≥对任意n∈N*都成立.令b n=,则b n+1﹣b n=﹣=,<b n;当n=8时,b9=b8;当n<8时,b n+1>b n.所以当n>8时,b n+1所以b n的最大值为b9=b8=,所以m的最小值为;(3)因为数列{a n}不是常数列,所以T≥2,=a n恒成立,从而a3=a1,a4=a2,①若T=2,则a n+2所以,所以λ(a2﹣a1)2=0,又λ≠0,所以a2=a1,可得{a n}是常数列,矛盾.所以T=2不合题意.②若T=3,取a n=(*),满足a n+3=a n恒成立.由a22=a1a3+λ(a2﹣a1)2,得λ=7.则条件式变为a n2=a n+1a n﹣1+7.由22=1×(﹣3)+7,知a3k﹣12=a3k﹣2a3k+λ(a2﹣a1)2;由(﹣3)2=2×1+7,知a3k2=a3k﹣1a3k+1+λ(a2﹣a1)2;由12=2×(﹣3)+7,知a3k+12=a3k a3k+2+λ(a2﹣a1)2;所以,数列(*)适合题意.所以T的最小值为3.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b 的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.【解答】解:(1)由f(x)=lnx,得f(1)=0,又f′(x)=,所以f′(1)=1,当c=0时,g(x)=ax+,所以g′(x)=a﹣,所以g′(1)=a﹣b,因为函数f(x)与g(x)的图象在x=1处有相同的切线,所以,即,解得a=,b=﹣;(2)当x0>1时,则f(x0)>0,又b=3﹣a,设t=f(x0),则题意可转化为方程ax+﹣c=t(t>0)在(0,+∞)上有相异两实根x1,x2.即关于x的方程ax2﹣(c+t)x+(3﹣a)=0(t>0)在(0,+∞)上有相异两实根x1,x2.所以,得,所以c>2﹣t对t∈(0,+∞),a∈(0,3)恒成立.因为0<a<3,所以2≤2•=3(当且仅当a=时取等号),又﹣t<0,所以2﹣t的取值范围是(﹣∞,3),所以c≥3.故c的最小值为3.(3)当a=1时,因为函数f(x)与g(x)的图象交于A,B两点,所以,两式相减,得b=x1x2(1﹣),要证明x1x2﹣x2<b<x1x2﹣x1,即证x1x2﹣x2<x1x2(1﹣)<x1x2﹣x1,即证<<,即证<ln<,即证1﹣<ln<﹣1,令=t,则t>1,此时即证1﹣<lnt<t﹣1.令φ(t)=lnt+﹣1,所以φ′(t)=﹣=>0,所以当t>1时,函数φ(t)单调递增.又φ(1)=0,所以φ(t)=lnt+﹣1>0,即1﹣<lnt成立;再令m(t)=lnt﹣t+1,所以m′(t)=﹣1=<0,所以当t>1时,函数m(t)单调递减,又m(1)=0,所以m(t)=lnt﹣t+1<0,即lnt<t﹣1也成立.综上所述,实数x1,x2满足x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.【解答】解:如图,连接AE,OE,因为直线DE与⊙O相切于点E,所以DE⊥OE,又因为AD⊥DE于D,所以AD∥OE,所以∠DAE=∠OEA,①在⊙O中,OE=OA,所以∠OEA=∠OAE,②…(5分)由①②得∠DAE=∠OAE,即∠DAE=∠FAE,又∠ADE=∠AFE,AE=AE,所以△ADE≌△AFE,所以DE=FE,又DE=4,所以FE=4,即E到直径AB的距离为4.…(10分)[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.【解答】解:设P(x0,y0)是圆x2+y2=1上任意一点,则=1,设点P(x0,y0)在矩阵M对应的变换下所得的点为Q(x,y),则=,即,解得,…(5分)代入=1,得=1,∴圆x2+y2=1在矩阵M的变换下所得的曲线方程为=1.…(10分)[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.【解答】解:直线ρcos(θ+)=1,转化为:,曲线ρ=r(r>0)转化为:x2+y2=r2,由于直线和圆相切,则:圆心到直线的距离d=.所以r=1.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【解答】解:由柯西不等式,得[x2+()2][12+()2]≥(x•1+)2,即≥(x+y)2.而x2+3y2=1,所以(x+y)2,所以﹣,…(5分)由,得,所以当且仅当x=,y=时,(x+y)max=.所以当x+y取最大值时x值为.…(10分)25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.【解答】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(﹣2,0,0),M(﹣1,0,2).=(﹣2,0,4),=(01,﹣1,2),cos<,>===.故直线AP与BM所成角的余弦值为.…(5分)(2)=(﹣2,1,0),=(﹣1,﹣1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<>===.故平面ABM与平面PAC所成锐二面角的余弦值为.…(10分)26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.【解答】解:(1)由条件,nf(n)=C C C C①,在①中令n=1,得f(1)=1.在①中令n=2,得2f(2)=6,得f(2)=3.在①中令n=3,得3f(3)=30,故f(3)=10.(2)猜想f(n)=.要证猜想成立,只要证等式n=•+2•+…+n•成立.由(1+x)n=+x+x2+…+x n①,两边同时对x求导数,可得n(1+x)n﹣1=+2x+3x2+n x n﹣1②,把等式①和②相乘,可得n(1+x)2n﹣1=(+x+x2+…+x n)•(+2x+3x2+n x n﹣1)③.等式左边x n的系数为n,等式右边x n的系数为•+•2+•3+…+n•n=•+2•+3•+…+n•=C C C C,根据等式③恒成立,可得n=C C C C.故f(n)=成立.。
2018年江苏省盐城市、南京市高考高三数学一模试卷及解析

2018年江苏省盐城市、南京市高考数学一模试卷一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B=.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p的值为.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是.8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是.10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是.12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为.二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T=a n对任意的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.2018年江苏省盐城市、南京市高考数学一模试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.(5分)已知集合A={x|x(x﹣4)<0},B={0,1,5},则A∩B={1} .【试题解答】解:∵集合A={x|x(x﹣4)<0}={x|0<x<4},B={0,1,5},∴A∩B={1}.故答案为:{1}.2.(5分)设复数z=a+i(a∈R,i为虚数单位),若(1+i)•z为纯虚数,则a的值为1.【试题解答】解:∵z=a+i,∴(1+i)•z=(1+i)(a+i)=a﹣1+(a+1)i,又(1+i)•z为为纯虚数,∴a﹣1=0即a=1.故答案为:1.3.(5分)为调查某县小学六年级学生每天用于课外阅读的时间,现从该县小学六年级4000名学生中随机抽取100名学生进行问卷调查,所得数据均在区间[50,100]上,其频率分布直方图如图所示,则估计该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为1200.【试题解答】解:由频率分布直方图得:该县小学六年级学生中每天用于阅读的时间在[70,80)(单位:分钟)内的频率为:1﹣(0.005+0.035+0.020+0.010)×10=0.3,∴估计该县小学六年级4000名学生中每天用于阅读的时间在[70,80)(单位:分钟)内的学生人数为:4000×0.3=1200.故答案为:1200.4.(5分)执行如图所示的伪代码,若x=0,则输出的y的值为1.【试题解答】解:根据题意知,执行程序后,输出函数y=,当x=0时,y=e0=1.故答案为:1.5.(5分)口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.【试题解答】解:口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,从袋中一次随机摸出2个球,基本事件总数n==6,摸出的2个球的编号之和大于4包含的基本事件有:(1,4),(2,3),(2,4),(3,4),共4个,∴摸出的2个球的编号之和大于4的概率为p=.故答案为:.6.(5分)若抛物线y2=2px的焦点与双曲线的右焦点重合,则实数p的值为6.【试题解答】解:∵双曲线的方程,∴a2=4,b2=5,可得c==3,因此双曲线的右焦点为F(3,0),∵抛物线y2=2px(p>0)的焦点与双曲线的右焦点重合,∴=3,解之得p=6.故答案为:6.7.(5分)设函数y=e x﹣a的值域为A,若A⊆[0,+∞),则实数a的取值范围是(﹣∞,2] .【试题解答】解:函数y=e x﹣a的值域为A∵e x=2,∴值域为A=[2﹣a,+∞).又∵A⊆[0,+∞),∴2﹣a≥0,即a≤2.故答案为:(﹣∞,2].8.(5分)已知锐角α,β满足(tanα﹣1)(tanβ﹣1)=2,则α+β的值为.【试题解答】解:∵(tanα﹣1)(tanβ﹣1)=2,可得:tanα+tanβ+1=tanαtanβ,∴tan(α+β)=═﹣1,∵锐角α,β,可得:α+β∈(0,π),∴α+β=.故答案为:.9.(5分)若函数y=sinωx在区间[0,2π]上单调递增,则实数ω的取值范围是(0,] .【试题解答】解:由函数y=sinωx,图象过原点,可得ω>0在区间[0,2π]上单调递增,∴,即.故答案为:(0,]10.(5分)设S n为等差数列{a n}的前n项和,若{a n}的前2017项中的奇数项和为2018,则S2017的值为4034.【试题解答】解:因为S n为等差数列{a n}的前n项和,且{a n}的前2017项中的奇数项和为2018,所以S=a1+a3+a5+…+a2017=1009×(a1+a2017)×=1009×a1009=2018,得奇a1009=2.=a2+a4+a6+…+a2016=1008×(a2+a2016)×=1008×a1009=1008×2=则S偶2016则S2017=S奇+S偶=2018+2016=4034.故答案为:4034.11.(5分)设函数f(x)是偶函数,当x≥0时,f(x)=,若函数y=f(x)﹣m 有四个不同的零点,则实数m的取值范围是[1,).【试题解答】解:由0≤x≤3可得f(x)∈[0,],x>3时,f(x)∈(0,1).画出函数y=f(x)与y=m的图象,如图所示,∵函数y=f(x)﹣m有四个不同的零点,∴函数y=f(x)与y=m的图象有4个交点,由图象可得m的取值范围为[1,),故答案为:[1,).12.(5分)在平面直角坐标系xOy中,若直线y=k(x﹣3)上存在一点P,圆x2+(y﹣1)2=1上存在一点Q,满足=3,则实数k的最小值为﹣.【试题解答】解:设P(x1,y1),Q(x2,y2);则y1=k(x1﹣3)①,+(y2﹣1)2=1②;由=3,得,即,代入②得+=9;此方程表示的圆心(0,3)到直线kx﹣y﹣3k=0的距离为d≤r;即≤3,解得﹣≤k≤0.∴实数k的最小值为﹣.故答案为:﹣.13.(5分)如图是蜂巢结构图的一部分,正六边形的边长均为1,正六边形的顶点称为“晶格点”.若A,B,C,D四点均位于图中的“晶格点”处,且A,B的位置所图所示,则的最大值为24.【试题解答】解:建立如图的直角坐标系,则A(,),B(0,0),那么容易得到C(0,5)时,D的位置可以有三个位置,其中D1(﹣,),D2(﹣,0),D3(﹣,),此时=(﹣,﹣),=(﹣,﹣),=(﹣,﹣5),=(﹣,﹣),则•=21,•=24,•=22.5,则的最大值为24,故答案为:24.14.(5分)若不等式ksin2B+sinAsinC>19sinBsinC对任意△ABC都成立,则实数k的最小值为100.【试题解答】解:∵ksin2B+sinAsinC>19sinBsinC,由正弦定理可得:kb2+ac>19bc,∴k>,只需k大于右侧表达式的最大值即可,显然c>b时,表达式才能取得最大值,又∵c﹣b<a<b+c,∴﹣b﹣c<﹣a<b﹣c,∴<19+()=20﹣()2=100﹣(﹣10)2,当=10时,20﹣()2取得最大值20×10﹣102=100.∴k≥100,即实数k的最小值为100.故答案为:100二、解答题(共6小题,满分90分)15.(14分)如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.(1)求证:BN∥平面A1MC;(2)若A1M⊥AB1,求证:AB1⊥A1C.【试题解答】证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.所以四边形A1NBM是平行四边形,从而A1M∥BN.又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,所以侧面ABB1A1⊥底面ABC.又CA=CB,且M是AB的中点,所以CM⊥AB.则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.又AB1⊂侧面ABB1A1,所以AB1⊥CM.又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,所以AB1⊥平面A1MC.又A1C⊂平面A1MC,所以AB⊥A1C.16.(14分)在△ABC中,角A,B,C的对边分别为a,b,c 已知c=.(1)若C=2B,求cosB的值;(2)若=,求cos(B)的值.【试题解答】解:(1)因为c=,则由正弦定理,得sinC=sinB. …(2分)又C=2B,所以sin2B=sinB,即2sinBcosB=sinB. …(4分)又B是△ABC的内角,所以sinB>0,故cosB=. …(6分) (2)因为=,所以cbcosA=bacosC,则由余弦定理,得b2+c2﹣a2=b2+a2﹣c2,得a=c. …(10分)从而cosB==,…(12分)又0<B<π,所以sinB==.从而cos(B+)=cosBcos﹣sinBsin=. …(14分)17.(14分)有一矩形硬纸板材料(厚度忽略不计),一边AB长为6分米,另一边足够长.现从中截取矩形ABCD(如图甲所示),再剪去图中阴影部分,用剩下的部分恰好能折卷成一个底面是弓形的柱体包装盒(如图乙所示,重叠部分忽略不计),其中OEMF 是以O为圆心、∠EOF=120°的扇形,且弧,分别与边BC,AD相切于点M,N.(1)当BE长为1分米时,求折卷成的包装盒的容积;(2)当BE的长是多少分米时,折卷成的包装盒的容积最大?【试题解答】解:(1)在图甲中,连接MO交EF于点T.设OE=OF=OM=R,在Rt△OET中,因为∠EOT=∠EOF=60°,所以OT=,则MT=0M﹣OT=.从而BE=MT=,即R=2BE=2.故所得柱体的底面积S=S扇形OEF ﹣S△OEF=πR2﹣R2sin120°=﹣,又所得柱体的高EG=4,所以V=S×EG=﹣4.答:当BE长为1(分米)时,折卷成的包装盒的容积为﹣4立方分米.(2)设BE=x,则R=2x,所以所得柱体的底面积S=S扇形OEF﹣S△OEF=πR2﹣R2sin120°=(﹣)x2,又所得柱体的高EG=6﹣2x,所以V=S×EG=(﹣2)(﹣x3+3x2),其中0<x<3.令f(x)=﹣x3+3x2,0<x<3,则由f′(x)=﹣3x2+6x=﹣3x(x﹣2)=0,解得x=2.列表如下:x(0,2)2(2,3)f′(x)+0﹣f(x)增极大值减所以当x=2时,f(x)取得最大值.答:当BE的长为2分米时,折卷成的包装盒的容积最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C:(a>b>0)的下顶点为B,点M,N是椭圆上异于点B的动点,直线BM,BN分别与x轴交于点P,Q,且点Q是线段OP的中点.当点N运动到点()处时,点Q的坐标为().(1)求椭圆C的标准方程;(2)设直线MN交y轴于点D,当点M,N均在y轴右侧,且=2时,求直线BM的方程.【试题解答】解:(1)由N(),点Q的坐标为(),得直线NQ的方程为y=x﹣,令x=0,得点B的坐标为(0,﹣).所以椭圆的方程为+=1.将点N的坐标(,)代入,得+=1,解得a2=4.所以椭圆C的标准方程为+=1.(2):设直线BM的斜率为k(k>0),则直线BM的方程为y=x﹣.在y=kx﹣中,令y=0,得x P=,而点Q是线段OP的中点,所以x Q=.所以直线BN的斜率k BN=k BQ==2k.联立,消去y,得(3+4k2)x2﹣8kx=0,解得x M=.用2k代k,得x N=.又=2,所以x N=2(x M﹣x N),得2x M=3x N,故2×==3×,又k>0,解得k=.所以直线BM的方程为y=x﹣19.(16分)设数列{a n}满足a=a n+1a n﹣1+λ(a2﹣a1)2,其中n≥2,且n∈N,λ为常数.(1)若{a n}是等差数列,且公差d≠0,求λ的值;(2)若a1=1,a2=2,a3=4,且存在r∈[3,7],使得m•a n≥n﹣r对任意的n∈N*都成立,求m的最小值;(3)若λ≠0,且数列{a n}不是常数列,如果存在正整数T,使得a n+T=a n对任意的n∈N*均成立.求所有满足条件的数列{a n}中T的最小值.【试题解答】解:(1)由题意,可得a=(a n+d)(a n﹣d)+λd2,化简得(λ﹣1)d2=0,又d≠0,所以λ=1.(2)将a1=1,a2=2,a3=4,代入条件,可得4=1×4+λ,解得λ=0,所以a=a na n﹣1,所以数列{a n}是首项为1,公比q=2的等比数列,+1所以a n=2n﹣1.欲存在r∈[3,7],使得m•2n﹣1≥n﹣r,即r≥n﹣m•2n﹣1对任意n∈N*都成立,则7≥n﹣m•2n﹣1,所以m≥对任意n∈N*都成立.令b n=,则b n+1﹣b n=﹣=,所以当n>8时,b n+1<b n;当n=8时,b9=b8;当n<8时,b n+1>b n.所以b n的最大值为b9=b8=,所以m的最小值为;(3)因为数列{a n}不是常数列,所以T≥2,①若T=2,则a n+2=a n恒成立,从而a3=a1,a4=a2,所以,所以λ(a2﹣a1)2=0,又λ≠0,所以a2=a1,可得{a n}是常数列,矛盾.所以T=2不合题意.②若T=3,取a n=(*),满足a n+3=a n恒成立.由a22=a1a3+λ(a2﹣a1)2,得λ=7.则条件式变为a n2=a n+1a n﹣1+7.由22=1×(﹣3)+7,知a3k﹣12=a3k﹣2a3k+λ(a2﹣a1)2;由(﹣3)2=2×1+7,知a3k2=a3k﹣1a3k+1+λ(a2﹣a1)2;由12=2×(﹣3)+7,知a3k+12=a3k a3k+2+λ(a2﹣a1)2;所以,数列(*)适合题意.所以T的最小值为3.20.(16分)设函数f(x)=lnx,g(x)=ax+(a,b,c∈R).(1)当c=0时,若函数f(x)与g(x)的图象在x=1处有相同的切线,求a,b的值;(2)当b=3﹣a时,若对任意x0∈(1,+∞)和任意a∈(0,3),总存在不相等的正实数x1,x2,使得g(x1)=g(x2)=f(x0),求c的最小值;(3)当a=1时,设函数y=f(x)与y=g(x)的图象交于A(x1,y1),B(x2,y2)(x1<x2)两点.求证:x1x2﹣x2<b<x1x2﹣x1.【试题解答】解:(1)由f(x)=lnx,得f(1)=0,又f′(x)=,所以f′(1)=1,当c=0时,g(x)=ax+,所以g′(x)=a﹣,所以g′(1)=a﹣b,因为函数f(x)与g(x)的图象在x=1处有相同的切线,所以,即,解得a=,b=﹣;(2)当x0>1时,则f(x0)>0,又b=3﹣a,设t=f(x0),则题意可转化为方程ax+﹣c=t(t>0)在(0,+∞)上有相异两实根x1,x2. 即关于x的方程ax2﹣(c+t)x+(3﹣a)=0(t>0)在(0,+∞)上有相异两实根x1,x2.所以,得,所以c>2﹣t对t∈(0,+∞),a∈(0,3)恒成立.因为0<a<3,所以2≥2•=3(当且仅当a=时取等号),又﹣t<0,所以2﹣t的取值范围是(﹣∞,3),所以c≥3.故c的最小值为3.(3)当a=1时,因为函数f(x)与g(x)的图象交于A,B两点,所以,两式相减,得b=x1x2(1﹣),要证明x1x2﹣x2<b<x1x2﹣x1,即证x1x2﹣x2<x1x2(1﹣)<x1x2﹣x1,即证<<,即证1﹣<ln<﹣1令=t,则t>1,此时即证1﹣<lnt<t﹣1.令φ(t)=lnt+﹣1,所以φ′(t)=﹣=>0,所以当t>1时,函数φ(t)单调递增.又φ(1)=0,所以φ(t)=lnt+﹣1>0,即1﹣<lnt成立;再令m(t)=lnt﹣t+1,所以m′(t)=﹣1=<0,所以当t>1时,函数m(t)单调递减,又m(1)=0,所以m(t)=lnt﹣t+1<0,即lnt<t﹣1也成立.综上所述,实数x1,x2满足x1x2﹣x2<b<x1x2﹣x1.[选做题](在21.22.23.24四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内)[选修4-1:几何证明选讲]图21.(10分)如图,已知AB为⊙O的直径,直线DE与⊙O相切于点E,AD垂直DE于点D.若DE=4,求切点E到直径AB的距离EF.【试题解答】解:如图,连接AE,OE,因为直线DE与⊙O相切于点E,所以DE⊥OE,又因为AD⊥DE于D,所以AD∥OE,所以∠DAE=∠OEA,①在⊙O中,OE=OA,所以∠OEA=∠OAE,②…(5分)由①②得∠DAE=∠OAE,即∠DAE=∠FAE,又∠ADE=∠AFE,AE=AE,所以△ADE≌△AFE,所以DE=FE,又DE=4,所以FE=4,即E到直径AB的距离为4.…(10分)[选修4-2:矩阵与变换]22.(10分)已知矩阵M=,求圆x2+y2=1在矩阵M的变换下所得的曲线方程.【试题解答】解:设P(x0,y0)是圆x2+y2=1上任意一点,则=1,设点P(x0,y0)在矩阵M对应的变换下所得的点为Q(x,y),则=,即,解得,…(5分)代入=1,得=1,∴圆x2+y2=1在矩阵M的变换下所得的曲线方程为=1.…(10分)[选修4-4:坐标系与参数方程]23.在极坐标系中,直线ρcos(θ+)=1与曲线ρ=r(r>0)相切,求r的值.【试题解答】解:直线ρcos(θ+)=1,转化为:,曲线ρ=r(r>0)转化为:x2+y2=r2,由于直线和圆相切,则:圆心到直线的距离d=.所以r=1.[选修4-5:不等式选讲]24.已知实数x,y满足x2+3y2=1,求当x+y取最大值时x的值.【试题解答】解:由柯西不等式,得[x2+()2][12+()2]≥(x•1+)2,即≥(x+y)2.而x2+3y2=1,所以(x+y)2,所以﹣,…(5分)由,得,所以当且仅当x=,y=时,(x+y)max=.所以当x+y取最大值时x值为.…(10分)25.(10分)如图,四棱锥P﹣ABCD的底面ABCD是菱形,AC与BD交于点O,OP⊥底面ABCD,点M为PC中点,AC=4,BD=2,OP=4.(1)求直线AP与BM所成角的余弦值;(2)求平面ABM与平面PAC所成锐二面角的余弦值.【试题解答】解:(1)因为ABCD是菱形,所以AC⊥BD.又OP⊥底面ABCD,以O为原点,直线OA,OB,OP分别为x轴,y轴,z轴,建立如图所示空间直角坐标系.则A(2,0,0),B(0,1,0),P(0,0,4),C(﹣2,0,0),M(﹣1,0,2).=(﹣2,0,4),=(01,﹣1,2),cos<,>===.故直线AP与BM所成角的余弦值为.…(5分)(2)=(﹣2,1,0),=(﹣1,﹣1,2).设平面ABM的一个法向量为=(x,y,z),则,令x=2,得=(2,4,3).又平面PAC的一个法向量为=(0,1,0),∴cos<>===.故平面ABM与平面PAC所成锐二面角的余弦值为.…(10分)26.(10分)已知n∈N*,nf(n)=C n0C n1+2C n1C n2+…+nC n n﹣1C n n.(1)求f(1),f(2),f(3)的值;(2)试猜想f(n)的表达式(用一个组合数表示),并证明你的猜想.【试题解答】解:(1)由条件,nf(n)=C C C C①,在①中令n=1,得f(1)=1.在①中令n=2,得2f(2)=6,得f(2)=3.在①中令n=3,得3f(3)=30,故f(3)=10.(2)猜想f(n)=.要证猜想成立,只要证等式n=•+2•+…+n•成立.由(1+x)n=+x+x2+…+x n①,两边同时对x求导数,可得n(1+x)n﹣1=+2x+3x2+n x n﹣1②,把等式①和②相乘,可得n(1+x)2n﹣1=(+x+x2+…+x n)•(+2x+3x2+n x n﹣1 ) ③.等式左边x n的系数为n,等式右边x n的系数为•+•2+•3+…+n•n=•+2•+3•+…+n•=C C C C,根据等式③恒成立,可得n=C C C C.故f(n)=成立.。
2018年高考数学江苏卷(含答案与解析)

数学试卷 第1页(共42页) 数学试卷 第2页(共42页)绝密★启用前江苏省2018年普通高等学校招生全国统一考试数 学本试卷共160分.考试时长120分钟.参考公式:锥形的体积公式13V Sh =,其中S 是椎体的底面积,h 是椎体的高。
一、填空题:本大题共14小题,每小题5分,共计70分. 1.已知集合{0,1,2,8}A =,{1,1,6,8}B =-,那么AB = .2.若复数z 满足i 12i z =+,其中i 是虚数单位,则z 的实部为 .3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 .4.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 .5.函数()f x =的定义域为 .6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 .7.已知函数ππsin(2)()22y x ϕϕ=+-<<的图象关于直线π3x =对称,则ϕ的值是 .8.在平面直角坐标系xOy 中,若双曲线22221(0)x y a b a b-=>>0,的右焦点(,0)F c 到一条渐近线的距离为2,则其离心率的值是 . 9.函数()f x 满足(4)()()f x f x x +=∈R ,且在区间(2,2]-上,()cos (2)2102x x f x x x π⎧⎪⎪=⎨⎪+⎪⎩0<≤,(-2<≤),,则((15))f f 的值为 . 10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .11.若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点,则()f x 在[1,1]-上的最大值与最小值的和为 .12.在平面直角坐标系xOy 中,A 为直线:2l y x =上在第一象限内的点,点(5,0)B ,以AB 为直径的圆C 与直线l 交于另一点D .若0AB CD =,则点A 的横坐标为 .13.在ABC △中,角A ,B ,C 所对应的边分别为a ,b ,c ,120ABC ∠=,ABC ∠的平分线交AC 于点D ,且1BD =,则4a c +的最小值为 .14.已知集合{21,}A x x n n ==-∈*N ,{2,}n B x x n ==∈*N .将AB 的所有元素从小到大依次排列构成一个数列{}n a ,记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为 .毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共42页) 数学试卷 第4页(共42页)二、解答题:本大题共6小题,共计90分,解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分14分)在平行六面体1111ABCD A B C D -中,1AA AB =,111AB B C ⊥. 求证:(Ⅰ)AB ∥平面11A B C ; (Ⅱ)平面11ABB A ⊥平面1A BC .16.(本小题满分14分)已知α,β为锐角,4tan 3α=,cos()αβ+=.(Ⅰ)求cos2α的值; (Ⅱ)求tan()αβ-的值.数学试卷 第5页(共42页) 数学试卷 第6页(共42页)17.(本小题满分14分)某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧MPN (P 为此圆弧的中点)和线段MN 构成,已知圆O 的半径为40米,点P 到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD ,大棚Ⅱ内的地块形状为CDP △,要求点A ,B 均在线段MN 上,C ,D 均在圆弧上.设OC 与MN 所成的角为θ.(Ⅰ)用θ分别表示矩形ABCD 和CDP △的面积,并确定sin θ的取值范围; (Ⅱ)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C过点1)2,焦点1(F,2F ,圆O 的直径为12F F .(Ⅰ)求椭圆C 及圆O 的方程;(Ⅱ)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; ②直线l 与椭圆C 交于A ,B 两点.若OAB △,求直线l 的方程.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共42页) 数学试卷 第8页(共42页)19.(本小题满分16分)记()f x ',()g x '分别为函数()f x ,()g x 的导函数.若存在0x ∈R ,满足00()()f x g x =且00()()f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.(Ⅰ)证明:函数()f x x =与2()22g x x x =+-不存在“S 点”; (Ⅱ)若函数2()1f x ax =-与()ln g x x =存在“S 点”,求实数a 的值;(Ⅲ)已知函数2()f x x a =-+,e ()xb g x x=.对任意0a >,判断是否存在0b >,使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”,并说明理由.20.(本小题满分16分)设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项1b ,公比为q 的等比数列. (Ⅰ)设10a =,11b =,2q =若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围; (Ⅱ)若110a b =>,m ∈*N,q ∈,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,1n m =+…,均成立,并求d 的取值范围(用1b ,m ,q 表示).数学试卷 第9页(共42页) 数学试卷 第10页(共42页)数学Ⅱ(附加题)本试卷均为非选择题(第21题~第23题). 本卷满分40分,考试时间为30分钟.21.【选做题】本题包括A ,B ,C ,D 四小题,请选定其中两小题并作答...........,若多做,则按作答的前两小题评分、解答时应写出文字说明、证明过程或演算步骤。
2018年数学真题及解析_2018年江苏省高考数学试卷

2018年江苏省高考数学试卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5.00分)已知集合A={0,1,2,8},B={﹣1,1,6,8},那么A∩B=.2.(5.00分)若复数z满足i•z=1+2i,其中i是虚数单位,则z的实部为.3.(5.00分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为.4.(5.00分)一个算法的伪代码如图所示,执行此算法,最后输出的S的值为.5.(5.00分)函数f(x)=的定义域为.6.(5.00分)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为.7.(5.00分)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.8.(5.00分)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为.9.(5.00分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x)=,则f(f(15))的值为.10.(5.00分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.11.(5.00分)若函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[﹣1,1]上的最大值与最小值的和为.12.(5.00分)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为.13.(5.00分)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.14.(5.00分)已知集合A={x|x=2n﹣1,n∈N*},B={x|x=2n,n∈N*}.将A∪B 的所有元素从小到大依次排列构成一个数列{a n},记S n为数列{a n}的前n项和,成立的n的最小值为.则使得S n>12a n+1二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14.00分)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.16.(14.00分)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.17.(14.00分)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D 均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(16.00分)如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.19.(16.00分)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x﹣2不存在“S点”;(2)若函数f(x)=ax2﹣1与g(x)=lnx存在“S点”,求实数a的值;(3)已知函数f(x)=﹣x2+a,g(x)=.对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.20.(16.00分)设{a n}是首项为a1,公差为d的等差数列,{b n}是首项为b1,公比为q的等比数列.(1)设a1=0,b1=1,q=2,若|a n﹣b n|≤b1对n=1,2,3,4均成立,求d的取值范围;(2)若a1=b1>0,m∈N*,q∈(1,],证明:存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,并求d的取值范围(用b1,m,q表示).数学Ⅱ(附加题)【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.(10.00分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若PC=2,求BC的长.B.[选修4-2:矩阵与变换](本小题满分10分)22.(10.00分)已知矩阵A=.(1)求A的逆矩阵A﹣1;(2)若点P在矩阵A对应的变换作用下得到点P′(3,1),求点P的坐标.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的方程为ρsin(﹣θ)=2,曲线C的方程为ρ=4cosθ,求直线l被曲线C截得的弦长.D.[选修4-5:不等式选讲](本小题满分0分)24.若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.25.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.26.设n∈N*,对1,2,……,n的一个排列i1i2……i n,如果当s<t时,有i s>i t,则称(i s,i t)是排列i1i2……i n的一个逆序,排列i1i2……i n的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n(k)为1,2,…,n的所有排列中逆序数为k的全部排列的个数.(1)求f3(2),f4(2)的值;(2)求f n(2)(n≥5)的表达式(用n表示).2018年江苏省高考数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5.00分)已知集合A={0,1,2,8},B={﹣1,1,6,8},那么A∩B={1,8} .【分析】直接利用交集运算得答案.【解答】解:∵A={0,1,2,8},B={﹣1,1,6,8},∴A∩B={0,1,2,8}∩{﹣1,1,6,8}={1,8},故答案为:{1,8}.【点评】本题考查交集及其运算,是基础的计算题.2.(5.00分)若复数z满足i•z=1+2i,其中i是虚数单位,则z的实部为2.【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案.【解答】解:由i•z=1+2i,得z=,∴z的实部为2.故答案为:2.【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.(5.00分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为90.【分析】根据茎叶图中的数据计算它们的平均数即可.【解答】解:根据茎叶图中的数据知,这5位裁判打出的分数为89、89、90、91、91,它们的平均数为×(89+89+90+91+91)=90.故答案为:90.【点评】本题考查了利用茎叶图计算平均数的问题,是基础题.4.(5.00分)一个算法的伪代码如图所示,执行此算法,最后输出的S的值为8.【分析】模拟程序的运行过程,即可得出程序运行后输出的S值.【解答】解:模拟程序的运行过程如下;I=1,S=1,I=3,S=2,I=5,S=4,I=7,S=8,此时不满足循环条件,则输出S=8.故答案为:8.【点评】本题考查了程序语言的应用问题,模拟程序的运行过程是解题的常用方法.5.(5.00分)函数f(x)=的定义域为[2,+∞).【分析】解关于对数函数的不等式,求出x的范围即可.【解答】解:由题意得:≥1,解得:x≥2,∴函数f(x)的定义域是[2,+∞).故答案为:[2,+∞).【点评】本题考查了对数函数的性质,考查求函数的定义域问题,是一道基础题.6.(5.00分)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为0.3.【分析】(适合理科生)从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,根据概率公式计算即可,(适合文科生),设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,根据概率公式计算即可【解答】解:(适合理科生)从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,故选中的2人都是女同学的概率P==0.3,(适合文科生),设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,故选中的2人都是女同学的概率P==0.3,故答案为:0.3【点评】本题考查了古典概率的问题,采用排列组合或一一列举法,属于基础题.7.(5.00分)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.【分析】根据正弦函数的对称性建立方程关系进行求解即可.【解答】解:∵y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,∴2×+φ=kπ+,k∈Z,即φ=kπ﹣,∵﹣φ<,∴当k=0时,φ=﹣,故答案为:﹣.【点评】本题主要考查三角函数的图象和性质,利用正弦函数的对称性建立方程关系是解决本题的关键.8.(5.00分)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为2.【分析】利用双曲线的简单性质,以及点到直线的距离列出方程,转化求解即可.【解答】解:双曲线=1(a>0,b>0)的右焦点F(c,0)到一条渐近线y=x的距离为c,可得:=b=,可得,即c=2a,所以双曲线的离心率为:e=.故答案为:2.【点评】本题考查双曲线的简单性质的应用,考查转化思想以及计算能力.9.(5.00分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x)=,则f(f(15))的值为.【分析】根据函数的周期性,进行转化求解即可.【解答】解:由f(x+4)=f(x)得函数是周期为4的周期函数,则f(15)=f(16﹣1)=f(﹣1)=|﹣1+|=,f()=cos()=cos=,即f(f(15))=,故答案为:【点评】本题主要考查函数值的计算,根据函数的周期性结合分段函数的表达式利用转化法是解决本题的关键.10.(5.00分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【分析】求出多面体中的四边形的面积,然后利用体积公式求解即可.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:2×=.故答案为:.【点评】本题考查几何体的体积的求法,考查空间想象能力以及计算能力.11.(5.00分)若函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[﹣1,1]上的最大值与最小值的和为﹣3.【分析】推导出f′(x)=2x(3x﹣a),x∈(0,+∞),当a≤0时,f′(x)=2x(3x ﹣a)>0,f(0)=1,f(x)在(0,+∞)上没有零点;当a>0时,f′(x)=2x(3x﹣a)>0的解为x>,f(x)在(0,)上递减,在(,+∞)递增,由f(x)只有一个零点,解得a=3,从而f(x)=2x3﹣3x2+1,f′(x)=6x(x﹣1),x ∈[﹣1,1],利用导数性质能求出f(x)在[﹣1,1]上的最大值与最小值的和.【解答】解:∵函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,∴f′(x)=2x(3x﹣a),x∈(0,+∞),①当a≤0时,f′(x)=2x(3x﹣a)>0,函数f(x)在(0,+∞)上单调递增,f(0)=1,f(x)在(0,+∞)上没有零点,舍去;②当a>0时,f′(x)=2x(3x﹣a)>0的解为x>,∴f(x)在(0,)上递减,在(,+∞)递增,又f(x)只有一个零点,∴f()=﹣+1=0,解得a=3,f(x)=2x3﹣3x2+1,f′(x)=6x(x﹣1),x∈[﹣1,1],f′(x)>0的解集为(﹣1,0),f(x)在(﹣1,0)上递增,在(0,1)上递减,f(﹣1)=﹣4,f(0)=1,f(1)=0,∴f(x)min=f(﹣1)=﹣4,f(x)max=f(0)=1,∴f(x)在[﹣1,1]上的最大值与最小值的和为:f(x)max+f(x)min=﹣4+1=﹣3.【点评】本题考查函数的单调性、最值,导数的运算及其应用,同时考查逻辑思维能力和综合应用能力,是中档题.12.(5.00分)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为3.【分析】设A(a,2a),a>0,求出C的坐标,得到圆C的方程,联立直线方程与圆的方程,求得D的坐标,结合=0求得a值得答案.【解答】解:设A(a,2a),a>0,∵B(5,0),∴C(,a),则圆C的方程为(x﹣5)(x﹣a)+y(y﹣2a)=0.联立,解得D(1,2).∴=.解得:a=3或a=﹣1.又a>0,∴a=3.即A的横坐标为3.故答案为:3.【点评】本题考查平面向量的数量积运算,考查圆的方程的求法,是中档题.13.(5.00分)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为9.【分析】根据面积关系建立方程关系,结合基本不等式1的代换进行求解即可.【解答】解:由题意得acsin120°=asin60°+csin60°,即ac=a+c,得+=1,得4a+c=(4a+c)(+)=++5≥2+5=4+5=9,当且仅当=,即c=2a时,取等号,故答案为:9.【点评】本题主要考查基本不等式的应用,利用1的代换结合基本不等式是解决本题的关键.14.(5.00分)已知集合A={x|x=2n﹣1,n∈N*},B={x|x=2n,n∈N*}.将A∪B 的所有元素从小到大依次排列构成一个数列{a n},记S n为数列{a n}的前n项和,则使得S n>12a n成立的n的最小值为27.+1【分析】采用列举法,验证n=26,n=27即可.【解答】解:利用列举法可得:当n=26时,A∪B中的所有元素从小到大依次排列,构成一个数列{a n},所以数列{a n}的前26项分别1,3,5,7,9,11,13,15,17,19,21,23.25,…41,2,4,8,16,32.S26=,a27=43,⇒12a27=516,不符合题意.当n=27时,A∪B中的所有元素从小到大依次排列,构成一个数列{a n},所以数列{a n}的前26项分别1,3,5,7,9,11,13,15,17,19,21,23.25,…41,43,2,4,8,16,32.S27==546,a28=45⇒12a28=540,符合题意,故答案为:27.【点评】本题考查了集合、数列的求和,属于中档题.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14.00分)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.【分析】(1)由⇒AB∥平面A1B1C;(2)可得四边形ABB1A1是菱形,AB1⊥A1B,由AB1⊥B1C1⇒AB1⊥BC⇒AB1⊥面A1BC,⇒平面ABB1A1⊥平面A1BC.【解答】证明:(1)平行六面体ABCD﹣A1B1C1D1中,AB∥A1B1,AB∥A1B1,AB⊄平面A1B1C,A1B1⊂∥平面A1B1C⇒AB∥平面A1B1C;(2)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,⇒四边形ABB1A1是菱形,⊥AB1⊥A1B.在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1⇒AB1⊥BC.∴⇒AB1⊥面A1BC,且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC.【点评】本题考查了平行六面体的性质,及空间线面平行、面面垂直的判定,属于中档题.16.(14.00分)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.【分析】(1)由已知结合平方关系求得sinα,cosα的值,再由倍角公式得cos2α的值;(2)由(1)求得tan2α,再由cos(α+β)=﹣求得tan(α+β),利用tan(α﹣β)=tan[2α﹣(α+β)],展开两角差的正切求解.【解答】解:(1)由,解得,∴cos2α=;(2)由(1)得,sin2,则tan2α=.∵α,β∈(0,),∴α+β∈(0,π),∴sin(α+β)==.则tan(α+β)=.∴tan(α﹣β)=tan[2α﹣(α+β)]==.【点评】本题考查三角函数的恒等变换及化简求值,考查同角三角函数基本关系式的应用,是中档题.17.(14.00分)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D 均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.【分析】(1)根据图形计算矩形ABCD和△CDP的面积,求出sinθ的取值范围;(2)根据题意求出年总产值y的解析式,构造函数f(θ),利用导数求f(θ)的最大值,即可得出θ为何值时年总产值最大.【解答】解:(1)S=(40sinθ+10)•80cosθ矩形ABCD=800(4sinθcosθ+cosθ),S△CDP=•80cosθ(40﹣40sinθ)=1600(cosθ﹣cosθsinθ),当B、N重合时,θ最小,此时sinθ=;当C、P重合时,θ最大,此时sinθ=1,∴sinθ的取值范围是[,1);(2)设年总产值为y,甲种蔬菜单位面积年产值为4t,乙种蔬菜单位面积年产值为3t,则y=3200t(4sinθcosθ+cosθ)+4800t(cosθ﹣cosθsinθ)=8000t(sinθcosθ+cosθ),其中sinθ∈[,1);设f(θ)=sinθcosθ+cosθ,则f′(θ)=cos2θ﹣sin2θ﹣sinθ=﹣2sin2θ﹣sinθ+1;令f′(θ)=0,解得sinθ=,此时θ=,cosθ=;当sinθ∈[,)时,f′(θ)>0,f(θ)单调递增;当sinθ∈[,1)时,f′(θ)<0,f(θ)单调递减;∴θ=时,f(θ)取得最大值,即总产值y最大.=800(4sinθcosθ+cosθ),答:(1)S矩形ABCDS△CDP=1600(cosθ﹣cosθsinθ),sinθ∈[,1);θ=时总产值y最大.【点评】本题考查了解三角形的应用问题,也考查了构造函数以及利用导数求函数的最值问题,是中档题.18.(16.00分)如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.【分析】(1)由题意可得.,又a2﹣b2=c2=3,解得a=2,b=1即可.(2)①可设直线l的方程为y=kx+m,(k<0,m>0).可得.由,可得(4k2+1)x2+8kmx+4m2﹣4=0,△=(8km)2﹣4(4k2+1)(4m2﹣4)=0,解得k=﹣,m=3.即可②设A(x1,y1),B(x2,y2),联立直线与椭圆方程得(4k2+1)x2+8kmx+4m2﹣4=0,O到直线l的距离d=,|AB|=|x2﹣x1|=,△OAB的面积为S===,解得k=﹣,(正值舍去),m=3.即可【解答】解:(1)由题意可设椭圆方程为,∵焦点F1(﹣,0),F2(,0),∴.∵∴,又a2﹣b2=c2=3,解得a=2,b=1.∴椭圆C的方程为:,圆O的方程为:x2+y2=3.(2)①可知直线l与圆O相切,也与椭圆C,且切点在第一象限,∴可设直线l的方程为y=kx+m,(k<0,m>0).由圆心(0,0)到直线l的距离等于圆半径,可得.由,可得(4k2+1)x2+8kmx+4m2﹣4=0,△=(8km)2﹣4(4k2+1)(4m2﹣4)=0,可得m2=4k2+1,∴3k2+3=4k2+1,结合k<0,m>0,解得k=﹣,m=3.将k=﹣,m=3代入可得,解得x=,y=1,故点P的坐标为(.②设A(x1,y1),B(x2,y2),由⇒k<﹣.联立直线与椭圆方程得(4k2+1)x2+8kmx+4m2﹣4=0,|x2﹣x1|==,O到直线l的距离d=,|AB|=|x2﹣x1|=,△OAB的面积为S===,解得k=﹣,(正值舍去),m=3.∴y=﹣为所求.【点评】本题考查了椭圆的方程,直线与圆、椭圆的位置关系,属于中档题.19.(16.00分)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x﹣2不存在“S点”;(2)若函数f(x)=ax2﹣1与g(x)=lnx存在“S点”,求实数a的值;(3)已知函数f(x)=﹣x2+a,g(x)=.对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.【分析】(1)根据“S点”的定义解两个方程,判断方程是否有解即可;(2)根据“S点”的定义解两个方程即可;(3)分别求出两个函数的导数,结合两个方程之间的关系进行求解判断即可.【解答】解:(1)证明:f′(x)=1,g′(x)=2x+2,则由定义得,得方程无解,则f(x)=x与g(x)=x2+2x﹣2不存在“S 点”;(2)f′(x)=2ax,g′(x)=,x>0,由f′(x)=g′(x)得=2ax,得x=,f()=﹣=g()=﹣lna2,得a=;(3)f′(x)=﹣2x,g′(x)=,(x≠0),由f′(x0)=g′(x0),假设b>0,得b=﹣>0,得0<x0<1,由f(x0)=g(x0),得﹣x02+a==﹣,得a=x02﹣,令h(x)=x2﹣﹣a=,(a>0,0<x<1),设m(x)=﹣x3+3x2+ax﹣a,(a>0,0<x<1),则m(0)=﹣a<0,m(1)=2>0,得m(0)m(1)<0,又m(x)的图象在(0,1)上连续不断,则m(x)在(0,1)上有零点,则h(x)在(0,1)上有零点,则存在b>0,使f(x)与g(x)在区间(0,+∞)内存在“S”点.【点评】本题主要考查导数的应用,根据条件建立两个方程组,判断方程组是否有解是解决本题的关键.20.(16.00分)设{a n}是首项为a1,公差为d的等差数列,{b n}是首项为b1,公比为q的等比数列.(1)设a1=0,b1=1,q=2,若|a n﹣b n|≤b1对n=1,2,3,4均成立,求d的取值范围;(2)若a1=b1>0,m∈N*,q∈(1,],证明:存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,并求d的取值范围(用b1,m,q表示).【分析】(1)根据等比数列和等差数列的通项公式,解不等式组即可;(2)根据数列和不等式的关系,利用不等式的关系构造新数列和函数,判断数列和函数的单调性和性质进行求解即可.【解答】解:(1)由题意可知|a n﹣b n|≤1对任意n=1,2,3,4均成立,∵a1=0,q=2,∴,解得.即≤d≤.证明:(2)∵a n=a1+(n﹣1)d,b n=b1•q n﹣1,若存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,则|b1+(n﹣1)d﹣b1•q n﹣1|≤b1,(n=2,3,…,m+1),即b1≤d≤,(n=2,3,…,m+1),∵q∈(1,],∴则1<q n﹣1≤q m≤2,(n=2,3,…,m+1),∴b1≤0,>0,因此取d=0时,|a n﹣b n|≤b1对n=2,3,…,m+1均成立,下面讨论数列{}的最大值和数列{}的最小值,①当2≤n≤m时,﹣==,当1<q≤时,有q n≤q m≤2,从而n(q n﹣q n﹣1)﹣q n+2>0,因此当2≤n≤m+1时,数列{}单调递增,故数列{}的最大值为.②设f(x)=2x(1﹣x),当x>0时,f′(x)=(ln2﹣1﹣xln2)2x<0,∴f(x)单调递减,从而f(x)<f(0)=1,当2≤n≤m时,=≤(1﹣)=f()<1,因此当2≤n≤m+1时,数列{}单调递递减,故数列{}的最小值为,∴d的取值范围是d∈[,].【点评】本题主要考查等比数列和等差数列以及不等式的综合应用,考查学生的运算能力,综合性较强,难度较大.数学Ⅱ(附加题)【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.(10.00分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若PC=2,求BC的长.【分析】连接OC,由题意,CP为圆O的切线,得到垂直关系,由线段长度及勾股定理,可以得到PO的长,即可判断△COB是等边三角形,BC的长.【解答】解:连接OC,因为PC为切线且切点为C,所以OC⊥CP.因为圆O的半径为2,,所以BO=OC=2,,所以,所以∠COP=60°,所以△COB为等边三角形,所以BC=BO=2.【点评】本题主要考查圆与直线的位置关系,切线的应用,考查发现问题解决问题的能力.B.[选修4-2:矩阵与变换](本小题满分10分)22.(10.00分)已知矩阵A=.(1)求A的逆矩阵A﹣1;(2)若点P在矩阵A对应的变换作用下得到点P′(3,1),求点P的坐标.【分析】(1)矩阵A=,求出det(A)=1≠0,A可逆,然后求解A的逆矩阵A﹣1.(2)设P(x,y),通过•=,求出=,即可得到点P的坐标.【解答】解:(1)矩阵A=,det(A)=2×2﹣1×3=1≠0,所以A可逆,从而:A的逆矩阵A﹣1=.(2)设P(x,y),则•=,所以=A﹣1=,因此点P的坐标为(3,﹣1).【点评】本题矩阵与逆矩阵的关系,逆矩阵的求法,考查转化思想的应用,是基本知识的考查.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的方程为ρsin(﹣θ)=2,曲线C的方程为ρ=4cosθ,求直线l被曲线C截得的弦长.【分析】将直线l、曲线C的极坐标方程利用互化公式可得直角坐标方程,利用直线与圆的相交弦长公式即可求解.【解答】解:∵曲线C的方程为ρ=4cosθ,∴ρ2=4ρcosθ,⇒x2+y2=4x,∴曲线C是圆心为C(2,0),半径为r=2得圆.∵直线l的方程为ρsin(﹣θ)=2,∴﹣=2,∴直线l的普通方程为:x﹣y=4.圆心C到直线l的距离为d=,∴直线l被曲线C截得的弦长为2.【点评】本题考查了极坐标方程化为直角坐标方程、直线与圆的相交弦长关系、点到直线的距离公式,属于中档题.D.[选修4-5:不等式选讲](本小题满分0分)24.若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.【分析】根据柯西不等式进行证明即可.【解答】解:由柯西不等式得(x2+y2+z2)(12+22+22)≥(x+2y+2z)2,∵x+2y+2z=6,∴x2+y2+z2≥4是当且仅当时,不等式取等号,此时x=,y=,z=,∴x2+y2+z2的最小值为4【点评】本题主要考查不等式的证明,利用柯西不等式是解决本题的关键.,【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.25.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.【分析】设AC,A1C1的中点分别为O,O1,以{}为基底,建立空间直角坐标系O﹣xyz,(1)由|cos|=可得异面直线BP与AC1所成角的余弦值;(2)求得平面AQC1的一个法向量为,设直线CC1与平面AQC1所成角的正弦值为θ,可得sinθ=|cos|=,即可得直线CC1与平面AQC1所成角的正弦值.【解答】解:如图,在正三棱柱ABC﹣A1B1C1中,设AC,A1C1的中点分别为O,O1,则,OB⊥OC,OO1⊥OC,OO1⊥OB,故以{}为基底,建立空间直角坐标系O﹣xyz,∵AB=AA1=2,A(0,﹣1,0),B(,0,0),C(0,1,0),A1(0,﹣1,2),B1(,0,2),C1(0,1,2).(1)点P为A1B1的中点.∴,∴,.|cos|===.∴异面直线BP与AC1所成角的余弦值为:;(2)∵Q为BC的中点.∴Q()∴,,设平面AQC1的一个法向量为=(x,y,z),由,可取=(,﹣1,1),设直线CC1与平面AQC1所成角的正弦值为θ,sinθ=|cos|==,∴直线CC1与平面AQC1所成角的正弦值为.【点评】本题考查了向量法求空间角,属于中档题.26.设n ∈N *,对1,2,……,n 的一个排列i 1i 2……i n ,如果当s <t 时,有i s >i t ,则称(i s ,i t )是排列i 1i 2……i n 的一个逆序,排列i 1i 2……i n 的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n (k )为1,2,…,n 的所有排列中逆序数为k 的全部排列的个数.(1)求f 3(2),f 4(2)的值;(2)求f n (2)(n ≥5)的表达式(用n 表示).【分析】(1)由题意直接求得f 3(2)的值,对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置,由此可得f 4(2)的值;(2)对一般的n (n ≥4)的情形,可知逆序数为0的排列只有一个,逆序数为1的排列只能是将排列12…n 中的任意相邻两个数字调换位置得到的排列,f n (1)=n ﹣1.为计算f n +1(2),当1,2,…,n 的排列及其逆序数确定后,将n +1添加进原排列,n +1在新排列中的位置只能是最后三个位置,可得f n +1(2)=f n (2)+f n (1)+f n (0)=f n (2)+n ,则当n ≥5时,f n (2)=[f n (2)﹣f n ﹣1(2)]+[f n ﹣1(2)﹣f n ﹣2(2)]+…+[f 5(2)﹣f 4(2)]+f 4(2),则f n (2)(n ≥5)的表达式可求.【解答】解:(1)记μ(abc )为排列abc 得逆序数,对1,2,3的所有排列,有μ(123)=0,μ(132)=1,μ(231)=2,μ(321)=3,∴f3(0)=1,f3(1)=f3(2)=2,对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置.因此,f4(2)=f3(2)+f3(1)+f3(0)=5;(2)对一般的n(n≥4)的情形,逆序数为0的排列只有一个:12…n,∴f n(0)=1.逆序数为1的排列只能是将排列12…n中的任意相邻两个数字调换位置得到的排列,f n(1)=n﹣1.为计算f n+1(2),当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排列,n+1在新排列中的位置只能是最后三个位置.因此,f n+1(2)=f n(2)+f n(1)+f n(0)=f n(2)+n.当n≥5时,f n(2)=[f n(2)﹣f n﹣1(2)]+[f n﹣1(2)﹣f n﹣2(2)]+…+[f5(2)﹣f4(2)]+f4(2)=(n﹣1)+(n﹣2)+…+4+f4(2)=.因此,当n≥5时,f n(2)=.【点评】本题主要考查计数原理、排列等基础知识,考查运算求解能力和推理论证能力,是中档题.。
2018年江苏省苏州市高考数学一模试卷

2018年江苏省苏州市高考数学一模试卷一、填空题:本大题共14个小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1. 已知集合A={−1, 1},B={−3, 0, 1},则集合A∩B=________.【答案】{1}【考点】交集及其运算【解析】根据交集的定义写出集合A∩B.【解答】解:集合A={−1, 1},B={−3, 0, 1},则集合A∩B={1}.故答案为:{1}.2. 已知复数z满足z⋅i=3−4i(i为虚数单位),则|z|=________.【答案】5【考点】复数的模复数代数形式的乘除运算【解析】z⋅i=3−4i(i为虚数单位),可得z⋅i⋅(−i)=−i(3−4i),化简利用模的计算公式即可得出.【解答】解:∵z⋅i=3−4i(i为虚数单位),∴z⋅i⋅(−i)=−i(3−4i),则z=−4−3i,则|z|=√(−4)2+(−3)2=5.故答案为:5.3. 双曲线x24−y23=1的渐进线方程是________.【答案】√3x±2y=0【考点】双曲线的渐近线【解析】由x24−y23=0,可得双曲线x24−y23=1的渐近线方程【解答】解:由x24−y23=1,双曲线x24−y23=1的渐近线方程为y=±bax=±√32x,即√3x±2y=0.故答案为:√3x±2y=0.4. 某中学共有1800人,其中高二年级的人数为600.现用分层抽样的方法在全校抽取n 人,其中高二年级被抽取的人数为21,则n=________.【答案】63【考点】分层抽样方法【解析】根据分层抽样的定义建立比例关系即可得到结论.【解答】解:∵高二年级被抽取的人数为21,∴21600=n1800,得n=63,故答案为:63.5. 将一颗质地均匀的正四面体骰子(每个面上分别写有数字1,2,3,4)先后抛掷2次,观察其朝下一面的数字,则两次数字之和等于6的概率为________.【答案】316【考点】列举法计算基本事件数及事件发生的概率古典概型及其概率计算公式【解析】基本事件总数n=4×4=16,利用列举法求出两次数字之和等于6包含的基本事件个数,由此能求出两次数字之和等于6的概率.【解答】解:将一颗质地均匀的正四面体骰子(每个面上分别写有数字1,2,3,4)先后抛掷2次,观察其朝下一面的数字,基本事件总数n=4×4=16.则两次数字之和等于6包含的基本事件有(2, 4),(4, 2),(3, 3),共3个,∴两次数字之和等于6的概率为p=316.故答案为:316.6. 如图是一个算法的流程图,则输出S的值是________.【答案】25【考点】程序框图【解析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,可得答案.【解答】解:当n=1时,满足进行循环的条件,S=1,n=3;当n=3时,满足进行循环的条件,S=4,n=5;当n=5时,满足进行循环的条件,S=9,n=7;当n=7时,满足进行循环的条件,S=16,n=9;当n=9时,满足进行循环的条件,S=25,n=11;当n=11时,不满足进行循环的条件,故输出的S值为25.故答案为:25.7. 若正四棱锥的底面边长为2cm,侧面积为8cm2,则它的体积为________cm3.【答案】4√33【考点】柱体、锥体、台体的体积计算【解析】根据侧面积计算出棱锥的斜高,利用勾股定理计算棱锥的高.【解答】解:设四棱锥为P−ABCD,底面ABCD的中心为O,取CD中点E,连结PE,OE,如图所示,则PE⊥CD,OE=12BC=1cm,∵S侧面=4S△PCD=4×12×CD×PE=8cm2,∴PE=2cm.∴PO=√PE2−OE2=√3cm,∴正四棱锥体积为V=13×S正方形ABCD×PO=13×22×√3=4√33cm3.故答案为:4√33.8. 设S n是等差数列{a n}的前n项和,若a2+a4=2,S2+S4=1,则a10=________.【答案】8【考点】等差数列的前n项和等差数列的通项公式【解析】设等差数列{a n}的公差为d,由a2+a4=2,S2+S4=1,可得2a1+4d=2,6a1+d+4×32d=1,联立解出利用通项公式即可得出.【解答】解:设等差数列{a n}的公差为d,∵a2+a4=2,S2+S4=1,∴2a1+4d=2,6a1+d+4×32d=1,解得:a1=−1,d=1,则a10=−1+9=8.故答案为:8.9. 已知a>0,b>0,且2a +3b=√ab,则ab的最小值是________.【答案】2√6【考点】基本不等式在最值问题中的应用【解析】根据a>0,b>0,即可得出2a +3b≥√6√ab,从而得出√ab≥√6√ab,从而可求出ab的最小值.【解答】解:a>0,b>0;∴√ab=2a +3b≥√6√ab,即√ab≥√6√ab,∴ab≥2√6,∴ab的最小值是2√6.故答案为:2√6.10. 设三角形ABC的内角A,B,C的对边分别为a,b,c,已知tanAtanB =3c−bb,则cosA=________.【答案】13【考点】余弦定理正弦定理同角三角函数间的基本关系【解析】先化切为弦,再由正弦定理及余弦定理求解.【解答】解:由tanAtanB =3c−bb,得sinAcosBcosAsinB=3c−bb,则acosBbcosA =3c−bb,即acosB=(3c−b)cosA,3ccosA=acosB+bcosA=a×a2+c2−b22ac +b×b2+c2−a22bc=c,∴cosA=13.故答案为:13.11. 已知函数f(x)={a −e x ,x <1,x +4x ,x ≥1, 若y =f(x)的最小值是4,则实数的取值范围为________. 【答案】 [e +4, +∞) 【考点】基本不等式在最值问题中的应用 分段函数的应用指数函数单调性的应用 函数的最值及其几何意义 【解析】考虑x <1的函数的单调性,可得f(x)的范围;由基本不等式可得x ≥1时f(x)的最小值,即可得到所求a 的范围. 【解答】解:函数f(x)={a −e x ,x <1,x +4x ,x ≥1, 当x <1时,f(x)=a −e x 递减,可得f(x)>a −e , 由x ≥1时,f(x)=x +4x≥2√x ⋅4x=4,当且仅当x =2时,取得最小值4, 由题意可得a −e ≥4, 即a ≥e +4.故答案为:[e +4, +∞).12. 在△ABC 中,点P 是边AB 的中点,已知|CP →|=√3,|CA →|=4,∠ACB =2π3,则CP →⋅CA →=________.【答案】 6【考点】平面向量数量积的性质及其运算律 向量的三角形法则 【解析】用CA →,CB →表示出CP →,根据CP =√3计算CB ,再计算CP →⋅CA →的值. 【解答】解:∵ 点P 是边AB 的中点, ∴ CP →=12CA →+12CB →,∴ CP →2=14CA →2+12CA →×CB →+14CB →2, ∴ 3=4+12×4×|CB →|×cos 2π3+14×|CB →|2,∴ CA →×CB →=4×2×cos 2π3=−4,∴ CP →⋅CA →=(12CA →+12CB →)×CA →=12CA →2+12CB →×CA →=6.故答案为:6.13. 已知直线l:x −y +2=0与x 轴交于点A ,点P 在直线l 上.圆C :(x −2)2+y 2=2上有且仅有一个点B 满足AB ⊥BP ,则点P 的横坐标的取值集合为________. 【答案】{13,5} 【考点】圆与圆的位置关系及其判定 直线与圆的位置关系 【解析】由题意得A(−2, 0),以AP 为直径的圆与圆C 相切.设P(m, m +2),则以AP 为直径的圆的圆心为(m−22,m+22),半径为√22|m +2|,由外切和内切两种情况进行讨论,能求出m .【解答】解:由题意得A(−2, 0),以AP 为直径的圆与圆C 相切, 设P(m, m +2),则以AP 为直径的圆的圆心为(m−22,m+22),半径为√22|m +2|,外切时,√22|m +2|+√2=√(m−62)2+(m+22)2,解得m =13, 内切时,√22|m +2|−√2=√(m−62)2+(m+22)2,解得m =5.综上,点P 的横坐标的取值集合为{13, 5}. 故答案为:{13, 5}.14. 若二次函数f(x)=ax 2+bx +c(a >0)在区间[1, 2]上有两个不同的零点,则f(1)a的取值范围为________. 【答案】 [0, 1) 【考点】由函数零点求参数的取值范围 二次函数的性质求线性目标函数的最值 简单线性规划 【解析】【解答】解:二次函数f(x)=ax 2+bx +c(a >0)在区间[1, 2]上有两个不同的零点, 则:{1<−b2a <2,f(1)≥0,f(2)≥0,f(−b 2a )<0, 即:{1<−b 2a <2,a +b +c ≥0,4a +2b +c ≥0,4ac−b 24a <0, 设:ba =x,c a =y , 即有:{−4<x <−21+x +y ≥0,4+2x +y ≥0,4y −x 2<0,画出可行域,如图,由A ,B ,C 组成的图形(包括线段AB ,AC ,不包括曲线BC ), 由f(1)a=1+b a +ca =1+x +y ,可得:1+x +y 的最小值为0, 当1+x +y 经过点(−4, 4), 可得:1+x +y =1, 则:1+x +y ∈[0, 1) 故:f(1)a的取值范围是:[0, 1).故答案为:[0, 1).二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答应写出文字说明、证明过程或演算步骤.→→π(1)若角α的终边过点(3, 4),求a→⋅b→的值;(2)若a→ // b→,求锐角α的大小.【答案】解:(1)角α的终边过点(3, 4),∴r=√32+42=5,∴sinα=yr =45,cosα=xr=35,∴a→⋅b→=√2sinα+sin(α+π4)=√2sinα+sinαcos π4+cosαsinπ4=√2×45+45×√22+35×√22=3√22.(2)若a→ // b→,则√2sinαsin(α+π4)=1,即√2sinα(sinαcosπ4+cosαsinπ4)=1,∴sin2α+sinαcosα=1,∴sinαcosα=1−sin2α=cos2α,对锐角α有cosα≠0,∴tanα=1,∴锐角α=π4.【考点】两角和与差的正弦公式任意角的三角函数平面向量数量积的性质及其运算律平面向量共线(平行)的坐标表示平行向量的性质同角三角函数间的基本关系【解析】(1)由三角函数的定义求出sinα、cosα,再根据平面向量数量积的定义计算a→⋅b→的值;(2)根据a→ // b→,列方程求出α的三角函数值以及锐角α的值.【解答】解:(1)角α的终边过点(3, 4),∴r=√32+42=5,∴sinα=yr =45,cosα=xr=35,→→π=√2sinα+sinαcos π4+cosαsinπ4=√2×45+45×√22+35×√22=3√22.(2)若a→ // b→,则√2sinαsin(α+π4)=1,即√2sinα(sinαcosπ4+cosαsinπ4)=1,∴sin2α+sinαcosα=1,∴sinαcosα=1−sin2α=cos2α,对锐角α有cosα≠0,∴tanα=1,∴锐角α=π4.如图,正三棱柱ABC−A1B1C1的高为√6,其底面边长为2.已知点M,N分别是棱A1C1,AC的中点,点D是棱CC1上靠近C的三等分点.求证:(1)B1M // 平面A1BN;(2)AD⊥平面A1BN.【答案】证明:(1)连结MN,正三棱柱ABC−A1B1C1中,如图,AA1 // CC1且AA1=CC1,则四边形AA1C1C是平行四边形,所以MN // AA1且MN=AA1,又正三棱柱ABC−A1B1C1中AA1 // BB1且AA1=BB1,所以MN // BB1且MN=BB1,所以四边形MNBB1是平行四边形,所以B1M // BN,又B1M平面A1BN,BN⊂平面A1BN,所以B1M // 平面A1BN.(2)正三棱柱ABC−A1B1C1中,AA1⊥平面ABC,BN⊂平面ABC,所以BN⊥AA1,正△ABC中,N是AC的中点,所以BN⊥AC,又AA1、AC⊂平面AA1C1C,AA1∩AC=A,所以BN⊥平面AA1C1C,又AD⊂平面AA1C1C,所以AD⊥BN,由题意,AA1=√6,AC=2,AN=1,CD=√63,所以AA1AC =ANCD=√32,又∠A1AN=∠ACD=π2,所以△A1AN与△ACD相似,则∠AA1N=∠CAD,所以∠ANA1+∠CAD=∠ANA1+∠AA1N=π2,则AD⊥A1N,又BN∩A1N=N,BN,A1N⊂平面A1BN,所以AD⊥平面A1BN.【考点】直线与平面垂直的判定直线与平面平行的判定【解析】(1)证明四边形MNBB1是平行四边形得出B1M // BN,故而B1M // 平面A1BN;(2)根据BN⊥平面ACC1A1可得BN⊥AD,根据三角形相似可得AD⊥A1N,故而AD⊥平面A1BN.【解答】证明:(1)连结MN,正三棱柱ABC−A1B1C1中,如图,AA1 // CC1且AA1=CC1,则四边形AA1C1C是平行四边形,因为点M、N分别是棱A1C1,AC的中点,所以MN // AA1且MN=AA1,又正三棱柱ABC−A1B1C1中AA1 // BB1且AA1=BB1,所以MN // BB1且MN=BB1,所以四边形MNBB 1是平行四边形,所以B 1M // BN ,又B 1M 平面A 1BN ,BN ⊂平面A 1BN , 所以B 1M // 平面A 1BN .(2)正三棱柱ABC −A 1B 1C 1中,AA 1⊥平面ABC ,BN ⊂平面ABC , 所以BN ⊥AA 1,正△ABC 中,N 是AC 的中点,所以BN ⊥AC ,又AA 1、AC ⊂平面AA 1C 1C ,AA 1∩AC =A , 所以BN ⊥平面AA 1C 1C ,又AD ⊂平面AA 1C 1C , 所以AD ⊥BN ,由题意,AA 1=√6,AC =2,AN =1,CD =√63,所以AA 1AC=AN CD=√32,又∠A 1AN =∠ACD =π2,所以△A 1AN 与△ACD 相似,则∠AA 1N =∠CAD , 所以∠ANA 1+∠CAD =∠ANA 1+∠AA 1N =π2,则AD ⊥A 1N ,又BN ∩A 1N =N ,BN ,A 1N ⊂平面A 1BN , 所以AD ⊥平面A 1BN .已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)经过点(√3,12),(1,√32),点A 是椭圆的下顶点. (1)求椭圆C 的标准方程;(2)过点A 且互相垂直的两直线l 1,l 2与直线y =x 分别相交于E ,F 两点,已知OE =OF ,求直线l 1的斜率. 【答案】解:(1)根据题意,椭圆C:x 2a 2+y 2b2=1(a >b >0)经过点(√3,12),(1,√32), 则有{3a 2+14b 2=1,1a 2+34b 2=1, 解得{1a 2=14,1b 2=1, 所以椭圆C 的标准方程为x 24+y 2=1.(2)由题意知A(0, −1),直线l 1,l 2的斜率存在且不为零, 设直线l 1:y =k 1x −1,与直线y =x 联立方程有{y =k 1x −1y =x , 得E(1k1−1,1k 1−1),设直线l 2:y =−1k 1x −1,同理F(1−1k 1−1,1−1k 1−1),因为OE =OF , 所以|1k 1−1|=|1−1k 1−1|,①1k 1−1=1−1k 1−1,k 1+1k 1=0无实数解;②1k 1−1=−1−1k 1−1,k 1−1k 1=2,k 12−2k 1−1=0,解得k 1=1±√2,综上可得,直线l 1的斜率为1±√2. 【考点】直线与椭圆结合的最值问题 椭圆的标准方程两条直线垂直与倾斜角、斜率的关系 【解析】(1)根据题意,将两点的坐标代入椭圆的方程有{3a 2+14b 2=11a 2+34b 2=1,解可得1a 2、1b 2的值,即可得椭圆的方程;(2)设直线l 1:y =k 1x −1,与直线y =x 联立方程有{y =k 1x −1y =x,可得E 的坐标,设直线l 2:y =−1k 1x −1,同理可得F 的坐标,又由OE =OF ,所以|1k 1−1|=|1−1k 1−1|,解可得k 的值,即可得答案. 【解答】解:(1)根据题意,椭圆C:x 2a+y 2b =1(a >b >0)经过点(√3,12),(1,√32),则有{3a 2+14b 2=1,1a+34b=1, 解得{1a 2=14,1b=1,所以椭圆C 的标准方程为x 24+y 2=1.(2)由题意知A(0, −1),直线l 1,l 2的斜率存在且不为零, 设直线l 1:y =k 1x −1,与直线y =x 联立方程有{y =k 1x −1y =x , 得E(1k1−1,1k1−1),设直线l 2:y =−1k 1x −1,同理F(1−1k 1−1,1−1k 1−1),因为OE =OF , 所以|1k 1−1|=|1−1k 1−1|,①1k 1−1=1−1k 1−1,k 1+1k 1=0无实数解;②1k 1−1=−1−1k 1−1,k 1−1k 1=2,k 12−2k 1−1=0,解得k 1=1±√2,综上可得,直线l 1的斜率为1±√2.如图,某景区内有一半圆形花圃,其直径AB 为6,O 是圆心,且OC ⊥AB .在OC 上有一座观赏亭Q ,其中∠AQC =2π3.计划在BC 上再建一座观赏亭P ,记∠POB =θ(0<θ<π2).(1)当θ=π3时,求∠OPQ 的大小;(2)当∠OPQ 越大,游客在观赏亭P 处的观赏效果越佳,求游客在观赏亭P 处的观赏效果最佳时,角θ的正弦值. 【答案】解:(1)设∠OPQ =α,由题,Rt △OAQ 中,OA =3, ∠AQO =π−∠AQC =π−2π3=π3,所以OQ =√3,在△OPQ 中,OP =3, ∠POQ =π2−θ=π2−π3=π6, 由正弦定理得OQ sin∠OPQ =OPsin∠OQP , 即√3sinα=3sin(π−α−π6),所以√3sinα=sin(π−α−π6)=sin(5π6−α), 则√3sinα=sin 5π6cosα−cos5π6sinα=12cosα+√32sinα, 所以√3sinα=cosα,因为α为锐角,所以cosα≠0,所以tanα=√33,得α=π6.(2)设∠OPQ =α,在△OPQ 中,OP =3,∠POQ =π2−θ, 由正弦定理得OQ sin∠OPQ =OPsin∠OQP , 即√3sinα=3sin(π−α−(π2−θ)),所以√3sinα=sin(π−α−(π2−θ)) =sin(π2−(α−θ)),从而(√3−sinθ)sinα=cosαcosθ,其中√3−sinθ≠0,cosα≠0, 所以tanα=√3−sinθ,记f(θ)=√3−sinθ,f ′(θ)=√3sinθ(√3−sinθ)2,θ∈(0,π2),令f ′(θ)=0,sinθ=√33,存在唯一θ0∈(0,π2)使得sinθ0=√33,当θ∈(0, θ0)时f ′(θ)>0,f(θ)单调增,当θ∈(θ0,π2)时f ′(θ)<0,f(θ)单调减, 所以当θ=θ0时,f(θ)最大,即tan∠OPQ 最大,又∠OPQ 为锐角,从而∠OPQ 最大,此时sinθ=√33.答:观赏效果达到最佳时,θ的正弦值为√33.【考点】利用导数研究函数的最值 两角和与差的正弦公式 利用导数研究函数的单调性 正弦定理 【解析】(1)根据题意,设∠OPQ =α,由正弦定理得OQsin∠OPQ =OPsin∠OQP ,变形可得√3sinα=sin5π6cosα−cos5π6sinα=12cosα+√32sinα,所以√3sinα=cosα,由同角三角函数基本关系式分析可得答案;(2)设∠OPQ =α,在△OPQ 中,由正弦定理得OQsin∠OPQ =OPsin∠OQP ,变形可得(√3−sinθ)sinα=cosαcosθ,即tanα=√3−sinθ,记f(θ)=√3−sinθ,求导可得f ′(θ)=√3sinθ(√3−sinθ)2,由导数与函数的单调性的关系分析可得答案.【解答】解:(1)设∠OPQ =α,由题,Rt △OAQ 中,OA =3, ∠AQO =π−∠AQC =π−2π3=π3,所以OQ =√3,在△OPQ 中,OP =3, ∠POQ =π2−θ=π2−π3=π6,由正弦定理得OQ sin∠OPQ =OPsin∠OQP , 即√3sinα=3sin(π−α−π6),所以√3sinα=sin(π−α−π6)=sin(5π6−α), 则√3sinα=sin 5π6cosα−cos5π6sinα=12cosα+√32sinα, 所以√3sinα=cosα,因为α为锐角,所以cosα≠0,所以tanα=√33,得α=π6.(2)设∠OPQ =α,在△OPQ 中,OP =3,∠POQ =π2−θ,由正弦定理得OQ sin∠OPQ =OPsin∠OQP , 即√3sinα=3sin(π−α−(π2−θ)),所以√3sinα=sin(π−α−(π2−θ)) =sin(π2−(α−θ)),从而(√3−sinθ)sinα=cosαcosθ,其中√3−sinθ≠0,cosα≠0, 所以tanα=3−sinθ,记f(θ)=√3−sinθ,f ′(θ)=√3sinθ(√3−sinθ)2,θ∈(0,π2), 令f ′(θ)=0,sinθ=√33,存在唯一θ0∈(0,π2)使得sinθ0=√33,当θ∈(0, θ0)时f ′(θ)>0,f(θ)单调增,当θ∈(θ0,π2)时f ′(θ)<0,f(θ)单调减, 所以当θ=θ0时,f(θ)最大,即tan∠OPQ 最大, 又∠OPQ 为锐角,从而∠OPQ 最大,此时sinθ=√33.答:观赏效果达到最佳时,θ的正弦值为√33.已知函数f(x)=x 3+ax 2+bx +c ,g(x)=lnx .(1)若a =0,b =−2,且f(x)≥g(x)恒成立,求实数c 的取值范围;(2)若b =−3,且函数y =f(x)在区间(−1, 1)上是单调递减函数. ①求实数a 的值;②当c =2时,求函数ℎ(x)={f(x),f(x)≥g(x),g(x),f(x)<g(x) 的值域.【答案】解:(1)根据题意,函数g(x)=lnx ,其定义域为(0, +∞). 当a =0,b =−2,f(x)=x 3−2x +c , ∵ f(x)≥g(x)恒成立,∴ x 3−2x +c ≥lnx 恒成立,即c ≥lnx −x 3+2x . 令φ(x)=lnx −x 3+2x , 则φ′(x)=1x −3x 2+2 =1+2x−3x 3x=(1−x)(1+3x+3x 2)x,令φ′(x)≥0,得x ≤1,∴ φ(x)在(0, 1]上单调递增, 令φ′(x)≤0,得x ≥1,∴ φ(x)在[1, +∞)上单调递减, ∴ 当x =1时,[φ(x)]max =φ(1)=1. ∴ c ≥1.(2)①当b =−3时,f(x)=x 3+ax 2−3x +c ,f ′(x)=3x 2+2ax −3, 由题意,f ′(x)=3x 2+2ax −3≤0对x ∈(−1, 1)恒成立, ∴ {f ′(1)=3+2a −3≤0,f ′(−1)=3−2a −3≤0,当a =0,b =−3,c =2时,f(x)=x 3−3x +2, f ′(x)=3x 2−3,令f ′(x)=3x 2−3=0,得x =1,对于g(x)=lnx ,当x ∈(0, 1)时,g(x)<0,当x =1时,g(x)=0,当x ∈(1, +∞)时,g(x)>0, ∴ 当x ∈(0, 1)时,ℎ(x)=f(x)>0,当x =1时,ℎ(x)=0,当x ∈(1, +∞)时,ℎ(x)>0.故函数y =ℎ(x)的值域为[0, +∞). 【考点】利用导数研究函数的最值利用导数研究不等式恒成立问题 分段函数的应用 【解析】(1)根据题意,f(x)≥g(x)恒成立,即x 3−2x +c ≥lnx 恒成立,变形可得c ≥lnx −x 3+2x ,令φ(x)=lnx −x 3+2x ,对其求导,利用函数的导数与函数的单调性分析可得[φ(x)]max =φ(1)=1,分析可得c 的范围;(2)①,当b =−3时,f(x)=x 3+ax 2−3x +c ,f ′(x)=3x 2+2ax −3.利用函数的导数与函数的单调性分析可得f ′(x)=3x 2+2ax −3≤0对x ∈(−1, 1)恒成立,即可得{f ′(1)=3+2a −3≤0f ′(−1)=3−2a −3≤0,解可得a 的值,即可得答案; ②,由①的结论,当a =0,b =−3,c =2时,f(x)=x 3−3x +2,利用函数的导数与函数的单调性分析可得当x ∈(0, 1)时,f(x)>0,当x =1时,f(x)=0,当x ∈(1, +∞)时,f(x)>0,g(x)=lnx ,当x ∈(0, 1)时,g(x)<0,当x =1时,g(x)=0,当x ∈(1, +∞)时,g(x)>0,结合函数ℎ(x)的解析式,分析可得答案. 【解答】解:(1)根据题意,函数g(x)=lnx ,其定义域为(0, +∞). 当a =0,b =−2,f(x)=x 3−2x +c , ∵ f(x)≥g(x)恒成立,∴ x 3−2x +c ≥lnx 恒成立,即c ≥lnx −x 3+2x . 令φ(x)=lnx −x 3+2x , 则φ′(x)=1x −3x 2+2 =1+2x−3x 3x=(1−x)(1+3x+3x 2)x,令φ′(x)≥0,得x ≤1,∴ φ(x)在(0, 1]上单调递增, 令φ′(x)≤0,得x ≥1,∴ φ(x)在[1, +∞)上单调递减, ∴ 当x =1时,[φ(x)]max =φ(1)=1. ∴ c ≥1.(2)①当b =−3时,f(x)=x 3+ax 2−3x +c ,f ′(x)=3x 2+2ax −3, 由题意,f ′(x)=3x 2+2ax −3≤0对x ∈(−1, 1)恒成立, ∴ {f ′(1)=3+2a −3≤0,f ′(−1)=3−2a −3≤0,当a=0,b=−3,c=2时,f(x)=x3−3x+2,f′(x)=3x2−3,令f′(x)=3x2−3=0,得x=1,对于g(x)=lnx,当x∈(0, 1)时,g(x)<0,当x=1时,g(x)=0,当x∈(1, +∞)时,g(x)>0,∴当x∈(0, 1)时,ℎ(x)=f(x)>0,当x=1时,ℎ(x)=0,当x∈(1, +∞)时,ℎ(x)>0.故函数y=ℎ(x)的值域为[0, +∞).已知S n是数列{a n}的前n项和,a1=3,且2S n=a n+1−3(n∈N∗).(1)求数列{a n}的通项公式;(2)对于正整数i,j,k(i<j<k),已知λa j,6a i,μa k成等差数列,求正整数λ,μ的值;(3)设数列{b n}前n项和是T n,且满足:对任意的正整数n,都有等式a1b n+a2b n−1+a3b n−2+⋯+a n b1=3n+1−3n−3成立.求满足等式T na n =13的所有正整数n.【答案】解:(1)由2S n=a n+1−3(n∈N∗),得:2S n+1=a n+2−3,两式作差得2a n+1=a n+2−a n+1,即a n+2=3a n+1(n∈N∗)由于a1=3,a2=2S1+3=9,所以a n+1=3a n(n∈N∗),a n≠0,则a n+1a n=3(n∈N∗),所以数列{a n}是首项为3,公比为3的等比数列,所以a n=3n(n∈N∗).(2)已知λa j,6a i,μa k成等差数列,所以:λa j+μa k=2⋅6a i,即λ3j+μ3k=2⋅6⋅3i,所以λ3j−i+μ3k−i=12,其中j−i≥1,k−i≥2,所以λ3j−i≥3λ≥3,μ3k−i≥9μ≥9,12=λ3j−i+μ3k−i≥12,所以j−i=1,k−i=2,λ=μ=1.(3)由a1b n+a2b n−1+a3b n−2+⋯+a n b1=3n+1−3n−3,得:a1b n+1+a2b n+a3b n−1+...+a n b2+a n+1b1=3n+2−3(n+1)−3,a1b n+1+3(a1b n+a2b n−1+...+a n−1b2+a n b1)=3n+2−3(n+1)−3,a1b n+1+3(3n+1−3n−3)=3n+2−3(n+1)−3,所以3b n+1=3n+2−3(n+1)−3−3(3n+1−3n−3),即3b n+1=6n+3,所以b n+1=2n+1(n∈N∗),又因为a 1b 1=31+1−3⋅1−3=3,得b 1=1, 所以b n =2n −1(n ∈N ∗),从而T n =1+3+5+...+(2n −1) =1+2n−12n =n 2(n ∈N ∗),T n a n=n 23n(n ∈N ∗),当n =1时,T1a 1=13;当n =2时,T 2a 2=49;当n =3时,T 3a 3=13;下面证明:对任意正整数n >3都有T na n<13,T n+1a n+1−T na n=(n +1)2(13)n+1−n 2(13)n=(13)n+1[(n +1)2−3n 2]=(13)n+1(−2n 2+2n +1),当n ≥3时,−2n 2+2n +1=(1−n 2)+n(2−n)<0, 即T n+1an+1−Tn a n<0,所以当n ≥3时,T na n递减,所以对任意正整数n >3都有T n a n<T 3a 3=13;综上可得,满足等式T na n=13的正整数n 的值为1和3.【考点】 等差中项数列与不等式的综合 数列的求和 数列递推式 等比关系的确定 数列的函数特性 【解析】(1)直接利用递推关系式求出数列的通项公式. (2)利用构造法求出结果.(3)利用已知条件和上步的结论求出结果. 【解答】解:(1)由2S n =a n+1−3(n ∈N ∗), 得:2S n+1=a n+2−3,两式作差得2a n+1=a n+2−a n+1, 即a n+2=3a n+1(n ∈N ∗)由于a 1=3,a 2=2S 1+3=9,所以a n+1=3a n (n ∈N ∗),a n ≠0, 则a n+1a n=3(n ∈N ∗),所以数列{a n }是首项为3,公比为3的等比数列, 所以a n =3n (n ∈N ∗).(2)已知λa j ,6a i ,μa k 成等差数列, 所以:λa j +μa k =2⋅6a i , 即λ3j +μ3k =2⋅6⋅3i ,所以λ3j−i +μ3k−i =12,其中j −i ≥1,k −i ≥2,所以λ3j−i ≥3λ≥3,μ3k−i ≥9μ≥9,12=λ3j−i +μ3k−i ≥12, 所以j −i =1,k −i =2,λ=μ=1.(3)由a 1b n +a 2b n−1+a 3b n−2+⋯+a n b 1=3n+1−3n −3,得:a 1b n+1+a 2b n +a 3b n−1+...+a n b 2+a n+1b 1=3n+2−3(n +1)−3, a 1b n+1+3(a 1b n +a 2b n−1+...+a n−1b 2+a n b 1)=3n+2−3(n +1)−3, a 1b n+1+3(3n+1−3n −3)=3n+2−3(n +1)−3, 所以3b n+1=3n+2−3(n +1)−3−3(3n+1−3n −3), 即3b n+1=6n +3,所以b n+1=2n +1(n ∈N ∗),又因为a 1b 1=31+1−3⋅1−3=3,得b 1=1, 所以b n =2n −1(n ∈N ∗),从而T n =1+3+5+...+(2n −1) =1+2n−12n =n 2(n ∈N ∗),T n a n=n 23n(n ∈N ∗),当n =1时,T1a 1=13;当n =2时,T 2a 2=49;当n =3时,T 3a 3=13;下面证明:对任意正整数n >3都有T na n<13,T n+1a n+1−T na n=(n +1)2(13)n+1−n 2(13)n=(13)n+1[(n +1)2−3n 2]=(13)n+1(−2n 2+2n +1),当n ≥3时,−2n 2+2n +1=(1−n 2)+n(2−n)<0, 即T n+1an+1−Tn a n<0,所以当n ≥3时,T na n递减,所以对任意正整数n >3都有T n a n<T 3a 3=13;综上可得,满足等式T na n=13的正整数n 的值为1和3.【选做题】在21,22,23,24四小题中只能选做两题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.[选修4-1:几何证明选讲]如图,AB是圆O的直径,D为圆O上一点,过点D作圆O的切线交AB的延长线于点C,且满足DA=DC.(1)求证:AB=2BC;(2)若AB=2,求线段CD的长.【答案】(1)证明:连接OD,BD,如图所示,因为AB是圆O的直径,所以∠ADB=90∘,AB=2OB.因为CD是圆O的切线,所以∠CDO=90∘,又因为DA=DC,所以∠A=∠C,于是△ADB≅△CDO,得到AB=CO,所以AO=BC,从而AB=2BC.(2)解:由AB=2及AB=2BC得到CB=1,CA=3.由切割线定理,CD2=CB⋅CA=1×3=3,所以CD=√3.【考点】与圆有关的比例线段【解析】(1)连接OD,BD.推导出∠CDO=90∘,∠A=∠C,从而△ADB≅△CDO,进而AB=CO,由此能证明AB=2BC.(2)由AB=2及AB=2BC得到CB=1,CA=3.由此利用切割线定理能求出线段CD.【解答】(1)证明:连接OD,BD,如图所示,因为AB 是圆O 的直径,所以∠ADB =90∘,AB =2OB .因为CD 是圆O 的切线,所以∠CDO =90∘,又因为DA =DC ,所以∠A =∠C ,于是△ADB ≅△CDO ,得到AB =CO ,所以AO =BC ,从而AB =2BC .(2)解:由AB =2及AB =2BC 得到CB =1,CA =3.由切割线定理,CD 2=CB ⋅CA =1×3=3,所以CD =√3.[选修4-2:矩阵与变换]已知矩阵A =[4001],B =[1205],列向量X =[a b ]. (1)求矩阵AB ;(2)若B −1A −1X =[51],求a ,b 的值. 【答案】解:(1)AB =[4001][1205]=[4805]. (2)由B −1A −1X =[51], 解得X =AB [51]=[4805][51]=[285], 又因为X =[a b], 所以a =28,b =5.【考点】矩阵与矩阵的乘法的意义特征向量的意义逆变换与逆矩阵【解析】(1)根据矩阵的乘法,即可求得AB ;(2)根据矩阵乘法计算公式,求得X =AB [51],即可求得X ,即可求得a 和b 的值. 【解答】解:(1)AB =[4001][1205]=[4805]. (2)由B −1A −1X =[51],解得X =AB [51]=[4805][51]=[285], 又因为X =[a b], 所以a =28,b =5.[选修4-4:坐标系与参数方程]在极坐标系中,已知圆C 经过点P(2√2,π4),圆心为直线ρsin(θ−π3)=−√3与极轴的交点,求圆C 的极坐标方程.【答案】解:在ρsin(θ−π3)=−√3中,令θ=0,得ρ=2,所以圆C 的圆心的极坐标为(2, 0),因为圆C 的半径PC =√(2√2)2+22−2×2√2×2×cos π4=2, 于是圆C 过极点,所以圆的极坐标方程为ρ=4cosθ.【考点】圆的极坐标方程【解析】先求出圆C 的圆心的极坐标为(2, 0),再求出圆C 的半径PC ,由圆C 过极点,能求出圆的极坐标方程.【解答】解:在ρsin(θ−π3)=−√3中,令θ=0,得ρ=2,所以圆C 的圆心的极坐标为(2, 0),因为圆C 的半径PC =√(2√2)2+22−2×2√2×2×cos π4=2, 于是圆C 过极点,所以圆的极坐标方程为ρ=4cosθ.[选修4-5:不等式选讲]已知x ,y 都是正数,且xy =1,求证:(1+x +y 2)(1+y +x 2)≥9.【答案】证明:因为x ,y 都是正数,xy =1,所以1+x +y 2≥3√xy 23>0, 1+y +x 2≥3√yx 23>0,(1+x +y 2)(1+y +x 2)≥9xy ,所以(1+x +y 2)(1+y +x 2)≥9,当且仅当x =y =1时,取得等号.【考点】基本不等式在最值问题中的应用【解析】由x ,y >0,且xy =1,运用三元均值不等式,由不等式的可乘性,即可得到结论.【解答】证明:因为x ,y 都是正数,xy =1,所以1+x +y 2≥3√xy 23>0, 1+y +x 2≥3√yx 23>0,(1+x +y 2)(1+y +x 2)≥9xy ,所以(1+x +y 2)(1+y +x 2)≥9,当且仅当x =y =1时,取得等号.【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.如图,在四棱锥P −ABCD 中,底面ABCD 是矩形,PD 垂直于底面ABCD ,PD =AD =2AB ,点Q 为线段PA (不含端点)上一点.(1)当Q 是线段PA 的中点时,求CQ 与平面PBD 所成角的正弦值;(2)已知二面角Q −BD −P 的正弦值为23,求PQ PA 的值.【答案】解:(1)以D 为原点,DA ,DC ,DP 为x ,y ,z 轴,建立如图所示空间直角坐标系.设AB =t ,则D(0, 0, 0),A(2t, 0, 0),B(2t, t, 0),C(0, t, 0),P(0, 0, 2t),Q(t, 0, t), ∴ CQ →=(t,−t,t),DB →=(2t,t,0),DP →=(0,0,2t),设平面PBD 的法向量n 1→=(x,y,z),则{DB →⋅n 1→=0,DP →⋅n 1→=0,即{2tx +ty =0,2tz =0, 取x =1,得平面的一个法向量n 1→=(1,−2,0),, ∴ cos <n 1→,CQ →>=n 1→⋅CQ →|n 1→||CQ →|=√5×√3t=√155, 则CQ 与平面PBD 所成角的正弦值为√155.(2)由(1)知平面PBD 的一个法向量为n 1→=(1,−2,0),设PQ PA =λ(0<λ<1),则PQ →=λPA →,DQ →=DP →+PQ →=(0, 0, 2t)+λ(2t, 0, −2t)=(2tλ, 0, 2t(1−λ)), DB →=(2t,t,0),设平面QBD 的法向量n 2→=(x,y,z),则{DQ →⋅n 2→=0,DB →⋅n 2→=0,即{2tλx +2t(1−λ)z =0,2tx +ty =0, 取z =−λ,得平面QBD 的一个法向量n 2→=(1−λ,2λ−2,−λ),由题意得,√1−(23)2=|cos <n 1→,n 2→>|=|n 1→⋅n 2→|n 1→||n 2→|| =√5√(1−λ)2+(2λ−2)2+(−λ)2, ∴ 59=5(1−λ)26λ2−10λ+5,即(λ−2)(λ−23)=0,∵ 0<λ<1,∴ λ=23,则PQ PA =23.【考点】二面角的平面角及求法用空间向量求平面间的夹角用空间向量求直线与平面的夹角【解析】(1)以D 为原点,DA ,DC ,DP 为x ,y ,z 轴,建立如图所示空间直角坐标系.设AB =t ,求出CQ →的坐标及平面PBD 的法向量n 1→,由CQ →与n 1→所成角的余弦值可得CQ 与平面PBD 所成角的正弦值;(2)由(1)知平面PBD 的一个法向量为n 1→=(1,−2,0),设PQ PA =λ(0<λ<1),则PQ →=λPA →,把平面QBD 的法向量n 2→的坐标用含有λ的代数式表示,再由二面角Q −BD −P 的正弦值为23列式求得λ值,则答案可求.【解答】解:(1)以D 为原点,DA ,DC ,DP 为x ,y ,z 轴,建立如图所示空间直角坐标系.设AB =t ,则D(0, 0, 0),A(2t, 0, 0),B(2t, t, 0),C(0, t, 0),P(0, 0, 2t),Q(t, 0, t), ∴ CQ →=(t,−t,t),DB →=(2t,t,0),DP →=(0,0,2t),设平面PBD 的法向量n 1→=(x,y,z),则{DB →⋅n 1→=0,DP →⋅n 1→=0,即{2tx +ty =0,2tz =0, 取x =1,得平面的一个法向量n 1→=(1,−2,0),, ∴ cos <n 1→,CQ →>=n 1→⋅CQ →|n 1→||CQ →|=√5×√3t =√155, 则CQ 与平面PBD 所成角的正弦值为√155. (2)由(1)知平面PBD 的一个法向量为n 1→=(1,−2,0),设PQ PA =λ(0<λ<1),则PQ →=λPA →,DQ →=DP →+PQ →=(0, 0, 2t)+λ(2t, 0, −2t)=(2tλ, 0, 2t(1−λ)), DB →=(2t,t,0),设平面QBD 的法向量n 2→=(x,y,z),则{DQ →⋅n 2→=0,DB →⋅n 2→=0,即{2tλx +2t(1−λ)z =0,2tx +ty =0, 取z =−λ,得平面QBD 的一个法向量n 2→=(1−λ,2λ−2,−λ),由题意得,√1−(23)2=|cos <n 1→,n 2→>|=|n 1→⋅n 2→|n 1→||n 2→|| =5√(1−λ)2+(2λ−2)2+(−λ)2, ∴ 59=5(1−λ)26λ2−10λ+5,即(λ−2)(λ−23)=0, ∵ 0<λ<1,∴ λ=23, 则PQ PA =23.在含有n个元素的集合A n={1, 2, ..., n}中,若这n个元素的一个排列(a1, a2,…,a n)满足a i≠i(i=1, 2,…,n),则称这个排列为集合A n的一个错位排列(例如:对于集合A3={1, 2, 3},排列(2, 3, 1)是A3的一个错位排列;排列(1, 3, 2)不是A3的一个错位排列).记集合A n的所有错位排列的个数为D n.(1)直接写出D1,D2,D3,D4的值;(2)当n≥3时,试用D n−2,D n−1表示D n,并说明理由;(3)试用数学归纳法证明:D2n(n∈N∗)为奇数.【答案】(1)解:根据错位排列的定义得出:D1=0,D2=1,D3=2,D4=9.(2)解:D n=(n−1)(D n−1+D n−2 ),理由如下:对A n的元素的一个错位排列(a1, a2,…,a n),若a1=k(k≠1),分以下两类:若a k=1,这种排列是n−2个元素的错位排列,共有D n−2个;若a k≠1,这种错位排列就是将1,2,…,k−1,k+1,…,n.排列到第2到第n个位置上,1不在第k个位置,其他元素也不在原先的位置,这种排列相当于n−1个元素的错位排列,共有D n−1个.∵k≠1,∴k共有n−1个不同的取值,∴D n=(n−1)(D n−1+D n−2 ).(3)证明:根据(2)的递推关系及(1)的结论,D n均为自然数;当n≥3,且n为奇数时,n−1为偶数,从而D n=(n−1)(D n−1+D n−2 )为偶数,又D1=0也是偶数,故对任意正奇数n,有D n均为偶数.下面用数学归纳法证明D2n(其中n∈N∗)为奇数.当n=1时,D2=1为奇数;假设当n=k时,结论成立,即D2k是奇数,则当n=k+1时,D2(k+1)=(2k+1)(D2k+1+D2k),注意到D2k+1为偶数,又D2k是奇数,所以D2k+1+D2k为奇数,又2k+1为奇数,所以D2(k+1)=(2k+1)(D2k+1+D2k),即结论对n=k+1也成立;根据前面所述,对任意n∈N∗,都有D2n为奇数.【考点】数学归纳法【解析】(1)根据错位排列的定义得出;(2)设A n的一个错位排列(a1, a2,…,a n),令a1=k(k≠1),根据a k是否为1讨论得出D n与D n−2,D n−1的关系;(3)根据(2)的结论可知D2k+1为偶数,再利用数学归纳法证明即可.【解答】(1)解:根据错位排列的定义得出:D1=0,D2=1,D3=2,D4=9.(2)解:D n=(n−1)(D n−1+D n−2 ),理由如下:对A n的元素的一个错位排列(a1, a2,…,a n),若a1=k(k≠1),分以下两类:若a k=1,这种排列是n−2个元素的错位排列,共有D n−2个;若a k≠1,这种错位排列就是将1,2,…,k−1,k+1,…,n.排列到第2到第n个位置上,1不在第k个位置,其他元素也不在原先的位置,这种排列相当于n−1个元素的错位排列,共有D n−1个.∵k≠1,∴k共有n−1个不同的取值,∴D n=(n−1)(D n−1+D n−2 ).(3)证明:根据(2)的递推关系及(1)的结论,D n均为自然数;当n≥3,且n为奇数时,n−1为偶数,从而D n=(n−1)(D n−1+D n−2 )为偶数,又D1=0也是偶数,故对任意正奇数n,有D n均为偶数.下面用数学归纳法证明D2n(其中n∈N∗)为奇数.当n=1时,D2=1为奇数;假设当n=k时,结论成立,即D2k是奇数,则当n=k+1时,D2(k+1)=(2k+1)(D2k+1+D2k),注意到D2k+1为偶数,又D2k是奇数,所以D2k+1+D2k为奇数,又2k+1为奇数,所以D2(k+1)=(2k+1)(D2k+1+D2k),即结论对n=k+1也成立;根据前面所述,对任意n∈N∗,都有D2n为奇数.。
2018年江苏省高考数学试卷(含详细答案解析)

2018年江苏省高考数学试卷一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5分)已知集合A={0,1,2,8},B={﹣1,1,6,8},那么A∩B=.2.(5分)若复数z满足i•z=1+2i,其中i是虚数单位,则z的实部为.3.(5分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为.4.(5分)一个算法的伪代码如图所示,执行此算法,最后输出的S的值为.5.(5分)函数f(x)=的定义域为.6.(5分)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为.7.(5分)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.8.(5分)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为.9.(5分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x)=,则f(f(15))的值为.10.(5分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.11.(5分)若函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[﹣1,1]上的最大值与最小值的和为.12.(5分)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为.13.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.14.(5分)已知集合A={x|x=2n﹣1,n∈N*},B={x|x=2n,n∈N*}.将A∪B的所有元素从小到大依次排列构成一个数列{a n},记S n为数列{a n}的前n项和,则成立的n的最小值为.使得S n>12a n+1二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.16.(14分)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.17.(14分)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P 为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(16分)如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.19.(16分)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x﹣2不存在“S点”;(2)若函数f(x)=ax2﹣1与g(x)=lnx存在“S点”,求实数a的值;(3)已知函数f(x)=﹣x2+a,g(x)=.对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.20.(16分)设{a n}是首项为a1,公差为d的等差数列,{b n}是首项为b1,公比为q的等比数列.(1)设a1=0,b1=1,q=2,若|a n﹣b n|≤b1对n=1,2,3,4均成立,求d的取值范围;(2)若a1=b1>0,m∈N*,q∈(1,],证明:存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,并求d的取值范围(用b1,m,q表示).数学Ⅱ(附加题)【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.(10分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若PC=2,求BC的长.B.[选修4-2:矩阵与变换](本小题满分10分)22.(10分)已知矩阵A=.(1)求A的逆矩阵A﹣1;(2)若点P在矩阵A对应的变换作用下得到点P′(3,1),求点P的坐标.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的方程为ρsin(﹣θ)=2,曲线C的方程为ρ=4cosθ,求直线l被曲线C截得的弦长.D.[选修4-5:不等式选讲](本小题满分0分)24.若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.25.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.26.设n∈N*,对1,2,……,n的一个排列i1i2……i n,如果当s<t时,有i s>i t,则称(i s,i t)是排列i1i2……i n的一个逆序,排列i1i2……i n的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n(k)为1,2,…,n的所有排列中逆序数为k的全部排列的个数.(1)求f3(2),f4(2)的值;(2)求f n(2)(n≥5)的表达式(用n表示).2018年江苏省高考数学试卷参考答案与试题解析一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.(5分)已知集合A={0,1,2,8},B={﹣1,1,6,8},那么A∩B={1,8} .【分析】直接利用交集运算得答案.【解答】解:∵A={0,1,2,8},B={﹣1,1,6,8},∴A∩B={0,1,2,8}∩{﹣1,1,6,8}={1,8},故答案为:{1,8}.【点评】本题考查交集及其运算,是基础的计算题.2.(5分)若复数z满足i•z=1+2i,其中i是虚数单位,则z的实部为2.【分析】把已知等式变形,再由复数代数形式的乘除运算化简得答案.【解答】解:由i•z=1+2i,得z=,∴z的实部为2.故答案为:2.【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.3.(5分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为90.【分析】根据茎叶图中的数据计算它们的平均数即可.【解答】解:根据茎叶图中的数据知,这5位裁判打出的分数为89、89、90、91、91,它们的平均数为×(89+89+90+91+91)=90.故答案为:90.【点评】本题考查了利用茎叶图计算平均数的问题,是基础题.4.(5分)一个算法的伪代码如图所示,执行此算法,最后输出的S的值为8.【分析】模拟程序的运行过程,即可得出程序运行后输出的S值.【解答】解:模拟程序的运行过程如下;I=1,S=1,I=3,S=2,I=5,S=4,I=7,S=8,此时不满足循环条件,则输出S=8.故答案为:8.【点评】本题考查了程序语言的应用问题,模拟程序的运行过程是解题的常用方法.5.(5分)函数f(x)=的定义域为[2,+∞).【分析】解关于对数函数的不等式,求出x的范围即可.【解答】解:由题意得:≥1,解得:x≥2,∴函数f(x)的定义域是[2,+∞).故答案为:[2,+∞).【点评】本题考查了对数函数的性质,考查求函数的定义域问题,是一道基础题.6.(5分)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为0.3.【分析】(适合理科生)从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,根据概率公式计算即可,(适合文科生),设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,根据概率公式计算即可【解答】解:(适合理科生)从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,故选中的2人都是女同学的概率P==0.3,(适合文科生),设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,故选中的2人都是女同学的概率P==0.3,故答案为:0.3【点评】本题考查了古典概率的问题,采用排列组合或一一列举法,属于基础题.7.(5分)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.【分析】根据正弦函数的对称性建立方程关系进行求解即可.【解答】解:∵y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,∴2×+φ=kπ+,k∈Z,即φ=kπ﹣,∵﹣φ<,∴当k=0时,φ=﹣,故答案为:﹣.【点评】本题主要考查三角函数的图象和性质,利用正弦函数的对称性建立方程关系是解决本题的关键.8.(5分)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为2.【分析】利用双曲线的简单性质,以及点到直线的距离列出方程,转化求解即可.【解答】解:双曲线=1(a>0,b>0)的右焦点F(c,0)到一条渐近线y=x的距离为c,可得:=b=,可得,即c=2a,所以双曲线的离心率为:e=.故答案为:2.【点评】本题考查双曲线的简单性质的应用,考查转化思想以及计算能力.9.(5分)函数f(x)满足f(x+4)=f(x)(x∈R),且在区间(﹣2,2]上,f(x)=,则f(f(15))的值为.【分析】根据函数的周期性,进行转化求解即可.【解答】解:由f(x+4)=f(x)得函数是周期为4的周期函数,则f(15)=f(16﹣1)=f(﹣1)=|﹣1+|=,f()=cos()=cos=,即f(f(15))=,故答案为:【点评】本题主要考查函数值的计算,根据函数的周期性结合分段函数的表达式利用转化法是解决本题的关键.10.(5分)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【分析】求出多面体中的四边形的面积,然后利用体积公式求解即可.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:2×=.故答案为:.【点评】本题考查几何体的体积的求法,考查空间想象能力以及计算能力.11.(5分)若函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,则f(x)在[﹣1,1]上的最大值与最小值的和为﹣3.【分析】推导出f′(x)=2x(3x﹣a),x∈(0,+∞),当a≤0时,f′(x)=2x(3x ﹣a)>0,f(0)=1,f(x)在(0,+∞)上没有零点;当a>0时,f′(x)=2x(3x﹣a)>0的解为x>,f(x)在(0,)上递减,在(,+∞)递增,由f(x)只有一个零点,解得a=3,从而f(x)=2x3﹣3x2+1,f′(x)=6x(x﹣1),x ∈[﹣1,1],利用导数性质能求出f(x)在[﹣1,1]上的最大值与最小值的和.【解答】解:∵函数f(x)=2x3﹣ax2+1(a∈R)在(0,+∞)内有且只有一个零点,∴f′(x)=2x(3x﹣a),x∈(0,+∞),①当a≤0时,f′(x)=2x(3x﹣a)>0,函数f(x)在(0,+∞)上单调递增,f(0)=1,f(x)在(0,+∞)上没有零点,舍去;②当a>0时,f′(x)=2x(3x﹣a)>0的解为x>,∴f(x)在(0,)上递减,在(,+∞)递增,又f(x)只有一个零点,∴f()=﹣+1=0,解得a=3,f(x)=2x3﹣3x2+1,f′(x)=6x(x﹣1),x∈[﹣1,1],f′(x)>0的解集为(﹣1,0),f(x)在(﹣1,0)上递增,在(0,1)上递减,f(﹣1)=﹣4,f(0)=1,f(1)=0,∴f(x)min=f(﹣1)=﹣4,f(x)max=f(0)=1,∴f(x)在[﹣1,1]上的最大值与最小值的和为:f(x)max+f(x)min=﹣4+1=﹣3.【点评】本题考查函数的单调性、最值,导数的运算及其应用,同时考查逻辑思维能力和综合应用能力,是中档题.12.(5分)在平面直角坐标系xOy中,A为直线l:y=2x上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为3.【分析】设A(a,2a),a>0,求出C的坐标,得到圆C的方程,联立直线方程与圆的方程,求得D的坐标,结合=0求得a值得答案.【解答】解:设A(a,2a),a>0,∵B(5,0),∴C(,a),则圆C的方程为(x﹣5)(x﹣a)+y(y﹣2a)=0.联立,解得D(1,2).∴=.解得:a=3或a=﹣1.又a>0,∴a=3.即A的横坐标为3.故答案为:3.【点评】本题考查平面向量的数量积运算,考查圆的方程的求法,是中档题.13.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为9.【分析】根据面积关系建立方程关系,结合基本不等式1的代换进行求解即可.【解答】解:由题意得acsin120°=asin60°+csin60°,即ac=a+c,得+=1,得4a+c=(4a+c)(+)=++5≥2+5=4+5=9,当且仅当=,即c=2a时,取等号,故答案为:9.【点评】本题主要考查基本不等式的应用,利用1的代换结合基本不等式是解决本题的关键.14.(5分)已知集合A={x|x=2n﹣1,n∈N*},B={x|x=2n,n∈N*}.将A∪B的所有元素从小到大依次排列构成一个数列{a n},记S n为数列{a n}的前n项和,则成立的n的最小值为27.使得S n>12a n+1【分析】采用列举法,验证n=26,n=27即可.【解答】解:利用列举法可得:当n=26时,A∪B中的所有元素从小到大依次排列,构成一个数列{a n},所以数列{a n}的前26项分成两组:1,3,5,7,9,11,13,15,17,19,21,23.25,…41;2,4,8,16,32.S26=,a27=43,⇒12a27=516,不符合题意.当n=27时,A∪B中的所有元素从小到大依次排列,构成一个数列{a n},所以数列{a n}的前27项分成两组:1,3,5,7,9,11,13,15,17,19,21,23,25,…41,43;2,4,8,16,32.S27==546,a28=45⇒12a28=540,符合题意,故答案为:27.【点评】本题考查了集合、数列的求和,属于中档题.二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(14分)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.【分析】(1)由⇒AB∥平面A1B1C;(2)可得四边形ABB1A1是菱形,AB1⊥A1B,由AB1⊥B1C1⇒AB1⊥BC⇒AB1⊥面A1BC,⇒平面ABB1A1⊥平面A1BC.【解答】证明:(1)平行六面体ABCD﹣A1B1C1D1中,AB∥A1B1,AB∥A1B1,AB⊄平面A1B1C,A1B1⊂∥平面A1B1C⇒AB∥平面A1B1C;(2)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,⇒四边形ABB1A1是菱形,⊥AB1⊥A1B.在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1⇒AB1⊥BC.∴⇒AB1⊥面A1BC,且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC.【点评】本题考查了平行六面体的性质,及空间线面平行、面面垂直的判定,属于中档题.16.(14分)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.【分析】(1)由已知结合平方关系求得sinα,cosα的值,再由倍角公式得cos2α的值;(2)由(1)求得t an2α,再由cos(α+β)=﹣求得tan(α+β),利用tan(α﹣β)=tan[2α﹣(α+β)],展开两角差的正切求解.【解答】解:(1)由,解得,∴cos2α=;(2)由(1)得,sin2,则tan2α=.∵α,β∈(0,),∴α+β∈(0,π),∴sin(α+β)==.则tan(α+β)=.∴tan(α﹣β)=tan[2α﹣(α+β)]==.【点评】本题考查三角函数的恒等变换及化简求值,考查同角三角函数基本关系式的应用,是中档题.17.(14分)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P 为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.【分析】(1)根据图形计算矩形ABCD和△CDP的面积,求出sinθ的取值范围;(2)根据题意求出年总产值y的解析式,构造函数f(θ),利用导数求f(θ)的最大值,即可得出θ为何值时年总产值最大.【解答】解:(1)S=(40sinθ+10)•80cosθ矩形ABCD=800(4sinθcosθ+cosθ),S△CDP=•80cosθ(40﹣40sinθ)=1600(cosθ﹣cosθsinθ),当B、N重合时,θ最小,此时sinθ=;当C、P重合时,θ最大,此时s inθ=1,∴sinθ的取值范围是[,1);(2)设年总产值为y,甲种蔬菜单位面积年产值为4t(t>0),乙种蔬菜单位面积年产值为3t,则y=3200t(4sinθcosθ+cosθ)+4800t(cosθ﹣cosθsinθ)=8000t(sinθcosθ+cosθ),其中sinθ∈[,1);设f(θ)=sinθcosθ+cosθ,则f′(θ)=cos2θ﹣sin2θ﹣sinθ=﹣2sin2θ﹣sinθ+1;令f′(θ)=0,解得sinθ=,此时θ=,cosθ=;当sinθ∈[,)时,f′(θ)>0,f(θ)单调递增;当sinθ∈(,1)时,f′(θ)<0,f(θ)单调递减;∴θ=时,f(θ)取得最大值,即总产值y最大.S矩形ABCD=800(4sinθcosθ+cosθ),S△CDP=1600(cosθ﹣cosθsinθ),sinθ∈[,1);答:θ=时总产值y最大.【点评】本题考查了解三角形的应用问题,也考查了构造函数以及利用导数求函数的最值问题,是中档题.18.(16分)如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.【分析】(1)由题意可得.,又a2﹣b2=c2=3,解得a=2,b=1即可.(2)①可设直线l的方程为y=kx+m,(k<0,m>0).可得.由,可得(4k2+1)x2+8kmx+4m2﹣4=0,△=(8km)2﹣4(4k2+1)(4m2﹣4)=0,解得k=﹣,m=3.即可②设A(x1,y1),B(x2,y2),联立直线与椭圆方程得(4k2+1)x2+8kmx+4m2﹣4=0,O到直线l的距离d=,|AB|=|x2﹣x1|=,△OAB的面积为S===,解得k=﹣,(正值舍去),m=3.即可【解答】解:(1)由题意可设椭圆方程为,∵焦点F1(﹣,0),F2(,0),∴.∵∴,又a2﹣b2=c2=3,解得a=2,b=1.∴椭圆C的方程为:,圆O的方程为:x2+y2=3.(2)①可知直线l与圆O相切,也与椭圆C,且切点在第一象限,因此k一定小于0,∴可设直线l的方程为y=kx+m,(k<0,m>0).由圆心(0,0)到直线l的距离等于圆半径,可得.由,可得(4k2+1)x2+8kmx+4m2﹣4=0,△=(8km)2﹣4(4k2+1)(4m2﹣4)=0,可得m2=4k2+1,∴3k2+3=4k2+1,结合k<0,m>0,解得k=﹣,m=3.将k=﹣,m=3代入可得,解得x=,y=1,故点P的坐标为(.②设A(x1,y1),B(x2,y2),由⇒k<﹣.联立直线与椭圆方程得(4k2+1)x2+8kmx+4m2﹣4=0,|x2﹣x1|==,O到直线l的距离d=,|AB|=|x2﹣x1|=,△OAB的面积为S===,解得k=﹣,(正值舍去),m=3.∴y=﹣为所求.【点评】本题考查了椭圆的方程,直线与圆、椭圆的位置关系,属于中档题.19.(16分)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x﹣2不存在“S点”;(2)若函数f(x)=ax2﹣1与g(x)=lnx存在“S点”,求实数a的值;(3)已知函数f(x)=﹣x2+a,g(x)=.对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.【分析】(1)根据“S点”的定义解两个方程,判断方程是否有解即可;(2)根据“S点”的定义解两个方程即可;(3)分别求出两个函数的导数,结合两个方程之间的关系进行求解判断即可.【解答】解:(1)证明:f′(x)=1,g′(x)=2x+2,则由定义得,得方程无解,则f(x)=x与g(x)=x2+2x﹣2不存在“S 点”;(2)f′(x)=2ax,g′(x)=,x>0,由f′(x)=g′(x)得=2ax,得x=,f()=﹣=g()=﹣lna2,得a=;(3)f′(x)=﹣2x,g′(x)=,(x≠0),由f′(x0)=g′(x0),假设b>0,得b=﹣>0,得0<x0<1,由f(x0)=g(x0),得﹣x02+a==﹣,得a=x02﹣,令h(x)=x2﹣﹣a=,(a>0,0<x<1),设m(x)=﹣x3+3x2+ax﹣a,(a>0,0<x<1),则m(0)=﹣a<0,m(1)=2>0,得m(0)m(1)<0,又m(x)的图象在(0,1)上不间断,则m(x)在(0,1)上有零点,则h(x)在(0,1)上有零点,则存在b>0,使f(x)与g(x)在区间(0,+∞)内存在“S”点.【点评】本题主要考查导数的应用,根据条件建立两个方程组,判断方程组是否有解是解决本题的关键.20.(16分)设{a n}是首项为a1,公差为d的等差数列,{b n}是首项为b1,公比为q的等比数列.(1)设a1=0,b1=1,q=2,若|a n﹣b n|≤b1对n=1,2,3,4均成立,求d的取值范围;(2)若a1=b1>0,m∈N*,q∈(1,],证明:存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,并求d的取值范围(用b1,m,q表示).【分析】(1)根据等比数列和等差数列的通项公式,解不等式组即可;(2)根据数列和不等式的关系,利用不等式的关系构造新数列和函数,判断数列和函数的单调性和性质进行求解即可.【解答】解:(1)由题意可知|a n﹣b n|≤1对任意n=1,2,3,4均成立,∵a1=0,q=2,∴,解得.即≤d≤.证明:(2)∵a n=a1+(n﹣1)d,b n=b1•q n﹣1,若存在d∈R,使得|a n﹣b n|≤b1对n=2,3,…,m+1均成立,则|b1+(n﹣1)d﹣b1•q n﹣1|≤b1,(n=2,3,…,m+1),即b1≤d≤,(n=2,3,…,m+1),∵q∈(1,],∴则1<q n﹣1≤q m≤2,(n=2,3,…,m+1),∴b1≤0,>0,因此取d=0时,|a n﹣b n|≤b1对n=2,3,…,m+1均成立,下面讨论数列{}的最大值和数列{}的最小值,①当2≤n≤m时,﹣==,当1<q≤时,有q n≤q m≤2,从而n(q n﹣q n﹣1)﹣q n+2>0,因此当2≤n≤m+1时,数列{}单调递增,故数列{}的最大值为.②设f(x)=2x(1﹣x),当x>0时,f′(x)=(ln2﹣1﹣xln2)2x<0,∴f(x)单调递减,从而f(x)<f(0)=1,当2≤n≤m时,=≤(1﹣)=f()<1,因此当2≤n≤m+1时,数列{}单调递递减,故数列{}的最小值为,∴d的取值范围是d∈[,].【点评】本题主要考查等比数列和等差数列以及不等式的综合应用,考查学生的运算能力,综合性较强,难度较大.数学Ⅱ(附加题)【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.(10分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若PC=2,求BC的长.【分析】连接OC,由题意,CP为圆O的切线,得到垂直关系,由线段长度及勾股定理,可以得到PO的长,即可判断△COB是等边三角形,BC的长.【解答】解:连接OC,因为PC为切线且切点为C,所以OC⊥CP.因为圆O的半径为2,,所以BO=OC=2,,所以,所以∠COP=60°,所以△COB为等边三角形,所以BC=BO=2.【点评】本题主要考查圆与直线的位置关系,切线的应用,考查发现问题解决问题的能力.B.[选修4-2:矩阵与变换](本小题满分10分)22.(10分)已知矩阵A=.(1)求A的逆矩阵A﹣1;(2)若点P在矩阵A对应的变换作用下得到点P′(3,1),求点P的坐标.【分析】(1)矩阵A=,求出det(A)=1≠0,A可逆,然后求解A的逆矩阵A﹣1.(2)设P(x,y),通过•=,求出=,即可得到点P的坐标.【解答】解:(1)矩阵A=,det(A)=2×2﹣1×3=1≠0,所以A可逆,从而:A的逆矩阵A﹣1=.(2)设P(x,y),则•=,所以=A﹣1=,因此点P的坐标为(3,﹣1).【点评】本题矩阵与逆矩阵的关系,逆矩阵的求法,考查转化思想的应用,是基本知识的考查.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的方程为ρsin(﹣θ)=2,曲线C的方程为ρ=4cosθ,求直线l被曲线C截得的弦长.【分析】将直线l、曲线C的极坐标方程利用互化公式可得直角坐标方程,利用直线与圆的相交弦长公式即可求解.【解答】解:∵曲线C的方程为ρ=4cosθ,∴ρ2=4ρcosθ,⇒x2+y2=4x,∴曲线C是圆心为C(2,0),半径为r=2得圆.∵直线l的方程为ρsin(﹣θ)=2,∴﹣=2,∴直线l的普通方程为:x﹣y=4.圆心C到直线l的距离为d=,∴直线l被曲线C截得的弦长为2.【点评】本题考查了极坐标方程化为直角坐标方程、直线与圆的相交弦长关系、点到直线的距离公式,属于中档题.D.[选修4-5:不等式选讲](本小题满分0分)24.若x,y,z为实数,且x+2y+2z=6,求x2+y2+z2的最小值.【分析】根据柯西不等式进行证明即可.【解答】解:由柯西不等式得(x2+y2+z2)(12+22+22)≥(x+2y+2z)2,∵x+2y+2z=6,∴x2+y2+z2≥4是当且仅当时,不等式取等号,此时x=,y=,z=,∴x2+y2+z2的最小值为4【点评】本题主要考查不等式的证明,利用柯西不等式是解决本题的关键.,【必做题】第25题、第26题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.25.如图,在正三棱柱ABC﹣A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.【分析】设AC,A1C1的中点分别为O,O1,以{}为基底,建立空间直角坐标系O﹣xyz,(1)由|cos|=可得异面直线BP与AC1所成角的余弦值;(2)求得平面AQC1的一个法向量为,设直线CC1与平面AQC1所成角的正弦值为θ,可得sinθ=|cos|=,即可得直线CC1与平面AQC1所成角的正弦值.【解答】解:如图,在正三棱柱ABC﹣A1B1C1中,设AC,A1C1的中点分别为O,O1,则,OB⊥OC,OO1⊥OC,OO1⊥OB,故以{}为基底,建立空间直角坐标系O﹣xyz,∵AB=AA1=2,A(0,﹣1,0),B(,0,0),C(0,1,0),A1(0,﹣1,2),B1(,0,2),C1(0,1,2).(1)点P为A1B1的中点.∴,∴,.|cos|===.∴异面直线BP与AC1所成角的余弦值为:;(2)∵Q为BC的中点.∴Q()∴,,设平面AQC1的一个法向量为=(x,y,z),由,可取=(,﹣1,1),设直线CC1与平面AQC1所成角的正弦值为θ,sinθ=|cos|==,∴直线CC1与平面AQC1所成角的正弦值为.【点评】本题考查了向量法求空间角,属于中档题.26.设n ∈N *,对1,2,……,n 的一个排列i 1i 2……i n ,如果当s <t 时,有i s >i t ,则称(i s ,i t )是排列i 1i 2……i n 的一个逆序,排列i 1i 2……i n 的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记f n (k )为1,2,…,n 的所有排列中逆序数为k 的全部排列的个数.(1)求f 3(2),f 4(2)的值;(2)求f n (2)(n ≥5)的表达式(用n 表示).【分析】(1)由题意直接求得f 3(2)的值,对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置,由此可得f 4(2)的值;(2)对一般的n (n ≥4)的情形,可知逆序数为0的排列只有一个,逆序数为1的排列只能是将排列12…n 中的任意相邻两个数字调换位置得到的排列,f n (1)=n ﹣1.为计算f n +1(2),当1,2,…,n 的排列及其逆序数确定后,将n +1添加进原排列,n +1在新排列中的位置只能是最后三个位置,可得f n +1(2)=f n (2)+f n (1)+f n (0)=f n (2)+n ,则当n ≥5时,f n (2)=[f n (2)﹣f n ﹣1(2)]+[f n ﹣1(2)﹣f n ﹣2(2)]+…+[f 5(2)﹣f 4(2)]+f 4(2),则f n (2)(n ≥5)的表达式可求.【解答】解:(1)记μ(abc )为排列abc 得逆序数,对1,2,3的所有排列,有μ(123)=0,μ(132)=1,μ(231)=2,μ(321)=3,∴f3(0)=1,f3(1)=f3(2)=2,对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置.因此,f4(2)=f3(2)+f3(1)+f3(0)=5;(2)对一般的n(n≥4)的情形,逆序数为0的排列只有一个:12…n,∴f n(0)=1.逆序数为1的排列只能是将排列12…n中的任意相邻两个数字调换位置得到的排列,f n(1)=n﹣1.为计算f n+1(2),当1,2,…,n的排列及其逆序数确定后,将n+1添加进原排列,n+1在新排列中的位置只能是最后三个位置.因此,f n+1(2)=f n(2)+f n(1)+f n(0)=f n(2)+n.当n≥5时,f n(2)=[f n(2)﹣f n﹣1(2)]+[f n﹣1(2)﹣f n﹣2(2)]+…+[f5(2)﹣f4(2)]+f4(2)=(n﹣1)+(n﹣2)+…+4+f4(2)=.因此,当n≥5时,f n(2)=.【点评】本题主要考查计数原理、排列等基础知识,考查运算求解能力和推理论证能力,是中档题.。
2018年江苏高考数学全真模拟试卷附答案

(第3题)2018年江苏高考数学全真模拟试卷(1)试题Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案直接填写在答题卡相应.....位置上.... 1.已知集合{}1A =,{}1,9B =,则A B =U ▲ . 2.如果复数2i12ib -+(i 为虚数单位)的实部和虚部互为相反数,那么b = ▲ . 3.对一批产品的长度(单位:mm )进行抽样检测,样 本容量为400,检测结果的频率分布直方图如图 所示.根据产品标准可知:单件产品的长度在区间 [25,30)内的为一等品,在区间[20,25)和[30, 35)内的为二等品,其余均为三等品.那么样本中 三等品的件数为 ▲ . 4.执行下面两段伪代码.若Ⅰ与Ⅱ的输出结果相同,则Ⅱ输入的x 的值为 ▲ .5.若将一枚质地均匀的骰子(各面上分别标有1,2,3,4,5,6的正方体玩具)先后抛掷两次,向上的点数依次为m ,n ,则方程220x mx n ++=无实数根的概率是 ▲ . 6.如图1,在△ABC 中,CE 平分∠ACB ,则AEC BEC S ACS BC∆∆=.将这个结论类比到空间:如图2,在三棱锥A BCD -中,平面DEC 平分二面角A CD B --且与AB 交于点E ,则类比的结论为 ▲ .7.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 ▲ .8.已知集合{}()0A x x x a =-<,{}27180B x x x =--<.若A B ⊆,则实数a 的取值范围是 ▲ . 9.已知函数24()2.x x a f x x x x a +<⎧=⎨-≥⎩,,,若对任意的实数b ,总存在实数0x ,使得0()f x b =,则实数a 的取值范围是 ▲ .10.若函数()f x 满足(1)(1)f x f x +=-,且当[]1 1x ∈-,时,2()f x x =,则函数(第6题)1x ← 2x x ← 3x x ← Print x I Read x 26y x ←+ Print y (第4题)4()() log F x f x x =-的零点个数为 ▲.11.若πtan 2tan 5α=,则3πcos()10πsin()5αα-=- ▲ .12.如图,在△ABC 中,D 为BC 的中点,E 为AD 的中点,直线BE 与边AC 交于点F .若6AD BC ==,则AB CF ⋅=u u u r u u u v▲ .13.如图,点C 在半圆的直径AB 的延长线上,2AB BC ==,过动点P 作半圆的切线PQ .若3PC PQ =,则△PAC 面积的最大值为 ▲ .14.已知等差数列{}n a 的公差d 不为0,等比数列{}n b 的公比q 是小于1的正有理数.若1a d =,21b d =,且222123123a a ab b b ++++是正整数,则q 的值是 ▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,角A B C ,,的对边分别为a b c ,,,且sin 6sin a C c B =. (1)求ab的值; (2)若126b c ==,,求cos C 及△ABC 的面积.(第12题)(第13题)如图,在四棱柱1111ABCD A B C D -中,平面11A ABB ⊥平面ABCD ,且∠π2ABC =. (1)求证:BC ∥平面11AB C ; (2)求证:平面11A ABB ⊥平面11AB C .17.(本小题满分14分)某企业拟建造如图所示的容器(不计厚度),容器的中间为圆柱形,左、右两端均为半球形.按照设计要求,容器的体积为80π3m 3,且l ≥2r .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米的建造费用为3000元,半球形部分每平方米的建造费用为c (c >3000)元.设该容器的建造费用为y 元. (1)写出y 关于r 的函数表达式,并求该函数的定义域; (2)求该容器的建造费用最小时r 的值.(第16题) (第17题)已知椭圆2222 1(0)x y C a b a b+=>>:的右焦点为F ,过椭圆C 的中心的弦PQ 的长为2,且∠90PFQ =o,△PQF 的面积为1. (1)求椭圆C 的方程;(2)设12A A ,分别为椭圆C 的左、右顶点,S为直线x =上的一个动点,直线1A S 交椭圆C 于点M ,直线2A S 交椭圆C 于点N ,若12S S ,分别为△12A SA ,△MSN 的面积,求12S S 的最大值. 19.(本小题满分16分)已知数列{}n a 是各项均为正数的等比数列,其前n 项和为n S ,且1564a a =,5348S S -=.(1)求数列{}n a 的通项公式;(2)若存在正整数(5)m l m l <<,,使得5 5m l a a a ,,成等差数列,求m l ,的值; (3)设 k m l *∈N ,,,k m l <<,对于给定的k ,求5 k m l a a a ,,经适当排序后能构成等差数列的充要条件.20.(本小题满分16分)已知函数211()log 22a f x x x =+-,且曲线()f x 上任意一点处的切线的斜率不小于2. (1)求a 的最大值;(2)当a 取最大值时,若()()2()g x f x kx k =-∈R 有两个极值点12x x ,,且12x x <,求证:2()()4g x g k +<-.试题Ⅱ(附加题)21.【选做题】本题包括A 、B 、C 、D 四小题,请选定其中两小题........,并在相应的答题区域.........内作答....若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4-1:几何证明选讲](本小题满分10分)如图,已知AD 是△ABC 的外角∠EAC 的平分线,交BC 的延长线于点D ,延长DA 交△ABC 的外接圆于点F ,连接FB ,FC . (1)求证:FB FC =; (2)求证:2FB FA FD =⋅.B .[选修4-2:矩阵与变换](本小题满分10分)在平面直角坐标系中,已知A (0,0),B (2,0),C (2,2),D (0,2),先将正方形ABCD 绕原点逆时针旋转90°,再将所得图形上所有点的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵M . C .[选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,圆C 的参数方程为cos 2sin 2x r y r θθ=+⎧⎨=+⎩,(θ为参数,0r >).以原点O 为极点,x 轴的正半轴为极轴,建立极坐标系,直线l 的极坐标方程为π2sin()104ρθ++=.(1)求圆C 的圆心的极坐标;(2)当圆C 与直线l 有公共点时,求r 的取值范围.(第21-A 题)D .[选修4-5:不等式选讲](本小题满分10分)设a b ,为互不相等的正实数,求证:3334()()a b a b +>+.【必做题】第22题、第23题,每小题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)如图,在底面为正方形的四棱锥P ABCD -中,侧棱PD ⊥底面ABCD ,PD DC =,E 是线段PC 的中点.(1)求异面直线AP 与BE 所成角的大小;(2)若点F 在线段PB 上,且二面角F DE B --的平面角的正弦值为3,求PF PB的值.23.(本小题满分10分)已知数列{}n a 的前n 项和为n S ,通项公式为1n a n =,且2211()2n n n S n f n S S n -=⎧=⎨-≥⎩,,,. (1)计算(1)(2)(3)f f f ,,的值;(2)比较()f n 与1的大小,并用数学归纳法证明你的结论.(第22题)2018年江苏高考数学全真模拟试卷(1)试题Ⅰ参考答案一、填空题 1.{}1,9 2.23-3.100 4.0 5.7366.A CDE ACD B CDE BDC V S V S -∆-∆=7.3 8.[]2,9- 9.[]5,4- 10.4 11.3 12.18- 1314.12二、解答题15.解:(1)因为sin 6sin a C c B =,所以6ac bc =, ……………………………………………………4分 所以6a b =,即6ab=. ……………………………………………………6分 (2)因为6ab=,1b =, 所以6a =,故2223612611cos 226112a b c C ab +-+-===⨯⨯,………………………………………………10分所以sin 12C =因此1sin 24ABC S ab C ∆==. ……………………………………………………14分 16.证明:(1)在四棱柱1111ABCD A B C D -中,BC ∥11B C , 又因为BC ⊄平面11AB C ,11B C ⊂平面11AB C ,所以BC ∥平面11AB C . ……………………………………………………6分 (2)因为平面11A ABB ⊥平面ABCD ,平面11A ABB I 平面ABCD AB =,BC ⊂平面ABCD ,又由∠π2ABC =知AB ⊥BC , 所以BC ⊥平面11A ABB . ……………………………………………………10分 又因为BC ∥11B C ,故11B C ⊥平面11A ABB . ……………………………………………………12分 而11B C ⊂平面11AB C ,所以平面11A ABB ⊥平面11AB C . ……………………………………………………14分 17.解:(1)设该容器的体积为V . 由题意知23480πππ33V r l r =+=, 故32224π8044203()π333V r l r r r r r -==-=-.由于2l r ≥,因此02r <≤,所以建造费用2224202π30004π2π()30004π3y rl r c r r r c r=⨯+=⨯-⨯+ 2160000π4π(2000)02c r r r=-+<≤,.…………………………………………………6分 (2)由(1)得:322160000π8π(2000)200008π(2000)()022000c y c r r r r r c -'=--=-<≤-,. 由于3000c >,因此20000c ->. 当32000002000r c -=-时,r =m =,则0m >,所以2228π(2000)()()c y r m r rm m r-'=-++. ① 当02m <<,即4500c >时,易得r m =是函数y 的极小值点,也是最小值点. ② 当2m ≥,即30004500c <≤时,由于(]0 2r ∈,,故0y '≤,因此函数y 单调递减, 所以2r =是函数y 的最小值点.综上,当30004500c <≤,且建造费用最小时,2r =;当4500c >,且建造费用最小时,r =. …………………………………………………14分18.解:(1)因为弦PQ 过椭圆C 的中心,且∠90PFQ =o, 所以112c OF PQ ===. 不妨设0000(,)(,0)P x y x y >,所以000121012PFQ S OF y y x b ∆=⋅==⇒=⇒=, 所以椭圆C 的方程为2212x y +=. …………………………………………………6分 (2)由(1)得:1(A,2A,设)S t , 可得直线1A S的方程为:x y =跟椭圆C 的方程2212x y +=联立得:221812(2)0y y t t+-=, 解得12260,9ty y t ==+, 代入直线1A S的方程得:2269t x t ===+,所以2226(,)99tM t t ++. …………………………………………………9分 同理可得直线2A S的方程为:x y t=, 跟椭圆C 的方程2212x y +=联立得:2224(2)0y y t t++=, 解得12220,1ty y t ==-+, 代入直线2A S的方程得:222222()111t x t t t t =⋅-=-+=+++,所以22)1tN t -+. ………………………………………………12分 因此121211221sin 21sin 2SA SA A SA S SA SA S SM SN SM SN MSN ⋅⋅∠⋅==⋅⋅⋅∠=222222222(9)(33)2911433(3)33t t t t t t t ⎡⎤+++⎢⎥++⎣⎦=⋅≤⋅=+++,当且仅当22933t t +=+,即t ==”.………………………………………16分 19.解:(1)因为数列{}n a 是各项均为正数的等比数列, 所以设数列{}n a 的公比为q ,且0q >.因为215364a a a ==,且30a >,所以38a =. 又因为5348S S -=,所以2458848a a q q +=+=,解得2q =,所以2nn a =. …………………………………………………3分(2)因为5 5m l a a a ,,成等差数列, 所以510m l a a a =+,即510222m l ⋅=+, 所以66522m l --=+, 故62m -,62l -中有且只有一个等于1.因为正整数m ,l 满足5m l <<,所以662124m l --⎧=⎪⎨=⎪⎩,解得68m n =⎧⎨=⎩. …………………………………………………8分(3)设5k a ,m a ,l a 经适当排序后能构成等差数列. ① 若25k m l a a a ⋅=+,则10222k m l⋅=+,所以11522m k l k ----=+.因为正整数k ,m ,l 满足k m l <<,所以110l k m k -->--≥,且11l k --≥, 所以11221l k m k ---->≥,122l k --≥.即112124m k l k ----⎧=⎪⎨=⎪⎩,解得13m k l k =+⎧⎨=+⎩. …………………………………………………10分 ② 若25m k l a a a =+,则22522m k l ⋅=⋅+,所以1225m k l k +---=(*).因为12m k +-≥,2l k -≥,所以12m k +-与2l k -都为偶数,而5是奇数,所以等式(*)不成立,从而等式25m k l a a a =+不成立. …………………………………………………12分 ③ 若25l k m a a a =+,则同②可知,该等式也不成立.综上所述,1m k =+,3l k =+.故5k a ,m a ,l a 为5k a ,1k a +,3k a +,即5k a ,2k a ,8k a .调整顺序后易知2k a ,5k a ,8k a 成等差数列.……………………………………………15分 因此,5k a ,m a ,l a 经适当排序后能构成等差数列的充要条件为13m k l k =+⎧⎨=+⎩.………16分 20.解:(1)由题意知1()ln f x x x a'=+. 当01a <<时,()2f x '≥不能恒成立,则1a >,此时1()2ln f x x x a '=+≥,即ln 1a ≤,故1e a <≤. 因此a 的最大值为e . …………………………………………………4分 (2)因为211()()2ln 2(0)22g x f x kx x x kx x =-=+-->, 所以1()2g x x k x'=+-. ① 当1k ≤时,1()22220g x x k k k x '=+-≥=-≥, 所以函数()g x 在(0,+∞)上单调递增,故函数()g x 在(0,+∞)上无极值.……6分③ 当1k >时,2121()2x kx g x x k x x-+'=+-=. 由()0g x '=得2210x kx -+=,24(1)0k ∆=->.设方程2210x kx -+=的两根分别为1x ,2x (12x x <),则122x x k +=,121x x =,其中1201x k x k <=<<=+所以()g x 在(0,1x )上单调递增,在(1x ,2x )上单调递减,在(2x ,+∞)上单调递增,从而()g x 有两个极值点1x ,2x . …………………………………………………9分222221()ln 222x g x x kx =+-- 2221221ln ()22x x x x x =+-+- 22222211ln ()22x x x x x =+-+- 2223ln 22x x =--, 构造函数23()ln (1)22x h x x x =-->,则1()0h x x x'=-<, 所以()h x 在(1,+∞)上单调递减,且(1)2h =-,故2()2g x <-.…………………12分 又231()ln (1)22k g k k k =-->, 构造函数231()ln (1)22x x x x ϕ=-->,则1()30x x xϕ'=-<, 所以()x ϕ在(1,+∞)上单调递减,且(1)2ϕ=-,故()2g k <-.…………………15分 所以2()()4g x g k +<-. …………………………………………………16分试题Ⅱ(附加题)参考答案21-A .证明:(1)因为AD 平分∠EAC ,所以∠EAD =∠DAC .因为四边形AFBC 是圆的内接四边形,所以∠DAC =∠FBC .因为∠EAD =∠FAB =∠FCB ,所以∠FBC =∠FCB ,所以FB =FC . …………………………………………………5分(2)因为∠FAB =∠FCB =∠FBC ,∠AFB =∠BFD ,所以△FBA ∽△FDB , 所以FB FA FD FB=,即2FB FA FD =⋅. ………………………………………………10分21-B .解:设将正方形ABCD 绕原点逆时针旋转90°所对应的矩阵为A , 则01cos90sin 9010sin 90cos90-⎡⎤-⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦o o o o A . ………………………………………………3分 设将所得图形上所有点的纵坐标压缩为原来的一半、横坐标不变对应的矩阵为B , 则10102⎡⎤⎢⎥=⎢⎥⎣⎦B . …………………………………………………6分 所以连续两次变换所对应的矩阵10010111100022-⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦M BA =.……………10分21-C .解:(1)由圆C :cos 2sin 2x r y r θθ=+⎧⎨=+⎩,得222(2)(2)x y r -+-=, 所以圆C 的圆心的直角坐标为(2,2), 故圆C的圆心的极坐标为,π)4. ………………………………………………5分(2)将直线lπsin()104θ++=化为10x y ++=,从而圆心(2,2)到直线l的距离为2d ==. 因为圆C 与直线l 有公共点,所以d r ≤,即2r ≥,故r 的取值范围是52,2⎡⎫+∞⎪⎢⎪⎣⎭. ………………………………………………10分 21-D .证明:因为0a >,0b >,所以要证3334()()a b a b +>+,只要证2234()()()a b a ab b a b +-+>+,即要证2224()()a ab b a b -+>+,只需证23()0a b ->.而a b ≠,故23()0a b ->成立. ………………………………………………10分22.解:(1)在四棱锥P ABCD -中,底面ABCD 为正方形,侧棱PD ⊥底面ABCD , 所以DA ,DC ,DP 两两垂直, 故以{},,DA DC DP u u u r u u u r u u u r 为正交基底,建立如图所示的空间直角坐标系D xyz -. 因为PD DC =,所以DA DC DP ==.不妨设2DA DC DP ===,则D (0,0,0),A (2,0,0),C (0,2,0),P (0,0,2),B (2,2,0). 因为E 是PC 的中点,所以E (0,1,1),故AP u u u r =(-2,0,2),BE u u u r =(-2,-1,1)所以cos ,AP BE 〈〉u u u r u u u r =AP BE AP BE⋅⋅u u u r u u u r u u u r u u u r =3, 从而,AP BE 〈〉u u u r u u u r =π6. 因此异面直线AP 与BE 所成角的大小为π6.………………………………………………4分 (2)由(1)可知DE u u u r =(0,1,1),DB u u u r =(2,2,0),PB u u u r =(2,2,-2). 设PF u u u r =PB λu u u r ,则PF u u u r =(2λ,2λ,-2λ),从而DF u u u r =DP u u u r +PF u u u r =(2λ,2λ,2-2λ).设m =(1x ,1y ,1z )为平面DEF 的一个法向量,则00DF DE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r m m ,即1211122(22)00x y z y z λλλ++-=⎧⎨+=⎩. 取1z =λ,则1y =-λ,1x =2λ-1,所以m =(2λ-1,-λ,λ)为平面DEF 的一个法向量.…………………………………6分 设n =(2x ,2y ,2z )为平面DEB 的一个法向量,则00DB DE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n ,即22222200x y y z +=⎧⎨+=⎩. 取2x =1,则2y =-1,2z =1,所以n =(1,-1,1)为平面DEB 的一个法向量.………………………………………8分 因为二面角F DE B --, 所以二面角F DE B --即cos ,⋅〈〉===⋅m nm n m n , 化简得241λ=.因为点F 在线段PB 上,所以0≤λ≤1,故λ=12,即PF PB =12.……………………………………………………………………10分23.解:(1)213(1)122f S ==+=, 4111113(2)23412f S S =-=++=, 62111119(3)345620f S S =-=+++=.………………………………………………………3分 (2)由(1)知(1)1f >,(2)1f >.下面用数学归纳法证明:当3n ≥时,()1f n <.由(1)知当3n =时,()1f n <.……………………………………………………………5分 假设当(3)n k k =≥时,()1f n <,即111()112f k k k k=++⋅⋅⋅+<+,那么11111(1)1222122f k k k k k k +=++⋅⋅⋅+++++++ 1111111()1222122k k k k k k k=+++⋅⋅⋅+++-++++ 11111()()212222k k k k<+-+-++ 2(21)2(22)12(21)2(22)k k k k k k k k -+-+=++++ 11112(21)(22)k k k k =--<++, 所以当1n k =+时,()1f n <也成立.………………………………………………………8分 因此,当3n ≥时,()1f n <.综上,当1n =和2n =时,()1f n >;当3n ≥时,()1f n <.…………………………10分。
2018江苏高考数学试题及答案解析

2018年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知集合{}8,2,1,0=A ,{}8,6,1,1-=B ,那么=⋂B A .2.若复数z 满足i z i 21+=⋅,其中i 是虚数单位,则z 的实部为 .3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 .4.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 .5.函数()1log 2-=x x f 的定义域为 .6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 .7.已知函数()⎪⎭⎫ ⎝⎛<<-+=222sin ππϕx x y 的图象关于直线3π=x 对称,则ϕ的值是 .8.在平面直角坐标系xOy 中,若双曲线()0,012222>>=-b a by a x 的右焦点()0,c F 到一条渐近线的距离为c 23,则其离心率的值是 . 9.函数()x f 满足()()()R x x f x f ∈=+4,且在区间]2,2(-上,()⎪⎪⎩⎪⎪⎨⎧≤<-+≤<=02,2120,2cos x x x xx f π, 则()()15f f 的值为 .10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .11.若函数()()R a ax x x f ∈+-=1223在()+∞,0内有且只有一个零点,则()x f 在[]1,1-上的最大值与最小值的和为 .12.在平面直角坐标系xOy 中,A 为直线x y l 2:=上在第一象限内的点,()0,5B ,以AB 为直径的圆C 与直线l 交于另一点D .若0=⋅CD AB ,则点A 的横坐标为 .13.在ABC ∆中,角C B A 、、所对的边分别为c b a 、、,120=∠ABC ,ABC ∠的平分线交AC 于点D ,且1=BD ,则c a +4的最小值为 .14.已知集合{}*∈-==Nn n x x A ,12|,{}*∈==N n x x B n,2|.将B A ⋃的所有元素从小到大依次排列构成一个数列{}n a ,记n S 为数列{}n a 的前n 项和,则使得112+>n n a S 成立的n 的最小值为 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在平行六面体1111ABCD A B C D -中,1111,AA AB AB B C =⊥. 求证:(1)11AB A B C 平面∥; (2)111ABB A A BC ⊥平面平面.16.(本小题满分14分)已知,αβ为锐角,4tan 3α=,5cos()αβ+=.(1)求cos2α的值; (2)求tan()αβ-的值.17.(本小题满分14分)某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧MPN (P 为此圆弧的中点)和线段MN 构成.已知圆O 的半径为40米,点P 到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD ,大棚Ⅱ内的地块形状为CDP △,要求,A B 均在线段MN 上,,C D 均在圆弧上.设OC 与MN 所成的角为θ.(1)用θ分别表示矩形ABCD 和CDP △的面积,并确定sin θ的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C 过点1(3,)2,焦点12(3,0),(3,0)F F -,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标; ②直线l 与椭圆C 交于,A B 两点.若OAB △26,求直线l 的方程.19.(本小题满分16分)记(),()f x g x ''分别为函数(),()f x g x 的导函数.若存在0x ∈R ,满足00()()f x g x =且00()()f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.(1)证明:函数()f x x =与2()22g x x x =+-不存在“S 点”; (2)若函数2()1f x ax =-与()ln g x x =存在“S 点”,求实数a 的值;(3)已知函数2()f x x a =-+,e ()xb g x x=.对任意0a >,判断是否存在0b >,使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”,并说明理由.20.(本小题满分16分)设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列. (1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围;(2)若*110,,a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+均成立,并求d 的取值范围(用1,,b m q 表示).数学Ⅱ(附加题)21.【选做题】本题包括A、B、C、D 四小题,请选定其中两小题,并在相应的答题区域内作答......................若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A.[选修4—1:几何证明选讲](本小题满分10分)如图,圆O的半径为2,AB为圆O的直径,P为AB延长线上一点,过P作圆O的切线,切点为C.若23PC=,求BC的长.B.[选修4—2:矩阵与变换](本小题满分10分)已知矩阵2312⎡⎤=⎢⎥⎣⎦A.(1)求A的逆矩阵1-A;(2)若点P在矩阵A对应的变换作用下得到点(3,1)P',求点P的坐标.C.[选修4—4:坐标系与参数方程](本小题满分10分)在极坐标系中,直线l的方程为πsin()26ρθ-=,曲线C的方程为4cosρθ=,求直线l被曲线C截得的弦长.D.[选修4—5:不等式选讲](本小题满分10分)若x,y,z为实数,且x+2y+2z=6,求222x y z++的最小值.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.学科#网22.(本小题满分10分)如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.23.(本小题满分10分)设*n ∈N ,对1,2,···,n 的一个排列12n i i i ,如果当s <t 时,有s t i i >,则称(,)s t i i 是排列12n i i i 的一个逆序,排列12n i i i 的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记()n f k 为1,2,···,n 的所有排列中逆序数为k 的全部排列的个数.(1)求34(2),(2)f f 的值;(2)求(2)(5)n f n ≥的表达式(用n 表示).数学Ⅰ试题参考答案一、填空题:本题考查基础知识、基本运算和基本思想方法.每小题5分,共计70分. 1.{1,8}2.23.904.8 5.[2,+∞) 6.310 7.π6-8.2 9.2210.4311.–312.313.914.27二、解答题15.本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,考查空间想象能力和推理论证能力.满分14分.证明:(1)在平行六面体ABCD -A 1B 1C 1D 1中,AB ∥A 1B 1. 因为AB ⊄平面A 1B 1C ,A 1B 1⊂平面A 1B 1C , 所以AB ∥平面A 1B 1C .(2)在平行六面体ABCD -A 1B 1C 1D 1中,四边形ABB 1A 1为平行四边形. 又因为AA 1=AB ,所以四边形ABB 1A 1为菱形, 因此AB 1⊥A 1B .又因为AB 1⊥B 1C 1,BC ∥B 1C 1, 所以AB 1⊥BC .又因为A 1B ∩BC =B ,A 1B ⊂平面A 1BC ,BC ⊂平面A 1BC , 所以AB 1⊥平面A 1BC . 因为AB 1⊂平面ABB 1A 1, 所以平面ABB 1A 1⊥平面A 1BC .16.本小题主要考查同角三角函数关系、两角和(差)及二倍角的三角函数,考查运算求解能力.满分14分.解:(1)因为4tan 3α=,sin tan cos ααα=,所以4sin cos 3αα=. 因为22sin cos 1αα+=,所以29cos 25α=, 因此,27cos22cos 125αα=-=-. (2)因为,αβ为锐角,所以(0,π)αβ+∈.又因为5cos()5αβ+=-,所以225sin()1cos ()5αβαβ+=-+=, 因此tan()2αβ+=-.因为4tan 3α=,所以22tan 24tan 21tan 7ααα==--, 因此,tan 2tan()2tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+.17.本小题主要考查三角函数的应用、用导数求最值等基础知识,考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.满分14分.解:(1)连结PO 并延长交MN 于H ,则PH ⊥MN ,所以OH =10. 过O 作OE ⊥BC 于E ,则OE ∥MN ,所以∠COE =θ, 故OE =40cos θ,EC =40sin θ,则矩形ABCD 的面积为2×40cos θ(40sin θ+10)=800(4sin θcos θ+cos θ), △CDP 的面积为12×2×40cos θ(40–40sin θ)=1600(cos θ–sin θcos θ). 过N 作GN ⊥MN ,分别交圆弧和OE 的延长线于G 和K ,则GK =KN =10. 令∠GOK =θ0,则sin θ0=14,θ0∈(0,π6). 当θ∈[θ0,π2)时,才能作出满足条件的矩形ABCD , 所以sin θ的取值范围是[14,1). 答:矩形ABCD 的面积为800(4sin θcos θ+cos θ)平方米,△CDP 的面积为 1600(cos θ–sin θcos θ),sin θ的取值范围是[14,1). (2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,设甲的单位面积的年产值为4k ,乙的单位面积的年产值为3k (k >0), 则年总产值为4k ×800(4sin θcos θ+cos θ)+3k ×1600(cos θ–sin θcos θ) =8000k (sin θcos θ+cos θ),θ∈[θ0,π2). 设f (θ)= sin θcos θ+cos θ,θ∈[θ0,π2), 则222()cos sin sin (2sin sin 1)(2sin 1)(sin 1)f θθθθθθθθ=--=-+-=--+′. 令()=0f θ′,得θ=π6, 当θ∈(θ0,π6)时,()>0f θ′,所以f (θ)为增函数;当θ∈(π6,π2)时,()<0f θ′,所以f (θ)为减函数, 因此,当θ=π6时,f (θ)取到最大值. 答:当θ=π6时,能使甲、乙两种蔬菜的年总产值最大. 18.本小题主要考查直线方程、圆的方程、圆的几何性质、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系等知识,考查分析问题能力和运算求解能力.满分16分. 解:(1)因为椭圆C的焦点为12(),F F -,可设椭圆C 的方程为22221(0)x y a b a b +=>>.又点1)2在椭圆C 上,所以2222311,43,a ba b ⎧+=⎪⎨⎪-=⎩,解得224,1,a b ⎧=⎪⎨=⎪⎩ 因此,椭圆C 的方程为2214x y +=.因为圆O 的直径为12F F ,所以其方程为223x y +=.(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>,则22003x y +=, 所以直线l 的方程为0000()x y x x y y =--+,即0003x y x y y =-+. 由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩,消去y ,得222200004243640()x y x x x y +-+-=.(*)因为直线l 与椭圆C 有且只有一个公共点,所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=. 因为00,0x y >,所以001x y =. 因此,点P的坐标为. ②因为三角形OAB,所以1 2AB OP ⋅AB =. 设1122,,()(),A x y B x y ,由(*)得2200022001,22448(2)2(4)x y x x x y ±-=+,所以2222121()()x B y y x A =-+- 222000222200048(2)(1)(4)x y x y x y -=+⋅+.因为22003x y +=,所以22022016(2)32(1)49x AB x -==+,即42002451000x x -+=, 解得22005(202x x ==舍去),则2012y =,因此P 的坐标为102(,)22.综上,直线l 的方程为532y x =-+.19.本小题主要考查利用导数研究初等函数的性质,考查综合运用数学思想方法分析与解决问题以及逻辑推理能力.满分16分.解:(1)函数f (x )=x ,g (x )=x 2+2x -2,则f ′(x )=1,g ′(x )=2x +2. 由f (x )=g (x )且f ′(x )= g ′(x ),得 222122x x x x ⎧=+-⎨=+⎩,此方程组无解, 因此,f (x )与g (x )不存在“S ”点. (2)函数21f x ax =-(),()ln g x x =, 则12f x ax g x x'='=(),(). 设x 0为f (x )与g (x )的“S ”点,由f (x 0)与g (x 0)且f ′(x 0)与g ′(x 0),得200001ln 12ax x ax x ⎧-=⎪⎨=⎪⎩,即200201ln 21ax x ax ⎧-=⎪⎨=⎪⎩,(*) 得01ln 2x =-,即120e x -=,则1221e 22(e )a -==. 当e2a =时,120e x -=满足方程组(*),即0x 为f (x )与g (x )的“S ”点.因此,a 的值为e2.(3)对任意a >0,设32()3h x x x ax a =--+.因为(0)0(1)1320h a h a a =>=--+=-<,,且h (x )的图象是不间断的,所以存在0x ∈(0,1),使得0()0h x =,令03002e (1)x x b x =-,则b >0.函数2e ()()xb f x x a g x x=-+=,,则2e (1)()2()x b x f x x g x x -=-=′,′. 由f (x )与g (x )且f ′(x )与g ′(x ),得22e e (1)2xx b x a x b x x x ⎧-+=⎪⎪⎨-⎪-=⎪⎩,即00320030202e e (1)2e (1)2e (1)x x xx x x a x x x x x x x ⎧-+=⋅⎪-⎪⎨-⎪-=⋅⎪-⎩(**) 此时,0x 满足方程组(**),即0x 是函数f (x )与g (x )在区间(0,1)内的一个“S 点”. 因此,对任意a >0,存在b >0,使函数f (x )与g (x )在区间(0,+∞)内存在“S 点”.20.本小题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.满分16分. 解:(1)由条件知:112(,)n n n a n d b -=-=. 因为1||n n a b b -≤对n =1,2,3,4均成立, 即1 12|()1|n n d ---≤对n =1,2,3,4均成立, 即1≤1,1≤d ≤3,3≤2d ≤5,7≤3d ≤9,得7532d ≤≤. 因此,d 的取值范围为75[,]32.(2)由条件知:111(1),n n n a b n d b b q -=+-=.若存在d ,使得1||n n a b b -≤(n =2,3,···,m +1)成立, 即1111|1|2,3,,(1())n b n d b q b n m -+--≤=+,即当2,3,,1n m =+时,d 满足1111211n n q q b d b n n ---≤≤--.因为q ∈,则112n m q q -<≤≤,从而11201n q b n --≤-,1101n q b n ->-,对2,3,,1n m =+均成立.因此,取d =0时,1||n n a b b -≤对2,3,,1n m =+均成立.下面讨论数列12{}1n q n ---的最大值和数列1{}1n q n --的最小值(2,3,,1n m =+). ①当2n m ≤≤时,111 2222111()()()n n n n n n n n q q nq q nq n q q q n n n n n n -------+--+-==---, 当112mq <≤时,有2n m q q ≤≤,从而1() 20n n n n q q q ---+>.因此,当21n m ≤≤+时,数列12{}1n q n ---单调递增,故数列12{}1n q n ---的最大值为2m q m-. ②设()()21x f x x =-,当x >0时,ln 21(0(n )l 22)x f x x '=--<, 所以()f x 单调递减,从而()f x <f (0)=1.当2n m ≤≤时,111112111()()()nn n q q n n f q n n n n --=≤-=<-, 因此,当21n m ≤≤+时,数列1{}1n q n --单调递减,故数列1{}1n q n --的最小值为mq m. 因此,d 的取值范围为11(2)[,]m mb q b q m m-.数学Ⅱ(附加题)参考答案21.【选做题】A .[选修4—1:几何证明选讲]本小题主要考查圆与三角形等基础知识,考查推理论证能力.满分10分. 证明:连结OC .因为PC 与圆O 相切,所以OC ⊥PC .又因为PC =OC =2,所以OP .又因为OB =2,从而B 为Rt △OCP 斜边的中点,所以BC =2. B .[选修4—2:矩阵与变换]本小题主要考查矩阵的运算、线性变换等基础知识,考查运算求解能力.满分10分. 解:(1)因为2312⎡⎤=⎢⎥⎣⎦A ,det()221310=⨯-⨯=≠A ,所以A 可逆, 从而1-A 2312-⎡⎤=⎢⎥-⎣⎦. (2)设P (x ,y ),则233121x y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,所以13311x y -⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A , 因此,点P 的坐标为(3,–1). C .[选修4—4:坐标系与参数方程]本小题主要考查曲线的极坐标方程等基础知识,考查运算求解能力.满分10分. 解:因为曲线C 的极坐标方程为=4cos ρθ, 所以曲线C 的圆心为(2,0),直径为4的圆.因为直线l 的极坐标方程为πsin()26ρθ-=,则直线l 过A (4,0),倾斜角为π6, 所以A 为直线l 与圆C 的一个交点. 设另一个交点为B ,则∠OAB =π6. 连结OB ,因为OA 为直径,从而∠OBA =π2,所以π4cos6AB ==因此,直线l 被曲线C 截得的弦长为23. D .[选修4—5:不等式选讲]本小题主要考查柯西不等式等基础知识,考查推理论证能力.满分10分. 证明:由柯西不等式,得2222222()(122)(22)x y z x y z ++++≥++. 因为22=6x y z ++,所以2224x y z ++≥, 当且仅当122x y z ==时,不等式取等号,此时244333x y z ===,,, 所以222x y z ++的最小值为4.22.【必做题】本小题主要考查空间向量、异面直线所成角和线面角等基础知识,考查运用空间向量解决问题的能力.满分10分.学科%网解:如图,在正三棱柱ABC −A 1B 1C 1中,设AC ,A 1C 1的中点分别为O ,O 1,则OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,以1,{},OB OC OO 为基底,建立空间直角坐标系O −xyz . 因为AB =AA 1=2,所以1110,1,0,3,0,0,0,1,0,0,1,()()()()(2,3,0,2,0,1,2)()A B C A B C --.(1)因为P 为A 1B 1的中点,所以31(,2)2P -, 从而131(,,2)(0,2,222),BP AC ==--, 故111|||310|cos ,|||||522BP AC BP AC BP AC ⋅-===⋅⨯. 因此,异面直线BP 与AC 1310.(2)因为Q 为BC的中点,所以1,0)2Q , 因此33(,0)22AQ =,11(0,2,2),(0,0,2)AC CC ==. 设n =(x ,y ,z )为平面AQC 1的一个法向量, 则10,0,AQ AC ⎧⎪⎨⎪⎩⋅=⋅=n n 即30,2220.y y z +=⎪+=⎩ 不妨取1,1)=-n ,设直线CC 1与平面AQC 1所成角为θ,则111||sin |cos |,|||CC CC CC |θ==⋅⋅==n n n 所以直线CC 1与平面AQC 1. 23.【必做题】本小题主要考查计数原理、排列等基础知识,考查运算求解能力和推理论证能力.满分10分.解:(1)记()abc τ为排列abc 的逆序数,对1,2,3的所有排列,有(123)=0(132)=1(213)=1(231)=2(312)=2(321)=3ττττττ,,,,,,所以333(0)1(1)(2)2f f f ===,.对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置.因此,4333(2)(2)(1)(0)5f f f f =++=.(2)对一般的n (n ≥4)的情形,逆序数为0的排列只有一个:12…n ,所以(0)1n f =.逆序数为1的排列只能是将排列12…n 中的任意相邻两个数字调换位置得到的排列,所以(1)1n f n =-. 为计算1(2)n f +,当1,2,…,n 的排列及其逆序数确定后,将n +1添加进原排列,n +1在新排列中的位置只能是最后三个位置.因此,1(2)(2)(1)(0)(2)n n n n n f f f f f n +=++=+. 当n ≥5时,112544(2)[(2)(2)][(2)(2)][(2)(2)](2)n n n n n f f f f f f f f ---=-+-++-+…242(1)(2)4(2)2n n n n f --=-+-+⋯++=, 因此,n ≥5时,(2)n f =222n n --.。
2018年江苏省南通市高考模拟试卷(九)数学(文)试题(word版)

(第3题)2018年江苏省南通市高考模拟试卷(九)数学(文)试题第Ⅰ卷(必做题,共160分)一、填空题:本大题共14小题,每小题5分,共70分.1. 设集合A = {1,x },B = {2,3,4},若A ∩B ={4},则x 的值为 ▲ . 2. 若复数z 1=2+i ,z 1·z2()2z =5,则z 2= ▲ .3. 对一批产品的长度(单位:毫米)进行抽样检测,样本容量为200,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为 ▲ .4. 执行如图所示的流程图,会输出一列数,则这列数中的第3个数为 ▲ . 5. 为活跃气氛,某同学微信群进行了抢红包活动.某同学发了一个“长长久久”随机分配红包,总金额为9.9元,随机分配成5份,金额分别为2.53元,1.19元,3.21元, 0.73元,2.33元,则身处海外的两名同学抢得的金额之和不低于5元的概率为 ▲ . 6. 函数22log (32)y x x =--的值域为 ▲ .7. 已知P -ABC 是正三棱锥,其外接球O 的表面积为16π,且∠APO =∠BPO =∠CPO=30°,则三棱锥的体积为 ▲ .8. 已知双曲线2214y x -=的左、右顶点为A 、B ,焦点在y 轴上的椭圆以A 、B 为顶点,A 作斜率为k 的直线l 交双曲线于另一点M ,交椭圆于另一点N ,若AN NM =,则k 的值为 ▲ .(第4题)9. 已知函数f (x )=cos x (sin x +cos x )12-,若()f α=,则cos(2)4πα-的值为 ▲ .10.已知{}n a 是首项为1,公比为2的等比数列,数列{}n b 满足11b a =,且12n b a a =++1121n n n a a a a a --++++++(2,n n *∈N ≥),若(28)2018m m a b +-=,则m 的值为 ▲ .11.定义在[]1,1-上的函数()sin (1)f x x ax b a =-+>的值恒非负,则a b -的最大值为 ▲ . 12.在△ABC 中,若352115CA AB AB BC BC CA==⋅⋅⋅,则cos C 的值为 ▲ .13.在平面直角坐标系xOy 中,圆O :221x y +=,直线:l 30x ay +-=,过直线l 上一点Q 作圆O 的切线,切点为,P N ,且23Q P Q N ⋅=,则正实数a 的取值范围是 ▲ . 14.已知偶函数()y f x =满足(2)(2)f x f x +=-,且在[]2,0x ∈-时,2()1f x x =-+,若存在12n x x x ,,,满足120n x x x <<<≤,且()()()()1223f x f x f x f x -+-+()()12017n n f x f x -+-=,则n x 最小值为 ▲ .二、解答题:本大题共6小题,共计90分. 15.(本小题满分14分)已知函数()()()sin 0,0f x A x A ϕϕ=+><<π的最小值是-2,其图象经过 点(,1)3M π.(1)求()f x 的解析式;(2)已知,(0,)2αβπ∈,且8()5f α=,24()13f β=,求()f αβ-的值.16.(本小题满分14分)如图,在四棱锥P ABCD -中,90BAD ∠=︒,AD BC ∥,2AD BC =,AB PA ⊥. (1)求证:平面PAD ⊥平面ABCD ;(2)若E 为PD 的中点,求证:CE ∥平面PAB17.(本小题满分14分)有一块以点O 为圆心,半径为2百米的圆形草坪,草坪内距离O D 点有一用于灌溉的水笼头,现准备过点D 修一条笔直小路交草坪圆周于A ,B 两点,为了方便居民散步,同时修建小路OA ,OB ,其中小路的宽度忽略不计. (1)若要使修建的小路的费用最省,试求小路的最短长度;(2)若要在△ABO 区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和π)18.(本小题满分16分)如图,点128n n a a +=+,{}n b ,n S 分别为椭圆2214+25n n n b b S ++=的左、右顶点和右焦点,过点n *∈N 的直线{}n a (异于{}n b 轴)交椭圆C 于点{}n b ,n n n c a b =+.(第16题)(1)若3AF =,点4r s t ,,与椭圆C 左准线的距离为5,求椭圆C 的方程; (2)已知直线()r s t <<的斜率是直线r s t ,,斜率的()()f m x f x +<倍. ① 求椭圆C 的离心率;② 若椭圆C 的焦距为()()f m x f x +<,求△AMN 面积的最大值.19.(本小题满分16分)已知函数2()ln f x x x ax =+.(1)若曲线()y f x =在1x =处的切线过点(22)A -,. ① 求实数a 的值;② 设函数()()f x g x x =,当0s >时,试比较()g s 与1()g s的大小; (2)若函数()f x 有两个极值点1x ,2x (12x x <),求证:11()2f x >-.20.(本小题满分16分)设数列{}n a 的各项均为不等的正整数,其前n 项和为n S ,我们称满足条件“对任意的*m n ∈N ,,均有()()()n m n m n m S n m S S +-=+-”的数列{}n a 为“好”数列.(1)试分别判断数列{}n a ,{}n b 是否为“好”数列,其中21n a n =-,12n n b -=,*n ∈N ,并给出证明;(2)已知数列{}n c 为“好”数列.① 若20172018c =,求数列{}n c 的通项公式;② 若1c p =,且对任意给定正整数p s ,(1s >),有1s t c c c ,,成等比数列, 求证:2t s ≥.2018年高考模拟试卷(9)参考答案数学Ⅰ一、填空题: 1.【答案】4 2.【答案】2+i 3.【答案】50 4.【答案】30 5.【答案】156.【答案】(],2-∞7.8.【答案】9.【答案】13解析一:f (x )=cos x (sin x +cos x )-12=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12=12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4,因为()f α=,所以1sin(2)43πα+=,所以1cos(2)cos (2)sin(2)42443ππππ⎡⎤-α=-α+=α+=⎢⎥⎣⎦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第3题)(第6题) 2018年江苏省高考数学模拟试卷(9)第Ⅰ卷(必做题,共160分)一、填空题:本大题共14小题,每小题5分,共70分 .1. 全集{}1,2,3,4,5U =,集合{}1,3,4A =,则U C A = ▲ .2. 设复数i z a b =+(a b ∈,R ,i 是虚数单位),若()2i i z -=则a b +的值为 ▲ .3. 在如图所示的算法流程图中,若输出的y 的值为26,则输入的x 的值为 ▲ .4. 概率为0.8,乙不输的概率为0.7,则两人下成和棋的概率为 ▲ .5. 顶点在原点且以双曲线1322=-y x 的右准线为准线的抛物线方程是 ▲ .6. 为了解学生课外阅读的情况,随机统计了n 名学生的课外阅读时间,所得数据都在[50,150]中, 其频率分布直方图如图所示.已知在[50 100),中 的频数为24,则n 的值为 ▲. 7. 甲,乙两种食物的维生素含量如下表:100,120单位,则混合物重量的最小值为 ▲ kg .8. 60°,则该棱锥的体积为 ▲ .9.在平面直角坐标系xOy 中,已知圆C :22(3)2x y +-=,点A 是x 轴上的一个动点,AP ,AQ 分别切圆C 于P ,Q 两点,则线段PQ 长的取值范围为 ▲ . 10.若函数 0,2,()0ln ,≤x x x f x x ax x ⎧+=⎨>-⎩在其定义域上恰有两个零点,则正实数a 的值为 ▲ .11.设直线l 是曲线343ln y x x =+的切线,则直线l 的斜率的最小值为 ▲ .12.扇形AOB 中,弦1AB =,C 为劣弧AB 上的动点,AB 与OC 交于点P ,则OP BP ⋅的最小值是 ▲ .13.在平面直角坐标系xOy 中,已知(cos sin )A αα,,(cos sin )B ββ,是直线y =+上的两点,则tan()αβ+的值为 ▲ .14.已知函数3()2f x x a a x=--+-有且仅有三个零点,且它们成等差数列,则实数a 的取值集合为 ▲ .二、解答题:本大题共6小题,共90分. 15.(本小题满分14分)已知tan α=2,cos β=- 7210,且α,β∈(0,π), (1)求cos2α的值; (2)求2α-β的值.16.(本小题满分14分)如图,在四棱锥P ABCD -中,△ACD 是正三角形,BD 垂直平分AC ,垂足为M , ABC ∠=120°,=1PA AB =,2PD =,N 为PD 的中点. (1)求证:AD ⊥平面PAB ; (2)求证:CN ∥平面PAB .D(第16题)PA P BPCM N17. (本小题满分14分)在平面直角坐标系xOy 中,已知A B ,分别是椭圆22221(0)y x a b a b+=>>的上、下顶点, 点()102M ,为线段AO的中点,AB .(1)求椭圆的方程;(2)设(2)N t ,(0t ≠),直线NA ,NB 分别 交椭圆于点P Q ,,直线NA ,NB ,PQ 的斜率分别为1k ,2k ,3k . ① 求证:P M Q ,,三点共线; ② 求证:132312k k k k k k +-为定值.18.(本小题满分16分)如图,一个角形海湾AOB ,∠AOB =2θ(常数θ为锐角).拟用长度为l (l 为常数)的围网围成一个养殖区,有以下两种方案可供选择: 方案一:如图1,围成扇形养殖区OPQ ,其中⌒PQ =l ; 方案二:如图2,围成三角形养殖区OCD ,其中CD =l ;(1)求方案一中养殖区的面积S 1 ;(2)求证:方案二中养殖区的最大面积S 2=l 24tan θ;(3)为使养殖区的面积最大,应选择何种方案?并说明理由.(第17题)llAOBAOB图1Q PAOBC D 图2(第18题)2θ2θ2θ19.(本小题满分16分)已知数列{}n a 的首项为2,前n 项的和为n S ,且111241n n n a a S +-=-(*n ∈N ).(1)求2a 的值; (2)设1nn n na b a a +=-,求数列{}n b 的通项公式;(3)若m p r a a a ,,(*m p r ∈,,N ,m p r <<,)成等比数列,试比较2p 与mr 的大小,并证明.20.(本小题满分16分)已知函数2()ln )xf x e a x b x=++(,其中,a b R ∈. 2.71828e =是自然对数的底数. (1)若曲线()y f x =在1x =处的切线方程为(1)y e x =-.求实数,a b 的值;(2)① 若2a =-时,函数()y f x =既有极大值,又有极小值,求实数b 的取值范围; ② 若2a =,2b ≥-.若()f x kx ≥对一切正实数x 恒成立,求实数k 的最大值(用b 表示).1O 2OABP QDC第II 卷(附加题,共40分)21.【选做题】本题包括A, B,C,D 四小题,每小题10分,请选定其中两小题,并在相应的答题.......区域内作答...... A ,(选修4-1;几何证明选讲)如图,1O ,2O 交于两点P Q ,,直线AB 过点P ,与1O ,2O 分别交于点A B ,,直线CD 过点Q ,与1O ,2O 分别交于点C D ,. 求证:AC ∥BD . B .(选修4-2:矩阵与变换)若二阶矩阵M 满足:12583446M ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭. (1)求二阶矩阵M ;(2)若曲线22:221C x xy y ++=在矩阵M所对应的变换作用下得到曲线C ',求曲线C '的方程.C .(选修4-4:坐标系与参数方程)已知点(1)P αα-+(其中[)0,2)απ∈,点P 的轨迹记为曲线1C ,以坐标原点 为极点,x 轴的正半轴为极轴建立极坐标系,点Q 在曲线21:)4C ρπθ=+上. (1)求曲线1C 的极坐标方程和曲线2C 的直角坐标方程;(2)当0,02ρθπ≥≤<时,求曲线1C 与曲线2C 的公共点的极坐标. D .(选修4-5:不等式选讲)已知实数0x >,0y >,0z >,证明:1239()()2462yx z x y z ++++≥.【选做题】第22题、23题,每题10分,共计20分.22.已知正六棱锥S ABCDEF -的底面边长为2,高为1.现从该棱锥的7个顶点中随机选取3个点构成三角形,设随机变量X 表示所得三角形的面积.(1)求概率(P X =的值;(2)求X 的分布列,并求其数学期望()E X .23.已知数列{a n }满足:a 1=1,对任意的n ∈N *,都有a n +1=(1+1n 2+n )a n +12n. (1)求证:当n ≥2时,a n ≥2;(2)利用“∀x >0,ln(1+x )<x ”,证明:a n <2e 34(其中e 是自然对数的底数).2018年江苏省高考数学模拟试卷(9)参考答案一、填空题1. {}2,5.2. 15.3.-4. 4. 0.5. 5. 26y x =-.6. 60.7. 30. 线性规划或待定系数法,设甲、乙混货物分别为x ,y 克,由题意3x+4y 1005x+2y 120≥⎧⎨≥⎩,设x+y=34)(52)x y x y λμ+++(,解得,31==1414λμ,,即可.8.9.. 设CA=x,则PQ=2CPcos<CAP=([3,))x ∈+∞,据此可得2PQ ≤< . 10. 1e. 易知函数()f x 在(],0-∞上有一个零点,所以由题意得方程ln 0ax x -=在()0+∞,上恰有一解,即ln x a x =在()0+∞,上恰有一解. 令ln ()x g x x =,21ln ()0x g x x-'==,得e x =,当()0,e x ∈时,()g x 单调递增,当()e,+x ∈∞时,()g x 单调递减,所以()1e e a g ==.11.9.223331212922k x x x x x=+=++≥=,也可以求导. 12. 116-.设弦AB 中点为M ,则()OP BP OM MP BP MP BP ⋅=+⋅=⋅, 若MP BP ,同向,则0OP BP ⋅>;若MP BP ,反向,则0OP BP ⋅<, 故OP BP ⋅的最小值在MP BP ,反向时取得, 此时1||||2MP BP +=,2||||1||||()216MP BP OP BP MP BP +⋅=-⋅-=-≥, 当且仅当1||||4MP BP ==时取等号,即OP BP ⋅的最小值是116-.13.(方法一)由题意,得sin sin ααββ⎧=⎪⎨=⎪⎩所以αβ,是方程sin x x即方程()πsin 3x -=5ππ()26k k αβ+=+∈Z,所以tan()αβ+=.(方法二)同上,αβ,sin 0x x -的两根.设()sin f x x x -()cos f x x x '=-.令()0f x '=,得0tan x =,所以02x αβ+=,所以(方法三)直线210x y +-=交单位圆于A B ,两点, 过O 作OH AB ⊥,垂足为H ,易知OH =因为OC =,所以60COH ∠=︒,即1502αβ+=︒,所以tan()tan 300αβ+=︒=14.95⎧-⎨⎩⎭.32()322x x a x f x x a x a x ⎧--⎪=⎨⎪--+-<⎩,≥,,,当x a ≥时,320x x --=,得11x =-,23x =,结合图形知,① 当1a <-时,313x -,,成等差数列,则35x =-,代入3220x a x --+-=得,95a =-;② 当13a -≤≤时,方程3220x a x --+-=,即22(1)30x a x +-+=的根为34x x ,,则343x x =,且3432x x +=,解得4x ,又342(1)x x a +=-,所以a =.③ 当3a >时,显然不符合. 所以a 的取值集合95⎧-⎨⎩⎭. 二、解答题:本大题共6小题,共90分. 15. (1)因为tan α=2,所以sin αcos α=2,即sin α=2cos α. 又sin 2α+cos 2α=1,所以5cos 2α=1,即cos 2α=15.所以 cos2α=2cos 2α-1=-35.(2)由α∈(0,π),且tan α=2>1,得α∈(π4,π2),所以2α∈(π2,π).由题知cos2α=-35,所以sin2α=45.又因为β∈(0,π),cos β=-7210∈(-1,0),所以β∈(π2,π), 所以sin β=210,且2α-β∈(-π2,π2). 因为sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22,所以2α-β=-π4.16.(1)因为BD 垂直平分AC ,所以BA BC =,在△ABC 中,因为120ABC ∠=︒, 所以30BAC ∠=︒.因为△ACD 是正三角形,所以60DAC ∠=︒, 所以90BAD ∠=︒,即AD AB ⊥.因为=1AB ,120ABC ∠=︒,所以AD AC = 又因为1PA =,2PD =,由222PA AD PD +=, 知90PAD ∠=︒,即AD AP ⊥. 因为AB AP ⊂,平面PAB ,AB AP A =,所以AD ⊥平面PAB .(2)(方法一)取AD 的中点H ,连结CH ,NH . 因为N 为PD 的中点,所以HN ∥PA , 因为PA ⊂平面PAB ,HN ⊄平面PAB , 所以HN ∥平面PAB .由△ACD 是正三角形,H 为AD 的中点,所以CH AD ⊥.由(1)知,BA AD ⊥,所以CH ∥BA , 因为BA ⊂平面PAB ,CH ⊄平面PAB , 所以CH ∥平面PAB . 因为CH HN ⊂,平面CNH ,CHHN H =,HPABCDMN所以平面CNH ∥平面PAB . 因为CN ⊂平面CNH , 所以CN ∥平面PAB .(方法二)取PA 的中点S ,过C 作CT ∥AD 交AB 的延长线于T ,连结ST ,SN .因为N 为PD 的中点,所以SN ∥AD ,且12SN AD =,因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB AD ⊥,所以CT AT ⊥, 在直角△ CBT 中,1BC =,60CBT ∠=︒, 得CT =由(1)知,AD ,所以12CT AD =,所以CT SN =.所以四边形SNCT 是平行四边形, 所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB , 所以CN ∥平面PAB .17.(1)由题意知,124()2b b =-=,解得a =1b =,所以椭圆的方程为2212x y +=.(2)① 由(2)N t ,,(01)A ,,(01)B -,,则直线NA 的方程为11y x t =+,直线NB 的方程为31y x t=-.由221122y x t x y ⎧=+⎪⎨⎪+=⎩,得,222422.2t x t t y t ⎧=-⎪+⎨-⎪=+⎩,,故()2224222t t t t P --++,. P ABCDMNTS由223122y x t x y ⎧=-⎪⎨⎪+=⎩,得,222121818.18t x t t y t ⎧=⎪+⎨-⎪=+⎩,,故()22212181818t t t t Q -++,. 所以直线PM 的斜率222221262482PMt t t k t t t ---+==-+, 直线QM 的斜率2222181261812818QMt t t k t t t ---+==+, 所以PM QM k k =,故P M Q ,,三点共线.② 由①知,11k t =,213k t=,2368t k t -=.所以21323122463182t k k k k k k t t t-+-=⨯-=-, 所以132312k k k k k k +-为定值12-.18.(1)设OP =r ,则l =r ·2θ,即r =l2θ,所以S 1=12lr =l 24θ,θ∈(0,π2).(2)设OC =a ,OD =b .由余弦定理,得l 2=a 2+b 2-2ab cos2θ,所以 l 2≥2ab -2ab cos2θ.所以 ab ≤l 22(1-cos2θ),当且仅当a =b 时“=”成立.所以S △OCD =12ab sin2θ≤l 2sin2θ4(1-cos2θ)=l 24tan θ,即S 2=l 24tan θ.(3)1S 2-1S 1=4l 2(tan θ-θ),θ∈(0,π2),. 令f (θ)=tan θ-θ,则f '(θ)=(sin θcos θ)'-1=sin 2θcos 2θ.当θ∈[0,π2)时,f '(θ)>0,所以f (θ)在区间[0,π2)上单调增.所以,当θ∈(0,π2)时,总有f (θ)>f (0)=0,即1S 2-1S 1>0,即S 1>S 2.答:为使养殖区面积最大,应选择方案一. 19. (1)易得2143a =.(2)由111241n n n a a S +-=-,得11241n nn n n a a a a S ++-=-,所以11241n n n n na a S a a ++-=-①.所以12121241n n n n n a a S a a +++++-=-②,由②-①,得12112112n n n n n n n n na a a aa a a a a +++++++=---.因为10n a +≠,所以22112n nn n n na a a a a a ++++=---. 所以121112n n n n n n a a a a a a +++++-=--,即12111n nn n n na a a a a a ++++-=--,即11n n b b +-=,所以数列{}n b 是公差为1的等差数列. 因为112134a b a a ==-,所以数列{}n b 的通项公式为14n b n =-.(3)由(2)知,114n n n a n a a +=--,所以114311414n n an a n n ++=+=--,所以14(1)141n n a a n n +=+--,所以数列41n a n ⎧⎫⎨⎬-⎩⎭是常数列.由124113a =⨯-,所以2(41)3n a n =-.(方法一)由m p r a a a ,,(m p r <<)成等比数列,则41m -,41p -,41r -成等比数列,所以2(41)(41)(41)p m r -=--, 所以2168164()0p p mr m r --++=,即2424()0p p mr m r --++=(*). (途径一)(*)式即为2424()4p p mr m r mr -=-+<-,所以2211(2))22p -<,即11222p -<,所以p <2p mr <.(途径二)(*)式即为24241p p rm r -+=-.由222222(42)(42)(41)()0414141p p r p p r r r p p r mr p r p r r r -+-+----=⋅-==>---, 所以2p mr <.(方法二)由m p r a a a ,,(m p r <<)成等比数列,则41m -,41p -,41r -成等比数列, 记4m α=,4p β=,4r γ=(1αβγ<<<), 则有1α-,1β-,1γ-成等比数列,所以2(1)(1)(1)βαγ-=--,即22()ββαγαγ-=-+.若2βαγ=,即2p mr =时,则2αγβ+=,所以αβγ==,矛盾; 若2βαγ>,则22()0βαγβαγ-+=->,所以1()12βαγ>+>,所以[][]2221(2)()()()()()024αγββαγαγαγαγαγαγ+---+>-+--+=->, 矛盾.所以2βαγ<,即2p mr <.20. (1) 由题意知曲线()y f x =过点(1,0),且'(1)e f =;又因为222'()ln e xa f x a xb xx+=-++⎛⎫ ⎪⎝⎭,则有(1)e(2)0,'(1)e()e,f b f a b =+==+=⎧⎨⎩解得3,2a b ==-.(2) ①当2a =-时,函数()y f x =的导函数22'()e 2ln 0xf x x b x =--+=⎛⎫ ⎪⎝⎭,若'()0f x =时,得222ln b x x=+, 设22()2ln g x x x =+(0)x > .由2332424'()x g x x x x-=-=0=,得x =1ln 2g =+.当0x <<时,'()0g x <,函数()y g x =在区间上为减函数,()(1ln 2,)g x ∈++∞;仅当1ln 2b >+时,()b g x =有两个不同的解,设为1x ,2x 12()x x <.此时,函数()y f x =既有极大值,又有极小值.②由题意2e ln xa xb xkx ++⎛⎫≥ ⎪⎝⎭对一切正实数x 恒成立,取1x =得(2)e k b ≤+.下证2e ln e (2)xa xb xb x ++⎛⎫≥+ ⎪⎝⎭对一切正实数x 恒成立.首先,证明e e xx ≥. 设函数()e e xu x x =-,则'()e e xu x =-,当1x >时,'()0u x >; 当1x <时,'()0u x <;得e e (1)0xx u -=≥,即e e xx ≥,当且仅当都在1x =处取到等号.再证1ln 1x x +≥. 设1()ln 1v x x x =+-,则21'()x v x x-=,当1x >时,'()0v x >;当1x <时,'()0v x <;得()(1)0v x v =≥,即1ln 1x x+≥,当且仅当都在1x =处取到等号. 由上可得2e ln (2)e xa xb xb x ++⎛⎫≥+ ⎪⎝⎭,所以min()(2)e f x b x ⎛⎫=+⎪⎝⎭,即实数k 的最大值为(2)e b +.数学Ⅱ(附加题)21. A. 连结PQ ,因为四边形ACQP 是1O 的内接四边形, 所以A PQD ∠=∠, 又在2O 中,PBD PQD ∠=∠,所以A PBD ∠=∠, 所以AC ∥BD .B .(1) 设1234A ⎛⎫= ⎪⎝⎭,则12234A ==-, 1213122A --⎛⎫⎪∴= ⎪-⎝⎭,21582131461122M -⎛⎫⎛⎫⎛⎫ ⎪∴== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭. (2)11112x x x x x M M y y y y y -'''-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=∴== ⎪ ⎪ ⎪ ⎪ ⎪⎪'''-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,即,2,x x y y x y ''=-⎧⎨''=-+⎩ 代入22221x xy y ++=可得()()()()2222221x y x y x y x y ''''''''-+--++-+=,即22451x x y y ''''-+=,故曲线C '的方程为22451x xy y -+=.C. (1)曲线1C :22(1)2x y ++=,极坐标方程为22cos 10ρθ+-= 曲线2C 的直角坐标方程为1y x =-; (2) 曲线1C 与曲线2C 的公共点的坐标为(0,1)-,极坐标为3(1,)2π. D. 因为0x >,0y >,0z >,所以1233x y z ++,2463y x z ++, 所以1239()()2462yx z x y z ++++≥.当且仅当::1:2:3x y z =时,等号成立.22.(1)从7个顶点中随机选取3个点构成三角形,共有37=35C种取法.其中X =ABF , 这类三角形共有6个.因此(376635P X C ===. (2)由题意,X2,其中X =ABF ,这类三角形共有6个;其中2X =的三角形有两类,如△P AD (3个),△P AB (6个),共有9个;其中X =PBD ,这类三角形共有6个;其中X =CDF ,这类三角形共有12个;其中X =的三角形如△BDF ,这类三角形共有2个.因此(635P X =,()9235P X ==, (635P X =,(1235P X ==,(235P X ==. 所以随机变量X 的概率分布列为:所求数学期望()E X 69612223535353535+⨯+++. 23. (1)①当n =2时,a 2=2,不等式成立.②假设当n =k (k ≥2)时不等式成立,即a k ≥2,则当n =k +1时,a k +1=(1+1k (k +1))a k +12k >2.所以,当n =k +1时,不等式也成立. 根据①,②可知,对所有n ≥2,a n ≥2成立.(2)当n ≥2时,由递推公式及(1)的结论有a n +1=(1+1n 2+n )a n +12n ≤(1+1n 2+n +12n +1)a n (n ≥2).两边取对数,并利用已知不等式ln(1+x )<x ,得 ln a n +1≤ln(1+1n 2+n +12n +1)+ln a n <ln a n +1n 2+n +12n +1,故 ln a n +1-ln a n <1n 2+n +12n +1(n ≥2),求和可得ln a n -ln a 2<12⨯3+1 3⨯4+…+1 (n -1)n +123+124+…+12n=(12-13)+(13-14)+…+(1n -1-1n )+123·1-12n -21-12=12-1n +122-12n <34. 由(1)知,a 2=2,故有ln a n 2<34,即a n <2e 34(n ≥2),而a 1=1<2e 34,所以对任意正整数n ,有a n <2e 34.。
