中考二次函数压轴题(共23道题目)
中考数学二次函数-经典压轴题含详细答案

一、二次函数 真题与模拟题分类汇编(难题易错题)1.如图,已知抛物线2y ax bx c =++经过A (-3,0),B (1,0),C (0,3)三点,其顶点为D ,对称轴是直线l ,l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求△PBC 周长的最小值;(3)如图(2),若E 是线段AD 上的一个动点( E 与A 、D 不重合),过E 点作平行于y 轴的直线交抛物线于点F ,交x 轴于点G ,设点E 的横坐标为m ,△ADF 的面积为S . ①求S 与m 的函数关系式;②S 是否存在最大值?若存在,求出最大值及此时点E 的坐标; 若不存在,请说明理由.【答案】(1)2y x 2x 3=--+.(2)3210. (3)①2S m 4m 3=---.②当m=﹣2时,S 最大,最大值为1,此时点E 的坐标为(﹣2,2). 【解析】 【分析】(1)根据函数图象经过的三点,用待定系数法确定二次函数的解析式即可.(2)根据BC 是定值,得到当PB+PC 最小时,△PBC 的周长最小,根据点的坐标求得相应线段的长即可.(3)设点E 的横坐标为m ,表示出E (m ,2m+6),F (m ,2m 2m 3--+),最后表示出EF 的长,从而表示出S 于m 的函数关系,然后求二次函数的最值即可. 【详解】解:(1)∵抛物线2y ax bx c =++经过A (-3,0),B (1,0), ∴可设抛物线交点式为()()y a x 3x 1=+-.又∵抛物线2y ax bx c =++经过C (0,3),∴a 1=-. ∴抛物线的解析式为:()()y x 3x 1=-+-,即2y x 2x 3=--+. (2)∵△PBC 的周长为:PB+PC+BC ,且BC 是定值. ∴当PB+PC 最小时,△PBC 的周长最小. ∵点A 、点B 关于对称轴I 对称,∴连接AC 交l 于点P ,即点P 为所求的点.∵AP=BP ,∴△PBC 的周长最小是:PB+PC+BC=AC+BC.∵A (-3,0),B (1,0),C (0,3),∴2,10. ∴△PBC 的周长最小是:3210.(3)①∵抛物线2y x 2x 3=--+顶点D 的坐标为(﹣1,4),A (﹣3,0),∴直线AD 的解析式为y=2x+6∵点E 的横坐标为m ,∴E (m ,2m+6),F (m ,2m 2m 3--+) ∴()22EF m 2m 32m 6m 4m 3=--+-+=---.∴()22DEF AEF 1111S S S EF GH EF AG EF AH m 4m 32m 4m 32222∆∆=+=⋅⋅+⋅⋅=⋅⋅=⋅---⋅=---.∴S 与m 的函数关系式为2S m 4m 3=---. ②()22S m 4m 3m 21=---=-++,∴当m=﹣2时,S 最大,最大值为1,此时点E 的坐标为(﹣2,2).2.如图,抛物线y =﹣x 2﹣2x+3的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,点D 为抛物线的顶点. (1)求点A 、B 、C 的坐标;(2)点M(m ,0)为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N ,可得矩形PQNM .如图,点P 在点Q 左边,试用含m 的式子表示矩形PQNM 的周长;(3)当矩形PQNM 的周长最大时,m 的值是多少?并求出此时的△AEM 的面积; (4)在(3)的条件下,当矩形PMNQ 的周长最大时,连接DQ ,过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G(点G 在点F 的上方).若FG =2,求点F 的坐标.【答案】(1)A(﹣3,0),B(1,0);C(0,3) ;(2)矩形PMNQ的周长=﹣2m2﹣8m+2;(3) m=﹣2;S=12;(4)F(﹣4,﹣5)或(1,0).【解析】【分析】(1)利用函数图象与坐标轴的交点的求法,求出点A,B,C的坐标;(2)先确定出抛物线对称轴,用m表示出PM,MN即可;(3)由(2)得到的结论判断出矩形周长最大时,确定出m,进而求出直线AC解析式,即可;(4)在(3)的基础上,判断出N应与原点重合,Q点与C点重合,求出DQ=DC=2,再建立方程(n+3)﹣(﹣n2﹣2n+3)=4即可.【详解】(1)由抛物线y=﹣x2﹣2x+3可知,C(0,3).令y=0,则0=﹣x2﹣2x+3,解得,x=﹣3或x=l,∴A(﹣3,0),B(1,0).(2)由抛物线y=﹣x2﹣2x+3可知,对称轴为x=﹣1.∵M(m,0),∴PM=﹣m2﹣2m+3,MN=(﹣m﹣1)×2=﹣2m﹣2,∴矩形PMNQ的周长=2(PM+MN)=(﹣m2﹣2m+3﹣2m﹣2)×2=﹣2m2﹣8m+2.(3)∵﹣2m2﹣8m+2=﹣2(m+2)2+10,∴矩形的周长最大时,m=﹣2.∵A(﹣3,0),C(0,3),设直线AC的解析式y=kx+b,∴303k bb-+=⎧⎨=⎩解得k=l,b=3,∴解析式y=x+3,令x=﹣2,则y=1,∴E(﹣2,1),∴EM=1,AM=1,∴S =12AM×EM =12. (4)∵M(﹣2,0),抛物线的对称轴为x =﹣l , ∴N 应与原点重合,Q 点与C 点重合, ∴DQ =DC ,把x =﹣1代入y =﹣x 2﹣2x+3,解得y =4, ∴D(﹣1,4), ∴DQ =DC =2. ∵FG =22DQ , ∴FG =4.设F(n ,﹣n 2﹣2n+3),则G(n ,n+3), ∵点G 在点F 的上方且FG =4, ∴(n+3)﹣(﹣n 2﹣2n+3)=4. 解得n =﹣4或n =1, ∴F(﹣4,﹣5)或(1,0). 【点睛】此题是二次函数综合题,主要考查了函数图象与坐标轴的交点的求法,待定系数法求函数解析式,函数极值的确定,解本题的关键是用m 表示出矩形PMNQ 的周长.3.如图,已知二次函数的图象过点O (0,0).A (8,4),与x 轴交于另一点B ,且对称轴是直线x =3.(1)求该二次函数的解析式;(2)若M 是OB 上的一点,作MN ∥AB 交OA 于N ,当△ANM 面积最大时,求M 的坐标;(3)P 是x 轴上的点,过P 作PQ ⊥x 轴与抛物线交于Q .过A 作AC ⊥x 轴于C ,当以O ,P ,Q 为顶点的三角形与以O ,A ,C 为顶点的三角形相似时,求P 点的坐标.【答案】(1)21342y x x =-;(2)当t =3时,S △AMN 有最大值3,此时M 点坐标为(3,0);(3)P 点坐标为(14,0)或(﹣2,0)或(4,0)或(8,0).【解析】 【分析】(1)先利用抛物线的对称性确定B (6,0),然后设交点式求抛物线解析式; (2)设M (t ,0),先其求出直线OA 的解析式为12y x =直线AB 的解析式为y=2x-12,直线MN 的解析式为y=2x-2t ,再通过解方程组1222y x y x t ⎧=⎪⎨⎪=-⎩得N (42t,t 33),接着利用三角形面积公式,利用S △AMN =S △AOM -S △NOM 得到AMN 112S 4t t t 223∆=⋅⋅-⋅⋅然后根据二次函数的性质解决问题; (3)设Q 213m,m m 42⎛⎫- ⎪⎝⎭,根据相似三角形的判定方法,当PQ PO OC AC=时,△PQO ∽△COA ,则213m m 2|m |42-=;当PQ POAC OC=时,△PQO ∽△CAO ,则2131m m m 422-=,然后分别解关于m 的绝对值方程可得到对应的P 点坐标. 【详解】解:(1)∵抛物线过原点,对称轴是直线x =3, ∴B 点坐标为(6,0),设抛物线解析式为y =ax (x ﹣6), 把A (8,4)代入得a•8•2=4,解得a =14, ∴抛物线解析式为y =14x (x ﹣6),即y =14x 2﹣32x ; (2)设M (t ,0),易得直线OA 的解析式为y =12x , 设直线AB 的解析式为y =kx+b ,把B (6,0),A (8,4)代入得6084k b k b +=⎧⎨+=⎩,解得k 2b 12=⎧⎨=-⎩,∴直线AB 的解析式为y =2x ﹣12, ∵MN ∥AB ,∴设直线MN 的解析式为y =2x+n , 把M (t ,0)代入得2t+n =0,解得n =﹣2t , ∴直线MN 的解析式为y =2x ﹣2t ,解方程组1222y x y x t ⎧=⎪⎨⎪=-⎩得4323x t y t ⎧=⎪⎪⎨⎪=⎪⎩,则42N t,t 33⎛⎫ ⎪⎝⎭, ∴S △AMN =S △AOM ﹣S △NOM1124t t t 223=⋅⋅-⋅⋅ 21t 2t 3=-+21(t 3)33=--+,当t =3时,S △AMN 有最大值3,此时M 点坐标为(3,0); (3)设213m,m m 42⎛⎫- ⎪⎝⎭, ∵∠OPQ =∠ACO , ∴当PQ PO OC AC =时,△PQO ∽△COA ,即PQ PO 84=, ∴PQ =2PO ,即213m m 2|m |42-=, 解方程213m m 2m 42-=得m 1=0(舍去),m 2=14,此时P 点坐标为(14,0); 解方程213m m 2m 42-=-得m 1=0(舍去),m 2=﹣2,此时P 点坐标为(﹣2,0); ∴当PQ PO AC OC =时,△PQO ∽△CAO ,即PQ PO 48=, ∴PQ =12PO ,即2131m m m 422-=,解方程2131m m m 422=-=得m 1=0(舍去),m 2=8,此时P 点坐标为(8,0); 解方程2131m m m 422=-=-得m 1=0(舍去),m 2=4,此时P 点坐标为(4,0); 综上所述,P 点坐标为(14,0)或(﹣2,0)或(4,0)或(8,0). 【点睛】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;灵活运用相似比表示线段之间的关系;会运用分类讨论的思想解决数学问题.4.已知抛物线2(5)6y x m x m =-+-+-. (1)求证:该抛物线与x 轴总有交点;(2)若该抛物线与x 轴有一个交点的横坐标大于3且小于5,求m 的取值范围;(3)设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ,若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ,求m 的值.【答案】(1)证明见解析;(2)1?<?m?3<;(3)56m m ==或 【解析】 【分析】(1)本题需先根据判别式解出无论m 为任何实数都不小于零,再判断出物线与x 轴总有交点.(2)根据公式法解方程,利用已有的条件,就能确定出m 的取值范围,即可得到结果. (3)根据抛物线y=-x 2+(5-m )x+6-m ,求出与y 轴的交点M 的坐标,再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标,列方程可得结论. 【详解】(1)证明:∵()()()222454670b ac m m m ∆=-=-+-=-≥ ∴抛物线与x 轴总有交点.(2)解:由(1)()27m ∆=-,根据求根公式可知,方程的两根为:x =即1216x x m =-=-+, 由题意,有 3<-m 6<5+1<?m 3∴<(3)解:令 x = 0, y =6m -+ ∴ M (0,6m -+)由(2)可知抛物线与x 轴的交点为(-1,0)和(6m -+,0), 它们关于直线y x =-的对称点分别为(0 , 1)和(0, 6m -), 由题意,可得:6166m m m 或-+=-+=- 56m m ∴==或 【点睛】本题考查对抛物线与x 轴的交点,解一元一次方程,解一元一次不等式,根的判别式,对称等,解题关键是熟练理解和掌握以上性质,并能综合运用这些性质进行计算.5.已知,抛物线y =﹣x 2+bx +c 经过点A (﹣1,0)和C (0,3). (1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P ,使PA +PC 的值最小?如果存在,请求出点P 的坐标,如果不存在,请说明理由;(3)设点M 在抛物线的对称轴上,当△MAC 是直角三角形时,求点M 的坐标.【答案】(1)223y x x =-++;(2)当PA PC +的值最小时,点P 的坐标为()1,2;(3)点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭. 【解析】 【分析】()1由点A 、C 的坐标,利用待定系数法即可求出抛物线的解析式;()2连接BC 交抛物线对称轴于点P ,此时PA PC +取最小值,利用二次函数图象上点的坐标特征可求出点B 的坐标,由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式,利用配方法可求出抛物线的对称轴,再利用一次函数图象上点的坐标特征即可求出点P 的坐标;()3设点M 的坐标为()1,m ,则22CM (10)(m 3)=-+-,()22AC [01](30)10=--+-=,()22AM [11](m 0)=--+-,分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况,利用勾股定理可得出关于m 的一元二次方程或一元一次方程,解之可得出m 的值,进而即可得出点M 的坐标. 【详解】解:()1将()1,0A -、()0,3C 代入2y x bx c =-++中,得:{103b c c --+==,解得:{23b c ==,∴抛物线的解析式为223y x x =-++.()2连接BC 交抛物线对称轴于点P ,此时PA PC +取最小值,如图1所示.当0y =时,有2230x x -++=, 解得:11x =-,23x =,∴点B 的坐标为()3,0.抛物线的解析式为2223(1)4y x x x =-++=--+,∴抛物线的对称轴为直线1x =.设直线BC 的解析式为()0y kx d k =+≠, 将()3,0B 、()0,3C 代入y kx d =+中, 得:{303k d d +==,解得:{13k d =-=,∴直线BC 的解析式为3y x =-+.当1x =时,32y x =-+=,∴当PA PC +的值最小时,点P 的坐标为()1,2.()3设点M 的坐标为()1,m ,则22(10)(3)CM m =-+-,()22[01](30)10AC =--+-=,()22[11](0)AM m =--+-.分三种情况考虑:①当90AMC ∠=时,有222AC AM CM =+,即22101(3)4m m =+-++,解得:11m =,22m =,∴点M 的坐标为()1,1或()1,2;②当90ACM ∠=时,有222AM AC CM =+,即224101(3)m m +=++-,解得:83m =, ∴点M 的坐标为81,3⎛⎫⎪⎝⎭;③当90CAM ∠=时,有222CM AM AC =+,即221(3)410m m +-=++,解得:23m =-, ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述:当MAC 是直角三角形时,点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【点睛】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理,解题的关键是:()1由点的坐标,利用待定系数法求出抛物线解析式;()2由两点之间线段最短结合抛物线的对称性找出点P 的位置;()3分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况,列出关于m 的方程.6.如图,抛物线y=ax 2+bx 过点B (1,﹣3),对称轴是直线x=2,且抛物线与x 轴的正半轴交于点A .(1)求抛物线的解析式,并根据图象直接写出当y≤0时,自变量x 的取值范围; (2)在第二象限内的抛物线上有一点P ,当PA ⊥BA 时,求△PAB 的面积.【答案】(1)抛物线的解析式为y=x 2﹣4x ,自变量x 的取值范图是0≤x≤4;(2)△PAB 的面积=15. 【解析】 【分析】(1)将函数图象经过的点B 坐标代入的函数的解析式中,再和对称轴方程联立求出待定系数a 和b ;(2)如图,过点B 作BE ⊥x 轴,垂足为点E ,过点P 作PE ⊥x 轴,垂足为F ,设P (x ,x 2-4x ),证明△PFA ∽△AEB,求出点P 的坐标,将△PAB 的面积构造成长方形去掉三个三角形的面积. 【详解】(1)由题意得,322a b b a+-⎧⎪⎨-⎪⎩==,解得14a b -⎧⎨⎩==,∴抛物线的解析式为y=x 2-4x , 令y=0,得x 2-2x=0,解得x=0或4, 结合图象知,A 的坐标为(4,0),根据图象开口向上,则y≤0时,自变量x 的取值范围是0≤x≤4;(2)如图,过点B 作BE ⊥x 轴,垂足为点E ,过点P 作PE ⊥x 轴,垂足为F ,设P (x ,x 2-4x ), ∵PA ⊥BA ∴∠PAF+∠BAE=90°, ∵∠PAF+∠FPA=90°, ∴∠FPA=∠BAE 又∠PFA=∠AEB=90° ∴△PFA ∽△AEB,∴PF AF AE BE =,即244213x x x--=-, 解得,x= −1,x=4(舍去) ∴x 2-4x=-5∴点P 的坐标为(-1,-5),又∵B 点坐标为(1,-3),易得到BP 直线为y=-4x+1 所以BP 与x 轴交点为(14,0) ∴S △PAB=115531524⨯⨯+= 【点睛】本题是二次函数综合题,求出函数解析式是解题的关键,特别是利用待定系数法将两条直线表达式解出,利用点的坐标求三角形的面积是关键.7.如图,(图1,图2),四边形ABCD 是边长为4的正方形,点E 在线段BC 上,∠AEF=90°,且EF 交正方形外角平分线CP 于点F ,交BC 的延长线于点N, FN ⊥BC . (1)若点E 是BC 的中点(如图1),AE 与EF 相等吗?(2)点E 在BC 间运动时(如图2),设BE=x ,△ECF 的面积为y . ①求y 与x 的函数关系式;②当x 取何值时,y 有最大值,并求出这个最大值.【答案】(1)AE=EF ;(2)①y=-12x 2+2x (0<x <4),②当x=2,y 最大值=2. 【解析】 【分析】(1)在AB 上取一点G ,使AG=EC ,连接GE ,利用ASA ,易证得:△AGE ≌△ECF ,则可证得:AE=EF ;(2)同(1)可证明AE=EF ,利用AAS 证明△ABE ≌△ENF ,根据全等三角形对应边相等可得FN=BE ,再表示出EC ,然后利用三角形的面积公式即可列式表示出△ECF 的面积为y ,然后整理再根据二次函数求解最值问题. 【详解】(1)如图,在AB 上取AG=EC , ∵四边形ABCD 是正方形, ∴AB=BC ,有∵AG=EC ,∴BG=BE , 又∵∠B=90°, ∴∠AGE=135°,又∵∠BCD=90°,CP 平分∠DCN , ∴∠ECF=135°,∵∠BAE +∠AEB=90°,∠AEB +∠FEC=90°, ∴∠BAE=∠FEC , 在△AGE 和△ECF 中,AGE ECF AG ECGAE CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AGE ≌△ECF , ∴AE=EF ;(2)①∵由(1)证明可知当E 不是中点时同理可证AE=EF , ∵∠BAE=∠NEF ,∠B=∠ENF=90°, ∴△ABE ≌△ENF , ∴FN=BE=x , ∴S △ECF =12(BC-BE)·FN , 即y=12x(4-x ), ∴y=-12x 2+2x (0<x <4), ②()()222111y x 2x x 4x x 22222=-+=--=--+, 当x=2,y 最大值=2. 【点睛】本题考查了正方形的性质,全等三角形的判定与性质,二次函数的最值问题,综合性较强,正确添加辅助线、熟练掌握相关知识是解题的关键.8.如图,在平面直角坐标系中,抛物线y=ax 2+2x+c 与x 轴交于A (﹣1,0)B (3,0)两点,与y 轴交于点C ,点D 是该抛物线的顶点. (1)求抛物线的解析式和直线AC 的解析式;(2)请在y 轴上找一点M ,使△BDM 的周长最小,求出点M 的坐标;(3)试探究:在拋物线上是否存在点P ,使以点A ,P ,C 为顶点,AC 为直角边的三角形是直角三角形?若存在,请求出符合条件的点P 的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为y=﹣x 2+2x+3;直线AC 的解析式为y=3x+3;(2)点M 的坐标为(0,3);(3)符合条件的点P 的坐标为(73,209)或(103,﹣139), 【解析】分析:(1)设交点式y=a (x+1)(x-3),展开得到-2a=2,然后求出a 即可得到抛物线解析式;再确定C (0,3),然后利用待定系数法求直线AC 的解析式;(2)利用二次函数的性质确定D 的坐标为(1,4),作B 点关于y 轴的对称点B′,连接DB′交y 轴于M ,如图1,则B′(-3,0),利用两点之间线段最短可判断此时MB+MD 的值最小,则此时△BDM的周长最小,然后求出直线DB′的解析式即可得到点M的坐标;(3)过点C作AC的垂线交抛物线于另一点P,如图2,利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b,把C点坐标代入求出b得到直线PC的解析式为y=-13x+3,再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==得此时P点坐标;当过点A作AC的垂线交抛物线于另一点P时,利用同样的方法可求出此时P点坐标.详解:(1)设抛物线解析式为y=a(x+1)(x﹣3),即y=ax2﹣2ax﹣3a,∴﹣2a=2,解得a=﹣1,∴抛物线解析式为y=﹣x2+2x+3;当x=0时,y=﹣x2+2x+3=3,则C(0,3),设直线AC的解析式为y=px+q,把A(﹣1,0),C(0,3)代入得3p qq-+=⎧⎨=⎩,解得33pq=⎧⎨=⎩,∴直线AC的解析式为y=3x+3;(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4),作B点关于y轴的对称点B′,连接DB′交y轴于M,如图1,则B′(﹣3,0),∵MB=MB′,∴MB+MD=MB′+MD=DB′,此时MB+MD的值最小,而BD的值不变,∴此时△BDM的周长最小,易得直线DB′的解析式为y=x+3,当x=0时,y=x+3=3,∴点M的坐标为(0,3);(3)存在.过点C作AC的垂线交抛物线于另一点P,如图2,∵直线AC的解析式为y=3x+3,∴直线PC的解析式可设为y=﹣13x+b,把C(0,3)代入得b=3,∴直线PC的解析式为y=﹣13x+3,解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩==,解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩,则此时P点坐标为(73,209);过点A作AC的垂线交抛物线于另一点P,直线PC的解析式可设为y=﹣x+b,把A(﹣1,0)代入得13+b=0,解得b=﹣13,∴直线PC的解析式为y=﹣13x﹣13,解方程组2231133y x xy x⎧-++⎪⎨--⎪⎩==,解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩,则此时P点坐标为(103,﹣139).综上所述,符合条件的点P的坐标为(73,209)或(103,﹣139).点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式,理解两直线垂直时一次项系数的关系,通过解方程组求把两函数的交点坐标;理解坐标与图形性质,会运用两点之间线段最短解决最短路径问题;会运用分类讨论的思想解决数学问题.9.已知抛物线C1:y=ax2﹣4ax﹣5(a>0).(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.【答案】(1)(﹣1,0)或(5,0)(2)①(0,﹣5),(4,﹣5)②y=﹣ax2+4ax﹣5(3)a=或【解析】试题分析:(1)将a=1代入解析式,即可求得抛物线与x轴交点;(2)①化简抛物线解析式,即可求得两个点定点的横坐标,即可解题;②根据抛物线翻折理论即可解题;(3)根据(2)中抛物线C2解析式,分类讨论y=2或﹣2,即可解题试题解析:(1)当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,∴对称轴为y=2;∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0);(2)①抛物线C1解析式为:y=ax2﹣4ax﹣5,整理得:y=ax(x﹣4)﹣5;∵当ax(x﹣4)=0时,y恒定为﹣5;∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);②这两个点连线为y=﹣5;将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;∴抛物线C2解析式为:y=﹣ax2+4ax﹣5,(3)抛物线C2的顶点到x轴的距离为2,则x=2时,y=2或者﹣2;当y=2时,2=﹣4a+8a﹣5,解得,a=;当y=﹣2时,﹣2=﹣4a+8a﹣5,解得,a=;∴a=或;考点:1、抛物线与x轴的交点;2、二次函数图象与几何变换10.抛物线,若a,b,c满足b=a+c,则称抛物线为“恒定”抛物线.(1)求证:“恒定”抛物线必过x轴上的一个定点A;(2)已知“恒定”抛物线的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.【答案】(1)证明见试题解析;(2),或.【解析】试题分析:(1)由“恒定”抛物线的定义,即可得出抛物线恒过定点(﹣1,0);(2)求出抛物线的顶点坐标和B的坐标,由题意得出PA∥CQ,PA=CQ;存在两种情况:①作QM⊥AC于M,则QM=OP=,证明Rt△QMC≌Rt△POA,MC=OA=1,得出点Q的坐标,设抛物线的解析式为,把点A坐标代入求出a的值即可;②顶点Q在y轴上,此时点C与点B重合;证明△OQC≌△OPA,得出OQ=OP=,得出点Q坐标,设抛物线的解析式为,把点C坐标代入求出a的值即可.试题解析:(1)由“恒定”抛物线,得:b=a+c,即a﹣b+c=0,∵抛物线,当x=﹣1时,y=0,∴“恒定”抛物线必过x轴上的一个定点A(﹣1,0);(2)存在;理由如下:∵“恒定”抛物线,当y=0时,,解得:x=±1,∵A(﹣1,0),∴B(1,0);∵x=0时,y=,∴顶点P的坐标为(0,),以PA,CQ为边的平行四边形,PA、CQ是对边,∴PA∥CQ,PA=CQ,∴存在两种情况:①如图1所示:作QM⊥AC于M,则QM=OP=,∠QMC=90°=∠POA,在Rt△QMC和Rt△POA中,∵CQ=PA,QM=OP,∴Rt△QMC≌Rt△POA(HL),∴MC=OA=1,∴OM=2,∵点A和点C是抛物线上的对称点,∴AM=MC=1,∴点Q的坐标为(﹣2,),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为,把点A(﹣1,0)代入得:a=,∴抛物线的解析式为:,即;②如图2所示:顶点Q在y轴上,此时点C与点B重合,∴点C坐标为(1,0),∵CQ∥PA,∴∠OQC=∠OPA,在△OQC和△OPA中,∵∠OQC=∠OPA,∠COQ=∠AOP,CQ=PA,∴△OQC≌△OPA(AAS),∴OQ=OP=,∴点Q坐标为(0,),设以Q为顶点,与x轴另一个交点为C的“恒定”抛物线的解析式为,把点C(1,0)代入得:a=,∴抛物线的解析式为:;综上所述:存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形,抛物线的解析式为:,或.考点:1.二次函数综合题;2.压轴题;3.新定义;4.存在型;5.分类讨论.。
(二次函数的应用)30道中考动点压轴题和函数压轴题
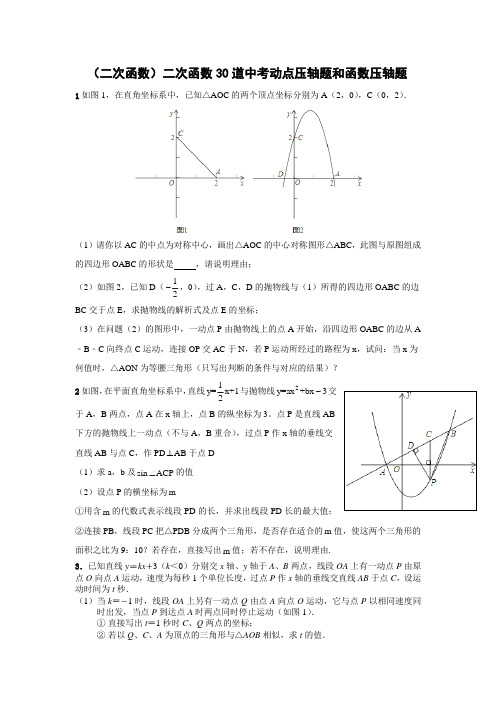
(二次函数)二次函数30道中考动点压轴题和函数压轴题1如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2).(1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是,请说明理由;(2)如图2,已知D(12-,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;(3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A ﹣B﹣C向终点C运动,连接OP交AC于N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)?2如图,在平面直角坐标系中,直线1y=x+12与抛物线2y=ax+bx3-交于A,B两点,点A在x轴上,点B的纵坐标为3。
点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D(1)求a,b及sin ACP∠的值(2)设点P的横坐标为m①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;②连接PB,线段PC把△PDB分成两个三角形,是否存在适合的m值,使这两个三角形的面积之比为9:10?若存在,直接写出m值;若不存在,说明理由.3.已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).①直接写出t=1秒时C、Q两点的坐标;②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.(2)当k =-34时,设以C 为顶点的抛物线y =(x +m)2+n 与直线AB 的另一交点为D (如图2).① 求CD 的长;② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大?4.已知二次函数的图象经过A (2,0)、C (0,12)两点,与x 轴的另一交点为点B ,且对称轴为直线x =4,设顶点为点D .(1)求二次函数的解析式及顶点D 的坐标;(2)如图1,在直线y =2x 上是否存在点E ,使四边形ODBE 为等腰梯形?若存在,求出点E 的坐标;若不存在,请说明理由;(3)如图2,点P 是线段OD 上的一个动点(不与O 、D 重合),以每秒 2 个单位长度的速度由点D 向点O 运动,过点P 作直线PQ ∥x 轴,交BD 于点Q ,将△DPQ 沿直线PQ 对折,得到△D 1PQ .在点P 运动的过程中,设△D 1PQ 与梯形OPQB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.5.A 、C 上,抛物线y =-2 3). (1)求抛物线的表达式;(2)如果点P 由点A 出发,沿AB 边以2cm /s 的速度向点B 运动,同时点Q 由点B 出发,沿BC 边以1cm /s 的速度向点C 运动,当其中一点到达终点时,另一点也随之停止运动.设S =PQ2(cm 2).①试求出S 与运动时间t 之间的函数关系式,并写出t 的取值范围;②当S 取54时,在抛物线上是否存在点R ,使得以点P 、B 、Q 、R 为顶点的四边形是平行图1图2图2 图1四边形?如果存在,求出R 点的坐标;如果不存在,请说明理由;(3)在抛物线的对称轴上求点M ,使得M 到D 、A 的距离之差最大,求出点M 的坐标.6.在梯形OABC 中,CB ∥OA ,∠AOC =60°,∠OAB =90°,OC =2,BC =4,以O 点为原点,OA 所在的直线为x 轴,建立平面直角坐标系,另有一边长为2的等边△DEF ,DE 在x 轴上(如图1),如果让△DEF 以每秒1个单位的速度向左作匀速直线运动,开始时点D 与点A 重合,当点D 到达坐标原点时运动停止.(1)设△DEF 运动时间为t ,△DEF 与梯形OABC 重叠部分的面积为S ,求S 关于t 的函数关系式;(2)探究:在△DEF 运动过程中,如果射线DF 交经过O 、C 、B 三点的抛物线于点G ,是否存在这样的时刻t ,使得△OAG 的面积与梯形OABC 的面积相等?若存在,求出t 的值;若不存在,请说明理由.7.已知二次函数y =ax2+bx -2的图象与x 轴交于A 、B 两点,与y 轴交于点C ,点A 的坐标为(4,0),且当x =-2和x =5时二次函数的函数值y 相等. (1)求实数a 、b 的值;(2)如图1,动点E 、F 同时从A 点出发,其中点E 以每秒2个单位长度的速度沿AB 边向终点B 运动,点F 以每秒 5个单位长度的速度沿射线AC 方向运动.当点E 停止运动时,点F 随之停止运动.设运动时间为t 秒.连接EF ,将△AEF 沿EF 翻折,使点A 落在点D 处,得到△DEF .①当t 为何值时,线段DF 平分△ABC 的面积?②是否存在某一时刻t ,使得△DCF 为直角三角形?若存在,求出t 的值;若不存在,请说明理由.③设△DEF 与△ABC 重叠部分的面积为S ,求S 关于t 的函数关系式;(3)如图2,点P 在二次函数图象上运动,点Q 在二次函数图象的对称轴上运动,四边形PQBC 能否成为以PQ 为底的等腰梯形?如果能,直接写出P 、Q 两点的坐标;如果不能,请说明理由.8.如图,直线y=-43x+4与x轴交于点B,与y轴交于点C,二次函数的图象经过A(-1,0)、B、C三点.(1)求二次函数的表达式;(2)设二次函数图象的顶点为D,求四边形OCDB的面积;(3)若动点E、F同时从O点出发,其中点E以每秒32个单位长度的速度沿折线OBC按O→B→C的路线运动,点F以每秒4个单位长度的速度沿折线OCB按O→C→B的路线运动,当E、F两点相遇时,整个运动随之结束.设运动时间为t(秒),△OEF的面积为S(平方单位).①在E、F两点运动过程中,是否存在EF∥OC?若存在,求出此时t的值;若不存在,请说明理由;②求S关于t的函数关系式,并求S的最大值.9.已知抛物线y=4,0)点B作BC∥x轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).(1)求抛物线的解析式;(2)记△EF A的面积为S,求S关于t的函数关系式,并求S的最大值,指出此时△EF A的形状;(3)是否存在这样的t值,使△EF A、F两点的坐标;若不存在,请说明理由.10.如图,抛物线y=ax2+bx+4与x轴交于A(-2,0)、B(4,0)两点,与y轴交于C 点.(1)求抛物线的解析式;(2)T是抛物线对称轴上的一点,且△ATC是以AC为底的等腰三角形,求点T的坐标;(3)M、Q两点分别从A、B点以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M 到达原点时,点Q 立刻掉头并以每秒32个单位长度的速度向点B 方向移动,当点M 到达抛物线的对称轴时,两点停止运动.过点M 的直线l ⊥x 轴交AC 或BC 于点P .求点M 的运动时间t 与△APQ 面积S 的函数关系式,并求出S 的最大值.11.如图,对称轴为直线x =-1的抛物线经过点A (-3,0)和点C (0,3),与x 轴的另一交点为B .点P 、Q 同时从B 点出发,均以每秒1个单位长度的速度分别沿BA 、BC 边运动,其中一个点到达终点时,另一点也随之停止运动.设运动时间为t (秒). (1)求抛物线的解析式;(2)连接PQ ,将△BPQ 沿PQ 翻折,所得的△B ′PQ 与△ABC 重叠部分的面积记为S ,求S 与t 之间的函数关系式,并求S 的最大值; (3)若点D 的坐标为(-4,3),当点B ′ 恰好落在抛物线上时,在抛物线的对称轴时是否存在点M ,使四边形MADB ′的周长最小,若存在,求出这个最小值;若不存在,请说明理由.12.如图,抛物线y =ax2+bx +152(a ≠0)经过A (-3,0)、C (5,0)两点,点B 为抛物线的顶点,抛物线的对称轴与x 轴交于点D . (1)求此抛物线的解析式;(2)动点P 从点B 出发,沿线段BD 向终点D 作匀速运动,速度为每秒1个单位长度,运动时间为t s ,过点P 作PM ⊥BD 交BC 于点M ,过点M 作MN ∥BD ,交抛物线于点N . ①当t 为何值时,线段MN 最长;②在点P 运动的过程中,是否有某一时刻,使得以O 、P 、形?若存在,求出此刻的t 值;若不存在,请说明理由.13.如图,抛物线y =-x2-2x +3与x 轴相交于点A 、B (A 在B 的左侧),与y 轴交于点C . (1)求线段AC 所在直线的解析式;(2)点M 是第二象限内抛物线上的一点,且S △MAC=12S △MAB,求点M 的坐标; (3)点P 以每秒1个单位长度的速度,沿线段BA 由B 向A 运动,同时,点Q 以每秒2个单位长度的速度,从A 开始沿射线AC 运动,当P 到达A 时,整个运动随即结束.设运动的时间为t 秒.①求△APQ 的面积S 与t 的函数关系式,并求当t 为何值时,△APQ 的面积最大,最大面积是多少?②在整个运动过程中,以PQ 为直径的圆能否与直线BC 相切?若能,请直接写出相应的t 值;若不能,请说明理由;③直接写出线段PQ 的中点在整个运动过程中所经过路径的长.14.如图,二次函数c x y +-=221的图象经过点D ⎪⎭⎫ ⎝⎛-29,3,与x 轴交于A 、B 两点. ⑴求c 的值;⑵如图①,设点C 为该二次函数的图象在x 轴上方的一点,直线AC 将四边形ABCD 的面积二等分,试证明线段BD 被直线AC 平分,并求此时直线AC 的函数解析式; ⑶设点P 、Q 为该二次函数的图象在x 轴上方的两个动点,试猜想:是否存在这样的点P 、Q ,使△AQP ≌△ABP ?如果存在,请举例验证你的猜想;如果不存在,请说明理由.(图②供选用)15.(2010福建福州)如图,在△ABC 中,∠C =45°,BC =10,高AD =8,矩形EFPQ 的一边QP 在BC 边上,E 、F 两点分别在AB 、AC 上,AD 交EF 于点H . (1)求证:AH AD =EFBC;(2)设EF =x ,当x 为何值时,矩形EFPQ 的面积最大?并求其最大值;(3)当矩形EFPQ 的面积最大时,该矩形EFPQ 以每秒1个单位的速度沿射线QC 匀速运动(当点Q 与点C 重合时停止运动),设运动时间为t 秒,矩形EFFQ 与△ABC 重叠部分的面积为S ,求S 与t 的函数关系式.16.(2010福建福州)如图1,在平面直角坐标系中,点B 在直线y =2x 上,过点B 作x 轴的垂线,垂足为A ,OA =5.若抛物线y =16x 2+bx +c 过O 、A 两点.(1)求该抛物线的解析式;(2)若A 点关于直线y =2x 的对称点为C ,判断点C 是否在该抛物线上,并说明理由; (3)如图2,在(2)的条件下,⊙O 1是以BC 为直径的圆.过原点O 作⊙O 1的切线OP ,P 为切点(点P 与点C 不重合).抛物线上是否存在点Q ,使得以PQ 为直径的圆与⊙O 1相切?若存在,求出点Q 的横坐标;若不存在,请说明理由17.(2010江苏无锡)如图,矩形ABCD 的顶点A 、B 的坐标分别为(-4,0)和(2,0),BC=设直线AC 与直线x =4交于点E .(1)求以直线x =4为对称轴,且过C 与原点O 的抛物线的函数关系式,并说明此抛物线一定过点E ;(2)设(1)中的抛物线与x 轴的另一个交点为N ,M 是该抛物线上位于C 、N 之间的一动点,求△CMN 面积的最大值.(第2题)(图1) (图2)18.(2010湖南邵阳)如图,抛物线y =2134x x -++与x 轴交于点A 、B ,与y 轴相交于点C ,顶点为点D ,对称轴l 与直线BC 相交于点E ,与x 轴交于点F 。
精选中考二次函数压轴题包括答案

精选中考二次函数压轴题(含答案)1.如图,二次函数y1 x2c的图象经过点D23,9,与x轴交于A、B两点.2⑴求 c 的值;⑵如图①,设点 C 为该二次函数的图象在x 轴上方的一点,直线AC 将四边形ABCD 的面积二均分,试证明线段BD 被直线 AC 均分,并求此时直线AC 的函数剖析式;⑶设点 P、Q 为该二次函数的图象在x 轴上方的两个动点,试猜想:可否存在这样的点P、Q,使△ AQP≌△ ABP?若是存在,请举例考据你的猜想;若是不存在,请说明原由.(图②供采纳)2.( 2010 福建福州)如图,在△ ABC 中,∠ C= 45°, BC= 10,高 AD = 8,矩形 EFPQ 的一边 QP 在 BC 边上, E、 F 两点分别在 AB、 AC 上, AD 交 EF 于点 H.AH=EF;(1)求证:AD BC(2)设 EF = x,当 x 为何值时,矩形EFPQ 的面积最大 ?并求其最大值;( 3)当矩形 EFPQ 的面积最大时,该矩形EFPQ 以每秒 1 个单位的速度沿射线QC 匀速运动 ( 当点 Q 与点 C 重合时停止运动 ),设运动时间为t 秒,矩形EFFQ 与△ ABC 重叠部分的面积为S,求 S 与 t 的函数关系式.( 第 2(图 1)(图3.( 2010 福建福州)如图 1,在平面直角坐标系中,点 B 在直线 y=2x 上,过点 B 作 x 轴的垂线,垂足为 A,OA= 5.若12抛物线 y=x + bx+ c 过 O、A 两点.6(1)求该抛物线的剖析式;(2)若 A 点关于直线 y= 2x 的对称点为 C,判断点 C 可否在该抛物线上,并说明原由;( 3)如图 2,在( 2)的条件下,⊙O1是以 BC 为直径的圆.过原点O 作⊙ O1的切线 OP, P 为切点 (点 P 与点 C 不重合 ).抛物线上可否存在点Q,使得以 PQ 为直径的圆与⊙ O1相切 ?若存在,求出点Q 的横坐标;若不存在,请说明原由4.(2010 江苏无锡)如图,矩形ABCD的极点 A、B 的坐标分别为(-4,0)和(2,0),BC=2 3 .设直线AC与直线x=4交于点 E.(1)求以直线x=4为对称轴,且过C与原点 O的抛物线的函数关系式,并说明此抛物线必然过点E;(2)设( 1)中的抛物线与x 轴的另一个交点为N,M是该抛物线上位于C、 N之间的一动点,求△ CMN面积的最大值.yD C EA OB xx= 45.( 2010 湖南邵阳)如图,抛物线y= 1 x2x 3 与x轴交于点A、B,与y轴订交于点C,极点为点D,对称轴l4与直线 BC 订交于点 E,与 x 轴交于点 F 。
二次函数压轴题专题分类训练(完整资料).doc

【最新整理,下载后即可编辑】中考二次函数压轴题专题分类训练题型一:面积问题【例1】如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式; (2)求△CAB 的铅垂高CD 及S △CAB ;(3)设点P 是抛物线(在第一象限内)上的一个动点,是否存在一点P ,使S △PAB =89S △CAB存在,请说明理由.【变式练习】1.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB . (1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由. (4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.图22.如图,抛物线y = ax 2 + bx + 4与x 轴的两个交点分别为A (-4,0)、B (2,0),与y 轴交于点C ,顶点为D .E (1,2)为线段BC 的中点,BC 的垂直平分线与x 轴、y 轴分别交于F 、G .(1)求抛物线的函数解析式,并写出顶点D 的坐标; (2)在直线EF 上求一点H ,使△CDH小周长;(3)若点K 在x 轴上方的抛物线上运动,当K 时,△EFK 的面积最大?并求出最大面积.3.如图,已知:直线3+y交x轴于点A,交y轴于点B,抛=x-物线y=ax2+bx+c经过A、B、C(1,0)三点.(1)求抛物线的解析式;(2)若点D的坐标为(-1,0),在直线3+y上有一点=x-P,使ΔABO与ΔADP相似,求出点P的坐标;(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使ΔADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.题型二:构造直角三角形【例2】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求此时点M的坐标;(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90º的点P的坐标.E【变式练习】1.如图,抛物线y=与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.(1)求点A、B的坐标;(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.O 11x y2.在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且310。
中考数学与二次函数有关的压轴题含详细答案

中考数学与二次函数有关的压轴题含详细答案一、二次函数1.如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.(1)求出抛物线C1的解析式,并写出点G的坐标;(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N 为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.【答案】(1)抛物线C1的解析式为y=﹣x2+2x+3,点G的坐标为(1,4);(2)k=1;(3)M1113+0)、N1131);M2113+,0)、N2(1,﹣1);M3(4,0)、N3(10,﹣1);M4(4,0)、N4(﹣2,﹣1).【解析】【分析】(1)由点A的坐标及OC=3OA得点C坐标,将A、C坐标代入解析式求解可得;(2)设抛物线C2的解析式为y=﹣x2+2x+3﹣k,即y=﹣(x﹣1)2+4﹣k,′作G′D⊥x轴于点D,设BD′=m,由等边三角形性质知点B′的坐标为(m+1,0),点G′的坐标为(1,3m),代入所设解析式求解可得;(3)设M(x,0),则P(x,﹣x2+2x+3)、Q(x,﹣x2+2x+2),根据PQ=OA=1且∠AOQ、∠PQN均为钝角知△AOQ≌△PQN,延长PQ交直线y=﹣1于点H,证△OQM≌△QNH,根据对应边相等建立关于x的方程,解之求得x的值从而进一步求解即可.【详解】(1)∵点A的坐标为(﹣1,0),∴OA=1,∴OC=3OA,∴点C的坐标为(0,3),将A、C坐标代入y=ax2﹣2ax+c,得:203a a cc++=⎧⎨=⎩,解得:13a c =-⎧⎨=⎩,∴抛物线C 1的解析式为y=﹣x 2+2x+3=﹣(x ﹣1)2+4, 所以点G 的坐标为(1,4);(2)设抛物线C 2的解析式为y=﹣x 2+2x+3﹣k ,即y=﹣(x ﹣1)2+4﹣k , 过点G′作G′D ⊥x 轴于点D ,设BD′=m ,∵△A′B′G′为等边三角形, ∴G′D=3B′D=3m ,则点B′的坐标为(m+1,0),点G′的坐标为(1,3m ), 将点B′、G′的坐标代入y=﹣(x ﹣1)2+4﹣k ,得:24043m k k m⎧-+-=⎪⎨-=⎪⎩, 解得:1104m k =⎧⎨=⎩(舍),2231m k ⎧=⎪⎨=⎪⎩,∴k=1;(3)设M (x ,0),则P (x ,﹣x 2+2x+3)、Q (x ,﹣x 2+2x+2), ∴PQ=OA=1,∵∠AOQ 、∠PQN 均为钝角, ∴△AOQ ≌△PQN ,如图2,延长PQ 交直线y=﹣1于点H ,则∠QHN=∠OMQ=90°, 又∵△AOQ ≌△PQN , ∴OQ=QN ,∠AOQ=∠PQN , ∴∠MOQ=∠HQN ,∴△OQM ≌△QNH (AAS ), ∴OM=QH ,即x=﹣x 2+2x+2+1, 解得:x=1132±(负值舍去), 当x=1132+时,HN=QM=﹣x 2+2x+2=1312-,点M (1132+,0), ∴点N 坐标为(1132++1312-,﹣1),即(13,﹣1); 或(113+﹣131-,﹣1),即(1,﹣1); 如图3,同理可得△OQM ≌△PNH ,∴OM=PH ,即x=﹣(﹣x 2+2x+2)﹣1, 解得:x=﹣1(舍)或x=4,当x=4时,点M 的坐标为(4,0),HN=QM=﹣(﹣x 2+2x+2)=6,∴点N 的坐标为(4+6,﹣1)即(10,﹣1),或(4﹣6,﹣1)即(﹣2,﹣1); 综上点M 1113+0)、N 1131);M 2113+0)、N 2(1,﹣1);M 3(4,0)、N 3(10,﹣1);M 4(4,0)、N 4(﹣2,﹣1).【点睛】本题考查的是二次函数的综合题,涉及到的知识有待定系数法、等边三角形的性质、全等三角形的判定与性质等,熟练掌握待定系数法求函数解析式、等边三角形的性质、全等三角形的判定与性质、运用分类讨论思想是解题的关键.2.一座拱桥的轮廓是抛物线型(如图所示),拱高6m ,跨度20m ,相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图所示),其表达式是2y ax c =+的形式.请根据所给的数据求出a ,c 的值.(2)求支柱MN 的长度.(3)拱桥下地平面是双向行车道(正中间是一条宽2m 的隔离带),其中的一条行车道能否并排行驶宽2m 、高3m 的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.【答案】(1)y=-350x 2+6;(2)5.5米;(3)一条行车道能并排行驶这样的三辆汽车. 【解析】试题分析:(1)根据题目可知A .B ,C 的坐标,设出抛物线的解析式代入可求解. (2)设N 点的坐标为(5,y N )可求出支柱MN 的长度.(3)设DN 是隔离带的宽,NG 是三辆车的宽度和.做GH 垂直AB 交抛物线于H 则可求解.试题解析: (1) 根据题目条件,A 、B 、C 的坐标分别是(-10,0)、(0,6)、(10,0).将B 、C 的坐标代入2y ax c =+,得 6,0100.c a c =⎧⎨=+⎩解得3,650a c =-=. ∴抛物线的表达式是23650y x =-+. (2) 可设N (5,N y ), 于是2356 4.550N y =-⨯+=. 从而支柱MN 的长度是10-4.5=5.5米.(3) 设DE 是隔离带的宽,EG 是三辆车的宽度和, 则G 点坐标是(7,0)(7=2÷2+2×3).过G 点作GH 垂直AB 交抛物线于H ,则23176335050H y =-⨯+=+>. 根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.3.如图所示,已知平面直角坐标系xOy ,抛物线过点A(4,0)、B(1,3)(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,设抛物线上的点P(m,n)在第四象限,点P 关于直线l 的对称点为E ,点E 关于y 轴的对称点为F ,若四边形OAPF 的面积为20,求m 、n 的值. 【答案】(1)y=-224(2)4y x x x =-+=--+,对称轴为:x=2,顶点坐标为:(2,4) (2)m 、n 的值分别为 5,-5 【解析】(1) 将点A(4,0)、B(1,3) 的坐标分别代入y =-x 2+bx +c ,得: 4b+c-16=0,b+c-1="3" , 解得:b="4" , c=0.所以抛物线的表达式为:24y x x =-+. y=-224(2)4y x x x =-+=--+,所以 抛物线的对称轴为:x=2,顶点坐标为:(2,4). (2) 由题可知,E 、F 点坐标分别为(4-m ,n ),(m-4,n ). 三角形POF 的面积为:1/2×4×|n|= 2|n|, 三角形AOP 的面积为:1/2×4×|n|= 2|n|,四边形OAPF 的面积= 三角形POF 的面积+三角形AOP 的面积=20, 所以 4|n|=20, n=-5.(因为点P(m,n)在第四象限,所以n<0) 又n=-2m +4m ,所以2m -4m-5=0,m=5.(因为点P(m,n)在第四象限,所以m>0) 故所求m 、n 的值分别为 5,-5.4.红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的 日销售量(件)与时间(天)的关系如下表: 时间(天) 1 3 6 10 36 … 日销售量(件)9490847624…未来40天内,前20天每天的价格y 1(元/件)与t 时间(天)的函数关系式为:y 1=t+25(1≤t≤20且t 为整数);后20天每天的价格y 2(原/件)与t 时间(天)的函数关系式为:y 2=—t+40(21≤t≤40且t 为整数).下面我们来研究 这种商品的有关问题.(1)认真分析上表中的数量关系,利用学过的一次函数、二次函数 、反比例函数的知识确定一个满足这些数据之间的函数关系式;(2)请预测未来40天中那一天的销售利润最大,最大日销售利润是多少?(3)在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程,公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.【答案】(1)y=﹣2t+96;(2)当t=14时,利润最大,最大利润是578元;(3)3≤a<4.【解析】分析:(1)通过观察表格中的数据日销售量与时间t是均匀减少的,所以确定m与t是一次函数关系,利用待定系数法即可求出函数关系式;(2)根据日销售量、每天的价格及时间t可以列出销售利润W关于t的二次函数,然后利用二次函数的性质即可求出哪一天的日销售利润最大,最大日销售利润是多少;(3)列式表示前20天中每天扣除捐赠后的日销售利润,根据函数的性质求出a的取值范围.详解:(1)设数m=kt+b,有,解得∴m=-2t+96,经检验,其他点的坐标均适合以上析式故所求函数的解析式为m=-2t+96.(2)设日销售利润为P,由P=(-2t+96)=t2-88t+1920=(t-44)2-16,∵21≤t≤40且对称轴为t=44,∴函数P在21≤t≤40上随t的增大而减小,∴当t=21时,P有最大值为(21-44)2-16=529-16=513(元),答:来40天中后20天,第2天的日销售利润最大,最大日销售利润是513元.(3)P1=(-2t+96)=-+(14+2a)t+480-96n,∴对称轴为t=14+2a,∵1≤t≤20,∴14+2a≥20得a≥3时,P1随t的增大而增大,又∵a<4,∴3≤a<4.点睛:解答本题的关键是要分析题意根据实际意义准确的求出解析式,并会根据图示得出所需要的信息.同时注意要根据实际意义准确的找到不等关系,利用不等式组求解.5.二次函数y=x2-2mx+3(m>)的图象与x轴交于点A(a,0)和点B(a+n,0)(n >0且n为整数),与y轴交于C点.(1)若a=1,①求二次函数关系式;②求△ABC的面积;(2)求证:a=m-;(3)线段AB(包括A、B)上有且只有三个点的横坐标是整数,求a的值.【答案】(1)y=x2-4x+3;3;(2)证明见解析;(3)a=1或a=−.【解析】试题分析:(1)①首先根据a=1求得A的坐标,然后代入二次函数的解析式,求得m的值即可确定二次函数的解析式;②根据解析式确定抛物线与坐标轴的交点坐标,从而确定三角形的面积;(2)将原二次函数配方后即可确定其对称轴为x=m,然后根据A、B两点关于x=m对称得到a+n-m=m-a,从而确定a、m、n之间的关系;(3)根据a=m-得到A(m-,0)代入y=(x-m)2-m2+3得0=(m--m)2-m2+3,求得m 的值即可确定a的值.试题解析:(1)①∵a=1,∴A(1,0),代入y=x2-2mx+3得1-2m+3=0,解得m=2,∴y=x2-4x+3;②在y=x2-4x+3中,当y=0时,有x2-4x+3=0可得x=1或x=3,∴A(1,0)、B(3,0),∴AB=2再根据解析式求出C点坐标为(0,3),∴OC=3,△ABC的面积=×2×3=3;(2)∵y=x2-2mx+3=(x-m)2-m2+3,∴对称轴为直线x=m,∵二次函数y=x2-2mx+3的图象与x轴交于点A和点B∴点A和点B关于直线x=m对称,∴a+n-m=m-a,∴a=m-;(3)y=x2-2mx+3(m>)化为顶点式为y=(x-m)2-m2+3(m>)①当a为整数,因为n>0且n为整数所以a+n是整数,∵线段AB(包括A、B)上有且只有三个点的横坐标是整数,∴n=2,∴a=m-1,∴A(m-1,0)代入y=(x-m)2-m2+3得(x-m)2-m2+3=0,∴m2-4=0,∴m=2,m=-2(舍去),∴a=2-1=1,②当a不是整数,因为n>0且n为整数所以a+n不是整数,∵线段AB(包括A、B)上有且只有三个点的横坐标是整数,∴n=3,∴a=m-∴A(m-,0)代入y=(x-m)2-m2+3得0=(m--m)2-m2+3,∴m2=,∴m=,m=-(舍去),∴a=−,综上所述:a=1或a=−.考点:二次函数综合题.6.如图1,在平面直角坐标系中,直线122y x=+与x轴交于点A,与y轴交于点C,抛物线212y x bx c=++经过A、C两点,与x轴的另一交点为点B.(1)求抛物线的函数表达式;(2)点D为直线AC上方抛物线上一动点,①连接BC、CD、BD,设BD交直线AC于点E,△CDE的面积为S1,△BCE的面积为S2.求:12SS的最大值;②如图2,是否存在点D,使得∠DCA=2∠BAC?若存在,直接写出点D的坐标,若不存在,说明理由.【答案】(1)213222y x x=--+;(2)①当2a=-时,12SS的最大值是45;②点D 的坐标是(2,3)-【解析】 【分析】(1)根据题意得到A (-4,0),C (0,2)代入y=-12x 2+bx+c ,于是得到结论; (2)①如图,令y=0,解方程得到x 1=-4,x 2=1,求得B (1,0),过D 作DM ⊥x 轴于M ,过B 作BN ⊥x 轴交于AC 于N ,根据相似三角形的性质即可得到结论;②根据勾股定理的逆定理得到△ABC 是以∠ACB 为直角的直角三角形,取AB 的中点P ,求得P (-32,0),得到PA=PC=PB=52,过D 作x 轴的平行线交y 轴于R ,交AC 的延线于G ,∠DCF=2∠BAC=∠DGC+∠CDG ,解直角三角形即可得到结论. 【详解】解:(1)根据题意得A (-4,0),C (0,2),∵抛物线y=-12x 2+bx+c 经过A .C 两点, ∴1016422b c c ⎧-⨯-+⎪⎨⎪⎩==, ∴3b=-2c=2⎧⎪⎨⎪⎩, 抛物线解析式为:213222y x x =--+ ; (2)①令0y =, ∴2132022x x --+= 解得:14x =- ,21x = ∴B (1,0)过点D 作DM x ⊥轴交AC 于M ,过点B 作BN x ⊥轴交AC 于点N ,∴DM ∥BN ∴DME BNE ∆∆∽∴12S DE DM S BE BN== 设:213222D a a a ⎛⎫--+ ⎪⎝⎭,∴122M a a ⎛⎫+ ⎪⎝⎭, ∵()10B , ∴51,2N ⎛⎫⎪⎝⎭∴()22121214225552a aS DM a S BN --===-++ ∴当2a =-时,12S S 的最大值是45;②∵A (-4,0),B (1,0),C (0,2), ∴AC=25,BC=5,AB=5, ∴AC 2+BC 2=AB 2,∴△ABC 是以∠ACB 为直角的直角三角形, 取AB 的中点P , ∴P (-32,0), ∴PA=PC=PB=52, ∴∠CPO=2∠BAC , ∴tan ∠CPO=tan (2∠BAC )=43, 过D 作x 轴的平行线交y 轴于R ,交AC 的延长线于G ,如图,∴∠DCF=2∠BAC=∠DGC+∠CDG , ∴∠CDG=∠BAC ,∴tan∠CDG=tan∠BAC=12,即RC:DR=12,令D(a,-12a2-32a+2),∴DR=-a,RC=-12a2-32a,∴(-12a2-32a):(-a)=1:2,∴a1=0(舍去),a2=-2,∴x D=-2,∴-12a2-32a+2=3,∴点D的坐标是()2,3-【点睛】本题是二次函数综合题,涉及待定系数法求函数的解析式,相似三角形的判定和性质,解直角三角形等知识点,正确的作出辅助线是解题的关键,难度较大.7.若三个非零实数x,y,z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x,y,z构成“和谐三组数”.(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;(2)若M(t,y1),N(t+1,y2),R(t+3,y3)三点均在函数y=kx(k为常数,k≠0)的图象上,且这三点的纵坐标y1,y2,y3构成“和谐三组数”,求实数t的值;(3)若直线y=2bx+2c(bc≠0)与x轴交于点A(x1,0),与抛物线y=ax2+3bx+3c(a≠0)交于B(x2,y2),C(x3,y3)两点.①求证:A,B,C三点的横坐标x1,x2,x3构成“和谐三组数”;②若a>2b>3c,x2=1,求点P(ca,ba)与原点O的距离OP的取值范围.【答案】(1)不能,理由见解析;(2)t的值为﹣4、﹣2或2;(3)①证明见解析;②2≤OPOP≠1.【解析】【分析】(1)由和谐三组数的定义进行验证即可;(2)把M、N、R三点的坐标分别代入反比例函数解析式,可用t和k分别表示出y1、y2、y3,再由和谐三组数的定义可得到关于t的方程,可求得t的值;(3)①由直线解析式可求得x 1=﹣c b,联立直线和抛物线解析式消去y ,利用一元二次方程根与系数的关系可求得x 2+x 3=﹣b a ,x 2x 3=c a ,再利用和谐三数组的定义证明即可;②由条件可得到a+b+c =0,可得c =﹣(a+b),由a >2b >3c 可求得b a的取值范围,令m =b a,利用两点间距离公式可得到OP 2关于m 的二次函数,利用二次函数的性质可求得OP 2的取值范围,从而可求得OP 的取值范围.【详解】(1)不能,理由如下:∵1、2、3的倒数分别为1、12、13, ∴12+13≠1,1+12≠13,1+13≠12, ∴实数1,2,3不可以构成“和谐三组数”; (2)∵M(t ,y 1),N(t+1,y 2),R(t+3,y 3)三点均在函数k x (k 为常数,k≠0)的图象上, ∴y 1、y 2、y 3均不为0,且y 1=k t ,y 2=1k t +,y 3=3k t +, ∴11y =t k ,21y =1t k +,31y =3t k+, ∵y 1,y 2,y 3构成“和谐三组数”,∴有以下三种情况: 当11y =21y +31y 时,则t k =1t k ++3t k+,即t =t+1+t+3,解得t =﹣4; 当21y =11y +31y 时,则1t k +=t k +3t k+,即t+1=t+t+3,解得t =﹣2; 当31y =11y +21y 时,则3t k +=t k +1t k+,即t+3=t+t+1,解得t =2; ∴t 的值为﹣4、﹣2或2;(3)①∵a 、b 、c 均不为0,∴x 1,x 2,x 3都不为0,∵直线y =2bx+2c(bc≠0)与x 轴交于点A(x 1,0),∴0=2bx 1+2c ,解得x 1=﹣c b, 联立直线与抛物线解析式,消去y 可得2bx+2c =ax 2+3bx+3c ,即ax 2+bx+c =0,∵直线与抛物线交与B(x 2,y 2),C(x 3,y 3)两点,∴x 2、x 3是方程ax 2+bx+c =0的两根,∴x 2+x 3=﹣b a ,x 2x 3=c a, ∴21x +31x =2323x x x x +=b a c a-=﹣b c =11x , ∴x 1,x 2,x 3构成“和谐三组数”;②∵x 2=1,∴a+b+c =0,∴c =﹣a ﹣b ,∵a >2b >3c , ∴a >2b >3(﹣a ﹣b),且a >0,整理可得253a b b a>⎧⎨>-⎩,解得﹣35<b a <12, ∵P(c a ,b a), ∴OP 2=(c a )2+(b a )2=(a b a --)2+(b a )2=2(b a )2+2b a +1=2(b a +12)2+12, 令m =b a ,则﹣35<m <12且m≠0,且OP 2=2(m+12)2+12, ∵2>0,∴当﹣35<m <﹣12时,OP 2随m 的增大而减小,当m =﹣35时,OP 2有最大临界值1325,当m =﹣12时,OP 2有最小临界值12, 当﹣12<m <12时,OP 2随m 的增大而增大,当m =﹣12时,OP 2有最小临界值12,当m =12时,OP 2有最大临界值52, ∴12≤OP 2<52且OP 2≠1, ∵P 到原点的距离为非负数,∴2≤OP且OP≠1. 【点睛】本题为二次函数的综合应用,涉及新定义、函数图象的交点、一元二次方程根与系数的关系、勾股定理、二次函数的性质、分类讨论思想及转化思想等知识.在(1)中注意利用和谐三数组的定义,在(2)中由和谐三数组得到关于t 的方程是解题的关键,在(3)①中用a 、b 、c 分别表示出x 1,x 2,x 3是解题的关键,在(3)②中把OP 2表示成二次函数的形式是解题的关键.本题考查知识点较多,综合性较强,特别是最后一问,难度很大.8.如图,关于x 的二次函数y=x 2+bx+c 的图象与x 轴交于点A (1,0)和点B 与y 轴交于点C (0,3),抛物线的对称轴与x 轴交于点D .(1)求二次函数的表达式;(2)在y 轴上是否存在一点P ,使△PBC 为等腰三角形?若存在.请求出点P 的坐标; (3)有一个点M 从点A 出发,以每秒1个单位的速度在AB 上向点B 运动,另一个点N 从点D 与点M 同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M 到达点B 时,点M 、N 同时停止运动,问点M 、N 运动到何处时,△MNB 面积最大,试求出最大面积.【答案】(1)二次函数的表达式为:y=x 2﹣4x+3;(2)点P 的坐标为:(0,2(0,3﹣2)或(0,-3)或(0,0);(3)当点M 出发1秒到达D 点时,△MNB 面积最大,最大面积是1.此时点N 在对称轴上x 轴上方2个单位处或点N 在对称轴上x 轴下方2个单位处.【解析】【分析】(1)把A (1,0)和C (0,3)代入y=x 2+bx+c 得方程组,解方程组即可得二次函数的表达式;(2)先求出点B 的坐标,再根据勾股定理求得BC 的长,当△PBC 为等腰三角形时分三种情况进行讨论:①CP=CB ;②BP=BC ;③PB=PC ;分别根据这三种情况求出点P 的坐标; (3)设AM=t 则DN=2t ,由AB=2,得BM=2﹣t ,S △MNB=12×(2﹣t )×2t=﹣t 2+2t ,把解析式化为顶点式,根据二次函数的性质即可得△MNB 最大面积;此时点M 在D 点,点N 在对称轴上x 轴上方2个单位处或点N 在对称轴上x 轴下方2个单位处.【详解】解:(1)把A (1,0)和C (0,3)代入y=x 2+bx+c ,103b c c ++=⎧⎨=⎩解得:b=﹣4,c=3,∴二次函数的表达式为:y=x 2﹣4x+3;(2)令y=0,则x 2﹣4x+3=0,解得:x=1或x=3,∴B (3,0),∴BC=32,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=32,∴OP=OC+PC=3+32或OP=PC﹣OC=32﹣3∴P1(0,3+32),P2(0,3﹣32);②当PB=PC时,OP=OB=3,∴P3(0,-3);③当BP=BC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+32)或(0,3﹣32)或(﹣3,0)或(0,0);(3)如图2,设AM=t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=1×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,2当点M出发1秒到达D点时,△MNB面积最大,最大面积是1.此时点N在对称轴上x 轴上方2个单位处或点N在对称轴上x轴下方2个单位处.9.在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=14x与抛物线交于A、B两点,直线l为y=﹣1.(1)求抛物线的解析式;(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.【答案】(1)抛物线的解析式为y=14x2﹣x+1.(2)点P的坐标为(2813,﹣1).(3)定点F的坐标为(2,1).【解析】分析:(1)由抛物线的顶点坐标为(2,0),可设抛物线的解析式为y=a(x-2)2,由抛物线过点(4,1),利用待定系数法即可求出抛物线的解析式;(2)联立直线AB与抛物线解析式成方程组,通过解方程组可求出点A、B的坐标,作点B关于直线l的对称点B′,连接AB′交直线l于点P,此时PA+PB取得最小值,根据点B的坐标可得出点B′的坐标,根据点A、B′的坐标利用待定系数法可求出直线AB′的解析式,再利用一次函数图象上点的坐标特征即可求出点P的坐标;(3)由点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征,即可得出(1-12-12y0)m2+(2-2x0+2y0)m+x02+y02-2y0-3=0,由m的任意性可得出关于x0、y0的方程组,解之即可求出顶点F的坐标.详解:(1)∵抛物线的顶点坐标为(2,0),设抛物线的解析式为y=a(x-2)2.∵该抛物线经过点(4,1),∴1=4a,解得:a=14,∴抛物线的解析式为y=14(x-2)2=14x2-x+1.(2)联立直线AB与抛物线解析式成方程组,得:214114y x y x x ⎧⎪⎪⎨⎪-+⎪⎩==,解得:11114x y ⎧⎪⎨⎪⎩==,2241x y ⎧⎨⎩==, ∴点A 的坐标为(1,14),点B 的坐标为(4,1). 作点B 关于直线l 的对称点B′,连接AB′交直线l 于点P ,此时PA+PB 取得最小值(如图1所示).∵点B (4,1),直线l 为y=-1,∴点B′的坐标为(4,-3).设直线AB′的解析式为y=kx+b (k≠0),将A (1,14)、B′(4,-3)代入y=kx+b ,得: 1443k b k b ⎧+⎪⎨⎪+-⎩==,解得:131243k b ⎧-⎪⎪⎨⎪⎪⎩==, ∴直线AB′的解析式为y=-1312x+43, 当y=-1时,有-1312x+43=-1, 解得:x=2813, ∴点P 的坐标为(2813,-1). (3)∵点M 到直线l 的距离与点M 到点F 的距离总是相等,∴(m-x 0)2+(n-y 0)2=(n+1)2,∴m 2-2x 0m+x 02-2y 0n+y 02=2n+1.∵M (m ,n )为抛物线上一动点,∴n=14m 2-m+1, ∴m 2-2x 0m+x 02-2y 0(14m 2-m+1)+y 02=2(14m 2-m+1)+1, 整理得:(1-12-12y 0)m 2+(2-2x 0+2y 0)m+x 02+y 02-2y 0-3=0. ∵m 为任意值,∴000220001110222220230y x y x y y ⎧--⎪⎪-+⎨⎪+--⎪⎩===,∴0021x y ⎧⎨⎩==, ∴定点F 的坐标为(2,1).点睛:本题考查了待定系数法求二次(一次)函数解析式、二次(一次)函数图象上点的坐标特征、轴对称中的最短路径问题以及解方程组,解题的关键是:(1)根据点的坐标,利用待定系数法求出二次函数解析式;(2)利用两点之间线段最短找出点P 的位置;(3)根据点M 到直线l 的距离与点M 到点F 的距离总是相等结合二次函数图象上点的坐标特征,找出关于x 0、y 0的方程组.10.如图,在平面直角坐标系xOy 中,A 、B 为x 轴上两点,C 、D 为y 轴上的两点,经 过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C 的坐标为(0,),点M 是抛物线C 2:2y mx 2mx 3m =--(m <0)的顶点.(1)求A 、B 两点的坐标;(2)“蛋线”在第四象限上是否存在一点P ,使得△PBC 的面积最大?若存在,求出△PBC 面积的最大值;若不存在,请说明理由;(3)当△BDM 为直角三角形时,求m 的值.【答案】(1)A (,0)、B (3,0).(2)存在.S △PBC 最大值为2716 (3)2m 2=-或1m =-时,△BDM 为直角三角形. 【解析】【分析】 (1)在2y mx 2mx 3m =--中令y=0,即可得到A 、B 两点的坐标.(2)先用待定系数法得到抛物线C 1的解析式,由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式,根据二次函数最值原理求出最大值.(3)先表示出DM 2,BD 2,MB 2,再分两种情况:①∠BMD=90°时;②∠BDM=90°时,讨论即可求得m 的值.【详解】解:(1)令y=0,则2mx 2mx 3m 0--=,∵m <0,∴2x 2x 30--=,解得:1x 1=-,2x 3=.∴A (,0)、B (3,0).(2)存在.理由如下:∵设抛物线C 1的表达式为()()y a x 1x 3=+-(a 0≠),把C (0,32-)代入可得,12a =. ∴C1的表达式为:()()1y x 1x 32=+-,即213y x x 22=--. 设P (p ,213p p 22--), ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+(). ∵3a 4=-<0,∴当3p 2=时,S △PBC 最大值为2716. (3)由C 2可知: B (3,0),D (0,3m -),M (1,4m -),∴BD 2=29m 9+,BM 2=216m 4+,DM 2=2m 1+.∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况:当∠BMD=90°时,BM 2+ DM 2= BD 2,即216m 4++2m 1+=29m 9+,解得:12m 2=-,22m 2=(舍去). 当∠BDM=90°时,BD 2+ DM 2= BM 2,即29m 9++2m 1+=216m 4+,解得:1m 1=-,2m 1=(舍去) .综上所述,2m =或1m =-时,△BDM 为直角三角形.11.如图,直线y =﹣x +4与x 轴交于点B ,与y 轴交于点C ,抛物线y =﹣x 2+bx +c 经过B ,C 两点,与x 轴另一交点为A .点P 以每秒2个单位长度的速度在线段BC 上由点B 向点C 运动(点P 不与点B 和点C 重合),设运动时间为t 秒,过点P 作x 轴垂线交x 轴于点E ,交抛物线于点M .(1)求抛物线的解析式;(2)如图①,过点P 作y 轴垂线交y 轴于点N ,连接MN 交BC 于点Q ,当12MQ NQ =时,求t 的值;(3)如图②,连接AM 交BC 于点D ,当△PDM 是等腰三角形时,直接写出t 的值.【答案】(1)y =﹣x 2+3x +4;(2)t 的值为12;(3)当△PDM 是等腰三角形时,t =1或t 2﹣1.【解析】【分析】(1)求直线y=-x+4与x 轴交点B ,与y 轴交点C ,用待定系数法即求得抛物线解析式. (2)根据点B 、C 坐标求得∠OBC=45°,又PE ⊥x 轴于点E ,得到△PEB 是等腰直角三角形,由2PB =求得BE=PE=t ,即可用t 表示各线段,得到点M 的横坐标,进而用m 表示点M 纵坐标,求得MP 的长.根据MP ∥CN 可证MPQ NCQ V V ∽,故有12MP MQ NC NQ ==,把用t 表示的MP 、NC 代入即得到关于t 的方程,求解即得到t 的值. (3)因为不确定等腰△PDM 的底和腰,故需分3种情况讨论:①若MD=MP ,则∠MDP=∠MPD=45°,故有∠DMP=90°,不合题意;②若DM=DP ,则∠DMP=∠MPD=45°,进而得AE=ME ,把含t 的式子代入并解方程即可;③若MP=DP ,则∠PMD=∠PDM ,由对顶角相等和两直线平行内错角相等可得∠CFD=∠PMD=∠PDM=∠CDF 进而得CF=CD .用t 表示M 的坐标,求直线AM 解析式,求得AM 与y 轴交点F 的坐标,即能用t 表示CF 的长.把直线AM 与直线BC 解析式联立方程组,解得x 的值即为点D 横坐标.过D 作y 轴垂线段DG ,得等腰直角△CDG ,用DG 即点D 横坐标,进而可用t 表示CD 的长.把含t 的式子代入CF=CD ,解方程即得到t 的值.【详解】(1)直线y =﹣x +4中,当x =0时,y =4∴C (0,4)当y =﹣x +4=0时,解得:x =4 ∴B (4,0)∵抛物线y =﹣x 2+bx +c 经过B ,C 两点∴1640004b c c -++=⎧⎨++=⎩ 解得:34b c =⎧⎨=⎩∴抛物线解析式为y =﹣x 2+3x +4(2)∵B (4,0),C (0,4),∠BOC =90° ∴OB =OC∴∠OBC =∠OCB =45° ∵ME ⊥x 轴于点E ,PBt ∴∠BEP =90°∴Rt △BEP 中,2PE sin PBE PB ∠==∴2BE PE PB t ===, ∴4M P P x x OE OBBE t y PE t ===﹣=﹣,== ∵点M 在抛物线上∴2243445M y t t t t +++=﹣(﹣)(﹣)=﹣, ∴24MP MP y y t t +=﹣=﹣ , ∵PN ⊥y 轴于点N∴∠PNO =∠NOE =∠PEO =90° ∴四边形ONPE 是矩形 ∴ON =PE =t ∴NC =OC ﹣ON =4﹣t ∵MP ∥CN ∴△MPQ ∽△NCQ ∴12MP MQ NC NQ == ∴24142t t t -+=-解得:12142t t =,=(点P 不与点C 重合,故舍去) ∴t 的值为12(3)∵∠PEB =90°,BE =PE ∴∠BPE =∠PBE =45° ∴∠MPD =∠BPE =45°①若MD =MP ,则∠MDP =∠MPD =45°∴∠DMP =90°,即DM ∥x 轴,与题意矛盾 ②若DM =DP ,则∠DMP =∠MPD =45° ∵∠AEM =90° ∴AE =ME∵y =﹣x 2+3x +4=0时,解得:x 1=﹣1,x 2=4 ∴A (﹣1,0)∵由(2)得,x M =4﹣t ,ME =y M =﹣t 2+5t ∴AE =4﹣t ﹣(﹣1)=5﹣t ∴5﹣t =﹣t 2+5t解得:t 1=1,t 2=5(0<t <4,舍去)③若MP =DP ,则∠PMD =∠PDM如图,记AM 与y 轴交点为F ,过点D 作DG ⊥y 轴于点G ∴∠CFD =∠PMD =∠PDM =∠CDF ∴CF =CD∵A (﹣1,0),M (4﹣t ,﹣t 2+5t ),设直线AM 解析式为y =ax +m∴()2045a m a t m t t -+=⎧⎨-+=-+⎩解得:a t m t =⎧⎨=⎩ , ∴直线AM :y tx t +=∴F (0,t ) ∴CF =OC ﹣OF =4﹣t ∵tx +t =﹣x +4,解得:41tx t -=+, ∴41D x tt DG -=+==, ∵∠CGD =90°,∠DCG =45° ∴)2421t CD DG t -+==,∴)2441t t t -+﹣ 解得:21t =﹣综上所述,当△PDM 是等腰三角形时,t =1或21t =﹣. 【点睛】本题考查了二次函数的图象与性质,解二元一次方程组和一元二次方程,等腰直角三角形的性质,相似三角形的判定和性质,涉及等腰三角形的分类讨论,要充分利用等腰的性质作为列方程的依据.12.在平面直角坐标系xOy 中(如图),已知抛物线y =x 2-2x ,其顶点为A . (1)写出这条抛物线的开口方向、顶点A 的坐标,并说明它的变化情况; (2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点” ①试求抛物线y =x 2-2x 的“不动点”的坐标;②平移抛物线y =x 2-2x ,使所得新抛物线的顶点B 是该抛物线的“不动点”,其对称轴与x 轴交于点C ,且四边形OABC 是梯形,求新抛物线的表达式.【答案】(l)抛物线y =x 2-2x 的开口向上,顶点A 的坐标是(1,-1),抛物线的变化情况是:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的;(2)①(0,0)、(3,3); ②新抛物线的表达式是y =(x +1)2-1. 【解析】 【分析】(1)Q 10a =>,故该抛物线开口向上,顶点A 的坐标为()1,1-;(2)①设抛物线“不动点”坐标为(),t t ,则22t t t =-,即可求解;②新抛物线顶点B 为“不动点”,则设点(),B m m ,则新抛物线的对称轴为:x m =,与x 轴的交点(),0C m ,四边形OABC 是梯形,则直线x m =在y 轴左侧,而点()1,1A -,点(),B m m ,则1m =-,即可求解. 【详解】(l)Q 10a =>,抛物线y =x 2-2x 的开口向上,顶点A 的坐标是(1,-1),抛物线的变化情况是:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的. (2)①设抛物线y =x 2-2x 的“不动点”坐标为(t ,t). 则t =t 2-2t ,解得t 1=0,t 2=3.所以,抛物线y =x 2-2x 的“不动点”的坐标是(0,0)、(3,3). ②∵新抛物线的顶点B 是其“不动点”,∴设点B 的坐标为(m ,m)∴新抛物线的对称轴为直线x=m,与x轴的交点为C(m,0)∵四边形OABC是梯形,∴直线x=m在y轴左侧.∵BC与OA不平行∴OC∥AB.又∵点A的坐标为(1,一1),点B的坐标为(m,m),m=-1.∴新抛物线是由抛物线y=x2-2x向左平移2个单位得到的,∴新抛物线的表达式是y=(x+1)2-1.【点睛】本题为二次函数综合运用题,涉及到二次函数基本知识、梯形基本性质,此类新定义题目,通常按照题设顺序,逐次求解即可.13.如图1,抛物线经过平行四边形的顶点、、,抛物线与轴的另一交点为.经过点的直线将平行四边形分割为面积相等的两部分,与抛物线交于另一点.点为直线上方抛物线上一动点,设点的横坐标为.(1)求抛物线的解析式;(2)当何值时,的面积最大?并求最大值的立方根;(3)是否存在点使为直角三角形?若存在,求出的值;若不存在,说明理由.【答案】(1)抛物线解析式为y=﹣x2+2x+3;(2)当t=时,△PEF的面积最大,其最大值为×,最大值的立方根为=;(3)存在满足条件的点P,t的值为1或【解析】试题分析:(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;(2)由A、C坐标可求得平行四边形的中心的坐标,由抛物线的对称性可求得E点坐标,从而可求得直线EF的解析式,作PH⊥x轴,交直线l于点M,作FN⊥PH,则可用t表示出PM的长,从而可表示出△PEF的面积,再利用二次函数的性质可求得其最大值,再求其最大值的立方根即可;(3)由题意可知有∠PAE=90°或∠APE=90°两种情况,当∠PAE=90°时,作PG⊥y轴,利用等腰直角三角形的性质可得到关于t的方程,可求得t的值;当∠APE=90°时,作PK⊥x 轴,AQ⊥PK,则可证得△PKE∽△AQP,利用相似三角形的性质可得到关于t的方程,可求得t的值.试题解析:(1)由题意可得,解得,∴抛物线解析式为y=﹣x2+2x+3;(2)∵A(0,3),D(2,3),∴BC=AD=2,∵B(﹣1,0),∴C(1,0),∴线段AC的中点为(,),∵直线l将平行四边形ABCD分割为面积相等两部分,∴直线l过平行四边形的对称中心,∵A、D关于对称轴对称,∴抛物线对称轴为x=1,∴E(3,0),设直线l的解析式为y=kx+m,把E点和对称中心坐标代入可得,解得,∴直线l的解析式为y=﹣x+,联立直线l和抛物线解析式可得,解得或,∴F(﹣,),如图1,作PH⊥x轴,交l于点M,作FN⊥PH,∵P点横坐标为t,∴P(t,﹣t2+2t+3),M(t,﹣t+),∴PM=﹣t2+2t+3﹣(﹣t+)=﹣t2+t+,∴S△PEF=S△PFM+S△PEM=PM•FN+PM•EH=PM•(FN+EH)=(﹣t2+t+)(3+)=﹣(t﹣)+×,∴当t=时,△PEF的面积最大,其最大值为×,∴最大值的立方根为=;(3)由图可知∠PEA≠90°,∴只能有∠PAE=90°或∠APE=90°,①当∠PAE=90°时,如图2,作PG⊥y轴,∵OA=OE,∴∠OAE=∠OEA=45°,∴∠PAG=∠APG=45°,∴PG=AG,∴t=﹣t2+2t+3﹣3,即﹣t2+t=0,解得t=1或t=0(舍去),②当∠APE=90°时,如图3,作PK⊥x轴,AQ⊥PK,则PK=﹣t2+2t+3,AQ=t,KE=3﹣t,PQ=﹣t2+2t+3﹣3=﹣t2+2t,∵∠APQ+∠KPE=∠APQ+∠PAQ=90°,∴∠PAQ=∠KPE,且∠PKE=∠PQA,∴△PKE∽△AQP,∴,即,即t2﹣t﹣1=0,解得t=或t=<﹣(舍去),综上可知存在满足条件的点P,t的值为1或.考点:二次函数综合题14.复习课中,教师给出关于x的函数(k是实数).教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选择如下四条:①存在函数,其图像经过(1,0)点;②函数图像与坐标轴总有三个不同的交点;③当时,不是y随x的增大而增大就是y随x的增大而减小;④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数;教师:请你分别判断四条结论的真假,并给出理由,最后简单写出解决问题时所用的数学方法.【答案】①真,②假,③假,④真,理由和所用的数学方法见解析.【解析】试题分析:根据方程思想,特殊与一般思想,反证思想,分类思想对各结论进行判断.试题解析:①真,②假,③假,④真.理由如下:①将(1,0)代入,得,解得.∴存在函数,其图像经过(1,0)点.∴结论①为真.②举反例如,当时,函数的图象与坐标轴只有两个不同的交点.∴结论②为假.③∵当时,二次函数(k是实数)的对称轴为。
中考数学压轴题专练之二次函数综合(含20题)
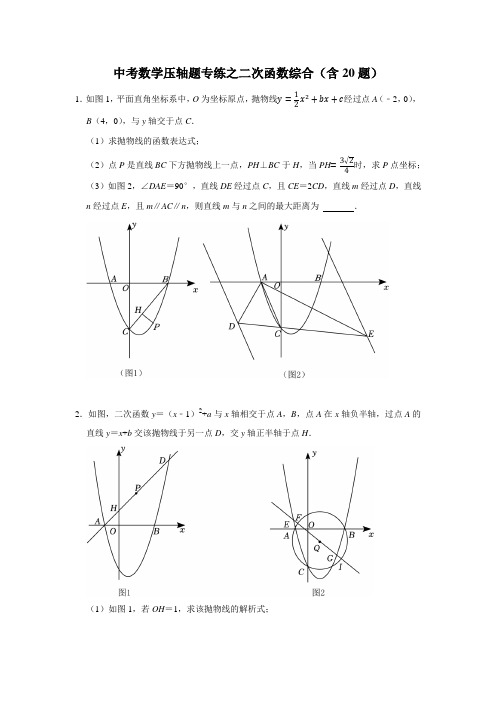
中考数学压轴题专练之二次函数综合(含20题)1.如图1,平面直角坐标系中,O为坐标原点,抛物线y=12x2+bx+c经过点A(﹣2,0),B(4,0),与y轴交于点C.(1)求抛物线的函数表达式;(2)点P是直线BC下方抛物线上一点,PH⊥BC于H,当PH=3√24时,求P点坐标;(3)如图2,∠DAE=90°,直线DE经过点C,且CE=2CD,直线m经过点D,直线n经过点E,且m∥AC∥n,则直线m与n之间的最大距离为.2.如图,二次函数y=(x﹣1)2+a与x轴相交于点A,B,点A在x轴负半轴,过点A的直线y=x+b交该抛物线于另一点D,交y轴正半轴于点H.(1)如图1,若OH=1,求该抛物线的解析式;(2)如图1,若点P是线段HD上一点,当1AH +1AD=3AP时,求点P的坐标(用含b的代数式表示);(3)如图2,在(1)的条件下,设抛物线交y轴于点C,过A,B,C三点作⊙Q,经过点Q的直线y=hx+q交⊙Q于点F,I,交抛物线于点E,G.当EI=GI+FI时,求2h2的值.3.如图1,在平面直角坐标系中,直线y=1与抛物线y=4x2相交于A,B两点(点B在第一象限),点C在AB的延长线上.且BC=n•AB(n为正整数).过点B,C的抛物线L,其顶点M在x轴上.(1)A点的坐标为;B点的坐标为;(2)当n=1时,抛物线L的函数表达式为;(3)如图2,抛物线E:,经过B、C两点,顶点为P.且O、B、P三点在同一直线上,求a n与n的关系式.4.如图,在平面直角坐标系中,二次函数y=14x2+bx+c的图象经过点A(6,0)、C(0,﹣3),点P为抛物线上一动点,其横坐标为m(m≥1).(1)求该抛物线对应的函数表达式.(2)若此抛物线在点P右侧部分(包括点P)的最低点的纵坐标为﹣5+m时,求m的值.(3)已知点M(m,m﹣3),点N(m﹣1,m﹣4),以MP、MN为邻边作▱PMNQ.①当抛物线在▱PMNQ 内部的部分的函数值y 随x 的增大而增大时,直接写出m 的取值范围;②当抛物线在▱PMNQ 内部的部分的函数值y 随x 的增大而增大或y 随x 的增大而减小时,抛物线与▱PMNQ 的边交点的纵坐标之差为12时,直接写出m 的值.5.综合与探究如图1,平面直角坐标系xOy 中,抛物线y =−38x 2+bx +3与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(﹣2,0),抛物线上有一动点P ,点P 在第一象限,过点P 作y 轴的平行线分别交x 轴和直线BC 于点D 和点E . (1)求抛物线及直线BC 的函数关系式;(2)当点E 为线段DP 的中点时,求点E 的坐标;(3)如图2,作射线OP ,交直线BC 于点F ,当△OBF 是等腰三角形时,求点F 的坐标.6.如图,抛物线y=ax2+bx﹣4(a≠0).与x轴交于A(4,0)和B(﹣1,0)两点,与y 轴交于点C,点P是直线AC下方的抛物线上一动点.(1)求抛物线的解析式;(2)过点P作PD⊥x轴于点D,交直线AC于点E,求线段PE的最大值及此时点P的坐标;(3)取(2)中PE最大值时的P点,在坐标平面内是否存在点Q,使得以点A、C、P、Q为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标,若不存在,请说明理由.7.如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与x轴交于A(﹣2,0)、B(4,0)两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点,连接OP交BC于点Q.(1)求抛物线的函数表达式;(2)当PQOQ 的值最大时,求点P的坐标和PQOQ的最大值;(3)把抛物线y=−12x2+bx+c向右平移1个单位,再向上平移2个单位得新抛物线y',M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,写出所有符合条件的N点的坐标,并写出求解点N的坐标的其中一种情况的过程.8.如图,△ABC的三个顶点坐标分别为A(﹣1,0),B(0,32),C(3,0),抛物线y=ax2+bx+c(a≠0)经过△ABC的三个顶点.(1)求抛物线y=ax2+bx+c(a≠0)的函数表达式;(2)点M是抛物线在第一象限上一点.①连接AM与BC相交于点E,即将△ABC分为两个三角形,若这两个三角形的面积之比为1:2时,则点M的坐标为,直线AM的函数表达式为;②将△ABO沿着x轴正方向平移,当点B与点M重合时停止,点A的对应点为A',点O 的对应点为点O'.求出△A'MO'与△BOC重合部分的图形的周长;(3)在抛物线y=ax2+bx+c(a≠0)的对称轴上取一点K,连接CK,使∠ACK+∠BAO =90°,延长CK交抛物线于点P,连接AK.动点Q从C点出发,沿射线CA以每秒1个单位长度的速度运动,是否存在某一时刻,使∠AQP=∠AKP?若存在,请直接写出此时t的值;若不存在,请说明理由.9.在平面直角坐标系中,抛物线y=x2+bx+c(b、c为常数)与x轴交点坐标为(1,0),与y轴交点的坐标为(0,3),点A、点B均在这个抛物线上,点A的横坐标为m,点B 的横坐标为1﹣m.当B在A的左侧时,抛物线上A、B两点之间的部分(包括A、B两点)记为图象G.(1)求此抛物线对应的函数表达式;(2)当图象G对应的函数值y随x的增大而减小时,求m的取值范围;(3)图象G最大值与最小值差为h,求h与m之间的函数关系式;(4)设点E的坐标为(m﹣3,2),点F的坐标(m﹣3,m﹣3),连结EF,以EF为边长向右作正方形EFPQ,当抛物线与正方形EFPQ的边只有两个交点,且交点的纵坐标之差为1时,直接写出m的值.10.如图,在平面直角坐标系中,抛物线y=x2+bx+c与直线AB交于点A(0,﹣2),B(2,0).(Ⅰ)求该抛物线的解析式;(Ⅱ)点P是直线AB下方抛物线上的一动点,过点P作x轴的平行线交AB于点C,过点P作y轴的平行线交x轴于点D,交线段AB于点H.求PC的最大值及此时点P的坐标;(Ⅲ)若点M是抛物线的顶点,在x轴上存在一点N,使△AMN的周长最小,求此时点N的坐标.11.在平面直角坐标系中,∠ACB=90°,AB∥x轴,如图1,C(1,0),且OC:OA=AC:BC=1:2.(1)求点A、点B的坐标;(2)已知抛物线y=ax2+bx+c(a≠0)过A、B、C三点,求该抛物线的表达式;(3)如图2,抛物线对称轴与AB交于点D,现有一点P从点A出发,以每秒1个单位的速度在AB上向点B运动,另一点Q从点D与点P同时出发,以每秒5个单位在抛物线对称轴上运动.当点P到达B点时,点P、Q同时停止运动,问点P、Q运动到何处时,△PQB面积最大,并求出最大面积.12.如图,抛物线y =ax 2+bx +2与x 轴交于点A (﹣1,0)、B (4,0)两点,与y 轴交点C ,连接AC ,BC .抛物线的对称轴交x 轴于点E ,交BC 于点F ,顶点为M . (1)求抛物线的解析式及顶点M 的坐标;(2)若D 是直线BC 上方抛物线上一动点,连接OD 交BC 于点E ,当DE OE的值最大时,求点D 的坐标;(3)已知点G 是抛物线上的一点,连接CG ,若∠GCB =∠ABC ,求点G 的坐标.13.如图,抛物线y =ax 2﹣8ax +12a (a <0)与x 轴交于A ,B 两点(点A 在点B 的左侧),抛物线上另有一点C 在第一象限,满足∠ACB 为直角,且使∠OCA =∠OBC . (1)求线段OC 的长;(2)求该抛物线的函数关系式;(3)在抛物线的对称轴上是否存在一点P ,使得△BCP 是以BC 为腰的等腰三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由.14.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0),B (4,0)两点,与y轴交于点C,且OC=2OA.(1)试求抛物线的解析式;(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线在第一象限交于点P,与直线BC交于点M,记m=S△CPMS△CDM,试求m的最大值及此时点P的坐标;(3)在(2)的条件下,m取最大值时,是否存在x轴上的点Q及坐标平面内的点N,使得P,D,Q,N四点组成的四边形是矩形?若存在,请直接写出所有满足条件的Q点和N点的坐标;若不存在,请说明理由.15.已知:y=12x2+bx+c经过点A(﹣2,﹣1),B(0,﹣3).(1)求函数的解析式;(2)平移抛物线使得新顶点为点P(m,n).①当m>0时,若S△OPB=3,且在直线x=k的右侧,两函数值y都随x的增大而增大,求k的取值范围;②点P在原抛物线上,新抛物线与y轴交于点Q,当∠BPQ=120°时,求点P的坐标.16.已知抛物线y =﹣x 2+bx +c 与x 轴交于A (﹣1,0),B (3,0)两点,交y 轴于点C ,M 是抛物线顶点.(1)直接写出抛物线的函数解析式;(2)如图1,点P 在抛物线上,若直线AP 经过△CBM 外接圆的圆心,判断△CBM 的形状并求点P 的横坐标;(3)以点P (1,t )为圆心的⊙P 与x 轴相切且与抛物线只有两个公共点,求t 的取值范围.17.如图,在平面直角坐标系中,抛物线y =ax 2+bx +c 与x 轴交于点A (4,0),C (﹣1,0)与y 轴交于点B ,已知tan ∠BAC =34. (1)求抛物线的函数表达式;(2)如图1,点P 为抛物线上的点,且点P 的横坐标为3,F 是抛物线上异于点P 的点,连接P A ,PB ,当S △P AB =S △F AB ,求点F 的横坐标;(3)如图2,点Q 为直线AB 上方抛物线上一点,OQ 交AB 于点D ,QE ∥BO 交AB 于点E .记△QDE ,△QDB ,△BDO 的面积分别为S 1,S 2,S 3.求S 1S 2+S 2S 3的最大值.18.如图1,对于平面上小于或等于90°的∠MON,我们给出如下定义:若点P在∠MON 的内部或边上,作PE⊥OM于点E,PF⊥ON于点F,则将PE+PF称为点P与∠MON 的“点角距”,记作d(∠MON,P).如图2,在平面直角坐标系xOy中,x、y正半轴所组成的角记为∠xOy.(1)已知点A(4,0)、点B(3,1),则d(∠xOy,A)=,d(∠xOy,B)=.(2)若点P为∠xOy内部或边上的动点,且满足d(∠xOy,P)=4,在图2中画出点P 运动所形成的图形.(3)如图3与图4,在平面直角坐标系xOy中,射线OT的函数关系式为y=43x(x≥0).①在图3中,点C的坐标为(4,1),试求d(∠xOT,C)的值;②在图4中,抛物线y=−12x2+2x+c经过A(5,0),与射线OT交于点D,点Q是A,D两点之间的抛物线上的动点(点Q可与A,D两点重合),求c的值和当d(∠xOT,Q)取最大值时点Q的坐标.19.如图,已知抛物线y=ax2+bx+c(a>0)与x轴交于A、B两点,与y轴交于点C(0,2),抛物线的对称轴为直线x=52,且OB=2OC.连接BC,点D是线段OB上一点(不与点O、B重合),过点D作x轴的垂线,交BC于点M,交抛物线于点N.(1)求抛物线的表达式;(2)当线段MN最大时,求点M的坐标;(3)连接BN,以B、D、N为顶点的三角形是否能够与△OBC相似?若能,请求出点N 的坐标;若不能,请说明理由.20.如图,已知抛物线y=﹣x2﹣2x+3的顶点为D点,且与x轴交于B,A两点(B在A的左侧),与y轴交于点C.点E为抛物线对称轴上的一个动点:(1)当点E在x轴上方且CE∥BD时,求sin∠DEC的值;(2)若点P在抛物线上,是否存在以点B,E,C,P为顶点的四边形是平行四边形?请求出点P的坐标;(3)若抛物线对称轴上有点E,使得AE+√55DE取得最小值,连接AE并延长交第二象限抛物线为点M,从请直接写出AM的长度.。
九年级二次函数压轴题专题训练(含答案和方式指导)

九年级二次函数压轴题专题训练(含答案)方式:面积法 ,化斜为直,韦达定理,几何变换等.1,如图1,在平面直角坐标系中,抛物线C1:22abxaxy-+=关于y轴对称且有最小值1-。
〔1〕求抛物线C1的解析式;〔2〕在图1中抛物线C1极点为A,将抛物线C1绕点B旋转180°后取得抛物线C2,直线y=kx﹣2k+4总通过必然点M,假设过定点M的直线与抛物线C2只有一个公共点,求直线l的解析式.〔3〕如图2,先将抛物线C1向上平移使其极点在原点O,再将其极点沿直线y=x平移取得抛物线C3,设抛物线C3与直线y=x交于C、D两点,求线段CD的长;〔1〕∴y=x2﹣1.‥‥‥‥‥‥‥2分〔2〕依题意可求出抛物线C2的解析式为:y=﹣〔x﹣2〕2+1,∵直线y=kx﹣2k+4总通过必然点M,∴定点M为〔2,4〕,‥‥‥‥‥‥‥4分①通过定点M〔2,4〕,与y轴平行的直线l:x=2与抛物线C3总有一个公共点〔2,1〕.②通过定点M〔2,4〕的直线l为一次函数y=kx﹣2k+4时,与y=﹣〔x﹣2〕2+1联立方程组,消去y得x2﹣4x+3+kx ﹣2k+4=0,即x2﹣〔4﹣k〕x+7﹣2k=0,△=k2﹣12=0,得k1=2,k2=﹣2,∴y=2x+4﹣4或y=﹣2x+4+4,综上所述,过定点M,共有三条直线l:x=2 或y=2x+4﹣4或y=﹣2x+4+4,它们别离与抛物线C2只有一个公共点.〔3〕设抛物线C3的极点为〔m,m〕,依题意抛物线C3的解析式为:y=〔x﹣m〕2+m,与直线y=x联立,解方程组得:,,∴C〔m,m〕,D〔m+1,m+1〕过点C作CM∥x轴,过点D作DM∥y轴,∴CM=1,DM=1,∴CD=.2,如图,抛物线y=ax2-4ax+b交x轴正半轴于A、B两点,交y轴正半轴于C,且OB=OC =3(1) 求抛物线的解析式(2) 如图1,D位抛物线的极点,P为对称轴左侧抛物线上一点,连OP交直线BC于G,连GD.是不是存在点P,使2=GOGD?假设存在,求点P的坐标;假设不存在,请说明理由(3) 如图2,将抛物线向上平移m个单位,交BC于点M、N.假设∠MON=45°,求m的值〔1〕243 y x x=-+3〔此题12分〕如图1,抛物线y =ax 2+(1-3a )x -3〔a >0〕与x 轴交于A 、B 两点,与y 轴交于C 点,直线y =-x +5与抛物线交于D 、E ,与直线BC 交于P (1) 求点P 的坐标 (2) 求PD ·PE 的值(3) 如图2,直线y =t 〔t >-3〕交抛物线于F 、G ,且△FCG 的外心在FG 上,求证:t a -1为常数.解:(1) 令y =0,那么ax 2+(1-3a )x -3=0,解得x 1=a 1-,x 2=3∴B (3,0)令x =0,那么y =-3∴直线BC 的解析式为y =x -3 联立⎩⎨⎧+-=-=53x y x y ,解得⎩⎨⎧==14y x∴P (4,1)(2) 设D (x 1,y 1)、E (x 2,y 2)那么PD =2(4-x 1),PE =2(4-x 2)联立⎪⎩⎪⎨⎧+-=--+=53)31(2x y x a ax y ,整理得ax 2+(2-3a )x -8=0∴x 1+x 2=a a 23-,x 1x 2=a 8-∴PD ·PE =2(4-x 1)(4-x 2)=2[16-4(x 1+x 2)+x 1x 2]=8]881216[2=-+-a a(3) ∵△FCG 的外心在FG 上 ∴∠FCG =90°设FG 与y 轴交于点H ,那么CH 2=FH ·GH ∴(t +3)2=-x F ·x G联立⎪⎩⎪⎨⎧--+==3)31(2x a ax y t y ,整理得ax 2+(1-3a )x -3-t =0∴x F ·x G =a t--3∴(t +3)2=a t+3 ∴31=-t a4.〔梅苑中学九月月考〕如图,在平面直角坐标系xOy 中,一次函数m x y +=45的图象与x轴交于A (-1,0),与y 轴交于点C .以直线x =2为对称轴的抛物线C 1:y =ax 2+bx +c 〔a ≠0〕通过A 、C 两点,并与x 轴正半轴交于点B (1) 求m 的值及抛物线C 1:y =ax 2+bx +c 〔a ≠0〕〔a ≠0〕的函数表达式(2) 设点D (0,1225),假设F 是抛物线C 1:y =ax 2+bx +c 〔a ≠0〕对称轴上使得△ADF 的周长取得最小值的点,过F 任意作一条与y 轴不平行的直线交抛物线C 1于M 1(x 1,y 1),M 2(x 2,y 2)两点,试探讨FM F M 2111+是不是为定值?请说明理由(3) 将抛物线C 1作适当平移,取得抛物线C 2:y 2=-41(x -h )2,h >1.假设当1<x ≤m 时,y 2≥-x 恒成立,求m 的最大值如图1,抛物线C1:y=x2﹣2x+c和直线l:y=﹣2x+8,直线y=kx〔k>0〕与抛物线C1交于两不同点A、B,与直线l交于点P.且当k=2时,直线y=kx〔k>0〕与抛物线C1只有一个交点.〔1〕求c的值;〔2〕求证:,并说明k知足的条件;〔3〕将抛物线C1沿第一象限夹角平分线的方向平移t〔t>0〕个单位,再沿y轴负方向平移〔t2﹣t〕个单位取得抛物线C2,设抛物线C1和抛物线C2交于点R;如图2.①求证不管t为何值,抛物线C2必过定点,并判定该定点与抛物线C1的位置关系;②设点R关于直线y=1的对称点Q,抛物线C1和抛物线C2的极点别离为点M、N,假设∠MQN=90°,求现在t的值.8、如图1,二次函数y=〔x+m〕〔x﹣3m〕〔其中m>0〕的图象与x轴别离交于点A,B 〔点A位于点B的左侧〕,与y轴交于点C,点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,使得AB平分∠DAE.〔1〕当线段AB的长为8时,求m的值.〔2〕当点B的坐标为〔12,0〕时,求四边形ADBE的面积.〔3〕请判定的值是不是为定值?假设是,请求出那个定值;假设不是,请说明理由.〔4〕别离延长AC和EB交于点P,如图2.点A从点〔﹣2,0〕动身沿x轴的负方向运动到点〔﹣4,0〕为止,求点P所通过的途径的长〔直接写出答案〕.解:〔1〕∵二次函数y=〔x+m〕〔x﹣3m〕〔其中m>0〕的图象与x轴别离交于点A,B〔点A位于点B的左侧〕,令y=0,得0=〔x+m〕〔x﹣3m〕,∴x=﹣m或x=3m,∴点A的坐标为〔﹣m,0〕,点B的坐标为〔3m,0〕,由题意,得AB=3m﹣〔﹣m〕=4m.∴4m=8,即m=2.〔2〕∵点B的坐标为〔12,0〕,∴m=4,∴A〔﹣4,0〕,C〔0,﹣3〕,如图,过点D,E别离作x轴的垂线,垂足为M,N.∵CD∥AB,∴点D 的坐标为〔8,﹣3〕,点M的坐标为〔8,0〕.∵AB平分∠DAE,∴∠DAM=∠EAN.∵∠DMA=∠ENA=90°,∴△ADM∽△AEN.∴=.设E点的坐标为〔〕,∴解得x1=16,x2=﹣4〔舍去〕,∴E点的坐标为〔16,5〕.因此S ADBE=S△ADB+S△ABE=,〔3〕为定值.∵A〔﹣m,0〕,B〔3m,0〕,C〔0,﹣3〕,过点D,E别离作x轴的垂线,垂足为M,N.由〔2〕有,=.∵CD∥AB,∴点D 的坐标为〔2m,﹣3〕,点M的坐标为〔2m,0〕.设E点的坐标为〔〕,可得解得x1=4m,x2=﹣m〔舍去〕.∴E点的坐标为〔4m,5〕,∴EN=5,DM=3∵△ADM∽△AEN.∴==;〔4〕由〔1〕有,A〔﹣m,0〕,B〔3m,0〕,C〔0,﹣3〕,E〔4m,5〕,∴直线AC解析式为y=﹣x﹣3①,直线BE解析式为y=x﹣15②,联立①②得,∴P〔,﹣〕,∴点A在运动时,点P的纵坐标不变,即:点A从运动到停顿,点P的途径是一条线段,∵点A从点〔﹣2,0〕动身沿x轴的负方向运动到点〔﹣4,0〕为止,∴当m=2时,P〔3,﹣〕,当m=4时,P〔6,﹣〕∴点P所通过的途径的长为6﹣3=3.9、如图,二次函数y=ax2﹣2amx﹣3am2〔a,m是常数,且m<0〕的图象与x轴交于A、B 〔点A位于点B的左侧〕,与y轴交于点C〔0,3〕,作CD∥AB交抛物线于点D,连接BD,过点B作射线BE交抛物线于点E,使得AB平分∠DBE.〔1〕求点A,B的坐标;〔用m表示〕〔2〕是不是为定值?假设是,求出那个定值;假设不是,请说明理由.〔3〕抛物线y=ax2﹣2amx﹣3am2的极点为F,直线DF上是不是存在唯一一点M,使得∠OMA=90°?假设存在,求出现在m的值;假设不存在,请说明理由.解:〔1〕由ax2﹣2amx﹣3am2=0得,x1=﹣m,x2=3m,那么B〔﹣m,0〕,A〔3m,0〕,〔2〕是定值,为;理由:过点D作DH⊥AB于H,过点E作EG⊥AB于G,将点C〔0,3〕代入y=ax2﹣2amx﹣3am2得,a=﹣;∴y=ax2﹣2amx﹣3am2=﹣x2+x+3,∵CD∥AB,∴点D的坐标为〔2m,3〕,∴OH=﹣2m,DH=3,∴BH=﹣3m∵AB平分∠DBE,∴∠DBH=∠EBG,又∠DHB=∠EGB=90°,∴△BDH∽△BEG,∴,设E〔n,﹣×n2+×n+3〕,∴OG=﹣n,EG=×n2﹣×n﹣3,∴BG=﹣m﹣n,∴,∴n=4m,∴E〔4m,5〕,∵BH=BO+OH=﹣m﹣2m=﹣3m,BG=BO+OG=﹣m﹣4m=﹣5m,∴,〔3〕存在,理由:如图2,∵B〔﹣m,0〕,A〔3m,0〕,∴F〔m,4〕,∵D〔2m,3〕,∴直线DF的解析式为y=﹣x+5,∴N〔5m,0〕,P〔0,5〕,∴OP=5,PN==5取OA的中点M,∵A〔3m,0〕,N〔5m,0〕,∴M〔〕,∴OM=﹣m.MN=﹣m,假设直线DF上是存在唯一一点M,使得∠OMA=90°,∴以OA为直径的⊙M与PN,PO相切,∴PM是∠OPN的角平分线,∴,∴,∴m=〔舍〕或m=﹣.。
初三二次函数压轴题集锦

初三二次函数集锦一.解答题(共30小题)1.如图,已知直线y=kx﹣6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,﹣4)为抛物线的顶点,点B在x轴上.(1)求抛物线的解析式;(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.2.如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式及点B坐标;(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.3.已知抛物线y=x2+bx+c的顶点为P,与y轴交于点A,与直线OP交于点B.(1)如图1,若点P的横坐标为1,点B的坐标为(3,6),试确定抛物线的解析式;=3,(2)在(1)的条件下,若点M是直线AB下方抛物线上的一点,且S△ABM求点M的坐标;(3)如图2,若点P在第一象限,且PA=PO,过点P作PD⊥x轴于点D.将抛物线y=x2+bx+c平移,平移后的抛物线经过点A、D,该抛物线与x轴的另一个交点为C,请探究四边形OABC的形状,并说明理由.4.如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣x2+bx+c经过点A、C,与AB交于点D.(1)求抛物线的函数解析式;(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.①求S关于m的函数表达式;②当S最大时,在抛物线y=﹣x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.5.如图,点A(﹣2,0)、B(4,0)、C(3,3)在抛物线y=ax2+bx+c上,点D 在y轴上,且DC⊥BC,∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F.(1)求抛物线的解析式;(2)CF能否经过抛物线的顶点?若能,求出此时点E的坐标;若不能,说明理由;(3)若△FDC是等腰三角形,求点F的坐标.6.如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=x2+bx+c交于第四象限的F点.(1)求该抛物线解析式与F点坐标;(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.②若△PMH是等腰三角形,请直接写出此时t的值.7.如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C 的位置,一条抛物线正好经过点O,C,A三点.(1)求该抛物线的解析式;(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.8.如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(点A在点B的左侧),直线l与抛物线交于A,C两点,其中点C的横坐标为2.(1)求A,B两点的坐标及直线AC的函数表达式;(2)P是线段AC上的一个动点(P与A,C不重合),过P点作y轴的平行线交抛物线于点E,求△ACE面积的最大值;(3)若直线PE为抛物线的对称轴,抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点,则在x轴上是否存在一点N,使四边形DMNQ 的周长最小?若存在,求出这个最小值及点M,N的坐标;若不存在,请说明理由.(4)点H是抛物线上的动点,在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由.9.已知抛物线y=ax2+bx+c的顶点为(1,0),且经过点(0,1).(1)求该抛物线对应的函数的解析式;(2)将该抛物线向下平移m(m>0)个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B、C,若△ABC为等边三角形.①求m的值;②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使四边形CBDP 为菱形?若存在,写出点P的坐标;若不存在,请说明理由.10.已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.(1)求实数a、b的值;(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式;11.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.12.如图,抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7)且与直线y=kx﹣2k﹣3相交于点P(m,2m﹣7).(1)求抛物线的解析式;(2)求直线y=kx﹣2k﹣3与抛物线y=ax2﹣(2a+1)x+b的对称轴的交点Q的坐标;(3)在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在请说明理由.13.如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.(1)试求抛物线的解析式;(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD 重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?14.如图,在平面直角坐标系中,直线y=x﹣与抛物线y=﹣x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.(1)求该抛物线的解析式;(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x 轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l 的最大值;②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P 的坐标.15.已知:m、n是方程x2﹣6x+5=0的两个实数根,且m<n,抛物线y=﹣x2+bx+c 的图象经过点A(m,0)、B(0,n).(1)求这个抛物线的解析式;(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.16.如图,在平面直角坐标系中,点O是原点,点A的坐标为(4,0),以OA 为一边,在第一象限作等边△OAB(1)求点B的坐标;(2)求经过O、A、B三点的抛物线的解析式;(3)直线y=x与(2)中的抛物线在第一象限相交于点C,求点C的坐标;(4)在(3)中,直线OC上方的抛物线上,是否存在一点D,使得△OCD的面积最大?如果存在,求出点D的坐标和面积的最大值;如果不存在,请说明理由.17.如图,二次函数的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.(1)试求此二次函数的解析式;(2)试证明:∠BAO=∠CAO(其中O是原点);(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.18.如图1,在平面直角坐标系xOy中,直线l:与x轴、y轴分别交于点A和点B(0,﹣1),抛物线经过点B,且与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;(2)点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.19.在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B (﹣3,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)点Q在直线BC上方的抛物线上,点Q到直线BC的距离最远,求点Q坐标.20.如图,直线y=kx+b分别交y轴、x 轴于A(0、2)、B(4、0))两点,抛物线y=﹣x2+bx+c过A、B两点.(1)求直线和抛物线的解析式;(2)设N(x、y)是(1)所得抛物线上的一个动点,过点N作直线MN垂直x 轴交直线AB于点M,若点N在第一象限内.试问:线段MN的长度是否存在最大值?若存在,求出它的最大值及此时x的值;若不存在,请说明理由;(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.21.如图,菱形ABCD的边长为6且∠DAB=60°,以点A为原点、边AB所在的直线为x轴且顶点D在第一象限建立平面直角坐标系.动点P从点D出发沿折线DCB向终点B以2单位/每秒的速度运动,同时动点Q从点A出发沿x轴负半轴以1单位/秒的速度运动,当点P到达终点时停止运动,运动时间为t,直线PQ 交边AD于点E.(1)求出经过A、D、C三点的抛物线解析式;(2)是否存在时刻t使得PQ⊥DB,若存在请求出t值,若不存在,请说明理由;(3)设AE长为y,试求y与t之间的函数关系式;(4)若F、G为DC边上两点,且点DF=FG=1,试在对角线DB上找一点M、抛物线ADC对称轴上找一点N,使得四边形FMNG周长最小并求出周长最小值.22.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.23.如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.24.在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.(1)求抛物线的解析式;(2)在AC上方的抛物线上有一动点P.①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.25.如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.(1)求抛物线的解析式;(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.26.如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x 刻画,斜坡可以用一次函数y=x刻画.(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.27.已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣).(1)求抛物线l2的函数表达式;(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.28.已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).(1)求抛物线的函数表达式;(2)求直线BC的函数表达式和∠ABC的度数;(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.29.如图,已知抛物线y=﹣x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式:;(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED 的面积最大?最大面积是多少?(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD 的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.30.如图,已知二次函数y=ax2+x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.(1)请直接写出二次函数y=ax2+x+c的表达式;(2)判断△ABC的形状,并说明理由;(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB 于点M,当△AMN面积最大时,求此时点N的坐标.初三二次函数压轴题集锦参考答案一.解答题(共30小题)1.;2.;3.;4.;5.;6.;7.;8.;9.;10.;11.;12.;13.;14.;15.;16.;17.;18.;19.;20.;21.;22.;23.;24.;25.;26.;27.;28.;29.y=﹣x2+3x+8;30.;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考二次函数压轴题(共23道题目)一.选择题(共10小题)1.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b <0,b2+8a>4ac,a<﹣1,其中结论正确的有()A.1个 B.2个 C.3个 D.4个2.如图是某二次函数的图象,将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有()(1)a>0;(2)c<0;(3)2a﹣b=0;(4)a+b+c>0.A.1个 B.2个 C.3个 D.4个3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c >0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0;其中正确的个数为()A.1个 B.2个 C.3个 D.4个4.已知点(x1,y1)、(x2,y2)、(x3,y3)都在抛物线y=x2+bx上,x1、x2、x3为△ABC的三边,且x1<x2<x3,若对所有的正整数x1、x2、x3都满足y1<y2<y3,则b的取值范围是()A.b>﹣2 B.b>﹣3 C.b>﹣4 D.b>﹣55.如图,点A(m,n)是一次函数y=2x的图象上的任意一点,AB垂直于x轴,垂足为B,那么三角形ABO的面积S关于m的函数关系的图象大致为()A.B.CD.6.抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限,那么下列结论成立的是()A.a>0,b>0,c=0 B.a>0,b<0,c=0 C.a<0,b>0,c=0 D.a<0,b<0,c=07.已知抛物线y=x2﹣(4m+1)x+2m﹣1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,)的下方,那么m的取值范围是()A.B.C.D.全体实数8.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.9.已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为()A.|2+b||b+1|B.c(1﹣c) C.(b+1)2D.10.下列关于函数y=(m2﹣1)x2﹣(3m﹣1)x+2的图象与坐标轴的公共点情况:①当m≠3时,有三个公共点;②m=3时,只有两个公共点;③若只有两个公共点,则m=3;④若有三个公共点,则m≠3.其中描述正确的有()个.A.一个B.两个C.三个D.四个二.填空题(共10小题)11.已知:如图,过原点的抛物线的顶点为M(﹣2,4),与x轴负半轴交于点A,对称轴与x轴交于点B,点P是抛物线上一个动点,过点P作PQ⊥MA于点Q.(1)抛物线解析式为.(2)若△MPQ与△MAB相似,则满足条件的点P的坐标为.12.将抛物线y=x2﹣2向左平移3个单位,所得抛物线的函数表达式为.13.如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE﹣EO|,再以CM、CO为边作矩形CMNO.令m=,则m=;又若CO=1,CE=,Q为AE上一点且QF=,抛物线y=mx2+bx+c经过C、Q两点,则抛物线与边AB的交点坐标是.15.在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大值时,点P的坐标是.16.如图为二次函数y=ax2+bx+c的图象,在下列结论中:①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=5;③a+b+c<0;④当x<2时,y随着x的增大而增大.正确的结论有(请写出所有正确结论的序号).17.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是.18.如图,已知一动圆的圆心P在抛物线y=x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是.19.如图,四边形ABCD是矩形,A、B两点在x轴的正半轴上,C、D两点在抛物线y=﹣x2+6x上.设OA=m(0<m<3),矩形ABCD的周长为l,则l与m的函数解析式为.20.若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(﹣1,0),则y=a+b+c的取值范围是.三.解答题(共4小题)21.已知抛物线y=ax2﹣2x+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=﹣x+1交y轴于点D.(1)求抛物线的解析式;(2)求证:△BCE∽△BOD;(3)点P是抛物线上的一个动点,当点P运动到什么位置时,△BDP的面积等于△BOE的面积?22.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.23.已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.(1)求抛物线的函数表达式;(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC 于点Q.①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.24.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l 于点H,连结OP,试求△OPH的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.二次函数压轴题(共24道题目)参考答案与试题解析一.选择题(共10小题)1.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b <0,b2+8a>4ac,a<﹣1,其中结论正确的有()A.1个 B.2个 C.3个 D.4个【分析】由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上,得c>0,对称轴为x=<1,∵a<0,∴2a+b<0,而抛物线与x轴有两个交点,∴b2﹣4ac>0,当x=2时,y=4a+2b+c<0,当x=1时,a+b+c=2.∵>2,∴4ac﹣b2<8a,∴b2+8a>4ac,∵①a+b+c=2,则2a+2b+2c=4,②4a+2b+c<0,③a﹣b+c<0.由①,③得到2a+2c<2,由①,②得到2a﹣c<﹣4,4a﹣2c<﹣8,上面两个相加得到6a<﹣6,∴a<﹣1.故选:D.2.如图是某二次函数的图象,将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c(a≠0),则下列结论中正确的有()(1)a>0;(2)c<0;(3)2a﹣b=0;(4)a+b+c>0.A.1个 B.2个 C.3个 D.4个【分析】如图是y=ax2+bx+c的图象,根据开口方向向上知道a>0,又由与y轴的交点为在y轴的负半轴上得到c<0,由对称轴x==﹣1,可以得到2a﹣b=0,又当x=1时,可以判断a+b+c的值.由此可以判定所有结论正确与否.【解答】解:(1)∵将其向左平移2个单位后的图象的函数解析式为y=ax2+bx+c (a≠0)(如虚线部分),∴y=ax2+bx+c的对称轴为:直线x=﹣1;∵开口方向向上,∴a>0,故①正确;(2)∵与y轴的交点为在y轴的负半轴上∴c<0,故②正确;(3)∵对称轴x==﹣1,∴2a﹣b=0,故③正确;(4)当x=1时,y=a+b+c>0,故④正确.故选:D.3.已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c >0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0;其中正确的个数为()A.1个 B.2个 C.3个 D.4个【分析】由抛物线开口向上得到a大于0,再由对称轴在y轴右侧得到a与b异号,即b小于0,由抛物线与y轴交于正半轴,得到c大于0,可得出abc的符合,对于(3)作出判断;由x=1时对应的函数值小于0,将x=1代入二次函数解析式得到a+b+c小于0,(1)错误;根据对称轴在1和2之间,利用对称轴公式列出不等式,由a大于0,得到﹣2a小于0,在不等式两边同时乘以﹣2a,不等号方向改变,可得出不等式,对(2)作出判断;由x=﹣1时对应的函数值大于0,将x=﹣1代入二次函数解析式得到a﹣b+c大于0,又4a大于0,c大于0,可得出a﹣b+c+4a+c大于0,合并后得到(4)正确,综上,即可得到正确的个数.【解答】解:由图形可知:抛物线开口向上,与y轴交点在正半轴,∴a>0,b<0,c>0,即abc<0,故(3)错误;又x=1时,对应的函数值小于0,故将x=1代入得:a+b+c<0,故(1)错误;∵对称轴在1和2之间,∴1<﹣<2,又a>0,∴在不等式左右两边都乘以﹣2a得:﹣2a>b>﹣4a,故(2)正确;又x=﹣1时,对应的函数值大于0,故将x=﹣1代入得:a﹣b+c>0,又a>0,即4a>0,c>0,∴5a﹣b+2c=(a﹣b+c)+4a+c>0,故(4)错误,综上,正确的有1个,为选项(2).故选:A.4.已知点(x1,y1)、(x2,y2)、(x3,y3)都在抛物线y=x2+bx上,x1、x2、x3为△ABC的三边,且x1<x2<x3,若对所有的正整数x1、x2、x3都满足y1<y2<y3,则b的取值范围是()A.b>﹣2 B.b>﹣3 C.b>﹣4 D.b>﹣5【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,结合已知条件,可知x1、x2、x3的最小一组值是2、3、4;根据抛物线,知它与x轴的交点是(0,0)和(﹣b,0),对称轴是x=﹣.因此要满足已知条件,则其对称轴应小于2.5.【解答】解:∵x1、x2、x3为△ABC的三边,且x1<x2<x3,∴x1、x2、x3的最小一组值是2、3、4.∵抛物线y=x2+bx与x轴的交点是(0,0)和(﹣b,0),对称轴是x=﹣,∴若对所有的正整数x1、x2、x3都满足y1<y2<y3,则﹣<2.5解,得b>﹣5.故选:D.5.如图,点A(m,n)是一次函数y=2x的图象上的任意一点,AB垂直于x轴,垂足为B,那么三角形ABO的面积S关于m的函数关系的图象大致为()A.B.C.D.【分析】因为A(m,n)是一次函数y=2x的图象上的任意一点,所以n=2m.根据三角形面积公式即可得出S与m之间的函数关系,根据关系式即可解答.【解答】解:由题意可列该函数关系式:S=|m|•2|m|=m2,因为点A(m,n)是一次函数y=2x的图象上的任意一点,所以点A(m,n)在第一或三象限,又因为S>0,所以取第一、二象限内的部分.故选:D.6.抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限,那么下列结论成立的是()A.a>0,b>0,c=0 B.a>0,b<0,c=0 C.a<0,b>0,c=0 D.a<0,b<0,c=0【分析】先根据图象经过象限的情况判断出a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理.【解答】解:∵抛物线经过原点,∴c=0,∵抛物线经过第一,二,三象限,可推测出抛物线开口向上,对称轴在y轴左侧∴a>0,∵对称轴在y轴左侧,∴对称轴为x=<0,又因为a>0,∴b>0.故选:A.7.已知抛物线y=x2﹣(4m+1)x+2m﹣1与x轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与y轴的交点在点(0,)的下方,那么m的取值范围是()A.B.C.D.全体实数【分析】因为抛物线y=x2﹣(4m+1)x+2m﹣1与x轴有一个交点的横坐标大于2,另一个交点的横坐标小于2,且抛物线开口向上,所以令f(x)=x2﹣(4m+1)x+2m﹣1,则f(2)<0,解不等式可得m>,又因为抛物线与y轴的交点在点(0,)的下方,所以f(0)<﹣,解得m<,即可得解.【解答】解:根据题意,令f(x)=x2﹣(4m+1)x+2m﹣1,∵抛物线y=x2﹣(4m+1)x+2m﹣1与x轴有一个交点的横坐标大于2,另一个交点的横坐标小于2,且抛物线开口向上,∴f(2)<0,即4﹣2(4m+1)+2m﹣1<0,解得:m>,又∵抛物线与y轴的交点在点(0,)的下方,∴f(0)<﹣,解得:m<,综上可得:<m<,故选:A.8.函数y=与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是()A.B.C.D.【分析】本题可先由反比例函数的图象得到字母系数的正负,再与二次函数的图象相比较看是否一致.【解答】解:由解析式y=﹣kx2+k可得:抛物线对称轴x=0;A、由双曲线的两支分别位于二、四象限,可得k<0,则﹣k>0,抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上;本图象与k的取值相矛盾,故A错误;B、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象符合题意,故B正确;C、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故C错误;D、由双曲线的两支分别位于一、三象限,可得k>0,则﹣k<0,抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上,本图象与k的取值相矛盾,故D错误.故选:B.9.已知抛物线y=x2+bx+c(c<0)经过点(c,0),以该抛物线与坐标轴的三个交点为顶点的三角形面积为S,则S可表示为()A.|2+b||b+1|B.c(1﹣c) C.(b+1)2D.【分析】把点(c,0)代入抛物线中,可得b、c的关系式,再设抛物线与x轴的交点分别为x1、x2,则x1、x2满足x2+bx+c=0,根据根的判别式结合两点间的距离公式可求|x1﹣x2|,那么就可得到以该抛物线与坐标轴的三个交点为顶点的三角形面积.【解答】解:∵抛物线y=x2+bx+c(c<0)经过点(c,0),∴c2+bc+c=0;∴c(c+b+1)=0;∵c<0,∴c=﹣b﹣1;设x1,x2是一元二次方程x2+bx+c=0的两根,∴x1+x2=﹣b,x1•x2=c=﹣b﹣1,∴抛物线与x轴的交点间的距离为|x1﹣x2|=====|2+b|,∴S可表示为|2+b||b+1|.故选:A.10.下列关于函数y=(m2﹣1)x2﹣(3m﹣1)x+2的图象与坐标轴的公共点情况:①当m≠3时,有三个公共点;②m=3时,只有两个公共点;③若只有两个公共点,则m=3;④若有三个公共点,则m≠3.其中描述正确的有()个.A.一个B.两个C.三个D.四个【分析】令y=0,可得出(m2﹣1)x2﹣(3m﹣1)x+2=0,得出判别式的表达式,然后根据m的取值进行判断,另外要注意m的取值决定函数是一次函数还是二次函数,不要忘了考虑一次函数的情况.【解答】解:令y=0,可得出(m2﹣1)x2﹣(3m﹣1)x+2=0,△=(3m﹣1)2﹣8(m2﹣1)=(m﹣3)2,①当m≠3,m=±1时,函数是一次函数,与坐标轴有两个交点,故错误;②当m=3时,△=0,与x轴有一个公共点,与y轴有一个公共点,总共两个,故正确;③若只有两个公共点,m=3或m=±1,故错误;④若有三个公共点,则m≠3且m≠±1,故错误;综上可得只有②正确,共个.故选:A.二.填空题(共10小题)11.已知:如图,过原点的抛物线的顶点为M(﹣2,4),与x轴负半轴交于点A,对称轴与x轴交于点B,点P是抛物线上一个动点,过点P作PQ⊥MA于点Q.(1)抛物线解析式为y=﹣x2﹣4x.(2)若△MPQ与△MAB相似,则满足条件的点P的坐标为(﹣,)、(﹣,).【分析】(1)设抛物线的解析式为:y=a(x+2)2+4,因为抛物线过原点,把(0,0)代入,求出a即可.(2)由于PQ⊥MA,即∠MQP=∠MBA=90°;所以只要满足∠PMQ=∠MAB或∠PMQ=∠AMB.①∠PMQ=∠AMB时,先找出点B关于直线MA的对称点(设为点C),显然有AC=AB=2、MC=MB=4,可根据该条件得到点C的坐标,进而求出直线MC(即直线MP)的解析式,联立抛物线的解析式即可得到点P的坐标;②∠PMQ=∠MAB时,若设直线MP与x轴的交点为D,那么△MAD必为等腰三角形,即MD=AD,根据此条件先求出点D的坐标,进而得出直线MP的解析式,联立抛物线的解析式即可得解.【解答】解:(1)∵过原点的抛物线的顶点为M(﹣2,4),∴设抛物线的解析式为:y=a(x+2)2+4,将x=0,y=0代入可得:4a+4=0,解得:a=﹣1,∴抛物线解析式为:y=﹣(x+2)2+4,即y=﹣x2﹣4x;(2)∵PQ⊥MA∴∠MQP=∠MBA=90°;若△MPQ、△MAB相似,那么需满足下面的其中一种情况:①∠PMQ=∠AMB,此时MA为∠PMB的角平分线,如图①;取点B关于直线MA的对称点C,则AC=AB=2,MC=MB=4,设点C(x,y),有:,解得(舍),∴点C的坐标为(﹣,);设直线MP的解析式:y=kx+b,代入M(﹣2,4)、(﹣,)得:,解得∴直线MP:y=x+联立抛物线的解析式,有:,解得,∴点P的坐标(﹣,);②∠PMQ=∠MAB,如右图②,此时△MAD为等腰三角形,且MD=AD,若设点D (x,0),则有:(x+4)2=(x+2)2+(0﹣4)2,解得:x=1∴点D(1,0);设直线MP的解析式:y=kx+b,代入M(﹣2,4)、D(1,0)后,有:,解得:∴直线MP:y=﹣x+联立抛物线的解析式有:,解得:,∴点P的坐标(﹣,)综上,符合条件的P点有两个,且坐标为(﹣,)、(﹣,).故答案:(1)y=﹣x2﹣4x;(2)(﹣,)、(﹣,).12.将抛物线y=x2﹣2向左平移3个单位,所得抛物线的函数表达式为y=x2+6x+7.【分析】根据二次函数图象的平移规律:左右平移,x改变:左加右减,y不变;上下平移,x不变,y改变,上加下减进行计算即可.【解答】解:根据平移规律:将抛物线y=x2﹣2向左平移3个单位得到:y=(x+3)2﹣2,y=x2+6x+7.故答案为:y=x2+6x+7.13.如图所示,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE﹣EO|,再以CM、CO为边作矩形CMNO.令m=,则m=1;又若CO=1,CE=,Q为AE上一点且QF=,抛物线y=mx2+bx+c经过C、Q两点,则抛物线与边AB的交点坐标是(,).【分析】求出CM=OE﹣CE,求出四边形CFGH的面积是CO×(OE﹣CE),求出四边形CMNO的面积是(OE﹣CE)×CO,即可求出m值;求出EF值,得出EF=QF,得出等边三角形EFQ,求出EQ,求出∠CEF、∠OEA,过Q作QD⊥OE于D,求出Q坐标,代入抛物线求出抛物线的解析式,把x=代入抛物线即可求出y,即得出答案.【解答】解:∵沿AE折叠,O和F重合,∴OE=EF,∵在Rt△CEF中,EF>CE,即OE>CE,∴CM=|CE﹣EO|=OE﹣CE,=CF2=EF2﹣EC2=EO2﹣EC2=(EO+EC)(EO﹣EC)=CO×(EO﹣EC),∵S四边形CFGHS四边形CMNO=CM×CO=(OE﹣CE)×OC,∴m==1;∵CO=1,CE=,QF=,∴EF=EO==QF,C(0,1),∴sin∠EFC==,∴∠EFC=30°,∠CEF=60°,∴∠FEA=×(180°﹣60°)=60°,∵EF=QF,∴△EFQ是等边三角形,∴EQ=,过Q作QD⊥OE于D,ED=EQ=.∵由勾股定理得:DQ=,∴OD=﹣=,即Q的坐标是(,),∵抛物线过C、Q,m=1代入得:,解得:b=﹣,c=1,∴抛物线的解析式是:y=x2﹣x+1,AO=EO=,∵把x=代入抛物线得:y=,∴抛物线与AB的交点坐标是(,),故答案为:1,.14.该试题已被管理员删除15.在平面直角坐标系中,点A、B、C的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是△ABC围成的区域(含边界)上的点,那么当w=xy取得最大值时,点P的坐标是(,5).【分析】分别求得线段AB、线段AC、线段BC的解析式,分析每一条线段上横、纵坐标的乘积的最大值,再进一步比较.【解答】解:线段AB的解析式是y=x+1(0≤x≤4),此时w=x(x+1)=+x,则x=4时,w最大=8;线段AC的解析式是y=x+1(0≤x≤2),此时w=x(x+1)=+x,此时x=2时,w最大=12;线段BC的解析式是y=﹣2x+10(2≤x≤4),此时w=x(﹣2x+10)=﹣2x2+10x,此时x=时,w最大=12.5.综上所述,当w=xy取得最大值时,点P的坐标是(,5).16.如图为二次函数y=ax2+bx+c的图象,在下列结论中:①ac>0;②方程ax2+bx+c=0的根是x1=﹣1,x2=5;③a+b+c<0;④当x<2时,y随着x的增大而增大.正确的结论有②④(请写出所有正确结论的序号).【分析】根据抛物线的开口向下判断出a<0,再根据与y轴的交点判断出c>0,然后判断出①错误;根据与x轴的交点坐标判断出②正确;取x=1的函数值判断出③错误;先求出抛物线对称轴为直线x=2,然后根据二次函数的增减性判断出④正确.【解答】解:∵抛物线开口向下,∴a<0,∵与y轴的正半轴相交,∴c>0,∴ac<0,故①错误;∵抛物线与x轴的交点坐标为(﹣1,0),(5,0),∴方程ax2+bx+c=0的根是x1=﹣1,x2=5,故②正确;由图可知,当x=1时,函数值y>0,即a+b+c>0,故③错误;抛物线对称轴为直线x==2;当x<2时,y随着x的增大而增大,故④正确;综上所述,正确的结论是②④.故答案为:②④.17.已知当x1=a,x2=b,x3=c时,二次函数y=x2+mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是m>﹣.【分析】根据三角形的任意两边之和大于第三边判断出a最小为2,再根据二次函数的增减性和对称性判断出对称轴在2、3之间偏向2,即小于2.5,然后列出不等式求解即可.【解答】方法一:解:∵正整数a,b,c恰好是一个三角形的三边长,且a<b<c,∴a最小是2,∵y1<y2<y3,∴﹣<2.5,解得m>﹣2.5.方法二:解:当a<b<c时,都有y1<y2<y3,即,∴,∴,∵a,b,c恰好是一个三角形的三边长,a<b<c,∴a+b<b+c,∴m>﹣(a+b),∵a,b,c为正整数,∴a,b,c的最小值分别为2、3、4,∴m>﹣(a+b)≥﹣(2+3)=﹣,∴m>﹣,故答案为:m>﹣.18.如图,已知一动圆的圆心P在抛物线y=x2﹣3x+3上运动.若⊙P半径为1,点P的坐标为(m,n),当⊙P与x轴相交时,点P的横坐标m的取值范围是3﹣<m<2或4<m<3+.【分析】由圆心P在抛物线y=x2﹣3x+3上运动,点P的坐标为(m,n),可得n=m2﹣3m+3,又由⊙P半径为1,⊙P与x轴相交,可得|m2﹣3m+3|<1,继而可求得答案.【解答】解:∵圆心P在抛物线y=x2﹣3x+3上运动,点P的坐标为(m,n),∴n=m2﹣3m+3,∵⊙P半径为1,⊙P与x轴相交,∴|n|<1,∴|m2﹣3m+3|<1,∴﹣1<m2﹣3m+3<1,解m2﹣3m+3<1,得:3﹣<m<3+,解m2﹣3m+3>﹣1,得:m<2或m>4,∴点P的横坐标m的取值范围是:3﹣<m<2或4<m<3+.故答案为:3﹣<m<2或4<m<3+.19.如图,四边形ABCD是矩形,A、B两点在x轴的正半轴上,C、D两点在抛物线y=﹣x2+6x上.设OA=m(0<m<3),矩形ABCD的周长为l,则l与m的函数解析式为l=﹣2m2+8m+12.【分析】求l与m的函数解析式就是把m当作已知量,求l,先求AD,它的长就是D点的纵坐标,再把D点纵坐标代入函数解析式求C点横坐标,C点横坐标与D点横坐标的差就是线段CD的长,用l=2(AD+CD),建立函数关系式.【解答】解:把x=m代入抛物线y=﹣x2+6x中,得AD=﹣m2+6m把y=﹣m2+6m代入抛物线y=﹣x2+6x中,得﹣m2+6m=﹣x2+6x解得x1=m,x2=6﹣m∴C的横坐标是6﹣m,故AB=6﹣m﹣m=6﹣2m∴矩形的周长是l=2(﹣m2+6m)+2(6﹣2m)即l=﹣2m2+8m+12.20.若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(﹣1,0),则y=a+b+c的取值范围是0<y<2.【分析】由二次函数的解析式可知,当x=1时,所对应的函数值y=s=a+b+c.把点(0,1),(﹣1,0)代入y=ax2+bx+c,得出c=1,a﹣b+c=0,然后根据顶点在第一象限,可以画出草图并判断出a与b的符号,进而求出y=a+b+c的变化范围.【解答】解:∵二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(﹣1,0),∴易得:c=1,a﹣b+c=0,a<0,b>0,由a=b﹣1<0得到b<1,结合上面b>0,所以0<b<1①,由b=a+1>0得到a>﹣1,结合上面a<0,所以﹣1<a<0②,∴由①②得:﹣1<a+b<1,且c=1,得到:0<a+b+c<2,则y=a+b+c的取值范围是0<y<2.故答案为:0<y<2三.解答题(共4小题)21.已知抛物线y=ax2﹣2x+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C,对称轴为x=1,顶点为E,直线y=﹣x+1交y轴于点D.(1)求抛物线的解析式;(2)求证:△BCE∽△BOD;(3)点P是抛物线上的一个动点,当点P运动到什么位置时,△BDP的面积等于△BOE的面积?【分析】(1)在抛物线y=ax2﹣2x+c中,已知对称轴x=﹣=1,可求出a的值;再将点A的坐标代入抛物线的解析式中,可确定c的值,由此得解.(2)首先由抛物线的解析式,确定点B、C、E的坐标,由直线BD的解析式能得到点D的坐标;在求出△BCE、△BOD的三边长后,由SSS来判定这两个三角形相似.(3)△BOE的面积易得,而在(2)中求出了BD的长,由△BDP、△BOE的面积相等先求出点P到直线BD的距离,如何由这个距离求出点P的坐标?这里需要进行适当的转化;首先在y轴上取一点(可设为点M),使得点M到直线BD 的距离等于点P到直线BD的距离,通过解直角三角形先求出DM的长,由此确定点M的坐标,然后过M作平行于直线BD的直线,再联立抛物线的解析式即可确定点P的坐标.【解答】解:(1)抛物线y=ax2﹣2x+c中,对称轴x=﹣=﹣=1,∴a=1;将点A(﹣1,0)代入y=ax2﹣2x+c中,得:1+2+c=0,c=﹣3;∴抛物线的解析式:y=x2﹣2x﹣3.(2)∵抛物线的解析式:y=x2﹣2x﹣3=(x﹣1)2﹣4=(x+1)(x﹣3),∴点C(0,﹣3)、B(3,0)、E(1,﹣4);易知点D(0,1),则有:OD=1、OB=3、BD=;CE=、BC=3、BE=2;∴==,∴△BCE∽△BOD.(3)S△BOE=×BO×|y E|=×3×4=6;∴S△BDP =×BD×h=S△BOE=6,即h=.在y轴上取点M,过点M作MN1⊥BD于N1,使得MN1=h=;在Rt△MN1D中,sin∠MDN1=,且MN1=;则MD==4;∴点M(0,﹣3)或(0,5).过点M作直线l∥MN2,如右图,则直线l:y=﹣x﹣3或y=﹣x+5,联立抛物线的解析式有:或解得:、、、∴当点P的坐标为(0,﹣3)、(,﹣)、(,)、(,)时,△BDP的面积等于△BOE的面积.22.如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.【分析】(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.【解答】解:(1)∵B(4,m)在直线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx+6上,∴,解得,∴抛物线的解析式为y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)∵△PAC为直角三角形,i)若点P为直角顶点,则∠APC=90°.由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;ii)若点A为直角顶点,则∠PAC=90°.如答图3﹣1,过点A(,)作AN⊥x轴于点N,则ON=,AN=.过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,∴MN=AN=,∴OM=ON+MN=+=3,∴M(3,0).设直线AM的解析式为:y=kx+b,则:,解得,∴直线AM的解析式为:y=﹣x+3 ①又抛物线的解析式为:y=2x2﹣8x+6 ②联立①②式,解得:x=3或x=(与点A重合,舍去)∴C(3,0),即点C、M点重合.当x=3时,y=x+2=5,∴P1(3,5);iii)若点C为直角顶点,则∠ACP=90°.∵y=2x2﹣8x+6=2(x﹣2)2﹣2,∴抛物线的对称轴为直线x=2.如答图3﹣2,作点A(,)关于对称轴x=2的对称点C,则点C在抛物线上,且C(,).当x=时,y=x+2=.∵点P1(3,5)、P2(,)均在线段AB上,∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(,).23.已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.(1)求抛物线的函数表达式;(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC 于点Q.①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)已知了A,B的坐标,可用待定系数法求出函数的解析式.(2)①QP其实就是一次函数与二次函数的差,二次函数的解析式在(1)中已经求出,而一次函数可根据B,C的坐标,用待定系数法求出.那么让一次函数的解析式减去二次函数的解析式,得出的新的函数就是关于PQ,x的函数关系式,那么可根据函数的性质求出PQ的最大值以及相对应的x的取值.(3)分三种情况进行讨论:当∠QOA=90°时,Q与C重合,显然不合题意.因此这种情况不成立;当∠OAQ=90°时,P与A重合,因此P的坐标就是A的坐标;当∠OQA=90°时,如果设QP与x轴的交点为D,那么根据射影定理可得出DQ2=OD•DA.由此可得出关于x的方程即可求出x的值,然后将x代入二次函数式中即可得出P的坐标.【解答】解:(1)∵抛物线过A(3,0),B(6,0),解得:,∴所求抛物线的函数表达式是y=x2﹣x+2.(2)①∵当x=0时,y=2,∴点C的坐标为(0,2).设直线BC的函数表达式是y=kx+h.则有,解得:.∴直线BC的函数表达式是y=﹣x+2.∵0<x<6,点P、Q的横坐标相同,∴PQ=y Q﹣y P=(﹣x+2)﹣(x2﹣x+2)=﹣x2+x=﹣(x﹣3)2+1∴当x=3时,线段PQ的长度取得最大值.最大值是1.②解:当∠OAQ′=90°时,点P与点A重合,∴P(3,0)当∠Q′OA=90°时,点P与点C重合,∴x=0(不合题意)当∠OQ′A=90°时,设PQ′与x轴交于点D.∵∠OQ′D+∠AOQ′=90°,∠Q′AD+∠AQ′D=90°,∴∠OQ′D=∠Q′AD.又∵∠ODQ′=∠Q′DA=90°,∴△ODQ′∽△Q′DA.∴,即DQ′2=OD•DA.∴(﹣x+2)2=x(3﹣x),10x2﹣39x+36=0,∴x1=,x2=,∴y1=×()2﹣+2=;y2=×()2﹣+2=;∴P(,)或P(,).∴所求的点P的坐标是P(3,0)或P(,)或P(,).24.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l 于点H,连结OP,试求△OPH的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)利用待定系数法求出抛物线的解析式;(2)①如答图1,作辅助线,利用关系式S△OPH =S△OMH﹣S△OMP求解;②本问涉及复杂的分类讨论,如答图2所示.由于点P可能在OC、BC、BK、AK、OA上,而等腰三角形本身又有三种情形,故讨论与计算的过程比较复杂,需要耐心细致、考虑全面.【解答】解:(1)由题意得:A(4,0),C(0,4),对称轴为x=1.设抛物线的解析式为y=ax2+bx+c,则有:,解得.∴抛物线的函数解析式为:y=﹣x2+x+4.(2)①当m=0时,直线l:y=x.∵抛物线对称轴为x=1,∴CP=1.如答图1,延长HP交y轴于点M,则△OMH、△CMP均为等腰直角三角形.∴CM=CP=1,∴OM=OC+CM=5.S△OPH=S△OMH﹣S△OMP=(OM)2﹣OM•CP=×(×5)2﹣×5×1=﹣=,=.∴S△OPH②当m=﹣3时,直线l:y=x﹣3.设直线l与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).假设存在满足条件的点P.a)当点P在OC边上时,如答图2﹣1所示,此时点E与点O重合.设PE=a(0<a≤4),则PD=3+a,PF=PD=(3+a).过点F作FN⊥y轴于点N,则FN=PN=PF,∴EN=|PN﹣PE|=|PF﹣PE|.在Rt△EFN中,由勾股定理得:EF==.若PE=PF,则:a=(3+a),解得a=3(+1)>4,故此种情形不存在;若PF=EF,则:PF=,整理得PE=PF,即a=3+a,不成立,故此种情形不存在;若PE=EF,则:PE=,整理得PF=PE,即(3+a)=a,解得a=3.∴P1(0,3).b)当点P在BC边上时,如答图2﹣2所示,此时PE=4.若PE=PF,则点P为∠OGD的角平分线与BC的交点,有GE=GF,过点F分别作FH⊥PE于点H,FK⊥x轴于点K,∵∠OGD=135°,∴∠EPF=45°,即△PHF为等腰直角三角形,设GE=GF=t,则GK=FK=EH=t,∴PH=HF=EK=EG+GK=t+t,∴PE=PH+EH=t+t+t=4,解得t=4﹣4,则OE=3﹣t=7﹣4,∴P2(7﹣4,4)c)∵A(4,0),B(2,4),∴可求得直线AB解析式为:y=﹣2x+8;联立y=﹣2x+8与y=x﹣3,解得x=,y=.设直线BA与直线l交于点K,则K(,).当点P在线段BK上时,如答图2﹣3所示.设P(a,8﹣2a)(2≤a≤),则Q(a,a﹣3),∴PE=8﹣2a,PQ=11﹣3a,∴PF=(11﹣3a).。
