倍长中线巧解题__几何图形中点问题

合集下载

中考数学几何辅助线：倍长中线法

中考数学几何添加辅助线：倍长中线中线或中点是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法。

此法常用于构造全等三角形，利用中线的性质、辅助线、对顶角进而用“SAS”证明对应边之间的关系。

常规的倍长中线可以出全等，但需要证明“三点共线”，遇到“中点+平行”，我们“延长出全等”，而非“倍长出全等”. 用“倍长中线法”作辅助线解几何题，是一种重要的技巧套路。

它可以有效地生发出全等、平行等基本条件，关联好多基本图形，帮助解题，大家务必好好掌握。

也给我们解题的启示：抓住核心，找到关键，才能快速解题。

逢中点，便倍长，全等观，平行现.倍长中线法:是指加倍延长中线，使所延长部分与中线相等，然后连接相应的顶点，构造“8字形”的全等三角形。

在与中点有关的线段尤其是涉及线段的等量关系时，倍长中线应用较常见，常见添加如图（AD是底边中线）典例1．已知：AD是ΔABC的中线，AE=EF．求证：AC=BF．名师指点：延长AD到M，使AD＝DM，连接BM，根据SAS证△ADC≌△MDB，推出BM＝AC，∠CAD＝∠M，根据AE＝EF，推出∠CAD＝∠AFE＝∠BFD，求出∠BFD＝∠M，再根据等腰三角形的性质证明即可．满分解答：证明：延长AD 到M ，使AD ＝DM ，连接BM ，∵AD 是△ABC 中线，∴CD ＝BD ，∵在△ADC 和△MDB 中，{CD ＝BD∠ADC ＝∠MDB AD ＝DM，∴△ADC ≌△MDB （SAS ），∴BM ＝AC ，∠CAD ＝∠M ，∵AE ＝EF ，∴∠CAD ＝∠AFE ，∵∠AFE ＝∠BFD ，∴∠BFD ＝∠CAD ＝∠M ，∴BF ＝BM ＝AC ，即AC ＝BF ．名师点评：倍长中线是常见的辅助线、全等中相关的角、线段的代换是解决问题的关键． 1．如图，在平行四边形ABCD 中，28CD AD ==，E 为AD 上一点，F 为DC 的中点，则下列结论中正确的是（）A ．4BF =B ．2ABC ABF ∠>∠。

1初中数学《几何辅助线秘籍》中点模型地构造1(倍长中线法;构造中位线法)

实用标准文案开场:1 •行礼；2•晨读；3•检查作业；4•填写表格5•如图所示,已知在-ABC中，AD是BC边上的中线f F是AD上的一点，连接BE并延长交AC于点F , AE二EF ,求证：AC = BF.6•如图所示.在二ABC中，分别以AB、AC为直角边向夕卜做等腰直角三角形^ABD和SCE , F为BC边上中点，FA的延长线交DE于点G ,求证：①DE二2AF ;②FG丄DE .7•如图所示，在R2ABC中，ZBAC二90。

，点D为BC的中点，点巳F分别为AB、AC上的点，且EDJLFD.以线段BE、EF、FC为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形，或者是钝角三角形？8•四边形ABCD是矩形岸是BC边上的中点，MBE沿看直线AE翻折，点B落在点F处. 直线AF与直线CD交于点G,请探究线段AB、AG、GC之间的关系.2•已知r如图,四边形ABCD中,AC. BD相交于点6 且AC = BD Z E x F分别是AD. BC 的中点，EF分别交AC、BD于点M. N・求证：0M二ON.CA p B3.BD、CE分别是的-ABC外角平分线，过A作AF丄BD , AG丄CE ,垂足分别是F、G ,易证FG=|( AB+BC+AC](1)若BD、CE分别是-ABC的内角平分线，FG与△ ABC三边有怎样的数量关系？画出图形实用标准文案3 •如图川ABC 中，AB 二BC,zABC 二90J 点E、F 分别在AB. AC 上.且AE 二EF,点QCE;(2)0BW0M.M分别为AF、CE的中点.求证：(1)OM詁实用标准文案4•如图r zDBC = zBCE 二90°, M 为DE 的中点.求证:MB 二MC.教学后记学生签名：家长签名:。

中点模型1---倍长中线(辉哥秘籍)

A
E
F
B

C
【例9】如图所示，在 ABC 中，AB AC ，延长 AB 到 D ，使 BD AB ，E 为 AB 的中点，连接 CE 、 CD ，求证 CD 2EC ．
板块三、求证中点
【例10】已知 ACB ，B ACB ，D ，E 分别是 AB 及 AC 延长线上的一点，且 BD CE ，连接 DE 交底 BC 于 G ，求证 GD GE ．
BA E
C
D
【例3】如图，在△ACB 和△AED 中，AC=BC，AE=DE，∠ACB＝∠AED＝90°,点 E 在 AC 上，连结 BD，取 BD 的中点 F，连结 FE、CF，求证：CF 与 EF 的关系
A
A
A
E
D
D
F
C
B
图1
E
F C
图2
D
B
C
【例4】如图，正方形 CGEF 的边 CG 与正方形 ABCD 的边 BC 在同一直线上（CG＞BC），连结 AE,取线段 AE 的中点 M．探究：线段 MD、MF 的关系，并加以证明.
A
F E
B
D
C
【例7】如图所示，已知 ABC 中，AD 平分 BAC ，E 、F 分别在 BD 、AD 上．DE CD ， EF AC ．求证： EF ∥ AB
A
F
BE
D
C
【例8】已知 AM 为 ABC 的中线， AMB ， AMC 的平分线分别交 AB 于 E 、交 AC 于
F ．求证： BE CF EF ．
A
D
B
G
C
E
【例11】已知△ABC 中，过 AB 边和 BC 边在三角形外分别作正方形 ABEF 和正方形 BCPQ，连接 EQ，过 B 点作 BM⊥EQ，延长 MB 与 AC 交于 D 点，求证：D 是 AC 中点．

倍长中线法(经典例题)2

倍长中线法〔加倍法〕知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法〞添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么〔延长的那一条〕，用SAS证全等〔对顶角〕倍长中线最重要的一点，延长中线一倍，完成SAS全等三角形模型的构造。

经典例题讲解：例1：△ABC中，AB=5，AC=3，求中线AD的取值范围。

例2：在△ABC中，AB=AC，D在AB上，E在AC的延长线上，DE交BC于F，且DF=EF，求证：BD=CE例3：在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+例5：CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE第 14 题图DF CBEAB自检自测：1、如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE 。

2、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.3、：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠F EAB C DABFDEC4、如图，CB、CD分别是钝角△AEC和锐角△ABC的中线，且AC=AB．求证：①CE=2CD．②CB平分∠DCE．5、如图△ABC，AD是BC边上的中线，分别以AB边、AC边为直角边各向形外作等腰直角三角形，求证EF＝2AD.4、：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.倍长中线法〔加倍法〕知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法〞添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么〔延长的那一条〕，用SAS 证全等〔对顶角〕倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模型的构造。

中点出来技巧(一)中线倍长法(作平行线)

中点出来技巧（一）中线倍长法（作平行线）
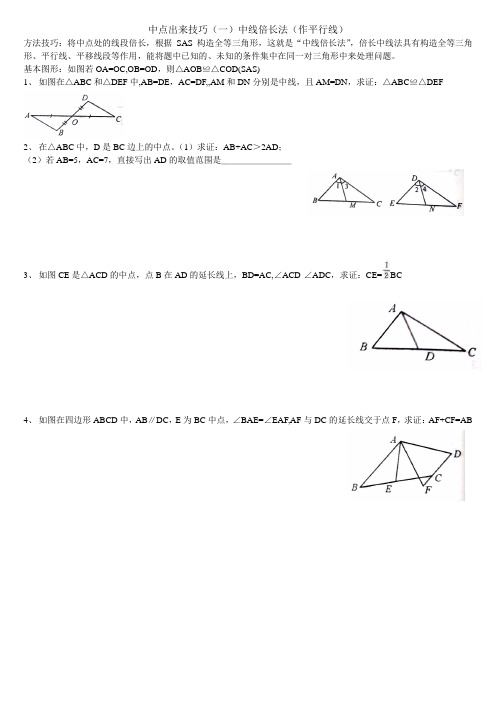
方法技巧：将中点处的线段倍长，根据SAS构造全等三角形，这就是“中线倍长法”，倍长中线法具有构造全等三角形、平行线、平移线段等作用，能将题中已知的、未知的条件集中在同一对三角形中来处理问题。

基本图形：如图若OA=OC,OB=OD，则△AOB≌△COD(SAS)
1、如图在△ABC和△DEF中,AB=DE，AC=DF,,AM和DN分别是中线，且AM=DN，求证：△ABC≌△DEF
2、在△ABC中，D是BC边上的中点。

（1）求证：AB+AC＞2AD；
（2）若AB=5，AC=7，直接写出AD的取值范围是＿＿＿＿＿＿＿＿
3、如图CE是△ACD的中点，点B在AD的延长线上，BD=AC,∠ACD-∠ADC，求证：CE=BC
4、如图在四边形ABCD中，AB∥DC，E为BC中点，∠BAE=∠EAF,AF与DC的延长线交于点F，求证：AF+CF=AB。

倍长中线法(经典例题)

倍长中线法知识网络详解：中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法的过程：延长某某到某点，使某某等于某某，使什么等于什么（延长的那一条），用SAS 证全等（对顶角）倍长中线最重要的一点，延长中线一倍，完成SAS 全等三角形模型的构造。

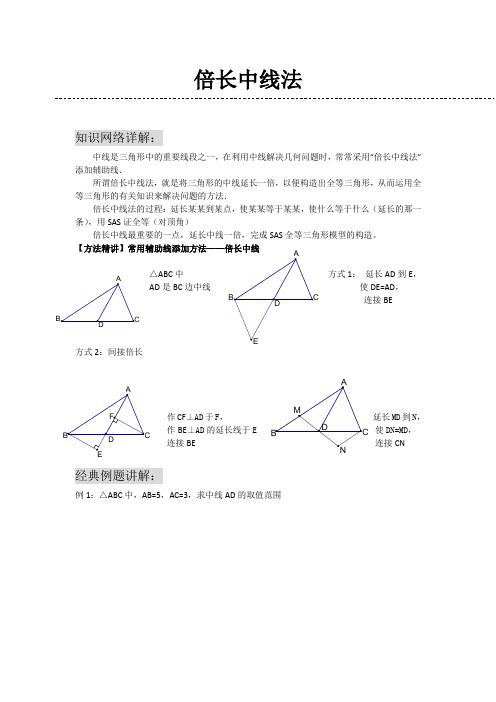
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中方式1：延长AD 到E ，AD 是BC 边中线使DE=AD ，连接BE方式2：间接倍长作CF ⊥AD 于F ，延长MD 到N ，作BE ⊥AD 的延长线于E 使DN=MD ，连接BE 连接CN经典例题讲解：例1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围D ABCEDAB C F EDC B AN D C B AM例2：已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE例3：已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例4：已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC.求证：AE 平分BAC ∠FE DA B CFEC ABD AB F D E C例5：已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE自检自测：1、如图，△ABC 中，BD=DC=AC,E 是DC 的中点，求证，AD 平分∠BAE.2、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

试探究线段AB 与AF 、CF 之间的数量关系，并证明你的结论.E D ABCF EAB C D3、如图，AD 为ABC ∆的中线，DE 平分BDA ∠交AB 于E ，DF 平分ADC ∠交AC 于F. 求证：EF CF BE >+4、已知：如图，∆ABC 中，∠C=90︒，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE//AB 交BC 于E ，求证：CT=BE.第 14 题图DF CBEADABCMTE。

初中几何中点问题之倍长中线

初中几何中点问题之倍长中线
中点，顾名思义，把一条线段分为两条相等的线段的点,叫做这条线段的中点。

题型一：倍长中线
你需要的知识点：中线，三角形全等
你遇到它的时间：初一下学期至中考
你觉得难点在这：辅助线构造
你需要会的技能：加倍，加倍，加倍！
在你眼中，这类题应该长这个样子
结论：这类题型倍长中线后一般会构造出一组全等，一组平行，常用于构造全等三角形。

倍长中线多用于构造全等三角形和证明边之间的关系(通常用"SAS"证明)
目的：在于进行边和角的转移，并且可以构造出两倍的线段。

注:一般都是原题已经有中线（或类中线）时用，不太会有自己画中线的时候。

题型二：倍长类中线
当然有时候题中会只出现中点，但是没有中线，这时候我们一般习惯于把这条线称之为类中线。

拓展：倍长中线之两次全等
通常，在综合题型中，倍长中线后的第一组全等只是一个基础，往往还需证明第二组全等，但是难点就在于如何去倍长中线，倍长中线后去连接什么线，这是问题的关键。

这时一般需要去试错，尤其是当有两个中点时，一般是倍长中线后大概率会有另一组的全等。

如下题，其实倍长CE后不管连接FA还是连接FB，这两种方法都可以继续下去。

最后，不是所有的中点问题都是可以进行倍长中线的，还有斜边中线，中位线，三线合一等多种中点问题，倍长中线只是其中一个，其余的问题我们下期再见。

初中几何中点问题之倍长中线

初中几何中点问题之倍长中线
中点，顾名思义，把一条线段分为两条相等的线段的点,叫做这条线段的中点。

倍长中线多用于构造全等三角形和证明边之间的关系(通常用"SAS"证明)
目的：在于进行边和角的转移，并且可以构造出两倍的线段。

注:一般都是原题已经有中线（或类中线）时用，不太会有自己画中线的时候。

题型二：倍长类中线
当然有时候题中会只出现中点，但是没有中线，这时候我们一般习惯于把这条线称之为类中线。

这时一般需要去试错，尤其是当有两个中点时，一般是倍长中线后大概率会有另一组的全等。

如下题，其实倍长CE后不管连接FA还是连接FB，这两种方法都可以继续下去。

初中数学倍长中线法(最全最新倍长中线法专题)

课堂练习
练习3.如图，在正方形ABCD中，E为AB边的中点，G，F分别为AD，BC边上的点，若AG＝1， BF＝2，∠GEF＝90°，求GF的长.
课堂练习
练习4.如图，在梯形ABCD中，AD∥BC，点E在BC上，AE＝BE，点F是CD的中点，且AF⊥AB，若AD＝2.7，AF＝4，AB＝6. 求CE的长.
课后练习
4.在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG、CG，如图（1），易证EG＝CG且EG⊥CG.
（1）将△BEF绕点B逆时针旋转90°，如图（2），证明: EG＝CG且EG⊥CG．（2）如图（3）将△BEF绕点B逆时针旋转180°，证明: EG＝CG且EG⊥CG．
几何模型四：倍长中线法
倍长中线法
当线段出现一个中点时，特别是三角形中，常常采用“倍长中线法”添加辅助线．倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．倍长中线法: △ABC中AD是BC边中线方式1: 延长AD到E，使DE=AD，连接BE
课堂练习
练习7.如图，已知D是△ABC的边BC上的一点，CD＝AB，∠BDA＝∠BAD，AE是△ABD的中线．求证: AD是∠EAC的平分线．
例题讲解
例5.如图，在△ABC中，AD平分∠BAC，E为BC的中点，过点E作EF∥AD交AB于点G，交CA的延长线于点F．求证: BG＝CF．
证明: 作CM∥AB交FE的延长线于M．∵BG∥CM， ∴∠B＝∠MCE，∵E是BC中点， ∴BE＝EC，在△BEG和△CEM中，
证明: 如图，过点D作DG∥AE，交BC于点G；则△DGF≌△ECF， ∴DG＝CE； ∵AB＝AC， ∴∠B＝∠ACB；

中考数学基本模型—中点模型,初三数学专题复习总结倍长中线练习题

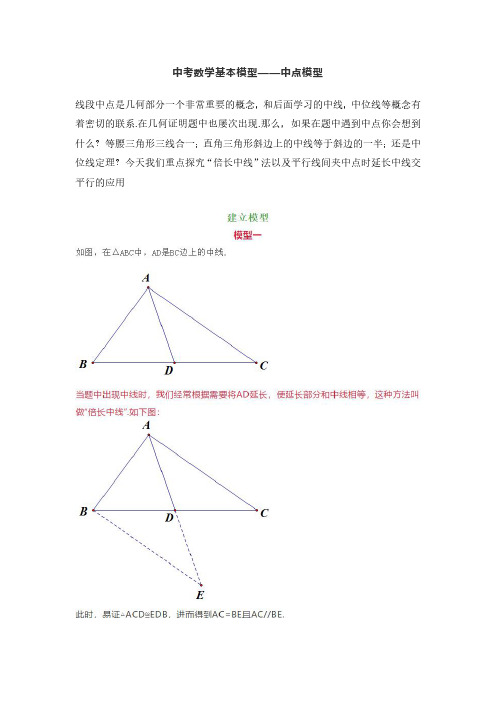
中考数学基本模型——中点模型线段中点是几何部分一个非常重要的概念，和后面学习的中线，中位线等概念有着密切的联系.在几何证明题中也屡次出现.那么，如果在题中遇到中点你会想到什么？等腰三角形三线合一；直角三角形斜边上的中线等于斜边的一半；还是中位线定理？今天我们重点探究“倍长中线”法以及平行线间夹中点时延长中线交平行的应用线相交.即“延长中线交平行”此时，易证△BEF≌△CED模型三如图，在△ABC中，点D是AB边的中点.可作另一边AC的中点，构造三角形中位线.如下图所示：时，只需将AE延长和DC的延长线相交，就一定会得到全等三角形，进而得到我们需要的结果.证明：如图，延长AE交DC的延长线于点F.∵四边形ABCD是平行四边形∴AB//CD，即AB//DF∴∠BAE=∠CFE，∠B=∠FCE又∵点E是BC中点∴BE=CE∴△ABE≌△FCE∴CF=AB=CD，AE=FE∴DF=2CD,又∵AD=2CD∴AD=DF,又因为点E是AF的中点∴DE⊥AF即∠AED=90°.反思：对于本题，还可以延长AE至点F使EF=AE，连接CF.通过证明△ABE ≌△FCE得到AB//CF,利用经过直线外一点有且只有一条直线与已知直线平行，得到D、C、F三点共线.再证明△DAF是等腰三角形，利用等腰三角形三线合一得到结论.对于第二种方法，同学们可以自己尝试.例2、在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．分析：由题可知，DE//BF，且点G是BE的中点，满足平行线间夹中点，所以可将DG延长与BF相交.证明：（1）AG=DG，且AG⊥DG.如图，延长DG交BF于点H，连接AH，AD.∵四边形CDEF是正方形，∴DE//CF即DE//BC∴∠GBH=∠GED，∠GHB=∠GDF又∵点G是BF的中点∴GB=GF∴△GBH≌△GDF(AAS)∴GD=GH，BH=DF∵DE=DC，∴BH=CD因为△ABC是等腰直角三角形∴AB=AC,∠ACD=180°-45°-90°=45°=∠ABC∴△ABH≌△ACD∴AH=AD，∠BAH=∠CAD∴∠DAH=∠CAD+∠CAH=∠BAH+∠CAH=∠BAC=90°∴△DAH是等腰直角三角形，又∵点G是DH的中点∴AG=DG且AG⊥DG.反思：若将正方形绕点C旋转任意角度，在旋转的过程中，上述结论还成立吗？试试看(2)AG⊥DG，AG=√3DG如图，延长DG交BF于点H，连接AH，AD.∵四边形CDEF是菱形，∴DE//CF即DE//BC∴∠GBH=∠GED，∠GHB=∠GDF又∵点G是BF的中点∴GB=GF∴△GBH≌△GDF(AAS)∴GD=GH，BH=DF∵DE=DC，∴BH=CD因为△ABC是等边三角形∴AB=AC,∠ACD=180°-60°-60°=60°=∠ABC∴△ABH≌△ACD∴AH=AD，∠BAH=∠CAD∴∠DAH=∠CAD+∠CAH=∠BAH+∠CAH=∠BAC=60°∴△DAH是等边三角形，又∵点G是DH的中点∴AG⊥DG.∠DAG=1/2∠DAH=30°∴AG=√3DG（3）AG⊥DG，DG=AG×tan(α/2)证明：延长DG与BC交于H，连接AH、AD，∵四边形CDEF是菱形，∴DE=DC，DE∥CF，∴∠GBH=∠GED，∠GHB=∠GDE，∵G是BE的中点，∴BG=EG，∴△BGH≌△EGD（AAS），∴BH=ED，HG=DG，∴BH=DC，∵AB=AC，∠BAC=∠DCF=α，∴∠ABC=90°﹣α/2，∠ACD=90°﹣α/2，∴∠ABC=∠ACD，∴△ABH≌△ACD（SAS），∴∠BAH=∠CAD，AH=AD，∴∠BAC=∠HAD=α；∴AG⊥HD，∠HAG=∠DAG=α/2，∴tan∠DAG=tan(α/2)，∴DG=AGtan（α/2）．反思：在本题的证明中，我们结合题目中给出的平行线间夹中点这一条件，将DG进行延长和BC相交，通过全等使问题得证.对于本题我们也可以采用倍长中线法进行证明.下面用倍长中线法对第一种情况加以证明.证明：如图，延长AG至点H，使GH=AG.连接EH，AD，DH.在△ABG和△HEG中BG=EG,∠AGB=∠HGE，AG=HG∴△ABG≌△HEG∴AB=HE，∠ABG=∠HEG∵AB=AC∴AC=HE∵DE//BC∴∠DEG=∠EBC∴∠HED=∠HEB+∠DEG=∠ABG+∠EBC=∠ABC=45°又∠ACD=180°-45°-90°=45°∴∠ACD=∠HED在△ACD和△HED中AC=HE，∠ACD=∠HED，DC=DE∴△ACD≌△HEDDA=DH，∠ADC=∠HDE∴∠ADC-∠HDC=∠HDE-∠HDC即∠ADH=∠CDE=90°所以△ADH是等腰直角三角形又因为点G是AH的中点所以DG=AG，DG⊥AG.上面我们用倍长中线证明了第一种情况，请你对第二三问加以证明.反思：在本题的证明过程中，容易犯的一个错误是，许多同学看到HE经过点C，就说∠HED=45°.而这一结论是需要证明的.小试身手如图1，在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG、CG.易证：EG=CG且EG⊥CG.（1）将△BEF绕点B逆时针旋转90°，如图2所示，则线段EG和CG有怎样的数量和位置关系？请直接写出你的猜想.（2）将△BEF绕点B逆时针旋转180°，如图3所示，则线段EG和CG又有怎样的数量和位置关系？请写出你的猜想，并加以证明.（3）将△BEF绕点B旋转一个任意角度α，如图4所示，则线段EG和CG 有怎样的数量和位置关系？请直接写出结论.前两问较简单，请同学们自行完成，这里只给出第三问的几种解法，仅供大家参考.解法一：如图，延长EG至点H，使GH=EG.连接DH，CE，CH.因为点G是DF的中点，所以GF=GD.根据SAS易证△GEF≌△GHDEF=HD且∠GEF=∠GHD，所以EF//DH.分别延长HD与EB交于点K，HD的延长线交BC于点M.如下图：因为EB⊥EF，而EF//DH，所以EK⊥HK，即∠BKM=∠MCD=90°.又∠BMK=∠CMD.根据三角形的内角和，可得∠KBM=∠MDC.所以∠EBC=∠HDC.又EB=HD，BC=DC所以△EBC≌△HDC.所以CE=CB且∠ECB=∠HCD.所以∠ECB=90°，即△BCE是等腰直角三角形，又因为点G是斜边EB的中点，所以CG⊥GE且CG=GE.解法二：如图，延长CG至点N，是GN=CG.连接FN，EN，EC.以下过程可参照解法一自行完成解法三：延长FE至点P使得EP=EF，连接BP；延长DC至点Q，使得CQ=CD，连接BQ.连接FQ，DP。

初中数学几何中点问题题型总结

初中数学几何中点问题题型总结1、还原中心对称图形（倍长中线法）中心对称与中心对称图形知识：把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心。

这两个图形中的对应点叫做关于中心的对称点。

中心对称的两条基本性质：(1)关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分。

(2)关于中心对称的两个图形是全等图形。

中心对称图形把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。

（一个图形）线段本身就是中心对称图形，中点就是它的对称中心，所以遇到中点问题，依托中点借助辅助线还原中点对称图形，可以把分散的条件集中起来（集散思想）。

例如图，D 是△ABC 的边BC 上的点，且CD=AB ，∠ADB=∠BAD ，AE 是△ABD的中线。

求证：AC=2AE练习 1、已知：如图，梯形ABCD 中，AD ∥BC ，∠ABC=90°．若BD=BC ，F 是CD的中点，试问：∠BAF 与∠BCD 的大小关系如何？请写出你的结论并加以证明；A BCDF2、Rt △ABC 中，∠BAC=90°，M 为BC 的中点，过A 点作某直线l ，过B 作BD l ⊥于点D ，过C 作CE l ⊥于点E 。

（1）中的结论是否任然成立？2、两条平行线间线段的中点（“八字型”全等）如图，1l ∥2l ，C 是线段AB 的中点，那么过点C 直线都可以和AB 构造“8字型”全等例已知梯形ABCD ，AD ∥BC ，点E 是AB 的中点，连接DE 、CE 。

求证：ABCD 12DECSS =梯分析：如果直接证明，是不容易，联想到AD ∥BC ，点E 是AD 的中点，我们延长DE ，与CB 的延长线交于点F ，这样，我们就构造出一对八字型的三角形，并且这对三角形是全等的。

初中数学几何专题- 辅助线专题(1)-中线倍长问题

B N E
A
C
MD
【拓】等腰 Rt△ABC 和等腰 Rt△ADE 有公共的直角顶点 A，分别连接 CD、BE. （1）如图，若 N 为 BE 的中点，求证：2AN＝CD；
A
D
M
C
E
N
B
（2）如图，若 N 为 BE 的中点，点 M 为 AN 和 CD 的交点，求证：AM⊥CD； A
D
M
C
E
N
B
（3）如图，若 AM⊥CD 于点 M，点 N 为 MA 与 BE 的交点，求证：N 为 BE 的中点．
D
A
E
B
P
C
【家庭作业】 1、在△ABC 中，AD 是 BC 边上的中线，若 AB＝3，AD＝4，则 AC 长的取值范围是______________. 2、已知：如图，AD 是△ABC 的中线，点 E 在 AD 上，BE＝AC，延长 BE 交于 AC 于 F，求证：AF＝EF．
3、如图，在△ABC 中，AB＞AC，E 为 BC 边的中点，AD 为∠BAC 的平分线，过 E 作 AD 的平行线，交 AB 于 F，交 CA 的延长线于 G．求证：BF＝CG．
（2）如图 2，△ABC 为一般三角形时线段 AM 与 ED 的关系是_________．试证明你的结论；（3）如图 3，若以△ABC 的边 AB、AC 为直角边，向内作等腰直角△ABD 和△ACE，其它条件不变，
试探究线段 AM 与 DE 之间的关系，不要求证明你的结论．
D E
ED
A
A
A
C M
B MC 图1
B
D
E
C
【例 2】如图，△ABC 中， AC<AB ， AD 是中线．求证： DAB<DAC ． A

专题02 中点四大模型(知识解读)(学生版)

专题02中点四大模型（知识解读）【专题说明】线段中点是几何部分一个非常重要的概念，和后面学习的中线，中位线等概念有着密切的联系.在几何证明题中也屡次出现.那么，如果在题中遇到中点你会想到什么？等腰三角形三线合一；直角三角形斜边上的中线等于斜边的一半；还是中位线定理？今天我们重点探究“倍长中线”法以及平行线间夹中点时延长中线交平行等的应用。

【方法技巧】模型1：倍长中线法如图，在△ABC中，AD是BC边上的中线.当题中出现中线时，我们经常根据需要将AD延长，使延长部分和中线相等，这种方法叫做“倍长中线”.如下图：此时，易证△ACD≌EDB，进而得到AC=BE且AC//BE.模型2：平行线夹中点如图，AB//CD，点E是BC的中点.可延长DE交AB于点F.模型3：中位线如图，在△ABC中，点D是AB边的中点.可作另一边AC的中点，构造三角形中位线.如下图所示：由中位线的性质可得，DE//BC且DE=1/2BC.【模型1倍长中线法】【典例1】【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：（1）由已知和作图能得到△ADC≌△EDB的理由是．A．SSS B．SAS C．AAS D．HL（2）求得AD的取值范围是．A．6＜AD＜8B．6≤AD≤8C．1＜AD＜7D．1≤AD≤7【感悟】解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．【问题解决】（3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．求证：AC＝BF．【变式1-1】（1）在△ABC中，AB＝5，AC＝3，求BC边上的中线AD的取值范围．（2）受到（1）启发，请你证明下面的问题：如图，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．求证：BE+CF＞EF.【变式1-2】如图，在△ABC中，已知：点D是BC中点，连接AD并延长到点E，连接BE．（1）请你添加一个条件使△ACD≌△EBD，并给出证明．（2）若AB＝5，AC＝3，求BC边上的中线AD的取值范围．【变式1-3】阅读下面的题目及分析过程，并按要求进行证明．已知：如图，E是BC的中点，点A在DE上，且∠BAE＝∠CDE．求证：AB＝CD．分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等，因此，要证明AB＝CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．现给出如下三种添加辅助线的方法，请任意选择其中两种对原题进行证明．（1）延长DE到F，使得EF＝DE；（2）作CG⊥DE于G，BF⊥DE于F交DE的延长线于F；（3）过点C作CF∥AB交DE的延长线于F．【模型2平行线夹中点】【典例2】如图，已知AB＝12，AB⊥BC，垂足为点B，AB⊥AD，垂足为点A，AD＝5，BC＝10，点E是CD的中点，求AE的长．【变式2-1】如图，AB∥CD，∠BCD＝90°，AB＝1，BC＝4，CD＝3，取AD的中点E，连结BE，则BE＝．【变式2-2】如图，公园有一条“Z”字形道路AB﹣BC﹣CD，其中AB∥CD，在E、M、F处各有一个小石凳，且BE ＝CF，M为BC的中点，连接EM、MF，请问石凳M到石凳E、F的距离ME、MF是否相等？说出你推断的理由．【变式2-3】如图：已知AB∥CD，BC⊥CD，且CD＝2AB＝12，BC＝8，E是AD的中点，①请你用直尺（无刻度）作出一条线段与BE相等；并证明之；②求BE的长．【模型3中位线】【典例3】如图，△ABC中，AD平分∠BAC，E是BC中点，AD⊥BD，AC＝7，AB＝4，则DE的值为（）A．1B．2C．D．【变式3-1】如图，在△ABC中，D，E，F分别是边AB，BC，CA的中点，若△DEF的周长为10，则△ABC的周长为．【变式3-2】如图，等边△ABC的边长是4，D，E分别为AB，AC的中点，延长BC至点F，使，连接CD 和EF．（1）求证：CD＝EF；（2）四边形DEFC的面积为．【变式3-3】如图，在平行四边形ABCD中，点E在BC的延长线上，CE＝DE＝2BC．CD的中点为F，DE的中点为G，连接AF，FG．（1）求证：四边形AFGD为菱形；（2）连接AG，若BC＝2，，求AG的长．【模型4】【典例4】用三种方法证明：直角三角形斜边上的中线等于斜边的一半．已知：如图，∠BCA＝90°，AD＝DB．求证：CD＝AB．【变式4-1】直角三角形斜边上的中线长为10，则该斜边长为（）A．5B．10C．15D．20【变式4-2】如图，点E是△ABC内一点，∠AEB＝90°，D是边AB的中点，延长线段DE交边BC于点F，点F 是边BC的中点．若AB＝6，EF＝1，则线段AC的长为（）A．7B．C．8D．9【变式4-3】用两种方法证明“直角三角形斜边上的中线等于斜边的一半”．已知：如图1，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线．求证：CD＝AB．证法1：如图2，在∠ACB的内部作∠BCE＝∠B，CE与AB相交于点E．∵∠BCE＝∠B，∴．∵∠BCE+∠ACE＝90°，∴∠B+∠ACE＝90°．又∵，∴∠ACE＝∠A．∴EA＝EC．∴EA＝EB＝EC，即CE是斜边AB上的中线，且CE＝AB．又∵CD是斜边AB上的中线，即CD与CE重合，∴CD＝AB．请把证法1补充完整，并用不同的方法完成证法2．。

倍长中线巧解题

B ADBCE图2-1倍长中线巧解题一、证明线段不等例1 如图1，在△ABC 中，AD 为BC 边上的中线．求证：AB +AC ＞2AD变式1：如图，点D 、E 三等分△ABC 的BC 边，求证：二、证明线段相等例2 如图2，在△ABC 中，AB ＞AC ，E 为BC 边的中点，AD 为∠BAC 的平分线，过，交CA 的延长线于G ．求证：BF =CG ．AB 上取异于D 的点C ，分别以AC 、BC 为斜边在AB 同侧作等腰直角三角形ACE 与BCF ，连结DE 、DF 、EF ，求证：△DEF 为等腰三角形三、求线段的长四、证明线段倍分例4 如图4，CB ，CD 分别是钝角△AEC 和锐角△ABC 的中线，且AC =AB ．求“截长补短法”在几何证明问题中的运用例1. 已知，如图1-1，在四边形ABCD 中，BC ＞AB ，AD =DC ，BD 平分∠ABC .求证：∠BAD +∠BCD =180°.例2. 如图2-1，AD ∥BC ，点E 在线段AB 上，∠ADE =∠CDE ，∠DCE =∠ECB .求证：CD =AD +BC .例3. 已知，如图3-1，∠1=∠2，P 为BN 上一点，且PD ⊥BC 于点D ，AB +BC =2BD . 求证：∠BAP +∠BCP =180°.B ABCD图1-1ABCDP12N图3-1BF例4. 已知：如图4-1，在△ABC 中，∠C ＝2∠B ，∠1＝∠2.求证：AB =AC +CD .练习：1、已知，如右图：Rt △ABC 中，∠C=90°，AC=BC ， AD 平分∠BAC.求证：AC+ CD =AB2、已知：如右图，AC ‖BD ，EA 、EB 分别平分∠CAB 和 ∠DBA ，CD 过E 点，求证：AB=AC+BD ．3.已知：如下左图，D 是EF 的中点,BE=CF,求证：△ABC 是等腰三角形。

4.已知：如下中图，AD 平分∠BAC,AB ⊥BD,∠BAC=2∠C,求证:AC=2AB5.已知：如下右图，∠BED =∠CAD,D 是BC 的中点,求证:BE=ACBDCB A 12图4-1ACDEBABDC。

【辅助线方法总结】倍长中线，不止是倍长这么简单

【辅助线方法总结】倍长中线，不止是倍长这么简单必须可以！基本图形：△ABC内有一条中线AD基本操作：延长中线AD到E，使得DE=AD，连接EC（或BE）基本结论：△ADB≌△EDC这是倍长中线的基本模型。

当题目中出现中点或者中线时，就需要考虑倍长中线这个方法。

而实际操作中好像看到中点的第一个方法并不是倍长中线，可能是三线合一或者直角三角形斜边中线更多一些。

那什么时候要考虑倍长中线呢？这就需要了解倍长中线到底做了什么。

来看一道题题目中有“点D是BC中点”，这个条件该怎么用？图中没有等腰或者直角三角形，那么中点的用法也就是倍长中线了。

而有同学会说：D是中点，但没有三角形，构不成中线，怎么用倍长中线呢？（也是因为这一点，不少孩子不认为这个题需要倍长中线，或者不知道该如何倍长）仔细观察一下倍长中线的基本操作，就会发现，是否有三角形并没有啥影响。

我们回头看方法基本操作，会发现整个过程中△ABC的边AC没有任何用处，如果去掉这个边，从题目到结论没有任何影响（只是题目叙述会麻烦一些）。

现在再来看这个题，是不是倍长ED或者AD，都能解决问题了？所以想真正掌握一个方法，需要对其模型做深入研究。

倍长中线深入理解图形结论：其实这个图形的结论并不是全等，而是旋转。

返回文章第一个图，观察倍长中线后，原图发生了什么变化可以看到△ABD绕着点D旋转了180°，把AB挪到了CE，同时把∠BAD和∠ABD同时转到了对面。

因此在做题时发现需要将边旋转，或者角需要挪位置，而题目中恰好有个中点，这时候考虑倍长中线才是最合适的。

再进一步，连接BE，这时四边形ABEC就是平行四边形（对角线互相平分）。

此时有关平行四边形的性质及常用方法，就可以在图中实现了。

通过上面的介绍，倍长中线这个方法是不是更清晰了。

真正学会一个方法，并不是知道个名字，知道辅助线是咋做的就可以了，而是要深入的研究，搞清楚方法究竟做了哪些。

这时再看定理或者方法，就不会出现“需要别人提醒辅助线该怎么做”了。

数学方法之“倍长中线法”和“折半中点法”

“倍长中线法”和“折半中点法”在几何证明题中，若要证明一条线段是另一条线段的2倍或者一半时，通常使用的方法有“倍长中线法”和“折半中点法”。

“倍长中线法”就是加倍延长底边的中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等；“折半中点法”正好相反，它是取底边的中点，然后也是需要连接相应的顶点，则对应角对应边都对应相等。

这两种方法主要用于构造全等三角形或者证明边之间的关系，常用到的知识点是“全等三角形”、“中位线定理”、“等腰三角形”等。

下面就这两种方法我举个例题展示一下：例如图所示，已知AD是△ABC的中线，点E在BC的延长线上，CE=AB，∠BAC= ∠BCA。

求证：AE=2AD分析1：“倍长中线法”是解决这类问题的有效途径之一。

延长AD至F使DF=AD，连接CF，先证△FCD≌△ABD，再证∠ACF=∠ACE，再证△ACF≌△ACE即可。

证明：延长AD至F使DF=AD，连接CF。

在⊿ABD和⊿FCD中AD=FD∠ADB=∠FDCBD=DC∴⊿ABD≌⊿FCD (SAS)∴AB=FC，∠B=∠DCF∵CE=AB，∠BAC=∠BCA，∠ACE=∠BAC+∠B ∴CF=CE，∠ACE=∠BCA+∠DCF=∠ACF在⊿ACF和⊿ACE中AC=AC∠ACE=∠ACFCF=CE∴⊿ACF≌⊿ACE (SAS)∴AE=AF=2AD即AE=2ADF分析2：“折半中点法”也是解决这类问题的有效途径之一。

取AE 中点G ，连接CG ，再运用“等边对等角” 、“中位线定理”可直接证出△ABD ≌△ECG 或△ACD ≌△ACG 得出结论。

证明：取AE 中点G ，连接CG 。

∵∠BAC=∠BCA∴AB=BC又∵AB=CE∴BC=CE又∵AG=EG∴CG ∥21AB ∴∠B=∠ECG 又∵BD=CD=21BC=21AB ∴CG=BD在△ABD 和△ECG 中AB=EC∠B=∠ECGBD=CG∴△ABD ≌△ECG （SAS ）∴AD=EG=21AE 即AE=2AD注：证明△ACD ≌△ACG 这个思路同学们可以自己思考下，我就不再赘述。