2011年衢州中考数学试题

合集下载

2011年中考数学试题分类9 一元二次方程

B． ( x 2)2 9
C． ( x 1)2 6
D． ( x 2)2 9
15. （2011 江苏苏州，8,3 分）下列四个结论中，正确的是
1 x 1 B.方程 x＋ x 1 C.方程 x＋ x 1 D.方程 x＋ x
A.方程 x＋【答案】D
=－2 有两个不相等的实数根 =1 有两个不相等的实数根 =2 有两个不相等的实数根 =a（其中 a 为常数，且|a|>2）有两个不相等的实数根
2பைடு நூலகம்
2
【答案】1 11. （2011 四川宜宾,12,3 分）已知一元二次方程 x 2 6 x 5 0 的两根为 a、 b，则值是____________．【答案】
1 1 的 a b
6 5
12. （2011 四川宜宾,15,3 分）某城市居民最低生活保障在 2009 年是 240 元，经过连续两年的增加，到 2011 年提高到 345.6 元，则该城市两年来最低生活保障的平均年增长率是 _______________．【答案】20% 13. （2011 江苏淮安，13，3 分）一元二次方程 x -4=0 的解是【答案】±2 14. （2011 上海，9，4 分）如果关于 x 的方程 x 2 x m 0 （m 为常数）有两个相等实
2 2 m，b 均为常数，a≠0），则方程 a( x m 2) b 0 的解是
。
【答案】x1=－4，x2=－1 8. （2011 广东株洲，13，3 分）孔明同学在解一元二次方程 x -3x+c=0 时，正确解得 x1=1， x2=2，则 c 的值为【答案】2 ．
2
9. （2011 江苏苏州，15,3 分）已知 a、b 是一元二次方程 x －2x－1=0 的两个实数根，则代数式（a－b）（a＋b－2）＋ab 的值等于________. 【答案】-1 10．（201 1 江苏宿迁,16,3 分）如图，邻边不等的矩形花圃 ABCD，它的一边 AD 利用已有的．．围墙，另外三边所围的栅栏的总长度是 6m．若矩形的面积为 4m ，则 AB 的长度是 ▲ m （可利用的围墙长度超过 6m）．

2011浙江金华丽水衢州中考数学(word)

书法绘画舞蹈其他第6题图浙江省2011年初中毕业生学业考试(金华衢州卷)数学试题卷考生须知：1.全卷共三大题,24小题，满分为120分.考试时间为120分钟,本次考试采用开卷形式.2.全卷分为卷Ⅰ（选择题）和卷Ⅱ（非选择题）两部分，全部在答题纸上作答.卷Ⅰ的答案必须用2B 铅笔填涂；卷Ⅱ的答案必须用黑色字迹钢笔或签字笔写在答题纸相应位置上.3.请用黑色字迹钢笔或签字笔在答题纸上先填写姓名和准考证号.4.作图时,可先使用2B 铅笔,确定后必须使用黑色字迹的钢笔或签字笔描黑. 参考公式：方差公式()()()[]2222121x x x x x xnS n -++-+-=.卷 Ⅰ说明：本卷共有1大题，10小题，共30分.请用2B 铅笔在答题纸上将你认为正确的选项对应的小方框涂黑、涂满.一、选择题(本题有10小题,每小题3分,共30分) 1.下列各组数中，互为相反数的是（ ▲ )A ．2和-2B ．-2和12C ．－2和12-D ．12和22.如图是六个棱长为1的立方块组成的一个几何体，其俯视图的面积是（ ▲ )A ．6B .5C .4D .3 3.下列各式能用完全平方公式进行分解因式的是（ ▲ )A ．x 2+ 1B ．x 2+2x －1C ．x 2＋x ＋1D ．x 2＋4x ＋44.有四包真空小包装火腿，每包以标准克数（450克）为基准，超过的克数记作正数，不足的克数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的是（ ▲ )A .＋2B .-3C .＋3D .+45.如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20o ，那么∠2的度数是（ ▲ )A .30oB .25oC .20oD .15o6.学校为了解七年级学生参加课外兴趣小组活动情况，随机调查了40名学生，将结果绘制成了如图所示的频数分布直方图，则参加绘画兴趣小组的频率是（ ▲ ) A ．0.1 B ．0.15C ．0.25D ．0.3 7.计算111aa a ---的结果为（ ▲ )A ．11a a +- B ．1a a -- C ．－1 D ．2第2题图第5题图8.不等式组211420x x ->⎧⎨-⎩，≤的解在数轴上表示为（ ▲ )9.如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为（ ▲ )A.600m B .500mC .400mD .300m10.如图，在平面直角坐标系中，过格点A ，B ，C 作一圆弧，点B 与下列格点的连线中，能够与该圆弧相切的是（ ▲ )A .点（0，3）B . 点（2，3）C .点（5，1）D . 点（6，1）卷 Ⅱ说明：本卷共有2大题，14小题，共90分.请用黑色字迹钢笔或签字笔将答案写在答题纸的相应位置上.二、填空题 (本题有6小题,每小题4分,共24分) 11.“x 与y 的差”用代数式可以表示为 ▲ .12.已知三角形的两边长为4，8，则第三边的长度可以是 ▲ (写出一个即可). 13.在中国旅游日（5月19日），我市旅游部门对2011年第一季度游客在金华的旅游时间作抽样调查，统计如下：的扇形圆心角的度数为 ▲ .14.从-2，-1，2这三个数中任取两个不同的数作为点的坐标，该点在第四象限的概率是 ▲ .15.如图,在□ABCD 中，AB =3，AD =4，∠ABC =60°，过BC 的中点E 作EF ⊥AB ，垂足为点F ，与DC 的延长线相交于点H ，则△DEF 的面积是 ▲ .16.如图，将一块直角三角板OAB 放在平面直角坐标系中， B (2，0)，∠AOB =60°，点A 在第一象限，过点A 的双曲线为k y x=.在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ´B ´.（1）当点O ´与点A 重合时，点P 的坐标是 ▲ ；（2）设P (t ，0)，当O ´B ´与双曲线有交点时，t 的取值范围是 ▲ .第10题图1 02 C1 02D1 02 A1 02BOB A B PO ´ 第15题图D三、解答题 (本题有8小题,共66分,各小题都必须写出解答过程) 17.(本题6分)计算:()15cos45π---+4.18.(本题6分)已知213x -=，求代数式2(3)2(3+)7x x x -+-的值．19.(本题6分)生活经验表明，靠墙摆放的梯子，当50°≤α≤70°时（α为梯子与地面所成的角），能够使人安全攀爬. 现在有一长为6米的梯子AB , 试求能够使人安全攀爬时，梯子的顶端能达到的最大高度AC .（结果保留两个有效数字，sin70°≈0.94，sin50°≈0.77， cos70°≈0.34，cos50°≈0.64）20.(本题8分)王大伯几年前承包了甲、乙两片荒山，各栽100棵杨梅树，成活98%．现已挂果，经济效益初步显现，为了分析收成情况，他分别从两山上随意各采摘了4棵树上的杨梅，每棵的产量如折线统计图所示.（1）分别计算甲、乙两山样本的平均数，并估算出甲、乙两山杨梅的产量总和；（2）试通过计算说明，哪个山上的杨梅产量较稳定？21.(本题8分)如图，射线PG 平分∠EPF ，O 为射线PG 上一点，以O 为圆心，10为半径作⊙O ，分别与∠EPF 的两边相交于A 、B 和C 、D ，连结OA ，此时有OA//PE ．（1）求证：AP =AO ；（2）若tan ∠OPB =12，求弦AB 的长；（3）若以图中已标明的点（即P 、A 、B 、C 、D 、O ）构造四边形，则能构成菱形的四个点为 ▲ ，能构成等腰梯形的四个点为 ▲ 或 ▲ 或第21题图第19题图 C杨梅树编号第20题图22.(本题10分)某班师生组织植树活动，上午8时从学校出发，到植树地点植树后原路返校，如图为师生离校路程s与时间t之间的图象.请回答下列问题：（1）求师生何时回到学校？（2）如果运送树苗的三轮车比师生迟半小时出发，与师生同路匀速前进，早半小时到达植树地点，请在图中，画出该三轮车运送树苗时，离校路程s与时间t之间的图象，并结合图象直接写出三轮车追上师生时，离学校的路程；（3）如果师生骑自行车上午8时出发，到植树地点后，植树需2小时，要求14时前返回到．．．．学校，往返平均速度分别为每时10km、8km.现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km，试通过计算说明哪几个植树点符合要求.23.(本题10分)在平面直角坐标系中，如图1，将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上, 设抛物线2y ax bx c=++（a＜0）过矩形顶点B、C.（1）当n=1时，如果a=-1，试求b的值；（2）当n=2时，如图2，在矩形OABC上方作一边长为1的正方形EFMN，使EF在线段CB上，如果M，N两点也在抛物线上，求出此时抛物线的解析式；（3）将矩形OABC绕点O顺时针旋转，使得点B落到x轴的正半轴上，如果该抛物线同时经过原点O.①试求当n=3时a的值；②直接写出a关于n的关系式．24.(本题12分)如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结（1）当∠AOB=30°时，求弧AB的长度；（2）当DE=8时，求线段EF的长；（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似，若存在，请求出此时点E的坐标；若不存在，请说明理由．第22题图时)第24题图浙江省2011年初中毕业生学业考试(金华卷)数学试卷参考答案及评分标准一、二、11．x －y 12.答案不惟一，在4＜x ＜12之间的数都可 13. 144° 14. 1315. 32 16. （1）（4，0）；（2）4≤t ≤-t ≤－4（各2分）三、解答题（本题有8小题，共66分） 17.(本题6分)()15cos45π---+4=111422-⨯-+⨯（写对一个2分，两个3分，三个4分，四个5分）= ……1分 18.(本题6分)由2x -1=3得x =2, ……2分又2(3)2(3+)7x x x -+-=2269627x x x x -+++-=232x +，……2分 ∴当x =2时，原式=14. …2分 19.(本题6分)当α=70°时，梯子顶端达到最大高度, ……1分 ∵sin α=ABAC , ……2分∴ AC = sin70°×6=0.94×6=5.64 ……2分≈5.6(米)答：人安全攀爬梯子时，梯子的顶端达到的最大高度约5.6米．……1分 20.(本题8分)（1）40=甲x (千克)， ……1分40=乙x (千克)， ……1分总产量为78402%9810040=⨯⨯⨯（千克）；……2分（2）()()()()[]3840344040403640504122222=-+-+-+-=甲S(千克2)， ……1分()()()()[]2440364048404040364122222=-+-+-+-=乙S(千克2)， ……1分∴22S S 乙甲＞. ……1分答：乙山上的杨梅产量较稳定． ……1分21.（本题8分）（1）∵PG 平分∠EPF ， ∴∠DPO =∠BPO ， ∵OA//PE ，∴∠DPO =∠POA ，∴∠BPO =∠POA ，∴PA =OA ； ……2分（2）过点O 作OH ⊥AB 于点H ，则AH =HB =12AB ， (1)∵ tan ∠OPB =12O H P H=，∴PH =2OH ， ……1分设OH =x ，则PH =2x ，由（1）可知PA =OA = 10 ，∴AH =PH －P A =2x －10，∵222AH OH OA +=， ∴222(210)10x x -+=，……1分解得10x =（不合题意，舍去），28x =，∴AH =6， ∴AB=2AH=12； ……1分（3）P 、A 、O 、C ；A 、B 、D 、C 或 P 、A 、O 、D 或P 、C 、O 、B .……2分(写对1个、2个、3个得1分，写对4个得2分) 22.(本题10分)（1）设师生返校时的函数解析式为b kt s +=，把（12，8）、（13，3）代入得，⎩⎨⎧+=+=b k b k 133,128 解得：⎩⎨⎧=-=68,5b k ∴685+-=t s ，当0=s 时，t =13.6 ， ∴师生在13.6时回到学校；……3分（2）图象正确２分.由图象得，当三轮车追上师生时，离学校4km ； ……2分（3）设符合学校要求的植树点与学校的路程为x （km ），由题意得：88210+++x x ＜14, 解得：x ＜9717，答：A 、B 、C 植树点符合学校的要求．……3分 23.(本题10分)（1）由题意可知，抛物线对称轴为直线x =12，∴122b a-=,得b = 1； ……2分（2）设所求抛物线解析式为21y ax bx =++，由对称性可知抛物线经过点B （2，1）和点M （12，2）∴1421112 1.42a b a b =++⎧⎪⎨=++⎪⎩，解得4,38.3a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线解析式为248133y x x =-++；……4分（3）①当n =3时，OC=1，BC =3，设所求抛物线解析式为2y ax bx =+，8.5 9.5 O 时)过C 作CD ⊥OB 于点D ，则Rt △OCD ∽Rt △CBD ， ∴13O D O C C DB C==,设OD =t ，则CD =3t ， ∵222OD CD OC +=， ∴222(3)1t t +=，∴10t ==,∴C（10，）, 又 B0），∴把B 、C 坐标代入抛物线解析式，得 0101.1010a a ⎧=+⎪=+，解得:a =3-； ……2分②a n=-. ……2分24.(本题12分) （1）连结BC ,∵A （10，0）, ∴OA =10 ,CA =5, ∵∠AOB =30°,∴∠ACB =2∠AOB =60°,∴弧AB 的长=35180560ππ=⨯⨯; ……4分（2）连结OD,∵OA 是⊙C 直径, ∴∠OBA =90°, 又∵AB =BD,∴OB 是AD 的垂直平分线, ∴OD =OA =10, 在Rt △ODE 中， OE ==-22DE OD681022=-,∴AE =AO －OE=10-6=4,由 ∠AOB =∠ADE =90°-∠OAB ，∠OEF =∠DEA ，得△OEF ∽△DEA, ∴OEEF DEAE =,即684EF =，∴EF =3；……4分（3）设OE =x ，①当交点E 在O ，C 之间时，由以点E 、C 、F 为顶点的三角形与△AOB 相似，有∠ECF =∠BOA 或∠ECF =∠OAB ，当∠ECF =∠BOA 时，此时△OCF 为等腰三角形，点E 为OC中点，即OE =25，∴E 1（25，0）；当∠ECF =∠OAB 时，有CE =5-x , AE =10-x ，∴CF ∥AB ,有CF =12A B ,∵△ECF ∽△EAD, ∴ADCF AECE =,即51104x x-=-,解得：310=x ,∴E 2（310，0）;②当交点E 在点C 的右侧时，∵∠ECF ＞∠BOA ，∴要使△ECF 与△BAO 相似，只能使∠ECF =∠BAO ，连结BE ，∵BE 为Rt △ADE 斜边上的中线， ∴BE =AB =BD, ∴∠BEA =∠BAO, ∴∠BEA =∠ECF, ∴CF ∥BE, ∴OE OC BECF =,∵∠ECF =∠BAO , ∠FEC =∠DEA =Rt ∠， ∴△CEF ∽△AED, ∴C F C E A D A E=,而AD =2BE , ∴2O C C E O EA E=,即55210x xx-=-, 解得417551+=x , 417552-=x ＜0（舍去），∴E 3（41755+，0）;③当交点E 在点O 的左侧时，∵∠BOA =∠EOF ＞∠ECF .∴要使△ECF 与△BAO 相似，只能使∠ECF =∠BAO 连结BE ，得BE =AD 21=AB ，∠BEA =∠BAO∴∠ECF =∠BEA, ∴CF ∥BE, ∴OEOC BECF =,又∵∠ECF =∠BAO , ∠FEC =∠DEA =Rt ∠，∴△CEF ∽△AED, ∴ADCF AE CE =，而AD =2BE , ∴2O C C E O EA E =,∴5+5210+x xx=, 解得417551+-=x , 417552--=x ＜0（舍去）,∵点E 在x 轴负半轴上, ∴E 4（41755-，0）,综上所述：存在以点E 、C 、F 为顶点的三角形与△AOB 相似,此时点E 坐标为： 1E （25，0）、2E （310，0）、3E （41755+，0）、4E （41755-，0）．……4分。

2011年中考数学试题精选汇编《矩形、菱形、正方形》

2011年中考数学试题精选汇编《矩形、菱形、正方形》一、选择题1. （2011浙江省舟山，10，3分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（）（A ）48cm（B ）36cm （C ）24cm （D ）18cm【答案】A 2. （2011山东德州8,3分）图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n 个图形的周长是（A ）2n （B ）4n （C ）12n + （D ）22n +【答案】C3. （2011山东泰安，17 ，3分）如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2，则S 1+S 2的值为A.17B.17C.18D.19图1图2 图3……（第10题） FA B C D H E① ②③ ④ ⑤4. （2011山东泰安，19 ，3分）如图，点O是矩形ABCD的中心，E是AB上的点，沿CE 折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为A.23B. 332C. 3D.6【答案】A5. （2011浙江杭州，10，3）在矩形ABCD中，有一个菱形B F D E(点E，F分别在线段AB，CD上)，记它们的面积分别为ABCD BFDES S和．现给出下列命题：（）①若ABCDBFDESStan EDF∠=．②若2,DE BD EF=∙则2DF AD=．则:A．①是真命题，②是真命题 B．①是真命题，②是假命题C．①是假命题，②是真命题 D，①是假命题，②是假命题【答案】A6. （2011浙江衢州，1,3分）衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF AG、分别架在墙体的点B、点C处，且AB AC=,侧面四边形BDEC为矩形，若测得100FAG∠=︒，则FBD∠=( )A. 35°B. 40°C. 55°D. 70°【答案】C7. （2011浙江温州，6，4分）如图，在矩形ABCD中，对角线AC，BD交于点O．已知∠AOB= 60°，AC＝16，则图中长度为8的线段有( )A．2条B．4条C．5条D．6条8. 2011四川重庆，10，4分）如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( )A ．1B ．2C ．3D ．4【答案】C9. （2011浙江省嘉兴，10，4分）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（）（A ）48cm（B ）36cm （C ）24cm （D ）18cm【答案】A 10．（2011台湾台北，29）如图(十二)，长方形ABCD 中，E 为BC 中点，作AEC 的角平分线交AD 于F 点。

2011年全国各地中考数学真题分类汇编：第23章等腰三角形

第23章等腰三角形一、选择题1. （2011浙江省舟山，7，3分）如图，边长为4的等边△ABC 中，DE 为中位线，则四边形BCED 的面积为（）（A ）32（B ）33 （C ）34 （D ）36【答案】B2. （2011四川南充市，10，3分）如图，⊿ABC 和⊿CDE 均为等腰直角三角形，点B,C,D 在一条直线上，点M 是AE 的中点，下列结论：①tan ∠AEC=CDBC ;②S ⊿ABC +S ⊿CDE ≧S ⊿ACE ;③BM ⊥DM;④BM=DM.正确结论的个数是（）（A ）1个（B ）2个（C ）3个（D ）4个MEDCBA【答案】D3. （2011浙江义乌，10，3分）如图，△ABC 和△ADE 都是等腰直角三角形，∠BAC =∠DAE =90°，四边形ACDE 是平行四边形，连结CE 交AD 于点F ，连结BD 交 CE 于点G ，连结BE . 下列结论中：① CE =BD ； ② △ADC 是等腰直角三角形； ③ ∠ADB =∠AEB ； ④ CD ·AE =EF ·CG ；一定正确的结论有ABCDEF G （第7题）AB CDEA．1个B．2个C．3个D．4个【答案】D4. （2011台湾全区，30）如图(十三)，ΔABC中，以B为圆心，BC长为半径画弧，分别交AC、AB于D、E两点，并连接BD、DE．若∠A=30∘，AB＝AC，则∠BDE的度数为何？A．45 B．52．5 C．67．5 D．75【答案】Ｃ5. （2011台湾全区，34）如图(十六)，有两全等的正三角形ABC、DEF，且D、A分别为△ABC、△DEF的重心．固定D点，将△DEF逆时针旋转，使得A落在DE上，如图(十七)所示．求图(十六)与图(十七)中，两个三角形重迭区域的面积比为何？A．2：1 B．3：2 C．4：3 D．5：4【答案】Ｃ6. （2011山东济宁，3，3分）如果一个等腰三角形的两边长分别是5cm和6cm，那么此三角形的周长是A．15cm B．16cmC．17cm D．16cm或17cm【答案】D7. （2011四川凉山州，8，4分）如图，在ABC△中，13AB AC==，10BC=，点D 为BC的中点，D E D E AB⊥，垂足为点E，则D E等于（）A．1013B．1513C．6013D．7513【答案】C 8.二、填空题1. （2011山东滨州，15，4分）边长为6cm 的等边三角形中，其一边上高的长度为________.【答案】2. （2011山东烟台，14,4分）等腰三角形的周长为14，其一边长为4，那么，它的底边为 . 【答案】4或63. （2011浙江杭州，16，4）在等腰Rt △ABC 中，∠C =90°，AC ＝1，过点C 作直线l ∥AB ，F 是l 上的一点，且AB ＝AF ，则点F 到直线BC 的距离为．224. （2011浙江台州，14,5分）已知等边△ABC 中，点D,E 分别在边AB,BC 上，把△BDE 沿直线DE 翻折，使点B 落在点B ˊ处，DB ˊ,EB ˊ分别交边AC 于点F ，G ，若∠ADF=80º ，则∠EGC 的度数为【答案】80º5. （2011浙江省嘉兴，14，5分）如图，在△ABC 中，AB =AC ，︒=∠40A ，则△ABC 的外角∠BCD ＝ °．【答案】1106. （2011湖南邵阳，11，3分）如图（四）所示，在△ABC 中，AB=AC ，∠B=50°，则∠A=_______。

2011年浙江省衢州市中考数学试卷

2011年浙江省衢州市中考数学试卷一、选择题（本大题共有10小题，每小题3分，共30分，请选出一个符合题意的正确的选项填涂在答题纸上，不选、多选、错选均不给分）1．（3分）2-的相反数为( )A ． 2B ．12C ．2-D ．12- 2．（3分）衢州市“十二五”规划纲要指出，力争到2015年，全市农民人均年纯收入超13000元，数字13000用科学记数法可以表示为( )A ．31310⨯B ．41.310⨯C ．40.1310⨯D ．213010⨯3．（3分）在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）:44，45，42，48，46，43，47，45．则这组数据的极差为( )A ．2B ．4C ．6D ．84．（3分）如图，下列几何体的俯视图是右面所示图形的是( )A ．B ．C ．D ．5．（3分）衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF 、AG 分别架在墙体的点B 、点C 处，且AB AC =，侧面四边形BDEC 为矩形．若测得110FAG ∠=︒，则(FBD ∠= )A ．35︒B ．40︒C ．55︒D ．70︒6．（3分）如图，OP 平分MON ∠，PA ON ⊥于点A ，点Q 是射线OM 上的一个动点，若2PA =，则PQ 的最小值为( )A ．1B ．2C ．3D ．47．（3分）5月19日为中国旅游日，衢州推出“读万卷书，行万里路，游衢州景”的主题系列旅游惠民活动，市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点；下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩，则王先生恰好上午选中孔氏南宗家庙，下午选中江郎山这两个地的概率是( )A ．19B ．13C ．23D ．298．（3分）一个圆形人工湖如图所示，弦AB 是湖上的一座桥，已知桥AB 长100m ，测得圆周角45ACB ∠=︒，则这个人工湖的直径AD 为( )A ．B ．C ．D ．9．（3分）小亮同学骑车上学，路上要经过平路、下坡、上坡和平路（如图），若小亮上坡、平路、下坡的速度分别为1v ，2v ，3v ，123v v v <<，则小亮同学骑车上学时，离家的路程s 与所用时间t 的函数关系图象可能是( )A ．B ．C ．D ．10．（3分）如图，一张半径为1的圆形纸片在边长为(3)a a …的正方形内任意移动，则该正方形内，这张圆形纸片“不能接触到的部分”的面积是( )A ．2a π-B ．2(4)a π-C ．πD ．4π-二、填空题（本大题共有6小题，每小题4分，共24分，请将答案填在答题纸上）11．（4分）方程220x x -=的解为．12．（4分）如图，直尺一边AB 与量角器的零刻度线CD 平行，若量角器的一条刻度线OF 的读数为70︒，OF 与AB 交于点E ，那么AEF ∠= ．13．（4分）在一自助夏令营活动中，小明同学从营地A 出发，要到A 地的北偏东60︒方向的C 处，他先沿正东方向走了200m 到达B 地，再沿北偏东30︒方向走，恰能到达目的地C （如图），那么，由此可知，B 、C 两地相距 m ．14．（4分）下列材料来自2006年5月衢州有关媒体的真实报道：有关部门进行民众安全感满意度调查，方法是：在全市内采用等距抽样，抽取32个小区，共960户，每户抽一名年满16周岁并能清楚表达意见的人，同时，对比前一年的调查结果，得到统计图如下：写出2005年民众安全感满意度的众数选项是；该统计图存在一个明显的错误是．15．（4分）在直角坐标系中，有如图所示的Rt ABO ∆，AB x ⊥轴于点B ，斜边10AO =，3sin 5AOB ∠=，反比例函数(0)k y k x=>的图象经过AO 的中点C ，且与AB 交于点D ，则点D 的坐标为．16．（4分）木工师傅可以用角尺测量并计算出圆的半径r ，用角尺的较短边紧靠O ，并使较长边与O 相切于点C ，假设角尺的较长边足够长，角尺的顶点为B ，较短边8AB cm =，若读得BC 长为acm ，则用含a 的代数式表示r 为．三、解答题（本大题共有8小题，共66分，请将答案写在答题纸上，务必写出解答过程）17．（8分）（1）计算：0|2|(3)2cos45π---+︒；（2）化简：3a b a b a b a b-++--． 18．（6分）解不等式113x x +-…，并把解在数轴上表示出来．19．（6分）有足够多的长方形和正方形卡片，如下图：（1）如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．这个长方形的代数意义是．（2）小明想用类似方法解释多项式乘法22(3)(2)273a b a b a ab b ++=++，那么需用2号卡片张，3号卡片张．20．（6分）研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，放回盒中，再继续．活动结果：摸球实验活动一共做了50次，统计结果如下表：推测计算：由上述的摸球实验可推算：（1）盒中红球、黄球各占总球数的百分比分别是多少？（2）盒中有红球多少个？21．（8分）某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系，每盆植入3株时，平均单株盈利3元，以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应该植多少株？小明的解法如下：解：设每盆花苗增加x 株，则每盆花苗有(3)x +株，平均单株盈利为(30.5)x -元，由题意得(3)(30.5)10x x +-=，化简，整理得：2320x x -+=解这个方程，得：11x =，22x =，答：要使每盆的盈利达到10元，每盆应该植入4株或5株．（1）本题涉及的主要数量有每盆花苗株数，平均单株盈利，每盆花苗的盈利等，请写出两个不同的等量关系：．（2）请用一种与小明不相同的方法求解上述问题．22．（10分）如图，ABC ∆中，AD 是边BC 上的中线，过点A 作//AE BC ，过点D 作//DE AB ，DE 与AC 、AE 分别交于点O 、点E ，连接EC ．（1）求证：AD EC =；（2）当90BAC ∠=︒时，求证：四边形ADCE 是菱形．23．（10分）ABC ∆是一张等腰直角三角形纸板，90C ∠=︒，2AC BC ==，（1）要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1)，比较甲、乙两种剪法，哪种剪法所得的正方形面积大？请说明理由．（2）图1中甲种剪法称为第1次剪取，记所得正方形面积为1s ；按照甲种剪法，在余下的ADE ∆和BDF ∆中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为2s （如图2)，则2s = ；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为3s ，继续操作下去⋯，则第10次剪取时，10s = ；（3）求第10次剪取后，余下的所有小三角形的面积之和．24．（12分）已知两直线1l ，2l 分别经过点(1,0)A ，点(3,0)B -，并且当两直线同时相交于y正半轴的点C 时，恰好有12l l ⊥，经过点A 、B 、C 的抛物线的对称轴与直线1l 交于点K ，如图所示．（1）求点C 的坐标，并求出抛物线的函数解析式；（2）抛物线的对称轴被直线1l ，抛物线，直线2l 和x 轴依次截得三条线段，问这三条线段有何数量关系？请说明理由；（3）当直线2l 绕点C 旋转时，与抛物线的另一个交点为M ，请找出使MCK ∆为等腰三角形的点M ，简述理由，并写出点M 的坐标．2011年浙江省衢州市中考数学试卷参考答案与试题解析一、选择题（本大题共有10小题，每小题3分，共30分，请选出一个符合题意的正确的选项填涂在答题纸上，不选、多选、错选均不给分）1．（3分）2-的相反数为( )A ． 2B ．12C ．2-D ．12- 【解答】解：与2-符号相反的数是 2 ，所以，数2-的相反数为 2 ．故选：A ．2．（3分）衢州市“十二五”规划纲要指出，力争到2015年，全市农民人均年纯收入超13000元，数字13000用科学记数法可以表示为( )A ．31310⨯B ．41.310⨯C ．40.1310⨯D ．213010⨯【解答】解：将13000 用科学记数法表示为41.310⨯．故选：B ．3．（3分）在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）:44，45，42，48，46，43，47，45．则这组数据的极差为( )A ．2B ．4C ．6D ．8【解答】解：数据的最大值为48，最小值为42，∴极差为：48426-=次/分．故选：C ．4．（3分）如图，下列几何体的俯视图是右面所示图形的是( )A ．B ．C ．D ．【解答】解：几何体的俯视图是两圆组成，∴只有圆台才符合要求．故选：A ．5．（3分）衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF 、AG 分别架在墙体的点B 、点C 处，且AB AC =，侧面四边形BDEC 为矩形．若测得110FAG ∠=︒，则(FBD ∠= )A ．35︒B ．40︒C ．55︒D ．70︒【解答】解：在ABC ∆中，AB AC =，110FAG ∠=︒，35ABC ACB ∴∠=∠=︒，又四边形BDEC 为矩形，90DBC ∴∠=︒，180180359055FBD ABC DBC ∴∠=︒-∠-∠=︒-︒-︒=︒．故选：C ．6．（3分）如图，OP 平分MON ∠，PA ON ⊥于点A ，点Q 是射线OM 上的一个动点，若2PA =，则PQ 的最小值为( )A ．1B ．2C ．3D ．4【解答】解：过点P 作PQ OM ⊥，垂足为Q ，则PQ 为最短距离， OP 平分MON ∠，PA ON ⊥，PQ OM ⊥，2PA PQ ∴==，故选：B ．7．（3分）5月19日为中国旅游日，衢州推出“读万卷书，行万里路，游衢州景”的主题系列旅游惠民活动，市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点；下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩，则王先生恰好上午选中孔氏南宗家庙，下午选中江郎山这两个地的概率是()A．19B．13C．23D．29【解答】解：画树状图得：∴一共有9种等可能的结果，王先生恰好上午选中孔氏南宗家庙，下午选中江郎山这两个地的有一种情况，∴王先生恰好上午选中孔氏南宗家庙，下午选中江郎山这两个地的概率是19．故选：A．8．（3分）一个圆形人工湖如图所示，弦AB是湖上的一座桥，已知桥AB长100m，测得圆周角45ACB∠=︒，则这个人工湖的直径AD为()A．B．C．D．【解答】解：连接OB．45 ACB∠=︒，12ACB AOB∠=∠（同弧所对的圆周角是所对的圆心角的一半），90AOB∴∠=︒；在Rt AOB ∆中，(OA OB O =的半径），100AB m =，∴由勾股定理得，AO OB ==，2AD OA ∴==；故选：B ．9．（3分）小亮同学骑车上学，路上要经过平路、下坡、上坡和平路（如图），若小亮上坡、平路、下坡的速度分别为1v ，2v ，3v ，123v v v <<，则小亮同学骑车上学时，离家的路程s 与所用时间t 的函数关系图象可能是( )A ．B ．C ．D ．【解答】解：A 、从图象上看小亮的路程走平路不变是不正确的，故不是．B 、从图象上看小亮走的路程随时间有一段更少了，不正确，故不是．C 、小亮走的路程应随时间的增大而增大，两次平路的两条直线互相平行，此图象符合，故正确．D 、因为平路和上坡路及下坡路的速度不一样，所以不应是一条直线，不正确，故不是．故选：C ．10．（3分）如图，一张半径为1的圆形纸片在边长为(3)a a …的正方形内任意移动，则该正方形内，这张圆形纸片“不能接触到的部分”的面积是( )A ．2a π-B ．2(4)a π-C ．πD ．4π-【解答】解：小正方形的面积是：1；当圆运动到正方形的一个角上时，形成扇形BAO ，它的面积是：4π．则这张圆形纸片“不能接触到的部分”的面积是4(1)44ππ-=-．故选：D ．二、填空题（本大题共有6小题，每小题4分，共24分，请将答案填在答题纸上） 11．（4分）方程220x x -=的解为 10x =，22x = ．【解答】解：220x x -=， (2)0x x -=， 0x =或20x -=，10x = 或22x =．故答案为：10x =，22x =．12．（4分）如图，直尺一边AB 与量角器的零刻度线CD 平行，若量角器的一条刻度线OF 的读数为70︒，OF 与AB 交于点E ，那么AEF ∠= 70︒ ．【解答】解：由已知量角器的一条刻度线OF 的读数为70︒，即70COF ∠=︒， //AB CD ，70AEF COF ∴∠=∠=︒，故答案为：70︒．13．（4分）在一自助夏令营活动中，小明同学从营地A出发，要到A地的北偏东60︒方向的C处，他先沿正东方向走了200m到达B地，再沿北偏东30︒方向走，恰能到达目的地C（如图），那么，由此可知，B、C两地相距200m．【解答】解：由已知得：∠=︒+︒=︒，ABC9030120∠=︒-︒=︒，906030BACACB ABC BAC∴∠=︒-∠-∠=︒-︒-︒=︒，1801801203030∴∠=∠，ACB BAC∴==．200BC AB故答案为：200．14．（4分）下列材料来自2006年5月衢州有关媒体的真实报道：有关部门进行民众安全感满意度调查，方法是：在全市内采用等距抽样，抽取32个小区，共960户，每户抽一名年满16周岁并能清楚表达意见的人，同时，对比前一年的调查结果，得到统计图如下：写出2005年民众安全感满意度的众数选项是安全；该统计图存在一个明显的错误是．【解答】解：安全选项小组小长方形的高最高，∴众数为安全选项；统计图存在一个明显的错误是2004年满意度统计选项总和不到100%故答案为：安全；2004年满意度统计选项总和不到100%．15．（4分）在直角坐标系中，有如图所示的Rt ABOAO=，∆，AB x⊥轴于点B，斜边103sin 5AOB ∠=，反比例函数(0)ky k x=>的图象经过AO 的中点C ，且与AB 交于点D ，则点D 的坐标为 3(8,)2．【解答】解：斜边10AO =，3sin 5AOB ∠=， 3sin 105AB AB AOB OA ∴∠===， 6AB ∴=，8OB ∴==，A ∴点坐标为(8,6)，而C 点为OA 的中点， C ∴点坐标为(4,3)，又反比例函数(0)ky k x =>的图象经过点C ，4312k ∴=⨯=，即反比例函数的解析式为12y x=， D 点在反比例函数的图象上，且它的横坐标为8，∴当8x =，12382y ==，所以D 点坐标为3(8,)2．故答案为3(8,)2．16．（4分）木工师傅可以用角尺测量并计算出圆的半径r ，用角尺的较短边紧靠O ，并使较长边与O 相切于点C ，假设角尺的较长边足够长，角尺的顶点为B ，较短边8AB cm =，若读得BC 长为acm ，则用含a 的代数式表示r 为 8r cm …时，r a =； 8r cm >时，21416r a =+ ．【解答】解：①如图所示，8r …时，OA BA ⊥，OC BC ⊥，90B ∠=︒，∴四边形OABC 是矩形，BC AO ∴=， r a ∴=；②当8r >时，如图：连接OC ， BC 与O 相切于点C ， OC BC ∴⊥，连接OA ，过点A 作AD OC ⊥于点D ，则四边形ABCD 是矩形，即AD BC =，CD AB =．在Rt AOD ∆中，222OA OD AD =+，即：222(8)r r a =-+，整理得：21416r a =+．故答案是：8r =时，r a =；当8r >时，21416r a =+．三、解答题（本大题共有8小题，共66分，请将答案写在答题纸上，务必写出解答过程） 17．（8分）（1）计算：0|2|(3)2cos45π---+︒；（2）化简：3a b a ba b a b-++--．【解答】解：（1）原式212=-+1=；（2）原式3a b a ba b-++=-，22a ba b-=-， 2=．18．（6分）解不等式113xx +-…，并把解在数轴上表示出来．【解答】解：去分母，得3(1)1x x -+…，整理，得24x …，2x ∴…．在数轴上表示为：．19．（6分）有足够多的长方形和正方形卡片，如下图：（1）如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．这个长方形的代数意义是 2232()(2)a ab b a b a b ++=++ ．（2）小明想用类似方法解释多项式乘法22(3)(2)273a b a b a ab b ++=++，那么需用2号卡片张，3号卡片张．【解答】解：（1）或2232()(2)a ab b a b a b ++=++，故答案为2232()(2)a ab b a b a b ++=++；（2）1号正方形的面积为2a ，2号正方形的面积为2b ，3号长方形的面积为ab ，所以需用2号卡片3张，3号卡片7张，故答案为：3；7．20．（6分）研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球与黄球，怎样估算不同颜色球的数量？操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球实验，摸球实验的要求：先搅拌均匀，每次摸出一个球，放回盒中，再继续．活动结果：摸球实验活动一共做了50次，统计结果如下表：推测计算：由上述的摸球实验可推算：（1）盒中红球、黄球各占总球数的百分比分别是多少？（2）盒中有红球多少个？【解答】解：（1）由题意可知，50次摸球实验活动中，出现红球20次，黄球30次，∴红球所占百分比为205040%÷=，黄球所占百分比为305060%÷=，答：红球占40%，黄球占60%；（2）由题意可知，50次摸球实验活动中，出现有记号的球4次，∴总球数为4810050÷=， ∴红球数为10040%40⨯=，答：盒中红球有40个．21．（8分）某花圃用花盆培育某种花苗，经过试验发现每盆的盈利与每盆的株数构成一定的关系，每盆植入3株时，平均单株盈利3元，以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元，要使每盆的盈利达到10元，每盆应该植多少株？小明的解法如下：解：设每盆花苗增加x株，则每盆花苗有(3)x+株，平均单株盈利为(30.5)x-元，由题意得(3)(30.5)10x x+-=，化简，整理得：2320x x-+=解这个方程，得：11x=，22x=，答：要使每盆的盈利达到10元，每盆应该植入4株或5株．（1）本题涉及的主要数量有每盆花苗株数，平均单株盈利，每盆花苗的盈利等，请写出两个不同的等量关系：平均单株盈利⨯每盆株数=每盆盈利平均单株盈利30.5=-⨯每盆增加的株数．（2）请用一种与小明不相同的方法求解上述问题．【解答】解：（1）平均单株盈利⨯每盆株数=每盆盈利，平均单株盈利30.5=-⨯每盆增加的株数；（2）解法1（列表法）答：要使每盆的盈利达到10元，每盆应该植入4株或5株；解法2（图象法）如图，纵轴表示平均单株盈利，横轴表示株数，则相应长方形面积表示每盆盈利．从图象可知，每盆植入4株或5株时，相应长方形面积都是10 答：要使每盆的盈利达到10元，每盆应该植入4株或5株．解法3（函数法）解：设每盆花苗增加x ，每盆的盈利为y 元，根据题意得可得：(3)(30.5)y x x =+-，当10y =时，(3)(30.5)10x x +-=，解这个方程得：11x =，22x =，答：要使每盆的盈利达到10元，每盆应该植入4或5株；解法4（列分式方程）解：设每盆花苗增加x 株时，每盆盈利10元，根据题意，得： 1030.53x x =-+，解这个方程得：11x =，22x =，经检验，11x =，22x =都是所列方程的解，答：要使每盆的盈利达到10元，每盆应该植入4或5株．22．（10分）如图，ABC ∆中，AD 是边BC 上的中线，过点A 作//AE BC ，过点D 作//DE AB ，DE 与AC 、AE 分别交于点O 、点E ，连接EC ．（1）求证：AD EC =；（2）当90BAC ∠=︒时，求证：四边形ADCE 是菱形．【解答】证明：（1）//DE AB ，//AE BC ，∴四边形ABDE 是平行四边形，//AE BD ∴，且AE BD =又AD 是BC 边的中线，BD CD ∴=， AE CD ∴=， //AE CD ，∴四边形ADCE 是平行四边形，AD EC ∴=；（2）90BAC ∠=︒，AD 是斜边BC 上的中线， AD BD CD ∴==，又四边形ADCE 是平行四边形，∴四边形ADCE 是菱形．23．（10分）ABC ∆是一张等腰直角三角形纸板，90C ∠=︒，2AC BC ==，（1）要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1)，比较甲、乙两种剪法，哪种剪法所得的正方形面积大？请说明理由．（2）图1中甲种剪法称为第1次剪取，记所得正方形面积为1s ；按照甲种剪法，在余下的ADE ∆和BDF ∆中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为2s （如图2)，则2s =12；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为3s ，继续操作下去⋯，则第10次剪取时，10s = ；（3）求第10次剪取后，余下的所有小三角形的面积之和．【解答】解：（1）解法1：如图甲，由题意，得AE DE EC ==，即1EC =，211CFDE S ==正方形如图乙，设MN x =，则由题意，得AM MQ PN NB MN x =====，∴3x =，解得3x =∴289PNMQ S ==正方形又819>∴甲种剪法所得的正方形面积更大．说明：图甲可另解为：由题意得点D 、E 、F 分别为AB 、AC 、BC 的中点，1OFDE S =正方形．解法2：如图甲，由题意得AE DE EC ==，即1EC =，如图乙，设MN x =，则由题意得AM MQ QP PN NB MN x ======，则3x =，解得x =又13>，即EC MN >． ∴甲种剪法所得的正方形面积更大．（2）212S =，10912S =．（3）解法1：探索规律可知：112n n S -=剩余三角形面积和为1210991112()2(1)222S S S -++⋯+=-++⋯+=解法2：由题意可知，第一次剪取后剩余三角形面积和为1121S S -==第二次剪取后剩余三角形面积和为12211122S S S -=-==，第三次剪取后剩余三角形面积和为233111244S S S -=-==，⋯第十次剪取后剩余三角形面积和为91010912S S S -==． 24．（12分）已知两直线1l ，2l 分别经过点(1,0)A ，点(3,0)B -，并且当两直线同时相交于y 正半轴的点C 时，恰好有12l l ⊥，经过点A 、B 、C 的抛物线的对称轴与直线1l 交于点K ，如图所示．（1）求点C 的坐标，并求出抛物线的函数解析式；（2）抛物线的对称轴被直线1l ，抛物线，直线2l 和x 轴依次截得三条线段，问这三条线段有何数量关系？请说明理由；（3）当直线2l 绕点C 旋转时，与抛物线的另一个交点为M ，请找出使MCK ∆为等腰三角形的点M ，简述理由，并写出点M 的坐标．【解答】解：（1）解法121:l l ⊥， 90ACB ∴∠=︒，即90ACO BCO ∠+∠=︒，又90ACO CAO ∠+∠=︒，BCO CAO ∴∠=∠，又90COA BOC ∠=∠=︒ BOC COA ∴∆∆∽，∴CO AOBO CO =，即13CO CO=，∴CO ，∴点C的坐标是，由题意，可设抛物线的函数解析式为2y ax bx =+ 把(1,0)A ，(3,0)B -的坐标分别代入2y ax bx =+得0930a b a b ⎧+⎪⎨-+=⎪⎩，解这个方程组，得a b ⎧=⎪⎪⎨⎪=⎪⎩，∴抛物线的函数解析式为2y x =+解法2：由勾股定理，得2222222()()OC OB OC OA BC AC AB +++=+=，又3OB =，1OA =，4AB =，∴OC =，∴点C 的坐标是，由题意可设抛物线的函数解析式为(1)(3)y a x x =-+，把C 代入函数解析式得a =，所以，抛物线的函数解析式为21)(3)y x x =-+=（2）解法1：截得三条线段的数量关系为KD DE EF ==．理由如下：设直线1l 的解析式为y kx b =+，把(1,0)A ，C ，代入解析式，解得k =，b所以直线1l 的解析式为y =+，同理可得直线2l 的解析式为y =，抛物线的对称轴为直线1x =-，由此可求得点K 的坐标为(-，点D 的坐标为(-，点E 的坐标为(-，点F 的坐标为(1,0)-，KD ∴=，DE ，EF KD DE EF ∴==．解法2：截得三条线段的数量关系为KD DE EF ==，理由如下：由题意可知Rt ABC ∆中，30ABC ∠=︒，60CAB ∠=︒，则可得tan30EF BF =⨯︒=，tan 60KF AF =⨯︒=由顶点D 坐标(-得DF =KD DE EF ∴===；（3）当点M 的坐标分别为(-，(-时，MCK ∆为等腰三角形．理由如下：()i 连接BK ，交抛物线于点G ，(1,0)F -，直线1l 的解析式为y =+，(1K ∴-，， (3,0)B -，∴直线BK 的解析式为：y =+①，抛物线的函数解析式为2y ==+；①②联立即可求出点G 的坐标为(-，又点C 的坐标为，则//GC AB ，可求得4AB BK ==，且60ABK ∠=︒，即ABK ∆为正三角形， CGK ∴∆为正三角形∴当2l 与抛物线交于点G ，即2//l AB 时，符合题意，此时点1M 的坐标为(-，()ii 连接CD ，由KD =，2CK CG ==，30CKD ∠=︒，易知KDC ∆为等腰三角形，∴当2l 过抛物线顶点D 时，符合题意，此时点2M 坐标为(-， ()iii 当点M 在抛物线对称轴右边时，只有点M 与点A 重合时，满足CM CK =，但点A 、C 、K 在同一直线上，不能构成三角形，综上所述，当点M 的坐标分别为(-，(-时，MCK ∆为等腰三角形．。

2011年中考数学试题分类30 解直角三角形

第30章解直角三角形一、选择题1. （2011湖北武汉市，10，3分）如图，铁路MN和公路PQ在点O处交汇，∠QON=30°．公路PQ上A处距离O点240米．如果火车行驶时，周围200米以内会受到噪音的影响．那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时，A处受噪音影响的时间为 A．12秒． B．16秒． C．20秒． D．24秒．【答案】B2. （2011湖南衡阳，9，3分）如图所示，河堤横断面迎水坡AB的坡比是1BC=5m，则坡面AB的长度是（）A．10m B．C．15m D．m【答案】A3. （2011山东东营，8，3分）河堤横断面如图所示，堤高BC＝5米，迎水坡AB的坡比1：BC与水平宽度AC之比），则AC的长是（）A．5B．10米C．15米D．米【答案】A4. （2010湖北孝感，10，3分）如图，某航天飞船在地球表面P点的正上方A处，从A处观测到地球上的最远点Q，若∠QAP=α，地球半径为R，则航天飞船距离地球表面的最近距离AP，以及P、Q两点间的地面距离分别是（）A.sin R α，180Rπα B.sin R R α-，()90180Rαπ-C. sin R R α-，()90180Rαπ+ D. cos R R α-，()90180Rαπ-【答案】B5. （2011宁波市，9，3分）如图，某游乐场一山顶滑梯的高为h ，滑梯的坡角为a ，那么滑梯长l 为A ． h sin aB ． h tan aC ． hcos a D ． h ·sin a【答案】A6. （2011台湾台北，34）图(十六)表示一个时钟的钟面垂直固定于水平桌面上，其中分针上有一点A ，且当钟面显示3点30分时，分针垂直于桌面，A 点距桌面的高度为10公分。

如图(十七)，若此钟面显示3点45分时，A 点距桌面的高度为16公分，则钟面显示3点50分时，A 点距桌面的高度为多少公分？A ．3322－B ．π＋16C ．18D ．19 【答案】D7. （2011山东潍坊，10，3分）身高相等的四名同学甲、乙、丙、丁参加风筝比赛，四人放出风筝的线长、线与地面的夹角如下表（假设风筝线是拉直的），则四名同学所放的风筝中最高的是（）同学甲乙丙丁放出风筝线长140m100m95m90m线与地面夹角30°45°45°60°A.甲B.乙C.丙D.丁【答案】D8. （2011四川绵阳10，3）周末，身高都为1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度.如图，小芳站在A处测得她看塔顶的仰角α为45°，小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米。

衢州中考数学试题答案.doc

浙江省2011年初中毕业生学业考试(衢州卷)数学参考答案一、选择题(本大题共10小题，每小题3分，共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案ABCACBABCD二、填空题(本大题共6小题，每小题4分，共24分) 11、2x 0x 21==， 12、70 13、200 14、安全；2004年满意度统计选项总和不到100% 15、(8，23) 16、当时8a 0≤<，a r =；时当8a >，4a 161r 2+=；或时8r 0≤<，a r =；时当8r >，4a 161r 2+=；三、(本大题共8小题，第17小题8分，第18、19、20小题各6分，第21题8分，第22、23小题各10分，第24小题12分，共66分) 17、解：(1)原式=22212⨯+- 21+=(2)原式=b a ba b 3a -++-=ba b2a 2--=218、解：去分母，得x 1)1x (3+≤- 整理，得4x 2≤ 2x ≤∴ 19、解：(1))b 2a )(b a (b 2ab 3a 22++=++(2)需用2号卡片 3 张，3号卡片 7 张。

20、解：(1)由题意可知，50次摸球实验活动中，出现红球20次，黄球30次， ∴红球所占百分比为20÷50=40%；黄球所占百分比为30÷50=60%；答：红球占40%，黄球占60%。

(2)由题意可知，50次摸球实验活动中，出现有记号的球4次，1- 0 1 2 3∴总球数为1008450=⨯ ∴红球数为40%40100=⨯答：盒中红球有40个21、解：(1)平均单株盈利⨯株数=每盆盈利平均单株盈利=⨯-5.03每盆增加的株数每盆的株数=3+每盆增加的株数 (2)解法1(列表法)每盆植入株数平均单株盈利(元)每盆盈利(元)3 3 94 2.5 10 5 2 106 1.5 97 1 7 ………答：要使每盆的盈利达到10元，每盆应该植入4株或5株；解法2(图象法)如图，纵轴表示平均单株盈利，横轴表示株数，则相应长方形面积表示每盆盈利。

2011年中考数学试题精选汇编《实数》

A.－4 B.－1 C.－ D.
【答案】B
7.（2011山东济宁，1，3分）计算―1―2的结果是
A．－1 B．1 C．－3 D．3
【答案】C
8.（2011四川广安，2，3分）下列运算正确的是（）
A． B．
C． D． [来源:学科网]
【答案】C
9.（2011重庆江津，1，4分）2－3的值等于( )
A.1 B.－5 C.5 D.－1·
2011年中考数学试题精选汇编
《实数》
一、选择题
1.（2011福建泉州，1，3分）如在实数0，－，，｜－2｜中，最小的是（）.
A． B．－ C．0D．｜－2｜
【答案】B
2.（2011广东广州市，1，3分）四个数－5，－0.1，，中为无理数的是().
A.－5B.－0.1C. D.
【答案】D
3.（2011山东滨州，1， 3分）在实数π、、、sin30°,无理数的个数为( )
16.（2011广东汕头，11，6分）计算：
【解】原式=1+ -4
=0
17.（2011浙江省嘉兴，17，8分）（1）计算：．
【答案】原式=4+1-3=2
18.（2011浙江丽水，17，6分）计算：|－1|－－(5－π)0+4cos45°.
【解】原式=1－ ×2 －1+4× =1－－1+2 = .
A．3B．30C．1D．0
【答案】C
26.（2011湖南湘潭市，1，3分）下列等式成立是
A. B. C. ÷ D.
【答案】A
27．（2011台湾全区，2）计算之值为何？
A．9 B．27 C．279 D．407
【答案】Ｃ
28.（2011台湾全区，12）12．判断312是96的几倍？

2011年中考数学试题汇编---一元一次不等式(组)

选择题（每小题x 分，共y 分）（2011•潜江市）4．某不等式组的解集在数轴上表示如图，则这个不等式组可能是B A .23x x -⎧⎨⎩≥≤ B .23x x -⎧⎨<⎩≥ C .⎩⎨⎧<->32x x D .23x x >-⎧⎨⎩≤〔2011•浙江省台州市〕6．不等式组⎩⎨⎧2x －4≤x ＋2x ≥3的解集是【 C 】A ．x ≥3B ．x ≤6C ．3≤x ≤6D ．x ≥6 （2011•宁波）3．不等式1x >在数轴上表示正确的是C(B) (C) (D)(2011•威海市)11．如果不等式组()2131x x x m--⎧⎪⎨⎪⎩＞＜的解集是2x ＜，那么m 的取值范围是 DA ．m =2B ．m ＞2C ．m ＜2D ．m ≥2(2011•苏州市)6．不等式组30,32x x -≥⎧⎪⎨<⎪⎩的所有整数解之和是BA ．9B ．12C ．13D ．15〔2011•湖北省武汉市〕3.如图，数轴上表示的是某不等式组的解集，则这个不等式组可能是BA.x+1>0，x-3>0.B.x+1>0，3-x>0.C.x+1<0，x-3>0.D.x+1<0，3-x>0.（2011•益阳市）6．不等式312->+x-2 0ABC D（第4题图）〔2011•浙江省义乌〕7．不等式组⎨⎧≥->+125523x x 的解在数轴上表示为C〔2011•日照市〕6．若不等式2x ＜4的解都能使关于x 的一次不等式（a -1）x ＜a +5成立，则a 的取值范围是A（A ）1＜a ≤7 （B ）a ≤7 （C ） a ＜1或a ≥7 （D ）a =71．〔2011•凉山州〕下列不等式变形正确的是（ B ）A ．由a b >，得ac bc >B ．由a b >，得22a b ->-C ．由a b >，得a b ->-D ．由a b >，得22a b -<-（2011•茂名市）4、不等式组⎩⎨⎧≥+<-0302x x 的解集在数轴上正确．．表示的是 D （2011•金华市）8.不等式组211420x x ->⎧⎨-⎩，≤的解在数轴上表示为（C ▲ )二、填空题（每小题x 分，共y 分）〔2011•大理〕10．不等式：2x +6＜0的解集是 x ＜-3 ．（2011•株洲市）9．不等式10x ->的解集是 1x > ．（2011•黄冈市）7．若关于x ，y 的二元一次方程组3133x y ax y +=+⎧⎨+=⎩的解满足2x y +＜，则1 02C1 02D1 02A1 02BA ．B ．C ．D ．a的取值范围为__ a＜4____．三、解答题：（共x分）（2011•呼和浩特市）23、（6分）生活中，在分析研究比赛成绩时经常要考虑不等关系.例如：一射击运动员在一次比赛中将进行10次射击，已知前7次射击共中61环，如果他要打破88环（每次射击以1到10的整数环计数）的记录，问第8次射击不能少于多少环？我们可以按以下思路分析：首先根据最后二次射击的总成绩可能出现的情况，来确定要打破88环的记录，第8次射击需要得到的成绩，并完成下表：根据以上分析可得如下解答：解：设第8次射击的成绩为x环，则可列出一个关于x的不等式：_______________________________________解得 _______________所以第8次设计不能少于________环.23、8环或9环或10环…………………………………（1分）9环或10环………………………………………………………（2分）10环…………………………………………………………………（3分）++x…………………………………………………………（4分）2061>88x………………………………………………（5分）7>8环 ……………………………………………………………………（6分）（2011•桂林市）24．（本题满分8分）某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人，如果给每个老人分5盒，则剩下38盒，如果给每个老人分6盒，则最后一个老人不足5盒，但至少分得一盒．（1）设敬老院有x 名老人，则这批牛奶共有多少盒？（用含x 的代数式表示）．（2）该敬老院至少有多少名老人？最多有多少名老人？解：（1）牛奶盒数：(538)x +盒 …………1分（2）根据题意得:5386(1)55386(1)1x x x x +--<⎧⎨+--≥⎩…………4分∴不等式组的解集为：39＜x ≤43 …………6分 ∵x 为整数∴x =40，41，42，43答：该敬老院至少有40名老人，最多有43名老人. …………8分（2011•天津）解不等式组215432x x x x +>-⎧⎨≤+⎩解：∵21543 2 x x x x +>-⎧⎨≤+⎩①②解不等式①．得6x >-．解不等式②．得2x ≤．∴原不等式组的解集为62x -<≤．（2011•黄石市）23.（本小题满分8分）今年，号称“千湖之省”的湖北正遭受大旱，为提高学生环境意识，节约用水，某校数学教师编制了一道应用题：为了保护水资源，某市制定一套节水的管理措施，其中对居民生活用水收费作如下规定：（1）若某用户六月份用水量为18吨，求其应缴纳的水费；（2）记该用户六月份用水量为x 吨，缴纳水费为y 元，试列出y 与x 的函数式；（3）若该用户六月份用水量为40吨，缴纳水费y 元的取值范围为7090y ≤≤，试求m 的取值范围。

2011年全国各地中考数学试卷试题分类汇编——第17章《事件与概率》

1 9
B.
1 3
C.
2 3
D.
2 9
【答案】A 8. （2011 浙江绍兴，7，4 分）在一个不透明的盒子中装有 8 个白球，若干个黄球，它们除颜色不同外，其余均相同.若从中随机摸出一个球，它是白球的概率为（） A.2 【答案】B 9. （2011 浙江义乌，9，3 分）某校安排三辆车，组织九年级学生团员去敬老院参加学雷锋活动，其中小王与小菲都可以从这三辆车中任选一辆搭乘，则小王与小菲同车的概率为（） 1 A． 3 【答案】A 10．（2011 浙江省嘉兴，12，5 分）从标有 1 到 9 序号的 9 张卡片中任意抽取一张，抽到序号是 3 的倍数的概率是【答案】． 1 B． 9 1 C． 2 2 D． 3 B.4 C.12 D.16
【答案】Ｃ 21. （2011 山东临沂，10，3 分）如图，A、B 是数轴上的亮点，在线段 AB 上任取一点 C，则点 C 到表示－1 的点的距离不大于．．．2 的概率是（ A．） D．
1 2
B．
2 3
C．
3 4
4 5
【答案】D 22. （2011 四川凉山州，4，4 分）下列说法正确的是（ A．随机抛掷一枚均匀的硬币，落地后反面一定朝上。 B．从 1，2，3，4，5 中随机取一个数，取得奇数的可能性较大。 C．某彩票中奖率为 36 0 0 ，说明买 100 张彩票，有 36 张中奖。 D．打开电视，中央一套正在播放新闻联播。【答案】B 23. （2011 四川绵阳 3，3）掷一个质地均匀且六个面上分别刻有 1 到 6 的点数的正方体骰子，如图.观察向上的ー面的点数，下列属必然事件的是）
1 【答案】 3 2. （2011 浙江省舟山，12，4 分）从标有 1 到 9 序号的 9 张卡片中任意抽取一张，抽到序号是 3 的倍数的概率是【答案】．

2011年中考数学试题分类37_投影与视图

第37章投影与视图一、选择题1. （2011浙江金华，2，3分）如图是六个棱长为1的立方块组成的一个几何体，其俯视图的面积是（）A ．6B ．5C ．4D ．3 【答案】B2. （2011湖北鄂州，12，3分）一个几何体的三视图如下：其中主视图都是腰长为4、底边为2的等腰三角形，则这个几何体的侧面展开图的面积为（） A ．2πB ．12π C ． 4πD ．8π【答案】C3. （2011安徽芜湖，3，4分）如图所示，下列几何体中主视图、左视图、俯视图都相同的是（）.【答案】C4. （2011福建福州，3，4分）在下列几何体中,主视图、左视图与俯视图都是相同的圆,该几何体是（）第12题图42 2 4左视图右视图俯视图ABDC【答案】A5. （2011江苏扬州，5,3分）如图是由几块小立方块所搭成的几何体的俯视图，小正方体中的数字表示该位置小立方块的个数，则该几何体的主视图是（）【答案】A6. （2011山东德州2,3分）一个几何体的主视图、左视图、俯视图完全相同，它一定是（Ａ）圆柱（B）圆锥（C）球体（D）长方体【答案】C7. （2011山东济宁，8，3分）如图，是有几个相同的小正方体搭成的几何体的三种视图，则搭成这个几何体的小正方体的个数是（）A. 3个B. 4个C. 5个D. 6个【答案】B8. （2011山东日照，5，3分）如图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主视图为（）【答案】C9. （2011山东泰安，6 ，3分）下列几何体：（第8题）其中，左视图是平等四边形的有（）A.4个B.3个C. 2个D.1个` 【答案】B10．（2011山东威海，10，3分）如图是由一些大小相同的小立方体组成的几何体的主视图和左视图，则组成这个几何体的小立方体的个数不可能是（）A ．3个B ．4个C ． 5个D ．6个【答案】D11. （2011山东烟台，2,4分）从不同方向看一只茶壶，你认为是俯视效果图的是（）【答案】A12. （2011浙江杭州，8，3）如图是一个正六棱柱的主视图和左视图，则图中的a ＝（）A ．23B ．3C ．2 D．1【答案】B13. （2011宁波市，6，3分）如图所示的物体的府视图是ABCD（第4题图）【答案】D14. （2011浙江衢州，1,3分）如下图，下列几何体的俯视图是右面所示图形的是（）【答案】A15. （2011浙江绍兴，4，4分）由5个相同的正方体搭成的几何体如图所示，则它的左视图是（）A. B. C. D.主视方向【答案】D16. （2011浙江台州，2,4分）下列四个几何体中，主视图是三角形的是（）【答案】B17. （2011浙江温州，3，4分）如图所示的物体由两个紧靠在一起的圆柱体组成，它的主视图是( )【答案】A主视方向A.B. C. D. (第4题)A.B. C. D.18. （2011浙江义乌，4，3分）如图，下列水平放置的几何体中，主视图不是．．长方形的是（）【答案】B19. （2011浙江省嘉兴，5，4分）两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视图是（）（A ）两个外离的圆（B ）两个外切的圆（C ）两个相交的圆（D ）两个内切的圆【答案】D20．（2011浙江丽水，2，3分）如图是六个棱长为1的立方块组成的一个几何体，其俯视图的面积是（）A ．6B ．5C ．4D ．3【答案】B21. （2011江西，3，3分）将两个大小完全相同的杯子（如图甲）叠放在一起（如图乙），则图乙中实物的俯视图是（）.【答案】C22. （2011甘肃兰州，6，4分）如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，这个几何体的主视图是水平面主视方向（第5题）A ．B ．C ．D ．A ．B ．C ．D ．【答案】D23. （2011湖南常德，10，3分）如图3，是由四个相同的小正方形组成的立体图形，它的左视图是（）【答案】A24. （2011江苏连云港，8，3分）如图，是由8个相同的小立方块搭成的几何体，它的三个视图都是2×2的正方形，若拿掉若干个小立方块后（几何体不倒掉．．．），其三个视图仍都为2×2的正方形，则最多能拿掉小立方块的个数为（） A ．1B ．2C ．3D ．4【答案】B25. （2011江苏宿迁,3,3分）下列所给的几何体中，主视图是三角形的是（▲）【答案】B26. （2011江苏泰州，4，3分）右图是一个几何体的三视图，则这个几何体是图3主视方向A B CD21 11正面A ．B ．C ．D ．俯视图左视图主视图A ．圆锥B ．圆柱C ．长方体D ．球体【答案】A27. （2011山东济宁，10，3分）如图，是某几何体的三视图及相关数据，则下面判断正确的是A ．a c >B ．b c >C ．2224a b c += D ．222a b c +=【答案】D28. （2011山东聊城，2，3分）如图，空心圆柱的左视图是（）【答案】C29. （2011四川成都，2,3分）如图所示的几何体的俯视图是D【答案】Dac2b第10题30. （2011四川广安，9，3分）由n 个相同的小正方体堆成的几何体，其视图如下所示，则n 的最大值是（） A ．18 B ．19 C ．20 D ．21【答案】A31. （2011四川内江，8，3分）由一些大小相同的小正方体搭成的几何体的俯视图如右图所示，其正方形中的数字表示该位置上的小正方体的个数，那么该几何体的主视图是12213ABCD【答案】B32. （2011四川宜宾,6,3分）如图所示的几何体的正视图是（）【答案】D33. (2011重庆綦江，3，4分)如图，是由两个相同的小正方体和一个圆锥体组成的立体图形，其俯视图是（）A ．B ．C ．D ．【答案】：CA ．Ｂ．Ｃ．Ｄ．（第6题图）主视图俯视图34.（2011江西南昌，3，3分）将两个大小完全相同的杯子（如图甲）叠放在一起（如图乙），则图乙中实物的俯视图是（）.A. B. C. D. 图甲图乙第3题图【答案】C35.（2011江苏淮安，4，3分）如图所示的几何体的主视图是（）A. B. C. D.【答案】B36.（2011江苏南通，6，3分）下列水平放置的几何体中，俯视图是矩形的是【答案】B37.（2011四川绵阳8，3）由四个相同的小正方体搭建了一个积木，它的三视图如右图所示，则这个积木可能是【答案】B38. （2011四川乐山4，3分）如图（2），在正方体ABCD-A 1B 1C 1D 1中，E 、F 、G 分别是 AB 、BB 1、BC 的中点，沿EG 、EF 、FG 将这个正方体切去一个角后，得到的几何体的俯视图是【答案】 B39. （2011四川凉山州，11，4分）一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的表面积为（）A ．66B ．48C ．48236D ．57【答案】A40. （2011安徽芜湖，3,4分）如图所示，下列几何体中主视图、左视图、俯视图都相同的是【答案】CABCD41. （2011湖北武汉市，8，3分）右图是某物体的直观图，它的俯视图是A ．B ．C ．D ．【答案】A42. （2011湖北黄石，5，3分）如图（1）所示的几何体的俯视图是【答案】B43. （2011湖南衡阳，3，3分）如图所示的几何体的主视图是（）A ．B ．C ．D ．【答案】B44. （2011贵州贵阳，4，3分）一个几何体的三视图如图所示，则这个几何体是主视图左视图俯视图（第4题图）（A ）圆柱（B ）三棱锥（C ）球（D ）圆锥【答案】D45. （2011广东肇庆，3，3分）如图是一个几何体的实物图，则其主视图是图DCBA【答案】C46. （2011湖北襄阳，8，3分）有一些相同的小立方块搭成的几何体的三视图如图2所示，则搭成该几何体的小立方块有A.3块B.4块C.6块D.9块【答案】B47. （2011湖南永州，10，3分）如图所示的几何体的左视图是（）【答案】B ．48. （2011江苏盐城，3，3分）下面四个几何体中，俯视图为四边形的是【答案】D49. （2011山东东营，3，3分）一个几何体的三视图如图所示,那么这个几何体是（）【答案】C50. (2011江苏镇江,3,2分)已知某几何体的三个视图(如图),此几何体是( )A B CD A ． B ． C ．D（第10题）图2主视图左视图俯视图A.正三棱柱B. 三棱锥C. 圆锥D. 圆柱【答案】C51.（2011内蒙古乌兰察布，5，3分）如图是由五个相同的小正方体搭成的几何体，它的主视图是（）【答案】B52．（2011重庆市潼南,6,4分）如图，在四个几何体中，主视图与其它几何体的主视图的形状不同的是【答案】C53.（2011安徽，3，4分）下图是五个相同的小正方体搭成的几何体，其左视图是（）A． B．C．D．【答案】A54.（2011广东湛江4,3分）下面四个几何体中，主视图是四边形的几何体有6题图A B CD第5题图A CB D正面圆锥圆柱球正方体 A 1个 B 2个 C 3个 D 4个【答案】B55. （2011贵州安顺，6，3分）如图是几个小立方块所搭的几何体俯视图，小正方形中的数字表示该位置上小立方块的个数，则这个几何体的主视图是（）A ．B ．C ．D ．【答案】A56. （2011湖南湘潭市，4，3分）一个几何体的三视图如下图所示，这个几何体是A.球B. 圆柱C.长方体D.圆锥【答案】B57. （2011湖北荆州，4，3分）如图，位似图形由三角尺与其灯光照射下的中心投影组成，相似比为2：5，且三角尺的一边长为8cm ，则投影三角尺的对应边长为 A ． 8cm B ．20cm C ．3.2 cm D ．10cm【答案】B左视图俯视图主视图58. （2011湖北宜昌，6，3分）如图，在一间黑屋子里用一盏白炽灯照一个球，球在地面上的阴影的形状是一个圆，当把白炽灯向远移时，圆形阴影的大心的变化情况是( ). A.越来越小 B.越来越大 C.大小不变 D.不能确定【答案】A59．（2011湖北宜昌，8，3分）一个圆锥体按如图所示摆放，它的主视图是( ).【答案】A二、填空题1. （2011山东菏泽，12，3分）如图是正方体的展开图，则原正方体相对两个面上的数字之和的最小值的是．【答案】62. （2011山东东营，17，4分）如图，观察由棱长为1的小立方体摆成的图形，寻找规律：如图①中; 共有1个小立方体，其中1个看得见，0个看不见；如图②中;把共有8个小立方体，其中7个看得见，1个看不见；如图③中；共有27个小立方体，其中19个看得见，8个看不见；……，则第⑥个图中，看得见的小立方体有______________个【答案】913. （2011山东枣庄，14，4分）如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中面积最小的是 .【答案】左视图4. （2010湖北孝感，14，3分）一个几何体是由一些大小相同的小正方体摆成的，其主视图与左视图如图所示，则组成这个几何体的小正方体最少有个.主视图左视图【答案】5 三、解答题1. （2011广东广州市，20，10分）5个棱长为1的正方体组成如图5的几何体．（1）该几何体的体积是（立方单位），表面积是（平方单位）（2）画出该几何体的主视图和左视图【答案】（1）5，22正面图5主视图左视图。

2011年中考数学试题精选汇编《有理数》

A. B. C. D. 8
【答案】D
33.（2011安徽芜湖，2，4分）我们身处在自然环境中，一年接受的宇宙射线及其它天然辐射照射量约为3100微西弗（1西弗等于1000毫西弗，1毫西弗等于1000微西弗），用科学记数法可表示为（）.
A．西弗B．西弗C．西弗D．西弗
【答案】C
34.（2011福建福州，1，4分）的相反数是（）
【答案】D
46.（2011山东泰安，4，3分）第六次人口普查公布的数据表明,登记的全国人口数量约为1340 000 000人,这个数据用科学记数法表示为（）
A.134×107人B.13.4×108人C.1.34×109人D.1.34×1010人
【答案】C
47.（2011山东烟台，1,4分）（－2）0的相反数等于（）
A．2. 89×104B．2.89×105C．2.89×106 D．2 89×107
【答案】C
51.（2011湖南邵阳，6，3分）地球上的水的总储量约为1.39×1018m3，但目前能被人们生产、生活利用的水只占总储量的0.77%，即约为0.0107×1018m3，因此我们要节约用水。请将0.0107×1018m3用科学计数法表示是（）
A.1 B.－1 C.2 D.－2
【答案】B
48.（2011浙江杭州，3，3）（）
A． B． C． D．
【答案】D
49.(2011浙江湖州，1，3)－5的相反数是
A．5B．－5C． D．-1
【答案】A
50.(2011浙江湖州，3，3)根据全国第六次人口普查统计，湖州市常住人口约为2890000人，近似数2890000用科学记数法可表示为
【答案】B
17.（2011台湾全区，11）图(二)数在线有O、A、B、C、D五点，根据图中各点所表示的数，判断 [来源:]

衢州市2011年中考数学模拟试题

衢州市2011年中考数学模拟试题说明：考试时间90分钟，满分120分．一、选择题（本题共5小题，每题3分，共15分）1、实施西部大开发战略是党中央面向21世纪的重大决策，西部地区占我国国土面积的32，我国国土面积约960万平方千米，用科学记数法表示我国西部地区的面积为（） A 、64×105km 2 B 、6.4×106km 2 C 、6.4×107km 2 D 、640×104km 22、已知a －b ＝3，b ＋c ＝－5，则代数式2ac bc a ab -+-的值是A ．15-B ．2-C ．6-D ．6 3、如图，在函数中 xy 1=的图象上有三点 A 、B 、C ，过这三点分别向x 轴、y 轴作垂线，过每一点所作两条垂线与 x 轴、y 轴围成的矩形的面积分别为S 1、S 2、S 3，则( )(Ａ)S 1＞S 2＞S 3 (Ｂ)S 1＜S 2＜S 3 (Ｃ)S 1＜S 3＜S 2 (Ｄ)S 1＝S 2＝S 3 4、正常人的体温一般在37℃左右，但一天中的不同时刻不尽相同.下图反映了一天24小时内小明体温的变化情况，下列说法错误的是（A ）清晨5时体温最低（B ）下午5时体温最高（C ）这一天中小明体温T(单位：℃)的范围是36.5≤T≤37.5（D ）从5时至24时，小明体温一直是升高的. 5、已知下列命题① 一组对边平行且相等的四边形是平行四边形; ② 两条对角线互相垂直且相等的四边形是正方形; ③ 一组对边平行且两条对角线相等的四边形是矩形; ④ 两条对角线互相垂直的平行四边形是菱形. 其中正确的命题的个数是( )(Ａ)0 (Ｂ)1 (Ｃ)2 (Ｄ)3 二、填空题（本题共５小题，每小题４分，共２０分） 6、若∠A 是锐角，sinA ＝23，则∠A ＝。

7、不等式组⎩⎨⎧≥++〈xx xx 1443的解集为。

8、函数2+-=x x y 中，自变量x 的取值范围是．9、如图3，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为P ，若AP ：PB ＝1：4．CD ＝8，则AB ＝。

2011浙江衢州中考数学(word)

2011年浙江省衢州市中考试题数学参考公式：二次函数 2(0)y ax bx c a =++≠图像的顶点坐标是2424b ac b a a-（-,）.一、选择题（本大题共10小题，每小题3分，满分30分。

请选出一个符合题意的正确的选项填涂在答题纸上，不选、多选、错选均不给分） 1.（2011浙江衢州，1,3分）数2-的相反数为（） A.2 B.12 C. 2- D.12- 【答案】A2. （2011浙江衢州，1,3分）衢州市“十二五”规划纲要指出，力争到2015年，全市农民人均年纯收入超过13000元，数13000用科学记数法可以表示为（） A.31310⨯ B. 41.310⨯ C. 50.1310⨯ D.213010⨯【答案】B3.（2011浙江衢州，1,3分）在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生（每组8人）测试成绩如下（单位：次/分）：44,45,42,48,46,47,45.则这组数据的极差为（） A.2 B.4 C.6 D.8 【答案】C4. （2011浙江衢州，1,3分）如下图，下列几何体的俯视图是右面所示图形的是（）【答案】A5.（2011浙江衢州，1,3分）衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF AG 、分别架在墙体的点B 、点C 处，且AB AC =,侧面四边形BDEC 为矩形，若测得100FAG ∠=︒，则FBD ∠=( )A. 35°B. 40°C. 55°D. 70°【答案】C6.（2011浙江衢州，1,3分）如图，OP 平分,MON PA ON ∠⊥于点A ，点Q 是射线OM上的一个动点，若2PA =，则PQ 的最小值为（）A.1B.2C.3D. 4【答案】B7.（2011浙江衢州，1,3分）5月19日为中国旅游日，衢州推出“读万卷书，行万里路，游衢州景”的主题系列旅游惠民活动，市民王先生准备在优惠日当天上午从孔氏南宗家庙。

2011年中考数学试题精选汇编《全等三角形》

2011年中考数学试题精选汇编《三角形全等》一、选择题1. （2011安徽芜湖，6，4分）如图，已知A B C △中，45ABC ∠= ， F 是高A D 和B E 的交点，4C D =，则线段D F 的长度为（）.A． B ． 4 C． D．【答案】B2. （2011山东威海，6，3分）在△ABC 中，AB ＞AC ，点D 、E 分别是边AB 、AC 的中点，点F 在BC 边上，连接DE ,DF ,EF .则添加下列哪一个条件后，仍无法判定△BFD 与△EDF 全等（）．A ． EF ∥AB B ．BF =CFC ．∠A =∠DFED ．∠B =∠DFE【答案】C3. （2011浙江衢州，1,3分）如图，O P 平分,MON PA ON ∠⊥于点A ，点Q 是射线O M 上的一个动点，若2PA =，则PQ 的最小值为（）A.1B.2C.3D. 4O N【答案】B4. （2011江西，7，3分）如图下列条件中，不能．．证明△ABD ≌△ACD 的是（）. A.BD =DC ，AB =AC B.∠ADB =∠ADCC.∠B =∠C ，∠BAD =∠CADD.∠B =∠C ，BD =DC第7题图【答案】D5. （2011江苏宿迁,7,3分）如图，已知∠1＝∠2，则不一定．．．能使△ABD ≌△ACD 的条件是（▲）A ．AB ＝AC B ．BD ＝CD C ．∠B ＝∠C D ．∠ BDA ＝∠CDA【答案】B6. （2011江西南昌，7，3分）如图下列条件中，不能．．证明△ABD ≌△ACD 的是（）. A.BD =DC ，AB =AC B.∠ADB =∠ADCC.∠B =∠C ，∠BAD =∠CADD.∠B =∠C ，BD =DC第7题图【答案】D7. （2011上海，5，4分）下列命题中，真命题是（）．(A)周长相等的锐角三角形都全等； (B) 周长相等的直角三角形都全等；(C)周长相等的钝角三角形都全等； (D) 周长相等的等腰直角三角形都全等．【答案】D8. （2011安徽芜湖，6,4分）如图，已知A B C △中，45ABC ∠=， F 是高A D 和B E 的交点，4C D =，则线段D F 的长度为（）.A ．B ． 4C ．D ．【答案】B9.10．二、填空题1. （2011江西，16，3分）如图所示，两块完全相同的含30°角的直角三角形叠放在一起，且∠DAB=30°。

2011年中考数学试题分类11 函数与一次函数

【答案】C
30.（2011湖北黄石，10，3分）已知梯形ABCD的四个顶点的坐标分别为A（－1，0），B（5，0），C（2，2），D（0，2），直线y=kx+2将梯形分成面积相等的两部分，则k的值为
A.－ B.－ C.－ D.－
【答案】A
31.（2011湖南衡阳，6，3分）函数中自变量x的取值范围是（）
【答案】A
46.（2011江苏南通，9，3分）甲、乙两人沿相同的路线由A地到B地匀速前进，A，B两地间的路程为20千米，他们前进的路程为s（单位：千米），甲出发后的时间为t（单位：小时），甲、乙前进的路程与时间的函数图像如图所示.根据图像信息，下列说法正确的是
A.甲的速度是4千米/小时
B.乙的速度是10千米/小时
【答案】B
3.（2011广东广州市，9，3分）当实数x的取值使得有意义时，函数y=4x+1中y的取值范围是（）．
A．y≥－7B．y≥9C．y＞9D．y≤9
【答案】B
4.（2011山东滨州，6，3分）关于一次函数y=－x+1的图像，下列所画正确的是( )
【答案】C
5.（2011重庆江津，4，4分）直线y=x－1的图像经过象限是( )
C.x≥D.x＜
【答案】A
25.（2011四川乐山3，3分）下列函数中，自变量x的取值范围为x＜1的是
A． B． C． D．
【答案】D
26.（2011四川乐山8，3分）已知一次函数的图象过第一、二、四象限，且与x轴交于点（2，0），则关于x的不等式的解集为
A．x<－1 B．x>-1 C．x>1 D．x<1
A.第一、二、三象限B.第一、二、四象限
C.第二、三、四象限D.第一、三、四象限

2011年中考数学试题分类32 圆的有关性质

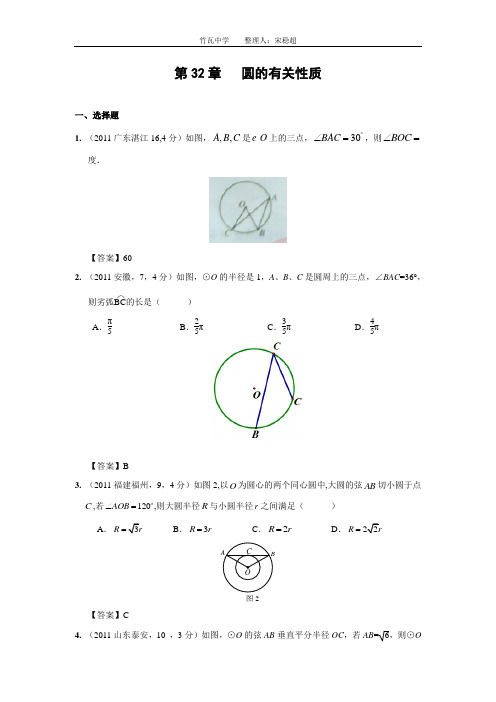
第32章圆的有关性质一、选择题1. （2011广东湛江16,4分）如图，,,A B C 是O 上的三点，30BAC ︒∠=，则BOC ∠= 度．【答案】602. （2011安徽，7，4分）如图，⊙O 的半径是1，A 、B 、C 是圆周上的三点，∠BAC =36°，则劣弧 ⌒BC 的长是（） A ．π5B ．25πC ．35πD ．45π【答案】B3. （2011福建福州，9，4分）如图2,以O 为圆心的两个同心圆中,大圆的弦AB 切小圆于点C ,若120AOB ∠= ,则大圆半径R 与小圆半径r 之间满足（）A．R = B ．3R r =C ．2R r =D．R =【答案】C4. （2011山东泰安，10 ，3分）如图，⊙O 的弦AB 垂直平分半径OC ，若AB =6，则⊙O图2的半径为（）A. 2B.2 2C.22D.62【答案】A5. （2011四川南充市，9，3分）在圆柱形油槽内装有一些油。

截面如图，油面宽AB 为6分米，如果再注入一些油后，油面AB 上升1分米，油面宽变为8分米，圆柱形油槽直径MN 为（）（A ）6分米（B ）8分米（C ）10分米（D ）12分米【答案】C6. （2011浙江衢州，1,3分）一个圆形人工湖如图所示，弦AB 是湖上的一座桥，已知桥AB 长100m ，测得圆周角45ACB ∠=︒，则这个人工湖的直径AD 为（）A.B.C.D.【答案】B7. （2011浙江绍兴，4，4分）如图，AB O 为的直径，点C 在O 上，若16C ∠=︒,则BOC ∠的度数是（）A.74︒B. 48︒C. 32︒D. 16︒【答案】C8. （2011浙江绍兴，6，4分）一条排水管的截面如图所示.已知排水管的截面圆半径10OB ，截面圆圆心O 到水面的距离OC 是6，则水面宽AB 是（）A.16B.10C.8D.6【答案】A9. （2011浙江省，5，3分）如图，小华同学设计了一个圆直径的测量器，标有刻度的尺子OA 、OB 在O 点钉在一起，并使它们保持垂直，在测直径时，把O 点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为（） A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位【答案】B10．（2011四川重庆，6，4分）如图，⊙O 是△A BC 的外接圆，∠OCB ＝40°则∠A 的度数等于( )A ． 60°B ． 50°C ． 40°D ． 30°【答案】B11.（2011浙江省嘉兴，6，4分）如图，半径为10的⊙O中，弦AB的长为16，则这条弦的弦心距为（）（A）6 （B）8 （C）10 （D）12【答案】A12.（2011台湾台北，16）如图(六)，BD为圆O的直径，直线ED为圆O的切线，A、C两点在圆上，AC平分∠BAD且交BD于F点。