圆锥曲线求圆锥曲线方程

合集下载

圆锥曲线基本题型总结

锥曲线基本题型总结:提纲:一、定义的应用：1、定义法求标准方程：2、涉及到曲线上的点到焦点距离的问题：3、焦点三角形问题：二、圆锥曲线的标准方程：1、对方程的理解2、求圆锥曲线方程（已经性质求方程）3、各种圆锥曲线系的应用：三、圆锥曲线的性质：1、已知方程求性质：2、求离心率的取值或取值范围3、涉及性质的问题：四、直线与圆锥曲线的关系：1、位置关系的判定：2、弦长公式的应用：3、弦的中点问题：4、韦达定理的应用：一、定义的应用：1.定义法求标准方程：（1）由题目条件判断是什么形状，再由该形状的特征求方程：（注意细节的处理）1•设F-F2为泄点,∣F1F2∣=6 ,动点M满足IMF I I+∣M F2I= 6 ,则动点M的轨迹是（）1/1C.圆D.线段【注:2a>|Fi F2I是椭圆，2a=∣Fι F2 I是线段】2.设％4, O), C(4,0) ,KZLlSC的周长等于18侧动点/1的轨迹方程为()A.5J+= 1 (yH0) -B.+ ∖ f ( X2,9)=1 (yH 0 )C错误!-错误!=1 G∙≠ 0) °D∙错误! + = 1 (y≠0)【注:检验去点】3.已知力(0, — 5)、B(0,5),昭I 一砂∣=2α,当α=3或5时，P点的轨迹为()A.双曲线或一条直线B.双曲线或两条直线C.双曲线一支或一条直线D.双曲线一支或一条射线【注:2a<|F I F2∣是双曲线，2a=∣ F1F2∣⅛射线，注意一支与两支的判断】4•已知两左点巧(一 3,0),尸2(3.0),在满足下列条件的平而内动点P的轨迹中,是双曲线的是()A↑∖PF i∖-∖PF2 I |=5B.∣ I PFll-I PF2∖ I =6C.∣∣PF1∣-∣PF2∣∣=7D.∣ I PF1∖-∖PF2∖ I =0 【注ι2a<∣Fι F2∣是双曲线】5•平而内有两个泄点Fι(-5,0)和F2( 5 ,0),动点P满足IPF I l-I PF沪6 ,则动点P的轨迹方程是()A.∖ f(x2, 1 6)- 错误! = l(xW-4) "B.错误!∙=l(xW∙3)C- = I(XM 4) 。

圆锥曲线与其方程

圆锥曲线与其方程圆锥曲线是数学中一个非常有趣且重要的概念，它是由一个平面与一个圆锥相交而形成的曲线。

圆锥曲线包括圆、椭圆、双曲线和抛物线四种类型，每种类型都有其独特的特点和方程。

首先，让我们来了解一下圆锥曲线中最简单的一种类型——圆。

圆可以被描述为一个平面上与一个圆心和半径相关联的点的集合。

其方程可以表示为(x-a)²+(y-b)²=r²，其中(a,b)是圆心的坐标，r是半径的长度。

圆的方程可以用来确定圆上的任意一点的坐标，从而使我们能够对圆进行研究和分析。

接下来，我们来讨论椭圆。

椭圆是圆锥曲线中另一种常见的类型，它具有两个焦点和一个长轴和短轴。

椭圆的方程可以表示为(x-h)²/a²+(y-k)²/b²=1，其中(h,k)是椭圆的中心坐标，a和b分别是长轴和短轴的长度。

椭圆的方程可以帮助我们确定椭圆上的点，并且可以用来计算椭圆的周长和面积。

双曲线是另一种重要的圆锥曲线类型。

它有两个分离的曲线分支，并且具有两个焦点和一个虚线的对称轴。

双曲线的方程可以表示为(x-h)²/a²-(y-k)²/b²=1，其中(h,k)是双曲线的中心坐标，a和b分别是曲线分支的长度。

双曲线的方程可以帮助我们确定双曲线上的点，并且可以用来研究双曲线的性质和特征。

最后，我们来谈谈抛物线。

抛物线是圆锥曲线中最具有特色的一种类型，它具有一个焦点和一条对称轴。

抛物线的方程可以表示为y=ax²+bx+c，其中a、b和c 是常数。

抛物线的方程可以帮助我们确定抛物线上的点，并且可以用来研究抛物线的形状和性质。

通过了解圆锥曲线和它们的方程，我们可以更好地理解和应用这些曲线。

圆锥曲线在几何学、物理学、工程学和计算机图形学等领域都有广泛的应用。

例如，在物理学中，椭圆轨道被用来描述行星的运动；在工程学中，抛物线被用来设计抛物面反射器；在计算机图形学中，圆锥曲线被用来生成二维和三维图形。

圆锥曲线方程

叫做椭圆
椭圆就是集合: P={ M| |MF1|+|MF2|=2a }
A1 F1
演示
y
B1 M
o F2
B2
椭圆的焦距：|F1F2|=2c A2 x 椭圆的长轴: |A1A2|=2a
椭圆的短轴： |B1B2|=2b
返回
椭圆的标准方程不论k为何实数，直线y=ax+b与椭圆
总有
Ⅰ直接法：将动点运动的规律直接转化为代数语言，
注意轨迹的完备性和纯粹性，即“除伪补缺”
离心率e=
c a
(
0<e<1
)
我国对圆锥曲线的研究也有相当的历史，很多史书均
叫做椭圆
1.范围 2.对称 3.顶点椭圆第一定义：把平面内与两个定点F1,F2的距离的
我国对圆锥曲线的研究也有相当的历史，很多史书均椭圆就是集合: P={ M| |MF1|+|MF2|=2a }
差的绝对值等于常数（小于
c o P的=点{ M的|轨迹叫A做1抛}物线F，1点F叫做抛物线的焦F点2.
（+c, 0) c2=a2+b2
A2 x
c2 = a2 - b2
不论k为何实数，直线y=ax+b与椭圆
方问题”时，就涉及圆锥曲线。 B2
他取三个顶点分别为直角
总有
椭圆的简单几何性质：在坐标系中计算得，椭圆的标准方程：
我国对圆锥曲线的研究也有相当的历史，很多史书均有这方面的记载。《恒星历指》一书中既有椭圆的名称，《交食历指》一书则记为长圆，《测量全义》中即记载了
椭圆产生于圆柱，也记载圆锥曲线源自圆锥。返回
椭圆 ellipse
椭圆第一定义：把平面内与两个定点F1,F2的距离的和等于常数（大于/F1F2/ ）的点的轨

圆锥曲线公式大全（高中珍藏版）

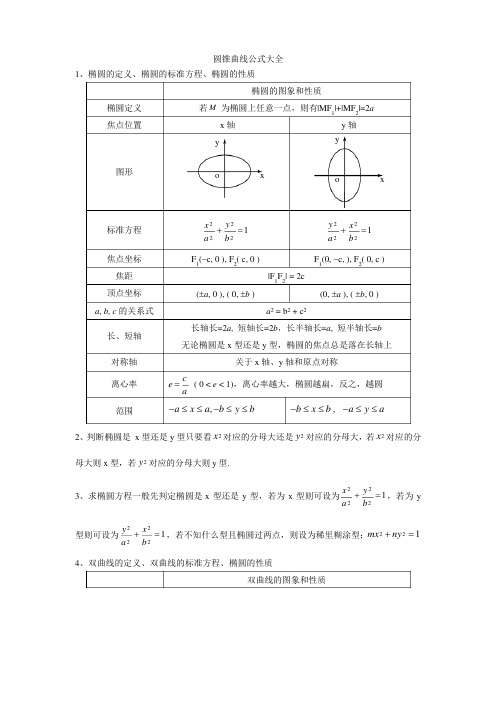
圆锥曲线公式大全1、椭圆的定义、椭圆的标准方程、椭圆的性质椭圆定义焦点位置椭圆的图象和性质若M 为椭圆上任意一点，则有|MF 1|+|MF 2|=2ax 轴y图形o xy 轴y o x标准方程焦点坐标焦距顶点坐标a ,b ,c 的关系式长、短轴对称轴离心率范围x 2y 2+2=12a b F 1(-c, 0 ), F 2( c, 0 )|F 1F 2| = 2c(±a , 0 ), ( 0,±b )a 2 =b 2 +c 2y 2x 2+2=12a b F 1(0,-c, ), F 2( 0, c )(0,±a ), (±b , 0 )长轴长=2a ,短轴长=2b ，长半轴长=a ,短半轴长=b 无论椭圆是x 型还是y 型，椭圆的焦点总是落在长轴上关于x 轴、y 轴和原点对称e =c ( 0 <e < 1)，离心率越大，椭圆越扁，反之，越圆a-a ≤x ≤a ,-b ≤y ≤b 2-b ≤x ≤b ，-a ≤y ≤a22、判断椭圆是x 型还是y 型只要看x 对应的分母大还是y 对应的分母大，若x 对应的分母大则x 型，若y 对应的分母大则y 型.22x 2y 23、求椭圆方程一般先判定椭圆是x 型还是y 型，若为x 型则可设为2+2=1，若为y a b y 2x 222型则可设为2+2=1，若不知什么型且椭圆过两点，则设为稀里糊涂型：mx +ny =1a b 4、双曲线的定义、双曲线的标准方程、椭圆的性质双曲线的图象和性质若M为双曲线上任意一点，则有MF1-MF2=2a(2a<2c)双曲线定义若MF1-MF2=2a=2c,则点M的轨迹为两条射线若MF1-MF2=2a>2c,则点M无轨迹焦点位置x轴y轴图形标准方程焦点坐标焦距顶点坐标(±a, 0 )x2y2-2=12a bF1(-c, 0 ), F2( c, 0 )|F1F2| = 2cy2x2-2=12a bF1(0,-c, ), F2( 0, c )(0,±a )a,b,c的关系式椭圆形状长的像a,所以a是老大，a2 = b2 + c2；双曲线形状长的像c,所以c是老大，c2 = a2 + b2实轴、虚轴对称轴离心率范围渐近线实轴长=2a,虚轴长=2b，实半轴长=a,虚半轴长=b无论双曲线是x型还是y型，双曲线的焦点总是落在实轴上关于x轴、y轴和原点对称e=c(e >1)aa≤x或x≤-a,y∈R a≤y或y≤-a,x∈Ry=±bxay=±axb2、判断双曲线是x 型还是y 型只要看x 前的符号是正还是y 前的符号是正，若x 前的符号为正则x 型，若y 前的符号为正则y 型，同样的，哪个分母前的符号为正，则哪个分母就为a 22222x 2y 23、求双曲线方程一般先判定双曲线是x 型还是y 型，若为x 型则可设为2-2=1，若a b y 2x 2为y 型则可设为2-2=1，若不知什么型且双曲线过两点，则设为稀里糊涂型：a b mx 2-ny 2=1(mn <0)6、若已知双曲线一点坐标和渐近线方程y =mx ，则可设双曲线方程为y 2-m 2x 2=λ(λ≠0)，而后把点坐标代入求解7、椭圆、双曲线、抛物线与直线l :y =kx +b 的弦长公式：AB =(k 2+1)(x 1-x 2)2=(12+1)(y -y )122k 8、椭圆、双曲线、抛物线与直线问题出现弦的中点往往考虑用点差法9、椭圆、双曲线、抛物线与直线问题的解题步骤：（1）假化成整(把分式型的椭圆方程化为整式型的椭圆方程)，联立消y 或x (2)求出判别式，并设点使用伟大定理（3）使用弦长公式1、抛物线的定义：平面内有一定点F 及一定直线l (F 不在l 上)P 点是该平面内一动点，当且仅当点P 到F 的距离与点P 到直线l 距离相等时，那么P 的轨迹是以F 为焦点，l 为准线的一条抛物线.————见距离想定义！！！2、（1）抛物线标准方程左边一定是x 或y 的平方（系数为1），右边一定是关于x 和y 的一次项，如果抛物线方程不标准，立即化为标准方程！（2）抛物线的一次项为x 即为x 型，一次项为y 即为y 型!(3)抛物线的焦点坐标为一次项系数的四分之一，准线与焦点坐标互为相反数！一次项为x ，则准线为”x=多少”，一次项为y ，则准线为”y=多少”!(4)抛物线的开口看一次项的符号，一次项为正，则开口朝着正半轴，一次项为负，则开口朝着负半轴！（5）抛物线的题目强烈建议画图，有图有真相，无图无真相！3、求抛物线方程，如果只知x 型，则设它为y =ax (a ≠0),a>o,开口朝右；a<0,开口朝左；如果只知y 型，则设它为x =ay (a ≠0),a>o,开口朝上；a<0,开口朝下。

圆锥曲线全部公式及概念

1. 椭圆l τ + ∑- = i(a>b>O)的参数方程是V Cr Zr 2,2»2准线到中心的距离为L ,焦点到对应准线的距离(焦准距)p =—・通径的一半(焦参数)：丄.C Ca2 22. 椭圆∆τ + l τ = l(rt >∕7>θ)焦半径公式及两焦半径与焦距构成三角形的面积： Cr Zr| PF l | = e(x + —) = a+ ex , ∖PF 21 = e(-— X) = U-ex ↑ S 斗严；=b 2 tan '丫 F22 223.椭圆的的内外部：(1)点PesyO)在椭圆丄v + L = l(α>b>0)的内部O⅛- + ⅛<l. Cr 泸Cr b'2 2 2 2(2)点 P(X o o to)在椭圆上τ +丄r = l(α>b>O)的外部 <≠>⅛ + ⅛>ι.Cr Zr Cr Zr的距离(焦准距)P = — •通径的一半(焦参数)：— C a5. 双曲线的内外部：(1)点P(X o o tO)在双曲线=Cr Ir/2 2 2 2 ⑵点P(X (P y 0)在双曲线一一二~ = l(α > 0,b > 0)的外部o —⅛■-汙V1・Cr IrCr Zr6. 双曲线的方程与渐近线方程的关系：(1)若双曲线方程为二一二=1二>渐近线方程：Δ1-22 = O^> y = ±-χ・α~ Ir Cr 少a-> 2A χ∙ V r β,V*⑵若渐近线方程为y = ±-x<=>-±- = O=>¾曲线可设为r — — = λ・ a a b Cr Zr2 22 2⑶若双曲线与亠一亠=1有公共渐近线，可设为=T 一亠=λCr XCr Ir(λ>0,焦点在X 轴上；九<0,焦点在y 轴上)・ (4)焦点到渐近线的距离总是b ∙7. 抛物线y 2= 2px 的焦半径公式：拋物线y 2=2px(p>0)焦半径ICFI = X O + -^・过焦点弦长IcQl = “+上+心+ £ = “+“ + 〃 . 2 2 28. 拋物线y 2 = IPX JL 的动点可设为P(±-,儿)或P(2∕"[2p∕) P(x , V ),其中y 2= 2PX ・2 P '•、 b A ,ac — b~9. 二次函数y = ax 1 +bx + c = a(x + —)2+ ------------- (a ≠ 0)的图象是抛物线：(1 )顶点坐标为Ia 4aZb 4“C — b~ z. .. ... I . . h ^CIC — /?" +1、 Z -S Λ /V ∙ z t , CT^CIC — b~ — 1 ,—:——)：(2)焦点的坐标为,——； ---------------- ):(3)准线万程是y = IABl = 5J(1+^2)(X 2 "ΛI )2 =I 比 _兀21 Vl +tan 2 a =I y l _y 21 √l + c^t 2ay = kx + b . .α(弦端点ACv 1,y 1X B(X^y 2),由方程<消去y 得到αL +bx + c = O 9 Δ>0, α为直线AB 的圆锥曲线X = Cl COS θ 亠亠 C• 离心率£ =—= y = bs ∖nθ aV»*■ C 4. 双曲线亠一 — = 1(« > 0.Z? > 0)的离心^e =— a ∕Γa • 2ι2 「，准线到中心的距离为∙，焦点到对应准线焦半径公式\PF }\ =I e(x + —) I=I a + <?xI, ∖PF 2∖ =I e(-^x) I=I a-ex ∖9 C 两焦半径与焦距构成三角形的面积S λj.ιp l .y = b 2 COt 'F'] F .2 22L = l(">0d>0)的内部 o ⅛-4>l. • - Cr Zr2a 4a2a 4a" 4a10. 以抛物线上的点为圆心，焦半径为半径的圆必与准线相切：以拋物线焦点弦为直径的圆，必与准线相切; 以抛物线的焦半径为直径的圆必与过顶点垂直于轴的直线相切・11. 直线与圆锥曲线相交的弦长公式：IABI = √(x 1-x 2)2+(y 1-y 2)2或F(x,y) = O倾斜角，&为直线的斜率，I召I= J(XI +心)‘ _4召心・12.圆锥曲线的两类对称问题：(1)曲线F(X,y) = O关于点P(X o,儿)成中心对称的曲线是F(2x0-x t2y0 -y)=0.(2)曲线F(X,y) = 0关于直线Av + Bv + C = O成轴对称的曲线是—2A(Ar + By+ C) 2B(Ax + By + C)x CFa ------ —R——、y --------- -V———)=0・√Γ+歹A" + B'特别地，曲线F(X9 y) = 0关于原点O成中心对称的曲线是F(-x,-y) = 0・曲线F(X9 y) = 0关于直线X轴对称的曲线是F(X^y) = 0.曲线F(X9 y) = 0关于直线y轴对称的曲线是F(-x, y) = 0・曲线F(X9 y) = 0关于直线y = x轴对称的曲线是F{y.x) = 0.曲线F(X,y) = 0关于直线y = -x轴对称的曲线是F(-y,-x) = 0・13 •圆锥曲线的第二定艾：动点M到定点F的距离与到定直线/的距离之比为常数£,若0 VfVl, M的轨迹为椭圆；若e = ∖9 M的轨迹为抛物线；若e>∖9 M的轨迹为双曲线.注意：J还记得圆锥曲线的两种定义吗解有关题是否会联想到这两个定狡2、还记得圆锥曲线方程中的：2(1)在椭圆中：α是长半轴，〃是短半轴，C是半焦距，其中b2 =a2-C29 f = (Ovwvl)是离心率，—a C• 2. 2是准心距，-L是准焦距，-L是半通径.C a2(2)在双曲线中："是实半轴，b是虚半轴，C是半焦距，其中b2 =c2-a29 e = -∖e>l)是离心率，L是a C准心距，伫是准焦距，冬是半通径.C a(3)在抛物线中：0是准焦距，也是半通径.3、在利用圆锥曲线统一定狡解题吋，你是否注意到定艾中的定比的分子分母的顺序(到定点的距离比到定直线的距离)4、离心率的大小与曲线的形状有何关系(圆扁程度，张口大小)等轴双曲线的离心率是多少(0 = √Σ)5、在用圖锥曲线与直线联立求解时，消元后得到的方程中要注意：二次项的系数是否为零判别式A 2 0的限制. (求交点，弦长，中点，斜率，对称，存在性问题都在Δ >0下进行).注意：尤其在求双曲线与直线的交点时：当A>0时：直线与双曲线有两个交点(包括直线与双曲线一支交于两点和直线与双曲线两支各交于一点两种情况)：当A = O时，直线与双曲线有且只有一个交点(此时称指向与双曲线相切)，反之，当直线与双曲线只有一个交点时，直线与双曲线不一定相切，此时直线与双曲线的一条渐近线平行，当AvO时，直线与双曲线没有交点.6、椭圆中，注意焦点.中心.短轴端点所组成的直角三角形•此时Cr =b2+c2・7、通径是抛物线的所有焦点弦中最短的弦.(想一想在双曲线中的结论)8、你知道椭圆、双曲线标准方程中aj∖c之间关系的差异吗9、如果直线与双曲线的渐近线平行吋，直线与双曲线相交，只有一个交点；如果直线与拋扬线的轴平行时，直线与抛物线相交，只有一个交点•此时两个方程联立，消元后为方程变为一次方程.椭圆练习1・过椭圆二+二=1 (a>b>O)的左焦点F I任做一条不与长轴重合的弦AB, F2为椭圆的右焦点，則AABA的周长是/ b^( )(A)2a (B)4a (C)2b (D) 4b2•设a,beR.a2+2b2 =6,则α + b 的最小值是( )(A) - 2√2 (B)-垃(0-3 (D)-2323. 椭圆的两个焦点和短轴的两个顶点，是一个含60°角的菱形的四个顶点，则椭圆的离心率为( )(A)丄 (B)遇 (C)遇 (D)丄或遇2 23 2 24. 设常数m>0,椭圆x 2+m 2y 2=m 2的长轴是短轴的两倍，則m 的值等于( )(A) 2(B) √2(C) 2 或丄 (D) √Σ 或空2 22 25. 过椭圆二+ L = l(°>b> 0)的左焦点片作X 轴的垂线交椭圆于点P,化为右焦点，若ZF i PF. = 60 ,则Cr "椭圆的离心率为()(A)^⑻迟 (C)I(D)I23236. 如果椭圆的两个焦点将长轴分成三等份，那么这个椭圆的两条准线间的距离是焦距的() (A) 18 倍 (B) 12 倍 (C) 9 倍 (D) 4 倍7. 当关于X, y 的方程X 2Sin^ -y 2COSCr=I 表示的曲线为椭圆时，方程(x+cos α)'+(y+ Sinaf)Jl 所表示的圆的國心在()(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限8. 已知椭圆的焦点为F b F 2,P 是椭圆上的一个动点，如果延长F 卩到Q,使得I PQ I=I PF 2I,那么动点Q 的轨迹是( )(A)圆 (B)椭圆 (C)直线 (D)其它9. 已知椭圆—÷-= 1与圆(χ-a)⅛Λ=9有公共点，则a 的取值范围是()9 4 (A)-6<a<6(B)0<a≤5(C)a 2<25(D) ∣a∣≤610•设椭圆的两个焦点分别为F-、F 2,过F?作椭圆长轴的垂线交椭圆于点P,若AFPFz 为等腰直角三角形，则椭圆的离心率是()(A)YZ(B)幺二！ (C) 2-√2(D) √2-l2 2SS11. 在椭圆—÷γ-≈ 1上取三点，其横坐标满足X I +×3=2X 2,三点依次与某一焦点连结的线段长为r b r 2, r 3,则有 α∙ b・I I 7()(A) r b r 2, r 3成等差数列 (B)丄+丄=二 (C) r b r 2,r 3^等比数列 (C)以上都不对 12•已知椭圆C ι- + y 2= 1的右焦点为F,右准线为/,点Ae/ ,线段4F 交C 于点B,若FA = 3FB, »■]2伍若椭圆之+「I 的离心率是、则W*16 •椭圆X 2COs 2 α +y 2=1 (0< a <ΛR, a≠ y )的半长轴= ------- ,半短轴= -------- ,半焦距= -------- ,离心率= ----------------- = --------- ,則该椭圆的离心率的取值范围为 ____________________ ・(A) (0.1)(B) (0.1)(0(0,#)(D)哼,1)13.已知片、耳是椭國的两个焦点，满足・"庁=0的点M 总在椭圆内部•则椭圆离心率的取值范围是()14. 一个椭圆中心在原点，焦点斤、C 在X 轴上，P (2, √J)是椭圆上一点，且1卩斤1、1斥巴I 、IP 耳I 成等差数列，則椭圆方程为()(A) ⅞4- ⑻护汀<C) ⅜÷⅞ = ∙ I 丽二()(A) √2 (B) 2 (C)^(D) 317.已知椭圆⅛4= ↑(a>b>O)的左、右焦点分别为斤(一c,0),耳(c,0), 若椭圆上存在一点P 使Sin PI71F2 Sin PF l F X是椭圆二+ 2_ = i上的一A,F I,F2是椭圆的焦点，且ZF I MF2=9O o,则ZkFNF?的面积等于9 419•与圆(x+1)2+y2=1相外切，且与IS(X-I)2÷y2=9相内切的动圆圆心的轨迹方程是X = 4COSa , …Ir20•设椭圆( L (□为参数)上一点P与X轴正向所成角ZPOx=-, 点P的坐标是y = 2√3 Sin a 321.在平面直角坐标系.9y中，椭E)4÷4 = 1G∕>∕7>O)的焦距为2c,以0为圆心，为半径作圆M ,若过P(Qe) Cr Iy C作圆M的两条切线相互垂直，则椭圆的离心率为 _________________22•已知直线/ : y=mx+b,椭圆C: (A ^.I)÷y2=1,若对任意实数叫/与C总有公共点，則a, b应满足的条件“是 _________ •23•椭圆F=4cos0 (。

圆锥曲线求解方程

圆锥曲线求解方程全文共四篇示例，供读者参考第一篇示例：圆锥曲线是几何学中的一个重要概念，它包括圆、椭圆、双曲线和抛物线。

圆锥曲线经常出现在数学问题中，我们经常需要求解这些曲线的方程。

本文将介绍如何求解圆锥曲线的方程，并且以具体的实例来解释每种曲线的特点和解法。

我们来看圆的方程。

圆是一种平面上所有点到圆心的距离相等的曲线。

圆的方程一般形式为(x-a)² + (y-b)² = r²，其中(a,b)是圆心的坐标，r是圆的半径。

对于圆心坐标为(2,3)，半径为4的圆，其方程为(x-2)² + (y-3)² = 4²。

第三种圆锥曲线是双曲线。

双曲线是一条开口向内或向外的曲线，其形状介于椭圆和抛物线之间。

双曲线的一般方程形式为(x-h)²/a² - (y-k)²/b² = 1或(y-k)²/b² - (x-h)²/a² = 1，其中(h,k)是双曲线的中心坐标，a和b分别是双曲线在x轴和y轴上的半轴长度。

对于中心坐标为(0,0)，x轴半轴长度为3，y轴半轴长度为2的双曲线，其方程可以是x²/9 - y²/4 = 1或者y²/4 - x²/9 = 1。

最后是抛物线的方程。

抛物线是一种对称的曲线，其形状可以根据焦点的位置而有所不同。

抛物线的一般方程形式为y = ax² + bx + c或者x = ay² + by + c，其中a、b、c是常数。

对于抛物线y = 2x² + 4x + 1，其焦点的位置可以根据方程中的a、b、c来确定。

当遇到圆锥曲线的方程时，我们可以通过观察曲线的形状和特点来快速判断出曲线的类型，并且用数学方法来求解方程。

通过本文的介绍，希望读者能够更加深入地理解圆锥曲线的求解方法，并且能够灵活运用这些方法解决实际问题。

利用圆锥曲线的参数方程解题

利用圆锥曲线的参数方程解题圆锥曲线是数学中常见的曲线类型，它可以通过参数方程来进行描述和求解。

利用圆锥曲线的参数方程，我们可以解决各种与这类曲线相关的问题。

本文将介绍圆锥曲线的参数方程及其解题方法。

一、圆锥曲线的参数方程圆锥曲线包括椭圆、双曲线和抛物线三种类型。

它们的参数方程可以分别表示如下：1. 椭圆的参数方程设椭圆的长半轴为a，短半轴为b，则椭圆的参数方程为：x = a * cos(t)y = b * sin(t)其中，t为参数，范围为[0, 2π)。

2. 双曲线的参数方程双曲线有两种类型：横双曲线和纵双曲线。

它们的参数方程分别为：横双曲线：x = a * sec(t)y = b * tan(t)纵双曲线：x = a * tan(t)y = b * sec(t)其中，t为参数，范围为(-∞, +∞)。

3. 抛物线的参数方程设抛物线的焦点为F，准线为l，焦点到准线的距离为p，则抛物线的参数方程为：x = 2 * p * ty = p * t^2其中，t为参数，范围为(-∞, +∞)。

二、利用圆锥曲线的参数方程解题方法利用圆锥曲线的参数方程解题时，一般需要根据题目给出的条件来确定参数的具体取值范围，并通过参数方程的形式将曲线转化为参数的函数。

然后，可以利用参数方程进行曲线的绘图、求解焦点、顶点、直线与曲线的交点等问题。

下面以一个具体的例子来说明如何利用圆锥曲线的参数方程解题。

例题：已知椭圆的长半轴为2，短半轴为1，求椭圆上与直线y=x+1相交的点的坐标。

解：根据椭圆的参数方程可知：x = 2 * cos(t)y = sin(t)将直线方程代入参数方程中，得：sin(t) = 2 * cos(t) + 1经过一系列的化简与变形，可求得参数t的解。

然后，将参数t的解代入参数方程，即可求得与直线相交的点的坐标。

三、实例分析通过以上的介绍，我们可以看到，利用圆锥曲线的参数方程解题需要对参数方程进行化简、求解方程等操作。

(完整版)解圆锥曲线问题常用方法及性质总结

解圆锥曲线问题常用方法+椭圆与双曲线的经典结论+椭圆与双曲线的对偶性质总结解圆锥曲线问题常用以下方法：1、定义法（1）椭圆有两种定义。

第一定义中，r 1+r 2=2a 。

第二定义中，r 1=ed 1 r 2=ed 2。

（2）双曲线有两种定义。

第一定义中，a r r 221=-，当r 1>r 2时，注意r 2的最小值为c-a ：第二定义中，r 1=ed 1，r 2=ed 2，尤其应注意第二定义的应用，常常将半径与“点到准线距离”互相转化。

（3）抛物线只有一种定义，而此定义的作用较椭圆、双曲线更大，很多抛物线问题用定义解决更直接简明。

2、韦达定理法因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用。

3、解析几何的运算中，常设一些量而并不解解出这些量，利用这些量过渡使问题得以解决，这种方法称为“设而不求法”。

设而不求法对于直线与圆锥曲线相交而产生的弦中点问题，常用“点差法”，即设弦的两个端点A(x 1,y 1),B(x 2,y 2),弦AB 中点为M(x 0,y 0)，将点A 、B 坐标代入圆锥曲线方程，作差后，产生弦中点与弦斜率的关系，这是一种常见的“设而不求”法，具体有：（1）)0(12222>>=+b a b y a x 与直线相交于A 、B ，设弦AB 中点为M(x 0,y 0)，则有02020=+k b y a x 。

（2）)0,0(12222>>=-b a b y a x 与直线l 相交于A 、B ，设弦AB 中点为M(x 0,y 0)则有02020=-k by a x （3）y 2=2px （p>0）与直线l 相交于A 、B 设弦AB 中点为M(x 0,y 0),则有2y 0k=2p,即y 0k=p.椭圆与双曲线的对偶性质总结椭圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b +=上，则过0P 的椭圆的切线方程是00221x x y ya b +=.6. 若000(,)P x y 在椭圆22221x y a b+=外，则过Po 作椭圆的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y y a b +=. 7. 椭圆22221x y a b+= (a ＞b ＞0)的左右焦点分别为F 1，F 2，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=（a ＞b ＞0）的焦半径公式：10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点，A 为椭圆长轴上一个顶点，连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点，则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点，A 1P 和A 2Q 交于点M ，A 2P和A 1Q 交于点N ，则MF ⊥NF.11. AB 是椭圆22221x y a b +=的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则22OM AB b k k a ⋅=-，即0202y a x b K AB -=。

圆锥曲线(抛物线、椭圆、双曲线)标准方程推导

圆锥曲线(抛物线、椭圆、双曲线)标准方程推导几何定义是在平面中，由所有满足到一定点与到一定直线距离相等的点所组成的图形，把这个定点称为焦点(focus)、定直线称为准线(directrix)。

为了方便推导，把这一定点放在x轴正方向上，定直线垂直x 轴放在x轴负半轴上，且原点刚好在两者中间。

上面这些都仅仅是为了推导方便而已。

设曲线上的点坐标为(x,y)，于是，\begin{aligned} d(F, P) &=d(P, D) \\ \sqrt{(x-a)^{2}+(y-0)^{2}} &=|x+a| \\ (x-a)^{2}+y^{2}&=(x+a)^{2} \\ x^{2}-2 a x+a^{2}+y^{2} &=x^{2}+2 ax+a^{2} \\ y^{2} &=4 a x \end{aligned}四种不同开口的标准型：二、椭圆(Ellipse)几何意义是在平面中，由所有到两个顶点距离之和为定值的点所组成的图形，把这两个定点称为焦点(foci)，也是为了推导的方便，把这两个焦点对称放在x轴正负半轴上，令两段距离之和为2a，根据两点之间距离公式进行如下推导：\begin{aligned} d\left(F_{1}, P\right)+d\left(F_{2}, P\right) &=2 a \\ \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}} &=2 a \\ \sqrt{(x+c)^{2}+y^{2}}=& 2 a-\sqrt{(x-c)^{2}+y^{2}} \\ (x+c)^{2}+y^{2}=& 4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}} \\ &+(x-c)^{2}+y^{2} \\x^{2}+2 c x+c^{2}+y^{2}=& 4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}} \\ &+x^{2}-2 c x+c^{2}+y^{2} \\ 4 c x-4 a^{2}=&-4 a \sqrt{(x-c)^{2}+y^{2}} \\ c x-a^{2}=&-a\sqrt{(x-c)^{2}+y^{2}} \\ \left(c x-a^{2}\right)^{2}=& a^{2}\left[(x-c)^{2}+y^{2}\right] \\ c^{2} x^{2}-2a^{2} c x+a^{4}=& a^{2}\left(x^{2}-2 cx+c^{2}+y^{2}\right) \\ \left(c^{2}-a^{2}\right)x^{2}-a^{2} y^{2} &=a^{2} c^{2}-a^{4} \\ \left(a^{2}-c^{2}\right) x^{2}+a^{2} y^{2} &=a^{2}\left(a^{2}-c^{2}\right) \end{aligned}令 b^2=a^2-c^2 （根据三角形两边之和大于第三边推出c<a）所以，\begin{aligned} b^{2} x^{2}+a^{2} y^{2} &=a^{2} b^{2} \\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1\end{aligned}常见的两种椭圆标准方程，一种是横躺在x轴上，一种是“站立”着，关键就是看x和y下面哪个数值比较大，哪个大，那么长的对称轴就在哪个方向上。

圆锥曲线方程知识点总结

圆锥曲线方程知识点总结一、圆锥曲线的基本方程椭圆的标准方程如下：$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. (a > b > 0)$$其中椭圆的长轴为$2a$，短轴为$2b$，焦距为$\sqrt{a^2 - b^2}$，离心率为$c/a$。

双曲线的标准方程如下：$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1. (a > 0, b > 0)$$其中双曲线的两个分支的焦点到中心的距离为$c = \sqrt{a^2 + b^2}$。

抛物线的标准方程如下：$$x^2 = 4ay. (a > 0)$$其中抛物线的焦点为$(0, a)$，顶点为$(0, 0)$。

二、圆锥曲线的参数方程圆锥曲线还可以用参数方程表示。

以椭圆为例，其参数方程为：$$\begin{cases}x = a \cos \theta, \\y = b \sin \theta. \\\end{cases}$$其中$\theta$的取值范围为$[0, 2\pi]$。

双曲线和抛物线的参数方程也可以类似地表示。

三、圆锥曲线的极坐标方程圆锥曲线还可以用极坐标方程表示。

以椭圆为例，其极坐标方程为：$$r = \frac{ab}{\sqrt{a^2 \sin^2 \theta + b^2 \cos^2 \theta}}.$$其中$r$为极径，$\theta$为极角。

双曲线和抛物线的极坐标方程也可以类似地表示。

四、圆锥曲线的性质1. 圆锥曲线关于坐标轴的对称性：- 椭圆关于$x$轴和$y$轴都对称；- 双曲线关于$x$轴和$y$轴都对称；- 抛物线关于$y$轴对称。

2. 圆锥曲线的焦点、直径、离心率等：- 椭圆的焦点到中心的距离为$c = \sqrt{a^2 - b^2}$，离心率为$e = c/a$；- 双曲线的焦点到中心的距离为$c = \sqrt{a^2 + b^2}$，离心率为$e = c/a$；- 抛物线的焦点到中心的距离为$c = a$，离心率为$e = 1$。

专题六第2讲圆锥曲线的方程与性质

易错提醒
求圆锥曲线的标准方程时的常见错误双曲线的定义中忽略“绝对值”致错；椭圆与双曲线中参数的关系式弄混，椭圆中的关系式为a2＝b2＋c2，双曲线中的关系式为c2＝a2＋b2；圆锥曲线方程确定时还要注意焦点位置.
跟踪演练1 (1)已知双曲线的渐近线方程为 y＝± 22x，实轴长为 4，则该双曲线的方程为
cos∠AF1B＝|AF1|22＋|AF|B1F|·|1B|2F－1||AB|2 ＝4m22＋·29mm·23－m9m2＝13，
在△AF1F2中， cos∠F1AB＝|AF1|22＋·|A|AFF1|2·||2A－F|2F| 1F2|2 ＝4m22＋·2mm2·－m 4c2＝cos∠AF1B＝13，
即 cos∠NMM′＝|M|MMN′| |＝ 55，
所以 cos∠OFA＝cos∠NMM′＝ 55， p
而 cos∠OFA＝||OAFF||＝
2＝ 2p2＋22
55，解得
p＝2.
(2)( 多选 )(2022·新高考全国 Ⅱ) 已知 O 为坐标原点，过抛物线 C ： y2 ＝
对于 B，由选项 A 的分析，知直线 AB 的方程为 y＝2 6x－p2，代入 y2＝2px，得 12x2－13px＋3p2＝0，解得 x＝34p 或 x＝13p，所以 xB＝13p，所以 yB＝－ 36p，所以|OB|＝ x2B＋y2B＝ 37p≠|OF|，故 B 不正确；
对于C，由抛物线的定义及选项A，B的分析，得|AB|＝xA＋xB＋p＝1123p＋p＝2152p>2p，即|AB|>4|OF|，故 C 正确；对于 D，易知|OA|＝ 433p，|AM|＝54p，
在抛物线 C 上，射线 FM 与 y 轴交于点 A(0,2)，与抛物线 C 的准线交于

新教材高中数学第三章圆锥曲线的方程章末复习练习含解析新人教A版选择性必修第一册

章末复习一、圆锥曲线的定义及标准方程 1．求圆锥曲线方程的常用方法(1)直接法：动点满足的几何条件本身就是几何量的等量关系,只需把这种关系“翻译”成含x ,y 的等式就得到曲线的轨迹方程．(2)定义法：动点满足已知曲线的定义,可先设定方程,再确定其中的基本量．(3)代入法：动点满足的条件不便用等式列出,但动点是随着另一动点(称之为相关点)而运动的．如果相关点所满足的条件是明显的,或是可分析的,这时我们可以用动点坐标表示相关点坐标,根据相关点所满足的方程即可求得动点的轨迹方程．(4)待定系数法：根据条件能确定曲线的类型,可设出方程形式,再根据条件确定待定的系数． 2．求圆锥曲线方程体现了逻辑推理和数学运算、直观想象的数学素养．例1 (1)已知动点M 的坐标满足方程5x 2＋y 2＝|3x ＋4y －12|,则动点M 的轨迹是( ) A ．椭圆 B ．双曲线 C ．抛物线 D ．以上都不对答案 C解析把轨迹方程5x 2＋y 2＝|3x ＋4y －12|写成x 2＋y 2＝|3x ＋4y －12|5.∴动点M 到原点的距离与它到直线3x ＋4y －12＝0的距离相等．∴点M 的轨迹是以原点为焦点,直线3x ＋4y －12＝0为准线的抛物线．(2)在圆x 2＋y 2＝4上任取一点P ,设点P 在x 轴上的正投影为点D .当点P 在圆上运动时,动点M 满足PD →＝2MD →,动点M 形成的轨迹为曲线C .求曲线C 的方程．解方法一由PD →＝2MD →,知点M 为线段PD 的中点,设点M 的坐标为(x ,y ),则点P 的坐标为(x ,2y )．因为点P 在圆x 2＋y 2＝4上, 所以x 2＋(2y )2＝4,所以曲线C 的方程为x 24＋y 2＝1.方法二设点M 的坐标为(x ,y ),点P 的坐标是(x 0,y 0), 由PD →＝2MD →,得x 0＝x ,y 0＝2y , 因为点P (x 0,y 0)在圆x 2＋y 2＝4上, 所以x 20＋y 20＝4,(*)把x 0＝x ,y 0＝2y 代入(*)式,得x 2＋4y 2＝4, 所以曲线C 的方程为x 24＋y 2＝1.反思感悟 (1)应用定义解题时注意圆锥曲线定义中的限制条件．(2)涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常用定义结合解三角形的知识来解决．(3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转化为到准线的距离,结合几何图形,利用几何意义去解决．跟踪训练1 (1)已知抛物线y 2＝8x 的准线过双曲线x 2a 2－y 2b2＝1(a >0,b >0)的一个焦点,且双曲线的离心率为2,则该双曲线的方程为________．答案 x 2－y 23＝1解析由题意得⎩⎪⎨⎪⎧c ＝2，ca＝2，解得⎩⎪⎨⎪⎧a ＝1，c ＝2，则b 2＝c 2－a 2＝3,因此双曲线方程为x 2－y 23＝1.(2)点P 是抛物线y 2＝8x 上的任意一点,F 是抛物线的焦点,点M 的坐标是(2,3),求|PM |＋|PF |的最小值,并求出此时点P 的坐标．解抛物线y 2＝8x 的准线方程是x ＝－2,那么点P 到焦点F 的距离等于它到准线x ＝－2的距离,过点P 作PD 垂直于准线x ＝－2,垂足为D ,那么|PM |＋|PF |＝|PM |＋|PD |.如图所示,根据平面几何知识,当M ,P ,D 三点共线时,|PM |＋|PF |的值最小, 且最小值为|MD |＝2－(－2)＝4, 所以|PM |＋|PF |的最小值是4.此时点P 的纵坐标为3,所以其横坐标为98,即点P 的坐标是⎝ ⎛⎭⎪⎫98，3. 二、圆锥曲线的几何性质1．本类问题主要有两种考查类型：(1)已知圆锥曲线的方程研究其几何性质,其中以求椭圆、双曲线的离心率为考查重点． (2)已知圆锥曲线的性质求其方程,基本方法是待定系数法,其步骤可以概括为“先定位、后定量”．2．圆锥曲线的性质的讨论和应用充分体现了直观想象和逻辑推理的数学素养．例2 (1)如图,F 1,F 2是椭圆C 1：x 24＋y 2＝1与双曲线C 2的公共焦点,A ,B 分别是C 1,C 2在第二、四象限的公共点．若四边形AF 1BF 2为矩形,则C 2的离心率是( )A. 2B. 3C.32D.62答案 D解析由椭圆可知|AF 1|＋|AF 2|＝4,|F 1F 2|＝2 3.因为四边形AF 1BF 2为矩形, 所以|AF 1|2＋|AF 2|2＝|F 1F 2|2＝12,所以2|AF 1||AF 2|＝(|AF 1|＋|AF 2|)2－(|AF 1|2＋|AF 2|2)＝16－12＝4, 所以(|AF 2|－|AF 1|)2＝|AF 1|2＋|AF 2|2－2|AF 1|·|AF 2|＝12－4＝8, 所以|AF 2|－|AF 1|＝22,因此对于双曲线有a ＝2,c ＝3, 所以C 2的离心率e ＝c a ＝62.(2)已知a >b >0,椭圆C 1的方程为x 2a 2＋y 2b 2＝1,双曲线C 2的方程为x 2a 2－y 2b2＝1,C 1与C 2的离心率之积为32,则C 2的渐近线方程为________．答案 x ±2y ＝0解析设椭圆C 1和双曲线C 2的离心率分别为e 1和e 2,则e 1＝a 2－b 2a ,e 2＝a 2＋b 2a.因为e 1·e 2＝32,所以a 4－b 4a 2＝32,即⎝ ⎛⎭⎪⎫b a 4＝14,所以b a ＝22. 故双曲线的渐近线方程为y ＝±ba x ＝±22x , 即x ±2y ＝0.反思感悟求解离心率的三种方法(1)定义法：由椭圆(双曲线)的标准方程可知,不论椭圆(双曲线)的焦点在x 轴上还是y 轴上都有关系式a 2－b 2＝c 2(a 2＋b 2＝c 2)以及e ＝c a,已知其中的任意两个参数,可以求其他的参数,这是基本且常用的方法．(2)方程法：建立参数a 与c 之间的齐次关系式,从而求出其离心率,这是求离心率的十分重要的思路及方法．(3)几何法：求与过焦点的三角形有关的离心率问题,根据平面几何性质以及椭圆(双曲线)的定义、几何性质,建立参数之间的关系,通过画出图形,观察线段之间的关系,使问题更形象、直观．跟踪训练2 (1)已知椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的半焦距是c ,A ,B 分别是长轴、短轴的一个端点,O 为原点,若△ABO 的面积是3c 2,则此椭圆的离心率是( ) A.12 B.32 C.22 D.33 答案 A解析 12ab ＝3c 2,即a 2(a 2－c 2)＝12c 4,所以(a 2＋3c 2)(a 2－4c 2)＝0,所以a 2＝4c 2,a ＝2c ,故e ＝c a ＝12.(2)已知双曲线x 2a 2－y 2b2＝1(a >0,b >0)的焦距为2c ,右顶点为A ,抛物线x 2＝2py (p >0)的焦点为F .若双曲线截抛物线的准线所得线段长为2c ,且|FA |＝c ,则双曲线的渐近线方程为_________．答案 x ±y ＝0 解析 c 2＝a 2＋b 2,①由双曲线截抛物线的准线所得线段长为2c 知, 双曲线过点⎝⎛⎭⎪⎫c ，－p 2,即c 2a 2－p 24b2＝1.② 由|FA |＝c ,得c 2＝a 2＋p 24,③由①③得p 2＝4b 2.④将④代入②,得c 2a 2＝2.∴a 2＋b 2a 2＝2,即ba＝1,故双曲线的渐近线方程为y ＝±x ,即x ±y ＝0. 三、直线与圆锥曲线的位置关系1．直线与圆锥曲线的位置关系,可以通过讨论直线方程与曲线方程组成的方程组的实数解的个数来确定,通常消去方程组中变量y (或x )得到关于变量x (或y )的一元二次方程,考虑该一元二次方程的判别式．2．借用直线与圆锥曲线问题培养数学运算的数学核心素养．例 3 已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)经过点(0,3),离心率为12,左、右焦点分别为F 1(－c ,0),F 2(c ,0)．(1)求椭圆的方程；(2)若直线l ：y ＝－12x ＋m 与椭圆交于A ,B 两点,与以F 1F 2为直径的圆交于C ,D 两点,且满足|AB ||CD |＝534,求直线l 的方程．解 (1)由题设知⎩⎪⎨⎪⎧b ＝3，c a ＝12，b 2＝a 2－c 2，解得a ＝2,b ＝3,c ＝1, ∴椭圆的方程为x 24＋y 23＝1. (2)由(1)知,以F 1F 2为直径的圆的方程为x 2＋y 2＝1,∴圆心到直线l 的距离d ＝2|m |5, 由d <1得|m |<52.(*) ∴|CD |＝21－d 2＝21－45m 2＝255－4m 2. 设A (x 1,y 1),B (x 2,y 2), 由⎩⎪⎨⎪⎧y ＝－12x ＋m ，x 24＋y 23＝1，得x 2－mx ＋m 2－3＝0,由根与系数的关系可得x 1＋x 2＝m ,x 1x 2＝m 2－3. ∴|AB |＝⎣⎢⎡⎦⎥⎤1＋⎝ ⎛⎭⎪⎫－122[m 2－4m 2－3]＝1524－m 2. 由|AB ||CD |＝534,得 4－m25－4m2＝1, 解得m ＝±33,满足(*)． ∴直线l 的方程为y ＝－12x ＋33或y ＝－12x －33.反思感悟 (1)直线与圆锥曲线的位置关系可以通过代数法判断． (2)一元二次方程的判别式Δ、弦长公式是代数法解决问题的常用工具．跟踪训练3 已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0),其焦点为F 1,F 2,离心率为22,直线l ：x ＋2y－2＝0与x 轴,y 轴分别交于点A ,B .(1)若点A 是椭圆E 的一个顶点,求椭圆的方程；(2)若线段AB 上存在点P 满足|PF 1|＋|PF 2|＝2a ,求a 的取值范围．解 (1)由椭圆的离心率为22,得a ＝2c , 由A (2,0),得a ＝2, ∴c ＝2,b ＝2, ∴椭圆方程为x 24＋y 22＝1.(2)由e ＝22,设椭圆方程为x 2a 2＋2y2a2＝1,联立⎩⎪⎨⎪⎧x 2a 2＋2y 2a2＝1，x ＋2y －2＝0，得6y 2－8y ＋4－a 2＝0,若线段AB 上存在点P 满足|PF 1|＋|PF 2|＝2a ,则线段AB 与椭圆E 有公共点,等价于方程6y 2－8y ＋4－a 2＝0在y ∈[0,1]上有解．设f (y )＝6y 2－8y ＋4－a 2,∴⎩⎪⎨⎪⎧Δ≥0，f 0≥0，即⎩⎪⎨⎪⎧a 2≥43，4－a 2≥0，∴43≤a 2≤4, 故a 的取值范围是⎣⎢⎡⎦⎥⎤233，2. 四、圆锥曲线的综合问题1．圆锥曲线的综合问题包括位置关系证明及定值、最值问题,解决的基本思路是利用代数法,通过直线与圆锥曲线的方程求解．2．圆锥曲线的综合问题的解决培养学生的逻辑推理和数学运算素养．例4 已知抛物线C ：y 2＝2px (p >0)经过点P (2,2),A ,B 是抛物线C 上异于点O 的不同的两点,其中O 为原点．(1)求抛物线C 的方程,并求其焦点坐标和准线方程； (2)若OA ⊥OB ,求△AOB 面积的最小值．解 (1)由抛物线C ：y 2＝2px 经过点P (2,2)知4p ＝4,解得p ＝1. 则抛物线C 的方程为y 2＝2x .抛物线C 的焦点坐标为⎝ ⎛⎭⎪⎫12，0,准线方程为x ＝－12.(2)由题意知,直线AB 不与y 轴垂直,设直线AB ：x ＝ty ＋a ,由⎩⎪⎨⎪⎧x ＝ty ＋a ，y 2＝2x ，消去x ,得y 2－2ty －2a ＝0.设A (x 1,y 1),B (x 2,y 2),则y 1＋y 2＝2t ,y 1y 2＝－2a . 因为OA ⊥OB ,所以x 1x 2＋y 1y 2＝0,即y 21y 224＋y 1y 2＝0,解得y 1y 2＝0(舍去)或y 1y 2＝－4. 所以－2a ＝－4,解得a ＝2.所以直线AB ：x ＝ty ＋2. 所以直线AB 过定点(2,0)．S △AOB ＝12×2×||y 1－y 2＝y 21＋y 22－2y 1y 2＝y 21＋y 22＋8≥2||y 1y 2＋8＝4. 当且仅当y 1＝2,y 2＝－2或y 1＝－2,y 2＝2时,等号成立．所以△AOB 面积的最小值为4.反思感悟 (1)解决最值问题常见的题型,可用建立目标函数的方法求解．(2)圆锥曲线的综合问题可以从分析问题的数量关系入手,利用直线系或曲线系方程或函数方程思想,通过联想与类比,使问题获解．跟踪训练4 已知动圆P 与圆O 1：x 2－x ＋y 2＝0内切,且与直线x ＝－1相切,设动圆圆心P 的轨迹为曲线C . (1)求曲线C 的方程；(2)过曲线C 上一点M (2,y 0)(y 0>0)作两条直线l 1,l 2与曲线C 分别交于不同的两点A ,B ,若直线l 1,l 2的斜率分别为k 1,k 2,且k 1k 2＝1.证明：直线AB 过定点．(1)解由题意可知,动圆圆心P 到点⎝ ⎛⎭⎪⎫12，0的距离与到直线x ＝－12的距离相等,所以点P 的轨迹是以⎝ ⎛⎭⎪⎫12，0为焦点,直线x ＝－12为准线的抛物线,所以曲线C 的方程为y 2＝2x .(2)证明易知M (2,2),设点A (x 1,y 1),B (x 2,y 2),直线AB 的方程为x ＝my ＋b ,联立⎩⎪⎨⎪⎧x ＝my ＋b ，y 2＝2x ，得y 2－2my －2b ＝0,所以⎩⎪⎨⎪⎧y 1＋y 2＝2m ，y 1y 2＝－2b ，所以⎩⎪⎨⎪⎧x 1＋x 2＝2m 2＋2b ，x 1x 2＝b 2，因为k 1k 2＝y 1－2x 1－2·y 2－2x 2－2＝1, 即y 1y 2－2(y 1＋y 2)＝x 1x 2－2(x 1＋x 2), 所以b 2－2b －4m 2＋4m ＝0, 所以(b －1)2＝(2m －1)2, 所以b ＝2m 或b ＝－2m ＋2.当b ＝－2m ＋2时,直线AB 的方程为x ＝my －2m ＋2过定点(2,2)与M 重合,舍去；当b ＝2m 时,直线AB 的方程为x ＝my ＋2m 过定点(0,－2),所以直线AB 过定点(0,－2)．1．(2019·全国Ⅰ)双曲线C ：x 2a 2－y 2b2＝1(a >0,b >0)的一条渐近线的倾斜角为130°,则C 的离心率为( ) A ．2sin 40° B ．2cos 40° C.1sin 50°D.1cos 50°答案 D解析由题意可得－b a＝tan 130°, 所以e ＝1＋b 2a2＝1＋tan 2130° ＝1＋sin 2130°cos 2130° ＝1|cos 130°|＝1cos 50°.2．(2019·全国Ⅱ)若抛物线y 2＝2px (p >0)的焦点是椭圆x 23p ＋y 2p＝1的一个焦点,则p 等于( )A ．2B ．3C ．4D ．8 答案 D解析由题意知,抛物线的焦点坐标为⎝ ⎛⎭⎪⎫p2，0,椭圆的焦点坐标为(±2p ,0), 所以p2＝2p ,解得p ＝8,故选D.3．(2019·全国Ⅰ)已知椭圆C 的焦点为F 1(－1,0),F 2(1,0),过F 2的直线与C 交于A ,B 两点．若|AF 2|＝2|F 2B |,|AB |＝|BF 1|,则C 的方程为( ) A.x 22＋y 2＝1 B.x 23＋y 22＝1 C.x 24＋y 23＝1 D.x 25＋y 24＝1 答案 B解析由题意设椭圆的方程为x 2a 2＋y 2b2＝1(a >b >0),连接F 1A ,令|F 2B |＝m ,则|AF 2|＝2m ,|BF 1|＝3m .由椭圆的定义知,4m ＝2a ,得m ＝a2,故|F 2A |＝a ＝|F 1A |,则点A 为椭圆C 的上顶点或下顶点．令∠OAF 2＝θ(O 为坐标原点),则sin θ＝c a＝1a.在等腰三角形ABF 1中,cos 2θ＝2m2＋3m 2－3m 22×2m ·3m＝13,因为cos 2θ＝1－2sin 2θ,所以13＝1－2⎝ ⎛⎭⎪⎫1a 2,得a 2＝3.又c 2＝1,所以b 2＝a 2－c 2＝2,椭圆C 的方程为x 23＋y 22＝1,故选B.4．(2019·北京)已知椭圆C ：x 2a 2＋y 2b2＝1的右焦点为(1,0),且经过点A (0,1)．(1)求椭圆C 的方程；(2)设O 为原点,直线l ：y ＝kx ＋t (t ≠±1)与椭圆C 交于两个不同点P ,Q ,直线AP 与x 轴交于点M ,直线AQ 与x 轴交于点N .若|OM |·|ON |＝2,求证：直线l 经过定点． (1)解由题意,得b 2＝1,c ＝1, 所以a 2＝b 2＋c 2＝2.所以椭圆C 的方程为x 22＋y 2＝1.(2)证明设P (x 1,y 1),Q (x 2,y 2), 则直线AP 的方程为y ＝y 1－1x 1x ＋1. 令y ＝0,得点M 的横坐标x M ＝－x 1y 1－1.又y 1＝kx 1＋t ,从而|OM |＝|x M |＝⎪⎪⎪⎪⎪⎪x 1kx 1＋t －1.同理,|ON |＝⎪⎪⎪⎪⎪⎪x 2kx 2＋t －1.由⎩⎪⎨⎪⎧y ＝kx ＋t ，x 22＋y 2＝1，得(1＋2k 2)x 2＋4ktx ＋2t 2－2＝0,则x 1＋x 2＝－4kt 1＋2k 2,x 1x 2＝2t 2－21＋2k 2.所以|OM |·|ON |＝⎪⎪⎪⎪⎪⎪x 1kx 1＋t －1·⎪⎪⎪⎪⎪⎪x 2kx 2＋t －1＝⎪⎪⎪⎪⎪⎪x 1x 2k 2x 1x 2＋k t －1x 1＋x 2＋t －12＝2⎪⎪⎪⎪⎪⎪1＋t 1－t .又|OM |·|ON |＝2,所以2⎪⎪⎪⎪⎪⎪1＋t 1－t ＝2.解得t ＝0,所以直线l 经过定点(0,0)．。

求圆锥曲线的方程

求圆锥曲线的方程【复习要点】求指定的圆锥曲线的方程是高考命题的重点，主要考查识图、画图、数形结合、等价转化、分类讨论、逻辑推理、合理运算及创新思维能力，解决好这类问题，除要求熟练掌握好圆锥曲线的定义、性质外，命题人还常常将它与对称问题、弦长问题、最值问题等综合在一起命制难度较大的题，解决这类问题常用定义法和待定系数法.一般求已知曲线类型的曲线方程问题，可采用“先定形，后定式，再定量”的步骤. 定形——指的是二次曲线的焦点位置与对称轴的位置.定式——根据“形”设方程的形式，注意曲线系方程的应用，如当椭圆的焦点不确定在哪个坐标轴上时，可设方程为mx 2+ny 2=1(m ＞0,n ＞0).定量——由题设中的条件找到“式”中特定系数的等量关系，通过解方程得到量的大小. 【例题】【例1】双曲线2224by x -=1(b ∈N )的两个焦点F 1、F 2，P 为双曲线上一点， |OP |＜5,|PF 1|,|F 1F 2|,|PF 2|成等比数列，则b 2=_________.解：设F 1(－c ,0）、F 2(c ,0)、P (x ,y ),则|PF 1|2+|PF 2|2=2(|PO |2+|F 1O |2)＜2(52+c 2), 即|PF 1|2+|PF 2|2＜50+2c 2, 又∵|PF 1|2+|PF 2|2=(|PF 1|－|PF 2|)2+2|PF 1|·|PF 2|, 依双曲线定义，有|PF 1|－|PF 2|=4, 依已知条件有|PF 1|·|PF 2|=|F 1F 2|2=4c 2∴16+8c 2＜50+2c 2,∴c 2＜317,又∵c 2=4+b 2＜317,∴b 2＜35,∴b 2=1.答案：1【例2】已知圆C 1的方程为()()3201222=-+-y x ，椭圆C 2的方程为 12222=+by ax ()a b >>0，C 2的离心率为22，如果C 1与C 2相交于A 、B 两点，且线段AB恰为圆C 1的直径，求直线AB 的方程和椭圆C 2的方程。

圆锥曲线的参数方程

圆锥曲线的参数方程圆锥曲线概述什么是圆锥曲线圆锥曲线是平面上的一类曲线，由一个固定点（焦点）和一个确定的线段（准线）组成。

圆锥曲线可以分为四种类型：椭圆、双曲线、抛物线和直线。

在本文中，我们将重点探讨圆锥曲线的参数方程，即用参数表示曲线上的点的坐标。

为什么使用参数方程参数方程是一种用参数表示曲线上的点的坐标的方法。

相比于直角坐标系下的方程，参数方程具有以下优点：1.可以更方便地描述曲线上的点的运动轨迹。

2.可以更容易地计算曲线上的点的坐标。

3.对于某些曲线，参数方程可以提供更简洁的表示方法。

圆锥曲线的参数方程示例在接下来的部分中，我们将分别介绍椭圆、双曲线、抛物线和直线的参数方程，并给出示例。

椭圆的参数方程椭圆的定义椭圆是由平面上到两个给定点的距离之和等于常数的点构成的图形。

这两个给定点分别称为焦点。

椭圆的参数方程对于以原点为中心的椭圆，其参数方程可以表示为：x = a cosθ y = b sinθ其中a和b分别表示长轴和短轴的长度，θ为参数。

参数θ通常取值范围为0到2π。

椭圆的示例以长轴长度为5，短轴长度为3的椭圆为例，其参数方程为：x = 5cosθ y = 3sinθ当θ的取值在0到2π范围内变化时，椭圆上的点的坐标将按照参数方程给出的公式进行计算。

双曲线的参数方程双曲线的定义双曲线是由平面上到两个给定点的距离之差等于常数的点构成的图形。

这两个给定点分别称为焦点。

双曲线的参数方程对于以原点为中心的双曲线，其参数方程可以表示为：x = a coshθ y = b sinhθ其中a和b分别表示长轴和短轴的长度，θ为参数。

参数θ通常取值范围为负无穷到正无穷。

双曲线的示例以长轴长度为5，短轴长度为3的双曲线为例，其参数方程为：x = 5coshθ y = 3sinhθ当θ的取值在负无穷到正无穷范围内变化时，双曲线上的点的坐标将按照参数方程给出的公式进行计算。

抛物线的参数方程抛物线的定义抛物线是由平面上到一个给定点和一条给定线段长度之和相等的点构成的图形。

圆锥曲线轨迹方程的求法

圆锥曲线轨迹方程的求法
一、直接法求轨迹方程
利用动点运动的条件得到等量关系，表示为x和y的等式。

例如，已知点A(-2,0)和B(3,0)，动点P(x,y)满足PA·PB=x²，
那么点P的轨迹是抛物线。

二、有定义法求轨迹方程
根据圆锥曲线的基本定义解题。

例如，已知圆O的方程
为x²+y²=100，点A的坐标为(-6,0)，M为圆O上的任意一点，AM的垂直平分线交OM于点P，那么点P的轨迹方程为
25/16=(x+3)²/y²，即椭圆。

三、用相关点法求轨迹方程
当动点M随着已知方程的曲线上另一动点C(x,y)运动时，找出点M与点C之间的坐标关系式，用(x,y)表示(x,y)，再将
x和y代入已知曲线方程，即可得到点M的轨迹方程。

例如，从双曲线x²-y²=1上一点Q引直线x+y=2的垂线，垂足为N，
求线段QN的中点P的轨迹方程。

设动点P的坐标为(x,y)，点
Q的坐标为(x₁,y₁)，则N点的坐标为(2x-x₁,2y-y₁)。

因为N
点在直线x+y=2上，所以2x-x₁+2y-y₁=2.又因为PQ垂直于直线x+y=2，所以x-y+y₁-x₁=0.将两个方程联立，得到
x₁=2x+2y-1和y₁=2x+2y-1.因为点Q在双曲线上，所以x₁²-y₁²=1.将x₁和y₁代入公式中，得到动点P的轨迹方程式为2x²-2y²-2x+2y-1=0.
四、用参数法求轨迹方程
选取适当的参数，分别用参数表示动点坐标得到动点轨迹的普通方程。

收藏：圆锥曲线综合五个类型

（一）求圆锥曲线方程求圆锥曲线方程分为五个类型，求解策略一般有以下几种： ①几何分析+方程思想； ②设而不求+韦达定理 ③定义+数形结合； ④参数法+方程思想类型1——待定系数法待定系数法本质就是通过对几何特征进行分析，利用图形，结合圆锥曲线的定义与几何性质，分析图中已知量与未知量之间的关系，列出含有待定系数的方程，解出待定的系数即可。

例1.2014年全国Ⅱ卷（理科20）设 F 1 、 F 2 分别是椭圆 C :x 2a 2+y 2b 2=1 a >b >0 的左、右焦点，M 是 C 上一点且 MF 2 与 x 轴垂直，直线 MF 1 与 C 的另一个交点为 N ．Ⅰ 若直线 MN 的斜率为 34，求 C 的离心率；Ⅱ 若直线 MN 在 y 轴上的截距为 2，且 ∣MN ∣=5∣F 1N ∣，求 a ，b ．【解法分析】第Ⅱ小题利用试题提供的几何位置关系和数量关系，结合椭圆的几何性质和方程思想，通过待定系数法进行求解。

着重考查椭圆的几何性质，将几何特征转化为坐标表示，突显数形结合的思想。

.21∴.2102-32.,4321∴4322222211的离心率为解得，联立整理得：且由题知，C e e e c b a c a b F F MF ==++==•=72,7.72,7.,,1:4:)23-(,:.23-,,.4,.42222211111122====+===+=+====•=b a b a c b a ace NF MF c e a NF ec a MF c c N M m MF m N F ab MF 所以，联立解得，且由焦半径公式可得两点横坐标分别为可得由两直角三角形相似，由题可知设，即知，由三角形中位线知识可类型2——相关点法求轨迹方程动点P(x ，y)依赖与另一个动点Q(x 0，y 0)变化而变化，并且动点Q(x 0，y 0)又在另一个已知曲线上，则可先用x ，y 表示x 0，y 0，再将x 0，y 0代入已知曲线，可得到所求动点的轨迹方程。