5-2_期权定价的二叉树模型概论

合集下载

第五讲期权定价理论I二叉树模型

15
记每步时长为Δt，那么单步二叉树模型下的期权价格为：
f=e-rΔt[pfu +(1-p)fd] 其中，p=(erΔt-d)/(u-d)。由此可以计算出期初和第一步
到期时各个节点的期权价值：
fu=e-rΔt[pfuu+(1-p)fud] fd=e-rΔt[pfud+(1-p)fdd]
f=e-rΔt[pfu+(1-p)fd] 把fu和fd代入f可得：
f=e-2rΔt[ p2 fuu+2p(1-p)fud+(1-p)2 fdd] 因此，期权的价格为期权预期收益以无风险利率进行
贴现的现值。想象一下，三步二叉树模型下期权的定价问题。
16
（四）看跌期权的情形
例5：考虑如下图11.7两年期的欧式看跌股票期权，执行价格为52元，股票的当期价格为50元，假设时期分为两步，每步期长为1年，且每步股票价格要么上涨20%，要么下跌20%，无风险利率为5%。
23
（七）Δ
回忆：Δ是什么？ Δ=(fu–fd)/(S0u-S0d) 什么意思？ Δ为期权价格变化与标的股票价格的变化之比； Δ为我们针对每个期权空头而持有的股票数量，
目的是构建一个无风险资产组合。 Δ对冲（delta hedging）通常是指构建一个无风险
对冲。看涨期权的Δ为正，看跌期权的Δ为负。计算图11.1和11.7中的Δ。
26
4. 期货期权的定价在风险中性世界里，期货的价格增长率为0。假设期货
的为期F0，初因价此格，为F0，时间长度为Δt的期货的期望价格也 E(FT)=pF0u+(1-p)F0d=F0 p=(1-d)/(u-d) 例10：一个期货的当前价格为31，波动率为30%，无风

期权定价的二叉树模型(ppt 39页)

第7章期权定价的二叉树模型
2022/3/23
22
ftrf S S f1 22S2 S 2f2rf f
c St N d1 X erf Tt N d2
St erf Tt N d1 X N d2 erf Tt
EST Nd1 X N d2 erf Tt EST Nd1 X N d2 erf Tt
2022/3/23
21
风险中性定理表达了资本市场中的这样的一个结论：即在市场不存在任何套利可能性的条件下，如果衍生证券的价格依然依赖于可交易的基础证券，那么这个衍生证券的价格是与投资者的风险态度无关的。
这个结论在数学量，尤其是期望收益率。
公平的入局费＝2000×50％+0×50％＝ 1000元
第7章期权定价的二叉树模型
2022/3/23
13
愿意支付的入局费风险类型数量入局费＜1000元风险厌恶者众多入局费＝1000元风险中性者入局费＞1000元风险喜好者极少
如果有人愿意无条件地参加公平的赌博，则这样的人被认为是风险中性。风险中性者对风险采取无所谓的态度。
考虑以下组合：
①买入1份股票看涨期权 ②卖空Δ股股票
显然，适当调整Δ可以使得上述组合为无风险组合。
第7章期权定价的二叉树模型
2022/3/23
3
如果这个组合是无风险组合，则其价值与状态无关，所以，以下数学表达式成立：
22118
解得，
0.25
也就是说，1份看涨期权多头加上0.25股股票空头构成的组合是无风险组合。
这就是风险中性定价的基本思想。
第7章期权定价的二叉树模型
2022/3/23
18
我们回到之前的示例中，在那里，我们可以把股票价格上升的概率定义为p，于是在到期日T时刻，股票价格的期望值为：

期权定价二叉树模型

9 e
0.10.25
8.78
• 这也应该是期初用于投资组合的资金，由此得：
1 30 C 8.78, C 10 8.78 1.22 3 • 买入期权的价格应该定为1.22元
三、期权定价的二项式公式
符号: S 0 股票在期初的价格, S X 期权确定的执行价格, u 股票价格在单个时间阶段内的上升因子 d 股票价格在单个时间阶段内的下降因子(-) Ru 期权在股票价格上升状态下的收益 Rd 期权在股票价格下降状态下的收益 r 年无风险收益率 T 期权的期限
7.14 qu max{ S 0 (1 u ) 3 (1 d ) S X ,0} q d max{ S 0 (1 u ) 2 (1 d ) 2 S X ,0}
0.33 qu max{ S 0 (1 u ) 2 (1 d ) 2 S X ,0} q d max{ S 0 (1 u )(1 d ) 3 S X ,0}
n n i i n i i C i qu q d max{ S 0 (1 u ) (1 d ) S X ,0} i 0
n
n n! n (n 1) (n i 1) , n 0,1, i (i 1) 1 i (n i )!i !
0 qu max{ S 0 (1 u ) 3 (1 d ) S X ,0} qd max{ S 0 (1 d ) 4 S X ,0}
对于第2阶段各状态期权价值有
2 13.7 qu 18.03 q d 7.14 qu max{ S 0 (1 u ) 4 S X ,0}
计算相关数据

u (e rT 1) ud 0.1 (e 0.05 1) 0.1 0.05 0.324859

期权定价公式的二叉树推导与分析

期权定价公式的二叉树推导与分析期权作为金融衍生品的重要组成部分，对于投资者和风险管理师来说具有重要意义。

期权的价值取决于多种因素，包括标的资产的价格、行权价格、剩余到期时间、无风险利率、波动率等。

期权的定价是金融领域的一个重要问题，准确的期权定价可以帮助投资者更好地进行投资决策和风险管理。

本文将介绍期权的定价公式，并通过二叉树的方法推导期权的价格，最后对各种情况下期权定价的计算方法与特点进行分析。

期权的定价公式是由费雪·布莱克、迈伦·斯科尔斯和罗伯特·默顿提出的布莱克-斯科尔斯模型。

该模型基于一些假设，例如无摩擦市场、无套利机会等，通过 Black-Scholes方程求解期权的定价。

具体公式如下：C = SₐN(d1) - XₐN(d2)其中， C为期权的公允价值； Sₐ为标的资产当前的价格； Xₐ为期权的行权价格； N(d1)和 N(d2)分别为正态分布变量的累积分布函数；d1和 d2分别为： d1 = (ln(Sₐ/Xₐ) + (r + σ²/2)T) / (σ√T) d2 = d1 - σ√T T为期权的剩余到期时间，以年为单位； r为无风险利率；σ为标的资产的年波动率。

二叉树方法是一种常用的期权定价模型，它可以用来推导期权的预期价格。

二叉树方法的思路是将期权的到期时间划分为若干个时间段，并假设标的资产在每个时间段内只有两种可能的价格，即上涨或下跌。

基于这个假设，我们可以构建一个二叉树来描述标的资产的价格变动情况。

假设初始时刻为 t0，标的资产的价格为 S0，行权价格为 X。

在每个时间段Δt内，标的资产的价格有两种可能的变化：上涨到 Su = S0 × u，或者下跌到 Sd = S0 × d，其中 u > 1，d < 1，u和 d分别为标的资产的上涨和下跌因子。

假设该期权的剩余到期时间为 T，共分为 n个时间段。

那么在 t0时，该期权的预期价格为：C0 = ∑CN(d1, d2, u, d) × (u × S0 - X)^+ ×Δt其中， N(d1, d2, u, d)为风险中性概率； (u × S0 - X)^+表示当标的资产价格上涨时，取 u × S0 - X，否则取 0；Δt为每个时间段的时间长度。

期权定价的二叉树模型

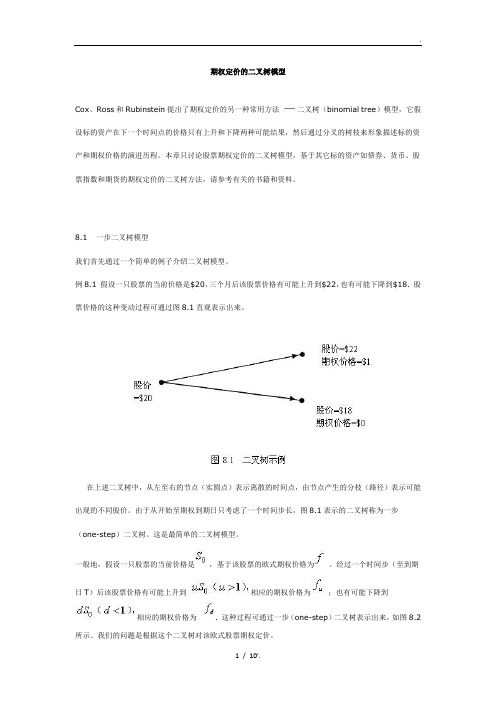
期权定价的二叉树模型Cox、Ross和Rubinstein提出了期权定价的另一种常用方法二叉树（binomial tree）模型，它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果，然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。

本章只讨论股票期权定价的二叉树模型，基于其它标的资产如债券、货币、股票指数和期货的期权定价的二叉树方法，请参考有关的书籍和资料。

8.1 一步二叉树模型我们首先通过一个简单的例子介绍二叉树模型。

例8.1 假设一只股票的当前价格是$20，三个月后该股票价格有可能上升到$22，也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。

在上述二叉树中，从左至右的节点（实圆点）表示离散的时间点，由节点产生的分枝（路径）表示可能出现的不同股价。

由于从开始至期权到期日只考虑了一个时间步长，图8.1表示的二叉树称为一步（one-step）二叉树。

这是最简单的二叉树模型。

一般地，假设一只股票的当前价格是，基于该股票的欧式期权价格为。

经过一个时间步（至到期日T）后该股票价格有可能上升到相应的期权价格为；也有可能下降到相应的期权价格为. 这种过程可通过一步（one-step）二叉树表示出来，如图8.2所示。

我们的问题是根据这个二叉树对该欧式股票期权定价。

为了对该欧式股票期权定价，我们采用无套利（no arbitrage）假设，即市场上无套利机会存在。

构造一个该股票和期权的组合（portfolio），组合中有股的多头股票和1股空头期权。

如果该股票价格上升到，则该组合在期权到期日的价值为；如果该股票价格下降到，则该组合在期权到期日的价值为。

根据无套利假设，该组合在股票上升和下降两种状态下的价值应该相等，即有由此可得(8.1)上式意味着是两个节点之间的期权价格增量与股价增量之比率。

在这种情况下，该组合是无风险的。

以表示无风险利率，则该组合的现值（the present value）为,又注意到该组合的当前价值是，故有即将(8.1)代入上式，可得基于一步二叉树模型的期权定价公式为(8.2)(8.3)需要指出的是，由于我们是在无套利（no arbitrage）假设下讨论欧式股票期权的定价，因此无风险利率应该满足： .现在回到前面的例子中，假设相应的期权是一个敲定价为$21，到期日为三个月的欧式看涨权，无风险的年利率为12%，求该期权的当前价值。

期权定价的二叉树模型

03
二叉树模型在期权定价中的应用
二叉树模型在欧式期权定价中的应用
欧式期权定义
二叉树模型原理
欧式期权是一种只能在到期日行权的期权。
二叉树模型是一种离散时间模型，通过构造一个二叉树来模拟股票价格的演变过程。
模型参数
定价过程
包括无风险利率、股票波动率、期权行权价等。
从到期日逆推至起始时间，考虑各种可能的价格路径，计算期权的预期收益，并使用无风险利率折现至起始时间。
与其他理论的结合
二叉树模型与其它金融理论的结合也是理论研究的一个重要方向，如将二叉树模型与随机过程理论、博弈论等相结合，以提供更深入、更全面的分析框架。
二叉树模型的应用研究进展
扩展到其他金融衍生品
二叉树模型在期权定价方面的应用已经非常成熟，研究者们正在将其应用于其他金融衍生品的定价，如期货、掉期等。
案例一：某公司股票期权定价
背景介绍
某上市公司股票期权激励计划需要为期权定价，以确定向员工发放的期权数量和行权价格。
模型应用
根据二叉树模型，预测股票价格的上涨和下跌幅度，并计算期权的内在价值和时间价值。
结论分析
根据计算结果，确定期权的行权价格和数量，实现了员工激励与公司发展的双赢。
案例二：某交易所债券期权定价
调整利率和波动率
根据市场数据和实际情况，调整利率和波动率的参数，可以提高模型的拟合度。
模型的选择与比较
1 2
基于误差
比较不同模型的预测误差，选择误差最小的模型。
基于风险
比较不同模型的风险指标，选择风险最小的模型。
3
基于解释性
选择更具有解释性的模型，以便更好地理解市场行为和风险。
05

期权定价的二叉树模型介绍

险利率。
计算期权的价值
计算期权的现值
根据预期收益和折现率，我们可以计算出期权的现值。看涨期权的现值是每个节点的股票价格与执行价格的差值与风险中性概率的乘积之和；看跌期权的现值是每个节点的执行价格与股票价格的差值与风险中性概率的乘积之和。
校准二叉树模型参数
为了使模型的预测结果与实际期权价格一致，我们需要校准模型参数。通常，我们使用历史数据来估计参数，例如股票价格的波动率和无风险利率。
建立二叉树
以时间步长为单位，从最后一个时间步长开始，依次向前建立二叉树，每个节点代表一个时间步长。
确定初始股票价格
确定股票的当前价格
通常以市场价格为基础确定初始股票价格。
考虑股息
如果股票在期权有效期内发放股息，需要在每个时间步长上调整股票价格。
确定无风险利率与时间步长
要点一
确定无风险利率
无风险利率是投资者在相同风险水平下可以获得的最低回报率。
05
二叉树模型的结果分析
模拟结果展示
假设一个股票价格变动模型，通过二叉树模型模拟股票价格的涨跌情况，并计算期权的价值。
根据不同的利率和波动率等参数设置，模拟不同的股票价格路径，从而得到期权价格的模拟结果。
结果分析与比较
将模拟结果与实际期权价格进行比较，分析二叉树模型定价的准确性。
对比不同参数设置下的模拟结果，分析利率和波动率等因素对期权价格的影响。
期权定价的二叉树模型介绍
2023-11-06
目录
• 引言 • 二叉树模型基本原理 • 构建二叉树模型 • 计算期权价值 • 二叉树模型的结果分析 • 二叉树模型在金融实践中的应用 • 结论与展望
01
引言
研究背景与意义

第八章期权及其二叉树模型-PPT文档资料

第八章期权及其二叉树模型
金融期权（financial option）简称为期权是主要的金融衍生产品，它是金融工程的主要工具,也是构成金融工程其它金融衍生产品的基础。
期权合约是买卖双方签定的一种协议，该协议赋予期权购买者在未来某一时刻以事先约定的价格购买(或出售）某一资产的权利。但是，那时他可以行使他的权利也可以不行使这个权利。如果到了规定的时间，而不行使这种权利，则这种权利就失效了。
令
1 r d p= ud
u 1 r 1-p= u d
1 r
p C u 1 pC d C
p称为套期保值概率。
事实上,若投资者是风险中性，则有
( 1) r Sq u S ( 1) q d S
由此得
1 r d q= ud
二、在(S,W)平面上欧式看涨期权和看跌期权的损益表示设股票初始价格为S, 期权的执行价格为股票初始价格，令
S S T S
W为期权的收益 (一) 在(S,W)平面上看涨期权多头和看涨期权空头的收益 (二) 在(S,W)平面上看跌期权多头和看跌期权空头的收益三、在(S,W)平面上, 股票和债券的收益:(为了说
3. 蝶式价差买卖(butterfly spread）：它是牛市价差买卖与熊市价差买卖的组合，即购入一份执行价格为 X1和一份执行价格为X2的看涨期权，再卖出两份执行价格为X3的看涨期权。其中，X2> X3 > X1 ，且 X1 X2 X3 2
4. 底部马鞍式组合（ bottom straddle 或买马鞍式）：购入一份看涨期权和一份看跌期权，执行价格均为 X 5. 顶部马鞍组合（top straddle 或卖马鞍式)：卖出一份看涨期权和一份看跌期权，执行价格均为 X 6. 底部梯形组合（Bottom vertical combination 或买入梯形组合)：买入一份看涨期权和一份看跌期权,执行价格分别是 X1和X2，其中X2 >X1。 7. 顶部梯形组合（Top vertical combination 或卖出梯形组合)：卖出一份看涨期权和一份看跌期权，执行价格分别为 X1和X2，其中X2 >X1 。

期权定价的二叉树模型

期权定价的二叉树模型期权定价是金融领域中的重要问题之一，而二叉树模型是一种经典的期权定价工具。

二叉树模型的主要思想是将期权到期日之间的时间划分为多个等长的时间段，并根据每个时间段内的股价变动情况来计算期权的价值。

下面将介绍二叉树模型的构建过程以及期权定价的基本原理。

首先，我们需要确定二叉树模型的参数。

主要包括股票价格的初始值、期权到期日、无风险利率、每个时间段的长度等。

其中，股票价格的初始值可以通过市场价格获取，期权到期日通常由合约确定，无风险利率可以参考国债收益率，而每个时间段的长度可以根据需要自行设置。

接下来，根据二叉树模型的思想，我们构建一个二叉树。

树的每个节点表示一个时间段，而每个节点下方的两个子节点分别表示股票价格在该时间段内上涨和下跌的情况。

具体构建二叉树的方式有很多种，常见的有Cox-Ross-Rubinstein模型和Jarrow-Rudd模型。

其中，Cox-Ross-Rubinstein模型是一种离散时间模型，每个时间段内股价上涨或下跌的幅度是固定的；而Jarrow-Rudd模型是一种连续时间模型，股价的变动是连续的。

在构建好二叉树之后，我们需要从期权到期日开始反向计算每个节点的期权价值。

通过回溯法，我们可以计算出每个节点的期权价值。

具体计算的方式是，对于期权到期日的节点，其价值等于股价与行权价格的差值（对于欧式期权而言）或者最大值（对于美式期权而言）。

而对于其他节点，其价值等于期权在上涨和下跌情况下的期望值，即其左右子节点的价值经过贴现后得到的值。

通过不断回溯，最终我们可以得到二叉树的根节点即为期权的实际价值。

需要注意的是，期权定价的准确性与二叉树模型的参数设定和树的构建方法有关。

参数的选择需基于市场数据和合理的假设，而构建二叉树的方法应能很好地反映实际股价的变动规律。

此外，二叉树模型也有一定的局限性，特别是在处理股价波动较为剧烈的情况下，可能无法准确地定价。

总之，二叉树模型是一种常用的期权定价工具，可以通过构建二叉树和回溯计算的方式来估计期权的价值。

期权定价-二叉树模型

期权定价-二叉树模型期权定价是金融市场中的重要内容，它是根据期权的特点和市场条件来确定期权价格的过程。

二叉树模型是一种常用的期权定价方法之一，其基本思想是将时间离散化，并通过构建一个二叉树来模拟标的资产价格的变动。

在二叉树模型中，每个节点代表了一个特定的时刻，而每个节点之间的关系是通过上涨和下跌两种情况进行连接的。

通过调整上涨和下跌的幅度，可以模拟出不同标的资产的价格变动情况。

期权的定价在二叉树模型中可以通过回溯法进行计算。

首先，在最后一个节点上，根据期权的特点以及市场条件来确定期权的价值。

然后，逐步向前回溯，通过考虑不同的路径来计算每个节点上的期权价值。

在回溯过程中，需要考虑每个节点的两个子节点的权重，即上涨和下跌的概率。

这可以根据市场条件来确定，通常是基于历史数据进行估计。

然后，在回溯过程中，可以根据节点上的期权价值和子节点的权重来计算每个节点的期权价格。

通过不断回溯，最终可以得到期权的初始价值，即在当前市场条件下，期权价格应该是多少。

这个初始价值可以用作参考，帮助投资者做出合理的投资决策。

需要注意的是，二叉树模型是一个简化的模型，它有一些假设和限制。

首先，它假设标的资产的价格只有上涨和下跌两种情况，而忽略了其他可能的情况。

其次，它假设市场条件在整个期权有效期内保持不变，而实际情况可能是变化的。

因此，在使用二叉树模型进行期权定价时，需要注意这些假设和限制。

总而言之，期权定价是金融市场中的重要内容，二叉树模型是一种常用的定价方法。

通过构建二叉树模型，并根据回溯法计算每个节点上的期权价值，可以得到期权的初始价格。

然而，需要注意二叉树模型的假设和限制，并结合实际情况进行综合分析和判断。

期权定价是金融市场中的重要内容，其旨在确定期权的合理价格。

期权是一种金融工具，赋予购买者在期权到期时以约定价格购买或出售标的资产的权利。

很多投资者都希望能够在市场上买入或者卖出期权，以便于在未来某个时刻获得利润。

因此，了解期权的合理价格对投资者来说至关重要。

金融数学第五讲期权定价二叉树方法ppt课件

推广到一般情形
一个依赖于股票的衍生证券，到期时间为 T
Su
S
ƒu
ƒ
Sd
ƒd
推广到一般情形
(continued)
考虑一个组合：持有D份股票，成为一份衍生证券的空头
当 D满足下面的条件时，组合为无Su风D –险ƒ：u
SuD
–
ƒu
=
Sd
DS–dDƒd–
or ƒd
D ƒu fd Su Sd
S*(iDt)S(iDt)
当 iDt 时
S * (iD t) S (iD t) D e r( iD t) 当 iDt 时（表示红利）
在 iDt 时刻：
当 iDt 时，这个树上每个结点对应的证券价格为：S0*ujdijD er(iDt) 当 iDt 时，这个树上每个结点对应的证券价格为：S0*u jdi j
无风险组合为: 持有 0.25份股票成为一份看涨期权的空头
三个月后组合的价值为 22´0.25 – 1 = 4.50 组合在时刻0的价值为 4.5e – 0.12´0.25 = 4.3670
期权的估值
资产组合为持有 0.25份股票
成为一份看涨期权的空头组合在时刻0的价值为4.3670 股票的价值是 5.000 (= 0.25×20 ) 从而，期权的价格为 0.633 (= 5.000 – 4.367 )
72 D0
48
E
4
32 F 20
美式期权该如何估值？
50 5.0894
A
60
B
1.4147
40
C
12.0
72 D0
48
E
4
32 F 20