材料力学课件 强度理论
合集下载
材料力学课件 强度理论讲诉

n
[s ]
可见:a) 与s2、s3无关; b) 应力su可用单向拉伸试样发生脆性断裂的
试验来确定。
实验验证:铸铁:单拉、纯剪应力状态下的破坏与 该理论相符;平面应力状态下的破坏和该理论基本 相符。
存在问题:没有考虑s2、s3对脆断的影响,无法解
释石料单压时的纵向开裂现象。
2)最大伸长线应变理论(第二强度理论)
1
2
s1
s 2 2
s 2
s 3 2
s1
s 3 2
ss
n
[s ]
实验验证: a) 较第三强度理论更接近实际值;
b) 材料拉压性能相同时成立。
强度理论的统一形式: s r [s ]
sr称为相当应力,分别为:
• 最大拉应力(第一强度)理论:
s r1 s1
• 最大伸长线应变(第二强度)理论:
可见:材料破坏的形式不仅与材料有关,还与 应力状态有关。
5)强度理论
根据一些实验资料,针对上述两种破坏形式, 分别针对它们发生破坏的原因提出假说,并认为不 论材料处于何种应力状态,某种类型的破坏都是由 同一因素引起,此即为强度理论。
常用的破坏判据有:
脆性断裂: s l max 塑性断裂: max
研究复杂应力状态下材料破坏的原因,根据一 定的假设来确定破坏条件,从而建立强度条件,这 就是强度理论的研究内容。
4)材料破坏的形式 常温、静载时材料的破坏形式大致可分为:
• 脆性断裂型: 例如: 铸铁:拉伸、扭转等; 低碳钢:三向拉应力状态。
• 塑性屈服型: 例如: 低碳钢:拉伸、扭转等; 铸铁:三向压缩应力状态。
s r2 s1 s 2 s 3
• 最大切应力(第三强度)理论: s r3 s1 s 3
[s ]
可见:a) 与s2、s3无关; b) 应力su可用单向拉伸试样发生脆性断裂的
试验来确定。
实验验证:铸铁:单拉、纯剪应力状态下的破坏与 该理论相符;平面应力状态下的破坏和该理论基本 相符。
存在问题:没有考虑s2、s3对脆断的影响,无法解
释石料单压时的纵向开裂现象。
2)最大伸长线应变理论(第二强度理论)
1
2
s1
s 2 2
s 2
s 3 2
s1
s 3 2
ss
n
[s ]
实验验证: a) 较第三强度理论更接近实际值;
b) 材料拉压性能相同时成立。
强度理论的统一形式: s r [s ]
sr称为相当应力,分别为:
• 最大拉应力(第一强度)理论:
s r1 s1
• 最大伸长线应变(第二强度)理论:
可见:材料破坏的形式不仅与材料有关,还与 应力状态有关。
5)强度理论
根据一些实验资料,针对上述两种破坏形式, 分别针对它们发生破坏的原因提出假说,并认为不 论材料处于何种应力状态,某种类型的破坏都是由 同一因素引起,此即为强度理论。
常用的破坏判据有:
脆性断裂: s l max 塑性断裂: max
研究复杂应力状态下材料破坏的原因,根据一 定的假设来确定破坏条件,从而建立强度条件,这 就是强度理论的研究内容。
4)材料破坏的形式 常温、静载时材料的破坏形式大致可分为:
• 脆性断裂型: 例如: 铸铁:拉伸、扭转等; 低碳钢:三向拉应力状态。
• 塑性屈服型: 例如: 低碳钢:拉伸、扭转等; 铸铁:三向压缩应力状态。
s r2 s1 s 2 s 3
• 最大切应力(第三强度)理论: s r3 s1 s 3
材料力学第9章 强度理论
由于物体在外力作用下所发生的弹性变形既包括 物体的体积改变,也包括物体的形状改变,所以可推 断,弹性体内所积蓄的变形比能也应该分成两部分: 一部分是形状改变比能(畸变能) ,一部分是体积改 变比能 。 在复杂应力状态下,物体形状的改变及所积蓄的 形状改变比能是和三个主应力的差值有关;而物体体 积的改变及所积蓄的体积改变比能是和三个主应力的 代数和有关。
注意:图示应力状态实际上为弯扭组合加载对 应的应力状态,其相当应力如下:
r 3 2 4 2 [ ] 2 2 [ ] r 4 3
可记住,便于组合变形的强度校核。
例1 对于图示各单元体,试分别按第三强度理论及第四强度理论 求相当应力。
120 MPa 140 MPa
r4
1 2 2 2 [(0 120) ( 120 120) ( 120 0) ] 120MPa 2
140 MPa
(2)单元体(b)
σ1 140MPa
σ 2 110MPa
σ3 0
110 MPa
σr 3 σ1 σ 3 140MPa 1 2 2 2 σr 4 [30 110 ( 140) ] 128MPa 2
1u
1u
E
b
E
1 1 1 2 3 E
1u
1u
E
b
E
1 2 3 b
强度条件为: 1 2 3
b
n
[ ]
实验验证: a) 可解释大理石单压时的纵向裂缝; b) 脆性材料在双向拉伸-压缩应力状态下,且压应 力值超过拉应力值时,该理论与实验结果相符合。
σ1 94 .72MPa σ 3 5 .28MPa
材料力学课件 第八章 强度理论

3
8
复杂应力状态下:单元体的三个主应力有无穷多个组合, 直接由试验得出的破坏条件一般不适应。
强度理论:是关于“构件发生强度失效(failure by lost strength)起因”的假说。
4
8
二、材料的破坏形式
铸铁与低碳钢的拉、压、扭试验的破坏现象 P M 低碳钢 铸铁拉伸 铸铁压缩 P
铸铁
r1
Wt
r 2 1
r 3 2
r 4 3
29
30
1 1 2 2 2 3 2 3 1 2 ux 6E
1、破坏判据: 2、强度准则
1 1 2 2 2 3 2 3 1 2 s 2
1 1 2 2 2 3 2 3 1 2 2
13
18
一、两个概念:1、极限应力圆:
2、极限曲线:极限应力圆的包络线(envelope)。
s极限应力圆
极限应力圆的包络线
s3
O
s2
s1
近似包络线
14
20
二、莫尔强度理论:任意一点的应力圆若与极限曲线相接触,
则材料即将屈服或剪断。 M P [ y] O2 3 N o O3 O1
3、实用范围:实用于破坏形式为屈服的构件。
16
§8–3
莫尔强度理论及其相当应力
莫尔认为:最大剪应力 是使物体破坏的主要因素, 但滑移面上的摩擦力也不可 忽略(莫尔摩擦定律)。综 合最大剪应力及最大正应力
的因素,莫尔得出了他自己
的强度理论。
¢ Ð Ä û °Í • ¶ (O.Mohr),1835¡ 1918 ª «
材料力学课件:强度理论-

r2 1 (2 3) []
§ 8 . 3 屈服准则
问题2 B点(正应力和剪应力均较大)处应力该如何校核?
梁弯曲的强度条件:
max
M max Wz
,
max
Fs
S
* max
Iz bBiblioteka .qzC
D
B
B
B
y y
它的强度条件是:
x
x
σx≤[σ] 、 σy≤[σ] 吗 ? τx≤[τ]、τy≤[τ]
不是! 实 践 证 明 : (1)强度与σ、τ 均有关,相互影响
例:
§ 8 . 1 强度理论的概念
易剪断
不易剪断
易动
不易动
§ 8 . 1 强度理论的概念
(2)强度与σx、σy、σz 、τx、τy和τz 间的比例有关
max 0
max -构件危险点的最大切应力 max (13)/ 2
0 -极限切应力,由单向拉伸实验测得 0 / 2 s
屈服条件
s1 - s3 = ss
强度条件
1 3
s
ns
实验表明:此理论对于塑性材料的屈服破坏能够得到较
为满意的解释。
§ 8 . 3 屈服准则
4. 形状改变比能理论(第四强度理论)
强度理论
§8.1 强度理论的概念 §8.2 断裂准则——第一、第二强度理论 §8.3 屈服准则——第三、第四强度理论
§8.1 强度理论的概念
§ 8 . 1 强度理论的概念
1、基本变形下强度条件的建立
max
FN,max A
[] (拉压)
max
M max Wz
[]
(弯曲)
(正应力强度条件)
max
1 0
§ 8 . 3 屈服准则
问题2 B点(正应力和剪应力均较大)处应力该如何校核?
梁弯曲的强度条件:
max
M max Wz
,
max
Fs
S
* max
Iz bBiblioteka .qzC
D
B
B
B
y y
它的强度条件是:
x
x
σx≤[σ] 、 σy≤[σ] 吗 ? τx≤[τ]、τy≤[τ]
不是! 实 践 证 明 : (1)强度与σ、τ 均有关,相互影响
例:
§ 8 . 1 强度理论的概念
易剪断
不易剪断
易动
不易动
§ 8 . 1 强度理论的概念
(2)强度与σx、σy、σz 、τx、τy和τz 间的比例有关
max 0
max -构件危险点的最大切应力 max (13)/ 2
0 -极限切应力,由单向拉伸实验测得 0 / 2 s
屈服条件
s1 - s3 = ss
强度条件
1 3
s
ns
实验表明:此理论对于塑性材料的屈服破坏能够得到较
为满意的解释。
§ 8 . 3 屈服准则
4. 形状改变比能理论(第四强度理论)
强度理论
§8.1 强度理论的概念 §8.2 断裂准则——第一、第二强度理论 §8.3 屈服准则——第三、第四强度理论
§8.1 强度理论的概念
§ 8 . 1 强度理论的概念
1、基本变形下强度条件的建立
max
FN,max A
[] (拉压)
max
M max Wz
[]
(弯曲)
(正应力强度条件)
max
1 0
材料力学第六章强度理论

r 3 1 3 2 4 2 209.5MPa [ ]
r4
1 2
[( 1 2 ) ( 2 3 ) ( 3 1 )
2 2
2
2 3 2 196.2MPa [ ]
需加大截面积,重选工字钢。改选32a号工字钢, a点处应力
这一极限值可由脆性材料单轴拉伸试验获得。 破坏条件 强度条件
σ 1σ b σ 1 ≤[ σ ]
(没有考虑σ2和σ3两个主应力对破坏的影响) 该理论由英国学者兰金(W.J.Rankine)于1859年提出, 对脆性材料如岩石、混凝土、铸铁、砖等在二向受拉或三向 受拉时较为合适。
2. 最大拉应变理论(第二强度理论)
200kN
200kN
A
420
C
1660 2500
D
420
B
解:1°作梁的FQ图 和M图。 2°正应力强度计算
FQ M
+
200kN
200kN +
-
200kN
2°正应力强度设计
A
420
C
1660 2500
200kN
200k D N
B
由 max
M max [ ] Wz
FQ M
420
+
200kN +
极限应力圆
O
包络线
以材料所有极限应 力圆的包络线来判断 材料是否破坏,即包 络线便是其破坏的临 界线。
M P N
K
L O1
O3O1 OO1 OO3
O2 O3 O
1 1 bt ( 1 3 ) 2 2
材料力学-第七章-强度理论

脆性断裂,最大拉应力准则
r1 = max= 1 [] 其次确定主应力
ma xx 2y 1 2 xy2 4x 2y 2.2 9 M 8 P
m inx 2y 1 2 xy2 4x 2y 3 .7M 2 P
1=29.28MPa,2=3.72MPa, 3=0
r113M 0 Pa
根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹 性失效准则;
考虑安全系数后,其强度条件
根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失 效准则;
考虑安全系数后,强度条件
建立常温静载复杂应力状态下的弹性失效准则: 强度理论的基本思想是:
确认引起材料失效存在共同的力学原因,提出关于这一 共同力学原因的假设;
像铸铁一类脆性材料均具有 bc bt 的性能,
可选择莫尔强度理论。
思考题:把经过冷却的钢质实心球体,放入沸腾的热油锅 中,将引起钢球的爆裂,试分析原因。
答:经过冷却的钢质实心球体,放入沸腾的热油锅中, 钢 球的外部因骤热而迅速膨胀,其内芯受拉且处于三向均 匀拉伸的应力状态因而发生脆性爆裂。
思考题: 水管在寒冬低温条件下,由于管内水结冰引起体 积膨胀,而导致水管爆裂。由作用反作用定律可知,水 管与冰块所受的压力相等,试问为什么冰不破裂,而水管 发生爆裂。
局限性:
1、未考虑 2 的影响,试验证实最大影响达15%。
2、不能解释三向均拉下可能发生断裂的现象, 此准则也称特雷斯卡(Tresca)屈服准则
4. 畸变能密度理论(第四强度理论) 材料发生塑性屈服的主要因素是 畸变能密度;
无论处于什么应力状态,只要危险点处畸变能密度达到 与材料性质有关的某一极限值,材料就发生屈服。
具有屈服极限 s
铸铁拉伸破坏
r1 = max= 1 [] 其次确定主应力
ma xx 2y 1 2 xy2 4x 2y 2.2 9 M 8 P
m inx 2y 1 2 xy2 4x 2y 3 .7M 2 P
1=29.28MPa,2=3.72MPa, 3=0
r113M 0 Pa
根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹 性失效准则;
考虑安全系数后,其强度条件
根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失 效准则;
考虑安全系数后,强度条件
建立常温静载复杂应力状态下的弹性失效准则: 强度理论的基本思想是:
确认引起材料失效存在共同的力学原因,提出关于这一 共同力学原因的假设;
像铸铁一类脆性材料均具有 bc bt 的性能,
可选择莫尔强度理论。
思考题:把经过冷却的钢质实心球体,放入沸腾的热油锅 中,将引起钢球的爆裂,试分析原因。
答:经过冷却的钢质实心球体,放入沸腾的热油锅中, 钢 球的外部因骤热而迅速膨胀,其内芯受拉且处于三向均 匀拉伸的应力状态因而发生脆性爆裂。
思考题: 水管在寒冬低温条件下,由于管内水结冰引起体 积膨胀,而导致水管爆裂。由作用反作用定律可知,水 管与冰块所受的压力相等,试问为什么冰不破裂,而水管 发生爆裂。
局限性:
1、未考虑 2 的影响,试验证实最大影响达15%。
2、不能解释三向均拉下可能发生断裂的现象, 此准则也称特雷斯卡(Tresca)屈服准则
4. 畸变能密度理论(第四强度理论) 材料发生塑性屈服的主要因素是 畸变能密度;
无论处于什么应力状态,只要危险点处畸变能密度达到 与材料性质有关的某一极限值,材料就发生屈服。
具有屈服极限 s
铸铁拉伸破坏
材料力学课件:强度理论-1

问题:1、主应力的方向与主应变的方向是否一致。 2、大小关系是怎样的。
Page5
二、主应力与主应变的关系
y
2
1 x
x
x
E
y
E
z
E
y
y
E
x
E
z
E
z
z
E
x
E
y
E
3 z
xy xy / G yz yz / G
1
1 E
[
1
( 2
3 )]
xz xz / G
2
1 E
[
2
( 1 3 )]
主应力。
主应力之一:
P
P A
4 300 103 502
153MPa
假设圆柱体膨胀塞满凹座:
5.001 5 0.0002 5
圆柱体为轴对称构件:
q
q
广义胡克定律:
1 [ ( )] 0.0002 E
若q为正值,说明假设正确
若q为负值,说明q应该等于零
Page8
拉应力过大导致材料失效 材料的失效有一定的规律
切应力过大导致材料失效
Page17
➢ 试验观察与分析
两类破坏现象
脆性断裂 屈服或显著的塑性变形
两类强度理论
关于断裂的强度理论 关于屈服的强度理论
广义胡克定律
微体的应变能密度:
1 2E
2 1
2 2
2 3
21 2
3 2
1 3
➢ 对于非主应力微体:
1 2
x x
y y
z z
xy xy
yz yz
zx zx
Page10
2
1
材料力学课件 第9章 强度理论

18
第九章 强度理论
首页
上一页
下一页
例题 一铸铁构件 bL= 400MPa, by= 1200MPa,一平面应力状
态点按莫尔强度理论屈服时,最大剪应力为450MPa,试求该点
的主应力值。 M
[ y]
P
O2 3
解:做莫尔理论分析图
KL
sinO2M O1L
oN
O3 O1 1 [ L]
O1O2
by
首页
上一页
下一页
例题 某铸铁构件危险点的应力如图所示,若许用拉应力
[ ] 30MPa ,试校核其强度。
y 20MPa
解 由图可知,x与y截面的应力为
10MPa x
15MPa
x 10MPa, x 15MPa, y 20MPa
计算最大正应力与最小正应力,得到
max m in
26.2MPa 16.2MPa
密度值,材料即发生屈服。
ud max uds
ud
1
6E
1 2 2 2 3 2 3 1 2
1)破坏判据: 2)强度准则
1
2
1
2 2
2
3 2
3
1 2
s
1
2
1
2 2
2
3 2
3
1 2
3)实用范围:实用于破坏形式为屈服的构件。
10
第九章 强度理论
即主应力为: 1 26.2MPa, 2 0, 3 16.2MPa
上式中主应力 3 虽为压应力,但其绝对值小于主应力 1 所以,宜采用
最大拉应力理论校核强度,显然有1
[
]
说明该构件满足强度要求。
11
第九章 强度理论
材料力学第9章强度理论幻灯片PPT

页 退出
材料力学
出版社 理工分社
9.3.2形状改变能密度理论〔第四强度理论〕 弹性体在外力作用下发生弹性变形,载荷在相应位移上可做功。如果所加外 力是静载荷,那么外力所作的功全部转化为弹性体的变形能。处在外力作用 下的微小体,其形状和体积都会发生改变,故变形能又可分为形状改变能和 体积改变能〔畸变能〕。单位体积内的形状改变能称为形状改变能密度〔畸 变能密度〕。在复杂应力状态下,形状改变能密度的一般表达式为
页 退出
材料力学
出版社 理工分社
法国科学家马里奥(E.Mariotte)在1682年提出最大线应变理论,后经修正为 最大伸长线应变理论,也称为第二强度理论。这一理论考虑了3个主应力对 脆性断裂的影响,能较好地解释石料或混凝土等脆性材料受轴向压应力而沿 纵向截面开裂的现象。铸铁受拉—压二向应力且压应力较大时,试验结果也 与这一理论接近。但是,按照这一理论,脆性材料在二向和三向受拉时比单 向拉伸承载能力会更高,而试验结果并不能证实这一点。 最大拉应力强度理论和最大伸长线应变理论均是针对脆性断裂的强度理论。 一般认为,前者适用于脆性材料以拉应力为主的工况,而后者适用于脆性材 料以压应力为主的工况。在工程实际应用中,以上两种强度理论均有应用。
页 退出
材料力学
出版社 理工分社
解〔1〕螺旋桨轴外外表A点的应力状态 如图9.1〔b〕所示,该点处于平面应力状态。根据公式〔8.5〕可得
那么3个主应力为
根据公式〔9.16〕得轴外外表A点的第三和第四强度理论的强度条件分别为
页 退出
材料力学
出版社 理工分社
〔2〕分析螺旋桨轴的内力 易得各横截面上的轴力及扭矩均一样。由根本变形的知识,在图示外载荷作 用下,横截面各点正应力相等,轴外外表各点的切应力到达最大值。由此可 知,轴外外表上的点即为危险点,且应力值分别为
材料力学课件 第八章应力状态与强度理论

二向应力状态(Plane State of Stress): 一个主应力为零的应力状态。
单向应力状态(Unidirectional State of Stress): 一个主应力不为零的应力状态。
x B x
zx
xz
x
x
A
§8–2 平面应力状态下的应力分析
y
y
y
xy x
等价 y
x
xy
x z
Ox
一、解析法
30
x
y
2
sin 2
x cos2
80 (40) sin(2 30 ) 60 cos(2 30 ) 2
21.96MPa
确定主平面方位,将单元体已知应力代入 8.3,得
20 45
tan 20
2 x x y
2 (60) 80 (40)
1
0 22.5
0 即为最大主应力1 与 x 轴的夹角。主应力为
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
解:由于主应力1 ,2 ,3 与主应变1 ,2 ,3 一一对应,故由已知数据可知,
已知点处于平面应力状态且 2 0 。由广义胡克定律
1
1 E
(1
3 )
3
1 E
( 3
1)
联立上式
单向应力状态(Unidirectional State of Stress): 一个主应力不为零的应力状态。
x B x
zx
xz
x
x
A
§8–2 平面应力状态下的应力分析
y
y
y
xy x
等价 y
x
xy
x z
Ox
一、解析法
30
x
y
2
sin 2
x cos2
80 (40) sin(2 30 ) 60 cos(2 30 ) 2
21.96MPa
确定主平面方位,将单元体已知应力代入 8.3,得
20 45
tan 20
2 x x y
2 (60) 80 (40)
1
0 22.5
0 即为最大主应力1 与 x 轴的夹角。主应力为
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
解:由于主应力1 ,2 ,3 与主应变1 ,2 ,3 一一对应,故由已知数据可知,
已知点处于平面应力状态且 2 0 。由广义胡克定律
1
1 E
(1
3 )
3
1 E
( 3
1)
联立上式
《强度理论教学》课件

这些理论各有其适用范围和局限性,应根据具体问题和材料的特性选择合适的强 度理论进行计算和分析。
02
最大拉应力理论
理论概述
最大拉应力理论,也称为第一 强度理论,认为材料在最大拉 应力作用下发生断裂破坏。
该理论忽略了其他应力分量对 材料强度的影响,只考虑了最 大拉应力。
该理论适用于脆性材料,如玻 璃、陶瓷等,这些材料的断裂 主要是由于拉应力引起的。
04
能量守恒理论
理论概述
能量守恒理论是物理学中的基本原理之 一,它指出在一个封闭系统中,能量不 能被创造或消灭,只能从一种形式转化
为另一种形式。
这一理论在许多领域都有广泛的应用, 如热力学、电磁学、光学和力学等。
能量守恒理论是自然科学和工程学科的 重要基础,为人类认识自然界和解决实
际问题提供了有力支持。
04
流动法则描述了材料在受力过 程中应变的发展规律。
流动法则是基于实验观察和理 论分析得到的,描述了材料在 受力过程中应变的分布和演化
。
流动法则对于预测材料的变形 行为和稳定性具有重要的意义
。
流动法则可以通过实验和数值 模拟进行验证和应用。
屈服准则与流动法则的关系
屈服准则和流动法则是描述材料力学 行为的两个重要方面,它们之间存在 密切的联系。
为的强度准则。
该理论认为,当材料所受剪应力 达到某一极限值时,材料发生屈
服或断裂。
该极限值即为材料的剪切强度极 限。
应用场景
最大剪应力理论主要应用于分析材料在复杂应力状态下的强 度和稳定性问题,如机械零件的强度分析、结构的稳定性分 析等。
在工程实践中,该理论常用于设计、优化和校核各种机械零 件和结构的承载能力。
源技术等方面。
02
最大拉应力理论
理论概述
最大拉应力理论,也称为第一 强度理论,认为材料在最大拉 应力作用下发生断裂破坏。
该理论忽略了其他应力分量对 材料强度的影响,只考虑了最 大拉应力。
该理论适用于脆性材料,如玻 璃、陶瓷等,这些材料的断裂 主要是由于拉应力引起的。
04
能量守恒理论
理论概述
能量守恒理论是物理学中的基本原理之 一,它指出在一个封闭系统中,能量不 能被创造或消灭,只能从一种形式转化
为另一种形式。
这一理论在许多领域都有广泛的应用, 如热力学、电磁学、光学和力学等。
能量守恒理论是自然科学和工程学科的 重要基础,为人类认识自然界和解决实
际问题提供了有力支持。
04
流动法则描述了材料在受力过 程中应变的发展规律。
流动法则是基于实验观察和理 论分析得到的,描述了材料在 受力过程中应变的分布和演化
。
流动法则对于预测材料的变形 行为和稳定性具有重要的意义
。
流动法则可以通过实验和数值 模拟进行验证和应用。
屈服准则与流动法则的关系
屈服准则和流动法则是描述材料力学 行为的两个重要方面,它们之间存在 密切的联系。
为的强度准则。
该理论认为,当材料所受剪应力 达到某一极限值时,材料发生屈
服或断裂。
该极限值即为材料的剪切强度极 限。
应用场景
最大剪应力理论主要应用于分析材料在复杂应力状态下的强 度和稳定性问题,如机械零件的强度分析、结构的稳定性分 析等。
在工程实践中,该理论常用于设计、优化和校核各种机械零 件和结构的承载能力。
源技术等方面。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验验证: a) 较第三强度理论更接近实际值;
b) 材料拉压性能相同时成立。
强度理论的统一形式:
s r [s ]
sr称为相当应力,分别为:
• 最大拉应力(第一强度)理论:
s r1 s 1
• 最大伸长线应变(第二强度)理论:
s r 2 s1 s 2 s 3 • 最大切应力(第三强度)理论: s r 3 s1 s 3
假设形状改变能密度 vd是引起材料塑性屈服的 因素,即:
vd vd u
vd u
所以:
可通过单拉试验来确定。
因为材料单拉屈服时有: s 1 s s
s2 s3 0
vd u
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 又: vd 6E
[ ] 0.5[s ]
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2 3 s
单拉: s r 4 3 s s s 由此可得: s
1
3 [ ] 0.577 [s ] 0.6[s ]
s s 0.577s s
可用28b号工字钢。
若用第三强度理论,则相当应力为:
s r ቤተ መጻሕፍቲ ባይዱ s 2 4 2
请自行计算最终结果。 注意:本例中对 a 点的强度校核是按简化后的 截面尺寸进行的。实际上,对符合国家标准的型钢 并不需要对该点进行校核;然而,对自行设计的焊 接而成的组合工字梁则需进行校核。
例 工字形截面简支梁由三根钢板焊接而成,已知: [s]=170MPa,[]=100MPa。试全面校核该梁的强度。 120 解: F F=200kN
可选用28a号工字钢,其截面系数为:
W 508106 m3
2. 再按切应力强度条件进行校核。
I z 71.14106 m4 2 d 0.8510 m
max
FS,max S z ,max Iz d
Iz S z ,max
24.62102 m
200103 24.62102 0.85102
其中
I zd
71.14106 0.0085
73.8MPa
E
0.0137 S z 0.122 0.0137 0.1263 2 223106 m3
s r 4 s 2 3 2 149.12 3 73.82 196.4MPa [s ] 170MPa
s max
M max ymax Iz
280 14
FS
z
C 420
D 420
2.5m
84 103 140 103 Pa -6 70.8 10
200kN
166 MPa
[s ]
M
.
200kN
84kN m 3 120 14 3 8.5 252 2 12 4 I z 2 133 14 120 10 m 12 12
• 形状改变能密度(第四强度)理论:
s r4
1 2 2 2 s1 s 2 s 2 s 3 s1 s 3 2
§7-7 强度理论的应用
应用范围: a) 仅适用于常温、静载条件下的均匀、连续、各 向同性的材料; b) 不论塑性或脆性材料,在三向拉应力状态都 发生脆性断裂,宜采用第一强度理论; c) 对于脆性材料,在二向拉应力状态下宜采用第 一强度理论; d) 对塑性材料,除三向拉应力状态外都会发生 屈服,宜采用第三或第四强度理论; e) 不论塑性或脆性材料,在三向压应力状态都发 生屈服失效,宜采用第四强度理论。
A
0.42m
C
1.66 m 2.50m
D
0.42m
B
(b) 200kN
FS图
C 、 D 截面为危险截面, 取C截面计算
FSC FS,max 200kN
200kN
(c)
M图
84kN· m
M C M max 84kN m
1.按正应力强度条件选择截面型号。
M max 84103 6 3 W 49610 m 6 [s ] 17010
s s
(a)
(b)
解:对图a所示应力状态,因为
1 s 2 s 1 s 5s 2 2 2
s
2
s2 0
1 s 2 s 3 s 5s 2 2 2
所以:
s
2
s r 3 s 1 s 3 s 4 5s
max [ ]
s max [s ]
研究复杂应力状态下材料破坏的原因,根据一 定的假设来确定破坏条件,从而建立强度条件,这 就是强度理论的研究内容。
4)材料破坏的形式 常温、静载时材料的破坏形式大致可分为: • 脆性断裂型: 例如: 铸铁:拉伸、扭转等; 低碳钢:三向拉应力状态。 • 塑性屈服型: 例如: 低碳钢:拉伸、扭转等; 铸铁:三向压缩应力状态。 可见:材料破坏的形式不仅与材料有关,还与 应力状态有关。
1 2s s2 6E
因此:
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 s s 2
由此可得强度条件为:
ss 1 2 2 2 s1 s 2 s 2 s 3 s1 s 3 [s ] 2 n
2 2
s r4
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2 s 3 2s
2 2
对图b所示应力状态,有:
s
s1 s 2 s
s 3 s
所以:
s r 3 s 1 s 3 2s
s r4
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2 2s
14
1.确定危险截面
8.5 z
A
280 14
C 420 2.5m
D 420
B
FS
200kN
. M 84kN m
200kN
例 工字形截面简支梁由三根钢板焊接而成,已知: [s]=170MPa,[]=100MPa。试全面校核该梁的强度。 120 F F=200kN 解: 1.正应力校核 A B 14 8.5
95.5MPa [ ] 100MPa
可选用28a号工字钢。
13.7
(d)
122 8.5
s max
126.3 280
max
E
3.工字型截面腹板和翼缘交界处(E点),正应 力和切应力都较大,因此还需对此进行强度校核。
(e)
s
E
s
13.7
126.3
E
sE E
8.5
E
u
su
E
因为:
1 1 s 1 s 2 s 3 E
因此有: s1 s 2 s 3 s u 强度条件为:
s 1 s 2 s 3
su
n
[s ]
实验验证: a) 可解释大理石单压时的纵向裂缝; b) 铸铁二向、三向拉应力状态下的实验不符; c) 对铸铁一向拉、一向压的二向应力状态偏于 安全,可用。
s1 s 3
ss
n
[s ]
实验验证: a) 仅适用于拉压性能相同的材料; b) 低碳钢单拉(压)对45滑移线吻合; c) 二向应力状态基本符合,偏于安全。 存在问题: a) 没考虑s2对屈服的影响,偏于安全, 但误差较大; b) 仅适用于拉压性能相同的材料。
4)形状改变能密度理论(第四强度理论)
3)最大切应力理论(第三强度理论)
假设最大切应力max是引起材料塑性屈服的因 素,则:
max u
对低碳钢等塑性材料,单向拉伸时的屈服是 由45°斜截面上的切应力引起的,因而极限应力u 可由单拉时的屈服应力求得,即:
u
因为: max
ss
2
常数
s1 s 3
2
由此可得,强度条件为:
不满足要求。
E
E
13.7
126.3
FS,max S z
200103 223106
126.3 280
M max y 84103 0.1263 sE 149 . 1 MPa Iz 71.14106
(d)
122
13.7
sE
可改用28b号工字钢,按同样的方法可得:
s r 4 173.2MPa [s ] 1.05 178.5MPa
1、概述
s
s
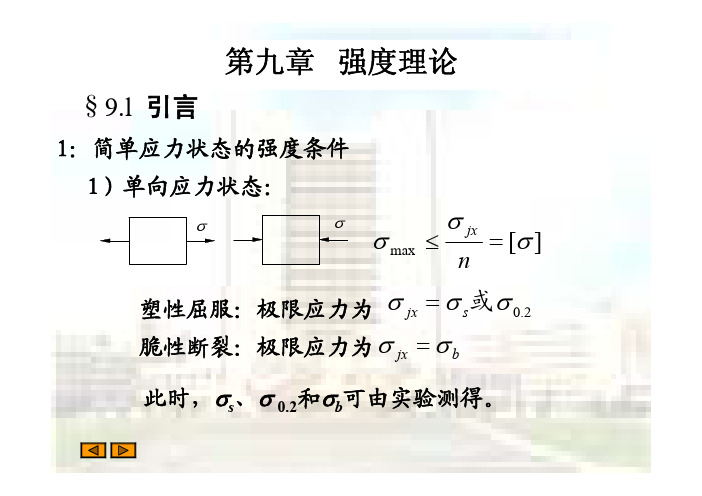
1)单向应力状态: 图示拉伸或压缩的单向应力状态,材料的破 坏有两种形式: 脆性断裂:极限应力为 s u s b 此时,ss、s p0.2和sb可由实验测得。由此可建 立如下强度条件: 塑性屈服:极限应力为 s u s s或s p0.2
s max
su
n
[s ]
其中n为安全系数。
可见:由第三强度理论,图 b 所示应力状态比 图 a 所示的安全;而由第四强度理论,两者的危险 程度一样。 注意:图a所示应力状态实际上为拉扭和弯扭组 合加载对应的应力状态,其相当应力如下:
s r 3 s 2 4 2
s r 4 s 2 3 2
例 工字钢梁如图a所示。已知材料(Q235钢)的许 用应力为 [s]=170MPa 和 []= 100MPa 。试按强度条 件选择工字钢号码。 (a) 200 kN 解:确定危险截面。 200 kN
b) 材料拉压性能相同时成立。
强度理论的统一形式:
s r [s ]
sr称为相当应力,分别为:
• 最大拉应力(第一强度)理论:
s r1 s 1
• 最大伸长线应变(第二强度)理论:
s r 2 s1 s 2 s 3 • 最大切应力(第三强度)理论: s r 3 s1 s 3
假设形状改变能密度 vd是引起材料塑性屈服的 因素,即:
vd vd u
vd u
所以:
可通过单拉试验来确定。
因为材料单拉屈服时有: s 1 s s
s2 s3 0
vd u
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 又: vd 6E
[ ] 0.5[s ]
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2 3 s
单拉: s r 4 3 s s s 由此可得: s
1
3 [ ] 0.577 [s ] 0.6[s ]
s s 0.577s s
可用28b号工字钢。
若用第三强度理论,则相当应力为:
s r ቤተ መጻሕፍቲ ባይዱ s 2 4 2
请自行计算最终结果。 注意:本例中对 a 点的强度校核是按简化后的 截面尺寸进行的。实际上,对符合国家标准的型钢 并不需要对该点进行校核;然而,对自行设计的焊 接而成的组合工字梁则需进行校核。
例 工字形截面简支梁由三根钢板焊接而成,已知: [s]=170MPa,[]=100MPa。试全面校核该梁的强度。 120 解: F F=200kN
可选用28a号工字钢,其截面系数为:
W 508106 m3
2. 再按切应力强度条件进行校核。
I z 71.14106 m4 2 d 0.8510 m
max
FS,max S z ,max Iz d
Iz S z ,max
24.62102 m
200103 24.62102 0.85102
其中
I zd
71.14106 0.0085
73.8MPa
E
0.0137 S z 0.122 0.0137 0.1263 2 223106 m3
s r 4 s 2 3 2 149.12 3 73.82 196.4MPa [s ] 170MPa
s max
M max ymax Iz
280 14
FS
z
C 420
D 420
2.5m
84 103 140 103 Pa -6 70.8 10
200kN
166 MPa
[s ]
M
.
200kN
84kN m 3 120 14 3 8.5 252 2 12 4 I z 2 133 14 120 10 m 12 12
• 形状改变能密度(第四强度)理论:
s r4
1 2 2 2 s1 s 2 s 2 s 3 s1 s 3 2
§7-7 强度理论的应用
应用范围: a) 仅适用于常温、静载条件下的均匀、连续、各 向同性的材料; b) 不论塑性或脆性材料,在三向拉应力状态都 发生脆性断裂,宜采用第一强度理论; c) 对于脆性材料,在二向拉应力状态下宜采用第 一强度理论; d) 对塑性材料,除三向拉应力状态外都会发生 屈服,宜采用第三或第四强度理论; e) 不论塑性或脆性材料,在三向压应力状态都发 生屈服失效,宜采用第四强度理论。
A
0.42m
C
1.66 m 2.50m
D
0.42m
B
(b) 200kN
FS图
C 、 D 截面为危险截面, 取C截面计算
FSC FS,max 200kN
200kN
(c)
M图
84kN· m
M C M max 84kN m
1.按正应力强度条件选择截面型号。
M max 84103 6 3 W 49610 m 6 [s ] 17010
s s
(a)
(b)
解:对图a所示应力状态,因为
1 s 2 s 1 s 5s 2 2 2
s
2
s2 0
1 s 2 s 3 s 5s 2 2 2
所以:
s
2
s r 3 s 1 s 3 s 4 5s
max [ ]
s max [s ]
研究复杂应力状态下材料破坏的原因,根据一 定的假设来确定破坏条件,从而建立强度条件,这 就是强度理论的研究内容。
4)材料破坏的形式 常温、静载时材料的破坏形式大致可分为: • 脆性断裂型: 例如: 铸铁:拉伸、扭转等; 低碳钢:三向拉应力状态。 • 塑性屈服型: 例如: 低碳钢:拉伸、扭转等; 铸铁:三向压缩应力状态。 可见:材料破坏的形式不仅与材料有关,还与 应力状态有关。
1 2s s2 6E
因此:
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 s s 2
由此可得强度条件为:
ss 1 2 2 2 s1 s 2 s 2 s 3 s1 s 3 [s ] 2 n
2 2
s r4
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2 s 3 2s
2 2
对图b所示应力状态,有:
s
s1 s 2 s
s 3 s
所以:
s r 3 s 1 s 3 2s
s r4
1 2 2 2 s 1 s 2 s 2 s 3 s 1 s 3 2 2s
14
1.确定危险截面
8.5 z
A
280 14
C 420 2.5m
D 420
B
FS
200kN
. M 84kN m
200kN
例 工字形截面简支梁由三根钢板焊接而成,已知: [s]=170MPa,[]=100MPa。试全面校核该梁的强度。 120 F F=200kN 解: 1.正应力校核 A B 14 8.5
95.5MPa [ ] 100MPa
可选用28a号工字钢。
13.7
(d)
122 8.5
s max
126.3 280
max
E
3.工字型截面腹板和翼缘交界处(E点),正应 力和切应力都较大,因此还需对此进行强度校核。
(e)
s
E
s
13.7
126.3
E
sE E
8.5
E
u
su
E
因为:
1 1 s 1 s 2 s 3 E
因此有: s1 s 2 s 3 s u 强度条件为:
s 1 s 2 s 3
su
n
[s ]
实验验证: a) 可解释大理石单压时的纵向裂缝; b) 铸铁二向、三向拉应力状态下的实验不符; c) 对铸铁一向拉、一向压的二向应力状态偏于 安全,可用。
s1 s 3
ss
n
[s ]
实验验证: a) 仅适用于拉压性能相同的材料; b) 低碳钢单拉(压)对45滑移线吻合; c) 二向应力状态基本符合,偏于安全。 存在问题: a) 没考虑s2对屈服的影响,偏于安全, 但误差较大; b) 仅适用于拉压性能相同的材料。
4)形状改变能密度理论(第四强度理论)
3)最大切应力理论(第三强度理论)
假设最大切应力max是引起材料塑性屈服的因 素,则:
max u
对低碳钢等塑性材料,单向拉伸时的屈服是 由45°斜截面上的切应力引起的,因而极限应力u 可由单拉时的屈服应力求得,即:
u
因为: max
ss
2
常数
s1 s 3
2
由此可得,强度条件为:
不满足要求。
E
E
13.7
126.3
FS,max S z
200103 223106
126.3 280
M max y 84103 0.1263 sE 149 . 1 MPa Iz 71.14106
(d)
122
13.7
sE
可改用28b号工字钢,按同样的方法可得:
s r 4 173.2MPa [s ] 1.05 178.5MPa
1、概述
s
s
1)单向应力状态: 图示拉伸或压缩的单向应力状态,材料的破 坏有两种形式: 脆性断裂:极限应力为 s u s b 此时,ss、s p0.2和sb可由实验测得。由此可建 立如下强度条件: 塑性屈服:极限应力为 s u s s或s p0.2
s max
su
n
[s ]
其中n为安全系数。
可见:由第三强度理论,图 b 所示应力状态比 图 a 所示的安全;而由第四强度理论,两者的危险 程度一样。 注意:图a所示应力状态实际上为拉扭和弯扭组 合加载对应的应力状态,其相当应力如下:
s r 3 s 2 4 2
s r 4 s 2 3 2
例 工字钢梁如图a所示。已知材料(Q235钢)的许 用应力为 [s]=170MPa 和 []= 100MPa 。试按强度条 件选择工字钢号码。 (a) 200 kN 解:确定危险截面。 200 kN
