水力学2

合集下载

水力学2(23)

3
由图（）、（b 由图（a）、（b）,建立1-1、2-2断面的能量方程，可以很容易推建立1 断面的能量方程，得类似于孔口、管嘴出流的流速和流量计算公式，现介绍如下。得类似于孔口、管嘴出流的流速和流量计算流速：管中流速：
1 v= 2gH0 L α + λ + ∑ξ d
1 Q = vA = A 2gH0 = µc A c 2gH0 L α + λ + ∑ξ d
管中流量：管中流量：
1 式中 µc = l α + λ + ∑ξ d
作用水头。作用水头。
——管道系统流量系数；管道系统流量系数；管道系统流量系数
2 α0v 0 1 断面的总水头， H0 = H + ≈ H ——1-1断面的总水头，称为短管自由出流的 2g
8
这一规定的流速需要从技术和经济两个方面来考虑。这一规定的流速需要从技术和经济两个方面来考虑。由连续性方程可知，当流量一定时，管中流速与管径的平方成反比。方程可知，当流量一定时，管中流速与管径的平方成反比。若选用较小的管径，则可节省管材，降低管道造价，用较小的管径，则可节省管材，降低管道造价，但过大的流速会引起较大的水头损失，从而又会使输水的运行费用增加，引起较大的水头损失，从而又会使输水的运行费用增加，同时还可能引起较大的噪音和较强的水击作用。反之，可能引起较大的噪音和较强的水击作用。反之，若选用较大的管虽可使运行费用降低，但管道造价将增高，径，虽可使运行费用降低，但管道造价将增高，对于水中挟带泥沙的管道，管中流速过小，还会引起泥沙的淤积作用。因此，沙的管道，管中流速过小，还会引起泥沙的淤积作用。因此，过大或过小的管中流速，在投资上都不会是最经济的，大或过小的管中流速，在投资上都不会是最经济的，在技术上也不会是最合理的。不会是最合理的。工程实际中，人们常通过技术与经济的比较，工程实际中，人们常通过技术与经济的比较，确定一个在符合技术要求的前提下，使供水总成本最低的经济流速v 合技术要求的前提下，使供水总成本最低的经济流速 e，作为确定管径d的依据。经济流速选定后，确定管径d的依据。经济流速选定后，即可按下式计算管径

水力学2复习资料（长理港航）.

⽔⼒学2复习资料（长理港航）.⽔⼒学（⼆）复习资料第⼀部分：判断题1、当⽔头H 降低，宽顶堰可能转化为实⽤堰。

（）2、堰流计算的特点是必须考虑局部⽔头损失j h 的影响。

（）3、堰流⾃由出流的能⼒⼩于淹没出流的能⼒。

（）4、消能池深的设计流量⼤于消能池长的设计流量（）5、均匀流⼀定是势流。

（）6、做圆周运动的液体⼀定是有涡流。

（）7、对明渠⾮恒定流⽽⾔，当0??SQ 时将产⽣涨⽔波。

（） 8、平⾯势流中，某根流线各点的流速势函数值均相等。

（）9、流⽹中每个⽹格的对⾓线应该正交。

（）10、边界层外的液体应视为实际液体，边界层内的液体可视为理想液体。

（）11、边界层内的液体型态只能是紊流（）12、确定底流式消能池深，应该采⽤最⼤流量来计算。

（）13、在其他情况相同的前提下，弧形闸门的过流能⼒强于平⾯闸门。

（）14、理想液体的流动不⼀定是有势流动。

（）15.只要下游⽔位不超过宽顶堰的堰顶，堰流就必然为⾃由出流。

（）16.正坡地下河槽中的浸润线可存在于a 区或b 区。

（）17.堰流⽔⼒计算时，⽔头损失必须同时考虑沿程与局部⽔头损失。

（）18.只要是运动液体，则其任⼀点的动⽔压强各⽅向是不相等的。

（）19.在远驱式⽔跃衔接的情况下，堰的过流能⼒按⾃由出流公式计算。

（）20. 底流式消⼒池池深和池长的设计流量都采⽤最⼤流量。

（）21.渗流系数及边界条件相同，作⽤⽔头不同，两者渗流流⽹相同。

（）22.⽆旋运动必须满⾜y x u u x y=。

（） 23.实际⽔深等于其相应的临界⽔深时的渗流，称为临界渗流。

（）24.底流消能设计中，取最⼤流量作为设计流量时，消⼒池的深度也最⼤。

（）25.堰顶厚度δ与堰上⽔头0H 之⽐0.67＜0H δ＜2.5时的堰流为实⽤堰流。

（）26.有旋运动是指流动过程中液体微团有绕⾃⾝轴旋转的流动。

（）27.均匀流的流线是相互平⾏的直线，所以是⽆涡流。

28.流⽹存在的充分必要条件是恒定渗流。

水力学第2章静水力学

水
静向作用面，作用线与矩形平面的交点就
力
学是压心D。
37
水力学
例：对三角形的压强分布图
第二章
水
静
力
学
其大小为： P 1 gh2b
2
其压心位于水面下2h/3处。
38
水力学
对压强分布图为梯形分布总压力的大小：
第
P p1 p2 ab 2
二
章
水静力学
对于梯形压心距平面底部的距离为：
A
A
33
水力学
I x y 2dA
A
第二章
则可得出： yD

Ix Sx

Ix yc A
水
利用惯性矩平行移轴定理： I x Ic yc2 A
静
力
学
34
水力学
将此定理代入上式可最后得出yD
第
二
章水
yD

Ic yc2A yc A

yc

Ic yc A
静
力
学
35
水力学
2.6.2 矩形平面静水压力——压力图法
静力
这样x方向的总压力为
学
Px= ρghcAx
42
水力学
总压力P 的铅垂分力Pz等于各微小面
第积上铅垂分力dPz的总合，即
二
章
Pz dPz ghdAz g hdAz gV
水
Az
Az
静力
式中： hdAz V 为压力体的体积
学
Az
43
水力学
压力体是由以下：
第
等压面是压强相等的点构成的面。

水力学2简答题

简答题
2014年6月26日 20:23
1. 达西、杜比公式的异同点
达西公式任意一点的渗流流速u=kj
恒定均匀层流渗流
杜比公式同一过水断面上各点的渗流流速都相等 v=kj 恒定非均匀渐变层流渗流
2. 闸孔出流和堰流的异同点相同点
重力作用下形成的水流运动
势能转化为动能的过程
属于明渠急变流，损失主要是局部水头损失
通过渗流模型任一断面的流量以及任一点的压力或水头均和实际水流相同
5. 泄水建筑物下游常用的水面衔接及消能措施有哪些，它们各自的水流特征有哪些
消能方消能机理式
主流位置衔接适用条件
底流消水跃能
底部
渠道
低水头建筑物，地质条件较差
挑流消空中耗Βιβλιοθήκη ，下游水体碰撞、旋垂直于河无能
滚
床
中高水头建筑物，地质条件较好
不同点
堰流
水面线为一条光滑的降落曲线
闸孔出流上、下游水面线是不连续的
水流特征过流能力 3. 为什么可以用水跃来消能，什么样的水跃消能形式最好
在水跃表面旋滚与主流的交界面附近漩涡强烈,从而导致该处水流的激烈紊动、混掺
使得紊动的附加切应力较一般渐变紊流为大
在水跃旋滚区内，由于水流要素的急剧变化，
特别是很大的紊流附加切应力使得跃前断面水流的大部分动能在水跃段内转化为热能而消失
Fr越大，水跃效能率越高，故强水跃的消能效率最高
（远驱式水跃消能效率高） 4. 什么是渗流模型，用渗流模型代替实际要遵循哪些原则
定义
用一种假想水流来代替真实的地下水流
假想水流的性质和真实的地下水相同
但它充满了既包括空隙空间，也包括颗粒所占据空间的整个渗流区域

第2章水力学基本知识

过流断面的几何要素
d--管径 h--水深 α--充满度, α=h/d θ--充满角,水深h所对应的圆心角。由几何关系可得水力要素导出量：过水面积 A d ( sin ) 湿周 d 水力半径
2
8
2
R
d sin (1 ) 4
2 1
流速
1 d sin 3 2 v [ (1 )] i n 4
波速判别
缓流急流临界流波速：
vc vc
vc
A c g B
c gh （矩形）
弗劳德数判别
缓流急流临界流
弗劳德数
Fr 1
Fr 1
Fr 1
v Fr c v g A B v gh

断面比能
断面比能
e h
v 2
2g
h
Q 2
2 gA2
de 0 dh
1 2 i tan lx
底坡可分为: 顺坡(i>0), 平坡(i=0), 逆坡(i<0)
常见的断面形状
过流断面的几何要素
底宽 b,水深 h,边坡系数 m(表示边坡倾斜程度的系数)
a m ctg h
水面宽过流断面面积湿周
水力半径
B b 2mh
A (b m h)h
2 1
流量
d2 1 d sin 3 2 Q ( sin ) [ (1 )] i 8 n 4
输水性能最优充满度
从上式可知,在水深很小时,水深增加,水面增宽,过流断面面积增加很快,接近管轴处增加最快，水深超过半管后，水深增加，水面宽减小，过流断面面积增加减慢，在满流前增加最慢。湿周随水深的增加与过流断面面积不同，接近管轴处增加最慢，在满流前增加最快，由此可知，在满流前，输水能力达到最大值，相应的充满度为最优充满度。

北航水力学课件s2 第二章流体静力学

水静压力的作用点（压力中心）：
Q p=gh，压强与水深成正比，深度越深，压强越大
\压力中心D在y轴上的位置必低于形心c。
力矩平衡原理：各微小面积dA上水静压力dP对x轴力矩之和＝整个受压面上的水静压力P对x轴的力矩左边
右边＝水静压力P对x轴力矩
yD －压力中心D至x轴的距离 Q左边＝右边，即各分力对某轴的力矩＝合力对同轴力矩之和
表示：压强在x, y, z三方向都无变化，表示流体空间各点压强相等
把流体平衡微分方程改写为：
结论：压强递增率的方向，就是单位质量力在各轴向分力的方向，
即质量力作用的方向就是压强递增的方向。
如，静止液体，压强增加的方向，就是重力作用的垂直向下的方向。
对不可压缩流体，r为常数，将上方程中各式分别乘以dx, dy, dz后相加，得：
过水静压力分布图ABE的形心，并位于对称面上。
流体力学中一般只考虑地球吸引力，惯性力。单位质量力：单位质量流体受到的质量力。
2. 表面力：作用在所取流体体积表面上的力，与作用的表面积大小成正比，是其它物体所直接施加的表面接触力
一般分解为两部分：
法向应力：垂直于作用表面的分量
切向应力：平行于作用表面的分量
静止流体中没有切向力，只存在法向力，因此，定义
2-2-2 重力作用下流体的压强分布规律
如图，均匀液体：
容器：开口液体密度：r
容器和液体：静止
流体所受质量力：重力单位质量力： X=0, Y=0, Z= -g
代入式 dp =r (Xdx+Ydy+Zdz) = -rgdz = -gdz
积分上式得：p = -gz + c
c：积分常数，由边界条件确定

水力学_第2章静水力学

A
c
A
P g sin S x g sin yc A ghc A pc A
31
水力学
上式表明：任意形状平面上的静水
第二章水静力学
总压力P 等于该平面形心点C 的压强 pc
与平面面积 A的乘积。
2.静水总压力的方向静水总压力P 的方向垂直指向受压面。
32
水力学
第二章水静力学
定义：在静止液体内部，将压强相等的各点连成的面称等压面。
由于在等压面上p C，则dp 0
则等压面方程为f x dx f y dy f z dz 0
特性：等压面上各点质量力与等压面正交。
f .ds f x dx f y dy f z dz 0
由z z0 , p p0代入上式得C p0 gz0
p p0 g ( z0 z )
p p0 gh
p A pB gh
17
水力学
第二章水静力学
p z C g
上式是重力作用下水静力学基本方程之
一。它表明：当质量力仅为重力时，静止液
第二章水静力学
则可得出： y D
利用惯性矩平行移轴定理： I x I c yc2 A
34
水力学
将此定理代入上式可最后得出yD
第二章水静力学
2 Ic yc A Ic yD yc yc A yc A
35
水力学
2.6.2 矩形平面静水压力——压力图法
第二章水静力学
12
水力学
上式为液体的平衡微分方程式。它是
第二章水静力学
欧拉（Euler)于1755年首先得出的，又称为欧拉平衡微分方程。它反映了平衡液体

【精品作文】水力学第二章课后答案

(2)图c和图d静水压力大小相等。以为两个面上的压强分布图是相同的，根据梯形压强分布图对应的压力计算式可知大小相等，作用点离水面距离相等。 2-11.（1）当容器向下作加速运动时，容器底部对水的作用力为F=m*(g-a),由牛顿第三定律知水对容器的压力也等于F，根据p=F/A,知底部的压强p=
m(g?a)
压强的传递有所改变。当施加外力时，液面压强增大了的各点压强都增加
?pA
?pA
，水面以下同一高度
。
2-8.（1）各测压管中水面高度都相等。
（2）标注如下，位置水头z,压强水头h,测压管水头p.
P
图2-8
2-9.选择A
2-10.(1)图a和图b静水压力不相等。因为水作用面的面积不相等，而且作用面的形心点压强大小不同。所以静水压力Pa>Pb.
（2）若容器盛的是汽油，则有
p?ρ?gh?0.75?9.8?1.5kPa?11.03kPa 0
2. 如图2-26所示封闭水箱两测压管的液面高程为：?液
面
高
程
为
?4?60cm
1
?100cm
，?
2
?20cm
，箱内少
。问
?3
为多?
解：由于水箱底部以上部分全都是水，且水银测压管开口与大气相通，故有
1-2．当空气温度从0℃增加至20℃时，运动粘度?增加15%，重度?减少10%，问此时动力粘度?增加多少（百分数）？ [解] ?
?????(1?0.15)?原(1?0.1)?原
?1.035?原?原?1.035?原
???原1.035?原??原
???0.035
?原?原
此时动力粘度?增加了3.5%
习题2
1. 一封闭容器如图2-35所示，测压管液面高于容器液面，h=1.5m,，若容器盛

水力学第2章水静力学

A点的相对压强为
pA gL sin
当被测点压强很大时：所需测压管很长，这时可以改用U形水银测压计。
2.6.2 U形水银测压计
在U形管内，水银面N-N为等压面，因而1点和2点压强相等。
对测压计右支 p2 pa m gh
对测压计左支
p1
p' A
gb
A点的绝对压强
p
A
pa
m gh
gb
A点的相对压强
量力只有重力的同一种连续介质。对不连续液体或一
个水平面穿过了两种不同介质，位于同一水平面上的
各点压强并不相等。
2－5 绝对压强与相对压强
2.5.1 绝对压强
假设没有大气存在的绝对真空状态作为零点计量的压强，称为绝对压强。总是正的。
2.5.2 相对压强把当地大气压作为零点计量的压强，称为相对压强。相
p
' A
p0
gh1
25
9.8 5
74 k Pa
pB' p0 gh2 25 9.8 2 44.6kPa
故A点静水压强比B点大。实际上本题不必计算也可得出此结论（因淹没深度大的点，其压强必大）。
例:如图，有一底部水平侧壁倾斜之油槽，侧壁角为300，被
油淹没部分壁长L为6m，自由面上的压强 pa =98kPa，油的密
面积所受的平均静水压力为：
p Fp
(1.1)
A
点的静水压强
p lim Fp A0 A
(1.2)
静水压力 Fp 的单位：牛顿（N）；静水压强 p 的单位：牛顿／米2（N／m2），
又称为“帕斯卡”（Pa）
2.1.2 静水压强的特性静水压强的两个重要特性：
1．静水压强的方向与垂直并指向受压面。

水力学-第2章-水静力学

2.2 液体平衡微分方程
2.2.1 液体平衡微分方程
静止液体内取边长分别为 dx, dy, dz 的微元六面体，
中心点 O’(x,y,z) 压强 p(x,y,z)。
pM
z
d dy c
dx d’
M c’ dz
a N O’
b
a’ pN
z
b’
y
O
y
x
x 由于六面体为静止，故作用在六面体上各个方向力满
足力平衡方程。以 x 方向为例：
欧拉 Leonhard Euler
1707年4月15日出生于瑞士的巴塞尔城，1783 年9月18日去逝于俄罗斯的彼得堡，享年76岁。
13岁时入读巴塞尔大学，15岁大学毕业，16岁获硕士学位。1727年任彼得堡科学院数学教授。1741年应普鲁士彼德烈大帝的邀请，到柏林担任科学院物理数学所所长。直到1766年，在沙皇喀德林二世的诚恳敦聘下重回彼得堡。
真空压强 — 绝对压强小于大气压强的差值，以符号pv 表示。根据定义有：
pv pa pabs 或
pv ( pabs pa ) p
真空压强又可表示为相对压强的负值，故又称负压。
压强关系图 p
pa
状态一
pabs1
p1
大气压
pv 状态二
pabs2
完全真空
2.3.4 测压管水头
以单位体积液体的重量ρg 除以水静力学基本方程不定
Xdx Ydy Zdz 0
上式称等压面方程。等压面方程中，X、Y、Z 为单位质量力在三个坐标轴的
分力，而 dx、dy、dz 则是等压面上任意线段在三个坐标轴的投影，由矢量代数得：
Xdx Ydy Zdz f dl

水力学2(31)

2.水跃基本方程水跃计算任务:求解水跃的跃前或跃后水深;水跃中的能量损失
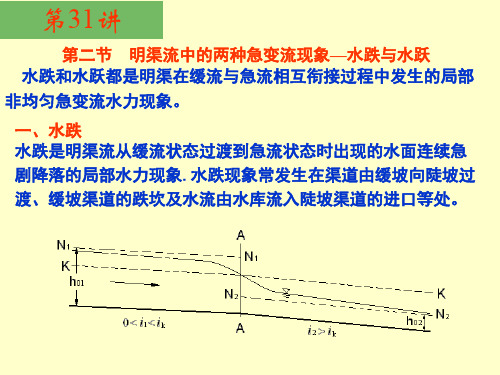
和水跃长度.下面以平坡棱柱形渠道中的完整水跃为例讨论如下由于水跃段内水流极为紊乱复杂,其阻力分布规律尚不清楚,无
法确定水跃中的水头损失hw,因此无法应用能量方程确定跃前水深 h′与跃后水深h″的相互关系.这时可应用恒定流动量方程讨论. 如上图,取1-1、2-2过水断面、渠道底面及水面为控制面,并且为
跃中的平均单位机械能损失也愈大。
2．水跃长度的计算
水跃长度L应理解为是水跃段长度Ly与跃后段长度L0之和，即
L Ly L0
水跃长度决定着有关渠段应加固的长度，所以水跃长度的确定具有重要的实际意义。由于水流在水跃过程中运动的复杂性，目前水跃长度还只能根据经验公式计算。
水跃段长度Ly的经验公式很多，而且因试验者的观察标准不完全一致，致使各经验公式的计算结果有一定差异。下面介绍两个矩形断面平坡棱柱形渠道水跃段长度的经验公式
θ(h)

βQ 2 gA
hcA
则
θ(h) θ(h)
上式表明，在棱柱形平坡渠道中，跃前水深h′与跃后水深h″具有相等的水跃函数值，所以又称这两个水深为共扼水深。
上述导出的水跃方程式，对于在底坡不大的棱柱形渠道中的水跃，也可近似应用。可以证明,当水跃函数θ(h)为最小值时,相应的水深为临界水深hk. 3.共扼水深的计算
如图是平坡渠道中闸下出流后形成的典型水跃形式,其水跃段可划分为上部的旋滚区和下部的主流区两部分.在上部旋滚区内, 水流质点无规则地旋回滚动并挟带有大量的气泡;下部的主流区则流速很大,水流急剧扩散,流线的扩散角和曲率都很大,属急变流.
在水跃段内,由于水流运动要素急剧变化,紊动、混掺强烈,旋滚区与主流区之间质量不断交换,能量损失很大,有时可达跃前断面能量的70%.因此,工程上常以水跃方式作为有效的消能手段.

水力学第2章.流体静力学

2.1 静止流体中应力的特性
特性一：静压强方向是垂直指向作用面（即沿作用面的内法线方向）.
p fs
N
τ
N
特性二：静止液体中任一点的静压强的大小与作用面方位无关。
pn1 pn 2
证明：
设在静止流体中任取一点O，围绕O点取微元直角四面体 OABC为隔离体。
px、py、pz、 pn
px
z z
相对压强 p（ relative pressure)
以当地大气压 pa 为基准起算的压强值：
p pabs pa
对于液体，也叫表压强 p ga ge (gage pressure).
在开口通大气容器中，液面的相对压强：
p0 0
深度为h的点相对压强： p gh
真空压强 p （ v vacuum pressure)
p po g ( zo z) po gh
z const
p const
推论四：静止连通的同种液体中，流体质量力仅有重力时，水平面必定是等压面。
注意：只适用于互相连通的同一种液体
◇ 压强的作用方向
压强的作用方向，应根据受力面的方位和承受压力的物质系统而定。静压强的作用方向垂直于作用面的切平面指向受力物质（流体或固体）系统表面的内法线方向.
2.1 静止流体中压强的性质
2.2 重力作用下静止流体中压强的分布规律
2.3 液体作用在平面壁上的总压力 2.4 液体作用在曲面壁上的总压力
流体质量力只有重力作用的情况下，研究静止流体压强的分布规律 . (X= 0; Y= 0; Z= -g)
2.2.1 流体静力学基本方程式
重力作用下的静止液体中，任取一倾斜放置的微元柱体受力分析:

水力学第二章液体运动的流束理论

pB 11.12m g
pB 11.12 9.8 108.98KN / m2
FA pA AA 3.768KN
FB pB AB 1.92KN

沿x轴方向取动量梁方程
FA FB cos Rx Q(BVB cos AVA )
解得 Rx 2.844KN
Q 0.02 v2 1m / s A2 0.02

列1－1，2－2断面得能量方程
2 p1 1v12 p2 2v2 z1 z2 hw g 2g g 2g
取1＝ 2＝ 1
p2 2.35m g

2-4 在水轮机的垂直锥形尾水管中（如图），已知1-1断面的直径为0.6m，断面平均流速v1为 6m/s，出口断面2-2的直径为0.9m，两断面间的水头损失hw为0.03，试求当z为5m时1-1断面处的真空度。
v2 3 2g
v 3 5 2g 9.9m / s
由连续原理： Q A 3 v 3 9.9 0.4 0.396m3 / s
1
3 0 1 3 0
（2）其它管段的流速及流速水头计算： v 1 Q 0.396 Q 0.396 7.93m/ s; v2 13.2m/ s A1 0.05 A2 0.03 v2 13.2 2 2 8.88 m; 2g 2 9.8

沿y轴方向取动量梁方程
Ry FB sin 60 Q(VB sin 60 )
解得 Ry 2.153KN
R Rx 2 Ry 2 3.567 KN

合力与水平方向的夹角 378'

2-13 一平板闸门宽b为2m，当通过流量Q为8m3/s时闸前水深H为4m，闸孔后收缩断面水深hc为0.5m，求作用于平板闸门上的动水总压力（不计摩擦力）。

水力学第二章课后题答案

r • H • D 2[ ]
rHD 2
9.8 14000 200 2 14000000
0.98cm
2.1 盛有同种介质（密度A =B
=1200kg/m 3 )的两容器，其中心
点A、B位于同一高程，今用U形
差压计测定A、B点之压差（差
压计内盛油，密度 0＝
800kg/m 3），A点还装有一水银
测压计。其它有关数据如图题1-
2所示（s=5cm,
h 1
=20cm,h=4cm）
问：
1. A、B两点之压差为多少？
解:当下游无水时: 水平分力
Px rhC 1Ax1 9.8 13 26 1 3312.4KN(水平向右）
垂直分力
Pz rV1 9.8 梯形abcd 1 9.8 0.5 (26 18) 4 1 862.04KN(竖直向下）
当下游有水时水平分力
Px rhC 1Ax1 rhc2Ax 2 3312.4 9.8 3 6 1 3316KN(水平向右）
（1）相同，不相等（2）减小，上升
2.5 压力体的概念是什么？如何确定压力体的范围及作用力方向？
压力体是计算总压力垂直分力 FPZ 的概念，只是作为计算
曲面上垂直压力的一个数值当量，不是由实际水体构成。
由受压曲面本身、通过曲面的四个边缘向自由液面作的
铅垂面、自由液面或其延伸面围成的体积就是压力体。压力体位于受压面同一侧的叫做实压力体，液体压力向下；压力体位于受压面异侧的叫做虚压力体，液体压力向上。
2
98
1 ctg 60
2
2
P
1 2
2 sin 60
则拉力 T 139.5KN
2.8 有—直立的矩形自动翻板闸门，门高H为5m，如果要求水面超过门顶h 为lm时，翻板闸门即可

水力学2

2.合力的方向：
合力的方向为受压面的内法向。
§2-6 静止液体作用在平面上的合力

§2-3 静止液体的压强分布
2. 绝对压强、相对压强、真空度
绝对压强的定义：
以绝对真空作为零点计量的压强值，称为绝对压强。
相对压强的定义：
以当地大气压作为零点计量的压强值，称为相对压强。
真空度（真空压强、真空值）的定义：
当液体中某点的绝对压强小于当地大气压时，当地大气压与该点绝对压强的差值，称为该点的真空度。
液体（水）静力学基本方程：
p z c 或 p p0 h
§2-3 静止液体的压强分布
注意: p p0 h 中的p0既可为液体表面上某点的压强，也可为液体内部某点的压强。
p p0 h
§2-3 静止液体的压强分布
二.压强的计量单位和表示方法： 1.压强的计量单位：
当液体中某点的绝对压强小于当地大气压时，当地大气压与该点绝对压强的差值，称为该点的真空度。
知识回顾
液体（水）静力学基本方程：
p z c 或 p p0 h

Z —— 单位重量液体所具有的位置势能（相对于某基准面）。 p/ —— 单位重量液体所具有的压强势能。 Z+p/ —— 单位重量液体所具有的总势能。
又 T T0 z 288 0.0065z

p
p0
dp g p R
dz T0 0.0065 z 0
z
取：g = 9.807m/s² ， = 0.0065K/m， R = 287 N•m/kg•K，T0 = 288K。则：
p 1 p0 T0
各向等值性
p x p y p z pn

水力学(2)水静力学

武汉理工大学土木工程与建筑学院
金溪
水力学
2.1 静水压强及其特性
第二章水静力学
一、定义水静力学：研究液体处于静止状态下的平衡规律和液体与固体边界间的作用力及其在工程中的应用。二、核心问题所谓静止包含两种情况：绝对静止、相对静止。绝对静止：液体与地球之间没有相对运动，液体内部质点之间没有相对运动。相对静止：液体与地球之间存在相对运动，液体与容器之间没有相对运动，液体质点之间不存在相对运动。
绝对静止 V=0,a=0 相对静止 V ≠ 0,a恒定且不为0 相对静止 V ≠ 0,a =0
2.1 静水压强及其特性
第二章水静力学
三、本章基本内容水静力学的核心问题是根据平衡条件来求得静水压强在空间的分布规律，进而确定静水压力的方向、大小和作用点。

平衡条件：受力的平衡压强分布规律：水静力学基本方程压力的求解：方向、大小、作用点
sin J x sin yc A
Jx yc A
Jx= JC＋yC2A，
★ yD＞ yC ，即D点一般在C点的下面。
Jc yc yc A
2.6 作用在平面壁上的静水总压力
第二章水静力学
2.6 作用在平面壁上的静水总压力
例2-4
第二章水静力学
同一静止液体中，不论哪一点 z+p/r总是常数。（能量守恒）
2.2 重力作用下静水压强的分布规律
2.2.2 静水压强基本方程的另一种形式及意义
第二章一、几何意义和水力学意义 1. z —位置水头（计算点位置高度） 2. p/r —压强水头（压强高度或测压管高度） 3. z+p/r —测压管水头 4. z＋p/r＝C—静止液体中各点位置高度与压强高度之和不变

水力学：第2章叶片式泵和风机

型号意义：
200S63A
200 —— 泵吸入口直径为 200mm；
S—单级双吸离心泵； 63 —— 扬程为63m； A —— 叶轮外径第一次
切割。
S型图
单级双吸中开离心泵
便拆式管道离心泵
DL型立式多级离心泵
IS型单吸离心泵
叶轮
S型双吸离心泵
二、离心泵的主要零件，作用材料和组成
1．叶轮：了解叶轮作用，材料，组成，按吸入口分类，按盖板情况分类
3、按叶轮进水方式分：单侧进水式泵：又叫单吸泵，图2－2，即叶轮上只有一个进水口双侧进水式泵：又叫双吸泵，即叶轮两侧都有一个进水口，它的流量比单吸式泵大一倍，可以近似看作是两个单吸泵叶轮背靠背放在一起。P101图2－93，图2－5。 4、按泵壳结合缝形式分：水平中开式泵：即在通过轴心线的水平面上开有结合缝垂直结合面缝：即结合面与轴心线相垂直
1、泵壳；2、镶在泵壳上的减漏环； 3、叶轮；4、镶在叶轮上的减漏环
轴封装置
泵轴穿出泵壳时，在轴与壳之间存在着间隙，如不采取措施，间隙处就会有泄漏。当间隙处的液体压力大于大气压力(如单吸式离心泵)时，泵壳内的高压水就会通过此间隙向外大量泄漏；当间隙处的液体压力为真空(如双吸式离心泵)时，则大气就会从间隙处漏入泵内，从而降低泵的吸水性能。为此，需在轴与壳之间的间隙处设置密封装置，称之为轴封。目前，应用较多的轴封装置有填料密封、机械密封。
立式轴流泵结构图
ZLB型立式轴流泵
叶轮 1、固定式 2、半调节
四、混流泵
1、混流泵的工作原理混流泵是介于离心泵和轴流泵之间的一种泵，
它是靠叶轮旋转而使水产生的离心力和叶片对水产生的推力双重作用而工作的。 2、混流泵的构造

水力学2

水力学2(23)

水力学2复习资料（长理港航）.

水力学第2章静水力学

水力学2简答题

第2章水力学基本知识

北航水力学课件s2 第二章流体静力学

水力学_第2章静水力学

【精品作文】水力学第二章课后答案

水力学第2章 水静力学

水力学-第2章-水静力学

水力学2(31)

水力学第2章.流体静力学

水力学 第二章液体运动的流束理论

水力学 第二章课后题答案

水力学2

水力学(2)水静力学

水力学：第2章 叶片式泵和风机

水力学第2章水静力学

水力学第二章液体运动的流束理论

水力学第二章课后题答案

水力学：第2章叶片式泵和风机