机械优化设计-无约束优化方法
机械优化设计方法第五章 多变量无约束优化方法

似极小点,则在X(k)点根据函数f(X)的性质,选择一个方向S(k),沿 此方向搜索函数值应是下降的,称S(k)为下降方向。
(3)当搜索方向S(k)确定以后,由X(k)点出发,沿S(k)方向进行搜索,
定出步长因子α(k),得新设计点 X(k+1)= X(k)+α(k) S(k) 并满足f(X(k+1))<f(X(k))。具有这种性质的算法称为下降算法。α(k) 可以是一维搜索方法确定的最优步长因子,亦可用其他方法确定。 (4)若新点X(k+1)满足迭代计算终止条件,则停止迭代,X(k+1)点就 作为近似局部极小点X*;否则,又从X(k+1)点出发,返回第(2)步 继续进行搜索迭代。
的极为有用的性质:从任意初始点X(0)出发,依次沿n个线性无关 的与A共扼的方向S1,S2,…, Sn各进行一维搜索,那么总能在第n 步或n步之前就能达到n维正定二次函数的极小点;并且这个性质 与所有的n个方向的次序无关。因而说共轭方向法具有有限步收敛 的特性。通常称具有这种性质的算法为二次收敛算法。 2.理论与实践证明,将二次收敛算法用于非二次的目标函数, 亦有很好的效果,但迭代次数不一定保证有限次,即对非二次n维 目标函数经n步共轭方向一维搜索不一定就能达到极小点。 3.对于非二次的目标函数寻优的另一种处理方法是循环迭代 法,即当达n步迭代终点X(n)时还未收敛,此时可将X(n)作为新的初 始点,再重新开始迭代,实践证明,这样做要比一直迭代下去具 有更好的效果。 4.即便对于正定二次函数,在数值计算中,由于数据的舍入 以及计算误差的累积,往往破坏了这种共轭性质。
(一)共轭方向的定义
设A为n×n阶实对称正定矩阵,如果有两个n维向量S1和S2满足
S1TAS2=0 则称向量S1与S2对于矩阵A共轭。 共轭向量的方向称为共轭方向。
《无约束优化方法》PPT课件

gk1 gk 与 d k 的共轭方向 d j 正交。
精选ppt
18
图4-9 共轭梯度法的几何说明
精选ppt
精选ppt
20
精选ppt
21
精选ppt
22
精选ppt
23
精选ppt
24
第六节变尺度法
变尺度法的基本思想:
前面讨论的梯度法和牛顿法,它们的迭代公式可以看作下列 公式的特例。
3
第二节 最速下降法
优化设计追求目标函数值最小,若搜索方向取该点的负梯度 方向,使函数值在该点附近的范围内下降最快。
按此规律不断走步,形成以下迭代算法:
xk1xkak f xk
以负梯度方向为搜索方向,所以称最速下降法或梯度法。
搜索方向确定为负梯度方向,还需确定步长因子a k
即求一维搜索的最佳步长,既有
xk 1xkkH f xk
变尺度法是对牛顿法的修正,它不是计算二阶导数的矩阵和 它的逆矩阵,而是设法构造一个对称正定矩阵H来代替Hesse 矩阵的逆矩阵。并在迭代过程中,使其逐渐逼近H-1 。
由于对称矩阵H在迭代过程中是不断修正改变的,它对于一 般尺度的梯度起到改变尺度的作用,因此H又称变尺度矩阵。
数值法
可以处理复杂函数及没有数学表达式 的优化设计问题
xk1xk akdk
搜索方向问题是无约束优化方法的关键。
各种无约束优化方法的区别:确定搜索方向的方法不同。
利用目标函数的一阶或二阶导数
无约束优化方法分类 (最速下降法、共轭梯度法、牛顿法)
利用目标函数值
(精坐选标ppt轮换法、鲍威尔等)
2
精选ppt
第四章常用的无约束优化方法

教学重点
1.鲍威尔法 2.梯度法 3.牛顿法
2
机械优化设计
概述
一、无约束优化方法的数学模型 有约束优化问题模型
L min F ( X * ) = F ( x1,x2, ,xn ), X ∈ R n D : g j ( X ) ≥ 0 j = 1,2,L, m hk ( X ) = 0 k = 1, 2,L, l
12
机械优化设计
一、Powell基本算法 Powell基本算法 1)开始采用坐标轴方向; 开始采用坐标轴方向; 2)每轮迭代产生一个新方向取代原来的第一 方向, 轮迭代后可产生n个彼此共轭的方向; 方向,n轮迭代后可产生n个彼此共轭的方向; 若目标函数为正定二次函数, 3)若目标函数为正定二次函数,n轮结束后 即可到达最优点。 即可到达最优点。
r (k ) r (k ) r (k ) r (k ) r (k ) r (k ) S 1 , S 2 , . . . , S m -1 , S m + 1 , . . . , S n , S n + 1 ,
22
第k+1环的方向组为:
机械优化设计
给定X 给定 0,Si=ei i=1,2,…n, ε
Powell 修正算法
K=0 i=1 方向搜索得一维最优点X 自Xi-1始,沿Si方向搜索得一维最优点 i
N
若powell法中不 需要换向,则 是否仍为共轭 方向法? 检查两次前后 sn+1是否对函数 的海塞矩阵共 轭即可。
Y
i< n Xn-X0 ≤ε
i=i+1
Y
输出X*=Xn 输出 F*=F(X*) ( )
x2
x2
o
x1
(2)等值线为如图脊线时--无效 (2)等值线为如图脊线时--无效 -o
第四章无约束优化方法

解: (1) 第一个搜索方向
对称正定
(0) (3) 从 X1 点沿S1方向求极小点x(1),即 点沿S 方向求极小点x
17
例
(0) 方向一维搜索求得该方向极小点x (4) 任取另初始点 x2 = 沿S1方向一维搜索求得该方向极小点 (2)
1 1
X(2)= 0.5 (5) 求与 1相共轭的方向 2 求与S 相共轭的方向S S2 =X(2)-X(1)=
x2
X(0)→X0
(1) (1) X1
终止准则: 终止准则:
( ( Xnk) − X0k) ≤ε
(2) X1
(1) (2) X2 →X0
(2) X2 →X0
(3)
( X* ←Xnk)
上式点距准则中的 两点应是一轮 轮 换 法 的 流 程 图
k Xi(−1)
Xi(k)
以最优步长原则确定α 以最优步长原则确定 2,即极小化
按最优步长原则确定步长α 按最优步长原则确定步长 1,即极小化
此问题可用某种一维优化方法求出α 此问题可用某种一维优化方法求出 1。 在这里, 在这里,我们暂且借用微分学求导解出 令其一阶导数为零, ,令其一阶导数为零,α1=5
得α2=4.5, ,
正定
10
4.2
鲍威尔(Powell)法 鲍威尔(Powell)法 (Powell)
鲍威尔法是直接搜索法中一个十分有效的算法。 鲍威尔法是直接搜索法中一个十分有效的算法。该算法是沿着 逐步产生的共轭方向进行搜索的,因此本质上是一种 共轭方向进行搜索的 本质上是一种共轭方向 逐步产生的共轭方向进行搜索的,因此本质上是一种共轭方向 鲍威尔法的收敛速率较快。 法,鲍威尔法的收敛速率较快。 以共轭方向作为搜索方向,不只限于鲍威尔法, 以共轭方向作为搜索方向,不只限于鲍威尔法,也用于其他一 共轭方向法。 些较为有效的方法,可以统称为共轭方向法 因此, 些较为有效的方法,可以统称为共轭方向法。因此,共轭方向 的概念在优化方法研究中占有重要的地位。 的概念在优化方法研究中占有重要的地位。 共轭方向在最优化问题中的应用是基于其具有一个重要性质, 共轭方向在最优化问题中的应用是基于其具有一个重要性质, 重要性质 个互相共轭的向量, 即:设 S1、S2、…、Sn是关于A的n个互相共轭的向量,则对于 、 是关于A 1 T 的极小点, 求正定二次函数 F ( X ) = c + bT X + X AX 的极小点,从任意初始 2…,n)方向进行一维最优化搜 点出发,依次沿S i=1, 点出发,依次沿Si (i=1,2, ,n)方向进行一维最优化搜 至多n步便可以收敛到极小点. 索,至多n步便可以收敛到极小点.
(06)第四章-无约束优化方法(坐标轮换法)

第四章 无约束优化方法 §4-7 坐标轮换法
§4-3 坐标轮换法
间接法:梯度法;牛顿法;变尺度法 共同点:求导数 直接法:直接用函数值 搜索方向如何定?
坐标轮换法的基本思想:
把n维无约束优化问题转化为一系列一维优化问题来求 解,即沿着n个坐标轴方向e1,e2……en顺次进行一维搜索, 每n次搜索记为一轮,轮换迭代,求解极值点。 基本迭代格式:
(1) T x = [0 0] ε = 0.1 初始点 0 的最优解。迭代精度 ,
z
课后练习题: 用坐标轮换法求目标函数(迭代两轮)
f ( x ) = x12 + 16 x 22 + 10 x1 x 2
(1) T x = [4 3] ε = 0.1 初始点 0 的最优解。迭代精度 ,
算法特点:
1)不需对目标函数求导,方法简单; 2)收敛速度通常较低(其有效性取决于目标 函数的性态),仅适于低维的情况。
x
(k ) i
=x
(k ) i −1
+α e
(k ) i i
(k = 1,2,3"; i = 1,2," n)
收敛准则:
(k ) x0( k ) − xn ≤ε
图4-12 坐标轮换法的基本原理示意图
计算步骤:
1)对于n个变量的函数,若在第k轮沿着第i个坐标 方向进行搜索,其迭代公式为: k k k i i −1 i i k 2)求最优搜索步长 α
x = x +α e
i
3)本轮所有方向搜索完毕,判断迭代终止条件:
x −x
k n
k 0
≤ε
k n
4)满足上式:
x =x
∗
第四章 无约束方法详解

[tt,ff]=opt_step_quad(xk1',dirk, th,epsx,epsf,maxiter); xk1=xk1+tt*dirk'; end xk0=xk1; xn=xk1; fn=ffx(xn); aa=norm(dir); if(aa<1e-30) aa=1e-30; end end
xn ]T
使目标函数 f ( x) min
min f ( x) x Rn
目前已研究出很多种无约束优化方法,它们的 主要不同点在于构造搜索方向上的差别。
(1)间接法(导数法)——确定搜索方向时用到一 阶或(和)二阶导数的方法。如梯度法、(阻尼) 牛顿法、变尺度法、共轭梯度法等。
(2)直接法——其搜索方向直接取定或由计算目标 函数值所得的信息来确定;即不使用导数信息,如 坐标轮换法、鲍威尔法等。
2020/9/23
5
无约束优化直接解法
坐标轮换法 鲍维尔(Powell)法 鲍维尔(Powell)修正算法
2020/9/23
6
§4-2 坐标轮换法(无约束优化直接解法)
一)搜索方向
依次沿n个正交坐标轴的方向搜索:
ee12
[1 [0
0 1
... ...
0]T 0]T
...
en [0 0 ... 1]T
坐标轮换法的Matlab程序由三部分组成。第一部分为坐标 轮换法计算函数coordinat(xk0,th,epsx, epsf,maxiter),函数引用 变量说明见程序注释。最优步长采用二次插值法计算,函数名 为opt_step_quad(xk0,dir0, th,TolX, TolFun,maxiter),该函数调 用区间搜索函数opt_range_serach(xk0,dir0,th)得出二次差值需 要的三个坐标点,区间搜索函数采用进退法。 第二部分为用户应用程序; 第三部分为定义目标函数,调用方式为fn=ffx(x)。 下面是坐标轮换法的Matlab计算程序:
《机械优化设计方法》第4章 无约束优化方法 (上课课件)

4.1.4 梯度法讨论
梯度法的收敛速度与设计变量的尺度关系很 大。对一般函数,梯度法的收敛速度较慢。 但对等值线为同心圆的目标函数,一次搜索 即可达到极小点。 若能通过点的坐标变换,改善目标函数的性 态,就可提高梯度法的收敛速度。
4.2 牛顿性方法
4.2 牛顿型方法
4.2.1 牛顿法的基本思想
1 * T * * f (X) f (X ) X X H ( X ) X X 2
*
结论:任意形式的目标函数在极值点附近的特 性,都近似于一个二次函数。 故以正定二元二次函数为例说明共轭方向对于 构造一种有效的最优化算法的重要性。
1 T T T f ( X ) X HX B X C , X x1 , x2 2
4.3.2共轭方向的产生
2 0 S f ( X ) e S 1 e0 0 S 0 e0 T S0 0 2 0 S f (X)S 0 T
S
k 1
e i s
k i 0
k
k
i
2 i S f (X) e k i T 2 i S f ( X ) e S 0 i i i T 2 i i o S f (X)S 2 i S f (X) e S k 1 ek T Si i 2 i i 0 S f (X)S k i T
若f(X)是二次函数,则X*就是f(X)的极小点;
否则只是一个近似点,需进一步迭代。
4.2.2牛顿法的迭代公式及迭代过程
故牛顿法的迭代公式为:
X k 1 X k [ H ( X K )]1 f ( X K ) k 1 k k X X S k k 1 k S [ H ( X )] f ( X )
机械优化设计方法总结

优化算法的总结一、总结优化设计算法(一维,多维无约束,多维有约束)的特点、使用条件及选择方法的原则。
1.1 一维搜索方法1.1.1 黄金分割法特点:简单,有效,成熟的一维直接搜索方法,应用广泛。
可以把区间缩小的任意长度。
使用条件:适用于[a,b]区间上使用原则:黄金分割点的内分点选取必须遵循每次区间缩短都取相等区间缩短率的原则。
1.2.2二次插值法特点:收敛速度较黄金分割法快,可靠性不如黄金分割法,初始点的选择影响收敛效果。
不可能一次就达到函数的最优解,必须重复多次,向最优值逐渐逼近。
原则:首先要选择一个初始步长,用外推法确定极值点存在的区间,然后用二次差值法求极值点的近似值。
1.2无约束多维优化方法1.2.1 最速下降法特点:1)最速下降法是求解无约束多元函数极值问题的古老算法之一;2)最速下降法理论明确,方法简单,概念清楚,每迭代一次除需进行一维搜索外,只需计算函数的一阶偏导数,计算量小;3)对初始点的要求较低,初始迭代效果较好,前后两步迭代的搜索方向相互正交,在极值点附近收敛很慢。
选用原则及条件:一般与其他算法配合,在迭代开始时使用。
1.2.2共轭梯度法特点:1)仅需计算函数的一阶偏导数,编程容易,准备工作量比牛顿法小,收敛速度远超过梯度法,但有效性比DFP(变尺度)法差;2)使用一阶倒数的算法,所用公式结构简单,并且所需的储存量少。
3)收敛速度很快,有超线性的手链速度。
使用条件:适用于维数较高(50维以上)、一阶偏导数易求的优化问题。
使用原则:共轭梯度法在第一个搜索方向取负梯度方向,而其余各步的搜索方向将负梯度偏转一个角度,即对负梯度进行修正,实质上是对最速下降法的改进。
在n次迭代后如果没有达到收敛精度,则通常以重置负梯度方向开始,直到满足精度为止。
1.2.3 牛顿法特点:牛顿法对初始点要求不严格,具有二次收敛性,最优点附近的收敛速度极快,对于正定二次函数的寻优,迭代一次即可达到极小点;当初始点选的合适的时候,是目前算法中收敛的最快的一种(尤其对二次函数)。
最新第4章无约束优化方法PPT课件

第机四械章优化设无计约束优化方法
第七节 坐标轮换法
基本思想:
每次仅对多元函数的一个变量沿其坐标轴进行 一维探索,其余各变量均固定不动,并依次轮换进行一
,
维探索的坐标轴,完成第一轮探索后再重新进行第二轮 探索,直到找到目标函数在全域上的最小点为止。
目的:将一个多维的无约束最优化问题,转化为一系
列的一维问题来求解。
第机四械章优化设无计约束优化方法
第六节 变尺度法(拟牛顿法)
DFP算法:
例 : 用 D F P 算 法 求 fx 1 ,x 2 x 1 2 2 x 2 2 4 x 1 2 x 1 x 2
,
的 极 值 解 。
H k 1 H k E k H k s s k T k s y k T k H y k k T y H ky k k T y H kk (k 0 ,1 ,2 , )
设法构造出一个对称正定矩阵 来H 代k 替 ,并 在迭G代( x过k )程1 中使 逐渐逼近 H,那k 么就简化G了(牛xk )顿1 法的计算,并且保持了牛顿法收敛快的优点。
变尺度法的
迭代公式:
x k 1 x k k H k fx k ( k 0 ,1 ,2)
第机四械优章化设无计约束优化方法
3)沿方向d k作,一维搜索得xk 1 xk k d k ; 4)判断收敛:若满足 f ( x(k 1) ) , 则令x* xk 1,f ( x* ) f ( xk 1),
无约束优化方法PPT课件-PPT精选文档

等式两边同乘 d
0
T
得
d Gd 0
0 T 1
fxa fx fx 0
k k T k k
k f x f x 0 k 1 T
d
k 1 T
dk 0
由此可知,在最速下降法中,相邻两个迭代点上 的函数梯度相互垂直。而搜索方向就是负梯度方 向,因此相邻两个搜索方向互相垂直。
第四章
无约束优化方法
第一节 概述
从第一章列举的机械设计问题,大多数实际问题 是约束优化问题。 约束优化问题的求解——转化为一系列的无约束 优化问题实现的。
因此,无约束优化问题的解法是优化设计方法 的基本组成部分,也是优化方法的基础。
无约束优化问题的极值条件
f x* 0
解析法(间接解法)
4.3.2 阻尼牛顿法 牛顿法的缺陷是,在确定极值点的过程中,并不含有沿 下降方向搜索的概念。因此对于非二次型函数,在迭代过 k 1 k 程中,可能出现 f( X )f( X )
的现象。为此人们提出了所谓的阻尼牛顿法。
令
k d H ( X ) f ( X ) k
1 k
以上二种经典方法中,人们不断努力,发掘,提出了不
同的改进方法。
第四节共轭方向及共轭方向法
为了克服最速下降法的锯齿现象,提高收敛速度,发展 了一类共轭方向法。搜索方向是共轭方向。
一、共轭方向的概念 共轭方向的概念是在研究二次函数
1T T f x x bx c xG 2
时引出的。 首先考虑二维情况
数值法(直接解法)
机械优化设计第四节无约束--坐标轮换法3-5解析
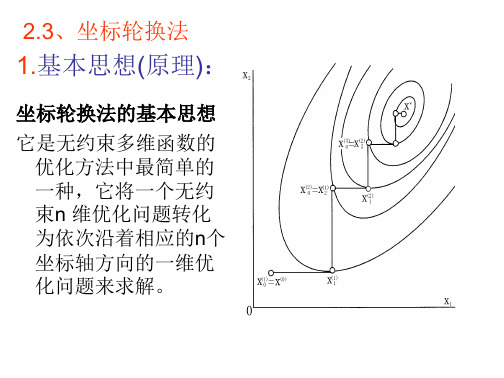
5
7.954 , 5.978 T 0.035 7.989 , 5.978T 0.018 7.989 , 5.996 T 0.04
计算第五轮的有
(5) (5)
x2 x0 (7.989 7.954)2 (5.996 5.978)2 0.0394
近似优化解为:
* (5) 7.989 x x2 5.996
*
f * f (x ) 8.000093
2.4、共轭方向法
1、共轭方向
坐标轮换法的收敛速度很慢,原因在于其搜索方向总是
平行于坐标轴,不适应函数变化情况如图所示若把一轮的起
点 与末点 (1)
(1)
x1
x2
连起来形成 一个新的搜索方向
S2
,
S2 与
S1 有何关系。
如图所示,设给定两个平行方向 S1 ,从两个任意初始点分别
)
e
i
否
in
是
(k) (k)
xn x0
否
是
k k 1
(0)
(k)
x xn
*
*
x x f f (x )
出口
特点: 简单易行,但由于它只能轮流沿几个坐标
方向前进,因而效率低下,特别是维数较高n>10 或目标函数性质不好的情况下收敛速度慢。本方 法的收敛效率在很大程度上取决于目标函数等值 线的形状。当椭圆簇的长短轴与坐标轴斜交,迭 代次数将大大增加,收敛速度很缓慢。目标函数
S2
*
x
S1
x
2
x1
S1
如图所示,同心椭圆簇具有 这样一个特点,就是二条任 意平行线的切点的连线必通 过椭圆族的中心。
沿这两个平行方向进行一维搜索求得极小点
机械优化设计之无约束优化方法培训课件

4x2 2x1
x0
4
2
取初始变尺度矩阵为单位矩阵A0=I,则第一次搜寻方向为
d0
A0f
(x0)
1 0
0 4 4
1
2
2
24
2020/
4.7 变尺度法
3/2
(9) DFP算例
上式即产生构造矩阵 Ak+1 应满足的一个重要条件,通常称为拟牛顿 条件或拟牛顿方程
15
2020/
4.7 变尺度法
3/2
(6) 变尺度矩阵的构造
拟牛顿条件 k Ak 1 yk 可写成 Ak Ak yk k 或 Ak yk k Ak yk (1)
DFP算法中的校正矩阵△ Ak取为下列形式:
选取初始矩阵A0,并以梯度方向快速收敛,通常取单位矩阵E 作为
初始矩阵,即A0=E。而后的矩阵均是在前一构造矩阵的基础上校正
得到,令
A1=A0+△A0
矩阵序列的
推广到一般的k+1次构造矩阵
基本迭代式
Ak+1=Ak+△Ak
△ Ak 称为校正矩阵
11
2020/
4.7 变尺度法
3/2
(5) 拟牛顿条件
构造矩阵Ak+1应该满足一个重要条件—拟牛顿条 件
yk
17
2020/
4.7 变尺度法
3/2
(6) 变尺度矩阵的构造
由上式可以看出,构造矩阵Ak+1的确定取决于第 k 次迭代中的下列 信息:
上次的构造矩阵:Ak 迭代点的位移矢量: 迭代点的梯度增量:
无约束优化方法PPT课件

从点xk出发,沿G某一共轭方向d k作一维搜索,到达xk 1
xk 1 xk ak d k
xk 1 xk ak d k 而在点xk、xk 1处的梯度分别为:
gk Gxk b gk1 Gxk1 b
gk1 gk G xk1 xk akGd k
等式两边同乘 d 0 T 得 d 0 T Gd1 0
d 0 d 1 是对G的共轭方向。
三、共轭方向法
1、选定初始点 x0 ,下降方向d 0 和收敛精度ε,k=0。
2、沿 d k 方向进行一维搜索,得 xk1 xk ak d k
3、判断 f xk1 是否满足,若满足则打印 xk1
xk1 xk k Hf xk
变尺度法是对牛顿法的修正,它不是计算二阶导数的矩阵和 它的逆矩阵,而是设法构造一个对称正定矩阵H来代替Hesse 矩阵的逆矩阵。并在迭代过程中,使其逐渐逼近H-1 。
由于对称矩阵H在迭代过程中是不断修正改变的,它对于一 般尺度的梯度起到改变尺度的作用,因此H又称变尺度矩阵。
第二节 最速下降法
优化设计追求目标函数值最小,若搜索方向取该点的负 梯度方向,使函数值在该点附近的范围内下降最快。 按此规律不断走步,形成以下迭代算法:
xk1 xk akf xk
以负梯度方向为搜索方向,所以称最速下降法或梯度法。
搜索方向确定为负梯度方向,还需确定步长因子ak
即求一维搜索的最佳步长,既有
共轭方向的概念是在研究二次函数
f x 1 xTGx bT x c
2 时引出的。 首先考虑二维情况
1 共轭方向
定义1:设G为 n n阶实对称正定矩阵,而 d i , d 为j 在n
无约束优化方法

第四章无拘束优化方法——最速降落法,牛顿型方法概括在求解目标函数的极小值的过程中,若对设计变量的取值范围不加限制,则称这种最优化问题为无拘束优化问题。
只管对于机械的优化设计问题,多半是有拘束的,无拘束最优化方法仍然是最优化设计的基本构成部分。
因为拘束最优化问题能够经过对拘束条件的办理,转变为无拘束最优化问题来求解。
为何要研究无拘束优化问题(1)有些实质问题,其数学模型自己就是一个无拘束优化问题。
(2)经过熟习它的解法能够为研究拘束优化问题打下优秀的基础。
(3)拘束优化问题的求解能够经过一系列无拘束优化方法来达到。
所以无拘束优化问题的解法是优化设计方法的基本构成部分,也是优化方法的基础。
依据构成搜寻方向所使用的信息性质的不一样,无拘束优化方法能够分为两类。
一:间接法——要使用导数的无拘束优化方法,如梯度法、(阻尼)牛顿法、变尺度法、共轭梯度法等。
二:直接法——只利用目标函数值的无拘束优化问题,如坐标轮换法、鲍威尔法纯真形法等。
无拘束优化问题的一般形式可描绘为:求 n 维设计变量X x1x2L x n T R n使目标函数 f ( X )min当前已研究出好多种无拘束优化方法,它们的主要不一样点在于结构搜寻方向上的差异。
无拘束优化问题的求解:1、分析法能够利用无拘束优化问题的极值条件求得。
马上求目标函数的极值问题变为求方程min f ( X * )0的解。
也就是*使其知足求Xf ( X *)0x1f ( X*)x2f ( X*)x n解上述方程组,求得驻点后,再依据极值点所需知足的充足条件来判断能否为极小值点。
但上式是一个含有n个未知量,n个方程的方程组,在实质问题中一般是非线性的,很难用分析法求解,要用数值计算的方法。
由第二章的叙述我们知道,优化问题的一般解法是数值迭代的方法。
所以,与其用数值方法求解非线性方程组,还不如用数值迭代的方法直接求解无拘束极值问题。
2、数值方法数值迭代法的基本思想是从一个初始点 X (0)出发,依据一个可行的搜寻方向 d ( 0)搜寻,确立最正确的步长0使函数值沿 d (0 )方向降落最大,获得 X (1)点。
机械优化设计 第5章 约束优化方法

2. 将(0,1)中的随机数 i 变换到(-1,1)中去;
yi 2i 1
3. 构成随机方向
y1
e
1
y2
n
i 1
yi2
...
yn
i 1,2,...,n
例: 对于三维问题: 1 0.2,2 0.6,3 0.8 变换得: y1 0.6, y2 0.2, y3 0.6
一. 基本思路
搜索方向----采用随机产生的方向 ① 若该方向不适用、可行,则 产生另一方向;
②若该方向适用、可行,则以加 速步长前进;
③若在某处产生的方向足够多, 仍无一适用、可行,则采用收缩 步长;
④若步长小于预先给定的误差限 则终止迭代。
2019/12/12
5
二.随机方向的构成
1.用RND(X)产生n个随机数 i , i 1,2,..., n(0 i 1)
j =1
给定内点 X 0 ,0 , m,
α =α 0, F0=F(X0)
K=0, j=0
0 初始步长; m 在一迭代点处允许产生的方向数; 终止误差限(步长)
产生随机方向
X X 0 S
否
X∈D
是
F=F(X)
否 F<F0 是
X0=X, F0=F
否 j =0
是
K=K+1
2019/12/12
2
二.迭代步骤
X (0) X (3) X (4)
X (1) X (2)
2019/12/12
3
三.存在问题
有时会出现死点, 导致输出“伪最优 点”.
* 为辨别真伪, 要用K-T条件进行检查.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f ( X k 1 )T f ( X k ) 0,
令
d k 1 f ( X k 1 ),
d k f ( X k ),
所以
d k 1 T d k 0.
最速下降法
由此可知: 在最速下降法中,相邻两个迭代点上的函数梯度 相互垂直。而搜索方向就是负梯度方向,因此 相邻两个搜索方向互相垂直。这就是说在迭代点向 函数极小点靠近的过程,走的是曲折的路线。形 成“之”字形的锯齿现象,而且越接近极小点锯齿 越细.
X k 1 X k k d k X k k H X k
1
f X k
牛顿型方法
其中是沿牛顿方向进行一维搜索的最佳步长,称为阻尼因子。 通过 f X k 1 f X k k d k min f X k k d k k 求得; f X k 1 f X k 这样就能保证
1
牛顿型方法
1. 一元函数求极值的牛顿型迭代法
对于一元函数,在 x 点进行泰勒展开,并忽略二次以上微量
f x f x k f x k x x k
k
根据一元函数极值存在的必要条件 f x 0 有
1 f x k x x k 2
2
0
2
沿负梯度方向 X 1 X 0 f ( X 0 ) 1 2 1 2 0 0 1 0 2 1 2 进行一维搜索 0 将 X 1 代入原方程,将n维问题化成一维问题。
最速下降法
f ( x) (1 20 )2 (1 20 )2 2(1 20 )2 (0 ),
解: 取初始点 x0 2,2
T
经过一次迭代即求得最小点 x* 0,0T
* 函数极小值 f x 0
1 2 2 1 0 2 0 1 0 x x f x f x 2 0
0 4 0 1 100 0 50
将 X 代入求梯度公式
1
2 x1 0 f ( X ) 2 x2 x1 0 0 x 0
1
2
最速下降法
显然 X 点满足收敛迭代准则,即 f ( X ) 1 。 因为该目标函数的等值线为圆簇,故只要经过一 轮迭代,即找到问题的极值点,计算效率很高。 其迭代示意图如图2所示。
牛顿型方法
阻尼牛顿法
牛顿法的缺陷是,在确定极值点的过程中,并不含 沿下降方向搜索的概念。因此对于非二次型函数, 在迭代过程中,可能出现 f X k 1 f X k 的现象。 为此人们提出了所谓的阻尼牛顿法 k k 1 令 d H X f X k 作为一个搜索方向,或称牛顿方向,则阻尼牛顿 法采用下述迭代公式:
最速下降法
图1
图2
最速下降法
2 (2) 求目标函数 f ( X ) x12 x2 的极小点 T X 0 1,1 解: 取初始点 则此点处函数值 f (X 0) 2
梯度
2 x1 2 f ( X ) 2 x2 x1 1 2 x 1
f x k f x k x x k 0
令
x x k 1
x
k 1 k
f xk x f x k
牛顿型方法
上式即为一元函数的牛顿型迭代 x k 可求得点 x k 1。 公式,即从 求 f x 的极小点,应满足极值 f x* 0 。所以求 f x 必要条件 的极小点,也就是求解方程 f x 0 的根,牛顿法又称作切 线法,如右图所示。
无约束优化方法
---最速下降法、牛顿型方 法
无约束优化方法
• 机械设计问题中,大部分都是约束优化问题。对于约束 优化问题的求解是通过转化为一系列的无约束优化问题 实现的。 • 因此,无约束优化问题的解法是优化设计方法的基本组 成部分,也就是优化方法的基础。
无约束优化方法
无约束问题的数学模型是: 迭代公式:
牛顿型方法
阻尼牛顿法的程序框图
•阻尼牛顿法程序框图如图所示。以上介绍的最速 下降法及牛顿法或称阻尼牛顿法,属于经典数学 方法。显然在这些方法中要用到某点函数的一阶 导数、二阶导数等信息,同时对牛顿法还要用到 逆矩阵的计算等。当变量维数较高时,计算工作 量相当大,影响计算速度。理论上,牛顿法的收 敛速度高于最速下降法。
1
f ( X ) 3.686164
最速下降法
将 X 1 的值代入求梯度公式得 2 x1 3.8 1 f ( x ) 0 0.15 50 x2 x 1.9
x2 0.003
1
显然 X 1 不是函数的极小点。仍需要继续迭代, 2 X 1 为初点,搜公式(1)可得 X , 第二轮迭代以 T X 10 0, 0 ,将 X 10代入公式 依此类推,经过10轮迭代
最速下降法
4.最速下降法步骤:
(1)给定初始点 x0 Rn,允许误差 0 ,令 k 0 。 (2)计算搜索方向 d k f ( xk ); d k ,则停止计算,x k 为所求极值点; (3)若 否则,求最优步长 k 使得 f ( x k k d k ) min f ( x k k d k ) 。 (4)令 x k 1 x k k d k ,令 k k 1 ,转(2)。
最速下降法
5.例题
的极小 T 点. X 0 2, 2 ,则初始点处函数值及梯度分别为 解:取初始点
f ( X ) x12 25x22 (1) 求目标函数
f ( X ) 104,
0
2 x1 4 f ( X ) 50 x2 x1 2 100 x 2
k
k
1
f X k ,(k=0,1,2,„,n)
这就是多元函数求极值的牛顿型迭代公式。 对于二次函数 ,海赛矩阵是一个常矩阵,其中各元素 均为常数。因此,无论从任何点出发,只需一步就可找 到极小点。
牛顿型方法
2 2 (3) 求目标函数 f x x1 25x2 的极小点。
T k k T k k
• 设 X k 1 为 X 的一个极小点,它作为 f X 极小点 X * 的一个近似点,根据极值必要条件: X k 1 0 即 f X k H X k X k 1 X k 0
牛顿型方法
由上式解得
X
k 1
X H X
(0 ) 4(1 20 )(2) 8(1 20 ). 1 令 (0 ) 0 即 8(1 20 ) 0 ,解得: 0 2 1 0 代入 X 式得 将 1 2 0 0 1 X 0 , 1 2 0
开始
给定 X 0 、
k 0
d k 2 f X k
1
k f kk 1 X
k k 1
X k 1 X k a k d k a k : min f X k a k d k k
a
X X
*
k 1
是
X k 1 X k
否
结束
0
2
沿负梯度方向进行一维搜索,有
2 2 4 0 0 4 X X 0f ( X ) 2 100 2 100 0
1 0 0
最速下降法
0 为一维搜索的最佳步长,应满足极值必要条件 f ( X ) min f ( X f ( X )) min (2 4 ) 25(2 100 ) min ( ),
min f ( X )
k k
X [ x1, x2 , x3 ,..., xn ]T , X Rn
X
k 1
X d
k
d k 为第k次探索的方向向量 X k 沿着 d k 方向迈出的步长, X k 1为k次搜索获得的一个新点
k 为第k次探索的初始值,
无约束优化方法
• 可以把初始点 X 、搜索方向 d 、迭代步长 k 称 为优化方法算法的三要素。其中以搜索方向 d 更 为突出和重要,它从根本上决定一个算法的成败、 收敛速率的快慢等。
k
k
k
• 搜索方向问题是无约束优化方法的关键。 • 各种无约束优化方法的区别就是确定搜索方向的 方法不同。
• 最速下降法
最速下降法
1.基本思想
min 优化设计是追求 f ( X ) ,因此,会自然想到 X 从某点 出发,以该点的负梯度方向即最速下降 方向为搜索方向,使函数值在该点附近范围内下降 最快。 按此规律形成以下迭代算法: X k 1 X k k f ( X k ),(k 1, 2,..., n) (1)
以负梯度方向为搜索方向,所以称为最速下降法或梯度法
最速下降法
2.搜索方向: d k f ( xk ) ,也称最速下降方向; 3.搜索步长:取最优步长,即满足 f ( X k 1 ) f ( X k k f ( X k )) min ( )
( )
f ( X ) dX [f ( X k k f ( X k ))]T (f ( X k )) 0 X d
牛顿型方法
2.多元函数求极值的牛顿型迭代法
X* • 对于多元函数 f X ,设 x k 为 f X 极小点 的一个近似点,在 X k 处将 f X 进行泰勒展开,保留 到二次项,得:
f X X f X k f X k
X X 1 X X H X X X 2
2 x1 0 f ( X ) 50 x2 x1 0 0 x 0
