车灯线光源的优化设计(第二组)
车灯线光源的优化设计模型
车灯线光源的优化设计模型
摘 要： 本文利用几何光学的原理,从线光源上某一点光源出发作反射;根
据能量守恒定律及光传播的球面性,给出直射光和反射光能量之间的关系.从而证明反射光远远强于直射光,故而,在计算测试屏某点的光强度时,可将直射光忽略,只考虑反射光. 根据点光源的反射强度,可计算出点光源到达B 和C 点的光强度,设线光源的长度为2a,则从-a 到a 对点光源积分,可算出B 点和C 点的光强度为:
a
a
B y I I --⋅⋅=
250001300arctan
25000459.00
0π
a a
c y I I --⋅⋅=
25000
2600arctan
25000459.00
0π
根据以知B 点的光强度为2单位,C 点的光强度为1单位,利用以上方程可求得:a=2.34mm. 通过点光源在抛物面上任一点处反射光线的计算机模拟，给出了线光源反射线在测试屏上形成的亮区。
关 键 词：光强度，点光源，线源的功率, 亮区光
一． 问题的提出：
汽车头部的车灯形状为一旋转抛物面,且已经告知开口半径和深度,所以可以得出抛物面的焦距,经过适当建立直角坐标系,可以得到抛物面的方程. 在焦点前放置的测试屏用以测试反射光的光强度,使其两点上的光强度各不小于某一额定值. 在设计规范的条件下,计算线光源长度,使线光源的功率最小. 且在此基础上,精确画出测试屏上反射光的亮区.最后提出对规范合理性的意见. 二． 基本假设：
1. 根据题目的要求,我们只考虑反射光的情形。
2. 在车灯内部,只考虑光线的一次反射。
3. 假设光线在抛物面内的每一点上都是镜面反射。
CUMCM历年赛题一览
中国大学生数学建模竞赛(CUMCM)历年赛题一览
CUMCM从1992年到2007年的16年中共出了45个题目,供大家浏览1992年
A.施肥效果分析问题(北京理工大学：叶其孝）
B.实验数据分解问题（复旦大学：谭永基）
1993年
A.非线性交调的频率设计问题（北京大学：谢衷洁）
B.足球排名次问题（清华大学：蔡大用）
1994年
A.逢山开路问题（西安电子科技大学：何大可）
B.锁具装箱问题（复旦大学:谭永基，华东理工大学:俞文此）
1995年
A.飞行管理问题（复旦大学:谭永基，华东理工大学:俞文此）
B.天车与冶炼炉的作业调度问题（浙江大学：刘祥官,李吉鸾）
1996年
A.最优捕鱼策略问题（北京师范大学：刘来福）
B.节水洗衣机问题（重庆大学：付鹂）
1997年
A.零件参数设计问题（清华大学：姜启源）
B.截断切割问题（复旦大学:谭永基，华东理工大学:俞文此）
1998年
A.投资的收益和风险问题（浙江大学：陈淑平）
B.灾情巡视路线问题（上海海运学院：丁颂康）
1999年
A.自动化车床管理问题（北京大学：孙山泽）
B.钻井布局问题（郑州大学：林诒勋）
C.煤矸石堆积问题（太原理工大学：贾晓峰）
2000年
A.DNA序列分类问题（北京工业大学：孟大志）
B.钢管订购和运输问题（武汉大学：费甫生）
C.飞越北极问题（复旦大学：谭永基）
D.空洞探测问题（东北电力学院：关信）
2001年
A.血管的三维重建问题（浙江大学：汪国昭）
B.公交车调度问题（清华大学：谭泽光）
C.基金使用计划问题（东南大学：陈恩水）
2002年
A.车灯线光源的优化设计问题（复旦大学:谭永基，华东理工大学:俞文此）
车灯线光源的最优设计
我们把这 N 个点光源在屏上某一小区域内的光子数进行求和,就可以求得该小区 域内的光照度值
l l 我们先分析一下任一个点光源 G(15,y1,0) ， （ y [ , ] ）在抛物面上任 1 2 2 一点 P(x0,y0,z0)的反射曲线. 为了直观的理解我们在平面上做出了大致反射 光线图,实际上这些点图并不是在一个平面上的（见图 2） 。G 是点光源，P 是反 射点，E 是 G 点关于过 P 点切平面的镜面对称点，PN 是反射方向。
Min P(l )
E C k E B2 k
其中 K 是某一要求的额定光强度,
E ,E
B
C
分别表示线光源在 B,C 两点的光强度
我们的目的就是求出满足 P 最小的
l
光子跟踪模型：
本题中线光源可以看成是许多个点光源的叠加，只有焦点处的那个点光源通 过抛物面后的反射光线是平行光束。其它点光源的反射光线都不是平行光束，因 此射到屏上的总光线分布比较复杂， 难以求出解析表达式。 但并不是无规律所寻， l l 给定了空间的一个点光源 G(15,y1,0) ， （其中 y [ , ] ） ，再给定抛物面 1 2 2 T: y z 60x
二、 模型假设：
1、基本假设 （1 ） （2 ） （3 ） （4 ） （5 ） 光线通过车灯的前玻璃时能量无损失。 光线在抛物面进行一次反射时，能量考虑成无损失。 不考虑二次反射。 不考虑光的干涉和衍射现象。 截取线光源上很小的一段 dl ，可以看成是在空间呈均匀辐射的 点光源。于是线光源可以看成是无穷多个点光源的叠加。 （6） 不考虑线光源对反射光能量的阻挡和吸收，即是说线光源不考 虑厚度，反射光线可以毫无影响地穿过线光源区域。
汽车车灯设计研究专题资料集锦(二)
讨论。
先进虚拟技术在车灯开发中的应用
重点说明了先进的虚拟技术和创新的开发方法在车灯开发过程中的应用,展现 了目前国际车灯设计开发的现状和未来的发展趋势。
考虑气动特性和热特性的车灯造型设计方法研究
以汽车前照灯为研究对象,分析现有成功的车灯造型设计案例,结合认知学、
形态学、产品语义学和美学等相关知识,提出了车灯造型设计的美学规律,表 现为“吸引人”,具体表现方法有认知性、功能美、创新性、象征性、幽默感
solidThinking在汽车车灯设计上的成功案例 Altair 公司的工业设计软件solidThinking为Automotive Lighting——全球
顶级车灯制造商在产品概念设计阶段提供了众多优势，使其在行业内更具竞
争力。
更多资料：http://www.yanfabu.com/Home.html
、区域的照度值的分析,较好地符合了GB4599-2007对近光的要求。该方法能 够大大缩短车灯设计周期,为未来大功率LED用于车灯设计提供参考。
汽车灯具光源建模和照明仿真计算 讨论了车灯设计中的光源建模的重要性,提出了灯丝发光能量分解的模型。通 过分析局部灯丝发光强度的分布,运用光学理论和数学方法完成了灯丝的建模 ,并实现计算机的光源仿真。把光源模型应用到车灯设计的实时仿真,得到灯
多曲面车灯CAD系统的建模技术 多曲面车灯的设计离不开CAD技术的支持 ,阐述了多曲面车灯计算机辅助配光
(整理)2002数学建模A题车灯线光源的优化设计参考答案.
A题车灯线光源的优化设计参考答案
A题车灯线光源的优化设计
安装在汽车头部的车灯的形状为一旋转抛物面，车灯的对称轴水平地指向正前方, 其开口半径36毫米，深度21.6毫米。经过车灯的焦点，在与对称轴相垂直的水平方向，对称地放置一定长度的均匀分布的线光源。要求在某一设计规范标准下确定线光源的长度。
该设计规范在简化后可描述如下。在焦点F正前方25米处的A点放置一测试屏，屏与FA垂直，用以测试车灯的反射光。在屏上过A点引出一条与地面相平行的直线，在该直线A点的同侧取B点和C点，使AC=2AB=2.6米。要求C点的光强度不小于某一额定值（可取为1个单位），B点的光强度不小于该额定值的两倍（只须考虑一次反射）。
请解决下列问题：
（1）在满足该设计规范的条件下，计算线光源长度，使线光源的功率最小。
（2）对得到的线光源长度，在有标尺的坐标系中画出测试屏上反射光的亮区。
（3）讨论该设计规范的合理性。
注意：以下答案是命题人给出的，仅供参考。各评阅组应根据对题目的理解及学生的解答，自主地进行评阅。
四. 反射光亮区的计算
分别将线光源和车灯反射面离散化为点光源和面元的集合，计算每一点光源关于每一车灯反射面元的反射光线，判断其是否与车灯反射面相交，若相交，一次反射光不能到达测试屏，否则求出该反射光线与反射屏平面的交点，即为反射亮点。所有这些亮点的集合即为反射光亮区。亮区的上半部分由下图所示(横坐标为x轴，纵坐标为y轴，单位为mm),下半部分与上半部分是关于x轴对称的。
汽车前照灯线光源的优化设计（2）
汽车前照灯分为"近"和"远"两个档位，"近光"的距离取的是汽车前照灯正前方的一恒定距离（国际通用的标准为25米远）。汽车的配光性能可以通过在接收屏上测光强等手段来衡量。针对一个已经提出配光性能要求的汽车前照灯光源设计问题，本文提出了"双向蒙特卡罗方法"，此方法能够大大节省计算量，使计算量至少降低了一个数量级（具体数据见正文中第五部分的表格）；同时，在具体求解时还根据题目特点，使用了进一步优化计算的逆向蒙特卡罗法。
车灯线光源的优化设计方案
车灯线光源的优化设计方案
薛武;杨铭和;倪冉
【期刊名称】《工程数学学报》
【年(卷),期】2003(020)005
【摘要】本问题是一个车灯线光源的优化设计问题.首先,我们建立了一个连续的数学模型来描述这个优化问题,此模型研究了线光源上任意一点发出的光线经过抛物面反射后到达光屏的情况, 对于给定的考察点(B或C)得到一个联系该点与光的发射点,反射点这3个点关系的方程组.由于光在传播过程中会有发散的现象,我们用Jacobi行列式做了一个变换来描述这种散射.根据C点的光强度必须大于一个确定的值(文中设为1),B点的光强度必须大于该值的2倍的约束条件将这个问题抽象成一个非线性规划问题.由于解非线性规划问题是很复杂的过程,我们选择了将连续模型简化成一个离散模型.但是离散模型将光离散成一条一条光线时,一般不能考虑光在传播过程中的散射问题.根据我们连续模型中用Jacobi行列式算出的结果知可以考虑光在传播过程中的散射问题,但是Jacobi行列式是很难求出来的,为了解决这个困难我们将光的散射用连续的方法做了一个简化.简化的方法是用向量投影的方法粗略作出了两个面积微元之间的关系,从而得到了光线打在光屏上的散射效果与光线的起始单位方向向量和该光线经抛物面反射时的反射点的坐标的关系.运用以上的离散模型的算法,得到最优的线光源长度为3.39mm.
【总页数】10页(P19-28)
【作者】薛武;杨铭和;倪冉
【作者单位】北京化工大学,北京,100029;北京化工大学,北京,100029;北京化工大学,北京,100029
车灯设计数学建模实例
材料
B点照度 （勒克 斯）
C点照度 （勒克 斯）
高压毛 细汞灯
卤素灯
50
30
30
20
2.0121
2.1267
1.3677
1.5122
4．2
7．9
（2） 反射光亮区的绘制
首先我们称光能照射到的区域为亮区。我们以 常用的高压毛细汞灯为例（即 = 4.2mm），来 绘制出测试屏上反射光的亮区。
亮区图的绘制步骤：
3、 此线光源均匀分布，各点同性。且任意一 点向整个空间各个方向均匀辐射能量。
假设
4、 光强额定值为1勒克斯 5、 不考虑光的干涉、衍射等现象。 6、 光强在某点叠加时，可直接取其 代数和。 7、 只考虑一次反射。
变量定义（符号）
c
E
p
焦准距 （m ） 线光源的功率 （W ） 光通量 （lm ——流明 ） 发光效率 （lm/W ） 照度 （lx(lm/m2) ——勒克斯
词汇:
1、线光源——宽度与其长度相比小得多
的发光体。 2、光通量 ——光源在单位时间内辐射出 的光能，用国际规定的眼（对光适应的 眼）的灵敏度来估定。 3、发光效率——光源每消耗1瓦特功率可 辐射出的光通量，又叫光效。 4、照度——单位面积所接受的光通量， 单位为勒克斯。
分析:
首先解决本问题的一个难点：由 于问题讨论的主要对象是线光源， 而线光源处理起来不太容易，因此 想到用微元法将线光源划分为若干 小段（微元），每一段可视为一个 点光源。这样就将线光源的问题转 化为了点光源的叠加问题。
历年数学建模题目
历年数学建模题目
以下是部分历年的数学建模题目：
1. 1992年：施肥效果分析问题、实验数据分解问题。
2. 1993年：非线性交调的频率设计问题、足球排名次问题。
3. 1994年：逢山开路问题、锁具装箱问题。
4. 2002年：车灯线光源的优化设计、彩票中的数学、车灯线光源的计算（大专组）、赛程安排（大专组）。
5. 2003年：SARS的传播、露天矿生产的车辆安排、奥运会临时超市网点设计、电力市场的输电阻塞管理、饮酒驾车、公务员招聘。
6. 2005年：出版社的资源配置、艾滋病疗法的评价及疗效的预测、易拉罐形状和尺寸的最优设计、煤矿瓦斯和煤尘的监测与控制。
7. 2008年：数码相机定位、高等教育学费标准探讨、地面搜索、NBA赛程的分析与评价。
8. 2009年：制动器试验台的控制方法分析、眼科病床的合理安排、卫星和飞船的跟踪测控、会议筹备。
以上信息仅供参考，如需历年数学建模题目，建议查阅数学建模论坛或相关网站获取。
车灯线光源的优化设计模型
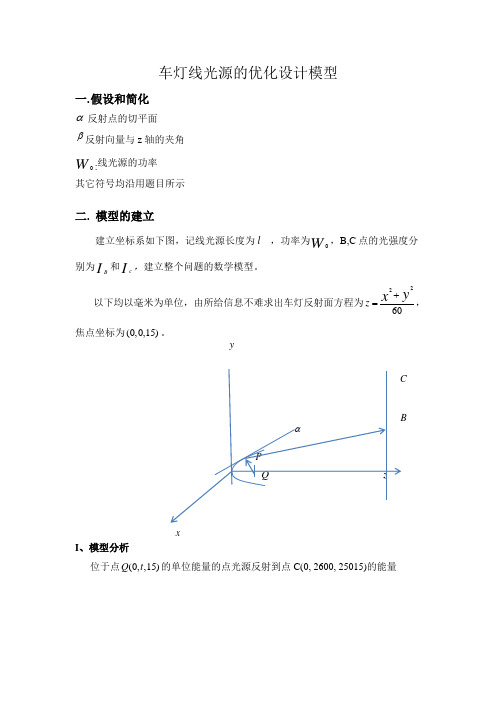
车灯线光源的优化设计模型
一.假设和简化
a反射点的切平面
P反射向量与z轴的夹角
W。•线光源的功率
其它符号均沿用题目所示
二.模型的建立
建立坐标系如下图，记线光源长度为I ，功率为w。，B，C点的光强度分
别为I B和I c，建立整个问题的数学模型。
2 2
以下均以毫米为单位，由所给信息不难求出车灯反射面方程为z= X +y
I、模型分析
位于点Q(0,t,15)的单位能量的点光源反射到点C(0, 2600, 25015)的能量
2 2
设反射点的坐标为p(x,y,x +y )。记入射向量为a ，该点反射面外法线方向
60
为b ，可以得到反射向量c = |-x,2600-y,25015-匚 满足与向量
V 60
丿
呻4
呻 2a 4 4 a -呻 2 b
b
共线. 记r 2
2 ，由 ■
a =(x,y -t. 2 j), 60 斗 x y
b =(——,——，一1)
30 30 从而得礬b 的表达式 C x^』^川III 川III 川III 川川川lil(i) 5 r +900
2
2
t(2y — r — 900)
C y= ----------- HIIIhllHIHIIH (2) 2 r
+900 r 4 + i800r
2 — 360ay -
810000”(⑶ 由反射向量c 满足与向量a b 2 + 900) b 共线，应
有
kc x —xHII 川川 1111卅I 川(4) kC y =2 600yil|| 川川 II (5) 2 kC z =2 50 1~560川川川 (6)
其中k 为常数。从上述 ⑴、(4)式可解得x=0或k = 2
thesis
车灯线光源的优化设计
摘要
本文讨论旋转抛物面车灯的线光源优化设计。在满足设计规范的前提下，寻找最佳长度线光源，达到最小功率的要求。
首先为了分析抛物面反射的几何关系，文章提出了光程极值模型和光路重建模型。光程极值模型从费马原理出发，用拉格朗日乘子法列出严格意义上的方程，运用恒等变形简化超越方程，把问题简化为多项式方程地求解。光路重建模型从几何光学的反射原理出发，利用矢量运算的技巧简化计算量，用遍历方法数值地进行求解。减少了解方程过程中的计算。
然后本文利用光程极值模型严格地计算了最节省功率时的光源长度。之后分别利用这两种模型计算了测试屏上的光强分布，给出了直观的图形表示。两种模型得出得结果非常吻合。
接着我们对这两种模型进行了误差分析，并综合比较了它们各自的优劣。最后文章从参数设置，反射面选择，增加检测点等方面对车灯设计规范进行讨论，得到了一些有益于实际的结果。
1 问题的提出
汽车前灯为一旋转抛物面，线光源经过车灯的焦点F，在对称轴垂直的水平方向对称放置，分布均匀。
测试车灯反射光的设计规范为：
1) 测试环境：测试屏置于F点正前方25m 的A点，垂直于FA。在屏上过A作平行于地面的直
线，并在直线上A的同侧取点B，C，使AC=2AB=2.6m 。
2) 达标条件：(只考虑一次反射) 当C点的光强度不小于某一额定值T，则B点的光强度不小于
2T。
我们的主要工作是：
1)在设计规范的约束下，给出线光源功率最小时的长度L。
2)在有标尺的坐标系中，就1) 的结果，在测试屏上画出反射光的亮区。
3)讨论给定的设计规范，并给出我们的改进方案和建议。
车灯线光源的优化设计方案42页PPT
61、辍学如磨刀之石，不见其损，日 有所亏 。 62、奇文共欣赞，疑义相与析。
63、暧暧远人村，依依墟里烟，狗吠 深巷中 ，鸡鸣 桑树颠 。 64、一生复能几，倏如流电惊。 65、少无适俗韵，性本爱丘山。
wk.baidu.com 谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
车灯线光源的优化设计
摘要
题目要求我们针对确定的设计规范，计算线光源的长度，然后再根据线光源的长度讨论该设计规范是否合理。
针对题目的任务，我们采用物理光学的知识和数学极限思想建立模型，根据题目的要求对线光源反射在屏幕上的光照强度进行了研究，并按照要求完成了线光源的优化设计。
对于问题一，采用了对线光源无限分割成线元的点光源的极限思想，并求出每个点光源经抛物面反射后照在测试屏幕上的光照强度，在B ,C 两点利用区
域法将圆区域的光照强度的和代替点的光照强度，再根据B ，
C 光照强度的关系，最后求得：
l =4mm
对于问题二，在问题一的基础上可以利用matlab 将带坐标的亮区绘出来，（结果见图5，第7页）
对于问题三，夜晚行车司机在看清障碍物时，从反应到到制动停止的距离为h ，其取值范围是：
23.6926.69m h m ≤≤
取26.69h m =>25m ,所以我们希望设计规范能够将25m 提高到30m 以外，提高司机的人身安全，同时考虑强度问题，为了确保在在30m 外能够辨出障碍物，屏幕上相应的B 和C 点的距离也要相应提高，并且线光源的长度也要适当增长，以确保有足够的强度。（具体长度呢？）
关键词：数学无限分割极限思想 光照度平方反比定理 光照强度
一、问题的重述
1.1问题背景
安装在汽车头部的车灯的形状为一旋转抛物面，车灯的对称轴水平地指向正前方, 其开口半径36mm，深度21.6mm。经过车灯的焦点，在与对称轴相垂直的水平方向，对称地放置一定长度的均匀分布的线光源。要求在某一设计规范标准下确定线光源的长度。
1.2目标任务
该设计规范在简化后可描述如下。在焦点F正前方25m处的A点放置一测试屏，屏与FA垂直，用以测试车灯的反射光。在屏上过A点引出一条与地面相平行的直线，在该直线A点的同侧取B点和C点，使AC=2AB=2.6m。要求C点的光强度不小于某一额定值（可取为1个单位），B点的光强度不小于该额定值的两倍（只须考虑一次反射）。解决如下问题：
（1）在满足该设计规范的条件下，计算线光源长度，使线光源的功率最小。（2）对得到的线光源长度，在有标尺的坐标系中画出测试屏上反射光的亮区。（3）讨论该设计规范的合理性。
二、问题分析
该问题属于物理学中的光学问题，对于线光源发射出来的光为无数条，我们无法运用整体思想进行建立模型。
对于问题一，我们运用无限分割成微元的极限思想，将线光源分成无限n （n=1,2,3…）份线元，然后计算出每份线元经过车灯抛物面反射后射在测光屏上的光照强度
E，进而可以对光照强度在,B C两点的极小区域进行求和，最后
n
要使线光源的发光功率最小，尽量满足B点处的光照强度接近C点处的两倍，由光照强度，功率与线光源之间个光线可以求出线光源的最小长度。
对于问题二，在问题一的基础上，在计算线元的光照强度时模拟光线的反射可得到反射光的亮区图。
对于问题三，结合实际与计算结果，以夜间行车的安全性讨论设计规范的合理性。
最后由模型和结果对该规范的合理性进行讨论修改。
三、基本假设
1.假设光线在经过抛物面反射所造成能量损失忽略不计，只考虑光线随距离的变化而产生的能量损失。
2.假设抛物面光滑，无凹凸不平，对光线无额外的作用，除了正常的反射。
3.由于要测试的,B C两点离屏幕A点距离远远大于旋转抛物面的最大口径故忽
略线光源对测光屏幕直射的光照强度，只考虑反射对测光屏幕光照强度的影响。
4.假设车灯发光均匀，光强均匀。
5.假设每份光线元经抛物面反射后，光强度为1个单位。
四、符号说明
五．模型的建立与求解
5.1问题一
对于问题一，要求在满足该设计规范的条件下，计算线光源的长度，使线光源的功率最小。
5.1.2模型的建立
首先以抛物面顶点为原心o，以抛物面的旋转中心轴为y轴，竖直向上为z 轴，建立空间直角坐标系，如图1：
图1 建立的坐标图
由题目所给的数据，抛物面开口半径为36mm ，深度为21.6mm ，我们根据抛物线旋转的知识求得抛物面方程：
2260x z y += (1)
设定线光源上任意一点p 坐标为（,15,0a ），a 的值取决于点的位置。同时已知了FA =25m ，2 2.6AC AB ==m 。则可以写出(1300,25015B ，(2600,25015,0)C 。当线光源上点光源P 发出的光经抛物面上(,,)D D D D x y z 反射后，照射到测屏试幕上的s 点，由空间几何知识，旋转抛物面在D 处的切平面的
法向量为(,30,)D D n x z =- 。如图2：
图2 点光源发出光线反射在屏幕上图
图3 入射光线与反射光线向量图
根据物理学中光的反射定律可知，光的入射角等于反射角，且入射光线和
反射光线同在反射平面一侧且分居法线两边。则向量PD 与向量n 的夹角和n 与
SD 的夹角相等，可知： 22()PD n SD n PD n
=+ （2）
由（2）式可求得发射光线的SD 的方向向量为SD =(,,)i j k ，则反射光线
的方程为：
D D D x x y y z z i j k
---== （3） 同时测试屏幕平面的方程为：
25015y = （4）
则运用matlab 软件编程可求出反射光线与测试屏幕的交点(,,)S S S S x y z 。算出S 点的坐标，可以求得光线从点光源射出到照射到测试屏幕所经过的路程： 1212,,PD R SD R R R R ===+ (5)
由光照度平方反比定理得光照度与点光源的发光强度I 成正比，与点光源到面的距离r 的平方成反比，并与面的法线与入射光线夹角余弦成正弦： 2
cos I E r β= （6） 由于在车灯抛物面中的法线与入射角的夹角较小，近似为0，且我们已假设点光源P 射出的光线元的光强度为I =1，经过反射后达到S 点的照度为： 21(1,2,3...)n E n R
== （7） 因为线光源的材质是均匀的，且单位长度发出的功率为一定值，故我们知道 必定存在：
p kl = （8）
其中k 与材质有关，为一常数。
要使功率最小，长度必须最小，但是必须符合反射光照到屏幕C 点和B 点光照强度近似两倍的关系：
2C B E E = （9）
5.1.3模型的求解 （建议求解的过程按算法步骤形式写，更具有可读性。）
实际中，我们很难测出一条光线正好就照到屏幕的某个点的光照强度，因此我们采取小区域加和在此区域所有光线的光照强度的方法,B C 两点进行处理，首先分别以,B C 两点为圆心取一个半径极小的圆，半径为30mm ，相对于1.3m 。圆也足够小，满足计算精度，然后将射在圆上的线元的光照度进行叠加，根据B 点的光照度近似是C 点的两倍，运用matlab 软件对整个模型过程进行编程求解：
l =4mm
这时,B C 两点的光照强度之比为1.96，近似为2。
5.2问题二
对于问题二，要求在第一问求得线光源强度的情况下，在有标尺的坐标系中画出测试屏上反射光的亮区。
5.2.1问题二的求解