2018年中考数学专题2实数

合集下载

全解八年级数学上第二章实数检测题及答案解析

第二章实数检测题（本检测题满分：100分，时间：90分钟）一、选择题（每小题3分，共30分） 1.（2018·天津中考）估计的值在（） A .1和2之间 B .2和3之间 C .3和4之间D .4和5之间2.（2018·安徽中考）与1+最接近的整数是（）A .4B .3C .2D .1 3.（2018·南京中考）估计介于（）A .0.4与0.5之间B .0.5与0.6之间C .0.6与0.7之间D .0.7与0.8之间 4.（ 2018·湖北宜昌中考）下列式子没有意义的是（） A .B .C .D .5.（2018 ）A. B. C. D.6. 若a ,b 为实数，且满足|a －2|+，则b －a 的值为（）A ．2B ．0C ．－2D ．以上都不对7.若a ，b 均为正整数，且a b a ＋b 的最小值是（） A.3 B.4 C.5 D.68.11，212c ⎛⎫- ⎪⎝⎭＝0，则abc 的值为（）A.0 B ．－1 C.－12 D.129.（2018·福州中考）若（m -1）20，则m ＋n 的值是（）A ．－1B ．0C ．1D ．210. 有一个数值转换器，原理如图所示：当输入的x =64时，输出的y 等于（）是有理数A ．2B ．8C ．D ．二、填空题（每小题3分，共24分）11.（2018·南京中考）4的平方根是_________;4的算术平方根是__________. 12.（2018·河北中考）若|a |=，则a =___________.13.已知： 1.910 6.042，≈ ，≈ . 14.绝对值小于π的整数有 .15.已知|a －5|＝0，那么a －b ＝ .16.已知a ，b 为两个连续的整数，且a b ，则a ＋b ＝ .17．（2018·福州中考）计算：1）1）＝________.18.（2018·贵州遵义中考） +＝ .三、解答题（共46分） 19.（6分）已知，求的值.21.（6分）先阅读下面的解题过程，然后再解答：形如n m 2±的化简，只要我们找到两个数a ，b ，使m b a =+，n ab =，即m b a =+22)()(，n b a =⋅，那么便有：b a b a n m ±=±=±2)(2)(b a >.例如：化简：347+. 解：首先把347+化为1227+，这里7=m ，12=n ，因为，，即7)3()4(22=+，1234=⨯，所以347+1227+32)34(2+=+.根据上述方法化简：42213-.22.（6分）比较大小，并说明理由：（1）与6；（2）与．23.（6分）大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不能全部写出来，于是小平用－1来表示的小数部分，你同意小平的表示方法吗？事实上小平的表示方法是有道理的，因为的整数部分是1，用这个数减去其整数部分，差就是小数部分. 请解答：已知：5＋的小数部分是，5－的整数部分是b ，求＋b 的值.24.（8分）计算：（1）862⨯-82734⨯+；（2）)62)(31(-+-2)132(-. 25.（8分）阅读下面计算过程：12)12)(12()12(1121-=-+-⨯=+；();23)23)(23(231231-=-+-⨯=+()25)25)(25(251251-=-+-⨯=+.试求：（1）671+的值；（2）nn ++11（n 为正整数）的值；（3++的值.第二章实数检测题参考答案一、选择题1.C 解析：11介于9和16之间，即9＜11＜16，则利用不等式的性质可以求得介于3和4之间．即∵ 9＜11＜16，∴ <<，∴ 3＜＜4，∴的值在3和4之间．故选C .2.B 解析：∵ 4.84＜5＜5.29，∴＜即2.22.3，∴ 1+2.2＜11+2.3，即3.2＜13.3，∴ 与13.3.C 解析：22 2.25 2.3, 2.2 2.3, 1.21 1.3,<<∴<<∴<<0.60.65∴<<，故选C . 4.A 解析：根据二次根式有意义的条件，当被开方数a ≥0时，二次根式有意义；当a <0时，在实数范围内没有意义.由于-3<0，所以没有意义.5.B ==6.C 解析：∵ |a －2|0，∴ a ＝2，b ＝0,∴ b －a ＝0－2=－2．故选C ．7.C 解析：∵ a ，b 均为正整数，且a b ∴ a 的最小值是3，b 的最小值是2，则a ＋b 的最小值是5．故选C ． 8.C解析：∵ 11，212c ⎛⎫- ⎪⎝⎭＝0，∴ a ＝－1，b ＝1，c ＝12，∴ abc ＝－12．故选C ．9.A 解析：根据偶次方、算术平方根的非负性，由（m -1）20,得m －1＝0，n ＋2＝0，解得m ＝1，n ＝－2，∴ m ＋n ＝1＋（－2）=－1.10.D解析：由图得64的算术平方根是8，8的算术平方根是故选D ．二、填空题11.2± 2 解析：∵ ()2224,24,=-=∴ 4的平方根是2±，4的算术平方根是2.12.1± 解析：因为02 0151=，所以1=a ，所以.1±=a13.604.2 ±0.019 1 ≈604.2； ≈±0.019 1. 14.±3，±2，±1,0 解析：π≈3.14，大于－π的负整数有：－3，－2，－1，小于π的正整数有：3，2，1，0的绝对值也小于π.15.8 解析：由|a －5|＝0，得a ＝5，b ＝－3，所以a －b ＝5－（－3）＝8.16.11 解析：∵ a b ， a ，b 为两个连续的整数，a ＝6，b ＝5，∴ a ＋b ＝11.17.1 解析：根据平方差公式进行计算，1）（2－1）＝()22－12＝2－1＝1.18. ==三、解答题19.解：因为，，即，所以.故，从而，所以，X|k | B| 1 . c |O |所以.20.解：∵ 2＜7＜3，∴ 7＜5+7＜8，∴a=7－2.又可得2＜5－7＜3，∴b=3－7.将a＝7－2，b=3－7代入ab＋5b中，得ab＋5b＝（7－2）（3－7）＋5（3－7）＝37－7－6＋27＋15－57＝2.21.解：根据题意，可知，因为，所以.22.分析：（1）可把6转化成带根号的形式，再比较它们的被开方数，即可比较大小；（2）可采用近似求值的方法来比较大小．解：（1）∵35＜36，∴ 6.（2）∵1≈－2.236+1＝－1.236≈－0.707，1.236＞0.707，∴1．23. 解：∵ 4＜5＜9，∴ 2＜＜3，∴ 7＜5＋＜8，∴＝－2.又∵－2＞－＞－3，∴ 5－2＞5－＞5－3，∴ 2＜5－＜3，∴b＝2，∴＋b＝－2＋2＝.（2(13-24.解：（1＝13.25.1=解：（（2==（3+＝－11＋10＝9.。

实数(运算问题2)备战2023年中考数学考点微专题

考向04 实数（运算问题2）例 1、（2018·浙江临安·中考真题）阅读下列题目的解题过程：已知a 、b 、c 为△ABC 的三边，且满足a 2c 2﹣b 2c 2=a 4﹣b 4，试判断△ABC 的形状．解：∵a 2c 2﹣b 2c 2=a 4﹣b 4 （A ）∴c 2（a 2﹣b 2）=（a 2+b 2）（a 2﹣b 2）（B ） ∴c 2=a 2+b 2 （C ） ∴△ABC 是直角三角形问：（1）上述解题过程，从哪一步开始出现错误？请写出该步的代号：；（2）错误的原因为：；（3）本题正确的结论为：．【答案】（1）C ；（2）没有考虑a=b 的情况；（3）△ABC 是等腰三角形或直角三角形．【分析】（1）根据题目中的书写步骤可以解答本题；（2）根据题目中B 到C 可知没有考虑a=b 的情况；（3）根据题意可以写出正确的结论．解答：（1）由题目中的解答步骤可得，错误步骤的代号为：C ，故答案为C ；（2）错误的原因为：没有考虑a=b 的情况，故答案为没有考虑a=b 的情况；（3）本题正确的结论为：△ABC 是等腰三角形或直角三角形，故答案为△ABC 是等腰三角形或直角三角形．【点拨】本题考查因式分解的应用、勾股定理的逆定理，解答本题的关键是明确题意，写出相应的结论，注意考虑问题要全面．例 2、（2021·贵州黔东南·中考真题）（1）计算：()012cos3021232+3.14--︒-π（2）先化简：2223+2+344+4x x x x x x x x-÷⋅--，然后x 从0、1、2三个数中选一个你认为合适的数代入求值．【答案】（1）32-；（2）2x +，当x ＝1时，原式＝3【分析】（1）根据实数的运算，零指数幂，负整数指数幂，特殊角的三角函数值进行计算即可；（2）先根据分式的混合运算法则化简，再代入求值即可得结果．解：（1）()012cos3022+3.14--︒-π＝(12212-+1212-+＝32-；（2）2223+2+344+4x x x x x x x x-÷⋅-- ＝()()()()23222··32x x x x x x x x ++--+- ＝2x +∵x 取0或2时，原式无意义， ∴x 只能取1 当x ＝1时，原式＝3【点拨】本题考查了分式的化简求值，实数的运算，零指数幂，负整数指数幂，特殊角的三角函数值，解决本题的关键是熟练掌握运算法则．例 3、（2021·辽宁鞍山·中考真题）先化简，再求值：22131242a a a a a-⎛⎫-÷ ⎪--+⎝⎭，其中2a ．【答案】2a a -，1 【分析】根据分式的混合运算的运算法则把原式化简为2aa -，再代入求值．解：22131242a a a a a-⎛⎫-÷ ⎪--+⎝⎭ ()()()2132221a a a a a a ⎡⎤+=-⨯⎢⎥-+--⎣⎦()()()21221a a a a a a +-=⨯+--2aa =-．当2a 时，原式1===【点拨】本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值．1、常用的因式分解方法：（1）提取公因式法：)(c b a m mc mb ma ++=++ （2）运用公式法：平方差公式：))((22b a b a b a -+=-；完全平方公式：222)(2b a b ab a ±=+± （3）十字相乘法：))(()(2b x a x ab x b a x ++=+++（4）分组分解法：将多项式的项适当分组后能提公因式或运用公式分解。

中考数学考点大串讲(北师大版)：专题02 实数

5的算术平方根的相反数是 5 ．
那么a 62 36 ， a 4b 的算术平方根是 4，a 4b 16 ，
【变式训练2】
解得：b 5 ；
已知： a 2 b 1 0 ，那么a b 2023 的值为 -1
【变式训练3】
（2）解：， a b2 2 36 52 2 36 25 2 9
∴ a 4，b 22 ．
已知2a 1 的平方根为3 ，a 3b 2 的立方根为4 ．（2）由（1）知 a 4，b 22 ，
(1)求a ，b 的值；
∴ a b 1 4 22 1 25 ，
(2)求a b1的算术平方根．
∵25 的算术平方根为 25 5 ，
∴ a b1的算术平方根是 5．
知识大全
知识大全
考点二平方根
1.正数有两个平方根，它们互为相反数 0只有一个平方根，它是0本身负数没有平方根
2.平方根的应用（1） a 叫做a的平方根，也称为二次方根。（2）一般地，正数a的正的平方根记作 a ，负的平方根记作 a ，正数a的平方根记作 a ，读作正、负根号a . （3）一个正数有 2 个平方根，它们互为相反数；0的平方根 0；负数没有平方根。（4）求一个数a的平方根的运算，叫做开平方；开平方运算与平方运算是互逆的运算.
．
那么其平方根为 3 ．
已知正数 a 的两个不同的平方根分别是2x 2 和63x ，a 4b
的算术平方根是 4．
(1)求 a，b 的值；
(2)求 a b2 2 的平方根．
知识大全
考点二004 0.0004 0.04 4 400 40000 …
正分数集合：⑤⑧⑨ ，
正分数集合：{ …}．非负整数集合：{ …}；

实数的运算(含二次根式三角函数特殊值的运算)(解析版)2018年数学全国中考真题-2

2018年数学全国中考真题实数的运算（含二次根式三角函数特殊值的运算）（试题二）解析版一、选择题 1. 计算的结果等于（） A. 5 B. C. 9 D.【答案】C【解析】分析：根据有理数的乘方运算进行计算．详解：（-3）2=9，故选C ．点睛：本题考查了有理数的乘方，比较简单，注意负号．2. （2018黑龙江绥化，4，3分）下列运算正确的是（） A.2a +3a =5a 2B.552-=-)( C.a 3·a 4=a12D.(π-3)0=1【答案】D.【解析】解：A 、235a a a +=，故错误； B 255-=()，故错误；C 、34347·a a a a +==，故错误；D 、0(3)1π-=，故正确.故选：D.【知识点】合并同类项，二次根式的性质，同底数幂的乘法，零指数幂的意义3. （湖北省咸宁市，1，3）咸宁冬季里某一天的气温为- 3℃〜2 ），则这一天的温差是( )A ．1℃B ．-1℃C ．5℃D ．-5℃ 【答案】C【解析】解：根据“温差=最高气温-最低气温”，2℃－（－3））=2℃+3℃=5℃，故选C ．【知识点】有理数的减法运算4. （2018吉林省，1, 2分）计算（﹣1）×（﹣2）的结果是（） A ．2B ．1C ．﹣2D ．﹣3【答案】A【解析】根据“两数相乘，同号得正”即可求出（﹣1）×（﹣2）=2．故选A ．【知识点】有理数的乘法5. （2018贵州铜仁，10，4）计算990013012011216121++++++ 的值为（） A. 1100 B. 99100 C. 199D. 10099【答案】B【解析】∵21-121121=⨯=，31-2132161=⨯=，41-31431121=⨯=，51-41541201=⨯=， 61-51651301=⨯=，……，1001-90110099199001=⨯=， ∴990013012011216121++++++ =11111111111122334455699100 =1991100100.6.（2018云南省昆明市，12，4分）下列运算正确的是（）A .2193-=⎛⎫ ⎪⎝⎭B . 020181-=- C . 32326(0)a a a a -⋅=≠ D =【答案】C ．【解析】A 选项是幂的乘方，213-⎛⎫ ⎪⎝⎭＝（13-）×（13-）＝19，故A 选项错误； B 选项02018-1－（－2）＝3，故B 选项错误；3232a a -⋅＝3×2·32a -＝6a ，故C 选项正确是同底数幂的乘法，其法则是底数不变，指数相加，即32325a a a a +⋅==，故C 选项正确；D ==故D 选项错误，故选C ．【知识点】幂的乘方；同底数幂的乘法；零指数幂；负指数幂；合并同类二次根式7. （2018湖北恩施州，16，3分）我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”．如图６，一位妇女在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量，由图可知，她一共采集到的野果数量为个．【答案】1838．【解析】本题为探索规律型，由题意可知，因为满六进一，从右到左依次排列的绳子分别代表绳结束乘以6的0次幂，6的1幂，6的2次幂，6的3次幂，6的4次幂．她一共采集到的野果数量为1838个．8. （2018辽宁锦州，6，3分）下列运算正确的是A 、7a －a=6B 、a 2·a 3=a 5C 、(a 3)3=a 6D 、(ab)4=ab 4【答案】B ，【解析】：根据合并同类项、幂的乘方、同底数幂的乘法、积的乘方法则进行解答．二、填空题1. （2018湖北省江汉油田潜江天门仙桃市，12，3分）112()2--= ．【答案】0【解析】直接利用二次根式的化简、绝对值的性质和负整数指数幂的性质分别化简，再计算．2323)21(23331=--+=--+-【知识点】二次根式分母有理化，绝对值，负整数指数幂2. （湖北省咸宁市，5，3）按一定顺序排列的一列数叫做数列，如数列：1111,,,,,261220则这个数列的前2018个数的和为__________. 【答案】20182019【解析】11111111,,,,,21262312342045====⨯⨯⨯⨯则第2018个数为120182019⨯ 则这个数列的前2018个数的和为111111223344520182019+++++⨯⨯⨯⨯⨯ =1111111111223344520182019-+-+-+-++- =112019-=20182019【知识点】探究规律3. （2018年黔三州，19,3）根据下列各式的规律，在横线处填空： 11+12−1=12，13+14−12=112，15+16−13=130，17+18−14=156，... (1)2017+12018− =12017×2018 . 【答案】11009【解析】按照等式顺序，第一个为11+12−1=12，第二个为13+14−1(3−1)÷2+1=13×4，第3个式子15+16−1（5−1）÷2+1=15×6，17+18−1(7−1)÷2+1=17×8，… …以此类推，12017+12018−1(2017−1)÷2+1 =12017×2018 . 【知识点】等式规律探索4. （2018江苏常州，9，2）计算:3-1-=_______．【答案】2 【解析】21313=-=--5. （2018四川巴中，21（1），6分）（1）计算：│－2│ －2cos 60°＋()－1－(2018－）0【答案】原式＝2－2×＋6－1＝2﹣1＋6﹣1＝6.【解析】依据数的绝对值意义，│－2│＝2；由特殊角的三角函数值得cos 60°＝；由负整数指数幂的意义得()－1＝611＝6或者()－1＝（6－1）－1＝6；根据a 0＝1（a ≠0）得(2018－）0＝1.6.（2018广西南宁，17，3）观察下列等式：30=1，31=3，32=9，33=27，34=81，35=243，…，根据其中规律可得30+31+32+…+32018的结果的个位数字是．【答案】3，【解析】∵30=1，31=3，32=9，33=27，34=81∴各位数4个数一循环， ∴(2018+1)÷4=504余3， ∴1+3+9=13∴30+31+32+…+32018的结果的个位数字3．7. （2018湖北十堰，14，3分）对于实数a ，b ，定义运算“）”如下，a ）b ＝a 2－ab ，例如，5）3＝52－5*3＝10．若（x ＋1））(x －2)＝6，则x 的值为．【答案】1【解析】由于（x ＋1））(x －2)＝6，所以（x ＋1）2－（x ＋1）（x －2）＝6，即有3x ＋3＝6，解得x ＝1，故答案为：1．8. （2018湖北随州11，3分）8|2－2＋2tan45°＝______．【答案】4．【解析】842⨯2根据“负数的绝对值等于它的相反数”可得|2－2|＝22－2；熟记特殊角的三角函数值可得2tan45°＝2×1＝2，所以原式＝222)＋2＝222＋2＝4．三、解答题1. （2018省市，题号，分值）计算：11220182-⎛⎫--+ ⎪⎝⎭【思路分析】先计算各项的值，进而求得结果，一个负数的绝对值为它的相反数，任何非零数的零次幂都为1，一个数的-1次幂相当于它的倒数【解题过程】原式=2-1+2=3【知识点】绝对值；零指数幂和负整指数幂；有理数加减2. （2018省市，题号，分值）先化简，再求值：22221644a a a aa-+-，其中a 【思路分析】先将分式化简，再将a 值代入求值【解题过程】()()()222244216224444a a a a a a a a a a a a +--==+-+-,当a =2时，原式【知识点】分式的乘除；二次根式3. （2018广西省桂林市，19，6分）1103)6cos 45+2---︒⎛⎫⎪⎝⎭．【思路分析】先算出每一个式子的值，再依据混合运算顺序，依次计算即可．1103)6cos 45+2---︒⎛⎫ ⎪⎝⎭＝6+121232-⨯=-=．【知识点】实数的四则运算；特殊角三角函数值的运用；负指数次幂；0次幂；二次根式的化简4. （2018黑龙江省龙东地区，21，5分）先化简，再求值：2221(1)21a a a a a a --÷+++，其中a ＝sin30°．【思路分析】先化简分式，再求a 的值，最后把a 的值代入计算即可．【解题过程】解：原式＝2222(1)()(1)(1)a a a a a a a a a a ++-+-++＝22(1)(1)(1)(1)a a a a a a +++-＝1aa -．当a ＝sin30°＝12时，原式＝－1．【知识点】分式的化简求值；特殊角的锐角三角函数值；平方差公式；完全平方公式5. （2018山东省东营市，19①，4分）计算：02018112133012)tan ()()--︒+-- 【思路分析】根据绝对值、0指数、三角函数、负数的偶次幂、分数的负整数指数幂的法则性质进行计算即可。

专题2：方程和不等式(组)常见题型和解题方法(终稿)

2017—2018学年度第二学期初三数学中考复习专题2：方程和不等式（组）常见题型和解题方法一、热点再练：1. 方程36x =的解为 .2. 关于x 的方程ax 2+bx +c =0（a ≠0）有一个根为1，则a +b +c = . 3．方程0532=++px x 的一个根为5，另一个根为______、p =_______.4．如果关于x 的方程(m –2)x 2–2x +1=0有解，则m 的取值范围是_______.5．已知关于x 的方程a (1–x 2)+2bx +c (1+x 2)=0有两个相等的实数根且a 、b 、c 均为正数，以a 、b 、c 为边围成一个三角形，则该三角形是________三角形.6．方程)2()2(2-=-x x 的根是________.方程组⎩⎨⎧=+=-1435y x y x 的解为________. 7．若关于x 的一元一次不等式组0122x a x x ->⎧⎨->-⎩有解，则a 的取值范围是________. 8．用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象（如图所示），则所解的二元一次方程组是【】A ．203210x y x y +-=⎧⎨--=⎩， B ．2103210x y x y --=⎧⎨--=⎩， C ．2103250x y x y --=⎧⎨+-=⎩， D ．20210x y x y +-=⎧⎨--=⎩， 9．下列方程中，两实数根之和是2的是【】A ．x 2–2x +5=0B ．x 2+2x –5=0C ．x 2+2x +5=0D ．x 2–2x –5=010．设1x 、2x 是关于x 的一元二次方程22x x n mx ++-=的两个实数根，且10x <，2130x x -<，则【】A ．1,2m n >⎧⎨>⎩B ．1,2m n >⎧⎨<⎩C ．1,2m n <⎧⎨>⎩D ．1,2m n <⎧⎨<⎩11．已知直线y =2x －b 经过点（－2，0），则关于x 的不等式2x －b ≥0的解集为__________．12．设一元二次方程(x －1)(x －2)＝m (m >0)的两根分别为α、β，且a <β，则a ，β满足【】A ．1<a <β<2B ．1<a <2<βC ．a <1<β<2D ．a <1且β>2（第9题）13．关于x 、y 的二元一次方程组5323x y x y p +=⎧⎨+=⎩的解是正整数，则整数p 的值为__________． 14．解分式方程225103x x x x-=+-．二、规律剖析例1. 解不等式组：331213(1)8x x x x-⎧+>+⎪⎨⎪---⎩，≤并在数轴上把解集表示出来．例2.已知关于x 的分式方程111x k k x x +-=+-的解为负数，求k 的取值范围．例3. 已知关于x 的一元二次方程mx 2－（3m ＋1）x ＋2m ＋2＝0的两实根为x 1，x 2．（1）请用含m 的代数式表示x 1，x 2；（2）且n ＝x 2－x 1－1，求在直角坐标系xOy 中动点P （m ，n ）所形成的曲线解析式．三、变式训练1. 若关于x 的不等式组10,233544(1)3x x x a x a+⎧+>⎪⎨⎪++>++⎩恰有三个整数解，求实数a 的取值范围．2. 若关于x 的分式方程121m x -=-的解为正数，则m 的取值范围是．3．已知关于x 的一元二次方程2(41)330mx m x m -+++=的两个实数根分别为1x ，2x ，212n x x =--，设点A （1，a ），B （b ，2）两点在动点P （m ，n ）所形成的曲线上，求直线AB 的解析式．四、分层作业1．一元二次方程(2x －1)2＝(3－x )2的解是．2．关于x 的方程12mx x -=的解为正实数，则m 的取值范围是【】A ．m ≥2B ．m ≤2C ．m ＞2D ．m ＜23．甲种电影票每张20元，乙种电影票每张15元．若购买甲、乙两种电影票共40张，恰好用去700元，则甲种电影票买了张．4．设α，β是一元二次方程x 2＋3x －7＝0的两个根，则α2＋4α＋β＝． 5. 下列关于x 的方程有实数根的是【】A ．x 2－x ＋1＝0B ．x 2＋x ＋1＝0C ．(x －1)(x ＋2)＝0D ．(x －1)2＋1＝06．若关于x 的一元二次方程x 2＋x ＋m =0有两个相等的实数根，则m = ．7．下列一元二次方程两实数根和为－4的是【】A ．x 2＋2x －4=0B ．x 2－4x ＋4=0C ．x 2＋4x ＋10=0D ．x 2＋4x －5=08．已知关于x 的一元二次方程x 2＋x ＋m =0的一个实数根为1，那么它的另一个实数根是【】A ．－2B ．0C ．1D ．29．若关于x 的一元一次不等式组10,0x x a -<⎧⎨->⎩无解，则a 的取值范围是（） A ．a ≥1 B ．a ＞1C ．a ≤－1D ．a ＜－1 10．关于x 的不等式x －b ＞0恰有两个负整数解，则b 的取值范围是（）A ．―3＜b ＜―2B ．―3＜b ≤―2C ．―3≤b ≤―2D ．―3≤b ＜―211．求不等式组364,213(1)x x x x --⎧⎨+>-⎩≥的解集，并写出它的整数解．12.已知2a－3x＋1＝0，3b－2x－16＝0，且a≤4＜b，求x的取值范围．13. 某省为解决农村饮用水问题，省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助．2008年，A市在省财政补助的基础上投入600万元用于“改水工程”，计划以后每年以相同的增长率投资，2010年该市计划投资“改水工程”1176万元．（1）求A市投资“改水工程”的年平均增长率；（2）从2008年到2010年，A市三年共投资“改水工程”多少万元？14. 关于x的一元二次方程ax2－3x＋1＝0的两个不相等的实数根都在0和1之间（不包括0和1），求a的取值范围．★15.已知a－b＝2，ab＋2b－c2＋2c＝0，当b≥0，－2≤c＜1时，求整数a的值．★16.已知关于x的方程kx2+（2k+1）x+2=0．（1）求证：无论k取任何实数时，方程总有实数根；（2）当抛物线y=kx2+（2k+1）x+2图象与x轴两个交点的横坐标均为整数，且k为正整数时，若P（a，y1），Q（1，y2）是此抛物线上的两点，且y1＞y2，请结合函数图象确定实数a的取值范围；（3）已知抛物线y=kx2+（2k+1）x+2恒过定点，求出定点坐标．。

2018数学中考专题--2-阅读理解型专题

2018年中考阅读理解题1、阅读下列材料，并解决后面的问题．材料：一般地，n 个相同的因数a 相乘：nn a a a a 记为个．如23＝8，此时，3叫做以2为底8的对数，记为 38log 8log 22 即．一般地，若 0,10 b a a b a n且，则n 叫做以a 为底b 的对数，记为 813.log log 4 如即n b b a a ，则4叫做以3为底81的对数，记为)481log (81log 33 即．问题：（1）计算以下各对数的值：64log 16log 4log 222 ．（2）观察（1）中三数4、16、64之间满足怎样的关系式？64log 16log 4log 222、、之间又满足怎样的关系式？（3）由（2）的结果，你能归纳出一个一般性的结论吗？ 0,0,10log logN M a a N M a a 且（4）根据幂的运算法则：m n mna a a 以及对数的含义证明上述结论．2、式子“1＋2＋3＋4＋5＋……＋100”表示从1开始的100个连续自然数的和.由于上述式子比较长，书写也不方便，为了简便起见，我们可将“1＋2＋3＋4＋5＋……＋100”表示为 1001n n，这里“”是求和符号.例如：“1＋3＋5＋7＋9＋……＋99”（即从1开始的100以内的连续奇数的和）可表示为 501)12(n n ；又如“13＋23＋33＋43＋53＋63＋73＋83＋93＋103”可表示为 1013n n.同学们，通过对以上材料的阅读，请解答下列问题：①2＋4＋6＋8＋10＋……＋100（即从2开始的100以内的连续偶数的和）用求和符号可表示为； ②计算：512)1(n n＝（填写最后的计算结果）3.计算机是将信息转换成二进制数进行处理的，二进制即“逢2进1”，如(1101)2表示二进制数，将它转换成十进制形式是1×23＋1×22＋0×21＋1×20＝13，那么将二进制(1111)2转换成十进制形式是数( ) A ．8 B ．15 C ．20 D ．304、先阅读下列材料，然后解答问题：材料1：从三张不同的卡片中选出两张排成一列，有6种不同的排法，抽象成数学问题就是从3个不同的元素中选取2个元素的排列，排列数记为23326A 。

北师大版八年级数学上册第2章《实数》中考试题及答案

八年级数学上实数的概念部分中考题1、（四川成都，1,3分）3-的绝对值是（）A ．3B ．3-C ．13D ．13- 【答案】A2、（四川成都，5,3分）成都地铁二号线工程即将竣工，通车后与地铁一号线呈“十”字交叉，城市交通通行和转换能力将成倍增长．该工程投资预算约为930 000万元，这一数据用科学记数法表示为（）A ． 59.310⨯ 万元B ． 69.310⨯万元C ．49310⨯万元D ． 60.9310⨯万元【答案】A3、（四川乐山，1，3分）如果规定收入为正，支出为负.收入500 元记作500元，那么支出237元应记作（）A ．500-元B ．237-元C ．237元D ．500元【答案】B4、（浙江舟山3，3分）南海资源丰富，其面积约为350万平方千米，相当于我国的渤海、黄海和东海总面积的3倍，其中350万用科学记数法表示为（）(A ) 0.35×108 (B )3.5×107(C ) 3.5×106 (D ) 35×105【答案】C5、（浙江温州，1，4分）给出四个数－1，0，0.5( )A ．－1B ．0C ．0.5D 【答案】D6、（浙江省衢州，1，3分）下列四个数中，最小的数是( )A .2B .－2C .0D . 12- 【答案】B7、（浙江省衢州，2，3分）衢州市是国家优秀旅游城市，吸引了众多的海内外游客.据衢州市2011年国民经济和社会发展统计公报显示，全年旅游总收入达121.04亿元.将121.04亿元用科学记数法可表示为( )A .12.104×10 9元B . 12.104×10 10元C .1.2104×10 10元D . 1.2104×10 11元【答案】C8、（浙江嘉兴，3，4分）南海资源丰富，其面积约为350万平方千米，相当于我国的渤海、黄海和东海总面积的3倍．其中350万用科学计数法表示为（）A．0.35×108B．3.5×107C．3.5×106D．35×105【答案】C9、（浙江绍兴，1，4分）3的相反数是（）A．3 B．-3 C．13D．13-【答案】B10、（浙江绍兴，3，4分）据科学家估计，地球的年龄大约是4600000000年，这个数用科学计数法表示为（）A．4.6×108B．46×108C．4.6×109D．0.46×1010【答案】C11、（浙江丽水，3，3分）如图，数轴的单位长度为1，如果点A，B表示的数的绝对值相等，那么点A表示的数是（）A．－4 B．－2 C．0 D．40【答案】B12、（山东临沂，2，3分）太阳的半径约为696000千米，把这个数据用科学记数法表示为( )A. 696×103千米B. 69.6×104千米C.6.96×105千米D. 6.96×106千米【答案】C13、（山东济宁，1，3分）在数轴上到原点距离等于2的点所表示的数是（）A．－2 B．2 C．2±D．不能确定【答案】C14、（江苏无锡，1，3分）如－2的相反数是( )A．2 B．一2 C．12D．一12【答案】A15、（江苏泰州，3，3分）过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为A．3.12×105B．3.12×106C．31.2×105D．0.312×107【答案】B。

中考初二实数专题讲解经典题及答案

4=1+3 9=3+616=6+10 …实数典型问题例1．的相反数是（）A． BC．2- D．2分析：本题考查实数的概念――相反数，要注意相反数与倒数的区别，实数a 的相反数是-a ，选A .要谨防将相反数误认为倒数，错选D.例3定义a ※b ＝a 2－b ，则(1※2)※3＝＿＿＿.解因为a ※b ＝a 2－b ，所以(1※2)※3＝(12－2)※3＝(－1)※3＝(－1)2－3＝－2.故应填上－2. 说明：求解新定义的运算时一定要弄清楚定义的含义，注意新定义的运算符号与有理数运算符号之间的关系，及时地将新定义的运算符号转化成有理数的运算符号.例4古希腊著名的毕达哥拉斯学派把1、3、6、10、…，这样的数称为“三角形数”，而把1、4、9、16、…，这样的数称为“正方形数”.从如图所示中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中，符合这一规律的是（）A.13＝3+10B.25＝9+16C.36＝15+21D.49＝18+31解因为15和21是相邻的两个“三角形数”，且和又是36，刚好符合“正方形数”，所以36＝15+21符合题意，故应选C .（说明本题容易错选B ，事实上，25虽然是“正方形数”，而9和16也是“正方形数”，并不是两个相邻“三角形数”）.例52()x y =+，则x －y 的值为（）A ．－1B ．1C ．2D ．3分析：因为x-1≥0，1-x ≥0，所以x ≥1，x ≤1，即x ＝1.2()x y =+，有1+y ＝0，所以y ＝-1，x －y ＝1-（1）＝2.例6．已知数据：13π，－2．其中无理数出现的频率为( ) A ．20％ B ．40％ C ．60％ D ．80％分析：，22都是无理数；л是无限不循环小数，也是无理数；而31，-2都是有理数，所以无理数出现的频率为53＝0.6＝60％，选C ．例7．为了求2008322221++++ 的值，可令S ＝2008322221++++ ，则2S ＝20094322222++++ ，因此2S-S ＝122009-，所以2008322221++++ ＝122009-．仿照以上推理计算出20093255551+++++ 的值是（）A ．152009- B.152010- C.4152009- D.4152010-解析：本题通过阅读理解的形式介绍了解决一类有理数运算问题的方法，利用例题介绍的方法，有：设S ＝20093255551+++++ ，则5S ＝201020093255555+++++ ，因此5S-S ＝20105-1，所以S ＝4152010-，选D.说明：你能从中得到解决这类问题的一般性规律吗？试一试.例8． a 是不为1的有理数，我们把11a-称为a 的差倒数．．．．如：2的差倒数是1112=--，1-的差倒数是111(1)2=--．已知113a =-，2a 是1a 的差倒数，3a 是2a 的差倒数，4a 是3a 的差倒数，…，依此类推，则2009a = ．解析：首先要理解差倒数．．．的概念，再按照要求写出一列数，从中找出规律，再应用规律来解决问题.根据题意可得到：113a =-，2a ＝433111=--）（，3a ＝4311-＝4，4a ＝31411-=-，…，可见这是一个无限循环的数列，其循环周期为3，而2009＝669×3+2，所以a 2009与a 2相同，即2009a =34．典型例题的探索（利用概念）例3. 已知：M a a b =++-82是a +8的算术数平方根，N b a b =--+324是b -3立方根，求M N +的平方根。

2018年成都市中考数学试题及答案详解

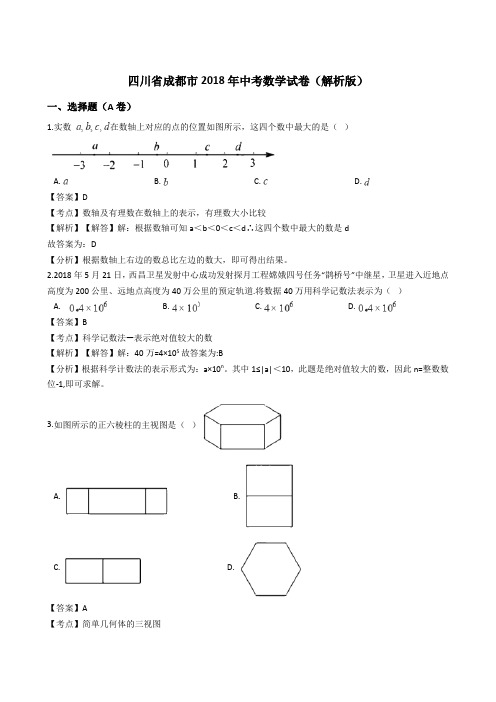
四川省成都市2018年中考数学试卷（解析版）一、选择题（A卷）1.实数在数轴上对应的点的位置如图所示，这四个数中最大的是（）A. B. C. D.【答案】D【考点】数轴及有理数在数轴上的表示，有理数大小比较【解析】【解答】解：根据数轴可知a＜b＜0＜c＜d∴这四个数中最大的数是d故答案为：D【分析】根据数轴上右边的数总比左边的数大，即可得出结果。

2.2018年5月21日，西昌卫星发射中心成功发射探月工程嫦娥四号任务“鹊桥号”中继星，卫星进入近地点高度为200公里、远地点高度为40万公里的预定轨道.将数据40万用科学记数法表示为（）A. B. C. D.【答案】B【考点】科学记数法—表示绝对值较大的数【解析】【解答】解：40万=4×105故答案为:B【分析】根据科学计数法的表示形式为：a×10n。

其中1≤|a|＜10，此题是绝对值较大的数，因此n=整数数位-1,即可求解。

3.如图所示的正六棱柱的主视图是（）A. B.C. D.【答案】A【考点】简单几何体的三视图【解析】【解答】解：∵从正面看是左右相邻的3个矩形，中间的矩形面积较大，两边的矩形面积相同，∴答案A符合题意故答案为：A【分析】根据主视图是从正面看到的平面图形，即可求解。

4.在平面直角坐标系中，点关于原点对称的点的坐标是（）A.B.C.D.【答案】C【考点】关于原点对称的坐标特征【解析】【解答】解：点关于原点对称的点的坐标为（3,5）故答案为：C【分析】根据关于原点对称点的坐标特点是横纵坐标都互为相反数，就可得出答案。

5.下列计算正确的是（）A. B. C. D.【答案】D【考点】同底数幂的乘法，完全平方公式及运用，合并同类项法则及应用，积的乘方【解析】【解答】解：A、x2+x2=2x2，因此A不符合题意；B、（x-y）2=x2-2xy+y2，因此B不符合题意；C、（x2y）3=x6y3，因此C不符合题意；D、，因此D符合题意；故答案为:D【分析】根据合并同类项的法则，可对A作出判断；根据完全平方公式，可对B作出判断；根据积的乘方运算法则及同底数幂的乘法，可对C、D作出判断；即可得出答案。

初中数学中考复习——实数专题(含答案)

初中数学中考复习——实数专题选择题下列各数中，绝对值最小的是（）A. -3B. 2C. 0D. π如果一个实数的相反数是它本身，那么这个数一定是（）A. 正数B. 负数C. 零D. 无法确定一个数的平方根是它本身的数有（）A. 0B. 1C. -1D. A和B实数-5和7在数轴上对应的点之间的距离是（）A. 2B. 12C. 10D. 14利用科学记数法表示的数，下列哪个选项是错误的（）A. 350 = 3.5 × 10²B. 0.05 = 5 × 10⁻²C. 500 = 5 × 10²D. 0.0006 = 6 × 10⁻⁴下列哪个数不是无理数（）A. πB. √2C. 0.333...（3无限重复）D. 22/7如果a和b是两个实数，且a的绝对值大于b的绝对值，那么|a| - |b|的值（）A. 一定为正B. 一定为负C. 可能是正数或负数D. 无法确定对于实数x，以下哪个条件可以保证x² - 4x + 4 = 0（）A. x = 2B. x = -2C. x = 0D. x = 4下列哪个表达式的结果不是实数（）A. √16B. √(-1)C. -√(-4)D. √9如果一个数的立方根是2，那么这个数是（）A. 6B. 8C. -8D. 4正确答案：CCDCBCAABC填空题实数包括有理数和无理数，其中有限小数和无限循环小数属于______。

一个数的相反数是与它符号相反的数，例如，数-7 的相反数是______。

一个数的绝对值是它到原点的距离，因此，|-5| 等于______。

如果一个数的平方根是4，则这个数的算术平方根是______。

立方根的定义是，如果一个数的立方等于a，则这个数叫做 a 的立方根。

例如，3 的立方根是______。

在实数大小比较中，数轴上右边的数总是比左边的数大。

因此，在数轴上，5 大于______。

2018中考数学知识点：实数的运算法则

2018中考数学知识点：实数的运算法则
实数的运算法则：
1、加法法则：
（1）同号两数相加，取相同的符号，并把它们的绝对值相加；
（2）异号两数相加，取绝对值大的加数的符号，并用较大的绝对值减去较小的绝对值。

可使用
①加法交换律：两个数相加，交换加数的位置，和不变；即：a+b=b+a；
②加法结合律：三个数相加，先把前两个数相加，或先把后两个数相加，和不变；即：（a+b）+c=a+（b+c）。

2、减法法则：减去一个数等于加上这个数的相反数。

即a-b=a+（-b）
3、乘法法则：
（1）两数相乘，同号取正，异号取负，并把绝对值相乘。

（2）n个实数相乘，有一个因数为0，积就为0；若n个非0的实数相乘，积的符号由负因数的个数决定，当负因数有偶数个时，积为正；当负因数为奇数个时，积为负。

（3）乘法可使用
①乘法交换律：两个数相乘，交换因数的位置，积不变，即：ab=ba；
②乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变，即：（ab）c=a（bc）；
③分配律：一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加,即：a（b+c）=ab+ac。

4、除法法则：
（1）两数相除，同号得正，异号得负，并把绝对值相除。

（2）除以一个数等于乘以这个数的倒数。

（3）0除以任何数都等于0，0不能做被除数。

5、乘方：所表示的意义是n个a相乘，即an，正数的任何次幂是正数，负数的偶次幂是正数，负数的奇次幂是负数，乘方与开方互为逆运算。

精心整理，仅供学习参考。

中考数学《实数》专题含解析

实数一、选择题1．某年哈尔滨市一月份的平均气温为﹣18℃，三月份的平均气温为2℃，则三月份的平均气温比一月份的平均气温高（）A．16℃B．20℃C．﹣16℃D．﹣20℃2．下列计算正确的是（）A．B．（a+b）2=a2+b2C．（﹣2a）3=﹣6a3D．﹣（x﹣2）=2﹣x3．下列计算正确的是（）A．（﹣1）﹣1=1 B．（﹣3）2=﹣6 C．π0=1 D．（﹣2）6÷（﹣2）3=（﹣2）24．数字，，π，，cos45°，中是无理数的个数有（）个．A．1 B．2 C．3 D．45．据报道，苏州市政府有关部门将在市区完成130万平方米老住宅小区综合整治工作．130万（即1300000）这个数用科学记数法可表示为（）A．1.3×104B．1.3×105C．1.3×106D．1.3×1076．数轴上的点A表示的数是﹣1，点B表示的数是﹣，则点B关于点A的对称点B′点表示的数为（）A．﹣2 B．﹣﹣2 C．﹣﹣1 D．07．下列计算结果正确的是（）A．（﹣a3）2=a9B．a2•a3=a6 C．D．（sin60°﹣）0=08．28cm接近于（）A．珠穆朗玛峰的高度B．三层楼的高度C．姚明的身高D．一张纸的厚度9．实数a、b在数轴上的位置如图所示，下列式子错误的是（）A．a＜b B．|a|＞|b|C．﹣a＜﹣b D．b﹣a＞0二．填空题10．地球与太阳之间的距离约为149 600 000千米，用科学记数法表示（保留2个有效数字）约为千米．11．化简：=．12．若将三个数表示在数轴上，其中能被如图所示的墨迹覆盖的数是．13．已知a、b为两个连续的整数，且，则a+b=．14．已知互为相反数，则a：b=．15．若的值在x与x+1之间，则x=．16．，则x y=．17．计算：=．18．化简二次根式：=．19．一个自然数的算术平方根是a，则相邻的下一个自然数的算术平方根是．三．计算题20．计算：﹣+|1﹣|+（）﹣1．21．计算：﹣2sin30°﹣（﹣）﹣2+（﹣π）0﹣+（﹣1）．22．．23．计算：．24．若x是不等于1的实数，我们把称为x的差倒数，如3的差倒数为，﹣5的差倒数为．现已知x1=﹣，x1的差倒数是x2，x2的差倒数是x3，…，以此类推，x的值是多少？实数参考答案与试题解析一、选择题1．某年哈尔滨市一月份的平均气温为﹣18℃，三月份的平均气温为2℃，则三月份的平均气温比一月份的平均气温高（）A．16℃B．20℃C．﹣16℃D．﹣20℃【考点】有理数的减法．【专题】应用题．【分析】根据题意用三月份的平均气温气温减去一月份的平均气温气温，再根据有理数的减法运算法则“减去一个数等于加上这个数的相反数”计算求解．【解答】解：2﹣（﹣18）=2+18=20℃．故选B．【点评】本题考查有理数的减法运算法则．2．下列计算正确的是（）A．B．（a+b）2=a2+b2C．（﹣2a）3=﹣6a3D．﹣（x﹣2）=2﹣x【考点】完全平方公式；去括号与添括号；幂的乘方与积的乘方；二次根式的加减法．【分析】利用完全平方公式、去括号与添括号法则、幂的乘方与积的乘方及二次根式的加减法等性质进行计算后即可确定答案．【解答】解：A、不是同类二次根式，因此不能进行运算，故本答案错误；B、（a+b）2=a2+b2+2ab，故本答案错误；C、（﹣2a）3=﹣8a3，故本答案错误；D、﹣（x﹣2）=﹣x+2=2﹣x，故本答案正确；故选D．【点评】本题考查了完全平方公式、去括号与添括号法则、幂的乘方与积的乘方及二次根式的加减法等性质，属于基本运算，要求学生必须掌握．3．下列计算正确的是（）A．（﹣1）﹣1=1 B．（﹣3）2=﹣6 C．π0=1 D．（﹣2）6÷（﹣2）3=（﹣2）2【考点】负整数指数幂；同底数幂的除法；零指数幂．【专题】计算题．【分析】根据平方根，负指数幂的意义，同底数的幂的除法的意义，分别计算出各个式子的值即可判断．【解答】解：A、（﹣1）﹣1=﹣1，故A错误；B、（﹣3）2=9，故B错误；C、任何非0实数的零次幂等于1，故C正确；D、（﹣2）6÷（﹣2）3=（﹣2）3，故D错误．故选C．【点评】解决此题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、同底数的幂的除法等考点的运算．4．数字，，π，，cos45°，中是无理数的个数有（）个．A．1 B．2 C．3 D．4【考点】无理数；特殊角的三角函数值．【分析】根据无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数，结合所给的数据判断即可．【解答】解：=2，cos45°=，所以数字，，π，，cos45°，中无理数的有：，π，cos45°，共3个．故选C．【点评】此题考查了无理数的定义，属于基础题，关键是掌握无理数的三种形式．5．据报道，苏州市政府有关部门将在市区完成130万平方米老住宅小区综合整治工作．130万（即1300000）这个数用科学记数法可表示为（）A．1.3×104B．1.3×105C．1.3×106D．1.3×107【考点】科学记数法—表示较大的数．【专题】应用题．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于1时，n是正数；当原数的绝对值小于1时，n是负数．【解答】解：130万=1 300 000=1.3×106．故选C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．6．数轴上的点A表示的数是﹣1，点B表示的数是﹣，则点B关于点A的对称点B′点表示的数为（）A．﹣2 B．﹣﹣2 C．﹣﹣1 D．0【考点】实数与数轴．【分析】先求出A、B之间的距离，然后根据对称的性质得出A、B′之间的距离，再设点B′表示的数为x，列出关于x的方程，解方程即可．【解答】解：∵数轴上的点A表示的数是﹣1，点B表示的数是﹣，∴AB=﹣1，∵点B和点B′关于点A对称，∴AB′=AB=﹣1．设点B′表示的数为x，则x+1=﹣1，x=﹣2．∴B′点表示的数为﹣2．故选A．【点评】本题考查了实数与数轴上的点的对应关系，以及对称的有关性质．7．下列计算结果正确的是（）A．（﹣a3）2=a9B．a2•a3=a6 C．D．（sin60°﹣）0=0【考点】负整数指数幂；同底数幂的乘法；幂的乘方与积的乘方；零指数幂．【分析】根据有理数的幂的乘方和同底数幂的乘法及负指数幂的运算法则计算．【解答】解：A、平方取正值，指数相乘，应为a6，故A错误；B、a2•a3=a5，故B错误；C、，故C正确；D、（sin60°﹣）0=1≠0，故D错误．故选C．【点评】本题主要考查了有理数的有关运算法则，解答此题时要注意任何非0数的0次幂等于1．8．28cm接近于（）A．珠穆朗玛峰的高度B．三层楼的高度C．姚明的身高D．一张纸的厚度【考点】有理数的乘方．【分析】根据有理数的乘方运算法则，计算出结果，然后根据生活实际来确定答案．【解答】解：28=24×24=16×16=256（cm）=2.56（m）．A、珠穆朗玛峰峰的高度约8848米，错误；B、三层楼的高度20米左右，错误；C、姚明的身高是2.23米，接近2.56米，正确；D、一张纸的厚度只有几毫米，错误．故选C．【点评】解答这样的题目有两个要点需要注意，一是有理数的乘方运算法则要记牢；二是根据生活实际情况来做出选择．9．实数a、b在数轴上的位置如图所示，下列式子错误的是（）A．a＜b B．|a|＞|b|C．﹣a＜﹣b D．b﹣a＞0【考点】实数与数轴．【分析】根据数轴表示数的方法得到a＜0＜b，数a表示的点比数b表示点离原点远，则a＜b；﹣a＞﹣b；b﹣a＞0，|a|＞|b|．【解答】解：根据题意得，a＜0＜b，∴a＜b；﹣a＞﹣b；b﹣a＞0，∵数a表示的点比数b表示点离原点远，∴|a|＞|b|，∴选项A、B、D正确，选项C不正确．故选C．【点评】本题考查了实数与数轴：数轴上的点与实数一一对应；数轴上原点左边的点表示负数，右边的点表示正数；右边的点表示的数比左边的点表示的数要大．二．填空题10．地球与太阳之间的距离约为149 600 000千米，用科学记数法表示（保留2个有效数字）约为 1.5×108千米．【考点】科学记数法与有效数字．【专题】计算题．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值是易错点，由于1 048 576有7位，所以可以确定n=7﹣1=6．有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字．用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．【解答】解：149 600 000=1.496×108≈1.5×108．故答案为1.5×108．【点评】此题考查科学记数法的表示方法，以及用科学记数法表示的数的有效数字的确定方法．11．化简：=．【考点】算术平方根．【分析】根据开平方的意义，可得答案．【解答】解：原式==，故答案为：．【点评】本题考查了算术平方根，先化成分数，再开方运算．12．若将三个数表示在数轴上，其中能被如图所示的墨迹覆盖的数是．【考点】实数与数轴．【专题】图表型．【分析】首先利用估算的方法分别得到﹣，，前后的整数（即它们分别在那两个整数之间），从而可判断出被覆盖的数．【解答】解：∵﹣2＜﹣＜﹣1，2＜＜3，3＜＜4，且墨迹覆盖的范围是1﹣3，∴能被墨迹覆盖的数是．【点评】本题考查了实数与数轴的对应关系，以及估算无理数大小的能力．13．已知a、b为两个连续的整数，且，则a+b=11．【考点】估算无理数的大小．【分析】根据无理数的性质，得出接近无理数的整数，即可得出a，b的值，即可得出答案．【解答】解：∵，a、b为两个连续的整数，∴＜＜，∴a=5，b=6，∴a+b=11．故答案为：11．【点评】此题主要考查了无理数的大小，得出比较无理数的方法是解决问题的关键．14．已知互为相反数，则a：b=．【考点】立方根．【分析】根据立方根互为相反数，可得被开方数互为相反数，根据互为相反数的两数的和为0，可得答案．【解答】解：互为相反数，∴（3a﹣1）+（1﹣2b）=0，3a=2b，故答案为：．【点评】本题考查了立方根，先由立方根互为相反数得出被开方数互为相反数，再求出的值．15．若的值在x与x+1之间，则x=2．【考点】估算无理数的大小．【分析】先估算的整数部分是多少，即可求出x的取值．【解答】解：∵2＜＜3，∴x=2．故答案为：2．【点评】此题主要考查了估算无理数的大小，确定无理数的整数部分即可解决问题．16．，则x y=﹣1．【考点】非负数的性质：算术平方根；非负数的性质：偶次方．【分析】首先根据非负数的性质，两个非负数的和是0，这两个数都是0求得x，y的值，代入即可求解．【解答】解：根据题意得：，解得：，∴x y=（﹣1）=﹣1．故答案是：﹣1．【点评】本题主要考查了非负数的性质，以及负指数幂的意义，正确求得x，y的值是解题的关键．17．计算：=．【考点】实数的运算；负整数指数幂；特殊角的三角函数值．【专题】计算题．【分析】根据负指数幂、二次根式化简、特殊角的三角函数3个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：原式=3+0.5﹣6×=，故答案为．【点评】本题是基础题，考查了实数的有关运算，还涉及了零指数幂、负指数幂、二次根式化简、绝对值等考点．18．化简二次根式：=﹣2．【考点】二次根式的混合运算．【分析】首先进行各项的化简，然后合并同类项即可．【解答】解：=3﹣（）﹣2=﹣2，故答案为﹣2．【点评】本题主要考查二次根式的化简、二次根式的混合运算，解题的关键在于对二次根式进行化简，然后合并同类项．19．一个自然数的算术平方根是a，则相邻的下一个自然数的算术平方根是．【考点】算术平方根．【分析】首先利用算术平方根求出这个自然数，然后即可求出相邻的下一个自然数的算术平方根．【解答】解：∵一个自然数的算术平方根是a，∴这个自然数是a2，∴相邻的下一个自然数为：a2+1，∴相邻的下一个自然数的算术平方根是：，故答案为：．【点评】此题主要考查算术平方根的定义及其应用，比较简单．三．计算题20．计算：﹣+|1﹣|+（）﹣1．【考点】实数的运算；负整数指数幂．【专题】计算题．【分析】原式第一项化为最简二次根式，第二项分母有理化，第三项利用绝对值的代数意义化简，最后一项利用负指数幂法则计算即可得到结果．【解答】解：原式=3﹣+﹣1+2=3+1．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．21．计算：﹣2sin30°﹣（﹣）﹣2+（﹣π）0﹣+（﹣1）．【考点】实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．【专题】计算题．【分析】本题涉及零指数幂、乘方、特殊角的三角函数值、立方根等考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：原式=﹣2×﹣+1﹣（﹣2）+1=﹣1﹣9+1+2+1=﹣6．【点评】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是掌握零指数幂、乘方、特殊角的三角函数值、立方根等考点的运算．22．．【考点】实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．【专题】计算题．【分析】根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=4+（1﹣）﹣1+2×+，再去括号和进行乘法运算，然后合并即可．【解答】解：原式=4+（1﹣）﹣1+2×+=4+1﹣﹣1++=4+．【点评】本题考查了实数的运算：先算乘方或开方，再算乘除，然后进行加减运算；有括号先算括号．也考查了零指数幂、负整数指数幂和特殊角的三角函数值．23．计算：．【考点】实数的运算；零指数幂；特殊角的三角函数值．【专题】计算题．【分析】本题涉及零指数幂、特殊角的三角函数值、二次根式化简、去绝对值4个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：原式=2+×﹣（﹣1）﹣1，=2+1﹣+1﹣1，=+1．【点评】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握特殊角的三角函数值、零指数幂、二次根式、绝对值等考点的运算．24．若x是不等于1的实数，我们把称为x的差倒数，如3的差倒数为，﹣5的差倒数为．现已知x1=﹣，x1的差倒数是x2，x2的差倒数是x3，…，以此类推，x的值是多少？【考点】规律型：数字的变化类．【分析】根据差倒数的定义分别计算出x1=﹣，x2=；x3=4，x4=﹣，则得到从x1开始每3个值就循环，而÷3=671，即可得出答案．【解答】解：∵x1=﹣，∴x2==；x3==4；x4==﹣；…，∴三个数一个循环，∵÷3=671，∴x=x3=4．【点评】此题考查了数字的变化类，是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．。

中考数学考点大串讲(北师大版)：专题02 实数必刷易错50题(原卷版)

专题02实数（易错50题6种题型）一、认识无理数1．（2022秋·陕西西安·八年级校考期中）下列实数中，属于无理数的是（）A ．3.14159B ．176C ．3D ．3642．（2021春·福建厦门·七年级校考期中）在2 ，4，2，3.14，327 ，3，这6个数中，无理数共有（）A ．4个B ．3个C ．2个D ．1个3．（2022秋·江苏连云港·七年级校考阶段练习）在“223,,2,0.1010010007 ”中无理数有个.4．（2023春·广西南宁·八年级校考阶段练习）如图，数轴上点A 表示的数是．5．（2022秋·江苏宿迁·七年级校考阶段练习）将下列各数填入相应的集合中：7,0, 2.55555,3.01,9,4.020020002,10%,2有理数集合：{…}；无理数集合：{…}；整数集合：{…}；分数集合：{…}6．（2023春·安徽六安·八年级统考期中）下面各图都是边长为1的小正方形组成的网格，小正方形的边所在直线的交点称为格点，若两个格点间的距离是无理数，则称该无理数为这两个格点的“无理间距”．例如，图①中无理间距有2，共有1个（数值相等的，不重复计数，下同）；图②中无理间距除了2外，还有5，22，共有123 个．观察图形，解决下面问题：(1)图③中无理间距应有1236 个，除了2，5，22外，还有________；(2)请在图③中画出端点为格点的线段，使它们的长度分别为你在（1）中所填的无理间距．（每个无理间距画一条线段即可）二、平方根7．（2023秋·山西长治·八年级长治市第六中学校校考阶段练习）9的平方根是（）A ．3B ．81C ．3D ．3 8．（2023秋·全国·八年级专题练习）已知 24a 与1b 互为相反数，则a b 的平方根是（）A ．5B ．3C ．5 D ．39．（2022春·江西新余·七年级校考期中）若12a ，24b ，且0ab ，则a b 的值是．10．（2023春·新疆阿克苏·七年级校考期末）若一个正数的两个不同平方根是35a 和7a ，则这个正数是．11．（2023秋·四川成都·八年级校考阶段练习）已知3m 的算术平方根是3，12n ，求m n 的算术平方根．12．（2023秋·甘肃武威·八年级统考开学考试）已知2a b 的平方根是3 ，52a b 的算术平方根是4，求3a b 的值．13．（2023秋·河北保定·八年级校考阶段练习）我们知道，负数没有算术平方根，但对于三个互不相等的负整数，若两两乘积的算术平方根都是整数，则称这三个数为“完美组合数”．例如：9 ，4 ，1 这三个数， 946 ， 913 ， 412 ，其结果6，3，2都是整数，所以9 ，4 ，1 这三个数为“完美组合数”．(1)18 ，8 ，2 这三个数是“完美组合数”吗？请说明理由．(2)若三个数3 ，m ，12 是“完美组合数”，其中有两个数乘积的算术平方根为12，求m 的值．三、立方根14．（2023秋·山西长治·八年级长治市第六中学校校考阶段练习）若一个数的立方根等于2 ，则这个数等于（）A ．4B ．8C ．8D ．815．（2023春·湖北襄阳·七年级校考阶段练习）已知x 是5的算术平方根，则213x 的立方根是（）A ．513-B ．513 C ．2D ．216.（2023春·云南昭通·七年级统考阶段练习）已知311x x ，则x 的值为．17．（2023春·湖南永州·八年级校考开学考试）（1）81的平方根是；（2）若 30.70.027x ，则x．18．（2023春·广东广州·七年级校考期中）已知一个正数的平方根是6a 与29a ，(1)求a 的值；(2)求关于x 的方程3640ax 的解．19．（2022秋·山西太原·八年级校考阶段练习）求下列未知数x 的值(1) 22511000x (2) 3823125x 20．（2021春·上海浦东新·七年级校考期中）已知一个正方体的棱长是7cm ，要再做一个正方体，使它的体积是原正方体的体积的8倍，求新做的正方体的棱长．四、估算21．（2023秋·重庆九龙坡·八年级重庆实验外国语学校校考阶段练习）估计1021 的值应在（）A ．4和5之间B ．5和6之间C ．6和7之间D ．7和8之间22．（2023春·山东滨州·七年级统考期中）如图，用两个面积为29cm 的小正方形拼成一个大的正方形．则大正方形的边长最接近的整数是()A ．4cmB ．5cmC ．6cmD ．7cm23．（2022·湖南株洲·株洲二中校考二模）写出一个大于7小于27的整数．24．（2023春·湖北恩施·七年级校考期中）已知511 的小数部分为m ，511 的小数部分为n ，则m n ．25．（2023秋·陕西榆林·八年级校考阶段练习）已知41a 的立方根是3 ，2 a b 的算术平方根是3，c 是15的整数部分．(1)求a ，b ，c 的值；(2)求5a b c 的平方根．26．（2023春·四川凉山·七年级校考阶段练习）我们知道2 1.414 ，于是我们说：“2的整数部分为1，小数部分则为21 ”．(1)21 的整数部分为_______，小数部分可以表示为______；(2)已知31 的小数部分为a ，51 的小数部分为b ，求a b 的值．五、实数27．（2023秋·广西南宁·八年级校考阶段练习）在下列四个实数中，最小的数是（）A ．5 B ．0C ．1D ．328．（2022春·河北邯郸·七年级校考期中）下列说法正确的有几个（）①两个无理数的和可能是有理数；②任意一个无理数都可以用数轴上的点表示；③2m 一定没有平方根；④实数包括有理数、无理数和零；⑤立方根等于本身的数是1．A ．1个B ．2个C ．3个D ．4个29．（2023秋·全国·七年级课堂例题）定义21*2a b ab b a b ．若2*3x ，则x 的值是（）A ．4B ．3C ．6D ．730．（2023秋·江苏淮安·九年级统考阶段练习）已知实数m 满足210m m ，则32232024m m m ．31．（2023秋·江西抚州·八年级校考阶段练习）把无理数3，5，11，17表示在数轴上，在这四个无理数中，最有可能被墨迹（如图所示）盖住的无理数是．32．（2023秋·重庆渝中·七年级重庆市求精中学校校考阶段练习）观察下列等式：133 ，239 ，3327 ，4381 ，53243 ，63729 ，…，则234202333333 的末位数字是．33．（2023春·河北沧州·七年级校考期中）实数a 在数轴上对应的点的位置如图，化简：2a a ．34．（湖南省长沙市明德教育集团2022-2023学年九年级期上学期中数学试题）计算：112633(3.14)2 35．（山西省临汾市两县一市2023-2024学年八年级上学期月考数学试题）计算．(1)33116827；(2)3912532 ．36．（2023春·吉林松原·八年级校考阶段练习）如图①是由8个同样大小的立方体组成的魔方，体积为8．(1)求出这个魔方的棱长；(2)图①中阴影部分是一个正方形ABCD ，求出阴影部分的面积及其边长；(3)把正方形ABCD 放到数轴上，如图②，使得点A 与1重合，那么点D 在数轴上表示的数为______．六、二次根式37．（山西省临汾市两县一市2023-2024学年九年级上学期月考数学试题）下列计算中正确的是（）A ．1553 B ．3223 C ．2510 D ．571238．（2022春·陕西安康·八年级校考期中）下列各式中，是最简二次根式的是（）A ．3B ．38C ．12D ．6339．（2023秋·四川眉山·九年级校考阶段练习）下列二次根式中与5是同类二次根式的是（）A ．10B ．20C ．25D ．3040.（2023春·河北沧州·八年级校考期中）当12a 时，式子221a a 的值为（）A ．32a B ．23a C ．1 D ．141．（山西省临汾市两县一市2023-2024学年九年级上学期月考数学试题）计算320154的结果是.42．（2023秋·陕西西安·八年级校考阶段练习）若88y x x 有意义，则3x ．43．（2023秋·四川内江·九年级校考阶段练习）∵2(21)322 ，∴32221 ；∵2(21)322 ，∴32221 ；∵2(23)743 ，∴74323 ．请你根据以上规律，结合你的经验化简843 ．44．（2023春·福建龙岩·八年级校考期中）已知实数a b 、在数轴上的位置如图所示，则化简代数式222(a b)a b 的结果45．（山西省临汾市两县一市2023-2024学年九年级上学期月考数学试题）计算(1) 26363253 ，(2)1512245153108846．（2023秋·贵州·八年级统考阶段练习）计算并解答：(1)12273(2)61822 (3)实数a b 、在数轴上的位置如图所示，且a b ，化简2a a b47．（2023秋·四川眉山·九年级校考阶段练习）已知,x y 为实数且229913x x y x ，求56x y 的平方根．48．（2023秋·河南南阳·九年级校考阶段练习）如图，面积为248cm 的正方形的四个角是面积为23cm 的小正方形，现将这四个角剪掉，制作一个无盖的长方体盒子，这个长方体盒子的底面边长和高分别是多少？（结果保留根号）49．（2022秋·山西太原·八年级校考阶段练习）阅读材料：材料一：两个含有二次根式而非雾的代数式相乘，如果它们的积不含二次根式，那么这两个代数式互为有理化因式．例如：333 ，6262624 ，我们称3的一个有理化因式是3，62 的一个有理化因式是62 ．材料二：如果一个代数式的分母中含有二次根式，通常可将分子、分母同乘分母的有理化因式，使分母中不含根号，这种变形叫做分母有理化．例如11333333 862883326224626262 请你仿照材料中的方法探索并解决下列问题：(1)13的有理化因式为______，75 的有理化因式为______；（均写出一个即可）(2)将下列各式分母有理化：①315；②11253 ．（要求；写出变形过程）50．（2023秋·四川宜宾·八年级校考阶段练习）若23(1)0xy y ．(1)求x ，y 的值；(2)求1111(2)(2)(4)(4)(2022)(2022)xy x y x y x y 的值．。

中考数学专题复习课件(第2讲_实数的运算及大小比较)

D )
4．－23×(－2)2＋2 的结果是( B ) A．18 B．－30 C．0
D．34
5．下列计算正确的是(
B
)
3 A. －27 ＝3 B．(π－3.14)0＝ 1 1－ C．( ) 1＝－2 D. 16 ＝± 4 2
目录首页上一页下一页末页
3 1－ 6．设 a＝20，b＝(－3)2，c＝－9，d＝( ) 1，则 a、b、c、d 按由小到大的顺序排列正 2 确的是( A ) A．c＜a＜d＜ b B．b＜d＜a＜c C．a＜c＜d＜b D．b＜c＜a＜d
)
(4)(2010· 毕节)若|m－3|＋(n＋2)2＝0，则 m＋2n 的值为( ) A．－4 B．－1 C．0 D．4 【点拨】本组题主要考查实数的简单运算及大小比较．(1)题画出数轴描出各点，最右边 1 的点表示的数即为最大的数；(2)题 A 选项结果为 1，C 选项结果为，D 选项结果为 3；(3) 3 题由图可知 a<0，b>0 且|a|>|b|，故 D 选项正确；(4)题因为 |m－ 3|≥0，且(n＋2)2≥0，又因为 |m－3|＋(n＋2) 2＝0，所以 m－3＝ 0 且 n＋2＝ 0.所以 m＝3，n＝－ 2，所以 m＋2n＝3＋2×(－ 2)＝－1.
下一页
末页
1．下列各数中，最大的数是( A．－1 B．0 C．1 D. 2
D )
2 2．如果□×(－ )＝1，则“□”内应填的实数是( 3 3 2 2 3 A. B. C．－ D ．－ 2 3 3 2
3．下列各式，运算结果为负数的是( D A．－(－2)－(－3) B．(－2)×(－3) －－ C．(－2) 2 D．(－ 3) 3 )
【解答】(1)原式＝ 1－3＋2－ 1＝－ 1. 2 (2)原式＝1＋(－ 3)－(2－ 2)－2× 2 ＝1－3－2＋ 2－ 2＝－4. (3)原式＝3－1＋ 3 2－4 2＝2－ 2. (4)原式＝3＋(－ 2)－ 2× 2 ＋1＝3－2－1＋1＝1. 2

云南中考数学 2_第2讲实数的大小比较及运算

第2讲实数的大小比较及运算
预学案·记易
考点一考点二考点三精讲案·学易类型一
平方根、算术平方根、立方根实数的运算实数的大小比较
平方根、算术平方根、立方根
类型二实数运算法则的判断
类型三实数的大小比较
类型四与实数有关的计算题试真题·练易
命题点一平方根、算术平方根、立方根
命题点二实数相关的计算题（高频考点）
7.(2014曲靖,17,6分)计算:|-2|-

1 4
1+( 2
-1.414)0+ 9
.
解原式=2-4+1+3=2.
探疑难·知易
1.“三根”转变先化简易错题1(2018安顺) 4 的算术平方根为 ( B ) A.± 2 B. 2 C.±2 D.2 解析 4=2,2的算术平方根是 2,选B. 错解 C或D

1 2
2

=4,∴原式=3-1+1-4=-1.
6.(2014昆明,15,5分)计算:| 2
|+(π-3)0+

1 2
1

-2cos

45°.
解
| 2
|= 2
,(π-3)0=1,

1 2
1

=-2,2cos

45°= 2
,∴原式= 2
+1-2- 2 =-1.
8.计算: 9
+|1- 5
|+( 5
+1)0-

1 4

2
.
解
9
=3,|1- 5
|= 5
-1,( 5

中考数学专题复习题实数(含解析)

2017-2018年中考数学专题复习题：实数一、选择题1.下列说法中，其中不正确的有任何数都有算术平方根；一个数的算术平方根一定是正数；的算术平方根是a；算术平方根不可能是负数．A. 0个B. 1个C. 2个D. 3个2.若x、y都是实数，且，则xy的值为A. 0B.C. 2D. 不能确定3.若一个数的平方根与它的立方根完全相同则这个数是A. 1B.C. 0D. ，04.已知，，则约等于A. B. C. D.5.如图，数轴上表示1、的对应点分别为点A、点若点A是BC的中点，则点C所表示的数为A. B. C. D.6.在实数，，，，，，，，相邻两个1中间一次多1个中，无理数有A. 2个B. 3个C. 4个D. 5个7.若，，则A. B. C. 或 D.或8.定义表示不超过实数x的最大整数，如，，函数的图象如图所示，则方程的解为A. 0或B. 0或2C. 1或D. 或9.若的小数部分为a，的小数部分为b，则的值为A. 0B. 1C.D. 210.用计算器计算，，根据你发现的规律，判断与为大于1的整数的值的大小关系为A. B. C. D. 与n的取值有关二、填空题11.若m是的算术平方根，则 ______ ．12.已知，则 ______ ．13.已知，则的平方根为______ ．14.若，，则 ______ ．15.已知实数a满足，那么的值是______ ．16.在实数，，，，，，0，，中，无理数的个数为______ ．17.定义新运算：对于任意实数a，b，都有，等式右边是通常的加法、减法及乘法运算比如：则的值为______．18.比较大小______填“”、“”、“”19.已知：m、n为两个连续的整数，且，则______．20.规定：表示a，b之间的一种运算．现有如下的运算法则：．例如：，，则 ______ ．三、计算题21.先化简，再求值：先化简，然后从的范围内选取一个合适的整数作为x的值代入求值．22.计算：．23.已知一个正数的两个平方根分别是和，求这个数的立方根．24.观察：，即，的整数部分为2，小数部分为，请你观察上述式子规律后解决下面问题．规定用符号表示实数m的整数部分，例如：，，填空： ______ ； ______ ．如果的小数部分为a，的小数部分为b，求的值．【答案】1. D2. C3. C4. A5. D6. C7. C8. A9. B10. C11. 512.13.14.15. 201616. 317. 518.19. 720.21. 解：原式，且，，，x是整数，，当时，原式．22. 解：原式．23. 解：根据题意得：，解得：，这个正数是100，则这个数的立方根是．24. 5；1。

中考数学专题复习课件专题二实数整式分式的运算与化简求值(共21张PPT(完整版)5

(4)(2017·张家界)先化简(1－x－1 1)÷x2－x24－x＋1 4，再从不等式 2x－1＜6 的正整数解中选一个适当的数代入求值；
解：原式＝xx－－21×（x＋（1x）－（2）x－2 1）＝xx＋－12， ∵2x－1＜6，∴2x＜7.∴x＜72.把 x＝3 代入上式，得原式＝33＋－12＝4.
解：原式＝－1－|1－ 33× 3|＋2×4＋1＝－1－0＋8＋1＝8.
2．化简： (1)(2017·十堰)化简：(a＋2 1＋aa2＋－21)÷a－a 1；
解：原式＝（2（a＋a－1）1）（＋a－a＋1）2 ·a－a 1＝2aa－（2a＋＋1a＋）2＝a（a3＋a 1）＝a＋3 1.
(2)(2017·乐山)(2aa22－＋12a－a2－a2－ 2a＋a 1)÷a－2a1. 解：原式＝[（a＋2a1（）a＋（1a－）1）－a（（aa－－11））2]÷a－2a1＝ (a－2a1－a－a 1)÷a－2a1＝a－a 1÷a－2a1＝a－a 1·a－2a1＝12.
(5)(2017·菏泽)(1＋3xx＋－11)÷x2－x 1，
其中 x 是不等式组1－x>－12－x，的整数解． x－1>0
解：1－x>－12－x①， x－1>0②，
解不等式①，得 x＜3；解不等式②，得 x＞1. ∴不等式组的解集为 1＜x＜3.∴不等式组的整数解为 x＝2. ∵(1＋3xx＋－11)÷x2－x 1＝x4＋x1×（x＋1）x（x－1）＝4(x－1)， ∴当 x＝2 时，原式＝4×(2－1)＝4.
1．计算： (1)(2017·温州)2×(－3)＋(－1)2＋ 8；解：原式＝－6＋1＋2 2＝－5＋2 2.
(2)(2017·黄石)(－2)3＋ 16＋10＋|－3＋ 3|；

中考数学复习考点知识讲解与提升强化训练2---实数的运算及大小比较(解析版)

中考数学复习考点知识讲解与提升强化训练第02讲实数的运算及大小比较1．实数的大小比较(1)数轴比较法：数轴上的两个数，右_边的数总大于_左__边的数； (2)代数比较法：正数＞0＞负数；两个负数，绝对值大的反而_小__； (3)差值比较法：①a －b ＞0⇔a ＞b ；②a －b ＝0⇔a ＝b ； ③a －b ＜0⇔a ＜b ；(4)求商比较法：若b ＞0，则①ab ＞1⇔a ＞b ； ②a b ＝1⇔a ＝b ；③a b ＜1⇔a ＜b ；(5)倒数比较法：若1a ＞1b 且a 与b 同号时，a ＜b ； (6)平方比较法：对于任意正实数a ，b 有a 2＞b ⇔a ＞ b. 3.非负数(1)常见非负数：|a|，a 2，a (a≥0)；(2)若几个非负数的和为0，则这几个非负数同时为0. 4．实数的运算(1)零指数幂：a 0＝1(a≠0)； (2)负整数指数幂：a －p＝1a p (a≠0)；(3)去绝对值符号：|a －b|＝⎩⎨⎧a －b （a>b ）0 （a ＝b ）；b －a （a<b ）(4)－1的奇偶次幂：(－1)n＝⎩⎨⎧ 1 ，n 为偶数－1，n 为奇数；注意：正数的任何次幂都是正数，负数的奇次幂为负数，负数的偶次幂为正数． (5)实数的运算顺序是先算乘方和开方，再算_乘除，最后算_加减_，如果有括号，先算小括号，再算中括号，最后算大括号，同级运算应_从左到右_依次计算．考点1：实数的大小比较【例题1】（2018•咸宁）写出一个比2大比3小的无理数（用含根号的式子表示）．【答案】【解析】：∵4＜5＜9，∴2＜＜3，即为比2大比3小的无理数．故答案为．归纳：两个实数比较大小，先将两个数化简成易于比较的同类数，再进行比较．考点2：实数的运算【例题2】(2018·石家庄十八县大联考)嘉琪在做家庭作业时，不小心将墨汁弄倒，恰好覆盖了题目的一部分：计算：(－7)0＋|1－3|＋(33)－1－□＋(－1)2 018. 经询问，王老师告诉题目的正确答案是1. (1)求被覆盖的这个数是多少？(2)若这个数恰好等于2tan(α－15)°，其中α为三角形一内角，求α的值．【解析】：(1)原式＝1＋3－1＋3－□＋1＝1， ∴□＝1＋3－1＋3＋1－1＝2 3. (2)∵α为三角形一内角， ∴0<α<180.∴－15°<(α－15)°<165°.∵2tan(α－15)°＝23，∴(α－15)°＝60°.∴α＝75.归纳：考查实数的运算，先分别计算出每一项的值，再根据实数混合运算的顺序进行计算，即先乘除，再加减，同级运算，按从左向右进行计算．一、选择题：1. （山东滨州1，3分）21-等于（）A．1 B．﹣1 C．2 D．﹣2【答案】B．【解答】解：112-=-，故选择B ．2. （江苏省扬州市，1，3分）与-2的乘积为1的数是( )A．2 B．-2 C．12D．12【答案】D【解答】解：与-2乘积为1的数就是-2的倒数，等于12，故选择D ．3. （江苏省淮安市，6，371+的值( ).A．在1和2之间B．在2和3之间C．在3和4之间D．在4和5之间【答案】C．【解答】解：∵4<7<9 479即27＜3 ∴2+17+1＜3+1 ∴37+1＜4，故选择C．4. （2018•福建）在实数|﹣3|，﹣2，0，π中，最小的数是（） A ．|﹣3| B ．﹣2 C ．0D ．π【答案】B【解答】解：在实数|﹣3|，﹣2，0，π中， |﹣3|=3，则﹣2＜0＜|﹣3|＜π，故最小的数是：﹣2．故选：B ．5. （江苏泰州，6，3分）实数a 、b 满足044122=++++b ab a a ，则a b 的值为 A ．2 B ．21 C ．−2 D ．−21 【答案】B【解答】解：由题意：2(2)0a b ++=，所以1020a a b +=⎧⎨+=⎩，解之得12a b =-⎧⎨=⎩，所以1122a b -==，故选择B ．二、填空题：6. （河南省，9，3分）计算：._________8)2(30=-- 【答案】-1【解答】解：（-2）0 -38=1-2 = -1，故答案为-1 .7. （2019•浙江嘉兴•4分）数轴上有两个实数a ，b ，且a ＞0，b ＜0，a+b ＜0，则四个数a ，b ，﹣a ，﹣b 的大小关系为（用“＜”号连接）．【答案】b ＜﹣a ＜a ＜﹣b【解析】解：∵a ＞0，b ＜0，a+b ＜0， ∴|b|＞a ，∴﹣b ＞a ，b ＜﹣a ，∴四个数a ，b ，﹣a ，﹣b 的大小关系为b ＜﹣a ＜a ＜﹣b ．故答案为：b ＜﹣a ＜a ＜﹣b8. （湖北省十堰市，12，3分）计算：|38-4|-（21）-2=______________【答案】-2【解答】解：（21）-2=|2-4|-211()2=|-2|-4=-2 . 9. （山东滨州18，4分）下列式子：22131=+⨯ 28197=+⨯ 22612725=+⨯ 28018179=+⨯ ……可猜想第个式子为．【答案】201620162016(32)3131-⨯+=-【解答】解：观察每个式子的第二个数依次是3，9，27，81这些数分别是13，23，33，43，因此第个式子的第2个数是20163，每个式子的第一个数总是比第2个数小2，因此第个式子的第1个数是201632-，每个式子的最后一个数总比第2个数小1，因此第个式子的最后一个数是201631-，所以第个式子是201620162016(32)3131-⨯+=-．故答案为：201620162016(32)3131-⨯+=- 三、解答题：10. (2019•云南•6分)计算：1021453--+---）（）（π．【分析】原式利用乘方，零指数幂、算术平方根、负整数指数幂法则计算即可求出值．【解析】解：原式＝9＋1－2－1＝7．11. （广东茂名，16，7分）计算：（－1）+8－2-－（π－3.14）0.【提示】本题考查了实数的运算，解题的关键是掌握乘方的意义、二次根式的化简、绝对值的意义、零整数指数幂的值和同类二次根式的合并法则．先分别计算（－1）、8、2-、（π－3.14）0的值，然后再进行实数、二次根式加减运算. 【解答】解：原式=1+22－2－1=22－2= 2 . 12. （江苏省扬州市，19（1），4分）计算：21()126cos303；【提示】本题考查了实数的混合运算，解题的关键是正确化简负整数指数幂、锐角三角函数值、二次根式等运算．本题先逐个化简负整数指数幂、锐角三角函数值、二次根式，再按照运算顺序计算．【解答】解：原式=9﹣23+6×32=9﹣23+33=9+3； 13. （江苏省宿迁市，17，6分）计算：4)12(330sin 201--++︒-【提示】根据特殊角的三角函数值，负指数、零指数幂的运算及算术平方根分别计算即可.【解答】解：原式=2×111-223++=31．14. （2019•甘肃武威•6分）计算：（﹣2）2﹣|﹣2|﹣2cos45°+（3﹣π）0【分析】先根据乘方的计算法则、绝对值的性质、零指数幂及特殊角的三角函数值分别计算出各数，再根据实数混合运算的法则进行计算即可．【解答】解：（﹣2）2﹣|﹣2|﹣2cos45°+（3﹣π）0，＝4﹣（2﹣）﹣2×+1，＝4﹣2+﹣+1，＝3．。