圆锥曲线与方程复习课件10
圆锥曲线专题题型小结ppt课件

2、两条直线 l1 : y k1x b1,l2 : y k2x b2 垂直:则 k1k2 1
3、一元二次方程根与系数的关系:若一元二次方程 ax2 bx c 0(a 0) 有两
个根 x1, x2 ,
则
x1
x2
b a
, x1x2
c a
。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
★ 变式1:过点P(8,1)的直线与双曲线 x2 y2 1
4
相交于A,B两点,且P为AB的中点,这样的直线 AB是否存在,如果存在,求出直线AB的直线方 程,若不存在,请说明理由。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
设
E(xE ,
yE ), F (xF ,
yF ) ,则
xE
(3 2k)2 12 3 4k 2
,
yE
k xE
3 2
k
以 - k代k得:xF
(3 2k)2 12 3 4k 2
,
yF
-k xF
3 2
k
KEF
yF xF
yE xE
k(xF xE ) 2k xF xE
1 2
即直线 EF 的斜率为定值,其值为 1 2
直线与圆锥曲线的位置关系
1.有关位置关系的问题:
例 1:已知直线 l : y kx 1与椭圆 C : x2 y2 1 4m
始终有交点,求 m 的取值范围
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
圆锥曲线PPT优秀课件

.
F0 A2 x
其中 a2 b2 c2 , a 0,b c 0 , F0 , F1, F2 是对应的焦点。 B1
(1)若三角形 F0 F1F2 是边长为 1 的等边三角形,求“果圆”的方程;
(2)若
A1 A
B1B
,求
b a
的取值范围;
解:(1)∵F0(c,0)F1(0, b2 c2 ),F2(0, b2 c2 )
①;
∵点 P1, P2 在双曲线上,∴点 P1, P2 的坐标适合方程①。
将 (3, 4
2
),
(
9 4
,
5)
分别代入方程①中,得方程组:
(4 2)2 a2
32 b2
25 a2
(
9)2 4 b2
1
1
将
1 a2
和
1 b2
1
看着整体,解得
a2 1
1 16
1
,
b2 9
∴
a 2 b2
16 即双曲线的标准方程为 y2
9
16
x2 9
1。
点评:本题只要解得 a2 ,b2 即可得到双曲线的方程,没有
必要求出 a,b 的值;在求解的过程中也可以用换元思想, 可能会看的更清楚。
(4) 与双曲线 x 2 y 2 1有共同渐近线, 9 16
且过点 (3,2 3) 。
解析:(4)设所求双曲线方程为 x2 y 2 ( 0) ,
3 m
5 n
1
定义,还要知道椭 圆中一些几何要素
所以,椭圆方程为 y2 x2 1 . 与椭圆方程间的关
10 6
系。
例 2.设椭圆的两个焦点分别为 F1、、F2,过 F2 作椭圆长轴的垂线交椭圆于点 P,若△F1PF2 为
高二数学圆锥曲线复习课PPT课件演示文稿

(2)设椭圆方程为 mx2+ny2=1(m>0,n>0 且 m≠n). ∵椭圆经过 P1、P2 点,将 P1,P2 两点坐标代入椭圆方程, 得63mm+ +n2n==1, 1. 解得 m=19,n=13. ∴所求椭圆方程为x92+y32=1.
b2 1
消元
一元二次方程
消y
消x
f (x) 0
g( y) 0
y
SABC
1 2
AB
•d
1 SABC 2 OC • y1 y2
B
c
O
x
A
第10页,共129页。
(3)直线与圆锥曲线有关弦的中点问题
解 题
思 路
直线与圆锥曲线联立消元得到一元二次方程
点差法
点的对称性
:
第11页,共129页。
5、焦点三角y形性质:
高二数学圆锥曲线复习课PPT 课件演示文稿
第1页,共129页。
(优质)高二数学圆
锥曲线复习课PPT课 件
第2页,共129页。
二、基础知识点梳理
1、圆锥曲线的定义
椭圆的定义:
双曲线的定义: 圆锥曲线的统一定义(第二定义) :
l
d . .M F
l d .M .
F
l d.M .
F
第3页,共129页。
2、圆锥曲线的标准方程
Image (2)(20191·新1课6标全国高考)在平面直角1坐6标系9xOy中,椭圆
C的中心为原点,焦点F1,F2在x轴上,离心率为 过F1的2直. 线l交C于A,B两点,且△ABF2的周长为16,那么C的方程2为____.
第33页,共129页。
【解析】(1)选C.不妨设E(-c,0),F(c,0),则
高教版中职数学基础模块《圆锥曲线》总复习课件

a,b,c的关系
a2=b2+c2
长轴、短轴
长轴长2a,短轴长2b
c
e = a (0<e<1)
离心率
一课一案 高效复习
二、双曲线
1、定义:
到两定点F1,F2的距离之差的绝对值为常数(<|F1F2|)
平面内______________________________________的点的轨迹叫做双曲线,
其中F1,F2是焦点,|F1F2|为焦距.
一课一案 高效复习
2、双曲线的标准方程和性质:
||MF1|-|MF2||=2a(a>0)
数学定义式
焦点位置
x轴
y轴
图形
标准方程
焦点
x2 - y2 =1(a>0,b>0)
a2 b2
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
|F1F2|=2c
y轴正半轴
y轴负半轴
y2=2px(p>0)
p
F( 2 ,0)
p
x=-2
y2=-2px(p>0)
p
F(- 2 ,0)
p
x= 2
x2=2py(p>0)
F(0, p
2 )
p
y=-2
x2=-2py(p>0)
p
F(0,- 2 )
p
y= 2
图形
标准方程
焦点
准线
顶点
对称轴
离心率
P的几何意义
O (0,0)
x轴
y轴
e=1
=1上的两个焦点,过F1的直线与椭圆
9
交于M、N两点,则△MNF2的周长为__________;
圆锥曲线 课件

利用线性代数知识求解圆锥曲线问题
线性方程组
线性方程组是线性代数中的基础内容, 它可以用来求解与圆锥曲线相关的问题 。例如,通过解线性方程组,可以找到 满足特定条件的点的坐标。
VS
特征值与特征向量
特征值和特征向量在解析几何中也有广泛 应用。通过计算圆锥曲线的特征值和特征 向量,可以深入了解曲线的性质,从而更 好地解决相关问题。
椭圆离心率的范围是0<e<1,双曲线的离心率范围是e>1。
圆锥曲线的光学性质
01
光线经过圆锥曲线上的点时,其 方向会发生改变,这种现象叫做 圆锥曲线的光学性质。
02
光线经过椭圆时,会沿着椭圆的 主轴方向折射;经过双曲线时, 会沿着双曲线的副轴方向折射。
圆锥曲线的对称性
圆锥曲线具有对称性,即如果将圆锥 曲线沿其对称轴旋转180度,它仍然 与原来的曲线重合。
02 圆锥曲线的性质
焦点与准线
焦点
圆锥曲线上的点到曲线的两个焦 点的距离之和等于常数,这个常 数等于椭圆的长轴长,等于双曲 线的实轴长。
准线
与圆锥的母线平行的线,在平面 内与准线相交的直线与圆锥相切 于一点,这个点叫做切点。
离心率
离心率:是描述圆锥曲线形状的一个重要参数,它等于圆锥顶点到曲线的距离与 圆锥的半径之比。离心率越大,圆锥曲线越扁平,反之则越接近于球形。
双曲线的极坐标 方程
$frac{rho^2}{a^2} frac{rho^2}{b^2} = 1$
圆锥曲线在极坐 标下的表…
将圆锥曲线问题转化为极 坐标形式,便于理解和求 解。
利用极坐标求解圆锥曲线问题
利用极坐标求解圆锥曲线问题的步骤
首先将问题转化为极坐标形式,然后利用极坐标的性质和公式进行求解。
2022版高考数学大一轮复习第10章圆锥曲线与方程第4讲圆锥曲线的综合应用1

第十章 圆锥曲线与方程第四讲 圆锥曲线的综合问题拓展变式1。
[2017浙江,21,15分]如图10—4—2,已知抛物线x 2=y ,点A (−12,14),B (32,94),抛物线上的点P (x ,y )(−12<x 〈32)。
过点B 作直线AP 的垂线,垂足为Q.图10—4-2(1)求直线AP 斜率的取值范围; (2)求|PA |·|PQ |的最大值。
2。
[2020全国卷Ⅰ,21,12分][文]已知A ,B 分别为椭圆E :x 2a 2+y 2=1(a 〉1)的左、右顶点,G 为E 的上顶点,AG ⃗⃗⃗⃗⃗ ·GB⃗⃗⃗⃗⃗ =8。
P 为直线x =6上的动点,PA 与E 的另一交点为C ,PB 与E 的另一交点为D.(1)求E 的方程;(2)证明:直线CD 过定点。
3.[2021武汉四地六校高三联考]已知椭圆C:x2a2+y2b2=1(a〉b〉0)的离心率为12,以原点为圆心,椭圆的短半轴为半径的圆与直线√7x−√5y+12=0相切。
(1)求椭圆C的方程.(2)已知A(-4,0),过点R(3,0)作与x轴不重合的直线l交椭圆C于P,Q两点,连接AP,AQ,分别交直线x=163于M,N两点,若直线MR,NR的斜率分别为k1,k2,问:k1k2是否为定值?若是,求出该定值;若不是,请说明理由.4。
[2021湖北省部分重点中学摸底联考]已知点A(1,−√32)在椭圆C:x2a2+y2b2=1(a〉b>0)上,O为坐标原点,直线l:xa2−√3y2b2=1的斜率与直线OA的斜率之积为−14.(1)求椭圆C的方程。
(2)不经过点A的直线m:y=√32x+t(t≠0)与椭圆C交于P,Q两点,P关于原点的对称点为R(与点A不重合),直线AQ,AR与y轴分别交于点M,N,求证:|AM|=|AN|.5。
[2020山西大同一联]已知椭圆C的中心在原点,焦点在坐标轴上,直线y=32x与椭圆C在第一象限内的交点是M,点M在x 轴上的射影恰好是椭圆C的右焦点F2,椭圆C的另一个焦点是F1,且MF1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF2⃗⃗⃗⃗⃗⃗⃗⃗ =94。
圆锥曲线课件

标准方程:x^2/a^2 - y^2/b^2 = 1 (a > 0, b > 0)
1. 范围:双曲线在x轴上的范围是[±a, ±∞],在y轴上 的范围是[0, b]。
3. 渐近线:双曲线有两条渐近线,斜率分别为y=±b/a 。
抛物线
定义:抛物线是指由平面内 与一个固定点F和一条直线l
的距离相等的点的轨迹。
极坐标系的基本概念
01
极坐标系是平面坐标系的一种形式,由极点、极轴和极径等构
成。
圆锥曲线在极坐标系中的表示
02
将圆锥曲线置于极坐标系中,探究其在极坐标系中的形式及其
性质。
极坐标与直角坐标的转换
03
掌握极坐标与直角坐标的转换公式,能够将极坐标方程转化为
直角坐标方程。
圆锥曲线在实际问题中的优化方案
实际问题的数学建模
折射定律
折射定律也是光学原理中的重要内容之一,它描述了 光线在不同介质之间传播时的偏转规律。在一些复杂 的光学系统中,如望远镜、显微镜等,需要对多个曲 面进行精确的设计和加工,而这些曲面常常是按照圆 锥曲线的形状进行设计和加工的。通过对这些曲面的 精确设计和加工,我们可以更好地控制光线的折射方 向和强度,从而制造出更好的光学器材和设备。
计算坐标
根据圆锥曲线的方程,计算出各个点的坐标 。
确定圆锥曲线的形状和大小
根据圆锥曲线的性质和特点,确定形状和大 小,选择合适的参数。
绘制图形
使用绘图软件或手绘,根据计算出的坐标绘 制圆锥曲线。
焦点半径法
01
02
03
确定焦点
根据圆锥曲线的类型和方 程,确定焦点位置。
计算半径
根据圆锥曲线的方程和焦 点的位置,计算出曲线的 半径。
圆锥曲线复习课课件

将问题转化为函数问题,利用函数的性质和图像,求解相关 问题。
05
圆锥曲线的问题与挑战
圆锥曲线中的难题与挑战
圆锥曲线中的复杂计算
圆锥曲线问题往往涉及大量的计算和复杂的数学公式,需要学生 具备较高的数学计算能力和逻辑思维能力。
圆锥曲线中的抽象概念
圆锥曲线问题常常涉及到抽象的概念和性质,需要学生具备较好的 数学基础和空间想象力。
利用圆锥曲线的参数方程,将问 题转化为参数的取值范围或最值 问题,简化计算。
圆锥曲线的特殊解题方法
焦点三角形法
利用圆锥曲线的焦点三角形,结合正 弦定理、余弦定理等,求解相关问题 。
切线法
通过圆锥曲线的切线性质,结合导数 和切线斜率,求解相关问题。
圆锥曲线的综合解题方法
数形结合法
将几何性质与代数表达式相结合,通过数形结合的方法,直 观地解决问题。
作用。
光线的弯曲程度与圆锥曲线的离 心率有关,离心率越大,光线弯
曲程度越明显。
圆锥曲线的对称性质
圆锥曲线具有对称性,包括中 心对称、轴对称和面对称等。
圆具有中心对称和轴对称,椭 圆和双曲线只有中心对称,抛 物线只有轴对称。
对称性是圆锥曲线的一个重要 性质,在解决几何问题时具有 广泛应用。
03
圆锥曲线的应用
路,提高解题能力。
培养数学思维
学生应注重培养数学思维,提高 逻辑推理能力和空间想象力,以
便更好地解决圆锥曲线问题。
如何进一步深化对圆锥曲线的研究
研究圆锥曲线的性质
01
学生可以进一步研究圆锥曲线的性质和特点,探索其内在规律
和数学之美。
探索圆锥曲线与其他数学领域的联系
02
学生可以探索圆锥曲线与其他数学领域之间的联系,例如与代
圆锥曲线的参数方程 课件

椭圆的参数方程及应用
将参数方程yx==35scionsθθ (θ 为参数)化为普通方 程,并判断方程表示曲线的焦点坐标.
【思路探究】 根据同角三角函数的平方关系,消去参 数,化为普通方程,进而研究曲线形状和几何性质.
【自主解答】
由yx==35scionsθθ
得csionsθθ==3y5x,,
两式平方相加,得x522+3y22=1.
抛物线的参数方程
设抛物线 y2=2px 的准线为 l,焦点为 F,顶点 为 O,P 为抛物线上任一点,PQ⊥l 于 Q,求 QF 与 OP 的交 点 M 的轨迹方程.
【思路探究】 解答本题只要解两条直线方程组成的方 程组得到交点的参数方程,然后化为普通方程即可.
【自主解答】 设 P 点的坐标为(2pt2,2pt)(t 为参数), 当 t≠0 时,直线 OP 的方程为 y=1t x, QF 的方程为 y=-2t(x-p2), 它们的交点 M(x,y)由方程组
∴a=5,b=3,c=4.
因此方程表示焦点在 x 轴上的椭圆,焦点坐标为 F1(4,0)
和 F2(-4,0).
椭圆的参数方程yx==bacsionsθθ,, (θ 为参数,a,b 为常数, 且 a>b>0)中,常数 a、b 分别是椭圆的长半轴长和短半轴长, 焦点在长轴上.
若本例的参数方程为yx==53scionsθθ ,(θ 为参数),则如何求 椭圆的普通方程和焦点坐标?
它到两渐近线的距离分别是 d1 和 d2,
则
d1·d2=|absec
φ+abtan b2+a2
φ| ·
|absec φ-abtan φ| b2+-a2
=|a2b2seac22+φ-b2tan2 φ|=aa2+2b2b2(定值).
高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质

> 0.
即 A=0(直线与抛物线的对称轴平行,即相交);
≠ 0,
(2)直线与抛物线相切⇔有一个公共点,即
= 0.
≠ 0,
(3)直线与抛物线相离⇔没有公共点,即
< 0.
课堂篇探究学习
探究一
探究二
探究三
当堂检测
变式训练2设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l
③当Δ<0时,即k>1时,l与C没有公共点,此时直线l与C相离.
综上所述,(1)当k=1或k=0时,直线l与C有一个公共点;
(2)当k<1,且k≠0时,直线l与C有两个公共点;
(3)当k>1时,直线l与C没有公共点.
课堂篇探究学习
探究一
探究二
探究三
当堂检测
反思感悟方程思想解决直线与抛物线的位置关系
题,通过我们学过的数学知识进行求解.利用抛物线模型解决问题
时,关键是建立坐标系得到抛物线的标准方程,一般都是将抛物线
的顶点作为坐标原点,将对称轴作为x轴或y轴建立坐标系,其次要注
意抛物线上关键点的坐标,并善于运用抛物线的对称性进行求解.
课堂篇探究学习
探究一
探究二
探究三
当堂检测
变式训练3如图是抛物线形拱桥,当水面到直线l时,拱顶离水面2
图形
对称轴
x轴
焦点
F
顶点
原点(0,0)
准线
x=-2
离心率
e=1
p
2
x轴
,0
p
开口方向 向右
p
F - ,0
2
p
y轴
F 0,
p
y轴
十、圆锥曲线与方程

十、圆锥曲线与方程高考模块检测一 圆锥曲线与方程1.(2014北京,理11)设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________;渐近线方程为________. 【答案】221312x y -=; 2y x =±【解析】解:双曲线2214y x -=的渐近线为2y x =±,故C 的渐近线为2y x =±;设C :224y x m -=,因为C 过()2,2,所以代入并解得3m =-,故C 的方程为221312x y -=,渐近线方程为2y x =±【考点】双曲线的简单性质【点评】本题主要考查双曲线的性质,利用渐近线之间的关系,再利用待定系数法解题是关键,比较基础.2.(2013北京,理6)若双曲线22221x y a-=( ).A .y =±2x B.y =C .12y x =± D.yx = 【答案】:B【解析】:c ,∴b . ∴渐近线方程为by x a=±=,故选B. 【考点】双曲线的简单性质【点评】本题考查双曲线的基本性质,渐近线方程的求法,考查计算能力。
3.(2012北京,理12)在直角坐标系xOy 中.直线l 过抛物线24y x =的焦点F.且与该撇物线相交于A 、B 两点.其中点A 在x 轴上方.若直线l 的倾斜角为60º.则△OAF 的面积为【答案】3【解析】根据y 2=4x 得焦点坐标F (1,0),因为直线l 的倾斜角为60º,所以直线的斜率为K=tan600=3,利用点斜式,直线方程为y=3x-3,将直线和曲线联立⇒⎪⎩⎪⎨⎧=-=xy x y 4)1(32A (3,23)B (332,31-),因此33212121=⨯⨯=⨯⨯=∆A OAF y OF S【考点】直线与圆锥曲线的综合问题;直线的倾斜角;抛物线的简单性质 【点评】直线与抛物线的关系可以转化为求交点坐标问题.4.(2012北京,理12)在直角坐标系xOy 中.直线l 过抛物线24y x =的焦点F.且与该撇物线相交于A 、B 两点.其中点A 在x 轴上方.若直线l 的倾斜角为60º.则△OAF 的面积为【答案】3【解析】根据y 2=4x 得焦点坐标F (1,0),因为直线l 的倾斜角为60º,所以直线的斜率为K=tan600=3,利用点斜式,直线方程为y=3x-3,将直线和曲线联立⇒⎪⎩⎪⎨⎧=-=xy x y 4)1(32A (3,23)B (332,31-),因此33212121=⨯⨯=⨯⨯=∆A OAF y OF S【考点】直线与圆锥曲线的综合问题;直线的倾斜角;抛物线的简单性质. 【点评】直线与抛物线的关系可以转化为求交点坐标问题.7(2011北京,理14)曲线C 是平面内与两个定点F1(-1,0)和F¬2(1,0)的距离的积等于常数)1(2>a a 的点的轨迹.给出下列三个结论:① 曲线C 过坐标原点;② 曲线C 关于坐标原点对称;③若点P 在曲线C 上,则△F 1PF 2的面积大于21a 2。
圆锥曲线与方程 课件 (共59张PPT)

(2) 、已知点 M 到点 F(4,0)的距离比它到直线 l:x+5=0 的距离小 1,求点 M 的轨迹方程.
解析: 如图, 设点 M 的坐标为(x, y), 由于点 M 到点 F(4,0) 的距离比它到直线 l:x+5 =0 的距离小 1,则点 M 到点 F(4,0) 的距离与它到直线 l′:x+4=0 的距离相等,根据抛物线的定 义可知点 M 的轨迹是以 F 为焦点,直线 l′为准线的抛物线, p 且 =4,即 p=8. ∴点 M 的轨迹方程为 y2=16x. 2
归纳总结
求轨迹方程时,如果能够准确把握一些曲线的定义,先判断 曲线类型再求方程,往往对解题起到事半功倍的效果.
学以致用
x2 y2 P 是椭圆上任 F2 是椭圆 2+ 2=1(a>b>0)的两焦点, (1)F1、 a b 垂足为点 Q, 从任一焦点引∠F1PF2 的外角平分线的垂线, 一点, 则点 Q 的轨迹为( A.圆 C.双曲线 ) B.椭圆 D.抛物线
问题探究 探究2: 直线与圆锥曲线的位置关系
例 2、 (1)设直线 l :y =kx +1,抛物线 C:y2=4x,当 k 为何值时,l 与 C 相切、相交、相离.
y=kx+1 解析 联立方程组 2 y =4x 整理得 k2x2+(2k-4)x+1=0. 当 k≠0 时,方程 k2x2+(2k-4)x+1=0 为一元二次方程. ∴Δ=(2k-4)2-4k2=16(1-k). ,消去 y,
∵|BC|=6,∴|BM|+|CM|=6. 又∵动圆过点 A,∴|CM|=|AM|,则|BM|+|AM|=6>4. 根据椭圆的定义知,点 M 的轨迹是以点 B(-2,0) 和点 A(2,0)为 焦点的椭圆,其中,2a=6,2c=4,∴a=3,c=2. ∴b2=a2-c2=5. x2 y2 故所求圆心的轨迹方程为 + =1. 9 5
第二章圆锥曲线与方程 章末归纳整合 课件

之间的关系式.
(3)定义法:如果所给几何条件正好符合圆、椭圆、双曲线、抛物线等曲线 的定义,则可直接利用这些已知曲线的方程写出动点的轨迹方程.
(4)参数法:当很难找到形成曲线的动点P(x,y)的坐标x,
y所满足的关系式时,借助第三个变量t,建立t和x,t和y的关 系式x=φ(t),y=φ(t),再通过一些条件消掉t就间接地找到了x 和y所满足的方程,从而求出动点P(x,y)所形成的曲线的普通 方程. (5)交轨法:有些情况下,所求的曲线是由两条动直线的 交点P(x,y)所形成的,既然是动直线,那么这两条直线的方程 就必然含有变动的参数,通过解两直线方程所组成的方程组,
就能将交点P(x,y)的坐标用这些参数表达出来,也就求出了动
点P(x,y)所形成的曲线的参数方程,消掉参数就得到了动点 P(x,y)所形成的曲线的普通方程.
专题三
求曲线的方程
求曲线方程是解析几何的基本问题之一,其基本方法有:
(1)直接法:建立适当的坐标系,设动点为(x,y),根据几何条件直接寻求x、 y之间的关系式. (2)代入法:利用所求曲线上的动点与某一已知曲线上的动点的关系,把所 求动点转换为已知动点.具体地说,就是用所求动点的坐标x、y来表示已知动 点的坐标并代入已知动点满足的曲线的方程,由此即可求得所求动点坐标x、y
【例 1】 如图所示,已知双曲线的焦点 在 x 轴上,离心率为 2,F1,F2 为左、右焦 点.P 为双曲线上一点,且∠F1PF2=60° , S PF1F2 =12 3,求双曲线的标准方程.
x2 y2 解:设双曲线的标准方程为a2-b2=1(a>0,b>0). c ∵ e=a=2,∴ c=2a. 由双曲线的定义有||PF1|-|PF2||=2a=c, 在△ PF1F2 中,由余弦定理,得|F1F2|2=|PF1|2+|PF2|2 -2|PF1||PF2|cos 60° =(|PF1|-|PF2|)2+2|PF1|· |PF2|· (1-cos 60° ), 即 4c2=c2+|PF1||PF2|.① 又 S PF1F2 =12 3 1 所以2|PF1||PF2|sin 60° =12 3,即|PF1||PF2|=48② 由①②得,c2=16,c=4,则 a=2,b2=c2-a2=12. x2 y2 所以所求的双曲线的标准方程为 4 -12=1.
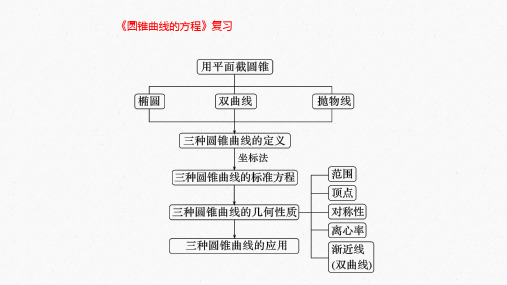
《圆锥曲线的方程》复习
由(1)知,以F1F2为直径的圆的方程为x2+y2=1, ∴圆心到直线 l 的距离 d=2|m5|,
由 d<1 得|m|< 25.
①
∴|CD|=2 1-d2=2
1-45m2=
2 5
5-4m2.
设A(x1,y1),B(x2,y2),
由yx4=2+-y3212=x+1,m,
得 x2-mx+m2-3=0,
由P→D=2M→D,得 x0=x,y0=2y,
因为点P(x0,y0)在圆x2+y2=4上,
所以 x20+y20=4,
(*)
把x0=x,y0=2y代入(*)式,得x2+4y2=4, 所以曲线 C 的方程为x42+y2=1.
(1)应用定义解题时注意圆锥曲线定义中的限制条件. (2)涉及椭圆、双曲线上的点与两个定点构成的三角形问题时,常 用定义结合解三角形的知识来解决. (3)在求有关抛物线的最值问题时,常利用定义把到焦点的距离转 化为到准线的距离,结合几何图形,利用几何意义去解决.
例3 已知椭圆ax22+by22=1(a>b>0)经过点(0, 3),离心率为12,左、右焦点分 别为 F1(-c,0),F2(c,0). (1)求椭圆的方程;
b= 3, 由题设知ac=21,
b2=a2-c2, 解得 a=2,b= 3,c=1,
∴椭圆的方程为x42+y32=1.
(2)若直线 l:y=-12x+m 与椭圆交于 A,B 两点,与以 F1F2 为直径的圆 交于 C,D 两点,且满足||CADB||=543,求直线 l 的方程.
Δ=m2-4(m2-3)=12-3m2>0.
②
由根与系数的关系可得x1+x2=m,x1x2=m2-3.
∴|AB|=
