第3章条件平差原理
附有参数的条件平差

4)按式(8)和式(9)计算参数近似值的改正
数 xˆ 和观测值L的改正数V。
xˆ
N
1 bb
B
T
N aa1W
V
P
1
AT
N
1 aa
(
Bxˆ
W
)
5)计算观测值和参数的平差值。
Lˆ L V , Xˆ X 0 xˆ
6)用平差值重新列平差值条件方程,检核整个 计算的正确性。
QLK QWK Q XˆK QKK QVK QLˆK
QLV QWV Q XˆV QKV QVV QLˆV
QLLˆ QWLˆ
Q XˆLˆ QKLˆ
QVLˆ
QLˆLˆ
Q
L
W
Xˆ
K
V
Lˆ
L
Q
QAT QAT Naa1BQXˆXˆ QA T QKK
QVV
Q QVV
W
AQ
N aa
BQXˆXˆ
解 : 本题n=3 ,t=2,r=n-t=1,又设u=1 ,故条件方
程的总数等于2。 两个平差值条件方程为
lˆ1lˆ2 lˆ3 0 lˆ3 Xˆ 0
将 Lˆi Li vi Xˆ X 0 xˆ,X 0 l3 , 代入以上条件方程,
并将它们线性化,可得
l2v1 l1v 2 v3 l1l2 l3 0 v3 xˆ 0
误差理论与测量平差
附有参数的条件平差
1.平差原理
一般地,附有参数的条件平差的函数模型为:
(1) A V B xˆ W 0
cn n1 cu u1 c1 c1
式中V为观测值L的改正数,xˆ 为参数近似值 X 0 的
改正数。其系数矩阵的秩分别为 rk(A) c, rk(B) u
条件平差原理

§9.1 条件平差原理在条件观测平差中,以n 个观测值的平差值1ˆ⨯n L 作为未知数,列出v 个未知数的条件式,在min =PV V T 情况下,用条件极值的方法求出一组v 值,进而求出平差值。
9.1.1基础方程和它的解设某平差问题,有n 个带有相互独立的正态随机误差的观测值 ,其相应的权阵为 , 它是对角阵,改正数为 ,平差值为 。
当有r 个多余观测时,则平差值 应满足r 个平差值条件方程为:⎪⎪⎭⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0ˆˆˆ221122112211οοοr L r L r L r b L b L b L b a L a L a L a n n n n n n (9-1) 式中i a 、i b 、…i r (i =1、2、…n )——为条件方程的系数;0a 、0b 、…0r ——为条件方程的常项数以ii i v L L +=ˆ(i =1、2、…n )代入(9-1)得条件方程(9-2)式中a w 、b w 、……r w 为条件方程的闭合差,或称为条件方程的不符值,即(9-3) 令⎪⎪⎪⎪⎪⎭⎫⎝⎛=⨯n n n n r r r r b b b a a a A212121⎪⎪⎭⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪⎭⎪⎪⎬⎫=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L ˆˆˆˆ2111⨯n L nn P ⨯1⨯n V 1ˆ⨯n L 1ˆ⨯n L则(9-1)及(9-2)上两式的矩阵表达式为0ˆ0=+A LA (9-4) 0=+W AV (9-5)上改正数条件方程式中V 的解不是唯一的解,根据最小二乘原理,在V 的无穷多组解中,取PV V T = 最小的一组解是唯一的,V 的这一组解,可用拉格朗日乘数法解出。
平差原理和方法的使用与分析

平差原理和方法的使用与分析一、引言平差作为一种测量数据处理的方法,广泛应用于测绘、空间定位、工程测量等领域。
平差的目的是通过处理观测数据,获得更为准确的测量结果。
在实际应用中,平差原理和方法的正确使用与分析将直接影响测量成果的质量。
二、平差原理的理解与应用平差的基本原理是通过最小二乘法,将观测数据的误差最小化。
在平差过程中,需要定义观测量、未知量和条件方程。
观测量是指通过测量得到的待确定的量,未知量是指需要求解的量,而条件方程则是将观测数据与未知量联系起来的等式。
在实际应用中,我们常用的平差方法有最小二乘平差、加权最小二乘平差和限差平差等。
最小二乘平差是指通过最小化观测数据的加权残差平方和,来获得最优的未知量组合。
加权最小二乘平差则是在最小二乘平差的基础上,考虑观测数据的精度权重,以提高平差结果的准确性。
限差平差是将观测数据的精度限制在一定范围内,以排除异常值的影响。
三、平差方法的适用性分析在选择平差方法时,我们需要根据实际情况进行适用性分析。
首先,应考虑观测数据的误差特点,如观测数据是否服从正态分布、是否存在系统误差等。
对于服从正态分布的数据,最小二乘平差是一种较为合适的方法。
对于存在系统误差的数据,可以考虑加权最小二乘平差来降低系统误差对结果的影响。
其次,应考虑观测数据的精度要求,以及所求未知量的敏感度。
如果精度要求较高或者所求未知量对结果较为敏感,可以采用限差平差来排除异常值的影响。
四、平差方法的误差分析在平差过程中,误差分析是至关重要的。
常见的误差包括观测误差、建模误差和未知量的估计误差。
观测误差是指测量仪器、环境等因素引起的误差,可以通过观测数据的重复测量来进行估计。
建模误差则是由于条件方程的建立不完善或者模型假设不准确而导致的误差。
未知量的估计误差是未知量的真值与估计值之间的差异。
误差分析的结果可用于判断平差结果的可靠性。
如果误差分析结果较小,说明平差结果较为可靠;如果误差分析结果较大,则需要重新考虑观测数据的准确性和建模的合理性。
条件平差与间接平差的相互关系

条件平差与间接平差的相互关系
一、条件平差与间接平差
1、条件平差与间接平差是指:条件平差是指基础数据是现有被观
测坐标信息,假定各点位置坐标值满足一定近似关系时(即解算中假
定有约束关系或条件,以达到所求结果的平差方法);而间接平差是指,基础数据是待测点的被观测量,包括方位量、距离量等,无任何
关系的前提条件,是一种完全无条件的平差方法。
二、条件平差
2、条件平差一般会把条件设置为两个系统中坐标值的差值最小,
这样就能够更容易地实现平差。
条件平差的典型应用是重叠法平差,
它会利用各观测值之间的内在联系,并通过设定一定的几何条件,使
其之间被观测量满足某一关系,以解决无条件方程组的平差问题。
三、间接平差
3、间接平差是指以被观测量构成的方程组,可以以各种迭代方法
求解,但是必须有一定的条件限制才能使解出的坐标值符合实际要求。
加拿大匹兹堡大学的Bloch教授认为,从下面几个原因考虑起,最好
用间接平差来解决坐标转换的问题:
(1)传统的解算序号很容易引起原点偏移和比例错误;
(2)间接平差可以很好地表示待解系统中的不确定性;
(3)使用间接平差可以很好地降低待解系统中分量精度和消隐关
系统时发生的偏差。
四、条件平差与间接平差的关系
4、条件平差与间接平差是有联系的,相互之间的联系是:可以把
条件平差看做是一种特殊的间接平差,即在无条件间接平差的基础上,再加入解算中的限制条件,以达到所求结果。
可以说,条件平差是间
接平差的分支,而间接平差是条件平差的总集合。
条件平差的基本原理

v1
V
n ,1
v2
vn
wa F1L1, L2 ,, Ln
wb F2 L1, L2 ,, Ln
wr Fr L1, L2 ,, Ln
则相应方程的矩阵表达式分别为
F Lˆ 0
AV W 0 W FL
3. 基础方程
按求函数极值的拉格朗日乘数法,设乘数
5)求观测值的平差值; Lˆ L V
6)检核。 F (Lˆ) 0
7)检核。
3. 实例分析 例6-1水准网如右图:观测值及其权矩阵如下:
L 0.023 1.114 1.142 0.078 0.099 1.216 T m
P diag1 1 1 2.5 2.5 2.5
求各水准路线的最或然值。
解: 1)列出条件方程
或
v1 v2 v3 v2
0 0 v4 4 0
v1
1 0
1 1
1 0
0 1
v2 vv43
0 4
0 0
令c=1,则由定权公式
,有 pi
C Si
1 Si
P 1
1 p1
0
0
0
0
1 p2
0
0
0
0
1 p3
0
0 s1 0 0 0 2 0 0 0
0 0
0 0
1 p4
0
K
r ,1
ka
kb
kr T
,称为联系数向量。组成函数
V T PV 2K T AV W
将 φ 对V 求一阶导数,并令其为零,得
d dV
2V T P
2KT
A
0
两边转置,得
《测量平差》学习辅导

《测量平差》学习辅导第一章测量平差及其传播定律一、学习要点(一)内容:测量误差的概念、测量误差来源、分类;偶然误差概率特性;各种精度指标;真误差定义;协方差传播律;权与定权的常用方法;协因数传播律;权逆阵及其传播规律。
(二)基本要求:1.了解测量平差研究的对象和内容;2.掌握偶然误差的四个概率特性;3.了解精度指标与误差传播偶然误差的规律;4.了解权的定义与常用的定权方法;5.掌握协方差传播率。
(三)重点:偶然误差的规律性,协方差、协因数的概念、传播律及应用;权的概念及定权的常用方法。
(四)难点:协方差、协因数传播率二、复习题(一)名词解释1.偶然误差2.系统误差3.精度4.单位权中误差(二)问答题1.偶然误差有哪几个概率特性?2.权是怎样定义的,常用的定权方法有哪些?(三)计算题σ的量测中误差1.在1:500的图上,量得某两点间的距离d=23.4mm,dσ。
σ=±0.2mm,求该两点实地距离S及中误差s三、复习题参考答案 (一)名词解释1.偶然误差:在一定条件下做一系列的观测,如果观测误差从表面上看其数值和符号不存在任何确定的规律性,但就大量误差总体而言,具有统计性的规律,这种误差称为偶然误差。
2.系统误差:在一定条件下做一系列的观测,如果观测的误差在大小、符号上表现出系统性,或者为某一常数,或者按照一定的规律变化,这种带有系统性和方向性的误差称为系统误差。
3.精度:表示同一量的重复观测值之间密集或吻合的程度,即各种观测结果与其中数的接近程度。
4.单位权中误差:权等于1的中误差称为单位权中误差。
(二)问答题1.答:有四个概率特性:①在一定观测条件下,误差的绝对值有一定的限值,或者说超出一定限值的误差出现的概率为零;②绝对值较小的误差比绝对值较大的误差出现的概率大;③绝对值相等的正负误差出现的概率相同;④偶然误差的数学期望为零。
2.答:设i L (i=1,2,3,…,n ),他们的方差为2i σ,如选定任一常数0σ,则定义:22ip σσ=,称为观测值L i 的权。
第3讲(三角网条件平差

第三章 条件平差
第四节
二、条件方程的列立 条件方程的种类:图形条件(内角和条件)、水平条件(圆周条件)、极条件、 条件方程的种类:图形条件(内角和条件)、水平条件(圆周条件)、极条件、 )、水平条件 )、极条件 方位角条件、边长条件、坐标条件。 方位角条件、边长条件、坐标条件。 1. 图形条件(n=15 图形条件(n=15 t=8 r=7 哪7个?) 每个三角形内角平差值和等于180 每个三角形内角平差值和等于180
sin L1 sin L4 sin L7 sin L10 sin L13 sin L1 sin L4 sin L7 sin L10 sin L13 v v cot L1 1 − cot L2 2 sin L2 sin L5 sin L8 sin L11 sin L14 ρ ′′ sin L2 sin L5 sin L8 sin L11 sin L14 ρ ′′
第三章 条件平差
第四节
三角网平差的目的 求待定点平面坐标平差值, 求待定点平面坐标平差值,并进行精度 评定。 评定。 三角网件方程个数等于多余观测个数。 条件方程个数等于多余观测个数。
r=nr=n-t
测角网、测边网、边角同测网。无 关键在于确定必要观测个数 t 。 测角网、测边网、边角同测网。 论网型多么复杂, 论网型多么复杂,都是由三角形和 大地四边形相互邻接或重叠而组成。 当网中有2个或2 大地四边形相互邻接或重叠而组成。 1.当网中有2个或2个以上已知点时 t=2 t=2倍待定点数 当网中仅具备4个必要起算数据( 当网中仅具备4个必要起算数据(一点 坐标、一条边的方位、 坐标、一条边的方位、一条边的边 2.当网中少于2个已知点时 当网中少于2 长或已知两点坐标) 称为自由 长或已知两点坐标)时,称为自由 这四个数据成为必要起算数据。 网。这四个数据成为必要起算数据。 (1)测角网 t=2倍总点数t=2倍总点数-4 多余四个必要起算数据时,成为非自由 多余四个必要起算数据时,成为非自由 网。 (2)测边或边角网 t=2倍总点数t=2倍总点数-3
条件平差

得法方程: AQATK-W=0 T 1 T N AQA AP A 令 aa r .r r .nn.nn.r 则有: NaaK-W=0
法方程系数阵Naa是一个r阶的满秩方阵,且可逆
N11k1 N12k 2 N1r k r W1 0 N 21k1 N 22k 2 N 2 r k r W2 0 N r1k1 N r 2 k 2 N rn k r Wr 0
目标函数:f x min n1 x a h x min F a , x f 1k 约束条件: h x 0 k 1 n1 F a, x
0 a F a, x 0 x
L2
L4 L1 L3 L2
A
B
C
§6-2 条件方程
条件方程的个数等于多余观测数r。条件方程之间 不能线性相关,在一个平差问题中,条件方程的个 数是固定不变的.
一、r的确定: r=n-t 二、条件方程的列立: 原则:足数(r个),线性无关,形式简单,易 于列立
控制网常见几何模型
水准网 三角网(测角网) 三边网(测边网) GPS基线向量网 单一附合导线
由此可得联系数K的解:
r ,1
K ( AQA ) W
T
T 1
V QA K
条件平差的 最小二乘解:
n,1
ˆ L V L
三、条件平差计算步骤:
1.根据平差问题的具体情况,列出条件方程,条 件方程的个数等于多余观测数r。 2.组成法方程式,法方程的个数等于多余观测数r 3.解法方程,求出联系数K值。 4.将K代入改正数方程式,求出V值,并求出观测 值的平差值=L+V。 5.检验平差计算的正确性(可用平差值重新列出 平差值条件方程式,看其是否满足方程)。
第三章条件平差
独立三角网
自由三角网
自由测角网
附合三角网(测角)
• 例:
∆ቤተ መጻሕፍቲ ባይዱ
α ∆
当n=35、n=22、n=35+22时,其条件式个数各为多 少?有哪些类型?
图形条件(内角和条件):
B
b1
a2
c1 D c2 a1 b3 c3 a3 b2 C
A
圆周条件(水平条件):
b1
a2
c1 a1 a3 c3
c2 b2 b3
5.1.06、 5.1.07
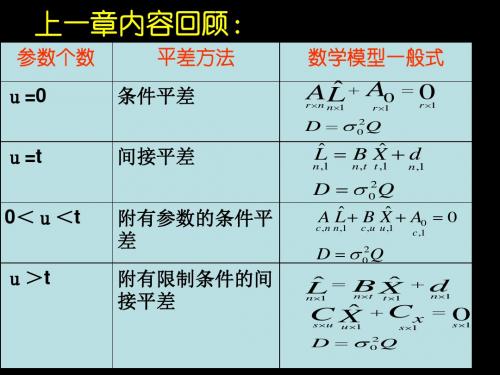
上节内容回顾:
改正数条件式 观测值的协方差阵 法方程
AV W 0
D P Q
2 0 1 2 0
r n n n
Naa K W 0 N aa AQ AT
r r n r
改正数方程
V P A K QA K
T
1 T
wr
T
• 则条件方程可写成:
ˆA 0 AL 0
• 以及改正数条件式:
W AL A0
AV W 0
这样一来,对于一个平差问题,我们能够得到 其数学模型:
AV W 0 D P Q
2 0 1 2 0
下面要解决的问题是: 由上述的数学模型来求改正数V。
不难发现,不能求得V的唯一解!!! 解决不唯一解的办法就是附加一个约束条件---“最小二乘估计” 即满足:
极条件(边长条件):
b1 a2
c1
a1 b3 c3
c2 b2 a3
极条件(边长条件)就是指由不同路线推算得到 的同一边长的长度应相等。
三角网的基本图形 1) 单三角形 2)大地四边形
3)中点多边形。
1-1条件平差原理--求取最或是值

V P 1 AT K
Lˆ L V
理论
感谢聆听,批评指导
公式
思考
平差
算例
转置
PTV AT K
两边左乘权逆阵P–1 V P 1 AT K
条件平差的平差值求取原理(第一任务)
2.基础方程
3.法方程
条件平差的基础方程
AV W 0
令
V P 1 AT K
构法方程
将改正数方程带入条件方程,得
AP 1 AT K W 0
令令
N aa AP 1 AT
1.条件方程
纯量形式
ab11LLˆˆ11 ab22LLˆˆ22 bannLLˆˆnnba0000 r1Lˆ1 r2Lˆ2 rnLˆn r0 0
带入
Lˆi Li vi
令
ALˆ A0 0
平差值条件方程
条件平差是经典平差的重要方法之一,其实质是观测值的改正数在满足一定条 件下,求改正数带权平方和的极值问题,可采用拉格朗日乘任务)
1.条件方程
设在某个测量几何模型中,必要观测数为 t ,观测了 n 个只含偶然误差的独立观测值 ,相应的权为 p1、p2、...、pn ,改正数 v1、v2、...、vn 、平差值 Lˆ1、Lˆ2、、Lˆn 。
将它们用向量(矩阵)表示为:
L1
L
L2
n,1
Ln
v1
V
v2
n,1
vn
p1
P
n,n
0
0
0 0
p2
0
第三章 条件平差

返回目录 返回本节
经化简即有
cv t c g v ta c gv t a c g v t a c g v t b c g v tb g b
1 a 1
2 a 2
3 a 3
1 b 1
2 b 1
33
(1
sina1 sinb1
sina2 sinb2
sina3)
sinb3
=0,
圆周条件,即
c ˆ1c ˆ2c ˆ336 o0
或
V V V W 0
c1
c2
c3
4
第三类是极条件或称边长条件。满足上述4个条件方程
的角值还不能使图3-5的几何图形完全闭合,例如,由边
长通过a2、b2、c2计算边长,通过a1、b1、c1由计算边长,
再由通过a3、b3、c3计算边长,计算的结果,其边长不会
(3-21)
这就是极条件(3-20)的线性形式。
三、测边网
和测角同一样,在测边网中也可分解为三角形,大地 四边形和中点多边形三种基本图形。对于测边三角形,决 定其形状和大小的必要观测为三条边长。所以t=3,此时 r=n-t=3-3=0,即测边三角形不存在的条件方程。对于测边 四边形,决定第一个三角形必须观测3条边长,决定第二 个三角形只需要再增加2条边长,所以确定一个四边形的 图形,必须观测5条边长,即t=5,所以r=n-t=6-5=1,存在 一个条件方程。对于中点多边形,例如中点五边形,它由 四个独立三角形组成,此t=3+2×3=9,故有r=n-t=10-9=1。
法,将上式用台劳公式展开取至次项,即可得线性形式的
极条件方程。
将 a ˆ a v,b ˆ b v,c ˆ c v代入(3-20)式,
测量平差复习题

《测量平差》复习题第一章:绪论1、什么是观测量的真值任何观测量,客观上总存在一个能反映其真正大小的数值,这个数值称为观测量的真值。
2、什么是观测误差观测量的真值与观测值的差称为观测误差。
3、什么是观测条件仪器误差、观测者和外界环境的综合影响称为观测条件。
4、根据误差对观测结果的影响,观测误差可分为哪几类根据误差对观测结果的影响,观测误差可分为系统误差和偶然误差两类。
5、在测量中产生误差是不可避免的,即误差存在于整个观测过程,称为误差公理。
6、观测条件与观测质量之间的关系是什么观测条件好,观测质量就高,观测条件差,观测质量就低。
7、怎样消除或削弱系统误差的影响一是在观测过程中采取一定的措施;二是在观测结果中加入改正数。
8、测量平差的任务是什么⑴求观测值的最或是值(平差值);⑵评定观测值及平差值的精度。
第二章:误差理论与平差原则1、描述偶然误差分布常用的三种方法是什么⑴列表法;⑵绘图法;⑶密度函数法。
2、偶然误差具有哪些统计特性(1) 有界性:在一定的观测条件下,误差的绝对值不会超过一定的限值。
(2) 聚中性:绝对值较小的误差比绝对值较大的误差出现的概率要大。
(3) 对称性:绝对值相等的正负误差出现的概率相等。
(4) 抵偿性:偶然误差的数学期望或偶然误差的算术平均值的极限值为0。
3、由偶然误差特性引出的两个测量依据是什么⑴制定测量限差的依据;⑵判断系统误差(粗差)的依据。
4、什么叫精度精度指的是误差分布的密集或离散的程度。
5、观测量的精度指标有哪些(1) 方差与中误差;(2) 极限误差;(3) 相对误差。
6、极限误差是怎样定义的在一定条件下,偶然误差不会超过一个界值,这个界值就是极限误差。
通常取三倍中误差为极限误差。
当观测要求较严时,也可取两倍中误差为极限误差。
7、误差传播律是用来解决什么问题的误差传播律是用来求观测值函数的中误差。
8、应用误差传播律的实际步骤是什么(1) 根据具体测量问题,分析写出函数表达式;(2) 根据函数表达式写出真误差关系式;(3) 将真误差关系式转换成中误差关系式。
第03章 条件平差

zqz99@
设观测值的权阵P为n×n的对角阵,又设联系
数矩阵K=(ka,kb,…,kr)T,则式(3-11)可用矩阵表 示为: Φ=VTPV-2KT(AV+W) 为求新函数Φ的极值,对上式的变量V求其一阶
偏导数,并令其为零。即
d d (V T PV ) d ( 2 K T ( AV W )) dV dV dV
zqz99@
2.1条件平差概述
在图3-1中,设HA为A点的已知高程,为了确定B、C 两点的高程,只要观测两个高差就够了,即必要观测数 为t=2,而图中按箭头方向观测了h1、h2、h3三个高差, 则n=3,因为有了多余观测(r=1),所以三个观测高差的 平差值产生了一个条件,即 ˆ h ˆ h ˆ 0 h
zqz99@
zqz99@
zqz99@
zqz99@
条 件 制约和影响事物存在、发展的
外部因素
zqz99@
第三章
1
2 3 4 5 6
条件平差
§1 条件平差原理
§2 必要观测与多余观测 §3 条件方程 §4 条件平差方程式 §5 条件平差的精度评定 §6 条件平差举例
式(3-13)称为改正数方程
vi
1 (ai ka bi kb ri kr ) pi
(3-13)
zqz99@
若多余观测为2, 即条件方程只有2个, 改正数方程为:
若多余观测为3, 即条件方程只有3个, 改正数方程为:
vi
v1
1 (ai ka bi kb ) pi
vi
v1
1 (ai ka bi kb ci kc ) pi
1 (a1ka b1kb ) p1 1 v2 (a2 ka b2 kb ) p2 1 vn (an ka bn kb ) pn
课件:第3章第1讲(条件平差原理)

ALˆ A0 0
AV W 0
(2)组成法方程; NK W 0
N AP1AT
(3)计算联系数K; K N 1W
三、解题步骤
(4)计算观测值改正数V ;
V P1 AT K
(5)计算观测值的平差值;
Lˆ L V
(6)检查平差计算的正确性,将平差值代入平差值 条件方程式,检验是否满足方程关系;
法方程的解: K N 1W
平差值: Lˆ L V
aa p
k
a
ab p
k
b
ar p
k
r
wa
0
apbk
a
bb
p
kb
br p
k
r
wb
0
ar
p
ka
br p
k
b
rr
p
kr
wr
0
二、精度评定
1. 单位权中误差的计算
ˆ 0
V T PV r
b0
0
a1v1 a2v2 anvn wa 0 b1v1 b2v2 bnvnwb0 r1v1 r2v2 rnvn wr 0
r1 Lˆ1
r2 Lˆ2
rn Lˆn
r0
0
wa (a1L1 a2 L2 an Ln a0 )
wb (b1L1 b2 L2 bn Ln b0
函数模型
W (AL A0 )
一、条件平差原理
AV W 0 按求函数极值的拉格朗日乘数法组成新函数
V T PV 2K T (AV W) 将Φ对V求导并令一阶导数为零:
K为乘系数(联系数)
K
r ,1
[ka
kb
kr ]T
d (V T PV) 2 (K T AV) 2V T P 2K T A 0
条件平差

1
线性化,并经整理后得
[ctga1 ctg(a1 b1 )]va1 ctg(a1 b1 )vb1 ctga2va2 ctgb2vb2 ctg(a3 b3 )va3 [ctg(a3 b3 ) ctgb3 ]vb3 w 0
w (1 sin(a1 b1 ) sin b2 sin b3 )
主要内容
第一节 条件平差原理 第二节 条件方程 第三节 精度评定 第四节 水准网平差示例
第1页/共37页
第一节 条件平差原理 ( ) 介绍条件平差原理,给出计算公式
一、基础方程及其解
设有r个观测值平差值线性条件方程:
ALˆ A 0 a1Lˆ1
a2 Lˆ2
...Βιβλιοθήκη an Lˆna00
b1Lˆ1 b2 Lˆ2 ... bn Lˆn b0 0( 4-1-5),矩阵形式为:
...
sin a1 sin a2 sin b1 sin b2
sin a3 sin b3
ctgb3
vb3
0
ctga1va1
...
ctga3va3
ctgb1vb1
... ctgb3vb3
(1 sin a1 sin a2 sin a3 ) 0
sin b1 sin b2 sin b3 第21页/共37页
..................................
0
r1Lˆ1 r2 Lˆ2 ... rn Lˆn r0
0
注意:第一个条件方程系数到最后一个条件方程系数分别 采用字母a-r,下标与观测值编号对应。r是最后一个条件方 程的编号,表示条件方程个数为r,但是r数目与r在英文字 母中序号无关。
求其一阶偏导数,并令其为0:
条件平差公式

条件平差公式
条件平差公式是一种用于对多个测量值进行分析和校正的数学方法。
其基本原理是,将所有测量值组成一个方程组,其中每个方程表示一个测量量与其他测量量之间的关系。
通过求解这个方程组,可以得到每个测量值的最优估计值和方差。
具体地说,条件平差公式可以分为两类:一类是基于观测方程的条件平差公式,另一类是基于误差方程的条件平差公式。
观测方程的条件平差公式是指,将所有测量值表示为观测方程的形式,然后通过最小二乘法求解得到最优估计值和方差。
观测方程通常表示为线性方程组的形式,即y=AX+e,其中y表示观测值,A表示系数矩阵,X表示未知数向量,e表示误差向量。
误差方程的条件平差公式是指,将所有误差表示为误差方程的形式,然后通过最小二乘法求解得到最优估计值和方差。
误差方程通常表示为非线性方程组的形式,即f(X)=e,其中f表示误差函数,X表示未知数向量,e表示误差向量。
无论是基于观测方程还是基于误差方程的条件平差公式,都具有很强的实用性和广泛的应用范围。
它们可以用于地理测量、航空测量、工程测量等领域,对于提高测量精度和减小误差具有重要意义。
- 1 -。
第9讲第三章条件平差-条件方程2pdf

如图平面三角网,其中 A、B、C 为已知点,P 为未知点,观测值为 cotL1v1 cotL3v3 cotL4v4 cotL6v6 w极 0 ,观测 各内角 Li ( i 1,2, ,6 )
(3)固定边条件一个
ˆ ,L ˆ L v , 值的平差值为 L i i i i
20
C 75
(2)圆周条件(水平条件) 圆周条件的个数等于中心点的条数。
9 3 6 D 4 2 B
ˆ L ˆ L ˆ 3600 0 L 3 6 9
A
8 1
ˆ L v 代入: 将L i i i L3 v 3 L6 v 6 L9 v 9 3600 0
v3 v6 v9 w4 0,w4 L3 L6 L9 3600
17
二、条件方程的形式
例 1:在右图所示的水准网中(箭头指 向高端) ,设观测高差为 h1 , h2 , h3 , h4 , h5 ,高 ˆ ,h ˆ ,h ˆ ,h ˆ ,h ˆ ,列出最或 差的最或然值为 h 1 2 3 4 5 然值及改正数应满足的条件关系式。
ˆ h ˆ ˆ h h 0 1 2 4 ˆ h ˆ ˆ 0 h h 2 3 5
28
观测值独立时
N AP 1 AT
C 75 6 D 3 A 8 1 4 2 B
n=9 t=4 r=n-t=9-4=5
9
19
(1)图形条件(内角和条件) 独立图形条件的个数等于互不重叠的三角形个数再加实 对角线的条数。
ˆ L ˆ L ˆ 180 0 0 ABD : L 1 2 3 ˆ L ˆ L ˆ 180 0 0 BCD : L 4 5 6 ˆ L ˆ L ˆ 180 0 0 ACD : L 7 8 9
第3章条件平差原理

v1 v2 v3 v4
573233
730305
1265125
1043317
推导如下:
VTPV VTP(P1ATK) VTATK(AV )TKWTK
纯量形式
20.09.2019 4
第三章 条件平差
第一节 条件平差原理
二、精度评定
则上述方程可表示为:
2. L、 W 、 K 、 V、 L ˆ的协因数阵及互 协因数阵
LL
W (A L A 0) A L A 0
DFFˆ02QFF
函数的方差
为了检查平差计算的正确性,可以将平差值代入平差值条件方程式,看是否满足 方程关系。
20.09.2019 10
第三章 条件平差
第一节 条件平差原理
[例3-1] n=4 t=3 r=1
A 1 P A TKW 0
p1
1
P
p2
1
n,n
Lˆ
n ,1
Lˆ Lˆ
1 2
Lˆ
n
L LV
n,1 n,1 n,1
Lˆ Lˆ
1 2
L1
பைடு நூலகம்
L
2
v1
v
2
Lˆ
n
L
n
vn
p1 P n,n
p2
kb
rr
(整理)测量平差中条件方程的建立

§3-4 三角网条件平差计算2学时三角网测量的目的,是通过观测三角形的各角度或边长,计算三角网中各未知点的坐标、边的长度及方位角等。
三角网按条件平差计算时,首要的问题是列出条件方程。
因此了解三角网的构成,总结其条件方程的种类及各种条件方程的组成规律是十分重要的。
三角网的种类比较多,网的布设形式也比较复杂。
根据观测内容的不同,有测角网、测边网、边角同测网等;根据网中起始数据的多少,有自由三角网和非自由三角网。
自由三角网是指仅具有必要起算数据的三角网,网中没有多余的已知数据。
如果测角三角网中,只有两个已知点(或者已知一个已知点的坐标、一条已知边的长度和一个已知的方位角),根据数学理论,以这两个已知点为起算数据,再结合必要的角度测量值,就能够解算出网中所有未知点的坐标。
如果三角网中除了必要的起算数据外还有其它的已知数据,或者说已知数据有冗余,就会增加对网形的约束,从而增强其可靠性,这种三角网称之为非自由三角网。
无论多么复杂的三角网,都是由单三角形、大地四边形和中点多边形组合而成的。
在本节,我们先讨论三角网条件平差中条件方程个数的确定问题,然后主要讨论测角三角网的条件方程的形式问题。
一、网中条件方程的个数三角网平差的目的,是要确定三角点在平面坐标系中的坐标最或然值。
如图3-9所示,根据前面学到的测量基础知识,我们知道,必须事先知道三角网中的四个数据,如两个三角点的4个坐标值,或者一个三角点的2个坐标值、一条边的长度和一个方位角,这4个已知数据我们称之为三角网的必要起算数据。
有了必要起算数据,就可以确定三角网在平面坐标系中的位置、网的大小及其方位,就可以计算三角网中未知点的坐标。
要对三角网进行平差计算,还必须先知道网中的总观测数n、判定必要观测数t,从而确定了多余观测数:r = n - t由条件平差原理知,多余观测数与条件方程数是相等的,有了多余观测数,也就确定出了条件方程的个数。
因此,问题的关键是判定必要观测数t。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A矩阵存在逆矩阵的充分必要条件 矩阵存在逆矩阵的充分必要条件 是A的行列式不等于0,称A为非奇 的行列式不等于 , 为非奇 异矩阵,否则为奇异矩阵。 异矩阵,否则为奇异矩阵。
2012-4-24
4
第三章 条件平差
复习知识
矩阵求逆方法 (1)伴随矩阵法: 伴随矩阵法: 设Aij为A的第i行j列元素aij的代数余 的第i 列元素a 子式,A的伴随矩阵A*为 子式, 的伴随矩阵A (2)初等变换法: 初等变换法:
OA = AO = O IA = AI = A A(B + C) = AB + AC ABC = A(BC)
2012-4-24
2
第三章 条件平差
复习知识
三、矩阵的转置 对于任意矩阵C 对于任意矩阵Cmn: 矩阵的转置的性质如下: 矩阵的转置的性质如下:
(4) (kA)T = kAT 将其行列互换,得到一个n*m阶矩阵, 阶矩阵, 将其行列互换,得到一个 阶矩阵
2012-4-24
9
第三章 条件平差
第一节
条件平差的数学模型为 函数模型: 函数模型: AV −W = 0
2 2 −1 随机模型: D 随机模型: n,n = σ 0 Q = σ 0 P,n n n,n
条件平差原理
L1 L L = 2 n ,1 M Ln
条件平差就是在满足 条件平差就是在满足r个条件方程 , , , 条件下,求解满足最小二乘法(V 条件下,求解满足最小二乘法( TPV = min)的V值,在数学中就是 min) 求函数的条件极值问题。 求函数的条件极值问题。 条件方程 一、条件平差原理
第三章 条件平差
复习知识
一、矩阵的定义及其某些特殊矩阵 (2) 若m=n,即行数与列数相同,称A ,即行数与列数相同, 为方阵。元素a 为方阵。元素 11、a22……,ann, , (1)由个数有个数排列成 行n列的表 个数有个数排列成m行 列的表 m×n个数排列成 称为主对角元素。 称为主对角元素。 叫矩阵,通常用一个大写字母表示, 叫矩阵,通常用一个大写字母表示, (3)若一个矩阵的元素全为 称零矩阵, 若一个矩阵的元素全为0, (3)若一个矩阵的元素全为 ,称零矩阵, 如: 一般用O表示 表示。 一般用 表示。
1× n
n× n n×1
A x ,式中 T, 式中A=A
2012-4-24
8
第三章 条件平差
补充知识
九、函数对向量的微分 m元函数向量对于 维向量 x的微分有 元函数向量对于n维向量 元函数向量对于 如下性质:(以下 为常数向量,F,G 如下性质: 以下C为常数向量, , 以下 为常数向量 为函数向量) 为函数向量 (1) dC = 0 (5 ) (4)当A为常数矩阵时 为常数矩阵时
复习知识
七、幂等矩阵 定义: 定义:称满足条件 为幂等矩阵。 为幂等矩阵。 幂等矩阵有下述重要性质: 幂等矩阵有下述重要性质: (1) 幂等矩阵 的特征值为 或1。 幂等矩阵A的特征值为 的特征值为0或 。 (2) 幂等矩阵A的秩,等于它的迹,即 幂等矩阵A的秩 等于它的迹, 的秩, R(A)=tr(A) (3) 若方阵A为R(A)=r的幂等矩阵 则E- A 若方阵 为 的幂等矩阵,则 的幂等矩阵 也为幂等矩阵, 也为幂等矩阵,且R(E-A)=n-r A2=A*A=A 八、二次型和正定阵
1 * 1 A = A = A* A det( A)
a11 a 21 L an1
0 a22 L a2n M 0 1 L L LML L an2 L ann M 0 0
a12 L a1n M 1
L L L L
0 0 L 1
2012-4-24
5
第三章 条件平差
复习知识
f 的方阵A 定义: ( x) = x 定义: 的方阵
T
上式称为二次型,A称为二次型矩阵。 上式称为二次型, 称为二次型矩阵。 称为二次型矩阵 若对于任意x≠0 若对于任意 称二次型是正定的, (1)xTAx>0 , 称二次型是正定的, ) A为正定矩阵,记为A A为正定矩阵,记为A>0 为正定矩阵 称二次型是半正定的, (2)xTAx≥0, 称二次型是半正定的, ) A为半正定矩阵,记为A≥0 为半正定矩阵,记为 为半正定矩阵 称二次型是负定的, (3)xTAx<0, 称二次型是负定的, ) A称为负定矩阵,记为A<0 称为负定矩阵,记为 称为负定矩阵 称二次型是半负定的, (4)xTAx≤0,称二次型是半负定的, ) 称二次型是半负定的 A称为半负定矩阵,记为A≤0 称为半负定矩阵,记为 称为半负定矩阵
d ( AF ) dF =A dx dx
dx
dF dG (F + G) = + dx dx dx T (3)d T d T T dG T dF 当A=A 时, (F G) = (G F) = F +G d ( xT Ax) dx dx dx dx = 2 xT A dx
(2 ) d
d ( xT Ax) T d T dx =x ( Ax) + ( Ax) dx dx dx = xT A + xT AT = xT ( A + AT )
b11 b A−1 = 21 n×n L bn1
b12 L b1n b22 L b2n L L L bn2 L bnn
R ( AB ) ≤ min { R( A), R ( B)}
2012-4-24
6
第三章 条件平差
复习知识
五、矩阵的迹 定义:方阵A 定义:方阵A的主对角元素之和称 为该方阵的迹,记为 为该方阵的迹, 六、满秩矩阵 定义: 阶方阵A的秩 定义:若n阶方阵 的秩 阶方阵 的秩R(A)=n,则称 , A为满秩方阵。若m*n阶矩阵 的秩 为满秩方阵。 阶矩阵A的秩 为满秩方阵 阶矩阵 R(A)=m,称A为行满秩阵;若R(A)=n, 为行满秩阵; 为行满秩阵 , 则称A为列满秩阵。 则称 为列满秩阵。 为列满秩阵 对于任意一m*n阶矩阵A, R(A)=r, 对于任意一m*n阶矩阵A,若R(A)=r, 阶矩阵 则A可分解为 可分解为
v1 v 2 V = n ,1 M v n
ˆ L1 ˆ L ˆ L = 2 n ,1 M ˆ Ln
n ,1
L = L+V
n ,1
n ,1
p1 ˆ L1 L1 + v1 ˆ L2 + v 2 P = L2 = M M n ,n ˆ Ln + v n Ln
m×n
tr ( A) = ∑ aii
i =1
n
对于矩阵的迹有下面的性质: 对于矩阵的迹有下面的性质: tr (AT)=tr (A) tr (A+B)=tr (A)+tr (B) tr (kA)=k tr (A) tr (AB)=tr (BA)
A = R⋅ S
m×r r ×n
2012-4-24
7
第三章 条件平差
p2
O pn
L 有n个观测值 n ,1 ,均含有相互独立 P 的偶然误差, 的偶然误差,相应的权阵为 n , n , L 改正数为 V1 ,平差值为 nˆ1 ,用 n, , 矩阵表示为: 矩阵表示为:
2012-4-24
必要 观测 数t, 多余 观测 数为r 数为r r=nr=n-t
(1) ( AB) = B A
(2) ( A−1)−1 = A (3) (I )−1 = I
−1
−1
−1
B= A
−1
(4) ( AT )−1 = ( A−1)T
(5) 对称矩阵的逆仍为对称矩阵。
(6) 对角矩阵的逆仍为对角矩阵且: A−1 = (diag(a11, a22 ,Lann ))−1 = diag( 1 1 1 , L ) a11 a22 ann
10
第三章 条件平差
第一节
改正数方程: 改正数方程:
条件平差原理
a1 b A= 1 r ,n L r1 a2 b2 L r2 L L L L an wa bn W = wb L r ,1 M rn wr
a 0 b A0 = 0 M r ,1 r0
a11 a12 a a22 21 A= m×n L L am1 am2
L a1n L a2n L L L amn
(4)对于 的方阵, (4)对于 n× n 的方阵,除主对角元素 外,其它全为零,称为对角矩阵。 其它全为零,称为对角矩阵。 如:
a11 0 0 a 22 A = m×n L L 0 0 L 0 L 0 L L L amn
(2)初等变换法: 初等变换法: 四、矩阵的秩
1 0 ቤተ መጻሕፍቲ ባይዱ L 0
则:
0 L 0 Mb11 1 L 0 Mb21 L L LL M 0 L 1 Mbn1
b12 L b1n b22 L b2n L L L bn2 L bnn
定义:矩阵A的最大线性无关的行( 定义:矩阵A的最大线性无关的行( 列)向量的个数r,称为矩阵A的行( 向量的个数r 称为矩阵A的行( 列)秩。由于矩阵的行秩等于列秩, 由于矩阵的行秩等于列秩, 故统称为矩阵的秩,记为R(A)。对 故统称为矩阵的秩,记为R(A)。 于矩阵的秩有性质: 于矩阵的秩有性质:
= diag(a11, a22 ,Lann )
2012-4-24 1
第三章 条件平差
复习知识
(5)对于对角阵, (5)对于对角阵,若a11=a22=……=ann =1, 对于对角阵 , 称为单位阵,一般用 、 表示 表示。 称为单位阵,一般用E、I表示。 则称A为对称矩阵。 (6)若aij=aji,则称A为对称矩阵。 二、矩阵的运算 (1)若具有相同行列数的两矩阵各对 应元素相同, 应元素相同,则: (2)具有相同行列数的两矩阵A、B相 具有相同行列数的两矩阵 、 相 A= B 加减,其行列数与 、 相同 相同, 加减,其行列数与A、B相同,其元 素等于A 对应元素之和、 素等于 、B对应元素之和、差。 对应元素之和 且具有可交换性与可结合性。 且具有可交换性与可结合性。 (3) 设A为m*s的矩阵,B为s*n的矩阵 为 的矩阵, 为 的矩阵, 的矩阵 的矩阵 相乘才有意义, 则A、B相乘才有意义,C=AB,C 、 相乘才有意义 , 的阶数为m*n。 。 的阶数为
