大学物理第四章静电场中的电介质
合集下载
静电场中的导体和电解质
Q + + + + ++ + + + + E= 0 S+ + + + + + + + ++
Q q + + + +++ + +-q + + - E= 0 S + 结论: 电荷分布在导体外表面, 导体 + q + + 内部和内表面没净电荷. + - - + + + + ++ 腔内有电荷q: E 0 q 0
i
结论: 电荷分布在导体内外两个表面,内表面感应电荷为-q. 外表面感应电荷为Q+q.
NIZQ
第 5页
大学物理学 静电场中的导体和电介质
结论: 在静电平衡下,导体所带的电荷只能分布在导体的 表面,导体内部没有净电荷. • 静电屏蔽 一个接地的空腔导体可以隔离内 外电场的影响. 1. 空腔导体, 腔内没有电荷 空腔导体起到屏蔽外电场的作用. 2. 空腔导体,腔内存在电荷 接地的空腔导 体可以屏蔽内、 外电场的影响.
NIZQ
第 3页
大学物理学 静电场中的导体和电介质
• 静电平衡时导体中的电场特性
E内 0
场强:
ΔVab
b
a
E dl 0
• 导体内部场强处处为零 E内 0 • 表面场强垂直于导体表面 E表面 // dS
• 导体为一等势体 V 常量 • 导体表面是一个等势面
S
0 E P dS qi
大学物理(6.2.1)--静电场中的电介质
d r
P
E
0 - -+- -+- -+- -+- -+-
E E0 0 r 0 r
'
(1
1 r
)
0
,
电极化率
10/13
电介质的击穿
理想电介质中没有自由电荷，但是实际的电 介质中总是存在一定的自由电荷。可以在电场作用 下产生微弱的电流。
加在电介质上的电场强度足够大时，电介质 中的电流迅速增加，其绝缘性能被破坏，甚至电介 质可能被烧毁。这叫电介质的击穿。
热释电性：温度的变化 表面产生极化电荷
电光效应：施加电场 晶体折射率发生变化
重要应用领域：
微电子学技术、超声波技术、电子光学、激光技术 、
新材料等
3/13
※ 电介质对电场的影响
( 电介质放在电场中）
U 0 E0
+
-
+
-
+
-
+
-
+
-
+
-
+
-
σ σ
电场
U E
+++++++
- - -εr- - - -
)
0
,
Q'
εr εr
1
Q0
9/13
※ 电极化强度与电场强度的关系
充满 r 的各向同性均匀电介质的平行板电容器
P
σ
'
r 1 r
0
,
P ( r 1)0E
P (r 1)0E
大学物理 电介质
电介质的种类和状态的不同而不同
χ = εr − 1 电极化率
令 ε r = (1 + χ e ) 为相对介电常量（相对电容率）
ε = ε 0ε r ～电介质的电容率
5
四、极化电荷与自由电荷的关系
E
=
E0
−
E'=
E0 εr
E'=
εr − 1 εr
E0
d
σ'=
εr − εr
1
σ
0
Q' =
εr − εr
即 D⇒ E ⇒ P ⇒σ′ ⇒q′
9
物理意义
E
单位试验电荷 的受力
单位体积内的 P 电偶极矩的矢
量和 无物理意义， D 只有一个数学 上的定义 D = ε0E + P
= ε 0ε r E
特点
真空中关于电场的讨论都 适用于电介质：高斯定律、 电势的定义、环路定理等
各向同性均匀电介质中
P = ε0χe E ，表面束缚电荷 σ ′ = P ⋅ n ，电介质中P ≠ 0
D = (1+ χ )ε0E
ε r = (1 + χ )
ε = ε rε 0
相对电容率或相对介电常量
电容率或介电常量
D＝ε0ε r E = εE
•注意： D 是辅助矢量，描写电场性质的物理量仍为 E ,V
对于真空 χ e = 0 ε r = 1 ε = ε 0 则 D = ε 0 E
3、有电介质时的高斯定理的应用
在垂直于电场方向的两个表面上，将产生极化电荷。
4.极化电荷
在外电场中，均匀介质内部各处仍呈电中性，但在介质表 面要出现电荷，这种电荷不能离开电介质到其它带电体，也不 能在电介质内部自由移动。我们称它为束缚电荷或极化电荷。 它不象导体中的自由电荷能用传导方法将其引走。
χ = εr − 1 电极化率
令 ε r = (1 + χ e ) 为相对介电常量（相对电容率）
ε = ε 0ε r ～电介质的电容率
5
四、极化电荷与自由电荷的关系
E
=
E0
−
E'=
E0 εr
E'=
εr − 1 εr
E0
d
σ'=
εr − εr
1
σ
0
Q' =
εr − εr
即 D⇒ E ⇒ P ⇒σ′ ⇒q′
9
物理意义
E
单位试验电荷 的受力
单位体积内的 P 电偶极矩的矢
量和 无物理意义， D 只有一个数学 上的定义 D = ε0E + P
= ε 0ε r E
特点
真空中关于电场的讨论都 适用于电介质：高斯定律、 电势的定义、环路定理等
各向同性均匀电介质中
P = ε0χe E ，表面束缚电荷 σ ′ = P ⋅ n ，电介质中P ≠ 0
D = (1+ χ )ε0E
ε r = (1 + χ )
ε = ε rε 0
相对电容率或相对介电常量
电容率或介电常量
D＝ε0ε r E = εE
•注意： D 是辅助矢量，描写电场性质的物理量仍为 E ,V
对于真空 χ e = 0 ε r = 1 ε = ε 0 则 D = ε 0 E
3、有电介质时的高斯定理的应用
在垂直于电场方向的两个表面上，将产生极化电荷。
4.极化电荷
在外电场中，均匀介质内部各处仍呈电中性，但在介质表 面要出现电荷，这种电荷不能离开电介质到其它带电体，也不 能在电介质内部自由移动。我们称它为束缚电荷或极化电荷。 它不象导体中的自由电荷能用传导方法将其引走。
静电场中的电介质
由定义
C 与 d S 0 有关
S
C ； d C
插入介质
0S q C u A uB d
C
0 r S
d
C
（2）球形电容器 已知
设+q、-q 场强分布： E 电势差：
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用，电矩方 向趋于外电场方向。但由于热运 动的存在，不会完全一致。
有极分子的取向极化！
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强，极化电荷越多； ②电介质不均匀，则不仅在电介质表面会出现极 化电荷，在电介质内部也会出现极化电荷； ③对均匀电介质，在其内部任一小区域内，正负 电荷数量仍然相等，因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义：描述了电介质极化强弱，反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中，P 0 E
称为电介质的电极化率，它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
C 与 d S 0 有关
S
C ； d C
插入介质
0S q C u A uB d
C
0 r S
d
C
（2）球形电容器 已知
设+q、-q 场强分布： E 电势差：
RB
RA RB
q
r q
B A
RA
q 4 0 r 2
q q
RB
1 1 u A uB dr ( ) 2 4 0 RA RB R A 4 0 r
f
pe
pe
3;
+ E + 外 + + + +
在外电场中有极分子的固有电 矩要受到一个力矩作用，电矩方 向趋于外电场方向。但由于热运 动的存在，不会完全一致。
有极分子的取向极化！
+ E + 外 + + + +
+
两端面出现极化电荷层
电介质被极化的宏观效果
①外电场越强，极化电荷越多； ②电介质不均匀，则不仅在电介质表面会出现极 化电荷，在电介质内部也会出现极化电荷； ③对均匀电介质，在其内部任一小区域内，正负 电荷数量仍然相等，因而仍然表现出电中性。
二、电极化强度和极化电荷
单位体积内分子电偶极矩的矢量和 P
1、电极化强度(矢量)
pi
V
物理意义：描述了电介质极化强弱，反映了电介质 内分子电偶极矩排列的有序或无序程度。
在各向同性的电介质中，P 0 E
称为电介质的电极化率，它取决于电介质的性质。
2、极化电荷和自由电荷 极化电荷
E E0
++++++ r + ------- C
(大学物理ppt)第 4 章 静电场中的电介质
第 4 章
静电场中的电介质
一、电介质对电场的影响 二、电介质的极化 三、电极化强度
四、极化电荷
五、D 的高斯定律
六、电容器和它的电容
七、电容器的能量
一、电介质对电场的影响
电介质也即绝缘体
特点是分子中正负电荷束缚得很紧，内
部几乎没有自由电荷，不导电，但在电场中会
受到电场的影响，反过来也会影响原有电场的
P
pi
V
P np
其中 n 表示电介质单位体积内的分子数。
三、电极化强度
2. 电极化强度与电场的关系
对 各向同性 的电介质，当电场不太强时， 试验表明：
P 0 ( r 1) E 0 E
其中 r 1 叫做电介质的电极化率。
四、极化电荷
1. 面束缚电荷
在介质中取一斜柱，长为 l ，则穿过 dS 面 的总正电荷为
dq qndV qnldScos
而 故 p ql， np P dq PcosdS
-q
e n
l
dS +q
面束缚电荷密度 dq P cos P e n dS
E
四、极化电荷
2. 体束缚电荷
穿过 dS面的总正电荷为 PcosdS P dS dqout 穿过整个封闭面 S 向外的 电荷应为 d qout P dS qout
S S
-q
e n
l
S
dS +q
E
留在封闭面 S 内的体束缚电荷应为 q in - q out P dS
二、电介质的极化 在电介质内部的宏观微小的区域内，正负电
静电场中的电介质
一、电介质对电场的影响 二、电介质的极化 三、电极化强度
四、极化电荷
五、D 的高斯定律
六、电容器和它的电容
七、电容器的能量
一、电介质对电场的影响
电介质也即绝缘体
特点是分子中正负电荷束缚得很紧，内
部几乎没有自由电荷，不导电，但在电场中会
受到电场的影响，反过来也会影响原有电场的
P
pi
V
P np
其中 n 表示电介质单位体积内的分子数。
三、电极化强度
2. 电极化强度与电场的关系
对 各向同性 的电介质，当电场不太强时， 试验表明：
P 0 ( r 1) E 0 E
其中 r 1 叫做电介质的电极化率。
四、极化电荷
1. 面束缚电荷
在介质中取一斜柱，长为 l ，则穿过 dS 面 的总正电荷为
dq qndV qnldScos
而 故 p ql， np P dq PcosdS
-q
e n
l
dS +q
面束缚电荷密度 dq P cos P e n dS
E
四、极化电荷
2. 体束缚电荷
穿过 dS面的总正电荷为 PcosdS P dS dqout 穿过整个封闭面 S 向外的 电荷应为 d qout P dS qout
S S
-q
e n
l
S
dS +q
E
留在封闭面 S 内的体束缚电荷应为 q in - q out P dS
二、电介质的极化 在电介质内部的宏观微小的区域内，正负电
2.静电场中的电介质
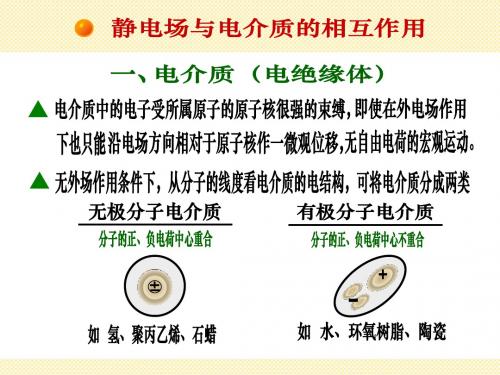
自由电荷 束缚电荷
1 E dS
S
0
q
S
0
1
0
P dS
S
( 0 E P) dS q0
S S
电位移矢量定义：
D 0E P
( 0 E P) dS q0
S S
自由电荷
3、极化（束缚）电荷与极化强度的关系： 对于均匀的电介质，极化电荷集中在它的表面。电介质 产生的一切宏观效果都是通过未抵消的束缚电荷来体现。
如图，在平板电容器两极板间的介 质内沿着方向取一长度为dl，横截面为 dS的小圆柱体，在其内部极化可视为 是均匀的。
dl
' dS
' dS
P
点的总场强为：
' 退极化场 是电介质中的总电场强度。 E E E 0 E0 是自由电荷产生的电场。
' E 是极化电荷产生的退极化场
E E0 E'
' '
2.电极化强度矢量
宏观上，电介质极化程度用电极化强度矢量来描述， 其定义式为：
P lim
pi
S S S in
Pn '
P dS dS
'
极化强度力线
在任一曲面内极化电荷的负值等于极化强度的通量。
四、电介质中的高斯定理
根据介质极化和 真空中高斯定律 ' P d S q
S S
S
电位移矢量
0
' ( q q 0 ) S
1 E dS
(2)对各向同性电介质( P e 0 E)
静电场中 的电介质
静电场中的电介质 ， ，
1.2 电介质的极化
1．电介质极化的机理
对于无极分子，在外电场的作用下，正、负电荷的中心被电场力拉开，使得正、负电荷中心产 生相对位移（这种极化称为位移极化），形成电偶极子。
在此力偶矩的作用下，有极分子的电偶极矩方向将转向与外电场基本一致的方向，这种极化称 为转向极化，其结果是电介质的两端出现等量异号的电荷.
真空中 r 1，空气中 r 1.005 ，可认为近似等于 1，其他电介质的 r 都大于 1。电介质的相对电容
率 r 和真空中电容率 0 的乘积称为电介质的电容率 ，即 r0
静电场中的电介质 ， ，
1.2 电介质的极化
3．电介质的击穿
如果外电场足够大，电介质分子就会摆脱分子的束缚成为自由电子，电介质的绝缘性被破坏而 成为导体，这个过程称为电介质的击穿，这个外电场的场强称为击穿场强。
大学物理
静电场中的电介质 ， ，
1.1 电介质的分类
电介质又称绝缘体。我们通常把气体、油类、蜡脂、玻璃、云母、陶瓷、橡胶等这些基本不导 电的物质称为电介质。
对于各向同性的电介质可分为无极分子和有极分子两类。
静电场中的电介质 ， ，
1.2 电介质的极化
电介质的极化是指在外电场作用下电介质表面产生极化电荷的现象。 其中，极化电荷又称束缚电荷，是指在外电场中，均匀介质内部各处仍成电中性，但在介质表 面出现的不能离开电介质到其他带电体，也不能在电介质内部自由移动的电荷。
静电场中的电介质 ， ，
1.2 电介质的极化
2．电介质对电场的影响
如果不存在电介质（真空），自由电荷激发的场强大小为 E0 ，引入均匀电介质后，当均匀电介质充
满电场不为零的空间，或几种均匀电介质分区充满电场且分界面都是等势面时，电介质的场强大小 E 将
静电场中的电介质参考答案
3.1 填空题3.1.1 位移极化、取向极化 3.1.2 无极分子、位移极化3.1.3 χ ，E P 0χε=3.1.4 7.08×10-5C·m -23.1.5 01W rε3.1.6 r ε、1、r ε3.1.7 增大、增大3.1.8 σ，r0εεσ、3.2 选择题3.2.1 B 3.2.2 C 3.2.3 B 3.2.4 C 3.2.5 C 3.2.6 D 3.2.7 D 3.2.8 B 3.2.9D3.2.10 C3.3证明及简答题3.3.1 证明：以球心为中心，作半径为r 的球形闭合曲面包围该金属球，其D 通量为24r D dS D dS D S d D r Sr r Ssπ===⋅⎰⎰⎰⎰⎰⎰由电介质中的高斯定律得 q rD r =24π，得 24rq D r π= ，或r e r q D24π= rr r e crb e r q e r q D E2224441ππεπεε==⋅==3.3.2证明：作柱面高斯面，其上底1S 位于介质中，下底2S 位于金属板中，3S 为侧面，柱轴线垂直于金属板。
由高斯定理，1211090cos 03S D DdS S S D S d D S n S n S=︒+⋅+=⋅=⎰⎰⎰⎰σ0σ=n D ，故 n e D0σ= ，n e D E εσε0==3.3.3答：从微观看，金属中有大量自由电子，在电场的作用下可以在导体内位移，使导体中的电荷重新分布，结果在导体表面出现感应电荷，达到静电平衡时感应电荷所产生的电场与外加电场相抵消，导体中的合场强为零，导体中自由电子的宏观移动停止。
在介质中，电子与原子核的结合相当紧密，电子处于束缚状态，在电场的作用下，只能作一微观的相对位移或者它们之间连线稍微改变方向，结果出现束缚电荷。
束缚电荷所产生的电场只能部分地抵消外场，达到稳定时，电介质内部的电场不为零。
3.4 计算题3.4.1解：分别用C 和0C 表示介质抽出前后电容器的电容，Q 和0Q 。
大学物理作业-静电场中的电介质一解答
02
圆柱形电容器储能计 算
对于圆柱形电容器，其储能$W = frac{1}{2} pi R^2 L varepsilon_0 E^2$，其中$R$为圆柱底面半径，$L$ 为圆柱高，$varepsilon_0$为真空介电 常数，$E$为电场强度。
03
实例分析
通过具体数值代入公式进行计算，可 得电容器储存的能量。
电介质在生物医学中的应用
近年来，电介质在生物医学领域的应用逐渐受到关注。例 如，利用电介质的生物相容性和导电性，可以开发出用于 生物组织工程、神经刺激和生物传感等方面的新型生物医 学器件和系统。
THANKS
感谢您的观看
绝缘体
绝缘体在静电场中不导电，其内部和 表面均可存在电荷分布。绝缘体的电 导率极低，因此可以保持电荷长时间 不变。
Part
02
电介质在静电场中表现
电介质极化现象
电介质极化定义
电介质在静电场作用下，内部正 负电荷中心发生相对位移，导致 电介质两端出现等量异号电荷的 现象。
极化方式
电介质极化方式包括电子极化、 原子极化和取向极化等。
不同类型电介质特性比较
绝缘体电介质 电阻率高，导电性能差， 1
极化率较低，主要用于电 气绝缘。
分子晶体电介质 4
由分子通过分子间作用力 结合而成，极化率和介电 常数均较低。
半导体电介质
2
电阻率介于导体和绝缘体之间
，具有一些特殊的电学性质，
如压电效应、热电效应等。
离子晶体电介质 3 由正负离子通过离子键结
相关领域前沿动态介绍
01 02 03
电介质材料的研究与应用
随着科技的发展，人们对于电介质材料的研究和应用不断 深入。新型的电介质材料不断涌现，如高介电常数材料、 压电材料、铁电材料等，它们在电子器件、传感器、能源 转换等领域具有广泛的应用前景。
静电场中的电介质特性
（1） 无极分子的位移极化 在外加电场作用下， 在外加电场作用下，无极分子原本重合的 正负电荷“重心”错开了， 正负电荷“重心”错开了，形成了一个电 偶极子， 偶极子，分子电偶极矩的方向沿外电场方 向。这种在外电场作用下产生的电偶极矩 称为感生电矩。 称为感生电矩。 在外电场的作用下电介质出现极化电荷的 现象，就是电介质的极化。 现象，就是电介质的极化。 在外场作用下，主要是电子位移， 在外场作用下，主要是电子位移，因而无 极分子的极化机制通常称为电子位移极化。 极分子的极化机制通常称为电子位移极化。
电介质体内一般没有自由电荷， 具有良好的绝缘性能 特点：具有极化能力和其中能够长期存在
电场的性质是电介质的基本属性
电介质的四大基本常数
介电常数:综合反映介质内部电极化行为的一个 介电常数 综合反映介质内部电极化行为的一个 主要的宏观物理量；以电极化的方式传递、 主要的宏观物理量；以电极化的方式传递、存 贮或记录电的作用与影响 电导是指电介质在电场作用下存在泄露电流 电导是指电介质在电场作用下存在泄露电流 介电损耗是电介质在电场作用下存在电能的损耗 介电损耗是电介质在电场作用下存在电能的损耗 击穿是指在强电场下可能导致电介质的破坏 击穿是指在强电场下可能导致电介质的破坏
1.无电场时 1.无电场时 有极分子 无极分子
分子热运动，各分子电偶极矩的取向杂乱无章， 分子热运动，各分子电偶极矩的取向杂乱无章， 整个电介质宏观上对外呈电中性 整个电介质宏观上对外呈电中性 2. 有电场时 有极分子介质-----取向极化 (orientation polarization) 有极分子介质 取向极化 orientation 无极分子介质-----位移极化(displacement polarization) 位移极化(displacement 无极分子介质 位移极化 边缘出现电荷 电荷分布 电介质的极化共同效果 电介质的极化共同效果 -----边缘出现电荷分布 极化 极化电荷( Polarization charges) 束缚电荷( bound charges)
静电场中的导体和电介质
静电场中的导体和电介质引言在物理学中，静电场是指当电荷处于静止状态时周围存在的电场。
导体和电介质是静电场中两种常见的物质类型。
理解导体和电介质在静电场中的行为对于理解静电现象和应用静电学原理具有重要意义。
本文将介绍导体和电介质在静电场中的特性和行为，包括导体的电荷分布和电场分布、导体内部电场为零的原因，以及电介质的电极化和电介质的介电常数。
导体导体的电荷分布在静电场中，导体具有特殊的电荷分布特性。
由于导体中的自由电子可以在导体内自由移动，一旦一个导体与其他带电体接触，自由电子将重新分布以达到平衡。
导体的外部表面电荷会分散在整个表面上，使得导体表面的电场强度为零。
这意味着在静电平衡条件下，导体表面任意一点的电势相等。
导体内部的电场分布特性在导体内部，电场强度为零。
这是由于自由电子可以在导体内自由移动，当导体中存在电场时，自由电子会沿着电场方向移动，直到达到平衡。
这种现象称为电荷迁移。
因此，导体内部的自由电子的运动将产生一个等量但相反方向的电场，导致导体内部的电场强度为零。
这也是为什么导体内部没有电场线存在的原因。
电介质电极化现象电介质是一种不易导电的物质，而其在静电场中的行为与导体有着显著不同。
当一个电介质暴露在静电场中时，电介质分子会发生电极化现象。
电极化是指电介质分子在电场作用下产生偶极矩。
在电场的作用下，电介质分子会发生形状变化，正负电荷分离，产生一个平均不为零的电偶极矩。
这种电极化现象可以分为两种类型：取向极化和感应极化。
取向极化是指电介质分子的取向方向在电场的作用下发生变化，而感应极化是指电场作用下导致电介质分子内部正负电荷的相对移动。
电介质的介电常数电介质的介电常数是描述电介质在电场中的响应特性的重要参数。
介电常数是一个比值，代表了电介质在电场力下的相对表现。
介电常数决定了电介质的极化程度和电场中的电场强度。
电介质的介电常数大于1，意味着电介质对电场的屏蔽效果更明显。
在实际应用中，通过选择合适的电介质和调整电场强度，可以改变静电场的分布和效果，用于电容器、绝缘材料等相关领域。
静电场中的电介质习题及答案
V
6、如果一平行板电容器始终连在电源两端，则充满均匀电介质后的介质中的场强与真空中 场强相等。
V
7、在均匀电介质中，如果没有体分布的自由电荷，就一定没有体分布的极化电荷。
V
8、在均匀电介质中，只有为恒矢量时，才没有体分布的极化电荷。
=恒矢量
X
9、电介质可以带上自由电荷，但导体不能带上极化电荷。
V
10、电位移矢量仅决定于自由电荷。
11、无限长的圆柱形导体，半径为R沿轴线单位长度上带电量入，将此圆柱形导体放在无
限大的均匀电介质中，则电介质表面的束缚电荷面密度是（）。
半径为a的长直导线，外面套有共轴导体圆筒，筒的内半径为 电常数为的均匀介质，沿轴线单位长度上导线带电为入，圆筒带电为
13、一圆柱形的电介质截面积为S,长为L,被沿着轴线方向极化，已知极化强度沿X方向,
X
15、介质存在时的静电能等于在没有介质的情况下，把自由电荷和极化电荷从无穷远搬到场
中原有位置的过程中外力作的功。
X
16、当均匀电介质充满电场存在的整个空间时，介质中的场强为自由电荷单独产生的场强的
分之一。
V
二、选择题
1.一平行板真空电容器， 充电到一定电压后与电源切断， 把相对介质常数为的均匀电介质 充满电容器。则下列说法中不正确的是：
A
3.在图中，A是电量的点电荷，B是一小块均匀的电介质，都是封闭曲面，下列说法中不
正确的是：
（A）
（B）
（C）
（D）
D
4.在均匀极化的电介质中，挖出一半径为r,高度为h的圆柱形空腔，圆柱的轴平行于极
化强度垂直，当h?r时，则空腔中心的关系为：
A)
B
（D）
C
5.在均匀极化的，挖出一半径为r，高度为h的圆柱形空腔，圆柱的轴平行于极化强度垂
6、如果一平行板电容器始终连在电源两端，则充满均匀电介质后的介质中的场强与真空中 场强相等。
V
7、在均匀电介质中，如果没有体分布的自由电荷，就一定没有体分布的极化电荷。
V
8、在均匀电介质中，只有为恒矢量时，才没有体分布的极化电荷。
=恒矢量
X
9、电介质可以带上自由电荷，但导体不能带上极化电荷。
V
10、电位移矢量仅决定于自由电荷。
11、无限长的圆柱形导体，半径为R沿轴线单位长度上带电量入，将此圆柱形导体放在无
限大的均匀电介质中，则电介质表面的束缚电荷面密度是（）。
半径为a的长直导线，外面套有共轴导体圆筒，筒的内半径为 电常数为的均匀介质，沿轴线单位长度上导线带电为入，圆筒带电为
13、一圆柱形的电介质截面积为S,长为L,被沿着轴线方向极化，已知极化强度沿X方向,
X
15、介质存在时的静电能等于在没有介质的情况下，把自由电荷和极化电荷从无穷远搬到场
中原有位置的过程中外力作的功。
X
16、当均匀电介质充满电场存在的整个空间时，介质中的场强为自由电荷单独产生的场强的
分之一。
V
二、选择题
1.一平行板真空电容器， 充电到一定电压后与电源切断， 把相对介质常数为的均匀电介质 充满电容器。则下列说法中不正确的是：
A
3.在图中，A是电量的点电荷，B是一小块均匀的电介质，都是封闭曲面，下列说法中不
正确的是：
（A）
（B）
（C）
（D）
D
4.在均匀极化的电介质中，挖出一半径为r,高度为h的圆柱形空腔，圆柱的轴平行于极
化强度垂直，当h?r时，则空腔中心的关系为：
A)
B
（D）
C
5.在均匀极化的，挖出一半径为r，高度为h的圆柱形空腔，圆柱的轴平行于极化强度垂
10-7 静电场中的电介质
15
板间电势差：
U AB
d1 d 2 E dl E1d1 E2d 2 1 2 AB
S
电容器的电容：
q S S C d1 d 2 d1 d2 U AB
r 1 0
r 2 0
r 1 0
r 2 0
P
pi
V
单位体积内分子电偶极矩的矢量和
描述了电介质极化强弱，反映了电介质内分子 电偶极矩排列的有序或无序程度。
pi :分子偶极矩 :电极化强度 P 2 的单位： Cm P
如果电介质内各处极化强度的大小和方向都相同， 就称为均匀极化。我们只讨论均匀极化的电介质。
5
三、极化强度与极化电荷的关系
D 0 r E E
例1 . 已知:导体球 R 、Q 、 r 求:1. 球外任一点的 E
(1101A)
r
R
2. 导体球的电势 u
解: 过P点作高斯面得 2 D 4 r Q D dS Q
S
r
S
电势
P
Q D 4r 2
D 方向：沿径向向外
0 r E
D E
电位移矢量 D
0 E 真空中
介质中
介质中的高斯定理 D dS q S
自由电荷
通过任意闭合曲面的电位移通量，等于该闭 合曲面所包围的自由电荷的代数和。
12
* D、E、P 三矢量之间关系
有电介质存在时的高斯定理的应用 SD dS q
即 或
n E2 E1 0
E1t = E2 t
上式表示，从一种介质过渡到另一种介质， 电场强度的切向分量不变。
板间电势差：
U AB
d1 d 2 E dl E1d1 E2d 2 1 2 AB
S
电容器的电容：
q S S C d1 d 2 d1 d2 U AB
r 1 0
r 2 0
r 1 0
r 2 0
P
pi
V
单位体积内分子电偶极矩的矢量和
描述了电介质极化强弱，反映了电介质内分子 电偶极矩排列的有序或无序程度。
pi :分子偶极矩 :电极化强度 P 2 的单位： Cm P
如果电介质内各处极化强度的大小和方向都相同， 就称为均匀极化。我们只讨论均匀极化的电介质。
5
三、极化强度与极化电荷的关系
D 0 r E E
例1 . 已知:导体球 R 、Q 、 r 求:1. 球外任一点的 E
(1101A)
r
R
2. 导体球的电势 u
解: 过P点作高斯面得 2 D 4 r Q D dS Q
S
r
S
电势
P
Q D 4r 2
D 方向：沿径向向外
0 r E
D E
电位移矢量 D
0 E 真空中
介质中
介质中的高斯定理 D dS q S
自由电荷
通过任意闭合曲面的电位移通量，等于该闭 合曲面所包围的自由电荷的代数和。
12
* D、E、P 三矢量之间关系
有电介质存在时的高斯定理的应用 SD dS q
即 或
n E2 E1 0
E1t = E2 t
上式表示，从一种介质过渡到另一种介质， 电场强度的切向分量不变。
静电场中的电介质
S
εr
ε0
σ + + + + + + −σ 0 - - - - - - - - - - '
闭合曲面内 自由电荷总数
闭合曲面内束 缚电荷总数
εr − 1 Q′ = Q0 εr
v v 1 ∫ E ⋅ dS = (Q0 − Q′)
S
ε0
εr − 1 Q′ = Q0 εr
v v Q0 ∫ E ⋅ dS =
v + E0 + + v＇ + E + v + E =0 + +
感应电荷 （自由电荷） 自由电荷）
v E0
v v v＇ E = E0 + E = 0
感应电荷电场强度
导体内电场强度 外电场强度
+σ0 + + + + + + + + + + + -σ ′
- - - - - v v v 导体 E0 E E'
感应电荷 自由电荷） （自由电荷）
注意 σ 0 ≠ σ ′
S
σ0 + + + + + + + + + +
d
-σ 0 -
v E0
--------S
σ′ E′ = ε0
+σ0 + + + + + + + + + + + -σ ′
- - - - - v v v ε r E0 E E'
+σ′ + + + + + + -σ 0 - - - - - - - - - - -
εr
ε0
σ + + + + + + −σ 0 - - - - - - - - - - '
闭合曲面内 自由电荷总数
闭合曲面内束 缚电荷总数
εr − 1 Q′ = Q0 εr
v v 1 ∫ E ⋅ dS = (Q0 − Q′)
S
ε0
εr − 1 Q′ = Q0 εr
v v Q0 ∫ E ⋅ dS =
v + E0 + + v＇ + E + v + E =0 + +
感应电荷 （自由电荷） 自由电荷）
v E0
v v v＇ E = E0 + E = 0
感应电荷电场强度
导体内电场强度 外电场强度
+σ0 + + + + + + + + + + + -σ ′
- - - - - v v v 导体 E0 E E'
感应电荷 自由电荷） （自由电荷）
注意 σ 0 ≠ σ ′
S
σ0 + + + + + + + + + +
d
-σ 0 -
v E0
--------S
σ′ E′ = ε0
+σ0 + + + + + + + + + + + -σ ′
- - - - - v v v ε r E0 E E'
+σ′ + + + + + + -σ 0 - - - - - - - - - - -
大学物理静电场中的导体和电介质
03
在静电场中，导体和电介质的 性质和行为表现出显著的差异 ，因此了解它们的特性是学习 大学物理静电场的重要基础。
学习目标
01
掌握导体和电介质的定义、性质和分类。
02
理解静电场中导体和电介质的电场分布和电荷分布。
03
掌握导体和电介质在静电场中的行为和相互作用， 以及它们在电路中的作用。
02
导体
导体的定义与性质
感应电荷的产生是由于导体内 部自由电荷受到电场力的作用 而重新分布，这种效应称为静 电感应现象。
静电感应现象在生产和生活中 的应用十分广泛，如静电除尘、 静电喷涂等。
导体的静电平衡状态
当导体放入静电场中并达到稳定状态时，导体内部的自由电荷不再发生定向移动， 此时导体的状态称为静电平衡状态。
在静电平衡状态下，感应电荷在导体内、外表面产生附加电场，该电场与外界电场 相抵消，使得导体内部的总电场为零。
应用
了解电场强度在电介质中 的分布和变化规律，有助 于理解电子设备和器件的 工作原理。
电介质的电位移矢量
01
02
03
04
定义
电位移矢量是指描述电场中电 荷分布情况的物理量。
特点
在静电场中，电位移矢量与电 场强度之间存在线性关系，可
以用介电常数表示。
计算
根据电位移矢量的定义和电场 强度的计算公式，可以计算出
定义
导体是指能够让电流通过的物质。在 静电场中，导体内部自由电荷会受到 电场力的作用而发生移动，从而形成 电流。
性质
导体具有导电性，其导电能力与温度 、光照、化学状态等因素有关。金属 导体是电导率最高的物质之一，而绝 缘体则几乎不导电。
导体的静电感应现象
当导体放入静电场中时，导体 表面会产生感应电荷，感应电 荷的分布与外界电场有关。
大学物理_4静电场中的电介质
S
i
自由电荷
各向同性 线性介质
P 0r 1E
D 0r E E 介质方程
r 0 称介质的介电常数（电容率）
在 斯具 定有 理某出种发对解称出性D的情况下，可以首先由高
即 D E P q
说明：
1.电位移在闭合面上的通量只和闭合面内的自
第十五章 静电场中的电介质
（Dielectric In Electrostatic Field）
§15.1 电介质对电场的影响 §15.2 电介质的极化 §15.3 D的高斯定律 §15.4 电容器及其电容 §15.5 电容器的能量
§15.1 电介质对电场的影响 电介质的特点：无自由电荷，不导电。 电场中置入各向同性均匀电介质时的影响
定义 C Q 单位:法拉 F
U
电容只与几何因素和介质有关 固有的容电本领
【例1】求真空中孤立导体球的电容
解：设球带电为 Q
导体球电势 U Q
4 0 R
导体球电容 C Q
U
4 0 R
问题
欲得到 1F的电容, 孤立导体球的半径R
由孤立导体球电容公式知
R
1
4 0
9109 m
R3
4π 0r 2
(r (r
R) R)
q2r2
we
0E2
2
32π2
q2
0
R
6
32π2 0 r 4
(r R) (r R)
静电能：We
V wedV
0
we
4πr
2dr