回形针9个意想不到的妙用只有1%的人知道

合集下载

第二章第1讲函数的概念及其表示-2025年高考数学备考

第二章函数第1讲函数的概念及其表示课标要求命题点五年考情命题分析预测1.了解构成函数的要素，能求简单函数的定义域.2.了解简单的分段函数，并能简单应用.求函数的定义域2022北京T11本讲是函数部分的基础，命题热点为分段函数的求值、含参和解不等式问题，题型以选择题、填空题为主，难度中等偏易.在2025年高考的备考中，要掌握函数的三要素和以分段函数为载体的有关应用.求函数的解析式分段函数2022浙江T14；2021浙江T12学生用书P0181.函数的概念及表示函数的定义一般地，设A ，B 是①非空的实数集，如果对于集合A 中的②任意一个数x ，按照某种确定的对应关系f ，在集合B 中都有③唯一确定的数y 和它对应，那么就称f ：A →B 为从集合A 到集合B 的一个函数，记作y ＝f （x ），x ∈A .三要素④定义域，⑤对应关系，⑥值域.定义域自变量x 的取值范围A .值域函数值的集合{f （x ）｜x ∈A }，是集合B 的⑦子集.相等函数⑧定义域相同，⑨对应关系完全一致.函数的表示法⑩解析法，⑪列表法，⑫图象法.注意（1）与x 轴垂直的直线和函数图象最多有一个交点；（2）解决函数问题时，优先考虑定义域.常用结论求函数的定义域时常用的结论（1）分式型1（）要满足f （x ）≠0；（2）偶次根式型2（）（n ∈N *）要满足f （x ）≥0；（3）[f （x ）]0要满足f （x ）≠0；（4）对数型log a f （x ）（a ＞0，且a ≠1）要满足f（x）＞0；（5）正切型tan f（x）要满足f（x）≠π2＋kπ，k∈Z.2.分段函数若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数.注意（1）分段函数虽由几个部分构成，但它表示的是一个函数；（2）分段函数的定义域是各段函数定义域的并集，值域是各段函数值域的并集.1.下列f（x）与g（x）表示同一个函数的是（B）A.f（x）＝2－1与g（x）＝－1·+1B.f（x）＝x与g（x）＝3＋2+1C.f（x）＝x与g（x）＝（）2D.f（x）＝2与g（x）＝332.下列函数中，其定义域和值域分别与函数y＝10lg x的定义域和值域相同的是（D）A.y＝xB.y＝lg xC.y＝2xD.y3.[教材改编]已知函数f（x 1，≤1，>1，则f（f（－2））＝（B）A.8B.12C.－34D.－109解析因为f（x）1，≤1，>1，所以f（－2）＝（－2）2－1＝3，所以f（f（－2））＝f（3）＝13－1＝12，故选B.4.已知函数f（x）＝2x－3，x∈{x∈N｜1≤x≤5}，则函数f（x）的值域为{－1，1，3，5，7}.学生用书P019命题点1求函数的定义域例1（1）[2022北京高考]函数f（x）＝1＋1－的定义域是（－∞，0）∪（0，1].解析因为f（x）＝1＋1－，所以x≠0，1－x≥0，解得x∈（－∞，0）∪（0，1].（2）若函数f（1－2x）的定义域为[－1，2]，则函数f（x）的定义域为[－3，3].解析因为函数f（1－2x）的定义域为[－1，2]，所以－1≤x≤2，所以－3≤1－2x≤3.所以函数f（x）的定义域为[－3，3].命题拓展若函数f（x）的定义域为[－1，2]，则函数f（1－2x）的定义域为[－12，1].解析由－1≤1－2x≤2，得－12≤x≤1，所以函数f（1－2x）的定义域为[－12，1].方法技巧1.求具体函数的定义域的策略根据函数解析式，构造使解析式有意义的不等式（组），求解不等式（组）即可；对实际问题，既要使函数解析式有意义，又要使实际问题有意义.2.求抽象函数的定义域的策略（1）若已知函数f（x）的定义域为[a，b]，则复合函数f（g（x））的定义域由不等式a≤g（x）≤b求出；（2）若已知函数f（g（x））的定义域为[a，b]，则f（x）的定义域为g（x）在[a，b]上的值域.注意无论函数的形式如何，定义域均是指其中的自变量x的取值集合.训练1（1）[2024浙江省宁波市余姚中学一检]已知函数y＝f（x）的定义域是[－2，3]，则函数y＝（2r1）r1的定义域是（A）A.[－32，－1）∪（－1，1]B.[－3，－1）∪（－1，7]C.（－1，7]D.[－32，－1）解析因为函数y＝f（x）的定义域是[－2，3]，所以－2≤2x＋1≤3，且x＋1≠0，解得x∈[－32，－1）∪（－1，1].故选A.（2）[2024江苏省镇江市丹阳市模拟]函数f（x）＝3－2＋（x－4）0的定义域为[23，4）∪（4，＋∞）.解析要使函数f（x）＝3－2＋（x－4）0有意义，则有3－2≥0，－4≠0，解得x≥23且x≠4，所以函数f（x）＝3－2＋（x－4）0的定义域为[23，4）∪（4，＋∞）.命题点2求函数的解析式例2（1）[2024河南省内乡高中模拟]已知f（x）是一次函数，且f（f（x））＝16x－25，则f（x）＝4x－5或－4x＋253.解析设f（x）＝kx＋b（k≠0），则f（f（x））＝k（kx＋b）＋b＝k2x＋kb＋b＝16x－25，∴2=16，B＋＝－25，∴=4，＝－5或＝－4，＝253，∴f（x）＝4x－5或f（x）＝－4x＋253.（2）已知f（x）满足2f（x）＋f（1）＝3x－1，则f（x）＝2x－1－13.解析已知2f（x）＋f（1）＝3x－1①，以1代替①中的x（x≠0），得2f（1）＋f（x）＝3－1②，①×2－②，得3f（x）＝6x－3－1，故f（x）＝2x－1－13.方法技巧求函数解析式的常用方法（1）待定系数法：若已知函数类型（如一次函数、二次函数等），则可用待定系数法求解.（2）换元法：若已知复合函数f（g（x））的解析式求解函数f（x）的解析式，可令g（x）＝t，解出x，然后代入f（g（x））中即可求得f（t），从而求得f（x）.此时要注意新元的取值范围.（3）配凑法：配凑法是将函数f（g（x））的解析式配凑成关于g（x）的形式，进而求出函数f（x）的解析式.（4）构造方程组法（消元法）：若已知f（x）与f（1），f（－x）等的表达式，则可通过赋值（如令x为1，－x等）构造出另一个等式，通过解方程组求出f（x）.注意求函数解析式时，若定义域不是R，一定要注明函数定义域.训练2（1）已知f（x2＋12）＝x4＋14，则f（x）的解析式为f（x）＝x2－2，x∈[2，＋∞）.解析因为f （x 2＋12）＝（x 2＋12）2－2，所以f （x ）＝x 2－2，x ∈[2，＋∞）.（2）[2024安徽淮南模拟]已知f （x ）是二次函数，且f （x ＋1）＋f （x －1）＝2x 2－4x ＋4，则f （x ）＝x 2－2x ＋1.解析因为f （x ）是二次函数，所以设f （x ）＝ax 2＋bx ＋c （a ≠0），则有a （x ＋1）2＋b （x ＋1）＋c ＋a （x －1）2＋b （x －1）＋c ＝2x 2－4x ＋4，即2ax 2＋2bx ＋2a ＋2c ＝2x 2－4x＋4，所以2=2，2＝－4，2+2=4，所以=1，＝－2，=1，所以f （x ）＝x 2－2x ＋1.（3）[2024湖北省钟祥市第一中学模拟]已知f （x ）满足3f （x ）＋2f （1－x ）＝4x ，则f （x ）的解析式为f （x ）＝4x －85.解析3f （x ）＋2f （1－x ）＝4x①，用1－x 代替①中的x 可得3f （1－x ）＋2f （x ）＝4（1－x ）②，由3×①－2×②可得f （x ）＝4x －85.命题点3分段函数角度1分段函数的求值（求参）问题例3（1）[山东高考]设f （x ）＝，0<<1，2（－1),≥1.若f （a ）＝f （a ＋1），则f （1）＝（C）A.2B.4C.6D.8解析作出f （x ）的图象，如图所示，因为a ＜a ＋1，所以要使f （a ）＝f （a ＋1），则有＝2（a ＋1－1），0＜a ＜1，所以解得a ＝14，所以f （1）＝f （4）＝6.（2）[2022浙江高考]已知函数f （x ）＝－2+2，≤1，＋1－1，>1，则f （f （12））＝3728；若当x ∈[a ，b ]时，1≤f （x ）≤3，则b －a 的最大值是3＋3.解析由题意知f （12）＝－（12）2＋2＝74，则f （f （12））＝f （74）＝74＋174－1＝74＋47－1＝3728.作出函数f （x ）的大致图象，如图所示，结合图象，令－x 2＋2＝1，解得x ＝±1；令x ＋1－1＝3，解得x ＝2±3，又x ＞1，所以x ＝2＋3.所以（b －a ）max ＝2＋3－（－1）＝3＋3.角度2分段函数的解不等式问题例4[全国卷Ⅰ]设函数f （x ）＝2－，≤0，1，>0，则满足f （x ＋1）＜f （2x ）的x 的取值范围是（D）A.（－∞，－1]B.（0，＋∞）C.（－1，0）D.（－∞，0）解析解法一当x ≤0时，函数f （x ）＝2－x 是减函数，则f （x ）≥f （0）＝1.作出f （x ）的大致图象如图所示，结合图象可知，要使f （x ＋1）＜f （2x ），则需+1<0，2<0，2＜+1或+1≥0，2<0，所以x ＜0，故选D.解法二当x ＝－12时，f （x ＋1）＝f （12）＝1，f （2x ）＝f （－1）＝2－（－1）＝2，满足f （x ＋1）＜f （2x ），排除A ，B ；当x ＝－1时，f （x ＋1）＝f （0）＝20＝1，f （2x ）＝f （－2）＝22＝4，满足f （x ＋1）＜f （2x ），排除C.故选D.方法技巧1.解分段函数的求值问题的思路：一般根据自变量所在区间代入相应的函数解析式求解，当出现f （f （a ））形式时，一般由内向外逐层求值.2.解分段函数的解不等式问题的思路：（1）若图象易画，可画出函数图象，数形结合求解；（2）根据分段函数的不同段分类讨论，最后取各段结果的并集.注意解得值或范围后，要注意检验其是否符合相应段的自变量的范围.训练3（1）[2024河南郑州外国语模拟]已知实数a ＜0，函数f （x ）＝2＋，<1，－－2，≥1，若f （1－a ）＝f （1＋a ），则a 的值为（A ）A.－34B.－32C.－35D.－1解析因为a＜0，所以1－a＞1，1＋a＜1.因为f（1－a）＝f（1＋a），所以－（1－a）－2a＝2（1＋a）＋a，解得a＝－34.故选A.（2）[2024四川达州外国语模拟]已知函数f（x）＝e－1，≤2，2（－2),>2，则f（7）＝8.解析由题意得f（7）＝2f（5）＝2×2f（3）＝4×2f（1）＝8e1－1＝8.（3）[2023江苏南通模拟]已知函数f（x）＝max{1－x，2x}，其中max{a，b}表示a，b中的较大者.则不等式f（x）＞4的解集为（－∞，－3）∪（2，＋∞）.解析作出f（x）的大致图象如图所示，结合图象可知f（x）＝1－，≤0，2，>0.当x≤0时，由1－x＞4，得x＜－3.当x＞0时，由2x＞4，得x＞2，所以f（x）＞4的解集为（－∞，－3）∪（2，＋∞）.1.[命题点1/2023黑龙江省齐齐哈尔市恒昌中学模拟]函数f（x－log3（1－2）的定义域是（A）A.[0，12）B.（－∞，12）C.（－∞，12]D.（－∞，1）解析由题意得1－>0，－log3（1－2）≥0，1－2>0，解得0≤x＜12，所以函数f（x）的定义域是[0，12），故选A.2.[命题点2]定义在（－1，1）上的函数f（x）满足2f（x）－f（－x）＝lg（x＋1），则f（x）＝23lg（x＋1）＋13lg（1－x），x∈（－1，1）.解析当x∈（－1，1）时，有2f（x）－f（－x）＝lg（x＋1）①.以－x代替x得，2f（－x）－f（x）＝lg（－x＋1）②.由①②消去f（－x）得，f（x）＝23lg（x＋1）＋13lg（1－x），x∈（－1，1）.3.[命题点3角度1]设函数f（x，≤1，>1，则满足2f（f（a））＝f（a）的a的取值范围是（D）A.（－∞，0]B.[0，2]C.[2，＋∞）D.（－∞，0]∪[2，＋∞）解析作出f（x）的图象（图略），可得f（x）的最小值为12，令t＝f（a），则t≥12，考虑f（t）＝2的解，作出y＝f（t）与y＝2在[12，＋∞）上的图象，如图1中实线所示，由图可知，当t≥1时，f（t）＝2，故t≥1.下面考虑f（a）≥1的解集，作出y＝f（a）与y＝1的图象如图2所示，由图可得a≤0或a≥2.故选D.图1图24.[命题点3角度2/2023山东济南模拟]已知函数f（x）＝－2+2B－2，≤，－，＞，若f（a2－4）＞f（3a），则实数a的取值范围是（B）A.（－1，4）B.（－∞，－1）∪（4，＋∞）C.（－4，1）D.（－∞，－4）∪（1，＋∞）解析由题意知f（x）＝－（－）2，≤，－，＞，易知函数f（x）在（m，＋∞），（－∞，m]上单调递增，且m－m＝－（m－m）2，所以函数f（x）在R上单调递增.则由f（a2－4）＞f（3a），得a2－4＞3a，解得a＞4或a＜－1，所以实数a的取值范围是（－∞，－1）∪（4，＋∞），故选B.学生用书·练习帮P2641.函数f（x）＝3－1＋1ln（2－）的定义域为（C）A.[13，1）∪（1，＋∞）B.[13，2）C.[13，1）∪（1，2）D.（0，2）解析要使函数f（x）＝3－1＋1ln（2－）有意义，则3－1≥0，2－>0，2－≠1，解得≥13，<2，≠1，故函数的定义域为[13，1）∪（1，2）.故选C.2.下列各组函数表示相同函数的是（C）A.f（x）＝2和g（x）＝（）2B.f（x）＝1和g（x）＝x0C.f（x）＝｜x｜和g（x）＝，≥0，－，<0D.f（x）＝e ln x和g（x）＝lg10x解析对于选项A，f（x）＝2＝｜x｜的定义域为R，g（x）＝（）2＝x的定义域为[0，＋∞），两个函数的定义域不相同，不是相同函数；对于选项B，f（x）＝1的定义域为R，g（x）＝x0＝1的定义域为{x｜x≠0}，两个函数的定义域不相同，不是相同函数；对于选项C，f（x）＝｜x｜＝，≥0，－，＜0，函数f（x），g（x）的定义域都是R，且对应法则相同，是相同函数；对于选项D，f（x）＝e ln x的定义域为（0，＋∞），g（x）＝lg10x的定义域为R，两个函数的定义域不相同，不是相同函数.故选C.3.[2023重庆模拟]已知函数f（＋1）＝x＋2，则f（x）的解析式为（C）A.f（x）＝x2－1B.f（x）＝x2－1，x∈（1，＋∞）C.f（x）＝x2－1，x∈[1，＋∞）D.f（x）＝x2－1，x∈[0，＋∞）解析解法一（配凑法）f（＋1）＝x＋2＝（＋1）2－1，令t＝＋1（t≥1），则f（t）＝t2－1，t∈[1，＋∞），所以f（x）＝x2－1，x∈[1，＋∞），故选C.解法二（换元法）令t＝＋1（t≥1），则＝t－1（t≥1），f（t）＝（t－1）2＋2（t －1）＝t2－1，t∈[1，＋∞），所以f（x）＝x2－1，x∈[1，＋∞），故选C.4.已知函数f（x）＝ln，≥1，0，0≤<1，，<0，若f（2a－1）－1≤0，则实数a的取值范围是（D）A.[e+12，＋∞）B.（－∞，－12]∪[0，e+12]C.[0，e+12]D.（－∞，e+12]解析因为f（2a－1）－1≤0，所以f（2a－1）≤1.作出函数y＝f（x）及y＝1的图象，如图所示，设两函数图象交于点P，则由图可知，2a－1≤x P＝e，所以a≤e+12，即a的取值范围是（－∞，r12]，故选D.5.[2024广东名校联考]已知函数f（x）的定义域是[0，4]，则函数y 的定义域是（2，5].解析由题意知0≤－1≤4，－2>0，解得2＜x≤5，即y2，5].6.[2024山东省部分学校阶段监测]已知函数f（x）＝3，≤0，l4，>0，则f（f（116））＝19.解析因为f（x）＝3，≤0，log4，>0，所以f（116）＝log4116＝－2，f（－2）＝3－2＝19，所以f（f（116））＝19.7.[2024惠州市一调]已知函数f（x）满足f（x＋1）＝f（x）＋2，则f（x）的解析式可以是f（x）＝2x（答案不唯一）.（写出满足条件的一个解析式即可）解析由f（x＋1）＝f（x）＋2知，函数f（x）的图象上移2个单位长度后得到的图象，与左移1个单位长度后得到的图象重合，f（x）＝2x＋k（其中k可取任意实数）满足要求.本题为开放题，答案可为f（x）＝2x，f（x）＝2x＋1等.8.[2024浙江名校联考]已知函数f（x）＝（12），∈（－∞，1),log4，∈（1，＋∞),则f（x）＞1的解集为（－∞，0）∪（4，＋∞）.解析由题意可得，f（0）＝（12）0＝1，结合指数函数y＝（12）x在定义域内单调递减可知，当x＜1时，f（x）＞1的解集为（－∞，0）；f（4）＝log44＝1，结合对数函数y＝log4x在定义域内单调递增可知，当x＞1时，f（x）＞1的解集为（4，＋∞）.所以不等式f（x）＞1的解集为（－∞，0）∪（4，＋∞）.9.[2023福建漳州联考]已知函数f（x）＝log2，>0，2+4+1，≤0，若实数a满足f（f（a））＝1，则实数a的所有取值的和为（C）A.1B.1716－5C.－1516－5D.－2解析作出y＝f（x）及y＝1的部分图象，如图所示，易得y＝f（x）与y＝1的图象有三个交点，设这三个交点分别为A，B，C，则易得x A＝－4，x B＝0，x C＝2.令f（a）＝－4，则由图可得log2a＝－4，解得a＝2－4＝116；令f（a）＝0，则由图可得a2＋4a＋1＝0或log2a＝0，解得a＝－2－3或a＝－2＋3或a＝1；令f（a）＝2，则由图可得a2＋4a＋1＝2（a≤0）或log2a＝2，解得a＝－2－5或a＝22＝4.所以实数a的所有取值的和为116＋（－2－3）＋（－2＋3）＋1＋（－2－5）＋4＝－1516－5，故选C.10.[2023西北工业大学附属中学模拟]设函数f（x）＝，0<<1，eln，≥1，若f（a）＝f（e a），则f（1）＝解析根据题意作出函数f（x）的图象，如图所示.由f（x）的定义域知，a＞0，所以e a＞1.易知y＝e x的图象与y＝x的图象无交点，所以e a≠a，所以要使f（a）＝f（e a），则0＜a＜1＜e a，所以＝e ln e a，变形可得＝e a，解得a＝1e，则f（1）＝f（e）＝e ln e＝e.11.[情境创新]德国著名数学家狄利克雷在数学领域成就显著，是解析数论的创始人之一.函数f（x）＝1，为有理数，0，为无理数被称为狄利克雷函数，则关于函数f（x），下列说法正确的是（D）A.f（x）的定义域为{0，1}B.f（x）的值域为[0，1]C.∃x∈R，f（f（x））＝0D.对于任意一个非零有理数T，f（x＋T）＝f（x）对任意x∈R恒成立解析由题意知f（x）的定义域为R，值域为{0，1}，故A，B错误；因为f（x）＝0或f（x）＝1，所以当f（x）＝0时，f（f（x））＝f（0）＝1，当f（x）＝1时，f（f（x））＝f（1）＝1，故C错误；对于任意一个非零有理数T，若x为有理数，则x＋T也为有理数，则f（x）＝f（x＋T）＝1，若x为无理数，则x＋T也为无理数，则f（x＋T）＝f（x）＝0，综上可得，对于任意一个非零有理数T，f（x＋T）＝f（x）对任意x∈R恒成立，故D正确.故选D.12.[探索创新/多选/2024江西名校联考]若存在M，使得f（x）≥M对任意x∈D恒成立，则函数f（x）在D上有下界，其中M为函数f（x）的一个下界，若存在N，使得f（x）≤N对任意x∈D恒成立，则函数f（x）在D上有上界，其中N为函数f（x）的一个上界，如果一个函数既有上界又有下界，那么称该函数有界，则下列说法正确的是（ABD）A.2是y＝x＋1（x∈（2，＋∞））的一个下界B.y＝ln有上界无下界C.y＝x e x有上界无下界D.y＝cos2+1有界解析对选项A，y＝x＋1在（2，＋∞）上单调递增，故y＞2＋12＝52≥2，A正确；对选项B，y＝ln，则y'＝1－ln2，当x∈（0，e）时，y'＞0，函数单调递增，当x∈（e，＋∞）时，y'＜0，函数单调递减，故函数在x＝e时有最大值为1e，无最小值，即y≤1e恒成立，B正确；对选项C，当x趋近于＋∞时，y＝x e x趋近于＋∞，C错误；对选项D，y＝Hs2+1，则｜y｜＝｜Hs｜2+1≤12+1≤1，即－1≤y≤1恒成立，D正确.故选ABD.。

延世大学韩国语教程1练习

延世大学韩国语教程1：第一课练习연습1. 다음보기와같이쓰십시오.请仿照例子填空。

[보기]2. 다음보기와같이문장을만드십시오. 请仿照例子造句。

[보기]한국사람-한국사람입니다.1) 미국사람 2) 일본사람3) 사전 4) 아이스크림5) 친구 6) 연세대학교3. 다음보기와같이문장을만드십시오请仿照例子造句。

[보기] 책-책입니까?1) 연필 2) 공책3) 중국사람 4) 영국사람5) 학생 6) 우유 7) 숙제4. 다음단어를이용하여대화를완성하십시오. 用下列单词完成对话。

[보기]버스가: 버스입니까? 나: 예, 버스입니다.1) 남자가: 남자입니까? 나: 예,2) 의자가: 의사입니까? 나: 아니요,3) 교과서가: 교과서입니까? 나: 예,4) 사과가: 가방입니까? 나: 아니요,5. 다음질문을만드십시오.请设计问句。

1) 가:______________________________________________________________?나: 예, 책상입니다.2) 가:______________________________________________________________?나: 예, 문입니다.3) 가:______________________________________________________________?나: 아니요, 창문이아닙니다.4) 가:______________________________________________________________?나: 아니요, 의자가아닙니다.5) 가:______________________________________________________________?나: 아니요, 잡지가아닙니다.6) 가:______________________________________________________________?나: 예, 사전입니다.7) 가:______________________________________________________________?나: 예, 학생입니다.8) 가:______________________________________________________________?나: 아니요, 선생님이아닙니다.6. 다음보기와같이대답하십시오. 请仿照例子回答问题。

聚四氟乙烯性能全参数

1．聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。

聚四氟乙烯以碳原子为骨架，氟原子对称而均匀地分布在它的周围，构成严密的屏障，使它具有非常宝贵的综合物理机械性能(表14—9)。

聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性，即使温度较高，也不会发生作用，其耐腐蚀性能甚至超过玻璃、瓷、不锈钢以至金、铂，所以，素有“塑料王”之称。

除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外，对酮类、醇类等有机溶剂均有耐蚀性。

只有熔融态的碱金属及元素氟等在高温下才能对它起作用。

聚四氟乙烯的介电性能优异，绝缘强度及抗电弧性能也很突出，介质损耗角正切值很低，但抗电晕性能不好。

聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好，在户外暴露3年，抗拉强度几乎保持不变，仅伸长率有所下降。

聚四氟乙烯薄膜与涂层由于有细孔，故能透过水和气体。

聚四氟乙烯在200℃以上，开始极微量的裂解，即使升温到结晶体熔点327℃，仍裂解很少，每小时失重为万分之二。

但加热至400℃以上热裂解速度逐渐加快，产生有毒气体，因此，聚四氟乙烯烧结温度一般控制在375～380℃。

聚四氟乙烯分子间的德华引力小，容易产生键间滑动，故聚四氟乙烯具有很低的摩擦系数及不粘性，摩擦系数在已知固体材料中是最低的。

聚四氟乙烯的导热系数小，该性能对其成型工艺及应用影响较大。

其不但导热性差，且线膨胀系数较大，加入填充剂可适当降低线膨胀系数。

在负荷下会发生蠕变现象，亦称作“冷流”，加入填充剂可减轻蠕变程度。

聚四氟乙烯可以添加不同的填充剂，选择的填充剂应基本满足下述要求：能耐380℃高温即四氟制品的烧结温度；与接触的介质不发生反应；与四氟树脂有良好的混入性；能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。

常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。

如填充玻璃纤维或石墨，可提高四氟制品的耐磨、耐冷流性，填充MoS2可提高其润滑性，填充青铜、钼、镍、铝、银、钨、铁等，可改善导热性，填充聚酰亚胺或聚苯酯，可提高耐磨性，填充聚苯硫醚后能提高抗蠕变能力，保证尺寸稳定等。

成都七中初中初二半期数学试卷及解析

‘ ｛·
．，工、 ·． .I_' L� u τ
m I 页，:J� ＇＂页
二 tlU豆
ω ［饷］他山乡份材咛于Wlr跺均锹
之一和·
/J.
土斗
－；
3
j与· C-3 ] -J)
，－易 llf. 5-,fo ［角手柯］枫：；
J .,-I斤·J.) = ;,+ ［－（巧’习习’巧
三角号槐 IS llJ锦帆二lff-Js t 项宁！
l 了灿仅
个蚊有〈
3.1川 131 L i 3 ,J
〉
（丰11专I！川之间阳一个 I ）叫主耐，，无理删
A. I个
B. 2个'
：τ2以下列八· 3.
M
5, 3
蚊踹为边陀仰叫 B. 6, 8, LO
3
个数的贷才C平／J 斗1
c. 3 A
D. 4 个〉
D. 6, 12, 13
.. 4.下列运算正确的｛
【某七初期中 9】
【初二暑假.勤思班.第六讲.例题 2】
【某七初期中 11】
【初二暑假.勤思班.第三讲.例题 1（2）】
【某七初期中 13】【某七初期中 18】【某七初期中 20】
【初二暑假.勤思班.第五讲.演练 5】【初二暑假.勤思班.第四讲.例题 3】【初二秋季.勤思班.第三讲.例题 2】
题 18 方程与不等式二元一次为程组解法
8
女
19 方程与不等式
为程的应用
8
女
20 勾股定理
勾股定理与金等综合 10
2018-2019 某七初学校初二（上）数学期中
匹配度分析
考试题目
【某七初期中 1】

01.数字码序(1-3d)3077.P0241-0260.P1046汉字基本集V186

01.數字碼序(1-3d)
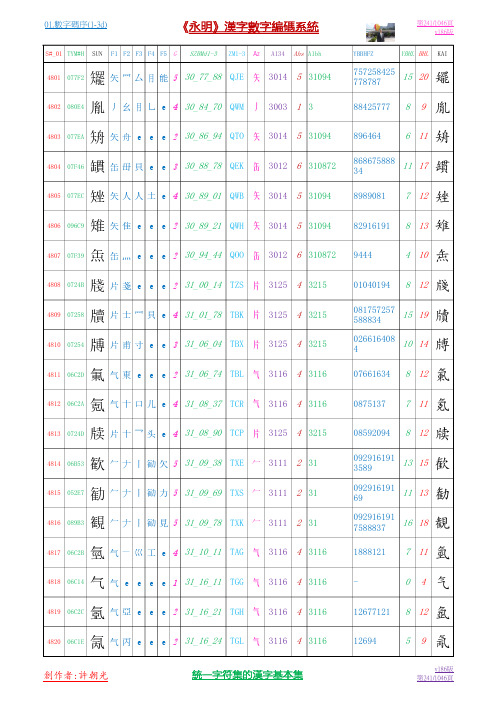
《永明》漢字數字編碼系統
F1 F2 F3 F4 F5 G
第241/1046頁 v186版 YBBHFZ
S#_01 TYM#H
SUN
SZBMd1-3
ZM1-3
Az
A134
Ahs A1bh
YBHL BHL
KAI
4801 077F2
矲胤矪罆矬雉缹牋牘牔氭氪牍歓勧観氫气氬氞
4822 06C29
4823 0520F
4824 06C19
4825 05C13
4826 07247
4827 0516A
4828 06C1D
4829 065A4
4830 06C18
4831 06C1A
4832 07248
4833 06C1B
4834 06C21
4835 07250
9 13 4 8
4836 06B23
S#_01 TYM#H
SUN
SZBMd1-3
ZM1-3
Az
A134
Ahs A1bh
YBHL BHL
KAI
4821 09880
颀氩刏氙尓片兪氝斤氘氚版氛氡牐欣氣牖牓牑
斤页 e e e 2 31_17_39 TFW 斤 3132 4 3312 气亚 e e e 2 31_17_71 TFH 气 3116 4 3116 气刂 e e e 2 31_22_22 TJJ 气 3116 4 3116 气山 e e e 2 31_22_72 TJJ 气 3116 4 3116 �� 小 e e e 2 31_24_34 TLW �� 3111 2 31 片 e e e e 1 31_25_12 TMF 片 3125 4 3215 �� ⺝巜 e e 3 31_27_88 TJE �� 3191 3 391 气内 e e e 2 31_29_64 TLS 气 3116 4 3116 斤 e e e e 1 31_32_13 TRD 斤 3132 4 3312 气介 e e e 2 31_32_22 TRJ 气 3116 4 3116 气川 e e e 2 31_32_72 TRJ 气 3116 4 3116 片⺁又 e e 3 31_33_65 TEA 片 3125 4 3215 气八刀 e e 3 31_34_53 TWC 气 3116 4 3116 气夂⺀ e e 3 31_35_92 TQU 气 3116 4 3116 片千臼 e e 3 31_38_36 TET 片 3125 4 3215 斤欠 e e e 2 31_38_59 TEX 斤 3132 4 3312 气米 e e e 2 31_40_34 TPW 气 3116 4 3116 片户甫 e e 3 31_41_06 TYB 片 3125 4 3215 片亠丷冖方 5 31_41_45 TYP 片 3125 4 3215 片户 �� e e 3 31_41_76 TYH 片 3125 4 3215

2025年高考数学一轮知识点复习1.5-一元二次不等式及其解法-专项训练【含答案】

第一章集合、常用逻辑用语与不等式第五节一元二次不等式及其解法1.不等式－x2＋3x＋10＞0的解集为（）A.（－2，5）B.（－∞，－2）∪（5，＋∞）C.（－5，2）D.（－∞，－5）∪（2，＋∞）2.下列不等式中解集为R的是（）A.－x2＋2x＋1≥0B.x2－25x＋5＞0C.x2＋6x＋10＞0D.2x2－3x＋4＜03.设m＋n＞0，则关于x的不等式（m－x）（n＋x）＞0的解集是（）A.{x｜x＜－n或x＞m}B.{x｜－n＜x＜m}C.{x｜x＜－m或x＞n}D.{x｜－m＜x＜n}4.不等式｜x｜（1－2x）＞0的解集为（）A.（－∞，0）∪（0，12）B.（－∞，12）C.（12，＋∞）D.（0，12）5.某小型服装厂生产一种风衣，日销售量x（件）与单价p（元）之间的关系为p＝160－2x，生产x 件所需成本为c（元），其中c＝500＋30x，若要求每天获利不少于1300元，则日销量x的取值范围是（）A.{x｜20≤x≤30，x∈N}B.{x｜20≤x≤45，x∈N}C.{x｜15≤x≤30，x∈N}D.{x｜15≤x≤45，x∈N}6.（多选）解关于x的不等式ax2＋（2－4a）x－8＞0，则下列说法中正确的是（）A.当a＝0时，不等式的解集为{x｜x＞4}B.当a＜0时，不等式的解集为{x｜x＞4或x＜－2}C.当a＜0时，不等式的解集为{x｜－2＜x＜4}D.当a＝－12时，不等式的解集为⌀7.不等式2x2－3｜x｜－35＞0的解集为.8.若不等式x2＋x＋m2＜0的解集不是空集，则实数m的取值范围为.9.若不等式ax2＋5x＋1≤0的解集为{x｜－12≤x≤－13}，则不等式－－3≤1的解集为.10.求下列关于x的不等式：（1）3r5－1＞x；（2）6x2＋ax－a2＜0.11.“m＜4”是“2x2－mx＋1＞0在x∈（1，＋∞）上恒成立”的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件12.若关于x的不等式x2－（m＋2）x＋2m＜0的解集中恰有4个整数，则实数m的取值范围为（）A.（6，7]B.[－3，－2）C.[－3，－2）∪（6，7]D.[－3，7]13.若不等式x2＋ax－2＞0在[1，5]上有解，则实数a的取值范围是.14.已知a，b，c∈R，关于x的不等式bx2－3x＋2＞0的解集为{x｜x＜1或x＞c}.（1）求b，c的值；（2）解关于x的不等式ax2－（ac＋b）x＋bc＜0.15.已知函数f（x）＝x2－2x＋1.（1）若f（x）≥0在R上恒成立，求实数a的取值范围；（2）若∃x∈[1，2]，f（x）≥2成立，求实数a的取值范围.参考答案与解析1.D存在量词命题的否定是全称量词命题，原命题的否定形式为“∀x∈R，f（x）≤1或f（x）＞2”.故选D.2.B对于A，∀x∈R，x2＋2x＋1＝（x＋1）2≥0，故A错误；对于B，含有全称量词“任意”，是全称量词命题且是真命题，故B正确；对于C，当x＝－1时，2x＝－2，为偶数，但x∉N，故C错误；对于D，π是无理数不是全称量词命题，故D错误.故选B.3.A若m＝－3，则a＝（9，－9）＝9b，所以a∥b；若a∥b，则m2×（－1）－（－9）×1＝0，解得m＝±3，得不出m＝－3.所以“m＝－3”是“a∥b”的充分不必要条件.故选A.4.B方程x2－4x＋4a＝0有实根，故Δ＝16－16a≥0，∴a∈（－∞，1]，函数f（x）＝（2－a）x 为增函数，故2－a＞1，∴a∈（－∞，1）.∵（－∞，1）⫋（－∞，1]，∴p是q的必要不充分条件，故选B.5.C法一因为xy≠0，且＋＝－2⇔x2＋y2＝－2xy⇔x2＋y2＋2xy＝0⇔（x＋y）2＝0⇔x＋y＝0.所以“x＋y＝0”是“＋＝－2”的充要条件.＝－1－1＝－2.法二充分性：因为xy≠0，且x＋y＝0，所以x＝－y，所以＋＝－＋－必要性：因为xy≠0，且＋＝－2，所以x2＋y2＝－2xy，即x2＋y2＋2xy＝0，即（x＋y）2＝0，所以x＋y＝0.所以“x＋y＝0”是“＋＝－2”的充要条件.6.AB由2≥1得0＜x≤2，依题意由选项组成的集合是（0，2]的真子集，故选A、B.7.AD A、B选项，p的否定是“∀x∈R，x2－2x＋a＋6≠0”，q的否定是“∃x∈R，x2＋mx＋1≤0”，所以A正确，B不正确；C选项，若p为假命题，则p的否定“∀x∈R，x2－2x＋a＋6≠0”是真命题，即方程x2－2x＋a＋6＝0在实数范围内无解，Δ＝4－4（a＋6）＜0，得a＞－5，C不正确；D 选项，q为真命题，则Δ＝m2－4＜0，解得－2＜m＜2，D正确.故选A、D.8.假解析：若直线l与平面α内的所有直线都不平行，则直线l与平面α相交，所以直线l与平面α不平行，所以命题p为真命题，所以p为假命题.9.－1（答案不唯一）解析：由于当x＞0时，x＋1≥2，当且仅当x＝1时等号成立，当x＜0时，x ＋1≤－2，当且仅当x＝－1时等号成立，所以x取负数，即可满足题意.例如x＝－1时，x＋1＝－2.10.（－∞，－2]解析：由命题p为真，得a≤0；由命题q为真，得Δ＝4a2－4（2－a）≥0，即a≤－2或a≥1，所以a≤－2.11.D∀改写为∃，∃改写为∀，n≤x2的否定是n＞x2，则该命题的否定形式为“∃x∈R，∀n∈N*，都有n＞x2”.12.C选项A：“开关A闭合”是“灯泡B亮”的充分不必要条件；选项B：“开关A闭合”是“灯泡B亮”的充要条件；选项C：“开关A闭合”是“灯泡B亮”的必要不充分条件；选项D：“开关A闭合”是“灯泡B亮”的既不充分也不必要条件.故选C.13.ABD对于A选项，若xc2＞yc2，则c2≠0，则x＞y，反之x＞y，当c＝0时得不出xc2＞yc2，所以“xc2＞yc2”是“x＞y”的充分不必要条件，故A正确；对于B选项，由1＜1＜0可得y＜x＜0，即能推出x＞y；但x＞y不能推出1＜1＜0（因为x，y的正负不确定），所以“1＜1＜0”是“x＞y”的充分不必要条件，故B正确；对于C选项，由｜x｜＞｜y｜可得x2＞y2，则（x＋y）（x－y）＞0，不能推出x＞y；由x＞y也不能推出｜x｜＞｜y｜（如x＝1，y＝－2），所以“｜x｜＞｜y｜”是“x ＞y”的既不充分也不必要条件，故C错误；对于D选项，若ln x＞ln y，则x＞y，反之x＞y得不出ln x＞ln y，所以“ln x＞ln y”是“x＞y”的充分不必要条件，故D正确.14.12（12，＋∞）解析：若A是B的充要条件，则A＝B，即x＝2是方程bx＝1的解，故b＝12；若A是B的充分不必要条件，则A⫋B，易知b＞0，则B＝{x｜x＞1}，故1＜2，即b＞12，故b的取值范围是（12，＋∞）.15.（－∞，0）解析：由题意知，当x∈[1，4]时，f（x）min＝f（1）＝2，g（x）max＝g（4）＝2＋m，则f（x）min＞g（x）max，即2＞2＋m，解得m＜0，故实数m的取值范围是（－∞，0）.1.A由－x2＋3x＋10＞0得x2－3x－10＜0，解得－2＜x＜5.2.C在C项中，对于方程x2＋6x＋10＝0，因为Δ＝36－40＝－4＜0，所以不等式x2＋6x＋10＞0的解集为R.3.B不等式（m－x）（n＋x）＞0可化为（x－m）·（x＋n）＜0，因为m＋n＞0，所以m＞－n，所以原不等式的解集为{x｜－n＜x＜m}，故选B.4.A由题意得x≠0，当x＞0时，原不等式即为x（1－2x）＞0，所以0＜x＜12；当x＜0时，原不等式即为－x（1－2x）＞0，所以x＜0，综上，原不等式的解集为（－∞，0）∪（0，12）.5.B设该厂每天获得的利润为y元，则y＝（160－2x）·x－（500＋30x）＝－2x2＋130x－500，0＜x＜80，x∈N.根据题意知，－2x2＋130x－500≥1300，解得20≤x≤45，x∈N.所以当20≤x≤45，x∈N 时，每天获得的利润不少于1300元，故选B.6.AD当a＝0时，不等式为2x－8＞0，解得x＞4，故选项A正确.由ax2＋（2－4a）x－8＞0可得（ax＋2）·（x－4）＞0，当<0，－2<4，即a＜－12时，不等式的解集为{x｜－2＜x＜4}；当<0，－2>4，即－12＜a＜0时，不等式的解集为{x｜4＜x＜－2}；当a＝－12时，－2＝4，此时不等式的解集为⌀，故选项B、C不正确，选项D正确.故选A、D.7.{x｜x＜－5或x＞5}解析：2x2－3｜x｜－35＞0⇔2｜x｜2－3｜x｜－35＞0⇔（｜x｜－5）（2｜x｜＋7）＞0⇔｜x｜＞5或｜x｜＜－72（舍去）⇔x＞5或x＜－5.8.（－12，12）解析：因为不等式x2＋x＋m2＜0的解集不是空集，所以Δ＞0，即1－4m2＞0，所以－12＜m＜12.9.{x｜x＞3}解析：因为不等式ax2＋5x＋1≤0的解集为{x｜－12≤x≤－13}，所以－12，－13是方程ax2＋5x＋1＝0的两根，所以a＝6，所以－－3≤1可化为－3－3≤0，解得x＞3，所以不等式－－3≤1的解集为{x｜x＞3}.10.解：（1）不等式3r5－1＞x化为以下两个不等式组－1<0，3+5<2－或－1>0，3+5>2－，由－1<0，3+5<2－，即<1，2－4－5>0，解得x＜－1，由－1>0，3+5>2－，即>1，2－4－5<0，解得1＜x＜5，所以原不等式的解集是（－∞，－1）∪（1，5）.（2）原不等式可化为（2x＋a）（3x－a）＜0，即（x＋2）·（x－3）＜0.①当－2＜3，即a＞0时，－2＜x＜3；②当－2＝3，即a＝0时，原不等式的解集为⌀；③当－2＞3，即a＜0时，3＜x＜－2.综上，当a＞0时，原不等式的解集为{x｜－2＜x＜3}；当a＝0时，原不等式的解集为⌀；当a＜0时，原不等式的解集为{x｜3＜x＜－2}.11.B2x2－mx＋1＞0在x∈（1，＋∞）上恒成立，即m＜2x＋1在x∈（1，＋∞）上恒成立，2x＋1∈（3，＋∞），故m≤3，“m＜4”是“m≤3”的必要不充分条件，故选B.12.C不等式x2－（m＋2）x＋2m＜0即（x－2）（x－m）＜0.当m＞2时，不等式解集为（2，m），此时要使解集中恰有4个整数，这四个整数只能是3，4，5，6，故6＜m≤7，当m＝2时，不等式解集为⌀，此时不符合题意；当m＜2时，不等式解集为（m，2），此时要使解集中恰有4个整数，这四个整数只能是－2，－1，0，1，故－3≤m＜－2.故实数m的取值范围为[－3，－2）∪（6，7]，故选C.13.（－235，＋∞）解析：对于方程x2＋ax－2＝0，∵Δ＝a2＋8＞0，∴方程x2＋ax－2＝0有两个不相等的实数根，又∵两根之积为负，∴必有一正根一负根，设f（x）＝x2＋ax－2，于是不等式x2＋ax－2＞0在[1，5]上有解的充要条件是f（5）＞0，即5a＋23＞0，解得a＞－235，故a的取值范围是（－235，＋∞）.14.解：（1）因为不等式bx2－3x＋2＞0的解集为{x｜x＜1或x＞c}，所以x1＝1与x2＝c是方程bx2－3x＋2＝0的两个实数根，由根与系数的关系，得1+＝3，1×＝2，解得b＝1，c＝2.（2）由（1）知不等式ax2－（ac＋b）x＋bc＜0为ax2－（2a＋1）x＋2＜0，即（ax－1）（x－2）＜0.①当a＝0时，易得不等式的解集为{x｜x＞2}.②当a＜0时，不等式可化为（x－1）（x－2）＞0，不等式的解集为{x｜x＜1或x＞2}.③当a＞0时，不等式可化为（x－1）（x－2）＜0，当1＞2，即0＜a＜12时，不等式的解集为{x｜2＜x＜1}，当1＝2，即a＝12时，不等式的解集为⌀，当1＜2，即a＞12时，不等式的解集为{x｜1＜x＜2}.15.解：（1）由题意得Δ＝24－4≤0，解得－4≤a≤4，∴实数a的取值范围为[－4，4].（2）由题意∃x∈[1，2]，使得2≤x－1成立.令g（x）＝x－1，x∈[1，2]，则g（x）在区间[1，2]上单调递增，∴g（x）max＝g（2）＝32，∴2≤32，解得a≤3，∴实数a的取值范围为（－∞，3].。

高中数学必修第一册《一元二次函数、方程和不等式》期末复习专项训练(学生版+解析版)

高中数学必修第一册《一元二次函数、方程和不等式》期末复习专项训练一、单选题l. (2022·四川绵阳·高一期末〉下列结论正确的是（〉A.若的b，则。

c>bc c.若。

＞b，则。

＋c>b+cl I B.若α＞b，则－〉－a D D.着。

＞b，则。

2> b22.(2022·辽宁·新民市第一高级中学高一期末〉已知α＜b<O，则（〉A.a2 <abB.ab<b2C.a1 <b1D.a2 >b i3.(2022·陕西汉中·高一期末〉若关于工的不等式，咐2+2x+m>O的解集是R，则m的取值范围是（〉A.(I, +oo)B.(0, I〕C.( -J, I)D.(J, +oo)4.(2022·广东珠海高一期末〉不等式。

＋l)(x+3)<0的解集是（〉A.RB.②c.｛对－3<x<-I} D.{xi x<-3，或x>-l}5. (2022·四川甘孜·高一期末〉若不等式似2+bx-2<0的解集为｛xl-2<x<I｝，则。

÷b=( )A.-2B.OC.ID.26. (2022·湖北黄石·商一期末〉若关于X的不等式x2-ax’＋7＞。

在（2,7）上有实数解，则α的取值范围是（〉A.（唱，8)B.（叫8] c.（叫2./7) D.（斗）7.(2022·新疆乌市一中高一期末〉已知y=(x-m)(x-n)+2022(n> m），且α，β（α〈别是方程y=O的两实数根，则α，β，111,n的大小关系是（〉A.α＜m<n＜βC.m＜α〈β＜nB.m＜α＜n＜βD.α＜m＜β＜n8.(2022·浙江·杭州四中高一期末〉已失11函数y＝κ－4+...2....(x>-1），当x=a时，y取得最小值b，则。

(完整word)Unicode汉字编码表

Unicode汉字编码表1 unicode编码表Unicode目前普遍采用的是UCS-2,它用两个字节来编码一个字符，比如汉字"经”的编码是0x7ECF，注意字符编码一般用十六进制来表示,为了与十进制区分,十六进制以0x开头,0x7ECF转换成十进制就是32463,UCS—2用两个字节来编码字符,两个字节就是16位二进制, 2的16次方等于65536,所以UCS-2最多能编码65536个字符。

编码从0到127的字符与ASCII编码的字符一样，比如字母"a"的Unicode 编码是0x0061,十进制是97,而”a”的ASCII编码是0x61,十进制也是97，对于汉字的编码，事实上Unicode对汉字支持不怎么好，这也是没办法的, 简体和繁体总共有六七万个汉字，而UCS—2最多能表示65536个，才六万多个，所以Unicode只能排除一些几乎不用的汉字，好在常用的简体汉字也不过七千多个,为了能表示所有汉字,Unicode也有UCS—4规范,就是用4个字节来编码字符，不过现在普遍采用的还是UCS—2，只用两个字节来编码,看一下Unicode对汉字的编码:——-------—----—--—---—--————----——————-—-—-—--——-————--—---—---——--——-—-2 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F—---—-—--—————--—-——-———————--------—---—————————---—4e00 一丁丂七丄丅丆万丈三上下丌不与丏4e10 丐丑丒专且丕世丗丘丙业丛东丝丞丟4e20 丠両丢丣两严並丧丨丩个丫丬中丮丯4e30 丰丱串丳临丵丶丷丸丹为主丼丽举丿4e40 乀乁乂乃乄久乆乇么义乊之乌乍乎乏4e50 乐乑乒乓乔乕乖乗乘乙乚乛乜九乞也4e60 习乡乢乣乤乥书乧乨乩乪乫乬乭乮乯4e70 买乱乲乳乴乵乶乷乸乹乺乻乼乽乾乿4e80 亀亁亂亃亄亅了亇予争亊事二亍于亏4e90 亐云互亓五井亖亗亘亙亚些亜亝亞亟4ea0 亠亡亢亣交亥亦产亨亩亪享京亭亮亯4eb0 亰亱亲亳亴亵亶亷亸亹人亻亼亽亾亿4ec0 什仁仂仃仄仅仆仇仈仉今介仌仍从仏4ed0 仐仑仒仓仔仕他仗付仙仚仛仜仝仞仟4ee0 仠仡仢代令以仦仧仨仩仪仫们仭仮仯4ef0 仰仱仲仳仴仵件价仸仹仺任仼份仾仿4f00 伀企伂伃伄伅伆伇伈伉伊伋伌伍伎伏4f10 伐休伒伓伔伕伖众优伙会伛伜伝伞伟4f20 传伡伢伣伤伥伦伧伨伩伪伫伬伭伮伯—-—-—-——---————-----—---—-—-—-————-——-——--------—-—-——3 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F----———-—-———-—--------——---—-—-—--—-———---———---—---4f30 估伱伲伳伴伵伶伷伸伹伺伻似伽伾伿4f40 佀佁佂佃佄佅但佇佈佉佊佋佌位低住4f50 佐佑佒体佔何佖佗佘余佚佛作佝佞佟4f60 你佡佢佣佤佥佦佧佨佩佪佫佬佭佮佯4f70 佰佱佲佳佴併佶佷佸佹佺佻佼佽佾使4f80 侀侁侂侃侄侅來侇侈侉侊例侌侍侎侏4f90 侐侑侒侓侔侕侖侗侘侙侚供侜依侞侟4fa0 侠価侢侣侤侥侦侧侨侩侪侫侬侭侮侯4fb0 侰侱侲侳侴侵侶侷侸侹侺侻侼侽侾便4fc0 俀俁係促俄俅俆俇俈俉俊俋俌俍俎俏4fd0 俐俑俒俓俔俕俖俗俘俙俚俛俜保俞俟4fe0 俠信俢俣俤俥俦俧俨俩俪俫俬俭修俯4ff0 俰俱俲俳俴俵俶俷俸俹俺俻俼俽俾俿5000 倀倁倂倃倄倅倆倇倈倉倊個倌倍倎倏5010 倐們倒倓倔倕倖倗倘候倚倛倜倝倞借5020 倠倡倢倣値倥倦倧倨倩倪倫倬倭倮倯5030 倰倱倲倳倴倵倶倷倸倹债倻值倽倾倿5040 偀偁偂偃偄偅偆假偈偉偊偋偌偍偎偏5050 偐偑偒偓偔偕偖偗偘偙做偛停偝偞偟5060 偠偡偢偣偤健偦偧偨偩偪偫偬偭偮偯5070 偰偱偲偳側偵偶偷偸偹偺偻偼偽偾偿-———-—---—--—-——--——————--—----———--——————--——-——------4 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F-—--—---—-—--—--—--——-—--——----————-———-—---——------—5080 傀傁傂傃傄傅傆傇傈傉傊傋傌傍傎傏5090 傐傑傒傓傔傕傖傗傘備傚傛傜傝傞傟50a0 傠傡傢傣傤傥傦傧储傩傪傫催傭傮傯50b0 傰傱傲傳傴債傶傷傸傹傺傻傼傽傾傿50c0 僀僁僂僃僄僅僆僇僈僉僊僋僌働僎像50d0 僐僑僒僓僔僕僖僗僘僙僚僛僜僝僞僟50e0 僠僡僢僣僤僥僦僧僨僩僪僫僬僭僮僯50f0 僰僱僲僳僴僵僶僷僸價僺僻僼僽僾僿5100 儀儁儂儃億儅儆儇儈儉儊儋儌儍儎儏5110 儐儑儒儓儔儕儖儗儘儙儚儛儜儝儞償5120 儠儡儢儣儤儥儦儧儨儩優儫儬儭儮儯5130 儰儱儲儳儴儵儶儷儸儹儺儻儼儽儾儿5140 兀允兂元兄充兆兇先光兊克兌免兎兏5150 児兑兒兓兔兕兖兗兘兙党兛兜兝兞兟5160 兠兡兢兣兤入兦內全兩兪八公六兮兯5170 兰共兲关兴兵其具典兹兺养兼兽兾兿5180 冀冁冂冃冄内円冇冈冉冊冋册再冎冏5190 冐冑冒冓冔冕冖冗冘写冚军农冝冞冟51a0 冠冡冢冣冤冥冦冧冨冩冪冫冬冭冮冯51b0 冰冱冲决冴况冶冷冸冹冺冻冼冽冾冿51c0 净凁凂凃凄凅准凇凈凉凊凋凌凍凎减-———---———--—--—-——-—--—-——————-——---—————---—---——-—--5 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F——-—----———--—------——-—--——-—-------------———--—-—--51D0 凐凑凒凓凔凕凖凗凘凙凚凛凜凝凞凟51E0 几凡凢凣凤凥処凧凨凩凪凫凬凭凮凯51F0 凰凱凲凳凴凵凶凷凸凹出击凼函凾凿5200 刀刁刂刃刄刅分切刈刉刊刋刌刍刎刏5210 刐刑划刓刔刕刖列刘则刚创刜初刞刟5220 删刡刢刣判別刦刧刨利刪别刬刭刮刯5230 到刱刲刳刴刵制刷券刹刺刻刼刽刾刿5240 剀剁剂剃剄剅剆則剈剉削剋剌前剎剏5250 剐剑剒剓剔剕剖剗剘剙剚剛剜剝剞剟5260 剠剡剢剣剤剥剦剧剨剩剪剫剬剭剮副5270 剰剱割剳剴創剶剷剸剹剺剻剼剽剾剿5280 劀劁劂劃劄劅劆劇劈劉劊劋劌劍劎劏5290 劐劑劒劓劔劕劖劗劘劙劚力劜劝办功52A0 加务劢劣劤劥劦劧动助努劫劬劭劮劯52B0 劰励劲劳労劵劶劷劸効劺劻劼劽劾势52C0 勀勁勂勃勄勅勆勇勈勉勊勋勌勍勎勏52D0 勐勑勒勓勔動勖勗勘務勚勛勜勝勞募52E0 勠勡勢勣勤勥勦勧勨勩勪勫勬勭勮勯52F0 勰勱勲勳勴勵勶勷勸勹勺勻勼勽勾勿5300 匀匁匂匃匄包匆匇匈匉匊匋匌匍匎匏5310 匐匑匒匓匔匕化北匘匙匚匛匜匝匞匟—--—--—----—--——--—-———————--——----—————-——-—-—-—------6 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F--—--——-———--——-———----——-——-——-—--—-—--—-———--—-————5320 匠匡匢匣匤匥匦匧匨匩匪匫匬匭匮匯5330 匰匱匲匳匴匵匶匷匸匹区医匼匽匾匿5340 區十卂千卄卅卆升午卉半卋卌卍华协5350 卐卑卒卓協单卖南単卙博卛卜卝卞卟5360 占卡卢卣卤卥卦卧卨卩卪卫卬卭卮卯5370 印危卲即却卵卶卷卸卹卺卻卼卽卾卿5380 厀厁厂厃厄厅历厇厈厉厊压厌厍厎厏5390 厐厑厒厓厔厕厖厗厘厙厚厛厜厝厞原53a0 厠厡厢厣厤厥厦厧厨厩厪厫厬厭厮厯53b0 厰厱厲厳厴厵厶厷厸厹厺去厼厽厾县53c0 叀叁参參叄叅叆叇又叉及友双反収叏53d0 叐发叒叓叔叕取受变叙叚叛叜叝叞叟53e0 叠叡叢口古句另叧叨叩只叫召叭叮可53f0 台叱史右叴叵叶号司叹叺叻叼叽叾叿5400 吀吁吂吃各吅吆吇合吉吊吋同名后吏5410 吐向吒吓吔吕吖吗吘吙吚君吜吝吞吟5420 吠吡吢吣吤吥否吧吨吩吪含听吭吮启5430 吰吱吲吳吴吵吶吷吸吹吺吻吼吽吾吿5440 呀呁呂呃呄呅呆呇呈呉告呋呌呍呎呏5450 呐呑呒呓呔呕呖呗员呙呚呛呜呝呞呟5460 呠呡呢呣呤呥呦呧周呩呪呫呬呭呮呯-——--——-—---—--——----—--------———--—-——----———--——-—-——7 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F———-—---—--—-————--——-————---—--—-—-——-——-————-------5470 呰呱呲味呴呵呶呷呸呹呺呻呼命呾呿5480 咀咁咂咃咄咅咆咇咈咉咊咋和咍咎咏5490 咐咑咒咓咔咕咖咗咘咙咚咛咜咝咞咟54a0 咠咡咢咣咤咥咦咧咨咩咪咫咬咭咮咯54b0 咰咱咲咳咴咵咶咷咸咹咺咻咼咽咾咿54c0 哀品哂哃哄哅哆哇哈哉哊哋哌响哎哏54d0 哐哑哒哓哔哕哖哗哘哙哚哛哜哝哞哟54e0 哠員哢哣哤哥哦哧哨哩哪哫哬哭哮哯54f0 哰哱哲哳哴哵哶哷哸哹哺哻哼哽哾哿5500 唀唁唂唃唄唅唆唇唈唉唊唋唌唍唎唏5510 唐唑唒唓唔唕唖唗唘唙唚唛唜唝唞唟5520 唠唡唢唣唤唥唦唧唨唩唪唫唬唭售唯5530 唰唱唲唳唴唵唶唷唸唹唺唻唼唽唾唿5540 啀啁啂啃啄啅商啇啈啉啊啋啌啍啎問5550 啐啑啒啓啔啕啖啗啘啙啚啛啜啝啞啟5560 啠啡啢啣啤啥啦啧啨啩啪啫啬啭啮啯5570 啰啱啲啳啴啵啶啷啸啹啺啻啼啽啾啿5580 喀喁喂喃善喅喆喇喈喉喊喋喌喍喎喏5590 喐喑喒喓喔喕喖喗喘喙喚喛喜喝喞喟55a0 喠喡喢喣喤喥喦喧喨喩喪喫喬喭單喯55b0 喰喱喲喳喴喵営喷喸喹喺喻喼喽喾喿-—-——-————---——-—-—----—-——-——--—-----—-——--——-—--———-—-8 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F-————----—---————---—---——-----————————-——-—-——————--55c0 嗀嗁嗂嗃嗄嗅嗆嗇嗈嗉嗊嗋嗌嗍嗎嗏55d0 嗐嗑嗒嗓嗔嗕嗖嗗嗘嗙嗚嗛嗜嗝嗞嗟55e0 嗠嗡嗢嗣嗤嗥嗦嗧嗨嗩嗪嗫嗬嗭嗮嗯55f0 嗰嗱嗲嗳嗴嗵嗶嗷嗸嗹嗺嗻嗼嗽嗾嗿5600 嘀嘁嘂嘃嘄嘅嘆嘇嘈嘉嘊嘋嘌嘍嘎嘏5610 嘐嘑嘒嘓嘔嘕嘖嘗嘘嘙嘚嘛嘜嘝嘞嘟5620 嘠嘡嘢嘣嘤嘥嘦嘧嘨嘩嘪嘫嘬嘭嘮嘯5630 嘰嘱嘲嘳嘴嘵嘶嘷嘸嘹嘺嘻嘼嘽嘾嘿5640 噀噁噂噃噄噅噆噇噈噉噊噋噌噍噎噏5650 噐噑噒噓噔噕噖噗噘噙噚噛噜噝噞噟5660 噠噡噢噣噤噥噦噧器噩噪噫噬噭噮噯5670 噰噱噲噳噴噵噶噷噸噹噺噻噼噽噾噿5680 嚀嚁嚂嚃嚄嚅嚆嚇嚈嚉嚊嚋嚌嚍嚎嚏5690 嚐嚑嚒嚓嚔嚕嚖嚗嚘嚙嚚嚛嚜嚝嚞嚟56a0 嚠嚡嚢嚣嚤嚥嚦嚧嚨嚩嚪嚫嚬嚭嚮嚯56b0 嚰嚱嚲嚳嚴嚵嚶嚷嚸嚹嚺嚻嚼嚽嚾嚿56c0 囀囁囂囃囄囅囆囇囈囉囊囋囌囍囎囏56d0 囐囑囒囓囔囕囖囗囘囙囚四囜囝回囟56e0 因囡团団囤囥囦囧囨囩囪囫囬园囮囯56f0 困囱囲図围囵囶囷囸囹固囻囼国图囿5700 圀圁圂圃圄圅圆圇圈圉圊國圌圍圎圏—----——--—-———-—--—--—-——--—-——--—--—--———-—--—-—--—-—--9 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F——---———-———-————-—--—---—--———-———————-—--——--—-—--—5710 圐圑園圓圔圕圖圗團圙圚圛圜圝圞土5720 圠圡圢圣圤圥圦圧在圩圪圫圬圭圮圯5730 地圱圲圳圴圵圶圷圸圹场圻圼圽圾圿5740 址坁坂坃坄坅坆均坈坉坊坋坌坍坎坏5750 坐坑坒坓坔坕坖块坘坙坚坛坜坝坞坟5760 坠坡坢坣坤坥坦坧坨坩坪坫坬坭坮坯5770 坰坱坲坳坴坵坶坷坸坹坺坻坼坽坾坿5780 垀垁垂垃垄垅垆垇垈垉垊型垌垍垎垏5790 垐垑垒垓垔垕垖垗垘垙垚垛垜垝垞垟57a0 垠垡垢垣垤垥垦垧垨垩垪垫垬垭垮垯57b0 垰垱垲垳垴垵垶垷垸垹垺垻垼垽垾垿57c0 埀埁埂埃埄埅埆埇埈埉埊埋埌埍城埏57d0 埐埑埒埓埔埕埖埗埘埙埚埛埜埝埞域57e0 埠埡埢埣埤埥埦埧埨埩埪埫埬埭埮埯57f0 埰埱埲埳埴埵埶執埸培基埻埼埽埾埿5800 堀堁堂堃堄堅堆堇堈堉堊堋堌堍堎堏5810 堐堑堒堓堔堕堖堗堘堙堚堛堜堝堞堟5820 堠堡堢堣堤堥堦堧堨堩堪堫堬堭堮堯5830 堰報堲堳場堵堶堷堸堹堺堻堼堽堾堿5840 塀塁塂塃塄塅塆塇塈塉塊塋塌塍塎塏5850 塐塑塒塓塔塕塖塗塘塙塚塛塜塝塞塟----—--——-—--——————------——--—-—-—-—-—--———-—---——-——-——10 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F-—-—-—---—--—————-—-——-————-——-—-————————---——-—---—-5860 塠塡塢塣塤塥塦塧塨塩塪填塬塭塮塯5870 塰塱塲塳塴塵塶塷塸塹塺塻塼塽塾塿5880 墀墁墂境墄墅墆墇墈墉墊墋墌墍墎墏5890 墐墑墒墓墔墕墖増墘墙墚墛墜墝增墟58a0 墠墡墢墣墤墥墦墧墨墩墪墫墬墭墮墯58b0 墰墱墲墳墴墵墶墷墸墹墺墻墼墽墾墿58c0 壀壁壂壃壄壅壆壇壈壉壊壋壌壍壎壏58d0 壐壑壒壓壔壕壖壗壘壙壚壛壜壝壞壟58e0 壠壡壢壣壤壥壦壧壨壩壪士壬壭壮壯58f0 声壱売壳壴壵壶壷壸壹壺壻壼壽壾壿5900 夀夁夂夃处夅夆备夈変夊夋夌复夎夏5910 夐夑夒夓夔夕外夗夘夙多夛夜夝夞够5920 夠夡夢夣夤夥夦大夨天太夫夬夭央夯5930 夰失夲夳头夵夶夷夸夹夺夻夼夽夾夿5940 奀奁奂奃奄奅奆奇奈奉奊奋奌奍奎奏5950 奐契奒奓奔奕奖套奘奙奚奛奜奝奞奟5960 奠奡奢奣奤奥奦奧奨奩奪奫奬奭奮奯5970 奰奱奲女奴奵奶奷奸她奺奻奼好奾奿5980 妀妁如妃妄妅妆妇妈妉妊妋妌妍妎妏5990 妐妑妒妓妔妕妖妗妘妙妚妛妜妝妞妟59a0 妠妡妢妣妤妥妦妧妨妩妪妫妬妭妮妯-——————--——--—--——-———-——-———--——---————-—---—-—-—-—--—-11 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F---——-—-—-—-----—-—-—————-----—-——-——————-———-—-—-———59b0 妰妱妲妳妴妵妶妷妸妹妺妻妼妽妾妿59c0 姀姁姂姃姄姅姆姇姈姉姊始姌姍姎姏59d0 姐姑姒姓委姕姖姗姘姙姚姛姜姝姞姟59e0 姠姡姢姣姤姥姦姧姨姩姪姫姬姭姮姯59f0 姰姱姲姳姴姵姶姷姸姹姺姻姼姽姾姿5a00 娀威娂娃娄娅娆娇娈娉娊娋娌娍娎娏5a10 娐娑娒娓娔娕娖娗娘娙娚娛娜娝娞娟5a20 娠娡娢娣娤娥娦娧娨娩娪娫娬娭娮娯5a30 娰娱娲娳娴娵娶娷娸娹娺娻娼娽娾娿5a40 婀婁婂婃婄婅婆婇婈婉婊婋婌婍婎婏5a50 婐婑婒婓婔婕婖婗婘婙婚婛婜婝婞婟5a60 婠婡婢婣婤婥婦婧婨婩婪婫婬婭婮婯5a70 婰婱婲婳婴婵婶婷婸婹婺婻婼婽婾婿5a80 媀媁媂媃媄媅媆媇媈媉媊媋媌媍媎媏5a90 媐媑媒媓媔媕媖媗媘媙媚媛媜媝媞媟5aa0 媠媡媢媣媤媥媦媧媨媩媪媫媬媭媮媯5ab0 媰媱媲媳媴媵媶媷媸媹媺媻媼媽媾媿5ac0 嫀嫁嫂嫃嫄嫅嫆嫇嫈嫉嫊嫋嫌嫍嫎嫏5ad0 嫐嫑嫒嫓嫔嫕嫖嫗嫘嫙嫚嫛嫜嫝嫞嫟5ae0 嫠嫡嫢嫣嫤嫥嫦嫧嫨嫩嫪嫫嫬嫭嫮嫯5af0 嫰嫱嫲嫳嫴嫵嫶嫷嫸嫹嫺嫻嫼嫽嫾嫿—---———----------—-——---—---—-———-—-——-—---—---—--—--12 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F—-—————-—--—----——--—----—--—--—-—---——------—-——--—-5b00 嬀嬁嬂嬃嬄嬅嬆嬇嬈嬉嬊嬋嬌嬍嬎嬏5b10 嬐嬑嬒嬓嬔嬕嬖嬗嬘嬙嬚嬛嬜嬝嬞嬟5b20 嬠嬡嬢嬣嬤嬥嬦嬧嬨嬩嬪嬫嬬嬭嬮嬯5b30 嬰嬱嬲嬳嬴嬵嬶嬷嬸嬹嬺嬻嬼嬽嬾嬿5b40 孀孁孂孃孄孅孆孇孈孉孊孋孌孍孎孏5b50 子孑孒孓孔孕孖字存孙孚孛孜孝孞孟5b60 孠孡孢季孤孥学孧孨孩孪孫孬孭孮孯5b70 孰孱孲孳孴孵孶孷學孹孺孻孼孽孾孿5b80 宀宁宂它宄宅宆宇守安宊宋完宍宎宏5b90 宐宑宒宓宔宕宖宗官宙定宛宜宝实実5ba0 宠审客宣室宥宦宧宨宩宪宫宬宭宮宯5bb0 宰宱宲害宴宵家宷宸容宺宻宼宽宾宿5bc0 寀寁寂寃寄寅密寇寈寉寊寋富寍寎寏5bd0 寐寑寒寓寔寕寖寗寘寙寚寛寜寝寞察5be0 寠寡寢寣寤寥實寧寨審寪寫寬寭寮寯5bf0 寰寱寲寳寴寵寶寷寸对寺寻导寽対寿5c00 尀封専尃射尅将將專尉尊尋尌對導小5c10 尐少尒尓尔尕尖尗尘尙尚尛尜尝尞尟5c20 尠尡尢尣尤尥尦尧尨尩尪尫尬尭尮尯5c30 尰就尲尳尴尵尶尷尸尹尺尻尼尽尾尿5c40 局屁层屃屄居屆屇屈屉届屋屌屍屎屏-—--——-——--——---———---———----——----—---—-—-—-----——-—-13 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F—---——-———--—---------—---—-—---—-—--—--—--——--—-——--5c50 屐屑屒屓屔展屖屗屘屙屚屛屜屝属屟5c60 屠屡屢屣層履屦屧屨屩屪屫屬屭屮屯5c70 屰山屲屳屴屵屶屷屸屹屺屻屼屽屾屿5c80 岀岁岂岃岄岅岆岇岈岉岊岋岌岍岎岏5c90 岐岑岒岓岔岕岖岗岘岙岚岛岜岝岞岟5ca0 岠岡岢岣岤岥岦岧岨岩岪岫岬岭岮岯5cb0 岰岱岲岳岴岵岶岷岸岹岺岻岼岽岾岿5cc0 峀峁峂峃峄峅峆峇峈峉峊峋峌峍峎峏5cd0 峐峑峒峓峔峕峖峗峘峙峚峛峜峝峞峟5ce0 峠峡峢峣峤峥峦峧峨峩峪峫峬峭峮峯5cf0 峰峱峲峳峴峵島峷峸峹峺峻峼峽峾峿5d00 崀崁崂崃崄崅崆崇崈崉崊崋崌崍崎崏5d10 崐崑崒崓崔崕崖崗崘崙崚崛崜崝崞崟5d20 崠崡崢崣崤崥崦崧崨崩崪崫崬崭崮崯5d30 崰崱崲崳崴崵崶崷崸崹崺崻崼崽崾崿5d40 嵀嵁嵂嵃嵄嵅嵆嵇嵈嵉嵊嵋嵌嵍嵎嵏5d50 嵐嵑嵒嵓嵔嵕嵖嵗嵘嵙嵚嵛嵜嵝嵞嵟5d60 嵠嵡嵢嵣嵤嵥嵦嵧嵨嵩嵪嵫嵬嵭嵮嵯5d70 嵰嵱嵲嵳嵴嵵嵶嵷嵸嵹嵺嵻嵼嵽嵾嵿5d80 嶀嶁嶂嶃嶄嶅嶆嶇嶈嶉嶊嶋嶌嶍嶎嶏5d90 嶐嶑嶒嶓嶔嶕嶖嶗嶘嶙嶚嶛嶜嶝嶞嶟———--——-—-—--—-—-————-——---—-———————--—--——--—--—--—-—14 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F--—--—--—-—-————-——-----—-——-——---———-—-————-—---—---5da0 嶠嶡嶢嶣嶤嶥嶦嶧嶨嶩嶪嶫嶬嶭嶮嶯5db0 嶰嶱嶲嶳嶴嶵嶶嶷嶸嶹嶺嶻嶼嶽嶾嶿5dc0 巀巁巂巃巄巅巆巇巈巉巊巋巌巍巎巏5dd0 巐巑巒巓巔巕巖巗巘巙巚巛巜川州巟5de0 巠巡巢巣巤工左巧巨巩巪巫巬巭差巯5df0 巰己已巳巴巵巶巷巸巹巺巻巼巽巾巿5e00 帀币市布帄帅帆帇师帉帊帋希帍帎帏5e10 帐帑帒帓帔帕帖帗帘帙帚帛帜帝帞帟5e20 帠帡帢帣帤帥带帧帨帩帪師帬席帮帯5e30 帰帱帲帳帴帵帶帷常帹帺帻帼帽帾帿5e40 幀幁幂幃幄幅幆幇幈幉幊幋幌幍幎幏5e50 幐幑幒幓幔幕幖幗幘幙幚幛幜幝幞幟5e60 幠幡幢幣幤幥幦幧幨幩幪幫幬幭幮幯5e70 幰幱干平年幵并幷幸幹幺幻幼幽幾广5e80 庀庁庂広庄庅庆庇庈庉床庋庌庍庎序5e90 庐庑庒库应底庖店庘庙庚庛府庝庞废5ea0 庠庡庢庣庤庥度座庨庩庪庫庬庭庮庯5eb0 庰庱庲庳庴庵庶康庸庹庺庻庼庽庾庿5ec0 廀廁廂廃廄廅廆廇廈廉廊廋廌廍廎廏5ed0 廐廑廒廓廔廕廖廗廘廙廚廛廜廝廞廟5ee0 廠廡廢廣廤廥廦廧廨廩廪廫廬廭廮廯——————--————————-------—--—-————-—————-—-—-——-——-————-15 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F-—-—-—-—-—-——---—--—--———-——-——---—-——-—----—-—--——--5ef0 廰廱廲廳廴廵延廷廸廹建廻廼廽廾廿5f00 开弁异弃弄弅弆弇弈弉弊弋弌弍弎式5f10 弐弑弒弓弔引弖弗弘弙弚弛弜弝弞弟5f20 张弡弢弣弤弥弦弧弨弩弪弫弬弭弮弯5f30 弰弱弲弳弴張弶強弸弹强弻弼弽弾弿5f40 彀彁彂彃彄彅彆彇彈彉彊彋彌彍彎彏5f50 彐彑归当彔录彖彗彘彙彚彛彜彝彞彟5f60 彠彡形彣彤彥彦彧彨彩彪彫彬彭彮彯5f70 彰影彲彳彴彵彶彷彸役彺彻彼彽彾彿5f80 往征徂徃径待徆徇很徉徊律後徍徎徏5f90 徐徑徒従徔徕徖得徘徙徚徛徜徝從徟5fa0 徠御徢徣徤徥徦徧徨復循徫徬徭微徯5fb0 徰徱徲徳徴徵徶德徸徹徺徻徼徽徾徿5fc0 忀忁忂心忄必忆忇忈忉忊忋忌忍忎忏5fd0 忐忑忒忓忔忕忖志忘忙忚忛応忝忞忟5fe0 忠忡忢忣忤忥忦忧忨忩忪快忬忭忮忯5ff0 忰忱忲忳忴念忶忷忸忹忺忻忼忽忾忿6000 怀态怂怃怄怅怆怇怈怉怊怋怌怍怎怏6010 怐怑怒怓怔怕怖怗怘怙怚怛怜思怞怟6020 怠怡怢怣怤急怦性怨怩怪怫怬怭怮怯6030 怰怱怲怳怴怵怶怷怸怹怺总怼怽怾怿6040 恀恁恂恃恄恅恆恇恈恉恊恋恌恍恎恏6050 恐恑恒恓恔恕恖恗恘恙恚恛恜恝恞恟6060 恠恡恢恣恤恥恦恧恨恩恪恫恬恭恮息6070 恰恱恲恳恴恵恶恷恸恹恺恻恼恽恾恿—-—-——--------——---———-—--——---———-—------—-—-—--———---16 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B C D E F——-——-—-—----————-—---——————--—---—---——-——--——-—----6080 悀悁悂悃悄悅悆悇悈悉悊悋悌悍悎悏6090 悐悑悒悓悔悕悖悗悘悙悚悛悜悝悞悟60a0 悠悡悢患悤悥悦悧您悩悪悫悬悭悮悯60b0 悰悱悲悳悴悵悶悷悸悹悺悻悼悽悾悿60c0 惀惁惂惃惄情惆惇惈惉惊惋惌惍惎惏60d0 惐惑惒惓惔惕惖惗惘惙惚惛惜惝惞惟60e0 惠惡惢惣惤惥惦惧惨惩惪惫惬惭惮惯60f0 惰惱惲想惴惵惶惷惸惹惺惻惼惽惾惿6100 愀愁愂愃愄愅愆愇愈愉愊愋愌愍愎意6110 愐愑愒愓愔愕愖愗愘愙愚愛愜愝愞感6120 愠愡愢愣愤愥愦愧愨愩愪愫愬愭愮愯6130 愰愱愲愳愴愵愶愷愸愹愺愻愼愽愾愿6140 慀慁慂慃慄慅慆慇慈慉慊態慌慍慎慏6150 慐慑慒慓慔慕慖慗慘慙慚慛慜慝慞慟6160 慠慡慢慣慤慥慦慧慨慩慪慫慬慭慮慯6170 慰慱慲慳慴慵慶慷慸慹慺慻慼慽慾慿6180 憀憁憂憃憄憅憆憇憈憉憊憋憌憍憎憏6190 憐憑憒憓憔憕憖憗憘憙憚憛憜憝憞憟61a0 憠憡憢憣憤憥憦憧憨憩憪憫憬憭憮憯61b0 憰憱憲憳憴憵憶憷憸憹憺憻憼憽憾憿61c0 懀懁懂懃懄懅懆懇懈應懊懋懌懍懎懏—-——--—-—-—-——---——————-—-—--------—---——-——-———--—--——----—-—------———-—---——-—17 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F——-——-—----—----——-—-—-—-—-———-—-—--——------—--—-——-—61d0 懐懑懒懓懔懕懖懗懘懙懚懛懜懝懞懟61e0 懠懡懢懣懤懥懦懧懨懩懪懫懬懭懮懯61f0 懰懱懲懳懴懵懶懷懸懹懺懻懼懽懾懿6200 戀戁戂戃戄戅戆戇戈戉戊戋戌戍戎戏6210 成我戒戓戔戕或戗战戙戚戛戜戝戞戟6220 戠戡戢戣戤戥戦戧戨戩截戫戬戭戮戯6230 戰戱戲戳戴戵戶户戸戹戺戻戼戽戾房6240 所扁扂扃扄扅扆扇扈扉扊手扌才扎扏6250 扐扑扒打扔払扖扗托扙扚扛扜扝扞扟6260 扠扡扢扣扤扥扦执扨扩扪扫扬扭扮扯6270 扰扱扲扳扴扵扶扷扸批扺扻扼扽找承6280 技抁抂抃抄抅抆抇抈抉把抋抌抍抎抏6290 抐抑抒抓抔投抖抗折抙抚抛抜抝択抟62a0 抠抡抢抣护报抦抧抨抩抪披抬抭抮抯62b0 抰抱抲抳抴抵抶抷抸抹抺抻押抽抾抿62c0 拀拁拂拃拄担拆拇拈拉拊拋拌拍拎拏62d0 拐拑拒拓拔拕拖拗拘拙拚招拜拝拞拟62e0 拠拡拢拣拤拥拦拧拨择拪拫括拭拮拯62f0 拰拱拲拳拴拵拶拷拸拹拺拻拼拽拾拿6300 挀持挂挃挄挅挆指挈按挊挋挌挍挎挏6310 挐挑挒挓挔挕挖挗挘挙挚挛挜挝挞挟-—-—-—---———---—--————----—-——-—-——-—-——--—-—-—-———--—18 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F—---——-——--—---—-—-—-—--——---—-—--—-—-—--——-——-—--——-6320 挠挡挢挣挤挥挦挧挨挩挪挫挬挭挮振6330 挰挱挲挳挴挵挶挷挸挹挺挻挼挽挾挿6340 捀捁捂捃捄捅捆捇捈捉捊捋捌捍捎捏6350 捐捑捒捓捔捕捖捗捘捙捚捛捜捝捞损6360 捠捡换捣捤捥捦捧捨捩捪捫捬捭据捯6370 捰捱捲捳捴捵捶捷捸捹捺捻捼捽捾捿6380 掀掁掂掃掄掅掆掇授掉掊掋掌掍掎掏6390 掐掑排掓掔掕掖掗掘掙掚掛掜掝掞掟63a0 掠採探掣掤接掦控推掩措掫掬掭掮掯63b0 掰掱掲掳掴掵掶掷掸掹掺掻掼掽掾掿63c0 揀揁揂揃揄揅揆揇揈揉揊揋揌揍揎描63d0 提揑插揓揔揕揖揗揘揙揚換揜揝揞揟63e0 揠握揢揣揤揥揦揧揨揩揪揫揬揭揮揯63f0 揰揱揲揳援揵揶揷揸揹揺揻揼揽揾揿6400 搀搁搂搃搄搅搆搇搈搉搊搋搌損搎搏6410 搐搑搒搓搔搕搖搗搘搙搚搛搜搝搞搟6420 搠搡搢搣搤搥搦搧搨搩搪搫搬搭搮搯6430 搰搱搲搳搴搵搶搷搸搹携搻搼搽搾搿6440 摀摁摂摃摄摅摆摇摈摉摊摋摌摍摎摏6450 摐摑摒摓摔摕摖摗摘摙摚摛摜摝摞摟6460 摠摡摢摣摤摥摦摧摨摩摪摫摬摭摮摯--—-—-——-————---———---—----———----—-—-—------—-———--—--19 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F—--————-———--—----——-———-—--————-—--—-—--—-——-——-———-6470 摰摱摲摳摴摵摶摷摸摹摺摻摼摽摾摿6480 撀撁撂撃撄撅撆撇撈撉撊撋撌撍撎撏6490 撐撑撒撓撔撕撖撗撘撙撚撛撜撝撞撟64a0 撠撡撢撣撤撥撦撧撨撩撪撫撬播撮撯64b0 撰撱撲撳撴撵撶撷撸撹撺撻撼撽撾撿64c0 擀擁擂擃擄擅擆擇擈擉擊擋擌操擎擏64d0 擐擑擒擓擔擕擖擗擘擙據擛擜擝擞擟64e0 擠擡擢擣擤擥擦擧擨擩擪擫擬擭擮擯64f0 擰擱擲擳擴擵擶擷擸擹擺擻擼擽擾擿6500 攀攁攂攃攄攅攆攇攈攉攊攋攌攍攎攏6510 攐攑攒攓攔攕攖攗攘攙攚攛攜攝攞攟6520 攠攡攢攣攤攥攦攧攨攩攪攫攬攭攮支6530 攰攱攲攳攴攵收攷攸改攺攻攼攽放政6540 敀敁敂敃敄故敆敇效敉敊敋敌敍敎敏6550 敐救敒敓敔敕敖敗敘教敚敛敜敝敞敟6560 敠敡敢散敤敥敦敧敨敩敪敫敬敭敮敯6570 数敱敲敳整敵敶敷數敹敺敻敼敽敾敿6580 斀斁斂斃斄斅斆文斈斉斊斋斌斍斎斏6590 斐斑斒斓斔斕斖斗斘料斚斛斜斝斞斟65a0 斠斡斢斣斤斥斦斧斨斩斪斫斬断斮斯65b0 新斱斲斳斴斵斶斷斸方斺斻於施斾斿—-——--——---———-—---—--———-——-——————---——-----———-—-——-—20 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F-—--————-—-——--—----——-—-—-——----—-——--——-——----—-———65c0 旀旁旂旃旄旅旆旇旈旉旊旋旌旍旎族65d0 旐旑旒旓旔旕旖旗旘旙旚旛旜旝旞旟65e0 无旡既旣旤日旦旧旨早旪旫旬旭旮旯65f0 旰旱旲旳旴旵时旷旸旹旺旻旼旽旾旿6600 昀昁昂昃昄昅昆昇昈昉昊昋昌昍明昏6610 昐昑昒易昔昕昖昗昘昙昚昛昜昝昞星6620 映昡昢昣昤春昦昧昨昩昪昫昬昭昮是6630 昰昱昲昳昴昵昶昷昸昹昺昻昼昽显昿6640 晀晁時晃晄晅晆晇晈晉晊晋晌晍晎晏6650 晐晑晒晓晔晕晖晗晘晙晚晛晜晝晞晟6660 晠晡晢晣晤晥晦晧晨晩晪晫晬晭普景6670 晰晱晲晳晴晵晶晷晸晹智晻晼晽晾晿6680 暀暁暂暃暄暅暆暇暈暉暊暋暌暍暎暏6690 暐暑暒暓暔暕暖暗暘暙暚暛暜暝暞暟66a0 暠暡暢暣暤暥暦暧暨暩暪暫暬暭暮暯66b0 暰暱暲暳暴暵暶暷暸暹暺暻暼暽暾暿66c0 曀曁曂曃曄曅曆曇曈曉曊曋曌曍曎曏66d0 曐曑曒曓曔曕曖曗曘曙曚曛曜曝曞曟66e0 曠曡曢曣曤曥曦曧曨曩曪曫曬曭曮曯66f0 曰曱曲曳更曵曶曷書曹曺曻曼曽曾替6700 最朁朂會朄朅朆朇月有朊朋朌服朎朏—-———-——--——-——————-——---—--—---————-————-----—---————-21 汉字编码表U+ 0 1 2 3 4 5 6 7 8 9 A B CD E F——--———-—--————--—---—--—--—-—--—-———--—-—--—--————-—6710 朐朑朒朓朔朕朖朗朘朙朚望朜朝朞期6720 朠朡朢朣朤朥朦朧木朩未末本札朮术6730 朰朱朲朳朴朵朶朷朸朹机朻朼朽朾朿6740 杀杁杂权杄杅杆杇杈杉杊杋杌杍李杏6750 材村杒杓杔杕杖杗杘杙杚杛杜杝杞束6760 杠条杢杣杤来杦杧杨杩杪杫杬杭杮杯6770 杰東杲杳杴杵杶杷杸杹杺杻杼杽松板6780 枀极枂枃构枅枆枇枈枉枊枋枌枍枎枏6790 析枑枒枓枔枕枖林枘枙枚枛果枝枞枟67a0 枠枡枢枣枤枥枦枧枨枩枪枫枬枭枮枯67b0 枰枱枲枳枴枵架枷枸枹枺枻枼枽枾枿67c0 柀柁柂柃柄柅柆柇柈柉柊柋柌柍柎柏67d0 某柑柒染柔柕柖柗柘柙柚柛柜柝柞柟67e0 柠柡柢柣柤查柦柧柨柩柪柫柬柭柮柯67f0 柰柱柲柳柴柵柶柷柸柹柺査柼柽柾柿6800 栀栁栂栃栄栅栆标栈栉栊栋栌栍栎栏6810 栐树栒栓栔栕栖栗栘栙栚栛栜栝栞栟6820 栠校栢栣栤栥栦栧栨栩株栫栬栭栮栯6830 栰栱栲栳栴栵栶样核根栺栻格栽栾栿6840 桀桁桂桃桄桅框桇案桉桊桋桌桍桎桏6850 桐桑桒桓桔桕桖桗桘桙桚桛桜桝桞桟。

2023年高考数学真题题源解密(新高考全国卷)专题07 数列(解析版)

专题07数列目录一览考向一等差数列1．（2023•新高考Ⅰ•第7题）记S n为数列{a n}的前n项和，设甲：{a n}为等差数列；乙：{��}为等差数列，则（）A．甲是乙的充分条件但不是必要条件B．甲是乙的必要条件但不是充分条件C．甲是乙的充要条件D．甲既不是乙的充分条件也不是乙的必要条件【答案】C解：若{a n}是等差数列，设数列{a n}的首项为a1，公差为d，则S n＝na1+�(�−1)2d，即��=a1+�−12d=�2n+a1−�2，故{��}为等差数列，即甲是乙的充分条件．��+1�+1−��=D，反之，若{��}为等差数列，则可设则��=S1+（n﹣1）D，即S n＝nS1+n（n﹣1）D，当n≥2时，有S n1＝（n﹣1）S1+（n﹣1）（n﹣2）D，﹣上两式相减得：a n＝S n﹣S n﹣1＝S1+2（n﹣1）D，当n＝1时，上式成立，所以a n＝a1+2（n﹣1）D，则a n+1﹣a n＝a1+2nD﹣[a1+2（n﹣1）D]＝2D（常数），所以数列{a n}为等差数列．即甲是乙的必要条件．综上所述，甲是乙的充要条件．考向二等比数列2．（2023•新高考Ⅱ•第8题）记S n为等比数列{a n}的前n项和，若S4＝﹣5，S6＝21S2，则S8＝（）A．120B．85C．﹣85D．﹣120【答案】C解：等比数列{a n}中，S4＝5，S6＝21S2，显然公比q≠1，设首项为a1，则�1(1−�4)1−�=−5①，�1(1−�6)1−�=21�1(1−�2)1−�②，化简②得q4+q2﹣20＝0，解得q2＝4或q2＝﹣5（不合题意，舍去），代入①得�11−�=13，所以S8=�1(1−�8)1−�=�11−�（1﹣q4）（1+q4）=13×（﹣15）×（1+16）＝﹣85．考向三数列综合3．（2023•新高考Ⅰ•第20题）设等差数列{a n}的公差为d，且d＞1．令b n=�2+��，记S n，T n分别为数列{a n}，{b n}的前n项和．（1）若3a2＝3a1+a3，S3+T3＝21，求{a n}的通项公式；（2）若{b n}为等差数列，且S99﹣T99＝99，求d．解：（1）∵3a2＝3a1+a3，S3+T3＝21，∴根据题意可得3(�1+�)=3�1+�1+2�3�1+3�+(2�1+6�1+�+12�1+2�)=21，∴�1=�6�+9�=21，∴2d 2﹣7d +3＝0，又d ＞1，∴解得d ＝3，∴a 1＝d ＝3，∴a n ＝a 1+（n ﹣1）d ＝3n ，n ∈N *；（2）∵{a n }为等差数列，{b n }为等差数列，且b n =�2+��，∴根据等差数列的通项公式的特点，可设a n ＝tn ，则��=�+1�，且d ＝t ＞1；或设a n ＝k （n +1），则��=��，且d ＝k ＞1，①当a n ＝tn ，��=�+1�，d ＝t ＞1时，则S 99﹣T 99=(�+99�)×992−(2�+100�)×992=99，∴50�−51�=1，∴50t 2﹣t ﹣51＝0，又d ＝t ＞1，∴解得d ＝t =5150；②当a n ＝k （n +1），��=��，d ＝k ＞1时，则S 99﹣T 99=(2�+100�)×992−(1�99�)×992=99，∴51�−50�=1，∴51k 2﹣k ﹣50＝0，又d ＝k ＞1，∴此时k 无解，∴综合可得d =5150．4．（2023•新高考Ⅱ•第18题）已知{a n }为等差数列，b n =��−6，�为奇数2��，�为偶数，记S n ，T n 为{a n }，{b n }的前n项和，S 4＝32，T 3＝16．（1）求{a n }的通项公式；（2）证明：当n ＞5时，T n ＞S n ．解：（1）设等差数列{a n }的公差为d ，S n ，T n 为{a n }{b n }的前n 项和，S 4＝32，T 3＝16，则�1+�2+�3+�4=32�1−6+2�2+�3−6=16，即4�1+4(4−1)2�=32�2=7，解得�1=5�=2，故a n＝5+2（n﹣1）＝2n+3；（2）证明：由（1）可知，��=2�−3，�为奇数4�+6，�为偶数，��=(5+2�+3)�2=(�+4)�，当n为偶数时，n＞5，T n＝﹣1+3+•••+2（n﹣1）﹣3+14+22+•••+4n+6=�2[−1+2(�−1)−3]2+�2(14+4�+6)2=�2(14+6�)2=�(3�+7)2，��−��=�2−�2＞0，当n为奇数时，n＞5，T n＝T n﹣1+b n=(�−1)(3�+4)2+2�−3=3�2+5�−102，T n﹣S n=�2−3�−102＞25−15−102=0，故原式得证．【命题意图】考查等差、等比数列的通项公式和前n项和公式，考查等差、等比数列的性质；考查数列的求和方法，考查根据数列的递推公式求通项公式，考查数列和其他知识结合等综合知识．【考查要点】数列是高考考查热点之一，其中等差、等比数列的通项公式、求和公式，以及与等差、等比数列有关的错位相消求和及裂项相消求和，是考查的重点．作为数列综合题，常和充要条件、方程、不等式、函数等结合，涉及到恒成立，存在，最值，解不等式或者证明不等式等，对于基础能力和基础运算要求较高．【得分要点】1．解决等差、等比数列有关问题的几点注意1 等差数列、等比数列公式和性质的灵活应用；2 对于计算解答题注意基本量及方程思想的运用；3 注重问题的转化，由非等差数列、非等比数列构造出新的等差数列或等比数列，以便利用相关公式和性质解题；4 当题目中出现多个数列时，既要纵向考察单一数列的项与项之间的关系，又要横向考察各数列之间的内在联系.2．数列求和问题一般转化为等差数列或等比数列的前n项和问题或已知公式的数列求和，不能转化的再根据数列通项公式的特点选择恰当的方法求解.,一般常见的求和方法有：（一）公式法②等比数列的前n 项和公式：③数列前n 项和重要公式：（2）1(21)n k k 13521n 2n（5）等差数列中，m n m n S S S mnd ；（6）等比数列中，n m m n n m m nS S q S S q S.二分组求和法：把一个数列分成几个可以直接求和的数列.三裂项相消法：有时把一个数列的通项公式分成两项差的形式，相加过程消去中间项，只剩有限项再求和.(1)适用条件：若{a n }是公差为d (d ≠0)的等差数列，{b n }是公比为q (q ≠1)的等比数列，求数列{a n b n }的前n 项和S n ；(2)基本步骤(3)注意事项：①在写出S n 与qS n 的表达式时，应特别注意将两式“错位对齐”，以便下一步准确写出S n －qS n ；②作差后，等式右边有第一项、中间n －1项的和式、最后一项三部分组成；③运算时，经常把b 2＋b 3＋…＋b n 这n －1项和看成n 项和，把－a n b n ＋1写成＋a n b n ＋1导致错误．五倒序相加法如果一个数列{a n}，与首末项等距的两项之和等于首末两项之和，可采用把正着写与倒着写的两个和式相加，就得到一个常数列的和，这一求和方法称为倒序相加法，等差数列前n项和公式的推导便使用了此法.用倒序相加法解题的关键，就是要能够找出首项和末项之间的关系，因为有时这种关系比较隐蔽.考向一等差数列5．（2022•新高考Ⅱ）图1是中国古代建筑中的举架结构，AA′，BB′，CC′，DD′是桁，相邻桁的水平距离称为步，垂直距离称为举．图2是某古代建筑屋顶截面的示意图，其中DD1，CC1，BB1，AA1是举，OD1，DC1，CB1，BA1是相等的步，相邻桁的举步之比分别为＝0.5，＝k1，＝k2，＝k3．已知k1，k2，k3成公差为0.1的等差数列，且直线OA的斜率为0.725，则k3＝（）A．0.75B．0.8C．0.85D．0.9【解答】解：设OD1＝DC1＝CB1＝BA1＝1，则CC1＝k1，BB1＝k2，AA1＝k3，由题意得：k1＝k3﹣0.2，k2＝k3﹣0.1，且，解得k3＝0.9，故选：D．考向二数列递推公式6.（多选）（2021•新高考Ⅱ）设正整数n＝a0•20+a1•21+…+a k1•2k﹣1+a k•2k，其中a i∈{0，1}，记ω（n）＝﹣a0+a1+…+a k，则（）A．ω（2n）＝ω（n）B．ω（2n+3）＝ω（n）+1C．ω（8n+5）＝ω（4n+3）D．ω（2n﹣1）＝n【解答】解：∵2n＝a0•21+a1•22+…+a k﹣1•2k+a k•2k+1，∴ω（2n）＝ω（n）＝a0+a1+…+a k，∴A对；当n＝2时，2n+3＝7＝1•20+1•21+1•22，∴ω（7）＝3．∵2＝0•20+1•21，∴ω（2）＝0+1＝1，∴ω（7）≠ω（2）+1，∴B错；∵8n+5＝a0•23+a1•24+•••+a k•2k+3+5＝1•20+1•22+a0•23+a1•24+•••+a k•2k+3，∴ω（8n+5）＝a0+a1+•••+a k+2．∵4n+3＝a0•22+a1•23+•••+a k•2k+2+3＝1•20+1•21+a0•22+a1•23+•••+a k•2k+2，∴ω（4n+3）＝a0+a1+•••+a k+2＝ω（8n+5）．∴C对；∵2n﹣1＝1•20+1•21+•••+1•2n﹣1，∴ω（2n﹣1）＝n，∴D对．故选：ACD．考向三数列的求和7．（2021•新高考Ⅰ）某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折．规格为20dm×12dm的长方形纸，对折1次共可以得到10dm×12dm，20dm×6dm两种规格的图形，它们的面积之和S1＝240dm2，对折2次共可以得到5dm×12dm，10dm×6dm，20dm×3dm三种规格的图形，它们的面积之和S2＝180dm2，以此类推．则对折4次共可以得到不同规格图形的种数为；如果对折n次，那么S k＝dm2．【解答】解：易知有，，共5种规格；由题可知，对折k次共有k+1种规格，且面积为，故，则，记，则，∴T n＝﹣＝1+（﹣）﹣＝，∴，∴．故答案为：5；．考向四数列综合8．（2021•新高考Ⅱ）记S n是公差不为0的等差数列{a n}的前n项和，若a3＝S5，a2a4＝S4．（Ⅰ）求数列{a n}的通项公式a n；（Ⅱ）求使S n＞a n成立的n的最小值．【解答】解：（Ⅰ）数列S n是公差d不为0的等差数列{a n}的前n项和，若a3＝S5，a2a4＝S4．根据等差数列的性质，a3＝S5＝5a3，故a3＝0，根据a2a4＝S4可得（a3﹣d）（a3+d）＝（a3﹣2d）+（a3﹣d）+a3+（a3+d），整理得﹣d2＝﹣2d，可得d＝2（d＝0不合题意），故a n＝a3+（n﹣3）d＝2n﹣6．（Ⅱ）a n＝2n﹣6，a1＝﹣4，S n＝﹣4n+×2＝n2﹣5n，S n＞a n，即n2﹣5n＞2n﹣6，整理可得n2﹣7n+6＞0，当n＞6或n＜1时，S n＞a n成立，由于n为正整数，故n的最小正值为7．9．（2021•新高考Ⅰ）已知数列{a n}满足a1＝1，a n+1＝（1）记b n＝a2n，写出b1，b2，并求数列{b n}的通项公式；（2）求{a n}的前20项和．【解答】解：（1）因为a1＝1，a n+1＝，所以a2＝a1+1＝2，a3＝a2+2＝4，a4＝a3+1＝5，所以b1＝a2＝2，b2＝a4＝5，b n﹣b n1＝a2n﹣a2n﹣2＝a2n﹣a2n﹣1+a2n﹣1﹣a2n﹣2＝1+2＝3，n≥2，﹣所以数列{b n}是以b1＝2为首项，以3为公差的等差数列，所以b n＝2+3（n﹣1）＝3n﹣1．另解：由题意可得a2n+1＝a2n﹣1+3，a2n+2＝a2n+3，其中a1＝1，a2＝a1+1＝2，于是b n＝a2n＝3（n﹣1）+2＝3n﹣1，n∈N*．（2）由（1）可得a2n＝3n﹣1，n∈N*，则a2n1＝a2n﹣2+2＝3（n﹣1）﹣1+2＝3n﹣2，n≥2，﹣当n＝1时，a1＝1也适合上式，所以a2n1＝3n﹣2，n∈N*，﹣所以数列{a n}的奇数项和偶数项分别为等差数列，则{a n}的前20项和为a1+a2+...+a20＝（a1+a3+…+a19）+（a2+a4+…+a20）＝10+×3+10×2+×3＝300．10．（2022•新高考Ⅰ）记S n为数列{a n}的前n项和，已知a1＝1，{}是公差为的等差数列．（1）求{a n}的通项公式；（2）证明：++…+＜2．【解答】解：（1）已知a1＝1，{}是公差为的等差数列，所以，整理得，①，故当n≥2时，，②，①﹣②得：，故（n﹣1）a n＝（n+1）a n﹣1，化简得：，，........，，；所以，故（首项符合通项）．所以．证明：（2）由于，所以，所以＝．11．（2022•新高考Ⅱ）已知{a n}是等差数列，{b n}是公比为2的等比数列，且a2﹣b2＝a3﹣b3＝b4﹣a4．（1）证明：a1＝b1；（2）求集合{k|b k＝a m+a1，1≤m≤500}中元素的个数．【解答】解：（1）证明：设等差数列{a n}的公差为d，由a2﹣b2＝a3﹣b3，得a1+d﹣2b1＝a1+2d﹣4b1，则d＝2b1，由a2﹣b2＝b4﹣a4，得a1+d﹣2b1＝8b1﹣（a1+3d），即a1+d﹣2b1＝4d﹣（a1+3d），∴a1＝b1．（2）由（1）知，d＝2b1＝2a1，由b k＝a m+a1知，，∴，即2k﹣1＝2m，又1≤m≤500，故2≤2k﹣1≤1000，则2≤k≤10，故集合{k|b k＝a m+a1，1≤m≤500}中元素个数为9个．重点考查等差、等比数列的概念、性质、通项公式和前n项和，考查错位相减、裂项相消等求和方法。

编译原理及实现课后习题答案孙悦红 (1)

|xyz|=7 | (xy)3 |=12
2.3 设有文法 G[S]�S∷=SS*|SS+|a�写出符号串 aa+a*规范推导�并构造语法树。
S => SS* => Sa* => SS+a* => Sa+a* => aa+a*
S
S
S
*
SS+a
aa
2.4 已知文法 G[Z]�Z∷=U0∣V1 、 U∷=Z1∣1 、 V∷=Z0∣0 ,请写出全部由此文法描述的只含有四个符号的句子。
+i#
POP,NEXTSYM
18
#E’T
i#
POP,PUSH(T’F)
所用产生式 E→TE’ T→FT’ F→i
T’→ε E’→+TE’
T→FT’ F→i
T’→*FT’
F→i
T’→ε E’→+TE’
T→FT’
19 20 21 22 23 �2�i*(i+i+i) 步骤
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
N 错误
INPUTSYM=下一个符号
INPUTSYM=’b’ Y
N 出口
4.2 设有文法 G[Z]� Z∷=(A) , A∷=a|Bb , B∷=Aab 若采用递归下降分析方法�对此文法来说�在分析过程中�能否避免回溯�为什么�
解�若采用递归下降分析方法�对此文法来说�在分析过程中不能避免回朔。因为规则 A ∷=a|Bb 和规则 B∷=Aab 构成了间接左递归�不满足实现没有回溯的递归下降分析方法的条件�1��书 P67��且规则 A: := a|Bb�FIRST(a)={a}�FIRST(Bb)={a}�即此规则候选式的首符号集有相交�不满足实现没有回溯的递归下降分析方法的条件�2��书 P67��在分析过程中�将造成回溯。

17J927-1车库建筑构造

.$Jf:lil!. (~) iif'f!k):l-*: .............................. 5-1
.$-)f.lj{Jt'f!k):l-*: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-4 ~$~ iif-fit):l-*: .................................. 5-6
<<Jt•3t1l#;t*1#!i. •1-$7}: ,~.. Y!~ }} GB 5768. 1-2009
<<1!LJ3.3t1(#;t*1#~ •2-$7}: JtJ3.3t3f!#;t>> GB 5768. 2-2009
<<Jt•3t1l#;t*1#!l. -3-$7}: ll•~1l#~}} GB 5768. 3-2009
~*~~~~¥J~wm ............................ 3-24
~~~JJ<.ll;J fl . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-25
~~fJiJj( l'J fl ( 1iJiPJ j\ ) . . . . . . . . . . . . . . . . . . . . . . . . . . 3-2 9 ~~fJiJj( Jl;J fl ( Jj( ;Ji }J ) . . . . . . . . . . . . . . . . . . . . . . . . . . 3-30
3.1 $ft: parking garage

高一数学同步备课系列(人教A版2019必修第一册)+1

①③④ 解析：①能构成集合，其中的元素满足三条边相等；
②不能构成集合，因为“比较接近1”的标准不明确，所以元素不确定，故不能构成集合；
③能构成集合，其中的元素是“某校高一年级16岁以下的学生”；
④能构成集合，其中的元素是“平面直角坐标系内到原点的距离等于1的点”；
⑤不能构成集合，因为“年轻”的标准是模糊的、不确定的，故不能构成集合；
典例5
下列关系中，正确的有
（ C ）
1
① ∈R；
2
②
④| 3 |∈Q；
⑤0＝{0}
A．1个
B．2个
2 Q ；
C．3个
③|－3|∈N；
D．4个
典例6
【多选题】下列所给关系正确的是( A B )
A. R
B. 6 Q
C. 0N*
D.| 5 |N*
练一练
1.思考辨析(正确的画“√”，错误的画“×”)
课本练习
教材P5练习1
1. 判断下列元素的全体是否组成集合，并说明理由．
(1) 与定点A，B等距离的点；
(2) 高中学生中的游泳能手．
解：(1) 能组成集合.
(2) 不能组成集合，因为不满足集合元素的确定性.
教材P5练习2
2. 用符号“∊”或“∉”填空：
1
∉
∉
∉ Z； ___
∊ Q；π ___
∊ R.
即的取值范围为{| ≥2}
题型四
集合中元素的特性
已知集合 A 含有两个元素 a 和 a2，若 1∈A，则实数 a 的值为________．
－1
解析：若 a＝1，则 a2＝1，此时集合 A 中两元素相同，与互异性矛盾，故 a≠1；
若 a2＝1，则 a＝－1 或 a＝1(舍去)，此时集合 A 中两元素为－1,1，故 a＝－1.

2021春浙教版数学七下第2章《二元一次方程组》提优练习

七年级下数学提优练习<1>班级___________ 姓名___________1.用加减法解方程组得时)2()1(,)2........(1572)1.....(..........974－y x y x ⎩⎨⎧-=+-=+〔〕 A .6x=－6 B .2x=24 C .2x=－6 D .6x=242.21x y =⎧⎨=⎩是二元一次方程组71ax by ax by +=⎧⎨-=⎩的解，那么a b -的值为〔〕A ．1B ．－1C ． 2D ．33.方程组5347x y x y m -=⎧⎨+=⎩中的x ，y 的值相等，那么m 等于( ) A ．2或－2 B ．4 C ．16． D ．－164.假设关于x ，y 的二元一次方程组⎩⎨⎧=-=+k y x ,k y x 95的解也是方程632=+y x 的解，那么k 的值为〔〕A ．43-B ．43C ． 34D ．34- 5.某校运发动分组训练，假设每组7人，余3人；假设每组8人，那么缺5人；设运发动人数为x 人，组数为y 组，那么列方程组为〔〕A 、⎩⎨⎧=++=x y x y 5837B 、⎩⎨⎧=-+=x y x y 5837C 、⎩⎨⎧+=-=5837x y x yD 、⎩⎨⎧+=+=5837x y x y6.足球比赛计分规那么为：胜一场得3分，平一场得1分，负一场得0分。

一个队打了11场，共得19分，那么这个队得胜得场数得可能性有〔〕A ．3种 B. 4种 C. 5种 D. 6种7.方程组：的解是：，那么方程组：的解是〔〕A 、B 、C 、D 、 8.?九章算术?中的“方程〞一章中，一次方程组是由算筹布置而成的．?九章算术?中的算筹图是竖排的，为看图方便，我们把它改为横排，如图〔1〕、图〔2〕．图中各行从左到右列出的算筹数分别表示未知数x ，y 系数与相应的常数项，把图〔1〕所示的算筹图用我们现在所熟悉的方程组形式表述出来就是3219423x y x y +=⎧⎨+=⎩类似地，图〔2〕所示的算筹图我们可以表述为〔〕(1) 〔2〕A .211211321926 (432743224234327)x y x y x y x y B C D x y x y x y x y +=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨+=+=+=+=⎩⎩⎩⎩ 9.假设关于x 、y 的方程组只有一个解，那么a 的值不等于〔〕A 、B 、﹣C 、D 、﹣10.假设方程组有无穷多组解，〔x ，y 为未知数〕，那么〔〕 A 、k≠2 B 、k=﹣2 C 、k ＜﹣2 D 、k ＞﹣211.当a= _________ 时，方程组无解． 12.假设()1321=+--y x a a 是二元一次方程，那么a = ．13.那么x 与y 之间的关系式为__________________．14.方程组的解适合x+y=2，那么m 的值为 _________ ． 15.假设那么x＝，y ＝．16.对于X,Y 定义一种新的运算“*〞：X*Y=aX+bY ，其中a,b 为常数，等式右边是通常的加减和乘法运算，3*5=15,4*7=28,那么2*3= ． 17.假设二元一次方程组⎩⎨⎧=+=-11532by ax y x 和⎩⎨⎧=+=-15y x ay cx 同解，那么可通过解方程组_ 求得这个解．18.方程组有正整数解〔a 为整数〕，求a 的值．19.小刚和小强同解二元一次方程组161ax by bx ay +=⎧⎨+=⎩，小刚把方程①抄错了，求得的解为13x y =-⎧⎨=⎩，小强把方程②抄错了，求得的解为32x y =⎧⎨=⎩，求原方程组的解． 20.甲、乙两地相距280 km ，一轮船在两地间航行，顺流用14 h ，逆流用20 h ．求这艘轮船在静水中的速度和水流速度．21.一列快车长70米，一列慢车长80米。

广东省揭阳市2024高三冲刺(高考物理)人教版测试(综合卷)完整试卷

广东省揭阳市2024高三冲刺（高考物理）人教版测试(综合卷)完整试卷一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题双缝干涉的实验装置的截面图如图所示，光源到双缝S1、S2的距离相等，O是S1、S2连线中垂线与光屏的交点。

若现在将该装置中垂线以下的部分没入水中，则原本处在O点的亮条纹将会（）A．向上移动B．向下移C．不动D．无法确定第(2)题图甲为一列简谐横波在t=0.10s时刻的波形图，图乙为质点P的振动图像。

下列说法正确的是（）A．在t=0.10s时，质点P的速度为零B．从t=0.10s到t=0.25s，质点P的路程为10cmC．这列简谐横波沿x轴正方向传播D．在t=0.25s时，质点P的加速度沿y轴负方向第(3)题蹦极是近些年来新兴的一项非常刺激的户外活动。

跳跃者站在桥梁、塔顶、高楼、吊车甚至热气球上，把一端固定的一根长长的橡皮条绑在踝关节处，然后两臂伸开，双腿并拢，头朝下跳下去。

如图是一位蹦极者从高处下落到速度为零的过程中的图像，当时，对应的速度值最大，则下面判断正确的是（）A．当下落距离小于15m时，蹦极者处于完全失重状态B．当下落距离小于15m时，蹦极者失重的数值（人自身重力与橡皮条拉力之差的绝对值）是个常量C．当下落距离大于15m时，蹦极者超重的数值（人自身重力与橡皮条拉力之差的绝对值）是个常量D．当下落距离大于15m时，蹦极者超重的数值（人自身重力与橡皮条拉力之差的绝对值）随距离的增大而增大第(4)题中国象棋的棋盘呈长方形，由九条竖线和十条横线相交组成，共有九十个交叉点，开局时红方和黑方各子的位置如图所示，现将电荷量为（）的两个点电荷分别固定在红方的“俥”位置，再将电荷量为（）的两个点电荷分别固定在黑方的左右“車”位置，点电荷在棋盘网格线所在的平面内，下列说法正确的是（）A．“將”所在位置与“帥”所在位置的电场强度大小相等方向不同B．棋盘中间“卒”与棋盘中间“兵”所在位置的电势相同C．电子在棋盘左侧“傌”所在位置的电势能小于在棋盘右侧“馬”所在位置的电势能D．一质子沿直线从红方正中间“兵”所在位置运动到黑方正中间“卒”所在位置，此过程中静电力始终不做功第(5)题质量是40kg的铁锤从5m高处落下，打在水泥桩上后不反弹，与水泥桩撞击的时间是0.05s。

刍甍、羡除、刍童及楔形四棱台的体积公式 (2019高考)数学考点分类解析 (2019高考)数学考点分类解析

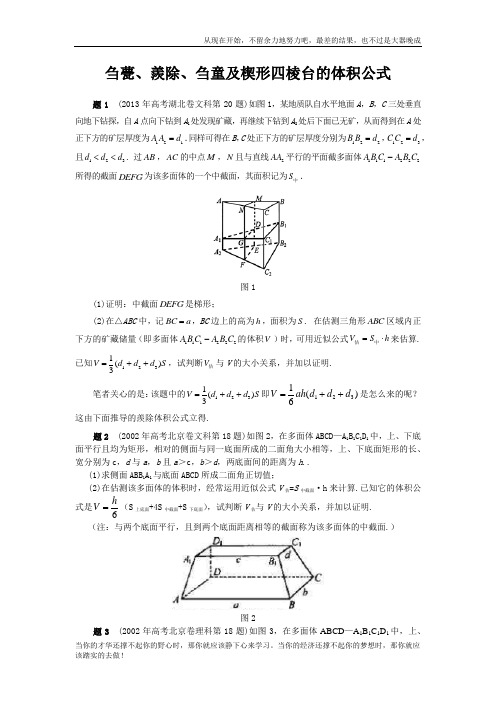
刍甍、羨除、刍童及楔形四棱台的体积公式题1 (2013年高考湖北卷文科第20题)如图1，某地质队自水平地面A ，B ，C 三处垂直向地下钻探，自A 点向下钻到A 1处发现矿藏，再继续下钻到A 2处后下面已无矿，从而得到在A 处正下方的矿层厚度为121A A d =．同样可得在B ，C 处正下方的矿层厚度分别为122B B d =，123C C d =，且123d d d <<. 过AB ，AC 的中点M ，N 且与直线2AA 平行的平面截多面体111222A BC A B C -所得的截面DEFG 为该多面体的一个中截面，其面积记为S 中．图1(1)证明：中截面DEFG 是梯形；(2)在△ABC 中，记BC a =，BC 边上的高为h ，面积为S . 在估测三角形ABC 区域内正下方的矿藏储量（即多面体111222A B C A B C -的体积V ）时，可用近似公式V S h =⋅估中来估算. 已知1231()3V d d d S =++，试判断V 估与V 的大小关系，并加以证明.笔者关心的是：该题中的1231()3V d d d S =++即)(61321d d d ah V ++=是怎么来的呢？这由下面推导的羨除体积公式立得.题2 (2002年高考北京卷文科第18题)如图2，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h .. (1)求侧面ABB 1A 1与底面ABCD 所成二面角正切值；(2)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图2题3 (2002年高考北京卷理科第18题)如图3，在多面体ABCD —A 1B 1C 1D 1中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E ，F 两点，上、下底面矩形的长、宽分别为c ，d 与a ，b 且a ＞c ，b ＞d ，两底面间的距离为h ..(1)求侧面ABB 1A 1与底面ABCD 所成二面角的大小； (2)证明：EF//面ABCD(3)在估测该多面体的体积时，经常运用近似公式V 估=S 中截面·h 来计算.已知它的体积公式是6hV =（S 上底面+4S 中截面+S 下底面），试判断V 估与V 的大小关系，并加以证明. （注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面.）图3笔者关心的是：高考题2,3中的6hV =（S 上底面+4S中截面+S下底面）即[(2)(2)]6hV a c b c a d =+++是怎么来的呢？这由下面推导的刍童体积公式立得.《九章算术·商功》篇有部分题目涉及到刍甍、羨除、刍童及楔形四棱台的体积公式，这些公式秦汉时人都已掌握，下面来推导它们.1.刍甍刍甍是图4所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是平行四边形.设a AB =，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)2(6c a HhV +=.图4证明如图5所示.设点F E ,在面ABCD 上的射影分别是点F E '',.图5我们把平面ABCD 分成三块区域：区域I 指该平面位于直线AD 左侧的部分(不包括直线AD )，区域II 指该平面夹在直线BC AD 、之间的部分(包括直线这两条直线)，区域III 指该平面位于直线BC 右侧的部分(不包括直线BC ).应分六种情形来证明： (1)点F E '',均位于区域I ；(2)点E '位于区域I ，点F '位于区域II ； (3)点E '位于区域I ，点F '位于区域III ；(4)点F E '',均位于区域II ；(5)点E '位于区域II ，点F '位于区域III ；(6)点F E '',均位于区域III .下面只对情形(5)予以证明：过点E '作CD GH ⊥于H '，交AB 于G ；过点F '作CD IJ ⊥于I ，交AB 于J ，得H E E h GH ='=,，所以=-+=-)(BJIC AGHD FJI EGH V V V V 四棱锥四棱锥直三棱柱=-+=-+)(32)(32GJIH ABCD BJIC AGHD S S Hc Hh S S H c Hh )2(6)(32c a Hh ch ah H c Hh +=-+=证毕！ 2.羨除羨除是图6所示中的五面体ABCDEF，其中EF DC AB ////，底面ABCD 是梯形.设)(,b a b DC a AB >==，直线CD AB 、之间的距离是h ，直线EF 与平面ABCD 之间的距离是H ，则其体积)(6c b a HhV ++=.图6证明用补形法可证.图7如图7所示，延长CD 至R ，使RC AB =，得刍甍ABCREF ，由刍甍的体积公式，得)(62)(3)2(6c b a Hh h b a H c a Hh V V V ADRE ABCREF ++=-⋅-+=-=-三棱锥刍甍注羨除的体积公式是由刍甍的体积公式推得的；当羨除的下底面梯形变成平行四边形时(即图4所示中的b a =时的情形)，羨除就变成了刍甍，也得刍甍的体积公式是羨除的体积公式的极限情形.3.刍童刍童是图8所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面A B C D 、底面D C B A ''''均是平行四边形.设b B A a AB =''=,，直线CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A A B C D ''''、之间的距离是H，则其体积])2()2[(6h a a h a a HV '+'+'+=.图8证明如图9所示，可得面A B AB ''与平行平面D C B A ABCD ''''、的交线B A AB ''、平行,所以CD B A //''.连结C BD A '',.图9由刍甍的体积公式，得])2()2[(6h a a h a a HV V V D C B A CD ABCD A B '+'+'+=+=''''''刍甍刍甍注刍童的体积公式是由刍甍的体积公式推得的；当刍童的上底面平行四边形变成线段时(即图4所示中的0='h 时的情形)，刍童就变成了刍甍，也得刍甍的体积公式是刍童的体积公式的极限情形. 4.楔形四棱台楔形四棱台是图10所示中的六面体D C B A ABCD ''''-，其中面//ABCD 面D C B A ''''，底面A B C D 、底面D C B A ''''均是梯形.设b D C b B A b CD a AB '=''=''==,,,，面CD AB 、之间的距离是h ，D C B A ''''、之间的距离是h '，面D C B A A BCD ''''、之间的距离是H ，则其体积])()[(6h b b a h a b a HV '+'+'+'++=.图10 图11证明如图11所示，可得CD B A //''.连结C B D A '',.由羨除的体积公式，得])()[(6h b b a h a b a HV V V D C B A CD ABCD A B '+'+'+'++=+=''''''羡除羡除注楔形四棱台的体积公式是由羨除的体积公式推得的；当楔形四棱台的上底面的梯形变成线段时(即图4中的0='h 时的情形)，楔形四棱台就变成了羨除，也得刍甍的体积公式是楔形四棱台的体积公式的极限情形.由刍甍的体积公式可推得羨除、刍童、楔形四棱台的体积公式，由楔形四棱台的体积公式也可推得刍甍的体积公式.题4 (1999年高考全国卷文科、理科第10题)如图12所示，在多面体ABCDEF 中，已知面ABCD 是边长为3的正方形，23,//=EF AB EF ，EF 与面ABCD 的距离为2，则该多面体的体积为( )A.29 B.5 C.6 D.215图12解 D.由刍甍的体积公式可得.题5 (2007年全国高中数学联赛江苏赛区复赛第一试第9题)如图13，在多面体ABCDEF 中，已知四边形ABCD 是边长为3的正方形，3//,2EF AB EF =.若该多面体的体积为152，则EF 与AC 的距离为 .图13解 2.设直线EF 与平面AC 的距离为H ，由刍甍的体积公式可得153323262H ⋅⎛⎫=⋅+ ⎪⎝⎭2H =进而可得：异面直线,EF AC 的距离为2H =.题6 (2005年高考全国卷I 理科第4题即文科第5题)如图14，在多面体ABCDEF 中，已知ABCD 是边长为1的正方形，且△ADE 、△BCF 均为正三角形，EF //AB ，EF =2，则该多面体的体积为( )A.32 B.33C.34D.23图14解 A.设棱,A D B C的中点分别是,S T ，在等腰梯形EFTS 中可得1,2,2ST EF ES FT ====，可求得该等腰梯形的高即直线EF 与平面ABCD 的距离22=H . 所以由刍甍的体积公式可得多面体ABCDEF的体积为12(212)63⋅+=. 题7 (1983年美国邀请赛题)图15中的多面体的底面是边长为s 的正方形，上面的棱平行于底面，其长为s 2，其余棱长也都为s ，若26=s ，求这个多面体的体积.图15解 288.由刍甍的体积公式可得(先算得s H 22=).在该题中，当1=s 时就是高考题2.用排除法简解2015年高考全国卷I 理科第12题高考题 (2015年高考全国卷I 理科第12题)设函数f (x )＝e x (2x －1)－ax ＋a ，其中a <1，若存在唯一的整数x 0使得f (x 0)<0，则a 的取值范围是( )A.3,12e ⎡⎫-⎪⎢⎣⎭ B.33,2e 4⎡⎫-⎪⎢⎣⎭C.33,2e 4⎡⎫⎪⎢⎣⎭D.3,12e ⎡⎫⎪⎢⎣⎭解法1 (数形结合法)D.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又函数g (x )在x <12时g (x )<0，在x >12时g (x )>0，所以其大致图象如图1所示．图1直线y ＝ax －a 过点(1，0)．若a ≤0，则f (x )<0的整数解有无穷多个，因此只能a >0. 结合函数图象可知，存在唯一的整数x 0，使得f (x 0)<0，即存在唯一的整数x 0，使得点(x 0，ax 0－a )在点(x 0，g (x 0))的上方，得x 0只能是0，所以实数a 应满足⎩⎪⎨⎪⎧f （－1）≥0，f （0）<0，f （1）≥0，即⎩⎪⎨⎪⎧－3e －1＋2a ≥0，－1＋a <0，e ≥0，解得32e≤a <1.即实数a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭.解法2 (分离常数法)D.令1+=t x 后，得题设即关于t 的不等式)0(1)e (21≠<++t at t t 有唯一的整数解.若0t >，由a <1，可得1(21)e (21)e t t t t at ++>+>>所以题设即关于t 的不等式1(21)e(0)t t at t ++<<即1(21)e (0)t t a t t++><有唯一的整数解，也即关于t 的不等式1(21)e (1)t t a t t++>≤-有唯一的整数解. 设1(21)e ()(1)t t g t t t ++=≤-，得12e ()(1)(21)(1)t g t t t t t+'=+-≤-，所以函数)(t g 在(,1]-∞-上是增函数，得最大值为(1)1g -=.又lim ()0,(1)1t g t g →-∞=-=，由此可作出函数)(t g 的图象如图2所示：图2注意到图象()y g t =过点32,2e B ⎛⎫- ⎪⎝⎭且1<a ，所以由图2可得：当32ea <时，满足()g t a >的整数t 有2,1--，所以此时不满足题意. 当1e23<≤a 时，满足()g t a >的整数t 只有1-，所以此时满足题意. 得所求a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭. 解法3 (排除法)D.当0a =时，不等式f (x )<0即e x (2x －1)<0也即12x <，它有无数个整数解，不满足题设.由此可排除选项A,B.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又g ′(0)＝1，所以可得曲线()y g x =在点(0,1)-处的切线为1y x =-，如图3所示．图3所以当a <1且1a →时满足题设(此时满足题设的唯一整数x 0=0).由此可排除选项C. 所以选D.注小题不大做，还是解法3(排除法)简洁.本题对函数与方程思想、数形结合思想、分类讨论思想都有所考查.例谈用验证法解题——2010年高考数学安徽卷理科第20题的另解题1 解方程：(1)2121+=+x x ；(2)c c x x 11-=-；(3)c c x x 11+=+. 解 (1)容易观察出212，=x 均是该方程的解.按常规方法解此方程时，先去分母得到一元二次方程，该一元二次方程最多两个解，再检验(舍去使原方程中分母为零的解)，所以原方程最多有两个解.而已经找到了原方程的两个解212，=x ，所以这两个解就是原方程的所有解.(2)同理，可得原方程的所有解是cc x 1-=，. (3)容易观察出cc x 1，=均是该方程的解.同上得原方程最多有两个解，而已经找到了原方程的两个解cc x 1，=(因为对于任意的非零实数c ，c 和c 1都是原方程的解，所以应当把c 和c1理解成原方程的两个解)，所以这两个解就是原方程的所有解.题2 解方程22=+++x x x .解设函数2)(+++=x x x x f ，易知它是增函数，所以方程2)(=x f 至多有一个根(当2在函数)(x f 的值域中时有一个根，否则没有根)，……所以原方程的根是2=x .题3 已知1tan ,51cos sin ->=+ααα，求αtan . 解由⎪⎩⎪⎨⎧=+=+1cos sin 51cos sin 22αααα及“勾三股四弦五”可以猜出该方程组有两组解：⎪⎪⎩⎪⎪⎨⎧-==53cos 54sin αα 或 ⎪⎪⎩⎪⎪⎨⎧=-=54c o s 53s i n αα 该方程组即⎪⎪⎩⎪⎪⎨⎧=⎪⎭⎫ ⎝⎛-+-=1sin 51sin sin 51cos 22αααα 因为关于αsin 的一元二次方程1sin 51sin 22=⎪⎭⎫ ⎝⎛-+αα最多有两个解，所以该方程组也最多有两组解，......所以上面猜出的两组解就是该方程组的全部解， (4)3tan -=α. 题4]1[ (2007年高考陕西卷理科第22(1)题)已知各项全不为零的数列}{k a 的前k 项和为k S ，且∈=+k a a S k k k (211N*)，其中11=a ，求数列}{k a 的通项公式. 解由题设得kk k k k a a a a a S a )(22211+++==+ ，所以当k a a a ,,,21 确定时，1+k a 也唯一确定.所以由11=a 知，数列}{k a 是唯一确定的.可以观察出k a k =满足题设的所有条件，所以数列{}k 是满足题设的唯一数列，得k a k =.另解 (2),2)()((211111k k k kk k k k k k k k S S S S S k S S S S a a S +-=≥--==-++-+因为)2)(01≥≠=--k a S S k k k ①由题设得3,121==S S ，再由①知{}k S 是唯一确定的数列⎪⎪⎭⎫ ⎝⎛⎩⎨⎧≥-==-2,1,11k S S k S a k k k .再同上得k a k =.题5]1[ (2005年高考江苏卷第23(1)(2)题)设数列}{n a 的前n 项和为n S ，已知11,6,1321===a a a ，且∈+=+--+n B An S n S n n n ()25()85(1N*)，其中B A ,为常数.(1)求A 与B 的值；(2)证明数列}{n a 为等差数列；解 (1)8,20-=-=B A . (2) ∈-+--+=+n n n S n n S n n (8582085251N*)，11=S ②所以{}n S 是唯一确定的数列，}{n a 也是唯一确定的数列.又由11,6,1321===a a a 知，若}{n a 为等差数列，则45-=n a n ，于是)35(21-=n n S n . 容易验证)35(21-=n n S n 满足②，所以题中的45),35(21-=-=n a n n S n n ，}{n a 为等差数.题6]2[ 已知数列}{n a 满足nn a a a n n ++==+2111,21，求n a ；解首先，由首项211=a 及递推关系nn a a n n ++=+211知，满足题意的数列}{n a 是唯一确定的.所以，若能找到一个数列满足该题目的所有条件，则该数列的通项公式就是所求的答案.易得⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+-=+-=+=-+n k n k n n n n a a n n 111111121，即nk a n1-=（k 是常数）满足递推关系n n a a n n ++=+211，再由211=a ，得n a n123-=满足题目的所有条件，所以本题的答案就是na n 123-=.题7]2[ 已知数列}{n a 满足n n a n n a a 1,3211+==+，求n a . 解易知本题的答案是是唯一确定的，所以只需寻求一个数列满足该题目的所有条件.易得k nk n kn na a n n (111+=+=+是非零常数），即n k a n =满足递推关系n n a n n a 11+=+，再由321=a ，得n a n 32=满足题目的所有条件，所以本题的答案就是na n 32=.注因为绝大部分求数列通项公式的题目答案都是唯一的，所以只要能观察或求出满足所有题设的一个通项公式，则该通项公式就是所求的唯一答案.对于要求解的问题Ω，若能证明它最多有n n (是确定的正整数)个解，又找出了它的n 个解n ωωω,,,21 ，则这n 个解就是该问题的所有解.这就是本文要阐述的用验证法解题.下面再用这种方法解答一道高考题：题8 (2010·安徽·理·20)设数列 ,,,,21n a a a 中的每一项都不为0.证明{}n a 为等差数列的充分必要条件是：对任何∈n N*，都有1113221111++=+++n n n a a na a a a a a .证明先证必要性.若数列{}n a 是公差为d 的等差数列：当0=d 时，易得欲证成立.当0≠d 时，有⎪⎪⎭⎫⎝⎛-++-+-=++++++1132232112132211111n n n n n n a a a a a a a a a a a a d a a a a a a 111111111322111111111111+++++=-⋅=⎪⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=n n n n n n a a na a a a d a a d a a a a a a d再证充分性.只需对)3(≥n n 用数学归纳法证明加强的结论：若),,3,2(1111113221n i a a ia a a a a a i i i ==+++++恒成立，则n a a a ,,,21 成等差数列，且na a n 1≠. 当3=n 时成立：当2=i 时，得2313132212,211a a a a a a a a a =+=+，所以321,,a a a 成等差数列，还可证313a a ≠(因为由313a a =可得023131313334=-=--+=+=a a a a a d a a ，而由3=i 时成立立知)04≠a .假设kn ,,4,3 =时成立：即ka a a ,,,21 成等差数列，且ka a a a a a k 11413,,4,3≠≠≠. 由k i ,,3,2 =时均成立及kaa a a a a k 11413,,4,3≠≠≠知，当21,a a 确定时，数列121,,,+n a a a 也是确定的，而由必要性的证明知，由21,a a 确定的等差数列121,,,+n a a a 满足题设，所以由题设及21,a a 确定的数列就是这个等差数列，即121,,,+n a a a 成等差数列，同上还可证111+≠+k a a k ，即1+=k n 时成立.所以要证结论成立，得充分性成立.参考文献1 甘志国.例谈用验证法求数列通项[J].中学数学月刊，2008(3)：462 甘志国著.初等数学研究(II)上[M].哈尔滨：哈尔滨工业大学出版社，2009.416-417用排除法简解2015年高考全国卷I 理科第12题高考题 (2015年高考全国卷I 理科第12题)设函数f (x )＝e x (2x －1)－ax ＋a ，其中a <1，若存在唯一的整数x 0使得f (x 0)<0，则a 的取值范围是( )A.3,12e ⎡⎫-⎪⎢⎣⎭ B.33,2e 4⎡⎫-⎪⎢⎣⎭C.33,2e 4⎡⎫⎪⎢⎣⎭D.3,12e ⎡⎫⎪⎢⎣⎭解法1 (数形结合法)D.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又函数g (x )在x <12时g (x )<0，在x >12时g (x )>0，所以其大致图象如图1所示．图1直线y ＝ax －a 过点(1，0)．若a ≤0，则f (x )<0的整数解有无穷多个，因此只能a >0. 结合函数图象可知，存在唯一的整数x 0，使得f (x 0)<0，即存在唯一的整数x 0，使得点(x 0，ax 0－a )在点(x 0，g (x 0))的上方，得x 0只能是0，所以实数a 应满足⎩⎪⎨⎪⎧f （－1）≥0，f （0）<0，f （1）≥0，即⎩⎪⎨⎪⎧－3e －1＋2a ≥0，－1＋a <0，e ≥0，解得32e≤a <1.即实数a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭.解法2 (分离常数法)D.令1+=t x 后，得题设即关于t 的不等式)0(1)e (21≠<++t at t t 有唯一的整数解.若0t >，由a <1，可得1(21)e (21)e t t t t at ++>+>>所以题设即关于t 的不等式1(21)e(0)t t at t ++<<即1(21)e (0)t t a t t++><有唯一的整数解，也即关于t 的不等式1(21)e (1)t t a t t++>≤-有唯一的整数解. 设1(21)e ()(1)t t g t t t ++=≤-，得12e ()(1)(21)(1)t g t t t t t+'=+-≤-，所以函数)(t g 在(,1]-∞-上是增函数，得最大值为(1)1g -=.又lim ()0,(1)1t g t g →-∞=-=，由此可作出函数)(t g 的图象如图2所示：图2注意到图象()y g t =过点32,2e B ⎛⎫- ⎪⎝⎭且1<a ，所以由图2可得：当32ea <时，满足()g t a >的整数t 有2,1--，所以此时不满足题意. 当1e23<≤a 时，满足()g t a >的整数t 只有1-，所以此时满足题意. 得所求a 的取值范围是3,12e ⎡⎫⎪⎢⎣⎭. 解法3 (排除法)D.当0a =时，不等式f (x )<0即e x (2x －1)<0也即12x <，它有无数个整数解，不满足题设.由此可排除选项A,B.令g (x )＝e x (2x －1)，得g ′(x )＝e x (2x ＋1).由g ′(x )>0得x >－12，由g ′(x )<0得x <－12，所以函数g (x )在11,,,22⎛⎫⎛⎫-∞--+∞ ⎪ ⎪⎝⎭⎝⎭上分别是减函数、增函数．又g ′(0)＝1，所以可得曲线()y g x =在点(0,1)-处的切线为1y x =-，如图3所示．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

回形针9个意想不到的妙用只有1%的人知道
生活中一些不起眼的小物件只要稍加利用往往能发挥
出意想不到的效果哦小幼今天要安利的主人公是一枚小小
的回形针回形针篇
1、变身缠线器「实用指数：★★★★★」
伴随着家里的电器越来越多，杂乱无章的电器线剪不断，理还乱！别着急，我们可以这样办：↓↓↓首先用橡皮筋在回形针上打个死结然后用橡皮筋缠绕住想绑的电线，绕完时再把橡皮筋固定在别针上，
轻松搞定！2、变身钥匙圈「实用指数：★★★」
新配的钥匙没有钥匙圈固定？别担心↓↓↓把回形针拉直并
围绕着笔转取出来的圆圈就可以当钥匙圈用咯！3、变身拉链拉环「实用指数：★★★★」
笔袋拉链的拉环坏了怎么办？
裤子上拉链的拉环坏了怎么办!莫慌↓↓↓
只要将回形针穿过拉链的环形洞就可以做成暂时性的拉环
so easy！有没有！4、变身食品封袋器「实用指数：★★★」零食开了没有及时吃完？回潮变软口感差或者只能干脆扔
掉浪费！别心塞↓↓↓把回形针拉直然后环绕绑住袋子就行妈妈再也不用担心我不爱惜食品了5、变身分页书签「实用指数：★★★★」
经常看书忘了看到哪一页
新买的书不舍得折书痕看过来！
↓↓↓在卡片、胶纸上剪出可爱的形状再把它们粘在回形针的头部简易书签诞生美观又实用！6、变身透明胶带「实用指数：★★★」上一次用过的胶带再次使用时很难找到头在哪里别捉急↓↓↓只要在胶带头部黏上回形针下次就能轻松找到7、固定肩带防止滑落「实用指数：★★★★★」夏天马上来临
女生想要穿的清凉性感一些又担心肩带露出不好看怎么
办!↓↓↓用回形针像图中那样在后面拉住不仅“隐形”
还能防止肩带滑落尴尬一秒解决！8、变身发卡「实用指数：★★★★★」
写作业的时候
工作的时候长长的刘海总是遮住眼睛很难受有木有偏偏又
忘记带发卡有了它↓↓↓女生又能省钱了！金属质感简单大方一不小心，就引领时尚了哦9、变身手机座「实用指数：★★★」人人都需要一个手机座
买的不如自己diy来的有成就感↓↓↓体力活可以请身边的男士代为效劳哦小小的回形针给我们的生活带来了很多的便
利只是不停地被掰成各种各样的形状你们考虑过它的感受
么回形针的内心是奔溃的创意美术｜儿童英语。