广东省广州市花都区2011届高三年级调研考试
广东省广州市花都区2011届高三调研考试(语文)

▁▂▃▄▅▆▇█▉▊▋▌精诚凝聚 =^_^= 成就梦想▁▂▃▄▅▆▇█▉▊▋▌2010学年花都区高三调研语文试卷本试卷共8页,24小题,满分为150分。
考试用时150分钟。
注意事项:1.答卷前,考生务必用2B铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校、以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回。
一、本大题4小题,每小题3分,共12分。
1、下列各组词语中加点的字读音完全相同的一组是A.劲敌痉挛不胫而走曲径通幽B.和面霍乱豁然开朗祸起萧墙C.甲壳撬动翘首以待七窍生烟D.筵席嫌隙垂涎三尺弦外之音2.下面语段中画线的成语,使用不恰当的一项是我国目前有1600万教育工作者,他们长期以来兢兢业业,默默耕耘,甘为人梯,培养了一批又一批优秀人才,为我国教育事业和现代化建设做出了不可磨灭的贡献。
他们耳濡目染,塑造出德才兼备的一代代新人,使漫漫教育征途薪火相传,生生不息。
A.兢兢业业B.不可磨灭C.耳濡目染D薪火相传3.下列各句中,没有语病的一句是A.藉天灾见亲情,书写人性的真诚及坚韧成为《唐山大地震》打动观众的主要元素,截至8月6日,票房已达4.96亿元。
B.专家组对圣元“早熟门”3女婴进行集体会诊,诊断认为“雌激素水平正常”,属于假性性早熟。
2011年调研测试语文答案-定稿
2011年广州市高三年级调研测试语文参考答案14.【断句和翻译】(1)窃料夷人张其凶暴/咆哮中国/深入腹地/得而不有/非有余力而不肯施/技止此也/使边将皆如莹等(/)出万死不一顾返之计/纵不百全/胜负之理/亦当相较/或未易量/ (3分,错3处扣1分。
……莹等/出万死……,本句可断,可不断。
扣完3分止。
)(2)①现在恐惧敌人不符合事实的话,将有功之臣说成有罪之臣。
(3分。
“怵”1分,“变易”1分,大意1分。
)②如果国家因抛弃城池处罚众将,(却)又因敢于作战而降罪姚莹。
(4分。
“委”1分,倒装句每处1分,大意1分。
)【参考译文】(一)陆游,字务观,名游,是山阴人。
大概是因为他母亲梦见秦少游后生了他,所以用秦少游的名作为陆游的字,而把秦少游的字作为陆游的名。
也有人说(这)是因为陆游仰慕秦少游的缘故。
绍兴末年,(陆游)才被赐及第。
他向茶山曾文清学习诗歌。
曾经跟从紫岩张公四处游历,详细地了解了西北边境的战事。
陆游天性激昂慷慨,喜欢行侠仗义,常常把策马草拟檄文作为自己的使命,而且喜好结交中原的英雄豪杰,以求消灭敌人。
从商人、道士、和尚到诗人、剑客,没有不广泛结交的。
在剑南做官的时候,写作诗词,都寄托着恢复中原的志向。
(他的诗词)在书肆广为流传,有人得到了这些诗词并把它们呈送到孝宗皇帝那里。
皇上勾画圈点他的诗作并且赞赏他的诗,立即决定授予他删定官的官职。
有人疑虑陆游交往过杂,由此他被品评的官员排斥。
皇上爱惜他的才华,马上重新任用他。
皇帝亲自批准陆游官职,授予陆游礼部郎的职位。
孝宗皇帝亲自任命官员,到陆游为止再也没有其他人,陆游得到孝宗皇帝的关爱到了这样的程度。
陆游请求提前退隐,在若耶、云门之间往来,接纳宾客亲切融洽,用饮酒做诗来自娱自乐。
他的官位已经升到了中大夫,就辞官退休了,发誓不再出来做官。
韩侂胄坚持想让他出山,陆游因为他而勉强再次做官。
韩侂胄很高兴陆游能归附自己,以至请出他最宠爱的四夫人弹奏着阮琴翩翩起舞,求取陆游的词章,故陆游写下了‚飞上锦裀红绉‛的诗句。
广东省广州市花都区2011届高三调研考试(理综)

2010年花都区高三调研理科综合试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第5页,第Ⅱ卷第5页至第10页。
考试时间150分钟,全卷满分300分。
第Ⅰ卷(选择题,共118分)一、单项选择题:本大题共16小题,每小题4分。
共64分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4分,选错或不答的得0分。
1.下列实验中,需要使用显微镜的是A.绿叶中色素的提取与分离B.检测苹果汁中的还原糖C.探究酵母菌细胞呼吸的方式D.低温或化学物质诱导染色体加倍实验2.下列说法错误的是A.种群是生物进化的基本单位B.突变和基因重组决定生物进化的方向C.生物多样性是共同进化的结果D.生物进化的实质是种群基因频率的改变3.以下为人体的体温与水盐平衡调节示意图,a、b、c、d代表激素。
有关叙述错误的是A.激素C能提高细胞的代谢速率B.当受到寒冷刺激时,a、b、c的分泌均会增加C.大量饮水后d的分泌增多,肾小管和集合管对水的重吸收增强D.体温和水盐平衡的维持都是神经调节和体液调节协调作用的结果4.以下与人体免疫有关的叙述,正确的是A.抗体是由浆细胞产生的免疫活性物质B.记忆细胞由造血干细胞直接分化而来C.吞噬细胞不参与细胞免疫过程D.免疫系统有防御功能,而没有调节功能5.下列有关细胞生命活动的叙述,正确的是A.细胞凋亡与基因表达无关B.人体各种组织细胞的衰老是同步进行的C.癌细胞转移与细胞膜上糖蛋白减少有关D.分裂期的细胞最重要的变化是进行染色体的复制6. 下列关于种群、群落和生态系统的叙述中,不正确的是A.生态系统中的组成成分越多,其抵抗力稳定性越高B.种群数量增加至K值时,其种群的出生率为零C.人类活动可改变群落演替的速度和方向D.建立大熊猫自然保护区有利于提高其环境容纳量7.下列各组离子在溶液中能大量共存的是A、Ca2+ 、HCO3-、Cl-、K+B、Al3+、AlO2-、OH-、Na+C、Fe3+、NH4+、SO42-、I-D、Fe3+、SCN-、Na+、CO32-8.下列关于NA说法正确的是A.0.1 mol 过氧化钠与足量水反应生成的O2分子数为0.1 NAB、100 mL 2.0 mol•L-1的盐酸与醋酸溶液中氢离子数均为0.2NAC .室温下,28.0g 乙烯和丙烯混合气体中含有的碳原子数为2NAD 、标准状况下,11.2L 臭氧中含有的氧原子数目为3NA 9.下列反应的离子方程式中,正确的是A .碳酸钙与醋酸反应:CO32-+2CH3COOH =CO2↑+H2O +2CH3COO -B .向氯化铝溶液中加入过量氨水:Al3+ + 3OH - = Al(OH)3↓C .次氯酸钙溶液中通入少量二氧化硫:Ca2++2ClO- + SO2 + H2O =CaSO3↓+ 2HClOD .硫酸与足量氢氧化钡溶液混合:2H ++SO42-+Ba2++2OH -=BaSO4↓+2H2O 10.下列涉及有机物的说法正确的是A .苯能与溴单质发生取代反应,因此不能用苯萃取溴水中的溴B .丙烷是一种清洁燃料,可用作燃料电池的燃料C .淀粉和纤维素水解产物都是葡萄糖,因此二者互为同分异构体D .苯乙烯、氯乙烯都是不饱和烃,均可用于合成有机高分子材料11.X 、Y 、Z 、Q 均为短周期元素,它们在周期表中位置如图1所示。
2011年广州市高三年级调研测试数学理科

试卷类型:A2011年广州市高三年级调研测试数学(理科)本试卷共4 页,共21 题,满分150 分。
考试用时120 分钟。
2011. 01 注意事项:1. 答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上, 并用2B 铅笔在答题卡上的相应位置填涂考生号。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只 有一项是符合题目要求的. 1. 函数()3g x x =+的定义域为A .{3x x ≥-} B .{3x x >-} C .{3x x ≤-} D .{3x x <-}2. 已知i 为虚数单位, 则复数i (1+i )的模等于A .12 B. 22C. 2D. 23. 已知,x y 满足约束条件,1,1.y x x y y ≤⎧⎪+≤⎨⎪≥-⎩则2z x y =+的最大值为A . 3- B. 32-C. 32D. 34. 已知:2p x ≤,:02q x ≤≤,则p 是q 的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5. 如果执行图1的程序框图,若输入6,4n m ==,那么输出的p 等于 图1A. 720 B . 360 C . 240 D. 120图2侧视图俯视图正视图4x33x46. 已知随机变量X 服从正态分布2(,)N μσ,且(22)0.9544P X μσμσ-<≤+=, ()0.6826P X μσμσ-<≤+=,若4μ=,1σ=, 则(56)P X <<=A .0.1358B .0.1359C .0.2716D .0.27187. 一空间几何体的三视图如图2所示, 该几何体的 体积为85123π+,则正视图中x 的值为 A. 5 B . 4 C. 3 D . 28.若把函数()=y f x 的图象沿x 轴向左平移4π个单位, 沿y 轴向下平移1个单位,然后再把图象上每个点的 横坐标伸长到原来的2倍(纵坐标保持不变),得到函数 sin =y x 的图象,则()=y f x 的解析式为A. sin 214⎛⎫=-+ ⎪⎝⎭y x π B. sin 212⎛⎫=-+ ⎪⎝⎭y x π C. 1sin 124⎛⎫=+-⎪⎝⎭y x π D. 1sin 122⎛⎫=+- ⎪⎝⎭y x π二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9. 某社区有500个家庭, 其中高收入家庭125户, 中等收入家庭280户, 低收入家庭95户. 为了调查社会购买力的某项指标, 采用分层抽样的方法从中抽取1个容量为若干户的样 本, 若高收入家庭抽取了25户, 则低收入家庭被抽取的户数为 .10. 已知直线l 经过坐标原点,且与圆22430x y x +-+=相切,切点在第四象限,则直线l 的 方程为 .11. 等比数列{a n }的前n 项和为S n ,若246,30S S ==,则6S = . 12. 922()2x x -展开式的常数项是 .(结果用数值作答) 13. 设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩ 若()4f x >,则x 的取值范围是 .图3ON M DCBAMDCBAP(二)选做题(14~15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图3,四边形ABCD 内接于⊙O ,BC 是直径,MN 与⊙O 相切, 切点为A ,MAB ∠35︒=,则D ∠= .15.(坐标系与参数方程选讲选做题)已知直线l 的参数方程为:2,14x t y t=⎧⎨=+⎩(t 为参数),圆C 的极坐标方程为22sin ρθ=,则直线l 与圆C 的位置关系为 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分) 在ABC ∆中,角,,A B C 的对边分别为,,a b c . 已知向量=m 2cos,sin 22A A ⎛⎫ ⎪⎝⎭, =n c o s,2s i n 22A A ⎛⎫- ⎪⎝⎭, 1=-m n . (1) 求cos A 的值;(2) 若23a =, 2b =, 求c 的值.17.(本小题满分12分)某商店储存的50个灯泡中, 甲厂生产的灯泡占60%, 乙厂生产的灯泡占40%, 甲厂生产 的灯泡的一等品率是90%, 乙厂生产的灯泡的一等品率是80%.(1) 若从这50个灯泡中随机抽取出一个灯泡(每个灯泡被取出的机会均等), 则它是甲厂生产的 一等品的概率是多少?(2) 若从这50个灯泡中随机抽取出两个灯泡(每个灯泡被取出的机会均等), 这两个灯泡中是甲 厂生产的一等品的个数记为ξ, 求E ξ的值.18.(本小题满分l4分)如图4,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,2PA AD ==,1AB =,BM PD ⊥于点M . (1) 求证:AM ⊥PD ;(2) 求直线CD 与平面ACM 所成的角的余弦值.图4OP n+1Q n +1P nP 1Q 1l 0P 0yx19.(本小题满分14分)已知椭圆()222:133x y E a a+=>的离心率12e =. 直线x t =(0t >)与曲线E 交于 不同的两点,M N ,以线段MN 为直径作圆C ,圆心为C . (1) 求椭圆E 的方程;(2) 若圆C 与y 轴相交于不同的两点,A B ,求ABC ∆的面积的最大值.20.(本小题满分14分) 已知函数()(af x x a x=+∈R ), ()ln g x x =. (1) 求函数()()()F x f x g x =+的单调区间;(2) 若关于x 的方程()()22g x f x e x=-(e 为自然对数的底数)只有一个实数根, 求a 的值.21.(本小题满分14分)如图5,过曲线C :x y e =上一点0(0,1)P 作曲线C 的切线0l 交x 轴于点11(,0)Q x ,又过1Q 作 x 轴的垂线交曲线C 于点111(,)P x y ,然后再过111(,)P x y 作曲线C 的切线1l 交x 轴于点22(,0)Q x ,又过2Q 作x 轴的垂线交曲线C 于点222(,)P x y ,,以此类推,过点n P 的切线n l与x 轴相交于点11(,0)n n Q x ++,再过点1n Q +作x 轴的垂线交曲线C 于点111(,)n n n P x y +++(n ∈N *). (1) 求1x 、2x 及数列{}n x 的通项公式;(2) 设曲线C 与切线n l 及直线11n n P Q ++所围成的图形面积为n S ,求n S 的表达式; (3) 在满足(2)的条件下, 若数列{}n S 的前n 项和为n T ,求证:11n n n nT x T x ++<(n ∈N *).图52011年广州市高三调研测试数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题 5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9.19 10.33y x =- 11. 126 12. 212- 13.()(),22,-∞-+∞14.125︒15.相交三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查平面向量, 同角三角函数的基本关系、解三角形等知识, 考查化归与转化的数学思想方法和运算求解能力) (1) 解: ∵=m 2cos ,sin 22A A ⎛⎫ ⎪⎝⎭,=n cos ,2sin 22A A ⎛⎫- ⎪⎝⎭, 1=-m n , ∴ 222cos2sin 122A A-=-. ……2分 ∴ 1cos 2A =-. ……4分(2)解: 由(1)知1cos 2A =-,且0A π<<,∴ 23A π=. ……6分∵23a =,2b =,题号 1 2 3 4 5 6 7 8 答案ACDBBBCB由正弦定理得sin sin a b A B=,即2322sin sin3B π=, ∴1sin 2B =. ……8分 ∵0,B B A π<<<, ∴6B π=. ……10分∴6C A B ππ=--=.∴2c b ==. ……12分17. (本小题满分12分)(本小题主要考查条件概率、数学期望等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)(1) 解法1: 设事件A 表示“甲厂生产的灯泡”, 事件B 表示“灯泡为一等品”, 依题意有()0.6P A =, ()0.9P B A =,根据条件概率计算公式得()()()0.60.90.54P AB P A P B A ==⨯=. ……4分 解法2: 该商店储存的50个灯泡中是甲厂生产的灯泡有5060%30⨯=个, 乙厂生产的灯泡 有5040%20⨯=个, 其中是甲厂生产的一等品有3090%27⨯=个, 乙厂生产的 一等品有2080%16⨯=个,故从这50个灯泡中随机抽取出一个灯泡, 它是甲厂生产的一等品的概率是 270.5450P ==. ……4分 (2) 解: ξ的取值为0,1,2, ……5分()22325025301225C P C ξ===, ()11272325062111225C C P C ξ===, ()22725035121225C P C ξ=== ……8分 ∴ξ的分布列为:∴2536213511323012 1.081225122512251225E ξ=⨯+⨯+⨯==. ……12分ξ 0 1 2P2531225 6211225 3511225zyxMD CB AP18.(本小题满分l4分)(本小题主要考查空间线面关系、直线与平面所成的角等知识, 考查数形结合的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)(1)证明:∵ PA ⊥平面ABCD ,AB ⊂平面ABCD ,∴PA AB ⊥.∵AB AD ⊥,,AD PA A AD =⊂平面PAD ,PA ⊂平面PAD ,∴AB ⊥平面PAD . ∵PD ⊂平面PAD∴AB PD ⊥, ……3分 ∵BM PD ⊥, AB BM B =,AB ⊂平面ABM ,BM ⊂平面ABM ,∴PD ⊥平面ABM . ∵AM ⊂平面ABM ,∴AM ⊥PD . ……6分 (2)解法1:由(1)知,AM PD ⊥,又PA AD =, 则M 是PD 的中点, 在Rt △PAD 中,得2AM =,在Rt △CDM 中,得223MC MD DC =+=,∴1622ACM S AM MC ∆=⋅=. 设点D 到平面ACM 的距离为h ,由D ACM M ACD V V --=, ……8分 得111332ACM ACD S h S PA ∆∆=. 解得63h =, ……10分设直线CD 与平面ACM 所成的角为θ,则6sin 3h CD θ==, ……12分 ∴3cos 3θ=.∴ 直线CD 与平面ACM 所成的角的余弦值为33. ……14分解法2: 如图所示,以点A 为坐标原点,建立空间直角坐标系A xyz -,则()0,0,0A ,()0,0,2P ,()1,0,0B ,()1,2,0C ,()0,2,0D ,()0,1,1M . ∴()()()1,2,0,0,1,1,1,0,0AC AM CD ===-. ……8分设平面ACM 的一个法向量为(,,)n x y z =,由,n AC n AM ⊥⊥可得:20,0.x y y z +=⎧⎨+=⎩令1z =,得2,1x y ==-.∴(2,1,1)n =-. ……10分设直线CD 与平面ACM 所成的角为α,则6sin 3CD n CD nα⋅==. ……12分 ∴3cos 3α=. ∴直线CD 与平面ACM 所成的角的余弦值为33. ……14分 19.(本小题满分14分)(本小题主要考查椭圆、圆、直线与圆的位置关系等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解:∵椭圆()222:133x y E a a+=>的离心率12e =, ∴2312a a -=. …… 2分解得2a =.∴ 椭圆E 的方程为22143x y +=. …… 4分 (2)解法1:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=. ∴ 圆C 的半径为21232t r -=. …… 6分∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴ 212302t t -<<,即22107t <<.∴ 弦长22222123||221274t AB r d t t -=-=-=-. …… 8分∴ABC ∆的面积211272S t t =⋅- …… 9分 ()21712727t t =⨯-()2271271227t t +-≤⨯377=. …… 12分 当且仅当27127t t =-,即427t =时,等号成立. ∴ ABC ∆的面积的最大值为377. …… 14分 解法2:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=. ∴ 圆C 的半径为21232t r -=. …… 6分∴ 圆C 的方程为222123()4t x t y --+=.∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴ 212302t t -<<,即22107t <<.在圆C 的方程222123()4t x t y --+=中,令0x =,得21272t y -=±,∴ 弦长2||127AB t =-. …… 8分 ∴ABC ∆的面积211272S t t =⋅- …… 9分 ()21712727t t =⨯-()2271271227t t +-≤⨯377=. ……12分当且仅当27127t t =-,即427t =时,等号成立. ∴ ABC ∆的面积的最大值为377. …… 14分 20.(本小题满分14分)(本小题主要考查函数、导数等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识) (1)解: 函数()()()ln aF x f x g x x x x=+=++的定义域为()0,+∞. ∴()'211a F x x x =-+22x x ax+-=. ① 当140a ∆=+≤, 即14a ≤-时, 得20x x a +-≥,则()'0F x ≥. ∴函数()F x 在()0,+∞上单调递增. ……2分 ② 当140a ∆=+>, 即14a >-时, 令()'0,F x = 得20x x a +-=, 解得121141140,22a ax x --+-++=<=. (ⅰ) 若104a -<≤, 则211402a x -++=≤. ∵()0,x ∈+∞, ∴()'0F x >,∴函数()F x 在()0,+∞上单调递增. …… 4分(ⅱ)若0a >,则1140,2a x ⎛⎫-++∈ ⎪ ⎪⎝⎭时, ()'0F x <; 114,2a x ⎛⎫-++∈+∞⎪ ⎪⎝⎭时, ()'0F x >, ∴函数()F x 在区间1140,2a ⎛⎫-++ ⎪ ⎪⎝⎭上单调递减, 在区间114,2a ⎛⎫-+++∞ ⎪ ⎪⎝⎭上单调递增. …… 6分 综上所述, 当0a ≤时, 函数()F x 的单调递增区间为()0,+∞;当0a >时, 函数()F x 的单调递减区间为1140,2a ⎛⎫-++ ⎪⎪⎝⎭, 单调递增区间为114,2a ⎛⎫-+++∞ ⎪ ⎪⎝⎭. …… 8分 (2) 解: 由()()22g x f x e x=-, 得2ln 2x a x e x x =+-, 化为2ln 2x x ex a x =-+. 令()ln x h x x =, 则()'21ln x h x x-=. 令()'0h x =, 得x e =.当0x e <<时, ()'0h x >; 当x e >时, ()'0h x <.∴函数()h x 在区间()0,e 上单调递增, 在区间(),e +∞上单调递减. ∴当x e =时, 函数()h x 取得最大值, 其值为()1h e e=. …… 10分 而函数()()2222m x x ex a x e a e =-+=-+-,当x e =时, 函数()m x 取得最小值, 其值为()2m e a e =-. …… 12分∴ 当21a e e -=, 即21a e e =+时, 方程()()22g x f x e x=-只有一个根. …… 14分21. (本小题满分14分)(本小题主要考查导数、数列、不等式、定积分等知识, 考查化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1) 解: 由x y e '=,设直线n l 的斜率为n k ,则n xn k e =.∴直线0l 的方程为1y x =+.令0y =,得11x =-, ……2分 ∴111xy e e ==, ∴11(1,)P e -. ∴111x k e e==. ∴直线1l 的方程为11(1)y x e e-=+.令0y =,得22x =-. ……4分 一般地,直线n l 的方程为()nn x x n y ee x x -=-,由于点11(,0)n n Q x ++在直线n l 上,∴11n n x x +-=-.∴数列{}n x 是首项为1-,公差为1-的等差数列.∴n x n =-. ……6分 (2)解:11(1)(1)111()()222|nn x x n n n n n n n n n n S e dx x x y e y e e e ------+-+-+=--=-=--⎰ =212ne e e -⋅. ……8分 (3)证明:1211[1()]2111221(1)1222(1)1n n n n e e e e e T e e e e e ee e e----⎛⎫=⋅+++=⋅=⋅- ⎪-⎝⎭-. ……10分∴111111111111n n n n n n n T e e e T e e e e e+++++---===+---,1(1)11n n x n x n n +-+==+-. 要证明11n n n nT x T x ++<,只要证明111n e e e n +-<-,即只要证明1(1)n e e n e +>-+. ……11分 证法1:(数学归纳法)① 当1n =时,显然222(1)021(1)e e e e e e ->⇔>-⇔>-+成立;② 假设n k =时,1(1)k ee k e +>-+成立,则当1n k =+时,21[(1)]k k e e e e e k e ++=⋅>-+,而2[(1)][(1)(1)](1)(1)0e e k e e k e e k -+--++=-+>.∴[(1)](1)(1)e e k e e k e -+>-++.∴2(1)(1)k ee k e +>-++.这说明,1n k =+时,不等式也成立.由①②知不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分 证法2: 110111111[1(1)](1)(1)n n n n n n n e e C C e C e +++++++=+-=+-++- 0111(1)1(1)(1)(1)n n C C e n e e n e ++>+-=++-=-+. ∴不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分 证法3:令()()11x f x e e x e +=---,则()()'11x fx e e +=--,当0x >时, ()()'11x f x e e +=--()110e e >--=>,∴函数()f x 在()0,+∞上单调递增.∴当0x >时, ()()00f x f >=.∵n ∈N *, ∴()0f n >, 即()110n ee n e +--->.∴()11n ee n e +>-+.∴不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分。
广东省广州市花都区2011届高三年级调研考试

广东省广州市花都区2011届高三年级调研考试数学试题(理)考试时间 120分钟 满分150分一、选择题(每小题5分,共40分)1.已知集合{2,3}A =,则集合A 的子集个数是( ) A .1个 B .2个C .3个D .4个 2.已知数列{}n a 满足120n n a a +-= ()n N +∈ ,则数列{}n a 一定是( )A .公差为12的等差数列 B .公差为2的等差数列C .公比为12的等比数列D .公比为2的等比数列3.函数1sin(),(0)26y x πωω=+>的最小正周期是4π,则ω=( )A .14B .12C .1D .24.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰 直角三角形,如果直角三角形的直角边长为2,那么这个几何体 的体积为 ( )A .13 B .23C . 43D .25.已知函数()y f x =在定义域[4,6]-内可导,其导函数'()y f x =的图象如右图,则函数()y f x =的单调递增区间为( )A .411[4,],[1,]33--B .7[3,0],[,5]3- C .411[,1],[,6]33-D .7[4,3],[0,],[5,6]3--6.为了解一片经济树林的生长情况,随机测量了其中100株树木的底部周长(单位:cm ),根据所得数据画出样本的频 率分布直方图如图所示.那么在这100株树木中,底部周 长小于110cm 的株数n 是 ( ) A .30 B .60 C .70 D .80 7.如图,平面内有三个向量,,,OA OB OC 其中OA 与OB 的夹角为60°, OA 与OC 、OB 与OC 的夹角都为30°,且∣OA ∣=∣OB ∣=1, ∣OC ∣=若OC =λOA +μOB , 则λμ+的值为( )A .4B.C.D .28.奇函数()f x 在(0,)+∞上是减函数,且(1)0f -=,则不等式()f x x >的解集为( )A .(,1)(1,)-∞-+∞B .(,1)(0,1)-∞-C .(1,0)(1,)-+∞D .(1,0)(0,1)-二、填空题(每小题5分,共30分)9.已知向量(3,2),(1,2),a x b x =-=且a b ⊥,则_______x =10.已知函数()(0)xf x a b a =+>的图象经过点(2,3)和原点,则(2)____f -=.11.若执行如右图所示的程序框图,则输出的S = . 12.在ABC ∆中,已知4,3,AB BC AC ===则ABC∆的最大角的大小为 .13.在区间[0,10]上随机取两个实数x ,y ,则事件“22x y +≥”的概率为_____14.若直线:10 l ax by ++=始终平分圆M :224210x y x y ++++=的周长,则()()2222a b -+-的最小值为_________.三、解答题15.(本题满分12分)已知()cos()sin 3f x x k xπ=+-,且()62f π=. (1)求实数k 的值;(2)求函数()f x 的最大值和最小值.16.(本题满分12分)某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘是41,21,43,且各汰.已知某选手通过初赛、复赛、决赛的概率分别阶段通过与否相互独立.(1)求该选手在复赛阶段被淘汰的概率; (2)设该选手在竞赛中回答问题的个数为,求的分布列、数学期望和方差.17.(本小题满分12分) 如图,在正方体1111D C B A ABCD -中,N M ,分别为棱BC AB ,的中点. (1)试判截面11A MNC 的形状,并说明理由;(2)证明:平面⊥1MNB平面11B BDD .18.(本小题满分14分)等差数列{}n a 中,13a =,前项和为nS ,等比数列{}n b 各项均为正数,11b =,且2212b S +=,{}n b 的公比22S q b =(1)求n a 与n b ;(2)求数列1{}n S 的前n 项和19.(本小题满分14分)已知函数2()ln f x a x bx =-图象上一点(2,(2))P f 处的切线方程为22ln 23++-=x y .(1)求b a ,的值;(2)若方程()0f x m +=在1[,]e e 内有两个不等实根,求的取值范围(其中为自然对数的底数);20.(本小题满分14分)在平面直角坐标系中,O 为坐标原点,已知两点(1,3),(5,1)M N -,若动点C 满足.NC t NM =且点C 的轨迹与抛物线24y x =交于,A B 两点.(1)求证:OA OB ⊥;(2)在x 轴上是否存在一点(,0)(0)P m m ≠,使得过点P 的直线l 交抛物线24y x =于,D E 两点,并以线段DE 为直径的圆都过原点。
2011年广州市高三数学 调研测试试题

2011年广州市高三调研测试说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9.19 10.33y x =- 11. 126 12. 212-13.()(),22,-∞-+∞14.125︒15.相交三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查平面向量, 同角三角函数的基本关系、解三角形等知识, 考查化归与转化的数学思想方法和运算求解能力)(1) 解: ∵=m 2cos ,sin 22A A ⎛⎫ ⎪⎝⎭,=n cos ,2sin 22A A ⎛⎫- ⎪⎝⎭, 1=-m n ,∴ 222cos2sin 122A A -=-. ……2分 ∴ 1cos 2A =-. ……4分(2)解: 由(1)知1cos 2A =-,且0A π<<,∴ 23A π=. ……6分∵23a =,2b =,由正弦定理得sin sin a b A B=,即2322sin sin3B π=,题号 1 2 3 4 5 6 7 8 答案ACDBBBCB∴1sin 2B =. ……8分 ∵0,B B A π<<<,∴6B π=. ……10分∴6C A B ππ=--=.∴2c b ==. ……12分17. (本小题满分12分) (本小题主要考查条件概率、数学期望等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)(1) 解法1: 设事件A 表示“甲厂生产的灯泡”, 事件B 表示“灯泡为一等品”, 依题意有()0.6P A =, ()0.9P B A =,根据条件概率计算公式得()()()0.60.90.54P AB P A P B A ==⨯=. ……4分解法2: 该商店储存的50个灯泡中是甲厂生产的灯泡有5060%30⨯=个, 乙厂生产的灯泡 有5040%20⨯=个, 其中是甲厂生产的一等品有3090%27⨯=个, 乙厂生产的 一等品有2080%16⨯=个,故从这50个灯泡中随机抽取出一个灯泡, 它是甲厂生产的一等品的概率是 270.5450P ==. ……4分(2) 解: ξ的取值为0,1,2, ……5分()22325025301225C P C ξ===, ()11272325062111225C C P C ξ===, ()22725035121225C P C ξ=== (8)分∴ξ的分布列为:∴2536213511323012 1.081225122512251225E ξ=⨯+⨯+⨯==. ……12分18.(本小题满分l4分)(本小题主要考查空间线面关系、直线与平面所成的角等知识, 考查数形结合的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)(1)证明:∵ PA ⊥平面ABCD ,AB ⊂平面ABCD ,∴PA AB ⊥.ξ 0 12P2531225 6211225 3511225zyxMD CB AP∵AB AD ⊥,,AD PA A AD =⊂平面PAD ,PA ⊂平面PAD ,∴AB ⊥平面PAD . ∵PD ⊂平面PAD∴AB PD ⊥, ……3分 ∵BM PD ⊥, AB BM B =,AB ⊂平面ABM ,BM ⊂平面ABM ,∴PD ⊥平面ABM . ∵AM ⊂平面ABM ,∴AM ⊥PD . ……6分 (2)解法1:由(1)知,AM PD ⊥,又PA AD =, 则M 是PD 的中点, 在Rt △PAD 中,得2AM =,在Rt △CDM 中,得223MC MD DC =+=,∴1622ACM S AM MC ∆=⋅=. 设点D 到平面ACM 的距离为h ,由D ACM M ACD V V --=, ……8分 得111332ACM ACD S h S PA ∆∆=. 解得63h =, ……10分设直线CD 与平面ACM 所成的角为θ,则6sin 3h CD θ==, ……12分 ∴3cos 3θ=.∴ 直线CD 与平面ACM 所成的角的余弦值为33. ……14分解法2: 如图所示,以点A 为坐标原点,建立空间直角坐标系A xyz -,则()0,0,0A ,()0,0,2P ,()1,0,0B ,()1,2,0C ,()0,2,0D ,()0,1,1M . ∴()()()1,2,0,0,1,1,1,0,0AC AM CD ===-. ……8分设平面ACM 的一个法向量为(,,)n x y z =, 由,n AC n AM ⊥⊥可得:20,0.x y y z +=⎧⎨+=⎩令1z =,得2,1x y ==-.∴(2,1,1)n =-. ……10分 设直线CD 与平面ACM 所成的角为α,则6sin 3CD n CD nα⋅==. ……12分 ∴3cos 3α=.∴直线CD 与平面ACM 所成的角的余弦值为33. ……14分 19.(本小题满分14分)(本小题主要考查椭圆、圆、直线与圆的位置关系等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解:∵椭圆()222:133x y E a a+=>的离心率12e =, ∴2312a a -=. …… 2分解得2a =.∴ 椭圆E 的方程为22143x y +=. …… 4分 (2)解法1:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y=⎧⎪⎨+=⎪⎩ 得221234t y -=. ∴ 圆C 的半径为21232t r -=. …… 6分∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =, ∴ 212302t t -<<,即22107t <<.∴ 弦长22222123||221274t AB r d t t -=-=-=-. …… 8分∴ABC ∆的面积211272S t t =⋅- …… 9分()21712727t t =⨯- ()2271271227t t +-≤⨯377=. …… 12分 当且仅当27127t t =-,即427t =时,等号成立.∴ ABC ∆的面积的最大值为377. …… 14分解法2:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩得221234t y -=.∴ 圆C 的半径为21232t r -=. …… 6分∴ 圆C 的方程为222123()4t x t y --+=.∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =, ∴ 212302t t -<<,即22107t <<.在圆C 的方程222123()4t x t y --+=中,令0x =,得21272t y -=±,∴ 弦长2||127AB t =-. …… 8分∴ABC ∆的面积211272S t t =⋅- …… 9分 ()21712727t t =⨯- ()2271271227t t +-≤⨯377=. ……12分 当且仅当27127t t =-,即427t =时,等号成立.∴ ABC ∆的面积的最大值为377. (14)分20.(本小题满分14分)(本小题主要考查函数、导数等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识) (1)解: 函数()()()ln aF x f x g x x x x=+=++的定义域为()0,+∞. ∴()'211a F x x x =-+22x x ax +-=.① 当140a ∆=+≤, 即14a ≤-时, 得20x x a +-≥,则()'0F x ≥. ∴函数()F x 在()0,+∞上单调递增. ……2分② 当140a ∆=+>, 即14a >-时, 令()'0,F x = 得20x x a +-=, 解得121141140,22a ax x --+-++=<=.(ⅰ) 若104a -<≤, 则211402a x -++=≤. ∵()0,x ∈+∞, ∴()'0F x >,∴函数()F x 在()0,+∞上单调递增. …… 4分(ⅱ)若0a >,则1140,2a x ⎛⎫-++∈ ⎪ ⎪⎝⎭时, ()'0F x <; 114,2a x ⎛⎫-++∈+∞ ⎪ ⎪⎝⎭时, ()'0F x >, ∴函数()F x 在区间1140,2a ⎛⎫-++ ⎪ ⎪⎝⎭上单调递减, 在区间114,2a ⎛⎫-+++∞ ⎪ ⎪⎝⎭上单调递增. …… 6分 综上所述, 当0a ≤时, 函数()F x 的单调递增区间为()0,+∞;当0a >时, 函数()F x 的单调递减区间为1140,2a ⎛⎫-++ ⎪ ⎪⎝⎭, 单调递增区间为114,2a ⎛⎫-+++∞ ⎪ ⎪⎝⎭. …… 8分(2) 解: 由()()22g x f x e x=-, 得2ln 2x a x e x x =+-, 化为2ln 2xx ex a x =-+. 令()ln x h x x =, 则()'21ln x h x x -=. 令()'0h x =, 得x e =.当0x e <<时, ()'0h x >; 当x e >时, ()'0h x <.∴函数()h x 在区间()0,e 上单调递增, 在区间(),e +∞上单调递减. ∴当x e =时, 函数()h x 取得最大值, 其值为()1h e e=. …… 10分而函数()()2222m x x ex a x e a e =-+=-+-,当x e =时, 函数()m x 取得最小值, 其值为()2m e a e =-. (12)分∴ 当21a e e -=, 即21a e e =+时, 方程()()22g x f x e x=-只有一个根. …… 14分21. (本小题满分14分)(本小题主要考查导数、数列、不等式、定积分等知识, 考查化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1) 解: 由x y e '=,设直线n l 的斜率为n k ,则n xn k e =.∴直线0l 的方程为1y x =+.令0y =,得11x =-, ……2分∴111xy e e ==, ∴11(1,)P e-. ∴111x k e e==. ∴直线1l 的方程为11(1)y x e e-=+.令0y =,得22x =-. ……4分一般地,直线n l 的方程为()nn x x n y ee x x -=-,由于点11(,0)n n Q x ++在直线n l 上, ∴11n n x x +-=-.∴数列{}n x 是首项为1-,公差为1-的等差数列.∴n x n =-. ……6分 (2)解:11(1)(1)111()()222|nn x x n n n n n n n n n n S e dx x x y e y e e e ------+-+-+=--=-=--⎰ =212ne e e -⋅. ……8分 (3)证明:1211[1()]2111221(1)1222(1)1n n n n e e e e e T e e e e e ee e e----⎛⎫=⋅+++=⋅=⋅- ⎪-⎝⎭-. ……10分∴111111111111n n n n n n n T e e e T e e e e e+++++---===+---,1(1)11n n x n x n n +-+==+-.要证明11n n n nT x T x ++<,只要证明111n e e e n +-<-,即只要证明1(1)n e e n e +>-+. ……11分 证法1:(数学归纳法)① 当1n =时,显然222(1)021(1)e e e e e e ->⇔>-⇔>-+成立; ② 假设n k =时,1(1)k e e k e +>-+成立, 则当1n k =+时,21[(1)]k k e e e e e k e ++=⋅>-+, 而2[(1)][(1)(1)](1)(1)0e e k e e k e e k -+--++=-+>. ∴[(1)](1)(1)e e k e e k e -+>-++. ∴2(1)(1)k e e k e +>-++.这说明,1n k =+时,不等式也成立. 由①②知不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分 证法2: 110111111[1(1)](1)(1)n n n n n n n e e C C e C e +++++++=+-=+-++- 0111(1)1(1)(1)(1)n n C C e n e e n e ++>+-=++-=-+. ∴不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分 证法3:令()()11x f x ee x e +=---,则()()'11x fx e e +=--,当0x >时, ()()'11x f x e e +=--()110e e >--=>,∴函数()f x 在()0,+∞上单调递增. ∴当0x >时, ()()00f x f >=. ∵n ∈N *, ∴()0f n >, 即()110n ee n e +--->.∴()11n e e n e +>-+. ∴不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分 [例1]求经过两点P 1(2,1)和P 2(m ,2)(m ∈R )的直线l 的斜率,并且求出l 的倾斜角α及其取值范围.选题意图:考查倾斜角与斜率之间的关系及斜率公式.解:(1)当m =2时,x 1=x 2=2,∴直线l 垂直于x 轴,因此直线的斜率不存在,倾斜角α=2π (2)当m ≠2时,直线l 的斜率k =21-m ∵m >2时,k >0. ∴α=arctan21-m ,α∈(0,2π), ∵当m <2时,k <0 ∴α=π+arctan21-m ,α∈(2π,π). 说明:利用斜率公式时,应注意斜率公式的应用范围. [例2]若三点A (-2,3),B (3,-2),C (21,m )共线,求m 的值. 选题意图:考查利用斜率相等求点的坐标的方法. 解:∵A 、B 、C 三点共线, ∴kAB =kAC ,.22132332+-=+--m 解得m =21. 说明:若三点共线,则任意两点的斜率都相等,此题也可用距离公式来解. [例3]已知两点A (-1,-5),B (3,-2),直线l 的倾斜角是直线AB 倾斜角的一半,求直线l 的斜率.选题意图:强化斜率公式.解:设直线l 的倾斜角α,则由题得直线AB 的倾斜角为2α.∵tan2α=kAB =.43)1(3)5(2=-----43tan 1tan 22=-∴αα 即3tan 2α+8tan α-3=0, 解得tan α=31或tan α=-3. ∵tan2α=43>0,∴0°<2α<90°, 0°<α<45°, ∴tan α=31. 因此,直线l 的斜率是31说明:由2α的正切值确定α的范围及由α的范围求α的正切值是本例解法中易忽略的地方.命题否定的典型错误及制作在教材的第一章安排了《常用逻辑用语》的内容.从课本内容安排上看,显得较容易,但是由于对逻辑联结词不能做到正确理解,在解决这部分内容涉及的问题时容易出错.下面仅对命题的否定中典型错误及常见制作方法加以叙述.一、典型错误剖析错误1——认为命题的否定就是否定原命题的结论在命题的否定中,有许多是把原命题中的结论加以否定.如命题:2是无理数,其否定是:2不是无理数.但据此就认为命题的否定就是否定原命题的结论就错了.例1写出下列命题的否定:⑴对于任意实数x,使x2=1;⑵存在一个实数x,使x2=1.错解:它们的否定分别为⑴对于任意实数x,使x2≠1;⑵存在一个实数x,使x2≠1.剖析:对于⑴是全称命题,要否定它只要存在一个实数x,使x2≠1即可;对于⑵是存在命题,要否定它必须是对所有实数x,使x2≠1.正解:⑴存在一个实数x,使x2≠1;⑵对于任意实数x,使x2≠1.错误2——认为命题的否定就是原命题中的判断词改和其意义相反的判断词在命题的否定中,有许多是把原命题中的判断词改为相反意义的词,如“是”改为“不是”、“等”改为“不等”、“大于”改为“小于或等于”等.但对于联言命题及选言命题,还要把逻辑联结词“且”与“或”互换.例2写出下列命题的否定:⑴线段AB与CD平行且相等;⑵线段AB与CD平行或相等.错解:⑴线段AB与CD不平行且不相等;⑵线段AB与CD不平行或不相等.剖析:对于⑴是联言命题,其结论的含义为:“平行且相等”,所以对原命题结论的否定除“不平行且不相等”外,还应有“平行且不相等”、“不平行且相等”;而⑵是选言命水产价格 /shuichan/ 水产价格吘莒咦题,其结论包含“平行但不相等”、“不平行但相等”、“平行且相等”三种情况,故否定就为“不平行且不相等”.正解:⑴线段AB与CD不平行或不相等;⑵线段AB与CD不平行且不相等.错误3——认为“都不是”是“都是”的否定例3写出下列命题的否定:⑴a,b都是零;⑵高一(一)班全体同学都是共青团员.错解:⑴a,b都不是零;⑵高一(一)班全体同学都不是共青团员.剖析:要注意“都是”、“不都是”、“都不是”三者的关系,其中“都是”的否定是“不都是”,“不都是”包含“都不是”;“至少有一个”的否定是“一个也没有”.正解:⑴a,b不都是零,即“a,b中至少有一个不是零”.⑵高一(一)班全体同学不都是共青团员,或写成:高一(一)班全体同学中至少有一人共青团员.错误4——认为“命题否定”就是“否命题”根据逻辑学知识,任一命题p都有它的否定(命题)非p(也叫负命题、反命题);而否命题是就假言命题(若p则q)而言的.如果一个命题不是假言命题,就无所谓否命题,也就是说,我们就不研究它的否命题.我们应清醒地认识到:假言命题“若p则q”的否命题是“若非p则非q”,而“若p则q”的否定(命题)则是“p且非q”,而不是“若p则非q”.例4写出命题“满足条件C的点都在直线F上”的否定.错解:不满足条件C的点不都在直线F上.剖析:对于原命题可表示为“若A,则B”,其否命题是“若┐A,则┐B”,而其否定形式是“若A,则┐B”,即不需要否定命题的题设部分.正解:满足条件C的点不都在直线F上.二、几类命题否定的制作1.简单的简单命题命题的形如“A是B”,其否定为“A不是B”.只要把原命题中的判断词改为与其相反意义的判断词即可.例5写出下列命题的否定:⑴ 3+4>6;⑵ 2是偶数.解:所给命题的否定分别是:⑴ 3+4≤6;⑵ 2不是偶数.2.含有全称量词和存在量词的简单命题全称量词相当于日常语言中“凡”,“所有”,“一切”,“任意一个”等,形如“所有A是B”,其否定为“存在某个A不是B”;存在量词相当于“存在一个”,“有一个”,“有些”,“至少有一个”,“至多有一个”等,形如“某一个A是B”,其否定是“对于所有的A都不是B”.全称命题的否定是存在命题,存在命题的否定是全称命题.例6写出下列命题的否定:⑴不论m取什么实数,x2+x-m=0必有实根.⑵存在一个实数x,使得x2+x+1≤0.⑶至少有一个整数是自然数.⑷至多有两个质数是奇数.解:⑴原命题相当于“对所有的实数m,x2+x-m=0必有实根”,其否定是“存在实数m,使x2+x-m=0没有实根”.⑵原命题的否定是“对所有的实数x,x2+x+1>0”.⑶原命题的否定是“没有一个整数是自然数”.⑷原命题的否定是“至少有三个质数是奇数”.3.复合命题“p且q”,“p或q”的否定“p且q”是联言命题,其否定为“非p或非q”(也写成┐p或┐q“;“p或q”是选言命题,其否定为“非p且非q”(也写成┐p且┐q“;例7写出下列命题的否定:⑴他是数学家或物理学家.⑵他是数学家又是物理学家.⑶2123x x+-≥0.解:⑴原命题的否定是“他既不是数学家也不是物理学家”.⑵原命题的否定是“他不能同时是数学家和物理学家”,即“他不是数学家或他不是物理学家”.⑶若认为┐p:2123x x +-<0,那就错了.┐p是对p的否定,包括2123x x+-<0或2123x x+-=0.或∵p :x >1或x <-3,∴┐p :-3≤x ≤1.第1章 第3节知能训练·提升考点一:命题真假的判断1.如果命题“非p 或非q ”是假命题,则下列结论中正确的为( )①命题“p 且q ”是真命题; ②命题“p 且q ”是假命题; ③命题“p 或q ”是真命题; ④命题“p 或q ”是假命题.A .①③B .②④C .②③D .①④解析:由“非p 或非q ”是假命题知,非p 和非q 都是假命题.即p 为真,q 为真.所以p 且q 为真,p 或q 也为真.①③正确.答案:A2.设命题p :若a >b ,则1a <1b ;命题q :1ab<0⇔ab <0.给出下列四个复合命题:①p 或q ;②p 且q ;③綈p 且q ;④綈p 或綈q .其中真命题的个数为( )A .0B .1C .2D .3解析:由题意知p 为假命题,q 为真命题,故p 或q 为真,p 且q 为假,綈p 且q 为真,綈p 或綈q 也为真,故真命题有3个.答案:D3.(2010·湖北质检)P :函数y =log a (x +1)在(0,+∞)内单调递减;Q :曲线y =x 2+(2a -3)x +1与x 轴交于不同的两点.如果P 与Q 有且只有一个正确,求a 的取值范围.解:当0<a <1时,函数y =log a (x +1)在(0,+∞)内单调递减;当a >1时,函数y =log a (x +1)在(0,+∞)内不单调递减.曲线y =x 2+(2a -3)x +1与x 轴交于不同两点等价于(2a -3)2-4>0,即a <12或a >52.情形(1):P 正确,但Q 不正确,因此a ∈(0,1)∩[12,52],即a ∈[12,1).情形(2):P 不正确,但Q 正确,因此a ∈(1,+∞)∩[(-∞,12)∪(52,+∞)],即a ∈(52,+∞).综上,a 的取值范围是[12,1)∪(52,+∞).考点二:反证法的应用4.用反证法证明命题“a ,b ∈N ,ab 可被5整除,那么a ,b 中至少有一个能被5整除”,那么假设的内容是( )A .a ,b 都能被5整除B .a ,b 都不能被5整除C .a 不能被5整除D .a ,b 有一个不能被5整除 答案:B5.已知函数f (x )对其定义域内的任意两个实数a 、b ,当a <b 时,都有f (a )<f (b ),求证:f (x )=0至多有一实根.证明:假设f (x )=0至少有两个不同的实根x 1,x 2,不妨设x 1<x 2,由方程的定义,f (x 1)=0,f (x 2)=0,则f (x 1)=f (x 2),①但是由已知,当x 1<x 2时,f (x 1)<f (x 2),②①式与②式矛盾,因此假设不成立.故f (x )至多有一个实根.考点三:充要条件的判断及证明6.若不等式|x -m |<1成立的充分不必要条件是13<x <12,则实数m 的取值范围是( )A .[-43,12]B .[-12,43]C .(-∞,-12]D .[43,+∞)解析:|x -m |<1⇔m -1<x <m +1.由题意m -1≤13且m +1≥12,得-12≤m ≤43.答案:B7.(2010·山东名校联考)已知命题p :-1≤4x -3≤1,命题q :x 2-(2a +1)x +a (a +1)≤0,,若綈p 是綈q 的必要不充分条件,则实数a 的取值范围是( )A .[0,12]B .[12,1]C .[13,12]D .(13,1]解析:由题知,命题p 为M =[12,1],命题q 为N =[a ,a +1].∵綈p 是綈q 的必要不充分条件,∴p 是q 的充分不必要条件,从而有M N ,于是可得⎩⎪⎨⎪⎧a <12,a +1>1.而当a =0或a =12时,同样满足M N 成立,故a 的取值范围是[0,12].答案:A8.(探究题)(1)是否存在实数p ,使“4x +p <0”是“x 2-x -2>0”的充分条件?如果存在,求出p 的取值范围.(2)是否存在实数p ,使“4x +p <0”是“x 2-x -2>0”的必要条件?如果存在,求出p 的取值范围.解:(1)因为x 2-x -2>0的解为x >2或x <-1.所以当x >2或x <-1时,x 2-x -2>0.由4x +p <0得x <-p 4.设A ={x |x >2或x <-1},B ={x |x <-p4}.由题意得B ⊆A .所以-p4≤-1,所以p ≥4.故存在实数p ≥4,使“4x +p <0”是“x 2-x -2>0”的充分条件.(2)由(1)知,要使“4x +p <0”是“x 2-x -2>0”的必要条件,则需满足A ⊆B ,但这不可能,故不存在实数p ,使“4x +p <0”是“x 2-x -2>0”的必要条件.1.(2009·浙江)已知a 、b 是实数,则“a >0且b >0”是“a +b >0且ab >0”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 解析:由a >0且b >0可得a +b >0,ab >0,由a +b >0有a 、b 至少一个为正,ab >0可得a 、b 同号, 两者同时成立,则必有a >0,b >0,故选C. 答案:C2.(2009·安徽)下列选项中,p 是q 的必要不充分条件的是( )A .p :a +c >b +d ,q :a >b 且c >dB .p :a >1,b >1,q :f (x )=a x-b (a >0,且a ≠1)的图像不过第二象限C .p :x =1,q :x 2=xD .p :a >1,q :f (x )=log a x (a >0,且a ≠1)在(0,+∞)上为增函数 解析:∵p :a +c >b +d ,q :a >b 且c <d , ∴pq ,q ⇒p .对于选项B :p ⇒q ,qp ,p 是q 的充分不必要条件.对于选项C :p ⇒q ,q p ,p 是q 的充分不必要条件. 对于选项D :p ⇔q ,p 是q 的充要条件.故选A. 答案:A3.(2009·江苏)设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直; (4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直. 上面命题中,真命题...的序号是________(写出所有真命题的序号). 解析:(1)由面面平行的判定定理可得,该命题正确; (2)由线面平行的判定定理可得,该命题正确.(3)如图(举反例),a ⊂α,α∩β=l ,a ⊥l ,使α与β不垂直.(4)l ⊥α,垂直的充要条件是l 与α内的两条相交直线垂直. 答案:(1)(2)1.对于函数:①f (x )=|x +2|,②f (x )=(x -2)2,③f (x )=cos(x -2),判断如下两个命题的真假;命题甲:f (x +2)是偶函数;命题乙:f (x )在(-∞,2)上是减函数,在(2,+∞)上是增函数;能使命题甲、乙均为真命题的所有函数的序号是( )A .①②B .②C .①③D .③解析:对于函数①,∵f (x +2)=|x +4|,∴命题甲是假命题;对于函数②,∵f (x +2)=x 2,∴命题甲是真命题,且命题乙是真命题; 对于函数③,∵f (x +2)=cos x ,∴命题甲是真命题,但命题乙是假命题. 答案:B2.已知集合A ={y |y =x 2-32x +1,x ∈[34,2]},B ={x |x +m 2≥1};命题p :x ∈A ,命题q :x ∈B ,并且命题p 是命题q 的充分条件,求实数m 的取值范围.解:化简集合A ,由y =x 2-32x +1,配方得y =(x -34)2+716.∵x ∈[34,2],∴y min =716,y max =2.∴y ∈[716,2].∴A ={y |716≤y ≤2}.化简集合B ,由x +m 2≥1,∴x ≥1-m 2, B ={x |x ≥1-m 2}.∵命题p 是命题q 的充分条件,∴A ⊆B .∴1-m 2≤716,解之,得m ≥34或m ≤-34.∴实数m 的取值范围是(-∞,-34]或[34,+∞).。
2011年广州市高三年级调研测试--数学(文)

试卷类型:A2011年广州市高三年级调研测试数学(文科)本试卷共4 页,共21 题,满分150 分。
考试用时120 分钟。
2011.01参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符 合题目要求的. 1. 函数()3g x x =+的定义域为A .{3x x ≥-}B .{3x x >-}C .{3x x ≤-} D .{3x x <-}2.已知i 为虚数单位, 则复数z =i (1+i )在复平面内对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限 3.设向量(2,0)=a ,(1,1)=b ,则下列结论中正确的是A .||||=a b B . 21=⋅b a C .//a b D .()-⊥a b b4.已知直线l 经过坐标原点,且与圆22430x y x +-+=相切,切点在第四象限,则直线l 的 方程为A .3y x =B .3y x =C .33y x =-D .33y x = 5.甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:从这四个人中选择一人参加奥运会射击项目比赛,最佳人选是 A .甲 B . 乙 C . 丙 D .丁甲 乙 丙 丁平均环数x8.6 8.9 8.9 8.2 方差2s3.53.52.15.6图2侧视图俯视图正视图6.如果执行图1的程序框图,若输入6,4n m ==,那么输出的p 等于A .720B .360C .240D .1207.“2>x ”是“0232>+-x x ”成立的 图1 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 8.定义3x y x y ⊗=-, 则()h h h ⊗⊗等于A .h -B .0C .hD .3h9. 一空间几何体的三视图如图2所示, 该几何体的体积为123π+,则正视图中x 的值为 A .5 B .4 C .3 D .2 10.若把函数()=y f x 的图象沿x 轴向左平移4π个单位, 沿y 轴向下平移1个单位,然后再把图象上每个点的 横坐标伸长到原来的2倍(纵坐标保持不变),得到函数 sin =y x 的图象,则()=y f x 的解析式为 A .sin 214⎛⎫=-+ ⎪⎝⎭y x π B .sin 212⎛⎫=-+ ⎪⎝⎭y x π C .1sin 124⎛⎫=+- ⎪⎝⎭y x π D .1sin 122⎛⎫=+- ⎪⎝⎭y x π二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题)11.已知等比数列{}n a 的公比是2,33a =,则5a 的值是 .12.△ABC 的三个内角A 、B 、C 所对边的长分别为a 、b 、c ,已知2,3a b ==,则sin sin()AA C =+ .图3ONMDCBA13.设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩ 若()4f x >,则x 的取值范围是 .(二)选做题(14~15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图3,四边形ABCD 内接于⊙O , BC 是直径,MN 与⊙O 相切, 切点为A ,MAB ∠35︒=,则D ∠= .15.(坐标系与参数方程选讲选做题)已知直线l 的参数方程为:2,14x t y t=⎧⎨=+⎩(t 为参数),圆C 的极坐标方程为22sin ρθ=,则直线l 与圆C 的位置关系为 . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知向量a (sin ,2)θ=,b (cos ,1)θ=, 且a //b ,其中(0,)2πθ∈.(1)求θsin 和θcos 的值; (2)若3sin(), 052πθωω-=<<,求cos ω的值. 17.(本小题满分12分)某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数 分布)如下表:学历 35岁以下 35~50岁 50岁以上本科 8030 20研究生x20y(1)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本 看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率;(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取N 个人,其中35岁以 下48人,50岁以上10人,再从这N 个人中随机抽取出1人,此人的年龄为50岁以上 的概率为539,求x 、y 的值.18.(本小题满分14分)如图4,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,AB DC ∥,A B CPD PAD △是等边三角形,已知24BD AD ==,2AB DC ==(1)求证:BD ⊥平面PAD ;(2)求三棱锥A PCD -的体积.19.(本小题满分14分) 图4已知椭圆(222:13x y E a a +=>的离心率12e =. 直线x t =(0t >)与曲线E 交于 不同的两点,M N ,以线段MN 为直径作圆C ,圆心为C . (1)求椭圆E 的方程;(2)若圆C 与y 轴相交于不同的两点,A B ,求ABC ∆的面积的最大值.20.(本小题满分14分)已知数列}{n a 的前n 项和为n S ,且满足1(n n S a n =-∈N *).各项为正数的数列}{n b 中,对于一切n ∈N *,有nk ==且1231,2,3b b b ===.(1)求数列{}n a 和{}n b 的通项公式;(2)设数列{}n n a b 的前n 项和为n T ,求证:2n T <.21.(本小题满分14分) 已知函数()(af x x a x=+∈R ), ()ln g x x =. (1)求函数()()()F x f x g x =+的单调区间;(2)若关于x 的方程()()22g x f x e x =-(e 为自然对数的底数)只有一个实数根, 求a 的值. 2011年广州市高三调研测试数学(文科)试题参考答案及评分标准一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.二、填空题:本大题主要考查基本知识和基本运算.本大题共5小题,考生作答4小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题. 11.12 12.2313.()(),22,-∞-+∞ 14.125︒ 15.相交三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查平面向量, 同角三角函数的基本关系、两角和与差的三角公式等知识, 考查化归与转化的数学思想方法和运算求解能力)(1)解:∵a (sin ,2)θ=,b (cos ,1)θ=, 且a //b , ∴sin cos 21θθ=,即θθcos 2sin =. …… 2分 ∵ 1cos sin22=+θθ, 0,2πθ⎛⎫∈ ⎪⎝⎭,解得sin θθ==, ∴55cos ,552sin ==θθ. …… 6分 (2)解:∵02πω<<,20πθ<<,∴22ππθω-<-<.∵3sin(), 5θω-=∴ 4cos()5θω-==. …… 8分 ∴cos cos[()]cos cos()sin sin()ωθθωθθωθθω=--=-+- …… 10分5=. …… 12分 17.(本小题满分12分)(本小题主要考查分层抽样、概率等知识, 考查或然与必然的数学思想方法,以及数据处理能力、 运算求解能力和应用意识)(1) 解: 用分层抽样的方法在35~50岁中抽取一个容量为5的样本, 设抽取学历为本科的人数为m , ∴30505m=, 解得3m =. …… 2分 ∴ 抽取了学历为研究生2人,学历为本科3人,分别记作S 1、S 2 ;B 1、B 2、B 3 .从中任取2人的所有基本事件共10个: (S 1, B 1),(S 1, B 2),(S 1, B 3),(S 2, B 1),(S 2, B 2), (S 2, B 3), (S 1, S 2), (B 1, B 2), (B 2, B 3), (B 1, B 3).O PDC BA其中至少有1人的学历为研究生的基本事件有7个: (S 1, B 1),(S 1, B 2),(S 1, B 3),(S 2, B 1), (S 2, B 2), (S 2, B 3), (S 1, S 2). …… 4分 ∴ 从中任取2人,至少有1人的教育程度为研究生的概率为710. …… 6分 (2)解: 依题意得:10539N =,解得78N =. …… 8分 ∴ 35~50岁中被抽取的人数为78481020--=. ∴482010805020x y==++. …… 10分解得40, 5x y ==.∴40, 5x y ==. …… 12分 18.(本小题满分14分)(本小题主要考查空间线面关系、锥体的体积等知识, 考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)(1)证明:在ABD △中,由于2AD =,4BD =,AB =∴222AD BD AB +=. …… 2分 ∴ AD BD ⊥.又平面PAD ⊥平面ABCD ,平面PAD平面ABCD AD =,BD ⊂平面ABCD ,∴BD ⊥平面PAD . …… 4分 (2)解:过P 作PO AD ⊥交AD 于O .又平面PAD ⊥平面ABCD , ∴PO ⊥平面ABCD . …… 6分∵PAD △是边长为2的等边三角形,∴PO =. 由(1)知,AD BD ⊥,在Rt ABD △中, 斜边AB边上的高为AD BD h AB ⨯==. …… 8分∵AB DC ∥,∴11222ACD S CD h =⨯==△. …… 10分∴11233A PCD P ACD ACD V V S PO --==⨯=⨯=△. …… 14分 19.(本小题满分14分)(本小题主要考查椭圆、圆、直线与圆的位置关系等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解:∵椭圆()222:133x y E a a +=>的离心率12e =,∴12a =. …… 2分解得2a =.∴ 椭圆E 的方程为22143x y +=. …… 4分 (2)解法1:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩得221234t y -=. ∴ 圆C的半径为2r =. …… 6分∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即0t <<.∴弦长||AB === ……8分∴ABC ∆的面积12S =⋅…… 9分)2127t =- )221272t +-≤= (12)分=,即t=. ∴ ABC ∆的面积的最大值为7. …… 14分 解法2:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=. ∴ 圆C的半径为r =. …… 6分∴ 圆C 的方程为222123()4t x t y --+=.∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即07t <<.在圆C 的方程222123()4t x t y --+=中,令0x =,得2y =±,∴弦长||AB =. …… 8分 ∴ABC ∆的面积12S =⋅…… 9分)2127t =- )221272t +-≤7= (12)分=,即7t =时,等号成立. ∴ ABC ∆. …… 14分 20.(本小题满分14分)(本小题主要考查数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1)解:∵1n n S a =-,当1n =时,1111a S a ==-, 解得112a =. ……1分当2n ≥时,1n n n a S S -=-()()111n n a a -=---, 得12n n a a -=, 即112n n a a -=. …… 3分 ∴数列}{n a 是首项为12, 公比为12的等比数列. ∴1111222n n n a -⎛⎫=⨯=⎪⎝⎭. …… 4分 ∵ 对于一切n ∈N *,有1nk ==, ①当2n ≥时, 有1n k -==, ②① - ②= 化简得: 11(1)0n n n b nb b +--+=, ③用1n +替换③式中的n ,得:211(1)0n n nb n b b ++-++=, ④ ……6分 ③-④ 整理得:211n n n n b b b b +++-=-, ∴当2n ≥时, 数列{}n b 为等差数列. ∵32211b b b b -=-=,∴ 数列{}n b 为等差数列. …… 8分 ∵ 121,2b b == ∴数列{}n b 的公差1d =.∴()11n b n n =+-=. …… 10分 (2)证明:∵数列{}n n a b 的前n 项和为n T ,∴231232222n n nT =++++, ⑤ ∴2211122222n n nT +=+++ , ⑥⑤-⑥得:21111122222n n n nT +=+++-…… 12分 1111221212nn n +⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦=--1212n n ++=-. ∴2222n n n T +=-<. ……14分 21.(本小题满分14分)(本小题主要考查函数、导数等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识) (1)解: 函数()()()ln aF x f x g x x x x=+=++的定义域为()0,+∞. ∴()'211a F x x x=-+22x x ax +-=.① 当140a ∆=+≤, 即14a ≤-时, 得20x x a +-≥,则()'0F x ≥. ∴函数()F x 在()0,+∞上单调递增. ……2分 ② 当140a ∆=+>, 即14a >-时, 令()'0,F x =得20x xa +-=, 解得120,x x =<=.(ⅰ) 若104a -<≤, 则20x =≤. ∵()0,x ∈+∞, ∴()'0F x >,∴函数()F x 在()0,+∞上单调递增. ……4分 (ⅱ)若0a >,则x ⎛∈⎝⎭时, ()'0F x <; 12x ⎛⎫-+∈+∞ ⎪ ⎪⎝⎭时, ()'0F x >, ∴函数()F x 在区间10,2⎛⎫-+ ⎪ ⎪⎝⎭上单调递减, 在区间12⎛⎫-++∞ ⎪ ⎪⎝⎭上单调递增.知识像烛光,能照亮一个人,也能照亮无数的人。
广东省广州市花都区2011届高三上学期学期初调研考试试题

广东省广州市花都区2011届高三上学期期初调研考试试题(英语)(本试卷三大题,满分135分。
考试用时120分钟。
)注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
I 语言知识及应用(共两节。
满分45分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1~15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
A man who knows how to write a personal letter has a very powerful tool. A letter can be enjoyed, read and 1 . It can set up a warm conversation between two people far apart; it can keep a 2 with very little effort.I will give 3 . A few years ago my older brother and I were not getting along well. We had been close as 4 but had grown apart. Our meetings were not 5 ; our conversation was filled with arguments and quarrels: and every effort to clear the air seemed to only 6 our misunderstanding. Then he 7 a small island in the Caribbean and we 8 touch. One day he wrote me a letter. He described his island and its people, told me what he was doing, said how he felt. Rereading the letter, I was 9 by its humor and clever expressions. These were all qualities for which I had 10 respected my older brother but 11 he no longer had them. I had never known he could write so well. And with that one letter we became friends 12 .It might never have occurred to him to write me if he had not been in a place where there were no 13 . For him, writing was a necessity. It also turned out to be the best way for us to get back in touch. Because we live in an age of 14 communication, people often forget that they don’t always have to phone or email. They have a 15 . And that is to write.1. A. received B. rewritten C. returned D. reread2. A. record B. promise C. friendship D. secret3. A. an example B. a lesson C. an experience D. a talk4.A.brothers B. children C.fellows D. classmates5. A.normal B. necessary C.pleasant D.possible6. A.deepen B. start C.express D.settle7. A.toured B. stopped over C.reached D.moved to8. A.lost B. kept in C.needed D.got in9.A.driven B. beaten C.surprised D.honored10. A.never B. seldom C.sometimes D.once11. A.realized B. judged C. thought D. expected.12. A.later B. anyhow C. too D. again.13. A.mail services B. transport services C. phones D. relative14. A.poor B. easy C. popular D. busy15.A. habit B. choice C. method D. plan第二节语法填空(共10小题;每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16~25的相应位置上。
广东省广州市花都区高三月调研英语试题

广东省花都区2011届高三上学期学期初调研考试试题(英语)(满分135分,时间120分钟)注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
I语言知识及应用(共两节。
满分45分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1~15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
A manwho knows howto writea personal letterhas a verypowerful tool。
A lettercan be enjoyed, readand 1 .Itcan set up awarm conversation betweentwopeople farapart; itcan keep a2wi thverylittle effort.I will give 3 。
Afewyears ago my older brother and I werenot gettingalong well.Wehad been closeas 4 but hadgrown apart. Our meetings were not 5 ;our conversationwas filled witharguments and quarrels: andevery effort toclear the air seemedtoonly 6ourmisunderstanding。
2011年广州高三年级调研测试

酶 2011年广州市高三年级调研测试理科综合参考答案一、单项选择题:本题包括16小题,每小题4分,共64分。
每小题给出的四个选项中,只有一个选项符合题目要求。
多选、错选均不得分。
二、双项选择题:本题包括9小题,每小题6分,共54分。
每小题给出的四个选项中,有两个选项符合题目要求。
全选对得6分,只选1个且正确得3分,错选、不选得0分。
三、非选择题:本题包括11小题,共182分。
26.(16分)(1)酵母菌、小球藻(2) C 6H 12O 6+6H 2O+6O 2→6CO 2+12H 2O+能量(3)B B 瓶的小球藻能获得A 瓶的酵母菌呼吸产生的CO 2 (4)抽样检测(显微镜直接计数) 对样液稀释后再取样计数 (5)反应时间 降低CO 2的浓度(或CO 2的浓度)(答“提高CO 2的浓度”不得分)27.(16分) (1)11(2)幼苗细胞分裂旺盛,DNA 复制时更容易发生基因突变 微型繁殖(植物组织培养) (3)①非同源染色体上的非等位基因 ②控制酶的合成来控制代谢过程 ③AAbb 、aaBB (全对才给分) 产油:不产油=9:7(全对才给分) 1/428.(16分)(1)血浆和淋巴 (2)静息 负 (3)突触小泡 突触后膜 阴 载体蛋白 控制物质进出细胞和进行细胞间的信息交流 29.(16分)(1)光合作用、细胞呼吸(或有氧呼吸)、水解反应(答对2点即可) 强 抵抗力 竞争 (2)①合理利用不同层次土壤的水分和无机盐 ②提高植物利用阳光的能力 (3)次生 (4)湿地 30.(16分)(1)大于(2分) (2)A (2分) D (2分) (3)(6分)CO 2(g )+3H 2(g )CH 3OH (g )+H 2O (g )起始物质的量/mol 6 8 0 0 物质的量变化/mol 2 6 2 2平衡物质的量/mol 4 2 2 2 (2分)(2分)(2分)(4)升高温度(2分) 增大压强(2分) 31.(16分)(1)3Cu +8H ++2NO 3- = 3Cu 2++2N O↑+4H 2O (3分) (2)AC (4分)(3)温度不是反应速率明显加快的主要原因。
花都区2011届9月高三调研文综政治 讲评

花都区2011届 花都区2011届9月高三调研文综政治 2011 参考答案
• 24 B 25 D 26 D 27 C 28 B 29 C 30 D 31 C 32 B 33 D 34 A 35 D
花都区2011届 花都区2011届9月高三调研文综政治参考答案 2011 • 36.(1)图中显示我国文化产业增加值与国 36.(1 .( 内生产总值都在快速增长。其中, 内生产总值都在快速增长。其中,文化产业增 加值的增长率持续上升,GDP的增长率先升后 加值的增长率持续上升,GDP的增长率先升后 降,且文化产业增加值的增长率一直高于同期 GDP的增长率。(5 的增长率。( GDP的增长率。(5分) • 启示: 启示:要促进国民经济又好又快发展必须 加快转变经济发展方式,推动产业结构优化升 加快转变经济发展方式, 提升文化等第三产业发展水平。( 。(4 级,提升文化等第三产业发展水平。(4分)
花都区2011届 花都区2011届9月高三调研文综政治 参考答案 2011
• (2)政府在推动文化建设和发展方面 应承担 ①组织社会主义文化建设的职 ;(3 能;(3分)②对社会主义市场经济条 件下文化事业和文化产业发展进行经 济调节、 济调节、市场监管等组织社会主义经 济建设的职能;( ;(3 济建设的职能;(3分)③加强公共文 化设施的提供社会公共服务的职能。 化设施的提供社会公共服务的职能。 (3分)
2010高考文综政治试题安徽卷 2010高考文综政治试题安徽卷
Байду номын сангаас
参考答案
• (2)我国是人民当家作主的社会主义国家,本质是人民当家作 (2)我国是人民当家作主的社会主义国家, 主。政府是国家权力机关的执行机关,是人民意旨的执行者和 政府是国家权力机关的执行机关, 人民利益的捍卫者。为人民服务是政府的宗旨, 人民利益的捍卫者。为人民服务是政府的宗旨,对人民负责是 政府工作的基本原则。(4分 政府工作的基本原则。(4分) • 加强“三农”工作,增加农民收入,体现了政府组织社会主义 加强“三农”工作,增加农民收入, 经济建设的职能;(2分 经济建设的职能;(2分) 完善社会保障体系等体现了政府提供 社会公共服务的职能;(2分)大力发展教育事业体现了政府组 社会公共服务的职能;(2分 织社会主义文化建设的职能;(2分 维护社会稳定, 织社会主义文化建设的职能;(2分)维护社会稳定,促进社会 和谐,体现了政府保障人民民主和维护国家长治久安的职能。 和谐,体现了政府保障人民民主和维护国家长治久安的职能。 (2分 (2分)
2011年广州市高三年级调研测试--数学(理)

x33x试卷类型:A2011年广州市高三年级调研测试数学(理科)本试卷共4 页,共21 题,满分150 分。
考试用时120 分钟。
2011. 01 参考公式:锥体的体积公式13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只 有一项是符合题目要求的. 1. 函数()3g x x =+的定义域为A .{3x x ≥-} B .{3x x >-} C .{3x x ≤-} D .{3x x <-}2. 已知i 为虚数单位, 则复数i (1+i )的模等于A .12B. 2C.2 D. 23. 已知,x y 满足约束条件,1,1.y x x y y ≤⎧⎪+≤⎨⎪≥-⎩则2z x y =+的最大值为A . 3- B. 32-C. 32D. 34. 已知:2p x ≤,:02q x ≤≤,则p 是q 的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5. 如果执行图1的程序框图,若输入6,4n m ==,那么输出的p 等于 图1A. 720 B . 360 C . 240 D. 1206. 已知随机变量X 服从正态分布2(,)N μσ,且(22)0.9544P X μσμσ-<≤+=,()0.6826P X μσμσ-<≤+=,若4μ=,1σ=, 则(56)P X <<=A .0.1358B .0.1359C .0.2716D .0.27187. 一空间几何体的三视图如图2所示, 该几何体的 体积为85123π+,则正视图中x 的值为 A. 5 B . 4图3N C. 3 D . 28.若把函数()=y f x 的图象沿x 轴向左平移4π个单位, 沿y 轴向下平移1个单位,然后再把图象上每个点的 横坐标伸长到原来的2倍(纵坐标保持不变),得到函数 sin =y x 的图象,则()=y f x 的解析式为 A. sin 214⎛⎫=-+ ⎪⎝⎭y x π B. sin 212⎛⎫=-+ ⎪⎝⎭y x π C. 1sin 124⎛⎫=+-⎪⎝⎭y x π D. 1sin 122⎛⎫=+- ⎪⎝⎭y x π二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9. 某社区有500个家庭, 其中高收入家庭125户, 中等收入家庭280户, 低收入家庭95户. 为了调查社会购买力的某项指标, 采用分层抽样的方法从中抽取1个容量为若干户的样 本, 若高收入家庭抽取了25户, 则低收入家庭被抽取的户数为 .10. 已知直线l 经过坐标原点,且与圆22430x y x +-+=相切,切点在第四象限,则直线l 的 方程为 .11. 等比数列{a n }的前n 项和为S n ,若246,30S S ==,则6S = . 12. 922()2x x-展开式的常数项是 .(结果用数值作答) 13. 设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩若()4f x >,则x 的取值范围是 .(二)选做题(14~15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图3,四边形ABCD 内接于⊙O , BC 是直径,MN 与⊙O 相切, 切点为A ,MAB ∠35︒=,则D ∠= .15.(坐标系与参数方程选讲选做题)已知直线l 的参数方程为:2,14x t y t=⎧⎨=+⎩(t 为参数),圆C 的极坐标方程为ρθ=,则直线l 与圆C 的位置关系为 .MDCBAP三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分) 在ABC ∆中,角,,A B C 的对边分别为,,a b c . 已知向量=m 2cos,sin 22A A ⎛⎫ ⎪⎝⎭, =n cos,2sin 22A A ⎛⎫- ⎪⎝⎭,.1-=⋅n m (1) 求cos A 的值;(2)若a =2b =, 求c 的值.17.(本小题满分12分)某商店储存的50个灯泡中, 甲厂生产的灯泡占60%, 乙厂生产的灯泡占40%, 甲厂生产 的灯泡的一等品率是90%, 乙厂生产的灯泡的一等品率是80%.(1) 若从这50个灯泡中随机抽取出一个灯泡(每个灯泡被取出的机会均等), 则它是甲厂生产的 一等品的概率是多少?(2) 若从这50个灯泡中随机抽取出两个灯泡(每个灯泡被取出的机会均等), 这两个灯泡中是甲 厂生产的一等品的个数记为ξ, 求E ξ的值.18.(本小题满分l4分)如图4,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,2PA AD ==,1AB =,BM PD ⊥于点M . (1) 求证:AM ⊥PD ;(2) 求直线CD 与平面ACM 所成的角的余弦值.图4 19.(本小题满分14分)已知椭圆(222:13x y E a a +=>的离心率12e =. 直线x t =(0t >)与曲线E 交于 不同的两点,M N ,以线段MN 为直径作圆C ,圆心为C . (1) 求椭圆E 的方程;(2) 若圆C 与y 轴相交于不同的两点,A B ,求ABC ∆的面积的最大值.20.(本小题满分14分)已知函数()(af x x a x=+∈R ), ()ln g x x =. (1) 求函数()()()F x f x g x =+的单调区间; (2) 若关于x 的方程()()22g x f x e x=-(e 为自然对数的底数)只有一个实数根, 求a 的值.21.(本小题满分14分)如图5,过曲线C :xy e =上一点0(0,1)P 作曲线C 的切线0l 交x 轴于点11(,0)Q x ,又过1Q 作 x 轴的垂线交曲线C 于点111(,)P x y ,然后再过111(,)P x y 作曲线C 的切线1l 交x 轴于点22(,0)Q x ,又过2Q 作x 轴的垂线交曲线C 于点222(,)P x y ,,以此类推,过点n P 的切线n l与x 轴相交于点11(,0)n n Q x ++,再过点1n Q +作x 轴的垂线交曲线C 于点111(,)n n n P x y +++(n ∈N *).(1) 求1x 、2x 及数列{}n x 的通项公式;图52011年广州市高三调研测试数学(理科)试题参考答案及评分标准一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题 5分,满分30分.其中14~15题是选做题,考生只能选做一题. 9.19 10.3y x =- 11. 126 12. 212- 13.()(),22,-∞-+∞14.125︒15.相交三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查平面向量, 同角三角函数的基本关系、解三角形等知识, 考查化归与转化的数学思想方法和运算求解能力) (1) 解: ∵=m 2cos ,sin 22A A ⎛⎫ ⎪⎝⎭,=n cos ,2sin 22A A ⎛⎫- ⎪⎝⎭, 1=-m n ,∴ 222cos2sin 122A A-=-. ……2分 ∴ 1cos 2A =-. ……4分(2)解: 由(1)知1cos 2A =-,且0A π<<, ∴ 23A π=. ……6分∵a =2b =,由正弦定理得sin sin a bA B =,2sin sin 3B =, ∴1sin 2B =. ……8分 ∵0,B B A π<<<,∴6B π=. ……10分∴6C A B ππ=--=.∴2c b ==. ……12分17. (本小题满分12分)(本小题主要考查条件概率、数学期望等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)(1) 解法1: 设事件A 表示“甲厂生产的灯泡”, 事件B 表示“灯泡为一等品”, 依题意有()0.6P A =, ()0.9P B A =,根据条件概率计算公式得()()()0.60.90.54P AB P A P B A ==⨯=. ……4分 解法2: 该商店储存的50个灯泡中是甲厂生产的灯泡有5060%30⨯=个, 乙厂生产的灯泡 有5040%20⨯=个, 其中是甲厂生产的一等品有3090%27⨯=个, 乙厂生产的 一等品有2080%16⨯=个, 故从这50个灯泡中随机抽取出一个灯泡,它是甲厂生产的一等品的概率是 270.5450P ==. ……4分 (2) 解: ξ的取值为0,1,2, ……5分()22325025301225C P C ξ===, ()11272325062111225C C P C ξ===, ()22725035121225C P C ξ=== ……8分 ∴ξ的分布列为:∴2536213511323012 1.081225122512251225E ξ=⨯+⨯+⨯==. ……12分 18.(本小题满分l4分)(本小题主要考查空间线面关系、直线与平面所成的角等知识, 考查数形结合的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)(1)证明:∵ PA ⊥平面ABCD ,AB ⊂平面ABCD ,∴PA AB ⊥.∵AB AD ⊥,,AD PA A AD =⊂平面PAD ,PA ⊂平面PAD ,∴AB ⊥平面PAD . ∵PD ⊂平面PAD∴AB PD ⊥, ……3分∵BM PD ⊥, ABBM B =,AB ⊂平面ABM ,BM ⊂平面ABM ,∴PD ⊥平面ABM .∵AM ⊂平面ABM ,∴AM ⊥PD . ……6分 (2)解法1:由(1)知,AM PD ⊥,又PA AD =, 则M 是PD 的中点,在Rt △PAD 中, 得AM =Rt △CDM 中,得MC ==,∴122ACM S AM MC ∆=⋅=. 设点D 到平面ACM 的距离为h ,由D ACM M ACD V V --=, ……8分得111332ACM ACD Sh S PA ∆∆=.解得3h =, ……10分 设直线CD 与平面ACM 所成的角为θ,则sin 3h CD θ==,……12分 ∴cos 3θ=.∴ 直线CD 与平面ACM 所成的角的余弦值为3. ……14分解法2: 如图所示,以点A 为坐标原点,建立空间直角坐标系A xyz -,则()0,0,0A ,()0,0,2P ,()1,0,0B ,()1,2,0C ,()0,2,0D ,()0,1,1M . ∴()()()1,2,0,0,1,1,1,0,0AC AM CD ===-. ……8分设平面ACM 的一个法向量为(,,)n x y z =, 由,n AC n AM ⊥⊥可得:20,0.x y y z +=⎧⎨+=⎩令1z =,得2,1x y ==-.∴(2,1,1)n =-. ……10分 设直线CD 与平面ACM 所成的角为α,则6sin 3CD n CD nα⋅==. ……12分 ∴cos α=.∴直线CD 与平面ACM 所成的角的余弦值为3. ……14分 19.(本小题满分14分)(本小题主要考查椭圆、圆、直线与圆的位置关系等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1)解:∵椭圆(222:13x y E a a +=>的离心率12e =, ∴12a =. …… 2分解得2a =. ∴ 椭圆E 的方程为22143x y +=. …… 4分 (2)解法1:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=. ∴ 圆C 的半径为2r =. …… 6分 ∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴02t <<,即07t <<.∴弦长||AB === …… 8分∴ABC ∆的面积12S =⋅ …… 9分)2127t =-)221272t +-≤7=. ……12分=7t=时,等号成立. ∴ ABC ∆ …… 14分 解法2:依题意,圆心为(,0)(02)C t t <<.由22,1,43x t x y =⎧⎪⎨+=⎪⎩ 得221234t y -=.∴ 圆C 的半径为2r =. …… 6分 ∴ 圆C 的方程为222123()4t x t y --+=.∵ 圆C 与y 轴相交于不同的两点,A B ,且圆心C 到y 轴的距离d t =,∴0t <<,即07t <<.在圆C 的方程222123()4t x t y--+=中,令0x =,得y=,∴ 弦长||AB =.…… 8分 ∴ABC ∆的面积12S=⋅ (9)分 )2127t =-)221272t +-≤=……12分=7t =时,等号成立.∴ ABC ∆的面积的最大值为7. …… 14分 20.(本小题满分14分)(本小题主要考查函数、导数等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识) (1)解: 函数()()()ln aF x f x g x x x x=+=++的定义域为()0,+∞. ∴()'211a F x x x=-+22x x ax +-=.① 当140a ∆=+≤, 即14a ≤-时, 得20x x a +-≥,则()'0F x ≥. ∴函数()F x 在()0,+∞上单调递增. ……2分 ② 当140a ∆=+>, 即14a >-时, 令()'0,F x = 得20x x a +-=,解得120,x x =<=.(ⅰ) 若104a -<≤, 则2102x -+=≤. ∵()0,x ∈+∞, ∴()'0Fx >, ∴函数()F x 在()0,+∞上单调递增. …… 4分(ⅱ)若0a >,则10,2x ⎛⎫-+∈ ⎪ ⎪⎝⎭时, ()'0F x <;x ⎫∈+∞⎪⎪⎝⎭时, ()'0F x >,∴函数()F x 在区间⎛ ⎝⎭上单调递减, 在区间⎫+∞⎪⎪⎝⎭上单调递增. …… 6分 综上所述, 当0a ≤时, 函数()F x 的单调递增区间为()0,+∞;当0a >时, 函数()F x 的单调递减区间为10,2⎛-+⎝⎭, 单调递增区间为12⎛⎫-++∞ ⎪ ⎪⎝⎭. …… 8分 (2) 解: 由()()22g x f x e x =-, 得2ln 2x a x e x x =+-, 化为2ln 2x x ex a x=-+. 令()ln x h x x =, 则()'21ln x h x x-=.令()'0h x =, 得x e =. 当0x e <<时, ()'0h x >; 当x e >时, ()'0h x <.∴函数()h x 在区间()0,e 上单调递增, 在区间(),e +∞上单调递减. ∴当x e =时, 函数()h x 取得最大值, 其值为()1h e e=. …… 10分 而函数()()2222m x x ex a x e a e =-+=-+-,当x e =时, 函数()m x 取得最小值, 其值为()2m e a e =-. …… 12分∴ 当21a e e -=, 即21a e e=+时, 方程()()22g x f x e x =-只有一个根. …… 14分21. (本小题满分14分)(本小题主要考查导数、数列、不等式、定积分等知识, 考查化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)(1) 解: 由xy e '=,设直线n l 的斜率为n k ,则n xn k e =.∴直线0l 的方程为1y x =+.令0y =,得11x =-, ……2分 ∴111xy e e ==, ∴11(1,)P e -.∴111x k e e==. ∴直线1l 的方程为11(1)y x e e-=+.令0y =,得22x =-. ……4分 一般地,直线n l 的方程为()nn x x n y ee x x -=-,由于点11(,0)n n Q x ++在直线n l 上,∴11n n x x +-=-.∴数列{}n x 是首项为1-,公差为1-的等差数列.∴n x n =-. ……6分(2)解:11(1)(1)111()()222|nnxx n n n n n n n n n n S e dx x x y e y e e e ------+-+-+=--=-=--⎰=212ne e e -⋅. ……8分 (3)证明:1211[1()]2111221(1)1222(1)1n n n n e e e e e T e e e e e e e e e----⎛⎫=⋅+++=⋅=⋅- ⎪-⎝⎭-. ……10分 ∴111111111111n n n n n n n T e e e T e e e e e +++++---===+---,1(1)11n n x n x n n +-+==+-. 要证明11n n n n T x T x ++<,只要证明111n e e e n+-<-,即只要证明1(1)n e e n e +>-+. ……11分 证法1:(数学归纳法)① 当1n =时,显然222(1)021(1)e e e e e e ->⇔>-⇔>-+成立; ② 假设n k =时,1(1)k e e k e +>-+成立,则当1n k =+时,21[(1)]k k e e e e e k e ++=⋅>-+,而2[(1)][(1)(1)](1)(1)0e e k e e k e e k -+--++=-+>.∴[(1)](1)(1)e e k e e k e -+>-++.∴2(1)(1)k ee k e +>-++.这说明,1n k =+时,不等式也成立. 由①②知不等式11n n n nT x T x ++<对一切n ∈N *都成立. ……14分 证法2: 110111111[1(1)](1)(1)n n n n n n n e e C C e C e +++++++=+-=+-++- 0111(1)1(1)(1)(1)n n C C e n e e n e ++>+-=++-=-+.∴不等式11n n n n T x T x ++<对一切n ∈N *都成立. ……14分 证法3:令()()11x f x e e x e +=---,则()()'11x f x e e +=--,当0x >时, ()()'11x f x e e +=--()110e e >--=>,∴函数()f x 在()0,+∞上单调递增.∴当0x >时, ()()00f x f >=. ∵n ∈N *,∴()0f n >, 即()110n e e n e +--->.∴()11n e e n e +>-+.∴不等式11n n n n T x T x ++<对一切n ∈N *都成立.……14分。
2011年广州市高三年级调研测试 文综答案

2011年广州市高三年级调研测试文科综合参考答案一、选择题:本题包括35小题,每小题4分,共140分。
每小题给出的四个选项中,只有一个选项符合题目要求。
多选、错选均不得分。
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 答案 D B A C D A A B C D C B D C A C A C 题号19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35答案 C B B B D D B D C D A C A D A A B二、非选择题:本题包括6小题,共160分。
36.(31分)(1)①图1和图2说明,改革开放以来,广东省劳动报酬在初次分配中的比重、居民收入在国民收入分配中的比重大幅下降,与国际比较,明显偏低。
(5分)②表说明,2001年以来,广东城乡居民收入分配呈现出两极分化的趋势。
(2分)(2)①科学发展观的第一要义是发展。
不合理的收入分配制度,会抑制消费需求,影响广东发展。
(3分)②科学发展观的核心是以人为本。
城乡居民收入分配两极分化,不利于维护劳动者公平分配、共享改革成果的权利,会严重挫伤劳动者发展生产的积极性,阻碍广东长远发展。
(3分)③科学发展观的基本要求是全面协调发展,不公平的收入分配,不利于协调广东城乡居民之间的经济利益,不利于广东经济社会的协调发展。
(3分)④科学发展观的根本方法是统筹兼顾。
不能统筹好政府、企业和居民三者的收人分配关系,不利于广东可持续发展。
(3分)(3)①矛盾是事物发展的源泉和动力。
做大“蛋糕”和分好“蛋糕”体现了效率与公平的矛盾,正确处理这一矛盾,才能促进广东又好又快发展。
(4分)②要坚持两点论与重点论的统一。
广东要继续以经济建设为中心,把“蛋糕”做大,更要处理好经济与社会协调发展中的问题,更加注重社会公平,分好“蛋糕”,保持发展的可持续性。
(4分)③要坚持具体问题具体分析。
广东省广州市2011届高三英语第一次调研考试试题

广东省广州市2010—2011学年度高三级第一次调研考试英语试题(本试卷三大题,满分135分。
考试用时120分钟。
)注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上,并用2B铅笔将相应的信息点涂黑。
不按要求填涂的,答卷无效。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;请注意每题答题空间,预先合理安排;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束后,将答题卡交回。
I. 语言知识及应用(共两节,满分45分)第一节完形填空(共15小题;每小题2分,满分30分)阅读下面短文,掌握其大意,然后从1—15各题所给的A、B、C和D项中,选出最佳选项,并在答题卡上将该项涂黑。
When I was a kid, my brother dropped the bomb: "No Santa Claus (Father Christmas)!" I fled to Grandma because I knew she would tell me the truth.I told her everything."No!" she said."Ridiculous! Don' t 1 it."After dinner, we went to General Store.Grandma handed me ten 2 ."Take it and buy something for whoever needs it.I'll wait in the car." I' d often gone shopping with Mother, but never had I shopped 3 .For moments, I stood there, confused, 4 what to do with it.I thought of everybody I knew. 5 I thought of Bobbie Decker.His mother always wrote a note, telling the teacher that he had a cough.We all knew that Bobbie would have no cough if he had a thicker coat.So I decided to buy Bobbie one."Is this a present for someone?" the saleslady asked me kindly.I 6 shyly.She smiled, handed it to me and wished me a merry Christmas.Then Grandma helped me wrap the coat in Santa Claus 7 and ribbons and write "To Bobbie, From Santa Claus " on it.Then she 8 me over to Bobbie's house.Grandma parked down the street from Bobbie' s house.We 9 noiselessly and hid in the 10 by his front walk."All right, Santa Claus," she 11 ,"get going." I rushed out, threw the present down at his front door, 12 his doorbell and flew back to the safety.Together we 13 breathlessly in the darkness for the front door to open.Forty years I haven' t forgotten those 14 I spent shivering (颤抖)in Bobbie' s bushes.That night, I realized that the stories about Santa Clause were really ridiculous .Santa Claus was alive, and we were on his 15 .1.A.remember B.believe C.understand D.consider 2.A.bags B.keys C.coats D.dollars 3.A.separately B.apart C.singly D.alone 4.A.wondering B.worrying C.expecting D.looking 5.A.Luckily B.Surprisingly C.Suddenly D.Firstly 6.A.nodded B.smiled C.replied D.denied7.A.gift B.name C.paper D.needle8.A.sent B.drove C.walked D.guided9.A.stole B.struggled C.stepped D.searched 10.A.cars .B.buildings C.stairs D.bushes 11.A.sighed B.whispered C.called D.shouted 12.A.knocked B.pushed C.pounded D.switched.13.A.rushed B.laughed C.paused D.waited 14.A.nights B.feelings C.moments D.bills15.A.side B.team C.part D.staff第二节语法填空(共10小题;每小题1.5分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卡标号为16—25的相应位置上。
广州市高三年级调研测试
学习必备欢迎下载2011 年广州市高三年级调研测试文科综合一、选择题:本题包括35小题,每小题4分,共140分。
每小题给出的四个选项中,只有一个选项符合题目要求。
多选、错选均不得分。
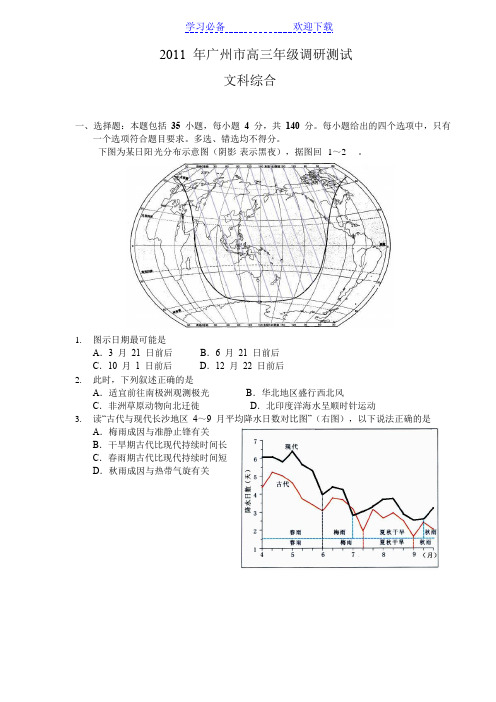
下图为某日阳光分布示意图(阴影表示黑夜),据图回1~2 。
1. 图示日期最可能是A.3 月21 日前后B.6 月21 日前后C.10 月1 日前后D.12 月22 日前后2. 此时,下列叙述正确的是A.适宜前往南极洲观测极光B.华北地区盛行西北风C.非洲草原动物向北迁徙D.北印度洋海水呈顺时针运动3. 读“古代与现代长沙地区4~9 月平均降水日数对比图”(右图),以下说法正确的是A.梅雨成因与准静止锋有关B.干旱期古代比现代持续时间长C.春雨期古代比现代持续时间短D.秋雨成因与热带气旋有关4. 形成草原带的气候类型是A.地中海气候B.温带季风气候C.温带大陆性气候D.温带海洋性气候5. 读“我国区域自然灾害脆弱性水平划分图”(右图),广东、江苏两省自然灾害水平属于轻度脆弱地区的最主要影响因素是A.地形因素B.人口密度C.城市化水平D.经济发展水平下图是我国各省区某项指标统计地图(省区面积大小表示指标值大小),回答6~7题。
6. 该指标最可能是A.人口数量B.石油储量C.耕地数量D.年降水量7. 造成图中东部省区面积大于西部省区的根本原因是A.自然地理环境的差异B.矿产资源储量的差异C.劳动力素质的差异D.城市化水平的差异8. 读“苹果种植的纬度分布示意图”(右下图),苹果特殊产地形成的主要因素是A.水分B.地形C.技术D.劳动力9. 据报道,北京至石家庄高速铁路将于2012 年开通运营,这将为石家庄的发展带来新机遇。
下列关于京石高速铁路的正确叙述是A.有利于“南粮北运”的实施B.有利于“西气东输”的实施C.有效减轻京广铁路的客运压力D.有利于加强沿海与内陆城市的联系10. 读“2006 年中国外资银行机构的城市分布图”(下图),影响其布局的最主要区位因素是A.气候条件B.劳动力C.高新技术水平D.城市经济地位11. 读“我国东部沿海某城市制造业与服务业空间分布模式图”(下图),下列叙述正确的是高XA.曲线X 表示服务业产业密度空间变化B.距市中心越远,制造业产业密度越低C.地价是影响服务业产业密度的重要因素D.目前该城市正处于逆城市化阶段40.(30 分)城市化与生态环境的和谐是实现和谐社会的重要基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17.解: (1)截面MNC1A1是等腰梯形, 连接AC,因为M、N分别为棱AB、BC的中点, 所以MN//AC,MN≠AC 又
AC / / A1C1 , MN / / A1C1 , 且MN A1C1 , MNC1 A1 是梯形,--------4分
--------6分 --------7分
长小于110cm的株数n是 A.30 C.70
( B.60 D.80
)
OA OC OB 夹角为60°, 与 、 与 OC 的夹角都为30°, 2 3 OA OB OC OC OA OB 且∣ ∣=∣ ∣=1, ∣ ∣= ,若 = + ,
20. (本小题满分14分) 在平面直角坐标系中, O 为坐标原点,已知两点 M (1, 3), N (5,1) ,若动点 C 满足
2 NC t NM . 且点 C 的轨迹与抛物线 y 4 x 交于 A, B 两点. OA OB (1)求证: ;
MN 平面BDD1 B1 , MN 平面B1MN
平面MNB 1 ⊥平面BDD 1 B 1
(注:对建立空间坐标系完成的,请酌情评分) 18.解: (1)由已知可得
--------12分
--------14分
q 3 a2 12 3 a2 q q ,
解方程组得, q 3 或 q 4 (舍去) ,
6. 为了解一片经济树林的生长情况, 随机测量了其中100株树 木的底部周长(单位:cm) ,根据所得数据画出样本的频 率分布直方图如图所示.那么在这100株树木中,底部周
OA , OB , OC , 其中 OA 与 OB 的 7.如图,平面内有三个向量
3 4
11. 420
12. 120
13. 7
14. 5
三、解答题 15.解: (1)由已知 f ( ) cos (2) f ( x ) cos( x
6
3 ,得 k 3 --------4 分 k sin 2 6 2
--------5 分 -------6 分
易证 RtAMA1 RtCNC1 , A1 M C1 N
MNC1 A1 是等腰梯形
(2)正方体ABCD—A1B1C1D1中
AC BD, BB1 平面ABCD, MN 平面ABCD, BB1 MN ,
--------9分
又MN // AC , MN BD, BD BB1 B ,
则 的值为 A. 4 B. 3 3 C. 2 3 D.2 ( )
f ( x) 0 8.奇函数 f ( x ) 在 (0, ) 上是减函数,且 f ( 1) 0 ,则不等式 x 的解集为(
A. ( , 1) (1, ) C. ( 1, 0) (1, ) 二、填空题(每小题5分,共30分) B. ( , 1) (0,1) D. ( 1, 0) (0,1)
赛三个阶段进行, 每个阶段选 竞赛,否则即遭淘汰.已知某
3 1 1 , , 选手通过初赛、复赛、决赛的概率分别是 4 2 4 ,且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率; (2)设该选手在竞赛中回答问题的个数为,求的分布列、数学期望和方差.
17. (本小题满分12分)
如图,在正方体 ABCD A1 B1C1 D1 中, M , N 分别为棱 AB, BC 的中点.
an
bn
1 } S n (2)求数列 的前 n 项和 {
19. (本小题满分14分)已知函数 f ( x ) a ln x bx 图象上一点 P (2, f (2)) 处的切线方程为 y 3 x 2 ln 2 2 . (1)求 a, b 的值;
2
1 [ , e] f ( x ) m 0 (2)若方程 在 e 内有两个不等实根,求的取值范围(其中为自然对数的底数) ;
h( x) 是减Βιβλιοθήκη 数--------11分1 [ , e] 则方程 h( x ) 0 在 e 内有两个不等实根的充要条件是
1 h( e ) 0, h (1) 0 , h(e) 0.
--------13分
解不等式组得 m 取值范围是
1 m 2
)
9.已知向量 a (3 x, 2), b (1, 2 x ), 且 a b ,则
x _______
10.已知函数 f ( x ) a b(a 0) 的图象经过点 (2,3) 和原 11.若执行如右图所示的程序框图,则输出的 S = 12. 在 ABC 中, 已知 AB 4, BC 3, AC 的大小为 . “ 2x y 2 ” 的 概 率 为
) 3 sin x 3 cos x cos sin x sin 3 sin x 3 3
1 3 cos x sin x 3 sin x 2 2
--------7 分
1 3 cos x sin x sin( x ) 2 2 6
--------9 分 --------11 分 --------12 分
1 A. 3 4 C. 3
2 B. 3
D. 2
5.已知函数 y f ( x) 在定义域 [ 4, 6] 内可导,其导函数 y f '( x) 的图象如右图,则函数 y f ( x) 的单调递增区间为 ( )
4 11 [4, ],[1, ] 3 3 A. 7 [3, 0],[ ,5] 3 B. 4 11 [ ,1],[ , 6] 3 C. 3 7 [4, 3],[0, ],[5, 6] 3 D.
--------3分
a2 6
--------5分 --------7分
an 3 ( n 1)3 3n
(2)
bn 3n 1
Sn
n(3 3n) 1 2 2 1 1 ( ) 2 S n n(3 3n) 3 n n 1
--------10分
当 x
2 k , k Z ,即 x 2 k , k Z 时 6 2 3
函数 f ( x ) 的最大值为 1.
16.解: (1)记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过 决赛”为事件C,则
P ( A)
3 1 1 , P ( B ) , P (C ) . 4 2 4 3 1 3 (1 ) 4 2 8.
--------2分 --------4分
a 4b 3 ∴2 ,且 a ln 2 4b 6 2 ln 2 2 .
--------6分 --------7分
解得 a 2, b 1 . ( 2) 令
f x 2 ln x x 2
, ,
--------8分
(2)在 x 轴上是否存在一点 P ( m, 0)( m 0) ,使得过点 P 的直线 l 交抛物线 y 4 x 于 D , E 两点,并以线段 DE 为直 径的圆都过原点。若存在,请求出 m 的值及圆心 M 的轨迹方程;若不存在,请说明理由
2
参考答案
一、选择题 题号 答案 二、填空题 9. 1 10. 1 D 2 C 3 C 4 B 5 B 6 C 7 A 8 D
1 A.公差为 2 的等差数列 1 C.公比为 2 的等比数列
B.公差为 2 的等差数列
D.公比为 2 的等比数列
1 y sin( x ), ( 0) 2 6 3.函数 的最小正周期是 4 ,则 1 A. 4 1 B. 2
C. 1 D. 2
(
)
4.如图,一个空间几何体的正视图、侧视图、俯视图为全等的等腰 直角三角形,如果直角三角形的直角边长为2,那么这个几何体 的体积为 ( )
(1)试判截面 MNC1 A1 的形状,并说明理由; (2)证明:平面 MNB1 平面 BDD1 B1 .
18. (本小题满分14分)等差数列
{an }
中,
a1 3
,前项和为
Sn
,等比数列
{bn }
各项均
为正数, (1)求
b1 1
与
,且 ;
b2 S2 12
,
{bn }
q
的公比
S2 b2
1 e2 .
--------14分
20.解: (1)由 NC t NM . 知点 C 的轨迹是过 M , N 两点的直线, 故点 C 的轨迹方程是:
--------1分
y3
1 (3) ( x 1) 4 ,
--------3分
即 y x4
y x 4 ( x 4)2 4 x x 2 12 x 16 0 2 y 4x x A xB 16, x A xB 12 y A yB ( x A 4)( xB 4) x A xB 4( x A xB ) 16 16.
的分布列为: 1 P 2
3 1 , 4 4
1 3 ) , 2 8 3 . 8
3
1 4
3 8
3 8
-------10分
的数学期望
E 1
的方差
1 3 3 17 2 3 . 4 8 8 8
-------11分
D (1
17 2 1 17 3 17 3 39 ) (2 ) 2 (3 ) 2 8 4 8 8 8 8 64 .-------12分
h x f ( x ) m 2 ln x x 2 m h/ x
则
2 2(1 x 2 ) 2x h/ x 0 x x ,令 ,
