投资学6
[经济学]证券投资学第六章
![[经济学]证券投资学第六章](https://img.taocdn.com/s3/m/8ebe95d0fab069dc502201ff.png)
30(1+I/2)20=100 I=12.44%
30(1+10I)=100 I=23.33%
因为不能利滚利,所以同样的现值为达到 同样的终值,单利的利率必须高一些。
五、债券利率与到期收益率的区别 是否获利我们用到期收益率来衡量。除零息 债券外,其它债券的到期收益率随利率的波动 而上下波动。 例:用1000美元买入一张面值为1000美元 息票利率 为10%的息票债券,持有一年后以 1200 美元的价格 售出,那么购买该债券的持有期收益率为多少? [(100+200)/1000] ×100%=30%
1、简单算术股价平均法。
是以上市的全部股票或选择股票为计算对象,将其 当天收盘价加总合计,除以采样数而得出。
采样股票的当天收盘价总和 简单算术股价平均法==————————————— — 采样股票数 例,某股票市场选定ABCDE五种股票为样本,这五 种股票当天的收盘价分别为10,20,30,40,50元, 简单平均股价 =(10+20+30+40+50)/5=30元
+108/(1+i/2)4
I=7%
2、 单利。债券到期收益率是指一定时期内债券投资收益 与投资额的比率。单利投资收益包括债券利息收入、债 券的资本损益(买卖差价),和复利不同的是单利不包 括债券利息再收益。
例1:一张面额为100元的债券,发行价格为98元,票面 利率为10%,偿还期限为5年,一次还本付息,投资者 的收益率是多少? 到期收益率= (到期本利和-认购价格)÷待偿年数 认购价格 解1:[(100+100×10%×5-98)/(98×5)] ×100%=10.61% 解2:{[100×10%+(100-98)÷5]/98}×100%=10.61% 单
证券投资学 第6章 技术分析 K线理论

实 体
L
(美)史蒂夫· 尼森 著 丁圣元 译
“假定蜡烛图技术是一柄削铁如泥的宝剑,使用它的人往往能 够最早地捕捉到市场趋势变化的最早信号,获取最大利润。那 么反过来,佩带这把宝剑的人一定要是精通武艺的名将,不然, 宝剑恐怕会先伤了主人。”
不同周期的K线图
道氏理论的主要内容
平均指数包含一切
尽管各个市场不可能预见地震或其他各种不同
的自然灾难,但是它们很快就能包含这种事件, 并几乎立即将它们的影响消化在价格行为中。
道氏理论认为,证券市场上同时存在着三种趋 势
主要趋势。表示股票市场价格长期趋势,主要趋 势一经形成,通常持续1年或1年以上。汉密尔顿 认为多头市场的平均长度为27个月,空头市场的 平均长度为15个月。 2. 次要趋势。指在主要趋势中,股价持续上涨过程 突然出现中期回跌现象,或者在股价持续下跌过 程中突然出现的中期反弹现象。次要趋势持续时 间为两周到1个月左右。这些中级调整通常回撤 至前面趋势运动的三分之一至三分之二之处,最 常见的大约足前面运动的一半或称50%处。 3. 短期趋势。也叫日常运动。指股价每天的小幅波 动。这种运动不大重要,也很难预测,一般持续 数小时至几天,很少持续三周的。
常用的交易指标
委比=(委买-委卖)/(委买+委卖)×100% 委买(卖)=买(卖)1+买(卖)2+· · · · +买(卖)5 委差=委买-委卖
涨跌=最新-前收;涨幅=涨跌/前收×100%
总额(总成交金额,单位:万元Amount) 总手(总成交量手数,1手=100股 VOLume)
均价=总成交金额/总成交量
•时间在进行行情判断时有很重要的作用。一个已经形成 的趋势在短时间内不会发生根本变化,中途出现的反方向 波动,对原来趋势不会产生大的影响。一个形成了的趋势 又不可能永远不变,经过了一定时间又会有新的趋势出现。 •空间在某种意义上讲,可以认为是价格的一方面,指的 是价格的位置、变动的幅度及可能达到的极限。
投资学基础讲义 第6章 风险资产配置

一个基本的更加符合现实的假设是:多数投资者是厌恶风险的,因而,投资者将考虑: 无风险资产
37
有正的风险溢价的投资品 投资组合的吸引力随着期望收益的增加和风险的减少而增加。 收益与风险同时增加是会怎么样呢?
表 6.1 可供选择的风险资产组(无风险利率 = 5%)
投资者会根据风险收益情况为每个资产组合给出一个效用值分数。 效用函数 U = 效用值 E ( r ) = 某一资产或资产组合的期望收益 A = 风险厌恶系数(A>0 厌恶、A=0 中性,A<0,偏好) s2 = 收益的方差 ½ = 一个约定俗成的数值
$ 96, 600 $210, 00
0.46
用 P 表示风险投资组合在完整资产组合中的比重,用 y 表示风险投资的比重,用 (1-y) 表示无风险投资的比重:
39
通常,只有政府可以发行无违约风险的债券。实际中无风险资产是一种理想的指数化 债券,只有在投资期限等于投资者愿意持有的期限时才能对投资者的实际收益率进行担 保。如果考虑利率风险,则指数化债券也有风险。
E(rc)=7%+(1.4X8%)=18.2%
C =1.4 22%=30.8%
41
Slope E rc rf 18.2 7 =0.36
c
30.8
图 借贷利率不相等时的可行集
P 的左侧是借出无风险资金,P 的右侧是借入无风险资金
6.7 风险容忍度与资产配置
投资者必须从可行集中选择一种最优的资产组合 C。完整资产组合的期望收益:
rf = 7% E(rp) = 15% y = % in p
srf = 0% sp = 22% (1-y) = % in rf
rc =yrp (1 y)rf
投资学-精要版-第九版-第6章-资本资产定价模

第6章资本资产定价模型一、单项选择题1、资本资产定价模型中,风险的测度是通过()进行的。
A、个别风险B、贝塔C、收益的标准差D、收益的方差2、无风险收益率和市场期望收益率分别是0.06和0.12。
根据CAPM模型,贝塔值为1.2的证券A的期望收益率是()。
A、0.06B、0.144C、0.12D、0.1323、就市场资产组合而言,下列哪种说法不正确?()A、它包括所有证券B、它在有效边界上C、市场资产组合中所有证券所占比重与它们的市值成正比D、它是资本市场线和无差异曲线的切点4、根据阿尔法的性质,下列说法正确的是()。
A、阿尔法为正则证券价格被高估B、阿尔法为零应买入C、阿尔法为负应买入D、阿尔法为正则证券价格被低估5、无风险收益率为0 . 0 7,市场期望收益率为0 . 1 5。
证券A期望收益率为0 . 1 2,贝塔值为1 . 3。
那么你应该()。
A、买入A,因为它被高估了B、卖空A,因为它被高估了C、卖空A,因为它被低估了D、买入A,因为它被低估了6、证券A 期望收益率为0 . 1 0,贝塔值为1 . 1。
无风险收益率为0 . 0 5,市场期望收益率为0 . 0 8。
这个证券的阿尔法是()。
A、1.7%B、-1 . 7%C、8.3%D、5.5%7、零贝塔值证券的期望收益率为()。
A、市场收益率B、零收益率C、负收益率D、无风险收益率8、标准差和贝塔值都是用来测度风险的,它们的区别在于()。
A、贝塔值既测度系统风险,又测度非系统风险B、贝塔值只测度系统风险,标准差是整体风险的测度C、贝塔值只测度非系统风险,标准差是整体风险的测度D、贝塔值既测度系统风险,又测度非系统风险,而标准差只测度系统风险9、资本资产定价模型认为资产组合的收益率最好用()来解释。
A、经济因素B、个别风险C、系统风险D、分散化10、一个被低估的证券将()。
A、在证券市场线上B、在证券市场线下方C、在证券市场线上方D、随着它与市场资产组合协方差的不同,或在证券市场线下方或在上方二、多项选择题1、下列说法正确的有()。
证券投资学之第六章

第六章资产组合管理主要内容资产组合的定义及理论源起,资产组合的收益与风险评价,资产组合的效率边界,投资组合的风险分散效应,资产组合理论的应用与局限。
重点难点•重点:资产组合的概念,资产组合的收益与风险评价,资产组合的效率边界。
•难点:资产组合的局限。
第一节投资收益和风险问题的引入•投资者制定投资目标应考虑回报和风险–投资者厌恶风险,承担风险需要补偿–不同的投资者对风险厌恶程度不一样,怎样刻画不同投资者对收益-风险之间的权衡关系•回报和风险的度量•例子:下一年你有5000块钱用于投资,投资一年,有六种投资机会供选择:–(1)30天到期、现在年收益率为6%的货币市场基金–(2)一年定期存款,利率为7.5%–(3)10年期长期国债,每年收益为9%–(4)一种股票,现价10元/股,下一年的预期股价为11.2元/股,且估计红利为0.2元–(5)一人向你借钱,期限一年,利率15%–(6)以8.4元人民币兑1美元买外汇•问题–各种投资的收益水平如何–各种投资有哪些风险,如何度量风险–各种投资的风险和收益的组合情况如何–如何进行投资决策(一种或多种组合投资)一、投资收益的度量-利率• 1.按计息的方式分:单利(simple rate);复利(compound rate)•TV-----total value P-----principal(1)终值(final value, FV)和现值(present value, PV)简式贷款中,贷款人向借款人提供一笔资金(本金,P),借款人于到期日连本带利偿还。
如p=1000,一年后偿还本金1000及利息I=100。
一年后的1100等于现在的1000元按一定的利率水平(10%)计算,现在的1000元,一年后的终值为1100元;或者说:一年后的1100元,现值为1000元•终值:计算某项资产P在n期后的价值,称为终值FV(final value)•计算过程中,利息以单利还是复利计呢•--复利•FV=P·(1+i)n•(期限是n,i为与期限一致的利率水平,按n期计复利)•例如:如果按月计复利,i为月利率1%,则现在的1000元6个月后的终值为•FV=1000×(1+1%)6•现值(PV,present value):•把未来的R元贴现到现在的价值,就是未来R元的现值,计算公式为•计算未来收入在今天的价值过程,称为对未来的贴现,利率i也称为贴现率(discount ratio)或贴现因子(discount factor)复利(年利率为6%)•复利频率n复利水平(%)•年 1 6.00000•半年 2 6.09000•季 4 6.13636•月12 6.16778•周52 6.17998•日365 6.18313(2)连续复利的计算•在上例中,e 0.06=1.0618365,因此,我们可以说,利息为6%的债券的连续复利为每年6.18365%。
投资学 实验六 债券久期的计算
实验六:债券久期的计算一、实验目的通过运用Excel软件,掌握债券久期、修正久期和凸度的计算,根据计算结果分析债券久期的影响因素,并且能够根据数据建立动态计算的债券久期模型,预测债券价格。
二、实验内容运用Excel软件,根据确定的数据,通过在Excel软件中输入有关债券久期、修正久期和凸度等公式计算相关的数值,通过对数值的观察,建立动态的久期分析模型。
最以后根据以上的实验结果来精确地预测出债券的未来价格。
三、实验步骤(一)基本久期的计算假设有两个债券,债券A刚刚发行,起面值1000元,票面利率与市场利率相同,均为7%,期限为10年。
债券B是五年前发行的,其面值为1000元,票面利率为11%,期限为15年,还有10年到期。
计算债券A与债券B的久期。
计算步骤:1、建立工作表,输入数据。
在B2、E2、A5:B14和E5:E14单元格中输入相应的数据。
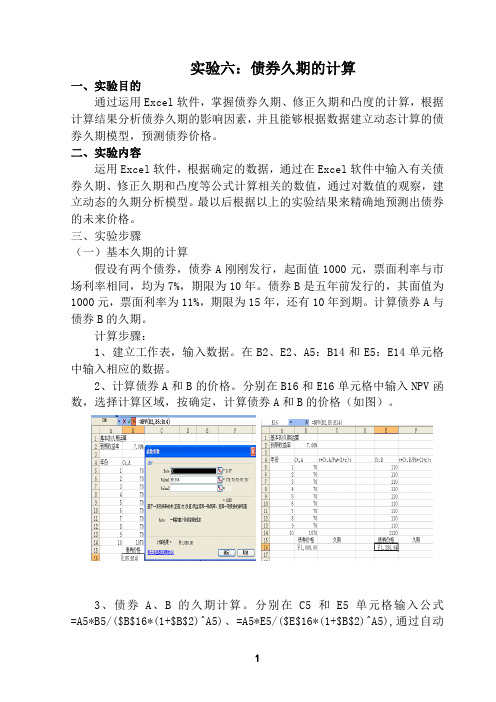
2、计算债券A和B的价格。
分别在B16和E16单元格中输入NPV函数,选择计算区域,按确定,计算债券A和B的价格(如图)。
3、债券A、B的久期计算。
分别在C5和E5单元格输入公式=A5*B5/($B$16*(1+$B$2)^A5)、=A5*E5/($E$16*(1+$B$2)^A5),通过自动填充单元格命令格式求出C5和F5单元区域的数据(如图)。
分别在C16和F16单元格输公式=SUM(C5:C14)和=SUM(F5:F14),按回车键,分别算出债券A和B的久期(如图)。
从计算结果来看,虽然债券A与债券B的到期期限都是10年,但债券A的久期大于债券B的久期。
(二)久期作为债券价格相对利率的弹性的计算。
已知债券A刚刚发行,其面值为1000元,票面利率为7%,期限为10年;债券B是5年前发行的,其面值为1000元,票面利率为11%,期限为15年,还有10年到期。
假设市场利率(贴现率)从当前的7%增加到7.02%。
请计算:(1)计算债券A与债券B的市场价格变化率;(2)作为债券价格相对市场利率的弹性来估计债券A、B的久期。
投资学-6投资组合有效边界计算

6最优投资组合选择最优投资组合选择的过程就是投资者将财富分配到不同资产从而使自己的效用达到最大的过程。
然而,在进行这一决策之前,投资者首先必须弄清楚的是市场中有哪些资产组合可供选择以及这些资产组合的风险-收益特征是什么。
虽然市场中金融资产的种类千差万别,但从风险-收益的角度看,我们可以将这些资产分为两类:无风险资产和风险资产。
这样一来,市场中可能的资产组合就有如下几种:一个无风险资产和一个风险资产的组合;两个风险资产的组合;一个无风险资产和两个风险资产的组合。
下面分别讨论。
一、一个无风险资产和一个风险资产的组合当市场中只有一个无风险资产和一个风险资产的时候,我们可以假定投资者投资到风险资产上的财富比例为w ,投资到无风险资产上的财富比例为1-w ,这样一来,投资组合的收益就可以写为:f P r w r w r )1(-+=其中,r 为风险资产收益,这是一个随机变量;f r 为无风险资产的收益,这是一个常数。
这样,资产组合的期望收益和标准差就可以写出下述形式:f P r w r wE r E )1()()(-+=σσw P =(因为122222122)1(2)1(σσσσw w w wP -+-+=,2112122,0σσρσσ===0)其中σ为风险资产的标准差。
根据上两式,我们可以消掉投资权重,并得到投资组合期望收益与标准差之间的关系:P ff P r r E r r E σσ-+=)()( 3-1当市场只有一个无风险资产和一个风险资产时,上式就是资产组合所以可能的风险-收益集合,又称为投资组合的可行集合。
在期望收益-标准差平面上,3-1是一条直线,我们称这条直线为资本配置线。
随着投资者改变风险资产的投资权重w ,资产组合就落在资本配置线上的不同位置。
具体来说,如果投资者将全部财富都投资到风险资产上1>w ,资产组合的期望收益和方差就是风险资产的期望收益和方差,资产组合与风险资产重合。
如果投资者将全部财富都投资在无风险资产上0>w ,资产组合的期望收益和方差就是无风险资产的期望收益和方差,资产组合与无风险资产重合。
《投资学(第6版)》教学大纲

人大社《投资学》(第6版)教学大纲制作人:郎荣燊裘国根制作时间:2021年3月一、课程介绍作为应用型院校财经专业的一门核心课程,“投资学”以培养学生投融资理论知识和基本实践技能为教学目的。
“投资学”课程遵循“理论与实践相结合”的教学原则,通过理解并掌握投融资决策应具备的基础理论、分析框架和决策方法,结合习题和案例辨析训练,培养学生在投融资领域进行分析、判断和决策的基本能力。
“投资学”主体教材内容包括导论、投资与经济发展、投资体制、投资结构、融资概论、项目融资、证券融资、项目投资、可行性研究与投资决策、项目投资的风险管理、证券投资分析、证券市场、投资组合与证券定价原理、现代投资银行、国际投资共十五章。
鉴于“投资学”课程具有理论知识与决策实践紧密结合的特点,我们在每个章节增加了相关案例,以帮助读者更好地理解相关知识要点。
另外,作为相关课内知识的补充,我们在部分章节推荐了课外书籍。
这些案例和补充读物可以帮助读者更好地理解我国具有中国特色社会主义市场经济发展历程、中外投资理论融合及资本市场演进,从而提升读者对投融资理论及决策方法在当代市场中的理解和运用能力。
本课程采用理论教学为主、实践教学(习题与案例教学或者实验教学)为辅的教学方式。
二、章节内容及建议课时本课程建议学时为72课时,其中:理论教学44课时,实践教学28课时。
课时少的学校可以将上述课时减半或者打折。
三、教学目标1.基本知识教学目标(1)掌握投资学基本理论、投资与经济增长、投资体制比较以及投资结构等要点。
(2)掌握融资的主要概念、融资方法和方式比较,特别是项目融资与证券融资。
(3)掌握投资的主要方法、分析工具、决策方法、相关市场及中介机构。
2.职业能力培养目标(1)学会运用所学的专业知识和分析方法来解决投融资实践过程中的疑难问题。
(2)独立操作、正确处理在实际工作当中经常涉及到的投融资决策问题。
3.思想素质教育目标(1)具有团队精神和协作精神。
证券投资学-06章简明教程PPT课件

P0
D1
1
D 表示所要求的持有期间年化收益率(简称收益率),
Dt 表示第
t 期支付的分红或派息。
证券投资学第6章 8
证券投资学第6章 9
如果期末价格是未知的(即未来的价格),则本节所谈到
的收益率为未来收益率。 如果期末价格是已知的,则本节所谈到的收益率为历史收 益率; 未来的价格是不确定的,所以根据上述方法计算出的收益率 也是不确定的。 假设未来某只股票的价格有 n种可能性,且第 i 种可能性下 的概率为 pi , i 1 n 。按照上述的方法计算出第 i 种可能 性下所对应的未来收益率 ri 。对各种可能性下未来收益率按 照发生的概率进行加权平均可以得到该资产的期望收益率 n E r :
E r pi ri
i 1
(6-4) 证券投资学第6章 10
利用表6.1的数据,可以得到该股票未来的期望收益率 14%: n E r pi ri
i 1
25% 0.44 50% 0.14 25% (0.16)
证券投资学第6章 2
典型的投资者:在不确定性决策的环境中,不但希望投资收 益最大化,还要求投资风险最小化,其决策是实现两个相互 制约目标之间的某种平衡。
马柯维茨的思路:分别用期望收益率和收益率的方差来衡量
投资的预期收益水平和不确定性(风险),建立均值方差模
型来阐述如何全盘考虑上述两个目标,从而进行投资决策。 结论:投资者应该通过同时购买多种证券而不是一种证券, 进行分散化投资。
证券投资学第6章 5
第一节
单个资产的收益和风险
收益度量:
对某一资产来说,持有期收益率(holding-period return, HPR)取决于投资期内资产价格上涨(或下跌)的程度,以及 分红或派息的收益:
投资学6~7章课后习题

证券投资学课后作业张娟管实1101 U201113738第六章风险厌恶与风险资产配置1.选e. 风险厌恶程度高的投资者会选择风险小的投资组合,或者说更愿意持有无风险资产.更高的风险溢价听着可能会很有吸引力,但是其风险一般也会很大,不能抵消掉风险厌恶者的恐惧;风险更高,那风险厌恶程度高的投资者更加不会考虑;夏普比率是说单位风险所获得的风险溢价,虽然夏普比率高,表明单位风险获得的风险溢价高,但是对于风险厌恶者来说,总的风险很高,那么他们同样会拒绝。
另外,夏普比率没有基准点,其大小本身没有意义,只有在与其他组合的比较中才有意义。
2.选b. 由夏普比率的公式S=E(r p)−r f B,当借入利率r f B升高时,若其它保持不变,σp则夏普比率升高。
3.如果预测股票市场的波动性增大,则说明其风险增大;假设投资者的风险容忍度不变,投资比例不变,那么预期收益会增加。
根据6-7的公式得出的。
13. E(r c)=70%*18%+30%*8%=15%;σc=70%∗28%=19.6%14.15.我的报酬-波动比率为(0.18-0.8)/0.28=0.3571. 客户的报酬-波动比率和我的一样。
斜率为0.357117.a. y=0.8b. 标准差为22.4%18.当标准差不大于18%时,投资比例y<=0.18/0.28=0.6429,最大投资收益为0.6429*0.18+0.3571*0.08=0.1443=14.43%,其中A=3.5,解得y∗=0.3644,即36.44%投资于风险资产,19.y∗=E(r p)−r fAσP263.56%投资于无风险资产。
20. a. y∗=0.4578,即45.78%投资于股票,54.22%投资于短期国债。
b. y∗=0.3080,即30.8%投资于股票,69.2%投资于短期国债。
c.但投资者的风险厌恶程度相等时,风险越大,投资于无风险资产的比重变大。
21.a. 0.5b. 7.5%c. 标准差不超过12%,要想收益最大化,则令标准差为12%,算出y=0.12/0.15=0.822.y=0.5, E(r c)=0.5∗12%+0.5∗5%=8.5%23分别有两条无差异曲线与上面这条折线的上下部分相切。
证券投资学-第六章技术分析

第一节 技术分析的理论基础
三、关于三大假设的合理性 1、任何一个因素对股票市场的影响最终都必然体
现在股票价格的变动上。从这一点来看,假设 一有一定的合理性。(p256)
证券投资学-第六章技术分析
*ST盛润A(000030):重组获批*ST盛润A“一”字涨停 ■北京商报 *ST盛润A(000030)2012年12月3日复牌并"一"字涨停。公司发布公告称,以新增股份换股吸 收合并富奥汽车零部件股份有限公司暨关联交易之重大资产证重券组投资事学项-第经六章证技监术分会析审核通过。
•宁波华翔(002048)2012年12月初的走势。 宁波华翔持有富奥股份2.00亿股,占总股本17.86%,可以换得ST盛润1.80亿股 新增A股股份,占重大资产重组后ST盛润总股本的13.89%。以ST盛润停牌前收盘 价8.61元估算,重组成功,宁波华翔对富奥股份的持股市值可达15.5亿元。宁 波华翔对富奥股份的持股(计入长期股权投资)成本为3.7亿元。由此可推测,宁 波华翔或可因ST盛润A重组成功而获得约12亿元股权增值。 证券投资学-第六章技术分析
证券投资学-第六章技术分析
第一节 技术分析的理论基础
l 三大假设是进行技术分析的基础,它不是十全 十美的,但不能因此而否定它存在的合理性。 承认它的存在,同时也应注意到它的不足。
证券投资学-第六章技术分析
第二节 市场行为的四个要素
l 价、量、时、空 证券市场中,价格、成交量、时间和空间
是进行分析的要素,这几个要素的具体情况和 相互关系是进行分析的基础。
析方法只注重市场的某个方面,不可能技术分 析方法每次都能全面周到的应付市场的变化, 如各种突然出现的偶然因素也会使技术分析方 法束手无策。完全避免是不可能的,投资者应 当争取做到尽量考虑周到,从而最大限度的降 低出现偏差的机会。
金融学投资经管课件教案-证券投资学06

什么是“反映所有可得信息”
价格对新信息反应的速度和程度
有效和非有效市场中价格对新信息的 反应
股票 价格
过激反应 和回归
有效市场对新 信息的反应
延迟 反应
0
宣布前(-)或者后(+)的天数
强形式有效性 半强形式有效性
弱形式有效性
例子:
总是在股价上涨后卖出股票,能赚到钱
There is no information out there that can be used to construct strategies that earn returns higher than required for their risk.
When we say ‘prices are correct’, we are implicitly statement what ‘correct’ is (i.e., we are assuming an asset pricing model)
Prices react to new information quickly and to the right extent
Market efficiency means
There is no free lunch
The only way you can get higher returns is by taking on more risk
1. 随机游走和有效市场
例子:一种模型预测股票价格三天后将 从20元/股涨至23元/股
The forecast of a future price increase will lead instead to an immediate price increase
第6章习题集-投资学教程

第六章因素模型与套利定价理论一、判断题1.大量的分析和经验表明,股票收益之间的协方差为正数或者负数的概率大致相同。
()2.单因素模型的提出者夏普将投资风险分为宏观因素带来的系统风险和企业特定因素带来的非系统风险。
()3.根据单因素模型,某种给定股票的收益率的变化仅仅来源于宏观经济因素的变动这个单因素的变动。
()4.套利组合中各种证券的权数之和等于零,意味着购买套利组合是不需要追加投资的。
()5.单因素模型中的宏观经济因素是对几乎所有上市公司具有影响的经济变量,通常包括:通货膨胀率、利率、GDP增速等。
()6.单因素模型中的宏观经济因素是“看不见,摸不着”的。
(),其期望收益由于不同公司经营状7.在市场模型中,影响股票超额收益的公司特有因素i况的不同而有所差别。
()8.市场模型可是单因素模型的一个特例,是将单因素模型中的宏观因素具体为具有代表性的市场指数。
()9.单因素模型的提出者是马克维茨。
()10.马柯威茨模型的缺点之一是计算太复杂。
()11.通常,证券价格和收益率的变化不会仅仅受到一个因素的影响。
如股票价格,其影响因素很多,除了国民生产总值的增长率外,还有银行存款利率、汇率、国债价格等影响因素。
()12.大量的分析和经验表明,股票收益之间的协方差一般是正的。
()13.单因素模型极大地简化了证券的期望收益率、方差及证券间协方差的计算。
()14.股票收益率与流动性之间是正相关的,股票流动性越高,预期收益率越高。
()15.单因素模型的残差项与因素相关。
()16.单因素模型中的残差项之间有可能相关。
()17.因素模型中残差项之间不相关。
()18.在多因素模型中,决定股票期望收益的因素完全包含在因素模型中,因此随机项的变动与因素变动具有相关性。
()19.在多因素模型中,由于股票收益共同变动的唯一原因是模型中共同因素的变动,因此不同股票的随机项之间相互独立,其协方差为0。
()20.Fama和French提出的三因素模型中,作为三因素之一的规模因素等于小市值公司与大市值公司股票的市值之差。
《投资学 》( Investments,(6th Edition))第六版[PDF]
![《投资学 》( Investments,(6th Edition))第六版[PDF]](https://img.taocdn.com/s3/m/de7bdf868762caaedd33d4f1.png)
《投资学》( Investments,(6th Edition))第六版[PDF]状态: 精华资源摘要: 发行时间: 2005年08月01日语言: 简体中文时间: 3月21日发布| 3月21日更新分类: 资料电子图书统计: 27000次浏览| 18次收藏相关:请登录举报: 举报资源•详细内容•相关资源•补充资源•用户评论eMule资源下面是用户共享的文件列表,安装eMule后,您可以点击这些文件名进行下载投资学.(第6版.).pdf 详情97.5MB全选97.5MB中文名: 投资学英文名: Investments,(6th Edition)资源格式: PDF版本: 第六版发行时间: 2005年08月01日地区: 大陆语言: 简体中文简介:资源介绍:《投资学》是由三名美国知名学府的著名金融学教授撰写的优秀著作,是美国最好的商学院和管理学院的首选教材,在世界各国都有很大的影响,被广泛使用。
自1999年《投资学》第4版以及2002年的第5版翻译介绍进中国以后,在国内的大学里,本书同样得到广泛运用和热烈反响。
此为本书的第6版,作者在前5版的基础上根据近年来金融市场、投资环境的变化和投资理论的最新进展做了大幅度的内容更新和补充,还亢分利用了网络资源为使用者提供了大量网上资料。
全书共分7大部分,27章。
详细讲解了投资领域中的风险组合理论、资本资产定价模型、套利定价理论、市场有效性、证券评估、衍生证券、资产组合管理等重要内容。
本书观点权威,阐述详尽,结构清楚,设计独特,语言生动活泼,学生易于理解,内容上注重理论与实践的结合。
本书适用于金融专业高年级本科生、研究生及MBA学生,金融领域的研究人员、从业者。
目录:第一部分引论第1章投资环境第2章金融工具第3章证券是如何交易的第4章共同基金和其他投资公司第二部分投资组合理论第5章利率史与风险溢价第6章风险与风险厌恶第7章风险资产与无风险资产之间的资本配置第8章最优风险资产组合第三部分资本市场均衡第9章资本资产定价模型第10章指数模型第11章套利定价理论与风险收益多因素模型第12章市场有效性和行为金融学第13章证券收益的经验根据第四部分固定收益证券第14章债券的价格与收益第15章利率的期限结构第16章债券资产组合的管理第五部分证券分析第17章宏观经济分析与行业分析第18章股权估价模型第19章财务报表分析第六部分期权、期货及其他衍生证券第20章期权市场介绍第21章期权定价第22章期货市场第23章期货与互换的详细分析第七部分积极的资产组合管理第24章资产组合业绩评估第25章投资国际分散化第26章资产组合的管理过程第27章积极的资产组合管理理论附录术语表。
投资学第6章风险厌恶与风险资产配置

投资学 第6章
5
你们是在投资还是赌博
▪ 1.购买彩票? ▪ 2.购买股票? ▪ 3.购买外汇? ▪ 4.老虎机?
投资学 第6章
6
投资者的风险态度
▪ 风险厌恶(Risk aversion) ▪ 风险中性(Risk neutral) ▪ 风险爱好(Risk lover)
投资学 第6章
7
如何判断你的类型
投资学 第6章
风险厌恶与风险资产的资本配置
本章主要内容
投资过程的分解: ➢选择一个风险资产组合 ➢在风险资产与无风险资产间决定配置比例
➢配置比例的技术性要求:效用优化
投资学 第6章
2
如何进行收益与风险的权衡
1.不同组别风险、收益的权衡 2.如何用一无量纲的数字来进行表示? 3.经济学如何刻画显示效用的?
Stand投a资r学d 第D6e章viation
12
表6.1 风险资产组合(无风险利率为 5%)
投资学 第6章
13
附录6A:圣彼德堡悖论
▪ 期望收益无限的赌局,为何参加者愿意付 出的门票价格非常有限?
▪ 边际效用递减规律
投资学 第6章
14
三、圣.彼得堡悖论(St.Petersburg paradox)
问题 ▪ 为何 风险厌恶者将拒绝参加公平博弈???
投资学 第6章
效用函数(Utility function)
▪ 一个风险厌恶投资者常用如下形式的效应函 数:
U E(r) 1 A 2
2
➢ 其中,A为投资者风险厌恶指数,收益率为小 数形式。
➢ 若A越大,表示投资者越害怕风险,在同等风 险的情况下,越需要更多的收益补偿。
连续执硬币直至落在地上出现“正面”为止。如果第一次出现正面,奖励 1 元, 第二次出现正面奖励 2 元,第三次出现正面奖励 4 元,第四次出现正面奖励 8 元,等 等。每多一次抛掷出现正面,就加倍地偿付。这个试验的可能结果可以总结如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 久期和凸度第一节 久期(Duration )一、久期的定义Macaulay(1938年)为了评估债券的平均还款期限,定义了久期。
他将每次支付现金所用时间的加权平均值定义为久期,而权重为每次支付的现金流的现值占现金流总和(即债券的价格)的比率。
称采用这种方法定义的久期为Macaulay 久期。
具体公式如下:Py M y C iMacaulay n i ni ∑=+++=1)1()1(久期 久期最初是用来表示平均还款期限,但实际上久期还可以表示债券价格的波动性。
由债券的定价公式()()n n i i y M y CP +++=∑=1111对y 求导数得到()()()()y Macaulaydy P dP yP Macaulay y y nM y Ci y nM y Ci dy dP n i n i n n i i +-=+⨯-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++-=+-+-=∑∑=+=+11111111111久期将上式变形得到久期 将yMacaulay +1久期定义修正久期,有的干脆将修正久期定义为久期。
即, ⎪⎪⎪⎪⎭⎫ ⎝⎛-=P dy dP D 则易知:收益率的变化久期债券价格变化的百分比⨯-=∆-=∆y D P P注意:利用久期计算价格变化相当于泰勒展开式的一阶近似。
由我们的久期定义易知:MD(Macaulay 久期)与D (久期)的关系为MD=(1+y)D二、久期的性质久期是债券分析中的核心概念,它有效地度量了债券的风险,在债券的风险管理中起到了非常重要的作用,另外它也是资产免疫管理中的一个核心概念。
由上述久期的定义知()()[]dy D P dP dy Var D P dP Var σσ=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛2 即,债券价格变化率(短期回报率)的标准差是收益率标准差的D 倍。
1.久期与债券息票率的关系为计算方便,假定债券一年付息一次,息票率为c ,面值为1,现在离到期日还有N 年,其收益率为y,债券的价格为:()[]N N N k N k y y y c y y c P )1(111)1(1)1(1+++-=+++=-=∑两边取对数,再对收益率求导数,得到:()()()()()[]()()()()[]y y c y c y N y MD y y y c N y y y y cN y dy dP P dy p d N N N N N N +-++--++=+++--++++++-=⨯=-------1111111111111ln 11整理得到:从此式可看出久期与息票率的关系:息票率c 越大,久期越小。
2.久期与收益率之间的关系类似地,我们可以得到下式:⎥⎦⎤⎢⎣⎡-++-=∑=-T t tt MD t P y c y dy dMD 12)()1(11 由上式,易知: 0≤dydMD ,即收益率越大,久期越小。
3. 久期与到期日的关系一般地说,债券的到期日越长,久期越大。
第二节 久期与风险管理一、资产组合的久期资产组合的久期:资产组合的久期等于组成资产组合的各个资产的久期的加权平均,权值是各个资产的现价占总资产的比率。
资产组合的收益率:是资产组合的现金流的到期收益率。
我们考虑两个资产构成的资产组合,资产组合的关系为:种资产的价格。
第种资产的数量;第其中,i B i N B N B N P i i 2211+=如果债券具有相同的收益率,则:212211222211112211111B B P D PB N D P B N D dy dB B P B N dy dB B P B N dy dP P dydB N dy dB N dy dP +=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=-+= 例1 一个资产组合由1B 和2B 组成,它们的价格、收益率、久期分别是:797968.1%,8.8,100,483092.0%,00.7,100222111======D y B D y B则资产组合的久期为:14053.1797968.1100100100483092.010*******=⨯++⨯+=P D由现金流计算出收益率:%422.8214.104214.4214.4219.107200432=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+++=y y y y y 将资产组合看成一个债券,通过久期的定义计算出资产组合的久期:193477.1200214.1042214.45.1214.41219.1075.0211432=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯+⎪⎭⎫ ⎝⎛+⨯+⎪⎭⎫ ⎝⎛+⨯++⨯+y y y y y 我们应该注意到这两种方法计算出的结果的差别。
二、久期的匹配我们在进行风险管理时,有时需要构造一个资产组合满足:1. 其价值与某个目标债券或债券组合相同;2. 当利率发生波动时,两者的价值变动也相同。
如果一个是多头,一个是空头。
可以构造对冲组合,规避利率风险。
例2 假定持有一个债券,10年后到期,息票率是6%,投资者要求的收益率也是6%,如果市场利率上升,债券价格有下降的风险。
投资者可以采取持有其他债券空头来对冲上述三种债券的面值都是100。
现在我们来确定应持有这两种债券的数量x ,y ,使这个资产组合能够对冲它的利率风险。
1004378.71008378.132596.949709.010********.94⨯=⨯⨯+⨯⨯=⨯+⨯y x y x 得到的解为:5027.05276.0==y x这个资产组合y 叫久期匹配的资产组合。
三、久期与免疫(immunization )从短期看,利率下降,债券的价格上涨,债券的短期投资者将会从利率下降获益。
反之,如果利率上升,短期持有债券就会受到损失。
从长期的角度考虑,情况正好相反,利率下降将会导致利息的再投资收益的下降,也会导致资本利得的下降。
反之则反之。
从以上的分析,我们可以猜测存在一个“中期”;从“中期”看投资者的收益基本上不受利率变化的影响。
这个“中期”恰好是债券的久期。
投资者的投资期限正好等于其持有的资产组合的久期,利率的任何变化对投资的收益不会造成影响。
第三节 浮动利率债券的久期浮动利率债券产生于20世纪80年代,也有到期日、面值,但它的息票率是不固定的。
一般地,一个浮动利率债券刚发行,或者,刚购买一个浮动利率债券,它的下一个利息支付已经确定。
则债券的价格与市场参考利率有关系:221221212121212221211212211212212211212212⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=+⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+++-=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+++=---=-=-∑∑R R R R R R dR dP R RR R R RR R R R R RR R P N N k k N N k k如果一个浮动利率债券的息票率是参考利率的两倍,这个债券被称为双倍浮动利率债券(double floater )。
可以证明双倍浮动利率债券的久期是负值。
第四节 凸 度把债券价格看成收益率的函数,把它用泰勒展开式展开得到:()()Pdy Pd y Pdy P d y P dy dPP P y dy P d y dy dP P 222222222121=∆+∆≈∆∆+∆≈∆凸度凸度定义为:例3 考虑一个10年后到期,面值是100元,息票率是6%,半年付息一次的平价债券,其久期和凸度经过计算分别为D=7.44,C=68.77。
假定收益率上升0.5%,利用凸度可以计算出价格变化为:37.9663.310063.32%177.681002144.72%11002=--=⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯-价格下降到: 如果收益率下降0.5%,导致的价格变化为:81.10381.310081.32%177.681002144.72%11002=+=⎪⎭⎫ ⎝⎛-⨯⨯⨯+⨯⎪⎭⎫ ⎝⎛-⨯-价格上升到:凸度的解释 首先从Macaulay 久期开始 ()"'2'111P P y P P P y P dy dMD P y dy dP MD +-⎥⎦⎤⎢⎣⎡+--=+⨯⎪⎪⎭⎫ ⎝⎛-=求导数得到由前述久期的性质中的公式知: ()()()()()()()()()()()[]1111111111c 11122"'"'2'11212+++==+++-=+-=+-⎥⎦⎤⎢⎣⎡+--=+--+=⎥⎥⎦⎤⎢⎢⎣⎡-++-=-=-=-∑∑MD MD S y C S C y MD MD C PP y MD P P C P P y P P P y P S y MD t P y S MD t P y c y dy dMD Tt t tT t t t 代入上式,得到:,则有:如果记凸度为有:记:上式给出了凸度的准确金融含义,台由两项构成,第一项S 是现金流的集中程度,第二项反映了久期的大小。
在久期给定的情况下,凸度就反映了债券带来的现金流的集中程度,现金流越集中,凸度越小,现金流越分散,凸度越大。
一个债券的凸度除了取决于现金流的集中程度外,还与收益率、到期日、息票率有关,收益率越高,凸度越小;到期日越远,凸度越大;息票率越大,凸度越小。
第五节 凸度与风险管理一、资产组合的凸度资产组合的凸度定义为:资产组合的凸度等于资产组合中的各个证券凸度的加权平均,权值是各个证券的价值占组合价值的比率。
不失一般性,假定资产组合P 由1N 份债券1B 和2N 份债券2B 组成,债券、债券组合的现价仍分别记成P B B ,,21,则价格之间有关系为:2211B N B N P +=求两次导数,然后除以价格P ,得到:21221122222221211122111B B P C P B N C P B N dy B d B PB N dy B d B P B N dy P d PC +=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛== 利率的变化,会导致债券的价格的变化,如果债券持有者不愿意承担这个利率风险,可以通过其他债券的组合把该利率风险对冲掉。
如果一个资产组合与目标债券具有相同的久期、凸度,现价也相同,则这一资产组合与目标债券持有反向的头寸,利率风险就可以对冲掉。
例4 为简便起见,假定本例中所有债券的收益率都是6%,目标资产为:为了构造久期、凸度匹配的资产组合,假定三种债券各需要的数量为x 、y 、z ,它们应该满足条件:1. 资产组合的价格=目标资产的价格:1001001002596.94=++z y x2. 资产组合的久期=目标资产的久期:1004378.71008378.131002651.42596.949709.0⨯=⨯+⨯+⨯z y x3. 资产组合的凸度=目标资产的凸度:1007748.681004700.2961007665.212596.94413.1⨯=⨯+⨯+⨯z y x求解结果为:1271.0,4669.1,6302.0==-=z y x二、凸度与免疫雷丁顿(F. M. Redington )1952年首先把久期、凸度等概念应用到债券免疫中。
