直线和圆曲线反算
2021年高考数学母题题源系列 专题09 直线与圆 理(含解析)

2021年高考数学母题题源系列专题09 直线与圆理(含解析)【母题来源】xx山东卷理–9【母题原题】一条光线从点射出,经轴反射后与圆相切,则反射光线所在直线的斜率为()(A)或(B)或(C)或(D)或【答案】【考点定位】1、圆的标准方程;2、直线的方程;3、直线与圆的位置关系.【命题意图】直线与圆的问题,意在考查学生对直线与直线、直线与圆的位置关系的理解与把握,考查待定系数法及点到直线的距离公式的运用.在考查相关基础知识的同时,较好地考查了考生的运算求解能力及数形结合思想.【方法、技巧、规律】求直线方程的基本方法是“待定系数法”,基本步骤有四:①设——根据题意,设出方程的形式;②列——根据题意,列出关于待定系数的方程或方程组;③解——解方程(组),求出待定系数;④代——将待定系数代入所设方程,即得所求.本题首先由光的反射原理,得到反射光线的反向延长线必过点,从而从设出直线方程的点斜式入手,根据直线与圆相切,利用圆心到直线的距离等于圆的半径,列出方程,求得直线的斜率.从历年高考题看,直线与圆的位置关系问题,是考查的重点之一,往往涉及直线与圆的几乎所有知识内容,如直线的斜率(倾斜角)、直线方程、距离公式、圆的方程、圆的几何特征等,通过直线与圆问题的考查,能较好的考查待定系数法、数形结合思想、分类讨论思想、转化与化归思想等重要的思想方法,亦能较好地考查考生全面、严谨的思维习惯及思维品质等.研究直线与圆的位置关系,往往是“几何法”优于“代数法”,但应根据具体题目,灵活选用.值得特别注意的是,研究直线与圆相切时,切线的斜率可能不存在,仅应用“待定系数法”,就会失解,必须数形结合,以形助数,准确求解;涉及圆的弦长问题,利用弦心距、半径和半弦长构成的直角三角形是关键;涉及两圆的公共弦问题,既要能通过布列方程组求解,又要注意数形结合,充分利用题中出现的直角三角形.【探源、变式、扩展】研读教材可以发现,此题源于人教B版必修二第二章,本章小结巩固与提高15题,而涉及反射原理的题目有:习题2-2B组11题,第二章,本章小结自测与评估2题等;涉及直线与圆相切,利用待定系数法求切线方程的题目,则在教科书唾手可得.研究近几年高考题可以发现,直线与圆的问题,易于与平面向量、圆锥曲线、基本不等式等相结合.【变式】【xx届山东省烟台市高三下学期一模】已知是直线()上一动点,是圆的一条切线,是切点,若线段长度最小值为,则的值为()A. B. C. D.【答案】D1.【xx年期中备考总动员高三理数学模拟卷【山东】5】若双曲线的渐近线和圆相切,则该双曲线的离心率等于()A. B. C. D.【答案】C2.【xx届广东省江门市普通高中高三调研测试】直线经过点且与圆相切,则直线的方程是()A. B.C. D.【答案】B3.【xx届江西省白鹭洲中学高三上学期期末】若直线过点,斜率为1,圆上恰有1个点到的距离为1,则的值为()A. B. C. D.【答案】B4.【xx年期中备考总动员高三理数学模拟卷【浙江】4】若点在直线上,过点的直线与曲线只有一个公共点,则的最小值为()A.2 B.4 C. D.16【答案】B5.【xx届安徽省安庆五校联盟高三下学期3月联考】若直线被圆所截得的弦长为,则()(A)或(B)或(C)或(D)或【答案】A6.【xx届浙江省衢州市高三4月教学质量检测】若直线被圆所截得的弦长为6,则的最小值为()A. B. C. D.【答案】C7.【xx届山东省济南市高三上学期期末考试】已知圆C过点,且圆心在x轴的负半轴上,直线被该圆所截得的弦长为,则过圆心且与直线l平行的直线方程为________.【答案】8.【xx届北京市丰台区高三上学期期末考试】过点作圆O:的切线,切点为,如果,那么切线的斜率是;如果,那么的取值范围是.【答案】9.【xx届山东省济南市高三上学期期末考试】已知直线和圆相交于A,B两点,当线段AB最短时直线l的方程为________.【答案】10.【xx届安徽省安庆五校联盟高三下学期3月联考】(本小题满分12分)已知圆:,直线过定点.(Ⅰ)若与圆相切,求的方程;(Ⅱ)若与圆相交于、两点,求的面积的最大值,并求此时直线的方程.【答案】(Ⅰ)或;(Ⅱ)面积最大值为,直线方程为或.37540 92A4 銤34776 87D8 蟘\34945 8881 袁X.' 33968 84B0 蒰&Vk39857 9BB1 鮱424144 5E50 幐。
超高设置与计算说明

超高设置与超高加宽计算说明一、超高设置1、《JTG D20-2006公路路线设计规范》取消了《JTJ 011-94公路路线设计规范》中的“圆曲线半径与超高值”表,各圆曲线半径所设置的超高值应根据设计速度、圆曲线半径、公路条件、自然条件等经计算确定。
路线程序根据《JTG D20-2006公路路线设计规范》送审稿提供的“圆曲线半径与超高值”表编制了圆曲线半径、设计速度等计算超高值的表格模板。
用户可以结合项目情况修改表格模板,该表格模板存储在路线程序安装目录下的“superelevation”文件夹中。
表5 最大超高值10%2、在超高自动计算前,用户可以先进行超高设置,程序中的命令:[数据处理]→[超高分段] →[超高值设置],设置窗体如图1图1 超高值设置3、路线程序根据最大超高值自动选用相应的表,若用户需要修改表格模板可点击“浏览”按钮弹出表格模板,然后修改表格模板。
点击“确定”按钮后,程序就会把用户设置的超高值存入数据库,超高自计算就会以用户设置的超高值进行计算。
若用户不进行超高设置,程序会按程序内默认的超高值进行计算。
4、表格模板格式不能修改,只能修改模板中的数据。
二、超高计算命令:[数据处理]→[超高分段] →[自动计算]图2 超高自动计算1、超高自动计算窗体说明(如图2)1、1 当选中窗体中的“全缓和曲线范围内超高”,程序不考虑渐变率计算的超高缓和长度,默认超高在缓和曲线上完成;反之考虑渐变率计算的超高缓和长度。
1、2 当选中窗体中的“S型曲线YH(HY)全超高”,程序认为S型曲线YH(HY)刚好达到全超高,然后向GQ点推;反之由GQ点向YH(HY)推。
1.3 当选中窗体中的“S型曲线公切点横坡0%”,则公切点超高为0%,若未选中,则公切点为正常路拱。
2、超高自动计算时,线元划分成如下单元进行计算:2、1直线——圆曲线和圆曲线——直线(1)中间没有缓和曲线,超高缓和长度直线和圆曲线上各一半。
工程测量坐标正反算通用程序(终极篇)

第五篇坐标正反算通用程序(终极篇)1. 坐标正算主程序(命名为ZBZS)第1行:Lbl 0:”K=”?K:”BIAN=”? Z:”α=”?B第2行:Prog “A”第3行:”X=”:N+Zcos(F+B)◢第4行:”Y=”:E+Zsin(F+B)◢第5行:”F=”:F►DMS◢第6行:Goto 0K——计算点的里程BIAN——计算点到中桩的距离(左负右正)α——取前右夹角为正2. 坐标反算桩号和偏距主程序(命名为ZBFS)第1行:”X1=”? C:”Y1=”?D:”K1=”?K第2行:Lbl 0:Prog “A”第3行:Pol(C-N,D-E):Icos(F-J)→S:K+S→K第4行:Abs(S)>0.0001=>Goto 0第5行:”K1=”:K◢第6行:”BIAN=”:Isin(J-F)→Z◢X1——取样点的X坐标Y1——取样点的Y坐标K1——输入时为计算起始点(在线路内即可),输出时为反算点的桩号Z——偏距(左负右正)注:在9860或9960中需将第3行替换为Pol(C-N,D-E): List Ans[1]→I :List Ans[2]→J:Icos(J-F)→S:K+S →K,正反算主程序所有输入赋值多加一赋值符号(→),其他所有除数据库外的程序均保持不变3. 计算坐标子程序(命名为XYF)为了简洁,本程序由数据库直接调用,上述中的正反算主程序不直接调用此程序第1行:K-A→S:(Q-P)÷L→I第2行:N+∫(cos(F+X(2P+XI)×90÷π),0,S)→N第3行:E+∫(sin(F+X(2P+XI)×90÷π),0,S)→E第4行:F+S(2P+S I)×90÷π→F第5行:F<0=>F+360→F: F>360=>F-360→F4. 数据库(命名为A)第1行:K≤175.191=>Stop(超出后显示Done)第2行:175.191→A:428513.730→N:557954.037→E:92°26′40″→F:0→P:1/240→Q:70.417→L:K≤A+L =>GoTo 1(第一缓和曲线)第3行:245.607→A: 428507.298→N:558024.092→E: 100°50′59.4″→F: 1/240→P:1/240→Q:72.915→L: K≤A+L =>Goto 1(圆曲线)第4行:318.522→A: 428482.988→N:558092.538→E: 118°15′25.2″→F: 1/240→P: 0→Q: 55.104→L: K≤A+L =>Goto 1(第二缓和曲线)第5行:373.627→A:428453.283→N:558138.912→E:124°50′4.5″→F:0→P:-1/180→Q:67.222→L:K≤A+L=>Goto 1:Stop(下一曲线的第一缓和曲线,示例为S型曲线,超出后显示Done)第6行:Lbl 1:Prog “XYF”A——曲线段起点的里程N——曲线段起点的x坐标E——曲线段起点的y坐标F——曲线段起点的坐标方位角P——曲线段起点的曲率(半径倒数,直线为0,左负右正)Q——曲线段终点的曲率(半径倒数,直线为0,左负右正)L——曲线段长度(尽量使用长度,为计算断链方便)说明:(1)正算主程序可以计算一般边桩的坐标,如要计算类似涵洞端墙的坐标需增加两个变量,具体方法参考本程序集中的第1篇辛普生公式的坐标计算通用程序(2)适用于任意线形:直线(0→P、0→Q)、圆曲线(圆半径倒数→P、圆半径倒数→Q)、缓和曲线(0或圆半径倒数→P、圆半径倒数或0→Q)、卵形曲线(接起点圆的半径倒数→P、接终点圆的半径倒数→Q),曲线左转多加一负号。
CASIO 4850 道路测量正反算程序(向量)

CASIO 4850 道路测量正反算程序变量意义(凡是坐标均按复数a+bi输入,所有的值均按数学坐标系考虑)以下所说的线元为直线、圆曲线、缓和曲线A 每个线元的起点坐标(由设计图提供,或者计算出来)B 直线线元的终点(方向)坐标(由设计图提供,或者计算出来)C 正反算时计算点的坐标结果(中间结果,不做事前计算)D 反算时计算点的坐标(现场实测值,手动输入)E 反算时计算桩号的向量(前一点)(中间结果,不做事前计算),显示结果时为正东坐标。
F 反算时计算桩号的向量(后一点)(中间结果,不做事前计算)G 反算时计算桩号的步长(程序设定为20米,可自定义设定,一般10--50)H 反算时计算桩号前一点的坐标结果(中间结果,不做事前计算)I (D-C)与E的夹角(中间结果,不做事前计算)J (D-H)与F的夹角(中间结果,不做事前计算)K 缓和曲线的曲线总长(由设计图提供,或者计算出来)L 正算时为偏移计算点的长度,反算时为0(正算时手动输入,左正右负)M 正反算判断,等于0时进入正算,等于1时进入反算N 反算时起点桩号,显示结果时为正北坐标。
O 圆曲线的圆心坐标(由设计图提供,或者计算出来)P 曲线左偏时为-1,右偏时为+1(根据设计图事先确定)Q 缓和曲线起点的切线角(由设计图提供,或者计算出来)R 圆曲线的半径,缓和曲线的终点半径(由设计图提供,或者计算出来)S 计算点桩号(正算时手动输入)T 每个线元的起点桩号(由设计图提供,或者计算出来)U 反算时终点桩号V 缓和曲线在标准位置时的坐标计算结果(中间结果,不做事前计算)W 与道路中线的偏角(手动输入,左偏转范围0度--180度,没有右偏)XYZ 缓和曲线在标准位置时的切线角计算结果(中间结果,不做事前计算)主程序清单(每个语句后均有回车键)说明:→条件判断△条件判断结束▲显示结果≠→条件判断的否则Lb1 0M=0:F=0:H=0:G=20:N=?:U=? 设定中间参数(N和U是起点和终点的桩号)Lb1 1"ZHENG SUAN=0""FAN SUAN=1":{M} 根据变量M的值确定正反算M=0→Goto 2△M=0,进入正算程序M=1→Goto 3△M=1,进入反算程序Goto 0 M=其他,回到起点Lb1 2Prog "计算程序":Goto 0 进入正算程序,Lb1 3 进入反算程序S=N 起点桩号是整个平曲线的起点,此时输入程序中,下同(可自定义起点)“JI SUAN DIAN”:{D} 输入计算点坐标(a+bi)S=S-GLb1 5S=S+GS>U→“GUO ZHONG DIAN”▲GOTO 0△终点桩号是整个平曲线的终点,下同.Pause 4,暂停2秒。
关于坐标正反算的应用

关于坐标正反算应用备注1、图纸上如果单纯只注明曲线的半径,就说明这段曲线是缓和曲线;2、如果有注明曲线的所有要素,就说明这段曲线是圆曲线;3、如果在图纸的下方有注明曲线的各要素,而且将切线分成几段,就说明这段曲线是缓和曲线带圆曲线;4、在同一条直线同一方向上任何点的方位角都是相同的。
5、在计算方位角时,两个坐标输入次序先后不同时,得出的方位角不同,但反算距离是一样的。
○1关于坐标正反算的应用(先点击解析交会和工具;曲线的转角=转向角也是偏角)一、以知两点坐标,求距离方位角?称为反算例:测站点坐标待定点坐标1、点击坐标正反算→点击坐标反算→输入起点坐标X(1234.5678),Y (8765.4321)→再输入终点坐标X(1293.7422),Y(8870.2181)。
2、点击计算,得出反算方位角60.324509(即至待定点方位角60º32´45.09")。
得出反算距离120.339999(即至待定点距离)。
下表是按上面算式计算的结果数据二、已知一个点坐标,至待定点距离(120.339999),坐标点至待定点方位角(60.324509,即60º32´45.09")。
求待定点坐标?称坐标正算例:已知坐标点待定点坐标1、点击坐标正反算→点击坐标正算→输入起点坐标X(1234.5678)→Y(8765.4321)。
2、再输入已知方位角(60.324509),输入已知距离(120.339999)。
3、点击计算,得出待定点坐标结果:X=1293.742201Y=8870.218099三、已知A、B两点坐标,B、C两点间距离(45.21),求C点坐标?例:点点点1、先求出A点至B点的方位角:1)、点击坐标正反算→点击坐标反算→先输入起点坐标即A点 X(18081.584),Y(101832.735),再输入终点坐标即B点X(18122.972),Y(101831.379)。
坐标正反算程序(4850)

坐标正反算程序(4850)正算主程序:ZS1.Prog “SJ”2.Lbl 0: {ZS}3.Z<A=>Rec(sqrt(S2+(Z-Q)2),F+180-tan-1(S÷(Q-Z))):X=N+I:Pause 0:Y=E+J◢4.Goto 0◣第一直线5.Z<B=>L=Z-A:W=F+90GL2÷πRU+90:H=U:O=Z[5]:P=Z[6]:T=F+90G:Goto 1◣第一回旋线6.Z<C=>L=Z-B7.W=F+G((90U+180L)÷πR+270)8.Rec(R-GS,W):X=Z[9]+I: Pause 0:Y=Z[10]+J◢9.Goto 0◣圆曲线10.Z<D=>L=D-Z:W=F+G(K-90L2÷πR V)+90:H=V:O=Z[7]:P=Z[8]:T=F+G(K+90):Goto 1◣第二回旋线11.Lbl 1:X=L-L5÷40R2V2+L9÷3456R4V412.Y=L3÷6RV-L7÷336R3V3+L11÷42240R5V513.Rec(sqrt(X2+Y2),T):X=O+I:Y=P+J14.Rec(S,W): X=X+I: Pause 0:Y=Y+J◢15.Goto 0◣16.Z>D=>Rec(sqrt(S2+(Z-D+Z[4])2),F+G(K+tan-1(S÷(Z-D+Z[4])))):X=N+I: Pause 0:Y=E+I◢17.Goto 0◣第二直线反算主程序:FS1.Prog"SJ"2.H=90U÷πR第一回旋线所对圆心角β013.T=90V÷πR第二回旋线所对圆心角β024.Rec((Z[3] +Z[4]÷cosK)/tanK,F+90G):Z[11]=Z[5]+I:Z[12]=Z[6]+J ZH、HZ点垂线交点坐标5.Z[13]=F+90G+180 ZH点与ZH、HZ点垂线交点连线方位角6.Z[14]=Z[13]+GH HY点与圆心连线方位角7.Z[15]=Z[13]+G(K-H) YH点与圆心连线方位角8.Z[16]=Z[15]+GT HZ点与ZH、HZ点垂线交点连线方位角9.Lbl 0:{XY}10.Pol(X-Z[11],Y-Z[12]):J<0=>J=J+360◣11.GJ<GZ[13]=> Pol(N-X,E-Y):Rec(I,F-J): “Z”:Z=Q-I:Pause 0:“S”:J◢12.Goto 0◣第一直线13.GJ>GZ[16]=> Pol(X-N,Y-E):Rec(I,J-F-GK): “Z”:Z=I-Z[4]+D:Pause 0:“S”:J◢14.Goto 0◣第二直线15.GJ>GZ[13]=>Pol(X-Z[9],Y-Z[10]):J<0=>J=J+360◣16.GJ<GZ[14]=>P=Z[13]:H=U:M=A:T=1:Z[17]=Z[5]:Z[18]=Z[6]:Z[19]=F:Goto 1◣第一缓和曲线17.GJ<GZ[15]=> “Z”:Z=B+RG(J-Z[14]):Pause 0:“S”:S=G(R-I)◢18.Goto 0◣圆曲线19.GJ>GZ[15]=>P=Z[16]:H=V:M=D:T=-1:Z[17]=Z[7]:Z[18]=Z[8]:Z[19]=F+GK+180:Goto 1◣第二缓和曲线20.Lbl 1:Pol(X-Z[11],Y-Z[12]):J<0=>J=J+360:L= Abs(J-P) πR÷180 “L=H×Abs(J-P)÷2÷(90H÷πR)”21.Lbl 2:O=L-L5÷40R2H2+L9÷3456R4H4-L13÷599040R6H622.P=L3÷6RH-L7÷336R3H3+L11÷42240R5H5-L15÷9676800R7H723.Rec(sqrt(O2+P2),Z[19]+TGtan-1(P÷O)):O=Z[17]+I:P=Z[18]+J24.Pol(X-O,Y-P):Rec(I,J-(Z[19]+90TGL2÷πRH)):AbsI>0.001=>L=L+I:Goto 2:≠>“Z”:Z=M+TL: Pause 0: “S”:TJ◢25.Goto 0◣子程序(曲线要素数据):SJ1.Defm 19:M:M=1=>F=*:K“ZJ”=*:G=*:U(Ls1)=*:V(Ls2)=*:R=*:Q=*:N“XJ”=*:E“YJ”=*:Goto 1◣2.M=2=>F=*:K“ZJ”=*:G=*:U(Ls1)=*:V(Ls2)=*:R=*:Q=*:N“XJ”=*:E“YJ”=*:Goto 1◣3.………………4.Lbl 1:Z[1]=U2÷24R-U4÷2688R3+U6÷506880R5Z[1]第一回旋线内移值P15.Z[2]=V2÷24R-V4÷2688R3+V6÷506880R5Z[2]第二回旋线内移值P26.M=(R+Z[2]-(R+Z[1])cosK)÷sinK7.P=(R+Z[1]-(R+Z[2])cosK)÷sinK8.Z[3]= M+U÷2-U3÷240R2Z[3]第一回旋线切线长T19.Z[4]= P+V÷2-V3÷240R2Z[4]第二回旋线切线长T210.L=RKπ÷180+(U+V)÷2曲线长(Ls1+圆+Ls2)11.A=Q-Z[3]:B=A+U:D=A+L:C=D-V ZH,HY,HZ,YH里程桩号12.I=0:J=0:Rec(Z[3],F+180):Z[5]=N+I:Z[6]=E+J ZH点坐标增量计算,ZH点坐标13.Rec(Z[4],F+GK):Z[7]=N+I:Z[8]=E+J HZ点坐标增量计算,HZ点坐标14.Rec(sqrt(M2+(R+Z[1])2),F+G(K+tan-1((R+Z[2])÷P))):Z[9]=N+I:Z[10]=E+J 圆心坐标注:F-起始边方位角K-转角G-线路左转为-,右转为+U-第一回旋线长V-第二回旋线长R-半径Q-交点桩号N,E-交点坐标Z-待求点桩号S-偏距(左偏为-,右偏为+)sqrt为根号。
线路测量坐标正、反算计算原理及卡西欧5800程序说明

线路测量坐标正、反算计算原理及卡西欧fx-5800P程序说明一、计算原理在各测量书中对于坐标正算的相关计算式均有说明,故在此不做详解,仅对正算过程中需要用到的原理及公式做一汇总。
对于坐标反算,虽然都采用无限趋近原理进行计算,但计算方式各有差别,本文仅对其中一种自认为相对简单易懂并便于操作的原理进行详解。
1.1 坐标转换[1]如图1,设X P、Y P为P点在国家控制网坐标系中的坐标;x P、y P为P点在工程独立控制网坐标系中的坐标。
X O、Y O为工程独立坐标系原点o在国家坐标系中的坐标,Δα为两坐标系纵坐标轴的交角。
如果一条边在国家坐标系中的坐标方位角为A,而在工程独立坐标系中的坐标方位角为α,则:∆α=A−α(1-1)当由工程独立坐标系坐标换算至国家坐标系坐标时,换算公式为:X=x cos∆α−y sin∆α+X O(1-2)Y=x sin∆α+y cos∆α+Y O}当由国家坐标系坐标换算至工程独立坐标系坐标时,也可使用式(1-2),此时应将X、Y与x、y互换,且∆α=α−A。
1.2 坐标方位角关系计算1.2.1 正、反坐标方位角[2]一条直线的坐标方位角与直线的前进方向有关,沿直线前进方向的坐标方位角称为正坐标方位角,与其相反方向的坐标方位角称为反坐标方位角。
如图2,由于轴子午线之间是互相平行的,因此同一直线的正、反坐标方位角相差180°,即:α正=α反±180°(2-1)当α反<180°时,取“+”号;当α反>180°时,取“-”号。
1.2.2 坐标方位角的推算[3] 1.2.2.1 转折角为右角如图3(a),α12为已知边坐标方位角,α23为推算边的坐标方位角,β右为该两边所夹的右角,则:α23=α12±180°−β右=α21−β右 (2-2)1.2.2.2 转折角为左角如图3(b),α12为已知边坐标方位角,α23为推算边的坐标方位角,β左为该两边所夹的右角,则:α23=α12+β左±180°=α21+β左(2-3) 无论用右角还是左角推算,如遇出现负数的情形,应加上360°。
【冲刺必刷】人教A版 高中数学2020届 高考复习专题--直线与圆的方程(含解析)

直线与圆的方程一、重点知识结构本章以直线和圆为载体,揭示了解析几何的基本概念和方法。
直线的倾斜角、斜率的概念及公式、直线方程的五种形式是本章的重点之一,而点斜式又是其它形式的基础;两条直线平行和垂直的充要条件、直线l1到l2的角以及两直线的夹角、点到直线的距离公式也是重点内容;用不等式(组)表示平面区域和线性规划作为新增内容,需要引起一定的注意;曲线与方程的关系体现了坐标法的基本思想,是解决解析几何两个基本问题的依据;圆的方程、直线(圆)与圆的位置关系、圆的切线问题和弦长问题等,因其易与平面几何知识结合,题目解法灵活,因而是一个不可忽视的要点。
二、高考要求1、掌握两条直线平行和垂直的条件,掌握两条直线所成的角和点到直线的距离公式,能够根据直线的方程判断两条直线的位置关系;3、会用二元一次不等式表示平面区域;4、了解简单的线性规划问题,了解线性规划的意义,并会简单的应用;5、了解解析几何的基本思想,了解用坐标法研究几何问题的方法;6、掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程的概念。
三、热点分析在近几年的高考试题中,两点间的距离公式,中点坐标公式,直线方程的点斜式、斜率公式及两条直线的位置关系是考查的热点。
但由于知识的相互渗透,综合考查直线与圆锥曲线的关系一直是高考命题的大热门,应当引起特别注意,本章的线性规划内容是新教材中增加的新内容,在高考中极有可能涉及,但难度不会大。
四、复习建议本章的复习首先要注重基础,对基本知识、基本题型要掌握好;求直线的方程主要用待定系数法,复习时应注意直线方程各种形式的适用条件;研究两条直线的位置关系时,应特别注意斜率存在和不存在的两种情形;曲线与方程的关系体现了坐标法的基本思想,随着高考对知识形成过程的考查逐步加强,对坐标法的要求也进一步加强,因此必须透彻理解。
既要掌握求曲线方程的常用方法和基本步骤,又能根据方程讨论曲线的性质;圆的方程、直线与圆的位置关系,圆的切线问题与弦长问题都是高考中的热点问题;求圆的方程或找圆心坐标和半径的常用方法是待定系数法及配方法,应熟练掌握,还应注意恰当运用平面几何知识以简化计算。
趋近法求算缓和曲线里程及偏距的计算原理
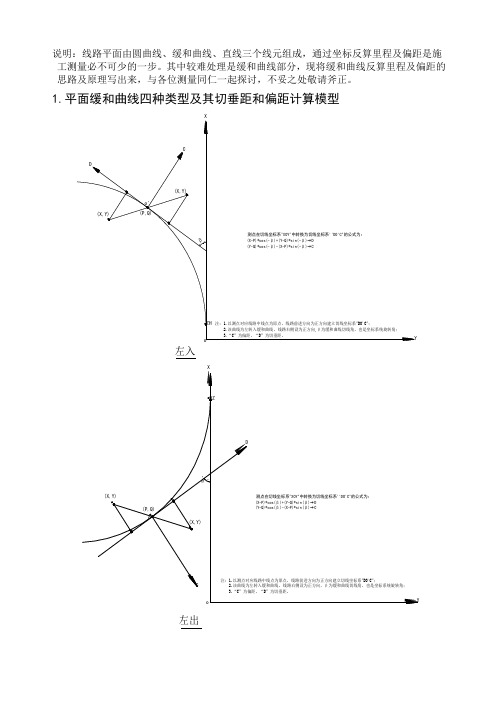
说明:线路平面由圆曲线、缓和曲线、直线三个线元组成,通过坐标反算里程及偏距是施工测量必不可少的一步。
其中较难处理是缓和曲线部分,现将缓和曲线反算里程及偏距的思路及原理写出来,与各位测量同仁一起探讨,不妥之处敬请斧正。
1.平面缓和曲线四种类型及其切垂距和偏距计算模型左入左出右入右出把以上左转曲线和右转曲线公式进行整理分析。
左转:入缓和曲线(X-P)*cos(-β)+(Y-Q)*sin(-β)→D(Y-Q)*cos(-β)-(X-P)*sin(-β)→C出缓和曲线(X-P)*cos(β)+(Y-Q)*sin(β)→D(Y-Q)*cos(β)-(X-P)*sin(β)→C右转:入缓和曲线(X-P)*cos(β)+(Y-Q)*sin(β)→D(Y-Q)*cos(β)-(X-P)*sin(β)→C出缓和曲线(X-P)*cos(-β)+(Y-Q)*sin(-β)→D(Y-Q)*cos(-β)-(X-P)*sin(-β)→C假设变量W为曲线方向判别符号,且规定W=1为右转,W=-1为左转,旋转角β=K,则以上公式简化为:入缓和曲线(X-P)×cos(W×K)+(Y-Q)×sin(W×K)→D(Y-Q)×cos(W×K)-(X-P)×sin(W×K)→C出缓和曲线(X-P)×cos(-W×K)+(Y-Q)×sin(-W×K)→D(Y-Q)×cos(-W×K)-(X-P)×sin(-W×K)→C2.趋近法求算缓和曲线里程及偏距(以上推导公式的应用)HHQX1 (计算入缓和曲线里程及偏距)程序清单:X:?Y:?W:(输入切线坐标和线路转向参数,1为左转,-1为右转X-S ZH→L:(测点对应缓和曲线长,估计值D O:S ZH+(L-L5÷(40×R2×l012)+ L9÷(3456×R4×l014))→P: W×(L3÷(6×R×l01)- L7÷(336×R3×l013))→Q:90×L2÷(π×R×l01)→K: (X-P)×cos(W×K)+(Y-Q)×sin(W×K)→D: (Y-Q)×cos(W×K)-(X-P)×sin(W×K)→C: L+D →L: LpWhile Abs(D)≥0.001: (循环语句。
《直线和圆的方程》教学分析和教学建议

本章教学建议
(三)教法、学法建议 1.抓住一切机会渗透解析几何的基本思想.
章节的地位与作用
解析几何是17世纪法国数学家笛卡尔和费马创立的,它的基本内 涵和方法是:通过坐标系,把几何的基本元素——点和代数的基本对 象——数(有序数对或数组)对应起来,在此基础上建立曲线的方程(点 的轨迹方程),从而把几何问题转化为代数问题,再通过代数方法研究 几何图形的性质.解析几何的创立是数学发展史上的一个里程碑,数学 从此进入变量数学时期,它为微积分的创建奠定了基础.
本章教学建议
(三)教法、学法建议
3.注重“曲线和方程”的内在逻辑关联,帮助学生在一般观念引领下构建和 把握曲线方程的整体结构.
曲线与方程之间一一对应的关系是解析几何的基石.虽然教科书正文中没有明确 提出曲线与方程的关系,但是两者的对应关系在直线的点斜式方程、圆的标准方 程的建立过程中有所体现. 从大的范围看,曲线与方程之间的一一对应反映了数量关 系与空间形式之间的关系.有了这种关系,就可以用方程表示曲线,对曲线进行“ 运算”;建立方程的几何直观表达,把方程“形象化”,进一步体会数形结合的 思想.
(2)求圆心在直线3x - y 0上,与x轴相切,且被直线x y 0截得的弦长为2 7的圆 的方程. 变式2: 求圆心在直线x y 4 0上,并且经过圆x2 y2 6x 4 0与圆x2 y2 6 y - 28 0 的交点的圆的方程.
本章教学建议
(三)教法、学法建议
9. 设计专题训练,结合解题过程,加强方法的总结,落实解题技能.
坐标正算反算公式讲解

一 方位角:在高斯直角坐标系中,由坐标纵轴方向的北端起,顺时针量到直线间的夹角,称为该直线的坐标方位角,常简称方位角,用a 表示。
1、第一象限的方位角YX第一象限第二象限第三象限第四象限oAa图12、第二象限的方位角Y X第一象限第二象限第三象限第四象限oAa图23、第三象限的方位角YX第一象限第二象限第三象限第四象限o Aa图34、第四象限的方位角YX第一象限第二象限第三象限第四象限oAa图4方位角计算公式:x=a -1tanA Y O Y -AX OX-方位角的计算器计算程序:Pol(X A -X O ,Y A -Y O )直线OA 方位角度值赋予给计算器的字母J ,0≤J <360。
直线段OA 的距离值赋予给计算器的字母I,I >0 直线OA 与直线AO 的方位角关系: 1、当直线OA 的方位角≤180°时,其反方位角等于a+180°。
2、 当直线OA 的方位角>180°时,其反方位角等于a-180°。
二 方位角的推算 (一)几个基本公式 1、坐标方位角的推算或:注意:若计算出的方位角>360°,则减去360°;若为负值,则加上360°。
例题:方位角的推算已知:α12=30°,各观测角β如图,求各边坐标方位角α23、α34、α45、α51。
13图5解: α23= α12-β2+180°=30°-130°+180°=80°α34= α23-β3+180°=80°-65°+180°=195°α45=α34-β4+180°=195°-128°+180°=247°α51=α45-β5+180°=247°-122°+180°=305°α12=α51-β1+180°=305°-95°+180°=30°(检查)三坐标正算一、直线段的坐标计算oB DACEaap图6设起点O的坐标(X O,Y O),直线OP的方位角为F op,求A、C、E点的坐标1、设直线段OA长度为L,则A点坐标为X A=X O+L×Cos(F op)Y A=Y O+L×Sin(F op)2、设直线段OB长度为L OB,直线段BC长度为L BC,则C点坐标为X B=X O+L OB×Cos(F op)Y B=Y O+L OB×Sin(F op)直线BC的方位角F BC=F op+aIF F B C>360°:Then F BC-360°→F BC:IfEndX C=X B+L BC×Cos(F BC)Y C=Y B+L BC×Sin(F BC)3、设直线段OD长度为L,直线段DE长度为L DE,则E点坐标为ODX D=X O+L OD×Cos(F op)Y D=Y O+L OD×Sin(F op)直线DE的方位角F DE=F op-aIF F DE<0°:Then F DE+360°→F DE:IfEndX E=X D+L DE×Cos(F DE)Y E=Y D+L DE×Sin(F DE)二、缓和曲线段的坐标计算x Y 00=L- +=L 40R L 52s 2L3456R L 94s 4L 6R L 3s L 336R L 7s 33-90 L πRL sO2切线角=设完整缓和曲线起点O 的坐标为O (XO,YO ),方位角为F ,曲线长度为L S ,曲线上任一点的曲线长度为L,当线路右转时直线CP 的方位角Fcp=F+90°IF F cp >360°:Then F cp-360°→F cp :IfEnd当线路左转时直线CP 的方位角Fcp=F-90°IF F cp<0°:Then F cp+360°→F cp:IfEndX P=X O+Abs(x O)×Cos(F)+Abs(y O)×COS(F CP)Y P=Y O+Abs(x O)×Sin(F)+Abs(y O)×Sin(F CP)三、圆曲线段的坐标计算圆曲线的已知点数据为起点S的桩号K s、走向方位角αs、起点S 坐标为(X o,Y o)、圆曲线半径为R与曲线长为L。
(十四)反设直线 巧算方程

1 2 c2 b 设函数 f(t)= b t+ t ≥a. 2ac c c2 1 2 所以b≥1,得 2≥ ,即 e≥ . a 2 2 故椭圆的离心率 e
速解技法——学一招
的取值范围为 2 ,1. 2
经典好题——练一手
常用结论——记一番
第二部分 板块(二) 反设直线
b2 所以|PF|=|t3|= , csin α
b c2 |PF| ab2 1 = a2sin α+a2b2sin α≥a, |AB| 2c
b 当且仅当 sin α=c时取等号, c c2 1 2 所以b≥1,得 2≥ ,即 e≥ . a 2 2 故椭圆的离心率 e
速解技法——学一招
速解技法——学一招
经典好题——练一手
常用结论——记一番
第二部分 板块(二) 反设直线
巧算方程
[经典好题——练一手] 1.已知过定点 P(2,0)的直线 l 交抛物线 y2=4x 于 A,B 两点,
则△AOB 面积的最小值为________.
结 束
解析:设直线 AB 为 x=ty+2,A(x1,y1),B(x2,y2),
9 G-4,0与以线段
答案:4 2
常用结论——记一番
经典好题——练一手
第二部分 板块(二) 反设直线
巧算方程
结 束
x2 y2 2.已知椭圆 E:2+ 2=1(a>b>0)过点(0, a b 2 2),且离心率 e 为 . 2 (1)求椭圆 E 的方程; (2)设直线 x=my-1(m∈R)交椭圆 E 于 A,B 两点,判断 点
巧算方程
结 束
法二:设直线
x=c+tcos l: y=tsin α
α,
(十八)反设直线 巧算方程

易知直线 PF:xy==tcs+intαco+sπ2α+,π2,
速解技法——学一招
经典好题——练一手
(t 为参数)
常用结论——记一番
第二部分 板块(二) 反设直线 巧算方程 结 束
由 x=ac2=c+t3cosα+π2. 所以|PF|=|t3|=csibn2 α, ||APFB||=a2bc2a2s1in α+ac2b2 2sin α≥ba,
速解技法——学一招
经典好题——练一手
常用结论——记一番
第二部分 板块(二) 反设直线 巧算方程 结 束
解:(1)由已知得 b= 2,e=ac= 22,且 a2=b2+c2,
解得 a=2, 所以椭圆 E 的方程为x42+y22=1.
(2)设点 A(x1,y1),B(x2,y2),
x=my-1,
由x42+y22=1
e 的取值范围.
[解] 法一:设直线 l:x=my+c,且 A(x1,y1),B(x2,y2).
x=my+c, 联立xa22+by22=1,
得(b2m2+a2)y2+2mcb2y-b4=0,
速解技法——学一招
经典好题——练一手
常用结论——记一番
第二部分 板块(二) 反设直线 巧算方程 结 束
得(m2+2)y2-2my-3=0.
速解技法——学一招
经典好题——练一手
常用结论——记一番
第二部分 板块(二) 反设直线 巧算方程 结 束
设函数 f(t)=21acb2t+ct2≥ba.
所以bc≥1,得ac22≥12,即
e≥
2 2.
故椭圆的离心率 e 的取值范围为 22,1.
速解技法——学一招
经典好题——练一手
常用结论——记一番
不设缓和曲线时圆曲线长度

不设置缓和曲线的情况下,圆曲线的长度会根据设计速度、圆曲线半径、以及曲线长度等因素而变化。
首先,缓和曲线是公路设计中的一个重要概念,它主要用于在直线段和曲线段之间进行平滑过渡。
在设置缓和曲线时,圆曲线长度通常会考虑车辆在曲线上行驶时的行驶半径、车辆速度以及缓和曲线的设置长度等因素。
如果不设置缓和曲线,那么车辆在曲线上行驶时的过渡就会更加直接,这可能会影响到车辆的行驶轨迹和稳定性。
在这种情况下,圆曲线的长度就需要根据车辆的速度、曲线的半径等因素进行计算。
具体来说,圆曲线的长度可以通过以下公式进行计算:L = v * T,其中L是圆曲线的长度,v 是设计速度(通常以km/h为单位),T是曲线所对应的圆心角。
这个圆心角通常会根据曲线的半径进行计算。
需要注意的是,这个公式只是一种近似计算方法,具体的圆曲线长度可能会因为各种因素的影响而有所不同,例如地形、土壤条件、桥梁结构等等。
另外,如果圆曲线长度过长,还需要考虑一些特殊情况。
例如,如果圆曲线长度超过了某个极限值(通常是根据设计规范确定的),那么就需要考虑设置反向弯道或弯道缓和曲线来改善车辆的行驶体验和安全性。
总的来说,不设置缓和曲线的情况下,圆曲线的长度需要综合考虑车辆速度、行驶半径、曲线半径、以及特殊情况等因素。
在进行公路设计时,需要根据实际情况进行计算和调整,以确保车辆行驶的安全性和舒适性。
fx-5800p全线坐标正反算带高程计算程序(线元法

曲线任意里程中边桩坐标正反算(CASIO fx-5800P计算器)程序一、程序功能及原理1.功能说明:本程序由一个主程序(TYQXJS)和五个子程——正算子程序(SUB-ZS)、反算子程序(SUB-FS)等构成,可以根据曲线段——直线、圆曲线、缓和曲线(完整或非完整型)的线元要素(起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径)及里程边距或坐标,对该曲线段范围内任意里程中边桩坐标进行正反算。
本修改版程序既可实现正算全线贯通,亦可实现反算全线贯通。
本程序在CASIO fx-5800P计算器运行。
2.计算原理:利用Gauss-Legendre 5点通用公式正算线路中边桩坐标、线外测点至曲线元起点和终点的垂距的符号是否相异(即Dca×Dcb<0=>该测点在其线元内)进行判断并利用该线元要素反算中桩里程、支距,最后计算出放样数据。
二、源程序1.主程序(TYQXJS)Deg:fix 3119→DimZ“INPUT(0) Or DATA(Else)”?ILbl 0:“1.SZ=>XY,2.XY=>SZ,3.TF=>CK,4.SD=>FY,5.TW=>FY”?NIf N=1 Or N=5:Then Goto 1Else If N=2 Or N=3 Or N=4:Then Goto 2Else Goto 3IfEnd:IfEndLbl 1:“K(m)=”?SIf S<0:Then Goto 0:IfEnd“JL(m)=”?ZIf Z≠0:Then “ANGLE→R(Deg)=”?M:IfEndIf I=0:Then Prog “DAT1”:Else Prog “DAT2”:IfEndS-O→W:If W<0:Then Goto 0:Else If W>H:Then Goto 0:IfEnd:IfEndProg “SUB-ZS”:Prog “SUB-GC”If Z<0:Then“XL(m)=”:X◢“YL(m)=”:Y◢If N=5:Then Prog “SUB-TW”:IfEndElse If Z>0:Then “XR(m)=”:X◢“YR(m)=”:Y◢If N=5:Then Prog “SUB-TW”:IfEndElse “X(m)=”:X◢“Y(m)=”:Y◢“Hs(m)=”:L◢“FWJ=”: F►DMS◢IfEnd:IfEndGoto 1Lbl 2:“X(m)=”?X:If X<0:Then Goto 0:IfEnd“Y(m)=”?YIf N=3 Or N=4:Then “H(m)=”?→Z[2]:IfEndX→Z[4]:Y→Z[5]:90→MIf I=0:Then Prog “DAT1”G+QEH(C+HD)→F:1→J:U→Z[8J]:V→Z[8J+1]G-M→A:F-M→B:Prog “SUB-ZX1”:Goto BG+M→A:F+M→B:Prog “SUB-ZX1”:Goto B:IfEnd0→J:Lbl A: Isz JZ[8J+3]-M→A:Z[8(J+1)+3]-M→B:Prog “SUB-ZX1”If Z[6]Z[7]<0:Then J→J:Prog“DAT1” :Goto B:IfEndZ[8J+3]+M→A:Z[8(J+1)+3]+M→B:Prog “SUB-ZX1”If Z[6]Z[7]<0:Then J→J:Prog “DAT1” :Goto B:Else Goto A:IfEndLbl B:Prog“SUB-FS”O+W→S:Prog “SUB-GC”“K(m)=”:S◢“Hs(m)=”:L◢“JL(m)=”:Z◢If N=3:Then Prog “WIDE”:IfEndIf N=4:Then Prog “SDFY”:IfEndGoto 2Lbl 3:“TYQXJS→END”2. 正算子程序(SUB-ZS)0.1184634425→A: 0.2393143352→B:0.2844444444→Z[1]:0.0469100770→K:0.2307653449→L:0.5→Z[3]U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Z[1]cos(G+QEZ[3]W(C+Z[3]WD))+Bcos(G+QE(1 -L)W(C+(1-L)WD))+Acos(G+QE(1-K)W(C+(1-K)WD)))→XV+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Z[1]sin(G+QEZ[3]W(C+Z[3]WD))+Bsin(G+QE(1-L)W(C+(1-L)WD))+Asin(G+QE(1-K)W(C+(1-K)WD)))→YG+QEW(C+WD)+M→FX+Zcos(F)→X:Y+Zsin(F)→YF-M→F:If F<0:Then F+360→F:IfEndReturn3. 反算子程序(SUB-FS)G-M→T:Abs((Y-V)cos(T)-(X-U)sin(T))→W:0→ZLbl C:Prog “SUB-ZS”T+QEW(C+WD)→L:(Z[5]-Y)cos(L)-(Z[4]-X)sin(L)→ZIf Abs(Z)<10-6:Then Goto D:Else W+Z→W:Goto C:IfEndLbl D:0→Z:Prog “SUB-ZS”:(Z[5]-Y)÷cos(F)→Z:Return4.高程计算子程序(SUB-GC)Prog “DAT3”0.5RAbs(0.01(E-D))→TIf E>D:Then 1→C:Else -1→C:IfEndIf S<A:Then -0.01D→W:Else 0.01E→W:IfEndAbs(A-S)→LIf L>T:Then B+WL→L:Else B+WL+C(T-L)2÷2÷R→L:IfEndReturn5. 垂距计算子程序(SUB-ZX1)(Z[5]-Z[8J+1])cos(A)-(Z[4]-Z[8J])sin(A)→Z[6](Z[5]-Z[8(J+1)+1])cos(B)-(Z[4]-Z[8(J+1)])sin(B)→Z[7]Return6.曲线元要素数据库:DAT1(两条线路,可扩充为多条线路)If I=0:Then Goto E: Else If I=2:Then Goto F:IfEnd:IfEndJ=1=>***→Z[8]:***→Z[9]:***→Z[10]:***→Z[11]:***→Z[12]:***→Z[13]:***→Z[14]:*** →Z[15]:IfEndJ=2=>***→Z[16]:***→Z[17]:***→Z[18]:***→Z[19]:***→Z[20]:***→Z[21]:***→Z[22]:***→Z[23]:IfEndJ=3=>***→Z[24]***→Z[25]:***→Z[26]:***→Z[27]:***→Z[28]:***→Z[29]:***→Z[30]:***→[31]:IfEnd………………………………………………..Goto HLbl F: J=1=>***→Z[8]:***→Z[9]:***→Z[10]:***→Z[11]:***→Z[12]:***→Z[13]:***→Z[14]:*** →Z[15]:IfEndJ=2=>***→Z[16]:***→Z[17]:***→Z[18]:***→Z[19]:***→Z[20]:***→Z[21]:***→Z[22]:***→Z[23]:IfEndJ=3=>***→Z[24]***→Z[25]:***→Z[26]:***→Z[27]:***→Z[28]:***→Z[29]:***→Z[30]:***→[31]:IfEnd(注:如有多个曲线元要素继续添加入数据库DAT1中)Goto GLbl E:“X0=”?U:“Y0=”?V:“S0=”?O:“F0=”?G:“LS=”?H:“R0=”?P:“RN=”?R:“Q=”?Q Lbl G:1÷P→C:(P-R)÷(2HPR)→D:180÷π→E:Return7.隧道放样子程序:SDFY5.5→A:8.5→B:L+1.5→CIf I=1:Then -1→K:Else 1→K:IfEnd 给左右隧道符号赋值1.25K→F:4.25K→L:7.25K→K 给各圆心距路线的偏距赋值Z[2]-C→D 计算测点至圆心的高差D,If D>A:Then Goto 1:Else If D<0:Then Goto 2:IfEnd:IfEndZ-L→E:Abs(E)→E:√(D2+E2)→W:W-A→T: 计算测点至圆心的平距E,实测半径W“R(m)=”:W◢“DR(m)=”:T◢If E≤A:Then D-√(A2-E2)→C:E-√(A2-D2)→L 计算测点水平偏移量L、垂直偏移量C “Dh(m)=”:C◢显示测点垂直偏移量C“DL(m)=”:L◢显示测点水平偏移量LElse E-√(A2-D2)→L“DL(m)=”:L◢IfEnd:ReturnLbl 1Z-L→E:Abs(E)→E:√(D2+E2)→W:W-A→T: 计算测点至圆心的平距E,实测半径W“R(m)=”:W◢“DR(m)=”:T◢If E≤A:Then D-√(A2-E2)→C“Dh(m)=”:C◢IfEnd:ReturnLbl 2:Abs(D)→D:Abs(Z)→Z:Abs(K)→K:Abs(F)→FIf Z>K:Then Z-F→E:Else Z+K→E:IfEnd√(D2+E2)→W:W-B→T“R(m)=”:W◢“Rc(m)=”:T◢If E≤B:Then D-√(B2-E2)→C:E-√(B2-D2)→L 计算测点水平偏移量L、垂直偏移量C “Dh(m)=”:C◢显示测点垂直偏移量C“DL(m)=”:L◢显示测点水平偏移量LElse E-√(B2-D2)→L“DL(m)=”:L◢显示测点水平偏移量LIfEnd:Return8.曲线元要素判断数据库:DAT2(两条线路,可扩充为多条线路)If I=2:Then Goto A:IfEndIf S<第一线元终点里程:Then 1→J:Prog “DAT1”:ReturnElse If S<第二线元终点里程:Then 2→J:Prog “DAT1”:ReturnElse If S<第三线元终点里程:Then 3→J:Prog “DAT1”:ReturnElse If S<第四线元终点里程:Then 4→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndIf S≥第四线元起点里程And S<第五线元终点里程:Then 5→J:Prog “DAT1”:Return .................................Else If S<第n线元里程:Then n→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndLbl AIf S<第一线元终点里程:Then 1→J:Prog “DAT1”:ReturnElse If S<第二线元终点里程:Then 2→J:Prog “DAT1”:ReturnElse If S<第三线元终点里程:Then 3→J:Prog “DAT1”:ReturnElse If S<第四线元终点里程:Then 4→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEndIf S≥第四线元起点里程And S<第五线元终点里程:Then 5→J:Prog “DAT1”:Return Else If S<第n线元里程:Then n→J:Prog “DAT1”:ReturnIfEnd:IfEnd:IfEnd:IfEnd .................................9.高程数据库子程序:DAT3(两条线路,可扩充为多条线路)If I=0:Then Goto A:Else If I=2:Then Goto B:IfEnd:IfEndIf S≤46500:Then 46150→A:361.26→B:40000→R:-0.3→D:-1.2→E:ReturnElse If S≤47200:Then 46800→A:353.46→B:20000→R:-1.2→D:1→E:ReturnElse If S≤48400:Then 47500→A:360.46→B:20000→R:1→D:-1.6→E:ReturnElse If S≤49600:Then 48700→A:341.26→B:10000→R:-1.6→D:2.45→E:Return IfEnd:IfEnd:IfEnd:IfEndIf S>49600 And S≤50300:Then 49840→A:369.19→B:100000→R:2.45→D:2.8→E:Return Else If I=2:Then49800→A:368.21→B:150000→R:2.45→D:2.7→E:ReturnIfEnd:IfEndLbl A:“C PEG(m)=”?→A“C H(m)=”?→B“R(m)=”?→R“I1=”?→D“I2=”?→EReturnLbl B49800→A:368.21→B:150000→K:2.45→D:2.7→E:Return10.填方路基宽度检查子程序(WIDE)“WIDTH CHECK”◢“H→MID(m)=”?→A 起坡点与中桩高差常数“DIST→MID(m)=”?→B 起坡点与中桩距离常数“i=”?→C 路基填筑坡度CAbs(Z[2]-L+A)→DAbs(Z)-B-D→E“DL(m)=”:E◢显示实有宽度与应有宽度之差值Return11.坡口坡脚线坐标计算子程序:SUB-TW“TIANWA LINE”◢“DIST→MID(m)=”?A 起坡点与中桩距离常数“H→MID(m)=”?B 起坡点与中桩高差常数“T(1) Or W(Else)=”?C 填方边坡为1,其它为挖方边坡“i=”?E 填方或挖方边坡坡度Abs(Z)-A→D: DE→KIf C=1:Then L-B-K→W:Else L+B+K→W:IfEnd“JS H(m)=”:W◢计算出应有高程“SC H(m)=”?→D 输入实测高程D-W→T“GC(m)=”:T◢显示实测高程与计算高程的差异Return三、使用说明1、规定(1) 以道路中线的前进方向(即里程增大的方向)区分左右;当线元往左偏时,Q=-1;当线元往右偏时,Q=1;当线元为直线时,Q=0。
CASIO fx-5800P线元法坐标正反算程序

CASIO fx-5800P线元法坐标正反算程序说明:本程序适用于卡西欧计算器 CASIO fx-5800P,可对全线贯通坐标正反算、竖曲线高程计算。
该程序可计算任意线型,包含(直线、圆曲线、缓和曲线、卵形曲线)等,还可以能通过坐标反推该点里程和距中线距离,适用测量员专用。
主程序名:ABCYT第1步Deg:Fix 3:10→DimZ第2步Lbl 3:"1.DK=>XY":"2.XY=>DK":"Q"?W:"DK"?S:Prog"ABCYTSJ":If P=0:Then 10^(45)→P:IfEnd:If R=0:Then 10^(45)→R:IfEnd第3步1÷P→C:(P-R)÷(2HPR)→D:180÷π→E:If W=1:Then Goto 1:Else Goto2:IfEnd第4步Lbl 1:"W"?Z:"α"?N:Abs(S-O)→W:Prog "ABCYTZ"第5步Cls:"F=":Locate 3,1,F°:"X=":Locate 3,2,X:"Y=":Locate 3,3,Y◢第6步Prog"ABCYTSQX":Cls:"H=":Locate 3,1,H◢第7步1→W:90→N:Goto 3第8步Lbl 2:?X:?Y:X→I:Y→J:Prog"ABCYTF":O+W→S第9步Cls:"K=":Locate 3,1,S:"S=":Locate 3,2,Z◢第10步2→W:Goto 3正算子程序名:ABCYTZ第1步0.1739274226→A:0.3260725774→B:0.0694318442→K:0.3300094782→L第2步1-L→F:1-K→M第3步U+W×(A×cos(G+Q×E×K×W×(C+K×W×D))+B×cos(G+Q×E×L×W×(C+L×W×D))+B×cos(G+Q×E×F×W×(C+F×W×D))+A×cos(G+Q×E×M×W×(C+M×W×D)))→X第4步V+W×(A×sin(G+Q×E×K×W×(C+K×W×D))+B×sin(G+Q×E×L×W×(C+L×W×D))+B×sin(G+Q×E×F×W×(C+F×W×D))+A×sin(G+Q×E×M×W×(C+M×W×D)))→Y第5步G+Q×E×W×(C+W×D)→F:F+ N→Z[1]第6步X+Z×cos(Z[1])→X:Y+Z×sin(Z[1])→Y反算子程序名:ABCYTF第1步Lbl 2:(S-O)→W:0→Z:Prog "ABCYTZ":F-90→Z[9]:(J-Y)×cos(Z[9])-(I-X)×sin(Z[9])→Z[10]第2步If Abs(Z[10])>0.001:Then S+Z[10]→S:Goto 2:Else Goto 1:IfEnd第3步Lbl 1:(Y-J)÷sin(Z[9])→Z第4步Pol(X-I,Y-J):If Z<0:Then -1×I→Z:Else 1×I→Z:IfEnd数据库名:ABCYTSJ第1步Goto1第2步Lbl 1:If S<7586.707 Or S>13346.96:Then Cls:Locate 2,2,"PQX":Locate 4,3,"CHAOXIAN":Locate 10,4,"→Stop"◢第3步Stop:IfEnd第4步Lbl 1:IF S<7946.707:Then 98°56′56″→G:7586.707→o:3378605.445→U:453648.704→V:0→P:4500→R:360→H:1→Q:Return:IfEnd第5步Lbl 1:IF S<11766.03:Then 101°14′26″→G:7946.707→o:3378544.714→U:454003.518→V:4500→P:4500→R:3819.323→H:1→Q:Return:IfEnd第6步Lbl 1:IF S<12126.03:Then 149°52′11″→G:11766.03→o:3376389.890→U:457018.324→V:4500→P:0→R:360→H:1→Q:Return:IfEnd第7步Lbl 1:IF S<13346.96:Then 152°09′41.68″→G:12126.03→o:3376073.846→U:457190.654→V:0→P:0→R:1220.93→H:0→Q:Return:IfEnd第n步……………………………………………………数据输入说明:第1步Goto1第2步Lbl 1:If S<本条线路起点里程S>本条线路止点里程Cls:Locate 2,2,"PQX":Locate 4,3,"CHAOXIAN":Locate 10,4,"→Stop"◢第3步Stop:IfEnd第4步Lbl 1:If S<本线元止点里程:Then线元起点切线方位角→G:线元起点桩号→O:线元起点坐标X→U:线元起点坐标Y→V:线元起点半径(直线为0、曲线为半径)→P:线元止点半径(直线为0、曲线为半径)→R:线元长度→H:线元转向(左转为-1、右转为1、直线为0)→Q:Return:IfEnd第n步Lbl 1:每增加一行则为增加一个线元要素。
直线和圆的参数方程重要知识

1.直线的参数方程
(1)过点 M0(x0,y0),倾斜角为 α 的直线 l 的参数方程为
x=x0+tcos α y=y0+t sin α
(t 为参数)
.
重点辅导
1
2 参数的几何意义 直线的参数方程中参数 t 的几何意义是:
直线上动点M到定点M0(x0,y0)的距离就是参数t的绝对值
M• 450 P x
O
的坐标为x, y,根据条件知
台风中心M移动形成的直线
图2 15
l 的方程为
x 300 40t cos1350 ,
y 40t sin1350 ,
t 为参数,t 0
x 300 20 2t ,
即 y 20 2t ,
t 为参数,t 0
重点辅导
18
当点M 300 20 2t,20 2t 在圆O内或在圆O上时,有
t为参数
②
思考 由M 0M te,你能得到直线l的参数 方 程②中 参 数t 的 几 何 意 义 吗?
重点辅导
4
因为e cos,sin ,所以| e | 1.由 M0M
te,得到| M0M || t | .所以,直线上的动点M 到定点M0的距离,等于② 中参数t 的绝对值.
当 0 时,sin 0,所以,直线l的单位
(2)设l与圆 x 2 y2 =4相交于两点A,B,求点P
到A,B两点的距离之积.
解:(1)直线的参数方程是
x=1+
3 2t
y=1+12t
(t 是参数).
重点辅导
7
(2)因为点 A,B 都在直线 l 上,所以可设它们对应的参数为 t1 和 t2,则点 A,B 的坐标分别为 A1+ 23t1,1+12t1,B1+ 23t2,1+21t2. 以直线 l 的参数方程代入圆的方程 x2+y2=4, 整理得到 t2+( 3+1)t-2=0.① 因为 t1 和 t2 是方程①的解,从而 t1t2=-2. 所以|PA|·|PB|=|t1t2|=|-2|=2.
圆曲线线元中反算里程和偏距

线元转向
说明
左转输入“-1 ” 白色区域为输入数据部分 右转输入“1” 此计算程序可判断计算点在直线线元中的里程和偏距(适合正 交,不适合斜交) 1 半径R 判断结果如下 K: 550.000 偏距: 右偏 17000.000 17.9994 示例图
9221.831 2388.674 起点至终点方 位角: 圆心至起点方 位角: 圆心至计算点 方位角: 235°01′ 50.17″ 110°21′ 34.09″ 177°28′ 19.47″ 9753.313907 177.4720744
圆曲线线元起点 K: X: 数 据 输 入 Y: 16355.765 9561.964 2880.850 计算点 X: Y: 弧长LC: 辅 助 计 算 圆心角O: 角1,角2: 夹角O1: 起点至终点方 位角: 665.6380 69°20′32.17 ″ 55°19′43.92 ″
圆曲线线元终点 K: X: Y: 17021.403 9203.321 2368.072
起点至圆心方 计算点至圆心距离: 532.0006 位角:
290°21′ 34.09″
Байду номын сангаас
67°06′45.38″ 圆心点坐标: 235.0306032 圆心至计算点 方位角:
2365.209415 角1,角2: 55.32887 夹角O1: 67.11261
圆心至起点方 位角:
110.3594686
圆心角O:
69.3422692
起点至圆心方 290.3595 位角:
计算点至起点弧长L
说明
输入数据部分 线线元中的里程和偏距(适合正 适合斜交)
结果如下 17000.000 17.9994 示例图
644.2348
圆曲线偏角计算公式

圆曲线偏角计算公式90L/(∏R)L为置镜点到测点的距离缓和曲线偏角计算公式:573L2/(RLs60)L为置镜点(ZH,HZ)到测点的距离,Ls为缓和曲线总长HY,YH点的切线方向是:两倍的缓和曲线总偏角后视ZH,或HZ点曲线要素:切线长T=Rtg(a/2)a为转折角曲线长L=∏Ra/180 a为转折角,R为半径外矢距E=R/cos(a/2)-R a为转折角,R为半径切曲差q=2T-L竖曲线:曲线长L=R(i2-i1)i2i1分别为交点相邻两边的纵坡度切线长T= R(i2-i1)/2外矢距E=T2/(2R)前进方向坐标计算公式:(坐标增量):X1=X+Dcosa D为距离a为方位角Y1=Y+Dsina后退方向坐标计算公式;Cx=X-DcosaCy=Y-Dsina直线段右侧坡脚点坐标计算公式:Ax1=AX+Dcos(a+90) Y 值同样直线段左侧坡脚点坐标计算公式:Ax1=AX+Dcos(a-90) Y值同样有已知两个坐标点计算方位角:例:A点坐标(X,Y),B点坐标(X1,Y1)A点方位角:tan-1a=(Y1-Y)/(X1-X)A,B两点间的距离AB=√(X-X1)2+(Y-Y1)2( 一).导线坐标计算的基本公式1.以纵坐标X的北端按顺时针方向到一直线的角度,称为该直线的方位角,通常以a表示。
有例说明,aAB表示直线AB方向的坐标方位角,aBA表示直线BA方向的坐标方位角,一般以直线的前进方向称为正方向,反之,称为反方向,直线AB的正、反方向的坐标方位角有如下关系:aBA=aAB加减180度2.坐标方位角的传递已知直线AB的方位角为aAB,在B点测得到直线B1的折角£左(或£右),直线B1的方位角aB1为:取左角£左时,aB1=aAB+£左—180度取右角£右时,aB1=aAB—£右+180度若计算的aB1<0度时应加360度若计算的aB1>360度时应减360度3坐标的正运算设A为已知点,其坐标XA、YA为已知,B是待定点。
