Matlab实验二
实验二-MATLAB-图形系统
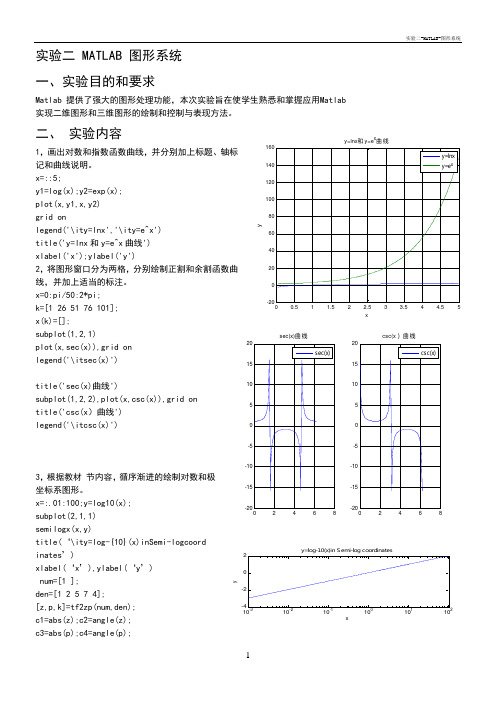
实验二 MATLAB 图形系统一、实验目的和要求Matlab 提供了强大的图形处理功能,本次实验旨在使学生熟悉和掌握应用Matlab 实现二维图形和三维图形的绘制和控制与表现方法。
二、实验内容1,画出对数和指数函数曲线,并分别加上标题、轴标记和曲线说明。
x=::5;y1=log(x);y2=exp(x);plot(x,y1,x,y2)grid onlegend('\ity=lnx','\ity=e^x')title('y=lnx和y=e^x曲线')xlabel('x');ylabel('y')2,将图形窗口分为两格,分别绘制正割和余割函数曲线,并加上适当的标注。
x=0:pi/50:2*pi;k=[1 26 51 76 101];x(k)=[];subplot(1,2,1)plot(x,sec(x)),grid onlegend('\itsec(x)')title('sec(x)曲线')subplot(1,2,2),plot(x,csc(x)),grid ontitle('csc(x)曲线')legend('\itcsc(x)')3,根据教材节内容,循序渐进的绘制对数和极坐标系图形。
x=:.01:100;y=log10(x);subplot(2,1,1)semilogx(x,y)title(‘\ity=log-{10}(x)inSemi-logcoord inates’)xlabel(‘x’),ylabel(‘y’)num=[1 ];den=[1 2 5 7 4];[z,p,k]=tf2zp(num,den);c1=abs(z);c2=angle(z);c3=abs(p);c4=angle(p);xyy=lnx和y=e x曲线sec(x)曲线csc(x)曲线101010101010y=log-10(x)in Semi-log coordinatesxypolar(c4,c3,'bx')hold on,polar(c2,c1,'ro')gtext('极坐标系中的零极点表示')4,根据教材 节内容,绘制多峰函数和三角函数的多条曲线。
实验二 MATLAB的数据类型与基本运算
实验二MATLAB的数据类型与基本运算一、实验目的掌握MATLAB中编程语言的表示和运算,了解常用基本数据类型,了解结构、元胞和表等复杂数据类型的基本概念;熟悉矩阵运算,掌握用矩阵求逆法解线性方程组的方法,熟悉多项式运算。
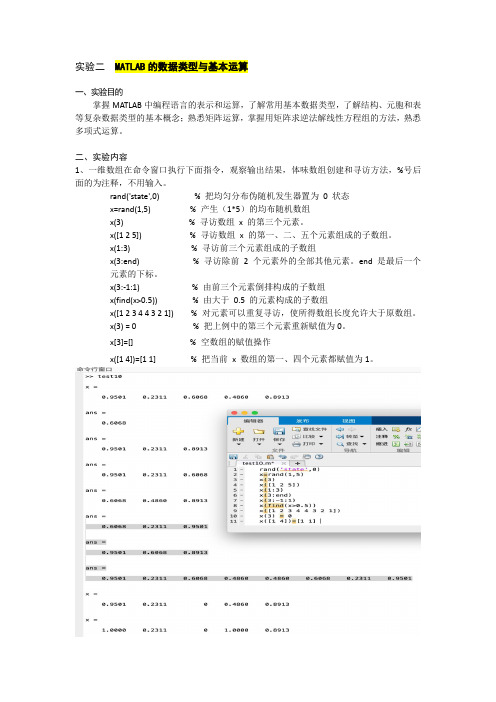
二、实验内容1、一维数组在命令窗口执行下面指令,观察输出结果,体味数组创建和寻访方法,%号后面的为注释,不用输入。
rand('state',0) % 把均匀分布伪随机发生器置为0 状态x=rand(1,5) % 产生(1*5)的均布随机数组x(3) % 寻访数组x 的第三个元素。
x([1 2 5]) % 寻访数组x 的第一、二、五个元素组成的子数组。
x(1:3) % 寻访前三个元素组成的子数组x(3:end) % 寻访除前2 个元素外的全部其他元素。
end 是最后一个元素的下标。
x(3:-1:1) % 由前三个元素倒排构成的子数组x(find(x>0.5)) % 由大于0.5 的元素构成的子数组x([1 2 3 4 4 3 2 1]) % 对元素可以重复寻访,使所得数组长度允许大于原数组。
x(3) = 0 % 把上例中的第三个元素重新赋值为0。
x[3]=[] % 空数组的赋值操作x([1 4])=[1 1] % 把当前x 数组的第一、四个元素都赋值为1。
2、在命令窗口执行下面指令,观察输出结果a=2.7358; b=33/79; % 这两条指令分别给变量 a , b 赋值。
C=[1,2*a+i*b,b*sqrt(a);sin(pi/4),a+5*b,3.5+i] % 这指令用于创建二维组C M_r=[1,2,3;4,5,6],M_i=[11,12,13;14,15,16] % 创建复数数组的另一种方法CN=M_r+i*M_i % 由实部、虚部数组构成复数数组3. 记录下面题目的程序和运行后的结果。
1⎥⎦⎤⎢⎣⎡=654321a ⎥⎦⎤⎢⎣⎡-=531142b ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=201c ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=063258741d下列运算是否合法,为什么?如合法,结果是多少?(1) result1 = a'=[1 4;2 5;3 6] (2) result2 = a * b 不合法(3) result3 = a + b=[3 6 2;5 8 11](4) result4 = b * d=[31 22 22;40 49 13](5) result5 = [b ; c' ] * d=[31 22 22;40 49 13;-5 -8 7] (6) result6 = a . * b=[2 8 -3;4 15 30](7) result7 = a . / b=[0.5000 0.5000 -3.0000;4.000 1.667 1.2000](8) result8 = a . * c 不合法(9) result9 = a . \ b=[2.0000 2.0000 -0.3333;0.2500 0.6000 0.8333] (10) result10 = a . ^2=[1 4 9;16 25 36] (11) result11 = a ^2不合法(12) result11 = 2 . ^ a=[2 4 8;16 32 64]4、设矩阵A =[311212123],B =[11−12−101−11]求(1)2A+B(2)4A 2-3B 2 (3)AB (4)BA (5)AB-BA5、设三阶矩阵A、B满足A-1BA=6A+BA,其中A=[13000140017],求矩阵B。
MATLAB数值分析实验二(复合梯形、辛普森和龙贝格求积,以及二重积分计算等)

佛山科学技术学院实验报告课程名称_______________ 数值分析________________________实验项目_______________ 数值积分____________________专业班级机械工程姓名余红杰学号2111505010 指导教师陈剑成绩日期月日一、实验目的b1、理解如何在计算机上使用数值方法计算定积分 a f ""X的近似值;2、学会复合梯形、复合Simpson和龙贝格求积分公式的编程与应用。
3、探索二重积分.11 f (x, y)dxdy在矩形区域D = {( x, y) | a _ x _ b, c _ y _ d}的数值D积分方法。
二、实验要求(1)按照题目要求完成实验内容;(2)写出相应的Matlab程序;(3)给出实验结果(可以用表格展示实验结果);(4)分析和讨论实验结果并提出可能的优化实验。
(5)写出实验报告。
三、实验步骤1、用不同数值方法计算积xln xdx =-- 0 9(1)取不同的步长h,分别用复合梯形及复合辛普森求积计算积分,给出误差中关于h的函数,并与积分精确值比较两公式的精度。
(2)用龙贝格求积计算完成问题(1 )。
2、给出一种求矩形区域上二重积分的复化求积方法,然后计算二重积分..e"y dxdy,其中积分区域D二{0乞x岂1,0岂y乞1}。
1.%lnt_t.m复化梯形:function F = Int_t(x1,x2,n)%复化梯形求积公式% x1,x2为积分起点和中点%分为n个区间,没选用步长可以防止区间数为非整数。
%样点矩阵及其函数值:x = lin space(x1,x2 ,n+1);y = f(x);m = len gth(x);%本题中用Matlab计算端点位置函数值为NaN,故化为零: y(1) = 0;y(m) = 0;%算岀区间长度,步长h:h = (x2 -x1)/n;a = [1 2*o nes(1,m-2) 1];%计算估计的积分值:F = h/2*sum(a.*y);%f.mfun cti on y = f(x)y = sqrt(x).*log(x);%run 11.mclc,clear;%分为10个区间,步长0.1的积分值:F = In t_t(0,1,10);F10 = F%分为100个区间F = In t_t(0,1,100);F100 = F%误差计算W10 = abs((-4/9)-F10);W100 = abs((-4/9)-F100);W = [W10 W100]%复化辛普森:%l nt_s.mfun cti on F = In t_s(x1,x2 ,n)%复化梯形求积公式% x1,x2区间,分为n个区间。
matlab实验二

北京工业大学Matlab实验报告**: ***学号: ************: **实验二、Matlab 的基本计算(一)实验目的1.掌握建立矩阵的方法。
2.掌握Matlab 各种表达式的书写规则以及常用函数的使用。
3.能用Matlab 进行基本的数组、矩阵运算。
4.掌握矩阵分析的方法以及能用矩阵运算或求逆法解线性方程组。
5.掌握Matlab 中的关系运算与逻辑运算。
(二)实验环境1.计算机2.MATLAB7.0集成环境(三)实验内容及要求1、熟练操作MATLAB7.0运行环境;2、自主编写程序,必要时参考相关资料;3、实验前应写出程序大致框架或完整的程序代码;4、完成实验报告。
(四)实验程序设计1.利用diag 等函数产生下列矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=032570800a ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=804050702b2.利用reshape 函数将1题中的a 和b 变换成行向量。
3.产生一个均匀分布在(-5,5)之间的随机矩阵(10×2),要求精确到小数点后一位。
4.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=731203321B求下列表达式的值:(1) B A K *611+=和I B A K +-=12(其中I 为单位矩阵)(2) B A K *21=和B A K *.22=(3) 331^A K =和3.32^A K =(4) B A K /41=和A B K \42=(5) ],[51B A K =和]2:);],3,1([[52^B A K = 5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x(1)求方程的解(矩阵除法和求逆法)(2)将方程右边向量元素3b 改为0.53,再求解,并比较3b 的变化和解的相对变化。
信号与系统MATLAB实验-实验二 Matlab中信号的运算

1、运用funtool对f(x)=sin(x)/x分别进行信号的尺度变换f(2x)、f(0.5x)和信号的移位运算f(x+1)、f(x-1)操作以及f(0.5x+1),分别记录相应波形。
f(x)=sin(x)/x f(x+1)f(2x) f(x-1)f(0.5x) f(0.5x+1)2、已知两连续时间信号如下图所示,1)写出信号的函数表达式,并计算f(t)=f1(t)* f2(t)的解析表达式; 2)用MATLAB 求f(t)=f1(t)* f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为dt )【实验思考】:通过不断改变dt 的取值并对比所得到的实验效果,观察当取样时间dt 为多大时,函数conv_cs()的计算结果就是连续时间卷积f(t)=f1(t)* f2(t)的较好近似结果?3、已知两连续时间信号如下图所示,1)写出信号的函数表达式,并计算f(t)=f1(t)* f2(t)的解析表达式;2)用MATLAB 求f(t)=f1(t)* f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为dt)【实验思考】:不断改变dt的取值并对比实验效果,当取样时间dt为多大时,函数conv_cs()的计算结果就是连续时间卷积f(t)=f1(t)* f2(t)的较好近似结果?clear alldt = 0.01;t1 = -3:dt:3;f1 = 2*(u(t1+1) - u(t1-1));figure;stairs(t1,f1);hold allgrid ont2 = -3:dt:3;f2 = u(t2+2)-u(t2-2);stairs(t2,f2)[fn, tn] = conv_cs(f1, t1, f2, t2, dt);plot(tn, fn)grid onlegend('f1', 'f2', 'f1*f2')。
MATLAB实验2 MATLAB的矩阵操作(1)

6、求特征值的方法求解方程
4x4+6x+3=0
(对比eig和roots、分析它们的不同和各自的应用范围)
7、P55思考练习3 , 5
实验过程中,请结合MATLAB的帮助系统。
四、实验操作过程与结果(写明使用到的函数及结算结果即可)
五、学生收获
MATLAB实验2MATLAB的矩阵操作(1)
班级专业:姓名:学号:日期:
一、实验目的
ห้องสมุดไป่ตู้1.熟悉MATLAB基本命令与操作;
2.熟悉MATLAB的矩阵运算;
3.了解MATLAB的多项式运算;
二、实验准备
通读书本第二章---MATLAB矩阵及其运算
三、实验内容
1.在命令窗口中键入表达式 ,并求 时 的值。
2. P54二.1
3.已知 , ,在MATLAB命令窗口中建立A、B矩阵并对其进行以下操作:
(1)计算矩阵A的行列式的值
(2)分别计算下列各式:
、 和 、 、 、 、
4、产生3阶随机方阵,其元素为[10,60]区间的随机整数,然后判断A的元素是否能被5整除。(分析fix、rand、rem函数的使用方法)
实验二MATLAB的矩阵操作_参考答案

1
5
>> A(k)
ans =
23
10
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
>> B=A([1,2,3],:)
B =
23.0000 10.0000 -0.7780 0
41.0000 -45.0000 65.0000 5.0000
32.0000 5.0000 0 32.0000
y =
-128.4271
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
A=[-1,5,-4;0,7,8;3,61,7]
B=[8,3,-1;2,5,3;-3,2,0]
>> A+6*B
ans =
47 23 -10
12 37 26
-15 73 7
&
ans =
-1.2768 -0.4743 0.2411
2.1229 1.3173 -0.2924
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
A=[23,10,-0.778,0;41,-45,65,5;32,5,0,32;6,-9.54,54,3.14]
>> k=find(A>=10&A<=25)
(2)
(3)
2.已知 ,
求下列表达式的值:
(1) , (其中I为单位矩阵)
(2)A*B、A.*B和B*A
(3)A/B及B/A
3.已知
完成下列操作
(1)输出A在[10,25]范围内的全部元素
(2)取出A前3行构成矩阵B,前两列构成矩阵C,右下角 子矩阵构成矩阵D,B与C的乘积构成矩阵E.
MATLAB实验报告

实验二MATLAB语言基础一、实验目的基本掌握MA TLAB向量、矩阵、数组的生成及其基本运算(区分数组运算和矩阵运算)、常用的数学函数。
了解字符串的操作。
二、实验内容1.向量的生成与运算;2.矩阵的创建、引用和运算;3.多维数组的创建及运算;4.字符串的操作。
三、实验步骤1.向量的生成与运算①向量的生成向量的生成有三种方法:直接输入法:生成行向量、列向量;冒号表达式法:变量=初值:间隔(可正可负):终值函数法:使用linspace线性等分函数,logspace对数等分函数。
格式为:linspace(初值,终值,个数)Logspace(初值,终值,个数), 初值及终值均为10的次幂。
②向量的运算A=[1 2 3 4 5],b=3:7,计算两行向量的转置,两行向量人加、减,两列向量的加、减;向量的点积与叉积。
a=[1 2 3 4 5];b=3:7;a =1 2 3 4 5b =3 4 5 6 7at=a',bt=b'at =12345bt =34567e1=a+b,e2=a-be1 =4 6 8 10 12 e2 =-2 -2 -2 -2 -2 f1=at+bt,f2=at-btf1 =4561012f2 =-2-2-2-2-2g1=dot(a,b),g2=a*bt>> g1=dot(a,b),g2=a*btg1 =85g2 =85g4=a.*b>> g4=a.*bg4 =3 8 15 24 35A=1:3;B=4:6;g3=cross(A,B)>> g3=cross(a,b)g3 =-3 6 -3注意:g1和g2的结果是否相同,为什么?g4的结果与g1和g2结果是否一样,为什么?g1和g2的结果相同,因为两者是同一种运算;g4与g1和g2不相同,因为两者一个是点乘一个是叉乘,运算不一样。
2.矩阵的创建、引用和运算矩阵是由n×m元素构成的矩阵结构。
实验二 MATLAB的科学计算

实验二 MATLAB的科学计算一、实验目的1、了解MATLAB的基本计算功能2、符号运算功能二、实验内容(一)基本计算功能例1、求[12+2× (7-4)]÷32的运算结果>>(12+2*(7-4))/3^2ans=2例2、用MATLAB求下面线性方程组的解3x1+ x2 - x3 = 3.6x1+2x2+4x3 = 2.1-x1+4x2+5x3 = -1.4>>A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];>>x=A\bx =1.4818-0.46060.3848例3、求两个矩阵的乘积a=[1 2 3;3 4 5;3 2 1]b=[1 2;3 4; 5 6]c=a*bc =22 2840 5214 20(二)符号运算功能1、求极限通常在MATLAB软件中,用limit 函数来求极限,其用法如表9-5所示:表9-5 limit 函数的用法例1、 求42cos lim 202x x e x -→.>> syms x % 把字符x 定义为符号 >>limit((cos(x)-exp(-x^2/2))/x^4)ans =-1/12例2 求42lim 22--→x x x .>> limit((x-2)/(x^2-4),x,2)ans =1/4例3 求t x t x t )cos()cos(lim 0-+→>> syms t x>> limit((cos(x+t)-cos(x))/t,t,0)ans =-sin(x)2 、求导数MATLAB 软件提供求函数导数的指令是diff ,具体使用格式如下:(1)diff(f, x) 表示对f (这里f 是一个函数表达式)求关于符号变量x 的一阶导数.若x 缺省,则表示求f 对预设独立变量的一阶导数.(2)diff(f, x, n) 表示对f 求关于符号变量x 的n 阶导数.若x 缺省,则表示求f 对预设独立变量的n 阶导数.例9-7 已知,c bx ax x f ++=2)(求)(x f 的一阶、二阶导数.>> syms a b c x>> f='a*x^2+b*x+c'f =a*x^2+b*x+c>> diff(f, x)ans =2*a*x+b>> diff(f,2)ans =2*a3 、求积分MATLAB软件提供求函数积分的指令是int,具体使用格式如下:(1)int(f) 返回f对预设独立变量的积分值;(2)int(f,v) 返回f对独立变量v的积分值;(3)int(f,a,b) 返回f对预设独立变量的积分值,积分区间为[a,b],a和b为数值式;(4)int(f,v,a,b) 返回f对独立变量的积分值,积分区间为[a,b],a和b为数值式;(5)int(f,m,n) 返回f对预设变量的积分值,积分区间为[m,n],m和n为符号式;例1、求下列函数的积分 :例:求不定积分⎰-dxex x23,⎰+12xxdx;>> syms x>> f=sym('x^3*exp(-x^2)') % 或 int('x^3*exp(-x^2)') f =x^3*exp(-x^2)>> int(f)ans =-1/2*x^2/exp(x^2)-1/2/exp(x^2)>> int('1/(x*sqrt(x^2+1))')ans =-atanh(1/(x^2+1)^(1/2))4 、数学表达式的化简例、 将下面表达式进行因式分解. 132-=a f>> f2=sym('a^3-1');>> factor(f2)ans =(a-1)*(a^2+a+1)。
实验二MATLAB程序设计含实验报告

实验二 MATLAB 程序设计一、 实验目的1.掌握利用if 语句实现选择结构的方法。
2.掌握利用switch 语句实现多分支选择结构的方法。
3.掌握利用for 语句实现循环结构的方法。
4.掌握利用while 语句实现循环结构的方法。
5.掌握MATLAB 函数的编写及调试方法。
二、 实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
M 文件的编写:启动MATLAB 后,点击File|New|M-File ,启动MATLAB 的程序编辑及调试器(Editor/Debugger ),编辑以下程序,点击File|Save 保存程序,注意文件名最好用英文字符。
点击Debug|Run 运行程序,在命令窗口查看运行结果,程序如有错误则改正三、 实验内容1.编写求解方程02=++c bx ax 的根的函数(这个方程不一定为一元二次方程,因c b a 、、的不同取值而定),这里应根据c b a 、、的不同取值分别处理,有输入参数提示,当0~,0,0===c b a 时应提示“为恒不等式!”。
并输入几组典型值加以检验。
(提示:提示输入使用input 函数)2.输入一个百分制成绩,要求输出成绩等级A+、A 、B 、C 、D 、E 。
其中100分为A+,90分~99分为A ,80分~89分为B ,70分~79分为C ,60分~69分为D ,60分以下为E 。
要求:(1)用switch 语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
(提示:注意单元矩阵的用法)3.数论中一个有趣的题目:任意一个正整数,若为偶数,则用2除之,若为奇数,则与3相乘再加上1。
重复此过程,最终得到的结果为1。
如:2?13?10?5?16?8?4?2?16?3?10?5?16?8?4?2?1运行下面的程序,按程序提示输入n=1,2,3,5,7等数来验证这一结论。
请为关键的Matlab 语句填写上相关注释,说明其含义或功能。
实验二matlab图形绘制精

、实验目的1、学习MATLAB图形绘制的基本方法;2、熟悉和了解MATLAB图形绘制程序编辑的基本指令;3、熟悉掌握利用MATLAB形编辑窗口编辑和修改图形界面,并添加图形的各种标注;、实验原理1.二维数据曲线图(1)绘制单根二维曲线plot(x,y;(2)绘制多根二维曲线plot(x,y当x是向量,y是有一维与x同维的矩阵时,则绘制多根不同颜色的曲线。
当x, y是同维矩阵时,则以x, y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3)含有多个输入参数的plot函数plot(x1,y1,x2,y2, …,xn,yn(4)具有两个纵坐标标度的图形plotyy(x1,y1,x2,y22.图形标注与坐标控制1)title (图形名称)2)xlabel (x 轴说明)3)ylabel (y 轴说明)4)text (x, y图形说明)5)lege nd (图例1,图例2,…)6) axis ([xmin xmax ymin ymax zmin zmax])3•图形窗口的分割subplot (m,n,p)4.三维曲线plot3 (x1,y1,z1,选项1, x2,y2,选项2,…,xn,yn,zn,选项n)5.三维曲面mesh(x,y,z,c与surf(x,y,z,c。
一般情况下,x, y, z是维数相同的矩阵。
X, y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的颜色范围。
三、实验内容及步骤1.绘制下列曲线:100V = --------(1grid on截图:v = —e亠(2xlabel('x';ylabel('y'; grid on截图:(3朮二了」1 6 t=-4:0.02:4; y=4*si n(t; x=4*cos(t;plot(x,y title('my first plot'; xlabel('x'; ylabel('y'; grid on截图:1r (4 "grid on截图:y Figuhr 1Q* liliwa Twlii M|4p'D u# k *■ □ u n2.在一个图形窗口绘制正弦和余弦曲线,要求给图形加标题正弦和余弦曲线”,X轴丫轴分别标注为时间t ”和正弦、余弦”,添加图例,在图形的某个位置标注“sin(t ”“co显示网格。
matlab2022实验2参考答案

matlab2022实验2参考答案报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:MATLAB实验二MATLAB符号计算试验报告说明:1做试验前请先预习,并独立完成试验和试验报告。
2报告解答方式:将MATLAB执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3报告以Word文档书写。
一目的和要求1熟练掌握MATLAB符号表达式的创建2熟练掌握符号表达式的代数运算3掌握符号表达式的化简和替换4熟练掌握符号微积分5熟练掌握符号方程的求解二试验内容1多项式运算(必做)1.1解方程:f(某)=某^4-10某某^3+34某某^2-50某某+25=0%采用数值方法:>>f=[1-1034-5025];>>root(f)%采用符号计算方法:f1=ym('某^4-10某某^3+34某某^2-50某某+25')olve(f1)1.2求有理分式R=(3某^3+某)(某^3+2)/((某^2+2某-2)(5某^3+2某^2+1))的商多项式和余多项式.a1=[3010];a2=[1002];a=conv(a1,a2);b1=[12-2];b2=[5201];b=conv(b1,b2);[p,r]=deconv(a,b);%注意:ab秩序不可颠倒。
%reidue用于实现多项式的部分分式展开,此处用deconv函数报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:%%此题,有同学程序如下:某1=[3010],某2=[1002],某3=[12-2],某4=[5201]某5=conv(某1,某2)[y6,r]=deconv(某5,某3)R=deconv(y6,某4)%%这种方法较第一种解法缺点:在除法运算中,会产生误差,故此题应先将分母的多项式相乘后,再与分子部分的多项式进行运算。
实验2利用MATLAB分析信号频谱及系统的频率特性

实验2利用MATLAB分析信号频谱及系统的频率特性引言:在信号处理领域,频谱分析是一项常见的任务。
通过分析信号的频谱,可以了解信号的频率特性以及信号中存在的频率成分。
而系统的频率特性是指系统对不同频率信号的响应情况。
本实验使用MATLAB对信号频谱和系统频率特性进行分析。
一、实验目标:本实验的主要目标是掌握使用MATLAB分析信号频谱及系统的频率特性的方法,包括信号频谱的计算、绘制和分析以及系统的频率响应计算和绘制。
二、实验原理:1.信号频谱分析:信号的频谱表示信号在频率域上的分布情况。
在MATLAB中,可以利用快速傅里叶变换(FFT)来计算信号的频谱。
FFT能够将时域信号转换为频域信号,从而得到信号的频谱信息。
频谱可以用幅度谱(或功率谱)和相位谱来表示。
2.系统的频率特性:系统的频率特性是指系统对不同频率信号的响应情况。
在MATLAB中,可以通过计算系统的频率响应来揭示系统的频率特性。
系统的频率响应是系统的输出信号与输入信号之比的幅度谱。
常见的方法包括系统传输函数法和单位冲激响应法。
三、实验步骤:1.生成信号:首先,我们可以使用MATLAB生成一个具有不同频率成分的信号。
例如,可以通过调用sin函数生成一个正弦信号并设置不同的频率参数。
2.信号频谱计算和绘制:利用MATLAB的FFT函数可以计算信号的频谱。
然后,可以使用MATLAB的plot函数将信号的频谱进行绘制。
在绘制频谱时,通常将频谱的幅度谱和相位谱绘制在同一图像上。
3.系统频率响应计算和绘制:对于系统的频率响应计算和绘制,可以采用系统传输函数法和单位冲激响应法。
对于系统传输函数法,可以通过给定系统的传输函数,使用MATLAB的freqz函数来计算系统的频率响应。
对于单位冲激响应法,可以通过给定系统的单位冲激响应,使用MATLAB的fft函数来计算系统的频率响应。
四、实验结果与分析:通过对实验数据进行处理和分析,可以得到信号的频谱和系统的频率特性信息。
MATLAB实验二答案

实验二报告人:王业成年级:机电131 学号:2013012496实验日期:2015.3.327报告完成日期:2015.3.30一、实验名称熟悉和掌握MA TLAB中关于矩阵变换以及矩阵运算的各种命令。
二、实验目的:熟悉和掌握MA TLAB中关于矩阵变换以及矩阵运算的各种命令。
三、实验内容:1.数、数组、矩阵的输入(1)数的输入a=5b=2-5i(2)数组的输入c=[1,3,5,7,9,11] %元素之间要用逗号用空格分开d=1:2:11e=linspace(1,11,6)体会以上输入有什么区别和联系。
(3)矩阵的输入A=[2,3,5;1,3,5;6,9,4] %行之间要用分别隔开2.矩阵大小的测试和定位A=[3,5,6;,2,5,8;3,5,9;3,7,9][n,m]=size(A)A(1,3)3. 矩阵的块操作A(2,:)A([1,3],:)A(2:3,1:2)问题2.1如何将A的2,3列互换?4.矩阵的四则运算A=[3,5,8;-2,3,6;1,4,9]B=rand(3,3)C=A+BD=A-BE=A*B问题2.2E为矩阵A、B的乘积运算结果,如果要求E的结果为A和B对应元素相乘的结果,应输入什么命令?F=A/B问题2.3 如果要求F为A,B对应元素作除法运算的结果,应输入什么命令?5.矩阵的点运算A=[1 2;3 4];B=[5 6;7 8];A*BA.*BA^2A.^26.矩阵的逻辑运算A=[1 2;3 4]; B=[0 6; 0 8]; A | BA&Bxor(A,B)a=-5;b=-10;(b~=0)&&(a/b>5)(b= =0)||(a/b>0)~a四、回答问题:问题2.1如何将A的2,3列互换?问题2.2 E为矩阵A、B的乘积运算结果,如果要求E的结果为A和B对应元素相乘的结果,应输入什么命令?问题2.3 如果要求F为A,B对应元素作除法运算的结果,应输入什么命令?五、思考题:1.输入一个矩阵A,取出A的第2行第1列的元素;取出A的第1,3,4列的所有元素;让A的第1列和第3列互换;删除A的第二列。
MATLAB实验二

本科实验报告课程名称《MATLAB电子信息应用》实验题目:矩阵和数组的操作实验地点:D001机房专业班级:学号:学生姓名:指导教师:一、实验环境计算机 MATLAB软件二、实验目的1.掌握矩阵和数组的一般操作,包括创建、保存、修改和调用等。
2.学习矩阵和数组的加减法运算与乘法。
3.掌握对数组中元素的寻访与赋值,会对数组进行一般的操作。
三、实验内容和步骤1.用三种方法创建一个3*3矩阵,然后利用矩阵编辑器,将其扩充为4*5矩阵,并保存,试着调用它。
(1)直接输入法如在命令区输入A=[3,2,1;4,5,6;7,8,9]。
(2)直接利用MATLAB提供的函数创建一个3*3矩阵如在命令区输入rand(3,3)即得到一个3*3的随机矩阵(3)利用MATLAB提供的“Matrix Editor”完成输入步骤1 在命令区输入A=1.步骤2 用鼠标单击工具栏的工作区浏览器,MATLAB弹出变量浏览器,选中变量A,鼠标左键双击A,打开矩阵编辑器。
步骤3 在左下角的两个文本框中分别输入希望得到的矩阵的行数和列数:3行3列,即得到一个3*3矩阵。
步骤4 要将上面矩阵改为一个4*5矩阵,只需改变矩阵的行数和列数即可。
如将3行3列改为4行5列,即可得到一个4*5矩阵。
若想修改其中的元素,只需用鼠标选中表格中我们想要修改的元素,将原来的元素修改为我需要的值。
步骤5 要命令区输入save data,即可保存上面例子中创建的矩阵A。
步骤6 在命令区输入 load data 即可把vabaocun在文件中的矩阵读到MATLAB的工作区的内存中来。
2.建立一个等差数列,然后由它产生一个对角阵。
步骤1 在命令区输入a=linspace(0,1.5,5)产生一个等差数列。
步骤2 在命令区输入B=diag(a)产生一个对角阵。
3.利用MATLAB的函数inv(A)求方阵A的逆矩阵。
步骤1 在命令区输入A=[1,2;5,6]得到一个2*2的方阵。
matlab实验报告实验二

matlab实验报告实验二Matlab实验报告实验二引言Matlab是一种功能强大的数学软件,广泛应用于科学研究和工程实践中。
在实验二中,我们将探索Matlab的图像处理功能,并通过实际案例来展示其应用。
图像处理基础图像处理是指对图像进行数字化处理的过程,其目的是改善图像质量、提取有用信息或实现特定的应用需求。
在Matlab中,我们可以利用各种函数和工具箱来实现图像处理的各种任务,如图像增强、滤波、分割和特征提取等。
实验步骤1. 图像读取与显示在Matlab中,我们可以使用imread函数读取图像文件,并使用imshow函数将图像显示在屏幕上。
例如,我们可以读取一张名为"lena.jpg"的图像,并显示出来:```matlabimg = imread('lena.jpg');imshow(img);```2. 图像灰度化图像灰度化是将彩色图像转换为灰度图像的过程。
在Matlab中,我们可以使用rgb2gray函数将彩色图像转换为灰度图像。
例如,我们可以将上一步读取的图像转换为灰度图像:```matlabgray_img = rgb2gray(img);imshow(gray_img);```3. 图像二值化图像二值化是将灰度图像转换为二值图像的过程,其中只包含黑色和白色两种颜色。
在Matlab中,我们可以使用imbinarize函数将灰度图像二值化。
例如,我们可以将上一步得到的灰度图像二值化:```matlabbinary_img = imbinarize(gray_img);imshow(binary_img);```4. 图像平滑图像平滑是指去除图像中的噪声或细节,使得图像更加平滑和清晰。
在Matlab 中,我们可以使用imfilter函数对图像进行平滑处理。
例如,我们可以对上一步得到的二值图像进行平滑处理:```matlabsmooth_img = imfilter(binary_img, fspecial('average'));imshow(smooth_img);```5. 图像边缘检测图像边缘检测是指提取图像中物体边缘的过程,常用于目标检测和图像分割。
MATLAB实验二

1 所以其解为 x=0.1342,y=0.9972,z=-0.0985,这三个方程的误差为 0.7690 10 8 ,
-0.0418 10 8 和-0.1054 10 8 ,且 h=1>0,这说明结果是可靠的
改进程序或思考: 此题也可以用更便捷的 inline 函数或匿名函数方式求解
>> [x, f, h]=fsolve(fun,[0,0,0]) Optimization terminated: first-order optimality is less than options.TolFun.
x=
0.1342 0.9972 -0.0985
f=
1.0e-008 *
0.7690 -0.0418 -0.1054
程序(或命令): % M 函数 eg4_4fun.m function f=fun(x) f(1)=9*x(1)^2+36*x(2)^2+4*x(3)^2-36; f(2)=x(1)^2-2*x(2)^2-20*x(3); f(3)=16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2;
>> [x ,f, h]=fsolve(@eg4_4fun ,[0,0,0]) Optimization terminated: first-order optimality is less than options. TolFun. x=
0.1342 0.9972 -0.0985
f=
1.0e-008 *
>> [x,f,h]=fsolve(@fun ,[0,0,0])得 Optimization terminated: first-order optimality is less than options.TolFun.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验课程:科学计算与数学软件专业:数学与应用数学班级:12070141学号:1207014145姓名:吴东中北大学理学院实验二线性方程组及矩阵特征值【实验目的】1.掌握线性方程组的解法以及学会使用Matlab求解线性方程。
2.掌握求解的全过程包括向量的运算以及如何求解矩阵特征值等。
【实验内容】1.向量的运算2. 用克莱姆(Cramer)法则求解四元线性方程组。
3. 现求解线性方程组bAx【实验过程】X=[-1 0 2];Y=[-2 -1 1];Z=dot(X,Y)sum(X.*Y)Z =4ans =4>> a=[1 2 3];b=[ 4 5 6];c=cross(a,b)c =-3 6 -3>> a=[1 2 3];b=[ 4 5 6];c=[-3 6 -3];X=dot(a,cross(b,c))X =54>> A=[1 2 3;4 5 6 ; 7 8 9];p=1.2;A^p[V,D]=eig(A);V*(D^p)*A^-1ans =2.4820 - 0.4841i3.6876 - 0.1313i4.8932 + 0.2214i7.0561 - 0.0534i 8.7403 - 0.0145i 10.4245 + 0.0244i11.6301 + 0.3772i 13.7930 + 0.1023i 15.9559 - 0.1725i警告: 矩阵接近奇异值,或者缩放错误。
结果可能不准确。
RCOND = 1.541976e-18。
ans =1.0e+17 *0.3590 + 0.0475i -0.7179 - 0.0950i 0.3590 + 0.0475i0.6721 + 0.0052i -1.3441 - 0.0105i 0.6721 + 0.0052i0.9852 - 0.0370i -1.9703 + 0.0740i 0.9852 - 0.0370i>> clearA = [-0.04 0.04 0.12 ; 0.56 -1.56 0.32 ; -0.24 1.24 -0.28]a=[A,eye(3)];atempo = a(2,:); a(2,:) = a(1,:); a(1,:)=tempo;aa(1,:) = a(1,:)/a(1,1)for i=2:3; a(i,:)=a(i,:) - a(i,1)*a(1,:); end;atempo = a(3,:); a(3,:) = a(2,:); a(2,:)=tempo;aa(2,:)=a(2,:)/a(2,2);afor i=1:3if i~=2, a(i,:)=a(i,:)-a(i,2)*a(2,:); endendaA =-0.0400 0.0400 0.12000.5600 -1.5600 0.3200-0.2400 1.2400 -0.2800a =-0.0400 0.0400 0.1200 1.0000 0 00.5600 -1.5600 0.3200 0 1.0000 0-0.2400 1.2400 -0.2800 0 0 1.0000a =0.5600 -1.5600 0.3200 0 1.0000 0-0.0400 0.0400 0.1200 1.0000 0 0 -0.2400 1.2400 -0.2800 0 0 1.0000a =1.0000 -2.7857 0.5714 0 1.7857 0-0.0400 0.0400 0.1200 1.0000 0 0 -0.2400 1.2400 -0.2800 0 0 1.0000a =1.0000 -2.7857 0.5714 0 1.7857 00 -0.0714 0.1429 1.0000 0.0714 00 0.5714 -0.1429 0 0.4286 1.0000a =1.0000 -2.7857 0.5714 0 1.7857 00 0.5714 -0.1429 0 0.4286 1.00000 -0.0714 0.1429 1.0000 0.0714 0a =1.0000 -2.7857 0.5714 0 1.7857 00 1.0000 -0.2500 0 0.7500 1.75000 -0.0714 0.1429 1.0000 0.0714 0a =1.0000 0 -0.1250 0 3.8750 4.87500 1.0000 -0.2500 0 0.7500 1.75000 0 0.1250 1.0000 0.1250 0.1250>> a(3,:)=a(3,:)/a(3,3)for i=1:3;if i~=3, a(i,:)=a(i,:)-a(i,3)*a(3,:); end;end;aa =1.0000 0 -0.1250 0 3.8750 4.87500 1.0000 -0.2500 0 0.7500 1.75000 0 1.0000 8.0000 1.0000 1.0000a =1.0000 0 0 1.0000 4.0000 5.00000 1.0000 0 2.0000 1.0000 2.00000 0 1.0000 8.0000 1.0000 1.0000>> A_inv = a(:,4:6)A*A_invD=[2,2,-1,1;4,3,-1,2;8,5,-3,4;3,3,-2,2]; %定义系数矩阵b=[4;6;12;6]; %定义常数项向量D1=[b,D(:,2:4)]; %用方程组的右端向量置换D的第1列D2=[D(:,1),b,D(:,3:4)]; %用方程组的右端向量置换D的第2列D3=[D(:,1:2),b,D(:,4:4)];%用方程组的右端向量置换D的第3列D4=[D(:,1:3),b];%用方程组的右端向量置换D的第4列DD=det(D);x1=det(D1)/DD;x2=det(D2)/DD;x3=det(D3)/DD;x4=det(D4)/DD;[x1,x2,x3,x4]A_inv =1.0000 4.0000 5.00002.0000 1.0000 2.00008.0000 1.0000 1.0000ans =1.0000 0.0000 0.00000 1.0000 0.00000 0.0000 1.0000ans =1.0000 1.0000 -1.0000 -1.0000>> D=[1,2,3,5;1,4,9,-2;1,8,27,6]; %定义系数矩阵b=[5;-2;6]; %定义常数项向量D1=[b,D(:,2:3)]; %用方程组的右端向量置换D的第1列D2=[D(:,1),b,D(:,3)]; %用方程组的右端向量置换D的第2列D3=[D(:,1:2),b];%用方程组的右端向量置换D的第3列DD=det(D);x1=det(D1)/DD;x2=det(D2)/DD;x3=det(D3)/DD;[x1,x2,x3]错误使用det矩阵必须为方阵。
>> D=[1,2,3;1,4,9,;1,8,27]; %定义系数矩阵b=[5;-2;6]; %定义常数项向量D1=[b,D(:,2:3)]; %用方程组的右端向量置换D的第1列D2=[D(:,1),b,D(:,3)]; %用方程组的右端向量置换D的第2列D3=[D(:,1:2),b];%用方程组的右端向量置换D的第3列DD=det(D);x1=det(D1)/DD;x2=det(D2)/DD;x3=det(D3)/DD;[x1,x2,x3]ans =23.0000 -14.5000 3.6667>>>> function [x,y]=line_solution(A,b)[m,n]=size(A);y=[];if norm(b)>0 %非齐次方程组if rank(A)==rank([A,b]) %方程组的相容性条件if rank(A)==n %有唯一解x=A\b;else %方程组有无穷多个解,基础解系disp('原方程组有有无穷个解,其齐次方程组的基础解系为y,特解为x');y=null(A,'r');x=A\b;endelse %方程组不相容,给出最小二乘解disp('方程组的最小二乘法解是:');x=A\b;endelse %齐次方程组if rank(A)==n %列满秩x=zeros(n,1) %0解else %非0解disp('方程组有无穷个解,基础解系为x');x=null(A,'r');endendfunction [x,y]=line_solution(A,b)|错误: 此上下文中不允许函数定义。
【实验结果分析及总结】1.当矩阵接近奇异值,结果可能不准确,应该尽量避免奇异值的出现以确保结论的准确性。
2.解方程组是输入的矩阵必须是方阵,否则结果会出错。
3.至于最后一个实验,实验时提示不允许函数定义,不知道指电脑所安装的Matlab版本问题还是怎么回事,在机房电脑能运行的,但是由于在机房的实验数据丢失,在重新在自己电脑上运行的时候出现了这种情况,没有找到原因。
4.向量运算以及矩阵运算等是解方程组的关键基础,我们应高熟练掌握。
