高三数学立体几何的综合与应用
2020高考数学解答题核心素养题型《专题07 立体几何综合问题》+答题指导)(解析版)

专题07 立体几何综合问题【题型解读】▶▶题型一 空间点、线、面的位置关系及空间角的计算(1)空间点、线、面的位置关系通常考查平行、垂直关系的证明,一般出现在解答题的第(1)问,解答题的第(2)问常考查求空间角,求空间角一般都可以建立空间直角坐标系,用空间向量的坐标运算求解.(2)利用向量求空间角的步骤:第一步:建立空间直角坐标系;第二步:确定点的坐标;第三步:求向量(直线的方向向量、平面的法向量)坐标;第四步:计算向量的夹角(或函数值);第五步:将向量夹角转化为所求的空间角;第六步:反思回顾.查看关键点、易错点和答题规范.【例1】 (2019·河南郑州高三联考)在如图所示的多面体中,四边形ABCD 是平行四边形,四边形BDEF是矩形,ED ⊥平面ABCD ,∠ABD =π6,AB =2AD . (1)求证:平面BDEF ⊥平面ADE ;(2)若ED =BD ,求直线AF 与平面AEC 所成角的正弦值.【答案】见解析【解析】(1)在△ABD 中,∠ABD =π6,AB =2AD ,由余弦定理,得BD =3AD ,从而BD 2+AD 2=AB 2,所以△ABD 为直角三角形且∠ADB =90°,故BD ⊥AD .因为DE ⊥平面ABCD ,BD ⊂平面ABCD ,所以DE ⊥BD .又AD ∩DE =D ,所以BD ⊥平面ADE .因为BD ⊂平面BDEF ,所以平面BDEF ⊥平面ADE .(2)由(1)可得,在Rt △ABD 中,∠BAD =π3,BD =3AD , 又由ED =BD ,设AD =1,则BD =ED = 3.因为DE ⊥平面ABCD ,BD ⊥AD ,所以可以点D 为坐标原点,DA ,DB ,DE 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示.则A (1,0,0),C (-1,3,0),E (0,0,3),F (0,3,3).所以AE →=(-1,0,3),AC →=(-2,3,0).设平面AEC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧ n ·A E →=0,n ·A C →=0,即⎩⎨⎧ -x +3z =0,-2x +3y =0,令z =1,得n =(3,2,1)为平面AEC 的一个法向量.因为A F →=(-1,3,3), 所以cos 〈n ,A F →〉=n ·A F →|n |·|A F →|=4214, 所以直线AF 与平面AEC 所成角的正弦值为4214. 【素养解读】本例问题(1)证明两平面垂直,考查了逻辑推理的核心素养;问题(2)计算线面所成的角时,考查了直观想象和数学运算的核心素养.【突破训练1】 (2018·北京卷)如图,在三棱柱ABC -A 1B 1C 1中,CC 1⊥平面ABC ,D ,E ,F ,G 分别为AA 1,AC ,A 1C 1,BB 1的中点,AB =BC = 5 ,AC =AA 1=2.(1)求证:AC ⊥平面BEF ;(2)求二面角B -CD -C 1的余弦值;(3)证明:直线FG 与平面BCD 相交.【答案】见解析【解析】(1)证明:在三棱柱ABC -A 1B 1C 1中,因为CC 1⊥平面ABC ,所以四边形A 1ACC 1为矩形.又E ,F 分别为AC ,A 1C 1的中点,所以AC ⊥EF .因为AB =BC .所以AC ⊥BE ,所以AC ⊥平面BEF .(2)由(1)知AC ⊥EF ,AC ⊥BE ,EF ∥CC 1.又CC 1⊥平面ABC ,所以EF ⊥平面ABC .因为BE ⊂平面ABC ,所以EF ⊥BE .如图建立空间直角坐称系Exyz .由题意得B (0,2,0),C (-1,0,0),D (1,0,1),F (0,0,2),G (0,2,1).所以CD →=(2,0,1),C B →=(1,2,0),设平面BCD 的法向量为n =(a ,b ,c ),所以⎩⎪⎨⎪⎧ n ·C D →=0,n ·C B →=0,所以⎩⎪⎨⎪⎧ 2a +c =0,a +2b =0.令a =2,则b =-1,c =-4,所以平面BCD 的法向量n =(2,-1,-4),又因为平面CDC 1的法向量为E B →=(0,2,0),所以cos 〈n ,E B →〉=n ·E B→|n ||EB →|=-2121. 由图可得二面角B -CD -C 1为钝二面角,所以二面角B -CD -C 1的余弦值为-2121. (3)证明:平面BCD 的法向量为n =(2,-1,-4),因为G (0,2,1),F (0,0,2),所以G F →=(0,-2,1),所以n ·G F →=-2,所以n 与G F →不垂直,所以GF 与平面BCD 不平行且不在平面BCD 内,所以GF 与平面BCD 相交. ▶▶题型二 平面图形折叠成空间几何体的问题1.先将平面图形折叠成空间几何体,再以其为载体研究其中的线、面间的位置关系与计算有关的几何量是近几年高考考查立体几何的一类重要考向,它很好地将平面图形拓展成空间图形,同时也为空间立体图形向平面图形转化提供了具体形象的途径,是高考深层次上考查空间想象能力的主要方向.2.(1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量.一般情况下,长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口.(2)在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图形,也要分析折叠前的图形.(3)解决翻折问题的答题步骤第一步:确定折叠前后的各量之间的关系,搞清折叠前后的变化量和不变量;第二步:在折叠后的图形中确定线和面的位置关系,明确需要用到的线面;第三步:利用判定定理或性质定理进行证明.【例2】 (2018·全国卷Ⅰ)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把△DFC 折起,使点C 到达点P 的位置,且PF ⊥BF .(1)证明:平面PEF ⊥平面ABFD ;(2)求DP 与平面ABFD 所成角的正弦值.【答案】见解析【解析】(1)证明:由已知可得,BF ⊥PF ,BF ⊥EF ,所以BF ⊥平面PEF .又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD .(2)作PH ⊥EF ,垂足为H .由(1)得,PH ⊥平面ABFD .以H 为坐标原点,HF →的方向为y 轴正方向,|B F →|为单位长,建立如图所示的空间直角坐标系Hxyz .由(1)可得,DE ⊥PE .又DP =2,DE =1,所以PE = 3.又PF =1,EF =2,故PE ⊥PF .可得PH =32,EH =32. 则H (0,0,0),P ⎝ ⎛⎭⎪⎫0,0,32,D ⎝ ⎛⎭⎪⎫-1,-32,0,D P →=⎝ ⎛⎭⎪⎫1,32,32,H P →=⎝ ⎛⎭⎪⎫0,0,32为平面ABFD 的法向量.设DP 与平面ABFD 所成角为θ,则sin θ=⎪⎪⎪⎪⎪⎪⎪⎪H P →·D P →|H P →|·|DP →|= 34 3=34. 所以DP 与平面ABFD 所成角的正弦值为34. 【素养解读】本例在证明或计算过程中都要考虑图形翻折前后的变化,因此综合考查了逻辑推理、数学运算、直观想象、数学建模的核心素养.【突破训练2】 如图1,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =1,AD =2,E 是AD 的中点,O 是AC 与BE 的交点,将△ABE 沿BE 折起到△A 1BE 的位置,如图2.(1)证明:CD ⊥平面A 1OC ;(2)若平面A 1BE ⊥平面BCDE ,求平面A 1BC 与平面A 1CD 所成锐二面角的余弦值.【答案】见解析【解析】(1)证明:在题图1中,因为AB =BC =1,AD =2,E 是AD 的中点∠BAD =π2,所以BE ⊥AC .即在题图2中,BE ⊥OA 1,BE ⊥OC ,从而BE ⊥平面A 1OC .又CD ∥BE ,所以CD ⊥平面A 1OC .(2)由已知,平面A 1BE ⊥平面BCDE ,又由(1)知,BE ⊥OA 1,BE ⊥OC .所以∠A 1OC 为二面角A 1-BE -C 的平面角,所以∠A 1OC =π2. 如图,以O 为原点,OB →,OC →,OA 1→分别为x 轴、y 轴、z 轴正方向建立空间直角坐标系,因为A 1B =A 1E =BC =ED =1,BC ∥ED ,所以B ⎝ ⎛⎭⎪⎫22,0,0,E ⎝ ⎛⎭⎪⎫-22,0,0,A 1⎝ ⎛⎭⎪⎫0,0,22,C ⎝ ⎛⎭⎪⎫0,22,0, 得BC →=⎝ ⎛⎭⎪⎫-22,22,0,A 1C →=⎝ ⎛⎭⎪⎫0,22,-22, CD →=BE →=(-2,0,0).设平面A 1BC 的一个法向量n 1=(x 1,y 1,z 1),平面A 1CD 的一个法向量n 2=(x 2,y 2,z 2),平面A 1BC 与平面A 1CD 的夹角为θ,则⎩⎪⎨⎪⎧ n 1·BC →=0,n 1·A 1C →=0,得⎩⎪⎨⎪⎧ -x 1+y 1=0,y 1-z 1=0,取n 1=(1,1,1); 由⎩⎪⎨⎪⎧ n 2·CD →=0,n 2·A 1C →=0,得⎩⎪⎨⎪⎧x 2=0,y 2-z 2=0,取n 2=(0,1,1), 从而cos θ=|cos 〈n 1,n 2〉|=23×2=63, 即平面A 1BC 与平面A 1CD 所成锐二面角的余弦值为63. ▶▶题型三 线、面位置关系中的探索性问题是否存在某点或某参数,使得某种线、面位置关系成立问题,是近几年高考命题的热点,常以解答题中最后一问的形式出现,解决这类问题的基本思路类似于反证法,即“在假设存在的前提下通过推理论证,如果能找到符合要求的点(或其他的问题),就肯定这个结论,如果在推理论证中出现矛盾,就说明假设不成立,从而否定这个结论”.【例3】 (2018·全国卷Ⅱ)如图,在三棱锥P -ABC 中,AB =BC =2 2 ,PA =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO ⊥平面ABC ; (2)若点M 在棱BC 上,且二面角M -PA -C 为30°,求PC 与平面PAM 所成角的正弦值.【答案】见解析【解析】(1)证明:因为AP =CP =AC =4,O 为AC 的中点,所以OP ⊥AC ,且OP =2 3.连接OB ,因为AB =BC =22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2. 由OP 2+OB 2=PB 2知PO ⊥OB .由OP ⊥OB ,OP ⊥AC 知PO ⊥平面ABC .(2)如图,以O 为坐标原点,OB →的方向为x 轴正方向,建立空间直角坐标系Oxyz .则O (0,0,0),B (2,0,0),A (0,-2,0),C (0,2,0),P (0,0,23),A P →=(0,2,23),取平面PAC 的一个法向量O B →=(2,0,0).设M (a,2-a,0)(0<a ≤2),则A M →=(a,4-a,0).设平面PAM 的法向量为n =(x ,y ,z ). 由A P →·n =0,A M →·n =0得⎩⎨⎧ 2y +23z =0,ax +(4-a)y =0,可取n =(3(a -4),3a ,-a ), 所以cos 〈O B →,n 〉=23(a -4)23(a -4)2+3a 2+a2.由已知得|cos 〈O B →,n 〉|=32. 所以23|a -4|23(a -4)2+3a 2+a2=32.解得a =-4(舍去),a =43. 所以n =⎝ ⎛⎭⎪⎫-833,433,-43.又P C →=(0,2,-23), 所以cos 〈P C →,n 〉=34.所以PC 与平面PAM 所成角的正弦值为34. 【素养解读】本例问题(1)中证明线面垂直直接考查了逻辑推理的核心素养;问题(2)中要探求点M 的位置,要求较高,它既考查了直观想象的核心素养,又考查了数学建模的核心素养.【突破训练3】 如图,在直三棱柱ABC -A 1B 1C 1中,平面A 1BC ⊥侧面ABB 1A 1,且AA 1=AB =2. (1)求证:AB ⊥BC ;(2)若直线AC 与平面A 1BC 所成的角为π6,请问在线段A 1C 上是否存在点E ,使得二面角A -BE -C 的大小为2π3,请说明理由.【答案】见解析【解析】(1)证明:连接AB 1交A 1B 于点D ,因为AA 1=AB ,所以AD ⊥A 1B ,又平面A 1BC ⊥侧面ABB 1A 1,平面A 1BC ⊂平面ABB 1A 1=A 1B ,所以AD ⊥平面A 1BC ,BC ⊂平面A 1BC ,所以AD ⊥BC .因为三棱柱ABC -A 1B 1C 1是直三棱柱,所以AA 1⊥底面ABC ,所以AA 1⊥BC ,又AA 1∩AD =A ,所以BC ⊥侧面ABB 1A 1,所以BC ⊥AB . (2)由(1)得AD ⊥平面A 1BC ,所以∠ACD 是直线AC 与平面A 1BC 所成的角,即∠ACD =π6,又AD =2,所以AC =22,假设存在适合条件的点E ,建立如图所示空间直角坐标系Axyz ,设A 1E →=λA 1C →(0≤λ≤1),则B (2,2,0),B 1(2,2,2),由A 1(0,0,2),C (0,22,0),得E (0,22λ,2-2λ),设平面EAB 的一个法向量m =(x ,y ,z ), 由⎩⎪⎨⎪⎧m ·AE →=0,m ·AB →=0,得⎩⎨⎧ 22λy +(2-2λ)z =0,2x +2y =0, 所以可取m =(1-λ,λ-1,2λ), 由(1)知AB 1⊥平面A 1BC ,所以平面CEB 的一个法向量n =(1,1,2), 所以12=⎪⎪⎪⎪⎪⎪cos 2π3=cos 〈m ,n 〉=m·n |m ||n |=2λ22(λ-1)2+2λ2,解得λ=12,故点E 为线段A 1C 中点时,二面角A -BE -C 的大小为2π3.。
高三理科数学立体几何复习专题
立体几何复习专题一、要求:(1)熟练掌握课本中的基本概念、定理。
(2)积累各种常见题型的解题方法:① 基本概念型题(直接证明、画图形举反例)② 证明类题:线面平行、线面垂直、面面平行、面面垂直。
③ 计算类题:异面直线所成角、线面角、面面角、点到面的距离、异面 直线间的距离、多面体的体积、球面距离。
(各自常用的方法是什么)(3)会用空间向量的方法去解决上述问题。
二、典型例题讲解例1. 如图,在直三棱柱111ABC A B C -中,1CC AC BC ==,90ACB ∠=︒,P 是1AA 的中点,Q 是AB 的中点.(1)求证: AB ⊥C 1CQ(2)求异面直线PQ 与1B C 所成角的大小; (3)求直线PQ 与面Q 1B C 所成角的正弦; (4)求二面角A 1-CQ-B 1的平面角的余弦。
例2.如图,在正方体ABCD —A 1B 1C 1D 1中, (1)在棱AD 上有一点P ,当P DP A为多少时,使二面角D 1-PC-D 的大小等于60°? (2)在(1)的条件下,求直线A 1B 1与平面CD 1P 所成的角.ABC1A 1B 1C PQ例3.如图,将长AA′=33,宽AA 1=3的矩形沿长的三等分线处折叠成一个三棱柱,如图所示:(1) 求平面APQ 与底面ABC 所成二面角的正切值; (2) 求三棱锥A 1—APQ 的体积.例4.如图,矩形ABCD 与ADQP 所在平面垂直,将矩形ADQP 沿PD 对折,使得翻折后点Q 落在BC 上,设AB=1,PA=h ,AD=y.(1)试求y 关于h 的函数解析式;(2)当y 取最小值时,指出点Q 的位置,并求出此时AD 与平面PDQ 所成的角; (3)在条件(2)下,求三棱锥P —ADQ 内切球的半径.三、巩固练习1、如图,已知面ABC ⊥面BCD ,AB ⊥BC ,BC ⊥CD ,且AB=BC=CD ,设AD 与面AB C 所成角为α,AB 与面ACD 所成角为β,则α与β的大小关系为(A )α<β (B )α=β (C )α>β (D )无法确定 2、下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面...的一个图是PP PPQ Q QQRRR R SSS SPPPPQQQQ RRRR SS SSPPPPQQQQ R RRR SSS S PPPPQQQQRRRR SSS S(A ) (B ) (C ) (D )3、在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,P ,Q 是对角线A 1C 上的点,且PQ =2a,则三棱锥P -BDQ 的体积为(A )3363a (B )3183a (C )3243a (D )无法确定 4、已知球的内接三棱锥的三条侧棱两两垂直,长度分别为3cm ,2cm 和3cm ,则此球的体积为(A )33312cm π (B )33316cm π (C )3316cm π (D )3332cm π5、如图,在一根长11cm ,外圆周长6cm 的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为(A ) 61cm (B )157cm (C )1021cm (D )1037cm6、设a 、b 是两条不同的直线,α、β是两个不同的平面,则下列四个命题:① 若b a ⊥,α⊥a ,α⊄b ,则α//b ;②若α//a , βα⊥,则β⊥a ; ③若β⊥a ,βα⊥,则α//a 或α⊂a ;④若b a ⊥,α⊥a ,β⊥b ,则βα⊥ 其中正确命题的个数为 ( )A .0B .1C .2D .37、正三棱锥ABC S —的侧棱长和底面边长相等,如果E 、F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成角为( ) A .090 B .060 C .045 D .030 8.右图是正方体的平面展开图,在这个正方体中: ①BM 与DE 平行; ②CN 与BE 是异面直线; ③CN 与BM 成60°角 ④DM 与BN 垂直以上四个命题中,正确的是 ( )A B C A BCAB CA BCP P P P A .①②③ B .②④ C .②③④ D .③④9.将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为( )A .π23 B .π32 C .6π D .34π 10.正方体ABCD -A 1B 1C 1D 1中,E 是BC 的中点,则A 1C 与DE 所成的角的余弦为( )A .1515 B .1510 C .630 D .1010 11.有3个命题(1)底面是正三角形,其余各个面都是等腰三角形的棱锥是三棱锥; (2)各个侧面都是等腰三角形的四棱锥是正四棱锥;(3)底面是正三角形,相邻两侧面所成的二面角都相等的三棱锥是正三棱锥。
高三数学二轮复习:立体几何

专题四 立体几何
第1讲 空间几何体
[考情考向分析]
1.以三视图为载体,考查空间几何体面积、体积的计算. 2.考查空间几何体的侧面展开图及简单的组合体问题.
内容索引
热点分类突破 真题押题精练
热规则 俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视 图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图 的宽度一样.即“长对正、高平齐、宽相等”. 2.由三视图还原几何体的步骤 一般先依据俯视图确定底面再利用正(主)视图与侧(左)视图确定几何体.
跟踪演练3 (1)(2018·咸阳模拟)在三棱锥P-ABC中,PA⊥平面ABC,
AB⊥BC,若AB=2,BC=3,PA=4,则该三棱锥的外接球的表面积为
A.13π C.25π
B.20π
√D.29π
解析 答案
(2)(2018·四川成都名校联考)已知一个圆锥的侧面积是底面积的2倍,
√ 记该圆锥的内切球的表面积为S1,外接球的表面积为S2,则SS12 等于
例3 (1)(2018·百校联盟联考)在三棱锥P-ABC中,△ABC和△PBC均为
边长为3的等边三角形,且PA=326 ,则三棱锥P-ABC外接球的体积为
13 13 A. 6 π
10 10 B. 3 π
√C.5
15 2π
55 D. 6 π
解析 答案
(2)(2018·衡水金卷信息卷)如图是某三棱锥的三视
跟踪演练1 (1)(2018·衡水模拟)已知一几何体的正(主)视图、侧(左)视 图如图所示,则该几何体的俯视图不可能是
√
解析 答案
(2)(2018·合肥质检)在正方体ABCD-A1B1C1D1中,E是棱 A1B1的中点,用过点A,C,E的平面截正方体,则位于 截面以下部分的几何体的侧(左)视图为
高中数学高考专题(5)立体几何的高考解答题型及求解策略

高中数学高考专题(5)立体几何的高考解答题型及求解策略立体几何的解答题型主要采用“论证与计算”相结合的模式,即首先是利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直,再计算几何体的体积.试题背景有折叠问题、探索性问题等,考查空间想象能力、逻辑思维能力及转化与化归思想的应用能力.题型一线面位置关系的证明题型概览:空间中线面的平行与垂直的证明有两种思路:一是利用相应的判定定理和性质定理去解决;二是利用空间向量法来论证,应用向量证明线、面的位置关系的关键是把空间线面位置关系的判定定理和性质定理与空间向量建立对应关系,把空间位置关系的证明转化为空间向量的运算,通过运算解决证明问题.这里以传统方法为例建立审题程序与答题模板,向量方法参照本专题题型二.如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN⊥平面ABCD,E、F分别为MA、DC的中点,求证:(1)EF∥平面MNCB;(2)平面MAC⊥平面BND.[审题程序]第一步:利用中位线、平行四边形的性质在四边形MNCB内确定与EF平行的直线;第二步:在平面MAC和平面BND中寻找与另一平面垂直的直线;第三步:应用面面垂直、菱形的性质,由线线垂直解决.[规范解答](1)如图,取NC的中点G,连接FG,MG.因为ME∥ND且ME=12ND,F、G分别为DC、NC的中点,FG∥ND且FG=12ND,所以FG与ME平行且相等,所以四边形MEFG是平行四边形,所以EF∥MG,又MG⊂平面MNCB,EF⊄平面MNCB,所以EF∥平面MNCB.(2)如图,连接BD、MC.因为四边形MADN是矩形,所以ND⊥AD.因为平面MADN⊥平面ABCD,平面ABCD∩平面MADN=AD,DN⊂平面MADN,所以ND⊥平面ABCD,所以ND⊥AC.因为四边形ABCD是菱形,所以AC⊥BD.因为BD∩ND=D,所以AC⊥平面BDN.又AC⊂平面MAC,所以平面MAC⊥平面BDN.[答题模板]解决这类问题的答题模板如下:1.(2016·北京西城区高三期末)如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE,CF的中点.(1)求证:AC⊥平面BDEF;(2)求证:平面BDGH∥平面AEF;(3)求多面体ABCDEF的体积.[解](1)证明:因为四边形ABCD是正方形,所以AC⊥BD.又平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,且AC⊂平面ABCD,所以AC⊥平面BDEF.(2)证明:在△CEF中,因为G,H分别是CE,CF的中点,所以GH∥EF.又GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面AEF.设AC∩BD=O,连接OH.在△ACF中,因为OA=OC,CH=HF,所以OH∥AF.因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF.因为OH∩GH=H,OH,GH⊂平面BDGH,所以平面BDGH∥平面AEF.(3)由(1)得AC⊥平面BDEF.因为AO=2,四边形BDEF的面积S▱BDEF=3×22=62,=4.所以四棱锥A-BDEF的体积V1=13×AO×S▱BDEF同理,四棱锥C-BDEF的体积V2=4.所以多面体ABCDEF的体积V=V1+V2=8.题型二求空间几何体的体积题型概览:计算几何体的体积,关键是根据条件找出相应的底面和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题.(1)直接法:对于规则几何体,直接利用公式计算即可.(2)割补法:当一个几何体的形状不规则时,常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体,然后再计算.经常考虑将三棱锥还原为三棱柱或长方体,将三棱柱还原为平行六面体,将台体还原为锥体.(3)等体积法:一般利用三棱锥的“等积性”求三棱锥体积,可以把任何一个面作为三棱锥的底面.注意两点:一是求体积时,可选择“容易计算”的方式来计算;二是利用“等积性”可求“点到面的距离”,关键是在面中选取三个点,与已知点构成三棱锥.(2016·全国卷Ⅲ)如图,四棱锥P-ABCD中,P A⊥底面ABCD,AD∥BC,AB=AD=AC=3,P A=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面P AB;(2)求四面体N-BCM的体积.[审题程序]第一步:由线线平行或面面平行证明(1);第二步:由N 为PC 中点,推证四面体N -BCM 的高与P A 的关系; 第三步:利用直接法求四面体的体积.[规范解答] (1)由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2.又AD ∥BC ,故TN 綊AM ,四边形AMNT 为平行四边形, 于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB , 所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A .取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5, 故S △BCM =12×4×5=2 5.所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. [答题模板] 解决这类问题的答题模板如下:2.(2016·深圳一模)如图所示,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧面SBC是正三角形,E是SB的中点,且AE⊥平面SBC.(1)证明:SD∥平面ACE;(2)若AB⊥AS,BC=2,求点S到平面ABC的距离.[解](1)证明:连接BD,交AC于点F,连接EF.∵四边形ABCD是平行四边形,∴F是BD的中点,又∵E是SB的中点,∴EF∥SD.∵SD⊄平面ACE,EF⊂平面ACE,∴SD∥平面ACE.(2)∵AB⊥AS,BC=BS=2,且E是SB的中点,∴AE=1.∵AE⊥平面SBC,BS、CE⊂平面SBC,∴AE⊥BS,AE⊥CE.∴AB=AE2+BE2= 2.又侧面SBC 是正三角形,∴CE =3, ∴AC =AE 2+CE 2=2,∴△ABC 是底边长为2,腰长为2的等腰三角形, ∴S △ABC =12×2×4-12=72.设点S 到平面ABC 的距离为h .由V 三棱锥S -ABC =V 三棱锥A -SBC ,得13h ·S △ABC =13AE ·S △SBC ,∴h =AE ·S △SBC S △ABC =237=2217.题型三 立体几何中的探索性问题题型概览:如果知道的是试题的结论,而要求的却是试题的某一个存在性条件(如存在某个定点、定直线、定值等),这种试题称为存在探索型试题.解题策略一般是先假设结论成立,然后以该结论作为一个已知条件,再结合题目中的其他已知条件,逆推(即从后往前推),一步一步推出所要求的特殊条件,即要求的存在性条件.若能求出,则存在;若不能求出,则不存在.(2016·石家庄调研)如图,在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,AC ⊥BC ,E 在线段B 1C 1上,B 1E =3EC 1,AC =BC =CC 1=4.(1)求证:BC ⊥AC 1;(2)试探究:在AC 上是否存在点F ,满足EF ∥平面A 1ABB 1?若存在,请指出点F 的位置,并给出证明;若不存在,请说明理由.[审题程序]第一步:由B 1E =3EC 1及EF ∥平面A 1ABB 1猜想点F 的位置;第二步:在平面A 1ABB 1内探求与EF 平行的直线或寻找经过EF 与平面A 1ABB 1平行的平面; 第三步:由线线平行或面面平行推理论证.[规范解答] (1)证明:∵AA 1⊥平面ABC ,BC ⊂平面ABC ,∴BC ⊥AA 1. 又∵BC ⊥AC ,AA 1∩AC =A ,∴BC ⊥平面AA 1C 1C . 又AC 1⊂平面AA 1C 1C ,∴BC ⊥AC 1.(2)解法一:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图1,在平面A1B1C1内过点E作EG∥A1C1交A1B1于点G,连接AG.∵B1E=3EC1,∴EG=34A1C1.又AF∥A1C1且AF=3,4A1C1∴AF∥EG且AF=EG,∴四边形AFEG为平行四边形,∴EF∥AG.又EF⊄平面A1ABB1,AG⊂平面A1ABB1,∴EF∥平面A1ABB1.解法二:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图2,在平面BCC1B1内过点E作EG∥BB1交BC于点G,连接FG. ∵EG∥BB1,EG⊄平面A1ABB1,BB1⊂平面A1ABB1,∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,∴FG∥AB.又AB⊂平面A1ABB1,FG⊄平面A1ABB1,∴FG∥平面A1ABB1.又EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面A1ABB1.∵EF⊂平面EFG,∴EF∥平面A1ABB1.[答题模板]解决这类问题的答题模板如下:3.如图,三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1⊥底面ABC,M为A1B1的中点.(1)证明:MC⊥AB;(2)若AA1=26,侧棱CC1上是否存在点P,使得MC⊥平面ABP?若存在,求PC的长;若不存在,请说明理由.[解](1)证明:取AB的中点N,连接MN,CN,则MN⊥底面ABC,MN⊥AB.因为△ABC是正三角形,所以NC⊥AB.因为MN∩NC=N,MN⊂平面MNC,NC⊂平面MNC,所以AB⊥平面MNC,所以AB⊥MC.(2)由(1)知MC⊥AB,若存在点P使得MC⊥平面ABP,则必有MC⊥BP.过M作MQ⊥B1C1,垂足为Q,连接QC,则QC是MC在平面BCC1B1内的射影,只需QC⊥BP即可,此时Rt△QC1C与Rt△PCB相似,QC1C1C =PCCB,所以PC=QC1·CBC1C=3×426=6,点P恰好是CC1的中点.。
高三数学一轮复习备考教学设计:高考中的立体几何问题说课稿

《高考中的立体几何问题》说课稿立体几何是高中数学知识体系的重要组成部分,是培养学生空间想象能力的重要载体,是每年高考必考的重要知识点!无论是从高考的现实出发,还是从学生个人的长远发展来看,学好立体几何这一模块的内容对于学生来说都是极为重要的。
在此,我仅从高考要求、命题趋势、考纲变化、复习意义四个方面来对立体几何模块谈谈我的看法。
一、高考要求1、空间几何体(1)认识柱、锥、台、球及其简单组合体的结构特征;(2)能画出简单空间图形的三视图,能识别相应三视图所表示的立体模型,会用斜二测画法画出他们的直观图;(3)会用平行投影方法画出简单空间图形的三视图与直观图,了解空间图形的不同表现形式;(4)了解球、棱柱、棱锥、台的表面积和体积的计算公式。
2、点、直线、平面之间的位置关系(1)理解空间直线、平面位置关系的定义,并了解四个公理及推论;(2)认识和理解空间中线面平行、垂直的有关性质与判定定理;(3)能够用公理、定理和已获得的结论证明一些空间位置关系的简单命题。
3、空间向量与立体几何(1)了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示;(2)掌握空间向量的线性运算及其坐标表示;(3)掌握空间向量的数量积及其坐标表示,能用向量数量积判断向量的共线与垂直;(4)理解直线的方向向量及平面的法向量;(5)能用向量语言表述线线、线面、面面的平行和垂直关系;(6)能用向量法证明立体几何中有关线面位置关系的一些简单定理;(7)能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究立体几何问题中的应用。
二、命题趋势通过分析最近5年全国卷在立体几何模块的命题可以发现如下规律:1、题型一般是两道小题一道大题(偶尔出现一道小题一道大题);2、小题中必考内容:三视图!三视图一般与特殊的柱体、锥体、球体及相关组合体的表面积与体积结合考查;3、小题中变化的内容:直线平面平行垂直的性质判定与命题结合、球的切接几何体问题、简单的空间角的计算等。
高三重点数学知识点:立体几何知识点总结

高三重点数学知识点:立体几何知识点总结
在高中复习阶段,大家一定要多练习题,掌握考题的规律,掌握常考的知识,这样有助于提高大家的分数。
编辑老师为大家整理了高三重点数学知识点,供大家参考。
1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决平行与垂直的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律--充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力。
2.判定两个平面平行的方法:
(1)根据定义--证明两平面没有公共点;
(2)判定定理--证明一个平面内的两条相交直线都平行于另一个平面;
(3)证明两平面同垂直于一条直线。
高中是人生中的关键阶段,大家一定要好好把握高中,编辑老师为大家整理了高三重点数学知识点,希望大家喜欢。
高三数学一轮专题4 高考中的立体几何问题(含解析)北师

专题四 高考中的立体几何问题1.如图,四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1)求证:CE ⊥平面PAD ;(2)若PA =AB =1,AD =3,CD =2,∠CDA =45°,求四棱锥P -ABCD 的体积.[解析] (1)∵PA ⊥底面ABCD ,CE 平面ABCD∴CE ⊥PA ,又∵AB ⊥AD ,CE ∥AB .∴CE ⊥AD .又∵PA ∩AD =A ,∴CE ⊥平面PAD .(2)由(1)可知CE ⊥AD .在Rt △ECD 中,DE =CD·cos45°=1,CE =CD·sin45°=1.又∵AB =CE =1,AB ∥CE ,所以四边形ABCE 为矩形.∴S 四边形ABCD =S 矩形ABCE +S △CDE =AB·AE +12CE·DE=1×2+12×1×1=52.又PA ⊥底面ABCD ,PA =1所以V 四棱锥p -ABCD =13S 四边形ABCD×PA =13×52×1=56.2.(2015·潍坊模拟)如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,AB =AD ,∠BAD =60°,E 、F 分别是AP 、AD 的中点.求证:(1)直线EF ∥平面PCD ;(2)平面BEF ⊥平面PAD .[证明] (1)在△PAD 中,因为E 、F 分别为AP 、AD 的中点,所以EF ∥PD .又因为E F ⃘平面PCD ,PD 平面PCD .所以直线EF ∥平面PCD .(2)连结BD .因为AB =AD ,∠BAD =60°,所以△ABD 为正三角形.因为F 是AD 的中点,所以BF ⊥AD .因为平面PAD ⊥平面ABCD ,BF平面ABCD,平面PAD∩平面ABCD=AD,所以BF⊥平面PAD.又因为BF平面BEF,所以平面BEF⊥平面PAD.3.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD、PC的中点,求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.[解析](1)因为平面PAD⊥底面ABCD,且PA垂直于这两个平面的交线AD,所以PA⊥底面ABCD.(2)因为AB∥CD,CD=2AB,E为CD的中点,所以AB∥DE,且AB=DE.所以四边形ABED为平行四边形.所以BE∥AD.又因为B E⃘平面PAD,AD平面PAD,所以BE ∥平面PAD .(3)因为AB ⊥AD ,而且四边形ABED 为平行四边形,所以BE ⊥CD ,AD ⊥CD .由(1)知PA ⊥底面ABCD .所以PA ⊥CD .所以CD ⊥平面PAD .所以CD ⊥PD .因为E 和F 分别是CD 和PC 的中点,所以PD ∥EF.所以CD ⊥EF ,又因为CD ⊥BE ,BE ∩EF =E ,所以CD ⊥平面BEF.所以平面BEF ⊥平面PCD .4.如图,在几何体P -ABCD 中,四边形ABCD 为矩形,PA ⊥平面ABCD ,AB =PA =2.(1)当AD =2时,求证:平面PBD ⊥平面PAC ;(2)若PC 与AD 所成的角为45°,求几何求P -ABCD 的体积.[解析] (1)证明:当AD =2时,四边形ABCD 是正方形,则BD ⊥AC .∵PA ⊥平面ABCD ,BD 平面ABCD ,∴PA ⊥BD .又∵PA ∩AC =A ,∴BD ⊥平面PAC .∵BD 平面PBD ,∴平面PBD ⊥平面PAC .(2)解:PC 与AD 成45°角,AD ∥BC ,则∠PCB =45°.∵BC ⊥AB ,BC ⊥PA ,AB ∩PA =A ,∴BC ⊥平面PAB ,PB 平面PAB .∴BC ⊥PB .∴∠CPB =90°-45°=45°.∴BC =PB =2 2.∴几何体P -ABCD 的体积为13×(2×22)×2=823.1.(2014·四川高考)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC ⊥BC ,证明:直线BC ⊥平面ACC1A1;(2)设D ,E 分别是线段BC ,CC1的中点,在线段AB 上是否存在一点M ,使直线DE ∥平面A1MC ?请证明你的结论.[解析] (1)因为四边形ABB1A1和ACC1A1都是矩形,所以AA1⊥AB ,AA1⊥AC .因为AB ,AC 为平面ABC 内两条相交直线,所以AA1⊥平面ABC .因为直线BC 平面ABC ,所以AA1⊥BC .又由已知,AC ⊥BC ,AA1,AC 为平面ACC1A1内两条相交直线,所以BC ⊥平面ACC1A1.(2)取线段AB 的中点M ,连接A1M ,MC ,A1C ,AC1,设O 为A1C ,AC1的交点. 由已知,O 为AC1的中点.连接MD ,OE ,则MD ,OE 分别为△ABC ,△ACC1的中位线,所以,MD 綊12AC ,OE 綊12AC ,因此MD綊OE.连接OM,从而四边形MDEO为平行四边形,则DE∥MO.因为直线D E⃘平面A1MC,MO平面A1MC.所以直线DE∥平面A1MC.即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.2.如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.(1)证明:AA1⊥BD;(2)证明:CC1∥平面A1BD.[解析](1)∵DD1⊥平面ABCD,BD平面ABCD∴DD1⊥BD,又∵AB=2AD且∠BAD=60°∴由余弦定理得BD2=AB2+AD2-2AB·ADcos∠BAD即BD=3AD,∴AD2+BD2=AB2,∴BD⊥AD又∵AD∩DD1=D∴BD⊥平面ADD1A1,又∵AA1平面ADD1A1,∴BD⊥AA1(2)连接AC,交BD于M,连接A1M,A1C1,∵底面ABCD 是平行四边形,∴AM =CM =12AC又∵AB =2AD =2A1B1∴A1G 綊CM ,即四边形A1MCC1是平行四边形;∴CC1∥AM1,又∵CC 1⃘平面A1BD ,A1M 平面A1BD∴CC1∥平面A1BD .3.(文)(2015·临沂模拟)如图,在边长为3的正三角形ABC 中,G ,F 为边AC 的三等分点,E ,P 分别是AB ,BC 边上的点,满足AE =CP =1,今将△BEP ,△CFP 分别沿EP ,FP 向上折起,使边BP 与边CP 所在的直线重合,B ,C 折后的对应点分别记为B1,C1.(1)求证:C1F ∥平面B1GE ;(2)求证:PF ⊥平面B1EF.[解析] (1)取EP 的中点D ,连接FD ,C1D .因为BC =3,CP =1,所以折起后C1为B1P 的中点.所以在△B1EP 中,DC1∥EB1.又因为AB =BC =AC =3,AE =CP =1,所以EP AC =EB AB ,所以EP =2且EP ∥GF.因为G ,F 为AC 的三等分点,所以GF =1.又因为ED =12EP =1,所以GF =ED ,所以四边形GEDF 为平行四边形.所以FD ∥GE.又因为DC1∩FD =D ,GE ∩B1E =E ,所以平面DFC1∥平面B1GE.又因为C1F 平面DFC1, 所以C1F ∥平面B1GE.(2)连接EF ,B1F ,由已知得∠EPF =60°,且FP =1,EP =2,由余弦定理,得EF2=12+22-2×1×2×cos60°=3,所以FP2+EF2=EP2,可得PF ⊥EF.因为B1C1=PC1=1,C1F =1,得FC1=B1C1=PC1,所以△PB1F 的中线C1F =12PB1,可得△PB1F 是直角三角形,即B1F ⊥PF.因为EF ∩B1F =F ,EF ,B1F 平面B1EF ,所以PF ⊥平面B1EF.(理)(2014·浙江高考)如图,在四棱锥A -BCDE 中,平面ABC ⊥平面BCDE ,∠CDE =∠BED =90°,AB =CD =2,DE =BE =1,AC = 2.(1)证明:DE ⊥平面ACD ;(2)求二面角B -AD -E 的大小.[解析] (1)在平面四边形BCDE 中,BC =2,在三角形ABC 中,AB=2,BC =2,AC = 2.根据勾股定理逆定理.∴AC ⊥BC .∵平面ABC ⊥平面BCOE ,而平面ABC ∩平面BCDE =BCAC ⊥BC ,∴AC ⊥平面BCDE ,∴AC ⊥DE ,又∵AC ⊥DE ,DE ⊥DC ,∴DE ⊥平面ACD .(2)由(1)知分别以CD →、CA →为x 轴、z 轴正方向.以过C 平行DE →为y 轴正向建立坐标系.则B(1,1,0),A(0,0,2),D(2,0,0),E(2,1,0)∴AB →=(1,1,-2),AD →=(2,0,-2),DE →=(0,1,0)设平面ABD 法向量n1=(x1,y1,z1),由n1·DE →=n1·AD →=0,解得n1=(1,1,2)设平面ADE 法向量n2=(x2,y2,z2),则n2·AE →=n2·AD →=0,解得:n2=(1,0,2)设平面ABD 与平面ADE 夹角为θ,cosθ=|cos 〈n1,n2〉|=1+0+22×3=32π∴平面ABD与平面ADE的二面角平面角为6.。
高三数学立体几何专题复习教案

(解题思想方法归纳)
问题一: 证明线线平行
1.证明两直线 、 平行,若直线 和直线 共面时,则可以用平面几何中常用的一些方法(如证明 和 是一个平行四边形的一组对边)证明它们无公共点。
在立体几何中一般还有以下几种思路:
①根据公理4
②根据“线面平行Байду номын сангаас的性质定理
③根据“线面垂直”的性质定理,若直线 和 都与平面 垂直,则 // 。
②利用中位法。如给出异面直线AB和CD,连接AC、AD、BC,然后再分别取这三条线段的中点E、F、G,连接EF、EG、FG得到△EFG,则∠FEG就是所求角或所求角的补角。这种方法优点是作异面直线所成角比较容易,但缺点是△EFG中有一边GF的长度不容易求。
3.向量方法:
转化成求两个向量的夹角(即等于所求的异面直线所成的角或其补角的大小)
2.向量方法:
①转化为证明向量共线。
②根据共面向量定理。
③证明向量与平面的法向量相互垂直。
问题三: 证明面面平行
1.传统几何方法:
①根据两个平面平行的定义
②根据两个平面平行的判定定理
③垂直于同一条直线的两个平面平行
④平行于同一平面的两个平面平行
2.思维过程:
线线平行 线面平行 面面平行
线线平行 线面垂直 面面平行
问题八: 求平面的斜线与平面所成角
1.传统几何方法:
①转化为求斜线与它在平面内的射影所成的角,通过直角三角形求解。
②利用三面角定理(即最小角定理) 求 。
2.向量方法:设 为平面 的法向量,直线 与平面 所成的角为 ,则
问题九: 求二面角
1.作出二面角的平面角并通过解三角形计算。作平面角常用方法如下:
高考数学最新真题专题解析—立体几何综合(新高考卷)

高考数学最新真题专题解析—立体几何综合(新高考卷)【母题来源】2022年新高考I卷【母题题文】已知正方体ABCD−A1B1C1D1,则()A. 直线BC1与DA1所成的角为90∘B. 直线BC1与CA1所成的角为90∘C. 直线BC1与平面BB1D1D所成的角为45∘D. 直线BC1与平面ABCD所成的角为45∘【答案】ABD【分析】本题主要考查直线与直线所成角及直线与平面所成角,属于中档题.【解答】解:如图,因为BC1⊥B1C,B1C//DA1,所以BC1⊥DA1,故A正确;对于选项B:因为直线BC1⊥平面CDA1B1,且CA1⊂平面CDA1B1,所以直线BC1⊥CA1,故B正确;对于选项C:连接A1C1与B1D1交于点O1,则∠O1BC1即为直线BC1与平面BB1D1D所成的角,sin∠O1BC1=O1C1BC1=12,所以∠O1BC1=30∘,故C错误;对于选项D:直线BC1与平面ABCD所成的角即为∠C1BC=45∘,所以D 正确.【母题来源】2022年新高考I卷【母题题文】如图,直三棱柱ABC−A1B1C1的体积为4,△A1BC的面积为2√2.(1)求A到平面A1BC的距离;(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A−BD−C的正弦值.【答案】解:(1)设A到平面A1BC的距离为d,因为直三棱柱ABC−A1B1C1的体积为4,即可得S△ABC·AA1=4,故V A1−ABC =13S△ABC·AA1=43,又V A1−ABC =V A−A1BC=13S△A1BC·d=13×2√2×d=43,解得d =√2,所以A 到平面A 1BC 的距离为√2;(2)连接AB 1,因为直三棱柱ABC −A 1B 1C 1中,AA 1=AB , 故AA 1B 1B 为正方形,即AB 1⊥A 1B ,又平面A 1BC ⊥平面ABB 1A 1,平面A 1BC ∩平面ABB 1A 1=A 1B ,AB 1⊂平面ABB 1A 1, 故AB 1⊥平面A 1BC ,所以AB 1⊥BC ,又因为AA 1⊥BC ,AB 1,AA 1⊂平面ABB 1A 1,且AB 1∩AB 1=A , 故BC ⊥平面ABB 1A 1,则BC ⊥AB , 所以BB 1,AB,BC 三条直线两两垂直, 故如图可以以B 为原点建立空间直角坐标系,设AA 1=AB =a ,BC =b ,则A 1B =√2a ,由条件可得{12a ×b ×a =412×√2a ×b =2√2,解得{a =2b =2, 则B(0,0,0),C(2,0,0),A(0,2,0),A 1(0,2,2),A 1C 的中点D(1,1,1), 所以BA ⃗⃗⃗⃗⃗ =(0,2,0),BD ⃗⃗⃗⃗⃗⃗ =(1,1,1),BC ⃗⃗⃗⃗⃗ =(2,0,0) 设平面ABD 的一个法向量为n 1⃗⃗⃗⃗ =(x,y,z),{n1⃗⃗⃗⃗ ⋅BA⃗⃗⃗⃗⃗ =0n1⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ =0⇒{2y=0x+y+z=0,取n1⃗⃗⃗⃗ =(1,0,−1),同理可求得平面BCD的一个法向量为n2⃗⃗⃗⃗ =(0,1,−1)所以|cos<n1⃗⃗⃗⃗ ,n2⃗⃗⃗⃗ >|=|n1⃗⃗⃗⃗⃗ ·n2⃗⃗⃗⃗⃗ ||n1⃗⃗⃗⃗⃗ |·|n2⃗⃗⃗⃗⃗ |=12,所以二面角A−BD−C的正弦值为√32.【母题来源】2022年新高考II卷【母题题文】如图,四边形ABCD为正方形,ED⊥平面ABCD,FB//ED,AB=ED=2FB,记三棱锥E−ABC,E−ACF,F−ABC的体积分别为V1,V2,V3,则()A. V3=2V2B. V3=2V1C. V3=V1+V2D. 2V3=3V1【答案】CD【解析】【分析】本题主要考查三棱锥的体积,属于基础题.【解答】解:设AB=ED=2FB=2,则V1=13×2×2=43,V2=13×2×1=23.连结BD交AC于M,连结EM、FM,则FM=√3,EM=√6,EF=3,故S△EMF=1 2⋅√3⋅√6=3√22,V3=13S△EMF×AC=2,V3=V1+V2,2V3=3V1.【母题来源】2022年新高考II卷【母题题文】如图,PO是三棱锥P−ABC的高,PA=PB,AB⊥AC,E是PB的中点.(1)证明:OE//平面PAC;(2)若∠ABO=∠CBO=30∘,PO=3,PA=5,求二面角C−AE−B正弦值.【答案】解:(1)法一:连接OA、OB,因为PO是三棱锥P−ABC的高,所以PO⊥平面ABC,所以PO⊥OA,PO⊥OB,所以∠POA=∠POB=90∘,又PA=PB,PO=PO,所以△POA≌△POB,所以OA=OB,作AB中点D,连接OD、DE,则有OD⊥AB,又AB⊥AC,所以OD//AC,又因为OD⊄平面PAC,AC⊂平面PAC,所以OD//平面PAC,又D、E分别为AB、PB的中点,所以,在△BPA中,DE//PA又因为平面PAC,PA⊂平面PAC,所以DE//平面PAC,又OD、DE⊂平面ODE,OD∩DE=D,所以平面ODE//平面PAC,又OE⊂平面ODE,所以OE//平面PAC;法二:(1)连接OA、OB,因为PO是三棱锥P−ABC的高,所以PO⊥平面ABC,所以PO⊥OA,PO⊥OB,所以∠POA=∠POB=90∘,又PA=PB,PO=PO,所以△POA≌△POB,所以OA=OB,又AB⊥AC,在Rt△ABF,O为BF中点,延长BO,交AC于F,连接PF,所以在△PBF中,O、E分别为BF、PB的中点,所以EO//PF,因为EO⊄平面PAC,PF⊂平面PAC,所以EO//平面PAC;(2)法一:过点D作DF//OP,以DB为x轴,DO为y轴,DF为z轴.建立如图所示的空间直角坐标系.因为PO=3,PA=5,由(1)OA=OB=4,又∠ABO=∠CBO=30∘,所以OD=2,DB=2√3,),所以P(0,2,3),B(2√3,0,0),A(−2√3,0,0),E(√3,1,32设AC=a,则C(−2√3,a,0),平面AEB的法向量设为n1⃗⃗⃗⃗ =(x1,y1,z1),直线AB的方向向量可设为a⃗=(1,0,0),直线DP⊂平面AEB,直线DP的方向向量为b⃗ =(0,2,3){a ⃗ ⋅n 1⃗⃗⃗⃗ =0b ⃗ ⋅n 1⃗⃗⃗⃗ =0,所以{x 1=02y 1+3z 1=0,所以x 1=0,设y 1=3,则z 1=−2,所以n 1⃗⃗⃗⃗ =(0,3,−2);平面AEC 的法向量设为n 2⃗⃗⃗⃗ =(x 2,y 2,z 2),AC ⃗⃗⃗⃗⃗ =(0,a,0),AE ⃗⃗⃗⃗⃗ =(3√3,1,32) {AC ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0AE ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0,所以{ay 2=03√3x 2+y 2+32z 2=0,所以y 2=0,设x 2=√3,则z 2=−6,所以n ⃗ =(√3,0,−6);所以cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >=n 1⃗⃗⃗⃗⃗ ·n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ |=√13×√39=13√3=4√313, 二面角C −AE −B 的平面角为θ,则sinθ=√1−cos 2θ=1113, 所以二面角C −AE −B 的正弦值为1113法二:(2)过点A 作AF//OP ,以AB 为x 轴,AC 为y 轴,AF 为z 轴 建立所示的空间直角坐标系.因为PO =3,PA =5,由(1)OA =OB =4,又∠ABO =∠CBO =30°,所以,AB =4√3,所以P(2√3,2,3),B(4√3,0,0), A(0,0,0),E(3√3,1,32),设AC =a ,则C(0,a,0),平面AEB 的法向量设为n 1⃗⃗⃗⃗ =(x 1,y 1,z 1),AB ⃗⃗⃗⃗⃗ =(4√3,0,0),AE ⃗⃗⃗⃗⃗ =(3√3,1,32) {AB ⃗⃗⃗⃗⃗ ⋅n 1⃗⃗⃗⃗ =0AE ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0,所以{4√3x 1=03√3x 1+y 1+32z 1=0,所以x 1=0设z 1=−2,则y 1=3, 所以n 1⃗⃗⃗⃗ =(0,3,−2);平面AEC 的法向量设为n 2⃗⃗⃗⃗ =(x,y,z),AC ⃗⃗⃗⃗⃗ =(0,a,0),AE ⃗⃗⃗⃗⃗ =(3√3,1,32) {AC ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0AE ⃗⃗⃗⃗⃗ ⋅n 2⃗⃗⃗⃗ =0,所以{ay 2=03√3x 2+y 2+32z 2=0,所以y 2=0,设x 2=√3,则z 2=−6,所以n 2⃗⃗⃗⃗ =(√3,0,−6);所以cos <n 1⃗⃗⃗⃗ ,n 2⃗⃗⃗⃗ >=n 1⃗⃗⃗⃗⃗ ·n 2⃗⃗⃗⃗⃗ |n 1⃗⃗⃗⃗⃗ |⋅|n 2⃗⃗⃗⃗⃗ |=√13×√39=√1213√3=4√313二面角C −AE −B 的平面角为θ,则sinθ=√1−cos 2θ=1113, 所以二面角C −AE −B 的正弦值为1113. 【命题意图】考察棱柱、棱锥棱台、圆柱、圆锥、圆台及其简单组合体的结构特征,能画出简单空间图形并能识别立体图形的模型,考察几何体中的点线面关系,考察线线、线面、面面之间的平行和垂直关系,考察异面直线所成的角,直线和平面所成的角,二面角的平面角等的求解,考察数形结合思想,空间想象力及逻辑推导能力。
高三数学第一轮复习立体几何的综合问题知识精讲

高三数学第一轮复习:立体几何的综合问题【本讲主要内容】立体几何的综合问题立体几何知识的综合应用及立体几何与其它知识点的综合问题【知识掌握】【知识点精析】1. 立体几何的综合问题融直线和平面的位置关系于平面与几何体中,有计算也有论证。
解决这类问题需要系统地掌握线线、线面、面面的位置关系,特别是平行与垂直的判定与性质.深刻理解异面直线所成的角、斜线与平面所成的角、二面角的平面角的概念,理解点到面的距离、异面直线的距离的概念.2. 立体几何横向可与向量、代数、三角、解析几何等综合.3. 应用性问题、探索性问题需综合运用所学知识去分析解决.【解题方法指导】例1. 如图所示,在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为()解析:P到直线BC的距离等于P到B的距离,动点P的轨迹满足抛物线定义.故选C.例2. 如图,四棱锥P-ABCD的底面是边长为a的正方形,PB⊥平面ABCD,(Ⅰ)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;(Ⅱ)证明不论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.(Ⅰ)解:∵PB⊥面ABCD,∴BA是PA在面ABCD上的射影,又DA⊥AB ∴PA⊥DA∴∠PAB是面PAD与面ABCD所成的二面角的平面角∴∠PAB=60°,PB=AB·tan60°=3a ,∴ V 锥=3233·3·31a a a =(Ⅱ)证明:不论棱锥的高怎样变化,棱锥侧面PAD 与PCD 恒为等腰三角形,作AE ⊥PD ,垂足为E ,连结CE ,则△ADE ≌△CDE ,因为AE =CE ,∠CED =90o,故∠CEA 是面PAD 与面PCD 所成的二面角的平面角. 设AC 与BD 交于点O ,连结EO ,则EO ⊥AC ,所以a AD AE OA a =<<=22,22a AE <, 在△AEC 中,02222cos 222222222<-=-=∙-+=∠AE a AE AE a AE EC AE AC EC AE CEA 所以面PAD 与面PCD 所成的二面角恒大于90o。
高中数学立体几何学习方法有哪些

高中数学立体几何学习方法有哪些高中数学立体几何学习方法有哪些立体几何的证明是数学学科中任一分之也替代不了的。
因此,历年高考中都有立体几何论证的考察。
论证时,首先要保持严密性,对任何一个定义、定理及推论的理解要做到准确无误。
所以学好立体几何要找到对的学习方法,下面是小编分享给大家的高中数学立体几何的学习方法的资料,希望大家喜欢!高中数学立体几何的学习方法一、逐渐提高逻辑论证能力论证时,首先要保持严密性,对任何一个定义、定理及推论的理解要做到准确无误。
符号表示与定理完全一致,定理的所有条件都具备了,才能推出相关结论。
切忌条件不全就下结论。
其次,在论证问题时,思考应多用分析法,即逐步地找到结论成立的充分条件,向已知靠拢,然后用综合法(“推出法”)形式写出。
二、立足课本,夯实基础直线和平面这些内容,是立体几何的基础,学好这部分的一个捷径就是认真学习定理的证明,尤其是一些很关键的定理的证明。
例如:三垂线定理。
定理的内容都很简单,就是线与线,线与面,面与面之间的关系的阐述。
但定理的证明在出学的时候一般都很复杂,甚至很抽象。
掌握好定理有以下三点好处:(1)深刻掌握定理的内容,明确定理的作用是什么,多用在那些地方,怎么用。
(2)培养空间想象力。
(3)得出一些解题方面的启示。
在学习这些内容的时候,可以用笔、直尺、书之类的东西搭出一个图形的框架,用以帮助提高空间想象力。
对后面的学习也打下了很好的基础。
三、“转化”思想的应用我个人觉得,解立体几何的问题,主要是充分运用“转化”这种数学思想,要明确在转化过程中什么变了,什么没变,有什么联系,这是非常关键的。
例如:(1)两条异面直线所成的角转化为两条相交直线的夹角即过空间任意一点引两条异面直线的平行线。
斜线与平面所成的角转化为直线与直线所成的角即斜线与斜线在该平面内的射影所成的角。
(2)异面直线的距离可以转化为直线和与它平行的平面间的距离,也可以转化为两平行平面的距离,即异面直线的`距离与线面距离、面面距离三者可以相互转化。
高三数学立体几何与概率统计的应用与解题策略

高三数学立体几何与概率统计的应用与解题策略立体几何与概率统计是高中数学中重要的两个分支,这两个部分的应用范围广泛,同时也是高考中常见的考点。
在高三阶段,学生需要充分掌握立体几何和概率统计的相关知识,并了解一些解题策略,以应对各类难题。
本文将探讨高三数学中立体几何与概率统计的应用和解题策略。
一、立体几何的应用立体几何是研究空间内的图形、体积和距离关系的一门学科。
在高三数学中,立体几何被广泛应用于各类几何证明、计算和问题求解中。
以下是几个常见的立体几何应用情景。
1. 体积计算:在考试中,经常会出现计算各种几何体的体积的题目。
例如,计算长方体、正方体、圆柱体、圆锥体、球体等的体积。
解决这类题目的关键是熟悉各种几何体的体积计算公式,并应用合适的方法进行计算。
2. 空间距离计算:在解决空间中点、直线和平面的位置关系问题时,需要计算各点之间的距离。
通过运用勾股定理或利用投影定理等方法,可以准确计算出空间中点与点、点与线、点与平面之间的距离。
这种应用在空间几何证明和解题中经常出现。
3. 空间几何证明:利用立体几何的相关知识,可以进行空间中图形的剖分和证明。
例如,证明平面和直线的垂直、平行关系,证明四面体的各边或各面之间的关系等。
在应用立体几何进行证明时,需要熟练掌握各种几何定理和推理思路。
二、概率统计的应用概率统计是研究一种事情发生可能性的大小以及数据的收集、整理和分析的数学分支。
在现实生活中,概率统计应用广泛,如市场调研、民意调查等。
在高三数学中,概率统计也是考试中的重点,以下是几个常见的概率统计应用情景。
1. 随机事件的概率计算:在解答概率题时,常常需要计算随机事件的概率。
对于简单的问题,可以利用概率计算公式进行计算;对于复杂的问题,需要灵活应用概率的性质和技巧,例如利用排列组合、条件概率等方法。
2. 数据收集与整理:在统计学中,收集数据是非常重要的一环。
在高考试卷中,会出现一些数据收集的题目,要求学生根据给定的条件,运用问卷调查、抽样调查等方法,收集和整理相关数据。
立体几何实际问题

立体几何实际问题
立体几何在实际生活中有着广泛的应用。
以下是一些常见的立体几何问题:
1. 建筑学:在建筑设计中,立体几何被用来构建和描述各种形状和结构,如柱子、墙壁、天花板、楼梯等。
设计师需要了解立体几何的基本原理,以确保结构的稳定性和安全性。
2. 工程学:在机械工程、航空航天工程和水利工程等领域,立体几何被用来设计和分析各种零件、设备和结构。
工程师需要了解立体几何的知识,以确保产品的功能和安全性。
3. 计算机图形学:在计算机图形学中,立体几何被用来描述和模拟三维形状和场景。
在游戏开发、电影制作、虚拟现实等领域,立体几何的应用越来越广泛。
4. 物理学:在物理学中,立体几何被用来描述和解释引力、电磁场、量子力学等领域的现象。
在物理学中,了解立体几何的基本原理可以帮助我们更好地理解物理现象的本质。
5. 数学:在数学中,立体几何是研究三维空间中的形状、曲线和曲面的学科。
在数学中,了解立体几何的基本原理可以帮助我们更好地理解数学概念的本质。
总之,立体几何在实际生活中有着广泛的应用,了解立体几何的基本原理可以帮助我们更好地解决各种实际问题。
高三数学复习(文科)立体几何知识点、方法总结
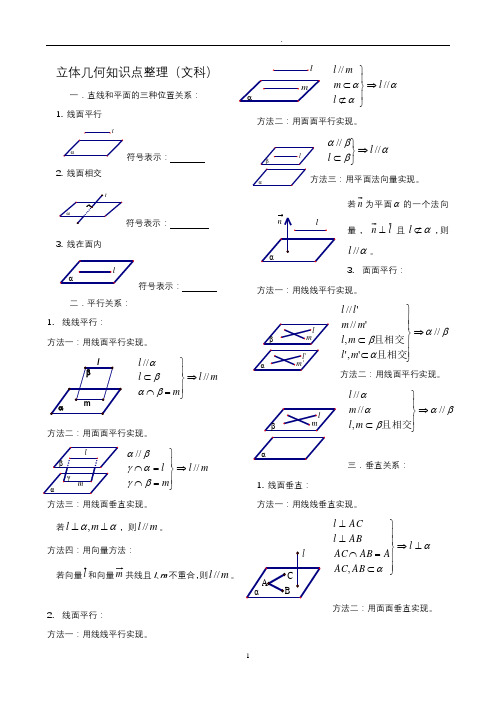
立体几何知识点整理(文科)一.直线和平面的三种位置关系:1. 线面平行符号表示:2. 线面相交符号表示:3. 线在面内符号表示:二.平行关系:1.线线平行:方法一:用线面平行实现。
mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法二:用面面平行实现。
mlml////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα方法三:用线面垂直实现。
若αα⊥⊥ml,,则ml//。
方法四:用向量方法:若向量l和向量m共线且l、m不重合,则ml//。
2.线面平行:方法一:用线线平行实现。
ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂方法二:用面面平行实现。
αββα////ll⇒⎭⎬⎫⊂方法三:用平面法向量实现。
若n为平面α的一个法向量,ln⊥且α⊄l,则α//l。
3.面面平行:方法一:用线线平行实现。
βααβ//',','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll方法二:用线面平行实现。
βαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:方法一:用线线垂直实现。
αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,方法二:用面面垂直实现。
llαββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m ,2. 面面垂直:方法一:用线面垂直实现。
βαβα⊥⇒⎭⎬⎫⊂⊥l l方法二:计算所成二面角为直角。
3. 线线垂直:方法一:用线面垂直实现。
m l m l ⊥⇒⎭⎬⎫⊂⊥αα方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭方法三:用向量方法:若向量l 和向量m 的数量积为0,则m l ⊥。
三.夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(︒︒ (2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理)余弦定理:abcb a 2cos 222-+=θ(计算结果可能是其补角)方法二:向量法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.四面体的一条棱长是x,其他 各条棱长为1.(1)把四面体的 体积V表示为x的函数f(x); (2)求f(x)的值域; (3)求f(x)的单调区间.
【解题回顾】本题(1)也可以用V=VB-SAD+VC-SAD求体积, (2)也可以对根号里的x2·(3-x2)求导得最大值, (3)当然可以考察导函数的符号定区间
4.如图,在直三棱柱ABC-A1B1C1中, 底面是等腰直角三角形,∠ACB=90° 侧棱AA1=2,D、E分别是CC1与A1B的 中点,点E在平面ABD上的射影是 △ABD的重心G.(1)求A1B与平面ABD 所成角的大小 (结果用反三角函数 值表示): (2)求点A1到平面AED的距离.
延伸·拓展
能力·思维·方法
1. 在直角坐标系 xoy 中,点A 、B 、C 、D的坐标分别为 (5,0)、(-3,0)、(0,-4)、(-4,-3), 将坐标平面沿y轴折成直二面角. (1)求AD、BC所成的角; (2)BC、OD相交于E,作 EF⊥AD于F, 求证:EF是AD、BC的公垂 线,并求出公垂线段EF的长; (3)求四面体C-AOD的体积. 【解题回顾】这是一道与解几结合的翻折题,画好折后 图将原平面图还原成四棱锥,进一步用三垂线定 理证明A纸片(如图1,图2), 要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼 成一个正三棱柱模型,使它们的全面积都与原三角形的 面积相等,请设计一种剪拼方法,分别用虚线标示在图 1、图2中,并作简要说明; (2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小; (3)(本小题为附加题) 如果给出的是一块任意三角形的纸片(如图3),要求 剪拼成一个直三棱柱模型,使它们的全面积与给出的三 角形的面积相等,请设计一种剪拼方法,用虚线标示在 图3中,并作简要说明.
B
B1 C A
【例3】 (2004年春季北京)如图,四棱锥S—ABCD
的底面是边长为1的正方形,SD垂直于底面ABCD,
SB=
3,
(1)求证:BC⊥SC; (2)求面ASD与面BSC所成二面角的大小; (3)设棱SA的中点为M,求异面直线DM与SB所成 角的大小.
M S
D
C
A
B
课前热身
1.一个立方体的六个面上分别标有字母 A、B、C、D、 F ,下图是此立方体的两种不同放置,则与 D 面相对 的面上的字母是 ( B )
2010届高考数学复习 强化双基系列课件
57《立体几何- 立体几何的综合与应用》
【教学目标】
1、初步掌握“立几”中“探索性”“发 散性”等问题的解法 2、提高立体几何综合运用能力,能正确 地分析出几何体中基本元素及其相互关 系,能对图形进行分解、组合和变形。
要点·疑点·考点
1. 初步掌握“立体几何”中“探索性”“发散性” 等命题的解法。
2.如图,以长方体ABCD-A1B1C1D1的顶点为顶点且四 A 1 - ABC 等 个面都是直角三角形的四面体是__________ ( 注:只写出其中的一个,并在图中画出相应的四面 体)
3.一间民房的屋顶有如图所示三种不同的盖法:①单 向倾斜;②双向倾斜;③四向倾斜. 记三种盖法屋顶面积分别为P1、P2、P3.若屋顶斜面与 水平面所成的角都是α ,则 ( D ) (A)P3>P2>P1 (B)P3>P2=P1 (C)P3=P2>P1 (D)P3=P2=P1
4.如图是正方体的平面展开图,在这个正方体中,① BM∥ED;②CN与BE是异面直线;③CN与BM成60°角; ④DM⊥BN以上四个命题中正确的序号是 ( D ) (A)①②③ (B)②④ (C)②③④ (D)③④
返回
5.已知甲烷CH4的分子结构是:中心一个碳原子,外围 有4个氢原子(这4个氢原子构成一个正四面体的四个顶 点).设中心碳原子到外围4个氢原子连成的四条线段两 两组成的角为θ ,则cosθ 等于 ( A) (A)-13 (B)13 (C)-12 (D)12
2. 在棱长为 a 的正方体 ABCD-A1B1C1D1 中, E 、 F 分别是 棱 AB 与 BC 的中点, (1) 求二面角 B-FB1-E 的大小; (2) 求点D到平面B1EF的距离;(3)在棱DD1上能否找一点M, 使BM⊥平面 EFB. 若能,试确定点 M 的位置,若不能, 请说明理由. 【解题回顾】此题也可以作面B1EF的垂线与DD1相交,再 说明可以找到一点M满足条件.过程如下:先证明面B1BDD1 ⊥面B1EF,且面B1BDD1∩面B1EF=B1G,在平面B1BDD1内作BM ⊥B1G,延长交直线DD1于M,由二平面垂直的性质可得: BM⊥面B1EF,再通过△B1BG∽△BDM可得M是DD1的中点, ∴在棱上能找到一点M满足条件. 此题是一道探索性命题.往往可先通过对条件的分析,猜 想出命题的结论,然后再进行证明.
2. 解应用题时,一定要注意审题,找出问题后面的图 形模型,将其转化为熟悉的几何体求解.
返回
; 广州私家侦探 广州私人侦探
dvh06eyc
色如新春刚抽的柳枝,翠中含金缕,黑子则如盛春满蓄的江水,蓝得发碧,质地为上等瑙、珀,加工技艺精湛绝伦,正是玩棋人所谓“云子”。 这一坛云子,包浆温润自然,叩之玉质金声,是难得一遇的古云子。若非唐静轩亲至,恪思阁绝不肯献宝。明柯进得门来,几个伙计从另一边也 把扬琴也抬到了。唐静轩令云子落回瓷坛,将瓷坛搁回桌上,起身迎明柯。伙计们把扬琴安放了之后,就识趣的退出去了。唐静轩凝视明柯: “她有回应吗?”明柯笑道:“你何不自己看看?”唐静轩就去摸琴身上的暗格,手法很熟练。这本来就是他自己拥有的古琴、是他发现的暗格。 手指伸进去,指尖立即触到一张纸。唐静轩的心沉下去,手指也抖了。他放进去的,就是一张纸。她不肯接受,所以退回给他?幸好他并没有把 手缩回去,指尖继续往前,明确无误的告诉他:这是一、张、纸。而他原先放进去的,确切说,是一封纸笺,厚薄与质地,是不一样的。唐静轩 的手还在抖,心却飞了起来。你如果没有在十七、八岁的时候爱上过一个女孩子,就绝想像不出好好一颗心怎么可以飞得那么高,那么高又是什 么样的感受。第四十章 梅香惹人约黄昏(2)唐静轩给明秀那封信笺里,写的是他的真实情感。从去年元夜之后,他就觉得自己在恋爱了。可他要 用三个月的时间抵制这奇怪的感情,三个月的时间发现这感情是恋爱,再用三个月的时间,去猜疑她是不是也爱他、他要用什么法子去问她。他 现在取出了这张纸。桑皮黑纸,还不到一个巴掌大,裁得整整齐齐,上头没有字迹、没有刻痕,什么都没有。唐静轩微微仰起脸,闭起眼睛,把 黑纸蒙在脸上,没有直接挨到,隔那么一点点。当女孩子挑选胭脂纸,想闻闻它的香气时,这是很正确的一种手法。他闻见了香气,横斜水清浅, 浮动月黄昏。梅香。那年元夜,月色如银,金吾不禁。人间诸般繁华灯火,隔了半个山头看,洒了一层银霜,仿佛也宁谥了。他在最热闹不堪的 佳节,爬上连最简单的六角琉璃灯都没有一盏的冷清山头,抱膝孤坐,回头去看夜市的灯火,以为这份情怀唯己独有,想不到又来了两个人。两 个女孩子,没有挑灯,其中一个娇滴滴抱怨:“表姊,怎的不命人多点些灯火来?”唐静轩听出这声音是他的堂姨,福珞。福珞这小家伙,年纪 虽不大,沾了母亲的光,辈份比他高了整整一层。福珞口中的表姊是谁呢?一堂已经三千里、一表又是三千里,这位“表姊”很可能已经不属于 他的亲属范畴了。他听到“表姊”回答说:“珞儿,你看月明如水,点起灯来,岂不乱了月色?要灯,夜市里尽有。你且立此处回头看,那些繁 华不堪的灯火,隔了这段距离,是不是被涤得净了?”唐静轩心里当时就“噔”的一下。他自己心底的话,从另一个人嘴里说出
2。提高立体几何综合运用能力。能正确地分析出几 何体中基本元素及其相互关系。能对图形进行分解、 组合和变形。
3。能用立体几何知识解决生活中的问题。
返回
点击双基
1.若Rt△ABC的斜边BC在平面α内,顶点A在α外, D 则△ABC在α上的射影是 A.锐角三角形 B.钝角三角形 C.直角三角形 D.一条线段或一钝角三角形
2.长方体AC1的长、宽、高分别为3、2、1,从A到C1沿 长方体的表面的最短距离为 D1 C C1 A.
1 3
B.
2 10
A1 D A 2 1
B1 C 3 B
C.
D.
3 2 2 3
3.设长方体的对角线长为4,过每个顶点的三条棱中总 有两条棱与对角线的夹角为60°,则长方体的体积是 A. 27 2 B.
AB =(1,0,0), OC =(2,0,0),OS =( 0,
OA =(0,1,0),
SC与 OB
的夹角α的大小;
(2)设n=(1,p,q),且n⊥平面SBC,求n; (3)求OA与平面SBC的夹角;
(4)求点O到平面SBC的距离;
(5)求异面直线SC与OB间的距离.
【例2】 如图,已知一个等腰三角形ABC的顶角 B=120°,过AC的一个平面α与顶点B的距离为1,根 据已知条件,你能求出AB在平面α上的射影AB1的长 吗?如果不能,那么需要增加什么条件,可以使AB1=2?
8 2
C.
8 3 D.16
B
4.棱长为a的正方体的各个顶点都在一个球面上,则 这个球的体积是____________
3π 3 a 2
5.已知△ABC的顶点坐标为A(1,1,1)、
B(2,2,2)、C(3,2,4),则△ABC的面积 是_____________.
6 2
典例剖析
【例1】在直角坐标系O—xyz中, 0, 1) . (1)求
图1
图2
【解题回顾】本题是2002年高考题,是一道集开放、 探索、动手于一体的优秀考题,正三角形剪拼正三棱 柱除参考答案的那种剪法外,还可以用如图 4 的剪法, 当然参考答案的剪法是其本质解,因为它为( 3 )的 解答提供了帮助.
图3
图4
返回
误解分析
1. 解探索性题目时,有些同学心浮气躁,没有根据 地胡乱猜测,最终导致错解.
