2.4 空间中的垂直关系
空间中两直线垂直的判定

空间中两直线垂直的判定在空间几何中,判断两条直线是否垂直是一个基本而重要的问题。
本文将介绍如何判定空间中两条直线的垂直关系,并提供相关的数学原理和具体的判定方法。
一、数学原理两条直线相交可以形成四个角,其中有特殊关系的一个角为90度,即两条直线垂直。
根据数学原理,我们可以通过以下方法来判定空间中两条直线是否垂直:1.利用向量法:设有两条非平行的直线L1和L2,分别有方向向量a和b。
如果a·b=0,则说明L1与L2垂直。
2.利用斜率法:设有两条非平行的直线L1和L2,分别有斜率k1和k2。
如果k1·k2=-1,则说明L1与L2垂直。
二、判定方法方法一:向量法步骤: 1. 确定两条非平行直线L1和L2,并求出它们的方向向量a和b。
2. 计算向量a与向量b的点积(内积)a·b。
3. 如果点积为0,则说明L1与L2垂直;否则,说明L1与L2不垂直。
示例代码:import numpy as npdef is_perpendicular(a, b):dot_product = np.dot(a, b)if dot_product == 0:return Trueelse:return False# 示例:判断直线L1和L2是否垂直a = np.array([1, 2, 3]) # 直线L1的方向向量b = np.array([-2, 1, -4]) # 直线L2的方向向量result = is_perpendicular(a, b)print(result) # 输出True表示L1与L2垂直方法二:斜率法步骤: 1. 确定两条非平行直线L1和L2,并求出它们的斜率k1和k2。
2. 计算斜率k1与斜率k2的乘积k1·k2。
3. 如果乘积为-1,则说明L1与L2垂直;否则,说明L1与L2不垂直。
示例代码:def is_perpendicular(k1, k2):product = k1 * k2if product == -1:return Trueelse:return False# 示例:判断直线L1和L2是否垂直k1 = 0.5 # 直线L1的斜率k2 = -2 # 直线L2的斜率result = is_perpendicular(k1, k2)print(result) # 输出True表示L1与L2垂直三、注意事项1.在使用向量法判定两条直线是否垂直时,需确保直线L1和L2非平行,否则无法求出其方向向量。
空间几何中的垂直关系

空间几何中的垂直关系空间几何是数学中的一个重要分支,研究了在三维空间中的图形、形态和位置关系。
其中垂直关系是几何中的基本概念之一,它在建筑、工程、设计等领域都有广泛的应用。
本文将介绍空间几何中的垂直关系及其相关概念和性质。
1. 垂直关系的定义在空间几何中,两条直线、两个平面或者两个曲面相互垂直,意味着它们的方向互相垂直,不在同一平面上,并且它们的夹角是90度。
具体来说,垂直关系可以分为以下几种情况:1.1 直线的垂直关系空间中的两条直线相互垂直的判定条件有多种,最常用的方法是利用两条直线的方向向量之间的垂直性。
设直线L1的方向向量为a,直线L2的方向向量为b,若a·b=0,则直线L1与直线L2垂直。
1.2 平面的垂直关系两个平面相互垂直的判定方法一般都涉及到它们的法向量。
设平面P1的法向量为n1,平面P2的法向量为n2,若n1·n2=0,则平面P1与平面P2垂直。
1.3 直线与平面的垂直关系直线与平面相互垂直的条件也涉及到它们的方向向量和法向量。
设直线L的方向向量为a,平面P的法向量为n,若a·n=0,则直线L与平面P垂直。
2. 垂直关系的性质垂直关系有一些重要的性质,下面将介绍几个常见的性质。
2.1 垂直平面的夹角如果两个平面相互垂直,则它们的夹角是90度。
这一性质在空间几何中非常重要,可以用来判断两个平面是否相互垂直。
2.2 垂直直线与平面的关系如果一条直线垂直于一个平面,那么它一定位于该平面上的某条直径上。
这一性质可以应用到建筑设计、物理力学等领域。
2.3 垂直向量与平面的关系设一个向量与平面上的任意一条向量都垂直,那么这个向量一定垂直于该平面。
这一性质常用于计算向量与平面的垂直关系。
3. 应用实例垂直关系在实际应用中有很多场景,下面举几个例子进行说明。
3.1 平面墙与地板的垂直关系在建筑设计中,我们常常需要确保墙面与地板垂直,以保证建筑的稳定性和美观性。
3.2 直线与曲面的垂直关系在机械制造中,我们需要确保某些直线与曲面垂直,来实现零件的配合与连接。
空间中的垂直关系

§7.5 空间中的垂直关系教案一.教学目标1.知识技能目标理解空间中直线与平面垂直、平面与平面垂直的概念,掌握证明线线垂直、线面垂直以及面面垂直的判定与性质,会利用有关的判定定理和性质定理进行空间中的垂直关系的证明。
2.过程方法目标学生通过积极主动地参与课堂活动,体会空间中的垂直关系,建构垂直关系相互转化的思维形式,培养空间想象能力。
3.情感态度,价值观目标学生通过主动探究、合作学习、相互交流,培养不怕困难、勇于探索的优良作风,增强了数学应用意识;通过体会成功,形成学习数学知识、了解数学文化的积极态度.二、教学重点、难点重点:利用有关垂直关系的相互转化进行推理与证明。
难点:合理准确地选用性质定理和判定定理。
三、教学方法启发发现法、课堂讨论法。
四、教学过程(一)定理回顾线面垂直定义:如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直。
判定定理:一条直线与一个平面内的___________________垂直,则该直线与此平面垂直。
性质定理:垂直于同一个平面的两条直线_____。
面面垂直定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
判定定理:一个平面过另一个平面的______,则这两个平面垂直.性质定理:两个平面垂直,则一个平面内______________的直线与另一个平面垂直. (二)基础自测例1: (1)下列命题中不正确的是 ( )A. 如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直.B. 垂直于三角形两边的直线必垂直于第三边.C. 过点A垂直于直线a的所有直线都在过点A且垂直于a的平面内.D. 如果三条共点直线两两垂直,那么其中一条直线垂直于另外两条所在的平面.(2) m、n是空间两条不同直线,α、β是两个不同平面,下面有四个命题:① m⊥α,n∥β,α∥β⇒m⊥n;② m⊥n,α∥β,m⊥α⇒n⊥β;③ m⊥n,α∥β,m∥α⇒n⊥β;④ m⊥α,m∥n,α∥β⇒n⊥β. 其中真命题的编号是( )A.①②B.②③C.①④D.③④PA B CD (三)典例研析例2:如图,斜三棱柱ABC —A 1B 1C 1的底面是直角三角形,∠ACB=90°,点B 1在底面ABC 内的射影恰好是BC 的中点,且BC=CA=AA 1.求证: (1) 平面ACC 1A 1⊥平面B 1C 1CB; (2) BC 1⊥AB 1.练习: 如图,四棱锥P-ABCD 的底面是矩形,AB=2,BC ,侧面PAB 是等边三角形,且侧面PAB ⊥底面ABCD.(1)证明:侧面PAB ⊥侧面PBC ; (2)求侧棱PC 与底面ABCD 所成的角.例3: 如图,在四棱锥P-ABCD 中,PA ⊥底面ABCD,AB ⊥AD,AC ⊥CD,∠ABC=60°,PA=AB=BC, E 是PC 的中点. 求证: (1) CD ⊥AE; (2) PD ⊥平面ABE.课外: 如图,在直三棱柱ABC —A 1B 1C 1中,∠ACB=90°,AA 1=BC=2AC=2,D 为AA 1中点.(1)求证:CD ⊥B 1C 1;(2)求证:平面B 1CD ⊥平面B 1C 1D;(3)求三棱锥C 1—B 1CD 的体积.(四)课堂总结。
高二第4讲 空间中的垂直关系(教师版)
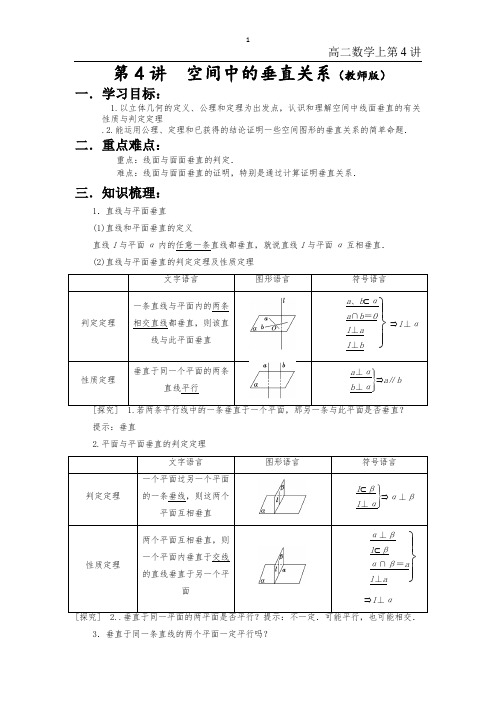
第4讲空间中的垂直关系(教师版)一.学习目标:1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题.二.重点难点:重点:线面与面面垂直的判定.难点:线面与面面垂直的证明,特别是通过计算证明垂直关系.三.知识梳理:1.直线与平面垂直(1)直线和平面垂直的定义直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直.(2)直线与平面垂直的判定定理及性质定理一条直线与平面内的两条相交直线都垂直,则该直垂直于同一个平面的两条[探究] 1.若两条平行线中的一条垂直于一个平面,那另一条与此平面是否垂直?提示:垂直2.平面与平面垂直的判定定理一个平面过另一个平面的一条垂线,则这两个两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平[探究] 2..垂直于同一平面的两平面是否平行?提示:不一定.可能平行,也可能相交.3.垂直于同一条直线的两个平面一定平行吗?提示:平行.可由线面垂直的性质及面面平行的判定定理推导出.四.典例剖析:题型一线面、面面垂直判断题例1(1)下列命题中,正确的序号是________.①若直线l与平面α内的一条直线垂直,则l⊥α;②若直线l不垂直于平面α,则α内没有与l垂直的直线;③若直线l不垂直于平面α,则α内也可以有无数条直线与l垂直;④若平面α内有一条直线与直线l不垂直则直线l与平面α不垂直.[思路探索] 利用线面垂直的定义并结合反例法,反证法判断.解析当l与α内的一条直线垂直时,不能保证l与平面α垂直,所以①不正确;当l与α不垂直时,l可能与α内的无数条平行直线垂直,所以②不正确,③正确.根据线面垂直的定义,若l⊥α则l与α的所有直线都垂直,所以④正确.答案③④(2)(2012·浙江省名校新高考研究联盟第二次联考)下列错误的是( )A.如果平面α⊥平面γ,如果平面β⊥平面γ,α∩β=l,那么l⊥γB.如果平面α⊥平面β,那么平面α内一定存在直线垂直于平面βC.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βD.如果平面α⊥平面β,过α内任意一点作交线的垂线,那么此垂线必垂直β解析:D中当过交线上任意一点作交线的垂线不在平面α内时,此垂线不垂直β,故选D.(3)(教材习题改编)PD垂直于正方形ABCD所在的平面,连接PB、PC,PA、AC、BD,则一定互相垂直的平面有( )A.8对B.7对C.6对D.5对解析:选B 由于PD⊥平面ABCD.故平面PAD⊥平面ABCD,平面PDB⊥平面ABCD,平面PDC⊥平面ABCD,平面PDA⊥平面PDC,平面PAC⊥平面PDB,平面PAB⊥平面PAD,平面PBC⊥平面PDC,共7对.课堂小结:(1)线面垂直的定义不易用来判定线面垂直,但能利用它判定线面不垂直.(2)要注意定义的等价性.课堂练习1:(1)下列命题中正确的个数是( )①如果直线l与平面α内的无数条直线垂直,则l⊥α;②如果直线l与平面α内的一条直线垂直,则l⊥α;③如果直线l不垂直于α,则α内没有与l垂直的直线;④如果直线l不垂直于α,则α内也可以有无数条直线与l垂直.A.0 B.1 C.2 D.3答:B(2)下列命题错误的是________(填序号).①若直线l与平面α内的两条直线垂直,则l⊥α;②若直线l与平面α内的两条相交直线垂直,则l与α的所有直线垂直;③过一点和已知直线垂直的平面有且只有一个;④a、b为异面直线,a∥α,b∥α,若l⊥a,l⊥b,则l⊥α.解析②③④正确,①不正确.答案①(3)(2012·金丽衢十二校第二次联考)已知平面α,β和直线m,给出条件:①m∥α;②m⊥α;③m⊂α;④α⊥β;⑤α∥β.当满足条件时,m⊥β.(填符合条件的序号)解析:当m⊥α且α∥β时,m⊥β,即应当填②⑤.题型二线面垂直的证明——————常运用线面垂直的判定定理证例2(等腰三角形中线即高证垂直)(2013年高考浙江卷(文))如图,在在四棱锥P-ABCD中,PA ⊥面ABCD,AB=BC=2,AD=CD=7,PA=3,∠ABC=120°,G 为线段PC 上的点.(Ⅰ)证明:BD ⊥面PAC ; (2)(3)(略)证明:(Ⅰ)由已知得三角形ABC 是等腰三角形,且底角等于30°,且6030AB CB AD CD ABD CBD ABD CBD BAC BD DB =⎫⎪=⇒∆≅∆⇒∠=∠=∠=⎬⎪=⎭且,所以;、BD AC ⊥,又因为PA ABCD BD PA BD PAC BD AC ⊥⇒⊥⎫⇒⊥⎬⊥⎭; 课堂练习2:(勾股定理证垂直)(2013年高考广东卷(文))如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 边上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G ,将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中BC =. (1) 证明:DE //平面BCF ;(2) 证明:CF ⊥平面ABF ;(3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -.图 4【答案】(1)在等边三角形ABC中,AD AE=AD AEDB EC∴=,在折叠后的三棱锥A BCF-中也成立,//DE BC∴,DE⊄平面BCF,BC⊂平面BCF,//DE∴平面BCF;(2)在等边三角形ABC中,F是BC的中点,所以AF BC⊥①,12BF CF==.在三棱锥A BCF-中,2BC=,222BC BF CF CF BF∴=+∴⊥②BF CF F CF ABF⋂=∴⊥平面;(3)由(1)可知//GE CF,结合(2)可得GE DFG⊥平面.11111113232333F DEG E DFGV V DG FG GF--⎛∴==⋅⋅⋅⋅=⋅⋅⋅⋅=⎝⎭题型三线线垂直的证明——————常转化为证线面垂直例3:(2013年高考课标Ⅰ卷(文))如图,三棱柱111ABC A B C-中,CA CB=,1AB AA=, 160BAA∠= .(Ⅰ)证明:1AB AC⊥;(Ⅱ)若2AB CB==,16AC=,求三棱柱111ABC A B C-的体积.【答案】(I)取AB的中点O,连接OC O、1OA O、1A B,因为CA=CB,所以OC AB⊥,由于AB=A A1,∠BA A1=600,故,AA B∆为等边三角形,所以OA1⊥AB.因为OC⨅OA1=O,所以AB⊥平面OA1C.又A1CC平面OA1C,故AB⊥AC. (II)由题设知12ABC AA B∆∆与都是边长为的等边三角形,12AA B都是边长为的等边三角形,所以2211111.OC OA AC AC OA OA OC ==+⊥又,故111111111,--= 3.ABC ABCOC AB O OA ABC OA ABC A B CABC S A B C V S OA=⊥∆⨯=因为所以平面,为棱柱的高,又的面积ABC的体积课堂练习3:(2013年高考大纲卷(文))如图,四棱锥902,P ABCD ABC BAD BC AD PAB PAD-∠=∠==∆∆中,,与都是边长为2的等边三角形.(I)证明:;PB CD⊥(II)(略)【答案】(Ⅰ)证明:取BC的中点E,连结DE,则ABED为正方形.过P作PO⊥平面ABCD,垂足为O. 连结OA,OB,OD,OE.由PAB∆和PAD∆都是等边三角形知PA=PB=PD, [来源:学科网]所以OA=OB=OD,即点O为正方形ABED对角线的交点, OE BD⊥,从而PB OE⊥.因为O是BD的中点,E是BC的中点, 所以OE//CD.因此,PB CD⊥.题型四面面垂直的证明——————常转化为证线面垂直例4(2013年高考山东卷(文))如图,四棱锥中,,,分别为的中点(Ⅰ)求证:;(Ⅱ)求证:课堂练习4:(2013年高考北京卷(文))如图,在四棱锥P ABCD -中,//AB CD ,AB AD ⊥,2CD AB =,平面PAD ⊥底面ABCD ,PA AD ⊥,E 和F 分别是CD 和PC 的中点,求证:(1)PA ⊥底面ABCD ;(2)//BE 平面PAD ;(3)平面BEF ⊥平面PCD【答案】(I)因为平面PAD⊥平面ABCD,且PA垂直于这个平面的交线AD所以PA垂直底面ABCD.(II)因为AB∥CD,CD=2AB,E为CD的中点,所以AB∥DE,且AB=DE所以ABED为平行四边形,所以BE∥AD,又因为BE⊄平面PAD,AD⊂平面PAD ,所以BE∥平面PAD.(III)因为AB⊥AD,而且ABED为平行四边形所以BE⊥CD,AD⊥CD,由(I)知PA⊥底面ABCD,所以PA⊥CD,所以CD⊥平面PAD[来源:学§科§网]所以CD⊥PD,因为E和F分别是CD和PC的中点所以PD∥EF,所以CD⊥EF,所以CD⊥平面BEF,所以平面BEF⊥平面PCD.题型五线面、面面垂直探究问题例5(2012北京文)如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点, 点F为线段CD上的一点.将△ADE沿DE折起到△A 1DE的位置,使A1F⊥CD,如图2.(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【考点定位】本题第二问是对基本功的考查,对于知识掌握不牢靠的学生可能不能顺利解决.第三问的创新式问法,难度比较大.解:(1)因为D,E分别为AC,AB的中点,所以DE∥BC.又因为DE⊄平面A1CB,所以DE∥平面A1CB.(2)由已知得AC⊥BC且DE∥BC,所以DE⊥AC.所以DE⊥A1D,DE⊥CD.所以DE⊥平面A1DC.而A1F⊂平面A1DC,所以DE⊥A1F.又因为A1F⊥CD,所以A1F⊥平面BCDE.所以A1F⊥BE(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.又因为DE∥BC,所以DE∥PQ.所以平面DEQ即为平面DEP.由(2)知DE⊥平面A1DC,所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C 的中点,所以A1C⊥DP,所以A1C⊥平面DEP,从而A1C⊥平面DEQ.故线段A1B上存在点Q,使得A1C⊥平面DEQ.课堂练习5:(2012北京理)如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB 上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.(1)求证:A1C⊥平面BCDE;(2)(略)(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.、、【考点定位】此题第二问是对基本功的考查,对于知识掌握不牢靠的学生可能不能顺利解答.第三问的创新式问法,难度非常大.解:(1) CD DE ⊥,1A E DE ⊥∴DE ⊥平面1A CD , 又 1AC ⊂平面1A CD , ∴1AC ⊥DE 又1AC CD ⊥, ∴1AC ⊥平面BCDE (3)设线段BC 上存在点P ,设P 点坐标为()00a ,,,则[]03a ∈,则(10A P a =- ,,,()20DP a = ,,设平面1A DP 法向量为()1111n x y z = ,,,则1111020ay x ay ⎧-=⎪⎨+=⎪⎩∴111112z x ay ⎧=⎪⎪⎨⎪=-⎪⎩∴()136n a =- , 假设平面1A DP 与平面1A BE 垂直,则10n n ⋅=,∴31230a a ++=,612a =-,2a =-∵03a << ∴不存在线段BC 上存在点P ,使平面1A DP 与平面1A BE 垂直五.品味高考(家庭作业):1.(2013年普通高等学校招生统一考试广东省数学(理)卷)设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )yCA .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥ 【答案】D2.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理))已知为异面直线,平面,平面.直线满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .,且B .,且C .与相交,且交线垂直于 D .与相交,且交线平行于【答案】D3.(2013年普通高等学校招生统一考试浙江数学(理)试题)在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A4.(2013年普通高等学校招生统一考试辽宁数学(理)试题)如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I)求证:PAC PBC ⊥平面平面;(II) (略)【答案】(略)5.(2013年普通高等学校招生全国统一招生考试江苏卷)本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC ,同理:FG∥平面ABC 又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC(2)∵平面⊥SAB 平面SBC ,平面SAB 平面SBC =BCAF ⊆平面SABAF⊥SB ,∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC 又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA6.(2013年普通高等学校招生统一考试广东省数学(理)卷)如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=. (Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ)(略)【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.COBDEC DO BE'A 图1 图2ABCSGFE连结,OD OE ,在OCD ∆中,由余弦定理可得OD ==,由翻折不变性可知A D '=所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O = ,所以A O '⊥平面BCDE .7.(2013年高考陕西卷(理))如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O为底面中心, A 1O ⊥平面ABCD, 1AB AA ==证明: A 1C ⊥平面BB 1D 1D ; (Ⅱ) (略)解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为, 在正方形ABCD中,BD C A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)8.(2013年高考江西卷(理))如图,四棱锥P ABCD -中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,1AC D OB E'A H,连接CE 并延长交AD 于F .(1) 求证:AD CFG ⊥平面;解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====, 故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG .。
空间中的垂直关系

8. 5 空间中的垂直关系1.线线垂直如果两条直线所成的角是______ ( 无论它们是相交还是异面),那么这两条直线互相垂直.2.直线与平面垂直(1)定义:如果直线I与平面a内的任意一条直线都垂直,我们就说__________________________ ,记作_______ .直线I叫做______________ ,平面a叫做_______________ .直线与平面垂直时,它们惟一的公共点P叫做________ .垂线上任意一点到垂足间的线段,叫做这个点到这个平面的垂线段,垂线段的长度叫做这个点到平面的______________ .(2)判定定理:一条直线与一个平面内的________________ 都垂直,则该直线与此平面垂直.推论:如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直于这个平面.用符号表示: a // b,(3)__________________________________________ 性质定理:垂直于同一个平面的两条直线 .3.直线和平面所成的角平面的一条斜线和它在平面上的射影所成的 ___________ ,叫做这条直线和这个平面所成的角.一条直线垂直于平面,我们说它们所成的角是直角;一条直线和平面平行,或在平面内,我们说它们所成的角是0°勺角.任一直线与平面所成角B的范围是 ____________ .4.二面角的有关概念(1)二面角:从一条直线出发的________________________ 叫做二面角.(2)二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作 ______________ 的两条射线,这两条射线所成的角叫做二面角的平面角.二面角的范围是 _______________ .5.平面与平面垂直(1)定义:一般地,两个平面相交,如果它们所成的二面角是_________________ ,就说这两个平面互相垂直.(2)判定定理:一个平面过另一个平面的__________ ,则这两个平面垂直.(3)性质定理:两个平面垂直,则一个平面内垂直于_____ 的直线与另一个平面垂直.自查自纠1.直角2.(1)直线I与平面a互相垂直I丄a平面a的垂线直线I 的垂面垂足距离(2)两条相交直线(3)平行3.锐角[0;90°4.(1)两个半平面所组成的图形(2)垂直于棱[0 ° 180°]5.(1)直二面角(2)垂线(3)交线0 (2017江西宜春四校联考)下列命题中错误的是( )A •如果平面a 丄平面3那么平面 a 内一定存在直线平行于平面 3B.如果平面 a 不垂直于平面 3,那么平面a 内一定不存在直线垂直于平面3C. 如果平面 a 丄平面 Y 平面3丄平面 Y a Q 3 =丨,那么I 丄平面 丫 D .如果平面a 丄平面3那么平面a 内所有直线都垂直于平面 3解:对于选项A ,可在a 内作直线平行于交线即可, A 正确;对于选项B ,假设在a 内存在直线垂直于平面 3则a 丄3这与已知矛盾,所以原命题成立,B 正确;对于选项C ,因为平面a 丄平面Y 所以在平面 丫内存在一条直线m 丄a 所以m i l.同理可知在平面 丫内存在直线n 丄3 n 丄I.若直线m , n 重合,则面a 与3重合或平 行,这与已知矛盾,所以直线 m , n 相交,又I 丄m , I 丄n ,所以I 丄面Y C 正确;对于选项 D ,易知a 与3的 交线I 并不垂直于面 3, D 错误.故选D.° (2017甘肃马营中学月考)若m 、n 是两条不同的直线,a 、3 丫是三个不同的平面,则下列命题中的真命题是( )A .若 m? 3 ,a 丄 3 ,贝U m 丄aB .若 aCl Y= m , 3C Y = n , m / n ,贝U a/ 3 C .若 m ± 3, m //a则a 丄3D .若 a 丄Y a 丄 3则 3-L Y解:若m? 3 , a 丄3 ,贝y m 与a 的关系可能平行也可能相交或 m? a ,贝y A 为假命题;选项 B 中,a 与3选C.而不充分条件.故填必要不充分.❺(2017重庆八中适应性考试)在正四面体P-ABC 中,D , E , F 分别是AB , BC , CA 的中点,下面四个结论 中正确的是 _________________ . ① BC //平面PDF ; ② DF 丄平面FAE ;③ 平面PDF 丄平面 ABC ; ④平面PAE 丄平面 ABC.解:由DF // BC 可得BC //平面PDF ,故①正确;若PO 丄平面ABC ,垂足为O ,贝U O 在AE 上,贝U DF 丄PO , 又DF 丄AE ,故DF 丄平面FAE ,故②正确;由PO 丄平面ABC , PO?平面PAE ,可得平面 FAE 丄平面 ABC , 故④正确,平面PDF 不过PO ,故③不正确.故填①②④.A . A 1E 丄 DC 1B . A 1E 丄 BDC . A 1E 丄 BC 1D . A 1E 丄AC解:由正方体的性质,得 A 1B 1 丄 BC 1 , BQ 丄 BC 1 ,所以 BG 丄平面 A 1B 1CD ,又 A 1E?平面 A 1B 1CD ,所以 A 1E 丄BC 1 ,故选C.(2017全国卷川)在正方体 ABCD-A i B i C i D i 中, E 为棱CD 的中点,贝U()❹ 若I , m 是两条不同的直线, m 垂直于平面a ,则"I 丄m ”是"I // a”的 _____________ 条件.解:若I 丄m , m 丄平面a,贝y I //a 或I? a ;若I //a, m 丄平面a,贝U I 丄m ,所以"I 丄m ”是"I // a”的必要 可能平行也可能相交,则B 为假命题;选项 D 中3与丫也可能平行或相交(不一定垂直),则D 为假命题.»为类解析触类旁邂类型一线线垂直问题EB 如图,在四棱台ABCD-A I B I C I D I中,D i D丄平面ABCD,底面ABCD是平行四边形,AB= 2AD, AD =A1B1,Z BAD = 60°(1)证明:AA i 丄BD ;⑵证明:CC i//平面A I BD.证明:(1)因为D I D丄面ABCD,且BD?面ABCD,所以D i D丄BD.又因为AB = 2AD,/ BAD = 60°在厶ABD 中,由余弦定理得BD2= AD2+ AB2—2AD ABcos60°= 3AD2,所以AD2+ BD2= AB2所以AD丄BD.又因为AD n D I D = D,所以BD丄面ADD i A i.又AA I?面ADD I A I,所以AA I±BD.(2)连接AC, A i C i,设AC n BD = E,连接A I E.i因为四边形ABCD为平行四边形,所以EC = ^AC.由棱台定义及AB = 2AD = 2A i B i知A i C i // EC且A i C i = EC,所以四边形A I ECC I为平行四边形.所以CC i// A I E.又因为A I E?面A I BD, CC i?面ABD,所以CC I // 面A I BD.【点拨】本题主要考查线线、线面位置关系•第(i)问证明线线垂直,其实质是通过证明线面垂直,再化归为线线垂直;第(2)问证明线面平行,需转化为证明线线平行,由于面A I BD中没有与CC I平行的直线,故需作辅助线.(20i7武汉市武钢第三子弟中学月考)如图,三棱柱ABC-A i B i C i 中,CA= CB , AB = AA i , / BAA i= 60°.f(i)证明:AB 丄A I C ;⑵若AB= CB = 2, A I C = .6,求三棱柱ABC-A i B i C i的体积. 解:⑴证明:取AB的中点O,连接OC, OA i, A I B.因为CA = CB,所以0C丄AB.由于AB = AA i,/ BAA i= 60° °故厶AA i B为等边三角形,所以OA i丄AB.因为OC A OA i= 0,所以AB丄平面OA i C.又A i C?平面OA i C,故AB丄A i C.⑵由题设知△ ABC与厶AA i B都是边长为2的等边三角形,所以OC = OA i = .3. 又A i C = ■.6,贝U A i C2= OC2+ OA i,故OA i丄OC.因为OC A AB= O,所以OA i丄平面ABC, OA i为三棱柱ABC-A i B i C i的高.乂△ ABC 的面积S SBC= , 3,故三棱柱ABC-A i B i C i 的体积为V = S^ABC X OA i = 3.类型二线面垂直问题GE 如图,四棱锥P-ABCD中,PA丄底面ABCD , AB丄AD,点E在线段AD上,且CE // AB.(i)求证:CE丄平面PAD ;⑵若PA= AB= i , AD = 3, CD =运,/ CDA = 45° 求四棱锥P-ABCD 的体积. 解:(1)证明:因为PA丄底面ABCD , CE?平面ABCD,所以PA丄CE.因为AB丄AD, CE / AB,所以CE丄AD.又PA A AD = A,所以CE丄平面PAD.(2)由(1)可知CE丄AD.在Rt △ ECD 中,CE = CD sin45 = 1, DE = CD c os45°= 1, 又因为AB = 1,贝U AB = CE.又CE // AB, AB丄AD,所以四边形ABCE为矩形,四边形ABCD为梯形.因为AD = 3,所以BC = AE= AD —DE = 2,1 1 5S ABCD = 2(BC + AD) AB =彳(2 + 3)X 1 = §,1 1 5 5VP-ABCD=3SABCD'PA=3x只1=6.于是四棱锥P-ABCD的体积为|.【点拨】证明线面垂直的基本思路是证明该直线和平面内的两条相交直线垂直,亦可利用面面垂直的性质定理来证明;第(2)问的难点在于求底面四边形ABCD的面积,注意充分利用题设条件,先证明底面ABCD是直角梯形,从而求出底面面积,最后求体积.(2017锦州市第二高级中学月考)如图,在正方体ABCD-A i B i C i D i中,E, F , P, Q, M, N分别是棱AB, AD , DD i, BB i, “B i, AQ i 的中点•求证:⑴直线BC i〃平面EFPQ ;⑵直线AC」平面PQMN.证明:(1)如图,连接AD i,由ABCD-A i B i C i D i是正方体,知AD i II BC i, 因为F , P分别是AD, DD i的中点,所以FP II AD i,从而BC i I FP.而FP?平面EFPQ,且BC i?平面EFPQ , 故直线BC i I平面EFPQ.⑵如图,连接AC, BD,贝U AC丄BD.由CC i丄平面ABCD , BD?平面ABCD,可得CC i丄BD .又AC A CC i = C,所以BD丄平面ACC i A i.而AC i?平面ACC i A i,所以BD丄AC i.因为M, N分别是A i B i, A i D i的中点,所以MN I BD,从而MN丄AC i. 同理可证PN丄AC i.又PN A MN = N,所以直线AC i±平面PQMN.类型三面面垂直问题GO)如图所示,在长方体ABCD-A i B i C i D i中,AB = AD = i, AA i= 2, M是棱CC i的中点.B C又A1B1Q B I M = B i,由①②得BM丄平面A I B I M.而BM?平面ABM,所以平面ABM丄平面A i B i M.【点拨】求异面直线所成的角,一般方法是通过平移直线,把异面问题转化为共面问题,通过解三角形求出所构造的角;证明面面垂直,可转化为证明线面垂直,而线面垂直又可以转化为证明线线垂直,在证明过程中,需充分利用规则几何体本身所具有的几何特征简化问题,有时还需应用勾股定理的逆定理,通过计算来证明垂直关系,这在高考题中是常用方法之一.变式.(2017武汉市第四十三中学月考)如图,在五棱锥P-ABCDE 中,PA丄平面ABCDE , AB// CD,/ ABC=45° AB= 2 2, BC = 2AE = 4,三角形PAB是等腰三角形.求证:平面PCD丄平面PAC.证明:因为/ABC = 45° AB= 2 2, BC = 4,所以在△ ABC 中,由余弦定理得,AC2= (2 _ 2)2+ 42-2 X 2_2X 4COS45 = 8,解得AC= 2 ,2,所以AB2+ AC2= 8 + 8 = 16= BC2,即卩AB丄AC,又PA丄平面ABCDE,所以PA丄AB.又FA n AC = A,所以AB丄平面PAC,又AB // CD,所以CD丄平面FAC. 又因为CD?平面PCD,所以平面PCD丄平面PAC.类型四垂直综合问题EE (2017大连经济技术开发区一中月考)如图1,在等腰直角三角形ABC中,/ A = 90° BC= 6, D, E分别是AC ,AB上的点,CD = BE= 2,O为BC的中点.将厶ADE沿DE折起,得到如图2所示的四棱锥A'B-DE ,其中AO = 3.(1)证明:A'O丄平面BCDE ;⑵求二面角A'C--B的平面角的余弦值.解:(1)证明:在图1中,易得OC = 3, AC = 3,2, AD = 2 2.如图示,连接OD , OE,在△ OCD中,由余弦定理可得OD = OC2+ CD2- 2OC CDcos45°= , 5•由翻折不变性可知AD = 2 _2,易得AO2+ OD2= AD2,所以A ‘0丄OD•同理可证A O丄OE.又因为OD n OE = O,所以A O丄平面⑵过O作OH丄CD交CD的延长线于H,连接A H,因为A ‘O丄平面BCDE,易知A H丄CD,所以/ A HO为二面角A‘ C--B的平面角.结合图1可知,H为AC中点,又O为BC中点,故OH = ^AB= 节,从而A H = OH2+ OA 2=亠3°, 所以cos/ A ‘ HO=-°^ =丘A ‘ H 5 '所以二面角A'CD-B 的平面角的余弦值为亠5【点拨】本题主要考查线面垂直及二面角的计算等.(2016全国卷I )如图,在以A , B , C , D , E , F 为顶点的五面体中,(1)证明:平面 ABEF 丄平面EFDC ;⑵求二面角E-BC-A 的余弦值.解:(1)证明:由已知可得 AF 丄DF , AF 丄FE ,又DF n FE = F ,所以AF 丄平面EFDC . 又AF?平面ABEF ,故平面ABEF 丄平面EFDC.⑵过D 作DG 丄EF ,垂足为 G ,由(1)知DG 丄平面ABEF.以G 为坐标原点, G F 的方向为x 轴正方向,|GF|为单位长,建立如图所示的空间直角坐标系 G -xyz.由(1)知/DFE 为二面角 D-AF-E 的平面角,故 / DFE = 60° 贝U DF = 2, DG可得 A(1 , 4, 0), B(-3,4, 0), E( — 3, 0, 0), D(0, 0, .3).由已知得,AB // EF ,所以 AB //平面 EFDC.又平面 ABCD n 平面 EFDC = CD ,故 AB / CD , CD // EF.由BE // AF ,可得BE 丄平面EFDC ,所以/CEF 为二面角C-BE-F 的平面角,故/CEF = 60°从而可得C(— 2,0, 3),连接 AC ,则 (1 , 0, . 3), EB = (0, 4, 0), AC = (— 3,— 4,3), AB = (— 4, 0, 0).设n = (x , y , z)是平面BCE 的法向量,贝Un EC =0,'x + T 3z = 0,厂即'所以可取n = (3, 0,—*3).InEB = 0,仆 0,m AC = 0,设m 是平面ABCD 的法向量,则m AB = 0,同理可取 m = (0, 3, 4),1. 判断(证明)线线垂直的方法 (1) 根据定义;(2) 如果直线a // b , a 丄c ,贝U b 丄c ;⑶如果直线 a 丄面a, c? a ,贝U a 丄c ;折叠要注意不变量;作二面角,往往要通过作垂线来实现.面ABEF 为正方形,AF = 2FD ,贝U cos 〈n , m >n m|n ||2「19 19 结合图形,得二面角 E-BC-A 的余弦值为一2 .'19/ AFD = 90° 且二面角揭示规漳⑷向量法:两条直线的方向向量的数量积为零.2.证明直线和平面垂直的常用方法(1)利用判定定理:两相交直线a, b? a , a丄c, b± c? c丄a;(2)a // b, a丄 a ? b± a ;⑶利用面面平行的性质:a// 3, a丄a ? a± 3 ;⑷利用面面垂直的性质:a丄3, a A 3 =m, a? a , a丄m? a丄3 ;a丄丫,3丄Y, a A 3 =m? m X 丫.3.证明面面垂直的主要方法(1)利用判定定理:a丄3, a? a ? a丄3 ;(2)用定义证明.只需判定两平面所成二面角为直二面角;(3)如果一个平面垂直于两个平行平面中的一个,则它也垂直于另一个平面:a// 3, a丄丫? 3丄丫.4.平面与平面垂直的性质的应用当两个平面垂直时,常作的辅助线是在其中一个面内作交线的垂线, 把面面垂直转化为线面垂直,进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系),构造(寻找)二面角的平面角或得到点到面的距离等.5.注意线线垂直、线面垂直、面面垂直间的相互转化判定定理判定定理线线垂直J *线面垂直・〜面面垂直性质定理性蜃定理6.线面角、二面角求法求这两种空间角的步骤:根据线面角的定义或二面角的平面角的定义,作(找)出该角,再解三角形求出该角,步骤是作(找)?证?求(算)三步曲.也可用射影法:设斜线段AB在平面a内的射影为A B AB与a所成角为0,贝U COS B 厂B厂I|AB|设厶ABC在平面a内的射影三角形为△ A B C 平面ABC与a所成角为0则COS 0 = S: B CS A ABC@|底翻科劃b查漏补缺折展延伸1.(2016浙江)已知互相垂直的平面 a , 3交于直线I •若直线m, n满足m// a, n丄3 ,则()A . m / lB . m / n C. n丄I D. m± n解:由题意知aA A l,所以l? 3 •因为n丄3所以n丄I•故选C.2.已知a, 3为两个不同的平面,I为直线,若a丄3, a A 3 = I,则()A .垂直于平面3的平面一定平行于平面aB.垂直于直线I的直线一定垂直于平面aC.垂直于平面3的平面一定平行于直线ID .垂直于直线I的平面一定与平面a, 3都垂直解:由面面垂直的判定定理可知,垂直于直线I的平面一定与平面a, 3都垂直.故选D.3.设m, n是两条不同的直线, a , 3是两个不同的平面.下列命题中正确的是()A .若a丄 3 m? a , n? 3 ,贝U m± nB.若a// 3 m? a , n? 3 ,则m// nC.若m l n , m? a , n? 3 ,贝U a丄3D .若m±a,m / n ,n / 3 ,贝U a丄3解:若a丄B, m? a , n?卩,贝U m与n可能平行、相交或异面,故A错;若a//®, m? a , n?卩,则m与n可能平行,也可能异面,故B错;若m丄n, m? a , n? B ,贝U a与®可能相交,也可能平行,故C错;对于D项,由m丄a, m / n,得n丄a,又知n // B,故a丄B,所以D项正确.故选D.4.(2017沈阳市第一中学月考)设平面a与平面B相交于直线m,直线a在平面a 内,直线b在平面B内,且b丄m,则"a丄B'是"a丄b”的( )A .充分不必要条件B.必要不充分条件C.充要条件D .既不充分也不必要条件解:当a丄B时,由面面垂直的性质定理知b丄a,则b丄a.所以“a丄B”是“a丄b”的充分条件.而当a? a ,且a // m时,因为b丄m,所以b丄a,而此时平面a与平面B不一定垂直.所以“a丄B”不是“ a丄b ”的必要条件.故选A.5.(2015福建质量检查)如图,AB是圆O的直径,VA垂直圆O所在的平面,C是圆周上不同于A, B的任意一点,M , N分别为VA, VC的中点,则下列结论正确的是( )CA . MN // ABB.MN与BC所成的角为45°C.OC X平面VACD .平面VAC丄平面VBC解:依题意,MN // AC,又直线AC与AB相交,因此MN与AB不平行,A错误;注意到AC丄BC,因此MN 与BC所成的角是90°, B错误;注意到直线OC与AC不垂直,因此OC与平面VAC不垂直,C错误;由于BC丄AC, BC丄VA,因此BC丄平面VAC.又BC?平面VBC,所以平面VBC丄平面VAC, D正确.故选D.6. (2017瓦房店市高级中学月考)如图,在正方形SGG2G3中,E, F分别是G1G2, G2G3的中点,D是EF的中点,现沿SE, SF及EF把这个正方形折成一个几何体,使G1, G2, G3三点重合于点G,这样,下列五个结论:(1)SG丄平面EFG ;(2)SD丄平面EFG ;(3)GF丄平面SEF;(4)EF丄平面GSD;(5)GD丄平面SEF.正确的是( )A. (1)和⑶B. ⑵和⑸C. (1)和⑷D. ⑵和⑷解因为正方形中折叠前后都有SG丄GE, SG丄GF,所以SG丄平面EFG.(1)正确,(2)错误:因为SG丄GF, SG丄GD,所以GF并不垂直于SF, GD并不垂直于SD,即卩⑶(5)错误.因为EF丄GD , EF丄SG, GD n SG= G ,所以EF丄面GSD.(4)正确.故选C.7.在正方体ABCD-A 'B 'C 'D中,过对角线BD '的一个平面交AA于E,交CC于F,贝U①四边形BFDE 一定是平行四边形;②四边形BFD E有可能是正方形;③四边形BFD E在底面ABCD内的投影一定是正方形;④平面BFD E有可能垂直于平面BB D.以上结论正确的为____________ .(写出所有正确结论的编号)解:根据两平面平行的性质定理可得BFD E为平行四边形,①正确;若四边形BFD E是正方形,则BE丄ED ', 又A ' D '丄EB, A ' D ' n ED ' = D ',所以BE丄面ADD A ',与已知矛盾,②错;易知四边形BFD E在底面ABCD内的投影是正方形ABCD,③正确;当E, F分别为棱AA ', CC '的中点时,EF // AC,又AC丄平面BB D, 所以EF丄面BB D,④正确.故填①③④.8.(2017沈阳市回民中学月考)ABCD是正方形,P为平面ABCD外一点,且PA丄平面ABCD,则平面PAB,平面PBC,平面PCD,平面PAD,平面ABCD这五个平面中,互相垂直的平面有 _________________ 对.解:因为PA丄平面ABCD,所以平面PAD丄平面ABCD,平面PAB丄平面ABCD.又因为AD丄平面FAB,所以平面FAD丄平面PAB,同理可得平面PBC丄平面PAB,平面PAD丄平面PCD,故互相垂直的平面有5对.故填5.9.(2017钟祥市实验中学月考)如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD = a, PA = PC =■, 2a.求证:(1)PD 丄平面ABCD ;⑵平面PAC丄平面PBD.证明:⑴因为PD = a, DC = a, PC= 2a,所以PC2= PD2+ DC2,所以PD 丄DC.同理可证PD丄AD,又AD n DC = D ,所以PD丄平面ABCD.⑵由⑴知PD丄平面ABCD ,所以PD丄AC,而四边形ABCD是正方形,所以AC丄BD,又BD n PD = D,所以AC丄平面PDB.同时AC?平面PAC ,所以平面PAC丄平面PBD.10. (2017谷城县第一中学月考)如图所示,在四棱锥P-ABCD中,PA丄底面ABCD , AB丄AD , AC丄CD,/ABC = 60° PA = AB = BC, E 是PC 的中点.证明:⑴CD丄AE;(2)PD丄平面ABE.证明:⑴ 因为PA丄底面ABCD , CD?平面ABCD,所以PA丄CD.因为AC丄CD , FA Q AC = A,所以CD丄平面FAC.而AE?平面PAC,所以CD丄AE.(2)由FA= AB= BC ,Z ABC= 60 °可得AC = PA•因为E是PC的中点,所以AE丄PC.由⑴知AE丄CD,且PC Q CD = C,所以AE丄平面PCD.而PD?平面PCD,所以AE丄PD.因为PA丄底面ABCD,所以PA丄AB.又因为AB丄AD且PA Q AD = A,所以AB丄平面PAD,而PD?平面PAD,所以AB丄PD.又因为AB Q AE= A,所以PD丄平面ABE.11. (2017 天津)如图,在四棱锥P- ABCD 中,AD 丄平面PDC , AD // BC, PD 丄PB, AD = 1 , BC = 3, CD = 4, PD = 2.AP 5因为PD丄平面PBC,故PF为DF在平面PBC上的射影,所以/ DFP为直线DF和平面PBC所成的角.由于AD // BC, DF // AB,故BF = AD = 1 ,由已知,得CF = BC- BF = 2.又AD 丄DC ,故BC 丄DC ,在Rt△ DCF 中,DF2= DC2+ CF2= 42+ 22= 20, DF = 2 5,所以在Rt△ DPF 中可得sin/ DFP = DD二亠5所以,直线AB与平面PBC所成角的正弦值为—.5(1)求三棱锥P-ABC的体积;(2)证明:在线段PC上存在点M,使得AC丄BM,并求MC的值.解:⑴由题设AB= 1, AC = 2,/ BAC = 60°, 可得S A ABC=I' AB - AC • sin60 °= ^3.由PA丄平面ABC,可知PA是三棱锥P-ABC的高,又PA = 1,所以三棱锥P-ABC的体积⑵证明:在平面ABC内,过点B 作BN丄AC,垂足为N.在平面FAC内,过点N作MN // PA,交PC于点M ,连接BM •由FA丄平面ABC知FA丄AC,又MN // PA,所以MN丄AC•又BN丄AC, BN P MN = N, BN?平面MBN ,MN?平面MBN,所以AC丄平面MBN.又BM?平面MBN,所以AC丄BM.I 3 PM AN 1在Rt△BAN中,AN=ABcos/BAC=2 从而NC=AC-AN乜由MN〃PA,得MM=AN二./ BAC= 60 °V=3 ABC,PA=卡. (2015安徽)如图,三棱锥AB= 1 , AC= 2,(1) 求异面直线A i M和C i D i所成的角的正切值;⑵证明:平面ABM丄平面A i B i M.解:⑴因为C i D i I B i A i,所以/ MA i B i为异面直线A i M和C i D i所成的角,因为A i B i丄平面BCC i B i,所以/ A i B i M =90°而A i B i= i , B i M = . B i C?+ MC i= 2,故tan/ MA i B i = = .2.A iB i(2) 证明:由A i B i丄平面BCC i B i, BM?平面BCC i B i,得"B i丄BM •①由(i)知,B i M = 2,又BM = BC1 2+ CM2= .2, B i B= 2,B i M2+ BM2= B i B2,从而BM 丄B i M.②(1) 求异面直线AP与BC所成角的余弦值;(2) 求证:PD丄平面PBC;⑶求直线AB与平面PBC所成角的正弦值.解:(1)如图,由已知AD // BC,故/DAP或其补角即为异面直线AP与BC所成的角.因为AD丄平面PDC,所以AD丄PD.在Rt△ PDA 中,由已知,得AP = AD1 2+ PD2= 5.故cos/ DAP = AD =血.所以,异面直线AP与BC所成角的余弦值为-?.5⑵证明:因为AD丄平面PDC,直线PD?平面PDC,所以AD丄PD.又因为BC // AD,所以PD丄BC.又PD丄PB,所以PD丄平面PBC.⑶过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.。
空间中的垂直关系常见题型及方法

⑷过一点有且只有一条直线垂直于已知直线。
1
例1 下列说法正确的有____.
⑸若一条直线平行于一个平面,则垂直于这个平面的直线 必垂直于这条直线。
⑹若一条直线垂直于一个平面,则垂直于这条直线的另一 条直线必平行于这个平面。
4
⑺若一条直线平行于一个平面,则它和这个平面内的任何 直线都不垂直。
⑻平行于同一平面的两条直线可能垂直。
三、面面垂直 定义: 如果两个相交平面的交线与第三个平面垂直,又这两个 平面与第三个平面相交所得的两条交线互相垂直,就称 这两个平面互相垂直。
面面垂直的判定定理: 如果一个平面过另一个平面的一条垂线,则这两个平 面互相垂直。 l ,l
这条直线叫做平面的垂线,这个平面叫做直线的垂面, 交点叫垂足。
线面垂直的判定定理: 如果一条直线与平面内的两条相交直线垂直,则这条直 线与这个平面垂直。 a ,b ,a b A,l a,l b l
线面垂直的性质定理: 如果两条直线垂直于同一个平面,那么这两条直线平行。
例1 下列说法正确的有____. ⑴如果一条直线垂直于平面内的无数条直线,那么这条直 线和这个平面垂直。
面面垂直的性质定理:
如果两个平面互相垂直,那么在一个平面内垂直于它们交 线的直线垂直于另一个平面。
2
∥
3
三垂线定理&其逆定理 三垂线定理: 平面内的一条直线,如果和穿过这个平面的一条斜线在这个 平面内的射影垂直,那么它也和这条斜线垂直。 逆定理: 如果平面内一条直线和穿过该平面的一条斜线垂直,那么这 条直线也垂直于这条斜线在平面内的射影。 证明异面垂直。
空间中的垂直关系常见题型及方法
空间中的垂直关系

空间中的三种垂直关系:
线线垂直: 所成角为直角 线面垂直: 线和面内所有直线都垂直
面面垂直: 所成的二面角为直二面角
问题: 如图,在四棱锥P ABCD中,PD 面ABCD, (1)请你添加一个条件,使PB AC成立;
问题: 如图,在四棱锥P ABCD中,PD 面ABCD, (1)请你添加CD中,PD 面ABCD, (6)若BC CD,PD CD, E是PC中点, 则在PB上是否存在点 F,使得PC 面DEF ?
在PB上是否存在点F,使得PB 面DEF ?
(7)若ABCD为正方形,PD CD, E、F是PC、PB的中点, 求二面角P DF E的正弦值;
(2)若PB AC, 求证:面 PAC 面PBD
(3)若PAD 面PBD, 求证:AD PB;
归纳:空间中垂直关系图
线线垂直
判
定
定
义
线面垂直
判
性
定
质
面面垂直
指出:转化思想是证明空间位置关系中最重要的思想
问题: 如图,在四棱锥 P ABCD中,PD 面ABCD, (4)若ABCD为矩形, AD 1,AB 2, E为AB中点,求证: PE CE; (5)若ABCD为矩形,AB kAD, 且在线段AB上存在一点E, 使得PE CE,求k的取值范围;
垂直关系

空间中的垂直关系●知识梳理线面垂直1.如果一条直线与平面相交并且与平面内的所有直线都垂直,那么就说这条直线与这个平面垂直.2.直线与平面垂直的判定:如果一条直线与平面内的两条相交直线都垂直,那么这条直线与这个平面垂直.3.直线与平面垂直的性质:如果两条直线都与同一个平面垂直,那么这两条直线平行.面面垂直1.两个平面垂直的定义:如果两个平面所成的二面角是直二面角,那么这两个平面互相垂直.2.两个平面垂直的判定定理:如果一个平面经过另一个平面的垂线,那么这两个平面垂直.3.两个平面垂直的性质定理:如果两个平面垂直,那么过其中一个平面内的一点作它的交线的垂线与另一个平面垂直.【基础练习】1.m、n表示直线,α、β、γ表示平面,给出下列四个命题,其中正确命题为①α∩β=m,n α,n⊥m,则α⊥β②α⊥β,α∩γ=m,β∩γ=n,则m⊥n③α⊥β,α⊥γ,β∩γ=m,则m⊥α④m⊥α,n⊥β,m⊥n,则α⊥βA.①②B.②③C.③④D.②④答案:C2.“直线l 垂直于平面α内的无数条直线”是“l α⊥”的 必要 条件。
3.如果两个平面同时垂直于第三个平面,则这两个平面的位置关系是 平行或相交 。
4.在正方体中,与正方体的一条对角线垂直的面对角线的条数是 6 。
5.两个平面互相垂直,一条直线和其中一个平面平行,则这条直线和另一个平面的位置关系是平行、相交或在另一个平面内 。
6.在正方体1111ABCD A BC D -中,写出过顶点A 的一个平面__AB 1D 1_____,使该平面与正方体的12条棱所在的直线所成的角均相等(注:填上你认为正确的一个平面即可,不必考虑所有可能的情况)。
7.设正方体ABCD —A 1B 1C 1D 1的棱长为1,则(1)A 点到CD 1的距离为________; (2)A 点到BD 1的距离为________;(3)A 点到面BDD 1B 1的距离为_____________; (4)A 点到面A 1BD 的距离为_____________; (5)AA 1与面BB 1D 1D 的距离为__________.答案:(1)26(2)36(3)22(4)33(5)22【范例导析】例1.如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD =DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F .(1)证明PA //平面EDB ; (2)证明PB ⊥平面EFD . 解析:本小题考查直线与平面平行,直线与平面垂直基础知识,考查空间想象能力和推理论证能力.证明:(1)连结AC ,AC 交BD 于O ,连结EO .∵底面ABCD 是正方形,∴点O 是AC 的中点 在PAC ∆中,EO 是中位线,∴PA // EO 而⊂EO 平面EDB 且⊄PA 平面EDB , 所以,PA // 平面EDB(2)∵PD ⊥底面ABCD 且⊂DC 底面ABCD ,∴DC PD ⊥∵PD =DC ,可知PDC ∆是等腰直角三角形,而DE 是斜边PC 的中线, ∴PC DE ⊥. ①同样由PD ⊥底面ABCD ,得PD ⊥BC .∵底面ABCD 是正方形,有DC ⊥BC ,∴BC ⊥平面PDC . 而⊂DE 平面PDC ,∴DE BC ⊥. ②由①和②推得⊥DE 平面PBC . 而⊂PB 平面PBC ,∴PB DE ⊥ 又PB EF ⊥且E EF DE = ,所以PB ⊥平面EFD .例2.如图,△ABC 为正三角形,EC ⊥平面ABC ,BD ∥CE ,CE =A CCA=2 BD,M是EA的中点,求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA。
高二数学空间中的垂直关系知识精讲

高二数学空间中的垂直关系【本讲主要内容】空间中的垂直关系直线与直线垂直、直线与平面垂直、平面与平面垂直【知识掌握】 【知识点精析】1. a ⊥α,b a b ⊥⇒α⊂2. b a //b a ⊥⇒αα⊥,3. 三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
4. 三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
5. α⊥⇒⊥⊥=α⊂α⊂c b c a c A b a b a ,,,,6. α⊥⇒α⊥a b b //a ,7. α⊥⇒⊥β⊂=βαβ⊥αa a a l l ,,, 8. α⊥⇒αββ⊥a //a ,9. γ⊥⇒γ⊥βγ⊥α=βαl l ,, 10. β⊥α⇒β⊥α⊂a a , 11. β⊥α⇒γβγ⊥α//, 12. β⊥α⇒βα⊥//a a ,【解题方法指导】垂直关系的证明可划分为直线与直线垂直、直线与平面垂直、平面与平面垂直三种类型。
这三种类型的垂直关系之间存在着较为紧密的联系,相互转化的特征十分明显。
因此,在解决垂直关系的证明问题时,可以分类逐一研究,但更要注意它们之间的相互联系与相互转化。
1. 直线与直线垂直的证明方法:证明直线与直线垂直,常从以下四个方面进行考虑。
(1)如果直线a 与直线b 是异面直线,可考虑使用异面直线所成角的方法进行,由勾股逆定理算出这个角为90°。
(2)可以转化为直线和平面垂直来考虑,将两条直线中的一条放在某个平面α内,只要能证出另一条与平面α垂直即可。
(3)如果存在两条直线的平行关系,若有直线c 平行于直线a ,又能证出直线b ⊥c ,则有b ⊥a 。
(4)三垂线定理及其逆定理是证明直线与直线垂直的重要定理,在使用的过程中,关键是寻找另一条直线c ,使得c 与b 在同一个平面α内,且b ⊥c ,又c 是直线a 在平面α内的射影,由三垂线定理得出b ⊥a 。
空间中的垂直关系

(2)如图,假设存在点F使平面 AFD⊥平面BFC, ∵AD∥BC,∴AD∥平面BFC, ∴AD平行于平面AFD与平面 BFC的交线l. 8分 ∵EP⊥平面ABCD, ∴EF⊥AD,而AD⊥AB, ∴AD⊥平面EAB, ∴l⊥平面EAB,
∴∠AFB是平面AFD与平面BFC 所成二面角的平面角, 10分 ∵P是AB中点,且FP⊥AB, ∴当∠AFB=90°时,FP=AP, FP ∴当 FP=AP,即 =1 时,平面 AP AFD⊥平面 BFC.… 12 分
规律方法总结
1.空间的垂直关系有直线与直线 垂直、直线与平面垂直、平面与平面垂 直.它们之间存在相互转化关系:
2.当有面面垂直时,一般是在 一个面内找(作)交线的垂线,则直线 垂直于面;在证面面垂直时,一般可 先从现有的直线寻找平面的垂线;在 证面面垂直时,一般可先从现有的直 线寻找平面的垂线,若没有,可作辅 助线解决.
(1)求证:DP⊥面EPC; (2)问在EP上是否存在点F使平面
FP AFD⊥平面 BFC?若存在,求出 的值. AP
解:(1)证明:∵EP⊥面 ABCD, ∴EP⊥DP, 又ABCD为矩形, AB=2BC, P、Q分别为AB、CD的中 点, 1 ∴PQ⊥DC且PQ= 2 DC, ∴DP⊥PC, 4分 又∵EP∩PC=P,∴DP⊥ 面EPC. 6分
2.直线a与b垂直,b⊥平面α,则a与α的 位置关系是( ) A.a⊥α B.a∥α C.a⊂α D.a⊂α或a∥α 答案:D
3.如图,如果MC⊥菱形ABCD所在 平面,那么MA与BD的位置关系是( ) A.平行 B.垂直但不相交 C.异面 D.相交但不垂直 答案:B
三基能力强化
4.(教材习题改编) △ABC中,∠ABC=90°, PA⊥平面ABC,则图中直角三 角形的个数是 . 答案:4
空间中的垂直关系

空间中的垂直关系1.线线垂直判断线线垂直的方法:所成的角是直角,两直线垂直;垂直于平行线中的一条,必垂直于另一条。
三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那麽它也和这条斜线的射影垂直 推理模式: ,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭。
注意:⑴三垂线指PA ,PO ,AO 都垂直α内的直线a 其实质是:斜线和平面内一条直线垂直的判定和性质定理⑵要考虑a 的位置,并注意两定理交替使用。
2.线面垂直定义:如果一条直线l 和一个平面α相交,并且和平面α内的任意一条直线都垂直,我们就说直线l 和平面α互相垂直其中直线l 叫做平面的垂线,平面α叫做直线l 的垂面,直线与平面的交点叫做垂足。
直线l 与平面α垂直记作:l ⊥α。
直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
3.面面垂直两个平面垂直的定义:相交成直二面角的两个平面叫做互相垂直的平面。
两平面垂直的判定定理:(线面垂直⇒面面垂直)如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
两平面垂直的性质定理:(面面垂直⇒线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
题型1:线线垂直问题例1.如图1所示,已知正方体ABCD —A 1B 1C 1D 1中,E 、F 、G 、H 、L 、M 、N 分别为A 1D 1,A 1B 1,BC ,CD ,DA ,DE ,CL 的中点,求证:EF ⊥GF 。
例2.如图,在直三棱柱ABC -A 1B 1C 1中,AB =BC ,D 、E 分别为BB 1、AC 1的中点,证明:ED 为异面直线BB 1与AC 1的公垂线。
空间中的垂直关系

③最小角定理:平面的斜线和它在平面内的射影所成的角, 是这条斜线和这个平面内任一条直线所成角中最小的角. cos =cos1cos2 (2)直线和平面所成的角: ①定义:平面的一条斜线和它在平面内的射影所成的锐 角,叫这条斜线和这个平面所成的角。 规定: 如果直线与平面垂直,那么这条直线和这平面所成的角 为90º ;如果直线与平面平行或直线在平面内,那么直线与平面 所成的角为0º . [0 ②范围: , 90 ] ③求法: 定义法:作出直线在平面上的射影. 向量法: 设n是平面的法向量,AB是平面的一条斜线,其中A∈,则 AB与平面所成的角为: | AB n | arcsin AB n
两个结论 1.如果一个角所在平面外一点到角的两边的距离相等,那么这 点在平面内的射影在这个角的平分线上. 2.过一个角的顶点引这个角所在平面的斜射线,设它与已知角 两边的夹角为锐角且相等,则这条射线在平面内的射影是这 个角的平分线.
唯一性命题
1.过直线外一点有且只有一条直线与已知直线平行. 2.过平面外一点有且只有一个平面与已知平面平行. 3.过一点有且只有一条直线与已知平面垂直. 4.过一点有且只有一个平面与已知直线垂直.
判定 性质 判定 性质
线面平行
线面垂直 线面垂直
判定 性质 判定 性质
面面平行
面面垂直 面面垂直
判定
性质
判定
性质
四.棱锥的顶点在底面上的射影与底面多边形的“心”的关 系 1.若棱锥的各侧棱长相等或棱锥的各侧棱与底面所成的角 相等,则顶点在底面上的射影是底面多边形的外心.
2.若棱锥的各侧面上的斜高相等或棱锥的各侧面与底面所成 的二面角的大小相等,则顶点在底面上的射影是底面多边形 的内心. 3.若三棱锥的各侧棱两两垂直或三棱锥的两相对棱互相垂直, 则顶点在底面上的射影是底面三角形的垂心.
空间中的垂直关系

直线在平面内
知识清单 垂直关系的相互转化 线线垂直 线面垂直 面面垂直
1.注意概念与定理的辨析 2.要证明想判定定理,由已知想性质定理 要证明想判定定理,由已知想性质定理 判定定理 性质
习题回顾 一.判断题: 判断题: 1.如果一条直线垂直于平面内的无数条直 那么这条直线和这个平面垂直.( 线,那么这条直线和这个平面垂直.( ) 2.过一点有且只有一条直线与已知直线 垂直. 垂直. 3.若l∥α,l⊥β ⊥ 则α ⊥β ( ( ) )
Gห้องสมุดไป่ตู้
条件的整合 隐含条件的挖掘
E C
D A
B
典型例题
2.直三棱柱ABC2.直三棱柱ABC-A1B1C中,A1A=AC=√2AB,AB=BC=a, 直三棱柱ABC D为BB1的中点(1)证明:平面ADC1⊥平面AA1C1C 的中点(1)证明:平面ADC 平面AA (1)证明 (2)求点B到平面ADC (2)求点B到平面ADC1的距离 求点
习题回顾 4.已知两个平面垂直,过一个平面内 已知两个平面垂直, 任意一点作交线的垂线,则垂线必垂直 任意一点作交线的垂线, 一点作交线的垂线 于另一个平面. 于另一个平面. ( ) 空间四点A,B,C.D.已知AB A,B,C.D.已知 5.空间四点A,B,C.D.已知AB ⊥ CD, AC ⊥ BD,AD ⊥ BC.则这四点可共面也 BC.则这四点可共面也 可不共面. 可不共面. ( ) 6.两个不重合平面α 6.两个不重合平面α,β.α内有不共 两个不重合平面 线的三点与 距离相等,那么α∥ ( 三点与β距离相等 线的三点与 距离相等,那么 ∥β( )
空间中的垂直关系
本溪市高级中学 姜志勇
知识清单
一.垂直关系的定义: 垂直关系的定义: 1.两条直线垂直-- 相交垂直与异面垂直 两条直线垂直-- 直线垂直于平面内的 任意一条直线 任意一条直线 3.平面与平面垂直-- 三条交线互相垂直 平面与平面垂直--
人教版高二数学必修第四册《空间中的垂直关系》说课稿

人教版高二数学必修第四册《空间中的垂直关系》说课稿一、引言《空间中的垂直关系》是人教版高二数学必修第四册的一章内容,本章主要介绍了三维空间中的垂直关系的概念、性质以及应用,并通过丰富的例题让学生深入理解垂直关系的几何特征和运用方法。
本说课稿将重点介绍该章节的教学目标、教学重点和难点、教学方法和教学过程的设计。
二、教学目标1.理解垂直关系的概念,掌握判断两条直线或两个平面是否垂直的方法;2.掌握垂直关系的性质和判定定理,并能运用定理解决问题;3.在三维空间中,能够熟练应用垂直关系的概念和性质,分析解决相关几何问题。
三、教学重点和难点3.1 教学重点1.垂直关系的定义和性质;2.垂直关系的判定定理。
3.2 教学难点1.理解垂直关系的几何特征,能准确判断两直线或两平面是否垂直;2.运用垂直关系的判定定理解决实际问题。
四、教学内容和安排4.1 教学内容1.垂直关系的概念和性质;2.垂直关系的判定定理;3.垂直关系在三维空间中的应用。
4.2 教学安排1.师生互动,通过引导问题引发学生对垂直关系的思考;2.展示垂直关系的定义和性质,以图例和实例帮助学生理解;3.通过演示和讨论,引入垂直关系的判定定理;4.练习和实践,通过例题和习题的讲解,巩固学生对垂直关系的理解和应用;5.总结与反思,让学生回顾本节课的重要内容和自己的学习体会。
五、教学方法本节课将采用多种教学方法来促进学生的主动参与和深入理解垂直关系的概念和运用方法。
具体教学方法包括:1.启发式教学法:通过提出问题、让学生自主发现、分析和总结,引导学生理解垂直关系的几何特征和性质;2.归纳法:通过示例与练习,让学生掌握垂直关系的判定定理,培养学生逻辑思维和推理能力;3.演示法:用图表和实例展示垂直关系的概念和运用方法,加深学生对知识点的理解;4.口头解答和板书:通过口头解答来激发学生思考和讨论,同时将关键内容通过板书方式呈现,方便学生复习和记忆。
六、教学过程设计6.1 Step 1 引入通过举例引发学生对垂直关系的思考,比如问“墙面上两个相交的直线之间是否存在垂直关系?”等问题。
《空间中的垂直关系》课件

垂直关系在空间中起着重要的作用。本PPT课件旨在介绍垂直关系的定义、 基本概念、应用和重要性,以及建筑结构中的具体应用。
引言
空间中的垂直关系是指物体在垂直方向上的位置和相互关系。垂直关系在建筑、城市规划等领域具有重 要作用,能够影响空间的布局和设计。
垂直方向的基本概念
2
垂直投影的定义和应用
垂直投影是指物体在某个垂直平面上的投影,可以用于建筑设计和工程测量等领 域。
3
垂直距离的测量方法
垂直距离是指两个物体之间在垂直方向上的距离,可以通过测量工具或基于三角 关系计算得出。
应用
1 垂直的重要性和应用
2 实例分析:建筑结构中的垂直关系
垂直关系在建筑结构、城市规划和室内设 计等领域中起着重要作用,能够优化空间 布局和提升空间感。
以高层建筑为例,垂直关系可以影响建筑 的稳定性、使用功能和美观性,是建筑设 计中不可忽视的因素。
总结
垂直关系在空间中具有重要性,能够决定空间的布局和设计。深入了解垂直 关系的定义、基本概念和应用,将有助于提升空间规划与设计的质量。
本PPT课件提供了垂直关系的基本知识和应用框架,以及建筑结构中的实例 分析,可根据实际需求进行具体运用。
垂线的定义
垂线是指与给定直线或平面垂直相交的直线。
垂直平面的定义
垂直平面是指与给定平面垂直相交的平面。
垂直角的定义
垂直角是指两条相交直线、弦或切线所夹的 角为90度。
空间中的垂直关系
1
不同垂直关系的分类
在空间中,垂直关系可以分为垂直与水平、垂直与斜面等不同类型。
参考文献
• 李宁,蔡明华. 理论建筑设计教程 [M]. 机械工业出版社,2015. • Thom as P.J. Architecture 101: From Frank Gehry to Ziggurats,
空间几何中的平行与垂直

空间几何中的平行与垂直在空间几何中,平行和垂直是两个重要的概念。
平行关系指的是两条直线或两个平面永远不会相交,在同一个平面内保持固定的距离;而垂直关系是指两条直线或两个平面相交时,彼此之间的夹角为90度。
平行和垂直关系在几何学中有广泛的应用,不仅帮助我们理解空间的结构和形态,也在实际生活中发挥着重要的作用。
1. 平行关系在空间几何中,平行关系是指两条直线或两个平面永远不会相交的关系。
当两条直线或两个平面的方向向量相等或相互垂直时,它们可以被认为是平行的。
1.1 直线的平行当两条直线的方向向量相等时,它们被称为平行直线。
我们可以使用向量的方法来判断两条直线是否平行。
假设有两条直线 l₁和 l₂,它们的方向向量分别为 a₁和 a₂。
若 a₁和 a₂相等,则 l₁和 l₂平行。
1.2 平面的平行两个平面是平行的,当且仅当它们的法向量相等或者互相垂直。
设两个平面的法向量分别为 n₁和 n₂,若 n₁和 n₂相等,则这两个平面平行。
平行关系在几何学中有许多应用。
例如,在平行四边形中,对角线之间的线段互相平分,每条对角线将平行四边形分成两个全等的三角形。
另外,在建筑设计中,平行关系也被广泛应用,如平行的墙壁或平行的连廊等。
2. 垂直关系垂直关系是指两条直线或两个平面相交时,彼此之间的夹角为90度。
垂直关系在空间几何中非常重要,常常用于求解角度,确定垂直平面等问题。
2.1 直线的垂直两条直线 l₁和 l₂垂直的充分必要条件是它们的方向向量的内积为0。
如果 l₁的方向向量 a₁和 l₂的方向向量 a₂满足 a₁·a₂=0,则 l₁和 l₂垂直。
2.2 平面的垂直两个平面P₁和P₂垂直的充分必要条件是它们的法向量相互垂直。
设平面 P₁的法向量为 n₁,平面 P₂的法向量为 n₂,若 n₁·n₂=0,则 P₁和 P₂垂直。
垂直关系在几何学中有许多应用。
例如,在直角三角形中,两条直角边互相垂直。
此外,垂直关系还可以应用于地理测量、建筑设计等领域。
空间中的垂直关系常见题型及方法
基本知识 二面PAD⊥面ABCD,AB=AD, ∠BAD=60°,E,F分别为AP、AD的中点 求证:(1)直线EF∥面PCD (2)面BEF⊥面PAD
1
【例4】四棱锥P-ABCD,侧面PAD为正三角形,且与底面 ABCD垂直,底面ABCD为边长为2的菱形,∠BAD= 60°,N是PB中点,过AND三点的平面交PC于 M,求证: 求 (1)DP∥面ANC (2)M是PC中点 (3)面PBC⊥面ADMN
【例7】 如右图,△ADP为正三角形,四边形ABCD为正方 形,平面PAD⊥面ABCD。M为平面ABCD内的动 点,且满足MP=MC,则点M在正方形ABCD内的 轨迹为(O为正方形ABCD的中心)
2
空间中的垂直关系常见题型及方法
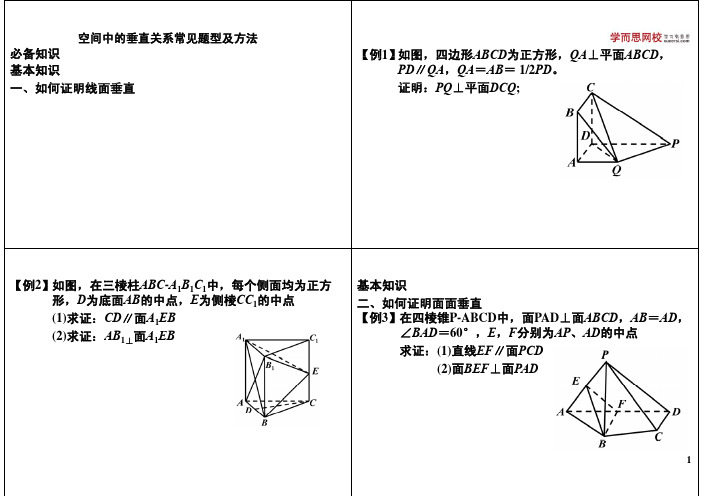
必备知识 基本知识 一、如何证明线面垂直 如何证明线面垂直
【例1】 如图,四边形ABCD为正方形,QA⊥平面ABCD, PD∥QA,QA=AB= 1/2PD。 证明 PQ⊥平面DCQ; 证明:
【例2】如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方 形,D为底面AB的中点,E为侧棱CC1的中点 (1)求证:CD∥面A1EB (2)求证: 求 AB1⊥面A1EB
【例5】 正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1及边界 上运动,并且总保持AP⊥BD1,则动点P的轨迹为?
【例6】 定点A和B都在平面α内,定点P在平面外, C是α内异 于A和B的动点,且PC⊥AC,那么动点C在平面 内的 轨迹是 ( ) A.一条线段,但要去掉两个点 条线段 但要去掉两个点 B.一个圆,但要去掉两个点 C.一个椭圆,但要去掉两个点 D.半圆,但要去掉两个点 半圆 但要去掉两个点
空间中的垂直关系

空间中的垂直关系1.两条直线互相垂直定义:如果两条直线相交于一点或经过平移后相交于一点,并且交角为直角,则称这两条直线互相垂直.2.直线与平面垂直(1)直线与平面垂直的定义:如果一条直线和一个平面相交于点O,并且和这个平面内过交点(O)的任何直线都垂直,就说这条直线和这个平面互相垂直.(2)直线与平面垂直的判定定理及其推论:文字语言图形语言符号语言判定定理如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直⎭⎪⎬⎪⎫a⊂αb⊂αa∩b=Ol⊥al⊥b⇒l⊥α推论1如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直于这个平面⎭⎪⎬⎪⎫a∥ba⊥α⇒b⊥α推论2如果两条直线垂直于同一个平面,那么这两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b3. 平面与平面垂直(1)平面与平面垂直的定义:如果两个相交平面的交线与第三个平面垂直,又这两个平面与第三个平面相交所得两条交线互相垂直,就称这两个平面互相垂直.(2)平面与平面垂直的判定定理:文字语言图形语言符号语言判定定理如果一个平面过另一个平面的一条垂线,则这两个平面互相垂直⎭⎪⎬⎪⎫l⊥αl⊂β⇒α⊥β(3)平面与平面垂直的性质定理:文字语言图形语言符号语言性质定理如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βl ⊂βα∩β=al ⊥a⇒l ⊥α1. 判断下面结论是否正确(请在括号中打“√”或“×”)(1)直线l 与平面α内的无数条直线都垂直,则l ⊥α.( ) (2)若直线a ⊥平面α,直线b ∥α,则直线a 与b 垂直. ( ) (3)直线a ⊥α,b ⊥α,则a ∥b . ( ) (4)若α⊥β,a ⊥β⇒a ∥α. ( ) (5)a ⊥α,a ⊂β⇒α⊥β.( )2. (2013·广东)设m ,n 是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )A .若α⊥β,m ⊂α,n ⊂β,则m ⊥nB .若α∥β,m ⊂α,n ⊂β,,则m ∥nC .若m ⊥n ,m ⊂α,n ⊂β,则α⊥βD .若m ⊥α,m ∥n ,n ∥β,则α⊥β3. 设a ,b ,c 是三条不同的直线,α,β是两个不同的平面,则a ⊥b 的一个充分条件是( )A .a ⊥c ,b ⊥cB .α⊥β,a ⊂α,b ⊂β C .a ⊥α,b ∥αD .a ⊥α,b ⊥α4. 将图1中的等腰直角三角形ABC 沿斜边BC 的中线折起得到空间四面体ABCD (如图2),则在空间四面体ABCD 中,AD 与BC 的位置关系是( )A .相交且垂直B .相交但不垂直C .异面且垂直D .异面但不垂直5. α、β是两个不同的平面,m 、n 是平面α及β之外的两条不同的直线,给出四个论断:①m ⊥n ;②α⊥β;③n ⊥β;④m ⊥α,以其中三个论断作为条件,剩余的一个论断作为结论,写出你认为正确的一个命题:____________________________.A 组 专项基础训练(时间:40分钟)一、选择题1.已知m是平面α的一条斜线,点A∉α,l为过点A的一条动直线,那么下列情形可能出现的是() A.l∥m,l⊥αB.l⊥m,l⊥αC.l⊥m,l∥αD.l∥m,l∥α2. 如图,已知△ABC为直角三角形,其中∠ACB=90°,M为AB的中点,PM垂直于△ABC所在平面,那么()A.P A=PB>PCB.P A=PB<PCC.P A=PB=PCD.P A≠PB≠PC3.在空间内,设l,m,n是三条不同的直线,α,β,γ是三个不同的平面,则下列命题中为假命题的是()A.α⊥γ,β⊥γ,α∩β=l,则l⊥γB.l∥α,l∥β,α∩β=m,则l∥mC.α∩β=l,β∩γ=m,γ∩α=n,若l∥m,则l∥nD.α⊥γ,β⊥γ,则α⊥β或α∥β4.正方体ABCD—A′B′C′D′中,E为A′C′的中点,则直线CE垂直于()A.A′C′B.BDC.A′D′D.AA′又∵BD∥B′D′,∴BD⊥CE.5. 如图所示,直线P A垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面P AC的距离等于线段BC的长,其中正确的是()A.①②B.①②③C.①D.②③二、填空题6.已知P为△ABC所在平面外一点,且P A、PB、PC两两垂直,则下列命题:①P A⊥BC;②PB⊥AC;③PC⊥AB;④AB⊥BC.其中正确的个数是________.7.在正三棱锥P-ABC中,D,E分别是AB,BC的中点,有下列三个论断:①AC⊥PB;②AC∥平面PDE;③AB⊥平面PDE.其中正确论断的序号为________.8.已知平面α,β和直线m,给出条件:①m∥α;②m⊥α;③m⊂α;④α∥β.当满足条件________时,有m⊥β.(填所选条件的序号)三、解答题9.在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.(1)求证:平面DEC⊥平面BDE;(2)求点A到平面BDE的距离.B组专项能力提升1.已知平面α与平面β相交,直线m⊥α,则() A.β内必存在直线与m平行,且存在直线与m垂直B.β内不一定存在直线与m平行,不一定存在直线与m垂直C.β内不一定存在直线与m平行,但必存在直线与m垂直D.β内必存在直线与m平行,不一定存在直线与m垂直2.(2012·江苏)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3 cm,AA1=2 cm,则四棱锥A-BB1D1D的体积为________ cm3.3.如图,已知六棱锥P-ABCDEF的底面是正六边形,P A⊥平面ABC,P A=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面P AE;④∠PDA=45°.其中正确的有________(把所有正确的序号都填上).。
空间几何中的垂直关系

空间几何中的垂直关系垂直关系是空间几何中的重要概念之一,它与直线和平面的相互关系密切相关。
本文将就空间几何中的垂直关系进行详细探讨。
一、垂直关系的定义和性质在空间几何中,我们称两条直线或一个直线和一个平面相互垂直,当且仅当它们的夹角为90度(或称直角)。
垂直关系具有以下性质:1. 垂直关系是相对的:两条直线或一个直线和一个平面相互垂直,可以理解为它们相互垂直的方向互为补角,即互为垂线。
2. 垂直关系具有传递性:如果直线AB垂直于直线BC,那么直线AB也将垂直于直线AC。
这个性质可以通过夹角定义和垂线的性质进行推导。
3. 平面与直线的垂直关系:当一条直线与一个平面垂直时,它与该平面的任意直线均垂直。
这一性质为建立空间几何中的垂直关系提供了便利。
4. 垂直关系与平行关系之间的关系:如果两个平面相互垂直,那么它们的任意一条公共直线与这两个平面都垂直;反之,如果两个平面的任意一条公共直线与这两个平面都垂直,那么这两个平面互相垂直。
二、垂直关系的应用垂直关系在几何学和实际生活中都有广泛的应用。
以下列举了几个常见的应用场景:1. 建筑学中的垂直关系:在建筑设计与施工中,垂直关系是十分重要的,用来确保建筑结构的稳定和整体美观。
例如,墙面的垂直性要求、柱子与楼梯之间的垂直关系等都是基于几何理论的。
2. 地质学中的垂直关系:地层与地层之间的垂直关系是地质学家研究地壳演化和地层分析的基础。
通过研究地质层的垂直关系,可以推断出地层的变动和地质历史的变迁。
3. 数学建模中的垂直关系:在数学建模中,垂直关系被广泛应用于平面几何、三维几何以及向量分析等学科中。
它在描述和解决实际问题时,起到了重要的作用。
4. 导航和测量中的垂直关系:在导航和测量领域,垂直关系被用于确定方向、角度和高度。
例如,地球上的经线与纬线垂直相交,使得我们可以准确测量位置和方向。
三、总结空间几何中的垂直关系是一种重要的几何概念,它与直线和平面之间的关系密不可分。
空间中的垂直关系教案

空间中的垂直关系教案一、教学目标1. 让学生理解垂直关系的概念,能够识别和描述物体之间的垂直关系。
2. 培养学生运用垂直关系解决实际问题的能力。
3. 培养学生的观察能力、动手能力和合作意识。
二、教学内容1. 垂直关系的定义及识别2. 垂直关系的应用3. 实际问题解决三、教学重点与难点1. 教学重点:让学生能够识别和描述物体之间的垂直关系,运用垂直关系解决实际问题。
2. 教学难点:培养学生运用垂直关系解决实际问题的能力。
四、教学方法1. 采用观察、讨论、实践、解决问题的教学方法。
2. 利用教具、模型等辅助教学。
五、教学准备1. 教具:垂直关系模型、实物图片等。
2. 学具:学生用书、练习本、画笔等。
六、教学过程1. 导入新课:通过展示实际生活中的垂直关系实例,引导学生发现和关注垂直关系。
2. 教学新课:讲解垂直关系的定义,让学生观察和描述实例中的垂直关系。
3. 实践操作:学生分组讨论,运用教具模型演示垂直关系,并互相评价。
4. 解决问题:引导学生运用垂直关系解决实际问题,如计算物体的高度、距离等。
5. 巩固拓展:出示不同类型的题目,让学生独立完成,提高运用垂直关系解决问题的能力。
七、课堂小结八、课后作业1. 完成学生用书上的练习题。
2. 观察生活中的垂直关系,拍照或绘图,下节课分享。
九、教学反思教师在课后对自己的教学进行反思,分析教学效果,针对学生的掌握情况调整教学策略。
十、章节测试设计一份章节测试题,检测学生对空间中垂直关系的掌握程度。
六、教学内容与活动1. 活动一:探索垂直关系的性质目的:让学生通过实践探索垂直关系的性质。
过程:学生分组,每组使用不同的材料(如直尺、三角板、绳子等)来构建垂直关系,并记录观察到的性质。
反馈:小组之间分享观察结果,讨论垂直关系的共同特点。
2. 活动二:垂直关系的应用游戏目的:培养学生将垂直关系应用于实际情境中。
过程:设计一个游戏,要求学生在游戏中识别和利用垂直关系,如在建筑游戏中使用垂直关系来构建稳定的结构。
