第二届全国大学生数学竞赛决赛非数学组题目
大学生高等数学竞赛试题汇总与答案

原式=
(ln(1t)t)1/(1t)111
2
2(1t)
t2t2
limelimelimee
t0t0t0
(3)
11
sxnnsxnsxsxn
Iexdx()xde()[xe|edx]
n0
000
ss
nnn(n1)n!n!
sxn1
exdxIII
n12n2n0n1
sssss
0
二、(15分)设函数f(x)在(,)上具有二阶导数,并且
''()(2'
t2t)2(t)''()(2'
3
dxdx/dt(22t)
=。。。
上式可以得到一个微分方程,求解即可。
四、(15分)设
n
a0,Sa,证明:
nnk
k1
(1)当1时,级数
a
n
S
nn
1
收敛;
(2)当1且()
sn时,级数
n
a
n
S
nn
1
发散。
解:
(1)
a>0,
n
s单调递增
n
当
n1
a收敛时,
n
aa
nn
一、(25分,每小题5分)
(1)设
n
22
x(1a)(1a)(1a),其中|a|1,求limxn.
n
n
(2)求
x
lim e1
x
1
x
2
x
。
(3)设s0,求
sxn
Iexdxn。
(1,2,)
0
(4)设函数f(t)有二阶连续导数,
第二届全国大学生数学竞赛(湖南赛区)暨2010年湖南省高校大学生数学竞赛获奖结果

关于第二届全国大学生数学竞赛(湖南赛区)暨2010年湖南省高校大学生数学竞赛获奖结果的通报各高校教务处、数学院(系):第二届全国大学生数学竞赛(湖南赛区)暨2010年湖南省高校大学生数学竞赛于2010年10月30日在湖南师范大学举行,来自全省的21所高校共计591名学生(不含国防科技大学赛区人数)报名参加了这次竞赛,竞赛取得了圆满成功。
本次竞赛分数学专业类和非数学专业类两大组,经过湖南省数学会竞赛委员会的认真评审,共有88人(不含国防科技大学赛区)获第二届全国大学生数学竞赛(湖南赛区)奖,其中数学专业类一等奖10名,二等奖12名,三等奖16名;非数学专业类一等奖10名,二等奖15名,三等奖25名。
有324人(含国防科技大学赛区)获2010年湖南省高校大学生数学竞赛奖,其中数学专业类一等奖29名,二等奖45名,三等奖63名;非数学专业类一等奖36名,二等奖67名,三等奖84名。
现将获奖结果予以公布(见附件1,附件2)。
第二届全国大学生数学竞赛决赛将于2011年3月在北京航空航天大学举行。
根据全国大学生数学竞赛委员会关于各赛区决赛指标的分配办法,经湖南省数学会竞赛委员会讨论决定,分别有10名数学类和8名非数学类选手被推选作为湖南赛区参加第二届全国大学生数学竞赛决赛的候选人上报第二届全国大学生数学竞赛组委会(名单见附件3),名单经第二届全国大学生数学竞赛组委会最终确认后,将由湖南省数学会通知到参加决赛选手所在学校,希各有关单位予以积极支持。
特此通报。
附件1:第二届全国大学生数学竞赛(湖南赛区)获奖结果附件2:2010年湖南省高校大学生数学竞赛获奖结果附件3:湖南赛区参加第二届全国大学生数学竞赛决赛推选人名单备注:获奖名单按获奖者所在学校名称“笔划”顺序排列。
附件1:第二届全国大学生数学竞赛(湖南赛区)获奖名单(数学专业类)(非数学专业类)附件2:2010年湖南省高校大学生数学竞赛获奖名单(数学专业类)2010年湖南省高校大学生数学竞赛获奖名单(非数学专业类)附件3:湖南赛区参加第二届全国大学生数学竞赛决赛推选人名单1.数学类2.非数学类。
第二届全国大学生数学竞赛决赛试题及详细解答

第二届全国大学生数学竞赛决赛试题及答案(非数学类,2011)一.计算下列各题(本题共3小题,每小题各5分,共15分。
)(1).求11cos 0sin lim xx x x -→⎛⎫ ⎪⎝⎭;解:方法一(用两个重要极限):()()20003221sin 1cos sin 1cos 001sin cos 12limlimlim sin 11331cos 3222sin sin lim lim 1lim x x x x x xxx x x x x x x x x x x x x x x x x x x x x x x ee eee→→→-∙---→→------→-⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭=====方法二(取对数):0202000322sin 1sin 1ln lim11cos lim1cos 201sin cos 12limlimlim 11333222sin lim x x x x x xx x x xx xx x x xx x x x x eex ee e e→→→→→-⎛⎫ ⎪⎝⎭--→----⎛⎫== ⎪⎝⎭====(2).求111lim ...12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭; 解:方法一(用欧拉公式)令111...12n x n n n n=++++++ 111ln =C+o 1211111ln 2=C+o 1212n nn n n n+++-++++++-+由欧拉公式得(),则(),其中,()1o 表示n →∞时的无穷小量,-ln2o 1n x ∴=两式相减,得:(),lim ln 2.n n x →∞∴=方法二(用定积分的定义)111lim lim lim()12n n n n x n n n→∞→∞→∞=++++111lim ()111n n n nn→∞=++++101ln 21dx x==+⎰(3)已知()2ln 1arctan tt x e y t e ⎧=+⎪⎨=-⎪⎩,求22d y dx 。
全国大学生数学竞赛(非数学类)大纲及历年预赛试卷

(*) 2 0 (1 2t 2 t 4 )dt 1
2
1 0
(1 2t 2
t 4 )dt
2t
2 t3 3
1 5
t
5
1 0
16 15
2.设 f (x) 是连续函数,且满足 f (x) 3x2
2
f (x)dx 2 , 则 f (x) ____________.
0
解 令 A 2 f (x)dx ,则 f (x) 3x2 A 2 , 0
n
x0
n
故
A lim ex e2x enx n e
x0
n
x
e lim ex e2x enx n
x0
nx
e lim ex 2e2x nenx e 1 2 n n 1 e
x0
n
n
2
因此
lim ( ex
e2x
e
nx
)
e x
eA
n1e
e 2
x0
n
解法 2 因
(x0 , y0 ) 处 的 法 向 量 为 (zx (x0 , y0 ), z y (x0 , y0 ),1) , 故 (zx (x0 , y0 ), z y (x0 , y0 ),1) 与
(2,2,1) 平行,因此,由 zx x , z y 2 y 知 2 zx (x0 , y0 ) x0 ,2 z y (x0 , y0 ) 2 y0 ,
y(1
f ( y))
因此
—4—
y
f ( y) [1 f ( y)]2 x2[1 f ( y)]3
二、(5
分)求极限 lim ( ex
e2x
e nx
e
)x
最近五届全国大学生高等数学竞赛真题及答案(非数学类)

目录第一届全国大学生数学竞赛预赛试卷 ........................................................................................... 1 第二届全国大学生数学竞赛预赛试卷 ........................................................................................... 7 第三届全国大学生数学竞赛预赛试卷 ......................................................................................... 11 第四届全国大学生数学竞赛预赛试卷 ......................................................................................... 18 第五届全国大学生数学竞赛预赛试卷 .. (23)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u uvu u u y x yx x yy x DDd d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
历届全国大学生高等数学竞赛真题及答案非数学类

前三届高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解: 因平面022=-+z y x 的法向量为)1,2,2(-,而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
全国大学生高等数学竞赛真题及答案(非数学类)-无答案

2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 4.设函数)(x y y =由方程29ln )(y y f e xe =确定,其中f 具有二阶导数,且1≠'f ,则=22d d x y________________. 二、(5分)求极限xenx x x x ne e e )(lim 20+++→ ,其中n 是给定的正整数.三、(15分)设函数)(x f 连续,⎰=10d )()(t xt f x g ,且A xx f x =→)(lim,A 为常数,求)(x g '并讨论)(x g '在0=x 处的连续性.四、(15分)已知平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:(1)⎰⎰-=---Lx y Lx yx ye y xe x ye y xed d d d sin sin sin sin ;(2)2sin sin 25d d π⎰≥--Ly yx ye y xe .五、(10分)已知xx e xe y 21+=,x x e xe y -+=2,xx x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.六、(10分)设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又已知该抛物线与x 轴及直线1=x 所围图形的面积为31.试确定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积最小.七、(15分)已知)(x u n 满足),2,1()()(1 =+='-n e x x u x u x n n n, 且neu n =)1(, 求函数项级数∑∞=1)(n nx u之和.八、(10分)求-→1x 时, 与∑∞=02n n x等价的无穷大量.2010年 第二届全国大学生数学竞赛预赛试卷一、(25分,每小题5分) (1)设22(1)(1)(1),nn x a a a =+++其中||1,a <求lim .n n x →∞(2)求21lim 1x x x e x -→∞⎛⎫+ ⎪⎝⎭。
历年全国大学生高等数学竞赛真题及答案(2009-2011非数学类).

1
1 2 4 2 3 1 5 16
2 (12t t )dt 2 t t t
令t 1u ,则u 1t2 ,du 2tdt ,u2 12t2 t4 ,u(1u) t2 (1t)(1t) ,
0
(*) 2 (12t2 t4 )dt
1
2
d y
则 2 ________________.
dx
f (y ) y
x
解方程xe e ln 29 的两边对 求导,得
y
(x y ) ln(1 ) u ln u u ln v
1x y
坐标轴所围成三角形区域.
0 1
解令 ,则 , ,
x y u,x v x v,y u v dxdy det dudv dudv
1 1
2 .设f (x) 是连续函数,且满足f (x) 3x 2 f (x)dx 2 , 则f (x) ____________.
0
处的切平面方程是2(x 2) 2(y 1) (z 5) 0 ,即曲面z y 2 平行平面
2
2x 2y z 0 的切平面方程是2x 2y z 1 0 。
4 .设函数y y (x) 由方程 f (y ) y 确定,其中 具有二阶导数,且 ,
xe e ln 29 f f 1
处的法向量为(z (x , y ), z (x , y ),1) ,故(z (x , y ), z (x , y ),1) 与(2,2,1) 平行,
x 0 0 y 0 0 x 0 0 y 0 0
D x dxdy D dudv
1x y 1u
1 u ln u u u u
4 2 10
解得A 。因此f (x) 3x 。
第二届全国大学生数学竞赛上海赛区赛暨第二届上海市大学生数学竞赛获奖名单(非数学类)
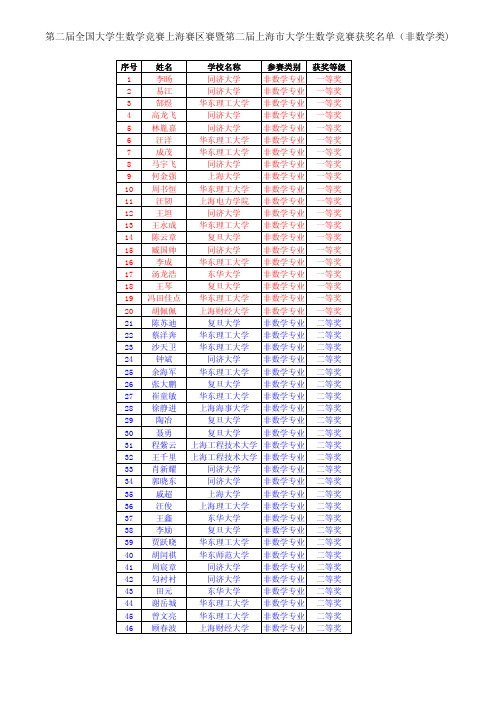
序号姓名学校名称参赛类别获奖等级1李旸同济大学非数学专业一等奖2易江同济大学非数学专业一等奖3郜煜华东理工大学非数学专业一等奖4高龙飞同济大学非数学专业一等奖5林胤嘉同济大学非数学专业一等奖6汪洋华东理工大学非数学专业一等奖7成茂华东理工大学非数学专业一等奖8马宇飞同济大学非数学专业一等奖9何金强上海大学非数学专业一等奖10周书恒华东理工大学非数学专业一等奖11汪韧上海电力学院非数学专业一等奖12王坦同济大学非数学专业一等奖13王永成华东理工大学非数学专业一等奖14陈云章复旦大学非数学专业一等奖15臧国帅同济大学非数学专业一等奖16李成华东理工大学非数学专业一等奖17汤龙浩东华大学非数学专业一等奖18王琴复旦大学非数学专业一等奖19冯田佳点华东理工大学非数学专业一等奖20胡佩佩上海财经大学非数学专业一等奖21陈苏迪复旦大学非数学专业二等奖22蔡洋奔华东理工大学非数学专业二等奖23沙天卫华东理工大学非数学专业二等奖24钟斌同济大学非数学专业二等奖25余海军华东理工大学非数学专业二等奖26张大鹏复旦大学非数学专业二等奖27崔童敏华东理工大学非数学专业二等奖28徐静进上海海事大学非数学专业二等奖29陶冶复旦大学非数学专业二等奖30聂勇复旦大学非数学专业二等奖31程紫云上海工程技术大学非数学专业二等奖32王千里上海工程技术大学非数学专业二等奖33肖新耀同济大学非数学专业二等奖34郭晓东同济大学非数学专业二等奖35戚超上海大学非数学专业二等奖36汪俊上海理工大学非数学专业二等奖37王鑫东华大学非数学专业二等奖38李励复旦大学非数学专业二等奖39贾跃晓华东理工大学非数学专业二等奖40胡闰祺华东师范大学非数学专业二等奖41周宸章同济大学非数学专业二等奖42勾衬衬同济大学非数学专业二等奖43田元东华大学非数学专业二等奖44谢岳城华东理工大学非数学专业二等奖45曾文亮华东理工大学非数学专业二等奖46顾春波上海财经大学非数学专业二等奖47吴永平上海大学非数学专业二等奖48江涛 上海大学非数学专业二等奖49胡祎同济大学非数学专业二等奖50陈辉同济大学非数学专业二等奖51邓达复旦大学非数学专业二等奖52孙方旭华东理工大学非数学专业二等奖53闵志伟华东理工大学非数学专业二等奖54汪 丰上海财经大学非数学专业二等奖55毛钰同济大学非数学专业二等奖56卢杰东华大学非数学专业二等奖57刘星星东华大学非数学专业二等奖58陈志宏东华大学非数学专业二等奖59练成华东理工大学非数学专业二等奖60盛博文上海大学非数学专业二等奖61黎萍上海工程技术大学非数学专业二等奖62王晓蓓同济大学非数学专业二等奖63周维华上海第二工业大学非数学专业二等奖64袁振东华大学非数学专业二等奖65刘小年复旦大学非数学专业二等奖66余刘柱华东理工大学非数学专业二等奖67朱诗倩华东师范大学非数学专业二等奖68蒋文斌上海工程技术大学非数学专业二等奖69徐建军上海理工大学非数学专业二等奖70吴超上海理工大学非数学专业二等奖71何超同济大学非数学专业二等奖72夏怀婷上海第二工业大学非数学专业三等奖73孔懿阳华东理工大学非数学专业三等奖74容尔益华东理工大学非数学专业三等奖75孙朦朦华东理工大学非数学专业三等奖76汪一鸣华东理工大学非数学专业三等奖77周阳华东理工大学非数学专业三等奖78周碧华华东师范大学非数学专业三等奖79黄志斌华东师范大学非数学专业三等奖80徐栋华东师范大学非数学专业三等奖81靳 轲上海财经大学非数学专业三等奖82佘 昀上海财经大学非数学专业三等奖83陈家诚上海大学非数学专业三等奖84朱绪嘉同济大学非数学专业三等奖85吴薇上海第二工业大学非数学专业三等奖86周文俊华东理工大学非数学专业三等奖87申 翔上海财经大学非数学专业三等奖88吴靖楠上海海事大学非数学专业三等奖89李清源上海理工大学非数学专业三等奖90张伟上海理工大学非数学专业三等奖91周庆昕同济大学非数学专业三等奖92关响生同济大学非数学专业三等奖93傅鹏复旦大学非数学专业三等奖94张阿龙华东理工大学非数学专业三等奖95顾凌峰华东师范大学非数学专业三等奖96曾秀兰华东师范大学非数学专业三等奖97李梁华东师范大学非数学专业三等奖98林正凯上海财经大学非数学专业三等奖99龚威上海理工大学非数学专业三等奖100李南同济大学非数学专业三等奖101彭程同济大学非数学专业三等奖102李萌同济大学非数学专业三等奖103丁婧东华大学非数学专业三等奖104姚胜东华大学非数学专业三等奖105李建东华大学非数学专业三等奖106李君楠华东理工大学非数学专业三等奖107邝斌上海大学非数学专业三等奖108张翔上海大学非数学专业三等奖109邱思择同济大学非数学专业三等奖110段鹏飞同济大学非数学专业三等奖111管道霞上海第二工业大学非数学专业三等奖112杨栩鑫复旦大学非数学专业三等奖113张雪蓉复旦大学非数学专业三等奖114徐颖婷华东理工大学非数学专业三等奖115吕梦晨上海财经大学非数学专业三等奖116李庄骅上海财经大学非数学专业三等奖117李为上海理工大学非数学专业三等奖118崔雨辰上海理工大学非数学专业三等奖119许国文同济大学非数学专业三等奖120沈剑同济大学非数学专业三等奖121王劲鹏同济大学非数学专业三等奖122杨光勇上海电力学院非数学专业三等奖123刘强上海海事大学非数学专业三等奖124张杰上海理工大学非数学专业三等奖125文苗上海理工大学非数学专业三等奖126黄荣蓉上海第二工业大学非数学专业三等奖127赵文强上海电力学院非数学专业三等奖128李杨上海工程技术大学非数学专业三等奖129徐锡明第二军医大学非数学专业三等奖130徐鹏程上海师范大学非数学专业三等奖131陈孝东上海工程技术大学非数学专业三等奖132江志浩上海海关学院非数学专业三等奖133徐清原上海师范大学非数学专业三等奖134陈 权上海应用技术学院非数学专业三等奖135喻红婕上海第二工业大学非数学专业三等奖136彭东升上海应用技术学院非数学专业三等奖。
全国大学生数学竞赛大纲(非专业组)

中国大学生数学竞赛竞赛大纲(初稿)为了进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,激励大学生学习数学的兴趣,发现和选拔数学创新人才,更好地实现“中国大学生数学竞赛”的目标,特制订本大纲。
一、竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是:激励大学生学习数学的兴趣,进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才。
“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。
二、竞赛的内容中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立.2.函数的性质:有界性、单调性、周期性和奇偶性.3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4.数列极限与函数极限的定义及其性质、函数的左极限与右极限.5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7.函数的连续性(含左连续与右连续)、函数间断点的类型.8.连续函数的性质和初等函数的连续性.9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理).二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital)法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1.原函数和不定积分的概念.2.不定积分的基本性质、基本积分公式.3.定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式.4.不定积分和定积分的换元积分法与分部积分法.5.有理函数、三角函数的有理式和简单无理函数的积分.6.广义积分.7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli )方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程:),()n (x f y =),,(y x f y '=''),(y y f y '=''.4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6. 简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7. 欧拉(Euler )方程.8. 微分方程的简单应用五、向量代数和空间解析几何1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2. 两向量垂直、平行的条件、两向量的夹角.3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4. 曲面方程和空间曲线方程的概念、平面方程、直线方程.5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.六、多元函数微分学1. 多元函数的概念、二元函数的几何意义.2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4. 多元复合函数、隐函数的求导法.5. 二阶偏导数、方向导数和梯度.6. 空间曲线的切线和法平面、曲面的切平面和法线.7. 二元函数的二阶泰勒公式.8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1. 二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标)、三重积分的计算(直角坐标、柱面坐标、球面坐标).2. 两类曲线积分的概念、性质及计算、两类曲线积分的关系.3. 格林(Green)公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4. 两类曲面积分的概念、性质及计算、两类曲面积分的关系.5.高斯(Gauss)公式、斯托克斯(Stokes)公式、散度和旋度的概念及计算.6.重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等)八、无穷级数1.常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2.几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz)判别法.3.任意项级数的绝对收敛与条件收敛.4.函数项级数的收敛域与和函数的概念.5.幂级数及其收敛半径、收敛区间(指开区间)、收敛域与和函数.6.幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)、简单幂级数的和函数的求法.7.初等函数的幂级数展开式.8.函数的傅里叶(Fourier)系数与傅里叶级数、狄利克雷(Dirichlei)定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。
第二届全国大学生数学竞赛决赛试卷(非数学类)

第二届全国大学生数学竞赛决赛试卷(非数学类,2011年3月)一、(本小题3分,每小题各5分,共15分)计算下列各题(要求写出重要步骤).(1)11cos 0sin lim x x x x -→⎛⎫ ⎪⎝⎭(2)111lim 12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭ (3)已知()2ln 1arctan t t x e y t e⎧=+⎪⎨=-⎪⎩,求22d d y x 二、(本题10分)求方程(24)d (1)d 0x y x x y y +-++-=的通解.三、(本题15分)设函数()f x 在0x =的某邻域内有二阶连续导数,且(0),(0),(0)f f f '''均不为零. 证明:存在唯一一组实数123,,k k k ,使得12320()(2)(3)(0)lim 0h k f h k f h k f h f h →++-=. 四、(本题17分)设2221222:1x y z a b c∑++=,其中0a b c >>>,2222:z x y ∑=+,Γ为1∑和2∑的交线. 求椭球面1∑在Γ上各点的切平面到原点距离的最大值和最小值.五、(本题16分)已知S 是空间曲线22310x y z ⎧+=⎨=⎩绕y 轴旋转形成的椭球面的上半部分(0z ≥)(取上侧),∏是S 在(,,)P x y z 点处的切平面,(,,)x y z ρ是原点到切平面∏的距离,,,λμν表示S 的正法向的方向余弦. 计算(1)d (,,)S z S x y z ρ⎰⎰; (2)(3)d Sz x y z S λμν++⎰⎰. 六、(本题12分)设()f x 是在(,)-∞+∞内可微函数,且()()f x mf x '<,其中01m <<.任取实数0a ,定义1ln ()n n a f a -=,1,2,n = .证明:11()n n n aa ∞-=-∑绝对收敛.七、(本题15分)是否存在区间[0,2]上的连续可微函数()f x ,满足(0)(2)1f f ==,()1f x '≤,20()d 1f x x ≤⎰?请说明理由.。
2010年第二届中国大学生数学竞赛四川赛区非数学专业组获奖名单

姓名
肖俊超 于涛 方斌 匡启帆 任其武 刘慧颖 陈通恒 袁银霞 周志云 朱小东 吴晨 涂新 刘尧 唐高民 冯玺祥 李辉 张也平
学校
四川大学 四川大学 四川大学 四川大学 四川大学 四川大学 四川大学 成都理工大学 成都理工大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学 电子科技大学
三等奖
(90项) 90项
张猛 曹英帅 王衍豪 李星辰 向济璇 邓小龙 马利锋 江海 陈钱 雷寿林 潘滔 王志 姜立茸 王耀辉 张焕 周才强 傅畅 俞水 纪东峰 刘章源 宁超 林川 郭伟 张浪 李志良 赖泽祺 廖小赛 何欢欢
代刚 李良 杨容 陈勇 赵旭 王亚飞 陆锦锦 舒展 王义 王瑞卓 赵俊博 彭磊 曹林强 张航 朱新明 李强 孙铜 周军
一等奖
(36项) 36项
许琛 贾逢德 邓波 付松林 阮涛 陈祎 易波 夏永敏 魏冰然 许皓天 汪波 徐放 鲍新春 张国彦
周舟 王冰川 刘丛志 陈前宇 田野 陈慧 王浩宇 吴博剑 王超 肖文健 安康 刘虎洋 卢坤 张进 周佃刚 赵鹏 王亚驰 倪尧 陈卓 李志希 李俊慧 艾兴胜 李小飞 李渝 王李波 李甜 徐洪闪 王海阳 黄杰 袁璐璐 张轩 吴宣 马宁
电子科技大学成都学院 西华大学 西南交通大学 西南交通大学 西南石油大学 四川大学 四川大学
四川大学
四川大学 四川大学 四川大学 四川大学 四川大学 成都大学 成都理工大学 成都理工大学
大学生高等数学竞赛试题汇总及答案

前三届高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009-2010年第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(16/15,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=,⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,2.设)(x f 是连续函数,且满足⎰--=222d )(3)(x x f x x f ,则=)(x f ____________.解:令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-,而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
最近五届全国大学生高等数学竞赛真题及答案(非数学类)

目录第一届全国大学生数学竞赛预赛试卷 ........................................................................................... 1 第二届全国大学生数学竞赛预赛试卷 ........................................................................................... 7 第三届全国大学生数学竞赛预赛试卷 ......................................................................................... 11 第四届全国大学生数学竞赛预赛试卷 ......................................................................................... 18 第五届全国大学生数学竞赛预赛试卷 .. (23)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u uvu u u y x yx x yy x DDd d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t 2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
全国大学生数学竞赛初赛2010年第二届《非数学专业》竞赛题目及答案解析高清无水印版

的 对 称 式 方 程 为 l1 :
1
1
0
,记两直线的方向向量分别为
l1 1, 1, 0 ,l2 4, 2, 1 ,两直线上两定点分别为P1(0, 0, 0), P2(2, 1, 3),并记
a
P1P2
2, 1, 3 ,l1
l2
1, 1,6;
a
l1
l2
| 2 1 18 |
19
其中 x, y, z | x2 y2 z2 1 而
a2 b2 c2
x2dV a x2 dx
a
y2 z2
dy dz
x2
a x2
a
ab 1
x2 a2
dx
4a 3bc 15
.
1
b2 c2
a2
4
或者使用换元法,有
x2dV
2
d
d
1
a
2r
2
0
0
0
sin2
cos2
abcr2
x2
dy
D
4xd x
dy
0.
6
C
x4 y2
的值为常数.
(1) 设 L 为正向闭曲线(x 2)2 y2 1 . 证明:
2xy d x (x)d y 0;
L
x4 y2
2xy d x (x)d y
(2) 求函数(x) ; (3) 设C 是围绕原点的光滑简单正向闭曲线,求
C
x4 y2
.
2xy d x (x)d y
【参考答案】设
L
x4 y2
I ,将曲线L 分割成两段L L1 L2 。设L0 不经过原点的
光滑曲线,使得 L0 L1 和 L0 L2 分别组成围绕原点的分段光滑闭曲线. 由已知条件可知 L0 L1 和
