一种分析和设计抗混叠滤波器的方法
抗混叠滤波器设计问题探讨

科技 一向导
21 年第 2 期 02 4
抗混叠滤波器设计问题探讨
吕彩 珍
( 上海奥波电子有限公 司 中国 上海
【 摘
2 07 ) 0 0 2
要】 电力谐 波分析 中, 为了最大程度 地抑制 或消除频谱 混叠对动 态测控 系统的影 响, 必须利 用抗混 叠滤波器。 设计抗 混叠滤波器时不
字长 N 1 , S = / 。依靠增 加采 样频率放宽对模 拟滤波 = 0时 1 B D ” L 2 器性 能的要求 是有 限度的. 带来 的问题是对 A D I 转换 器的性 能要 求提 高, 采样数据量增 加 , 系统 的运算 速率也必须提 高。为 了解决这 个问 题. 采用过采样 技术 12过采样 时模拟抗混叠滤波器 的设计 . 121 ..过采样技术与 ∑ △式 AD转换器 一 I 为了降低对模拟 滤波器 的技术要求 , 中先 以 Dv D >) 工程  ̄L 1 = 的 频率采样 , 经过 A D后 , I 再按照 1 L , 因子抽取 , / 使采样频率 降低到 0 模 拟滤 波器 的过渡带 n < < ・ , n LQ/ 其主要完成对高于 L 的高频 2 n, 2 分量 的滤除。这样 的预滤波必然导致采样得到的信号在 n < < F 内 2 fr 1 发生混 叠。 但这部分混叠在对信号抽 取前用数字滤波器滤 除。 这样使 模拟滤 波器就容易设计和实现 采用数字滤波加模拟滤波解决频谱 混 叠 问题 ,高 阶的数字滤波器可以 由 D P编程实现 . S S D P的运行速度 快 的特点可 以使 阶数很高 的数字低通滤波器 以级联形式实现 这种方 案 最终并不增加信号 的数据量也未加大对微处理器运算速度的要求 基 于过采 样技 术发展 起来 的 ∑一 △式 A D转 换器利 用过 采样 技 I 术、 噪声整形和数字滤波 已经使 AD转换器 的分辨率高达 2 位 I 4 1 . 过采样 中. .2 2 模拟抗混叠滤波器的设计 通 过程 序 设 定 A 7 3 0的采 样 频 率 n = i = 4 H ,取 0 : D 36 Lt 6k z 2 , . 5 计算各次谐 波电压和和 电流的 D T时 . F 假定单 周期采样点 数 18此 时取 nr1 8 5 = . H , = 0 2, = 2 x 0 64 z L 1 。模拟滤 波器的过渡带 25 H < k .k z l 2H , ' kz k3 主要完成对频率 大于 L / = 2 H 的高频信 号的滤除 此 n 23k z 时滤波器通带最大衰减取 0 ,阻带最小 衰减 : 2 1 I N — 2 1 . 1 一 0 g( 2 ̄ 0 g / 5 (2 ) 0d , 1 一1 2 B 抗混 叠滤波器 的阶数 n 5 可见 AD转 换器 的精度 提 /7 =。 I 高了6 倍( 4 精度由 1 增 加到 1 ) 但模拟滤波器的阶数降低 1 滤 0 6。 阶 除 n 到L D 之间无用信 号的任务 则交给 A D转换 之后 的数 字滤波 I 器完成 。 在谐波分析 中. 了克服相位误差 . 续的数字滤波器必须采 为 后 用 F 线性相位数字滤波器 . i r 本文篇幅原因不再赘述
一种与显示设备相关的抗颜色混叠新方法

色混叠滤波 方法 。 鉴于颜色 混叠 的区域及形状 与亚像 素排布 的多样性 紧密 相关, 在频域 内通过倒 晶格理论给 出不 同 亚像素排布各基色 的 Ny q u i s t 频率限制图 , 并 以此为依据设计各基色分量上 的抗混叠滤波器 。 对 图像进行滤波预处 理后再经亚像素采样 显示图像 , 达 到保持 图像清 晰度的同时消除或减 弱显示图像中颜色 混叠的 目的。理论分析和仿 真结果表 明,相对于 5 - t a p滤波法 ,在无 明显颜色错误 的前提下 ,该方法可将 图像亮度分量 的 P S NR 值提高 3 O % 左右 ;另外 ,该算法简 单,易于实现 。
-
( S c h o o l o f T e c h n i c a l P h y s i c s , X i d i a n U n i v e r s i t y , X i ’ a n 7 1 0 0 7 1 , C h i n a ) ( I n s t i t u t e C o m p u t e r S c i e n c e a n d T e c h n o l o g y , X i ’ a n U n i v e r s i t y
一
种 与显 示设 备相 关的抗颜 色混叠新方法
赵 小明 赵 园美 周筱媛
西安
袁胜春
7 1 0 0 7 1 )
( 西安 电子科技 大学技 术物 理学院
( 西安科技 大学计 算机科 学与技 术学院
摘
西安
7 1 0 0 5 4 1
要: 针对显示系统 中应用亚像素采样技术 引起 的颜 色混叠问题 , 该文提 出一种基于显示 设备亚像素排布 的抗颜
A No v e l Co l o r An t i — a l i a s i n g Me t h o d Re l a t e d t o Di s pl a y s
放大器噪声分析与ADC相关参数理解
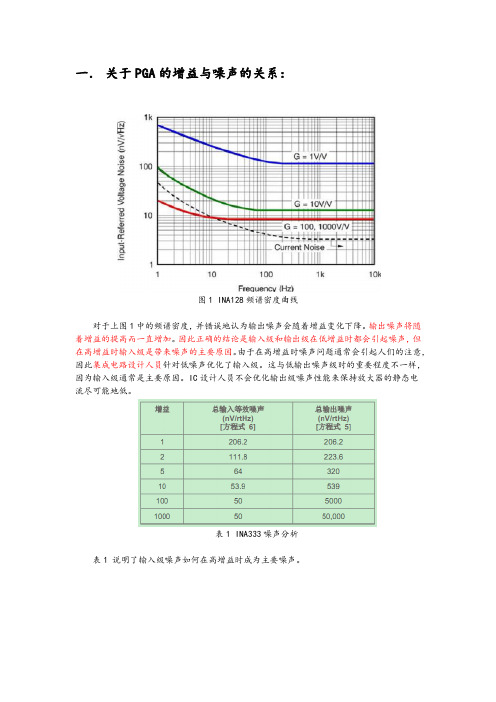
一.关于PGA的增益与噪声的关系:图1 INA128频谱密度曲线对于上图1中的频谱密度,并错误地认为输出噪声会随着增益变化下降。
输出噪声将随着增益的提高而一直增加。
因此正确的结论是输入级和输出级在低增益时都会引起噪声,但在高增益时输入级是带来噪声的主要原因。
由于在高增益时噪声问题通常会引起人们的注意,因此集成电路设计人员针对低噪声优化了输入级。
这与低输出噪声级时的重要程度不一样,因为输入级通常是主要原因。
IC设计人员不会优化输出级噪声性能来保持放大器的静态电流尽可能地低。
表1 INA333噪声分析表1 说明了输入级噪声如何在高增益时成为主要噪声。
下式为仪表放大器的噪声计算公式:RTO=G*RTI例如,AD620A 的噪声典型值规定为 eni=9 nV/√Hz 和 eno =72 nV/√Hz。
因此,AD620A 工作在增益为10 条件下的RTI 总噪声计算如下:二.ADC峰峰值分辨率与有效分辨率大多数应用不希望在系统输出时看到码闪烁。
例如,对于电子秤应用,无闪烁位数很重要。
可以将ADC产生的数字字截断,使得在电子秤监视器上看不到闪烁位。
无噪声分辨率或峰峰值分辨率是根据数据手册给出的噪声值计算出的。
首先计算信噪比(SNR):SNR = 20log(噪声/满量程输入)ADI公司一般规定使用峰峰值分辨率或无噪声码分辨率,这是使用峰值噪声(等于均方根噪声的6.6倍)计算SNR而获得的。
从信噪比计算中可以确定精度。
SNR = 6.02N + 1.76 = 20log(峰值噪声/满量程输入) 从AD7719数据手册可知,当模拟输入范围为+2.56 V且数据更新速率为5.35 Hz时,均方根噪声等于1.25μV。
根据该数据计算信噪比:(20log((6.6 × 1.25E–6)/(2.56 × 2)) = –115.85 dB 据此计算峰峰值分辨率:115.85 = 6.02N + 1.76 => N = (115.85 – 1.76)/6.02 = 19 Bits 因此,在上述条件下,19个MSB中无闪烁位。
适用于有源电力滤波器的抗混叠滤波器设计

U 刖 吾
在 当代煤矿 的电网 中, 由于大量大功率和 非线性设备的应 用, 致使 部分煤矿 电 网中的谐波含 量已 经远远超 出国家 标准 ,
在 国 内外 专 家 学 者 的 努 力 下 , 源 滤 波 器 在 煤 矿 电 网 谐 波 治 理 有
八 八 厂 八 \
t增摄杠攥罄
抗 混叠 滤 波 器 。
: 十一十… 高 :… {: {: {: … }:一 :一1 : : } …: :… :… …: ; … : …: …: :- …: : 吲 十… …: : 哥: { … } { . }
一 。 。
{ 十 一十 … } } } { { { { 十 一 十 … … L 一 L _ 。 … … … … … … … … … _ _-
…
一
; -{ … … … ; ; : … ÷ … … } ; ; ; 一 - … … … … … … … … 一
一… — … : : 1 。… f : … … … … … … … … … … … … 一1
本文针对煤 矿电网谐 波主要分布在 3 0次以内的实际情况 , 通 过理论分析 , t b软 件验证 , 计出 了一款具 有针 对性的 mal a 设
珏 0 “ 栳 拦,暑 强 =¨ .
. .
.._..__ .-_..一 4 .'.3 -¨ 1
~ 墨■ . 0 1 “ 三 . 土譬.7 图 - 三 I . - 三 I 三 ; ] L
中 的应用越 来越广泛 。滤除谐 波的前提 是要准 确地检 测出谐 波, 目前广 泛应 用于 实 践的谐 波 检测 算法 为 F T, F T计 F 用 F 算信 号频谱时 , 免信号 产生混叠 是首要任 务 , 避 因此抗 混叠滤 波器作为信 号的预处理环节 , 它在有源电力滤 波器 中是必不可
fir设计步骤

fir设计步骤FIR设计步骤一、引言FIR(Finite Impulse Response)滤波器是一种常用的数字滤波器。
它具有线性相位响应和有限的脉冲响应特性,被广泛应用于信号处理领域。
本文将详细介绍FIR设计的步骤。
二、确定滤波器的规格要求在进行FIR设计之前,首先需要明确滤波器的规格要求,包括截止频率、通带增益、抗混叠要求等。
这些规格要求将直接影响到滤波器的设计参数和性能。
三、选择窗函数FIR设计中常用的窗函数有矩形窗、汉宁窗、汉明窗、布莱克曼窗等。
选择合适的窗函数可以平衡滤波器的主瓣宽度和副瓣衰减。
在选择窗函数时,需要考虑滤波器的性能要求和实际应用场景。
四、确定滤波器的阶数滤波器的阶数决定了其频率响应的陡峭程度。
一般来说,阶数越高,滤波器的性能越好,但计算复杂度也会增加。
根据规格要求和计算资源的考虑,确定合适的滤波器阶数。
五、计算理想频率响应根据滤波器的规格要求,可以计算出理想的频率响应。
理想频率响应是指在所需的通带增益和副瓣衰减要求下,滤波器在频域上的理想响应。
六、设计滤波器的频率响应通过选择合适的窗函数,可以将理想频率响应转换为实际的频率响应。
窗函数的作用是在频域上对理想频率响应进行加权,以实现对滤波器性能的调节。
七、计算滤波器的时域响应通过对设计的频率响应进行反变换,可以得到滤波器的时域响应。
时域响应是指滤波器的脉冲响应,即滤波器对单位脉冲输入的响应。
八、优化滤波器的性能设计完成后,可以对滤波器的性能进行优化。
常见的优化方法包括增加滤波器的阶数、调整窗函数的参数、改变滤波器的截止频率等。
通过优化,可以进一步改善滤波器的性能。
九、验证滤波器的性能设计完成后,需要对滤波器的性能进行验证。
可以通过模拟仿真或实际测试来验证滤波器的频率响应、时域响应、抗混叠性能等。
如果发现性能不符合要求,可以返回上一步进行调整和优化。
十、总结本文介绍了FIR设计的步骤,包括确定规格要求、选择窗函数、确定滤波器阶数、计算理想频率响应、设计频率响应、计算时域响应、优化性能和验证性能等。
FIR滤波器设计

FIR滤波器设计FIR滤波器(Finite Impulse Response Filter)是一种数字滤波器,其输出仅取决于当前输入和以前的输入,而不取决于以前的输出。
FIR滤波器设计是指确定FIR滤波器的系数,使其具有所需的频率响应特性。
在设计FIR滤波器时,常见的方法包括窗函数法、四种极点分布法和最小二乘法。
窗函数法是FIR滤波器设计中最简单和最常用的一种方法。
该方法通过选择合适的窗函数来对理想滤波器的频率响应进行逼近。
常见的窗函数有矩形窗、汉宁窗、汉明窗等。
在进行设计时,首先确定所需的频率响应特性,然后选择合适的窗函数,并计算窗函数的系数。
最后,通过将理想滤波器的频率响应与窗函数进行卷积运算,得到FIR滤波器的系数。
四种极点分布法包括均匀采样法、线性相位法、最小相位法和Hilbert变换法。
这些方法通过在单位圆上选择合适的极点分布来设计FIR滤波器。
均匀采样法将极点均匀分布在单位圆上,线性相位法将极点分布在单位圆的实轴上,最小相位法将极点分布在单位圆的右半平面上,Hilbert变换法将极点分布在单位圆的上半平面上。
这些方法各有特点,根据实际需求选择合适的方法进行设计。
最小二乘法是一种经典的优化方法,用于确定FIR滤波器的系数。
该方法通过最小化实际输出与期望输出之间的误差来确定滤波器的系数。
常见的最小二乘法包括基于频域的最小二乘法和基于时域的最小二乘法。
在基于频域的最小二乘法中,通过选择合适的权重函数和目标函数来进行优化。
在基于时域的最小二乘法中,通过最小化滤波器的延迟和频率响应之间的误差来确定滤波器的系数。
在进行FIR滤波器设计时,需要考虑的因素包括滤波器的阶数、截止频率、过渡带宽和抗混叠性能。
滤波器的阶数取决于所需的频率响应特性,通常较高阶数的滤波器具有更陡峭的滚降斜率。
截止频率和过渡带宽决定了滤波器的频率响应特性,通常需要根据实际需求进行选择。
抗混叠性能是指滤波器在抽样过程中抑制混叠频率的能力,通常通过在设计过程中引入预留频率来实现。
抗混叠滤波matlab

抗混叠滤波matlab在MATLAB中,抗混叠滤波通常是指使用数字滤波器来减少信号采样时可能引入的混叠效应。
混叠效应是由于信号的频率超过了采样频率的一半而导致的。
以下是一种可能的方法来实现抗混叠滤波的示例:首先,你需要确定信号的采样频率和混叠效应的频率范围。
然后,你可以使用MATLAB中的数字滤波器设计工具,比如`fir1`或`fir2`来设计一个低通滤波器,以去除混叠效应。
例如,你可以使用`fir1`函数来设计一个截止频率为0.5的低通滤波器,代码如下:matlab.fs = 1000; % 采样频率。
f_cutoff = 100; % 截止频率。
normalized_cutoff = f_cutoff / (fs/2); % 归一化截止频率。
filter_order = 30; % 滤波器阶数。
b = fir1(filter_order, normalized_cutoff); % 设计滤波器系数。
然后,你可以使用`filter`函数将滤波器应用于信号。
假设你的信号是`x`,你可以这样应用滤波器:matlab.filtered_signal = filter(b, 1, x);这将产生一个经过抗混叠滤波处理的信号`filtered_signal`,其中混叠效应已经被减少。
除了使用`fir1`函数之外,MATLAB还提供了许多其他数字滤波器设计和应用的工具和函数,可以根据具体情况选择合适的方法来实现抗混叠滤波。
总之,抗混叠滤波在MATLAB中可以通过设计和应用数字滤波器来实现,具体的方法取决于信号的特性和混叠效应的频率范围。
希望这些信息能对你有所帮助。
抗混叠失真IIR数字滤波器的设计与仿真

抗混叠失真IIR数字滤波器的设计与仿真LIU Wen-fei【摘要】采用冲激响应不变法在IIR数字高通和数字带阻滤波器的设计过程中,如果在模拟信号频带之间进行频带变换将会发生频谱混叠失真,如果将频带变换放在数字信号频带中进行则可以消除冲激响应不变法带来的频谱混叠失真问题.通过巴特沃斯数字带阻滤波器的设计实例提出了抗混叠失真的具体设计方法和步骤,由仿真结果可以看出,采用\"数字-数字频带变换\"的设计方法能够有效避免混叠现象发生,是一种有效可行的设计IIR数字滤波器的方法.【期刊名称】《佳木斯大学学报(自然科学版)》【年(卷),期】2019(037)001【总页数】5页(P126-130)【关键词】频谱混叠;冲激响应不变法;数字-数字频带变换【作者】LIU Wen-fei【作者单位】【正文语种】中文【中图分类】TP3910 引言混叠失真[1]是指在信号采样过程中发生的频谱混叠现象,在对连续时间信号进行等间隔采样时,如果信号的最高频率成分大于采样频率的一半,即不满足奈奎斯特采样定理,那么采样后高于和低于采样频率的信号将混杂在一起,信号的频谱发生频谱分量的交叠现象,这就是频谱混叠失真。
发生频谱混叠失真的信号将无法重建,也就是信号将无法从采样信号中进行恢复还原。
1 IIR数字滤波器的设计中发生混叠失真的原因IIR(infinite impulse response)滤波器是数字滤波器中的一种。
数字滤波器按照系统的冲激响应的特点可以分成无限长单位冲激响应IIR滤波器和有限长单位冲激响应FIR(finite impulse response)滤波器。
IIR滤波器[2]具有结构简单、效率高、与模拟滤波器有对应关系、易于解析控制及计算机辅助设计等优点,与FIR滤波器相比,相同阶次滤波效果更好。
IIR数字滤波器一般采用间接设计的方法。
间接法设计是利用模拟滤波器来设计数字滤波器,因为模拟滤波器的设计方法已经比较成熟,有完整的设计公式以及数据表格可以直接使用,使得数字滤波器的设计更为方便、高效和快捷。
写出数字滤波的几种常用方法(一)

写出数字滤波的几种常用方法(一)数字滤波的几种常用方法引言数字滤波是一种信号处理技术,通过对信号进行处理,减少其噪声和干扰,并提升信号的质量和可靠性。
本文将介绍数字滤波的几种常用方法,包括: 1. 移动平均滤波 2. 中值滤波 3. 加权递推平均滤波 4. IIR滤波器 5. FIR滤波器1. 移动平均滤波移动平均滤波是一种简单而有效的滤波方法,通过计算窗口内数据的平均值来平滑信号。
该方法适用于平稳的信号,并且能够保留信号的整体趋势。
移动平均滤波的步骤如下: - 选择一个窗口大小,通常为奇数,例如5或9。
- 将窗口内的数据求平均值,并将该平均值替换窗口中心的数据点。
- 窗口向前移动一个位置,重复以上步骤,直到滤波完成。
2. 中值滤波中值滤波是一种非线性滤波方法,通过用窗口内的中间值来替换窗口中心的数据点,以抑制噪声和异常值的影响。
中值滤波的步骤如下: - 选择一个窗口大小,通常为奇数,例如3或5。
- 将窗口内的数据排序,并取中间值作为窗口中心的新数值。
- 窗口向前移动一个位置,重复以上步骤,直到滤波完成。
3. 加权递推平均滤波加权递推平均滤波是一种基于加权平均的滤波方法,通过给窗口内的数据点赋予不同的权重来进行滤波。
该方法对于快速变化的信号具有较好的滤波效果。
加权递推平均滤波的步骤如下: - 选择一个窗口大小,通常为奇数,例如3或5。
- 给窗口内的每个数据点赋予一个权重,权重可以根据具体的应用场景进行选择。
- 将窗口内的数据点乘以相应的权重,并计算加权平均值。
- 将加权平均值替换窗口中心的数据点。
- 窗口向前移动一个位置,重复以上步骤,直到滤波完成。
4. IIR滤波器IIR滤波器是一种基于递归差分方程的滤波方法,通过计算输入信号和输出信号的差分来进行滤波。
该方法具有较高的滤波效果和较少的计算复杂度。
IIR滤波器的设计和参数选择较为复杂,可以采用著名的巴特沃斯滤波器、切比雪夫滤波器等方法进行设计。
数字信号处理考试问题及答案

第1章 引 言1、数字信号处理的含义?数字信号处理—-Digital Signal Processing 采用数字技术的方式进行信号处理。
将信号转化为数字信号,利用数字系统进行处理。
2、什么是信号?信号主要采用什么方式表达? 传递信息的载体:进行变化的物理量;与日常生活密切相关: 语言、音乐、图片、影视模拟信号的表达:在电子技术中,通过传感器将信号转化为随时间连续变化的电压:模拟电压信号数字信号的表达:对模拟电压进行等间隔测量,将各测量值采用有限精度的数值表达,体现为顺序排布的数字序列。
3 、什么是模拟信号?什么是数字信号?信号在时间和数值上都是连续变化的信号称为模拟信号.模拟信号是指用连续变化的物理量表示的信息,其信号的幅度,或频率,或相位随时间作连续变化 数字信号指幅度的取值是离散的,幅值表示被限制在有限个数值之内。
时间和幅度上都是离散(量化)的信号。
二进制码就是一种数字信号。
二进制码受噪声的影响小,易于有数字电路进行处理,所以得到了广泛的应用。
4 、数字信号具有什么特点?信号采用抽象数字序列表达,与物理量没有直接关系,在传输、保存和处理过程中,信号精度不受环境因素影响,抗干扰性强.信号采用数字序列表达后,对模拟信号难以进行的很多处理能够方便地实现,例如:大规模长时间的信号存储、对信号的乘法调制和各种编码调制、信号的时间顺序处理、信号的时间压缩/扩张、复杂标准信号的产生。
5 、数字信号处理具有什么意义?数字信号处理是研究如何用数字或符号序列来表示信号以及对这些序列作处理的一门学科。
它具有精度高、可靠性高、灵活性、便于大规模集成化等特点。
6 、列举一些在生活中常见的数字技术的应用。
商业摄影领域;录音电话机;数码相机;数字电视;MP3播放器等等。
第2章信号的数字化1、信号数字化需要经过哪些基本步骤?信号数字化可以分为三步:1)等距采样,实现信号离散化;2)数值量化,用有限精度表达采样值;3) AD 转换,对量化值进行二进制编码。
滤波器设计有哪些步骤?

滤波器设计通常包括以下步骤:明确设计要求:确定滤波器的类型、频率范围、阻带衰减要求、插入损耗限制等,以及所需的性能指标和参数。
确定滤波器结构:根据设计要求,选择适合的滤波器结构,如低通、高通、带通、带阻等。
常见的滤波器结构包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
计算滤波器系数:根据设计要求和所选定的滤波器结构,计算滤波器的系数。
这一步通常需要运用数学和数字信号处理的基本原理,如傅里叶变换、拉普拉斯变换等。
优化滤波器性能:根据设计要求和计算出的滤波器系数,优化滤波器的性能,包括调整滤波器的阶数、调整系数的值等。
实现滤波器:将计算出的滤波器系数应用于实际的信号处理中,实现滤波器的功能。
这一步通常需要编写代码或使用相应的软件工具。
测试与验证:对实现的滤波器进行测试和验证,确保其性能符合设计要求。
测试过程中可以使用仿真信号或实际信号,通过比较滤波前后的信号,评估滤波器的性能。
总之,滤波器设计是一个复杂的过程,需要综合考虑设计要求、滤波器结构、性能优化和实现等多个方面。
在实际应用中,还需要根据具体情况选择合适的算法和工具进行滤波器设计。
抗混叠滤波器antialiasfilter是一个低通滤波器用以在输出

抗混叠滤波器 anti-alias filter是一个低通滤波器,用以在输出电平中
把混叠频率分量降低到微不足道的程度。
在对模拟信号进行离散化时,采
样频率f2至少应2倍于被分析的信号的最高频率f1,即:f2≥2 f1;否则可能出现因采样频率不够高,模拟信号中的高频信号折叠到低频段,出现
虚假频率成分的现象(如下图所示),称之为:混叠。
为解决频率混叠,在对模拟信号进行离散化采集前,采用低通滤波器滤除
高于1/2采样频率的频率成份。
实际仪器设计中,这个低通滤波器的截止
频率(fc) 为:
截止频率(fc)= 采样频率(fs) / 2.56
窗函数有截短和平滑的作用,窗函数选择的好,可以在相同阶次的情况下,提高滤波器的性能,或是在满足设计要求的情况下,减少滤波器阶数。
选窗标准:
1. 较低的旁瓣幅度,尤其是第一旁瓣;
2. 旁瓣幅度要下降得快,以利于增加阻带衰减;
3. 主瓣宽度要窄,这样滤波器过渡带较窄。
但这三点难以同时满足,当选用主瓣宽度较窄时,虽然得到的幅频特性较陡峭,
但通带、阻带波动会明显增加;当选用较低的旁瓣幅度时,虽然得到的幅频特性较平缓匀滑,但过渡带变宽。
因此,实际的选择往往是取折衷。
一般选这几个窗之一:矩形窗、三角窗、汉宁窗、海明窗、布拉克曼窗、凯塞窗,可以查查资料比较他们的旁瓣幅度,过渡带宽度和阻带最小衰减后再进行选择。
滤波器设计中的稳定性与抗混叠性能

滤波器设计中的稳定性与抗混叠性能稳定性与抗混叠性能在滤波器设计中扮演着重要的角色,对于信号处理和通信系统的性能至关重要。
本文将探讨滤波器设计中的稳定性和抗混叠性能,并介绍一些常见的设计方法和技巧。
一、引言滤波器是实现信号处理的重要工具,用于选择性地通过或阻断输入信号中的某些频率分量。
在滤波器设计中,稳定性和抗混叠性能是两个关键概念。
二、稳定性稳定性是指滤波器在输入信号有限、幅度受限的情况下,输出信号的幅度不会无限增长的性质。
滤波器的稳定性对于系统的可靠性和性能至关重要。
为了保证稳定性,滤波器的传递函数必须满足一些条件。
其中一个常见的条件是传递函数的极点必须位于单位圆内。
这些极点代表滤波器的特性和频率响应,位于单位圆内的极点意味着滤波器的输出将收敛到有限的范围内。
稳定性还可以通过频域的稳定性条件进行判断。
例如,滤波器的频率响应函数在整个频率范围内都必须是有界的,不能无限增长。
总的来说,在滤波器设计中,稳定性的保证可以通过合适的极点选取、迭代算法等方法来实现。
三、抗混叠性能抗混叠性能是指滤波器在滤除目标频率之外的频率分量时不引入失真或干扰。
在实际应用中,滤波器的输入信号通常包含多个频率分量,而滤波器只需要通过特定的频率分量,抑制其他频率分量。
为了获得良好的抗混叠性能,滤波器设计需要满足奈奎斯特采样定理,即采样频率必须大于信号中最高频率的两倍。
这是为了避免混叠现象的发生,即输入信号中的高频分量被错误地解释为低频分量,从而导致失真。
在滤波器设计中,常用的抗混叠方法包括低通滤波器的设计和采样频率的选择。
四、滤波器设计方法在滤波器设计中,有多种方法和技术可供选择,常见的有FIR滤波器和IIR滤波器。
FIR滤波器(Finite Impulse Response)是一种线性相位滤波器,其特点是稳定性好、无混叠问题、滤波器特性易于设计等。
FIR滤波器设计的关键是选取合适的滤波器系数,常见的设计方法包括窗函数法和最小二乘法。
抗混叠滤波器.

摘要文章是对抗混叠滤波器的设计研究,提出了一种过采样系统设计方案。
通过多次反复地对信号进行采样,然后通过将数字滤波和模拟滤波技术有机结合,充分发挥各自滤波器的特点来解决数据采集系统的抗混叠问题。
抗混叠滤波器的设计重点在数字滤波器部分,而FIR数字滤波器以其良好的线性特性、系统稳定等诸多优点,得到了广泛应用,也十分适合用于信号采集中的抗混叠滤波。
关键词:抗混叠滤波器;过采样;数字滤波器;目录摘要 (I)目录 (II)第1章绪论 (1)1.1课题研究背景和意义 (1)1.2课题研究现状 (1)1.3课题的目标与任务 (2)第2章抗混叠滤波器系统的构建 (3)2.1抗混叠滤波器设计的基本思路 (3)2.2数字滤波器的选择 (3)2.3过采样系统 (4)2.3.1过采样技术 (4)2.3.2过采样系统设计方案 (4)第3章抗混叠滤波器系统的仿真 (6)3.1FIR低通滤波器的设计 (6)3.1.1FIR数字滤波器的设计步骤 (6)3.1.2窗函数的选择 (6)3.1.3MATLAB相关函数的使用 (7)3.2过采样系统的构建与仿真 (8)结论 (11)参考文献 (12)致谢..................................................................................................错误!未定义书签。
附录. (13)第1章绪论1.1课题研究背景和意义现如今需要滤波器的领域十分多。
例如,采样视频系统中的信号混叠现象,当超出视频频段范围的高频信号通过数模转换器的采样过程混叠回视频频段时,就会产生混叠现象;随着电力电子技术的不断发展,电力电子装置广泛投入运行因而有大量的高次谐波注入电网,产生了严重的谐波污染,对于工农业生产造成了严重的影响;在当代煤矿的电网中,由于大量大功率和非线性设备的应用,致使部分煤矿电网中的谐波含量已经远远超出国家标准;在自动控制、测控系统的数据采集过程中,不可避免地会有高频干扰信号混杂在有用信号当中,当这些信号的数据采集频率超过采样定理所规定的范围时,就会采集到一些不确定的信号并对有用信号造成干扰,即频率混叠。
ADC抗混叠滤波与驱动问题

2 无源抗混叠滤波器的驱动
图 1 所示为前级运放驱动无源抗混叠滤波电路的简单示意图 。开关 K 和电容 C2 构成 了集成在 ADC 中的采样保持电路,当开关断开时处于保持阶段;开关闭合时为采样阶段。 无源抗混叠滤波器的设计中,考虑最差的情况,假设 ADC 前后两次转换之间,模拟量 的输入值相差 (即加到 C2 上的电压值) 最大即为 5V。 为保证 C1 对 C2 的分压小于 1LSB=5/212, 假设要求 C1=aC2,这样 C1 对 C2 的分压为 UC1=1/aUC2,UC2 最大为 5V,由 C1 分压所造成 的误差最大为 UC1=5/a,令 5/a<5/212=1LSB,即 a>212,C1>4096C2。在实际应用时,由于采 样频率往往高于信号中的最高频率数倍(>2)以上和高频信号频率往往幅值较低,对电容 C1 的要求 C1>212C2 可以适当的放宽。为保证测量的可信度,后面都同上考察最差情况,实际 应用中可适当放宽要求。 在 ADuC841 中的电容 C2 的值为 32pF,C1≥4096C2=131072pF,取标称值 C1=0.22uF。 现有的运算放大器对容性负载的驱动能力有限,当 R 较小 C1 值较大时,运放驱动大容 性负载时可能会产生振荡。AD8024 是一种四元组 350MHz、24V 的放大器,据其数据手册称 [8] 可驱动高电容性负载,其最大也可以驱动 1000pF 的容性负载 。可见,运放驱动能力限制 了无源抗混叠滤波器的应用, 尤其在高精度数据采集系统中。 这在实际应用中应该引起注意。
[7]
1
图1 放大器驱动无源抗混叠滤波器 Fig.1 Amplifier drives passive anti-aliasing filter
抗混叠滤波器的工作原理

抗混叠滤波器的工作原理抗混叠滤波器(Anti-aliasing Filter)是在信号采样之前使用的一种滤波器,其主要目的是防止混叠现象的发生。
混叠是指在模拟信号采样过程中,高频成分超过了采样频率的一半,导致无法恢复原始信号,产生频谱重叠,从而引入误差和失真。
工作原理:截止频率设置:抗混叠滤波器的首要任务是屏蔽超过采样频率一半的高频成分,以阻止混叠现象的发生。
因此,滤波器必须具备适当的截止频率,将原始信号的频率范围限制在一半采样频率之内。
滤波特性:抗混叠滤波器通常采用低通滤波器的形式,其频率响应在截止频率以下具有较高的传递函数增益,并在截止频率以上迅速下降。
这样可以有效地阻止高频成分的传递,从而减少或消除混叠。
模拟滤波:在模拟信号采样之前,抗混叠滤波器将信号传递到模拟滤波器中进行滤波处理。
模拟滤波器的功能是去除输入信号中超过截止频率的高频成分,确保输入信号频谱不会超过采样频率的一半。
数字滤波:在数字信号处理中,抗混叠滤波器可以实现数字滤波器形式。
在进行模拟到数字转换(ADC)之前,在信号采样之后应用这种数字滤波器。
数字滤波器的设计通常采用离散时间系统的方法,使用差分方程、滤波器系数等进行滤波处理。
总结:抗混叠滤波器的工作原理主要是通过限制信号频率范围和滤除高频成分来防止混叠现象。
它在信号采样之前采用模拟滤波或数字滤波的方式,以确保提供给采样器的信号不包含超过采样频率的一半的高频成分。
这样能够保证采样频率能够完整地包含信号的频谱,并避免混叠带来的误差和失真。
需要注意的是,抗混叠滤波器的设计需要根据具体应用场景的采样频率和信号频率范围来确定合适的滤波器类型、截止频率和滤波特性。
ATT7021

RESET REF
AGND ,DGND SCF S1,S0 G1,G0
CLKIN ,CLKOUT REVP CF F2 , F1
说
明
模拟电源 数字电源引脚
高通滤波器选择脚
不连接
电流取样信号输入
电压取样信号输入
复位引脚
参考电压引脚
模拟地和数字地
校验频率选择
频率转换系数选择引脚
通道 1 增益选择
外部时钟输入 频率输出
高电平 4
高电平 4.5
V
0.5
V
低电平
V
0.5
低电平 0.8
见指标说明部分
精度
动态范围 500 1
E
Pin22
0.1
G=1,2,8,16.
极限参数 ( T = 25 )
项目 数字电源电压 模拟电源电压 电流采样电压 电压采样电压
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一种分析和设计抗混叠滤波器的方法
作者:宋军赵明忠
来源:《现代电子技术》2008年第19期
摘要:信号采集通道中,一般采用高阶抗混叠滤波器来消除频率混叠现象,这同时也增加了滤波器设计难度。
为有效降低滤波器设计的难度,在详细分析并讨论了抗混叠滤波器的陡度、阶数与信号抽样频率以及A/D转换器的分辨率之间的内在关系后,提出了抗混叠滤波器、抽样频率和A/D转换器三者之间合理权衡设计的方法。
该分析方法为抗混叠滤波器乃至信号采集通道的设计提供了十分有益的参考。
关键词:滤波器;陡度;抽样频率;频率混叠
中图分类号:TN713文献标识码:B文章编号:1004373X(2008)1906702
Method of Analyzing and Designing Anti-aliasing Filter
SONG Jun,ZHAO Mingzhong
(College of Information Science and Technology,Nanjing Forests
University,Nanjing,210037,China)
Abstract:The high-rank anti-aliasing filter is often used to avoid spectrum aliasing in signal gathering system.In an effortto reduce the difficulty of designing filters,the relations among the anti-aliasing filter′s roll-off rate,rank,sampling frequency and the recognition of analog-to-digital converter are discussed and analysed in detail,then a reasonable method to choose and design these three ones are presented including anti-aliasing filter,sampling frequency and A/D converter.The results provide an effective reference for design of anti-aliasing filter and signal gathering channel.
Keywords:filter;roll-off rate;sampling frequency;spectrum aliasing
1 引言
信号采集中,当信号频率(f)超过1/2采样频率(fS),即f>12fS时,在时间域上会出现f′=fS -f的拍现象,其最大幅值与输入幅值的关系基本保持不变[1-3]。
在频域上出现频率为f′=fS-f 的假频,这就是折叠效应造成的混频现象,亦称频率混叠现象或频率混淆现象[4-6]。
为此,一般采用高滤波陡度的抗混叠滤波器,以消除频率混叠现象。
但如果单纯依靠提高滤波器的陡度来达到要求,无疑将提高滤波器设计难度和成本。
本文通过分析发现,综合考虑滤波器的陡度、阶数及系统抽样频率和ADC的分辨率可以在消除频率混叠现象的同时,有效降低滤波器设计的难度和成本。
2 滤波器陡度、系统抽样频率及ADC分辨率三者关系
2.1 理论分析
对信号不失真采样,一般需满足奈奎斯特抽样定理(Nyquist Sampling Theorem)[7]:
(1) 被抽样信号为带限信号,即信号最高频率fmax≠∞;
(2) 采样频率至少为被抽样信号最高频率的两倍,即fS≥2fmax。
这就要求信号在进行采样之前,必须进行低通滤波,通常称为抗混叠滤波,也称去混淆滤波。
由于抗混叠滤波器的截至频率fh直接决定被采样信号的最高频率fmax,且通常有fh=fmax,故采样频率fS与该截至频率fh的关系为:
fS=k·fh(k≥2)
(1)
此外,抗混叠滤波器在高于截频fh部分的陡度R也应满足一定的要求:将被采样信号中高于fS/2的噪音信号衰减到ADC(模数转换器)的量化阶梯q以下。
如图1是一低通滤波器的波特图。
其中,0~fh为有用信号频率范围,与该范围以fS/2为轴对称的频率范围是(fS-fh)~fS,若在这个频段上存在噪音干扰,则采样后这些噪音就会折叠到0~fh的信号频段上,这就是所谓的假频干扰,(fS-fh)对应的虚线也称有效假频线。
为了滤除假频干扰,就必须将(fS-fh)~fS 频段上的噪声衰减到ADC的可量化电平q以下。
从最坏情况考虑,假设有用信号的最大幅度(为VS)分量出现在频率f=fh处,干扰噪声中幅度最大(Vn)的频率分量出现在f=fS-fh处。
抗混叠滤波器的幅频特性为k(f),通带内理想,设:
图1 典型低通滤波器波特图
当f=fh时:
k(f)=kS=1(2)
当f=fS-fh时:
k(f)=kn
(3)
为了使抗混叠滤波后信号的最大幅度分量不超出ADC的最大量化电平E,噪音干扰的最大分量低于ADC的量化阶梯q,要求:
VS·kS=VS=E
(4)
Vn·kn=q
(5)
由式(4)和式(5)可得:
-20lg kn=20lgEq-20lgVSVn
(6)
若ADC量化的位数为m,则E=2m·q,并令B=-20lg kn代入式(6)得:
B=-20lg kn=6m-20lgVSVn
(7)
设0~(fS-fh)之间有fh的L个十倍频程(decade),即:
fS-fhfh=10L
(8)
由式(1)和式(8)可得:
L=lg(k-1)
(9)
这样,抗混叠滤波器的陡度R:
R=BL=Blg(k-1)
=6m-20lgVSVn·1lg(k-1)
(10)
2.2 三者关系讨论
由式(10)可见,抗混叠滤波器的陡度R与ADC的量化位数m、采样频率fS=k·fh以及信号噪声幅度比VS/Vn有密切关系:
(1) 当采样频率和ADC位数一定,即k和m固定时,信号噪声幅度比越大,对滤波器的陡度要求越小;
(2) 当采样频率和信号噪声幅度比一定,即k和VS/Vn一定时,ADC位数越少,对滤波器的陡度要求越小;
(3) 当信号噪声幅度比和ADC位数一定,即m和VS/Vn一定时,采样频率越高,对滤波器的陡度要求越小。
2.3 实际滤波器陡度设计分析
以最常见的模拟巴特沃斯(Butterworth)低通滤波器为例,分析如何针对不同分辨率的ADC 选取抗混叠滤波器的阶数、陡度及采样频率。
N阶巴特沃斯低通滤波器的幅频特性为:
k(f)=11+ff02n
(11)
f0为滤波器的截频,陡度为:
R=20n dB/dec
(12)
综合式(10)和式(12)可得:
n=0.3m-lgVSVn·1lg(k-1)
(13)
显然,信号噪声幅度比、采样频率和ADC的分辨率都直接影响巴特沃斯低通滤波器阶数的选取。
(1) 当lgVS/Vn≥0.3m时,则可以不必设置抗混叠滤波器。
例如,一个系统的ADC位数m=12,则需要信号噪声幅度比VS/Vn≥4×103才可以省略抗混叠滤波器,这在现实中一般很难保证。
(2) 当VS=Vn时,即噪声幅度和信号幅度相当,则有:
n=0.3m·1lg(k-1)
(14)
此时,若系统的采样ADC位数m=12,采样频率fS=4·fmax,即采样频率为信号最高频率的4倍(k=4),则根据式(14)有滤波器的阶数n至少为8才能满足要求;
而若ADC位数不变(m=12),提高采样频率到信号最高频率的5倍,即fS=5·fmax,则滤波器的阶数n为6就可以满足要求。
(3) 当k=2,即采样频率为信号最高频率的2倍时,只要信号噪声幅度比不满足上述讨论
的条件(1),就不能避免频谱的混叠。
3 结语
由于滤波器的阶数越高,成本和复杂程度也越高,而且信号通过滤波器的延时也越长,给系统的稳定性带来威胁,更给信号的后期数字滤波和处理带来不确定性。
因此在选择和设计系统前置抗混叠滤波器时,尤其需要综合考虑了采样频率、ADC的分辨率和噪声等因素对滤波器设计的影响。
只有权衡分析、选择抗混叠滤波器的阶数、系统采样频率以及ADC的分辨率,才能使系统达到最优化的设计。
参考文献
[1]黄振平.采用频率的合理选择[J].世界地震工程,1998,14(3):63-67.
[2]李德葆.振动模态分析及其应用[M].北京:宇航出版社,1989.
[3]谭清,龙杰强.便携式数据采集系统中自适应抗混叠滤波器的设计[J].现代电子技术,2007,30(5):105-107.
[4]李刚.高精度数据采集中抗混叠滤波器的设计[J].国外电子元器件,2007(8):31-34.
[5]齐永前,孙俊杰.振动信号的抗混叠跟踪滤波的实现[J].现代制造工程,2006(2):93-95.
[6]刘洪涛,吴云洁.高品质抗混叠滤波器的设计[J].仪器仪表用户,2006,13(1):97-98.
[7]赵传伟.数据采集的基本原理[J].大众科学,2007(16):57-58.
作者简介宋军男,1979年出生,江苏徐州人,硕士,讲师。
研究方向为信号处理和嵌入式系统。
赵明忠男,1964年出生,山东兖州人,硕士,副教授。
研究方向为单片机与数字信号处理。
注:本文中所涉及到的图表、注解、公式等内容请以PDF格式阅读原文。
