第9讲 数组
工程热力学第9讲第一部分复习热一律与热二律应用

______、______、______。
简答题
1. 气体膨胀时一定对外作功,气体压缩时一定耗功。此说 法是否正确?请说明理由。
即在恒温T1、T2下, t,任
t,R
推论一:在两个不同温度的恒温热源间工作的一切可逆热机,具 有相同的热效率,且与工质的性质无关。
推论二:在两个不同温度的恒温热源间工作的任何不可逆热机, 其热效率总小于这两个热源间工作的可逆热机的效率。
卡诺定理讨论
1、在两个不同 T 的恒温热源间工作的一切
可逆热机
传热
1851年 开尔文-普朗克表述
1850年 克劳修斯表述
热功转换的角度
热量传递的角度
不可能从单一热源取
热,并使之完全转变为有 用功而不产生其它影响。
热量不可能自发地、
不付代价地从低温物体 传至高温物体。
完全等效!!!
违反一种表述,必违反另一种表述!!!
卡诺定理
卡诺定理:在两个不同温度的恒温热源间工作的所有热机,以 可逆热机的热效率为最高。
各种表述等价不是偶然的,说明共同本质。 热力学第二定律的实质: 1. 自发过程是不可逆的。 2. 要使非自发过程得以实现,必须伴随一个适当的自发过
程作为补充条件。 热力学第二定律的推论: 1. 热二律推论之一:卡诺定理,给出热机的最高理想效率 2. 热二律推论之二:克劳修斯不等式,反映过程方向性 3. 热二律推论之三:熵,反映过程的方向性
c2
gz
ws
ws
△ c2/2
第9章 FORTRAN中的数组

• •
•
•
9.2 数组的引用方式
• 数组经过定义之后,就可以在程序中使用了。在 Fortran77标准中,数组只允许在输入输出语句中 进行整体操作。在其他场合,只能对数组的元素 通过下标索引的方式逐个进行操作。到了 Fortran90标准,这一限制被大大放宽了。数组除 了能够进行整体操作以外,还能对数组中的片断 和数组的整体进行操作。这进一步增强了Fortran 语言在数值处理方面的能力。Fortran中数组的引 用方式可以概括为以下几种:
9.1.3 定义形式三
• 第三种数组定义形式的语法格式如下所示。 • DIMENSION([下标下界:]下标上界[,„]) [::] 数组名[,„] • [类型说明 [::] 数组名[,„]] • 该定义形式通过DIMENSION语句直接说明了数组的 维数和维的范围。这种形式定义的数组全部具有 相同的维数和大小。如下代码表示了如何采用上 述形式进行数组的定义。 • DIMENSION(10, 4:10) :: A, B, N • INTEGER :: A • REAL(8) :: N
9.4 数组的类型
• 根据数组在定义时的特征,比如数组的秩、数组 的形状和每一维的大小,可以将数组划分为好几 种类型。这些不同类型的数组在程序单元中如何 使用?在哪些程序单元中使用?有什么特点?本 节将针对这些问题进行逐一介绍。
9.4.1 显形数组
• 显形(Explicit-shape)数组是Fortran中最简单、 最容易理解的一种数组类型。顾名思义,这种类 型的数组在定义阶段就通过数组定义语句明确的 规定了所有特征,比如数组的秩、数组的维数、 每一维的长度和上下界。通过这种方式定义的数 组具有确定的形状和大小,在程序运行过程中不 允许再对数组的任何特征进行改变。需要注意的 是,在显形数组的维说明中,还允许使用整型变 量或整型表达式来定义维的上下界。这涉及到两 种特殊的显形数组,会在随后的小节中进行介绍。
北京大学计算概论(C语言)经典课件Lecture 9——循环语句复习及数组(上)页PPT文档

数组元素的赋值
每个数组元素,就是一个变量。 每个数组元素占用的空间大小是由定义数组
变量时给定的类型决定的。例如:
cards每个元素占1字节(char类型的长度) distance每个元素占8字节(double 类型的长度)。
19
数组元素的赋值
在给数组元素赋值时,可以把数组元素看作 单个变量,例如:
给数组元素赋值,数据类型必须匹配。
20
数组元素的访问
数组元素可以用在任何单个变量可能出现的地 方。例如:
int max, min; max = score [0]; min = score[3];
17
数组元素
定义一个数组变量相当于定义一组变量,这组 变量中的每一个都可以通过“数组变量名[下 标]”形式来访问。例如:score[0], score[1], score[2] 等等。
这组变量在内存中是连续存放的,它们的下标 从0开始计数。
在数组中(设N是数组的元素总数)
第一个数组元素的下标是0 最后一个数组元素的下标是N-1
continue;
8
课堂练习
1.已知:int a=5;执行语句while(a>0)
{
a--;
}
a的值是(
)。
A. 5
B. 0 C. –1 D. -2
2.已知:int a=5;执行语句while(--a>0)
{
a--;
}
a的值是(
)。
A. 5
B. 0 C. –1 D. -2
3.已知:int a=5;执行语句while(a-->0)
表达式必须是数值表达式 一次循环
计算表达式的值 如果表达式值为真,执行循环体,为假退出
数组

(2)数组的下界默认为0,上界由Array函数括号内的参数个数决定。也可以通过函数 LBound()或 UBound()获得。
(3)Array只能给没有说明具体数组类型 (Variant)和元素个数的一维数组赋值。 (4)数组元素的类型可以是任意的。
略),语句形式为: Dim 数组名() [As 类型] (2)引用数组前在过程中用ReDim语句指明该数组的大小,语句形式为:
答案:C
【例3】一个二维数组可以存放一个矩形。在程序开始有语 句Option Base 0,则下面定义的数组中正好可以存放一个 4×3矩阵(即只有12个元素)的是______。
A)Dim a(-2 to 0,2) As Integer B)Dim c(3, 2) C)Dim d(4,3) As Integer 答案:B D)Dim b(-1 to -4,-1 to -3) As பைடு நூலகம்nteger
第一种:Dim 数组名(下标上界) [As 类型]
例:Dim a(10) As Integer,b!(6) 第二种:Dim 数组名([下标下界 to]下标上界) [As 类型] 2、说明: (1)数组的命名规则 与变量的命名规则相同,只能由字母、数字、下划线构成,第一个字符 只能是字母。 (2)下标不能是变量,必须为常数,可以是实数,小数点前面的数为奇数,四舍五入,小数 点前面的数为偶数,五舍六入。例3.5→ 4,4.5→ 4。 例:n=InputBox(“输入n的值”) Dim arr(n) „变量即使赋值也不能做下标 例: Dim a(0 to 10) As Integer
数据结构的第九讲

19
n 1
算法分析
在平均情况下的关键字比较次数和对象移动次 数约为 n2/4。 直接插入排序的时间复杂度为 o(n2)。 直接插入排序是一种稳定的排序方法。
20
插入排序 (Insert Sort)
2、折半插入排序 (Binary Insertsort)
基本思想 设在顺序表中有一 个对象序列 V[0], V[1], …, V[n-1]。其中, V[0], V[1], …, V[i-1] 是已经排好 序的对象。在插入V[i] 时, 利用折半搜索法寻 找V[i] 的插入位置。
28
冒泡排序的算法分析
时间效率: O(n2) 因为要考虑最坏情况 空间效率: O(1) 只在交换时用到一个缓冲单元 稳 定 性: 稳定 25和25*在排序前后的次序未改变
29
冒泡排序的算法分析
最好情况:
初始排列已经有序,只执行一趟起泡,做 n-1 次关 键码比较,不移动对象。 初始排列逆序,算法要执行n-1趟起泡,第i趟(1 i n) 做了n- i 次关键码比较,执行了n-i 次对象交换。 此时的比较总次数KCN和记录移动次数RMN为:
一个人接受科技教育 得到的最大收获,是那些 能够受用一生的一般性智 能工具。
—George Forsythe,《计算机科学家到来以前我们做什么》,1968
第九讲 基本排序算法和查找算法
主要内容
9.1 基本排序算法 9.2 基本查找算法
9.1 基本排序算法
9.1 基本排序算法
基本概念 插入排序 冒泡排序 选择排序
mid high
key ~ list [mid]
第9讲 向量组及其线性相关性

是否有非0解
方法二
考虑由
a1,a 2 ,a 3
组成的行列式
1 30 1 0 0 2 1 1 = 2 7 1 =1(1)11 7 1 = 31 0
10 3 3 1 3 3 10 3
方程组只有0解 所以: 向量组线性无关
定理3 向量组a1,a2, ,am线性相关 向量组中至少有一个向量能由其余向量
(1) 线性相关与线性无关定义:
设有向量组
a1,a2, ,am
如果存在不全为零的数 l 1,l2, ,lm,
使得 l1a1l2a2 lmam= o
则称向量组a1,a2, ,am线性相关
否则称它线性无关
(2) 线性相关与线性无关的判定
定理2 向量组a1,a2, ,am线性相关
齐次方程组 x1a1 x2a2 xm am =0 有非0
a1,n1
a2,n1
an,n1
r(A) = (a1 ,a2 ,...,an1) n
所以 a1 ,a2 ,...,an1 线性相关
(5) 推论 Rn中的任意n+1个向量一定线性相关 证明 证法二
设a1
,a 2
,...,a n1
为给定的n维向量
因为
a1
,a 2
,..
.
,a
组
n1
能被Rn
中的初单位向量组
a11 a12 a1n A= a21 a22 a2n
am1 am2 amn
1 =( a11 a12 a1n ) 2 =(a21 a22 a2n )
... ... ...
m = (am1 am2 amn)
a11
a1 =
a21
am1
a12
全国计算机二级c语言学习指南课件与历年真题精讲精析 第9章

2、1个数组元素,实质上就是1个变量,它具有和相 同类型单个变量一样的属性,可以对它进行赋值和参 与各种运算。 3、一个数组不能整体引用,数组名中存放的是一个地 址常量,它代表整个数组的首地址。 例如:double x[8], *p, q; p=x; q=x;
不能将数组名赋给一个类型不同的普通变量
C语言规定,数组名代表数组的首地址,因此, 数组名实际上也是指针,但它是一个固定不变的 指针常量。
如:int a[5]; a是数组名,也是指针,它永远指向数组的首地址 ,即不能将新地址赋给该指针。但可以通过形如 a+k的形式(k是整数)来表达该数组其它元素的地 址。 如:for(k=0;k<5;k++) scanf(“%d”,a+k);
15 67 3 26 98
a[0]
a[1] a[2] a[3] a[4]
高地址
9.1.2 一维数组元素的引用 数组名[下标表达式] 如:double x[8]; 则x[0]、x[j]、x[i+k]均合法。 注意:i+k是下标表达式而不是两个下标。 说明:
1、“下标表达式”可以是任何非负整型数据,取值范
for(k=0;k<10;k++) printf(“%4d”, *(p+k));
for( k=0;k<10;k++) {printf(“%4d”,*p);p++;}
for( k=0;k<10;k++) printf(“%4d”,*p++);
for( ;p-a<10;p++) printf(“%4d”,*p);
围是0~(元素个数-1)。
SAS讲义-第九课

SAS讲义-第九课一、Do循环1、大家回看第四课的例11,可以发现Do循环应该要和End搭配使用。
下面都是可行的Do语句。
do i=5;do i=2,3,5,7;do i=1 to 100;do i=1 to 100 by 2;do i=100 to 1 by -1;do i=1 to 5,7 to 9;do i=’01jan99’d,’25feb99’d;do i=’01jan99’d to ‘01jan2000’d by 1;例1 产生1,2,9,8 的序列。
data a;do i=1,2,9,8;output;end;run;思考:若output放在end之后,或者去掉output,那会怎样呢?例2 产生1-20的奇数序列。
data a;do i=1 to 20 by 2;output;end;run;例3 求1-100的自然数之和。
data a;do i=1 to 100 ;n+i;output;end;run;例4 求1-100的自然数的平方和。
data a;do i=1 to 100 ;n+i**2;output;end;run;例5用do循环处理数组。
(下课还会深入说数组)data a(drop=i);array day{7} d1-d7;do i=1 to 7;day{i}=i+1;end;run;2、do while语句。
先判断while表达式,若成立则执行,否则推测循环。
例6data a;n=0;do while (n<5);n+1;output;end;run;例7 计算1加到100的过程中,第一个大于等于2000的数。
data a;do i=1 to 100 while (n<2000) ;n+i;output;end;run;3、do until 语句。
先执行,直到until的表达式为真,推出循环。
4、do over 语句。
我们到下课再说。
二、select语句。
随机数学 第9讲 第六章平稳过程(1)

2 C X (τ ) = COV [ X (t ), X (t − τ )] = RX (τ ) − mX
2 C X (0) = DX ( t ) = RX (0) − mX .
则称 { X ( t ), t ∈ T }为宽平稳过程 , 或广义平稳过程 . 以下讨论中,若没有特别说明,平稳即指宽平稳。
第六章 平稳过程随机过程 6.1 平稳过程概念 平稳过程是指过程的统计特性不随时间的推移而变 化的随机过程。 一般,为了便于研究,我们只考虑随机过程的数字 特征特性的平稳性,即有如下宽平稳过程的 定义:
注1 平稳过程数字特征的特点
(1) 平稳过程的所有样本曲 线都在水平直线
x(t ) = mX 上下波动 , 平均偏离度为 σ X .
平稳过程X(t) 的“平均功率”
此式表明:
自相关 (自协方差 )函数都在 τ = 0处取到最大值 .
RX (0) ≥ 0.
RX (−τ ) = RX (τ ) ,
2 证明: RX (0) = E[ X (t ) X (t )] = E X (t ) 2 = Ψ X ≥ 0.
e − λt ( λt ) , k = 0,1, 2, k!
k
若随机点在[0,t]内出现偶数次 ,则
若随机点在[0,t]内出现奇数次 ,则 X ( t ) = −1; (1)计算 mX ( t ) , C X ( t1 , t2 )
⎛ ( λt )0 ( λt )2 ( λt )4 ⎞ = e − λt ⎜ + + + ⎟ ⎜ 0! ⎟ 2! 4! ⎝ ⎠ λt − λt −2 λ t ⎞ 1+ e − λt ⎛ e + e [0,t]内随机 = e ⎜ ⎟ = 2 2 ⎝ ⎠ 点出现奇数次
线性代数第9讲
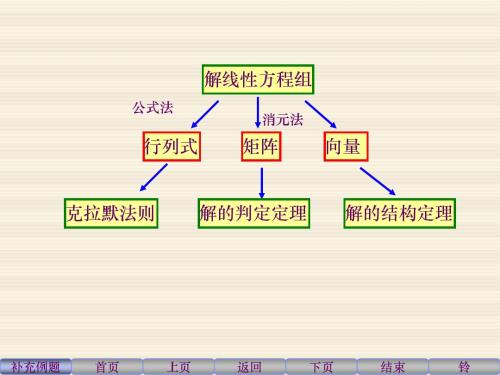
k11 k (b , b2, ⋅ ⋅ ⋅ , bl ) =(a1, a2, ⋅ ⋅ ⋅ , am) 21 1 ⋅⋅⋅ km1 即B=AK.
k12 k22 ⋅⋅⋅ km2
⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅
k1l k2l . ⋅⋅⋅ kml
>>>
反之, 若B=AK, 则 矩阵B的列向量组能由矩阵A的列向量组线性表示;
补充例题 首页 上页 返回
−3 2 −3c+2 x =c 2 +−1 = 2c−1 , 1 0 c 从而得表示式 b=(a1, a2, a3)x = =(−3c+2)a1+(2c−1)a2+ca3, 其中c可任意取值.
下页
结束
补充例题
首页
上页
返回
下页
结束
铃
线性组合与线性表示 设A: a1, a2, ⋅⋅⋅, am是一向量组, 表达式 k1a1+k2a2+ ⋅⋅⋅ +kmam, 称为向量组A的一个线性组合, 其中k1, k2, ⋅⋅⋅, km是一组实数, 称为这线性组合的系数. 如果向量b是向量组A的线性组合 b=λ1a1+λ2a2+ ⋅⋅⋅ +λmam, = 则称向量b能由向量组A线性表示.
结束
铃
向量组的等价 若向量组B: b1, b2, ⋅⋅⋅, bl中的每个向量都能由向量组A: a1, a2, ⋅⋅⋅, am线性表示, 则称向量组B能由向量组A线性表示. 若向量组A与B能相互表示, 则称这两个向量组等价. 使 若向量组B组能由向量组A线性表示, 则存在矩阵K=(kij),
k11 k (b , b2, ⋅ ⋅ ⋅ , bl ) =(a1, a2, ⋅ ⋅ ⋅ , am) 21 1 ⋅⋅⋅ km1
C语言第九章 数组总结

基本概念:数组 :一组具有相同名字、不同下标、个数固定的同类型变量的集合数组元素 :数组中的一个变量数组的类型 :数组元素的类型(基本类型包括:整型(int )浮点型(float )双精度浮点型(double )字符型(char )无值型(void ))数组的维数 :确定数组中各元素之间相对位置的下标个数(1.下标必须是正数常数或整形表达式 2.下标的取值从0开始,最大下标值为数组元素个数减一 3.下标不要越界)例如:int a[6];int 是类型,a[6]是一维数组说明符 为a 开辟a[0] a[1]a[2]a[3]a[4]a[5] 六个连续的存储单元。
一维数组的初始化:1.数组不初始化,其元素值为随机值 2.所赋初值少于定义个数系统为后面元素自动补零 3.当全部数组元素赋初值时,可不指定数组长度例如:int a[5]={1,2,3,4,5} 等价于a[0]=1;a[1]=2;a[2]=3;a[3]=4;a[4]=5;应用:例如:定义一个数组,使a[0]到a[7]的值为0~7,然后输出。
#include <stdio.h>main(){int i,a[8]; /*一维数组的定义*/for(i=0;i<=7;i++)a[i]=i; /*一维数组的初始化*/for(i=0;i<=7;i++)printf("%d ",a[i]); /*一维数组的引用*/}例如:读十个正数存入数组,找到其中最大值和最小值。
思路:1.用for 循环出入10个正数 2.处理:(a)先令max=x[0] (b)依次用x[i]和max 比较(循环)若max<x[i],令max=x[i] 3.输出:max#include <stdio.h>#define SIZE 10main(){ int x[SIZE],i,max;printf("Enter 10 integers:\n");for(i=0;i<SIZE;i++) scanf("%d",&x[i]);max=x[0];for(i=1;i<SIZE;i++)if(max<x[i])max=x[i];}二维数组的定义方式:数据类型 数组名[常量表达式][常量表达式] (按行序先)例如:int a[3][4]用for 出入10个正数(有一个m*n 的二维数组a ,其中i 行j 列元素a[i][j]在数组中的位置计算公式是:i*n+j+1)可把二维数组看作是一种特殊的一维数组:它的元素又是一个一维数组例如:把 a[3][4] 看作是一个一维数组,有3个组元素:a[0]、a[1]、a[2],每个组元素中又包含 4 个元素的一维数组。
C与数据结构 第9次课--一维数组和二维数组的定义和使用

第9次课----一维数组和二维数组的定义和使用
第4章
一维数组元素的引用
引用形式 数组名[整型表达式] 下标的取值 0≤ 整型表达式 ≤元素个数-1 例如 int a[10]; 表示有10个整型元素,分别为: a[0] a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[9]
第4章
二维数组的初始化
二维数组定义时赋值,可以按行分段赋值,也可以 按行连续赋值。 例如 按行分段赋值: int a[3][3]={ {80,75,92}, {61,65,71}, {59,63,70} }; 按行连续赋值: int a[3][3]={ 80,75,92,61,65,71,59,63,70 };
在全部元素赋值的情况下,这两种 赋初值的结果是完全相同的。
《C语言与数据结构》
第9次课----一维数组和二维数组的定义和使用
第4章
二维数组的初始化
例如 (1)int a[3][3]={ {80,75}, {61}, {59,63} }; (2)int a[3][3]={ 80,75,61,59,63 }; (3)int a[3][3]; 问题:这三行的结果如何? (1)
第4章
一维数组的定义
定义形式 类型标识符 数组名[整型常量表达式]; 本质 声明数组元素的类型和个数之后,编译器才能为 该数组分配合适的内存。 举例 #define M 20 int a[10]; 定义a是有10个整型元素的数组 float b[5]; 定义b是有5个浮点型元素的数组 char ch[M+6];定义ch是有M+6即26个元素的字符 型数组
《C语言与数据结构》
第9次课----一维数组和二维数组的定义和使用
第9讲 数学思想方法(一)——枚举法

第九讲数学思想方法(一)——枚举法哲理故事五岁的汉克和爸爸妈妈哥哥一起到森林干活,突然间下起雨来,可是他们只带了一块雨披。
爸爸将雨披给了妈妈,妈妈给了哥哥,哥哥又给了汉克。
汉克问道:“为什么爸爸给了妈妈,妈妈给了哥哥,哥哥又给了我呢?”爸爸回答道:“因为爸爸比妈妈强大,妈妈比哥哥强大,哥哥又比你强大呀。
我们都会保护比较弱小的人。
汉克左右看了看,跑过去将雨披撑开来挡在了一朵风雨中飘摇的娇弱小花上面。
生存之道:真正的强者不一定是多有力,或者多有钱,而是他对别人多有帮助。
责任可以让我们将事做完整,爱可以让我们将事情做好。
例1如下图所示,已知长方形的周长为20厘米,长和宽都是整厘米数,这个长方形有多少种可能形状?哪种形状的长方形面积最大?(边长为1厘米的正方形的面积叫做1平方厘米).我的思考:点睛一笔:例2 如右图所示,ABCD是一个正方形,边长为2厘米,沿着图中线段从A到C的最短长度为4厘米.问这样的最短路线共有多少条?请一一画出来.我的思考:点睛一笔:例3 在10和31之间有多少个数是3的倍数?我的思考:点睛一笔:例4 两个整数之积为144,差为10,求这两个数?我的思考:点睛一笔:例512枚硬币的总值是1元,其中只有5分和1角的两种,问每种硬币各多少个?我的思考:点睛一笔:例6 小虎给4个小朋友写信.由于粗心,在把信纸装入信封时都给装错了.4个好朋友收到的都是给别人的信.问小虎装错的情况共有多少种可能?我的思考:点睛一笔:课后札记:本章重点题型和解题方法:计算我最强:15+79= 51-34= 69-47= 46+21-26= 9×9= 每日一练:1.一个长方形的周长是22米,如果它的长和宽都是整米数,问:①这个长方形的面积有多少可能值?②面积最大的长方形的长和宽是多少?家长签字:2.有四种不同面值的硬币各一枚,它们的形状也不相同,用它们共能组成多少种不同钱数?家长签字:3.三个自然数的乘积是24,问由这样的三个数所组成的数组有多少个?如(1,2,12)就是其中的一个,而且要注意数组中数字相同但顺序不同的算作同一数组,如(1,2,12)和(2,12,1)是同一数组.家长签字:4.小虎给3个小朋友写信,由于粗心,把信装入信封时都给装错了,结果3个小朋友收到的都不是给自己的信,请问小虎错装的情况共有多少种可能?家长签字:5.一个学生假期往A、B、C三个城市游览.他今天在这个城市,明天就到另一个城市.假如他第一天在A市,第五天又回到A市.问他的游览路线共有几种不同的方案?家长签字:6.下图中有6个点,9条线段,一只甲虫从A点出发,要沿着某几条线段爬到F点.行进中甲虫只能向右、向下或向右下方运动.问这只甲虫有多少种不同的走法?家长签字:小幽默滥用成语刚上二年级的小明在爸爸出差的时候给爸爸写了一封信,信的内容如下:我最亲密无间的爸爸:你好!最近身体是否健壮如牛,工作是否蒸蒸日上。
部编版数学五年级暑假第9讲.数阵图综合.优秀A版

图1
图2
图3
8 第 9 级上 优秀 A 版 教师版
第9讲
九株十行 英国一位数学家 1821 年出了一道题智力题:春风艳阳暖,园中植树忙,每行植三株, 九株栽十行。意思就是有九棵树,种成十行,要求每行要有三棵树,应该怎么种? 答案:图中点表示树
1、辐射型数阵图 2、封闭型数阵图 3、复合型数阵图 解决数阵图问题的基本思路如下 : 1、区分数阵图中的普通格和关键格; 2、利用所有数之和、幻和(关系线或关系区域上的数之和)的数量关系;确定关键格的可能值
与幻和可能值; 3、运用已经得到的信息进行尝试填图.
2 第 9 级上 优秀 A 版 教师版
第9讲
11=2+9=4+7=5+6,将它们填入 B、C、D、E、F、G 中,最后填出所有数,如图所示(答案不 唯一)
例5
将自然数 1~11 填入下图的 11 个圆圈内(其中 3 和 8 已填入),使得每条直线(共 10 条)上的三个 数之和都相等.
(学案对应:学案 4) 【分析】本题中 A 由 5 条线共有,因此,应当首先确定 A 以及每条直线三个数的和 .设每条直线的三
例题思路
模块 1:例 1-3,基本数阵图 例 1:辐射型数阵图 例 2:封闭型数阵图 例 3:幻方变化型数阵图
模块 2:例 4-5,复合型数阵 例 4:简单复合型数阵图 例 5:综合复合型数阵图
第9讲 数论之质数合数 教师版

本讲中的知识点在小学课本内已经有所涉及,并且多以判断题考察。
质数合数的出现是对自然数的另一种分类方式,但是相对于奇数偶数的划分要复杂许多。
质数本身的无规律性也是一个研究质数结构的难点。
在奥数数论知识体系中我们要帮助孩子树立对质数和合数的基本认识,在这个基础之上能够会与之前的一些知识点结合运用。
分解质因数法是一个数论重点方法,本讲另一个授课重点在于让孩子对这个方法能够熟练并且灵活运用。
1. 质数与合数 一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数).一个数除了1和它本身,还有别的约数,这个数叫做合数.要特别记住:0和1不是质数,也不是合数.常用的100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个;除了2其余的质数都是奇数;除了2和5,其余的质数个位数字只能是1,3,7或9.考点:⑴ 值得注意的是很多题都会以质数2的特殊性为考点.⑵ 除了2和5,其余质数个位数字只能是1,3,7或9.这也是很多题解题思路,需要大家注意.2. 质因数与分解质因数质因数:如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数.互质数:公约数只有1的两个自然数,叫做互质数.分解质因数:把一个合数用质因数相乘的形式表示出来,叫做分解质因数.例如:30235=⨯⨯.其中2、3、5叫做30的质因数.又如21222323=⨯⨯=⨯,2、3都叫做12的质因数,其中后一个式子叫做分解质因数的标准式,在求一个数约数的个数和约数的和的时候都要用到这个标准式.分解质因数往往是解数论题目的突破口,因为这样可以帮助我们分析数字的特征.知识点拨教学目标第九讲:数论之质数合数3. 唯一分解定理任何一个大于1的自然数n 都可以写成质数的连乘积,即:312123k a a a a kn p p p p =⨯⨯⨯⨯ 其中为质数,12k a a a <<<为自然数,并且这种表示是唯一的.该式称为n 的质因子分解式.例如:三个连续自然数的乘积是210,求这三个数.分析:∵210=2×3×5×7,∴可知这三个数是5、6和7.4. 部分特殊数的分解111337=⨯;100171113=⨯⨯;1111141271=⨯;1000173137=⨯;199535719=⨯⨯⨯;1998233337=⨯⨯⨯⨯;200733223=⨯⨯;2008222251=⨯⨯⨯;10101371337=⨯⨯⨯.5. 判断一个数是否为质数的方法根据定义如果能够找到一个小于p 的质数q(均为整数),使得q 能够整除p ,那么p 就不是质数,所以我们只要拿所有小于p 的质数去除p 就可以了;但是这样的计算量很大,对于不太大的p ,我们可以先找一个大于且接近p 的平方数2K ,再列出所有不大于K 的质数,用这些质数去除p ,如没有能够除尽的那么p 就为质数.例如:149很接近1441212=⨯,根据整除的性质149不能被2、3、5、7、11整除,所以149是质数.【系列一:质数合数的基本概念的应用】【例 1】 下面是主试委员会为第六届“华杯赛”写的一首诗:美少年华朋会友,幼长相亲同切磋;杯赛联谊欢声响,念一笑慰来者多;九天九霄志凌云,九七共庆手相握;聚起华夏中兴力,同唱移山壮丽歌.请你将诗中56个字第1行左边第一字起逐行逐字编为1—56号,再将号码中的质数由小到大找出来,将它们对应的字依次排成一行,组成一句话,请写出这句话.【解析】 按要求编号排序,并画出质数号码:美 少 年 华 朋 会 友,幼 长 相 亲 同 切 磋;1 2 3 4 5 6 7 8 9 10 11 12 13 14杯 赛 联 谊 欢 声 响,念 一 笑 慰 来 者 多;例题精讲15 16 17 18 19 20 21 22 23 24 25 26 27 28九天九霄志凌云,九七共庆手相握;29 30 31 32 33 34 35 36 37 38 39 40 41 42聚起华夏中兴力,同唱移山壮丽歌.43 44 45 46 47 48 49 50 51 52 53 54 55 56将质数对应的汉字依次写出就是:少年朋友亲切联欢;一九九七相聚中山.【巩固】(2008年南京市青少年“科学小博士”思维训练)炎黄骄子菲尔兹奖被誉为“数学界的诺贝尔奖”,只奖励40岁以下的数学家.华人数学家丘成桐、陶哲轩分别于1982年、2006年荣获此奖.我们知道正整数中有无穷多个质数(素数),陶哲轩等证明了这样一个关于质数分布的奇妙定理:对任何正整数k,存在无穷多组含有k个等间隔质数(素数)的数组.例如,3k=时,3,5,7是间隔为2的3个质数;5,11,17是间隔为6的3个质数:而,,是间隔为12的3个质数(由小到大排列,只写一组3个质数即可).【解析】最小的质数从2开始,现要求每两个质数间隔12,所以2不能在所要求的数组中.而且由于个位是5的质数只有一个5,所以个位是3的质数不能作为第一个质数和第二个质数,可参照下表:【例 2】两个质数之和为39,求这两个质数的乘积是多少.【解析】因为和为奇数,所以这两个数必为一奇一偶,所以其中一个是2,另一个是37,乘积为74.我们要善于抓住此类题的突破口。
C语言第9讲 字符数组
1 2 3
4 7 5 8 a[i][j]=i*1+j*3+1 6 9 #include <stdio.h> void main(void) { int a[3][3],i,j; for(i=0;i<3;i++) 生成如下矩阵?? for(j=0;j<3;j++) 1 5 9 13 a[i][j]=i+j*3+1; 5 9 13 17 for(i=0;i<3;i++) 9 13 17 21 { for(j=0;j<3;j++) printf(“%4d”,a[i][j]); printf(“\n”); } }
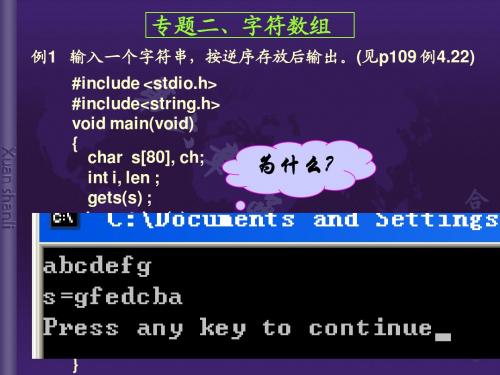
专题二、字符数组
例1 输入一个字符串,按逆序存放后输出。(见p109 例4.22) #include <stdio.h> #include<string.h> void main(void) { char s[80], ch; int i, len ; gets(s) ; len=strlen(s); for(i=0; i<len/2; i++) 交 { ch=s[i]; s[i]=s[len-i-1]; 换 s[len-i-1]=ch; 字 符 } printf("s=%s\n",s); }
合 肥 ★ 课堂作业: 输入一组整数给一个数组a[3][3],编程以矩阵形式输出该数 工 组,并求此矩阵的主对角线元素之和。 业 大 学
则输出的结果是 __________。
Xuan shanli
合 肥 工 业 大 学
⑵ 矩阵的转置运算
例1:将一个二维数组中的行和列元素互换,存放到另一个二 维数组中( p98~99 例4.7 )。
char9 数组

9.1.2 一维数组的引用 除了给指针变量赋地址值外,还可以给指针变量赋 NULL值。 例如:p=NULL; NULL是在stdio.h头文件中的预定义符。NULL的代码 值为0,当p=NULL时,称p为空指针。因为NULL的代码 值是0,所以上面语句等价于: p=’\0’; 或 p=0; 这时,指针p并不是指向地址为0的存储单元,而是具 有一个确定的值——“空”。企图通过一个空指针去访问 一个存储单元时,将会得到一个出错信息。
•编写程序,通过函数给数组输入若干大于等于5的整数,用0作为输入结束标志, 调用函数输出该数组中的元素。
#include <stdio.h> #define N 20 void aout(int *,int); int ain(int *); main() { int a[N], i; i = ain(a); aout(a, i); }
9.2 一维数组和指针
9.2.1 一维数组和数组元素的地址 一维数组在主存中占连续的存储空间,数组名 代表的是数组的首地址。可定义一个指针变量, 通过赋值或赋初值的形式,把数组名或数组的第 一个元素的地址赋值该指针变量,该指针变量就 指向了该数组。值得注意的是,这个指针变量中 的地址值不可改变,也就是说,不可以给数组名 重新赋值,因而数组名也可以认为是一个地址常 量。
在以下语句中,由于进入循环前指针变量pa指 向的是数组a的首地址,则pa++使得pa依次指了a 数组中的每一个元素: for(pa=a, i=0; i<5; i++) pa++; 同样也可以写成: for(pa=a, i=0; i<5; i++) { scanf(“%d”, pa); pa++;} 或 for(pa=a, i=0; i<5; i++) scanf(“%d”, pa++); 或 for(pa=a; pa-a<5; pa++) scanf(“%d”, pa);
第9讲数论板块综合卷解析

数论综合卷1.在黑板上写出三个整数,然后擦去一个换成其它两数之和,这样继续操作下去,最后得到 66,88,237。
问:原来写的三个整数能否为 1,3,5?分析:此题单从具体的数来,无从下手。
但抓住其操作过程中奇偶变化规律,问题就变得很简单了。
如果原来三个数为1、3、5,为三奇数。
无论怎样,操作一次后一定为二奇一偶,再往后操作,可能有以下两种情况:一是擦去一奇数,剩下一奇一偶,其和为奇,因此换上去的仍为奇数;二是擦去一偶数,剩下两奇,其和为偶,因此,换上去的仍为偶数。
总之,无论怎样操作,总是两奇一偶,而66、88、237是两偶一奇,这就发生矛盾.所以,原来写的不可能为1、3、5.2.有一批文章共 15 篇,各篇文章的页数是 1 页、2 页、3 页、 、14页和15页的稿纸,如果将这些文章按某种次序装订成册,并统一编上页码,那么每篇文章的第一页是奇数页码的文章最多有多少篇?分析:15篇中有偶数页码的7篇;奇数页码的8篇,每2篇奇数页码的文章合起来凑成的也是偶数页码。
所以第一页是奇数页码的最多可有7+(8÷2)=11(篇)。
3.桌子上有 5 个开口向上的杯子,现在允许每次同时翻动其中的 4 个,问能否经过若干次翻动,使得 5 个杯子的开口全都向下?分析:这不可能.我们将口向上的杯子记为:“0”,口向下的杯子记为“1”.开始时,由于5个杯子全朝上,所以这5个数的和为0,是个偶数.一个杯子每翻动一次,所记数由0变为1,或由l变为0,改变了奇偶性.每一次翻动四个杯子,因此,5个数之和的奇偶性仍与原来相同.所以,不论翻动多少次,5个数之和仍为偶数.而5个杯子全部朝下,和为5,是奇数,因此,不可能.4.我们把从 1 开始若干个自然数的连乘积用简单的符号表示,如:1×2×3 记作 3!读作 3 的阶乘;1×2×3×4×......×100 记作 100!读作 100 的阶乘; 1×2×3×......×n 记作 n!,读作 n 的阶乘。
I第九讲(十字链表及基本操作)

(b)每行 列设一个表头结点(结构同元素结点), 每行/列设一个表头结点 结构同元素结点), 每行 列设一个表头结点( 为链构成循环链表, 以down/right为链构成循环链表,即第 列头结点的 为链构成循环链表 即第i列头结点的 down指向该列上第 个非 元素,第i 行头结点的 指向该列上第1个非 元素, 指向该列上第 个非0元素 right指向该行第 个非 元素.第i列/行上最后一个 指向该行第1个非 元素. 列 行上最后一个 指向该行第 个非0元素 结点的down/right指向该列 行的头结点.若某列 行 指向该列/行的头结点 若某列/行 结点的 指向该列 行的头结点. 中无非0元素 则令它的头结点down/right域指向自 元素, 中无非 元素,则令它的头结点 域指向自 己. (c)设一个总头结点(结构同元素结点),令总 设一个总头结点( ),令总 设一个总头结点 结构同元素结点), 头结点和各个列/行头结点用 字段 按列/行序构 头结点和各个列 行头结点用val字段,按列 行序构 行头结点用 字段, 成一个循环单链表. 成一个循环单链表.
row元素在稀疏矩阵中的行号col元素在稀疏矩阵中的列号val元素值down指向同列中下一个非0元素结点right指向同行中下一个非0元素结点rowcolvaldownrightb每行列设一个表头结点结构同元素结点以downri上第1个非0元素第i行头结点的right指向该行第1个非0元素
(d)可令总头结点的 可令总头结点的row,col与val 分别表示矩阵的 , 与 可令总头结点的 最大行号,列号与非0元素个数 元素个数, 最大行号,列号与非 元素个数,而down/right指向 指向 行的头结点. 第1列/行的头结点.该总头结点可作为整个十字链表 列 行的头结点 的代表. 的代表. (e)由于行与列的头结点分别使用 由于行与列的头结点分别使用right域与 域与down域 由于行与列的头结点分别使用 域与 域 (不同时使用 ,故第i列与第 行头结点可合用同一个 不同时使用),故第 列与第i 不同时使用 列与第 头结点(对所有可能的i),以节省存储空间. ),以节省存储空间 头结点(对所有可能的i),以节省存储空间. (f)有时,为了快速访问行 列头结点,设置一个一维 有时, 列头结点, 有时 为了快速访问行/列头结点 数组headNodes[] ,使headNodes[i]指向 行/列的 数组 指向i行 列的 指向 头结点.但这并不是必须的,因为各行/列的头结点 头结点.但这并不是必须的,因为各行 列的头结点 已形成了一个循环单链表, 已形成了一个循环单链表,故若已知十字链表总头 结点,即可搜索到任一头结点. 结点,即可搜索到任一头结点.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用一个统一的名称(数组名)和下标来唯一确定
数组中的元素。 •新的解决办法: 可以通过数组来实现
4
#include <stdio.h> main( ) {char c[10]; int i,letter=0,space=0,digit=0,other=0; printf("请输入一行字符:\n"); for(i=0;i<10;i++) scanf("%c",&c[i]);
⑥ strlen函数,其一般形式为:strlen (字符数组) , strlen是测 试字符串长度的函数。函数的值为字符串中的实际长度(不包 括′\0′在内)。 ⑦ strlwr函数 其一般形式为:strlwr(字符串) strlwr函数的作用是将字符串中大写字母换成小写字母。 ⑧ strupr函数
如果一个字符数组中包含一个以上′\0′,则遇第一 个′\0′时输出就结束。
19
3.常用字符串处理函数
① puts函数 字符串的输出;其一般形式为: puts(字符数组) ② gets函数 字符串的输入;其一般形式为:gets(字符数组) ③ strcat函数 字符串的连接;其一般形式为:strcat(字符数组1,
a[3]=3;
9
3.初始化
一维数组
E.g int a[10]={0,1,2,3,4,5,6,7,8,9}//定义时初始化 int a[10]={0,1,2,3}//只给部分元素赋值
char c[10]={‘I’,’a’,’m’,’h’,’a’,’p’,’p’,’y’}//可逐个字符赋给
5
基本语法
1.数组的定义
一维数组: 类型说明符 数组名[常量表达式]
类型说明符---基本数据类型,如int、float、char等;
数组名---同变量名,命名规则一样 在定义数组时,需要指定数组中元素的个数。方括号中的常
量表达式用来表示元素的个数,即数组长度; 常量表达式可以包括常量和符号常量,不能包括变量。
例如
char c[10]; Scanf(“%s”,c) printf(″%s″,c);
18
说明
数组名表示数组的首地址;
用“%s”格式符输出字符串时,printf函数中的输 出项是字符数组名,而不是数组元素名。 如果数组长度大于字符串实际长度,也只输出到遇′ \0′结束。
输出字符不包括结束符′\0′。、
23
作业
1.将一个数组中的值逆序存放,如原来为1, 2,3,4,5,要求改为5,4,3,2,1 2.预习教材P166冒泡排序和P168选择排序算 法 3.复习本讲内容
24
7
思考
例: int a[10]如果要让变量t的值等于数组的 第6个元素,怎么办? t=a[6] or t=a[5] ? t=a[5] //因为第一个元素 的下标从0开始
8
注意
在使用数组元素时,应该注意下标值应在 已定义的数组大小的范围内。
常出现的错误有:
int a[3] /*定义a为含3个元素的数组 */
•附:对于一维数组,由于元素下标都从0开始,而且也知道数组的长 度(即元素的个数),所以在实际应用中,一般涉及到数组,都会涉 及到循环,且以for循环运用较普遍。
14
源程序
#include<stdio.h> void main() { int i ,a[10]; a[0]=a[1]=1; //前两项为1 for(i=2;i<10;i++) //为数组各元素赋值 a[i]=a[i-1]+a[i-2];
其一般形式为:strupr(字符串)
strupr函数的作用是将字符串中小写字母换成大写字母。
21
说明
使用字符串处理函数需加入字符串头文件, 如#include<string.h>, 在C++的编译环境 中可以省略。
22
例:
#include<stdio.h> #include<string.h> void main() { char str1[20],str2[20]; //定义字符数组str1,str2 printf("please input the string:\n"); gets(str1); //输入字符串1 printf("please input the string:\n"); gets(str2); //输入字符串2 puts(strcat(str1,str2)); //将字符串1和2连接的结果输 出 }
E.g int a[10],float score[5],char str[30]…
6
2.数组元素的引用
一维数组 说明: 数组名[下标]
数组必须先定义,后使用;(同变量一样) 只能逐个引用数组元素,而不能一次引用整个数组; 数组中,第一个元素的下标从o(零)开始。
e.g. int a[10];//定义了一个含10个元素的整型数组,这 10个元素分别是:a[0],a[1],a[2],a[3],…a[9];
16
二、字符串
1.字符串和字符串结束标志
在C中,字符串是通过字符数组来存储的 为了测定字符串的实际长度,C语言规定了一个“字 符串结束标志”——‘\0’。 ′\0′ 由系统自动添加。
17
2.字符串(字符数组)的输入输出
字符数组的输入输出可以有两种方法:
• 逐个字符输入输出。用格式符“%c”输入或输出 一个字符。 • 将整个字符串一次输入或输出。用“%s”格式符, 意思是对字符串的输入输出。
数组中各元素,不足的地方自动定为空字符
详见教材P132-133
10
补充
数组初始化时,如果要求其值从键盘输入,如何 操作?
对于一维数组(字符数组除外)有 2种方法 :数据
之间以空格隔开,以回车结束输入;数据之间以回车 隔开;
11
#include <stdio.h> 数组定义,字符数组,含10个元素 main( ) {char c[10]; 数组元素赋值 int i,letter=0,space=0,digit=0,other=0; printf("请输入一行字符:\n"); for(i=0;i<10;i++) 依次访问数组中的各个元素,进行判断 scanf("%c",&c[i]); for(i=0;i<10;i++) {if(c[i]>='a'&&c[i]<='z'|| c[i]>='A'&&c[i]<='Z') letter++; else if(c[i]==' ') space++; else if(c[i]>='0'&&c[i]<='9') digit++; else other++; } printf("字母数=%d,空格数=%d,数字数=%d,其他字符数 =%d\n",letter,space,digit,other); }
数据类型
基本数据类型
整型 字符型
实型
构造类型
数组类型 结构体类型 共用体类型
1
例:统计各种字符的个数(前面习题) #include <stdio.h> main() {char c; int letter=0,space=0,digit=0,other=0; printf("请输入一行字符:\n"); while ((c=getchar( ))!='\n') {if(c>='a'&&c<='z'|| c>='A'&&c<='Z') letter++; else if(c==' ') space++; else if(c>='0'&&c<='9') digit++; else other++; } printf("字母数=%d,空格数=%d,数字数=%d,其他字符数 =%d\n",letter,space,digit,other); }
分析: 有10个元素,都是int型,所以可定义一个含 10个元素的一维数组,如:int a[10]; 数组的前两项都等于1,即:a[0]=a[1]=1; 存在的递推关系: a[2]=a[1]+a[0],a[3]=a[2]+a[1],…a[9]=a[8]+a[7]. 即:a[i]=a[i-1]+a[i-2]
12
例2:fibonacci数列问题,求前10项
用变量来递推
#include<stdio.h> main() { int f1=1,f2=1,f; int i; for(i=3;i<=10;i++) { f=f1+f2; f1=f2; f2=f; printf("%d,",f); } }
13
用数组来处理
2
分析
从键盘上输入的字符都是同一种数据类型--字符类型(char); 字符的个数多于一个; 以前的解决办法:
char c; while ((c=getchar( ))!='\n')
还有没有其他办法?
