切线方程与切点弦方程
抛物线切点弦方程公式推导

抛物线切点弦方程公式推导
抛物线是一种常见的二次函数形式,其方程为y=ax+bx+c。
当抛物线上存在一点P(x0,y0),则通过该点的切线方程为
y-y0=2ax0(x-x0)。
现在我们来推导出抛物线切点弦的方程公式。
首先,我们假设抛物线的两个点P1(x1,y1)和P2(x2,y2)是位于该抛物线上的任意两个点。
我们知道,通过两个点的直线方程为
y-y1=(y2-y1)/(x2-x1)(x-x1)。
其次,我们要找到抛物线上与直线相交的切点P(x0,y0)。
我们可以将抛物线方程中的x替换为x0,从而得到y0=ax0+bx0+c。
接着,我们将y0代入直线方程,得到
y1+(y2-y1)/(x2-x1)(x0-x1)=ax0+bx0+c。
通过整理方程,我们可以得到抛物线切点弦的方程公式为
y=y1+(y2-y1)/(x2-x1)(x-x1)-a(x1+x2)/2(x1-x2)(x-x1)(x-x2)。
通过这个公式,我们可以求得抛物线与直线相交的切点P(x0,y0)的方程,从而更好地研究抛物线的性质和应用。
- 1 -。
圆的切线方程与切点弦方程关系探究

圆的切线方程与切点弦方程关系探究作者:杨福海来源:《黑河教育》2015年第10期解析几何的基本思想是用代数的方法研究几何问题,是数形结合思想的重要应用。
直线与圆的位置关系的判定中有几何法和代数法之分,几何法是通过圆心到直线的距离与圆的半径比大小,代数法是联立直线与圆的方程,通过方程组解的个数来判断直线与圆的位置关系。
通常情况下我们不探讨这两种方法之间的联系,特别是在学习直线与圆的位置关系时我们并不强调位置发生变化时直线方程之间有什么联系。
在课前预习时,学生遇到一道作业题,从中发现一个有趣的结论,却找不出所涉及知识的内在联系。
我也咨询了不少老师,但没有得到满意的答案,因此我尝试从另一个角度进行探讨。
作业题:已知圆C的方程为x2+y2=16 ,点P在直线X=8上,过p点引圆C的两条切线PA,PB,切点为A,B,求证:直线AB 恒过定点。
学生的解法:∵PA,PB是圆C的两条切线,∵OA⊥AP,OB⊥BP。
∵A,B在以OP 为直径的圆上。
设点P的坐标为(8,b),b∈R,则线段OP的中点Q坐标为4,。
∴以OP 为直径的圆Q方程为(x-4)2+y-2=42+2,b∈R。
化简得:x2+y2-8x-by=0,b∈R。
∵AB为圆Q和圆C的公共弦,∴直线AB的方程为8x+by=16,b∈R,所以直线AB恒过定点(2,0)。
这个解法是我们平时教学中常用的方法,但是有个别学生发现了直线AB的方程8x+by=16,b∈R与过圆x2+y2=16上一点(x0,y0)的切线方程x0x+y0y=16完全雷同,于是提出了疑问:为什么定点P在圆上时过点P(x0,y0)切线方程与定点P在圆外时过点p(x0,y0)引圆的切线方程(切点为A,B,直线AB )完全一样?在这里一条是切线一条是割线啊!为了解决这个问题,我们首先要了解,如果设P(x0,y0)为圆外一点,过P点引圆x2+y2=r2的两条切线PA,PB ,切点为A,B,则直线AB的方程称为切点弦方程。
悬链线的切线切点弦总结归纳(转换坐标系法)

悬链线的切线切点弦总结归纳(转换坐标系法)悬链线是一种重力均匀分布的链条所形成的曲线,运动学和动力学问题中经常用到该曲线。
在研究悬链线的过程中,切线切点弦是一个重要的概念。
在本文中,我们将通过转换坐标系的方法总结归纳悬链线的切线切点弦的相关知识。
悬链线的方程可以表示为:$\frac{d^2y}{dx^2}=\frac{T}{w\sqrt{1+(\frac{dy}{dx})^2}}$其中T和w分别为张力和重力,y是悬链线在x处的高度。
在某一点(x,y)处,悬链线的切线斜率可以表示为:$k=\frac{dy}{dx}=\frac{dw}{d\alpha}\frac{d\alpha}{ds}$其中,$\alpha$是链条与x轴的夹角,s是弧长。
通过对式子进行求导,可以得到:$\frac{dk}{ds}=\frac{dy}{dx}\frac{T}{w^2}\sqrt{1+(\frac{dy}{d x})^2}$当悬链线在某一点的切线斜率为k时,其切线方程可以表示为:$y-kx+\frac{Tw^2}{2}\ln|k+\sqrt{1+k^2}|=C$其中,C为常数。
切线与x轴的交点即为切点。
通过求解切点坐标,可以得到:$x=\frac{2w^2}{T}(e^{\frac{2(k-C)}{w^2}}-1)$$y=\frac{2w^2}{T}(ke^{\frac{2(k-C)}{w^2}}-k-\sqrt{1+k^2}+1)$关于悬链线的弦,如果已知其起点坐标为(x1,y1),终点坐标为(x2,y2),则弦的方程可以表示为:$\frac{y-y1}{y2-y1}=\frac{x-x1}{x2-x1}$如果以悬链线的最低点为起点,则该点处的切线与y轴平行,切点坐标为(0,h),弦的方程可以表示为:$y-h=\frac{2h}{L}x-\frac{h}{L^2}x^2$其中,h为悬链线的最低点处的高度,L为悬链线的长度。
课题∶圆锥曲线的切线方程和切点弦方程

课题:圆锥曲线的切线方程和切点弦方程主讲人: 安庆一中 李治国 教学目标:(1).掌握圆锥曲线在某点处的切线方程及切点弦方程。
(2).会用切线方程及切点弦方程解决一些问题。
(3)通过复习渗透数形结合、类比的思想,逐步培养学生分析问题和解决问题的能力。
(4) 掌握曲线与方程的关系。
教学重点:切线方程及切点弦方程的应用教学难点:如何恰当使用切线方程及切点弦方程教学过程:1. 引入:通过09年安徽省高考题及近几年各省考察圆锥曲线的实例引出本节课。
2. 知识点回顾:1.2. 3.4. 圆锥曲线切线的几个性质:性质1 过椭圆的准线与其长轴所在直线的交点作椭圆的两条切线,则切点弦长等于该椭圆的通径.同理:双曲线,抛物线也有类似的性质性质2 过椭圆的焦点F 1的直线交椭圆于A ,B 两点,过A ,B 两点作椭圆的切线交于点P ,则P 点的轨迹是焦点 的对应的准线,并且同理:双曲线,抛物线也有类似的性质3. 例题精讲:练习1:抛物线 与直线 围成的封闭的图形的面积为 ,若直线l 与抛物线相切,且平行于直线 ,则直线l 的方程为例1: 设抛物线 的焦点为F ,动点P 在直线22200(,)x y r M x y +=过圆 上一点 的切线方程:200xx yy r +=00221xx yy a b +=220022(,)1x y P x y a b +=设为椭圆上的点,则过该点的切线方程为:220022(,)1x y P x y a b -=设为双曲线上的点,则过该点的切线方程为:00221xx yy a b -=00(,)2P x y px =2设为抛物线y 上的点,则过该点的切线方程为:00()yy p x x =+1PF AB ⊥1F :20l x y --=2:C y x =2(0)y ax a =>1x =43260x y -+=上运动,过P 作抛物线C 的两条切线PA 、PB ,且与抛物线C 分别相切于A 、B 两点.求△APB 的重心G 的轨迹方程.4. 圆锥曲线的切点弦方程:1.2.3.4. 练习2:例题3:5.小结: 1.判断直线与圆锥曲线的位置关系时,注意数形结合;2. 掌握求曲线方程的方法:3. 两种方程两种思想作业: 6. 反思220022(,)1x y P x y a b +=设为椭圆外一点,过该点作椭圆的两条切线,切点为A ,B 则弦AB 的方程为:22200(,)P x y x y r +=设为圆外一点,则切点弦的方程为:200xx yy r +=220022(,)1x y P x y a b -=过为双曲线的两支作两条切线,则切点弦方程为:00221xx yy a b -=00(,)2P x y px =2设为抛物线y 开口外一点,则切点弦的方程为:00()yy p x x =+22221(,0). x y P m a bA B AB ±=≠对于圆锥曲线,过点,(m 0)作两条切线,切点为,则直线恒过定点22x 21,4312A,B AB OMN y P x y +=+=已知椭圆是在直线位于第一象限上一点,由P 向已知椭圆作两切线,切点分别为,问当直线与两坐标轴围成的三角形面积最小,最小值为多少?2l y x+3P y 2A,B.PAB P x ==∆已知是直线:上一点,过点作抛物线的两条切线,切点分别为求面积的最小值。
专题 切线与切点弦问题-高考数学大一轮复习

专题36 切线与切点弦问题【方法技巧与总结】1、点()00 M x y ,在圆222x y r +=上,过点M 作圆的切线方程为200x x y y r +=.2、点()00 M x y ,在圆222x y r +=外,过点M 作圆的两条切线,切点分别为 A B ,,则切点弦AB 的直线方程为200x x y y r +=.3、点()00 M x y ,在圆222x y r +=内,过点M 作圆的弦AB (不过圆心),分别过 A B ,作圆的切线,则两条切线的交点P 的轨迹方程为直线200x x y y r +=.4、点()00 M x y ,在圆222()()x a y b r -+-=上,过点M 作圆的切线方程为()()200()()x a x a y b y b r --+--=.5、点()00 M x y ,在圆222()()x a y b r -+-=外,过点M 作圆的两条切线,切点分别为 A B ,,则切点弦AB 的直线方程为()()200()()x a x a y b y b r --+--=.6、点()00 M x y ,在圆222()()x a y b r -+-=内,过点M 作圆的弦AB (不过圆心),分别过 A B ,作圆的切线,则两条切线的交点P 的轨迹方程为()()200()()x a x a y b y b r --+--=.7、点()00 M x y ,在椭圆2222x y a b +=1(0)a b >>上,过点M 作椭圆的切线方程为00221x x y y a b +=.8、点()00 M x y ,在椭圆2222x y a b +=1(0)a b >>外,过点M 作椭圆的两条切线,切点分别为 A B ,,则切点弦AB 的直线方程为00221x x y ya b+=. 9、点()00 M x y ,在椭圆2222x y a b+=1(0)a b >>内,过点M 作椭圆的弦AB (不过椭圆中心),分别过A B ,作椭圆的切线,则两条切线的交点P 的轨迹方程为直线02x x a +021y yb=. 10、点()00 M x y ,在双曲线2222x y a b -=1(0 0)a b >>,上,过点M 作双曲线的切线方程为00221x x y y a b -=.11、点()00 M x y ,在双曲线22x a-221(0 0)y a b b =>>,外,过点M 作双曲线的两条切线,切点分别为A B ,,则切点弦AB 的直线方程为00221x x y ya b-=. 12、点()00 M x y ,在双曲线22x a -221(0 0)y a b b =>>,内,过点M 作双曲线的弦AB (不过双曲线中心),分别过 A B ,作双曲线的切线,则两条切线的交点P 的轨迹方程为直线00221x x y ya b-=. 13、点()00 M x y ,在抛物线2y =2(0)px p >上,过点M 作抛物线的切线方程为()00y y p x x =+.14、点()00 M x y ,在抛物线2y =2(0)px p >外,过点M 作抛物线的两条切线,切点分别为 A B ,,则切点弦AB 的直线方程为()00y y p x x =+.15、点()00 M x y ,在抛物线2y =2(0)px p >内,过点M 作抛物线的弦AB ,分别过 A B ,作抛物线的切线,则两条切线的交点P 的轨迹方程为直线()00y y p x x =+.【题型归纳目录】 题型一:切线问题 题型二:切点弦过定点问题题型三:利用切点弦结论解决定值问题 题型四:利用切点弦结论解决最值问题 题型五:利用切点弦结论解决范围问题 【典例例题】 题型一:切线问题例1.已知平面直角坐标系中,点(4,0)到抛物线21:2(0)C y px p =>准线的距离等于5,椭圆22222:1(0)x y C a b a b+=>>,且过点. (1)求1C ,2C 的方程;(2)如图,过点(E m ,0)(2)m >作椭圆2C 的切线交1C 于A ,B 两点,在x 轴上取点G ,使得AGE BGE ∠=∠,试解决以下问题:①证明:点G 与点E 关于原点中心对称;②若已知ABG ∆的面积是椭圆2C 四个顶点所围成菱形面积的16倍,求切线AB 的方程.【解析】(1)解:因为点(4,0)到抛物线1C 的准线2px =-的距离等于5, 所以452p +=,解得2p =,所以抛物线1C 的方程为24y x =; 因为椭圆2C,且过点,所以222221314c aa b a b c ⎧=⎪⎪⎪+=⎨⎪-=⎪⎪⎩,解得2a =,1b =,所以椭圆2C 的方程为2214x y +=;(2)①证明:因为2m >,且直线AB 与椭圆2C 相切, 所以直线AB 的斜率存在,设直线AB 的方程为()y k x m =-, 联立22()14y k x m x y =-⎧⎪⎨+=⎪⎩,得22222(41)8440k x k mx k m +-+-=, 因为直线AB 与椭圆2C 相切,所以△42222644(41)(44)0k m k k m =-+-=,即2214k m =-,联立2()4y k x m y x=-⎧⎨=⎩,得2440ky y km --=,设1(A x ,1)y ,2(B x ,2)y ,则12124,4y y y y m k+==-;设(,0)G t ,因为AGE BGE ∠=∠,所以0AG BG k k +=, 则12120y yx t x t+=--,即211212()0x y x y t y y +-+=, 即121212()()04y y y y t y y +-+=,又120y y +≠,所以124y y t m ==-,即(,0)G m -, 即点G 与点E 关于原点中心对称;②解:椭圆2C 四个顶点所围成菱形面积为122242S a b ab =⨯⨯==,所以ABG ∆的面积为16464⨯=,则1211||||222ABG S GE y y ∆=-=⨯==,令64,即22(4)256m m m -+=, 即42342560m m m -+-=,即42(256)(4)0m m m -+-=, 即22(4)[(16)(4)]0m m m m -+++=, 即32(4)(51664)0m m m m -+++=,因为2m >,所以4m =,2211412k m ==-,k =所以直线AB 的方程为4)y x =-. 例2.某同学在探究直线与椭圆的位置关系时发现椭圆的一个重要性质:椭圆2222:1(0)x y C a b a b +=>>在任意一点0(M x ,0)y 处的切线方程为00221xx yy a b+=.现给定椭圆22:143x y C +=,过C 的右焦点F 的直线l 交椭圆C 于P ,Q 两点,过P ,Q 分别作C 的两条切线,两切线相交于点G . (1)求点G 的轨迹方程;(2)若过点F 且与直线l 垂直的直线(斜率存在且不为零)交椭圆C 于M ,N 两点,证明:11||||PQ MN +为定值.【解析】(1)解:设直线PQ 为1x ty =+,1(P x ,1)y ,2(Q x ,2)y , 易得在P 点处切线为11143x x y y +=,在Q 点处切线为22143x x y y+=, 由11221,431,43x x y yx x y y ⎧+=⎪⎪⎨⎪+=⎪⎩得2112214()y y x x y x y -=-,又111x ty =+,221x ty =+,可得4x =,故点G 的轨迹方程4x =.(2)证明:联立l 的方程与C 的方程221,1,43x ty x y =+⎧⎪⎨+=⎪⎩消去x ,得22(34)690t y ty ++-=.由韦达定理,得122634t y y t +=-+,122934y y t =-+,所以2212(1)||34t PQ t +==+, 因为PQ MN ⊥,将t 用1t -代,得222112(1)12(1)||13434t t MN t t ++==+⋅+, 所以22221134347||||12(1)12(1)12t t PQ MN t t +++=+=++. 例3.已知圆222:(0)O x y r r +=>.(1)求证:过圆O 上点0(M x ,0)y 的切线方程为200x x y y r +=.类比前面的结论,写出过椭圆2222:1(0)x y C a b a b+=>>上一点0(N x ,0)y 的切线方程(不用证明). (2)已知椭圆22:143x y C +=,Q 为直线4x =上任一点,过点Q 作椭圆C 的切线,切点分别为A 、B ,求证:直线AB 恒过定点.【解析】(1)证明:因为圆222:O x y r +=, 故圆心(0,0)O ,半径为r , 又0(M x ,0)y , 所以0OM y k x =, 因为0(M x ,0)y 在圆上, 所以过M 的圆的切线斜率0x k y =-,所以过M 的圆的切线方程为0000()x y y x x y -=--,① 又因为22200x y r +=,② 由①②整理得,为200x x y y r +=.所以过圆O 上点0(M x ,0)y 的切线方程为200x x y y r +=.过椭圆2222:1(0)x y C a b a b +=>>上一点0(N x ,0)y 的切线方程为00221x x y ya b+=;(2)设(4,)Q t ,()t R ∈,1(A x ,1)y ,2(B x ,2)y , 由(1),则直线QA 的方程11143x x y y +=, 因为Q 在QA 上,所以1113ty x +=,① 同理可得2213ty x +=,② 由①②可得直线AB 的方程为13tx y +=,令0y =,得1x =, 所以直线AB 恒过点(1,0).变式1.已知点(1,0)A -,(1,0)B ,动点P 满足||||4PA PB +=,P 点的轨迹为曲线C .(Ⅰ)求曲线C 的方程;(Ⅱ)已知圆222x y R +=上任意一点0(P x ,0)y 处的切线方程为:200x x y y R +=,类比可知椭圆:22221x y a b+=上任意一点0(P x ,0)y 处的切线方程为:00221x x y ya b+=.记1l 为曲线C 在任意一点P 处的切线,过点B 作BP 的垂线2l ,设1l 与2l 交于Q ,试问动点Q 是否在定直线上?若在定直线上,求出此直线的方程;若不在定直线上,请说明理由.【解析】解:(Ⅰ)由椭圆的定义知P 点的轨迹为以A ,B 为焦点,长轴长为4的椭圆,设椭圆方程为2222:1x y a b +=,则241a c =⎧⎨=⎩,∴2a b =⎧⎪⎨=⎪⎩曲线C 的方程为22143x y +=.(Ⅱ)设0(P x ,0)y ,由题知直线1l 的方程为00:143x x y y+=, 当01x ≠时,001PB y k x =-,2l ∴的斜率为0201x k y -=,0201:(1)x l y x y -=-,1l 与2l 的方程联立00001(1)143x y x y x x y y -⎧=-⎪⎪⎨⎪+=⎪⎩,消y 得000034(1)(1)120(4)4(4)x x x x x x x +---=⇒-=-, 4x ∴=.动点Q 在定直线4x =上, 当01x =时,032y =±,1:142x yl ±=, 2:0l y =,(4,0)Q ,Q 在直线4x =.综上所述,动点Q 在定直线4x =上.变式2.下面是某同学在学段总结中对圆锥曲线切线问题的总结和探索,现邀请你一起合作学习,请你思考后,将答案补充完整.(1)圆222:O x y r +=上点0(M x ,0)y 处的切线方程为 .理由如下: .(2)椭圆22221(0)x y a b a b+=>>上一点0(x ,0)y 处的切线方程为 ;(3)(,)P m n 是椭圆22:13x L y +=外一点,过点P 作椭圆的两条切线,切点分别为A ,B ,如图,则直线AB的方程是 .这是因为在1(A x ,1)y ,2(B x ,2)y 两点处,椭圆L 的切线方程为1113x xy y +=和2213x x y y +=.两切线都过P 点,所以得到了1113x m y n +=和2213x my n +=,由这两个“同构方程”得到了直线AB 的方程;(4)问题(3)中两切线PA ,PB 斜率都存在时,设它们方程的统一表达式为()y n k x m -=-,由22()33y n k x m x y -=-⎧⎨+=⎩,得222(13)6()3()30k x k n km x n km ++-+--=, 化简得△0=得222(3)210m x mnk n -++-=.若PA PB ⊥,则由这个方程可知P 点一定在一个圆上,这个圆的方程为 . (5)抛物线22(0)y px p =>上一点0(x ,0)y 处的切线方程为00()y y p x x =+;(6)抛物线2:4C x y =,过焦点F 的直线l 与抛物线相交于A ,B 两点,分别过点A ,B 作抛物线的两条切线1l 和2l ,设1(A x ,1)y ,2(B x ,2)y ,则直线1l 的方程为112()x x y y =+.直线2l 的方程为222()x x y y =+,设1l 和2l 相交于点M .则①点M 在以线段AB 为直径的圆上;②点M 在抛物线C 的准线上. 【解析】解:(1)圆222:O x y r +=上点0(M x ,0)y 处的切线方程为200y y x x r +=. 理由如下:①若切线的斜率存在,设切线的斜率为k ,则001OM OM k k y k x⋅=-⎧⎪⎨=⎪⎩,所以0x k y =-, 又过点0(M x ,0)y , 由点斜式可得,0000()x y y x x y -=--, 化简可得,220000y y x x x y +=+, 又22200x y r +=,所以切线的方程为200y y x x r +=; ②若切线的斜率不存在,则(,0)M r ±, 此时切线方程为x r =±.综上所述,圆222:O x y r +=上点0(M x ,0)y 处的切线方程为200y y x x r +=. (3)在1(A x ,1)y ,2(B x ,2)y 两点处,椭圆L 的切线方程为1113x x y y +=和2213x xy y +=, 因为两切线都过P 点(,)m n , 所以得到了1113x m y n +=和2213x my n +=, 由这两个“同构方程”得到了直线AB 的方程为13mxny +=; (4)问题(3)中两切线PA ,PB 斜率都存在时,设它们方程的统一表达式为()y n k x m -=-, 由22()33y n k x m x y -=-⎧⎨+=⎩,可得222(13)6()3()30k x k n km x n km ++-+--=, 由△0=,可得222(3)210(*)m k mnk n -++-=, 因为PA PB ⊥, 则1PA PB k k ⋅=-,所以(*)式中关于k 的二次方程有两个解且其乘积为1-,则2122113n k k m-⋅==--, 可得224m n +=,所以圆的半径为2,且过原点,其方程为224x y +=. 故答案为:(1)200y y x x r +=,理由见解析; (3)13mxny +=; (4)224x y +=.题型二:切点弦过定点问题例4.定义:若点0(P x ,0)y 在椭圆22221(0)x y a b a b +=>>上,则以P 为切点的切线方程为:00221x x y ya b+=.已知椭圆22:132x y C +=,点M 为直线260x y --=上一个动点,过点M 作椭圆C 的两条切线MA ,MB ,切点分别为A ,B ,则直线AB 恒过定点( ) A .11(,)23-B .11(,)23-C .12(,)23-D .12(,)23-【解析】解:因为M 在直线260x y --=上,则可设点M 的坐标为(26,)t t +,t R ∈, 设1(A x ,1)y ,2(B x ,2)y ,所以直线MA ,MB 的方程分别为: 11221,13232x x y y x x y y +=+=,显然点M 的坐标适合两个方程, 代入可得:1122(26)132(26)132x t y tx t y t +⎧+=⎪⎪⎨+⎪+=⎪⎩,则直线AB 的方程为:(26)132x t yt++=,即2(26)360t x yt ++-=, 即(43)612x y t x +=-,令4306120x y x +=⎧⎨-=⎩,解得12,23x y ==-,所以直线AB 过定点12(,)23-,故选:C .例5.已知经过圆2221:C x y r +=上点0(x ,0)y 的切线方程是200x x y y r +=.(1)类比上述性质,直接写出经过椭圆22222:1(0)x y C a b a b+=>>上一点0(x ,0)y 的切线方程;(2)已知椭圆22:16x E y +=,P 为直线3x =上的动点,过P 作椭圆E 的两条切线,切点分别为A 、B ,①求证:直线AB 过定点. ②当点P 到直线AB时,求三角形PAB 的外接圆方程. 【解析】解:(1)切线方程为:00221x x y ya b+=. (2)设切点为1(A x ,2)y ,2(B x ,2)y ,点(3,)P t ,由(1)的结论的AP 直线方程:1116x x y y +=,BP 直线方程:2216x xy y +=, 通过点(3,)P t ,∴有1122316316x y t x y t ⨯⎧+⨯=⎪⎪⎨⨯⎪+⨯=⎪⎩,A ∴,B 满足方程:12x ty +=,∴直线AB 恒过点:1020xy ⎧-=⎪⎨⎪=⎩即直线AB 恒过点(2,0).又已知点(3,)P t 到直线AB.∴22|354t t t-=+ 425410t t ⇒--=,22(51)(1)0t t +-=,1t ∴=±.当1t =时,点(3,1)P ,直线AB 的方程为:220x y +-=. 2222066x y x y +-=⎧⎨+=⎩求得交点121(0,1),(,),(3,1)55A B P -. 设PAB ∆的外接圆方程为:220x y Dx Ey F ++++=,代入得131012529E F D E F D E F +=-⎧⎪++=-⎨⎪-+=-⎩,解得:PAB ∆的外接圆方程为223210x y x y +--+= 即PAB ∆的外接圆方程为:2239()(1)24x y -+-=.例6.已知抛物线2:2C x py =的焦点为F ,抛物线上一点(A m ,2)(0)m >到F 的距离为3. (1)求抛物线C 的方程和点A 的坐标;(2)设直线l 与抛物线C 交于D ,E 两点,抛物线C 在点D ,E 处的切线分别为1l ,2l ,若直线1l 与2l 的交点恰好在直线2y =-上,证明:直线l 恒过定点. 【解析】(1)解:由题意知232p +=,得2p =,所以抛物线C 的方程为24x y =. 将点(A m ,2)(0)m >代入24xy =,得m =,所以点A 的坐标为.(2)证明:设221212(,),(,)44x x D x E x ,由题意知.直线l 的斜率存在,设直线l 的方程为y kx n =+, 联立方程24y kx nx y=+⎧⎨=⎩,得2440x kx n --=,所以△216160k n =+>,124x x k +=,124x x n =-,24x y =,即24x y =, 则2xy '=,所以抛物线C 在点D 处的切线1l 的方程为2111()24x x y x x =-+,化简得21124x x y x =-,同理直线2l 的方程为22224x x y x =-,联立方程2112222424x x y x x x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,解得121224x x x x x y +⎧=⎪⎪⎨⎪=⎪⎩. 又因为直线1l 与2l 的交点恰好在直线2y =-上,所以1224x x =-,即128x x =-. 所以1248x x n =-=-.解得2n =.故直线l 的方程为2y kx =+,所以直线l 恒过定点(0,2).题型三:利用切点弦结论解决定值问题例7.已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为(1,0)F,且点P 在椭圆C 上,O 为坐标原点(1)求椭圆C 的标准方程(2)过椭圆22122:153x y C a b +=-上异于其顶点的任一点Q ,作圆224:3O x y +=的切线,切点分别为M ,(N M ,N 不在坐标轴上),若直线MN 的横纵截距分别为m ,n ,求证:22113m n+为定值 【解析】解:(1)由题意得:1c =,所以221a b =+,又因为点P 在椭圆C 上,所以223314a b+=, 可解得24a =,23b =,所以椭圆标准方程为22143x y +=.(2)证明:由题意:2213:144x y C +=,设点1(Q x ,1)y ,2(M x ,2)y ,3(N x ,3)y ,因为M ,N 不在坐标轴上,所以1QM OMk k =-,直线QM 的方程为2222()x y y x x y -=-, 化简得:2243x x y y +=,① 同理可得直线QN 的方程为3343x x y y +=,② 把Q 点的坐标代入①、②得212131314343x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩,所以直线MN 的方程为1143x x y y +=---------------③, 令0y =,得143m x =,令0x =得143n y =,所以143x m=,143y n =,又点Q 在椭圆1C 上,所以2244()3()433m n+=, 即22113m n+为定值. 例8.已知1F 、2F 分别为椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,且右焦点2F 的坐标为(1,0),点P 在椭圆C 上,O 为坐标原点. (1)求椭圆C 的标准方程;(2)若过点2F 的直线l 与椭圆C 交于A ,B两点,且||AB =l 的方程; (3)过椭圆C 上异于其顶点的任一点Q ,作圆22:1O x y +=的两条切线,切点分别为M ,(N M ,N 不在坐标轴上),若直线MN 在x 轴、y 轴上的截距分别为m 、n ,那么2212m n +是否为定值?若是,求出此定值;若不是,请说明理由.【解析】解:(1)椭圆C 的右焦点2F 的坐标为(1,0),∴椭圆C 的左焦点1F 的坐标为(1,0)-,由椭圆的定义得12||||2PF PF a +=,2a ∴=a ∴=,22a =由题意可得1c =,即2221b a c =-=,即椭圆C 的方程为2212x y +=;(2)直线l 与椭圆C 的两个交点坐标为1(A x ,1)y ,2(B x ,2)y , ①当直线l 垂直x轴时,易得||AB = ②当直线l 不垂直x 轴时,设直线:(1)l y k x =-联立2212(1)x y y k x ⎧+=⎪⎨⎪=-⎩,消y 得,2222(12)4220k x k x k +-+-=,①则2122421k x x k +=+,21222221k x x k -=+,222222222121222224228(1)||(1)[()4](1)[()24]2121(21)k k k AB k x x x x k k k k -+∴=++-=+-⨯==+++,解得1k =±,∴直线方程l 的方程为10x y --=或10x y +-=(Ⅲ)设点0(Q x ,0)y ,3(M x ,3)y ,4(N x ,4)y ,连接OM ,ON , 0M MQ ⊥,ON NQ ⊥,M ,N 不在坐标轴上,303M y k x ∴=,404N y k x =-, ∴直线MQ 的方程为3333()y y y x x x -=-,即331xx yy +=,⋯① 同理直线NQ 的方程为441xx yy +=,⋯②, 将点Q 代入①②,得0303040411x x y y x x y y +=⎧⎨+=⎩,显然3(M x ,3)y ,4(N x ,4)y 满足方程001xx yy +=,∴直线MN 的方程为001xx yy +=,分别令0x =,0y =,得到01n x =,01m y =. 01y m ∴=,01x n=, 0(Q x ,0)y 满足2212x y +=;∴221112m n+=,即22122m n +=题型四:利用切点弦结论解决最值问题例9.已知抛物线22x py =上一点0(M x ,1)到其焦点F 的距离为2. (1)求抛物线的方程;(2)如图,过直线:2l y =-上一点A 作抛物线的两条切线AP ,AQ ,切点分别为P ,Q ,且直线PQ 与y 轴交于点N .设直线AP ,AQ 与x 轴的交点分别为B ,C ,求四边形ABNC 面积的最小值.【解析】解:(1)由||122pMF =+=,得2p =, 所以抛物线的方程为24x y =. (2)设1(P x ,1)y ,2(Q x ,2)y , 由12y x '=可得在P 处的切线方程为2111()42x x y x x -=-,整理可得112()x x y y =+,同理在Q 处的切线方程为222()x x y y =+,又因为两切线都过(,2)A t -,∴11222(2)2(2)tx y tx y =-⎧⎨=-⎩,即可得直线PQ 的方程为2(2)tx y =-,所以直线过点(0,2),即(0,2)N , 又1(2x B ,0),2(2xC ,0), ∴四边形ABNC 的面积122||||ABC NBC S S S BC x x ∆∆=+==-,联立122()4tx y y x y =+⎧⎨=⎩,可得2280x tx --=,122x x t ∴+=,128x x =-所以12||3242S x x =-.(当0t =时取等号),∴四边形ABNC 面积的最小值为例10.已知(,1)T m 为抛物线2:2(0)C x py p =>上一点,F 是抛物线C 的焦点,且||2TF =. (1)求抛物线C 的方程;(2)过圆22:(2)1E x y ++=上任意一点G ,作抛物线C 的两条切线1l ,2l ,与抛物线相切于点M ,N ,与x 轴分别交于点A ,B ,求四边形ABNM 面积的最大值.【解析】解:(1)||2TF =,由抛物线定义知,122p +=,2p ∴=,24x y ∴=. (2)设1(M x ,1)y ,2(N x ,2)y ,0(G x ,0)y ,0[3y ∈-,1]-, 切线11:2()AM x x y y =+,因此:11122A y x x x ==, 切线22:2()AN x x y y =+,因此:22222B y x x x ==, 另一方面,点0(G x ,0)y 在两切线上,从而满足:011020202()2()x x y y x x y y =+⎧⎨=+⎩,因此切点弦MN 的方程为:002()x x y y =+,直线MN 与抛物线24x y =进行方程联立:200240x x x y -+=, 从而1202x x x +=,1204x x y =,且||MN ==, ABMN GMN GAB S S S ∆∆=-212011||||2222x x y =⋅-33222220001200111[(4)||](4)242x y y x x x y =---=-2200000(4)(73)x y y y y =-+=---, 当0[3y ∈-,1]-1323=, 2200073773[()]924y y y ---=-++,∴93ABMN S ,当且仅当03y =-时,取到最大值.题型五:利用切点弦结论解决范围问题例11.已知椭圆2222:1(0)x y C a b a b+=>>的长轴长为6,C 上一点M 关于原点O 的对称点为N ,F 为C 的右焦点,若MF NF ⊥,设MNF α∠=,且3sin()44πα+=.(1)求椭圆C 的标准方程;(2)经过圆22:10O x y+=上一动点P 作椭圆C 的两条切线,切点分别记为A ,B ,求AOB ∆面积的取值范围.【解析】解:(1)由26a =,即3a =,又22122cos 2sin )4c c e a c c πααα====++所以c =2221b a c =-=,则椭圆的方程为2219x y +=;(2)设1(A x ,1)y ,2(B x ,2)y , 则直线PA 的方程为1119x x y y +=,直线PB 的方程为2219x xy y +=, 因为0(P x ,0)y 在直线PA ,PB 上, 所以101019x x y y +=,202019x x y y +=,所以直线AB 的方程为0019x xy y +=, 由00221999x xy y x y ⎧+=⎪⎨⎪+=⎩消去y ,结合220010x y +=,和220010x y =-,可得22200(810)1881810y x x x y +-+-=, △242018(8)y y =+,120|||AB x x -=0=202018108y y +=+,又点O 到直线AB的距离为d ==,2020018119||922108y S AB d y +=⋅=⋅=+,又2010y,记[1t ,9],所以9[6t t +∈,10], 所以9[10S ∈,3]2.例12.已知椭圆2222:1(0)x y C a b a b+=>>的左焦点1(F 0),点Q 在椭圆C 上.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)经过圆22:5O x y +=上一动点P 作椭圆C 的两条切线,切点分别记为A ,B ,直线PA ,PB 分别与圆O 相交于异于点P 的M ,N 两点. (ⅰ)求证:0OM ON +=; (ⅱ)求OAB ∆的面积的取值范围.【解析】解:(Ⅰ)由题意可得c =221314a b+=,222a b c =+,解得24a =,21b =, 所以椭圆的方程为:2214x y +=;(Ⅱ)()i 证明:设0(P x ,0)y ,①当直线PA ,PB 的斜率都存在时,设过P 与椭圆相切的直线方程为00()y k x x y =-+, 联立直线与椭圆的方程0022()440y k x x y x y =-+⎧⎨+-=⎩, 整理可得2220000(14)8()4()40k x k y kx x y kx ++-+--=,△2222000064()4(14)[4()4]k y kx k y kx =--+--,由题意可得△0=,整理可得222000(4)210x k x y k y -++-=, 设直线PA ,PB 的斜率分别为1k ,2k ,所以20122014y k k x -=-,又2205x y +=,所以220022001(5)4144x x x x ---==---, 所以PM PN ⊥,即MN 为圆O 的直径,所以0OM ON +=; ②当直线PA 或PB 的斜率不存在时,不妨设(2,1)P , 则直线PA 的方程为2x =,所以(2,1)M -,(2,1)N -,也满足0OM ON +=; ()ii 设点1(A x ,1)y ,2(B x ,2)y ,当直线PA 的斜率存在时,设直线PA 的方程为:111()y k x x y =-+,联立直线PA 与椭圆的方程11122()440y k x x y x y =-+⎧⎨+-=⎩,消y 可得2221111111(14)8()4()40k x k y k x x y k x ++-+--=,△22221111111164()4(14)[4()4]k y k x k y k x =--+--, 由题意△0=,整理可得222111111(4)210x k x y k y -++-=, 则11111122111444x y x y x k x y y -=-==--, 所以直线PA 的方程为:1111()4x y x x y y =--+, 化简可得22111144x x y y y x +=+, 即1114x xy y +=, 经验证,当直线PA 的斜率不存在时,直线PA 的方程为2x =或2x =-也满足1114x xy y +=,同理可得直线PB 的方程2214x xy y +=, 因为0(P x ,0)y 在直线PA ,PB 上,所以101020201414x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩,所以可得直线AB 的方程为0014x x y y +=,而P 在圆225x y +=上,所以22005x y +=, 联立直线AB 与椭圆的方程为00221444x xy y x y ⎧+=⎪⎨⎪+=⎩,整理可得22200(35)816160y x x x y +-+-=, 020853A B x x x y +=+,2020161653A B y x x y -=+, 所以O 到直线AB的距离d =,弦长0|||A B AB x x - 又点O 到直线AB的距离d ==,令t ,[1t ∈,4],则2144||424OAB t S d AB t t t∆=⋅==++,而4[4t t+∈,5],所以OAB ∆的面积的取值范围是4[5,1].例13.椭圆2222:1(0)x y C a b a b+=>>的两焦点分别为1F ,2F ,椭圆与y轴正半轴交于点Q ,122QF F S =.(1)求曲线C 的方程;(2)过椭圆C 上一动点P (不在x 轴上)作圆22:1O x y +=的两条切线PC 、PD ,切点分别为C 、D ,直线CD 与椭圆C 交于E 、G 两点,O 为坐标原点,求OEG ∆的面积S 的取值范围.【解析】解:(1)椭圆与y轴正半轴交于点Q ,122QF F S=.可得121222QF F b Sc b bc ==⨯⨯==,∴2c a ==, ∴椭圆方程为22142x y +=.(2)设0(P x ,0)y ,线段OP 的中点为00(,)22x y ,22222000001,2(1)24242x y x x y +==-=-,2004x <, 以OP以OP 为直径的圆的方程为22220000()()224x y x y x y +-+-=,即00()()0x x x y y y -+-=,又圆22:1O x y +=, 两式相减00:1CD x x y y +=,由0022124x x y y x y +=⎧⎨+=⎩,消去y 并化简得22220000(2)4240x y x x x y +-+-=, ∴22222220000000164(2)(24)8(412)x x y y y x y =-+-=-+22222000008[41(4)]24(1)y x x y x =-+-=+,0000||EG ==O EG d -=∴200000001||2222S EG d x =⋅====+-=由于2004x <,所以20115x +<,2011x +<对于函数211()3(15),()30h t t t h t tt '=+<=->,()h t在上递增.(1)4,h h ===所以20431x +<1114<,62<,∴62S <.S ∈. 变式3.已知椭圆22122:1(0)x y C a b a b+=>>的两个焦点1F ,2F ,动点P 在椭圆上,且使得01290F PF ∠=的点P 恰有两个,动点P 到焦点1F的距离的最大值为2+(1)求椭圆1C 的方程;(2)如图,以椭圆1C 的长轴为直径作圆2C ,过直线x =-T 作圆2C 的两条切线,设切点分别为A ,B ,若直线AB 与椭圆1C 交于不同的两点C ,D ,求||ABCD的取值范围.【解析】解:(1)动点P 在椭圆上,且使得01290F PF ∠=的点P 恰有两个,b c ∴=, 动点P 到焦点1F 的距离的最大值为2+∴2a c +=+可得2a =,b c =所以椭圆1C 的方程为:22142x y +=;(2)圆2C 的方程为224x y +=,设直线x =-T 的坐标为)t ,设1(A x ,1)y ,2(B x ,2)y ,则直线AT 的方程为114x x y y +=,直线BT 的方程为224x x y y +=,又)T t 在直线AT 和BT上,即112244ty ty ⎧-+=⎪⎨-+=⎪⎩,故直线AB 的方程为4ty -+=.由原点O 到直线AB的距离d =得||AB =联立224142ty x y ⎧-+=⎪⎨+=⎪⎩,消去x 得22(16)8160t y yt +--=,设3(C x ,3)y ,4(D x,4)y ,则343422816,1616t y y y y t t -+==++,从而222(8)16t CD t +==+记28(8)t m m +=,则||AB CD =11(0)8y y m =<,则||AB CD =11(0)8y y m =<,所以||AB CD3()112256f y y y =+-, 所以由2()127680f y y y '=-=得18y =, 所以3()112256f y y y =+-在1(0,]8上单调递增,()(1f y ∴∈,2]即||ABCD∈. 变式4.已知椭圆22122:1(0)x y C a b a b+=>>的两个焦点1F ,2F ,动点P 在椭圆上,且使得1290F PF ∠=︒的点P 恰有两个,动点P 到焦点1F 的距离的最大值为2+(Ⅰ)求椭圆1C 的方程;(Ⅱ)如图,以椭圆1C 的长轴为直径作圆2C ,过直线x =-T 作圆2C 的两条切线,设切点分别为A ,B ,若直线AB 与椭圆1C 交于不同的两点C ,D ,求弦||CD 长的取值范围.【解析】解:()I 由使得1290F PF ∠=︒的点P 恰有两个可得,b c a ==;动点P 到焦点1F 的距离的最大值为2+2a c +=2,a c ==所以椭圆1C 的方程是22142x y +=⋯(4分)()II 圆2C 的方程为224x y +=,设直线x =-T 的坐标为()t -设1(A x ,1)y ,2(B x ,2)y ,则直线AT的方程为114x x y y+=,直线BT的方程为224x x y y+=,又()t-在直线AT和BT上,即112244tyty⎧-+=⎪⎨-+=⎪⎩,故直线AB的方程为4ty-+=⋯(6分)联立224142tyx y⎧-+=⎪⎨+=⎪⎩,消去x得22(16)8160t y yt+--=,设3(C x,3)y,4(D x,4)y.则343422816,1616ty y y yt t-+==++,⋯(8分)从而21224(8)|||(16)tCD y yt+=-=⋯+(10分)232416t-=++,又21616t +,从而2322016t--<+,所以||[2CD∈,4)⋯(12分)变式5.已知椭圆22122:1(0)x yC a ba b+=>>的离心率为12,且直线1:1x yla b+=被椭圆1C截得的弦长为.()I求椭圆1C的方程;()II以椭圆1C的长轴为直径作圆2C,过直线2:4l y=上的动点M作圆2C的两条切线,设切点为A,B,若直线AB与椭圆1C 交于不同的两点C,D,求||||CD AB的取值范围.【解析】解:()I线1:1x yla b+=,经过点(,0)a,(0,)b,被椭圆1C227a b+=.又12ca=,222a b c=+,解得:24a=,23b=,1c=.∴椭圆1C的方程为22143x y+=.()II由()I可得:圆2C的方程为:224x y+=.设(2,4)M t,则以OM为直径的圆的方程为:222()(2)4x t y t-+-=+.与224x y+=联立可得:直线AB的方程为:2440tx y+-=,设1(C x,1)y,2(D x,2)y,联立222440143tx yx y+-=⎧⎪⎨+=⎪⎩,化为:22(3)480t x tx+--=,则12243tx xt+=+,12283x xt-=+,2236||43tCDt+==+.又圆心O到直线AB的距离d==||AB∴===,22222364||||243t tAB CD tt t+∴=+⨯=+令233t m+=,则||||8AB CD=3m,可得3233m-<,可得:2||||83AB CD<变式6.如图,已知点P在半圆22:(2)4(2)Q x y y++=-上一点,过点P作抛物线2:2(0)C x py p=>的两条切线,切点分别为A,B,直线AP,BP,AB分别与x轴交于点M,N,T,记TNB∆的面积为1S,TMA∆的面积为2S.(Ⅰ)若抛物线C的焦点坐标为(0,2),求p的值和抛物线C的准线方程;(Ⅱ)若存在点P,使得128SS=,求p的取值范围.【解析】解:(Ⅰ)22p=,4p=.准线方程为直线2y=-.(Ⅱ)设1(A x,1)y,2(B x,2)y,过点A的切线方程11:()Al x x p y y=+,于是1(,0)2xM;过点B的切线方程22:()Bl x x p y y=+,于是2(,0)2xN;点(P x,)y在两条切线上,所以10012002()()x x p y yx x p y y=+⎧⎨=+⎩,可得点P坐标为1212(,)22x x x xPp+.1212:()22ABx x x xl x p yp+=+,于是12112112121212()(,0).||||||22()x x x x x x x xT TMx x x x x x-=-=+++,2222121212()||||||22()x x x x x x TN x x x x -=-=++, 而23122111||||2||81||||2TN y S x S x TM y ⋅===⋅,所以212x x =-. 于是点211(,)2x x P p --,点P 的轨迹方程为24px y =-,问题转化为抛物线24p x y =-与半圆22:(2)4(2)Q x y y ++=-有交点. 记24()f x x p =-,则4(2)42f p=-⨯-,又因为0p >, 解得:08p <.所以p 的取值范围为(0,8].变式7.如图,设抛物线2:4C y x =的焦点为F ,点P 是半椭圆221(0)4y x x +=<上的一点,过点P 作抛物线C 的两条切线,切点分别为A 、B ,且直线PA 、PB 分别交y 轴于点M 、N . (Ⅰ)证明:FM PA ⊥; (Ⅱ)求||||FM FN ⋅的取值范围.【解析】解:(Ⅰ)设点P 的坐标为0(x ,0)y ,直线PA 方程为00()(0)x m y y x m =-+≠.令0x =,可知点M 的坐标为00(0,)x y m-. 由,消去x 得2004440y my my mx -+-=. 因为直线与抛物线只有一个交点, 故△0=,即2000m y m x -+=. 因为点F 的坐标为(1,0), 故00(1,)x FM y m =--,00(,)xPM x m=--.则20002()0x FM PM m y m x m⋅=-+=. 因此FM PM ⊥,亦即FM PA ⊥.(Ⅱ)设直线PB 的方程为00()(0)x n y y x n =-+≠. 由(1)可知,n 满足方程2000n y n x -+=.故m ,n 是关于t 的方程2000t y t x -+=的两个不同的实根. 所以.由(1)可知:FM PA ⊥,同理可得FN PB ⊥. 故||FM ||FN =.则||||FM FN ⋅= 因为22001(0)4y x x +=<.因此,||||FM FN ⋅的取值范围是.。
切点弦定理

切点弦定理切点弦定理,是初中数学中的重要定理之一。
它是指在一个圆上,如果有一条弦,那么这条弦所在直线与圆的交点,以及这条弦所在直线上离圆最近的点,这两个点所构成的线段,其长度相等。
这个定理的证明可以采用相似三角形的方法。
我们先将圆心与这条弦所在直线的交点连接起来,然后可以得到两个相似的三角形。
其中一个三角形的底边是弦,另一个三角形的底边是切线,而且这两个三角形的顶角相等。
因此,我们可以得到这样一个方程:弦的长度/切线的长度=切线上离圆最近的点到圆心的距离/圆心到弦中点的距离。
由于圆心到弦中点的距离是常数,因此我们可以得到:弦的长度=切线上离圆最近的点到圆心的距离×2。
这个定理有很多应用。
其中一个应用就是求解圆内接四边形的对角线长度。
我们可以先连接对角线,然后将对角线所在直线与圆相交,可以得到四个交点。
根据切点弦定理,我们可以得到对角线长度相等。
另外一个应用就是求解圆外接四边形对角线长度之积。
我们可以将这个四边形分割成两个三角形和一个内接四边形。
由于内接四边形的对角线长度相等,因此我们只需要求解两个三角形的斜边长度即可。
我们可以连接两个顶点和圆心,然后根据切点弦定理求解出斜边长度。
除了初中数学中的应用之外,切点弦定理在高中数学和大学数学中也有很多应用。
例如,在高中数学中,我们可以利用切点弦定理来证明某些三角函数恒等式;在大学数学中,切点弦定理也有很多应用,例如在微积分中,我们可以利用切点弦定理来证明某些导数公式。
总之,切点弦定理是一个非常重要的定理,它不仅有着广泛的应用,而且还是许多高级数学知识的基础。
在学习数学时,我们应该认真掌握这个定理,并善于运用它来解决各种问题。
【高中数学复习讲义】第8讲 直线与圆-原卷版
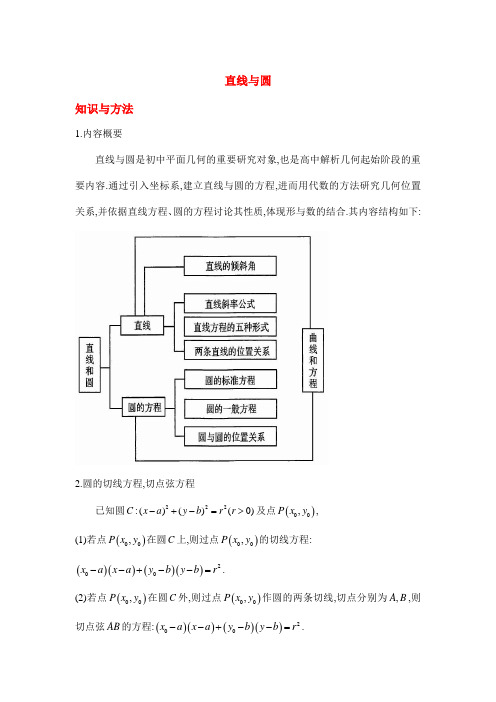
直线与圆知识与方法1.内容概要直线与圆是初中平面几何的重要研究对象,也是高中解析几何起始阶段的重要内容.通过引入坐标系,建立直线与圆的方程,进而用代数的方法研究几何位置关系,并依据直线方程、圆的方程讨论其性质,体现形与数的结合.其内容结构如下:2.圆的切线方程,切点弦方程已知圆222:()()(0)C x a y b r r -+-=>及点()00,P x y , (1)若点()00,P x y 在圆C 上,则过点()00,P x y 的切线方程:()()()()200x a x a y b y b r --+--=.(2)若点()00,P x y 在圆C 外,则过点()00,P x y 作圆的两条切线,切点分别为,A B ,则切点弦AB 的方程:()()()()200x a x a y b y b r --+--=.3.阿波罗尼斯圆在平面上给定两点,A B ,设点P 在同一平面上且满足PA PBλ=,当0λ>且1λ≠时,点P 的轨迹是圆,称为阿波罗尼斯圆(1λ=时点P 的轨迹是线段AB 的中垂线),其中阿波罗尼斯圆的直径为221a λλ-.典型例题【例1】直线()2110x a y +++=的倾斜角的取值范围是( )A.0,4π⎡⎤⎢⎥⎣⎦B.3,4ππ⎡⎫⎪⎢⎣⎭C.0,,42πππ⎡⎤⎛⎫⋃ ⎪⎢⎥⎣⎦⎝⎭D.3,,424ππππ⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【例2】设m ∈R ,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y (点P 与点,A B 不重合),则PAB 面积的最大值是( )A. B.5 C.52【例3】(多选题)设圆222220x y x y +---=的圆心为点C ,直线l 过点()0,3且与圆C 交于,A B 两点,且AB =则直线l 的方程是( ) A.4390x y -+= B.34120x y +-=C.0x =D.4390x y +-=【例4】直线()20mx y m +-=∈R 与圆22:210C x y y +--=相交于,A B 两点,弦长AB 的最小值为________;若ABC 则m 的值为________.【例5】已知圆22:1O x y +=上存在点P ,直线:40l kx y -+=上存在点Q ,使得6PQO π∠=,则实数k 的取值范围是( )A.⎡⎣B.(),∞∞-⋃+C.⎡⎣D.(),∞∞-⋃+【例6】在平面直角坐标系xOy 中,已知圆224x y +=上有且只有四个点到直线1250x y c -+=的距离为1,则实数c 的取值范围是________.【例7】过点()00,P x y 分别作圆221:1C x y +=与圆221:211C x y -+-=()()的切线,切点为,A B .若PA PB =,则2200x y +的最小值为( )B.54D.5【例8】已知P 是函数()2f x x =图像上的一点,过点P 作圆22:430M x y y +--=的两条切线,切点分别为,A B ,则PA PB ⋅的最小值为( )A.328- B.3C.0D.32【例9】已知两点()()2,0,2,0A B --以及圆222:(4)(3)(0)C x y r r ++-=>.若圆C 上存在点P ,满足0PA PB ⋅=,则实数r 的取值范围为( ) A.[]3,6B.[]3,7C.[]4,7D.[]4,6【例10】在平面直角坐标系xOy 中,已知两定点()()2,2,0,2A B -,动点P 满足PA PB=(1)求动点P 的轨迹C 的方程;(2)轨迹C 上有两点,E F ,它们关于直线:40l kx y +-=对称,且满足4OE OF ⋅=,求OEF 的面积.强化训练1.直线2cos 30,63x y ππαα⎛⎫⎡⎤--=∈ ⎪⎢⎥⎣⎦⎝⎭的倾斜角的变化范围是( ) A.,63ππ⎡⎤⎢⎥⎣⎦ B.,43ππ⎡⎤⎢⎥⎣⎦ C.,42ππ⎡⎤⎢⎥⎣⎦ D.2,43ππ⎡⎤⎢⎥⎣⎦2.已知直线1:310l mx y m --+=与直线2:310l x my m +--=相交于点P ,线段AB 是圆22:(1)(1)4C x y +++=上一条动弦,且AB =则PA PB +的最大值为( )A. B. C. D.23.已知过点()3,0P 的直线与圆22:(2)(1)4C x y -+-=交于,A B 两点(点A 在x 轴上方).若3BP PA =,直线AB 的斜率为________.4.已知直线:0l ax by c ++=被圆22:16C x y +=截得的弦的中点为M .若320,a b c O +-=为坐标原点,则点M 的轨迹方程为________,OM 的最大值为________.5.在设点()01,P y ,若圆22:1O x y +=上存在点Q ,使得6OPQπ∠,则0y 的取值范围是________.6.若圆222(3)(5)x y r -++=上有且只有两个点到直线432x y -=的距离等于1,则半径r 的取值范围是( ) A.(]4,6 B.[)4,6C.()4,6D.[]4,67.已知22:2220M x y x y +---=,直线:220,l x y P ++=为l 上的点,过点P 作M的切线,PA PB ,切点分别为,A B .当PM AB ⋅最小时,直线AB 的方程为( ) A.210x y --= B.210x y +-= C.210x y -+= D.210x y ++=8.过点32,4m A m +⎛⎫ ⎪⎝⎭向圆22:4690C x y x y +-++=作切线,切点为B .若AB λ>,则实数λ的取值范围为( )A.()1∞-B.(∞-C.()2∞-D.(∞-9.已知点((,A B ,作直线l ,使得点,A B 到直线l 的距离均为d ,且这样的直线l 恰有4条,则d 的取值范围是( )A.[)1,∞+B.()0,1C.(]0,1D.()0,210.已知圆22:230C x y x +--=,若等边PAB 的一边AB 为圆C 的一条弦,则线段PC 长度的最大值为( )B. C.4D.。
二次曲线中点弦、切线、切点弦及双切线方程

=(nla2 4-a;Ox;+(blb2+b A)《+
(aIb2+a2b1)XOYo一
[(alb2+a2b1)Yo+2ala2名o]名。一
[(aIb2+a2b1)茗o+2bIb2Yo]Yo,
且口A麟。算+A byoy=A似:+A 6_《.
从而,O;Xo髫+byoy=鲋j+6扼.
这说明,点M(戈。,Y。)关于双直线AC、
\ ∥~y /a。+2
O/
-x
/
都成等角.证明:这
图6
样的折线只能位于
抛物线对称轴的一侧.
(第22届全苏数学奥林匹克)
讲解:不妨设抛物线为Y=ax2(a>0).
依次取折线上三个相邻的顶点A;(并nax;)
(i=n,n+1,n+2,nE N).
由抛物线在点A。+。处的切线方程(或求
导数)可知其斜率
k七 l2j2:}2-ak=x^忌A+nl一, +l一An.++2.--=鼎掣叫=凸X(nX+n2+4"X石nn++I1)?).
即5菇一7y-鲁:o.
所以,Q也是MN的中点,即定点Q平分 线段MN.
注:从曲线的含变化参数的方程(实际
上就是曲线系方程)求出曲线上的定点,是
证明曲线过定点的常规方法.由于本题中的
切点弦MN只依赖点Jp的位置,因此,使用切
点弦方程正是时机.证明点Q平分线段MN
实际上是使用了同一法,同时也发挥了中点
弦方程的作用.
2009年第8期
7
二次曲线中点弦、切线、切点弦及双切线方程
胡圣团
(湖南省澧县一中,415500)
(本讲适合高中) 1知识简介
记G(x,Y)=Ax2+Bxy+Cy2+Dk+E|y+F 1.1二次曲线中点弦的方程
切点弦公式

切点弦公式切点弦公式:xx0+yy0=r²。
切弦亦称切点弦,是一条特殊弦。
从圆外一点向圆引两条切线,连结此两切点的弦称为切弦。
圆心与已知点点连线垂直平分切弦。
切点弦方程公式解析过圆x +y =r 外一点P(x0,y0)作切线PA,PB,A(x1,y1),B(x2,y2)是切点,则过AB的直线xx0+yy0=r ,称切点弦方程。
证明:x +y =r 在点A,B的切线方程是xx1+yy1=r ,xx2+yy2=r∵点P在两切线上∴x0x1+y0y1=r ,x0x2+y0y2=r此二式表明点A,B的坐标适合直线方程xx0+yy0=r ,而过点A,B的直线是唯一的∴切点弦方程是xx0+yy0=r说明:切点弦方程与圆x +y =r 上一点T(x0,y0)的切线方程相同。
过圆(x-a) +(y-b) =r 外一点P(x0,y0)作切线PA,PB,切点弦方程是(x-a)(x-x0)+(y-b)(y-y0)=r 。
切点弦方程的概念切弦亦称切点弦,是一条特殊弦。
从圆外一点向圆引两条切线,连结此两切点的弦称为切弦。
切点弦方程的性质圆心与已知点点连线垂直平分切弦,如图,P 是圆外一点,PA,PB 与⊙O 相切,切点是A,B,AB 是切弦,此时,OP 垂直平分AB。
切点弦方程证明设圆上一点A为(x0,y0),则该点与圆心O的向量OA(x0-a,y0-b)因为过该点的切线与该方向半径垂直,则有切线方向上的单位向量与向量OA的点积为0。
设直线上任意点B为(x,y)则对于直线方向上的向量AB(x-x0,y-y0)有向量AB与OA的点积。
椭圆的切点弦方程公式推导

椭圆的切点弦方程公式推导1.定义椭圆及其性质:椭圆是一个平面上的几何图形,它由平面上到两个定点F1和F2的距离之和恒定于常数2a的点P构成。
此外,椭圆还有一个重要性质,就是通过椭圆上的两个点和椭圆上与这两点垂直的直径,必定存在一条唯一的切线。
2.确定椭圆的标准方程:椭圆的标准方程是x^2/a^2+y^2/b^2=1,其中a和b是椭圆的半长轴和半短轴的长度。
3.确定椭圆上特定点的切线方程:假设椭圆上的一点P位于第一象限,其坐标为(x0,y0)。
要求得P的切线方程,需要先求得椭圆上过点P的切线的斜率k。
4.求切线的斜率:设椭圆上的点P的坐标为(x0,y0),则与切线垂直直径的斜率为-x0/y0,而切线的斜率为-y0/x0。
由此可得切线的斜率k=-y0/x0。
5.求切点的坐标:切线方程需要通过切点,因此需要求出切点的坐标。
设切点的坐标为(x1,y1),则切线方程为y-y1=k(x-x1)。
6. 求椭圆上的点 P 的坐标:代入椭圆的标准方程,得到 x0^2/a^2+ y0^2/b^2 = 1、由此可得 y0 = sqrt(b^2 - (b^2/a^2)*x0^2)。
7. 代入切线斜率得到切点的坐标:代入切线斜率 k 和切点的坐标(x1, y1),得到 k = -sqrt(b^2 - (b^2/a^2)*x0^2)/x1,再整理得 x1 = b^2*x0/sqrt(a^2*y0^2 + b^2*x0^2) 和 y1 = -a^2*y0/sqrt(a^2*y0^2 + b^2*x0^2)。
8.代入切点坐标得到切线方程:将切点的坐标(x1,y1)代入切线方程y-y1=k(x-x1),整理得y=(b^2*y0-a^2*y1)x+a^2y1-b^2y0。
至此,推导得到了椭圆的切点弦方程公式为y=(b^2*y0-a^2*y1)x+a^2y1-b^2y0,其中(x0,y0)为椭圆上的点的坐标,(x1,y1)为切点的坐标。
圆锥曲线的切线方程和切点弦方程的证明

点为 A(x1, y1)B(x2, y2)切点弦所在的直线方程为
y0y = p(x + x0)
−
b2x0 a2y0
[2x
−
(x1
+
x2)]
化简后得
x0x a2
+
y0y b2
=
1
同理过双曲线外一点 P(x0, y0)向双曲线做两条切线 PA 和 PB,切
点为 A(x1, y1)B(x2, y2)切点弦所在的直线方程为
x0x a2
−
y0y b2
=
1
同理过抛物线外一点 P(x0, y0)向抛物线做两条切线 PA 和 PB,切
为 A(x1, y1)B(x2, y2)切点弦所在的直线方程为
x0x a2
+
y0y b2
=
1
切线 PA 的方程和切线 PB 的方程分别为
x1x xa22x a2
+ +
y1y yb22y b2
= =
1 1
两式相减得
x(x1 − a2
x2
)
=
−
y(y1 − a2
y2)
−b2x a2y
=
(y1 (x1
− −
[2x
−
(x1
+
x2)]
切线 PA 的方程和切线 PB 的方程分别为
x1x xa22x a2
+ +
y1y yb22y b2
= =
1 1
两式相加得
x(x1 + a2
x2)
=
y(y1 + a2
y2)
+
2
y1
+
圆锥曲线的切线方程和切点弦方程

圆锥曲线的切线方程和切点弦方程课题:圆锥曲线的切线方程和切点弦方程教学目标:1) 掌握圆锥曲线在某点处的切线方程及切点弦方程。
2) 能够使用切线方程及切点弦方程解决一些问题。
3) 通过复渗透数形结合、类比的思想,逐步培养学生分析问题和解决问题的能力。
4) 掌握曲线与方程的关系。
教学重点:切线方程及切点弦方程的应用教学难点:如何恰当使用切线方程及切点弦方程教学过程:1.引入:通过09年安徽省高考题及近几年各省考察圆锥曲线的实例引出本节课。
2.知识点回顾:1) 过圆$x^2+y^2=r^2$上一点$(x_0,y_0)$的切线方程为:$xx_0+yy_0=r^2$2) 设$P(x,y)$为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$上的点,则过该点的切线方程为:$\frac{xx_0}{a^2}+\frac{yy_0}{b^2}=1$3) 设$P(x,y)$为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$上的点,则过该点的切线方程为:$\frac{xx_0}{a^2}-\frac{yy_0}{b^2}=1$4) 设$P(x,y)$为抛物线$y^2=2px$上的点,则过该点的切线方程为:$y=y_0+p(x+x_0)$圆锥曲线切线的几个性质:1) 过椭圆的准线与其长轴所在直线的交点作椭圆的两条切线,则切点弦长等于该椭圆的通径。
同理,双曲线,抛物线也有类似的性质。
2) 过椭圆的焦点$F_1$的直线交椭圆于$A$,$B$两点,过$A$,$B$两点作椭圆的切线交$PF_1\perp AB$于点$P$,则$P$点的轨迹是焦点$F_1$的对应的准线,并且同理,双曲线,抛物线也有类似的性质。
3.例题精讲:1) 练1:已知抛物线$y=ax^2(a>0)$与直线$x=1$围成的封闭图形的面积为3,若直线$l$与抛物线相切,且平行于直线$2x-y+6=0$,则直线$l$的方程为。
专题14 圆锥曲线切线方程 微点2 圆锥曲线切线方程的常用结论及其应用

(2)过抛物线 上一点 处的切线方程为 ;过抛物线 的外部一点 引两条切线,过两切点的弦所在直线方程为: ;
(3)过抛物线 上一点 处的切线方程为 ;过抛物线 的外部一点 引两条切线,过两切点的弦所在直线方程为: .
同理可得焦点在 轴上的情形.
【结论4】(1)过圆 上一点 切线方程为 ;
(2)当 在椭圆 的外部时,过M引切线有两条,过两切点的弦所在直线方程为 .
【结论5】(1)过双曲线 上一点 处的切线方程为 ;
(2)当 在双曲线 的外部时,过M引切线有两条,过两切点的弦所在直线方程为: .
证明:(1) 的两边对x求导,得 ,得 ,由点斜式得切线方程为 ,即 ,又 所求的切线方程为 .
(1)求椭圆的方程;
(2)直线 与椭圆有唯一的公共点 ,与 轴的正半轴交于点 ,过 与 垂直的直线交 轴于点 .若 ,求直线 的方程.
例6.
6.已知椭圆 与直线 相切于点 ,且点 在第一象限,若直线 与 轴、 轴分别交于点 、 .若过原点O的直线 与 垂直交与点 ,证明: 定值.
【强化训练】
7.若椭圆 的焦点在x轴上,过点 作圆 的切线,切点分别为A、B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是()
下面的结论是从斜率的角度得到已知曲线的切线方程.
【结论8】(1)斜率为k的双曲线 的切线方程为 ;
(2)斜率为k的双曲线 的切线方程为 .
证明:(1)设切线方程为 ,联立 方程得:
,
若 即 , ,
令 化简可得: , ,故切线方程为 .
同理可证情形(2).
【评注】 , ,过双曲线的对称中心不可能作出直线与双曲线相切.
抛物线切点弦方程公式推导

抛物线切点弦方程公式推导在数学中,抛物线是一种经典的曲线形式,它的形状类似于一个开口朝上或者朝下的碗。
抛物线在几何学、物理学、工程学等领域都有广泛的应用。
在本文中,我们将推导出抛物线的切点弦方程公式。
首先,我们假设有一条抛物线,其方程为:y = ax^2 + bx + c其中,a、b、c为常数,x、y为变量。
接着,我们需要确定抛物线上某一点P(x0, y0)处的切线方程。
为了求出切线方程,我们需要确定该点的一阶导数,即:y' = 2ax + b接下来,我们需要求出切线的斜率。
根据导数的定义,当x = x0时,切线的斜率即为y'的值:k = y' = 2ax0 + b知道了切线的斜率,我们就可以利用点斜式推导出切线方程:y - y0 = k(x - x0)代入k的值,得到:y - y0 = (2ax0 + b)(x - x0)这就是抛物线在点P(x0, y0)处的切线方程。
接着,我们需要求出切线所在的弦的方程。
在抛物线上任选两点P(x1, y1)和P(x2, y2),则它们所在的直线方程为:y - y1 = (y2 - y1) / (x2 - x1) * (x - x1)将抛物线方程代入,得到:ax^2 + bx + c - y1 = (y2 - y1) / (x2 - x1) * (x - x1) 这就是抛物线与任意两点所在的弦的方程。
最后,我们需要求出切点弦的方程。
切点弦即为切线所在的直线,因此它的方程为:y - y0 = (y2 - y1) / (x2 - x1) * (x - x0)其中,(x1, y1)和(x2, y2)为抛物线上任意两点,(x0, y0)为抛物线上与它们相切的点坐标。
综上所述,我们推导出了抛物线切点弦方程公式:y - y0 = (y2 - y1) / (x2 - x1) * (x - x0)在实际应用中,我们可以根据该公式求出抛物线上任意两点间的切点弦方程,从而得到更精确的计算结果。
切点弦方程的推导方法

切点弦方程的推导方法嘿,你知道切点弦方程不?这玩意儿超厉害的!咱先说说推导方法哈。
假设有个曲线方程,咱随便找个点在曲线上,那过这点的切线咋求呢?咱就把曲线方程看成一个神秘的宝藏地图,那个点就是咱的起点。
咱对曲线方程求导,就像拿到了一把神奇的钥匙,能打开找到切线斜率的大门。
然后用点斜式就能得到切线方程啦!这过程简单不?那切点弦方程呢,就是从曲线外一点引曲线的两条切线,这两条切线的切点连成的弦的方程。
咱先求出过曲线外那点和曲线上一点的直线方程,再让它和曲线方程联立,消去一个变量,得到一个关于另一个变量的二次方程。
这就好比在玩拼图游戏,把不同的碎片拼在一起。
利用韦达定理,找到两个切点的横坐标或纵坐标之间的关系。
然后根据两点确定一条直线,就可以得到切点弦方程啦!哇塞,是不是很神奇?这过程安全不?那必须安全啊!只要你按照步骤来,一步一步稳稳当当的,就不会出啥岔子。
就像走在平坦的大路上,只要你不瞎蹦跶,肯定不会摔跤。
稳定性也杠杠的,不管你用多少次这个方法,结果都是一样的靠谱。
那这切点弦方程有啥用呢?应用场景可多啦!比如在解析几何问题里,要求某条特殊弦的方程,用切点弦方程就超级方便。
它就像一把万能钥匙,能打开很多难题的大门。
优势也很明显啊,比传统方法简单快捷多了。
不用费老大劲去求切线,再求切点,然后再求弦的方程。
用切点弦方程,一步到位,爽不爽?咱来个实际案例哈。
比如说有个圆的方程,还有个点在圆外。
要求过这点的两条切线的切点弦方程。
咱就按照上面的方法来,先求导,再联立方程,最后得到切点弦方程。
一验证,哇,完全正确。
这效果,简直绝了!所以啊,切点弦方程就是解析几何里的大宝贝,谁用谁知道。
赶紧试试吧!。
切点弦方程公式推导

切点弦方程公式推导切线是曲线上一点的切线,它在该点处与曲线相切,并且与曲线在该点的切线有相同的斜率。
而弦是曲线上两点之间的直线段。
推导切点弦方程的过程如下:设曲线方程为y=f(x),其中f(x)是一个函数。
设曲线上有一点P(x0,y0),我们要找到曲线在该点处的切线方程。
1.首先,我们需要求得曲线在点P处的斜率k。
我们可以使用导数来求解,导数表示函数的斜率。
求导得到f'(x),表示函数f(x)在x点处的导数,也就是x0点处的切线的斜率。
2.接下来,我们可以使用点斜式的公式来写出直线的方程。
点斜式公式如下:y-y0=k(x-x0)将点P的坐标代入得到:y-y0=f'(x0)(x-x0)这就是曲线在点P处的切线方程。
我们现在来举个例子来具体说明以上步骤:例子:给定曲线y=x^2,求曲线在点P(2,4)处的切线方程。
1.首先,我们求导数。
对于y=x^2,求导得到f'(x)=2x。
因此,曲线在任意点x处的切线的斜率k为2x。
2.接下来,我们代入点P(2,4)的坐标来得到切线方程。
根据点斜式公式:y-y0=f'(x0)(x-x0)代入坐标得到:y-4=2(2)(x-2)简化得到:y-4=4(x-2)这就是曲线y=x^2在点P(2,4)处的切线方程。
通过以上推导,我们可以得到曲线在任意点处的切线方程。
这个方程可以用来求解曲线在该点处的切线的各种性质和问题,比如切线的斜率、与坐标轴的交点等。
同时,我们也可以推导切点弦的方程。
切点弦是通过曲线上两个点和它们的切线的交点所形成的直线。
设两点为P(x1,y1)和Q(x2,y2),切线方程分别为:y-y1=f'(x1)(x-x1)y-y2=f'(x2)(x-x2)通过求解这两个方程,我们可以得到切点弦的方程。
求解过程中会有一些代数运算和求导的过程,但是基本思路和切线方程推导是相似的。
总结起来,切点弦方程公式的推导是通过求导得到函数的斜率,然后使用点斜式公式得到切线方程,最后通过解方程得到切点弦方程。
圆的切点弦方程公式推导

圆的切点弦方程公式推导要推导圆的切点弦方程公式,首先我们需要了解一些基本知识。
1.圆的定义:圆是平面上离一个固定点的距离等于一定值的点的集合。
这个固定点叫做圆的圆心,距离等于一定值的这个值叫做圆的半径。
2. 圆的参数方程:圆的参数方程可以表示为:x = a + r * cosθ,y = b + r * sinθ,其中(a, b)为圆心的坐标,r为半径的长度,θ为参数的取值范围。
3.切线的定义:切线是与曲线在其中一点相切且与曲线在这一点处相切的直线。
推导切点弦方程的过程如下:设圆的圆心为C(a,b),半径为r。
圆上任意一点P(x,y)。
1.写出圆的参数方程:根据圆的参数方程可以得到:x = a + r * cosθ,(1)y = b + r * sinθ,(2)2.画出切线与圆的示意图:画出圆,并在圆上任意取一点P,然后在P点处画出一条切线。
假设切点为T(x1,y1)。
3.求出P点到圆心C的距离:根据圆的定义可知,点P到圆心C的距离等于圆的半径r。
因此可以得到以下关系:√((x-a)²+(y-b)²)=r,(3)4.P点到圆上任意一点T的距离等于0:由于P点在切线上,所以P点到切点T的距离为0。
根据距离公式,可以得到以下关系:√((x1-x)²+(y1-y)²)=0,(4)5.消除θ的影响:将式(1)和式(2)带入式(4)中,可以得到:√((x1 - [a + r * cosθ])² + (y1 - [b + r * sinθ])²) = 0。
6.化简方程:将上式进行展开和化简,可以得到:(x1 - a) * cosθ + (y1 - b) * sinθ = 0,(5)7.代入切点的坐标:由于切点的坐标为T(x1,y1)(x1 - a) * cosθ + (y1 - b) * sinθ = 0。
8.弦方程公式:令弦的斜率为k,根据切线与弦的关系可知,切线的斜率与弦的斜率相等。
0切线方程及切点弦

②切线方程及切点弦若曲线:022=++++F Ey Dx By Ax 上的点为()00,y x ,则该点外的切线方程为:()()0220000=++++++F y y E x x Dy By x Ax 如1、椭圆:12222=+b y a x 切点为()00,y x ,则切线方程为12020=+b yy a x x2、双曲线:12222=-b y a x 切点为()00,y x ,则切线方程为12020=-byy a x x3、抛物线:px y 22= 切点为()00,y x ,则切线方程为()x x p y y +=00椭圆上点()00,y x P 的切线的推导:12222=+b y a x Θ 02222='⋅+∴b y y a x(),由点斜式切0202,00y a x b y k y x -='=∴()002020:x x y a x b y y l --=-切整理得:02020220202=-+-x b x x b y a y y a 2022020202y a x b x x b y y a +=+∴12202202020=+=+∴b y a x b y y a x x ,12020=+∴b yy a x x P 处的切线方程为:点 例1、椭圆12:22=+y x E 过点()2,2P 引E 的两条切线,切点分别为B A ,,求AB l 解:设()11,y x A ,()22,y x B ,则E 的两条切线方程分别为:12:11=+y y xx l A ,12:22=+y y xx l B ,又P Θ点在切线A l ,B l 上12,122211=+=+∴y x y x 有 由此特征可得12:=+y x l AB 练习:(2018届茂名一模16)过抛物线y x E 42=:的准线上一点P 作抛物线E 的两条切线,切点分别为B A 、,若AB l 的倾斜角为6π,求P 点的横坐标③抛物线二级结论之相切过焦点的两直线QF l 和PF l 互相垂直,分别与准线抛物线的交点为P Q 、则PQ l 与抛物线相切 例、已知抛物线()02:2>=p px y E 的焦点为F ,准线为l ,A 使E 上一点,线段FA 的中点坐标为()22,. (1)求E 的方程(2)点M 为l 上一点,P 是E 上任意一点,若FP FM ⊥,试问直线MP 与E 是否有其他公共点?说明理由.解:(1)略x y 82=,(2)①取()42,P 易求得()42,P 点处的切线为2+=x y FP FM ⊥Θ,()02,-∴M 也在切线上②设E 上任意一点()y x P ,,由x y 82=两边取导数得yy 4=' P ∴点处的切线斜率为141y y y y ='=()x x y y l P +=∴114:切,则它与l 的交点为⎪⎪⎭⎫⎝⎛--1184x 2y N ,ΘFP FM ⊥,设()2y 2,-M ∴由0=⋅得()()0y 2y 4112=-⋅-,,x 11221184048y x y y y x -==+-∴即 ∴⎪⎪⎭⎫⎝⎛--1184x 2y M ,与N 点重合,综上,若FP FM ⊥时,MP l 与E 没有其他公共点 变式1、已知抛物线()022>=p px y 的焦点为F ,点P 在抛物线上,且x PF ⊥轴,过点P 且与抛物线相切的直线与x 轴相交于点Q ,若2=PQ ,则抛物线的标准方程为( )x y A 8.2= x y B 6.2= x y C 4.2= x y D 2.2=变式2、已知抛物线()02:2>=p py x C ,过点⎪⎭⎫⎝⎛-2,0p M 引抛物线C 的两条切线,切点分别为B A ,且4=∆MAB S ,若抛物线C 与直线01:=+-y x l 交于Q P 、两点,则=PQ ( )8.A 16.B 4.C 02.D。
切线方程与切点弦方程

切线方程与切点弦方程一、圆的切线方程一、圆的方程为:(x - a)²+ (y - b)²= r²1. 已知:圆的方程为:(x - a)²+ (y - b)²= r², 圆上一点P(x0, y0)。
求过点P的切线方程解:圆心C(a, b);直线CP的斜率:k1 = ( y0- b) / ( x0- a)因为直线CP与切线垂直, 所以切线的斜率:k2 = -1/k1 = - (x0 - a) / (y0 - b)根据点斜式, 求得切线方程:y - y0 = k2 (x - x0)y - y0 = [- (x0 - a) / (y0 - b)] (x - x0)整理得:(x - x0)(x0 - a) + (y - y0)(y0 - b) = 0 (切线方程公式)展开后: x0x - ax + ax0 + y0y - by + by0 - x0²- y0²= 0 (1)因为点P在圆上, 所以它的坐标满足方程:(x0 - a)²+ (y0 - b)²= r²化简: x0²- 2ax0 + a²+ y0²- 2by0 + b²= r²移项: - x0²- y0²= -2ax0 - 2by0 + a²+ b²- r²(2)由(2)代入(1), 得:x0x - ax + ax0 + y0y - by + by0 + (-2ax0 - 2by0 + a²+ b²- r²) = 0 化简:(x0x - ax - ax0 + a²) + (y0y - yb- by0 + b²) = r²整理:(x0 - a)(x - a) + (y0 - b)(y - b) = r²变式-1 已知:圆的方程为:(x - a)²+ (y - b)²= r², 圆外一点P(x0, y0)二、对于圆的一般方程:x²+ y²+ Dx + Ey + F = 0, 过圆上的点的切线方程.2.已知:圆的方程为:x²+ y²+ Dx + Ey + F = 0, 圆上一点P(x0, y0)解:圆心C( -D/2, -E/2 )直线CP的斜率:k1 = (y0 + E/2) / (x0 + D/2)因为直线CP与切线垂直, 所以切线的斜率:k2 = -1/k1 = - (x0 + D/2) / (y0 + E/2)根据点斜式, 求得切线方程:y - y0 = k2 (x - x0)y - y0 = [- (x0 + D/2) / (y0 + E/2)] (x - x0)整理得:x0x + y0y + Dx/2 + Ey/2 - Dx0/2 - Ey0/2 -x0²- y0²= 0 (3)因为点P在圆上, 所以它的坐标满足方程:x0²+ y0²+ Dx0 + Ey0 + F = 0移项: - x0²- y0²= Dx0 + Ey0 + F (4)由(4)代入(3), 得:x0x + y0y + Dx/2 + Ey/2 - Dx0/2 - Ey0/2 + Dx0 + Ey0 + F = 0整理, x0x + y0y + D(x + x0)/2 + E(y + y0)/2 + F = 0变式-2 已知:圆的方程为:x²+ y²+ Dx + Ey + F = 0 , 圆外一点P(x0, y0) 二、圆的切点弦方程三、圆锥曲线的切线方程和切点弦方程设P(x 0, y0)是圆锥曲线上(外)一点,过点P引曲线的两条切线,切点为A , B两点,则A , B两点所在的直线方程为切点弦方程。
抛物线切点弦方程公式推导

抛物线切点弦方程公式推导
本文将介绍抛物线切点弦方程公式的推导过程。
抛物线切线方程一般形式为y=mx+n,其中m为切线斜率,n为截距。
由于切点与切线的性质,切线的斜率等于抛物线在切点处的导数。
因此,我们可以先求解抛物线在切点处的导数,再代入切线方程中,得出切线方程的具体形式。
抛物线的一般式为y=ax+bx+c,其中a≠0。
为了方便推导,我们先将抛物线平移,使其顶点位于原点。
设抛物线的顶点为(0,0),则抛物线方程可化为y=ax。
求解y=ax在点(x0,y0)的导数,有:
y' = lim (h→0) [(ax0+h)-ax0]/h
= lim (h→0) [2ax0h+h]/h
= lim (h→0) [2ax0+h]/1 (当h趋近于0时,可以将分母约掉) = 2ax0
因此,抛物线在点(x0,y0)处的切线斜率为2ax0。
接下来,我们可以代入切点的坐标(x0,y0),得出切线方程为:y=2ax0x-y0。
接着,我们可以使用两点式求解过点(x0,y0)和(x,y)的弦方程。
弦方程的一般式为y=kx+b,其中k为斜率,b为截距。
弦的斜率为:
k = (y-y0)/(x-x0)
代入切点坐标,可得:
k = (ax-0)/(x-0) = ax
因此,弦方程为:y=ax(x-x0)+y0。
将切点坐标代入,即可得到抛物线切点弦方程的具体形式:y=ax(x-x0)+y0。
至此,我们成功地推导出了抛物线切点弦方程公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
切线方程与切点弦方程
一、圆的切线方程
一、圆的方程为:(x - a) 2 + (y - b) 2 = r 2
1. 已知:圆的方程为:(x - a) 2 + (y - b) 2 = r2,圆上一点P(x0, y0)。
求过点 P 的切线方程
解:圆心C(a,b);直线 CP 的斜率: k1 = ( y 0- b) / ( x 0- a)
因为直线CP 与切线垂直 , 所以切线的斜率:k2 = -1/k 1 = - (x 0 - a) / (y 0 - b)
根据点斜式 , 求得切线方程:
y - y 0 = k 2 (x - x 0)
y - y 0 = [- (x 0 - a) / (y 0 - b)] (x - x 0)
整理得: (x - x0)(x0 - a) + (y - y0)(y0 - b) = 0(切线方程公式 )
展开后 : x0 x - ax + ax 0 + y 0y - by + by 0 - x0 2 - y02= 0(1)
因为点 P 在圆上 , 所以它的坐标满足方程:
(x0 - a)2 + (y 0 - b) 2 = r 2
化简 : x02 - 2ax0 + a2 + y 02 - 2by 0 + b2 = r 2
移项 : - x 02 - y 02 = -2ax 0 - 2by0 + a2 + b2 - r2(2)
由 (2)代入 (1), 得: x0x - ax + ax 0 + y 0y - by + by 0 + (-2ax 0 - 2by0 + a2 + b2- r2) = 0化简: (x0x - ax - ax 0 + a2) + (y 0y - yb- by 0 + b2) = r 2
整理: (x0 - a)(x - a) + (y 0 - b)(y - b) = r 2
变式 -1 已知 :圆的方程为 :(x - a) 2 + (y - b) 2 = r2 ,圆外一点 P(x0, y0)
二、对于圆的一般方程:x2 + y2 + Dx + Ey + F = 0,过圆上的点的切线方程.
2. 已知 :圆的方程为 :x2 + y2 + Dx + Ey + F = 0,圆上一点P(x0, y0)
解:圆心C( -D/2,-E/2 )
直线 CP 的斜率 :k1 = (y 0 + E/2) / (x 0 + D/2)
因为直线CP 与切线垂直 , 所以切线的斜率:k2 = -1/k 1 = - (x 0 + D/2) / (y 0 + E/2)
根据点斜式 , 求得切线方程:
y - y 0 = k2 (x - x 0)
y - y 0 = [- (x 0 + D/2) / (y 0 + E/2)] (x - x 0)
整理得 :x 0x + y 0y + Dx/2 + Ey/2 - Dx 0 /2 - Ey 0/2 -x 02 - y02 = 0(3)
因为点 P 在圆上 , 所以它的坐标满足方程:
x02 + y 02 + Dx 0 + Ey 0 + F = 0
移项 : - x 02 - y02 = Dx 0 + Ey 0 + F(4)
+F=0由 (4) 代入 (3),得: x
0x + y 0y + Dx/2 + Ey/2 - Dx 0/2 - Ey 0/2 +Dx 0 + Ey 0
整理 , x0x + y 0y + D(x + x 0)/2 + E(y + y 0)/2 + F = 0
变式 -2已知 :圆的方程为:x2 + y2 + Dx + Ey + F = 0 ,圆外一点P(x0 , y0)二、圆的切点弦方程
三、圆锥曲线的切线方程和切点弦方程
设P(x0, y0)是圆锥曲线上(外)一点,过点 P 引曲线的两条切线,切点为 A , B 两点,则 A , B 两点所在的直线方程为切点弦方程。
标准方程切点弦方程圆
椭圆
双曲线
抛物线。
