中值定理及导数应用
中值定理与导数的应用

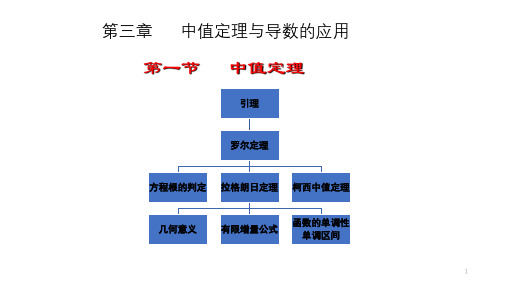
第三章 中值定理与导数的应用§3. 1 中值定理 一、罗尔定理 费马引理设函数f (x )在点x 0的某邻域U (x 0)内有定义, 并且在x 0处可导, 如果对任意x ∈U (x 0), 有 f (x )≤f (x 0) (或f (x )≥f (x 0)), 那么f '(x 0)=0.罗尔定理 如果函数)(x f 满足:(1)在闭区间],[b a 上连续, (2)在开区间),(b a 内可导, (3)在区间端点处的函数值相等,即)()(b f a f =, 那么在),(b a 内至少在一点)(b a <<ξξ , 使得函数)(x f 在该点的导数等于零,即0)('=ξf .例:设函数)(x f 在[0,1]上连续,在(0,1)上可导,0)1(=f ,证明:在(0,1)内存在ξ,使得ξξξ)()(f f -='.【分析】本题的难点是构造辅助函数,可如下分析:()0)(0)()(0)()()()(='→='+→='+→-='x xf x f x x f f f f f ξξξξξξ【证明】令)()(x xf x G =,则)(x G 在[0,1]上连续,在(0,1)上可导,且0)1(1G (1)0,0)(0)0(====f f G ,)()()(x f x x f x G '+=' 由罗尔中值定理知,存在)1,0(∈ξ,使得)()()(ξξξξf f G '+='.即ξξξ)()(f f -='例:设函数f (x ), g (x )在[a , b ]上连续,在(a , b )内具有二阶导数且存在相等的最大值,f (a )=g (a ), f (b )=g (b ), 证明:存在(,)a b ξ∈,使得()().f g ξξ''''=【分析】需要证明的结论与导数有关,自然联想到用微分中值定理,事实上,若令()()()F x f x g x =-,则问题转化为证明()0F ξ''=, 只需对()F x '用罗尔定理,关键是找到()F x '的端点函数值相等的区间(特别是两个一阶导数同时为零的点),而利用F (a )=F (b )=0, 若能再找一点(,)c a b ∈,使得()0F c =,则在区间[,],[,]a c c b 上两次利用罗尔定理有一阶导函数相等的两点,再对()F x '用罗尔定理即可。
中值定理与导数的应用

中值定理是反映函数与导数之间联系的重要定理,也是微积分学的理论基础。
在实际应用中,中值定理与导数的应用非常广泛。
以下是一些具体的应用:
1.判断函数的单调性:通过导数可以判断函数的单调性,如果函数在某个区间内的导数大于0,则
该函数在这个区间内单调递增;如果函数在某个区间内的导数小于0,则该函数在这个区间内单调递减。
2.求函数的极值:导数可以用来求函数的极值。
如果函数在某一点的导数为0,则该点可能是函数
的极值点。
在判断出极值点后,可以通过求导数在该点的左右两侧的符号变化来确定该点是极大值点还是极小值点。
3.判断函数的凹凸性:通过二阶导数可以判断函数的凹凸性。
如果函数在某一点的二阶导数大于0,
则该函数在该点附近是凹函数;如果二阶导数小于0,则该函数在该点附近是凸函数。
4.求函数的拐点:在判断出函数的极值点和凹凸性后,可以进一步求出函数的拐点。
拐点的定义是
函数图像在该点处的切线发生弯曲的地方。
通过求一阶导数在该点的左右两侧的符号变化,可以判断出拐点的位置。
5.判断函数的不等式:通过导数还可以判断函数的不等式。
如果两个函数在某个区间内的导数符号
相反,则这两个函数在该区间内的函数值一定不相等。
6.最优化问题:在工程和经济学中,经常需要解决最优化问题。
使用微积分中的中值定理和导数可
以找到最优解。
例如,在经济学中,可以使用微积分来找到最大化收益或最小化成本的最佳策略。
总的来说,中值定理与导数的应用非常广泛,它们是微积分学的重要基石,可以用于解决各种实际问题。
高等数学 第3章 第一节 中值定理
(函数
即
6
,
y
5
6
ln sin x
是 y
是初等函数, 且当
x
6
ln sin x 定义域内的一部分;
,
5
6
时,cossixn
y'
sin x
x
0,
cot x.)
且ln s in
lnsin 5
ln 1 .
6
62
令 y' cos x cot x 0, sin x
得 x , 5 .
F(b) F(a)
( x) 满足罗尔定理的全部条件,且:
'(x) f '(x) f (b) f (a) F '(x)
F(b) F(a)
Y F , f Fb, f b
C•
•B
由罗尔定理,至少存在一点 ∈(a,b) ,
即:
使
f
'( )
'( ) 0,
f (b) f (a) F '( ) 0
即 1、 2、 3都是方程 f 'x 0 的根。 注意到 f ' x 0 为三次方程, 它最多有三个根。
我们已经找到它的三个实根
1、 2、 3 ,
所以这三个根就是方程
f 'x 0 的全部根。
14
例3 证明当x 0时, x ln1 x x
1 x
证 设f x ln1 x, 显然,函数 f x 在 0, x 上满足
f (b) f (a)
O a
bx
结论等价于: f f b f a
ba
或: f f b f a 0
ba
AB的方程为:
中值定理与导数的应用

中值定理与导数的应用导数是微积分中的重要概念,它描述了函数在某一点的变化率。
而中值定理则是导数的重要应用之一,它揭示了函数在某一区间内必然存在某一点,使得该点的斜率等于该区间的平均斜率。
在实际问题中,中值定理具有广泛的应用,可以帮助我们解决各种与变化率相关的问题。
让我们来了解一下中值定理的基本原理。
根据中值定理,如果一个函数在闭区间[a, b]上连续,并且在开区间(a, b)内可导,那么在(a, b)内至少存在一点c,使得函数在c处的导数等于函数在[a, b]上的平均斜率。
换句话说,函数在区间内的某一点的瞬时变化率与整个区间的平均变化率相等。
中值定理的一个重要推论是拉格朗日中值定理。
根据拉格朗日中值定理,如果一个函数在闭区间[a, b]上连续,并且在开区间(a, b)内可导,那么在(a, b)内至少存在一点c,使得函数在c处的导数等于函数在[a, b]上的斜率。
换句话说,拉格朗日中值定理给出了函数在某一区间内某一点的瞬时变化率与该区间的斜率之间的对应关系。
中值定理的应用非常广泛。
一个常见的应用是求函数在某一区间内的最大值和最小值。
根据极值存在定理,如果一个函数在闭区间[a, b]上连续,那么它在该区间内必然存在最大值和最小值。
根据中值定理,我们可以通过求函数在该区间内的导数为0的点,来确定函数的极值点。
另一个常见的应用是求函数的单调性。
根据中值定理,如果一个函数在某一区间内的导数恒大于0(或恒小于0),那么该函数在该区间内必然是递增的(或递减的)。
因此,我们可以通过求函数的导数来确定函数在某一区间内的单调性。
中值定理还可以用来解决一些与速度和加速度相关的问题。
例如,在物理学中,我们经常需要计算物体在某一时间段内的平均速度和瞬时速度。
根据中值定理,我们可以通过求物体在该时间段内的位移与时间的比值,来确定物体在某一时刻的瞬时速度。
中值定理是导数的重要应用之一,它可以帮助我们解决各种与变化率相关的问题。
微分中值定理与导数的应用总结

微分中值定理与导数的应用总结一、微分中值定理1.拉格朗日中值定理拉格朗日中值定理是微分中值定理的最基本形式,它表述为:如果函数f(x)在区间[a,b]上连续,在开区间(a,b)内可导,则在(a,b)内至少存在一个数c,使得f(b)-f(a)=f'(c)(b-a),其中c属于(a,b)。
拉格朗日中值定理的几何意义是:如果一条曲线在两个点a和b上的斜率相等,则在这两个点之间必然存在一点c,使得曲线在c点和a、b两点之间的切线斜率相等。
2.柯西中值定理柯西中值定理是微分中值定理的推广形式,它给出了两个函数的导数的关系。
设f(x)和g(x)在[a,b]上连续,在开区间(a,b)内可导且g'(x)≠0,则存在一个数c,使得[f(b)-f(a)]/[g(b)-g(a)]=[f'(c)]/[g'(c)]。
柯西中值定理的几何意义是:如果曲线f(x)和g(x)在两个点a和b上的切线斜率之比等于f'(c)和g'(c)的比,则在这两个点之间必然存在一点c,使得曲线f(x)和g(x)在c点的切线斜率之比等于f'(c)和g'(c)的比。
3.罗尔中值定理罗尔中值定理是微分中值定理的特殊形式,它给出了导数为零的充分条件。
设函数f(x)在[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则在(a,b)内至少存在一个数c,使得f'(c)=0。
罗尔中值定理的几何意义是:如果一条曲线在两个端点上的函数值相等,则在这两个端点之间必然存在一个点c,使得曲线在c点的切线斜率为零。
微分中值定理的应用非常广泛,例如在证明极限存在或连续性、研究函数增减性和函数极值、解方程和不等式等问题中都有重要的作用。
在实际生活中,微分中值定理可以应用于求解速度、加速度、距离等问题,帮助我们更好地理解和解决实际问题。
二、导数的应用导数作为微积分的重要概念,具有很多实际应用。
中值定理与导数的应用(高等数学)省名师优质课赛课获奖课件市赛课一等奖课件
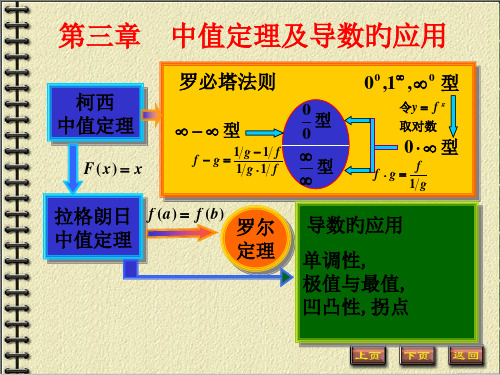
定义 使导数为零的点(即方程f ( x) 0的实根)叫 做函数f ( x)的驻点.
定理(必要条件) 设 f ( x) 在点x0 处具有导数,且 在 x0处取得极值,那末必定 f '( x0 ) 0.
注意:可导函数 f ( x) 的极值点必定是它的驻 点, 但函数的驻点却不一定 是极值点.
2、罗必塔法则
(1). 0 型及 型未定式 0
定义 这种在一定条件下经过分子分母分别求导再 求极限来拟定未定式旳值旳措施称为罗必塔法则.
(2). 0 , , 00,1 , 0型未定式
关键:将其他类型未定式化为罗必塔法则可处理 旳类型 ( 0 ), ( ) .
0
定理 设(1)当x 0时,函数 f ( x) 及 F ( x) 都趋于零; (2) 在 a 点的某领域内(点 a 本身可以除外 ), f ( x) 及 F ( x) 都存在且 F ( x) 0; (3) lim f ( x) 存在(或为无穷大);
(2) 在开区间 ( a , b ) 内可导
(3)在开区间 ( a , b ) 内F(x) 0
至少存在一点
(a,b) , 使
f (b) f (a) F (b) F (a)
f ( ) . F( )
注意:若令F(x)=x,则柯西中值定理变为拉氏中值 定理,即拉
0
原式
lim
x
1
1
x 1 x2
2
lim
x
1
x
2
x
2
1.
例8
求
lim
x0
tan x x2 tan
x x
.
解
微分中值定理与导数应用

F ( x) 的最小值. F( x) 0 ,即得 f ( x) x .证毕.
例 5 设 lim f ( x) 1,且 f ( x) 0 .试证: f ( x) x . x0 x
4 (b a)2
|{ f (b) [ f (b)
f (b)( a b 2
b)
1 2
f
(1
)(
a
2
b
b)2 ]}
{ f (a) [ f (a)
f (a)( a b 2
a)
1 2
f
(
2
)(
a
2
b
a)2 ]} |
4 (b a)2
|
1 2
{
f
(1
)
f
(
2
)}(
b
2
a
)2
0 ,根据极限的保号性即知,
在 x a 的右邻近,有 f ( x) f (a) 0 ,故有 f ( x) f (a) . xa
f (a) 不可能是 f ( x) 在[a, b] 上的最小值. 同理,由 f(b)
0 可知, f (b) 也不可能是 f ( x) 在[a, b] 上的最小值.
F ( x) F( x) F(0) F( x)x (其中 (0,1) )
{F( x) F(0)}x {F(1 x) x}x (其中1 (0,1) ) F (1 x) x2 0 ,即得 f ( x) x .证毕.
例 6 设 f ( x) 在[a,b] 上存在, f (a) f (b) 0 .试证:
中值定理及导数应用笔记

中值定理及导数应用笔记中值定理是数学中的一个重要定理,它是求函数在某一区间内的最大值或最小值的一种方法。
中值定理:设f(x)在[a, b]内可导,且f’(x)在(a,b)内存在,则存在c∈(a, b),使得f’(c)=0。
中值定理的应用:1.求函数在某一区间内的极值:由中值定理可知,如果函数f(x)在[a, b]内可导,且f’(x)在(a, b)内存在,则存在c∈(a,b)使得f’(c)=0。
因此,我们可以通过求解f’(x)=0的方程来求出函数在[a, b]内的极值。
2.求函数的泰勒公式:利用中值定理可以得出泰勒公式,即对于函数f(x)在x0处的泰勒展开式:f(x)=f(x0)+f’(x0)(x-x0)+O((x-x0)^2)。
导数是数学中的一个概念,它表示函数在某一点处的斜率。
导数的应用:1.求函数的单调性:如果函数f(x)在点x处的导数大于0,则函数在点x处单调递增;如果函数f(x)在点x处的导数小于0,则函数在点x处单调递减。
2.求函数的极值:如果函数f(x)在点x处的导数等于0,则函数可能在点x处取得极值。
通过对函数的二阶导数进行分析,可以判断函数在点x处的极值是最大值还是最小值。
1.求函数在某一点的切线:切线是函数在某一点的切线的图像。
切线的斜率等于函数在这个点的导数。
因此,我们可以通过求解函数在某一点的导数来求出函数在这个点的切线。
2.求函数在某一区间内的最小值和最大值:当函数在某一区间内单调递增或单调递减时,可以通过求解函数在区间端点处的导数来求出函数在该区间内的最小值和最大值。
以上是中值定理和导数的应用笔记。
通过对中值定理和导数的学习,可以帮助我们更好地理解函数的性质,并运用到数学和其他领域中。
需要注意的是,中值定理和导数的应用是有一定条件的,在使用这些工具时要注意满足这些条件。
此外,中值定理和导数是高等数学中的基础概念,在深入学习数学和其他科学领域之前,要先扎实地掌握这些概念。
中值定理与导数应用

嘉兴学院
10/5/2024
第四章 中值定理与导数应用
第17页
例7 证明当x [ 1 ,1]时,不等式 2
arctan x ln(1 x2 ) ln 2
4 成立.
例8 证明:若函数f (x)在(, )内 满足关系式 f (x) f (x),且f (0)=1,
则 f (x) ex.
嘉兴学院
f '() 0
嘉兴学院
10/5/2024
第四章 中值定理与导数应用
y 几何解释:
第4页
C y f (x)
o a 1
2 b x
在两端点高度相同的连续曲线弧AB上,
若除端点外处处均有不垂直于x轴的切
线存在,则此曲线弧上至少有一点C,
在该点处的切线平行于x轴.
嘉兴学院
10/5/2024
第四章 中值定理与导数应用
f (x1 x2 ) f (x2 ) f (x1)
f (x1 x2 ) f (x2 ) f (x1) f (0)
f (2 ) x1 f (1) x1 (x2 2 x1 x2 , 0 1 x1)
x1 f ( )(2 1) 0 (1 2 )
f (x1 x2 ) f (x1) f (x2 )
并求满足定理的值. 例4 证明 arcsin x arccos x
2 (1 x 1).
嘉兴学院
——证明恒等式旳一般措施
10/5/2024
第四章 中值定理与导数应用
第13页
例5 证明当x 0时, x ln(1 x) x. 1 x
例6 设 Lim f (x) K , 求 x+
Lim [ f (x a) f (x)].(a 0)
x+
嘉兴学院
微分中值定理及导数的应用

积分因子法
通过引入一个积分因子,将微分方程转化为可解的一 阶线性方程组。
感谢您的观看
THANKS
微分中值定理及导数的应用
目录
• 微分中值定理 • 导数的定义与性质 • 导数在函数中的应用 • 导数在实际问题中的应用 • 导数的进一步研究
01
微分中值定理
微分中值定理的定义
微分中值定理
若函数$f(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可 导,则存在$c in (a, b)$,使得$f'(c) = frac{f(b) - f(a)}{b - a}$。
导数与积分的关系
牛顿-莱布尼兹公式
用导数和积分相互转化的方式,将定积分转化为求和的 形式,从而简化计算。
微积分基本定理
定积分可以表示为被积函数的一个原函数在积分上下限 的函数值的差,即牛顿-莱布尼兹公式的特殊形式。
导数与微分方程
微分方程
描述一个变量关于另一个变量的导数等于某个给定函 数的方程。
初值问题
导数在科学计算中的应用
数值分析
导数在数值分析中有着广泛的应用,例如在求解微分方程、 积分方程和线性代数方程时,导数可以帮助我们找到近似 解。
图像处理
在图像处理中,导数可以帮助我们进行边缘检测、图像滤 波和图像增强等操作,从而提高图像的清晰度和质量。
信号处理
在信号处理中,导数可以用来分析信号的变化趋势和频率 特征,例如在音频处理和图像处理中,导数可以帮助我们 提取信号中的重要信息。
详细描述
如果一个函数在某区间的导数大于0, 则该函数在此区间单调递增;如果导 数小于0,则函数单调递减。
第四章中值定理与导数的应用1

例14. 求 lim n ( n n 1). 0型
则至少存在一点 (a, b) , 使得 f ( ) 0 .
y y f (x)
A
B
Oa
bx
实际上, 切线与弦线 AB 平行.
费马(Fermat)引理:
且
存在
(或 )
证:设
则
0 0
y O x0 x
y y f (x)
注意:
O a
bx
1) 定理条件条件不全具备, 结论不一定成立. 例如,
A
Oa
弦 AB 的方程: y f (a) f (b) f (a) (x a)
ba
bx
利用罗尔中值定理 证明
注1:在[a, b]内的任意闭区间 [ x1, x上2 ],拉格朗日中值 定理均成立.
特别地, 若 x 与 x +Δx为区间(a, b)内的任意两点,则有
y f (x x) f (x) f (x x)x (0 1)
(化简)
lim
x0
2 cos3
x
2
连续使 用罗必 达法则
下面的介绍的是利用倒数法 或取对数法将其它的不定型 转化为可以运用罗必达法则 计算的例题 .
例8 求 lim x ln x . 0
x0
用另一种形式 颠倒行不行 ?
解
倒数法
lim
x0
x ln
x
lim
x0
ln x 1
x
行 , 但繁些 .
f (1) f (2 ) f (3) 0 . 其中, 1 (a, b) , 2 (b, c) , 3 (c, d ) ,
即 f (x) 0 至少有三个实根.
f (x) 是四次多项式, f (x) 是三次多项式,
中值定理和导数应用总结

驻点和不可导点统称为临界点.
定理(第一充分条件) (1)如果 x ( x0 , x0 ), 有 f ' ( x ) 0;而 x ( x0 , x0 ) , 有 f ' ( x ) 0 ,则 f ( x )在 x0 处取得极大值. (2)如果 x ( x0 , x0 ), 有 f ' ( x ) 0;而 x ( x0 , x0 ) 有 f ' ( x ) 0 ,则 f ( x )在 x0 处取得极小值. ' x ( x , x ) x ( x , x ) f (3)如果当 时, ( x ) 符 0 0 及 0 0 号相同,则 f ( x )在 x0 处无极值.
第一步
' " f ( x ) 0 f 求出方程 和 ( x ) 0 在函数定义 域内的全部实根,用这些根同函数的间断点或导数 不存在的点把函数的定义域划分成几个部分区间.
第二步
确定在这些部分区间内 f ' ( x ) 和 f " ( x ) 的符 号,并由此确定函数的增减性与极值及曲线的凹 凸与拐点(可列表进行讨论) ;
第三步
确定函数图形的水平、铅直渐近线以及其 他变化趋势;
第五步 描出与方程 f ' ( x ) 0 和 f " ( x ) 0 的根对
第四步
应的曲线上的点,有时还需要补充一些点,再综 合前四步讨论的结果画出函数的图形.
如果对区间 I 上任意两点 x1 , x2 , 恒有 x1 x2 f ( x1 ) f ( x2 ) f( ) , 2 2 那末称 f ( x ) 在 I 上的图形是(向上)凸 的;
第三章 中值定理与导数的应用
第一节第三节 函数单调性的判别法
第四节
函数的极值及其求法
2019/10/10
第五节 函数的最大值与最小值
第六节 曲线的凹凸性与拐点
第七节
函数图形的描绘
第一节 中值定理
微分学中有三个中值定理应用非常广泛,它们 分别是罗尔定理、拉格朗日中值定理和柯西中值定 理.
从上述拉格朗日中值定理与罗尔定理的关系,自 然想到利用罗尔定理来证明拉格朗日中值定理.但在拉 格朗日中值定理中,函数f(x)不一定具备f(a)=f(b)这个 条件,为此我们设想构造一个与f(x)有密切联系的函数 φ(x)(称为辅助函数),使φ(x)满足条件φ(a)=φ(b).然后对 φ(x)应用罗尔定理,再把对φ(x)所得的结论转化到f(x) 上,证得所要的结果.
一、0/0型未定式
第三节 函数单调性的判定法
如图3-4所示,如果函数y=f(x)在区间[a,b]上 单调增加,那么它的图像是一条沿x轴正向上升的曲线 ,这时,曲线上各点切线的倾斜角都是锐角,它们的 切线斜率f′(x)都是正的,即f′(x)>0.同样地,如图3-5所 示,如果函数y=f(x)在[a,b]上单调减少,那么它的 图像是一条沿x轴正向下降的曲线,这时曲线上各点切 线的倾斜角都是钝角, 它们的斜率f′(x)都是负的,即 f′(x)<0.由此可见,函数的单调性与导数的符号有着密 切的联系.下面,我们给出利用导数判定函数单调性的 定理.
根据上面三个定理,如果函数f(x)在所讨论的区间内各点处 都具有导数,我们就以下列步骤来求函数f(x)的极值点和 极值:
(1) 求出函数f(x)的定义域;
(2) 求出函数f(x)的导数f′(x);
(3) 求出f(x)的全部驻点(即求出方程f′(x)=0在所讨论的区 间内的全部实根)以及一阶导数不存在的点;
理学微分中值定理与导数的应用
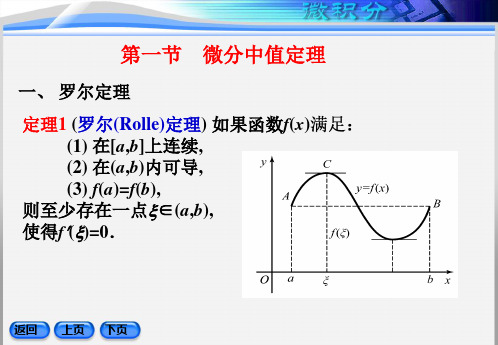
lim
x2 6x 4 2
注意: 如果
lim
f ( x)仍为 0
型未定式,且f(x),g(x)满足
x x0 g( x)
0
定理条件,则可继续使用洛必达法则.
返回 上页 下页
例2
求 lim x0
sin 2
x
x sin x4
x
cos
x
.
解
sin2 x x sin x cosx
lim
x0
x4
lim
x0
证 由于f(x)=ln(1+x)在[0,+∞)上连续、可导,
对任何x>0,在[0, x]上运用微分中值公式,
f(x)-f(0)=f′( x)x,
即
x
ln(1+x)= 1 x
由于
x 1 x
<
x
1
<x,lt;<1 ),
(0< <1).
x
1 x <ln(1+x)<x.
返回 上页 下页
x 0
x
x 0
x
返回 上页 下页
因f(x)在达到最大值,所以不论x是正的还是负的, 总有
f( + x)-f()≤0.
当x>0时, 当x<0时,
f ( x) f ( ) 0
x
f ( x) f ( ) 0
x
f ( ) lim f ( x) f ( ) 0
x 0
x
f ( ) lim f ( x) f ( ) 0
(3) lim f ( x) 存在(或为∞) x g( x)
lim f ( x) lim f ( x) x g( x) x g( x)
注 罗尔定理的三个条件缺少其中任何一个,定理的结 论将不一定成立.
2020年考研数学必背定理:中值定理与导数的应用

2020年考研数学必背定理:中值定理与导数的应用中值定理与导数的应用1、定理(罗尔定理)如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且在区间端点的函数值相等,即f(a)=f(b),那么在开区间(a,b)内至少有一点ξ(a2、定理(拉格朗日中值定理)如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,那么在开区间(a,b)内至少有一点ξ(a3、定理(柯西中值定理)如果函数f(x)及F(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且F’(x)在(a,b)内的每一点处均不为零,那么在开区间(a,b)内至少有一点ξ,使的等式[f(b)-f(a)]/[F(b)-F(a)]=f’(ξ)/F’(ξ)成立。
4、洛必达法则应用条件只能用与未定型诸如0/0、∞/∞、0×∞、∞-∞、00、1∞、∞0等形式。
5、函数单调性的判定法设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,那么:(1)如果在(a,b)内f’(x)>0,那么函数f(x)在[a,b]上单调增加;(2)如果在(a,b)内f’(x)如果函数在定义区间上连续,除去有限个导数不存有的点外导数存有且连续,那么只要用方程f’(x)=0的根及f’(x)不存有的点来划分函数f(x)的定义区间,就能保证f’(x)在各个部分区间内保持固定符号,因而函数f(x)在每个部分区间上单调。
6、函数的极值如果函数f(x)在区间(a,b)内有定义,x0是(a,b)内的一个点,如果存有着点x0的一个去心邻域,对于这去心邻域内的任何点x,f(x)f(x0)均成立,就称f(x0)是函数f(x)的一个极小值。
在函数取得极值处,曲线上的切线是水平的,但曲线上有水平曲线的地方,函数不一定取得极值,即可导函数的极值点必定是它的驻点(导数为0的点),但函数的驻点却不一定是极值点。
定理(函数取得极值的必要条件)设函数f(x)在x0处可导,且在x0处取得极值,那么函数在x0的导数为零,即f’(x0)=0.定理(函数取得极值的第一种充分条件)设函数f(x)在x0一个邻域内可导,且f’(x0)=0,那么:(1)如果当x取x0左侧临近的值时,f’(x)恒为正;当x去x0右侧临近的值时,f’(x)恒为负,那么函数f(x)在x0处取得极大值;(2)如果当x取x0左侧临近的值时,f’(x)恒为负;当x去x0右侧临近的值时,f’(x)恒为正,那么函数f(x)在x0处取得极小值;(3)如果当x取x0左右两侧临近的值时,f’(x)恒为正或恒为负,那么函数f(x)在x0处没有极值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应注意的问题: 如果定理的三个条件有一个不满足,则定理的结论
就可能不成立。
y
y
y
B
A
B
A
B
A
aO
bx a O c bx a O
bx
f(x)不满足条件(1) f(x)不满足条件(2) f(x)不满足条件(3)
二、拉格朗日中值定理
观察与思考: 设连续光滑的曲线y=f(x) 在端点A、B处的纵坐标不
相等。
简要证明: 令 j(x)=f(x)f(a) f (b) f (a) (xa),
ba
则函数j(x)在区间[a, b]上满足罗尔定理的条件,
于是至少存在一点x(a, b),使j (x)=0,即
由此得
j (x)=f (x) f (b) f (a) =0,
ba
f(b)f(a)=f (x)(ba)。
f
(x)=
f(x)=
lim
xx
f (x) f (x ) 0, x x
f
(x)=
f(x)=
lim
xx
f (x) f (x ) 0, x x
因此必有f (x)=0。
罗尔定理: 如果函数y=f(x)在闭区间[a, b]上连续,在开区间(a,
b)内可导,且有f(a)=f(b),那么在(a, b)内至少在一点x , 使得f (x)=0。
内可导,那么在(a, b)内至少有一点x,使得 f(b)f(a)=f (x)(ba)。
拉格朗日中值定理的几何意义:
y
C1
y=f(x) B
C2 A
O ax
hbx
拉格朗日中值定理:
如果函数f(x)在闭区间[a, b]上连续,在开区间(a, b)
内可导,那么在(a, b)内至少有一点x,使得 f(b)f(a)=f (的导数恒为零,那么f(x)
在区间I上是一个常数。
证明:在区间I上任取两点x1,x2(x1<x2),应用拉格 朗日中值定理,就得
f(x2)f(x1)=f (x)(x2x1) (x1<x < x2)。 由假定,f (x)=0,所以f(x2)f(x1)=0,即
f(x2)=f(x1)。 因此 f(x)在区间I上是一个常数。
§4. 1 中值定理
一、罗尔定理 二、拉格朗日中值定理
拉格朗日中值定理及中值公式 三、柯西中值定理
一、罗尔定理
观察与思考:
设连续光滑的曲线 y=f(x) 在端点 A、B 处的纵坐标 相等。
y
C
A
y=f(x) B
Oa x
bx
提问:f (x)=?
罗尔定理: 如果函数y=f(x)在闭区间[a, b]上连续,在开区间(a,
= lim 3x 2 3 = lim 6x = 3 。 x1 3x 2 2x 1 x1 6x 2 2
b)内可导,且有f(a)=f(b),那么在(a, b)内至少在一点x , 使得f (x)=0。
简要证明:(1)如果 f(x)=f(a) ,则 f (x)0,定理的结 论显然成立的。
(2)如果有 x(a, b),使 f(x)f(a),不妨设 f(x)f(a),
则函数f(x)的最大值点 x 必在(a, b)内。于是
解: lim sin ax = lim (sin ax) = lim a cos ax = a 。 x0 sin bx x0 (sin bx) x0 b cos bx b
例
2.求 lim x1
x3 x3
3x 2 x2 x 1
。
解:lim x3 3x 2 = lim (x3 3x 2) x1 x3 x 2 x 1 x1 (x3 x 2 x 1)
xa g (x)
那么
lim f (x) = lim f (x) 。 xa g(x) xa g (x)
说明:
在上述定理中,把xa换成x, 把条件(2)换成
(2)当|x|>N时f (x)及F (x)都存在且F (x)0;
结论仍成立。
“零比零”型未定式的定值法:
例 1.求 lim sin ax (b 0)。 x0 sin bx
例如,下列极限都是未定式:
lim
x0
x sin x x3
,
lim
x
ln x xn
(n>0),
lim xn ln x(n>0),lim (sec xtan x),
x0
x
lim
xx,lim
1 (1
2
)x,lim
1
(x 2a 2x)2
。
x0
x
x
x
二、洛必达法则
定理 如果函数f(x)与g(x)满足如下条件: (1)当xa时,函数极限都为零(或都为无穷大); (2)函数在点a的某去心邻域内都可导且g(x)0; (3) lim f (x) 存在(或为无穷大);
三、柯西中值定理
函数f(x)及F(x)在闭区间[a, b]上连续,在开区间(a, b) 内可导,且F (x)在(a, b)内恒不为零,那么在(a, b)内至
少有一点x ,使等式
f (b) f (a) = f (x ) 。 F (b) F (a) F (x )
§4.2 洛必达法则
一、未定式 二、洛必达法则
提问: 直线AB的斜率k=?
y
C1
y=f(x) B
f (x)=?, f (h)=?
C2
f(b)f(a)=?
A
答案:
k= f (b) f (a) , ba
O ax
f (x)=f (h)= k, f(b)f(a)=f (x)(ba) 。
hbx
拉格朗日中值定理:
如果函数f(x)在闭区间[a, b]上连续,在开区间(a, b)
“零比零”型未定式的定值法: “无穷比无穷”型未定式的定值法: 其它类型未定式的定值法:
一、未定式
在函数商的极限中,如果分子分母同是无穷小量或
同是无穷大量,那么极限可能存在,也可能不存在, 这种极限称为未定式。这种类型的未定式记为 -0 或 - 。
0 其它类型的未定式:0·、、00、1、0。
拉格朗日中值定理: 如果函数f(x)在闭区间[a, b]上连续,在开区间(a, b)
内可导,那么在(a, b)内至少有一点x,使得 f(b)f(a)=f (x)(ba)。
拉格朗日中值公式:
f(b)f(a)=f (x)(ba) , f(xDx)f(x)=f (xqDx)Dx (0<q <1), Dy= f (xqDx)Dx (0<q <1)。
