寿险精算原理 第二章
中国精算师《寿险精算》章节题库-人寿保险的精算现值(圣才出品)

第2章人寿保险的精算现值选择题1.30岁的人购买保额为1000元的特殊的35年期两全保险,已知条件如下:(1)在其购买保险时,其两个孩子的年龄分别是3岁和6岁;(2)特殊约定为:如果被保险人死亡时两个孩子的年龄都小于11岁,那么给付额为3000元;如果被保险人死亡时只有一个孩子的年龄小于11岁,那么给付额为2000元;(3)在被保险人死亡时立即给付保险金;(4)μ30+t=0.04,t≥0;(5)δ=0.06;(6)35E30=0.0302。
则此保单的趸缴纯保费为()元。
[2008年真题]A.638B.766C.777D.796E.800【答案】D【解析】由题意可知,该保险相当于保额1000元的35年期两全保险+1000元保额的8年期定期保险(5-8年内被保险人只有一个孩子小于11岁)+1000元保额的5年期定期保险(5年内两个孩子都小于11岁),故此保单的趸缴保险费为:=796(元)2.30岁的人购买两年期定期保险,保险金在被保险人死亡的年末给付,保单年度t 的保额为bt ,已知条件为:q30=0.1,b2=10-b1,q31=0.6,i=0 ,Z表示给付现值随机变量,则使得Var(Z)最小的b1的值为()。
[2008年真题]A.0.0B.5.0C.6.8D.8.6E.8.9【答案】C【解析】v=1,由题意得:Pr [K(30)=0]=q30=0.1,Pr [K(30)=1]=p30q31=(1-0.1)×0.6=0.54,所以E(Z)=b1×0.1+(10-b1)×0.54,E(Z)2= ×0.1+(10-b12)×0.54,故Var(Z)=E(Z2)-(E(Z))2= -6.048b1+24.84。
故当b1=6.048/(2×0.4464)=6.8时,Var(Z)最小。
3.50岁的人购买保险金在死亡时给付的特殊的递增型终身寿险,Z表示给付现值随机变量,已知:b t=1+0.1t,v t=(1+0.1t)-2,t p50·μ(50+t)=0.02 ,0≤t<50则Var(Z)的值为()。
保险专业《寿险精算原理》教学大纲

《寿险精算原理》教学大纲一、课程说明(一)编制依据本大纲依据“2010级保险实务专业人才培养方案”所编制。
(二)课程性质及任务本课程是保险专业的专业基础课之一,是一门实践性很强的学科。
通过本课程的学习要达到使学生既具有更扎实的保险理论知识与更坚实的专业思想,同时具备独立分析、研究具体寿险险种、设计保险保障计划、表述说明保单内容评价保障价值等工作的技能。
(三)本课程同其他课程的关系本课程以教学计划中的《保险学原理》为基础,同时又作为《人身保险》的前导课程。
(四)教学内容的设置本课程教学内容主要是根据“2010级保险实务专业人才培养方案”的培养目标来设置的。
(五)教学方法与教学手段的采用本课程教学主要采用讲解式、讨论式和模拟操作的形式进行教学。
(六)教材的选用根据教学大纲的规定,选用普通高等教育“十二五”应用型规划教材《保险精算原理与实务》,二、教学时数及分配表教学时数:60三、教学内容第一章寿险精算概述【目的要求】1、本章是寿险的总纲,通过教学使学生了解寿险精算的内涵、起源、发展及现状。
2、明确寿险精算在寿险经营中的运用领域、涉及内容及其作为寿险经营基础的重要意义。
3、寿险精算主要的具体研究内容。
【重点难点】重点:寿险精算的发展、作用与意义。
难点:寿险精算的研究内容。
【理论内容】第一节寿险精算的内涵一、精算的概念和分类二、保险精算的概念和分类三、寿险精算的概念和内容四、意外险精算的概念和内容第二节寿险精算的起源一、寿险保单的起源二、寿险早期的经营特点三、寿险早期经营的问题及障碍四、“老公平”的出现五、寿险死亡法则的建立六、第一张生命表的编制第三节寿险精算的发展与现状一、北美精算协会二、日本精算协会三、中国精算师四、中国的精算教育与精算科学应用第四节寿险精算的意义一、寿险经营对象的特点二、寿险精算的意义第五节寿险精算的内容一、利息度量二、现值、终值度量三、确定年金计量分析四、生命年金计量分析五、生命函数及死亡保险六、纯保险费及毛保险费的确定七、准备金的计提八、分红的计算九、寿险保单性价比评价【实验内容】无【作业测验】1、试述精算学的定义与分类。
社会保险精算原理第二章 人寿和年金保险

将来法和过去法
30
责任准备金以将来法计算,是未来给付精算现 值与未来净保费精算现值之差。对不同保单, 根据契约规定的保险责任、保险金额和保费缴 付方式,可以分别计算出计算时点的未来给付 精算现值和未来净保费精算现值。t年末的责任 准备金以tV表示。
过去法责任准备金是过去净保费的累积与过去 保险金累积之差。
社会保险精算原理第二章 人寿和年金保险 作者
终身寿险
6
在上式中,两边同乘以生命表x岁的存活人数lx
lxAx k1dxk k0
等式表明,lx个x岁的人投保终身寿险的趸缴净 保费总额正好满足按生命表死亡规律在死亡年 末ຫໍສະໝຸດ 单位的赔付。定期寿险7
对(x)的1单位赔付n年定期寿险,其现值随机变 量为:
以nEx表示1单位元n年纯粹生存保险现值:
nEx n n px
2.2.1纯粹的生存保险
21
与在复利下的现值系数νt和累积系数(1+i)t的作 用类似,nEx是在利率和生者利下n年的折现系 数, 1/ nEx为在利率和生者利下n年的累积系数。
1/nEx1/nnpx(1i)nlxl xn
它是利率累积因子(1+i)n与生存累积因子之 积。
2.2.2年付一次生存年金的精算现值
22
生存年金是以生存为条件发生的年金。如果被 保险人在规定的时期内存活,则发生年金的收 付,否则,停止收付。年金保险中,在保险期 内年金的发放以被保险人存活为条件。长期寿 险的缴费通常也采取生存年金的方式,在被保 险人生存期内缴付保费,被保险人死亡,则停 止缴费。生存年金有终身年金、定期年金、延 期年金几种基本类型,由首次支付的起点不同 分为期首付年金和期末付年金。
νK+1 k=0,1,2,……n-1
寿险精算学-ch2

未来寿命的生存函数示意图
• t p0 =S0 (t)
• 1 px 简记为 px
特别符号
• t u qx t px tu px
• tu px t px u pxt
未来寿命生存函数的性质
• 定理1: 0 px 1
•
定理2:
d dt
t
px
0
,t 0
•
定理3:
lim
t x
t
px
0
• 由于死亡是必然发生的, 所以还可以得到如下两个引理:
• 在新生婴儿时期寿命的密度函数有一个递减趋势。 这是 因为新生婴儿是脆弱的,各种先天不足都会在刚出生时暴 露, 所以新生婴儿阶段死亡概率是偏高的。 经过医学治疗 和自然淘汰, 婴儿死亡率迅速下降。
• 青少年时期是人一生中死亡率最低的一段时期。 这段时 期是人类的健康黄金期。
• 从40 岁左右开始, 随着年龄的增长, 人的器官逐渐老化, 开 始罹患各种疾病,身体进入失效期, 死亡率开始递增。 60 岁前后进入加速失效期, 80 岁前后达到死亡率的顶峰。
– 中老年时期属于人类的加速失效时期。 在这段时间里, 身体各器 官逐渐老化,开始罹患各种疾病。 通常一种疾病治好了, 不久又会 产生另外一种疾病。 人类进入加速失效期之后, 健康维持成本将 变得越来越大。
例2.5
• 假设某人群每10万个新生婴儿, 能活到40 岁的人数为 97369, 能活到85 岁的人数为33851, 而在85~86 岁这一年 死亡的人数为3758。
• 所以本例中, 40 岁的人在85 岁时未来寿命的密度函数和 死亡力函数(以年为最小计量单位) 为:
f40 (45)
3758 97369
0.0386
保险精算第二讲.

1
n 1
k 0
例3.5
在例3.2中,假设50岁的张某购买的是一份 30年 的两全保险,死亡年年 末给付, 保额为100000 元,求该保单的趸缴净 保费。
例3.5答案
1 100000 A50:30 100000 A50 100000 :30
A
1
50:30
20468 .70 100000 (1.08 ) 30 30 p50 20468 .70 100000 (1.08 ) 24985 .85 (元) 由例3.2,3.3和3.5可以看出: Ax:n Ax
k px qx k v k 1
k 0
4
d xk lx
四、延期m年终身寿险
对(x)的1单位元 m年延期终身寿险, 是从x m岁起到被保险人终身止 的1单位元保险,其现值随 机变量为: 0, Z k 1 v ,
k 0,1,2,...., m 1 k m, m 1, m 2,.....
1 65 t 保单精算现值为: 20000 A40=20000 v t 1 t p x q x t
t 0
由生存函数可以看出:
t
p40 0 t 65
64
1 t 1 65 t 1 因此20000 A40=20000 ( ) t 0 1.1 65 65 20000 64 1 t 1 ( ) t 0 1.1 65 65 1 1 20000 1.1 3070 .65(元) 1 65 1.1 1 1.1
x
例3.2答案
解:该生命表的最大年 龄时105 岁,所以t的取值范围是 0 到55岁。所求的赔付现值为 100000 A
寿险精算习题及答案
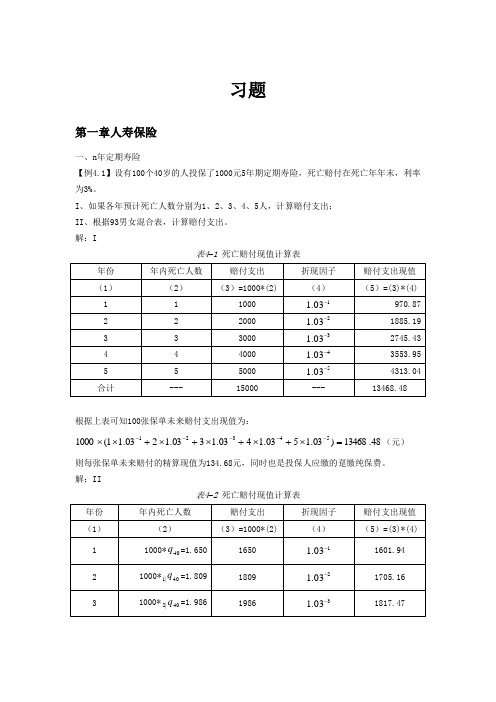
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
第二章 人寿保险

自愿、企业个人共同缴费 完全积累制 截至2017年底,全国近8万户企业 建立了企业年金,参加职工人数达 到了2300多万人,积累基金近1.3 万亿元;职业年金正随着机关事业 单位养老保险制度改革逐步建立。
个人自愿缴费
2018年5月,个人税收 递延型养老保险正式在 上海、福建、厦门、苏 州工业园区启动试点。
14
第二节 新型人寿保险
变额人寿保险 投资连结保险
Investment-link Life Insurance
Universal Life Insurance
万能人寿保险
包含保险保障功能并至少在一个投资 账户拥有一定资产价值的人身保险产 品。 没有最低保证利率,风险由投保人承 担。 缴费灵活、保额可调整。 设置独立投资账户,有最低保证利 率。 结合了万能险保费灵活的特征和变额 人寿保险中投保人可选择账户投向的特 征。 保险公司将其实际经营成果优于定价 假设的盈余,按一定比例向保单持有人 进行分配的人寿保险产品。 红利来源:死差益、费差益、利差 益。 分配方式:现金分红、保额分红。
非养老类一表(男) 非养老类二表(女)
这里输入学校或者班级的名称
非养老类一表(女) 养老类表(男)
非养老类二表(男) 养老类表(女)
PPT设计:PPT设计教程网 登陆网址: 4
第一节 人寿保险概述
三、人寿保险的分类
按保险责任划分 死亡保险 保费或保额是否可以调整 传统寿险 新型寿险
变额寿险 万能寿险
生存保险
两全保险
万能变额寿险
分红保险
这里输入学校或者班级的名称
PPT设计:PPT设计教程网
登陆网址:
5
第一节 人寿保险概述
《寿险精算学》实验指导书

《寿险精算学》实验指导书李新统计学院保险教研室山东工商学院目录实验一生存分布与生命表实验二人寿保险趸缴纯保费实验三人寿保险年缴均衡纯保费实验四寿险责任准备金的计算实验一生存分布与生命表实验目的:通过本次实验使学生学会如何利用Excel软件来计算各类死亡概率、生存概率及一些其它的生命表函数。
实验内容:Excel的基本用法;中国人寿保险业经验生命表(1990-1993)非养老金业务(混合表)(CL3)的输入;利用中国人寿保险业经验生命表(1990-1993)非养老金业务(混合表)(CL3)计算整数年龄各种死亡概率、生存概率;利用中国人寿保险业经验生命表(1990-1993)非养老金业务(混合表)(CL3)计算分数年龄各种死亡概率、生存概率;利用中国人寿保险业经验生命表(1990-1993)非养老金业务(混合表)(CL3)计算各类生命表函数。
实验步骤:1、在Excel输入中国人寿保险业经验生命表(1990-1993)非养老金业务(混合表)(CL3);2、利用生命表基础函数计算各整数年龄段的生存概率nx p 和死亡概率nx q 、x m n q 等。
如计算x 岁的人未来5年内死亡的概率,可以用5年内死亡人数比例来近似死亡概率,计算公式应为:55x x x xl l q l +-=。
先计算0岁的人未来5年内死亡的概率50q ,在单元格F2中输入公式“=(C2-C7)/C2”,按回车键得到结果;再拖动F2单元格右下角的填充柄,向下填充,就可以得到F 列所有整数年龄存活人在未来5年内的死亡概率。
结果如下图所示:其它两种死亡概率n x q 、x m n q 的计算方法类似。
3、在死亡均匀分布假设和常数死亡力假设的前提下计算分数年龄死亡率和生存率,,(0,1)t x tx q p t ∈。
比如计算死亡均匀分布假设下0.2x +的个体在未来0.5年内死亡的概率,公式为0.50.20.510.2xx xq q q +=-。
寿险精算实务精华版

寿险精算实务讲义第一章 人寿保险的主要类型1.1传统的人寿保险1.1.1 定期寿险定期寿险是指以死亡为给付保险金条件,且保险期限为固定年限的人寿保险。
1.1.2 终身寿险终身寿险是指以死亡为给付保险金条件,且保险期限为终身的人寿保险。
1.1.3 终身寿险两全保险是指在保险期限内以死亡或生存为支付保险金条件的人寿保险。
1.1.4 年金保险年金保险指以生存为支付保险金条件,按约定分期支付生存保险金,且分期支付生存保险金的间隔不超过一年(含一年)的人寿保险。
1.2 新型人寿保险1.2.1分红保险 1.2.2投资连结保险第二章 保单现金价值与红利2.1 保单现金价值2.1.1 保单现金价值的含义现金价值又称解约金、退保金、不丧失保单利益、不丧失价值或不丧失现金价值。
现金价值是指投保人或保险公司解除保险合同时,由保险公司向投保人退还的那部分金额。
现金价值往往特指以现金方式支付的不丧失保单利益。
,0kk k k CV V SC CV =-≥一般情况下,现金价值不大于责任准备金,主要原因是费用在毛保费中重新调整造成的。
其他原因:①财务风险;②死亡率风险;③效益风险;④退保成本。
2.1.2 保单现金价值的计算⑴ 调整保费法 ....()()()()k k C V A k P a k V P P a k αα=-=--, 1..A E P aα+=根据NAIC1941年规则:10.4m in(,0.04)0.25m in(,,0.04)0.02x E P P P ααα=++; 1980年规则:1 1.25m in(,0.04)0.01E P =+优点:是计算现金价值的主要方法,详细定义了费用的确定,得到的不丧失价值更为准确公平; 缺点:计算相对复杂。
⑵ 准备金比例法 k k k C V f V =⨯优点:①简单,便于管理;②不受公司定价假设的影响;③准备金是保单责任的保守估计,对客户较为公平;④能够及时地反映定价时市场利率的变化。
保险精算1-5章答案(第二版)李秀芳

第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
2011寿险精算数学大纲

《寿险精算数学》教学大纲课程编号:120320JS课程类别:专业基础课开课单位:理学系适用专业:数学与应用数学周学时:4学分:3先修课程:高等数学、概率论、利息理论建议修读学期:5一、课程介绍《寿险精算学》是数学与应用数学(保险精算师方向)专业的专业基础课。
它是以高等数学、概率论有关原理为基础,探讨寿险精算及其规律的一门科学。
通过本课程的学习,学生应能根据要求在理解的基础上牢固记忆本课程所涉及的基本概念,融会贯通所学理论知识并逐步培养分析问题和解决问题的能力,为进一步学习专业课打下基础。
二、教学内容和基本要求第1章生存分布与生命表基本要求1.掌握死亡年龄的概率分布函数2.掌握生存分布3.熟悉生命表教学重点1. 连续型的死亡年龄概率分布2. 离散型的死亡年龄概率分布3. 生存函数,死力教学内容1.1 死亡年龄的概率分布函数1.1.1 连续型的死亡年龄概率分布1.1.2 离散型的死亡年龄概率分布1.2 生存分布1.2.1 生存函数1.2.2 连续型未来寿命的生存分布1.2.3 离散型未来寿命的生存分布1.3 死力1.3.1 死力的定义及性质1.3.2 死力的若干解析形式1.4 生命表1.4.1 生命表函数1.4.2 生命表各函数之间的关系1.4.3 关于尾龄的若干种假设1.4.4 生命表实例1.4.5 选择—终极生命表1.4.6 随即变量T(x)与K(x)的方差公式第2章人寿保险的趸缴纯保费基本要求1.掌握离散型人寿保险模型2.掌握连续型人寿保险模型3.掌握死亡均匀分布假设下寿险模型教学重点1. 离散型人寿保险模型2. 连续型人寿保险模型3. 死亡均匀分布假设下寿险模型教学内容2.1 人寿保险概述2.2 离散型人寿保险模型2.2.1 死亡保险2.2.2 两全保险2.2.3 延期寿险2.2.4 非均衡给付保险2.3 连续型人寿保险模型2.3.1 死亡保险2.3.2 两全保险与延期寿险2.3.3 非均衡给付保险2.3.4 趸缴纯保费的换算函数表示式2.4 死亡均匀分布假设下的寿险模型2.4.1 连续型终身寿险与离散型终身寿险之间的关系2.4.2 实例2.5 递推方程式2.5.1 离散型终身寿险趸缴保费的递推方程式2.5.2 连续型终身寿险趸缴纯保费的微分方程式第3章生存年金的精算现值基本要求1.掌握精算现值的计算方法2.掌握离散型生存年金的计算方法3.掌握变额生存年金、连续型生存年金。
寿险精算原理课件(非数学专业选修课)

精算工作主要由精算师承担,在英国精算 行业业务报告中是这样描述精算师的作用 的:“在给金融投资等问题提供专家的、 恰如其分的解答方面,尤其是解释不确定 的未来事件方面,发挥精算行业的作用并 提高它的声誉。” 精算工作的对象是“不确定性”。 精算师工作范围:保险公司、政府部门、 咨询公司、证券公司、大型企业及人口统 计部门,等等。
第二节、预测未来
精算师常常必须对将来要发生的事件作出估 计(预测)。例如:估计一笔养老金作为特 殊的资产在未来10年中的利率;估计每10万 套同一类型的房屋在下一年将被火灾毁坏的 房屋数;估计已经参加了人身保险的人中有 多少将在未来10年中死亡;估计未来10年的 通货膨胀率进而估计一个具体的正在应运的 公司在支出方面将要受到的影响,等等。
m
d 1 d 1 m
m
m
d d 1 1 m
d
m
m
m
m 1
1 d
1 m
6、名义利率与名义贴现率之间的关系
i 1 m
m
m
d 1 p
A
t
A
0
e
0 r d r
t
②积累函数利息强度之间的关系:
a
t
a
0
e
0 r d r
t
e
0 r d r
t
③度量期内获得的利息与利息强度之间的关 n 系: n
0
A t t d t
0
A t d t A n A 0
In a
保险精算学2_li

如果每年年初支付:
4 0 0 0 a 60 : 20 4 0 0 0 N 60 N 80 D 60 4 1 9 4 9 .8 1 4 0
实验习题:利用excel编辑 a x : n 和 ax : n
的计算表。
3、2、5 n年延期期末付生存年金(从第n+1年开始支付到终生) n年延期生存年金是投保后经过n年才进入给付的年金。对(x)每 年l元的n年延期期末付生存年金现值以 n a x 表示。
如图:(相当于把 x +1 ~ ∞ 上每年1单位元的年金折算到x的时刻)
3 2 1
Ex Ex Ex
1 1 1
……
……
1
x
x +1
x +2
x +3
x 1
ω -1
(4· 4a)
a x 1E x 2 E x 3 E x
t
Ex
显然, 是保险期分为1年、2年、3年等一系列1元纯粹生存 ax 保险现值之和。 公式(4· 4a)的求和上限为x + t = ω -1 ,t =ω -1-x, ω -1是 生命表中的最大年龄。今后为了方便通常写为∞。
4 0 0 0 a 60 4 0 0 0 4 1 9 6 1 .0 8
6 0 1
4000
D 60
2 6 6 0 6 .0 2
这份保险的现值为41961.08元。 实验习题:利用excel制作 a x 的计算表。 3、2、2 期首付终身生存年金 对(x)岁投保的人每年1元的期初支付终身生存年金,其现值 以 ax 表示。
N x n 1 D x n D xn Dx
3、2、4 期首付n年定期生存年金 以 ax : n 表示对(x)的每年l元期首付n年定期生存年金现值,则
《寿险精算》学习指南

迄今为止,国内外对精算尚未达成完全统一的定义。不过,大多采用如下方 式来描述。所谓精算,就是运用数学、统计学、金融学、保险学及人口学等多学 科的知识和原理,定量解决金融保险等领域中有关问题,进而为决策提供科学依 据的一门应用型学科。精算与保险的结合形成保险精算,保险精算是精算的重要 组成部分。保险精算一般被描述为:运用数学、统计学、金融学、保险学及人口 学等学科的知识和原理,去解决商业保险与各种社会保障业务中有关项目,如死 亡率的测定、生命表的构造、费率的厘定、准备金的计提、利源分析、盈余分配、 偿付能力管理等,以此保证保险经营的稳定性和安全性。
4
叉和边缘学科。
§1.2 寿险精算的起源
寿险精算是从寿险经营的窘境中应运而生的一门新兴学科。寿险的前身是欧 洲中世纪的基尔特(Guild)制定。据记载,世界上最早的寿险保单之一,是在 16 世纪末,由一群海上保险承保人在伦敦对 William Gibbon 签发的,一年保险 期限,保险金额为 382.68 镑的定期保单。
18 世纪中期以前,英国早期的寿险组织、资格最老的要数于 1706 年在伦敦 特许成立的协和保险社。1721 年经特许成立的皇家交易保险公司和伦敦保险公 司开始经营寿险业务。此外,还有一些捐助团体以及联盟协会也经营寿险业务。 这些互助协会、保险公司以及其他团体经营寿险业务,这些业务概括起来,具有 如下几个特点:(1)寿险仅为火险、海险的副产品,尚未大规模独立地经营寿险。 (2)寿险业务所承保的对象限制较多。互助协会承保会员人数有限,主要局限 于商人、企业合伙人;特许保险公司经营的寿险,将病人、老年人及天花病人等 一概拒之门外。(3)寿险的保险费采用赋课式,未将年龄大小、死亡率高低等与 保险费挂钩。(4)寿险经营缺乏严密的科学基础,表现在有关计算单一、粗糙, 考虑因素较少。这样的寿险经营导致的是寿险业的不景气,保险技术的停滞不前。 也正是在这种经营思想的指导下,协和保险社在 1756 年以詹姆斯·道森(James Dodson)年龄偏大(那时 Dodson 实际年龄仅 46 岁)为由,拒绝吸收其为保险 社成员,其结果成为寿险精算兴起的导火线。
寿险精算原理 第二章

an
,s
n
。
例2、有两个连续还款模型A,B。A每期还 款额为2,还款期限为20年,B每期还款额 为3,还款期限为10年。求使A,B模型等 效的 。
将上式一般化后得到:
sn sn
1 i 1 i
m
sm n sm m n m s s
m
三、在付款期间某时刻的年金当前值
1 1 3 1 4 1 5 1 6 7 8 9
(付款额)
0
1
2
10 (时间)
a5
a5
V
4
s5
s5
分析上图可得:
V
4
a5
2
1 i
3
a5
3
1 i
2
v s5 s3 a 2
v 5 s 2 a 3 s
将上式一般化后得到:
an
1 i
m
v
nm
sn sm anm
an
1 i
m
v
nm
a sn sm nm
一、在首期付款前某时刻的年金现值
1 1 3 1 4 1 5 1 6 … 7 8 9
(付款额)
0
1
2
10 (时间)
a5
a5
分析上图可得:
V
0
va5 v a5
2
a 6 a1 a7 a2
将上式一般化后得到:
v
m
an amn am an amn am
an
sn
sn
寿险精算学

4、趸缴纯保费的厘定
4.2厘定原则
保费净均衡原则 解释 所谓净均衡原则(it is net because it has not been loaded), 即保费收入的期望现时值正好等于将来的保险赔付金 的期望现时值(expectation of the present value of the net premium equals expectation of the present value of the payment)。它的实质是在统计意义上的收支平衡。是 在大数场合下,收费期望现时值等于支出期望现时值
4、趸缴纯保费的厘定
4.3基本符号
—— 的人。 ( x 投保年龄 ) ——人的极限年龄 ——保险金给付函数。 t —— 贴现函数。 v t ——保险给付金在保单生效时的现时值 t
b
z
x
zt bt vt
4、趸缴纯保费的厘定
趸缴纯保费的定义
在保单生效日一次性支付将来保险赔付金的期望现时值
net single premium paid at the monent of death
死亡年末赔付保险趸缴纯保费的厘定
net single premium paid at the end of the year of death
递归方程 recursion equations 计算基数 commutation functions
非延期保险non-deferred
insurance 两全保险 endowment insurance
保障期是否有限
定期寿险 term year
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、在首期付款前某时刻的年金现值
1 1 3 1 4 1 5 1 6 … 7 8 9
(付款额)
0
1
2
10 (时间)
a5
a5
分析上图可得:
V
0
va5 v a5
2
a 6 a1 a7 a2
将上式一般化后得到:
v
m
an amn am an amn am
将上式一般化后得到:
sn sn
1 i 1 i
m
sm n sm m n m s s
m
三、在付款期间某时刻的年金当前值
1 1 3 1 4 1 5 1 6 7 8 9
(付款额)
0
1
2
10 (时间)
a5
a5
V
4
s5
s5
分析上图可得:
an
sn
sn
例1、某银行客户想通过零存整取方式在1 年后可得10000元,在月复利为0.5%的情 况下,问每月初需存入多少钱才能达到其 目的。
2.2 任意时刻的年金值
不论在理论上还是在实务中,都会遇到 要求计算任意 t 时刻年金值 V t 的问题。 一般而言,有三种时刻的年金值需要计算: ⑴首期付款前某时刻的年金现值; ⑵最后一期付款后某时刻的年金积累值; ⑶付款期间某时刻的年金当前值。
1 0 1 1 1 2 1 3 1 4 … … … … 1 n-2 1 n-1
(付款额)
n (时间)
二、期初支付年金的现值与积累值计算
1、期初支付年金在0时刻的现值记为 a n
2 n2 n 1 an 1 v v v v
,并有
1 v d
n
2、期初支付年金在 n 时刻的积累值记为 ,并有 sn n 1 i 1 n n 1 2 1 i 1 i 1 i 1 i sn
一、在相等时间间隔上进行的一系列支付 称为年金。 二、在每个付款期间末付款的年金称为期 末付年金。 假设一笔期末付年金,付款期限为 n 期, 每期期末付款额为1元,每期利率为 , i 那么各期付款如图所示。
1 0 1 1 2 1 3 1 4 … … … 1 n-2 1 n-1 1 (付款额) n (时间)
例4、已知年实际利率为8%,乙向银行贷 款10000元,期限为5年,计算下面的三种 还款方式中利息所占的额度。 ⑴贷款的本金和利息积累值在第5年年末 一次还清。 ⑵每年末支付贷款利息,第5年年末归还 本金。 ⑶贷款每年末均衡偿还(即采用年金的方 式)。
2.2 期初付年金
一、在每个付款期间初付款的年金称为期 初付年金。 假设一笔期初付年金,付款期限为 n 期,每期期初付款额为1元,每期利率 为 i , 那么各期付款如图所示。
an
,s
n
。
例2、有两个连续还款模型A,B。A每期还 款额为2,还款期限为20年,B每期还款额 为3,还款期限为10年。求使A,B模型等 效的 。
2.4
永续年金
定义:付款次数没有限制,永远持续的年 金称为永续年金。永续年金只有现值,积 累值不存在。 1、期末付永续年金的现值 其现值记为 a ,则计算公式为:
a v v
2
v
3
v 1 v
n
1 i
,
i 0
a
lim a n lim
n
1 v i
n
d
3、相关公式及其经济解释:
①
② ③ ④
1 dan v
n
(2.2.5)
1 i
sn
1 an
n
d n 1(2.2.6) s
an
1
1 i (2.2.7)
n
sn
d
(2.2.8)
三、期末支付与期初支付年金之间的联系 1、由现值与积累值可得到以下公式: a 1 i a ① (2.2.9)
i
3、相关公式及其经济解释:
① 1 ia n v
② 1 i
n
n
1 is n
n
③ s n a n 1 i ④
1 an 1 sn i
例1、计算年利率为6%的条件下,每年年 末投资1000元,投资10年的现值及积累值。 例2、某银行客户想通过零存整取方式在1 年后可得10000元,在月复利为0.5%的情 况下,问每月末需存入多少钱才能达到其 目的。 例3、甲在银行存入20000元,计划分4年 支取完,每半年支取一次,每半年计息一 次的年名义利率为7%。试计算每次的支 取金额。
第二章
2.1 2.2 2.3 2.4 2.5
年金
期末付年金 期初付年金 任意时刻的年金值 永续年金 连续年金
年金的概念:在相同间隔的时间上进行的一系 列支付称为年金。 例如:在未来十年中,每年年末支付1000元; 从1998年至2015年每年年初支付3800元等。
2.1
期末付年金
1 i
,
i 1
2、期初付永续年金的现值 其现值记为 a ,则计算公式为:
a
1 v v
2
1 d
3、相关等式及其经济行为解释
an a v a
n
a
an v a
n
※经济行为解释请看28页。
例1、某人去世后,保险公司将支付10万 元的保险金,期三个受益人协商,决定按 永续年金方式领取该笔款项,受益人A领 取前8年的年金,受益人B领取以后10年的 年金,然后由受益人C领取以后的所有年 金。所有的年金领取都发生在年初。保险 公司预定的利率为6.5%。计算A,B,C各 自所领取的保险金份额。
2.5 连续年金
定义:连续付款的年金称为连续年金。 n 连续付款 个计息期,每个计息期的付 款额之和为1的连续年金现值记为 a ,有
n
an
n 0
v dt
t
1 v
n
积累值记为 s
sn
n 0
n
,则有
nt
1 i
dt
1 i
n
1
例1、以 的形式表示
v
m
二、在最后一期付款后某时刻的年金积累 值
1 1 3 1 4 1 5 1 6 7 8 9
(付款额)
0
1
2
10 (时间)
s5
s5
4
V
1 0
分析上图可得:
V
1 0
s5 5 s
1 i 1 i
s9 s 4 8 3 s s
3
…
三、期末支付年金的现值与积累值计算 1、期末支付年金在0时刻的现值记为 a
an v v
2
n
,并有
v
3
v
n 1
v
n
1 v i
n
2、期末支付年金在 n 时刻的积累值记为 s n ,并有 n 1 i 1 n 1 n2 s n 1 i 1 i 1 i 1
V
4
a5
2
1 i
3
a5
3
1 i
2
v s5 s3 a 2
v 5 s 2
1 i
m
v
nm
sn sm anm
an
1 i
m
v
nm
a sn sm nm
n n
②
③ ④
s sn n
1 i
(2.2.10)
(2.2.11) (2.2.12)
a n a n 1 1 s sn 1 n 1
2、以上公式图解释:
1 0 1
1 2
1 3
1 4
… …
… …
1
1
(付款额)
n-1
n
n+1 (时间)
an
